Development of an Itemwise Efficiency Scoring Method: Concurrent, Convergent, Discriminant, and Neuroimaging-Based Predictive Validity Assessed in a Large Community Sample

Abstract

Traditional “paper-and-pencil” testing is imprecise in measuring speed and hence limited in assessing performance efficiency, but computerized testing permits precision in measuring itemwise response time. We present a method of scoring performance efficiency (combining information from accuracy and speed) at the item level. Using a community sample of 9,498 youths age 8-21, we calculated item-level efficiency scores on four neurocognitive tests, and compared the concurrent, convergent, discriminant, and predictive validity of these scores to simple averaging of standardized speed and accuracy-summed scores. Concurrent validity was measured by the scores' abilities to distinguish men from women and their correlations with age; convergent and discriminant validity were measured by correlations with other scores inside and outside of their neurocognitive domains; predictive validity was measured by correlations with brain volume in regions associated with the specific neurocognitive abilities. Results provide support for the ability of itemwise efficiency scoring to detect signals as strong as those detected by standard efficiency scoring methods. We find no evidence of superior validity of the itemwise scores over traditional scores, but point out several advantages of the former. The itemwise efficiency scoring method shows promise as an alternative to standard efficiency scoring methods, with overall moderate support from tests of four different types of validity. This method allows the use of existing item analysis methods and provides the convenient ability to adjust the overall emphasis of accuracy versus speed in the efficiency score, thus adjusting the scoring to the real-world demands the test is aiming to fulfill.

Most current methodology for scoring performance based on psychological testing is designed for traditional “paper-and-pencil” tests, in which precise measurement of performance speed is not feasible. Therefore, while performance accuracy could be readily obtained, the limited information on speed rendered problematic the assessment of performance efficiency. The increasing use of computerized testing has allowed psychometricians access to additional information about test-taker ability, the most obvious being speed of performance that can be measured with great precision. However, there appears to be no consensus on how to deal with that information in combination with the traditional measure, accuracy. One common strategy is simply to treat speed and accuracy as two separate scores, but there is good reason to seek one overall score, especially if speed and accuracy are correlated (positively or negatively), making inclusion of both simultaneously in a multivariate analysis potentially problematic. It also makes intuitive sense that speed and accuracy could be combined to arrive at a positive metric, efficiency.

The question is how best to combine accuracy and speed. One obvious method that has been applied in previous studies (e.g. Glenn & Parsons, 1992) is simply to divide a person's accuracy score (e.g. total correct) by his/her mean or, more commonly, median¹ response time. A large total correct (large numerator) and a short median response time (small denominator) thus results in a higher efficiency score, and vice versa, which is an intuitive and easily calculated method (for theoretical rationale, see R. Sternberg, 1977; S. Sternberg, 1969; Townsend & Ashby, 1978, 1983). A second method (e.g. Moore, 2015) is to calculate separate z-transformed accuracy and speed scores, where speed is the median response time multiplied by negative one, and average those two standardized values. Thus individuals who are very accurate and fast would receive high scores, and slow, inaccurate individuals would receive low scores. These two traditional methods will be referred to as the “ratio method” and “mean-z-score method,” respectively.

The purpose of the present study was to explore the utility of a more flexible and potentially more widely useful method for calculating efficiency, here termed the “Itemwise Method.” As the name suggests, the Itemwise Method involves calculating a separate efficiency score for each item:

$$S_{\mathit{\text{ij}}}=\{\begin{array}{c}-kln(T_{\mathit{\text{ij}}}),\text{if correct}\\ -ln(T_{\mathit{\text{ij}}})\text{otherwise}\end{array}$$ (1)

Where S_ij is the efficiency score on item i for person j, and T is the response time (e.g. in milliseconds) on item i for person j. Note that response times are log-transformed due to their notorious positive skew (McCormack & Wright, 1964). The constant k is a pre-determined constant between zero and one. For example, if k = 0.5 and the individual responded correctly in 2000 milliseconds [ln(2000) = 7.60], his/her item score would be -7.60(0.5) = -3.80; whereas, if incorrect, his/her item score would simply be -7.60. Note that all item scores are therefore negative, but because k is constrained to be between zero and one, a correct answer will always be less negative than an incorrect answer (holding response time constant). The item score thus retains the conventional ordering property where higher (less negative) scores are superior to lower (more negative) scores. Regardless of response, the examinee is penalized for taking a long time, but this penalty is lessened (by k) if the response is correct. Note, therefore, that a correct response can result in an item score that is inferior to an incorrect response if response time is too long, and vice versa. Also, because the uniformly negative scores described here are on a rather unintuitive scale, they can be z-transformed so that a score represents standard deviations above or below the mean. In all demonstrations below, however, we leave scores untransformed so they are directly linkable to Equation 1. The R code for quickly converting dichotomous responses and response times to itemwise efficiency scores by Equation 1 is available in the supplementary materials.

To illustrate, Figure 1 shows an example item from an Age Differentiation test (described below), scored using four different values of k. The top panel shows the distribution of item scores (N = 4,333; sample described below) when k = 0.1; there is clearly great incentive to respond correctly because correct response times result in a score one tenth as negative as for incorrect responses. When k = 0.9 (bottom panel), on the other hand, there is far more incentive to emphasize speed over accuracy because a correct response still receives nine tenths the response time penalty of an incorrect response.

Figure 1.

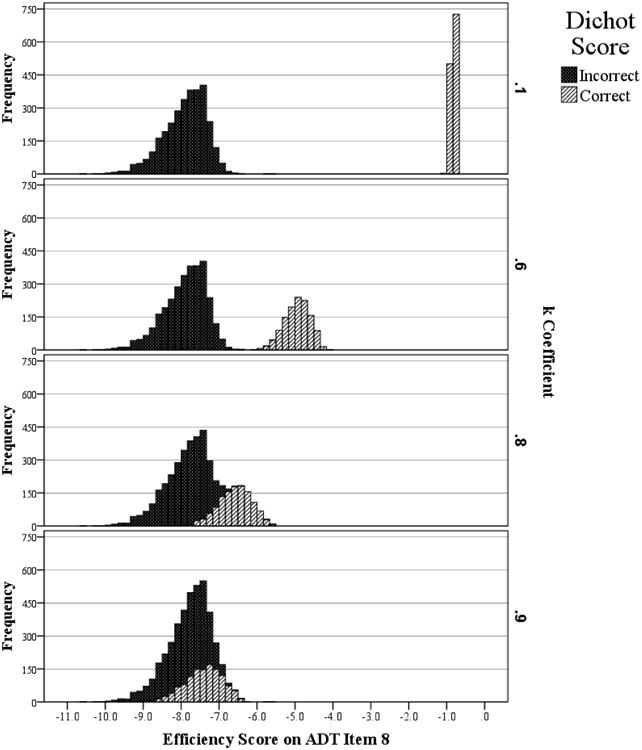
Histograms of Efficiency Scores for Item 8 on the Age Differentiations Test for Four Values of k, Separated by Dichotomous Score (Correct/Incorrect).

With an individual's items each scored in the above way, his/her total test score can then be calculated in a number of ways, the simplest being a basic sum score:

$$X_j=\sum _{i=1}^p{S}_{\mathit{\text{ij}}}$$ (2)

Where X_j is the total score for individual j, and p is the total number of items on the test. Alternatively, the items could be treated as continuous variables in a factor analysis, which could be used to find regression weights using, for example, Thurstone's (1935) method:

$$W=R^{-1}L$$ (3)

Where R is the matrix of correlations among the items, and L is the loading matrix from the factor analysis. The details of factor analysis methods are beyond the present scope, but see Kim and Mueller (1978) for review and Grice (2001) for a discussion of factor scoring methods and issues. Finally, a third possible scoring method is to apply a continuous Item Response Theory (IRT; Embretson & Reise, 2000; Lord, 1980) model such as the continuous response model (CRM; Samejima, 1973). For simplicity, here we use only sum scores, but encourage further investigation into the utility of the other scoring methods.

When introducing a new method, however, it is important to demonstrate that it contributes beyond the simple and available methods. Unless an investigator has a specific preference for emphasis of accuracy over speed, or does not wish to investigate which value of k is best—it would be helpful for us to recommend a single, reasonable value of k, and demonstrate that it produces scores at least as good as those produced by the traditional methods. Although we cannot recommend a single value of k, one reasonable approach would be to set k such that it emphasizes accuracy and speed equally (a characteristic rarely true for the traditional methods). For the convergent, discriminant, and predictive validity analyses described below, we use said approach to k, and the script for calculating the itemwise scores (see Supplement) includes an automatic algorithm for finding the k value that emphasizes accuracy and speed equally. This algorithm works by correlating the raw accuracy (total correct) and speed (sum of reaction times multiplied by -1) with the itemwise efficiency scores at values of k ranging from 0.05 to 0.95 in increments of 0.05. The value of k that generates the itemwise score with the minimum absolute difference between its correlation with accuracy and speed is considered optimal. We use “optimal” here only to mean that accuracy and speed are balanced; depending on the research question, emphasizing accuracy over speed (or vice versa) might be more appropriate.

We investigate the concurrent, convergent, discriminant, and predictive validity of the itemwise efficiency scores as compared to traditional methods. Note that we are using the term validity here not in the usual sense of the validity of the interpretation of test scores, but rather, as the relative validity of interpretations of two different types of efficiency scores on the same test. Nonetheless, we believe validity is still the most appropriate term.

Note that we do not have a specific rationale for why the interpretation of itemwise efficiency scores would be more valid than the traditional efficiency scoring methods, but only that they will perform at least as well and come with some additional advantages over the traditional scores. First, the itemwise method provides an easy way to balance accuracy and speed equally in the efficiency score by automatically finding the value of k necessary to do so for that test. Second, because k can be set by the researcher, it allows systematic exploration of what happens when the efficiency score is more associated with accuracy than speed, or vice versa. Third, the itemwise score allows one to examine efficiency during very specific parts of the test administration. This is especially important in functional neuroimaging studies where performance is tied to real-time physiologic activity and the investigator might be interested in that relationship during specific types of items or stimuli. For example, the emotion recognition test used here contains faces displaying various emotions, and one line of research (e.g. Loughead et al., 2008) examined the event-related performance-imaging relationship when different emotions were displayed (e.g. threat-related versus positive emotions). This is not possible using the traditional methods. Finally, measuring efficiency at the item level allows the use of existing item-analysis methods such as item response theory (IRT) applying, for example, the continuous response model (CRM; Samejima, 1973). The advantages of IRT are many (see Reise, Ainsworth, & Haviland, 2005), but a notable one is the ability to test for differential item functioning (DIF; Osterlind & Everson, 2010), sometimes called “measurement bias.”

It is also important to note that item response models incorporating response time have existed for over two decades (see Roskam, 1987), and have been continually developed since that time (De Boeck & Partchev, 2012; Fox, Klein Entink, & van der Linden, 2007; Klein Entink et al., 2009; Partchev & De Boeck, 2012; van der Linden, Klein Entink, & Fox, 2010; van der Maas et al., 2011; for review, see van der Linden, 2009). However, these models come with some disadvantages. First, and perhaps most importantly, although they are designed to model accuracy without ignoring information provided by speed (and vice versa), to our knowledge none of them provides a single efficiency score. Instead, they produce two scores (e.g. see Molenaar, Tuerlinckx, & van der Maas, 2015a; van der Linden 2007), one more related to accuracy and one more related to speed, which prohibits direct comparison of those scores with the efficiency score presented here. Another promising model, the Q-diffusion IRT model (Molenaar, Tuerlinckx, & van der Maas, 2015b) is unfortunately limited to items with only two response categories, and could therefore not be estimated in our data. A second weakness of the more advanced models is that, as with most cognitive-psychometric and IRT models, they require a minimum sample size for confident estimation of the item parameters. By contrast, calculation of the present itemwise efficiency scores requires no minimum sample size. Finally, perhaps due to their complexity and resultant occasional estimation difficulty, the advanced models appear simply not to appeal to most non-methodological applied researchers. This is not a weakness of the models as such, but it does suggest a need for simpler itemwise methods that can easily be adopted by applied researchers. We hope the itemwise model presented here fulfills that need.

Validity Assessment

For concurrent validity, we investigated how well the various efficiency scores (itemwise and traditional) distinguish between men and women (using basic t-tests) and, because the age of the sample ranges from 8 to 21 years during which performance shows marked improvement, how well they correlate with age. We selected from the battery tests on which performance has been shown to differ between the sexes (Gur et al., 2012; Halpern et al., 2007). Specifically, males perform better than females on spatial tasks (Linn & Petersen, 1985; Voyer, Voyer, & Bryden, 1995), such as the line orientation test used here. By contrast, females perform better than males on social cognition tasks and some memory tasks (e.g., Erwin et al., 1992; Hedges & Nowell, 1995; Hyde & Linn, 1988; Saykin et al., 1995; Williams et al., 2008), such as the emotion identification, age differentiation, and verbal memory tests used here. Additionally, there is substantial evidence that, within the age range of our participants, performance on these tests increases with age (Ang & Lee, 2008, 2010; Gow et al., 2011; Gur et al., 2012). However, so as not to limit our test selection only to their relationships with sex and age, we include an additional test (measuring spatial memory) that has not been shown to relate to either sex or age.

For convergent and discriminant validity, we investigated how well the alternative efficiency scores correlated with other measures in the same neurocognitive domain, and whether those correlations (and differences in correlations) were indeed lower for measures not in the same neurocognitive domain. Moore et al. (2015) showed that the battery from which these tests were taken has a four-factor structure of efficiency scores: Memory, Complex Reasoning, Executive Function, and Social Cognition. To demonstrate convergent and discriminant validity for the itemwise efficiency scores of the Penn Word Memory Test, for example, we hypothesize that it will correlate at least as highly as its traditional (mean-z-score) equivalent with the other two Memory tests' efficiency scores but not more highly than its traditional equivalent on the three tests of Executive Function.

Finally, for predictive validity we investigated how well the various efficiency scores correlated with neuroimaging measures of brain volume in regions that are established to be involved in the particular tests' neurocognitive demands. Our group has previously published studies showing the relationships between test scores and specific brain regions (Gur et al., 2000; Roalf et al., 2014), and we were guided by those results. Additionally, through an a priori literature search, we added some regions that we had not included in previous studies. Note that the reason we chose brain volume rather than other imaging modalities (e.g. gray matter density, cerebral blood flow, etc.) is that volume provides (by far) the largest effects of all available modalities. Also, a meta-analysis of brain-performance relationships (Pietschnig et al., 2015) found that volume is the best predictor of performance compared to other modalities.

For the line orientation test (PLOT), our previous research (Gur et al., 2000) suggested the parietal lobe white matter (also see Carpenter et al., 1999; Harris et al., 2000; Wolbers, Schoell, & Büchel, 2006; Zacks et al., 2003) and planum temporale. Additionally, there is some support for the importance of the occipital lobe white matter in mental rotation tasks. Because the spatial ability assessed here is ultimately visuo-spatial, and given the occipital lobe's well-established relationship to visual processing (Kandel, Schwartz, & Jessell, 2000, ch. 24-28; Riddoch, 1917), adequate occipital lobe function would aid in this task (Cohen et al., 1996).

For the verbal (CPW) and spatial (VOLT) episodic memory tests, hippocampus and fornix play a significant role (Aggleton & Brown, 1999; Kern et al., 2012; Kessler et al, 2001; Nestor et al., 2007; Penfield and Milner, 1958; Squire, 1992), and our previous results (Roalf et al., 2014) suggested additional brain regions of interest: central operculum, inferior frontal gyrus pars opercularis, inferior frontal gyrus pars triangularis (TrIFG), inferior temporal gyrus, anterior insula, posterior insula, medial frontal gyrus (MFG), occipital pole, inferior frontal gyrus (orbital), posterior cingulate gyrus, superior frontal gyrus, superior temporal gyrus, and fusiform gyrus (FuG; temporal and occipital).

For the two social cognition tests (ADT and ER40), our previous research (Roalf et al., 2014) suggested the following regions: amygdala, hippocampus, parahippocampal gyrus (PHG), posterior cingulate gyrus (PCgG; also see Frith & Frith, 1999; Hadland et al., 2003), fusiform gyrus, thalamus, inferior frontal gyrus pars opercularis (OpIFG), inferior frontal gyrus pars triangularis (TrIFG), and occipital lobe white matter (OCC WM). Additionally, there is substantial evidence that the corpus callosum (CC) is involved in social cognition tasks (Badaruddin et al., 2007; Bridgman et al., 2014; Lau et al., 2013; Symington et al., 2010).

Methods

Participants and Administration

The participants and recruiting methods used for the Philadelphia Neurodevelopmental Cohort (PNC) have been described in detail previously (Calkins et al., 2014; Gur et al., 2014; Moore et al., 2015). The sample included youths (age 8-21) recruited through an NIMH funded Grand Opportunity (GO) study characterizing clinical and neurobehavioral phenotypes in a genotyped prospectively accrued community cohort. All study participants were previously consented for genomic studies when they presented for pediatric services within the Children's Hospital of Philadelphia (CHOP) healthcare network. Note that this included visits for routine “well-child” check-ups, and thus the majority of the participants are physically and psychologically healthy. During the visit, they provided a blood sample for genetic studies, authorized access to Electronic Medical Records (EMRs) and gave written informed consent/assent to be re-contacted for future studies. Of the 50,540 genotyped subjects, 18,344 met criteria and were randomly selected, with stratification for age, sex and ethnicity.

The sample included ambulatory youths in stable health, proficient in English, physically and cognitively capable of participating in an interview and performing the computerized neurocognitive testing. Youths with disorders that impaired motility or cognition (e.g., significant paresis or palsy, intellectual disability) were excluded. Notably, participants were not recruited from psychiatric clinics and the sample is not enriched for individuals who seek psychiatric help. A total of 9,498 participants enrolled in the study between 11/2009 - 8/2013 and were included in this analysis, although because there were several alternate forms of some tests (described below), the sample sizes in the present study differed across tests. Participants provided informed consent/assent after receiving a complete description of the study and the Institutional Review Boards at Penn and CHOP approved the protocol.

Neuroimaging

Structural and functional neuroimaging was performed on a random subsample (N = 1601) of the 9498 PNC participants. The neuroimaging procedures have been described in detail (Satterthwaite et al., 2014, 2015). Briefly, all data were acquired on the same scanner (Siemens Tim Trio 3 Tesla, Erlangen, Germany; 32 channel head coil) using the same imaging sequences. Structural brain was completed using a magnetization-prepared, rapid acquisition gradient-echo (MPRAGE) T1-weighted image with the following parameters: TR 1810 ms, TE 3.51 ms, FOV 180×240 mm, matrix 256×192, 160 slices, TI 1100 ms, flip angle 9 degrees, effective voxel resolution of 0.9 × 0.9 × 1mm.

Regional volumes were estimated using an advanced multi-atlas regional segmentation (MARS) procedure (Doshi et al., 2013). A set of T1 MRI images from the OASIS data set were manually labeled according to 148 anatomic regions by Neuromorphometrics, Inc.(http://Neuromorphometrics.com/); the labeled atlases were registered to each subject's T1 image, and a final segmentation was arrived upon using an adaptive voting procedure for each region. While computationally intensive, such multi-atlas procedures provide much greater accuracy over regional measurements that utilize registration to a single atlas only. All registrations used DRAMMS, a highly-accurate deformable registration with attribute matching and mutual-salience weighting (Ou et al., 2011).

Tests Administered

The tests administered in the present study have been described in detail previously (Gur et al., 2001, 2010, 2012; Moore et al., 2015), but we provide brief descriptions below. Four tests were scored using the itemwise and traditional efficiency scoring methods, and are the focus of the present investigation. Additionally, eight other tests were scored using only the traditional Mean-z-score efficiency method, and those scores were used in a convergent and discriminant validity comparison (described below). The five tests that are the focus of the present paper are as follows:

Penn Word Memory Test (CPW)

The Penn Word Memory Test presents 20 target words that are then mixed with 20 foils equated for frequency, length, concreteness, and imageability (Gur et al., 1997). The participants are asked to memorize the target words as they are presented (1/sec) and after the presentation of the target words they are presented with target and foils and asked to indicate whether a word presented was included in the target list on a 1 to 4 scale (definitely yes; probably yes; probably not; definitely not).

Penn Line Orientation Test (PLOT)

The Penn Line Orientation Test presents two lines at an angle, and participants click on a button that makes one line rotate until they consider it to have the same angle as the other. The relative location of the lines, their sizes, and the number of degrees of rotation with each click differ across trials.

Penn Emotion Identification Test (ER40)

The Penn Emotion Identification Test displays faces expressing one of four emotions (happy, sad, anger, fear) and neutral faces, eight each. The faces are presented one at a time, and the participant is asked to identify the emotion displayed from the set of five choices. The facial stimuli are balanced for sex, age, and ethnicity (Carter et al., 2008; Gur et al., 2002; Gur et al., 2006; Mathersul et al., 2008).

Penn Age Differentiation Test (ADT)

The Penn Age Differentiation Test requires the participant to select which of two presented faces appears older, or if they are the same age. The stimuli were generated by morphing a young person's face with that of an older person who has similar facial features. The stimuli vary by percent of difference in age (calculated based on the percentage contributed by the older face) and are balanced for sex and ethnicity.

Visual Object Learning Test (VOLT)

The Visual Object Learning Test uses euclidean shapes as stimuli with the same paradigm as the word and face memory (Glahn, Gur, Ragland, Censits, & Gur, 1997; Gur et al., 2001, 2010). The presentation paradigm is otherwise identical to the verbal memory test.

The seven additional tests used in the validity comparison are as follows:

Penn Face Memory Test (CPF)

The Penn Face Memory Test presents 20 faces that are then mixed with 20 foils equated for age, sex, and ethnicity (Gur et al., 1997, 2001, 2010). The presentation paradigm is otherwise identical to the verbal and spatial memory tests.

Penn Verbal Reasoning Test (PVRT)

The Penn Verbal Reasoning Test consists of verbal analogy problems with simplified instructions and vocabulary (Gur et al., 1982, 2001, 2010).

Penn Matrix Reasoning Test (PMAT)

The Penn Matrix Reasoning Test consists of matrices requiring reasoning by geometric analogy and contrast principles (Gur et al., 2010).

Penn Emotion Differentiation Test (EDI)

The Penn Emotion Differentiation Test presents pairs of emotional expressions, each pair obtained from the same individual expressing the same emotion, one more intense than the other or of equal intensity. Gradations of intensity were obtained by morphing a neutral to an emotionally intense expression and the difference between pairs of stimuli ranged between 10 and 60% of mixture. The task is to click on the face that displays the more intense expression or indicate that they have equal intensity. The same emotions are used as for the Emotion Identification test but the faces are different.

Penn Conditional Exclusion Test (PCET)

Penn Conditional Exclusion Test is a measure of abstraction and concept formation. Participants decide which of four objects does not belong with the other three, based on one of three sorting principles (e.g., size, shape, line thickness). The participant is guided by feedback and, after 10 successful trials demonstrating that the principle was solved, the principle is changed without informing the participant (Gur et al., 2010; Kurtz, Ragland, Moberg, & Gur, 2004).

Penn Continuous Performance Test (PCPT)

The Penn Continuous Performance Test presents 7-segment displays at a rate of 1/sec. The participant's task is to press the space bar whenever the display forms a digit (for the first half of the test) or a letter (for the second half of the test). The original Penn Continuous Performance Test (Gur et al., 2001, 2010; Kurtz et al., 2001) has been abbreviated from 6 minutes (3 minutes for digits, 3 for letters) to 3 minutes (1.5 minutes for each).

Letter-N-Back (LNB)

The Letter N-back test displays sequences of uppercase letters with stimulus duration of 500 ms (ISI 2,500 ms.) In the 0-back condition, participants respond to a single target (i.e., X). In the 1-back condition they respond if the letter is identical to that preceding it. In the 2-back condition, they respond if the letter is identical to that presented two trials back (Gur et al., 2001, 2010; Ragland et al., 2002).

Data Analysis

All analyses described below were performed in R (R Core Team, 2014). First, items were scored based on equation 1, and sum scores were calculated from these itemwise scores. The sum scores were then used in analyses assessing validity.

The three validity investigations (concurrent, convergent/discriminant, and predictive) were calculated as follows:

1. For concurrent validity, male and female itemwise efficiency scores using k = 0.1, 0.3, 0.5, 0.7, 0.8, and 0.9 were compared using t-tests. For comparison, t-tests were also conducted comparing men's and women's scores on the traditional efficiency scores (Ratio method and Mean-z-score method) and on the pure accuracy and speed scores. Based on these results (described below), as well as Figure 2 (above), after this analysis we used only itemwise efficiency scores with k equal to a value that emphasized accuracy and speed equally. The rationale for showing the results using varying levels of k here was to demonstrate how validation results change as accuracy is emphasized over speed (and vice versa) when calculating efficiency scores. Of particular interest is whether the results change in predictable or unpredictable ways—e.g. will sex differences always become larger when accuracy is emphasized over speed (or vice versa)?

   Of the three possible overall scoring methods (sum, factor, and item-factor), for simplicity, from here, we use only the sum score method. Additionally, from here, when we refer to “traditional” efficiency scores, we are referring to the “Mean-z-score” method.

2. For convergent/discriminant validity, each itemwise efficiency score was correlated with the traditional efficiency scores of two tests that are within the same neurocognitive domain and three tests that are in a different neurocognitive domain (specifically, executive function). The same was done with the traditional scores. These correlations were then compared. For example, the CPW itemwise efficiency score was correlated with another memory test (CPF), the CPW traditional efficiency scores were correlated with the same test (CPF), and those correlations were compared. Because the two correlations shared a variable (CPF), the basic Fisher (1915) z-transformation could not be used. Instead, we used the Steiger (1980) method implemented using the ‘cocor’ package (Diedenhofen & Musch, 2015) in R. Note that, unlike for concurrent validity, itemwise efficiency scores were calculated using only one value of k—specifically, the one that emphasized accuracy and speed equally.

3. For predictive validity, the itemwise and traditional efficiency scores for the four tests were predicted by volume of brain regions of interest (ROIs). This was done using linear regression and controlling for age, age squared, and age cubed (for nonlinear effects). These analyses were conducted separately for men and women. The regression coefficients were then compared across score type (itemwise versus traditional) by converting them to partial correlations using the following equation:

   $$r=\frac{t}{\sqrt{t^2+{\mathit{\text{df}}}_{\mathit{\text{res}}}}}$$ (4)

   Where t is the t statistics for that coefficient. We then compared these correlations using the same Steiger (1980) method described above. As with convergent/discriminant validity, the value of k used was the one that emphasized accuracy and speed equally.

Figure 2.

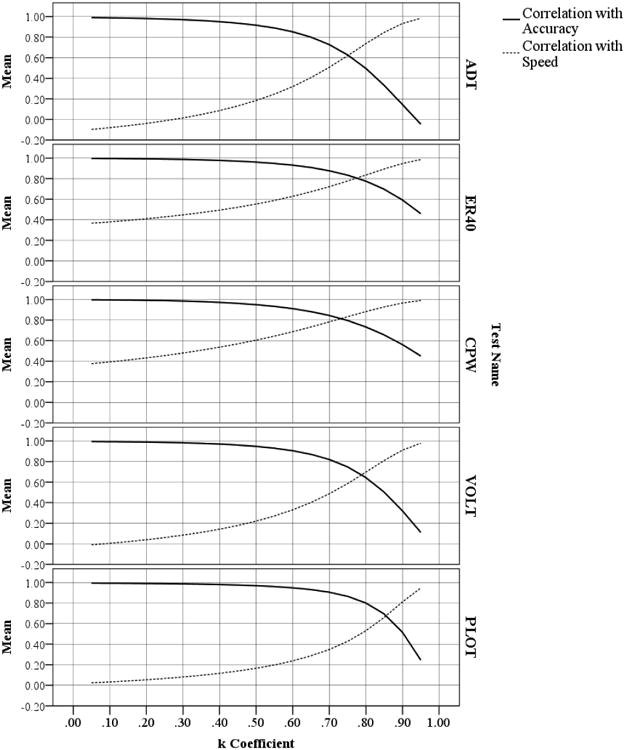
Correlations of Accuracy and Speed Scores with Itemwise Efficiency Scores, by k Coefficient, for Five Neurocognitive Tests.

Note that because the substantive scientific findings (e.g. sex differences) are not the focus of this study but rather a means for comparing two methods for calculating efficiency, we do not apply a familywise correction for the false discovery rate. Instead, we use the traditional p-value cutoff of 0.05 and emphasize the caveat that any substantive scientific findings herein should be interpreted with caution for this reason. On the other hand, some effects in the study are directly relevant to the main focus of the paper, namely, those for the comparison of effect sizes of the two methods (e.g. last five columns of Table 3 and comparisons of regression coefficients in Tables 4a-e). These effects are corrected for multiple comparisons using Bonferroni (1936) because they are directly related to the efficiency score comparison we are investigating.

Table 3. Correlations and differences of correlations among itemwise and traditional efficiency scores.

Test	Domain	Itemwise efficiency					Traditional efficiency					Difference
		ADT	ER40	CPW	VOLT	PLOT	ADT	ER40	CPW	VOLT	PLOT	ADT	ER40	CPW	VOLT	PLOT
ER40	Soc	.423					.460					-.037*
EDI	Soc	.559	.597				.599	.613				-.040*	-.016*
ADT	Soc		.533					.540					-.007
VOLT	Mem			.388					.385					.003
CPF	Mem			.493	.429				.490	.447				.003	-.018*
CPW	Mem				.361					.396					-.035*
PMAT	Comp					.464					.422					.042*
PVRT	Comp					.498					.441					.057*
ABF	Exec	.234	.360	.265	.249	.409	.262	.376	.268	.272	.359	-.028*	-.016*	-.003	-.023*	.050*
ATT	Exec	.325	.481	.404	.230	.383	.368	.491	.410	.240	.363	-.043*	-.010	-.006	-.010	.020*
WM	Exec	.268	.433	.364	.211	.383	.311	.446	.375	.239	.354	-.043*	-.013	-.011*	-.028*	.029*

Note.

^*= p < .05;

ER40 = Emotion Recognition; EDI = Emotion Differentiation; ADT = Age Differentiation; CPW = Word Memory; CPF = Face Memory; VOLT = Spatial Memory; PLOT = Spatial Ability; PMAT = Matrix Reasoning; PVRT = Verbal Reasoning; ABF = Abstraction and Mental Flexibility; ATT = Attention; WM = Working Memory; Soc = Social Cognition; Mem = Episodic Memory; Comp = Complex Reasoning; Exec = Executive Control.

Table 4.

a. Relationships of Itemwise Penn Line Orientation Test Efficiency Scores to Brain Volume in Three ROIs.

ROI	Males				Females
	Itemwise		Traditional		Itemwise		Traditional
	Coef	p-value	Coef	p-value	Coef	p-value	Coef	p-value
	Par WM	0.192	< .001	0.157	< .001	0.197	< .001	0.158	< .001
PT	0.160	< .001	0.138	< .001	0.189	< .001	0.161	< .001
Occ WM	0.155	< .001	0.133	< .001	0.134	< .001	0.120	< .001
Note. Coef = Standardized Coefficient; ROI = Region of Interest; Par = Parietal; Occ = Occipital; WM = White Matter; PT = Planum Temporale.

b. Relationships of Itemwise Word Memory Test Efficiency Scores to Brain Volume in Sixteen ROIs.
ROI	Males				Females
	Itemwise		Traditional		Itemwise		Traditional
	Coef	p-value	Coef	p-value	Coef	p-value	Coef	p-value
	CO	-0.008	0.802	-0.006	0.856	0.015	0.652	0.030	0.362
OpIFG	-0.019	0.563	-0.001	0.967	0.015	0.642	0.018	0.580
TrIFG	0.062	0.058	0.063	0.051	0.066	0.040	0.073	0.022
ITG	-0.022	0.494	-0.014	0.659	0.031	0.331	0.043	0.181
Ains	0.044	0.190	0.062	0.064	-0.031	0.344	-0.019	0.559
Pins	0.031	0.375	0.037	0.272	-0.004	0.901	0.007	0.829
MFG	-0.016	0.636	-0.001	0.986	0.058	0.085	0.072	0.032
OCP	-0.003	0.916	0.009	0.771	-0.032	0.319	-0.021	0.517
OrIFG	0.036	0.270	0.051	0.112	-0.013	0.686	-0.005	0.872
PCgG	0.021	0.532	0.031	0.343	0.030	0.381	0.044	0.194
SFG	-0.024	0.479	-0.009	0.790	0.021	0.528	0.035	0.296
STG	-0.047	0.150	-0.033	0.306	-0.002	0.947	0.016	0.630
FuG	0.043	0.191	0.066	0.041	0.050	0.126	0.061	0.060
OFuG	0.038	0.264	0.061	0.064	0.027	0.414	0.038	0.258
Fornix	-0.004	0.902	0.003	0.926	0.054	0.100	0.059	0.073
Hip	0.039	0.238	0.052	0.106	-0.031	0.326	-0.017	0.599
Note. Significant results bolded; Coef = Standardized Coefficient; ROI = Region of Interest; CO = Central Operculum; OpIFG = Inferior Frontal Gyrus pars Opercularis; TrIFG = Inferior Frontal Gyrus pars Triangularis; ITG = Inferior Temporal Gyrus; Ains = Anterior Insula; Pins = Posterior Insula; MFG = Medial Frontal Gyrus; OCP = Occipital Pole; OrIFG = Inferior Frontal Gyrus (Orbital); PCgG = Posterior Cingulate Gyrus; SFG = Superior Frontal Gyrus; STG = Superior Temporal Gyrus; FuG = Fusiform Gyrus; OFuG = Occipital Fusiform Gyrus; Hip = Hippocampus.

c. Relationships of Itemwise Spatial Memory Test Efficiency Scores to Brain Volume in Sixteen ROIs.
ROI	Males				Females
	Itemwise		Traditional		Itemwise		Traditional
	Coef	p-value	Coef	p-value	Coef	p-value	Coef	p-value
	CO	0.081	0.035	0.060	0.122	0.057	0.083	0.083	0.012
OpIFG	0.075	0.052	0.066	0.093	0.042	0.203	0.068	0.039
TrIFG	0.016	0.664	0.028	0.472	0.077	0.015	0.091	0.004
ITG	0.077	0.041	0.075	0.049	0.091	0.004	0.129	< .001
Ains	0.125	0.001	0.134	0.001	0.042	0.204	0.066	0.047
Pins	0.091	0.022	0.075	0.061	0.040	0.229	0.060	0.072
MFG	0.077	0.047	0.067	0.086	0.090	0.007	0.117	< .001
OCP	0.041	0.284	0.023	0.542	0.027	0.391	0.028	0.376
OrIFG	0.128	0.001	0.143	< .001	0.060	0.057	0.074	0.021
PCgG	0.078	0.042	0.076	0.051	0.083	0.014	0.104	0.002
SFG	0.056	0.145	0.053	0.173	0.071	0.031	0.079	0.017
STG	0.033	0.389	0.025	0.520	0.037	0.259	0.071	0.033
FuG	0.148	< .001	0.152	< .001	0.061	0.056	0.091	0.005
OFuG	0.077	0.045	0.078	0.045	0.061	0.063	0.075	0.024
Fornix	0.009	0.823	0.010	0.802	0.049	0.130	0.068	0.037
Hip	0.104	0.006	0.091	0.017	0.037	0.239	0.045	0.160
Note. Bold indicates that the difference between the itemwise and traditional effects is significant at the p < 0.05 level; Coef = Standardized Coefficient; ROI = Region of Interest; CO = Central Operculum; OpIFG = Inferior Frontal Gyrus pars Opercularis; TrIFG = Inferior Frontal Gyrus pars Triangularis; ITG = Inferior Temporal Gyrus; Ains = Anterior Insula; Pins = Posterior Insula; MFG = Medial Frontal Gyrus; OCP = Occipital Pole; OrIFG = Inferior Frontal Gyrus (Orbital); PCgG = Posterior Cingulate Gyrus; SFG = Superior Frontal Gyrus; STG = Superior Temporal Gyrus; FuG = Fusiform Gyrus; OFuG = Occipital Fusiform Gyrus; Hip = Hippocampus.

d. Relationships of Itemwise Emotion Recognition Test Efficiency Scores to Brain Volume in Ten ROIs.
ROI	Males				Females
	Itemwise		Traditional		Itemwise		Traditional
	Coef	p-value	Coef	p-value	Coef	p-value	Coef	p-value
	Amygdala	-0.038	0.545	-0.052	0.373	0.135	0.067	0.113	0.124
Hip	-0.041	0.532	-0.037	0.538	0.201	0.002	0.181	0.006
PHG	-0.023	0.686	-0.016	0.761	0.278	< .001	0.259	< .001
PCgG	-0.035	0.526	-0.022	0.675	0.304	< .001	0.307	< .001
FuG	-0.012	0.810	-0.002	0.961	0.266	< .001	0.277	< .001
Thalamus	0.073	0.257	0.064	0.283	0.266	< .001	0.258	< .001
OpIFG	-0.001	0.987	0.008	0.879	0.265	< .001	0.275	< .001
TrIFG	-0.047	0.413	-0.044	0.402	0.187	0.005	0.166	0.014
OCC WM	0.030	0.619	0.020	0.724	0.061	0.358	0.088	0.184
CC	0.037	0.524	0.025	0.643	0.198	0.004	0.201	0.003
Note. Significant results bolded; Coef = Standardized Coefficient; ROI = Region of Interest; Hip = Hippocampus; PHG = Parahippocampal Gyrus; PCgG = Posterior Cingulate Gyrus; FuG = Fusiform Gyrus; OpIFG = Inferior Frontal Gyrus pars Opercularis; TrIFG = Inferior Frontal Gyrus pars Triangularis; OCC = Occipital; WM = White Matter; CC = Corpus Callosum.

e. Relationships of Itemwise Age Differentiation Test Efficiency Scores to Brain Volume in Ten ROIs.
ROI	Males				Females
	Itemwise		Traditional		Itemwise		Traditional
	Coef	p-value	Coef	p-value	Coef	p-value	Coef	p-value
	Amygdala	0.042	0.381	0.000	0.997	-0.100	0.043	-0.099	0.032
Hip	0.048	0.324	0.045	0.344	0.064	0.201	0.080	0.090
PHG	0.089	0.077	0.049	0.312	0.118	0.017	0.132	0.004
PCgG	0.084	0.096	0.053	0.282	0.135	0.011	0.152	0.002
FuG	0.094	0.066	0.069	0.165	0.068	0.176	0.099	0.036
Thalamus	0.099	0.057	0.049	0.323	0.153	0.002	0.149	0.001
OpIFG	0.122	0.016	0.104	0.033	0.087	0.102	0.084	0.088
TrIFG	0.031	0.527	0.011	0.820	0.121	0.016	0.092	0.050
OCC WM	0.076	0.141	0.055	0.271	0.134	0.007	0.119	0.011
CC	0.074	0.157	0.023	0.652	0.188	0.000	0.203	< .001

Note. Significant results bolded; Coef = Standardized Coefficient; ROI = Region of Interest; Hip = Hippocampus; PHG = Parahippocampal Gyrus; PCgG Posterior Cingulate Gyrus; FuG = Fusiform Gyrus; OpIFG = Inferior Frontal Gyrus pars Opercularis; TrIFG = Inferior Frontal Gyrus pars Triangularis; OCC = Occipital; WM = White Matter; CC = Corpus Callosum.

Results

Concurrent Validity

Table 1 shows the differences in standardized efficiency scores (using the global mean and SD) between males and females for all five tests. Additionally, differences for pure accuracy and speed scores are reported at the bottom. Consistent with previous research, females outperform males (indicated by a negative effect) on the ADT, ER40, and CPW, males outperform females on the PLOT, and neither sex outperforms the other on the VOLT. These effects are further supported by the pure accuracy and speed scores, in which females are not only more accurate, but also faster on the first three tests; likewise, males are both more accurate and faster on the PLOT. Neither sex is faster or more accurate on the VOLT.

Table 1.

Standardized Differences between Male and Female Efficiency, Accuracy, and Speed Scores on Four Neurocognitive Tests, by Test, Score Type, and k Coefficient.

Efficiency Score Type	Differences in z-scores
	ADT	ER40	CPW	VOLT	PLOT
Sum (k = .1)	-.316	-.173	-.143	.050	.233
Sum (k = .3)	-.318	-.184	-.153	.052	.239
Sum (k = .5)	-.315	-.200	-.167	.054	.247
Sum (k = .7)	-.281	-.221	-.180	.056	.260
Sum (k = .8)	-.226	-.230	-.184	.054	.263
Sum (k = .9)	-.128	-.230	-.179	.044	.239
Ratio Method (score/RT ratio)	-.290	-.246	-.174	.059	.231
Mean-z-score Method	-.266	-.255	-.187	.042	.255
Pure Accuracy	-.314	-.210	-.144	.050	.181
Pure Speed	-.088	-.356	-.152	.008†	.120

Note. Negative values indicate Female > Male performance; all differences significant at the p < .05 level except where indicated by †; Max absolute values within each efficiency score type combination bolded; ADT = Age Differentiation Task; ER40 = Emotion Recognition Task; CPW = Word Memory Task; PLOT =Penn Line Orientation Task; Score/RT = total correct divided by median reaction time.

For the itemwise efficiency scores, effects are further broken down by k value (0.1, 0.3, 0.5, 0.7, 0.8, and 0.9), with the greatest effect in each score type bolded. The main question of interest here is whether the itemwise efficiency scores pick up equal or larger effects than the traditional (Ratio and Mean-z-score) efficiency scores. For two out of the five tests (ADT, and PLOT), at least one of the effects using itemwise scores is larger than either of the effects using traditional scores—e.g. for the ADT, the effect using an itemwise sum score with k = 0.3 is -0.318, compared to -0.290 and -0.266 for the traditional scores. For the other two tests in which a sex difference is expected (ER40 and CPW), at least one of the traditional methods outperforms the itemwise scores at all levels of k. Finally, for the test in which a sex difference is not expected, the traditional Ratio Method picks up a larger effect than the itemwise methods at any value of k.

Table 2 shows the correlations of the itemwise and standard efficiency scores with age, as well as the correlations of pure speed and accuracy with age. The results are similar to the sex differences insofar as, for some values of k and for some tests, the itemwise scores outperform the traditional scores. For the ADT and PLOT, the largest itemwise correlation is larger than either of the traditional scores; however, for the ER40 and CPW, the highest itemwise correlations with age (0.46 and 0.41, respectively) were larger than only one of the two traditional scores. Finally, for the VOLT, which is not expected to correlate with age, the traditional mean-z-score method finds a significant effect. Notably, in the case of the PLOT, the highest itemwise correlation with age is larger than either pure accuracy or pure speed, providing some evidence that an efficiency measure might provide more than the sum of its parts.

Table 2.

Correlations with Age, by Test, Score Type, and k Coefficient.

Efficiency Score Type	ADT	ER40	CPW	VOLT	PLOT
Itemwise Sum (k = .1)	.44	.39	.14	.07	.39
Itemwise Sum (k = .3)	.44	.40	.18	.08	.39
Itemwise Sum (k = .5)	.42	.43	.24	.10	.38
Itemwise Sum (k = .7)	.35	.46	.32	.12	.36
Itemwise Sum (k = .8)	.25	.46	.37	.14	.33
Itemwise Sum (k = .9)	.10	.45	.41	.14	.23
Ratio Method (score/RT ratio)	.33	.47	.43	.16	.34
Mean-z-score Method	.36	.45	.35	.17	.28
Pure Accuracy	.45	.29	.17	.07	.38
Pure Speed	.05	.36	.42	.17	.03

Note. All correlations significant at the p < .05 level; Max correlations within each efficiency score type combination bolded; ADT = Age Differentiation Task; ER40 = Emotion Recognition Task; CPW = Word Memory Task; PLOT = Penn Line Orientation Task; VOLT = Visual Object Learning Test; Score/RT = total correct divided by median reaction time.

Of course, comparison of the traditional methods to the itemwise method using a range of k values does not provide very conclusive information because it is unlikely that a researcher would vary k as widely in practice. These results would be more informative if we suggested a value of k a priori, and then compared effects using that specific k coefficient. Here, we used the k coefficient that results in scores that correlate with accuracy and speed equally. These values were 0.85, 0.80, 0.75, 0.75, and 0.75 for the PLOT, VOLT, ADT, ER40, and CPW, respectively.

Convergent and Discriminant Validity

Table 3 shows the correlations among the itemwise efficiency scores, efficiency scores on other tests within their neurocognitive domains, and efficiency scores from other tests not in their neurocognitive domains. The same is shown for the traditional (Mean-z-score) efficiency scores, and the five rightmost columns show the differences between them. As expected, the mean correlation of a test within its domain (e.g. the ADT with the ER40 and EDI) is larger than the mean correlation of that test with tests outside its domain (e.g. the ADT with the ABF, ATT, and WM).

For the ADT, ER40, and VOLT, convergent validity favors the traditional scores, indicated by the negative values: difference of correlations of -0.037 and -0.040 for the ADT's domain (social cognition), -0.016 for the ER40's domain (social cognition), and -0.018 and -0.035 for the VOLT's domain (episodic memory). For the CPW, there is no difference in prediction between the two score types, and for the PLOT, the itemwise scores perform better: difference in correlations of 0.042 and 0.057. For discriminant validity, the itemwise scores appear to perform better, indicated by the mostly negative values in the last three rows of Table 3. Again, the exception is the PLOT, indicated by its correlations with the ABF, ATT, and WM (executive domain) more positive than those of the traditional scores.

Predictive Validity

Tables 4a through 4e show the relationships between the efficiency scores (itemwise and traditional) and the brain regions of interest known to be associated with specific tasks; 4a-4e correspond to the PLOT, CPW, VOLT, ER40, and ADT, respectively. For the PLOT (Table 4a), volume of all regions predicts performance. Parietal lobe white matter has the largest effect (mean β across sex and score type = 0.18; p < 0.001), followed by the planum temporale (mean β = 0.16; p < 0.001) and occipital lobe white matter (mean β = 0.14; p < 0.001). For all six relationships (three male, three female), the effect using the itemwise efficiency scores is larger than the effect using the traditional efficiency scores, however none of these differences in effects is significant after correction for multiple comparisons.

For the CPW (Table 4b), only five out the sixteen regions predicted performance, and these differed between males and females. For males, the fusiform gyrus predicted traditional scores. For females, the TrIFG predicted both score types, and the MFG predicted only traditional scores. Overall, the CPW results appear to slightly favor the traditional scores, however none of these differences in effects is significant after correction for multiple comparisons.

For the VOLT (Table 4c), fifteen out of the sixteen regions predicted efficiency, with the strongest effect coming from the FuG (mean β across sex and score type = 0.11; p < 0.001), followed by the OrIFG (mean β = 0.10; p < 0.001) and ITG (mean β = 0.09; p < 0.001). The smallest effect came from the OCP (mean β = 0.09; mean p = 0.40). Of the significant effects (across both males and females), the itemwise efficiency scores produced larger effects in nine out of the thirty tests, providing small-to-moderate support for the traditional scores. However none of these differences in effects is significant after correction for multiple comparisons. For the ER40 (Table 4d), male scores were predicted by none of the regions of interest. Female scores were predicted by the hippocampus, PHG, PCgG, FuG, thalamus, OpIFG, TrIFG, and CC. The largest effect was for the thalamus (mean β across sex and score type = 0.17; p < 0.001), followed by the PCgG (mean β = 0.14; p < 0.001) and OpIFG (mean β = 0.14; p < 0.001). Of these eight effects, four were larger for the itemwise scores than for the traditional scores, however none of these differences in effects is significant after correction for multiple comparisons.

Finally, for the ADT (Table 4e), male scores were predicted by only the OpIFG. Female scores were predicted by the following: PHG, PCgG, FuG, thalamus, TrIFG, OCC WM, and CC. The largest effects were for the CC (mean β across score types = 0.12; p < 0.001) and thalamus (mean β = 0.11; p < 0.001). Additionally, amygdala predicted performance in females, but it was in the opposite direction (β = -0.10; mean p = 0.038) from what previous research has shown. Of the eight significant effects in the expected direction, four were larger for the itemwise scores than for the traditional scores, however none of these differences in effects is significant after correction for multiple comparisons.

Discussion

We present a new method for scoring computerized test results, which takes advantage of the availability of precise measures of itemwise speed to arrive at a single parameter of efficiency. We applied this scoring algorithm to five tests from a computerized battery that was administered to a large population-based sample of nearly 10,000 participants aged 8 to 21, of whom a subsample also received neuroimaging. With this dataset we demonstrated that the new efficiency scores, compared to traditional simple averaging of accuracy and speed or using them as separate indices, produce similar effect sizes for sensitivity to sex differences and age effects, depending on the test. We further showed that the new efficiency scores have slightly inferior convergent validity although slightly superior discriminant validity. Predictive validity, tested by regressions predicting performance with hypothesized brain indices derived from the neuroimaging data, was about equal for the new and traditional scoring algorithms, again depending on the test. It is also worth noting that the differences in effect sizes between the itemwise and traditional methods was usually quite small (rarely larger than 0.05). Based on this and the mixed results described above, we cannot make the claim that the interpretation of the itemwise scores is more valid than that of the traditional scores, but we do emphasize other advantages of the itemwise method.

The first major advantage of itemwise efficiency scores is that the continuous coefficient k allows a psychometrician to decide how much emphasis to place on accuracy versus speed. For example, if one wanted to focus almost exclusively on accuracy but penalize individuals who take an extremely long time, one could set k very low (e.g. 0.1; see top panel in Figure 1). On the other hand, if a psychometrician wanted to focus almost exclusively on speed but give individuals a very slight incentive for being correct, he/she could set k to be high (e.g. 0.9; see bottom panel in Figure 1). This variable emphasis on accuracy versus speed is illustrated in Figure 2, which shows the correlation of itemwise efficiency scores with pure accuracy and pure speed, at varying levels of k. The specific correlations vary by test (each described below), but in all four cases, itemwise efficiency scores calculated using low values of k correlate more highly with accuracy than speed, and vice versa. Additionally, as they are used presently, the parameter k can be set to emphasize accuracy and speed equally, a balance rarely achieved with the traditional methods.

A second advantage of this scoring method is in the context of neurocognitive testing in relation to brain parameters of structure and, even more so, function, where itemwise scoring can be correlated with regional brain activation. Furthermore, different brain parameters can relate differentially to accuracy and speed of processing, and this variability can be captured by itemwise efficiency scoring.

Finally, scoring efficiency at the item-level allows the use of IRT, which comes with several advantages. One is the ability to measure item bias (DIF), and a second is the ability to administer the test adaptively using computerized adaptive testing (CAT; Wainer et al., 2000). Although technically CAT is not necessary with continuous items due to their covering the full range of difficulty, they can differ by their discrimination parameter, which is another important determinant of the suitability of an item in a CAT administration. Also, note that the individual item scores are sometimes fully bimodal (depending on k), which means these item scores might not actually cover the full range of difficulty. We encourage further investigation of this topic.

One interesting finding that came out of the convergent and predictive validity analyses is that the itemwise efficiency scores appear to be especially valid in the case of visuo-spatial ability (PLOT) and should perhaps be used with caution for memory tests (CPW and VOLT). The latter, poorer performance of the itemwise scores for memory tasks might be related to a previous finding (see Moore et al., 2015) in which an exploratory factor analysis of neurocognitive performance speed revealed a separate memory factor. This could mean that speed of performance on memory tasks—specifically recognition memory in this case—is phenomenologically different from speed of performance on other tasks.

It is important to point out a limitation of the itemwise method presented here, specifically, it cannot be calculated for tests (e.g. the CPT) in which some “responses” are actually nonresponses. Regardless of whether the non-response is correct or incorrect, it does not produce a response time, and efficiency for that item can therefore not be calculated. Nonetheless, while more investigation of this and similar approaches is warranted, the proposed method can help advance the rate and scope of behavioral data that can be collected in ongoing and planned large-scale studies envisioned by the “precision medicine” initiative. This massive effort of data gathering will focus on biological parameters related to physical illnesses, but the brain is a valid organ in this context and its products, behavior and mental illness, deserve attention. Here the ability to reduce the number of parameters to be submitted for data mining is crucial to address the problem of Type I error containment. While it is of interest for a psychometrician to examine speed and accuracy separately, when test results have to be correlated with multiple measures derived from neuroimaging and genetic analyses then submitting both sets of scores for analysis will double the dimensionality of data. Of course, a positive finding with the efficiency index could justify a hypothesis-guided evaluation of the relative contribution of speed or accuracy to the effect. As a final note, these results are preliminary but we encourage further evaluation of this and similar procedures for deriving test scores that incorporate accuracy and speed parameters to measure performance efficiency.