A novel meta-analytic approach: Mining frequent co-activation patterns in neuroimaging databases

Abstract

In recent years, coordinate-based meta-analyses have become a powerful and widely used tool to study coactivity across neuroimaging experiments, a development that was supported by the emergence of large-scale neuroimaging databases like BrainMap. However, the evaluation of co-activation patterns is constrained by the fact that previous coordinate-based meta-analysis techniques like Activation Likelihood Estimation (ALE) and Multilevel Kernel Density Analysis (MKDA) reveal all brain regions that show convergent activity within a dataset without taking into account actual within-experiment co-occurrence patterns. To overcome this issue we here propose a novel meta-analytic approach named PaMiNI that utilizes a combination of two well-established data-mining techniques, Gaussian mixture modeling and the Apriori algorithm. By this, PaMiNI enables a data-driven detection of frequent co-activation patterns within neuroimaging datasets. The feasibility of the method is demonstrated by means of several analyses on simulated data as well as a real application. The analyses of the simulated data show that PaMiNI identifies the brain regions underlying the simulated activation foci and perfectly separates the co-activation patterns of the experiments in the simulations. Furthermore, PaMiNI still yields good results when activation foci of distinct brain regions become closer together or if they are non-Gaussian distributed. For the further evaluation, a real dataset on working memory experiments is used, which was previously examined in an ALE meta-analysis and hence allows a cross-validation of both methods. In this latter analysis, PaMiNI revealed a fronto-parietal “core” network of working memory and furthermore indicates a left-lateralization in this network. Finally, to encourage a widespread usage of this new method, the PaMiNI approach was implemented into a publicly available software system.

Introduction

Over the last decades, functional neuroimaging has been evolved to the most prevalent tool in cognitive neuroscience and the key method for investigations into the functional organization of the human brain. As a consequence, the neuroimaging community has generated a tremendous amount of studies concerning the localization of almost all cognitive domains. This growing number of published neuroimaging literature has prompted the development of meta-analysis techniques, which exploit the substantial amount of neuroimaging data in order to draw robust and more general inferences. Particularly coordinate-based meta-analyses (CBMA) provide powerful and easily accessible techniques, which operate on the three-dimensional coordinates of peak activation foci reported by these studies in standard reference space, i.e. the MNI (Evans et al., 1992) or Talairach (Talairach and Tournoux, 1988) spaces. CBMA allow a straightforward analysis of (the entire) previous literature, as it only relies on the published peak coordinates and hence may be employed without the need for obtaining additional data from the respective authors, e.g. image files. The latter aspect usually limits the capability of image-based methods to cover a broad range of (in particular older) studies. Furthermore, the work on those sparse representations of the image data is also profitable from a computational perspective. CBMA are particularly facilitated by large scale databases like BrainMap (www.brainmap.org) (Fox and Lancaster, 2002; Laird et al., 2005) or NeuroSynth (www.neurosynth.org) (Yarkoni et al., 2011) that collect the information and peak coordinates of neuroimaging studies and make them accessible.

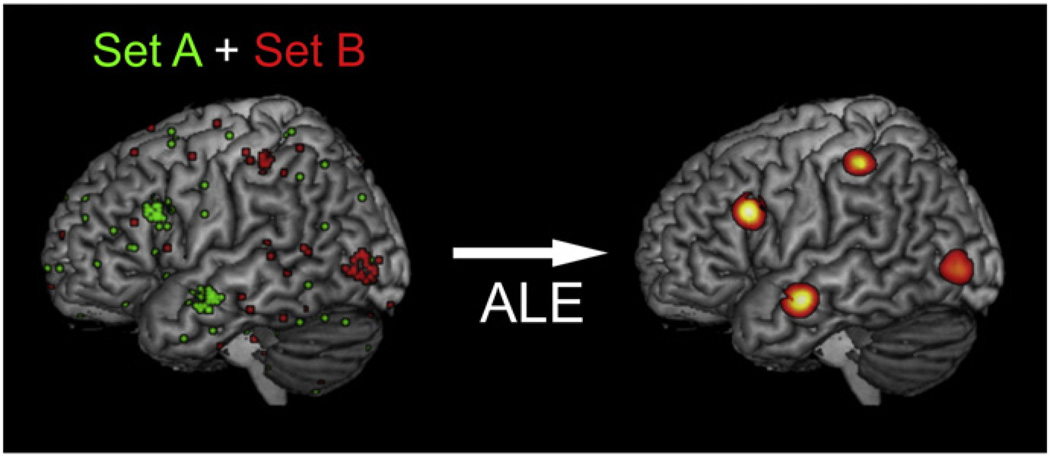
The most common previous CBMA techniques are Activation Likelihood Estimation (ALE: Eickhoff et al., 2009, 2012; Turkeltaub et al., 2002) and (Multilevel) Kernel Density Analysis (KDA and MKDA: Wager et al., 2004; Wager et al., 2007). In principle, both methods rely on similar concepts: first, they model each focus of a dataset; in ALE the activation foci are modeled as Gaussian distributions, in MKDA as spheres. Then, these representations are combined across experiments; in ALE via the union of the modeled activation (Turkeltaub et al., 2012), in MKDA via weighted averages of the modeled maps representing the studies (Wager et al., 2007). Finally, the resulting activation maps are tested for significance, i.e. above-chance convergence, using permutation tests. The results of both techniques, ALE and MKDA, are maps that indicate those locations in the brain, where the reported activations of all experiments in the underlying dataset significantly converge. The brain regions featuring this convergence of activity can then be interpreted as being robustly involved in the cognitive processes addressed by the experiments of the set. The co-activation patterns shown by the resulting maps can generally be regarded as functionally connected (Caspers et al., 2013; Eickhoff et al., 2010; Jakobs et al., 2012). That is, they fulfill the criteria of functional connectivity by representing temporal coincident and spatially distant neural activity (Friston, 1994). However, both described CBMA approaches have some disadvantages, when trying to evaluate connectivity, i.e. within experiment co-activity. That is, the resulting maps of ALE and MKDA indicate all brain regions consistently active within a specific dataset, without taking into account, if those brain regions are really co-active within single experiments. Hence, there is no information on the distributions of specific co-activation patterns across experiments. In order to demonstrate this aspect, we simulated a dataset containing two divergent subsets of experiments and subjected it to a standard ALE analysis (Fig. 1): While set A featured experiments with activation in the inferior frontal cortex and on the middle temporal gyrus, the experiments of set B provided activation foci in the intraparietal sulcus and on the middle occipital gyrus (Fig. 1, left). To simulate noise, all experiments had additional activation foci randomly distributed over the whole brain. The simulated dataset was analyzed with the latest version of the ALE algorithm (Eickhoff et al., 2012). The resulting ALE map revealed convergent activity in all four input regions (Fig. 1, right). However, the segregation into two underlying subsets cannot be recognized anymore in the ALE map as all four regions likewise show significant convergence. This leads to possible misinterpretations regarding co-activity within the ALE map. All four regions are represented in the same map, although there was for example no experiment within the simulation dataset in which the inferior frontal cortex was co-active with the intraparietal sulcus.

Fig. 1.

Left: Simulated dataset of two sets of experiments (simulation 2). Activation foci of all experiments are projected onto the MNI single subject brain. Set A (green) contained foci centered around the inferior frontal gyrus and the middle temporal gyrus, set B (red) contained foci centered around the intraparietal sulcus and the middle occipital gyrus. For both sets noise foci were generated. Right: ALE meta-analysis of the simulated dataset. The resulting ALE map is projected onto the MNI single subject brain.

To address this issue and provide a method for a more specific identification of co-activation patterns across experiments, we developed a novel meta-analytic approach based on well-established data-mining techniques. The proposed method identifies frequent co-activation patterns in coordinate-based neuroimaging datasets and reveals how often a specific brain region is co-active with other brain regions within the dataset. Here we present the novel method, named PaMiNI (Pattern Mining in NeuroImaging), and its implementation into a software tool. Some aspects of the PaMiNI method have already been described in (Caspers et al., 2012a, 2012b). The method is evaluated by means of five simulations and cross-validated with ALE using a real dataset on working memory.

Material and methods

The aim of the proposed method is to find frequent co-activation patterns, i.e. combinations of brain regions that frequently show co-occurrent activation in a dataset of neuroimaging experiments. It is based on the concepts of CBMA, that is, all information is provided as three-dimensional coordinates of activation maxima in the individual experiments. The method itself is then composed of two steps: first, the brain regions consistently activated in a specific dataset (set of experiments, each providing at least one focus of activation) are modeled using Gaussian mixture modeling on the three-dimensional coordinates making up this dataset, and the activation foci are assigned to the identified brain regions. In the second step, frequent co-activations patterns across experiments are identified using association analysis.

The method as well as the implemented software system will be referred to as PaMiNI, which stands for Pattern Mining in NeuroImaging.

Modeling of brain regions underlying a dataset

Let D = {E₁,…,E_n} be a dataset of experiments where every experiment E_i is a set of three-dimensional peak coordinates $E_i=\{C_1^i,\dots ,C_{m_i}^i\}$ with m_i ≥ 1 representing the number of peak coordinates of experiment E_i. The coordinates are triplets $C_j^i=(x_j^i,y_j^i,z_j^i)$ where $x_j^i,y_j^i$ and $z_j^i$ are the coordinate components for the three spatial dimensions in MNI reference space (Evans et al., 1992). If coordinates are given in Talairach space (Talairach and Tournoux, 1988), they are converted to the MNI reference space using the Lancaster transform (Laird et al., 2010; Lancaster et al., 2007). Hence, the set of coordinates in a dataset is given in a discrete metric space.

To reveal convergent activity within the coordinate data of the entire dataset D, common subsets of coordinates based on their spatial location are identified by applying Gaussian mixture modeling on the pooled coordinates $C=\{C_1^1,\dots ,C_{m_1}^1,\dots ,C_1^n,\dots ,C_{m_n}^n\}$ of all experiments in the dataset. That is, considering the coordinates as instances randomly drawn from a mixture of K_opt three-dimensional Gaussian distributions and thus fitting the Gaussians to optimally represent the coordinate data. K_opt indicates the optimal number of Gaussian distributions, which still has to be specified. The probability density function with which a coordinate $C_j^i$ is drawn from the mixture can be formalized as

$$f\left(C_j^i\right)=\sum _{k=1}^{K_{\mathit{\text{opt}}}}{p}_k·𝒩(C_j^i|{\mu }_k,{\sum }_k)$$

where p_k specifies the proportion of distribution k in the mixture of distributions with 0 < p_k < 1 and $\sum _{k=1}^{K_{\mathit{\text{opt}}}}{p}_k=1.𝒩(C_j^i|{\mu }_k,{\sum }_k)$ denotes the value of the Gaussian density function with the three-dimensional mean vector µ_k and the 3 × 3 full covariance-matrix Σ_k at $C_j^i$. Thus, in order to model the K_opt Gaussian distributions to the given coordinates the parameters for the proportion of each of the K_opt Gaussians in the mixture, their mean (location) and co-variance Θ = θ₁, …, θ_Kopt = p₁, …, p_Kopt, μ₁,…,μ_Kopt, Σ₁, … Σ_Kopt have to be estimated, which is done by maximum-likelihood estimation. At this, the log-likelihood function

$$LL(\Theta |C)=\mathrm{l}\mathrm{n}f(C_1^1,\dots ,C_{m_1}^1,\dots ,C_1^n,\dots ,C_{m_n}^n)=\sum _{i=1}^n\sum _{j=1}^m\mathrm{l}\mathrm{n}[\sum _{k=1}^{K_{\mathit{\text{opt}}}}{p}_k·𝒩(C_j^i|{\mu }_k,{\sum }_k\left)\right]$$

is optimized applying the expectation-maximization (EM) algorithm (Dempster et al., 1977). The EM algorithm repeatedly performs alternating steps of expectation, where the log-likelihood function is calculated based on the current estimate for the parameters, and steps of maximization, where the parameters are optimized given the current LL function. The procedure stops, when the optimization of the LL function converges, i.e. when the improvement for the estimation is smaller than a given threshold value. To reduce the risk of detecting local maxima in the LL function, the EM algorithm is replicated several times (in our case 1000 times) for different randomly chosen initializations of parameters, and the estimate yielding the largest log-likelihood value is used.

For the Gaussian mixture modeling the parameter K_opt specifying the number of components of the mixture has to be set. Obviously, however, it is usually not known a priori how many brain regions are underlying a given dataset, i.e. how many Gaussians are needed to represent the entire set of coordinates. Therefore, the optimal number of components should be determined by the method itself. This is done using the Bayesian Information Criterion (BIC), which is a statistical index for the estimation of the dimensionality of a model (Schwarz, 1978). For this, Gaussian mixture modeling is performed for ascending numbers of components between 1 and K_max. Then the model with dimension K_opt ∈ {1,…,K_max} is chosen, where the BIC is minimal, meaning that this model most appropriately fits to the given data. The choice of the parameter K_max influences the time of computation, as high values of K_max lead to more numerous and more complex calculations of Gaussian mixture models. On the other hand, K_max should be chosen large enough to surely contain the optimal dimensionality of the model, K_opt, which in turn strongly depends on the composition of the dataset. While testing the method, values for K_max between 15 and 30 have shown to be sufficient in most applications.

The described procedure yields a mixture with K_opt Gaussian distributions within the space of the reference brain with the estimates of their parameters θ_k for 1 ≤ k ≤ K_opt. These Gaussians can be interpreted as spatial estimates of the brain regions, which were commonly found in the experiments of the underlying dataset D. For each of these, μ_k ∈ θ_k indicates the center of a brain region and the parameter Σ_k ∈ θ_k its spatial spread.

It is important to notice, that a Gaussian mixture model will consider every coordinate of the set, including “noise” activations, i.e. foci that are none consistently (and hence effectively at random) activated in single experiments. However, from a neurophysiological perspective these “noise” activations are not fully at random, but can correspond to false positives or to idiosyncrasies of the experimental design or the examined population in a single experiment. Nevertheless, as these activations usually do not converge in specific brain regions, but are more or less randomly distributed over the brain, they are often “collected” by the mixture modeling in a few components with large spatial spreads. Since these “noise clusters” carry no neurophysiological information on the convergent activity of the set and are thus redundant for the pattern search, they should be eliminated prior to the mapping of coordinates. This is done by setting a threshold for the standard deviation of the Gaussian components in a mixture in order to restrict their sizes. That is, excluding Gaussians for the further analysis, whose standard deviations exceed a specific boundary value. Based on considerations regarding previous anatomical and functional neuroimaging parcellations of brain regions as well as first experiences with the PaMiNI method, threshold values between 20 and 25 mm have proven to yield quite reasonable results in most applications. That is, when using those threshold values in sample analyses, the pattern search usually included all brain regions that were covered by the studies of the investigated datasets, while the size of an included Gaussian did not exceed a range to still consider it as a single “brain region”. Furthermore, these threshold values correspond to approximately three to five times the expected standard deviation of a single activation focus regarding inter-subject and inter-template variability, which is empirically estimated to be $\sigma =\sqrt{\frac{{(7.3mm)}^2}{\sqrt{N_{\mathit{\text{subj}}}}}+{(3.6mm)}^2}$ based on the number of subjects N_subj of an experiment (Eickhoff et al., 2009).

In order to assess the brain regions activated in each individual experiment of the entire group of experiments, i.e. to represent each experiment as a set of the modeled brain regions, the coordinates have to be assigned to the Gaussian distributions of the resulting mixture. For this, every coordinate $C_j^i\in C$ is assigned to the Gaussian with index k* ∈ {1,…,K_opt}, where its posterior probability $P({\theta }_{k^{*}}|C_j^i)$ is maximal. To eliminate outliers, i.e. coordinates that are not located near the center of a Gaussian or that are located between two modeled regions, coordinates that show a maximal posterior probability below a specific threshold (e.g. P ≤ 0.50) are mapped to the value 0. Then, an experiment E_iactivates a modeled brain region with index k* ∈ {1,…,K_opt}, if at least one of its coordinates $C_j^i$ for 1 ≤ j ≤ m_i is mapped to region k* using the posterior probability, i.e. if at least one coordinate shows its maximal posterior probability in Gaussian k* and this probability is larger than the lower threshold. As a consequence of this mapping, each experiment can be regarded as a subset of the K_opt modeled brain regions.

At the end of this step the procedure yields a mixture of Gaussian distributions representing the underlying brain regions of a dataset and a direct mapping of the input coordinates of the individual experiments to those modeled brain regions.

Finding common co-activation patterns

The second step of the PaMiNI workflow aims at identifying frequent co-activation patterns across the experiments based on the set of modeled brain regions as identified above. For this, terms and methods from association analysis, which is primarily known from market-basket analyses in economy (Agrawal et al., 1993), are adapted.

A co-activation pattern, i.e. a (frequent) combination of co-occurrent activations, can be expressed as a subset of the K_opt modeled brain regions. Hence, to find frequent co-activation patterns means to identify the frequent subsets within the set representations of the experiments as combinations of modeled brain regions. For this, we introduce the following definitions: A co-activation pattern is supported by an experiment, if and only if the co-activation pattern is a subset of the components of the experiment, i.e. if all brain regions of the pattern showed activation within the particular experiment. The support of a co-activation pattern is then defined as the number of experiments in the dataset which support this pattern, that is, the number of experiments that feature activation in that set of brain regions. A co-activation pattern is frequent, if its support is equal to or greater than a lower limit value, the minimum support or minsup.

Having set these conventions, the identification of common co-activation patterns can be reduced to a typical problem of association analysis (see Agrawal et al., 1993), where the K_opt Gaussian distributions resemble the “items”, the experiments of the dataset resemble the “transactions” and the frequent co-activation patterns correspond to the “frequent itemsets”. To efficiently identify the frequent co-activation patterns, the Apriori algorithm (Agrawal and Srikant, 1994) is adapted. The Apriori algorithm utilizes a monotonicity property of frequent itemsets: any subset of a frequent itemset is frequent, or the other way around, an itemset can only be frequent, if all of its subsets are frequent. Hence, the Apriori algorithm first identifies the frequent single items (“1-itemsets”). Then, the algorithm inductively calculates the frequent k-itemsets from the frequent (k − 1)-itemsets by merging (k − 1)-itemsets that differ only in two items and testing, if their support in the dataset is larger than or equal to the given minsup (Agrawal and Srikant, 1994). Transferred to the problem of finding frequent co-activation patterns of modeled brain regions, the algorithm first identifies those brain regions that show activation in at least a specific number (minsup) of experiments, i.e. those regions whose frequency within the dataset (support) is larger or equal than the minsup. It then inductively generates the frequent k-patterns from the frequent (k − 1)-patterns for increasing values of k. The algorithm terminates, if at the respective level k no frequent pattern is found in the dataset. At the end of this step the procedure yields all co-activation patterns, which are frequently, i.e. at least as often as the given minsup, found within the dataset. A pseudocode representation of the adopted Apriori algorithm is given in Fig. 2.

Fig. 2.

Pseudocode representation of the adapted Apriori algorithm. Frequent co-activation patterns P are identified based on the Gaussian mixture components GC in a dataset D with a given minimum support minsup.

To visualize the distribution of frequent co-activation patterns, the identified patterns are recorded in a scatter plot, where the number of components, i.e. brain regions, of a pattern (abscissa) is plotted against the support of the respective pattern (ordinate).

In order to identify potentially interesting patterns within the distribution of frequent co-activation patterns, in particular the number of components of a pattern and its closedness are considered. In data-mining, closedness is a measure of the interestingness of patterns, which is defined as the difference between the support of a pattern and the support of its most supported direct super-pattern (Boley et al., 2009). Hence, closedness indicates the number of experiments that activate a specific pattern, but do not show any further activated brain regions. A strong closedness of a specific pattern thus means that adding a component to this pattern dramatically decreases its support, which indicates that this pattern is particularly stable and hence probably interesting.

Integration into a graphical user interface

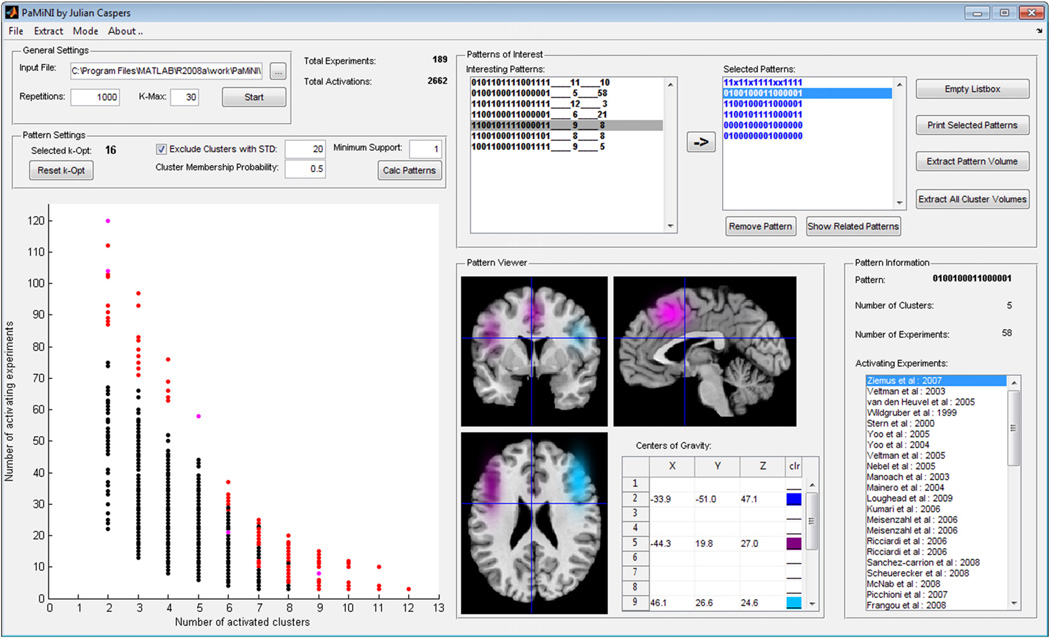
The PaMiNI method was integrated into a MATLAB implementation providing a graphical user interface (Fig. 3). This system facilitates the calculation steps introduced in the former two sections and further provides integrative visualization and analysis tools for the examination of frequent co-activation patterns. The system operates on datasets of neuroimaging experiments, which can be either obtained by extraction from the BrainMap database using the Sleuth software (Fox and Lancaster, 2002; Laird et al., 2005), or provided manually via Microsoft Excel spreadsheets. Input values, such as the number of repetitions or maximal number of components K_max for the Gaussian mixture modeling, as well as the threshold for the posterior probability and the minsup can be set by the user. The optimal number of clusters K_opt can be chosen by the user based on a BIC graph. For the further analysis of the co-activation patterns, the PaMiNI system provides a graph that illustrates the pattern distribution and enables the selection of single patterns. Furthermore, there is a cross-section viewer that facilitates the interactive inspection of specific patterns projected onto the MNI reference brain. In order to support the sharing of analysis data among different users, PaMiNI offers functions for saving and loading analyses and allows the extraction of three-dimensional image files of co-activation patterns in the NIfTI format (Neuroimaging Informatics Technology Initiative, http://nifti.nimh.nih.gov/). The PaMiNI software will be publicly available under http://www.fz-juelich.de/inm/inm-1/DE/Service/Download/download_node.html.

Fig. 3.

Screenshot of the PaMiNI graphical user interface.

Evaluation of the PaMiNI method

For the evaluation of the introduced method, several simulated datasets as well as a set from a real application were analyzed with the PaMiNI system outlined above.

The performance of the PaMiNI method regarding some specific features was studied by means of five simulations, which were generally based on the same dataset. For this, a set of 55 experiments was generated, each of which “reported” at least two activation foci that were randomly drawn from a Gaussian distribution centered in one of four specific brain region. Furthermore, each experiment comprised five activation foci, which were randomly placed within the gray matter to simulate noise, or more specifically foci that do not contribute to converging activation. The centers of the four brain regions were set at the inferior frontal gyrus (MNI: −54, 17, 28), the middle temporal gyrus (MNI: −60, −7, −15), the intraparietal sulcus (MNI: −40, −35, 50) and the middle occipital gyrus (MNI: −43, −83, 1). If not otherwise specified, datasets were analyzed in PaMiNI using 100 repetitions for the Gaussian mixture modeling and a K_max of 12. Gaussians of the resulting mixture were excluded, if their standard deviation was larger than 20 mm. For the mapping of the coordinates a lower threshold for the posterior probability of 0.5 was used and the minsup for the Apriori algorithm was set to 5. Simulation 1 investigated the general ability of PaMiNI to detect the four input regions and hence consisted of a dataset, where all 55 experiments showed activation foci in each of the four regions. In simulation 2 the set of experiments was split into two dichotomous subgroups in order to test PaMiNI's capacity to identify distinctive co-activation patterns. Here, 30 experiments (set A) had foci centered at the inferior frontal gyrus and the middle temporal gyrus, the other 25 experiments (set B) had foci centered at the intraparietal sulcus and the middle occipital gyrus (cf. the introduction). Simulation 3 provided a more complex distribution of co-activation patterns within the simulated set of experiments. For this, the dataset contained 20 experiments showing activation foci at the inferior frontal gyrus and the middle temporal gyrus (2-pattern), 15 experiments with foci at the intraparietal sulcus and the middle occipital gyrus (2-pattern), 10 experiments yielding activations at the inferior frontal gyrus, the middle temporal gyrus and the intraparietal sulcus (3-pattern), 7 experiments having foci at the middle temporal gyrus, the intraparietal sulcus and the middle occipital gyrus (3-pattern) and 3 experiments showing activation within all four brain regions (4-pattern). In order to be able to detect all input patterns including the 4-pattern, the minsup was set to 3 for this analysis. Simulation 4 investigated PaMiNI's ability to detect separate brain regions dependent on the distance between their centers. For this, the centers of the two regions of set B in simulation 2 were brought stepwise closer to the centers of the two regions of set A in three steps. More precisely, the brain region initially centered at the intraparietal sulcus was shifted towards the region in the inferior frontal gyrus on a straight line between the centers of both regions, while the region initially centered at the middle occipital gyrus was shifted towards the middle temporal gyrus, so that the distances between the respective two regions were decreased by a quarter of the initial distances (58 mm between the intraparietal sulcus and the inferior frontal gyrus; 80 mm between middle occipital gyrus and middle temporal gyrus) in each step. In the first of the resulting datasets, the centers of the posterior two regions were placed at MNI: −44, −22, 45 (distance 44 mm) and MNI: −47, −64, −3 (distance 60 mm), in the second dataset at MNI: −47, −9, 39 (distance 29 mm) and MNI: −52, −45, −7 (distance 40 mm) and in the third simulated set at MNI: −50, 4, 34 (distance 15 mm) and MNI: −56, −26, −11 (distance 20 mm). The centers of set A were kept unchanged at MNI: −54, 17, 28 and MNI: −60, −7, −15 in all three datasets. All three datasets were simulated with 30 experiments for set A and 25 experiments for set B. As the analysis of the third dataset (distances 15 mm/20 mm) yielded no separation between the anterior and posterior simulated regions, the analysis was repeated on a dataset with the same centers as in the third set but with an increased number of experiments, i.e. with 300 experiments for set A and 250 experiments for set B. Finally, to investigate how PaMiNI performs if the assumption of foci being normally distributed in a brain region is left, simulation 5 provided a dataset with the same settings as in simulation 2 but with foci randomly drawn from Laplace distributions centered at the respective brain regions instead of Gaussian distributions.

The set of real application data was provided by a recent meta-analysis on the neural correlates of working memory (Rottschy et al., 2012). This dataset comprised 189 fMRI experiments on a diverse range of working memory tasks, which were obtained from the BrainMap database and a PubMed literature search as well as reference tracing of retrieved studies (see Rottschy et al., 2012 for details and list of experiments). For the analysis of the working memory dataset in PaMiNI 1000 repetitions of Gaussian mixture modeling were computed for model dimensions up to a K_max of 30. Again, Gaussians with a standard deviation larger than 20 mm were excluded from the mixture, and coordinates were assigned to the Gaussian clusters using the maximum posterior probability with a lower threshold of 0.5. For the pattern search with the Apriori algorithm a minsup of 10 was chosen.

Results

Simulation datasets

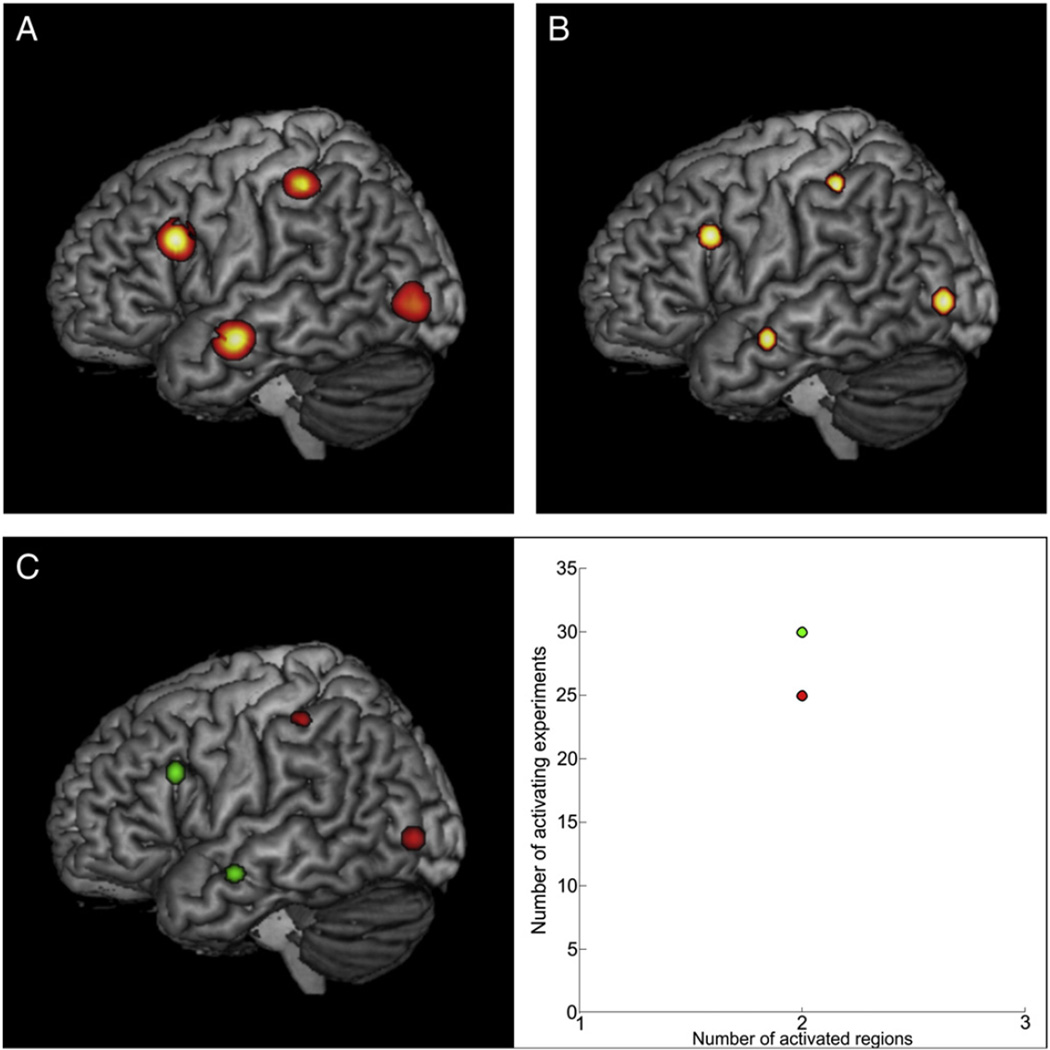
Simulation 1 provided a dataset for the analysis in PaMiNI, where all 55 experiments showed activation in each of the four simulated input regions. After Gaussian mixture modeling, the analysis in PaMiNI yielded a BIC graph with a minimum at five components, indicating that the model with five components most appropriately fitted the given data. Accordingly, this model was chosen for further analysis. Due to the given lower threshold for the Gaussian standard deviation of 20 mm, one of those five Gaussians was excluded from the mixture for the following pattern search. The remaining four Gaussian distributions were located on the right inferior frontal cortex (MNI: −54, 17, 29), the middle temporal gyrus (MNI: −59,−7,−15), the intraparietal sulcus (MNI: −40, −36, 50) and the middle occipital gyrus (MNI: −43, −83, 1) (see Fig. 4B). Hence, the centers of those Gaussians almost perfectly matched the MNI center foci used as input for the simulation data (inferior frontal gyrus: −54, 17, 28, distance: 0, 0, 1; middle temporal gyrus: −60, −7, −15, distance: 1, 0, 0; intraparietal sulcus: −40, −35, 50, distance: 0, 1, 0; middle occipital gyrus: −43, −83, 1, distance: 0, 0, 0). Each input focus of the set was then mapped to the Gaussian component, whose posterior probability given this specific focus was maximal across the four components. If this maximum posterior probability was less than the lower threshold of 0.5, the focus was not assigned to any brain region. Based on this mapping, one co-activation pattern was found by the adapted Apriori algorithm, which included all four components and was found in all 55 input experiments. Thus, the PaMiNI analysis was able to reproduce the ALE map resulting from the analysis of the same dataset (Fig. 4A) and to identify the 4-pattern build by the four input regions in every experiment of the input set.

Fig. 4.

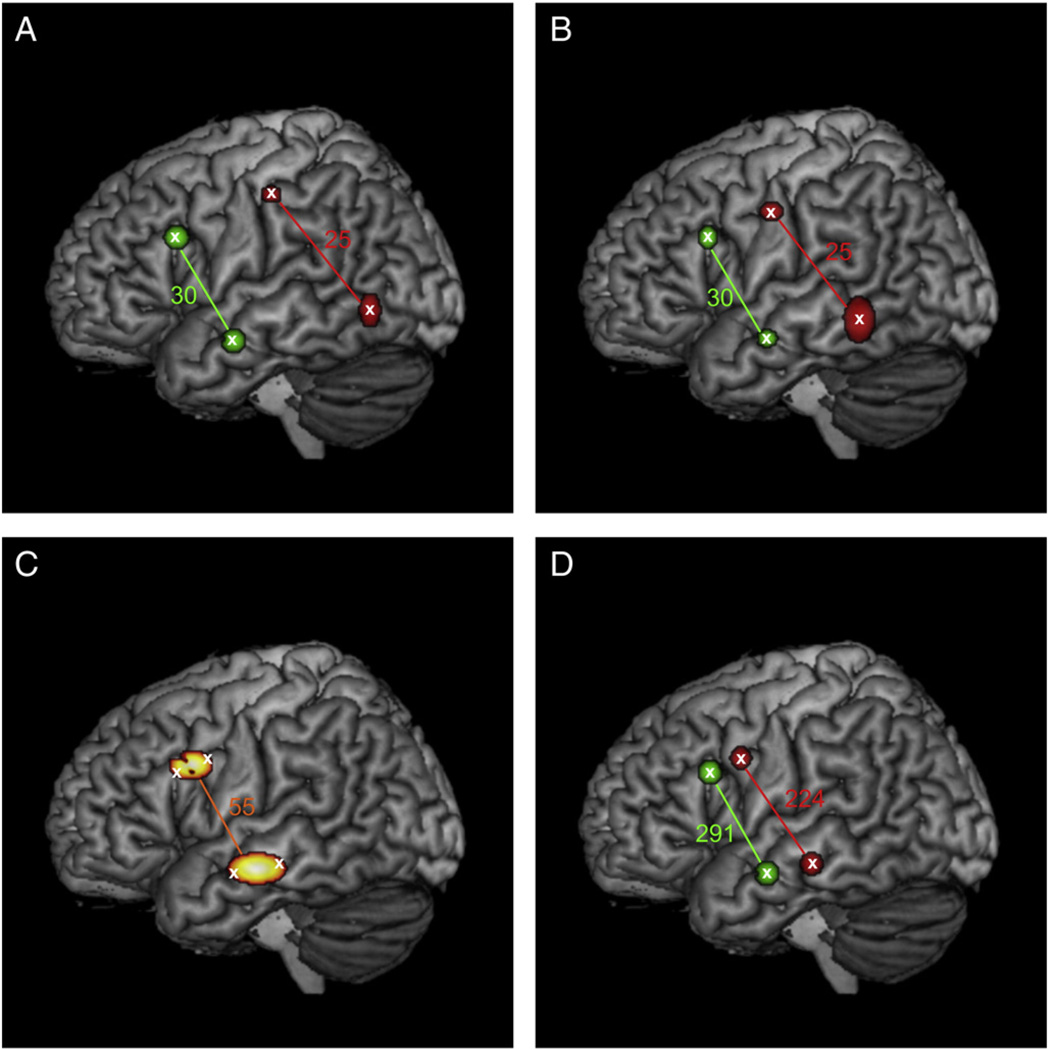
ALE and PaMiNI results of the simulated data. A ALE map of the simulated data projected onto the MNI single subject brain. B Result of the PaMiNI analysis of simulation 1. The Gaussian clusters (restricted to 1 FWHM) of the 4-pattern identified in all 55 experiments are projected onto the MNI single subject brain. C Results of the PaMiNI analysis of simulation 2. Left: Gaussian clusters (restricted to 1 FWHM) of the two identified 2-patterns projected onto the MNI single subject brain. Right: Scatter plot representing the pattern distribution of simulation 2. Patterns are color-coded: Anterior 2-pattern (set A) green, posterior 2-pattern (set B) red.

In Simulation 2 the simulated dataset was divided into two dichotomous groups of experiments, i.e. 30 experiments showing activation in the anterior two regions (set A) and 25 experiments showing activation in the posterior two regions (set B). The Gaussian mixture modeling in PaMiNI again found four Gaussians having a standard deviation larger than 20 mm. Likewise to simulation 1, these four Gaussians matched the centers of the input regions very well (Fig. 4C left). After allocating the foci to the modeled brain regions, the pattern search using the adapted Apriori algorithm yielded two co-activation patterns in the dataset with two involved brain regions each (Fig. 4C right). The first pattern was composed of the inferior frontal and the middle temporal clusters and was supported by 30 experiments. The analysis showed that all 30 experiments derived from set A of the input set. Accordingly, the second co-activation pattern consisted of the intraparietal and the middle occipital clusters and was supported by 25 experiments, which originated from set B without exception. Hence, the PaMiNI analysis yielded an exact separation of the data into the two subsets created for the simulation.

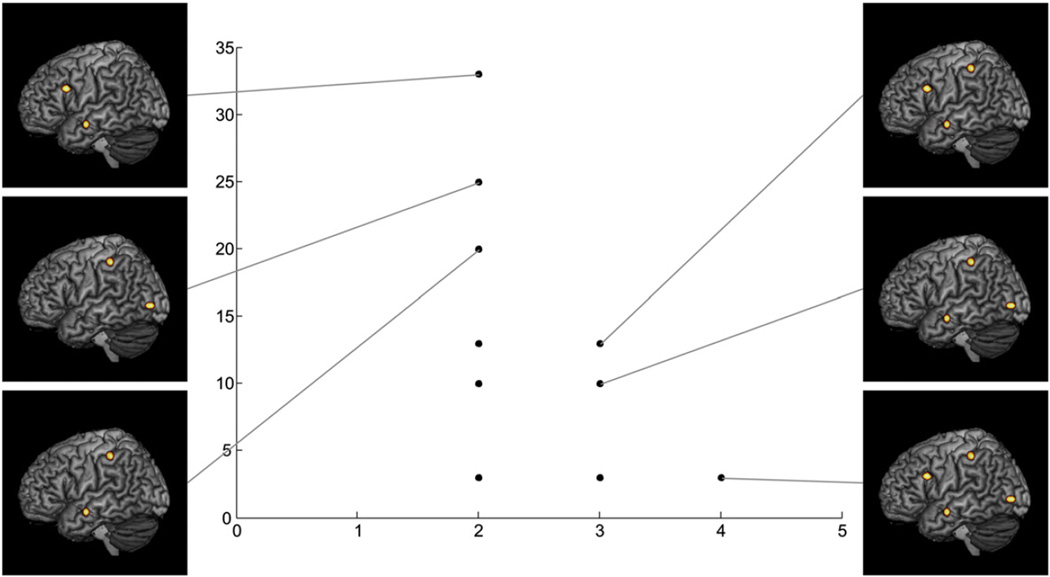
In simulation 3 the input dataset provided a more complex distribution of co-activation patterns but with the same input regions and the same total number of experiments as in simulation 1 and simulation 2. Likewise to these first two simulations, the Gaussian mixture modeling and thresholding of the Gaussian's standard deviation in PaMiNI yielded four Gaussians, which adequately represented the four input regions. The graph resulting from the pattern search in the second step of PaMiNI, which indicates the distribution of the identified co-activation patterns, is shown in Fig. 5. Here, the 4-pattern covering all four brain regions was found in 3 experiments. The 2-patterns and 3-patterns identified by PaMiNI showed a larger support than the number of experiments that were simulated for the respective pattern, when the pattern was a sub-pattern that was fully included in a supported pattern with more components (e.g. the 4-pattern). Hence, the 3-pattern with the inferior frontal gyrus, the middle temporal gyrus and the intraparietal sulcus was found in 13 experiments, i.e. 10 experiments that were simulated for this 3-pattern plus 3 experiments of the 4-pattern. The 3-pattern involving the middle temporal gyrus, the intraparietal sulcus and the middle occipital gyrus was supported by 10 experiments, i.e. 7 experiments that were simulated for this 3-pattern and the 3 experiments of the 4-pattern. When regarding the 2-patterns, the combination of the inferior frontal gyrus and the middle temporal gyrus was found in 33 experiments, i.e. the 20 experiments simulated for this 2-pattern plus the 10 experiments of the first 3-pattern and the 3 experiments of the 4-pattern, which also included these two regions. The combination of the intraparietal sulcus and the middle occipital gyrus was found in 25 experiments (15 experiments simulated for this combination plus 7 experiments of the second 3-pattern plus 3 experiments of the 4-pattern). Hence, the pattern search in PaMiNI perfectly resolved the distribution of co-activation patterns that was taken as the basis for this simulation. The remaining 2-patterns in the pattern-graph correspond to sub-patterns of the two 3-patterns and the 4-pattern where no further experiments were simulated for. Thus, their support corresponds to the sum of the support for the patterns that include these 2-patterns, i.e. the combination of the middle temporal gyrus and the intraparietal sulcus was supported by 20 experiments (both 3-patterns and the 4-pattern), the combination of the inferior frontal gyrus and the intraparietal sulcus by 13 experiments (the first 3-pattern and the 4-pattern) and the two co-activations of the middle temporal gyrus with the middle occipital gyrus and the intraparietal sulcus with the middle occipital gyrus were both supported by 10 experiments (the second 3-pattern and the 4-pattern). Finally, the co-activation of the inferior frontal gyrus and the middle occipital gyrus, as well as the remaining two possible 3-patterns (inferior frontal gyrus, middle temporal gyrus, middle occipital gyrus / inferior frontal gyrus, intraparietal sulcus, middle occipital gyrus) were only included in the 4-pattern and hence supported by 3 experiments.

Fig. 5.

Results of simulation 3. Scatter plot of the pattern distribution identified by PaMiNI is shown. Each scatter represents a single co-activation pattern and the number of supporting experiments (ordinate) is plotted against the number of included brain regions (abscissa). Images along both sides of the plot show the Gaussian representations (restricted to 1 FWHM) of the patterns they are linked to projected onto the MNI single subject brain. Composition of the unlabeled patterns can be deduced from the labeled patterns.

In simulation 4 the centers of the two brain regions of set B from simulation 2 were shifted towards the centers of the two regions of set A by reducing the distance between the anterior and posterior regions in three steps. The results of these analyses are shown in Fig. 6. When the distance between set A and set B was reduced to three quarter (60 mm/44 mm) or half (40 mm/29 mm) of the initial distance between both sets (Fig. 6A and B), PaMiNI was able to identify four separate Gaussians adequately representing the four input regions. In both cases, the co-activation of the anterior two regions were found in all 30 experiments simulated for set A, while each of the 25 experiments simulated for set B could be assigned to the co-activation of the posterior two regions by the pattern search in PaMiNI. When the distance between set A and set B was reduced to a quarter of the initial distance (20 mm/15 mm), only two Gaussian distributions were found by the mixture modeling in PaMiNI, which represented the superior two regions and the inferior two regions by a common Gaussian each (Fig. 6C). The centers of those Gaussians were located in the middle of the center coordinates of the respective two input regions. The pattern search in PaMiNI yielded only one co-activation pattern, which was composed of the two identified Gaussians and which was supported by all 55 input experiments. However, when the number of simulated experiments was increased to 300 for set A and 250 for set B at the same distance stage (quarter of initial distance: 20 mm/15 mm), PaMiNI was again able to separate the four input regions as single Gaussians representations (Fig. 6D). Here, 291 of the 300 input experiments could be correctly assigned to set A and 224 of the 250 experiments simulated for set B were assigned to the co-activation of the posterior two regions.

Fig. 6.

Results of simulation 4. Centers of the two posterior simulated regions (set B, red) are shifted stepwise closer to the two anterior simulated regions (set A, green). Gaussian clusters (restricted to 1 FWHM)of the PaMiNI analysis are projected onto the MNI single subject brain. Colored numbers indicate the number of experiments identified for the respective pattern in PaMiNI. A Distance between centers: 60mm (superior two regions), 44 mm (inferior two regions). Simulated experiments: 30 (set A), 25 (set B). B Distance between centers: 40 mm (superior two regions), 29 mm (inferior two regions). Simulated experiments: 30 (set A), 25 (set B). C Distance between centers: 20 mm (superior two regions), 15 mm (inferior two regions). Simulated experiments: 30 (set A), 25 (set B). The superior two regions were represented by a common Gaussian distribution in PaMiNI and the inferior two regions by another common Gaussian. D Distance between centers: 20 mm (superior two regions), 15 mm (inferior two regions). Simulated experiments: 300 (set A), 250 (set B). All four input regions could be identified by as single Gaussians by PaMiNI.

Simulation 5 investigated the performance of PaMiNI, when activation foci are not assumed to be Gaussian distributed in a brain region. Thus, a dataset was analyzed with the same constellation as in simulation 2, but with activation foci randomly drawn from a Laplace distribution centered in the respective brain regions instead of a Gaussian distribution. The Gaussian mixture modeling identified four Gaussian distributions, which adequately represented the four input regions and were comparable to those identified in simulation 2 (Supplement 1). The pattern search using the adapted Apriori algorithm yielded two co-activation patterns, which comprised the co-activation of the anterior two regions (set A) and the co-activation pattern including the posterior two regions (set B). 29 of the 30 experiments simulated for set A could be assigned to the co-activation of the anterior two regions, while the posterior co-activation pattern was found in 24 of the 25 experiments simulated for set B.

Working memory dataset

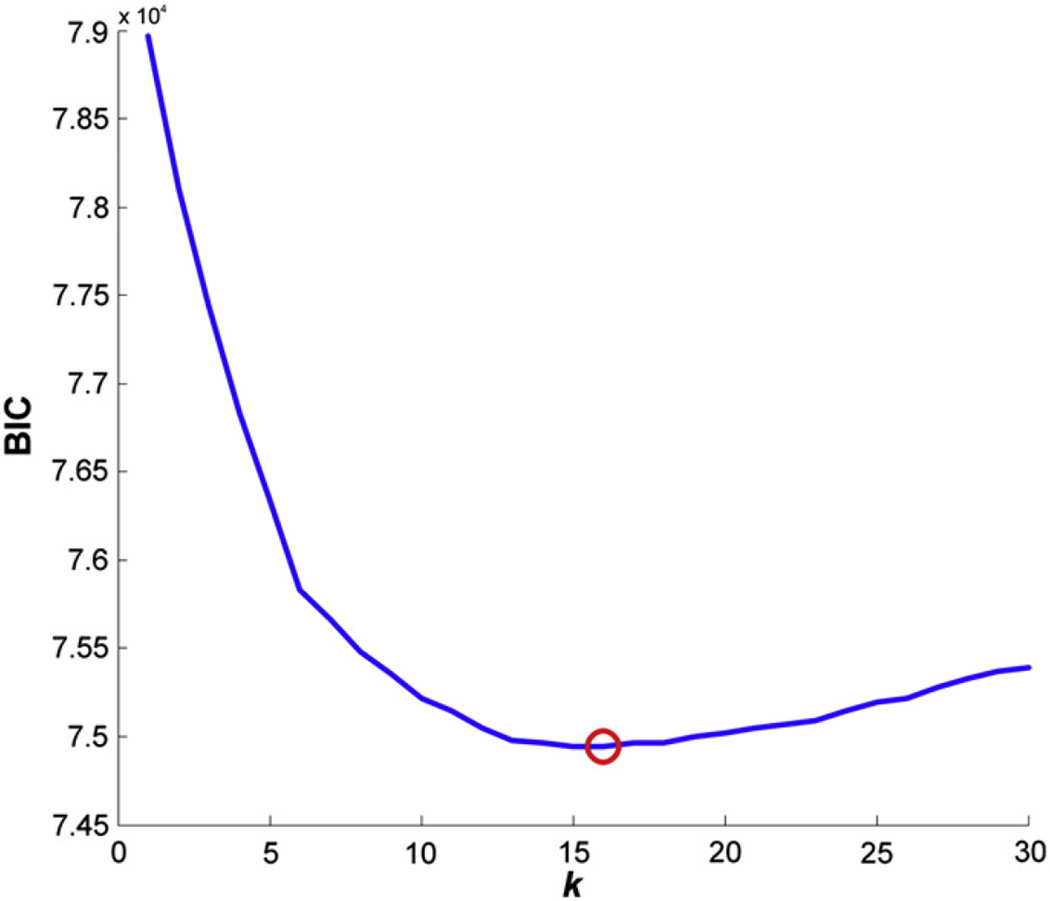
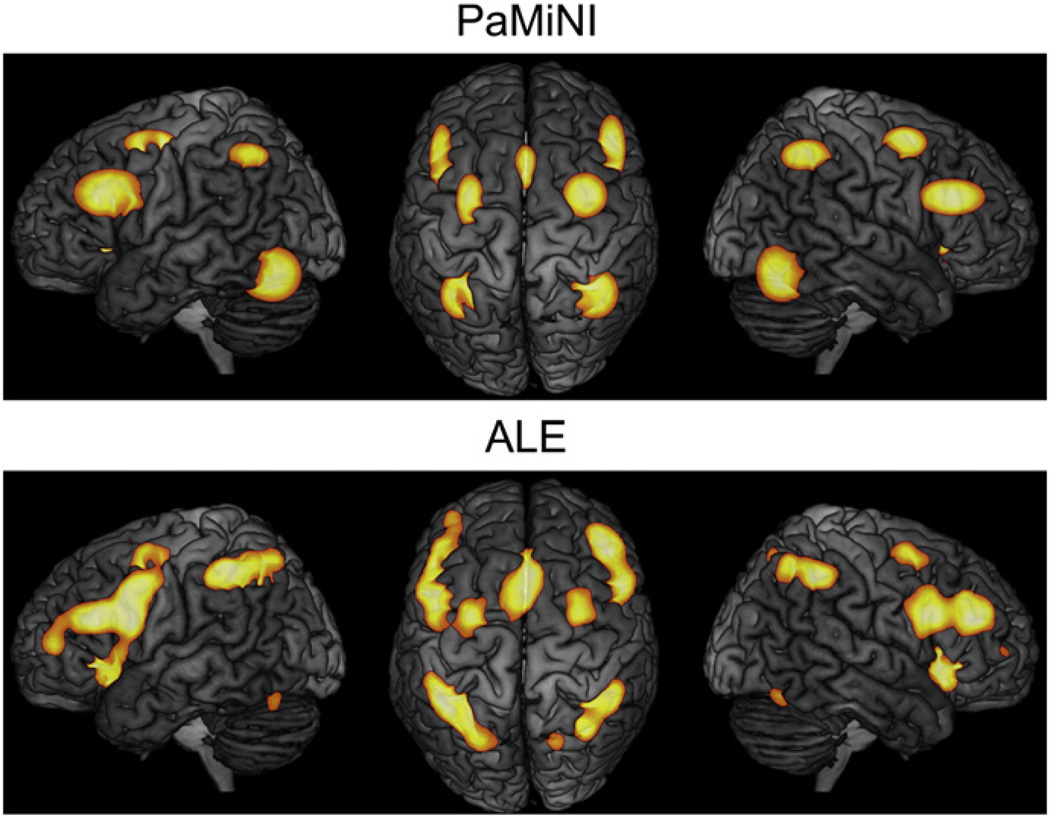
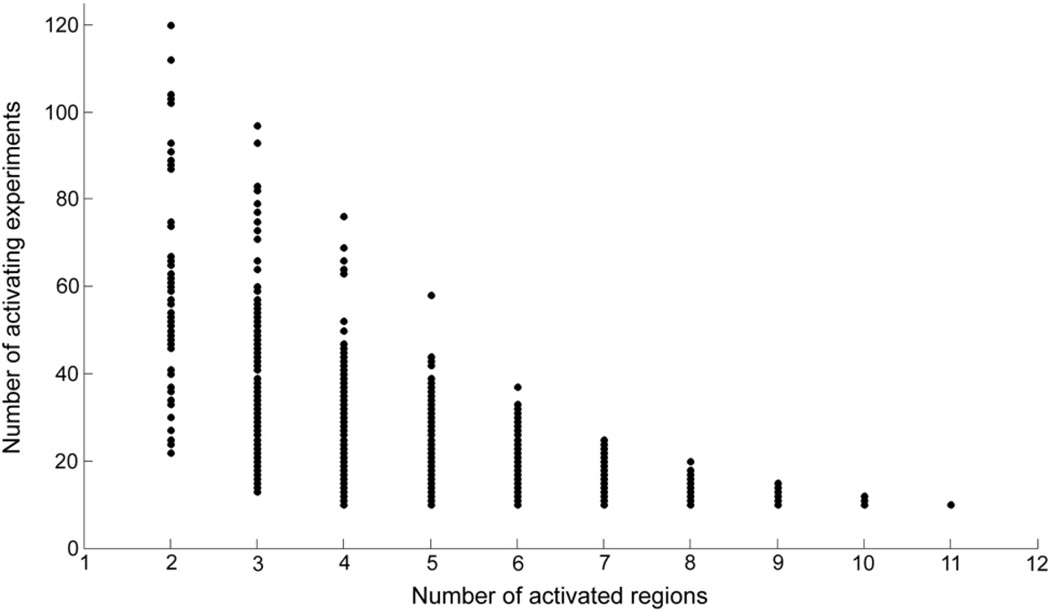
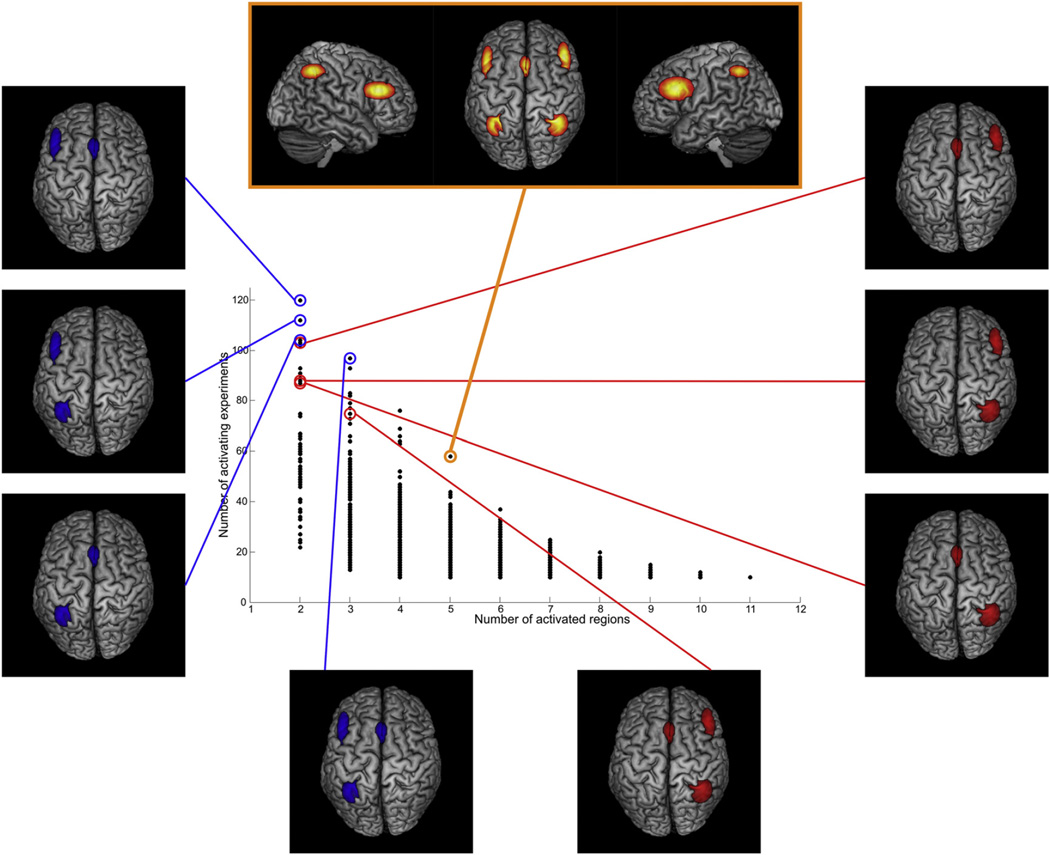
The analysis of the working memory dataset in PaMiNI yielded the BIC graph for the calculated Gaussian mixture models shown in Fig. 7. According to this graph, the model with the lowest BIC had 16 components and was considered the most appropriate model of our data. Four Gaussians had a standard deviation of more than 20 mm and were hence excluded from further analysis. The remaining 12 components were located on the bilateral posterior dorsolateral prefrontal cortex (DLPFC; left MNI: −44, 20, 27; right MNI: 46, 27, 25), the bilateral dorsal premotor cortex (dPMC; left MNI: −29, −1, 54; right MNI: 32, 2, 54), the supplementary/pre-supplementary motor area ((pre-)SMA; MNI: 0, 17, 47), the bilateral anterior insula (aIns; left MNI: −32, 23, −3; right MNI: 36, 24, −4), the bilateral intraparietal sulcus (IPS, left MNI: −34, −51, 47; right MNI: 37, −50, 47), the bilateral ventral occipitotemporal cortex (VOT; left MNI: −37, −65, −16; right MNI: 33, −64, −16) and the left basal ganglia (BG; MNI: −15, −2, 7). These brain regions largely correspond to those regions identified in the main effect of the previous ALE meta-analysis (Rottschy et al., 2012; see Fig. 8). Particularly, the location and extent of the SMA, the dPMC, the IPS and the left basal ganglia matched very well in both approaches. Compared to the respective Gaussian representations in PaMiNI, the DLPFC cluster in the ALE main effect extended more anteriorly and covered parts of the rostral lateral prefrontal cortex, especially on the left hemisphere. However, the position and expanse of the cluster centers of the DLPFC were again quite similar in both approaches. The anterior insula and the ventral occipitotemporal cortex also showed corresponding center locations. However, their expansions differed in both approaches. While the anterior insula showed quite large clusters in the ALE main effect that were partially confluent with the DLPFC clusters, the Gaussian representations of the anterior insula in PaMiNI had more narrow spatial extends. Opposed to this, the VOT was represented by rather small clusters in the ALE main effect, while its respective Gaussian representations in PaMiNI showed a much larger spread. The distribution of co-activation patterns found by the adapted Apriori algorithm is shown in Fig. 9. Here, the most frequent 5-pattern, that is the pattern consisting of 5 brain regions and showing the highest support in the set, was of special interest, as it showed a strong closedness and was considerably more frequently found than any other 5-pattern (58 experiments compared to 44 experiments for the second-most frequent 5-pattern). Furthermore, all most frequent patterns with 6 or more components fully included this 5-pattern but had a much lower support, highlighting its relevance. The 5-pattern consisted of the bilateral DLPFC, the bilateral IPS and the (pre)SMA (see Fig. 10). The previous ALE meta-analysis identified the same set of regions as the “core” network of working memory (Rottschy et al., 2012). This ALE “core” network additionally included the bilateral anterior insula. However, the corresponding pattern in PaMiNI consisting of the bilateral DLPFC, bilateral IPS, SMA and the bilateral anterior insula was found in 24 experiments and was not the most frequent 7-pattern. The two most frequent 7-patterns were the combination of the PaMiNI “core” 5-pattern with the bilateral dPMC and the combination of the “core” 5-pattern with the left dPMC and the left VOT, each found in 25 experiments. The bilateral activation of the anterior insula was found in 49 experiments, which was at an intermediate level within the 2-patterns.

Fig. 7.

BIC graph for the Gaussian mixture models of the working memory dataset. The Bayesian Information Criterion (BIC) of a model is plotted against its number of components. A red circle indicates the model with the lowest BIC, meaning that this model most appropriately fits to the given data.

Fig. 8.

Comparison of the identified brain regions in the working memory dataset between PaMiNI and ALE. Top: Gaussian distributions (restricted to 1 FWHM) representing the identified brain regions from the Gaussian mixture modeling in PaMiNI projected onto three views of the MNI single subject brain. Bottom: Map of the ALE meta-analysis of the same dataset (Rottschy et al., 2012) projected onto three views of the MNI single subject brain.

Fig. 9.

Pattern distribution of the working memory dataset. Each scatter represents a single co-activation pattern. The number of supporting experiments (ordinate) of a pattern is plotted against its number of included brain regions (abscissa).

Fig. 10.

The “core” 5-pattern of working memory and the lateralization of its sub-patterns. The scatter-plot representing the pattern distribution from Fig. 9 is shown. The “core” 5-pattern (top, orange) was identified as the most frequent pattern with five components. The sub-patterns of this “core” 5-pattern from the left hemisphere (left, blue) are noticeably more frequently found within the dataset than the right hemispheric ones (right, red).

When investigating the sub-patterns of the PaMiNI “core” 5-pattern it became obvious that the left hemispheric regions were more often found than the right sided ones (Fig. 10). In particular, the left DLPFC co-active with the (pre-)SMA was found in 120 experiments, which was the most frequent 2-pattern, while the right DLPFC with the (pre-) SMA was only found in 103 experiments. Likewise, the combination of the left IPS and the (pre-)SMA was found in 104 experiments, while the (pre-)SMA together with right IPS was supported by 87 experiments, and left sided DLPFC combined with left sided IPS was revealed in 112 experiments, while the respective right sided pattern was found in 88 experiments. The same ratio between left- and right-hemispheric parts of the “core” 5-pattern was also found for the 3-patterns, as the combination of the left DLPFC, the left IPS and the (pre-)SMA was the most frequent 3-pattern found in 97 experiments, while the respective right-hemispheric 3-pattern was only found in 79 experiments. In a similar manner, the analysis revealed a predominance of the frontal parts of the “core” 5-pattern. The bilateral DLPFC was found in 102 experiments and the combination of the bilateral DLPFC with the (pre-)SMA in 93 experiments. In contrast, the co-activation of the bilateral IPS was only revealed in 89 experiments and the combination of the bilateral IPS and the (pre-)SMA in 75 experiments. Notably, the (pre-)SMA was involved in the majority of the frequent patterns.

Discussion

In the current work, we introduced a novel meta-analytic approach for the identification of frequent co-activation patterns, named PaMiNI. The developed method bases on two established data mining techniques, Gaussian mixture modeling that derives from probabilistic cluster analysis and the Apriori algorithm from association analysis. The method is fully data-driven. It does not draw on any a priori assumptions regarding the specific dataset or a presupposed anatomic segregation of the human brain, but rather only uses the reported activation foci of the neuroimaging experiments.

Gaussian mixture modeling has been successfully used in several classification applications (e.g. Ashburner and Friston, 2005; Greenspan et al., 2006; Huang et al., 2005; Reynolds et al., 2000). In PaMiNI, a mixture of Gaussian distributions is fitted to the three-dimensional coordinates of a dataset, in order to separate spatially distinctive groups of activation foci from each other. The resulting Gaussians represent the spatial distribution of the input coordinates and can be interpreted as probabilistic estimators for the spatial location of the brain regions involved in the experiments of the dataset. For this purpose, Gaussian distributions are adequate representations, since the uncertainty of the spatial location of regions due to inter-subject variability and inter-template variability between experiments can be supposed to be normally distributed (Eickhoff et al., 2009). The results of simulation 5 furthermore show that PaMiNI still yields robust results when the distribution of activation foci in a brain region deviates from a Gaussian. Unlike other clustering techniques, Gaussian mixture modeling allows a non-deterministic a posteriori allocation of a set of activation foci to the brain regions based on probabilistic values.

The Apriori algorithm and association analysis per se originate from market-basket analyses (Agrawal et al., 1993). At that, department store chains or web-stores analyze the buying transactions of their customers to identify sets of frequently bought commodities for marketing purposes. We here adapted the Apriori algorithm in order to efficiently find the frequent co-activation patterns in a set of experiments based on the modeled brain regions. This is done by handling the modeled brain regions as the “items”, the frequent co-activation patterns as the “frequent itemsets” and the neuroimaging experiments analogous to the “transactions” from association analysis. Generally, the search for frequent co-activation patterns could also be solved by brute force, i.e. looking up the frequency of every possible combination of brain regions in the set of experiments. However, the number of possible combinations exponentially increases with the number of underlying brain regions. E.g., for a mixture of 20 brain regions, the number of possible co-activation patterns and hence necessary comparisons would be larger than one million (2²⁰ = 1,048,576). The Apriori algorithm significantly decreases the necessary computations by limiting the examination of the frequency of patterns to those sets, which can be combined from the patterns that have already been proven to be frequent. This makes the PaMiNI approach computationally applicable even for large and complex datasets.

The analyses of the test datasets demonstrate the feasibility of PaMiNI. In the simulated datasets, PaMiNI revealed an adequate representation of the input regions and a perfect segregation of the underlying co-activation patterns even for complex datasets. In contrast, the ALE analysis of the set from simulation 2 indicated all four regions within one map, which makes the distinction between the two underlying patterns impossible. This representational problem is a general issue of recent coordinate-based meta-analyses resulting in uncertainties and possible misinterpretation. The PaMiNI approach addresses this shortcoming by identifying the actual (within-experiment) co-activation patterns and analyzing their frequency across the dataset. Even though the simulated data in simulation 2 is an extreme example based on disjoint subsets in a dataset, the analysis clearly highlights the advantages of PaMiNI for the distinction of co-activation patterns.

The resolution capacity of PaMiNI for the identification of single brain regions was investigated in simulation 4. Here, PaMiNI still yielded a perfect segregation of the four simulated regions when the distance between the region centers was lowered to the half of the initial distance, i.e. 29 mm for the superior two regions. Only after reducing the distance to a quarter of the initial distance, i.e. 20 mm and 15 mm, PaMiNI was not able to find separate representations for the adjacent regions. In this latter case, the distance between the region centers was below 2 FWHM of the distributions used for the simulation of the activation foci. Thus, the 1-FWHM ranges of both adjoining regions already intersected. However, when the number of simulated experiments was increased by the factor 10, i.e. 550 instead of 55 experiments, PaMiNI again yielded a perfect segregation of the four underlying brain regions even for this setting of narrow region centers. This circumstance can be explained by an increase of the local signal-to-noise ratio when more simulated experiments are used. That is, there were more activation foci representing and hence converging in a brain region, while the noise foci were equally (at random) distributed throughout the brain. This observation demonstrates that, naturally, the accuracy for the identification of single brain regions in PaMiNI strongly depends on the number of experiments in the dataset under investigation, i.e. that fewer input foci yield a coarser segregation of brain regions, while an increasing number of activation foci improves the granularity for the detection of regions.

The analysis of the working memory dataset demonstrates the applicability of PaMiNI to real world data. Here, the brain regions found by the Gaussian mixture modeling in PaMiNI broadly correspond to those identified in the previous ALE meta-analysis (Rottschy et al., 2012). However, it should be noted that the ALE maps and the modeled brain regions in PaMiNI (like in Fig. 8) are not directly comparable, since the ALE maps indicate the quantity of convergent activation in a specific voxel, while the Gaussian distributions in PaMiNI are probabilistic spatial estimators for the activation foci of a dataset. Thus, specific constellations of the activations arrangement can cause discrepancies between the maps of both approaches. For example a group of activation foci showing a broad spatial spread around a specific region will be represented by a large Gaussian in PaMiNI, while the resulting convergent activity in ALE can be rather low, dependent on the number of activation foci in this region. The reason for this initially counter-intuitive behavior is as follows: In ALE each activation focus is modeled as a Gaussian with a spread depending on the number of subjects of the experiment. In a case where activation foci lie close together, the overlap of the Gaussians of the modeled activation foci is very high, resulting in a high convergence of activity throughout a wider region. When performing significance testing, most of these voxels will survive thresholding. That is, if many foci are close together, even the more peripheral voxels of this region of convergence may become statistically significant. In turn, if activation foci are more spread out over a brain region, the Gaussians of the modeled activation foci in ALE show low overlap, i.e. convergence of the modeled Gaussians. Convergence is thus lower than the threshold for most of the voxels in the region. Consequently, usually only a rather limited number of voxels in the center of the region are declared significant. These considerations may possibly explain the observed differences between the ALE and PaMiNI representations of the anterior insula and the ventral occipitotemporal cortex in the working memory dataset. Nevertheless, both types of maps indicate the spatial location of convergent activity within the input set, which allows general comparisons between both approaches. In this context, the examination of the working memory dataset can be regarded as a cross-validation for both methods, as it shows that the PaMiNI analysis largely reproduces the results of the ALE meta-analysis.

In addition to it, PaMiNI revealed several further aspects regarding co-activation patterns in the working memory dataset. The most frequent 5-pattern in PaMiNI, consisting of the bilateral dorsolateral prefrontal cortex, the bilateral intraparietal sulcus and the supplementary motor area, was shown to play a central role in this dataset. This 5-pattern directly matches the major parts of the “core-network” from the previous ALE analysis. There, the “core-network” was identified by subdividing the experiments of the set into topical groups and calculating a conjunction on the ALE maps of each group (Rottschy et al., 2012). The PaMiNI “core” 5-pattern is furthermore well in line with other meta-analyses on working memory (Owen et al., 2005; Wager and Smith, 2003). The salience of this 5-pattern for working memory might be explained by an integrative function of this network for fronto-parietal synchronization, which is essential for working memory tasks (Naghavi and Nyberg, 2005; Salazar et al., 2012; Wendelken et al., 2008). Albeit particularly relevant, this network is not specific for working memory, as it is also involved in other cognitive processes like attention (Langner and Eickhoff, 2013; Shulman et al., 2009) or motor tasks requiring orientation and movement integration (Marangon et al., 2011). Thus, this “core” network might act as a more general fronto-parietal integrator in different attention-demanding cognitive functions (Curtis and Lee, 2010).

Compared to the “core” network of the ALE meta-analysis (Rottschy et al., 2012), the PaMiNI “core” pattern did not include the bilateral anterior insula. Indeed, the respective 7-pattern, consisting of the “core” 5-pattern and the bilateral anterior insula, was significantly less often found within the dataset. This discrepancy might be explained by the circumstance that the anterior insula is particularly involved in saliency detection (Cauda et al., 2012; Menon and Uddin, 2010) and the implementation of task sets in general (Dosenbach et al., 2006; Kurth et al., 2010). Thus, the anterior insula might be activated in only some of the used tasks in its function for task set initiation and maintenance and with a less marked relation to the regions of the working memory “core” network.

The pattern analysis in PaMiNI revealed another aspect of the working memory “core” network, which is hemispheric lateralization. The pattern distribution indicated that all sub-sets of the “core” 5-pattern are considerably more often found on the left side, compared to the corresponding patterns of the right hemisphere. This might partially be explained by the obvious hemispheric asymmetry between verbal working memory, which is lateralized to the left hemisphere, and spatial working memory, which shows stronger activity on the right side (Nagel et al., 2013; Smith and Jonides, 1997; Thomason et al., 2009). The asymmetry in the PaMiNI analysis favoring the left hemisphere is probably indicative for an overrepresentation of verbal working memory tasks in the composition of experiments in the set. Indeed, 54 of the 97 experiments activating the 3-pattern consisting of the left DLPFC, the left IPS and the SMA had words or letters as stimuli, while only 38 of 75 experiments activating the respective right hemispheric 3-pattern used these verbal stimuli. The lateralization towards the left hemisphere in the working memory dataset could already be conjectured from the main effect of the ALE meta-analysis, as the convergent activity of the frontal regions is stronger on the left than on the right side. This notion is now quantitatively confirmed by the distribution of co-activation patterns in the PaMiNI analysis.

Another important finding of the PaMiNI analysis is that the (pre-) SMA is part of nearly all highly supported patterns in the working memory set. The (pre-)SMA is known to play a major role in cognitive control (Hoffstaedter et al., 2013; Lau et al., 2006; Mostofsky and Simmonds, 2008; Obeso et al., 2013). That is, the (pre-)SMA is accounted to be responsible for the initiation, switching and termination of tasks, which usually involves an alignment with working memory. In this context, the DLPFC is attributed a proactive function for the action inhibition of the (pre-)SMA in situations with high working memory load (Criaud and Boulinguez, 2013; Jahfari et al., 2010; Mostofsky et al., 2003). The PaMiNI analysis indeed showed that the co-activation pattern consisting of the (pre-)SMA and the bilateral DLPFC was the second most supported 3-pattern within the set, which highlights its role for working memory tasks.

The examination of the sample datasets shows that PaMiNI produces meaningful segregations of brain regions, which are comparable to the results yielded by a well-established previous approach, i.e. ALE. Beside this compatibility between both approaches, it was furthermore demonstrated that PaMiNI yields additional insight compared to previous approaches regarding the examination of co-activation patterns, as it separates the sets of co-occurrent activity and reveals their frequency in a set of neuroimaging experiments. Hence, PaMiNI complements the scope of present meta-analyses by using a yet different and novel approach. The integration of the PaMiNI method into a publicly available software system makes the analysis of datasets easily accessible and allows the efficient application to a wide range of examinations. The coordinate-based pattern mining with PaMiNI can now be used for any possible arrangement from the rich amount of neuroimaging data unraveling their underlying co-activation patterns and helping to answer yet unresolved questions concerning the functional organization of the human brain.

Conclusions

We here demonstrated a novel meta-analytic approach that extends the capabilities of previous coordinate-based meta-analytic techniques, i.e. ALE or MKDA, regarding the identification of co-activation patterns. This new method, named PaMiNI, combines two established pattern mining techniques, i.e. Gaussian mixture modeling and the Apriori algorithm from association analysis, in order to reveal the distribution of frequent co-activation patterns within sets of neuroimaging experiments represented by their coordinate data of peak activations. The applicability of the PaMiNI approach was evaluated using simulated datasets as well as a dataset on working memory findings. These evaluation analyses demonstrated the ability of PaMiNI to detect convergent activation foci within a dataset and to distinguish distinct co-activation patterns between experiments, as well as its feasibility for real applications. Furthermore, the analysis of the working memory data yielded a fronto-parietal “core” network of working memory similar to that of the ALE analysis but with additional insight regarding the distribution of sub-networks, i.e. a left-lateralization and a dominant role of the (pre-)SMA. By the integration into a publicly available software system PaMiNI can now be applied to any possible set of neuroimaging experiments to facilitate the validation of functional organization principles of the human brain and the generation of new hypotheses for future research.