Stock enhancement or sea ranching? Insights from monitoring the genetic diversity, relatedness and effective population size in a seeded great scallop population (Pecten maximus)

Abstract

The mass release of hatchery-propagated stocks raises numerous questions concerning its efficiency in terms of local recruitment and effect on the genetic diversity of wild populations. A seeding program, consisting of mass release of hatchery-produced juveniles in the local naturally occurring population of great scallops (Pecten maximus L.), was initiated in the early 1980s in the Bay of Brest (France). The present study aims at evaluating whether this seeding program leads to actual population enhancement, with detectable effects on genetic diversity and effective population size, or consists of sea ranching with limited genetic consequences on the wild stock. To address this question, microsatellite-based genetic monitoring of three hatchery-born and naturally recruited populations was conducted over a 5-year period. Results showed a limited reduction in allelic richness but a strong alteration of allelic frequencies in hatchery populations, while genetic diversity appeared very stable over time in the wild populations. A temporal increase in relatedness was observed in both cultured stock and wild populations. Effective population size (Ne) estimates were low and variable in the wild population. Moreover, the application of the Ryman-Laikre model suggested a high contribution of hatchery-born scallops to the reproductive output of the wild population. Overall, the data suggest that the main objective of the seeding program, which is stock enhancement, is fulfilled. Moreover, gene flow from surrounding populations and/or the reproductive input of undetected sub-populations within the bay may buffer the Ryman-Laikre effect and ensure the retention of the local genetic variability.

Introduction

The mass release of juvenile hatchery-produced individuals, of commercial species, into the wild commonly has one or more of three main purposes: restocking, stock enhancement or ranching. The practice has been applied to aquatic, as well as, terrestrial species and is commonly used to address the depletion of exploited marine species (Bell et al., 2008). The primary objective of restocking programs is to re-establish locally extinct or nearly extinct species using nonlocal or captive broodstock. On the other hand, when wild populations of marine species are declining but not extinct, owing to overfishing or degradation of environmental conditions, the mass release of cultivated individuals aims at increasing population size (sea ranching) and/or improving wild recruitment (stock enhancement).

Restocking and stock enhancement programs raise numerous questions related to their efficiency in terms of local recruitment and their eventual impact on the genetic diversity of the resulting population. First, the fitness of cultured versus wild individuals might differ because of unintentional domestication (Araki and Schmid, 2010) or poor adaptation to local environmental conditions (for example, Waal et al., 2013). Second, the effective population size (Ne) of cultured stocks is commonly much lower than wild stocks, potentially leading to a depletion of the local genetic variability due to strong genetic drift. This is particularly the case in marine bivalves, where very high fecundities associated with high variance in reproductive success lead to small Ne in cultured populations (Boudry et al., 2002; Appleyard and Ward, 2006; Lallias et al., 2010b). As a consequence, enhancing wild populations with hatchery-born individuals can induce a reduction of their effective population size. This phenomenon is known as the Ryman-Laikre effect, which corresponds to the consequence of mixing populations with different effective population sizes (Ryman and Laikre, 1991; Ryman et al., 1995). This effect has been documented in a wide range of species (Utter and Epifanio, 2002) but has appeared to be minimal in bivalve mollusks in light of their population biology (Gaffney, 2006). The risk of significantly reducing the effective population size of an enhanced population due to a Ryman-Laikre effect strongly increases as the ratio between the number of seeded individuals and the census size of the recipient population increases, and depends on the respective effective population sizes (Gaffney, 2006). A similar effect of highly variable reproductive success, called the Hedgecock effect or sweepstake reproductive success, has been documented in natural populations of bivalves in some locations (Hedgecock and Pudovkin, 2011).

Stock enhancement can also lead to a significant increase in relatedness among individuals and, ultimately, inbreeding depression. Although negative effects of inbreeding have been documented in shellfish for a variety of fitness-related traits, under experimental or aquaculture conditions (for example, Saavedra and Guerra 1996, Bierne et al., 1998), no comprehensive evaluation of the fitness of released mollusks in the wild have been performed so far. Overall, Araki and Schmid (2010) found ample evidence of negative impacts of hatchery-rearing on the fitness (evaluated as reproductive success of released animals) and diversity of cultured individuals. The vast majority of studies revealing a significantly lower reproductive success of hatchery-reared individuals have been conducted on fish (mainly salmonids and flatfishes, see Araki and Schmid (2010) for details), whereas similar studies on cultivated marine invertebrates, such as mollusks, are still scarce. In any case, it is recommended that a population enhancement program takes into account the maintenance of genetic diversity, specifically, by using the largest possible broodstock, renewing it regularly, releasing families in equal quantity, and performing genetic monitoring of the recipient populations (Bell et al., 2008). Examples of beneficial seeding programs in marine population are rare in the literature (but see Gonzales et al. (2008) for an example of apparent demographic recovery of the fishery of the black sea bream in Hiroshima Bay (Japan)).

The great scallop Pecten maximus is a benthic marine bivalve of high economical value. It is mainly harvested in the United Kingdom and France. Total landings amounted to 65 632T in 2013 (FAO, 2015). The main harvest method consists of dredging on natural beds with sea ranching supplementation implemented in specific locations to complement the natural production. This is particularly the case in the Bay of Brest (Beaumont and Gjedrem, 2006), where a seeding program was initiated in the early 1980s following the dramatic collapse of the local stock precipitated by a particularly cold winter in 1962–1963 (Dao et al., 1999). To that aim, a commercial hatchery was implemented in Le Tinduff harbor (Plougastel, France) in 1983.

The Tinduff hatchery produces between 5 and 10 million spat per year (F Breton, personal communication). The vast majority is seeded on wild beds in the Bay of Brest. The broodstock is renewed each year by sampling new genitors locally. Fifty to 140 genitors are used each year (F Breton, personal communication). Juveniles are then seeded on wild scallop beds of the recipient populations and harvested by dredge when they reach commercial size (10–10.5 cm in length). Hold et al. (2012) simulated the impact of seeding a Tinduff-produced cohort in populations of the Isle of Man to assess their potential genetic impact using the Ryman-Laikre approach. They found that under certain conditions, only a limited impact was to be expected. Morvezen et al. (2016) found no significant difference in terms of genetic variability between the heavily seeded population of the Bay of Brest and neighboring unseeded or low-seeded wild populations. However, a precise estimation of the genetic impact, assessing a possible Ryman-Laikre effect on the effective population size of seeded populations, remained to be conducted.

In this theoretical and empirical framework, the present study aims to evaluate whether the seeded individuals, in the Bay of Brest, contribute to the total reproductive output of the stock as was expected in the population enhancement program. Such a contribution should be detectable by the genetic impact on the genetic diversity and effective population size of the recipient wild population. If no genetic impact is found, the seeding could be classified as a sea ranching program with limited effect on the longer term demography of the scallop population in the Bay of Brest.

Materials and methods

Sample collection

Three different year-classes, born in 2007, 2009 and 2012, were sampled at age 2+ (estimated by counting annual winter ring on the shell, (Mason, 1957)) in the Bay of Brest, by dredging on wild seeded beds. For each year-class, hatchery-born scallops and wild-born scallops were differentiated by the double-ring method: hatchery-born scallops display a stress ring caused by the seeding procedure in addition to the winter ring in their first year (Fleury et al., 2005; Alban and Boncoeur, 2008). Each individual valve was checked by two to three independent readers for a robust assessment of the presence or absence of the double ring. Samples sizes are given in Table 1. For all individuals, a fragment of adductor muscle or mantle was collected and preserved in 70–95% ethanol for further DNA analyses.

Table 1. Genetic diversity, effective population size and family structure for each sampled cohort.

	W07	H07	W09	H09	W12	H12
N	96	55	40	100	69	76
Ar±s.e.	9.08±1.44	8.46±1.47	9.29±1.45	8.48±1.25	8.97±1.44	7.42±1.03
He±s.e.	0.69±0.08	0.70±0.07	0.68±0.08	0.69±0.08	0.70±0.07	0.70±0.06
Ne (single sample)
LD	932 (313.6–∞)	39.4 (32–49.9)	∞	28.7 (25–32.8)	∞ (255.7–∞)	27.6 (23.0–33.5)
Het_ex	∞	∞	∞	∞	∞	∞
Sibship	95 (75–130)	35 (22–59)	62 (41–99)	50 (33–80)	95 (68–137)	30 (19–51)
Coancestry	29.9 (10.4–59.5)	10.9 (3.8–21.8)	20.9 (6.3–44.2)	14.9 (4.8–30.4)	105.8 (0–531.2)	11.5 (6.1–18.7)
Ne (temporal)
Pollack	−127.2	NA	71.0	NA	161.7	NA
Nei and Tajima	−131.5	NA	66.2	NA	156.2	NA
Jorde and Ryman	−155.4	NA	38.1	NA	155.7	NA
Harmonic mean (unweighted)	302.47	27.45	58.62	32.80	179.55	25.56

W, wild samples (without double ring). H, hatchery samples (with double ring). Years of birth are given for each sample after their origin. Ar, Allelic richness; He, gene diversity; LD, estimation of Ne with the single sample method of linkage disequilibrium method (Waples and Do, 2008); Het_ex, heterozygote excess method (Zhdanova and Pudovkin, 2008); Sibship, parentage method (Wang, 2009); Coancestry, coancestry method (Nomura, 2008); Pollack, Estimation of Ne with the temporal method of Pollack (1983), then transformed in yearly Nb with Waples et al. (2007) method; Nei and Tajima, idem with Nei and Tajima (1981) method; Jorde and Ryman, idem with Jorde and Ryman (2007) method; Harmonic mean (unweighted), Harmonic mean of Ne estimators.

DNA extraction and microsatellite genotyping

DNA extraction was performed using the QIAamp DNA Mini Kit (Qiagen, Hilden, Germany), according to the manufacturer's instructions. DNA concentrations were estimated using a Nanodrop (Thermo Fisher Scientific Inc., Waltham, MA, USA) and diluted to 10 ng DNA per milliliter. Genetic variation at 12 microsatellite loci was assayed using three multiplex PCR amplifications (mx1, m2, mx4), as described in Morvezen et al. (2013, 2016).

Statistical analysis

Allelic richness (A_r) and gene diversity (H_e) were assessed for each locus and each population (that is, year-classes populations of each origin) using FSTAT v2.93 (Goudet, 2001), accounting for sample size differences by the rarefaction method implemented in the software. Null allele frequencies were estimated using the Van Oosterhout algorithm implemented in MICROCHECKER v2.2 (Van Oosterhout et al., 2004). Significant differences between samples were tested using a Friedman Chi-squared test for non-independent data, followed by pairwise paired Wilcoxon tests with false discovery rate correction for multiple testing (Benjamini and Hochberg, 1995) in R (R Core Team, 2013).

Pairwise F_ST values (Weir and Cockerham, 1984) were calculated with GENETIX v4.05 (Belkhir et al., 2001), and heterogeneity in allelic frequencies between pairs of samples was tested with GENEPOP v4.2 (G-test; 1000 dememorisations, 100 batches and 10 000 iterations per batch; Rousset, 2008). The presence of outlier loci was checked using LOSITAN (50 000 simulations, infinite mutation model, 95% confidence intervals; Antao et al., 2008).

Relatedness was calculated with COANCESTRY v1.0 (Wang, 2011), using the triadic likelihood method described by Wang (2007). This estimator was chosen because it is least biased when data contain many unrelated individuals (Wang, 2007), as expected in wild populations of marine mollusks. Significance of mean differences in relatedness between samples was assessed by 10 000 permutations in COANCESTRY.

Effective population size (Ne) was estimated according to seven different methods. NEESTIMATOR v2.01 (Do et al., 2014) was used to apply the heterozygosity method (Zhdanova and Pudovkin, 2008), the linkage disequilibrium method (Waples and Do, 2008), the coancestry method (Nomura, 2008), as well as three temporal methods (Nei and Tajima, 1981; Pollack, 1983, Jorde and Ryman, 2007). The sibship method (Wang, 2009) was calculated using COLONY (Jones and Wang, 2010). Temporal methods were calculated on the three possible time frames (that is, 2007–2012, 2007–2009, 2009–2012) and then decomposed into estimates of yearly effective number of breeders (Nb) using the method implemented in SALMONNB v1.1 (Waples et al, 2007). This method has been developed for the Pacific salmon, a semelparous species, but could be applicable in our case (Waples, personal communication, and see discussion for expanded explanation). All details concerning the options used for Ne calculations are presented in Supplementary Material.

All Ne estimates were combined using an unweighted harmonic mean, as suggested by Waples and Do (2010). Variance-weighted harmonic mean would have been preferable (Waples and Do, 2010), but variance estimates could not be obtained for all estimators, as some were equal to infinity. Negative estimates of Ne were also included in the harmonic mean. Negative values of Ne are most probably caused by sampling noise being greater than the signal, which is likely to happen with moderate to high Ne (Waples and Do, 2010). Therefore, not including those estimates would bias the mean (see Results).

Finally, the relative reproductive success (x) of hatchery-born scallops was estimated using the Ryman-Laikre equation (See below, Ryman and Laikre, 1991) for three possible time frames (i) combining 2007 wild and hatchery samples to produce 2009 wild samples, (ii) combining 2009 wild and hatchery samples to produce 2012 wild samples, and (iii) on overall data (2007–2012), using combined Ne estimates. Estimates of the relative reproductive success were used to predict Ne resulting from crossings between 2012 wild and hatchery populations.

Ryman-Laikre (1991) equation–N_C: Effective population size of the cultivated population.

N_W: effective population size of the recipient, wild population. N_E: Effective population size of the resulting offspring from the mixing of the two populations. x: relative reproductive contribution of the cultivated population.

Results

Genotype scoring and null alleles

One locus (PmRM007) was excluded from further analysis because of inconsistencies in allele scoring. Null alleles were detected at 3 (PmRM027, PmRM012, PmRM043) out of the 11 remaining loci, which is consistent with previous studies using the same markers (Morvezen et al., 2013, 2016). Most analyses (except the most computationally intensive, COANCESTRY and COLONY) were performed with and without those loci and provided similar results. Further results are thus given for all 11 loci.

Genetic diversity

Wild-born samples displayed the highest allelic richness values (Ar=8.97–9.29), whereas hatchery samples showed a lower Ar, which was approximately 0.5–1.5 lower (Table 1). Allelic richness differed significantly among samples (Friedman Chi-squared=14.32; df=5; P=0.013). However, no significant difference was detected in pairwise comparisons after Benjamini and Hochberg (1995) false discovery rate correction for multiple testing (paired Mann–Whitney test, P>0.05 for all comparisons). Observed heterozygosity appeared relatively similar among all samples (Ho~0.70), without any significant difference (Friedman Chi-squared=1.45, df=5, P=0.917). No significant differentiation was detected among wild populations (F_ST non-significantly different from zero; no significant heterogeneity in allelic frequencies (G-test, P>0.05), Table 2). All pairwise F_ST involving a hatchery cohort were significantly greater than zero (0.0049<F_ST<0.0265), except for the pair H07-N09 (F_ST=0.0045, P=0.087). The highest F_ST values were found among hatchery populations. All pairwise G-tests involving a hatchery sample were significant, indicating a strong heterogeneity in allelic frequencies (Table 2). No outlier loci was detected by LOSITAN (P>0.05 for all loci)

Table 2. F _ST (below diagonal) and G-test P-value (above diagonal) for all pairs of populations.

	W07	H07	W09	H09	W12	H12
W07	—	***	NS	***	NS	***
H07	0.0054**	—	***	***	***	***
W09	0.0013	0.0045	—	***	NS	***
H09	0.0077**	0.0107***	0.0068*	—	***	***
W12	—0.0006	0.0049*	0.0048	0.0064**	—	***
H12	0.0198***	0.0261***	0.0212***	0.0265***	0.0161***	—

Significance of F_ST are calculated by 10 000 permutations. Significance after Benjamini and Hochberg correction for multiple testing is given in bold: NS, non-significant, *P<0.05; **P<0.01, ***P<0.001. W, wild sample (without double ring); H, hatchery samples (with double rings). Year of birth is given for each sample after the origin.

Relatedness

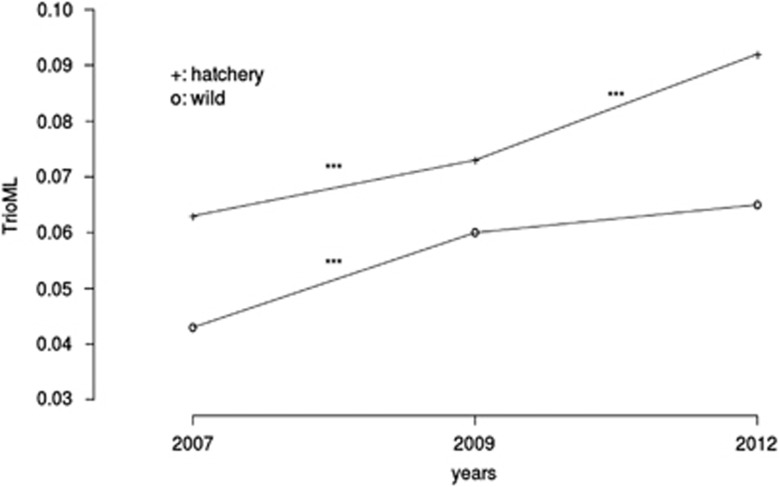
Relatedness was globally higher within hatchery populations (Figure 1). A small but notable trend in the increase of relatedness with time was observed in wild and hatchery populations. This temporal increase in relatedness was significant (10 000 permutations, P<0.001), except between 2009 and 2012 for the wild populations.

Figure 1.

Temporal evolution of relatedness in wild and hatchery populations. TrioML: relatedness estimator calculated by COANCESTRY (Wang, 2011), using Wang (2007) method. Significant values between time points are shown (***P<0.001).

Effective population sizes and reproductive contribution of the hatchery seed

Effective population size estimates varied largely among methods (Table 1). However, Ne estimates were systematically higher in wild populations than in hatchery populations in a given year, for all Ne estimates and for the combined estimates (varying between 58.62 and 302.47 for wild populations and between 25.56 and 32.80 for hatchery populations). The combined estimate without the negative values for the wild population of 2007 was 88.8 (302.47 when included), indicating that removing negative values did bias the mean toward a underestimation of Ne (see Waples and Do, 2010 for an extensive discussion about the biological meaning of negative Ne estimates). For the rest of the analysis, only the combined estimate including negative values was considered.

A high variability in Ne was observed among years in wild populations, with a particularly low Ne found in 2009 across all methods (mean Ne=58.62). The relative reproductive contribution of the 2007 hatchery cohort was estimated to be x=0.67 in the 2009 wild cohort, meaning an estimated reproductive output of 67% for hatchery-born scallops for this year. However, it was not possible to estimate x for the 2009 hatchery cohort in the 2012 wild cohort because Ne increased in 2012 compared with 2009, which is not mathematically possible if we assume that 2009 wild and hatchery samples are the breeding populations producing 2012 wild sample (see discussion). Over all data (2007–2012), x was estimated at a value of 0.34.

Discussion

Genetic diversity

Although hatchery populations displayed a lower allelic richness than wild-born ones, the difference was weak and not strongly supported statistically. This suggests that the genetic diversity of hatchery seed was not reduced much compared with the recipient wild population, contrary to what is often observed in hatchery production of bivalves (Taris et al., 2007; Lind et al., 2009; Lallias et al., 2010a). This might result from the care taken by the Tinduff hatchery in their crossing procedure (F Breton, personal communication): the great scallop being a simultaneous hermaphrodite, most individuals are commonly used both as male and female and batches of mixed spermatozoa from five to six individuals are used to individually fertilize ovocytes from each female. This likely maximizes parental contributions in he resulting progenies. However, F_ST and G-test results indicated a high genetic differentiation between wild and hatchery populations, as previously reported in other mollusks such as, the European flat oyster (Lallias et al., 2010a) and abalone (Hara and Sekino, 2007). This differentiation reflects a strong alteration of allelic frequencies in the hatchery that is most likely due to genetic drift resulting from the limited size of the broodstock (commonly 30–60 individuals), combined with high variance in reproductive success (Boudry et al., 2002; Morvezen et al., 2013).

Even if limited, the reduction in allelic diversity and alteration of allelic frequencies could potentially accumulate over generations, gradually eroding the genetic variability of the great scallop population in the Bay of Brest. However, no trend was observed over time in sampled wild populations (that is, stability in allelic richness, no significant F_ST or G-Test among wild samples), as would be expected if significant genetic erosion was occurring. This result must be interpreted cautiously and the study should be extended over a longer period of time to be able to detect a significant temporal trend. Moreover, analyzing years pre-dating the first seeding (that is, before 1980s) or corresponding to the first seeding events (early 1980s) would be ideal but is unfortunately precluded by the absence (to our knowledge) of historical samples. According to previous results (Morvezen et al., 2016), the level of genetic diversity in the wild population of the Bay of Brest is very similar to those in neighboring wild scallop populations, supporting the temporal stability found in the present study among wild populations.

The temporal stability of genetic diversity displayed by the wild population could be explained by four alternative (and not mutually exclusive) hypotheses. First, regular gene flow from wild populations surrounding the Bay of Brest may maintain a high diversity in the wild population harbored in the Bay. Such gene flow might be promoted by the large tidal amplitude in the Bay, leading to strong renewal of the water during each tidal cycle (~40% Delmas and Tréguer, 1983), and is congruent with observed F_ST estimates between populations along the French Atlantic coast and the English Channel (Morvezen et al., 2016). Second, military areas closed to fishing may harbor unexploited sub-populations, which could ensure the retention of genetic diversity within the Bay by contributing significantly to the total reproductive output of the Bay. Third, the reproductive success of hatchery-propagated scallops could be limited in the wild, as previously reported in salmonids (Araki et al., 2007; Christie et al., 2012, 2014; Milot et al., 2013), thus avoiding negative genetic impacts in the wild seeded population. However, to our knowledge, this observation has never been made in bivalves and this hypothesis is contradicted by estimates of the relative reproductive contribution of hatchery populations provided in the present study (see below). Fourth, practices implemented in the local scallop hatchery may limit the loss in genetic diversity: the broodstock is fully renewed every year by random dredging wild adults (identified according to the double-ring method) in the wild population (Alban and Boncoeur, 2008). However, this practice alone could not completely avoid erosion, even limited, of the genetic variability (Waples, 1999).

Relatedness

As expected, relatedness was higher in hatchery populations than in the wild ones owing to the inherently strong familial structure caused by the low number of breeders. The increase in relatedness over time in the wild population, albeit small, may reflect some introgression between highly related hatchery individuals and their wild counterparts. This temporal increase is also observed in hatchery populations, possibly because the broodstock originates from the local wild population, thus amplifying the effect with hatchery crosses over time. The increase in relatedness is concerning, as inbreeding depression has been shown to occur at relatively low levels of inbreeding over several generations in bivalve mollusks (Evans et al., 2004). Again, this observation must be interpreted with caution, as only three time points over 5 years have been studied and the increase is weakly supported statistically (notably between 2009 and 2012). Moreover, marker-based estimators of relatedness have been shown to be subject to bias when highly related and unrelated individuals are compared (Wang, 2014). The reliability of these estimates is particularly poor at the individual level (Taylor, 2015), but our results comparing populations should be accurate. To strengthen the results, genetic monitoring should be extended over a longer time.

Effective population sizes

The observed lack of consistency among the different Ne estimators is not surprising. Despite the increase in research interest, statistical and software refinements, and the development of new genetic markers and methods, estimating effective population size remains a challenge. This is particularly the case with organisms, such as the great scallop, which display complex life-history traits. Indeed, most methods for estimating effective population size have been developed for a narrow scope of life-history traits: non-overlapping generations, relatively small variance in reproductive success and separated sexes (Waples and Do, 2010). Those criteria are not met with the great scallop and as a consequence using and interpreting most Ne estimates should be carried out with caution. Moreover, the possibility of substantial immigration in the population could further bias estimates, as gene flow could have different impacts on different estimators (see Gilbert and Whitlock (2015), for a comprehensive analysis; for more details on the differences between estimation methods, see Barker (2011), Hare et al. (2011), Phillipsen et al. (2011) and Holleley et al. (2014)).

In a complex case, like the great scallop, the best estimate of Ne is usually the combination (via harmonic mean) of all available methods into one value to dilute the differential biases associated with each method and thereby improve the accuracy of Ne estimation (Waples and Do, 2010). However, this methodology can be challenging, especially combining estimates from single sample methods and temporal methods as they do not apply to the same time frames (Nomura, 2008; Waples and Do, 2010). One approach for combining single sample and temporal Ne consists of considering temporal Ne as equivalent to the harmonic mean of the effective number of breeders per generation (that is, yearly Nb) for the generations engulfed in the time period of interest. This oversimplification is more realistic when generations are not overlapping (as in semelparous species) and with a fixed age structure of breeders (Waples et al., 2007). Although this might not seem realistic for a marine bivalve, the case of the Bay of Brest is peculiar: scallops are harvested just after their first reproductive season (that is, age 2+) and, because of the high fishing pressure, individuals may reproduce only once (A Jollivet, personal communication). Therefore, Pecten maximus in the Bay of Brest can be functionally considered as a quasi-semelparous species with limited age structure among mature individuals. Thus, the method developed in salmon for estimating yearly Nb from temporal Ne estimates appears viable in the present study (Waples, personal communication).

For the hatchery broodstock, combined Ne estimates (which can be assimilated to yearly Nb) appear slightly lower than usual broodstock census size. This result can be explained by the high variance in reproductive success that strongly reduces the effective number of breeders. High variance in reproductive success is often observed in bivalve hatcheries (Boudry et al., 2002; Lallias et al., 2010b), including in the great scallop (Morvezen et al., 2013). For the wild populations, some estimates and some upper confidence interval included infinity. Most Ne estimation methods perform better in populations with small Ne (Waples and Do, 2010) and an estimation including infinity could be indicative of a moderate to large Ne. However, the mean Ne estimates are much lower than expected in a bivalve displaying large population census sizes and mass-spawing with fecundation in the open sea. Small Ne/N ratios have often been reported in the literature (Frankham, 2007), sometimes even as low as 10⁻⁶ in the Pacific oyster (Hedgecock et al., 1992). In the present study, estimating Ne/N is difficult because of the lack of data concerning the census size of the great scallop population in the Bay of Brest. However, considering the total annual landings for this stock (~100–300T, Alban and Boncoeur, 2008), the census size should be at least in the order of magnitude of 10⁶–10⁷, giving an approximation of Ne/N in the order of magnitude of 10⁻⁴–10⁻⁵. A small Ne/N ratio could be caused by sweepstake reproductive success where a small number of individuals contribute to the majority of the next generation (Hedgecock and Pudovkin, 2011). Although such a phenomenon could result in a strong variance in allelic frequencies through generations and induce chaotic genetic patchiness (Larson and Julian, 1999), a stable genetic diversity was found over the three successive wild populations studied. The estimation of Ne for the 2009 wild cohort is the most surprising. It is threefold to fivefold lower than Ne estimates for both 2007 and 2012 wild populations. This could be explained by a strong sampling bias, as the 2009 wild sample is the smallest in the data set and Ne estimators are sensitive to sampling errors (Waples and Do, 2010). It could also be an indicator of a strong Ryman-Laikre effect, due to a large reproductive contribution of hatchery-born individuals during this particular year (see below for Ryman-Laikre effect discussion).

Overall, the results suggest that the annual effective number of breeders is small and variable in the wild, consistent with a sweepstake reproductive success (Hedgecock and Pudovkin, 2011). Moreover, this effect could be amplified by genetic drift resulting from hatchery propagation if seeded scallops contribute significantly to reproduction.

Relative reproductive contribution of hatchery and wild-born populations

Estimates of the relative reproductive contribution were highly variable and sometimes not possible. This could indicate that the simplistic hypotheses underlying the Ryman-Laikre model might not be realistic enough to be informative in the case of the great scallop. In particular, the relative contribution could not be assessed for the 2009–2012 period, clearly showing that the hypothesis of a simple reproductive mixing between 2009 hatchery and wild populations is not sufficient to explain the observed Ne in 2012. Nevertheless, estimates of x (0.34–0.67) suggest a Ryman-Laikre effect, with a high contribution of hatchery stocks to the total reproductive output of the wild population. These values should not be considered as a definitive result but as a possible indication of reproductive contribution of the hatchery seeds. To our knowledge, no previous study has used the Ryman-Laikre equation to estimate relative reproductive success. A comprehensive assessment of potential bias, assumptions and limits of this methodology should be conducted to evaluate the reliability of this estimate.

Accordingly, the increase in relatedness over time is also an indicator that seeded individuals appear to contribute to some degree to the reproduction of the great scallop population in the Bay of Brest (see above). The Ryman-Laikre effect might be the cause for the relatively small Ne observed in the wild population (in particular in 2009), but it seems to be counterbalanced by other processes, as Ne appears to be able to increase even after a dramatic reduction (in 2012). Again, as explained above, gene flow from neighboring populations as well as undetected population sub-structure could explain both the retention of genetic diversity and the apparent recovering of effective population size.

Conclusion: sea ranching or stock enhancement?

The present study suggests that hatchery-born scallops may significantly contribute to the reproduction of the wild population, fulfilling the objective of the population enhancement program conducted in the Bay of Brest, which is to provide additional breeders. In spite of the relative alteration of the genetic diversity and lower effective population size in the hatchery populations, the genetic variability appears relatively stable over time in the wild population supplemented with hatchery seed. In particular, gene flow from surrounding populations and/or the reproductive input of putative unexploited sub-populations within the bay may buffer the Ryman-Laikre effect and ensure the retention of the local genetic variability. Although the first goal of the supportive breeding program is to enhance the local recruitment and improve the productivity of the scallop population in the Bay of Brest, the stock is far from having recovered to its historical levels (Alban and Boncoeur, 2008). Various factors may strongly limit the demographic growth of the local population, such as trophic competition with non-native invasive species like Crepidula fornicata (Thouzeau et al., 2000) or Crassostrea gigas (Lejart and Hily, 2011), increased predation, or emerging environmental pressures (eutrophication, toxic algal bloom; Anderson et al., 2002, 2012). Genetic monitoring of the population in the Bay of Brest should be continued over a longer period of time and extended to other seeded scallop populations. This would provide opportunities to better assess the extent of the reproductive success of hatchery-born scallops in the wild and their impact on the effective population size and genetic diversity of seeded populations. Moreover, further investigations are required to evaluate whether the reproductive contribution of hatchery populations may affect the local adaptation of wild populations and their adaptive potential to environmental changes (see Laikre et al., 2010). This issue appears particularly crucial to ensure the long-term persistence of enhanced populations, particularly in a context of global changes.

The authors declare no conflict of interest.