Three-dimensional all-dielectric metamaterial solid immersion lens for subwavelength imaging at visible frequencies

TiO₂ nanoparticles are demonstrated to assemble low-loss three-dimensional all-dielectric metamaterials working at visible frequencies.

Abstract

Although all-dielectric metamaterials offer a low-loss alternative to current metal-based metamaterials to manipulate light at the nanoscale and may have important applications, very few have been reported to date owing to the current nanofabrication technologies. We develop a new “nano–solid-fluid assembly” method using 15-nm TiO₂ nanoparticles as building blocks to fabricate the first three-dimensional (3D) all-dielectric metamaterial at visible frequencies. Because of its optical transparency, high refractive index, and deep-subwavelength structures, this 3D all-dielectric metamaterial-based solid immersion lens (mSIL) can produce a sharp image with a super-resolution of at least 45 nm under a white-light optical microscope, significantly exceeding the classical diffraction limit and previous near-field imaging techniques. Theoretical analysis reveals that electric field enhancement can be formed between contacting TiO₂ nanoparticles, which causes effective confinement and propagation of visible light at the deep-subwavelength scale. This endows the mSIL with unusual abilities to illuminate object surfaces with large-area nanoscale near-field evanescent spots and to collect and convert the evanescent information into propagating waves. Our all-dielectric metamaterial design strategy demonstrates the potential to develop low-loss nanophotonic devices at visible frequencies.

INTRODUCTION

Metamaterials are a class of artificial electromagnetic media structured on a subwavelength scale, aiming to provide specific electromagnetic properties that are not available in natural materials (1–3), such as negative, zero, or ultrahigh refractive index (4–7); subdiffraction confinement (1, 8); electromagnetic cloaking (9, 10); and unusual optical nonlinearities (11, 12). Most metamaterials involve the use of metallic resonant structures designed to achieve the response of electromagnetic waves (1). These metal-based metamaterials can operate with negligible electromagnetic energy loss at microwave and terahertz frequencies (4, 6, 10, 13) but suffer from high intrinsic loss at higher optical frequencies (for example, near-infrared and particularly the visible region) because of the coupling of light to plasmons in metallic nanostructures (1, 3, 8, 14). This metallic loss severely limits the performance of optical metamaterials and their scalability to dimensions for practical uses. For example, metal-based plasmonic components have low transmission efficiency at optical frequencies, thus making them less useful for optical waveguiding over long distances or through bulk three-dimensional (3D) structures (2, 15).

Substantial efforts have been devoted to developing low-loss optical metamaterials in recent years (7, 16–20), because they may have many important applications, such as in perfect lenses with diffraction-unlimited optical resolution (21–26), invisibility cloaks (27–29), and optical computers (30, 31). The most promising approach is the all-dielectric metamaterials that use the near-field coupling between transparent (low absorption), high–refractive index dielectric building blocks (19, 20, 32, 33). Coupling between dielectric nanoresonators can exhibit unusual optical phenomena similar to those of metallic nanoresonators, such as local field enhancement and confinement, but with much lower energy dissipation and thus significantly higher device performance (20, 34, 35). Moreover, the high transmission and diffraction efficiencies of dielectric components make it possible to move optical metamaterials from current 2D metasurfaces or layered metamaterials to truly 3D metamaterials (2). Nanostructured silicon is known as an excellent candidate for near-infrared metamaterials because of silicon’s high refractive index (n ≈ 3.6) and transparency in the near-infrared region, as well as its compatibility with current nanofabrication techniques, such as electron-beam lithography and focused ion beam (7, 34–37). Although a recent report indicates that silicon nanodimers can also induce near-field enhancement effects in the visible region (38), unfortunately, silicon is not ideal for visible light metamaterials because of its visible light absorption caused by electron transitions across the bandgap (39). The ideal dielectric for visible light metamaterials has not yet been reported, probably because there is a limited choice of visible-transparent, high-refractive-index dielectric materials and because fabricating these materials into desired nanostructures using the current top-down or bottom-up approaches remains a challenge.

Here, we report a new design and nanofabrication of a 3D TiO₂ metamaterial capable of working efficiently in the visible spectrum. This all-dielectric metamaterial is fabricated through a novel nano–solid-fluid assembly (NSFA) method using visible-transparent, high-refractive- index, and deep-subwavelength–sized anatase TiO₂ nanoparticles (15 nm; refractive index n = 2.55) as dense building blocks. We experimentally demonstrate that when this metamaterial is used as a solid immersion lens (mSIL), this novel dielectric superlens can produce a sharp-contrast, wide field-of-view virtual image with a super-resolution of at least 45 nm under a white-light optical microscope, which has surpassed the performance of all existing near-field imaging approaches (22–25, 40–42). We further show by simulations that the near-field coupling between contacting TiO₂ nanoparticles can lead to subdiffraction confinement of visible light at the nanoscale comparable to the size of TiO₂ nanoparticles. Because of the lack of energy dissipation in the all-dielectric media, large-area nanoscale evanescent wave illumination can thus be effectively guided onto the surface of the observed object, and the excited evanescent waves that carry subwavelength information about the object will also be readily coupled and propagated through the media into propagating waves for far-field super-resolution imaging. The all-dielectric metamaterial and its NSFA method that we present here may open a door to designing and fabricating a new type of metamaterial to understand and study novel physical phenomena and properties for more important applications.

RESULTS

Fabrication of the TiO₂ mSIL

Bottom-up assembly of dielectric nanoparticles may provide a simple route to all-dielectric metamaterials but often suffers from problems such as cracking, irreversible aggregation, and insufficient controllability of the assembled morphology. To address these issues, we develop the NSFA method that uses the oil/water interface to induce the plastic deformation of fluid-like TiO₂ nanoparticle precipitation into controllable 3D morphology during the assembly process and to solidify the TiO₂ nanoparticles into a more densely packed structure after dehydration.

Figure 1 illustrates the NSFA method for the assembly of the TiO₂ mSIL, which resembles a conventional SIL’s hemisphere or super-hemisphere appearance (43–45). Briefly, an aqueous suspension containing 15-nm anatase TiO₂ nanoparticles is centrifuged to obtain a tightly packed precipitate (Fig. 1A). The resulting supernatant is then completely removed from the precipitate and replaced by a water-immiscible organic solvent mixture consisting of hexane and tetrachloroethylene, resulting in a nano–solid-fluid of TiO₂ nanoparticles (Fig. 1B). This novel nano–solid-fluid consists of an inner aqueous phase that contains a high volume fraction of TiO₂ nanoparticles and residual water filling the voids between nanoparticles and an outer oil phase that contains tetrachloroethylene (with a high boiling point of 121.1°C) as a protective and lubricant layer to prevent the evaporation of interparticle water. Because the TiO₂ nanoparticles have limited mobility in this confined water-in-oil interface, the nano–solid-fluid can behave as a plastic solid capable of being molded into desired 3D shapes. To produce a hemispherical mSIL, we directly sprayed the nano–solid-fluid onto the surface of the observed object with a syringe. The dispersed droplets of the nano–solid-fluid collapse under gravity, and the oil/water interfacial tension, will drive the deformation of the nano–solid-fluid into a curved shape with a regular and smooth surface (Fig. 1C). Owing to the low surface tension of hexane (18.4 mN/m at 25°C), the organic solvent mixture can readily wet the surface of various objects, which will enhance the filling of nanoscale surface roughness by TiO₂ nanoparticles, causing an intimate contact between the mSIL and the object surface. After evaporation of the organic solvent mixture, these nanoparticles are expected to undergo a phase transition (from a fluid-like to a solid-like state) arising from the interparticle capillary attraction due to further evaporation of the residual water, thus forming an even more densely packed 3D structure (Fig. 1E). To produce a super-hemispherical mSIL, we used a precoated thin layer of organic solvent mixture on the sample surface to float and support the nanoparticle droplets (Fig. 1D), which will retain their shape after dehydration (Fig. 1F).

Fig. 1. Schematic illustration of the assembly of the all-dielectric TiO₂ mSIL.

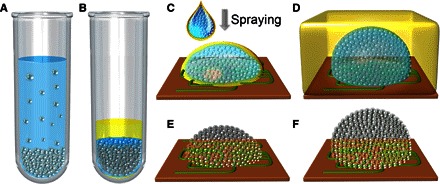
(A) Anatase TiO₂ nanoparticles (15 nm) were centrifuged into a tightly packed precipitate. (B) The supernatant was replaced by an organic solvent mixture consisting of hexane and tetrachloroethylene to form a TiO₂ nano–solid-fluid. (C) To prepare a hemispherical mSIL, the nano–solid-fluid was directly sprayed onto the sample surface. (D) To prepare a super-hemispherical mSIL, the nano–solid-fluid was sprayed onto the sample surface covered by a thin layer of organic solvent mixture. (E and F) After evaporation of the solvents, the nanoparticles underwent a phase transition to form a more densely packed structure.

Super-resolution properties of the TiO₂ mSIL

To investigate the parameters affecting the magnification factor and field of view of the TiO₂ mSIL, we compared the white-light optical microscopy images of a semiconductor wafer pattern with a lattice spacing of 200 nm (fig. S1) observed through these hemispherical or super-hemispherical mSILs. As shown in Fig. 2, the mSIL width is the same in each group of transverse images, around 10, 15, and 20 μm [see the inserted scanning electron microscopy (SEM) images]. Not surprisingly, as the height of the mSIL increases, we observed an increase in the magnification factor of around 1.8, 2.5, 3.0, 3.6, 4.7, and 5.3. This indicates that the magnification factor is determined by the shape (height-to-width ratio) of the mSIL. The magnification factor sharply increases with the height-to-width ratio of the mSIL approaching unity (a spherical shape) and reaches 5.3 at a height-to-width ratio of 0.82. With the further increase of this ratio, the contrast of the virtual image gradually disappears. Using geometrical optics ray tracing, we theoretically fit the experimental magnification curve and inversely derived that the mSIL media has an effective index of 1.95 and a high particle volume fraction of 61.3% (fig. S2). This packing fraction is close to the random close packing limit (~64%) of monodisperse hard spheres (46), indicating an intimate contact between TiO₂ nanoparticles throughout the media. Moreover, the mSIL presented here exhibits a wide field of view, which is approximately linearly proportional to the width of the mSIL (fig. S3).

Fig. 2. Magnification factor and field of view of the TiO₂ mSIL.

(A to R) Optical microscopy images of a wafer pattern with a lattice spacing of 200 nm observed through the TiO₂ mSIL with widths of about 10 μm (A to F), 15 μm (G to L), and 20 μm (M to R), corresponding to increasing magnification factors of 1.8 (A, G, and M), 2.5 (B, H, and N), 3.0 (C, I, and O), 3.6 (D, J, and P), 4.7 (E, K, and Q), and 5.3 (F, L, and R). Inset: Side-view SEM images of the corresponding mSIL located on the patterns.

To demonstrate the super-resolution capability of mSILs, we present in Fig. 3 the optical microscopy images of a recordable Blu-ray disk and a semiconductor wafer observed by the TiO₂ mSIL. Through SEM, the Blu-ray disk contains recording tracks with 200-nm-wide ridges separated by 100-nm-wide grooves (Fig. 3A), and the wafer contains parallel line patterns with a pitch of 60 nm (Fig. 3E) or point and line patterns with a pitch of 50 nm (Fig. 3I). Typically, the surface roughness on the wafer surface is below 5 nm, as revealed by atomic force microscopy (AFM) (Fig. 3, F and J). The SEM images of the bottom surfaces of the mSIL detached from the test samples (Fig. 3, B, C, G, and K) indicate that the nano–solid-fluid consisting of 15-nm nanoparticles has fully penetrated into different nanopatterns with a feature size down to a few tens of nanometers owing to their small size and fluidity.

Fig. 3. Super-resolution optical imaging through the TiO₂ mSIL.

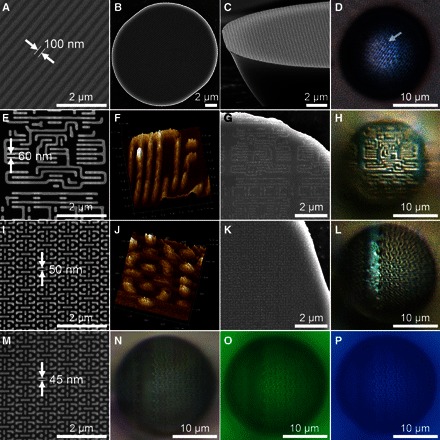
(A to P) SEM images of a Blu-ray disk containing 100-nm-wide grooves (A) and the wafer patterns with 60-nm (E), 50-nm (I), and 45-nm pitches (M) after gold coating of sample (I). (B) and (C), (G), and (K) are the bottom surfaces of the mSIL detached from the surface of samples (A), (E), and (I), respectively. AFM images of the wafer pattern with 60-nm (F) and 50-nm pitches (J). Optical microscopy images of the TiO₂ mSIL focused on the surface of a Blu-ray disk (D) and wafer patterns with 60-nm (H), 50-nm (L), and 45-nm pitches (N to P), with magnification factors of 1.8, 3.1, 3.0, and 3.1, respectively. The last mSIL was illuminated under white light (N), green light (λ ~ 540 nm) (O), or blue light (λ ~ 470 nm) (P). The mSIL had widths of about 20 μm.

The 100-nm-wide grooves on the disk surface are clearly visible through the 1.8× magnified virtual image created by a hemispherical TiO₂ mSIL (Fig. 3D). The mSIL also enables direct observation of the recorded data that are stored in the grooves as the difference in reflectivity (as indicated by the arrow in Fig. 3D) that cannot be detected even by SEM. Moreover, the hemispherical mSIL is formed into a semi-ellipsoid shape with its long axis parallel to the tracks on the disk (Fig. 3, B to D). This confirms that the nano–solid-fluid can plastically deform and flow along the grooves and ridges on the disk during the assembly process. Furthermore, after dehydration of interparticle water, the assembled morphology of TiO₂ nanoparticles can be maintained and reinforced because of the strong capillary attraction between nanoparticles.

Nonetheless, this type of hemispherical mSIL cannot efficiently resolve the wafer pattern with 75-nm features because of its low magnification factor (fig. S4). However, when a super-hemispherical mSIL is located on the pattern, a 60-nm pitch can be observed through the 3.1× magnified virtual image (Fig. 3H). This type of super-hemispherical mSIL can be further used to image a more complex structure with 50-nm Fig. 3L). By using an optical microscope equipped with a features (Fig. 3L). By using an optical microscope equipped with a higher-resolution CCD (charge-coupled device) camera, we can more clearly capture the subwavelength details of the 50-nm features (fig. S5) and even a gold-coated pattern with 45-nm features (Fig. 3M), in which the dots are distinguished from the lines under an illumination of white light, green light (λ ~ 540 nm), or blue light (λ ~ 470 nm) (Fig. 3, N to P). Obviously, these subwavelength features are far beyond the resolution of the optical microscope (fig. S6). The best super-resolution performance is achieved under the illumination of short-wavelength blue light. This suggests that the super-hemispherical mSIL can be used for the observation of sub–50-nm features, which significantly exceeds the resolution of 130 nm that can be obtained with conventional SIL made of polymer materials (45). Moreover, the mSIL also allows direct observation of 50-nm polystyrene latex beads located on the surface of a Blu-ray disk, which indicates that the super-resolution ability of the mSIL does not rely on the metallic properties of the observed object (fig. S7). In addition, the particle size of TiO₂ nanoparticles has a profound influence on the super-resolution performance, and the mSIL assembled from 45-nm anatase TiO₂ nanoparticles will reveal a lower contrast and a lower resolution than those from 15-nm TiO₂ nanoparticles (fig. S8).

Super-resolution mechanism of the mSIL

For classical hemispherical and super-hemispherical SILs composed of homogeneous material, the lateral resolution is enhanced by a factor of n and n², respectively, but their maximum lateral resolution will be capped at λ/2n (44, 47, 48). Along the axial direction, the resolution may be scaled by a factor of n³, which is out of the scope of current research (49). Accordingly, using a conventional SIL with a refractive index of n = 2.55, the best resolution attainable is λ/2n = 108 nm under an optical microscope with λ = 550-nm illumination. Obviously, the outstanding super-resolution capability of the mSIL presented here cannot be explained by classic geometrical optics. To explore the super-resolution mechanism of the mSIL, we performed full-wave 3D simulations of the all-dielectric metamaterial media. The basic simulation structure of the artificial media is a closely stacked 15-nm anatase TiO₂ nanoparticle composite, in which tiny air gaps between the particles exist, resulting in a dense scattering media. Figure 4 shows the simulation results of electric field distribution in the media when applying a plane wave illumination at a wavelength of 550 nm from the far field. Electric field confinements are observed in the gaps between nanoparticles, indicating the ability of the metamaterial media to modulate and confine visible light at the nanoscale (Fig. 4A). Because TiO₂ is nearly free of energy dissipation at visible wavelengths, this near-field coupling effect among neighboring nanoparticles can effectively propagate through the media over long distances, forming an arrayed “patterned illumination” landscape on the surface of an underlying substrate (Fig. 4B). These illumination spots are evanescent in nature, containing high–spatial frequency components. Their sizes are mainly determined by the size of TiO₂ nanoparticles, having a full width at half maximum (FWHM) resolution of ~8 nm (Fig. 4C).

Fig. 4. Propagating wave scattering by a dense all-dielectric medium.

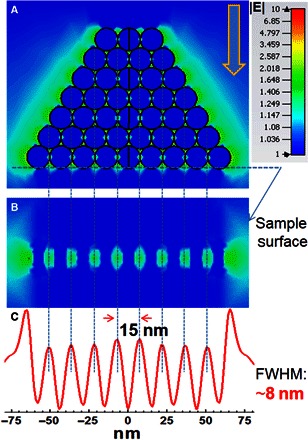
(A) Plane wave (λ = 550 nm) passing through the stacked TiO₂ nanoparticles. Electric field hotspots are generated in the gaps between contacting particles, which guides light to the underlying sample. (B) Large-area nanoscale evanescent wave illumination can be focused onto the sample surface because of the excitation of nanogap mode. (C) The size of the illumination spots is equal to the particle size, having an FWHM resolution of ~8 nm.

Therefore, it is expected that mSILs will have the unusual ability to transform the far-field illumination into large-area nanoscale evanescent wave illumination focused on the object surface within the near-field region. This novel nanophotonic effect is somewhat similar to that of aperture near-field scanning optical microscopy (NSOM), in which evanescent wave illumination is transmitted from the subwavelength aperture at the tip of a metal-coated optical fiber, and the size of the illumination spot is not limited by the incident wavelength but by the aperture size (40, 50). However, the single nanoaperture design in NSOM suffers from several limitations, such as low optical throughput, long scanning time, and insufficient contact between aperture probe and object surface (40). In our design, the array of TiO₂ nanoparticles can act as thousands of near-field probes to simultaneously illuminate the sample surface, and the strength of the focused evanescent wave illumination can be maximized owing to the near-perfect solid immersion of imaging object by TiO₂ nanoparticles. Moreover, theoretically, the size of the evanescent wave illumination spots can be further reduced by using smaller anatase TiO₂ nanoparticles or higher refractive index rutile (n = 2.70) TiO₂ nanoparticles, and this near-field illumination may also be useful for other applications such as nanoscale light harvesting and sensing.

According to the reciprocal principle (51), the conversion process in mSILs (Fig. 4) from propagating waves to evanescent waves can be optically reversed. In other words, an array of evanescent wave source located on the bottom surface of the mSIL will be converted back into propagating waves by the mSIL media. This is confirmed by two–point source calculation—a technique widely used to determine the imaging resolution of an optical system. In simulation, two incoherent point sources including all evanescent wave components were used; they were separated by a distance of 45 nm. For comparison purposes, both conventional media (homogeneous anatase TiO₂ material) and our metamaterial media (stacked 15-nm anatase TiO₂ nanoparticle) were simulated. Using slab geometry, we demonstrate in Fig. 5 that evanescent waves behave differently when interacting with conventional media (Fig. 5A) and metamaterial media (Fig. 5B). As shown in Fig. 5C, in conventional media, the evanescent waves decay exponentially as expected when the distance to point sources increases. The loss of evanescent waves causes reduced resolution. Figure 5E demonstrates the inability of conventional media to resolve two point sources in the far-field region (for example, z = 650 nm > λ = 550 nm). The two points are only resolvable in the near field when the distance to point sources is extremely small, typically smaller than 50 nm in the present case. However, in metamaterial media, the evanescent waves experience strong interaction with TiO₂ nanoparticles, which causes effective conversion of evanescent waves into propagating waves (Fig. 5D). The converted waves are mainly guided through the gaps between particles. Electric field received at the far-field region (z > λ) is about |E| ~ 0.45 (because source amplitude |E| = 1, this corresponds to |E|² = 20% of total evanescent energy), which is comparable to the field strength at z = 7.5 nm (near field). This means that near-field energy is converted and transported to the far field. The periodic modulation effect of electric field inside the metamaterial media can be seen as a signature of propagating waves. Because there is essentially no material loss in the media, the periodic propagation experiences an undamped modulation, showing an effective period of 160 nm. These waves propagate outward from the near field into the far field and contribute to super-resolution. This result confirms the validity of the reciprocal principle mentioned earlier. Figure 5F shows that the two point sources are reconstructed and discernible at the far field (for example, z = 650 nm). Compared to metal-based superlenses and hyperlenses whose resolution is limited by material loss in metal (22–25), the proposed mSIL is free from this problem. Its resolution is mainly affected by the excitation of evanescent waves and the conversion efficiency of evanescent waves into propagating waves, as well as the effective capture of the subwavelength information in the far field (for example, using an mSIL with a higher magnification factor and an optical microscope with a higher-resolution CCD camera). This makes it possible to design a perfect imaging device using dielectric nanoparticles as building blocks.

Fig. 5. Comparisons between conventional TiO₂ media and metamaterial TiO₂ media to convert evanescent waves into propagating waves.

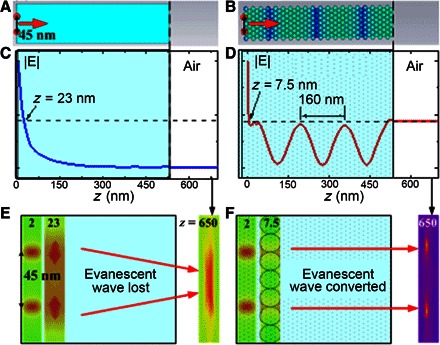
(A) Conventional media composed of homogeneous anatase TiO₂. (B) Metamaterial media derived from closely stacked 15-nm anatase TiO₂ nanoparticles. (C) Mean electric field amplitude as a function of distance from point sources (transverse electric–polarized, incoherent). The amplitude decays exponentially in conventional media, and most of the evanescent wave energy is lost within a distance of 50 nm. (D) In metamaterial media, evanescent waves interact with TiO₂ nanoparticles and turn into propagating waves that travel outward to the far field. A periodicity of 160 nm is observed. (E and F) Two point sources (45-nm separation) imaged with conventional (E) and metamaterial media (F), at positions z = 2 nm (near-source), z = 23 nm (near field, inside slab), and z = 650 nm (far field, outside slab). In the far field, the conventional media fails to resolve the two points, whereas the metamaterial media can successfully resolve them.

We would like to point out that there is a significant difference between propagating (for example, plane wave exciting) and evanescent wave scattering by TiO₂ nanoparticles. Under propagating wave excitation, there are theoretically no cross-polarization terms in the scattering matrix. However, in evanescent wave scattering, the exponentially decreasing amplitude introduces an asymmetry, which leads to polarization mixing. Moreover, as opposed to the propagating case, the scattering coefficients do not necessarily decrease with their order, and the magnetic terms can actually be enhanced (52). These factors have to be considered to understand the unusual conversion process in the metamaterial media subjected to an evanescent wave excitation.

CONCLUSION

In summary, we have demonstrated for the first time that TiO₂ nanoparticles can be used to assemble low-loss all-dielectric metamaterials working over the entire visible spectrum. Owing to the densely packed structure of deep-subwavelength–sized TiO₂ nanoparticles, the metamaterial can achieve both high refractive index and high transparency. The near-field coupling among neighboring TiO₂ nanoparticles can lead to unique photophysical properties that are not available with conventional optics. For instance, the mSIL presented here allows a deep subdiffraction-limited resolution down to 45 nm (~λ/12). This is attributed to the exceptional abilities of the metamaterial media to create an array of evanescent wave illumination focused on the sample surface and to effectively couple the evanescent information into propagating waves. Because of the inherent low loss in the all-dielectric metamaterial, these processes can be carried out in a truly 3D structure and over long distances. The NSFA method we have described is simple and versatile and can be readily extended to assemble TiO₂ nanoparticles or even other dielectric nanoparticles into arbitrarily shaped metamaterial-based photonic devices (for example, a TiO₂ wire used as an optical fiber; fig. S9). Further combining techniques such as nanoimprinting and nanofluidics may lead to compact and inexpensive nanophotonic devices for cloaking, optical interconnect networks, near-field sensing, solar energy utilization, etc.

MATERIALS AND METHODS

Preparation of TiO₂ nano–solid-fluid

To remove possible aggregates in TiO₂ aqueous sol (VK-TA33, Hangzhou Wanjing New Material Co. Ltd.), 35 ml of 15 wt % anatase TiO₂ sol with a peak number-average size of 15 nm measured by Zetasizer Nano ZS90 (Malvern Instruments Ltd.; see fig. S10) was centrifuged in a 50-ml centrifuge tube at 35,000g for 20 min at 10°C (GL-21M Refrigerated Centrifuge, Xiangyi Centrifuge Instrument Co. Ltd.). Then, 35 ml of the unprecipitated suspension was collected and further centrifuged at 35,000g for 60 min at 10°C. The supernatant was completely removed from the transparent precipitate and replaced by 10 ml of an organic solvent mixture consisting of hexane and tetrachloroethylene with a volume ratio of 1:2, resulting in a nano–solid-fluid of TiO₂ nanoparticles.

Self-assembly of TiO₂ mSILs

A small amount of TiO₂ nano–solid-fluid suspended in the organic solvent mixture was loaded into a 25-gauge syringe needle fitted with a stainless steel tube, with the exposed part of the tube removed. To prepare a hemispherical mSIL, the TiO₂ nano–solid-fluid was directly sprayed onto the surface of the observed sample via a 1-ml syringe, and the residual solvents were left to evaporate at ambient pressure and temperature (1 atm, 20°C) for 3 min. To prepare a super-hemispherical mSIL, a thin layer of the organic solvent mixture was spread over the sample surface and then the TiO₂ nano–solid-fluid was sprayed onto this surface. After 30 s, the excess organic solvent mixture was removed by touching the edge of the sample with a piece of filter paper and left for evaporation of residual solvents.

Optical super-resolution imaging

The optical micrographs in Fig. 3 (D, H, and L) were taken using a HIROX KH-7700 light microscope (HIROX Co. Ltd.) equipped with a 2.11-megapixel CCD camera, an MX-10C co-axial vertical lighting zoom lens, an OL-700II objective lens [numerical aperture (NA), 0.8], and an AD-10S directional lighting adapter at a total magnification of ×2100 in reflection mode. The optical micrographs in Fig. 3 (N to P) were taken using an Olympus BX63 light microscope (Olympus Corporation) equipped with a 5-megapixel CCD camera (Olympus, DP26) and a 100× objective lens (Olympus, LMPlanFL N; NA, 0.8) in reflection mode.

SEM and AFM observations

The nanoscale patterns on a recordable Blu-ray disk (after recording of data and removal of the cover layer) or a semiconductor wafer were observed on a Philips XL30 SEM operating at an accelerating voltage of 10 kV without gold coating. The wafer pattern with 45-nm features was obtained by sputter-coating the wafer with gold at a current of 30 mA for 180 s (BalTec SCD005). To observe the bottom surface of the mSIL, it was detached from the observed sample using double-sided adhesive tape. AFM images were taken on a Bruker MultiMode 8 AFM (Veeco Instruments) in tapping mode.

Optical simulation

Results presented in Fig. 5 were calculated using full-wave 3D electromagnetic software (CST MICROWAVE STUDIO). The frequency domain solver (finite element method) was used. Two incoherence point sources (y-polarized, perpendicular to the xz plane, set using a 1 nm × 1 nm rectangular waveguide port in software) were placed 45 nm away, and a convergence accuracy of 1 × 10⁻⁴ was used. Periodic boundary conditions were applied in xy directions. The computation was run on a server with a 16× 2.4-GHz central processing unit and 128-gigabyte memory. The averaged electric fields at different z planes were obtained using the postprocessing functions included in the software.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/8/e1600901/DC1

fig. S1. Wafer pattern used for evaluating the magnification factor and field of view of a TiO₂ mSIL.

fig. S2. Estimation of the effective refractive index and particle volume fraction of a TiO₂ mSIL.

fig. S3. Field of view of a TiO₂ mSIL.

fig. S4. The limiting resolution obtained with a TiO₂ hemispherical mSIL.

fig. S5. The super-resolution images obtained with a TiO₂ super-hemispherical mSIL.

fig. S6. Direct imaging of wafer patterns by an optical microscope.

fig. S7. Direct optical observation of 50-nm latex beads located on the surface of a Blu-ray disk.

fig. S8. Comparisons of TiO₂ hemispherical mSIL assembled from 15-or 45-nm anatase TiO₂ nanoparticles.

fig. S9. Nano–solid-fluid assembly for the TiO₂ optical fiber.

fig. S10. Characterizations of 15-nm anatase TiO₂ nanoparticles.