NEOCIVET: Towards accurate morphometry of neonatal gyrification and clinical applications in preterm newborns

Abstract

Cerebral cortical folding becomes dramatically more complex in the fetal brain during the 3rd trimester of gestation; the process continues in a similar fashion in children who are born prematurely. To quantify this morphological development, it is necessary to extract the interface between gray matter and white matter, which is particularly challenging due to changing tissue contrast during brain maturation. We employed the well-established CIVET pipeline to extract this cortical surface, with point correspondence across subjects, using a surface-based spherical registration. We then developed a variant of the pipeline, called NEOCIVET, that quantified cortical folding using mean curvature and sulcal depth while addressing the well-known problems of poor and temporally-varying gray/white contrast as well as motion artifact in neonatal MRI. NEOCIVET includes: i) a tissue classification technique that analyzed multi-atlas texture patches using the nonlocal mean estimator and subsequently applied a label fusion approach based on a joint probability between templates, ii) neonatal template construction based on age-specific sub-groups, and iii) masking of non-interesting structures using label-fusion approaches. These techniques replaced modules that might be suboptimal for regional analysis of poor-contrast neonatal cortex. The proposed segmentation method showed more accurate results in subjects with various ages and with various degrees of motion compared to state-of-the-art methods. In the analysis of 158 preterm-born neonates, many with multiple scans (n = 231; 26–40 weeks postmenstrual age at scan), NEOCIVET identified increases in cortical folding over time in numerous cortical regions (mean curvature:+0.003/week; sulcal depth:+0.04 mm/week) while folding did not change in major sulci that are known to develop early (corrected p < 0.05). The proposed pipeline successfully mapped cortical structural development, supporting current models of cerebral morphogenesis, and furthermore, revealed impairment of cortical folding in extremely preterm newborns relative to relatively late preterm newborns, demonstrating its potential to provide biomarkers of prematurity-related developmental outcome.

Introduction

Cerebral cortical gyration is one of the most striking morphological changes that occur in the fetal brain. It starts as early as 10 gestational weeks and most secondary sulci and gyri are formed during the 3rd trimester of gestation (White et al., 2010). Recent study has shown that the process may evolve differently in children who are born prematurely (Lefevre et al., 2015). To quantify such early morphological development by image analysis, it is necessary to extract cortical surface, especially the interface of the gray matter (GM) and white matter (WM). Only a few packages (Habas et al., 2012; Li et al., 2014b; Melbourne et al., 2014; Wright et al., 2014) have been proposed to perform this task. To enable regional analysis, they co-register an individual lobar atlas to each subject's cortical surface. However, this approach lacks point-wise correspondence across subjects and, consequently, spatial sensitivity.

Pure surface-based packages such as the MNI's CIVET pipeline (Kim et al., 2005; MacDonald et al., 2000) or FreeSurfer (Fischl, 2012) extract triangulated cortical surface and define point correspondence using surface-based spherical registration (Robbins et al., 2004). These pipelines have been broadly used in applications for adult brain MRI. However, these packages have not been optimized for fetal/neonatal analyses. Different degrees of myelination, neuronal proliferation and migration, and axonal sprouting and pathfinding among various cortical and subcortical regions, which are distinctive features of developing brain, are manifested as regionally- and temporally-varying gyral shapes and GM/WM contrast in structural MRI. This spatiotemporally dynamic tissue contrast challenges tissue classification techniques used in most pipelines since they are usually based on a tissue contrast histogram constructed from the whole brain across time. Furthermore, the spatial normalization obtained by registering an individual volume/surface to a single, average template that represents a whole population can be incomplete in fetal/neonatal brain MRI and may subsequently lack the point correspondence, as such a single volume or surface template cannot fully characterize the spatiotemporally dynamic brain anatomy.

A recent publication (Isgum et al., 2015) has summarized the result of the MICCAI Grand Challenge in 2012, which performed the systemic evaluation on neonatal brain segmentation approaches. The 8 methods presented were based on various techniques such as expectation–maximization framework with atlas prior, a method in the SPM toolkit, a Maximum a Posteriori Expectation–Maximization algorithm, large deformation of multiple atlases, prior knowledge of cortical morphology or use of single atlas combined with pattern learning of brain tissues/structures (Isgum et al., 2015). The segmentation accuracy of cortical GM for these techniques was generally relatively poor (Dice overlap index < 86%, range: 60–85%; Hausdorff distance > 5mm, range = 5.4–24 mm; note that the accuracy of cortical GM segmentation in adult brains often reaches above Dice = 90%). As this poor segmentation may be partly due to the fact that many of these methods were driven from those directly used for adult brain segmentation, special technical elements to characterize the large anatomical variability in the neonatal stage may be demanded. Techniques that combine a feature of local intensity variations into the deformable models have recently been proposed for tissue segmentation of neonatal brain (Wang et al., 2011). Another method from the same group improved the performance by the guidance of deformation with image features extracted from a late time point longitudinal scan (L. Wang et al., 2013). These techniques demonstrated excellent performance in their data set. However, deformable model-based techniques are generally known to be noise sensitive. Unfortunately, about 40–50% of neonatal MRI scans are affected by a degree of motion artifact and a large proportion of such noisy data should have been excluded in previous morphological analyses (Engelhardt et al., 2015; Melbourne et al., 2014). Other methods have not taken into account motion artifact in segmentation.

To enable the analysis of cortical morphology in neonates, we developed a variant of the CIVET pipeline, called NEOCIVET. This pipeline includes a number of new modifications and parameter tunings. In particular, we improved the cortical GM segmentation under motion-affected MRI using a patch-based texture modeling and label fusion based on the joint probability between templates. This algorithm learns patterns of anatomical morphology under a variable amount of motion artifacts using a well-adapted library. Also, we constructed spatiotemporally varying age-specific surface templates using an unbiased construction scheme and a large sized preterm neonatal dataset (231 scans; age range: 26–40 weeks gestation) to improve the surface registration performance across subjects.

Methods

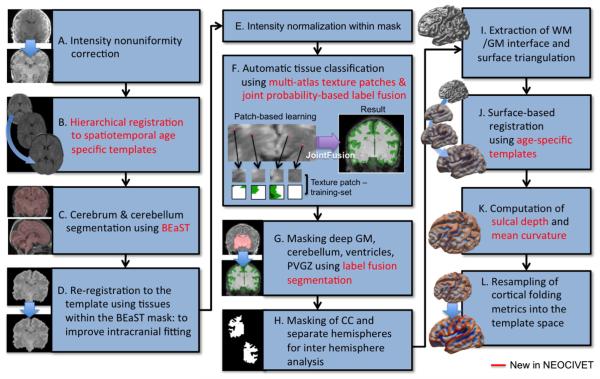
NEOCIVET includes a series of image processing steps to achieve the goal of extracting the interface between GM and WM. Briefly we describe the flow of the pipeline here as in Fig. 1: A) MRI images underwent intensity non-uniformity correction using N3 (Sled et al., 1998); B) these images were linearly registered to the spatiotemporal neonatal brain template from the Biomedical Image Analysis Group, Imperial College London (http://biomedic.doc.ic.ac.uk/brain-development/index.php?n=Main.Neonatal2). Non-linear registration between all pairs of images and performing nonlinear kernel regression (Serag et al., 2012) created this preterm newborn template that consisted of 9 brain images representing the mean shapes of different age groups (28–44 week gestational ages at every 2 weeks). The individual images were first registered to the closest age-template and further registered to the oldest brain template using the transformation matrix of the registration between the selected age-template and the oldest template; C) we segmented the cerebrum and cerebellum using a patch-based brain extraction algorithm (BEaST) (Eskildsen et al., 2012); D) these masked brains were re-registered to the template to improve the intracranial fitting; E) MRI intensities were re-corrected using N3 and normalized within the brain mask; F) the GM, WM, and CSF were classified within the mask by integrating the nonlocal mean estimation of multi-atlas texture patches (Coupé et al., 2011) with an advanced label fusion based on a joint probability between selected templates (H.Z. Wang et al., 2013). In order to overcome the poor segmentation, with varying tissue contrast and varying cortical folding patterns at different gestational ages as well as under heavy motion artifact, we constructed a patch library that contains individual atlases (image + manual segmentation; n = 27) scanned at various ages and under variable conditions of motion; G) a nonlinear registration and label-fusion approach (H.Z. Wang et al., 2013) was used to mask out non-cortical structures: deep GM, ventricles and the periventricular germinal zone (which looks like GM as neural cells migrate into this area and proliferate in neonates) and the cerebellum. While the cerebellum was removed, other masked structures were merged into the WM class; H) segmentation of the corpus callosum in the mid-plane divided the WM into hemispheres. This separation allowed for analysis of hemispheric asymmetry in morphometry by co-registering the flipped right hemisphere to the left; I) we parameterized the WM boundary by evolving an ellipsoid, triangulated using an icosahedral model and a multi-resolution deformation scheme, as in the CIVET (Kim et al., 2005); J) to improve point correspondence across subjects, a surface-based registration (Robbins et al., 2004) was performed with respect to age-specific templates that were constructed using an unbiased framework (Lyttelton et al., 2007); K) the cortical morphology was characterized by measuring sulcal depth and mean curvature; L) finally, these measurements were further re-sampled to the surface template using the transformation obtained in the surface registration, in order to allow inter-subject comparison.

Fig. 1.

Flowchart of NEOCIVET, a variant of CIVET used for neonatal brain analysis. New modules and parameters are in red. PVGZ: periventricular germinal zone.

In the following sections, we describe the new modules included in NEOCIVET and how they address technical challenges in neonatal brain MRI. We also discuss the choice of parameters for optimal performance. Finally, we investigate the ability of NEOCIVET to assess developmental trajectory and its clinical utility using a dataset of pretermborn neonates.

Subjects

Our initial dataset comprised 158 preterm newborns (mean postmenstrual age at birth [PMA] = 28.3 ± 2.4 weeks; range 24–33 weeks), admitted to UCSF Benioff Children's Hospital San Francisco between June 2006 and March 2015. Exclusion criteria included (i) clinical evidence of a congenital malformation or syndrome, (ii) congenital infection, and (iii) newborns too clinically unstable for transport to and from the MRI scanner. Parental consent was obtained for all cases following a protocol approved by the institutional Committee on Human Research. All patients were scanned postnatally as soon as clinically stable (PMA at scan: 31.6 ± 1.8 weeks; range 26–36 weeks), and 110 patients were re-scanned before discharge at late preterm age (PMA at scan: 35.9±2.0 weeks; range 32–40 weeks). Due to extremely severe motion artifact for which even an expert could hardly recognize the brain anatomy, 20 baseline and 17 follow-up scans were excluded. The final database included 138 baseline (PMA = 31.8 ± 1.8 weeks) and 93 follow-up scans (35.9 ± 1.8 weeks). No subject was excluded among the initial 158 newborns.

MRI acquisition

Customized MRI-compatible incubators with specialized head coils were used to provide a quiet, well-monitored environment for neonates during the MRI scan, minimizing patient movement and improving the signal-to-noise ratio. Newborns enrolled between June 2006 and July 2011 (n = 95) were scanned on a 1.5-Tesla General Electric Signa HDxt system (GE Medical Systems, Waukesha, WI, USA) using a specialized high-sensitivity neonatal head coil built within a custom-built MRI-compatible incubator. T1-weighted images were acquired using sagittal 3-dimensional inversion recovery spoiled gradient echo (3D SPGR) (repetition time [TR] = 35; echo time [TE] = 6.00; inversion time of 0.00 ms; field of view [FOV] = 256 × 192 mm²; number of excitations [NEX] = 1.00; and flip angle [FA] = 35°), yielding images with 1 × 1 × 1 mm³ spatial resolution. Newborns enrolled between July 2011 and March 2015 (n=63) were scanned on a 3-Tesla General Electric Discovery MR750 system in a different MR compatible incubator and using a specially designed (for 3 T imaging) neonatal head coil. T1-weighted images were also acquired using sagittal 3D IR-SPGR (TR = minimum; TE = minimum; inversion time of 450 ms; FOV = 180 × 180 mm²; NEX = 1.00; FA = 15°), and were reformatted in the axial and coronal planes, yielding images with 0.7 × 0.7 × 1 mm spatial resolution.

Classification of brain tissues

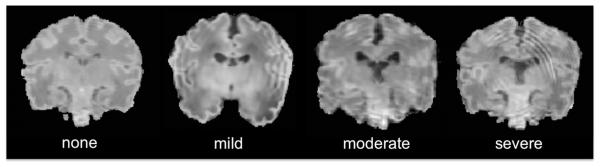
Regional variations in myelination and cell density in neonatal brains may cause MR intensity changes beyond the variability that can be captured by the analysis of a whole brain histogram. Moreover, even after excluding subjects with an extremely severe motion artifact such that brain anatomy is barely recognized (approximately 10–15%), a degree of this artifact may still affect 30–40% of remaining data (Fig. 2). Unfortunately, such noisy data should have been excluded in previous morphological analyses (Engelhardt et al., 2015; Melbourne et al., 2014). We addressed the aforementioned issues by combining a patch-based texture modeling (Coupe et al., 2011; Eskildsen et al., 2012; Hu et al., 2014) with a joint probability-based label fusion method (H.Z. Wang et al., 2013) and constructed a well adapted training-set as described below.

Fig. 2.

Various degrees of motion artifact on neonatal MRI.

We determine a label corresponding to a given voxel x_t in the target image based on the similarity of its surrounding patch P(x_t) to all the patches P(y_s) taken from atlases (s | s = 1,2,…, N) in the library (=training-set). A voxel y_s is selected inside a search volume (y ∈ η_xt). In other words, for the patch P centered at the voxel x_t of the target image, similar patches extracted from the N images are searched for within the surrounding neighborhood η_xt. This procedure has been demonstrated to result in a moderately improved performance in computing the consensus segmentation compared to conventional multiatlas label fusion algorithms that often have difficulty in finding optimal texture features due to misregistration.

A nonlocal means estimator v^l(x_t) is used to estimate the label at x_t:

$$V^l\left({\mathbf{x}}_t\right)=\frac{\sum _{s=1}^N\sum _{y\in \eta }{W}_l(x_t,y_s)l\left({\mathbf{y}}_s\right)}{\sum _{s=1}^N\sum _{y\in \eta }{W}_l(x_t,y_s)}$$ (1)

where l(y_s) is the label of voxel y on the current template image s. For the purpose of brain tissues, we define the label values as background=0, CSF=1, GM=2, and WM=3. Accordingly, we used l(y_s) ∈ [0,1,2,3]. In the original study, the weight w_l(x_t, y_s) of the label l(y_s) was computed based on the similarity between patches P(x_t) and P(y_s) as:

$$W_l(x_t,y_s)=e^{\frac{\parallel P\left({\mathbf{x}}_t\right)-P\left({\mathbf{y}}_s\right){\parallel }_2^2}{h}}$$ (2)

‖•‖₂ is the normalized L2 norm that is normalized by the number of patch elements and computed between each intensity of the elements of the patches P(x_t) and P(y_s). This image similarity based local weighted method has been used in other voting (or label fusion) approaches and has performed competitively (Artaechevarria et al., 2009; Heckemann et al., 2006; Lotjonen et al., 2010). Yet, H.Z. Wang et al. (2013) pointed that this method can be limited as it assigns voting weights to each atlas independently and, thus, cannot account for the case where labeling errors produced by different atlases may be correlated. For example, when a same (or very similar) atlas was copied to the library twice, the weight to this atlas in segmentation of a test image will be doubled, creating a biased result. Such biased results can occur in cases where the features of atlases included in a library do not distribute uniformly in terms of variability of the target anatomy. Thus, weighting using a joint probability as proposed in H.Z. Wang et al. (2013)) would improve the label fusion. We replace the weighting in Eq. (2) with the equation below:

$${\mathbf{W}}_{{\mathit{x}}_{\mathit{t}}}=\frac{{\mathbf{M}}_{{\mathit{x}}_{\mathit{t}}}^{-1}{1}_N}{1_N^t{\mathbf{M}}_{{\mathit{x}}_{\mathit{t}}}^{-1}{1}_N},\sum _{s=1}^N{\mathbf{W}}_{{\mathit{x}}_{\mathit{t}}}\left(S\right)=1$$ (3)

where Mx is a pairwise dependency matrix between two atlases s₁ and s₂, defined as:

$${\mathbf{M}}_{{\mathit{x}}_t}(s_1,s_2)=E_{{\delta }_{s1}\left(x\right){\delta }_{s2}\left(x\right)}[{\delta }_{s1}\left(x\right){\delta }_{s2}\left(x\right)\mid P\left({\mathbf{x}}_t\right),P\left({\mathbf{y}}_1\right),\dots ,P\left({\mathbf{y}}_{s1}\right),\dots ,P\left({\mathbf{y}}_{s2}\right),\dots ,P\left({\mathbf{y}}_N\right)]$$ (4)

$$=\mathit{p}({\delta }_{\mathit{s}1}\left(\mathit{x}\right){\delta }_{\mathit{s}2}\left(\mathit{x}\right)=1\mid P\left({\mathbf{x}}_t\right),P\left({\mathbf{y}}_1\right),\dots ,P\left({\mathbf{y}}_{s1}\right),\dots ,P\left({\mathbf{y}}_{s2}\right),\dots ,P\left({\mathbf{y}}_N\right))$$ (5)

where δ_s1(x)=[1,0] is the label difference between the s₁ atlas and the target image, and $E_{{\delta }_{s1}\left(x\right){\delta }_{s2}\left(x\right)}$ is an expected segmentation error when atlases s₁ and s₂ are considered together. Therefore, Mx(s₁,s₂) estimates how likely atlases s₁ and s₂ are to both produce wrong segmentations for the target image, given the observed feature images. H.Z. Wang et al. (2013) demonstrated that Eq. (5) could follow as:

$${\mathbf{M}}_{{\mathit{x}}_{\mathit{t}}}(s_1,s_2)\propto \parallel P\left({\mathbf{x}}_t\right)-P\left({\mathbf{y}}_{s1}\right){\parallel }_2^{\beta }\parallel P\left({\mathbf{x}}_t\right)-P\left({\mathbf{y}}_{s2}\right){\parallel }_2^{\beta }.$$ (6)

When s₁ = s₂, Eq. (6) can be collapsed to ${\mathbf{M}}_{{\mathbf{x}}_{\mathbf{t}}}(s_1,s_1)\propto \parallel P\left({\mathbf{x}}_t\right)-P\left({\mathbf{y}}_{s1}\right){\parallel }_2^{2\beta }$ and one can see that Eq. (2) is a particular case of M_xt (s₁, s₁) with β = exp(•). As observed in H.Z. Wang et al. (2013), the use of β = 2 resulted in the most stable and best accuracy in our tissue segmentation as well. Finally, the label probability, v^l(x_t) in Eq. (1), was estimated per label l using Eqs. (3) and (6), and the hard classification of brain tissues was made based on the highest probability among all the tissue types (GM/WM/CSF/background).

Construction of training-set for the patch-based tissue segmentation

To train the proposed automated tissue segmentation, we selected 27 scans from our database, taking into account: (i) uniform age distribution; and (ii) a variable degree of artifact (Table 1). A rater (RM) segmented manually the 3 tissue types of brain (GM, WM, CSF) using the MNI-BIC Display tool (http://www.bic.mni.mcgill.ca/ServicesSoftwareVisualization/Display). The images were spatially normalized prior to this process. The manual labeling is tedious and simultaneously demands consistency. To balance the time requirement and consistency when creating the training-set, a rater segmented a brain MRI on every 2nd slice through the coronal plane and the segmentation on the other slices was interpolated using a nearest neighborhood method (average time cost: 4 days per case). Later, the rater completed the manual labeling in the full resolution by revisiting the initial labels and correcting them on 3 orthogonal views (i.e., axial, coronal, and sagittal planes; this took another 4 days). After a month, to evaluate the manual labeling, the same rater independently performed the “complete” labeling for a randomly selected sample (n = 7) to calculate the intra-rater agreement. This resulted in an excellent agreement between the two segmentations (Dice index: WM = 97 ± 2%, GM = 96 ± 3%). We finally investigated whether the automated segmentation accuracy was different if the learning was from “incomplete” versus complete manual labeling (further details can be found in the sections ‘Evaluation of the segmentation accuracy’ and ‘Performance relative to manual labeling’).

Table 1.

Distribution of age and motion artifact among the templates (n = 27) used for training of the proposed tissue segmentation.

	Age				Motion artifact
	26-30	31-33	34-36	37-40	none	mild	moderate	severe
n(%)	5 (18%)	8 (30%)	8(30%)	6 (22%)	10(37%)	9 (33%)	4(15%)	4(15%)

Surface fitting

The WM/GM interface was extracted by deforming an ellipsoid triangulated using icosahedral sampling (MacDonald et al., 2000). The initial surface was sampled with 320 triangles and deformed towards the boundary of the hemispheric WM while smoothness and proximity (to prevent an intersection of the surface) were constrained. The surface was up-sampled to 81,920 triangles at the end of each deformation cycle.

Surface-based morphological measurements

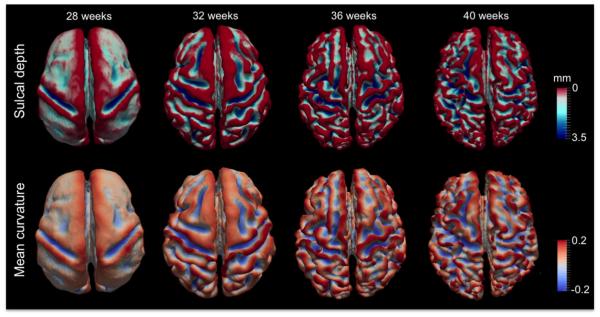
In most applications, CIVET is primarily used to measure cortical thickness between the inner and outer cortical surfaces. In contrast, NEOCIVET aims to characterize the cortical folding at the WM/GM interface (=inner cortical surface). We computed sulcal depth as gyration/sulcation index (Hill et al., 2010), and mean curvature that captures concavity/convexity as cortical complexity index (Fig. 3). To compute the sulcal depth, we first overlaid a brain hull model (extracted in Fig. 1C) on the cortical manifold to detect vertices on the gyral crowns (Hill et al., 2010), which were initialized with a depth of zero. Then, the depth was calculated using the geodesic distance from the crown (Hong et al., 2014). The mean curvature was estimated using a method (Do Carmo, 1976) that has been widely employed in neuroimaging studies (Luders et al., 2006; Scott et al., 2013).

Fig. 3.

Measurement of folding on the cortical surfaces. Top: sulcal depth was quantified using geodesic distance from the gyral crown (indexed in red); bottom: cortical complexity was computed using mean curvature.

$$H_{curvature}=\sum _{v=1}^{n_v}{\left(\frac{(x_v-{\tilde{x}}_v)\cdot N_v}{B_v}\right)}^2$$ (7)

where x_v is the 3D position of the vertex v, $\tilde{x}$ is the centroid of its neighbor vertices of vertex v, N_v is the unit normal vector at vertex v (i.e., this vector is normal to the polygon made by connecting the vertices neighboring v), and B_v is the average distance from the centroid of each of the neighbors.

Note that this morphometry was performed in the stereotaxic space (as in Fig. 1B) where the intracranial volume was normalized such that no effects of brain growth were on the actual measurement.

Construction of age-specific surface templates and registration

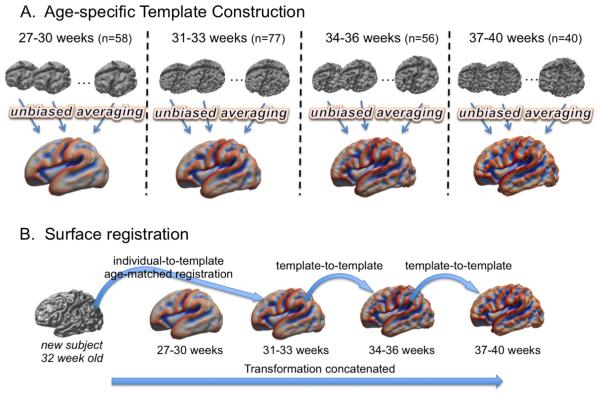
As seen in Fig. 3, cortical folding changes dramatically during perinatal development. This emphasizes the importance of constructing templates that capture the precise cortical morphology for specific age ranges, so as to ensure the accuracy of registration. We therefore subdivided our dataset into four age ranges: 27–30 (n = 58), 31–33 (n = 77), 34–36 (n = 56) and 37–40 (n = 40) weeks PMA. For each group, we constructed a surface template (Fig. 4A) using SURFTRACC, a surface registration algorithm included in CIVET (Robbins et al., 2004) and an unbiased template construction framework (Lyttelton et al., 2007). In brief, SURFTRACC first transposes individual sulcal depth maps into icosahedral spheres. It then iteratively searches for local optimal vertex correspondence between an individual and a template sphere based on a matching of a given feature (in this case, depth potential function; Boucher et al., 2009). Mapping the deformed meshes back to the original cortical surface coordinates allows a registration of the individual to the template surface. Inclusion of a regularization step further preserves local surface topology. This procedure was integrated into a hierarchical framework that allows for registration from coarse to fine scale. An initial template was created by a simple averaging of vertices among the surfaces in each age group. Thereafter, an iterative alignment proceeds from low dimensional warping of all individuals to the initial template, and towards higher dimensional warping to a new template that is constructed from the previous warping cycle as described in Lyttelton et al. (2007). Left and “flipped-right” hemispheres from all subjects were pooled to avoid subject- and hemisphere-specific bias in the evolution and averaging. Using the original warping cycle in Lyttelton et al., we observed that fitting was incomplete, likely due to a larger anatomical variation included in neonatal brains even after breaking down the age range. Therefore, by adding cycles with which no more changes were made in the template shape at the end of registrations using the given control mesh size, we optimized the warping cycle for our data as in Table 2. After construction, the youngest-age template was registered to the 2nd youngest and so on such that each template was registered to its closest older template, yielding a temporally continuous transformation. For inter-subject analyses, any given subject was first registered to the corresponding age template and then was ultimately transformed to the oldest template space by concatenating the sequence of transformations between age-specific templates (Fig. 4B).

Fig. 4.

Construction of spatiotemporal surface template and the used surface registration scheme. A. The whole dataset (n = 231) is split into 4 different age groups. Age-specific templates are created using an unbiased averaging framework (Lyttelton et al., 2007). B. A new subject will be registered to its age-matched template and ultimately registered to the oldest template space using template-to-template transformations.

Table 2.

Construction of an unbiased surface template. The number of control mesh sizes used for each cycle is shown. After each cycle, averaging was performed to create an intermediate template and a new template feature field (depth potential map) was generated.

Cycle no.	Control mesh size (polygons)
	320	1280	5120	20,480	81,920
Cycles1–2	y	N	N	N	N
Cycles3–4	Y	Y	N	N	N
Cycles 4–5	Y	Y	Y	N	N
Cycles 6–8	Y	Y	Y	Y	N
Cycles 9–12	Y	Y	Y	Y	Y

Other technical considerations and parameter selection

For optimal performance in our neonatal dataset, parameters in the NEOCIVET were empirically chosen. Also, some CIVET modules were updated with more recent publicly available techniques. Below, we describe these modifications in some detail so as to guide NEOCIVET users in their parameter selection with respect to MRI field strength, pulse sequence and spatial resolution:

• a) For intensity inhomogeneity correction using N3, we found that a smoothing distance for RF wavelength as 100 mm for 1.5 T and 40 mm for 3 T MRI yielded the best performance in brain masking and tissue classification, which also agreed with the result from a previous extensive analysis on the smoothing distance of N3 (Boyes et al., 2008).

• b) The FSL-BET-based brain masking and single atlas-based masking of deep GM and ventricles performed poorly for neonatal brains due to rapid changes in volume and intensity. We addressed this issue by introducing publicly available techniques that use patches of multiple templates or fuse multiple templates based on a similarity measure (Eskildsen et al., 2012; H.Z. Wang et al., 2013). The use of 25 manually labeled atlases (images were chosen by balancing 1.5 T and 3 T data and the uniformity of age range) achieved excellent segmentation accuracy for the whole brain mask and the mask combining the deep GM and ventricles (Dice > 0.90%).

• c) Our image data were scanned with an in-plane resolution of 1 × 1 mm² for 1.5 T and 0.6 × 0.6 mm² for 3 T MRI with 1 mm thickness for both MRIs whereas the used volumetric neonatal templates were sampled at 0.82 × 1.03 × 1.6 mm³. Registration to this template would cause image data loss. We up-sampled the templates to 0.6 × 0.6 × 0.6 mm³. This step did not necessarily improve registration, which we ultimately optimized using the age-specific templates.

• d) Parameters in the segmentation algorithm were chosen empirically. The nonlocal mean was computed on multi-resolution images to improve the performance against the local minima issue (as in Eskildsen et al., 2012). Three different resolutions (2.4 × 2.4 × 2.4 mm³; 1.2 × 1.2 × 1.2 mm³; 0.6 × 0.6 × 0.6 mm³) were used and parameters were set at each resolution as: the size of searching area η_xt = 3 × 3 × 3; 5 × 5 × 5; 13 × 13 × 13 voxels; and the size of patch = 3 × 3 × 3; 3 × 3 × 3; 5 × 5 × 5 voxels. In Eq. (6), β was chosen as 2. On a single core of Intel™ i7-3770 K, 3.5 GHz, the segmentation step and the whole pipeline process for a neonatal MRI took 15 min and 2.1 h, respectively.

Evaluation of NEOCIVET

Evaluation of the segmentation accuracy

We compared our classification against the two original methods, the nonlocal mean method (Coupé et al., 2011) and the JointFusion algorithm (H.Z. Wang et al., 2013), which we used for our combined approach. We also evaluated a non-training-based method (Dai et al., 2013; Wang et al., 2011) that has been included in a publicly open package iBEAT, version 1.1 (http://www.med.unc.edu/bric/ideagroup/free-softwares/libra-longitudinal-infant-brain-processing-package). This method was based on a level-sets deformable model that evolved using local intensity information and constraints of atlas spatial prior, and cortical thickness constraint, as well as longitudinal information if available (Wang et al., 2011; L. Wang et al., 2013). As our algorithm was based on learning, we segmented a test image using a leave-one-out strategy where the test image was omitted from the training-set to avoid possible bias. We also compared the automated segmentation resulting from the learning using “incomplete” manual labeling to the segmentation using complete annotation.

Performance relative to manual labeling

We used the complete manual labeling as the ground truth. Multiple comparisons for the following analyses were adjusted using false discovery rate (Benjamini and Hochberg, 1995).

• a) Global overlap assessment. To evaluate the volume-wise accuracy of automated approaches, we computed the Dice overlap between manual labeling and automatic labeling. To measure global contour differences between manual and automated labeling, we computed the mean Hausdorff distance, Hm (Kim et al., 2015). We measured Hm only for GM/WM interfaces. To assess the influence of larger cortical folding in older neonates or of amount of motion artifact on the segmentation accuracy, we correlated the accuracy metrics with age (i.e., PMA at scan) or the degree of artifact (none/mild/moderate/severe).

• b) Surface-based local analysis of contour accuracy. To localize the mis-segmentation, a surface-based framework was employed to spatially localize contour difference between manual and automated segmentations (Kim et al., 2015). We automatically extracted parametric surface models of the GM–WM interfaces (as described in the section ‘Surface fitting’) based on the manual labels, and based on the tissue classifications of each automated algorithm. Individual surfaces were aligned to their age-matched surface templates and ultimately to the oldest template (described in the section ‘Construction of age-specific surface templates and registration’). For each classification algorithm, we computed the point-wise surface-normal component of the displacement vector between automated and manual labels. Statistical analysis was performed using SurfStat (http://www.math.mcgill.ca/keith/surfstat/). We performed surface-based t-tests on these differences (Worsley et al., 2009). To improve statistical sensitivity and across-subject correspondence data were blurred using a surface-based diffusion kernel of 10 mm full-width-at-half-maximum (FWHM).

Evaluation of spatiotemporal surface template construction

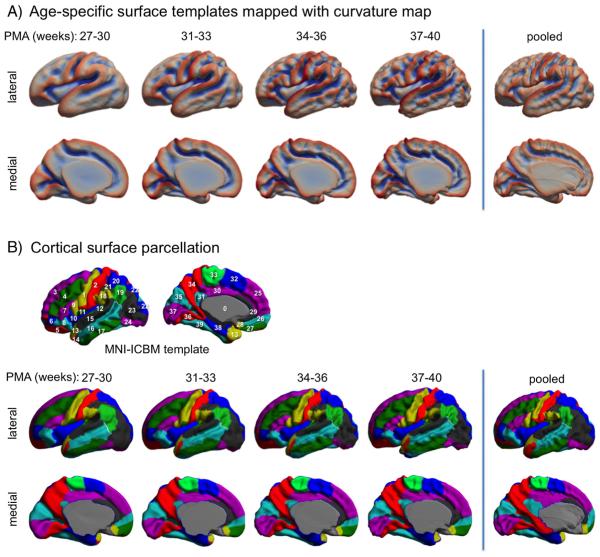
To assess whether the proposed age-specific template construction scheme would improve surface registration, we compared the shape between the age-specific templates and a template created by pooling all individuals in the section ‘Construction of age-specific surface templates and registration’. We also used a cortical parcellation (Tzourio-Mazoyer et al., 2002) that was originally mapped on the MNI-ICBM surface template. We projected this cortical subdivision to our oldest template (37–40 weeks) by the coregistration between this template and the MNI-ICBM template and subsequently mapped on the younger templates using the template-to-template coregistrations performed in the section ‘Construction of age-specific surface templates and registration’. We compared the anatomical correspondence of this map to that projected on the pooled template.

Results

Cross-method comparison of segmentation accuracy

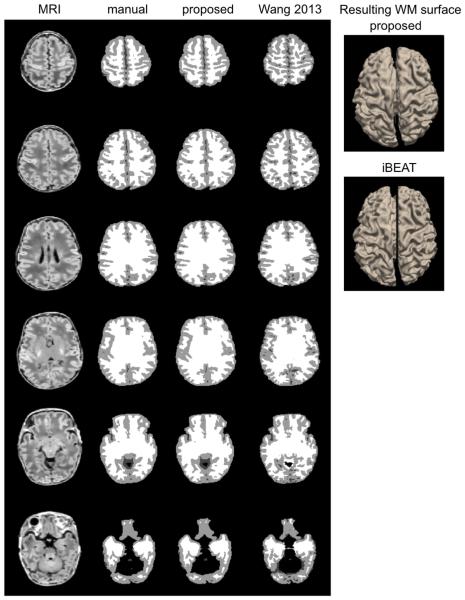
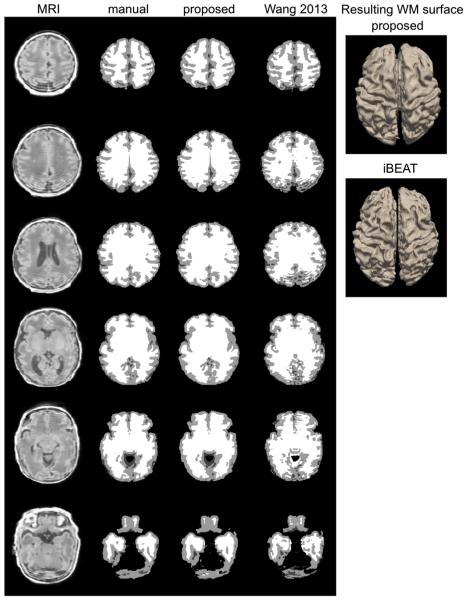
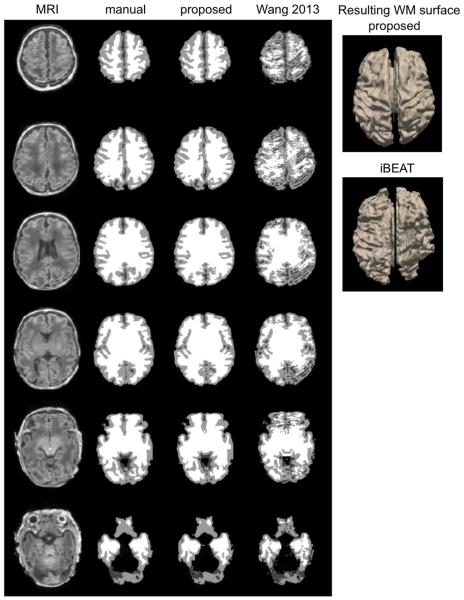
Manual labeling and all the automated segmentations for three representative subjects scanned at different ages and with different amounts of artifact are shown in Fig. 5. The proposed algorithm showed consistently similar tissue classification to the manual labeling, independent of the severity of motion artifact.

Fig. 5.

Segmentation and WM surface extraction. Three examples (top: 37 weeks PMA with minimal artifact; middle: 36 weeks PMA with moderate artifact; bottom: 34 weeks with severe artifact) are shown. The segmentation using the proposed method that was based on learning from incomplete manual labeling was compared to that using a nontraining-based method (iBEAT).

• a) Global assessment. Classification performance is listed in Table 3. Our method provided significantly higher accuracy than the three conventional methods: nonlocal mean method, joint fusion approach, and the iBEAT package, both in terms of overlap (Dice index: GM: 1.4–8.8%, WM: 1.9–4.2%; t > 3.2; FDR < 0.05) and boundary distance (Hm: 0.11–0.53 mm) to the manual labeling (t > 3.5; FDR < 0.01). The segmentation using our approach was slightly improved when using the “complete” manual labeling as training data (Dice index: 0.9–1.6%; Hm: 0.08 mm). There were trends that accuracy of the segmentation using “incomplete” labeling-based training decreased with increased age (r = 0.45; t = 2.5; FDR = 0.1) and increased motion artifact (r = 0.41; t = 2.2; FDR = 0.15), which disappeared when using “complete” labeling-based training (FDR > 0.3).

• b) Surface-based contour accuracy (Fig. 6). At the WM–GM interface, the proposed algorithm with “incomplete” manual labeling-based training underestimated bilaterally small areas of prefrontal, lateral and medial occipital cortical GM (i.e., WM–GM interface was misplaced inside the true cortex) and unilaterally a focal area of left middle temporal GM compared to manual labeling (mean: 0.15 ± 0.10 mm). In this area, the GM underestimation in the algorithm increased along with aging (t = 4.2; FDR < 0.01). We found no areas displaying significant correlations between GM underestimation and the degree of motion artifact (FDR = 0.2). The GM underestimation in our algorithm became insignificant when using “complete” labeling-based training (FDR = 0.2). No significant GM overestimation was observed (FDR > 0.3).

Table 3.

Performance of cortical GM/WM segmentation.

Algorithm	Dice similarity index (%)		Hausdorff distance (mm)
	GM	WM	WM
Wang et al. (2011)	84.6 ± 3.4	92.1 ± 2.2	0.81 ± 0.22
Nonlocal mean	91.2 ± 2.9	93.8 ± 1.9	0.48 ± 0.10
JointFusion	92.0 ± 2.4	94.4 ± 1.9	0.39 ± 0.08
NEOCIVET-I	93.4 ± 2.1	96.3 ± 1.6	0.28 ± 0.07
NEOCIVET-C	95.0 ± 1.8	97.2 ± 1.3	0.20 ± 0.05

NEOCIVET-I/-C indicates the proposed approach separately trained using incomplete/complete manual labeling. Nonlocal mean and JointFusion used incomplete manual labeling.

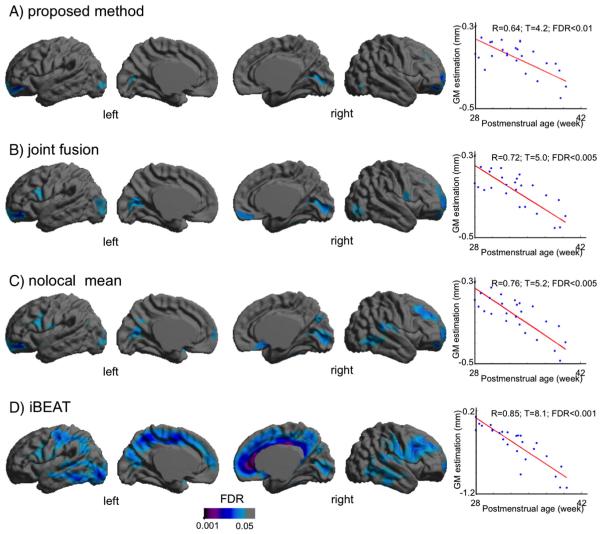
Fig. 6.

Regional segmentation error map. For each classification algorithm, we extracted the WM boundary and computed the point-wise surface-normal component of the displacement vector between automated and manual labels. The significant areas (FDR < 0.05) are those presenting GM underestimation in automated methods. The proposed approach exhibited only focal areas of significant segmentation error whereas other training-based methods (B, C) resulted in larger extents of the error and the non-training-based method (D) displayed broad areas of error. In the areas of significant error, all methods resulted in larger errors along with increased PMA.

The nonlocal mean and the joint fusion approaches had a similar pattern and larger extents of the segmentation errors (nonlocal: mean: 0.31 ± 0.24 mm; joint fusion: mean: 0.23 ± 0.16 mm; Fig. 6) relative to the proposed method. Underestimation of GM in the areas displaying segmentation errors were found to increase along with aging (nonlocal: t = 5.0, FDR > 0.005; joint fusion: t = 5.2, FDR > 0.005) and no significant GM under/overestimations were found in relation to motion artifact (FDR > 0.1).

The iBEAT segmentation algorithm showed GM overestimation in widespread areas of the cortex (mean: 0.93 ± 0.34 mm), with the primary area of large segmentation error located in the cingulate cortex. In the area demonstrating significant error, the GM overestimation of iBEAT significantly associated with the severity of motion artifact (t = 8.1; FDR < 0.001).

Evaluation of spatiotemporal surface templates

The constructed age-specific templates are shown in Fig. 7A. The templates captured general folding changes across different ages. Compared to the template created using the pooled dataset, the age-specific templates better characterized sulcal and gyral shapes, as sulcal fundi and gyral crowns presented with higher magnitudes of the mean curvature.

Fig. 7.

Results of spatiotemporal template construction. A. Age-specific surface templates and the template constructed using pooled data. The mean curvature was mapped on each template. The age-specific templates captured folding changes across different ages. B. Cortical surface parcellation. The parcellation was performed in the MNI-ICBM template and mapped to the neonatal templates by coregistration (see details in the section: ‘Evaluation of spatiotemporal surface template construction’). The pooled template displayed a noticeable misplacement of the mid-sagittal plane, which subsequently distort the placement of other labels on the medial surface. Cortical label index: 1. precentral; 2. postcentral; 3. superior frontal, dorsolateral; 4. middle frontal; 5. superior frontal, orbital; 6. middle frontal, orbital; 7. inferior frontal, triangular; 8. inferior frontal, orbital; 9. inferior frontal, opercular; 10. insula; 11. rolandic operculum; 12. Heschl; 13. temporal pole: superior temporal; 14. temporal pole: middle temporal; 15. superior temporal; 16. middle temporal; 17. inferior temporal; 18. supramarginal; 19. angular; 20. superior parietal; 21. inferior parietal; 22. superior occipital; 23. middle occipital; 24. inferior occipital; 25. superior frontal, medial; 26. superior frontal, medial orbital; 27. Rectus; 28. olfactory; 29. anterior cingulate; 30. median cingulate; 31. posterior cingulate; 32. supplementary motor area; 33. paracentral lobule; 34. precuneus; 35. cuneus; 36. lingual; 37. calcarine fissure & surrounding the cortex; 38. parahippocampal; 39. fusiform.

Mapping cortical parcellations (Fig. 7B), the spatiotemporal templates generally presented similar subdivisions of the cortex relative to the MNI-ICBM template. The labels were consistently located on the template between different ages. The pooled template, on the other hand, displayed a noticeable misplacement of mid-sagittal plane (gray in Fig. 7B), which subsequently distort the placement of other labels on the medial surface.

Application of NEOCIVET

Here we investigated the ability of the pipeline to assess developmental trajectory and the impact of brain injury on cortical structural development.

Cortical folding in brain development

Mixed-effect linear/polynomial nonlinear models were used to address both inter-subject effects and intra-subject changes between serial MRI scans by permitting multiple measurements per subject and thus increasing statistical power. For the subsequent analyses, we selected a linear or polynomial model that yielded the smallest fitting error. We first assessed a possible impact of MRI field strength on measurement of cortical folding by comparing the two groups (1.5 T vs. 3 T) while correcting for PMA at scan. We then assessed developmental trajectory of cortical folding by correlating the magnitudes of sulcal depth and curvature with PMA at the time of scanning. We included the presence of imaging evidence for moderate/severe perinatal brain injuries (i.e., intraventricular hemorrhage, cerebellar hemorrhage, white matter injury, and hydrocephalus) as covariates to correct for possible impact of such injuries on the cortical folding process.

Clinical utility of NEOCIVET

The brain of the extremely preterm (EPT) infant may grow and develop in a different way than it would in the womb. It has been suggested that EPT birth impedes brain growth even in the absence of major white-matter destruction or hemorrhage (Ajayi-Obe et al., 2000). We grouped our dataset into EPT (PMA at birth < 28 weeks; n = 71) and into moderately preterm (MPT) birth (32–34 weeks; n = 20; note that our neonatal dataset did not include anyone categorized as the late preterm birth [PMA > 34 weeks]). We then assessed difference in cortical folding between EPT and MPT groups while correcting for their PMA and the presence of imaging evidence for brain injuries.

Results

Measurement of cortical folding in development

MRI field strength slightly affected our morphometry as we found only a trend towards difference in cortical folding between the 1.5 T and 3 T groups (sulcal depth: t = 2.8, FDR = 0.08; mean curvature: t = 2.5, FDR = 0.1). As a result, cortical folding was underestimated in 1.5 T relative to 3 T data (overall depth = −0.002 mm/week; curvature = −0.0001/week). Even though this effect did not reach the significance after FDR correction, we included the field strength as a covariate in all the subsequent analyses in order to correct for its potential effects.

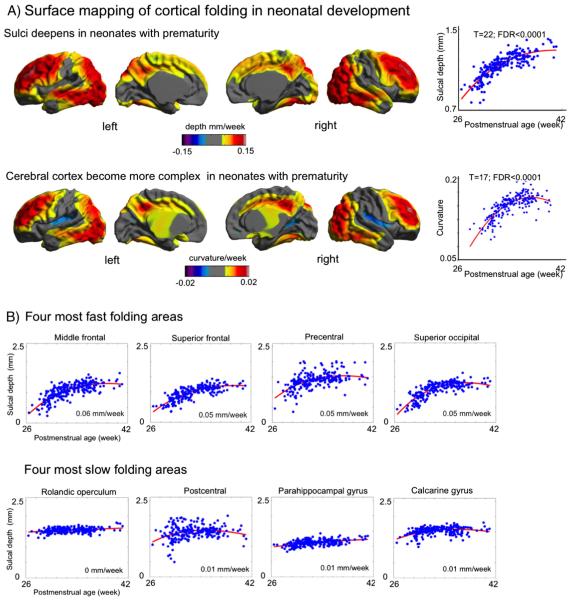
NEOCIVET identified increases in cortical folding over time in numerous cortical regions (overall sulcal depth: +0.021 mm/week; curvature: 0.0032/week) while folding was unchanged in major sulci that are known to develop earlier (FDR < 0.05; Fig. 8A). This pattern was nonlinear as 2nd order polynomial model fitted best (t = 22; FDR < 0.0001; vs. linear fitting: t = 18). A region of interest (ROI) analysis (Fig. 8B) showed that middle frontal, superior frontal, precentral, and superior occipital cortices displayed the most rapid cortical folding among all ROIs (depth 0.05–0.06 mm/week; curvature 0.005–0.008/week) whereas Rolandic operculum, postcentral, parahippocampal and calcarine cortices presented the slowest folding (depth: <0.008 mm/week; curvature: <0.001/week).

Fig. 8.

Trajectory of cortical folding in preterm newborns. A. NEOCIVET identified increases in cortical folding over time in numerous cortical regions while folding unchanged in major sulci that are known to develop earlier (FDR < 0.05). This pattern was nonlinear as 2nd order polynomial model fitted best. B. Analysis of the region of interests (ROIs) defined in Fig. 7. The folding trajectories measured using sulcal deepening are shown in the 4 fastest and 4 slowest folding areas.

Comparison of cortical folding between EPT and MPT

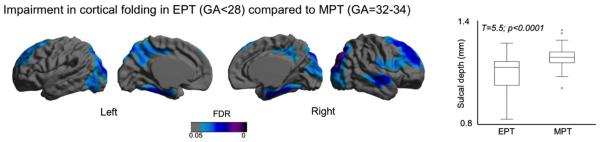
Comparing the folding pattern in the EPT to MPT, NEOCIVET found significant growth impairment in EPT, localized primarily in the regions developing postnatally (FDR < 0.05; Fig. 9), which included bilateral superior frontal, occipital, and basal temporal cortices, the bilateral precuneus, and the right superior/middle temporal cortex. The EPT group additionally was found to have growth impairment in bilateral parahippocampal gyri and part of the right central cortex that showed a slow growth postnatally (Fig. 8). We also tested the effects of birth weight on cortical morphology. The pattern was very similar to that found when comparing the EPT newborns with the MPT newborns (Supplementary Fig. 1). This is reasonable as birth weight and GA at birth was highly correlated (r = 0.7; p < 0.0001).

Fig. 9.

Impairment in cortical folding in extremely preterm (EPT, gestational age at birth < 28 weeks) newborns compared to moderate preterm newborns (MPT, 32–34 weeks). The significant areas (FDR < 0.05) indicate the shallower sulcal depth in the EPT group compared to MPT after correcting the postmenstrual at scan. The boxplot shows the folding distribution of the overall cortical surface for the two groups.

Discussion

We have introduced NEOCIVET, a variant of the CIVET pipeline that was designed to extract the cortical surface and measure relative morphometrics, for application to neonatal MRI. The patch-based joint-fusion approach for cortical tissue segmentation in NEOCIVET generally performed accurately across data with various ages and various motion artifacts. Nonetheless, it still presented focal areas of significant misclassification in the prefrontal and occipital cortices. This inaccurate segmentation was improved by refining the manual segmentation in the training data. NEOCIVET successfully characterized the developmental trajectory of cortical folding by improving a series of processes in CIVET. Our cross-data validation showed reliable performance of NEOCIVET when it was applied to two different sets of MRI images scanned under different field strengths. NEOCIVET revealed developmental disruption in extremely preterm (EPT) newborns relative to moderate preterm (MPT) newborns, demonstrating its potential to provide biomarkers of prematurity-related developmental outcome.

Given the complex nature of cortical folding, dramatic changes in brain structures in early development and relatively low and dynamically changing tissue contrast on MRI, improvement of performance in brain tissue segmentation is not trivial. We achieved this goal using the proposed method. Optimizing the whole cortical morphometry pipeline for neonatal brain MRIs, in particular for those with the motion artifact, is challenging and important in neonatal neuroimaging. In this context, the main novelty of the proposed technique lies in 1) a tissue segmentation method that is a mathematically sound integration of one label-fusion method to the other with different advantages and; 2) seamless incorporation of this segmentation technique into a well-established framework for cortical morphometry.

There have been numerous attempts to segment neonatal brain tissues. These works included the methods evaluated in the MICCAI 2012 Grand Challenge (Isgum et al., 2015) as well as more recent approaches that include a coupled level-set approach that utilized a population-based atlas and local intensity variability (Wang et al., 2011), a similar approach combined with the guidance of longitudinal scans (L. Wang et al., 2013), and a method that combined patch modeling with the level-set approach (Wang et al., 2014). More recent works uses a multi-step classifier utilizing supervised learning (Moeskops et al., 2015a), trains a classifier using multicontrast MRIs (Anbeek et al., 2013; Wang et al., 2015), or combines the patch analysis with Expectation–Maximization algorithm (Liu et al., 2016). Our segmentation algorithm, which combined patch analysis with a joint probabilistic label fusion, achieved a comparable accuracy in labeling brain tissues at various ages. Our approach, by modeling the pattern of motion artifacts through a strategic construction of the template library, further achieved reliable performance in segmentation of the neonatal MRIs with a degree of motion artifact that occurs in about 30% of acquisitions. None of the previous studies have evaluated the impact of motion artifact on their methods. The proposed method is training-based whereas iBEAT is not. By comparing training-based patch analysis techniques including our method with a non-training-based algorithm, we found an advisory result: i.e., patch-based approaches are more recommended for motion-corrupted data.

It is generally believed that use of prior information in (single/multiple) template-based approaches can bias the segmentation and may result in mis-segmentation. Our results showed a significant correlation between segmentation accuracy and the postmenstrual age when using incompletely annotated labeling in the training process. However, this effect became smaller using complete annotation. Our method did not show the relationship between segmentation accuracy and the severity of a motion artifact, suggesting that cooperation of a proper learning method such as patch-based segmentation with an inclusion of numerous motion-affected cases in the training set can improve the segmentation performance and can minimize the bias.

In the segmentation of neonatal brains, where intensity contrast and cortical morphology varies largely across different ages, the construction of a reliable template library is crucial for robust segmentation. Creation of a template (= atlas) inevitably involves an expert's manual labeling, which is very tedious and time-consuming. In our study, we tested the utility of partially annotated (or incomplete) segmentation that reduced the time of complete labeling by one half. Our evaluation showed that the overall performance using partial labeling showed only slightly reduced accuracy compared with complete annotation, which confirms a previous finding (Moeskops et al., 2015a). It is, nevertheless, worth noting that the regional mis-segmentation was significantly higher in partial labeling. The related cortical GM underestimation in older brains likely indicates that the higher cortical folding complexity in older neonatal brains may increase inaccuracy of the partial labeling, which was performed only through the coronal slices.

Previous studies that measured cortical folding have lacked point-wise correspondence between subjects, which challenges group-wise analysis of regional changes (Melbourne et al., 2014; Wright et al., 2014). We overcame this weakness using a surface registration that re-arranges mesh triangulation based on cortical morphology similarity between subjects. We initially hypothesized that a single averaged template cannot fully characterize the spatiotemporally dynamic brain anatomy and the co-registration of an individual surface to such a template may be erroneous. We indeed found that a template created from the whole population of our neonatal data could not capture the representative shape. By creating spatiotemporal surface templates and co-registering between templates, we optimized the point-wise correspondence between subjects with different ages.

Lyttelton et al. (2007) pointed out that a minimum of 30 subjects is required for a stable template construction. Using a large dataset obtained through the long-term UCSF Neonatal Brain Development Research Program, we constructed 4 different age-representative templates made using more than 40 subjects per each. To the best of our knowledge, there have been only two studies (Li et al., 2015; Wright et al., 2015) that constructed spatiotemporally varying surface templates. The temporal point-correspondence in this method was obtained using kernel regression. However, these age-specific templates were created based on a much smaller number of subjects than in our study (total scan numbers: 81 vs. 231).

Compared to the MNI-ICBM adult template, the flat area on the midsagittal plane was larger in our neonate templates due to our exclusion of part of the mesiotemporal lobe from the GM segmentation, where the tissue contrast was not sufficient for segmentation at this age. This shape difference from the adult atlas slightly influenced the registration performance in the neighboring area in the temporal lobe. However, a relatively small degree of manual correction would easily improve the current parcellation that was fully automatic and was based on the adult atlas.

The cortical folding in early development is known as an established biomarker to predict maturation (i.e., gestational age) and brain functional development (Dubois et al., 2008; Zilles et al., 2013). Visual inspection of brain MRI (Garel et al., 2001) and postmortem brains (Chi et al., 1977) could only identify the emergence of a new gyrus. By extracting parametric cortical surfaces, we could quantify the degree of cortical folding as well as identify gyral emergence. Our quantification of cortical gyration captured the nonlinear trajectory of folding increase in preterm newborns. Our finding of the nonlinear folding trajectory is supported by previous analyses of fetal brain MRI (Habas et al., 2012; Wright et al., 2014) that have found similar characteristics in an overlapped period of the fetal development.

The effects upon brain growth may differ in the presence of different perinatal clinical conditions such as preterm birth (Padilla et al., 2015), low body weight at birth (Parikh et al., 2013), prematurity-related brain injuries (Kim et al., accepted for publication; Kim et al., 2016; Tam et al., 2011b), and the related treatments (Tam et al., 2011a). Cortical folding may also be impaired as a result of such clinical factors (Engelhardt et al., 2015). We demonstrated the sensitivity of cortical folding metrics provided in NEOCIVET by revealing impaired cortical folding in extremely preterm (EPT) newborns compared to relatively late preterm newborns. The regions with decreased cortical folding in EPT newborns were mapped mostly in the cortical areas that rapidly fold postnatally, suggesting the presence of perinatal brain damage. The lack of overlap of our finding with a previous finding reporting areas of cortical volume loss in EPT (Padilla et al., 2015) suggests that a combined analysis of various morphological and microstructural measurements may be demanded to clarify the effects of the prematurity on brain development.

We focused only on reconstruction of the GM–WM interface (namely WM surface). Other measures such as cortical thickness and area were not considered in our study. It is also noted that cortical gyrification is conventionally measured on the middle surface created between pial and WM surfaces even though it has been done also on WM surface in numerous neonatal studies due to no modeling of the pial surface (Habas et al., 2012; Lefevre et al., 2015; Wright et al., 2014). We are currently expanding the current pipeline to derive the pial surface as in recent neonatal/infant brain studies (Li et al., 2014a; Lyall et al., 2015; Moeskops et al., 2015b).

The fast 2D MRI acquisition that creates stacks of image slices in many orientations is commonly used to correct for motion artifact in fetal brain imaging instead of using a post-processing like ours. After reconstructing a high-resolution volume image from these 2D image stacks, NEOCIVET is applicable to the analysis of cortical morphology in fetal brains.

We plan to include NEOCIVET in a future CIVET release that is open to the public through CBRAIN, a web-based platform for distributed processing and exchange of 3D/4D brain imaging data (http://mcin-cnim.ca/neuroimagingtechnologies/cbrain/).