Temporal dynamics of visual category representation in the macaque inferior temporal cortex

Decades of research indicate a temporal dynamic of visual-object categorization, depending on the level of category abstraction. To understand the neural mechanism of the temporal course of object categorization, we studied responses of neurons in inferotemporal cortex of macaque monkeys to presentation of natural object images. We observed that inferior temporal neurons represent mid-level categories (e.g., human faces) earlier than superordinate (e.g., animal)- and subordinate (e.g., face identity)-level categories.

Abstract

Object categories are recognized at multiple levels of hierarchical abstractions. Psychophysical studies have shown a more rapid perceptual access to the mid-level category information (e.g., human faces) than the higher (superordinate; e.g., animal) or the lower (subordinate; e.g., face identity) level. Mid-level category members share many features, whereas few features are shared among members of different mid-level categories. To understand better the neural basis of expedited access to mid-level category information, we examined neural responses of the inferior temporal (IT) cortex of macaque monkeys viewing a large number of object images. We found an earlier representation of mid-level categories in the IT population and single-unit responses compared with superordinate- and subordinate-level categories. The short-latency representation of mid-level category information shows that visual cortex first divides the category shape space at its sharpest boundaries, defined by high/low within/between-group similarity. This short-latency, mid-level category boundary map may be a prerequisite for representation of other categories at more global and finer scales.

NEW & NOTEWORTHY

Decades of research indicate a temporal dynamic of visual-object categorization, depending on the level of category abstraction. To understand the neural mechanism of the temporal course of object categorization, we studied responses of neurons in inferotemporal cortex of macaque monkeys to presentation of natural object images. We observed that inferior temporal neurons represent mid-level categories (e.g., human faces) earlier than superordinate (e.g., animal)- and subordinate (e.g., face identity)-level categories.

we recognize objects at different levels of hierarchical abstraction. Psychologists have commonly divided these levels of abstraction into three groups: superordinate (e.g., animal), mid-level or basic level (e.g., bird), and subordinate (e.g., eagle). Theoretical (Mack et al. 2009; Rosch et al. 1976) and psychophysical (Mack and Palmeri 2015; Murphy and Brownell 1985; Tanaka and Taylor 1991) studies have indicated a more rapid, perceptual access to the mid-level category information than the higher or the lower levels, suggesting speeded neural processing of the mid-level information. Other studies have challenged the mid-level advantage by demonstrating rapid access to the superordinate-level category information (Fabre-Thorpe et al. 2001; Macé et al. 2009; Poncet and Fabre-Thorpe 2014; Wu et al. 2014).

The time course of representation of category information in the neural responses involved in object recognition is poorly understood. Several studies have attempted to address this question using human magnetoencephalography (MEG) (Carlson et al. 2013; Pantazis et al. 2014) and event-related potential (ERP) (Thorpe et al. 1996), yielding conflicting results. MEG data show systematically longer latencies for more abstract category information (animate vs. inanimate) (Carlson et al. 2013; Pantazis et al. 2014), whereas ERP data show very short latencies for superordinate (animal) categories (Thorpe et al. 1996). However, MEG and ERP recordings have limited spatial resolutions and convey collective neural activities that may have originated from different parts of the brain. Furthermore, MEG and ERP signals reflect both the inputs and outputs to the cortex and may fail to reveal potential delays caused by local processing of information in the cortex. Thus the exact timing of the emergence of category information in specific neural structures cannot be revealed by these methods. The studying of the precise time course of the representation of categories requires recording the spiking activity of individual neurons.

In nonhuman primates, inferior temporal (IT) cortex lies at the end of the ventral visual pathway and is thought to be responsible for visual object recognition. IT is a purely visual area that contains various category-selective neurons (Bruce et al. 1981; Fujita et al. 1992; Kiani et al. 2007; Tanaka et al. 1991). It has been suggested that global (e.g., face category) and fine (e.g., face identity) information is conveyed by earlier and later parts of the IT neural responses, respectively (Matsumoto 2004; Sugase et al. 1999), indicating faster representation of more abstract information. This hypothesis, however, does not explain faster behavioral responses to basic-, mid-level categories.

To investigate the time course of categorical representation, we recorded the responses of IT neurons to a large number of diverse visual stimuli with multiple levels of hierarchical category abstraction. We show that IT population and single cells represented mid-level categories (e.g., faces and bodies) earlier than superordinate (e.g., animate/inanimate)- and subordinate (e.g., face identity)-level categories. These findings put constraints on models of visual object recognition by showing a stepwise processing of category information over time.

MATERIALS AND METHODS

We analyzed responses of neurons in the IT cortex of two male macaque monkeys (Kiani et al. 2005, 2007). Details of the experimental procedure have been explained in our previous publications. Briefly, responses of 674 neurons were recorded as the monkeys viewed a rapid presentation of a large number of natural and artificial visual stimuli. The stimulus set consisted of over 1,000 colored photographs of various objects on a gray background. The stimuli were presented at the center of a cathode ray tube monitor and were scaled to fit in a 7° window. To present our large stimulus set in the limited time that we could reliably record from each neuron, we used a rapid serial visual presentation (RSVP) (Edwards 2003; Földiák et al. 2004; Keysers et al. 2001). Each stimulus was shown for 105 ms without any interstimulus blank interval. During the presentation, the monkeys were required to maintain fixation within a window of ±2° at the center of the screen. The monkeys were rewarded with a drop of juice every 1.5–2 s for maintaining fixation

Calculation of the Temporal Dynamics of Category Information across the IT Population

At each moment in time, the representation of each stimulus by the IT neural population can be quantified by a vector whose elements are the firing rates of individual neurons. This population representation is a point in R^N space, where N is the number of recorded neurons. To ensure that the population representation is not biased by the high firing-rate neurons, we normalized the responses of each neuron by subtracting the mean and dividing by the SD of responses to all stimuli (z-score normalization).

We used nonclassical multidimensional scaling (MDS) on correlation distance (Shepard 1980; Torgerson 1958) and principal component analysis (PCA) (Pearson 1901) to illustrate the separation of IT responses for different categories in two dimensions. The MDS analysis was performed for a pair of categories, e.g., animate and inanimate, and two separate, 20 ms time intervals.

In the PCA method, the eigenvectors of covariance matrix were used to make a transform matrix from the high-dimensional neural space to the lower-dimensional data. We calculated the principle components for neural responses from 65 to 170 ms after stimulus onset. Then, with the use of the first two components with the greatest eigenvalues, we constructed a constant two-dimensional (2D) axis for representation of the high-dimensional neural-response space. The first two components (with the greatest eigenvalues) explain the most variance. We projected the neural responses in a 20-ms window on the 2D axis that was constructed by PCA. The window was moved in steps of 1 ms to make animations that show the arrangements of categories in time.

We used two different indices to quantify the discriminability of object categories based on the responses of the IT neural population: “separability index” (SI) and “classification accuracy.” Both indices were calculated using the neural response in a 20-ms window. The indices were, therefore, calculated for the high-dimensional neural responses. The window was moved in steps of 1 ms to measure the time course of the two indices.

Separability index.

The separation of two categories or groups of images based on IT population responses can be defined using the scatter matrix of the category members in R^N. The scatter matrix could be considered as an estimation of covariance in high-dimensional space. Two factors bear on separability: the within-category scatter and the between-category scatter (Duda et al. 2001). SI was defined as the ratio of between-category scatter and within-category scatter. The computation was performed in three steps. First, we calculated the center of mass of each category in R^N and also the mean across all categories, total mean.

Mean of each category

$${\mu }_i=\frac{1}{n_i}{\displaystyle \sum _{j\in C_i}\overrightarrow{r_j}}$$

Total mean

$$m=\frac{1}{n}{\displaystyle \sum _{i=1}^c{n}_i{\mu }_i}$$

where $\overrightarrow{r_j}$ is the population representation of stimulus j in category i, C_i is the set of stimuli that belong to category i, and n_i is the number of stimuli in C_i. n is the number of total stimuli.

Second, we calculated the between- and within-category scatters.

Within-category scatter for each category

$$S_i={{\displaystyle \sum _{j,k\in C_i}\left(\overrightarrow{r_j}-{\mu }_i\right)\left(\overrightarrow{r_k}-{\mu }_i\right)}}^T$$

Total within-category scatter

$$S_w={\displaystyle \sum _{i\in M}{S}_i}$$

Between-category scatter

$$S_B={\displaystyle \sum _{i\in M}{n}_i\left({\mu }_i-m\right){\left({\mu }_i-m\right)}^T}$$

where M is the set of categories for which SI is calculated. Note that S_i is the covariance matrix of neural responses calculated for the members of category i. S_W and S_B are estimates of neural covariance matrices based on category members and the categories, respectively. Because we use the representation of images in neural space, the dimension of S_W and S_B matrices is N·N (N is number of neurons).

Finally, SI was computed as

$$SI=\frac{\Vert S_B\Vert }{\Vert S_W\Vert }$$

where ||S|| indicates the norm of S. In this paper, we use a spectral norm (or ||S||) (Horn and Johnson 1990), because it takes into account both the variance and covariance of neural responses. Spectral norm is the largest singular value of S, and the singular value of matrix S describes the length of its geometrical expansion across major axes in the neural space. However, we obtained similar results with other matrix norms, such as trace and Frobenius norm (data not presented in this report).

Our method of calculating separability has several advantages. It can be applied to high-dimensional datasets (here, 674 neurons) with a limited number of data points. In our data, in some cases (such as human identity), it was as low as 6 and as high as 500. Finally, it properly takes into account both the variance and covariance of neural responses. Our method is closely related to Fisher information (Duda et al. 2001) and to the use of ANOVA in low-dimensional datasets (Lehmann and Romano 2006). Basically, SI is an index for evaluation of clustering quality. To calculate the SE of SI, we used a bootstrapping process (Efron and Tibshirani 1994). All of the calculations were repeated 500 times on a random selection of stimuli. We used the SD of bootstrap samples to compute confidence intervals and significances.

The SI was also used to measure the separation of two categories of stimuli that are described by physical shape features extracted from images. Each image is a point in R^N space, where N is the number of physical properties that define an image shape feature space. We calculated shape feature space using different physical models, including V1, V2, and V4 [the outputs of different layers in the Hierarchical Model (HMAX)] (Riesenhuber and Poggio 1999), foot print (Sripati and Olson 2010), and a combination of object area with three other basic global properties of the images—luminance, contrast, and aspect ratio (basic properties) (Baldassi et al. 2013). With the use of the foot-print model, we calculated the physical difference between each pair of images and made a distance matrix obtained from the foot-print model. Then, we used nonclassical MDS on the foot-print distance matrix to represent images on high-dimension feature space.

Classification accuracy.

For each category pair reported in this paper, we trained a support vector machine (SVM) classifier with a linear kernel (Cortes and Vapnick 1995) using the neural responses to 70% of the stimuli. Then, we measured the classification accuracy of the model for the remaining 30% of the stimuli. Training was done by using a least-square method for finding the separating hyperplane (Suykens and Vandewalle 1999). When classification among more than two categories was desired (face identity), a majority voting procedure between every pair of classes (one-vs.-one, max-wins voting strategy) was used (Hsu and Lin 2002). This means that all potential pairwise classifiers were run, and the label of test stimuli was obtained by majority vote of all classifiers. Because chance level depends on the number of categories involved in each classification, we report the normalized classification accuracy defined as (accuracy − chance)/(1 − chance). To calculate the SE of classification accuracy, we repeated the calculations 500 times. In each repetition, the stimuli were randomly partitioned into training and test sets.

To compare the time course of the representation of different categories, we measured the onset and peak times of the separability and classification accuracy indices. Peak time was defined as when the index exceeded 90% of its maximum for 2 ms or more. Onset time was defined as when the index exceeded 10% of its maximum for 10 ms or more. The main results are not sensitive to the change in the mentioned thresholds (10% and 90%). To measure the SE of the onset and peak times for SI and classification accuracy, we used a bootstrapping method. To compare latencies of different categories, we used the estimation confidence interval using bootstrap samples.

We also applied agglomerative cluster analysis (Johnson 1967) to the neural distances in the early (85–105 ms; poststimulus) and late (155–175 ms) phases of response and computed the tree structure. This is an unsupervised analysis, and no prior assumption is implied. Then, for all of the tested categories, we computed the nodes in the tree that best matched each category. The average of the two following ratios was used as a score for the match between category and the tree: ratio 1 = (number of category members under the node)/(total members of the category), and ratio 2 = (number of category members under the node)/(total stimuli under the node) (Kiani et al. 2007). To compare change in hierarchical clustering score for different categories in early and late phases of the response, we applied the estimation confidence interval using bootstrap samples.

Calculation of the Temporal Dynamics of Category Information in Individual Neurons

We used receiver operating characteristic (ROC) analysis (Green and Swets 1989) as a robust measure for the separation of response distributions elicited by each pair of the tested categories. The area under ROC (AUROC) quantifies the performance of an ideal observer for discriminating two categories based on the responses of a single neuron (0.5 indicates chance, and 1.0 indices perfect categorization performance). For each neuron and for each pair of categories, we measured AUROC for a sliding, 20-ms window in steps of 1 ms. For conditions in which separation of more than two categories was required (e.g., face identity) AUROC was calculated for all category pairs and then was averaged across the pairs. The peak and onset times of the ROC analysis were measured as they were done for the population indices.

A neuron was defined as category selective if its responses to images of a specific category (e.g., faces) were greater than its responses to other images (one-tailed t-test, P < 0.05). The degree of selectivity of each neuron for one category (C₁) vs. another category (C₂) was computed by d′ index, based on following formula (Green and Swets 1989)

$${d\prime }^{}=\frac{\left|M\left(C_1\right)-M\left(C_2\right)\right|}{\sqrt{\frac{{\sigma }^2\left(C_1\right)+{\sigma }^2\left(C_2\right)}{2}}}$$

where M(C₁) and M(C₂) are the mean response of the cell to categories C₁ and C₂, respectively, and σ²(C₁) and σ²(C₂) are the variances of the cell responses in categories C₁ and C₂, respectively.

RESULTS

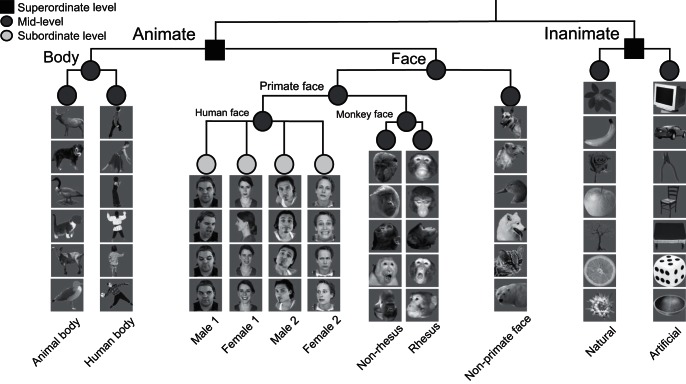
To examine the time course of category representation in the neural responses of IT cortex, we used our previously reported data of spiking activity of IT neurons (Kiani et al. 2005, 2007). In this experiment, two macaque monkeys passively viewed visual stimuli while responses of individual IT neurons (n = 674) were recorded. The recording sites included all subdivisions of IT except posterior IT (area TEO). The stimuli were images of >1,000 colored photographs of isolated natural and artificial objects. A large number of visual object categories at different levels of abstractions were included in the stimulus set, allowing us to explore the time course of category information at different levels of hierarchy (Fig. 1). Category structure of the stimulus set was first formed on an intuitive basis by dividing the stimuli into animate and inanimate categories. Animate stimuli were further divided into faces and bodies, inanimate stimuli into natural and artificial, bodies into human and animal body, and faces into primate and nonprimate faces. Finally, to provide a base for comparison of the relative time of emergence of category (mid-level or basic level) compared with identity (subordinate level) information, human faces were divided into four different individuals for whom we had at least six different images. Monkey faces were also divided into rhesus and nonrhesus faces. These categorical divisions are consistent with previous reports about natural categorical representations in the monkey and human IT (Chao et al. 1999; Kiani et al. 2007; Kriegeskorte et al. 2008; Martin et al. 1996).

Fig. 1.

Hierarchical category structure of the stimuli. Three category levels are defined: 1) superordinate level: animate vs. inanimate; 2) mid-level (basic level): face vs. body, primate faces vs. nonprimate faces, human body vs. animal body, rhesus face vs. nonrhesus face, and natural inanimate vs. artificial inanimate; 3) subordinate level: human individual identity. Photos courtesy of Hemera Photo-Objects/Jupiterimages.

Figure 2 shows the projection of the stimuli on a 2D map, created by applying MDS to the responses of the IT neural population. Each point represents one of the stimuli in the categories shown in each panel. MDS creates a low-dimensional map of the stimuli so that the distances of stimuli on the map match with the distances of the population response patterns elicited by the stimuli. We performed MDS for two separate time intervals: 1) the initial IT responses during 85–105 ms and 2) the later responses during 155–175 ms after stimulus onset. MDS analysis revealed that the early responses conveyed category information, separating faces and bodies and primate faces and nonprimate faces but failed to discriminate the higher (animates and inanimates) and lower level (face identities). The later responses, however, differentiated mid- as well as superordinate- and subordinate-level categories. On average, 67% of variance was captured by the first two dimensions of the MDS in the early phase of responses and 74% in the late phase.

Fig. 2.

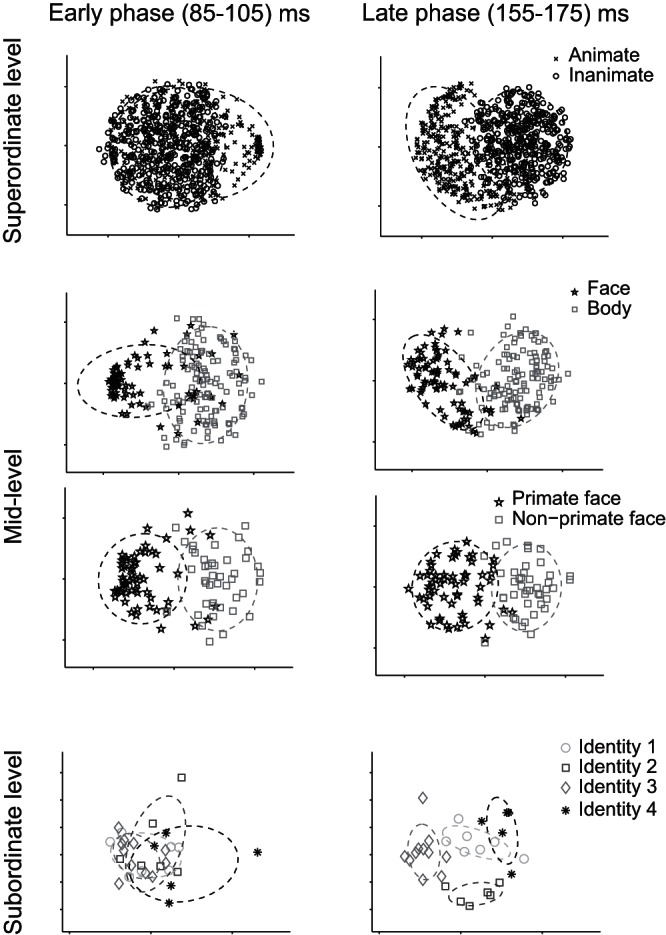
2D Representations of categories at 3 levels of hierarchy in early and late phases of neural responses. These representations are generated using multidimensional scaling on the neural population responses at 3 levels of the hierarchy. Early (85–105 ms; left) and late (155–175 ms; right) phases of the neural responses are shown. The rows show animate vs. inanimate, face vs. body, primate faces vs. nonprimate faces, and 4 human face identities. Ellipses demonstrate 2 SD of the distribution of category members in the 2D representations.

To visualize the time course of category representation, we constructed a constant 2D axis using the first two PCA components derived from the neural response, from 65–170 ms after stimulus onset. We projected the neural responses in a 20-ms window on the 2D axis. The window moved at 1 ms steps from 0 to 210 ms after stimulus onset (see materials and methods). We concatenated the 2D maps that were generated at consecutive times into a movie. In Supplemental Movie 1, the actual stimuli are shown. Sixty-two percent of variance was captured by the first two dimensions of the PCA (Fig. 3). Supplemental Movie 1 shows the temporal evolution of the differential representation of the categories by the IT population. Consistent with the MDS result shown in the movie, human and monkey (primate) faces start to move away from other stimuli soon after the stimulus onset. Later, bodies separate from faces and the other stimuli. Finally, animate and inanimate images form two distinct clusters. At this time, different human face stimuli form separate clusters.

Fig. 3.

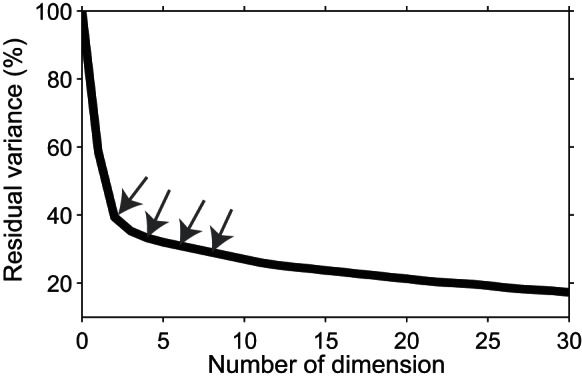
The percentage of unexplained variance. The percentage of unexplained (residual) variance against the number of PCA dimensions used for construction of the movie. The first 2 dimensions of the PCA analysis reported here were used to make the movie. The neural population responses to all stimuli in the 65- to 170-ms time window were used to extract the principle dimensions by PCA. The gray arrows indicate the values for second, fourth, sixth, and eighth dimensions. The explained (100 − unexplained) variance quantifies how well information is represented in the reduced, low-dimensional neural space.

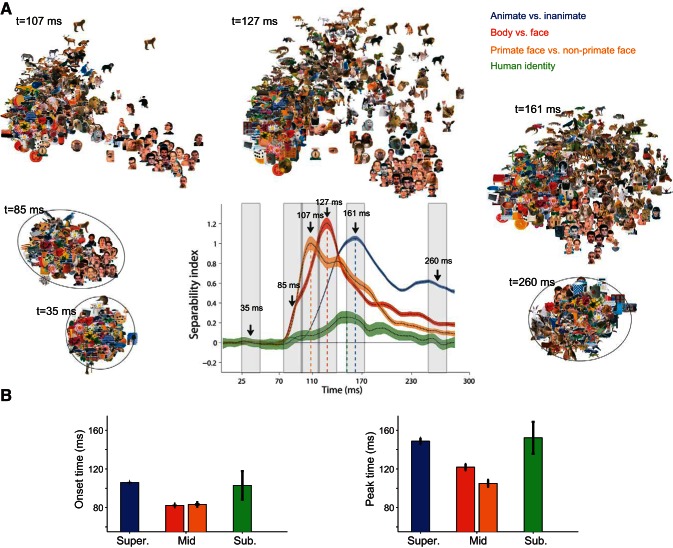
To quantify the strength and reliability of category representation in the IT neural population, we used an index that measures the ratio of between-category distances and within-category scatter of the stimuli based on IT neural responses (SI; see materials and methods). High values of SI indicate that the tested categories have large, between-category distances and small, within-category scatter. Figure 4A shows the time course of SI for different levels of object categorization. SI reached significant values for all categorization levels at some point after the stimulus onset. We observed earlier onset of significant SI values for body vs. face and for primate (monkey and human) vs. nonprimate faces (mid-level) compared with SI values for animates vs. inanimates (superordinate level) and for face identities (subordinate level). The mid-level categorizations had both an earlier onset (P < 0.001) and earlier peak (P < 0.001; Fig. 4B; onset latencies: animate vs. inanimate 105.9 ± 0.64 ms, face vs. body 82.3 ± 0.74 ms, primate faces vs. nonprimate faces 83.3 ± 1.26 ms, and face identity 103 ± 14.7 ms; peak latencies of the above-mentioned categories were 148.7 ± 3.3 ms, 121.9 ± 3.2 ms, 105.1 ± 3.6 ms, and 152.2 ± 16.5 ms, respectively). Six time windows of the movie were selected to illustrate the representation of stimuli at baseline and around onset and peak latencies of categorization. The earlier separation of mid-level categories in the movie is consistent with the earlier onset and peak latencies of SI.

Fig. 4.

Time course of the separability index (SI) for the 3 levels of hierarchy. A: time courses of SI. The time courses were offset by the mean value of index at the 1- to 50-ms interval from stimulus onset. Shaded areas represent SD, calculated using the bootstrap procedure. Surrounding scatter plots are 6 frames from Supplemental Movie 1. The 107-, 127-, and 161-ms time points correspond to SI peak times of primate faces vs. nonprimate faces, face vs. body, and animate vs. inanimate, respectively. B: onset (left) and peak (right) latencies of SI; onset latency is defined as the first time that the index exceeds 10% of its maximum value for 10 ms. Peak latency is defined as the time that the index exceeds 90% of its maximum value at least for 2 ms.

To examine the time course of representation of other mid-level categories, the onset latencies for a wide range of categories were calculated and are provided in Table 1. A trend toward earlier representation of mid-level categories was observed in all of the tested conditions.

Table 1.

Onset and peak latencies of SI for different levels of categorization

Category Name	Onset, ms	Peak, ms
Superordinate Level
Animate vs. inanimate	105.9 ± 0.64	148.7 ± 3.3
Mid-level
Human vs. animal	79.5 ± 0.73*	97.8 ± 4.00*
Monkey vs. animal	87.4 ± 4.74*	108.7 ± 4.75*
Face
Human vs. animal	82.9 ± 1.13*	102.4 ± 3.09*
Monkey vs. animal	87.5 ± 2.93*	123.4 ± 7.21*
Human vs. bird	88.8 ± 2.46*	139.2 ± 12.58
Monkey vs. bird	93.4 ± 4.84†	127.8 ± 8.88†
Human vs. cat	88.0 ± 2.04*	136.9 ± 6.83‡
Monkey vs. human	89.4 ± 2.18*	139.2 ± 3.74†
Rhesus vs. nonrhesus	100.3 ± 11.63	125.3 ± 7.34*
Body
Human vs. animal	98.7 ± 5.24	133.3 ± 10.7
Human vs. 4-limb	93.8 ± 3.26†	126.7 ± 9.74‡
Bird vs. 4-limb	97.8 ± 6.74	125.8 ± 13.78‡
Human vs. bird	101.4 ± 4.45	138.9 ± 11.6
Inanimate
Artificial vs. natural	91.6 ± 5.1†	126.4 ± 4.57*
Car vs. furniture	98.6 ± 9.07	131.2 ± 5.53†
Car vs. common tools	102.8 ± 7.91	134.8 ± 6.20†
Subordinate Level
Human identity	103.3 ± 14.70	152.2 ± 16.50
Woman vs. man	103.5 ± 15.61	173.6 ± 49.27
Monkey identity	128.5 ± 28.13	156.2 ± 24.75

SI, separability index.

Significant against superordinate:

^*P < 0.001;

^†P < 0.01;

^‡P < 0.05.

In our analysis of category time course, there was no impact of the selected level of the contrasted category (e.g., all other stimuli, higher-level category, and categories at the same level with the one being tested) on the main finding. Onset and peak times of almost all of the tested face and body categories were earlier than the related times for superordinate categorization (Tables 2 and 3).

Table 2.

The peak and onset latencies of SI for face and body categorizations against 3 different contrast categories (all other, inanimate, and other animate stimuli)

	Peak	Onset
Animate vs. Inanimate	105.9 ± 0.64	148.7 ± 3.3
Face
vs. all other	81.4 ± 0.56*	111.2 ± 2.71*
vs. inanimate	83.7 ± 0.54*	124 ± 3.15*
vs. other animate	81.4 ± 0.7*	117.2 ± 3.2*
Primate
vs. all other	81.3 ± 0.58*	100.8 ± 3*
vs. inanimate	84.3 ± 0.49*	111.7 ± 3.17*
vs. other animate	82.1 ± 0.65*	100.9 ± 2.65*
Nonprimate
vs. all other	91.8 ± 4.49*	131.7 ± 5.25†
vs. inanimate	97.8 ± 1.18*	126.2 ± 2.26*
vs. other animate	101.2 ± 7.21	139.2 ± 7.28
Monkey
vs. all other	86.9 ± 2.4*	108.6 ± 6.61*
vs. inanimate	92.1 ± 1.85*	124.3 ± 2.37*
vs. other animate	90 ± 3.29*	123.9 ± 4.61*
Human
vs. all other	82.5 ± 0.53*	98.3 ± 0.96*
vs. inanimate	84.4 ± 0.52*	108.2 ± 2.45*
vs. other animate	82.4 ± 0.53*	99.9 ± 1.51*
Cat
vs. all other	81.3 ± 9.81†	120.6 ± 70.41
vs. inanimate	103 ± 1.93	129 ± 3.49*
vs. other animate	NS	NS
Bird
vs. all other	82.3 ± 7.3*	88.6 ± 6.11*
vs. inanimate	101.9 ± 3.71	129.8 ± 5.87*
vs. other animate	NS	NS
Body
vs. all other	93.9 ± 0.63*	119.8 ± 3.21*
vs. inanimate	96.1 ± 0.58*	127.5 ± 2.81*
vs. other animate	93.6 ± 1.64*	124.6 ± 5.05*
Four-limb
vs. all other	95 ± 0.84*	120.5 ± 2.75*
vs. inanimate	97.9 ± 0.79*	126.4 ± 2.67*
vs. other animate	95 ± 1.43*	126.7 ± 5.45*
Human
vs. all other	89.2 ± 1.69*	131.7 ± 20.8
vs. inanimate	92.8 ± 2.65*	124.4 ± 4.06*
vs. other animate	88.3 ± 2.96*	154.7 ± 20.21
Monkey
vs. all other	95.9 ± 3.24*	118.4 ± 5.36*
vs. inanimate	99.1 ± 2.5†	128.1 ± 4.42*
vs. other animate	95.9 ± 4.7‡	127.5 ± 10.21‡
Bird
vs. all other	95.7 ± 1.64*	120.5 ± 4.63*
vs. inanimate	98.1 ± 1.41*	126.9 ± 3.19*
vs. other animate	95.8 ± 2.12*	125.4 ± 7.21*
Cat
vs. all other	NS	NS
vs. inanimate	99.3 ± 2.41†	124.8 ± 5.1*
vs. other animate	101.6 ± 4.99	121.5 ± 6.29*
Dog
vs. all other	NS	NS
vs. inanimate	99.8 ± 2.53†	127.4 ± 4.23*
vs. other animate	97 ± 5.54	124.8 ± 9.59†

NS, not significant.

Significant against superordinate:

^*P < 0.001;

^†P < 0.01;

^‡P < 0.05.

Table 3.

The peak and onset latencies of category information indexed by SI for several animate categories tested against inanimate stimuli

Category Name	Onset, ms	Peak, ms
Animate	105.9 ± 0.64	148.7 ± 3.3
Human	83.5 ± 0.52*	113.1 ± 4.18*
Animal	94.6 ± 0.61*	140.8 ± 5.17
Monkey	95.3 ± 1.19*	126.3 ± 3.02*
Bird	98.3 ± 1.41*	127 ± 2.65*
Cat	100.6 ± 1.75†	128.4 ± 3.77*
Reptile	93.7 ± 8.37	126.5 ± 6.38*
Insect	96.7 ± 4.59‡	122.5 ± 4.8*
Butterfly	97.1 ± 6.41	120.3 ± 4.15*
Hand	94.6 ± 2.49*	132.1 ± 7.11‡
Fish	99.5 ± 10.9	136 ± 6.78‡

Significant against superordinate:

^*P < 0.001;

^†P < 0.01;

^‡P < 0.05.

To examine the contribution and significance of face stimuli in the earlier emergence of mid- compared with superordinate-level categories, we discarded the neural responses to face stimuli and repeated the SI time course analysis. Mid-level advantage did not depend on responses to faces (Table 4). We also excluded face neurons from our cell population and calculated onset and peak times of various body category pairs (i.e., body images without visible faces). The mid-level advantage was observed in the nonface IT cell population using only body stimuli. To explore the effect of face information on representation of body categories, we used 29 pairs of exactly similar body images but with and without face (12 pairs of 4-limb; 9 pairs of bird body; and 8 pairs of other body images) and repeated the SI time course analysis for these categories against inanimate stimuli (Table 5; body category consists of all 29 pairs). In each selected pair, all shape features are the same except faces. The latencies extracted from the SI time course of bodies with and without face tested against inanimate, and the average of SI values [window (70–170) ms] was considered as a measure of represented category information. The results confirm the importance of face information in representation of category information (greater average SI value for bodies with face than bodies without face; SI_{bodies-with-face} = 0.58 ± 0.01, SI_{bodies-without-face} = 0.26 ± 0.01; P < 0.001) but also show that the main temporal structure reported here does not purely depend on face stimuli. Category information of both image groups (bodies with and without face) emerged earlier than superordinate. There was no significant difference between latencies of bodies with and without face.

Table 4.

Onset and peak latencies of SI for faceless animate

Category Name	Onset, ms	Peak, ms
Superordinate Level
Animate vs. inanimate	105.9 ± 0.64	148.7 ± 3.3
vs. inanimate
Nonface animate	96.4 ± 1.25*	129.3 ± 3.63*
Body	98.6 ± 1.83*	128.8 ± 3.83*
Human body	91.3 ± 3.25*	122.4 ± 2.49*
Four-limb body	96.4 ± 2.09*	126.6 ± 4.17*
Bird body	96.3 ± 1.27*	129.4 ± 4.08*
Other animate	93.4 ± 3.63*	123.6 ± 4.2*
vs. other animate
Body	97.2 ± 2.55*	129.4 ± 5.03*
Human body	97.8 ± 3.11†	128.8 ± 4.88*
Four-limb body	97.4 ± 3.01†	131 ± 6.04†
Bird body	100.7 ± 3.52	131.8 ± 6.68‡

Significant against superordinate:

^*P < 0.001;

^†P < 0.01;

^‡P < 0.05.

Table 5.

The peak and onset latencies of category information indexed by SI for bodies with and without face tested against inanimate stimuli

Category Name	Onset, ms		Peak, ms
Animate	105.9 ± 0.64		148.7 ± 3.3
	with Face	without Face	with Face	without Face
Body	98.1 ± 1.44*	95.8 ± 2.46*	125.2 ± 3.17*	125.6 ± 4.07*
Bird body	100.7 ± 2.91†	104.0 ± 7.81	125.2 ± 4.8*	126.7 ± 6.33*
Four-limb body	98.1 ± 2.47*	96.5 ± 3.31‡	123.5 ± 3.52*	123.5 ± 4.11*

Significant against superordinate:

^*P < 0.001;

^†P < 0.05;

^‡P < 0.01.

To test further the temporal dynamics of category information in the IT population code, we trained biologically plausible linear classifiers (Hung et al. 2005; Meyers et al. 2008) to discriminate categories at different levels of abstraction based on the IT neural responses. Fig. 5A shows the classification accuracy. The classification accuracy was cross validated and normalized so that zero indicates that the classifier is at chance, and one indicates that the classifier performs perfectly. As expected from our SI and MDS analysis, classification accuracy increased significantly sooner for the mid-level categorizations than for the low and high levels (Fig. 5A). The earliest time that a downstream structure could discriminate the mid-level categories above chance level was 72.5 ± 2.9 and 76.1 ± 1.7 ms after stimulus onset for faces/bodies and for primate/nonprimate faces, respectively (Fig. 5B). The earliest significant discriminations for the high- and low-level discrimination were 10–30 ms later (Fig. 5B; P < 0.01; animate and inanimate discrimination, 85.4 ± 4.7 ms; face-identity discrimination, 95.7 ± 8.2 ms). The differences were even larger (35–50 ms, P < 0.01) for the time of peak performance (Fig. 5B; faces vs. bodies, 116.6 ± 4.4 ms; primate vs. nonprimate faces, 106.8 ± 4.6 ms; animate vs. inanimate, 135 ± 7.5 ms; and face identity, 150.4 ± 5.1 ms).

Fig. 5.

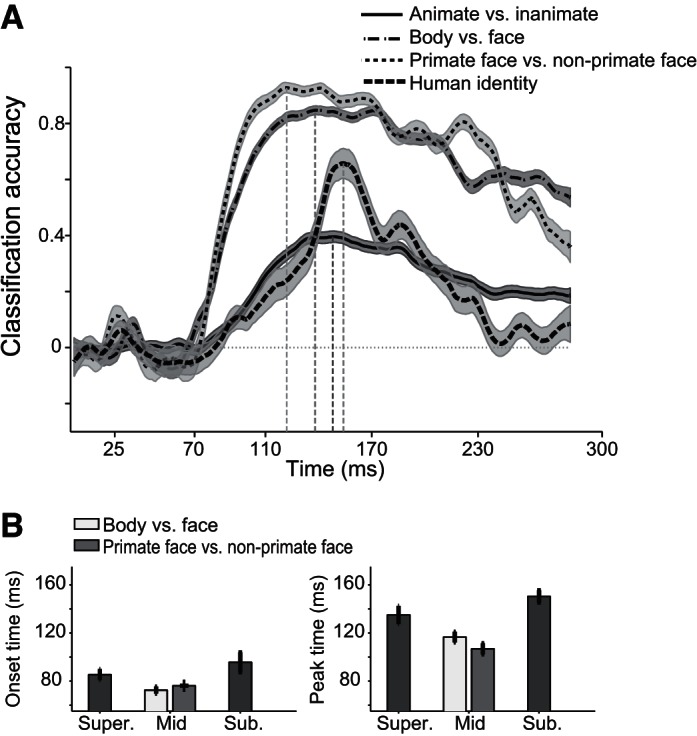
Time courses of classification accuracy for the 3 levels of hierarchy. A: time courses of normalized classification accuracy using SVM. Shaded areas are the SE. B: corresponding onset (left) and peak (right) latencies.

We used an agglomerative cluster analysis at early and late phases of response to examine the time course of category organization at a different level of hierarchy in an unsupervised way (see materials and methods for details). Figure 6 illustrates the hierarchical cluster trees computed at early (Fig. 6, A and B) and late (Fig. 6C) phases of neural response. Face, body, other animate, and inanimate category members at the lowest level of hierarchy are indicated. Face stimuli clustered at the earliest time interval (Fig. 6A; 85–105 ms), and following them, 10 ms later (Fig. 6B; 95–115 ms), body images clustered. Both face and body images (mid-level) clustered earlier than superordinate animate stimuli (Fig. 6C; 155–175 ms). Consistent with our previous analysis, the hierarchical analysis at different time bins provides unsupervised evidence for later clustering of superordinate rather than mid-level categories. For all tested categories depicted in Table 1, we calculated the hierarchical score based on ratios 1 and 2 [ratio 1 = (number of category members under the node)/(total members of the category), and ratio 2 = (number of category members under the node)/(total stimuli under the node)]. Table 6 shows the degrees of match between categories and nodes in the reconstructed tree for the early (85–105 ms) and late (155–175 ms) phases of responses. The categories with significant value across at least one of the phases were included in Table 6 (significance was computed against chance value calculated in 0–20 ms by 95% confidence interval). Table 6 also indicates the increase in hierarchical score from early to late phase of response [(Score_late − Score_early)/Score_late]. Consistent with our main finding, the superordinate categories (animate and inanimate) have a bigger change in hierarchical scores than all tested mid-level categories. So the unsupervised organization of mid-levels and superordinate in cluster tree at the early phase of response also supports earlier representation of mid-level categories in both animate and inanimate categories.

Fig. 6.

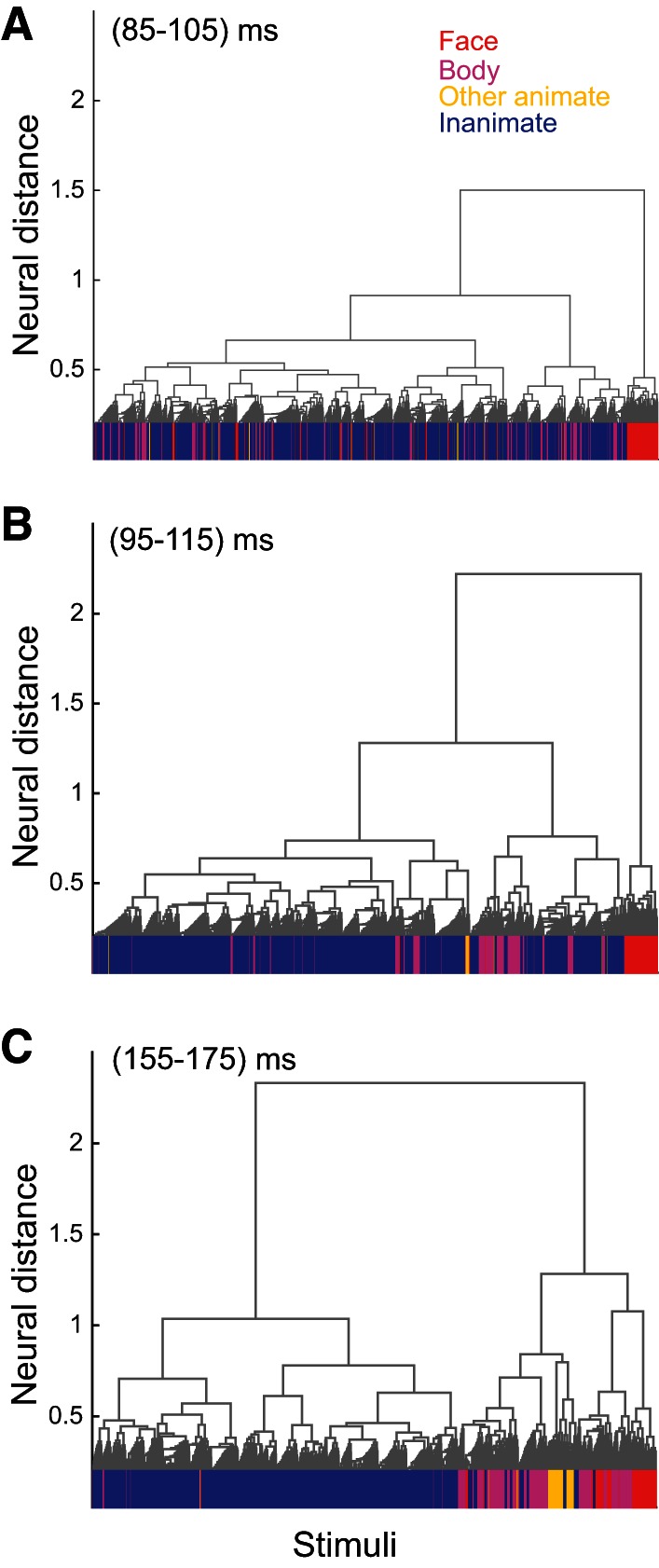
Hierarchical clustering of IT response patterns at early and late phase of response. Hierarchical cluster trees were computed at early (A and B; 85–105 and 95–115 ms, respectively) and late (C; 155–175 ms) phases of response. At the lowest level of the tree (horizontal axes), face, body, other animate, and inanimate exemplars are indicated by red, purple, yellow, and blue lines, respectively. All animates, excluding face and body categories, make “other animate” stimuli. The vertical axes indicates average neural distance between the stimuli of subclusters.

Table 6.

Degrees of match between categories and nodes in the tree, reconstructed from responses of IT cells in early and late phase of neural responses

Category Name	Scoreearly, 85–105 ms	Scorelate, 155–175 ms	(Slate − Searly)/Slate
Animate	0.68 ± 0.01	0.77 ± 0.05	0.13 ± 0.08
Human	0.78 ± 0.03	0.73 ± 0.04	−0.07 ± 0.05*
Animal	0.67 ± 0.00	0.62 ± 0.04	−0.06 ± 0.06*
Face	0.69 ± 0.03	0.67 ± 0.03	−0.03 ± 0.05†
Primate face	0.79 ± 0.03	0.71 ± 0.04	−0.09 ± 0.05*
Human face	0.94 ± 0.03	0.87 ± 0.05	−0.08 ± 0.06*
Rhesus face	0.51 ± 0.00	0.5 ± 0.04	−0.02 ± 0.08†
Body	0.60 ± 0.00	0.56 ± 0.03	−0.06 ± 0.05*
Four-limb body	0.56 ± 0.00	0.56 ± 0.02	0.00 ± 0.04†
Inanimate	0.76 ± 0.00	0.83 ± 0.03	0.09 ± 0.04
Natural	0.70 ± 0.00	0.73 ± 0.03	0.05 ± 0.05
Artificial	0.56 ± 0.01	0.55 ± 0.02	0.00 ± 0.03*

IT, inferior temporal; S_late, Score_late; S_early, Score_early.

Significant against corresponding superordinate:

^*P < 0.01;

^†P < 0.05.

To assess the timing of category representation in the single-cell responses, the AUROC was used (see materials and methods). AUROC quantifies the performance of an ideal observer for discriminating two categories based on the responses of a single neuron. The time courses of AUROC of individual neurons show later emergence of superordinate and subordinate categories.

To choose neurons for single-cell analysis, we defined selectivity of single cells, measured by d′ (see materials and methods), to three pairs of categories: animate vs. inanimate, face vs. body, and primate faces vs. nonprimate faces. For each of these category pairs, we performed a randomization test on the d′ (randomizing class labels) and defined selectivity based on the significance of a randomization test (P < 0.05). There were 126 neurons selective to all of the tested category pairs. Peak and onset time were defined as when the AUROC exceeded 90% and 10% of its maximum for 2 and 10 ms, respectively.

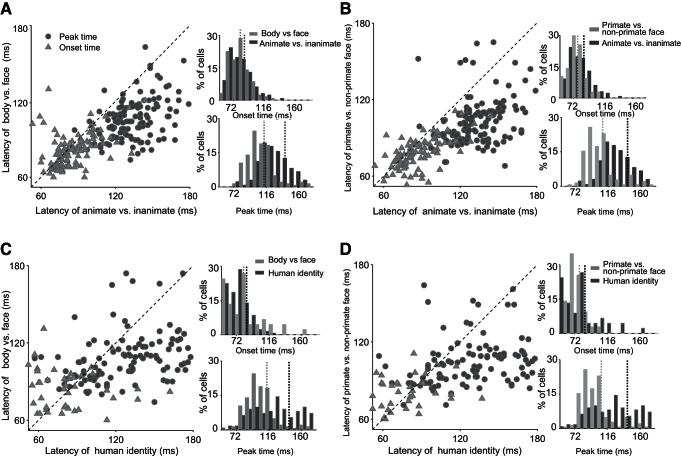
Figure 7 illustrates single-cell latencies for different levels of object categories. Each point in the scatter plots depicts one category-selective cell. Onset latencies are earlier for mid-level (faces vs. bodies, 81.6 ± 1.20 ms; primate faces vs. nonprimate faces, 78.3 ± 1.16 ms) compared with superordinate (animate vs. inanimate, 87.4 ± 1.43 ms, one-tailed t-test, P < 0.05)- and subordinate (human face identity, 85.7 ± 4.85 ms, one-tailed t-test against the latency of face vs. body categorization, P < 0.05)-level categorizations. A larger difference existed in the peak latencies (peak latency of faces vs. bodies, 113.1 ± 2.23 ms; primate vs. nonprimate faces, 107.8 ± 2.19 ms; animate vs. inanimate, 141.4 ± 2.62 ms, P < 0.001; face identity, 143.0 ± 3.77 ms, P < 0.001). Similar results were obtained when we used all responsive neurons with significant AUROC at 65–170 ms (one-tailed t-test).

Fig. 7.

Onset and peak-latency scatter plots of single cells. Each panel (A–D) shows the scatter plot of onset (triangles) and peak (circles) latencies of 1 pair of categories against another pair (A: face vs. body against animate vs. inanimate, B: primate faces vs. nonprimate faces against animate vs. inanimate, C: face vs. body against human identity, and D: primate faces vs. nonprimate faces against human identity). Each point represents 1 cell. The distributions of latencies (top: onset; bottom: peak) for the corresponding categories are depicted on the right side of the scatter plots. The dashed, vertical lines in distribution plots show the mean latencies.

To examine the relation between category selectivity of individual neurons and onset/peak time of category discrimination, we measured the correlation between d′ values of each neuron and onset/peak time of category discrimination for various category pairs. There was a significant correlation between selectivity and onset/peak latency for almost all of the tested category pairs (onset latencies: animate vs. inanimate r = −0.29, P < 0.001; face vs. body r = −0.15, P < 0.01; primate faces vs. nonprimate faces r = −0.13, P < 0.01; and face identity r = 0.15, P = 0.21; peak latencies of the above-mentioned categories: r = −0.36, P < 0.05; r = −0.41, P < 0.05; r = −0.32, P < 0.05; and r = −0.19, P < 0.05, respectively).

To examine further the temporal dynamic of category information in the IT neural ensemble, consisting of neurons without any category selectivity, we calculated SI for 157 neurons that show no significant response to face, body, animate, and inanimate categories (one-tailed t-test, P < 0.05). Interestingly, we found a similar trend for the time course of category representation in the population activity of these noncategory neurons (Fig. 8). The time course of SI in these neurons shows earlier manifestation of mid-level categories in responses of all of the IT subpopulation (Fig. 8B; onset latencies: animate vs. inanimate 135.6 ± 16.21 ms, face vs. body 96.2 ± 4.34 ms, primate faces vs. nonprimate faces 105.1 ± 10.87 ms, and face identity 132.9 ± 32.32 ms; peak latencies of the above-mentioned categories: 193.8 ± 7.91 ms, 190.8 ± 8.19 ms, 143.3 ± 7.05 ms, and 169.6 ± 44.83 ms, respectively).

Fig. 8.

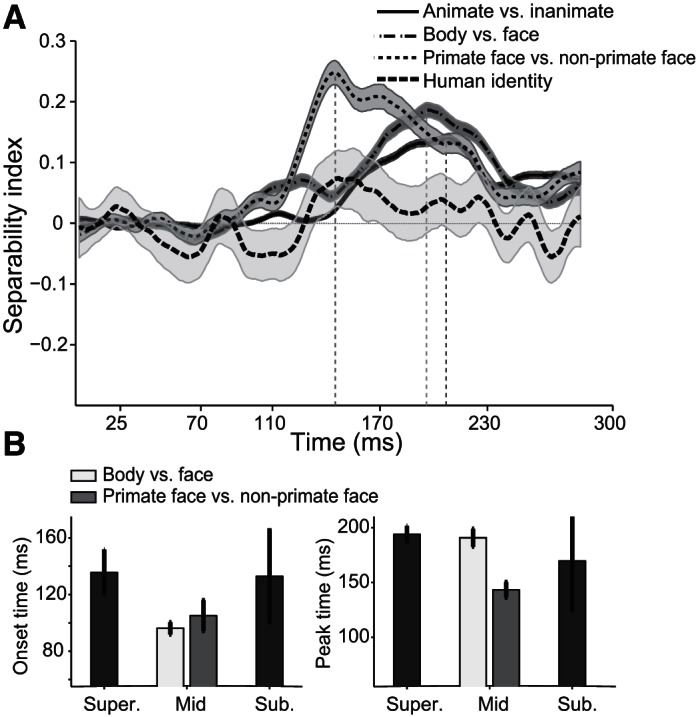
Time courses and latencies of separability index (SI) in the nonselective cell population at the 3 levels of hierarchy. A: time courses of nonselective cell population. Nonselective cells are those that show no significant selectivity to face, body, animate, or inanimate images. Selectivity of the target category against the other stimuli is examined by 1-tailed t-test, P < 0.05. B: the mean onset (left) and mean peak (right) latencies are shown. Shaded areas (A) and error bars (B) represent SE.

It is possible that within/between physical feature similarities of visual stimuli determine the time course of the tested pairs of categories. To address this issue, we measured the physical similarity of images using V1, V2, and V4 models. These models are constructed using the outputs of different layers in the HMAX model (Riesenhuber and Poggio 1999). In addition, we used foot-print (Sripati and Olson 2010) and basic global properties of the images (object area, luminance, contrast, and aspect ratio) (Baldassi et al. 2013). We then used the ratio of within/between class physical similarity values of different pairs of categories (25 mid-levels and 1 superordinate) to calculate SI. So SI was used to measure the separation of two categories of stimuli that are described by both physical shape features and neural response. The distributions of onset and peak latencies for 25 pairs of mid-level categories, which are extracted from the time course of SI computed by neural data, are shown in Fig. 9A. Animate/inanimate onset and peak category representation times were always later than the latencies of tested, 25 pairs of mid-levels categories. There is a significant difference between the mean of onset and peak latencies of 25 pairs of tested mid-level categories and the peak and onset latencies of animate vs. inanimate (Fig. 9A; t-test, P < 0.001). With the use of each of the above-mentioned physical models, we calculated SI values for physical distinction of different pairs of categories (25 mid-levels and 1 superordinate). All of the SI values for physical distinction were bias corrected by random shuffling of category labels, 1,000 times in each tested category pair. Here, the negative values show nonsignificant physical distinctions. We plotted the SI values extracted from physical features against the onset and peak latencies extracted from the time course of SI computed by neural data for each pair of 26 tested categories (Fig. 9B). These analyses revealed no correlation between latency of category representation and within/between physical similarity for any of the tested models.

Fig. 9.

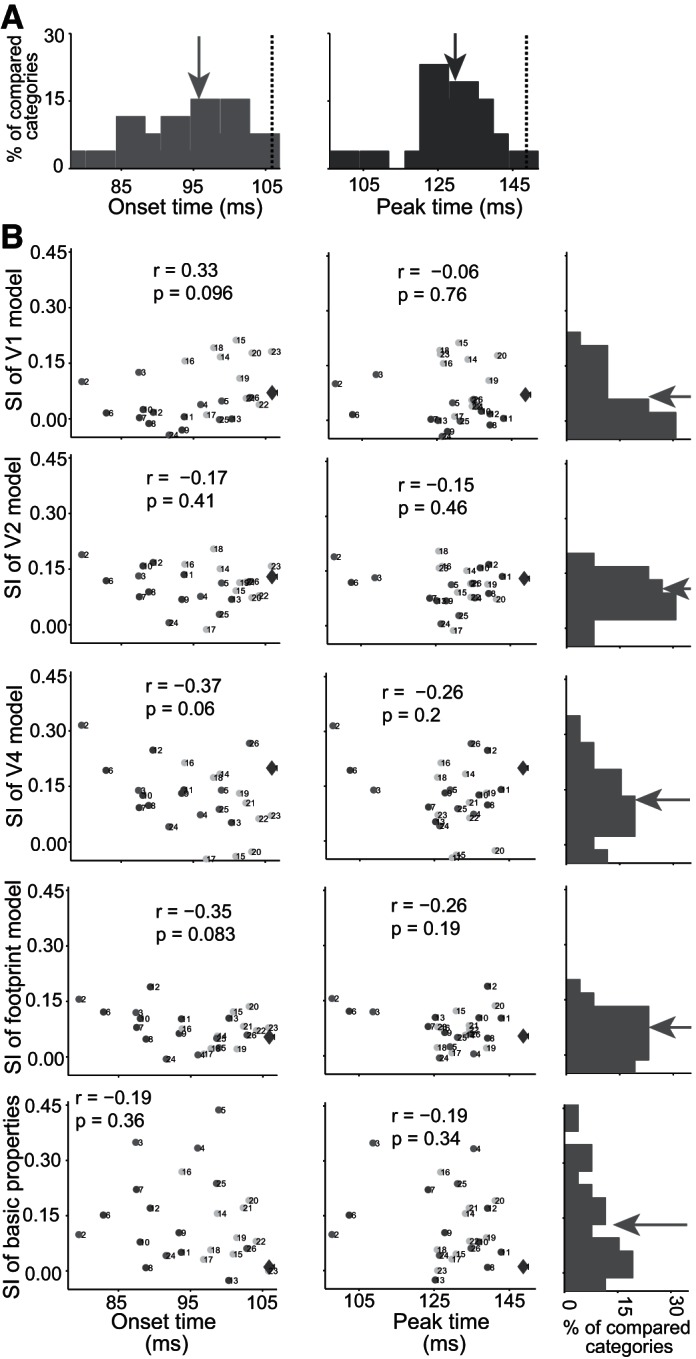
Distribution of latencies and relationship of physical similarity and latencies of category representation in IT cortex. A: the distribution of onset (left) and peak (right) latencies for 26 pairs of tested categories (25 mid-levels and 1 superordinate level). The dashed lines show the onset (left) and peak (right) latency of superordinate level, animate vs. inanimate, and the arrows show the mean value of latency distributions. B: in each panel, we calculated the within/between class physical distinction using SI and different physical models (V1, V2, V4, foot print, and basic properties). All of the SI values for physical distinction were bias corrected by random shuffling of category labels, 1,000 times in each tested mid-level contrast category. There was no significant correlation between latency of category representation and within/between physical similarity for any of the tested models (the correlation coefficient values with their P values are shown in each panel). The big diamond shows the animate vs. inanimate categorization; numbers next to each point indicate the following: 1, animate vs. inanimate; 2, human vs. animal; 3, monkey vs. animal; 4, hand vs. reptile; 5, hand vs. butterfly; 6, human face vs. animal face; 7, monkey face vs. animal face; 8, human face vs. bird face; 9, monkey face vs. bird face; 10, human face vs. cat face; 11, monkey face vs. cat face; 12, monkey face vs. human face; 13, rhesus face vs. nonrhesus face; 14, human body vs. animal body; 15, monkey body vs. animal body; 16, human body vs. 4-limb body; 17, monkey body vs. 4-limb body; 18, bird body vs. 4-limb body; 19, human body vs. bird body; 20, monkey body vs. bird body; 21, human body vs. cat body; 22, human body vs. dog body; 23, bird body vs. cat body; 24, artificial inanimate vs. natural inanimate; 25, car vs. furniture; 26, car vs. common tools. The arrows show the mean value of latency distributions.

To study further the effect of within-category member similarity on the neural representation of mid-level categories, we selected a subset of faces and bodies with equal within-similarity distances (diverse faces and similar bodies). The basic global properties of the images (object area, luminance, contrast, and aspect ratio) (Baldassi et al. 2013) were used to compute within-category distance. New animate, face, and body categories were made using face and body shape distance-matched stimuli. There is no significant difference in mean of within-similarity distances for selected bodies and faces (within-similarity distance before selection: face = 0.43 ± 0.24, body = 0.62 ± 0.41; within-similarity distance after selection: face = 0.51 ± 0.37, body = 0.50 ± 0.33; t-test, P = 0.14). Consistent with our main findings, the early representation of mid-level categories compared with superordinate was observed when using neural responses of these shape-distance-matched categories (Table 7). These results also suggest that highly similar face stimuli are not the major factor in the late representation of superordinate category.

Table 7.

The peak and onset latencies of category information for faces and bodies equalized within similarity

Category Name	Onset	Peak
Modified animate vs. inanimate	99.6 ± 2.00	146.9 ± 4.51
Diverse face vs. similar body	88.4 ± 5.33*	131.6 ± 3.96†
Divers face vs. inanimate	89.0 ± 1.37†	128.6 ± 2.94†
Similar body vs. inanimate	97.3 ± 0.75	127.1 ± 2.47†
Diverse face vs. other animate	83.6 ± 1.48†	120.7 ± 4.27†
Similar body vs. other animate	93.2 ± 1.93†	123.8 ± 6.8†

Significant against corresponding superordinate:

^*P < 0.05;

^†P < 0.001.

To examine a potential, functional difference between IT subdivisions, we compared the temporal dynamics of category representation using data of neurons located in areas lower bank of superior temporal sulcus (STS), ventral inferotemporal cortex (TEv), dorsal inferotemporal cortex (TEd), as well as the posterior part of TE (TEp)/anterior part of TE (TEa; with and without STS neurons). The locations of neurons were defined using MRI and electrophysiological mapping (Kiani et al. 2007). Whereas the results of the SI analysis were noisier, due to smaller sample sizes, earlier representation of mid-level categories compared with superordinate and subordinate was observed in all of the tested areas (Table 8).

Table 8.

The peak and onset category information latencies in different IT subdivisions

	Animate vs. Inanimate		Face vs. Body		Primate Face vs. Nonprimate Face		Human Identity
	Onset	Peak	Onset	Peak	Onset	Peak	Onset	Peak
STS	96.0 ± 0.88	131.3 ± 2.90	85.4 ± 0.84*	125.9 ± 4.47	84.9 ± 1.63*	119.3 ± 7.85	105 ± 20.86	145.7 ± 13.04
TEd	95.5 ± 0.83	138.4 ± 4.53	89.1 ± 0.75*	120.9 ± 2.18*	85.4 ± 1.40*	115.6 ± 9.77†	93.1 ± 6.63	160 ± 12.79
TEv	99.9 ± 0.59	145.8 ± 3.30	81 ± 0.83*	121.3 ± 3.69*	83.5 ± 1.38*	104.5 ± 7.52*	16.9 ± 16.23	158.9 ± 31.35
TEp (with STS)	93.1 ± 0.76	130.0 ± 2.94	89.2 ± 0.97*	119.4 ± 3.98†	88.3 ± 1.7†	124.0 ± 11.14	120.6 ± 15.73	155.3 ± 9.09
TEa (with STS)	99.8 ± 0.75	146.8 ± 2.85	81.0 ± 0.72*	124.8 ± 4.33*	82.5 ± 1.16*	103.1 ± 3.25*	104.6 ± 14.84	156.3 ± 19.46
TEp (without STS)	93.9 ± 0.77	130.2 ± 2.95	89.8 ± 0.93*	119.6 ± 3.75†	88.4 ± 1.69*	121.0 ± 6.67	134.7 ± 8.14	158.3 ± 10.11
TEa (without STS)	100 ± 0.80	148.5 ± 3.51	80.8 ± 0.74*	124.3 ± 3.89*	82.9 ± 1.47*	103 ± 2.23*	102.8 ± 13.81	155.5 ± 20.7

Significant against corresponding superordinate:

^*P < 0.001;

^†P < 0.01.

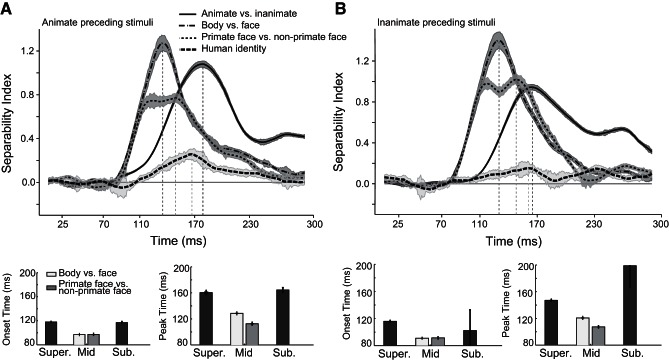
To control the potential impact of spike contamination evoked by preceding stimuli that may occur in RSVP, we divided trials into two groups: trials in which an animate image preceded the stimulus and those in which an inanimate image preceded the stimulus (Fig. 10). We then calculated the SI values of each group separately. The advantage of mid-level categories was preserved in both conditions (condition a, onset latencies: animate vs. inanimate 118 ± 0.14 ms, face vs. body 97.1 ± 0.31 ms, primate faces vs. nonprimate faces 97.4 ± 0.52 ms, and face identity 117.1 ± 1.62 ms; peak latencies of the above-mentioned categories: 160.4 ± 1.5 ms, 128.6 ± 0.89 ms, 112.6 ± 1.11 ms, and 164.4 ± 3.62 ms, respectively; condition b, onset latencies: animate vs. inanimate 116 ± 0.22 ms, face vs. body 91 ± 0 ms, primate faces vs. nonprimate faces 91.5 ± 0.52 ms, and face identity 102.4 ± 30.51 ms; peak latencies of the above-mentioned categories: 147.1 ± 0.69 ms, 120.7 ± 0.92 ms, 107.4 ± 0.61 ms, and 198.9 ± 32.5 ms, respectively).

Fig. 10.

The time course of category representation in trial with animate or inanimate preceding stimuli. Time courses of separability index, the mean onset, and mean peak latencies were computed in trials in which an animate image preceded the stimulus (A) and those in which an inanimate image preceded the stimulus (B). Shaded areas (top) and error bars (bottom) represent SE.

DISCUSSION

In this paper, we studied the time course of visual object category representation in neural responses of the IT cortex of macaque monkeys. We found that IT neurons represent mid-level categories (e.g., human faces) earlier than superordinate (e.g., animal)- and subordinate (e.g., face identity)-level categories. Responses of the IT neural population, both category-selective and nonselective neurons, show a temporal order of category information with earlier emergence of mid-level category information. A similar time course of category information was observed in the activity of individual neurons with strong category selectivity.

Psychophysical studies have shown that perceptual access to the mid-level category information occurs earlier than access to the higher- or lower-level categories. These findings suggest an expedited neural processing of the mid-level information (Mack and Palmeri 2015; Rosch et al. 1976; Tanaka and Taylor 1991). Our results suggest the neural signature of this mid-level advantage phenomenon. The short-latency emergence of mid-level category information shows that the category shape space is divided first at its sharpest boundaries, defined by high/low within/between-group similarity. This short-latency, mid-level category boundary map may be used for representation of category boundaries at higher or lower levels of abstraction in later stages of the neural processing. In addition, these findings put constraints on the models of object recognition by showing temporally structured processing of category information in the visual cortex. Our study surpasses past literature and reconciles seemingly contradictory results in previous studies, as we explain below. However, it should be noted that the neurophysiological data reported here were collected from passively viewing monkeys; therefore, relevance of the temporal course of neural responses to behavioral visual categorization cannot be directly established in our study and needs further investigations.

Neural correlates of object categorization have been widely investigated in the ventral visual pathway (Bruce et al. 1981; Kiani et al. 2007; Kriegeskorte et al. 2008; Tanaka 2003). Cells in IT cortex respond selectively to specific categories at different levels of abstraction (Desimone et al. 1984; Fujita et al. 1992; Kiani et al. 2007; Tsao 2006). However, previous studies have generated contradictory results about the time course of categorical representations. The recording of IT responses to faces of humans and monkeys has revealed that IT neurons distinguish monkey faces from human faces earlier than they distinguish face identities (Matsumoto 2004; Sugase et al. 1999). These authors have hypothesized a coarse-to-fine temporal gradient for the representation of information in IT and have speculated that global information could act as a header to prepare downstream areas for processing of finer-grained information.

On the other hand, recent MEG studies in humans have suggested an opposite temporal gradient in which finer-grained information about visual stimuli is represented before more global information. The decoding of MEG signals results in earlier recognition of exemplar members (i.e., image identities) than more abstract categories (e.g., animate vs. inanimate) (Carlson et al. 2013). Multivariate pattern classification of the time course of human MEG signals shows a delayed representation of superordinate categories compared with individual images (Pantazis et al. 2014). With the use of data from our lab [Kiani et al. (2007) and current results], Pantazis et al. (2014) report a similar pattern in their human MEG data and the category structure of the spiking activity of IT neurons. There is, however, an unresolved discrepancy between the latency of category representations in IT spiking activity and MEG and EEG studies. Unlike the MEG and EEG studies that show earlier representation of individual stimuli, IT-spiking activity supports an earlier representation of mid-level categories. The discrepancy is likely to originate from differences in signals recorded by the two techniques. Whereas spiking activity represents neuronal outputs, MEG and EEG signals reflect a complex combination of synaptic inputs, neuronal outputs, synchrony, and spatial alignment of charges along axons and dendrites in large populations of neurons (Ikeda et al. 2002; Murakami and Okada 2006; Okada et al. 1997). The resolution of the discrepancy between the two techniques requires a deeper understanding of the mapping of MEG and EEG signals to spiking activity. However, it is likely that the earlier representation of individual stimuli in MEG and EEG signals reflects a larger difference in IT input, whereas the earlier representation of mid-level categories in spiking activity emerges from the processing of the input information by IT neurons.

Our results are immune to several confounding factors that have been shown to bias measurements of response latencies. First, note that within-category heterogeneity of stimuli increases monotonically from subordinate- to mid- to superordinate-level categories. Therefore, delayed representation of superordinate and subordinate categories cannot be attributed to their higher diversity or stimulus dissimilarity compared with mid-level categories. Secondly, the differential time course of category representations cannot be attributed to the number of cells selective for each category. The temporal advantage of mid-level categories persisted even after exclusion of category-selective cells. Thirdly, our results were not biased by a preferential representation of mid-level categories in an individual monkey. The main results were independently replicated in each monkey. Fourthly, the observed results were not shaped by the number of stimuli that belonged to each category. To examine the potential impact of sample-size bias, we equalized the number of samples in pairs of categories and repeated the SI and SVM analyses. Mid-level category information emerged earlier in all of the tested category pairs. Fifthly, spike contamination, evoked by preceding stimuli that may occur in RSVP, did not impact the mid-level advantage. Finally, the differential time course of the category representations could not be attributed to a systematic difference in luminance or contrast across the categories. The nested structure of the hierarchical categories removes concerns about biases caused by such stimulus inhomogeneity. Ruling out these confounds enhances the reliability of our conclusions about the slower emergence of superordinate and subordinate category information in IT cortex.

To be able to present a large number of stimulus images, we used an RSVP paradigm with short stimulus-presentation duration and no interstimulus interval. It is plausible that neural responses in the RSVP condition are different than when longer-presentation duration with long interstimulus intervals is used. It should be noted that in natural life, as we explore the visual world, retinal images of visual stimuli change relatively rapidly without any no-stimulation intervals. So the potential interaction of stimuli in the RSVP condition on neural responses may mimic the real-world condition better than stimulation paradigms with long interstimulus intervals. In addition, cells in the monkey IT cortex preserve their stimulus selectivity in RSVP as fast as 14–28 ms/stimulus (Edwards 2003; Földiák et al. 2004; Keysers et al. 2001). Furthermore, backward masking has a minimal effect on the initial part of neuronal responses when the stimulus onset asynchrony is <80 ms (Kovács et al. 1995; Rolls and Tovee 1994). We have previously used the same image set and tested IT neural response latency of human and animal faces for two presentation methods: 245 ms presentation time with 245 ms blank interval and 105 ms presentation time without any blank interval (Kiani et al. 2005). We found no significant difference between face response latency of these two presentation methods.

With the consideration of the limitations of the stimulus set, we could calculate SI values for only 3 subordinate categories compared with 16 mid-level conditions. On the other hand, we only examine one superordinate category pair (animate vs. inanimate) with high within-member shape variability. A more balanced stimulus image set is needed to understand fully the subordinate vs. mid-level category information time courses.

The psychophysical studies that have challenged the mid-level advantage by demonstrating rapid access to the superordinate-level category information (Fabre-Thorpe et al. 2001; Macé et al. 2009; Poncet and Fabre-Thorpe 2014; Wu et al. 2014) are not necessarily contradictory to our findings. As in the animal-detection experiments, subjects could rely on detection of face or body (or even face or body components) and perform the task efficiently. The short-latency, mid-level category information (animal face or animal body) could underlie the short-latency behavioral responses in these animal-detection tasks. Consistent with our results, a new, functional MRI and psychophysics study with a large real-world object image set shows that participants were significantly faster for basic-level categorization than superordinate and subordinate. With the use of multivoxel analysis, it suggests that neural patterns of mid-level (basic-level) categories represent an optimal level of within-category similarity (category cohesion) and between-category dissimilarity (category distinctiveness) (Iordan et al. 2015).

One explanation for the mid-level advantage is that mid-level and superordinate categories might be represented in IT and prefrontal cortex, respectively. Mid-level categories have low within-class to between-class shape variability and high behavioral saliency. Recognition of these categories can take place earlier, since the perceptual processing of category information occurs within the visual cortex and does not need involvement of the higher brain areas, such as prefrontal cortex. Categorization of objects at higher levels of the category hierarchy requires more complex computations, since at these levels, within- to between-class shape variability is relatively high, and parsing the objects into correct groups is more time consuming, resulting in delayed perceptual access. Consistent with this hypothesis, neural representation of novel category boundaries has been shown in the prefrontal cortex (Freedman et al. 2003), whereas short-latency category information of highly familiar objects has been indicated in the IT neural responses (Anderson et al. 2008; Hung et al. 2005; Kiani et al. 2005).

An alternative explanation for earlier emergence of the mid-level categories in our data might be the impact of face images on the temporal course of category information reported here. Faces and bodies with face comprised a large proportion of our animate images. In our image set, faces—and especially human faces—were highly similar. The low within-category shape distance of faces and short-latency responses to faces (Kiani et al. 2005) may result in early emergence of the mid-level animate categories in our analysis. Our control analysis of neural responses to 29 pairs of exactly similar bodies, with and without face, suggests that earlier mid-level category information observed here does not exclusively depend on neural responses to faces.

Learning is shown to diminish the time difference between categorization at the mid- and subordinate levels (Johnson and Mervis 1997; Tanaka and Taylor 1991). Long-term learning can redefine the perceptual category boundaries mapped in IT (Baker et al. 2002; Seger and Miller 2010). Consistent with these findings, in our data, earlier onset of category information was observed for some of the more familiar mid-level categories (e.g., human and monkey face/body) but not the other less familiar ones (e.g., bird bodies). The peak response time of mid-level categories, however, was earlier than the superordinate and subordinate ones in all of the tested categories, including the less familiar ones (Table 1). This finding implies that the learning-dependent, expedited processing of some mid-level categories affects onset but not peak time of category representation in IT.

With the use of an entirely data-driven method, we have previously shown that neural responses in IT cortex discriminate animate from inanimate objects (Kiani et al. 2007; Kriegeskorte et al. 2008). However, this finding does not necessarily imply semantic representation of object categories. Animate/inanimate category boundary representation in IT could be defined by similarity of physical features within the animate images. The nature of these critical/diagnostic features is not known. Our current results, using the same data, show that the temporal order of emergence of category information is not affected by the degree of within/between-category shape similarity, defined by several predominant shape-representation models. We believe both phenomena emerge because of the selectivity of IT neurons to critical features that distinguish and discriminate biologically relevant categories. Some recent studies have questioned the presence of a true animate/inanimate boundary representation in IT (Baldassi et al. 2013; Yamins et al. 2014). The discrepancies observed in these studies and in our previous and current reports could be due to differences in the recorded IT area, stimulus set size, and stimulus shape variability. Neurons in the anterior IT tend to be more category selective (Kiani et al. 2007; Tanaka et al. 1991). Thus a population analysis performed using a larger proportion of posterior neurons could fail to show animate/inanimate differentiation. Furthermore, monkeys in our study were raised as pets and had far-richer visual experience than the regular experimental monkeys. Formation of category-boundary representation has been shown to be experience dependent (Anderson et al. 2008).

In summary, we examined the time course of category information in the neural responses of IT cortex of macaque monkeys viewing a large number of object images and found an earlier representation of mid-level categories both in the IT population and in single-unit responses. The faster emergence of mid-level category information suggests that visual cortex first divides the category shape space at its sharpest boundaries based on high within-group and low between-group similarity. This mid-level advantage in IT neural responses provides a mechanism for the mid-level advantage in perception and behavior.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

R.K. and H.E. conception and design of research; R.K. and H.E. performed experiments; M-R.A.D., A-H.V., and R.K. analyzed data; M-R.A.D., A-H.V., R.K., M.N.A., B.N.A., and H.E. interpreted results of experiments; M-R.A.D. prepared figures; M-R.A.D., A-H.V., R.K., M.N.A., B.N.A., and H.E. drafted manuscript; M-R.A.D., A-H.V., R.K., M.N.A., B.N.A., and H.E. edited and revised manuscript; M-R.A.D. and H.E. approved final version of manuscript.