Phasor Analysis of Local ICS Detects Heterogeneity in Size and Number of Intracellular Vesicles

Abstract

Organelles represent the scale of organization immediately below that of the cell itself, and their composition, size, and number are tailored to their function. Monitoring the size and number of organelles in live cells is relevant for many applications but can be challenging due to their highly heterogeneous properties. Image correlation spectroscopy is a well-established analysis method capable of extracting the average size and number of particles in images. However, when image correlation spectroscopy is applied to a highly heterogeneous system, it can fail to retrieve, from a single correlation function, the characteristic size and the relative amount associated to each subspecies. Here, we describe a fast, unbiased, and fit-free algorithm based on the phasor analysis of multiple local image correlation functions, capable of mapping the sizes of elements contained in a heterogeneous system. The method correctly provides the size and number of separate subspecies, which otherwise would be hidden in the average properties of a single correlation function. We apply the method to quantify the spatial and temporal heterogeneity in the size and number of intracellular vesicles formed after endocytosis in live cells.

Introduction

Organelles are by definition subcellular structures that perform specialized functions (1). They represent the scale of organization immediately below that of the cell itself, and their composition, size and number are tailored to their functions (2). Recent advances in live-cell imaging technology, including development of specific fluorescent markers, optimization of fluorescent labeling protocols, and availability of ever more sensitive and less invasive optical microscopes (3, 4, 5), have delivered the capability of observing almost any subcellular structure at high spatial and temporal resolution in living cells. The characterization of even the geometrically simplest organelles, such as spherically shaped vesicles, can be of primary importance in biology and medicine, as they are involved in almost any process of the cell, including, for instance, intracellular trafficking (6, 7), intercellular communication (8, 9), and delivery of nanomedicines (10, 11).

In contrast, an ongoing challenge in monitoring even the most fundamental geometrical features of any organelle, such as their size and number, is that it can be difficult to make measurements on morphologically complex and dynamic subcellular structures (12). The technical complexity is due, first of all, to the morphological properties, which can be highly heterogeneous in both space and time. This is often complicated by the limited specificity and photostability of the used fluorescent probes, giving rise to noisy microscopy images. To be able to detect morphological changes in subcellular structures, it is necessary to perform an analysis over relatively long acquisition times with a high temporal resolution in live-cell conditions, so the analysis technique should account for both morphological heterogeneity and a low signal/noise ratio (SNR).

Image correlation spectroscopy (ICS) is a general approach to quantitatively analyze fluorophore distribution in images (13). ICS is widely accepted as a highly versatile method for analyzing biological macromolecule organization, with applications ranging from clustering of membrane receptors (14, 15) to counting of dendritic spines (16), to characterization of collagen fibers (17, 18) or even cells in epithelial layers (19). Every ICS-based analysis starts with the calculation of the autocorrelation function (ACF) of the image I(x,y), defined as

$$G\left(\xi ,\eta \right)=\langle I\left(x,y\right)I\left(x+\xi ,y+\eta \right)\rangle ,$$ (1)

where the brackets indicate that the average is carried out over the entire image. The basic principles of ICS are largely similar to those of fluorescence correlation spectroscopy (FCS) (20, 21, 22), with the notable difference that FCS is the analysis of intensity fluctuations in time, whereas ICS is the analysis of intensity fluctuations in space (14). In both cases, fluctuations are characterized through a normalized ACF that contains average information about the typical width and relative magnitude of the fluctuations. The width of the spatial ACF is a parameter that can be used to measure the size of fluorescent elements, whereas its amplitude can be used to quantify their concentration. To this aim, a normalized autocorrelation function is usually defined as

$$\hat{G}\left(\xi ,\eta \right)=\frac{\langle I\left(x,y\right)I\left(x+\xi ,y+\eta \right)\rangle }{{\langle I\left(x,y\right)\rangle }^2}-1.$$ (2)

The correlation function is by definition obtained as the average of many fluctuations and thus can be a robust and precise characterization method, even when calculated on a very noisy data set. On the other hand, after the averaging process, it can be very hard to characterize the heterogeneity present in the system, and the correlation function of a heterogeneous system will only reveal its average properties.

In many cases, it can be of interest to isolate the different species forming a heterogeneous system and characterize them separately. In general, if the image can be approximated by a superposition of p independent contributions (i.e., there is no correlation between the species),

$$I\left(x,y\right)=\sum _{k=1}^p{I}_k\left(x,y\right),$$ (3)

then its correlation function, Ĝ(ξ,η), can be described as a combination of the correlation functions Ĝ_k(ξ,η), corresponding to the single species:

$$\hat{G}\left(\xi ,\eta \right)=\frac{\sum _{k=1}^p{\langle I_k\left(x,y\right)\rangle }^2\left[1+{\hat{G}}_k\left(\xi ,\eta \right)\right]}{{\langle \sum _{k=1}^p{I}_k\left(x,y\right)\rangle }^2}-1.$$ (4)

However, it can be a difficult task to recover, from the total correlation function, Ĝ(ξ,η), the relative concentration of each component species, and the shapes of the correlation functions Ĝ_k(ξ,η) of each component. If there is spatial heterogeneity, one can attempt to retrieve the correlation functions of multiple species by calculating a collection of local correlation functions by considering small portions of the image. In this way, we get a better description of the heterogeneity of the system by limiting the averaging process to small spatial intervals. This approach could compensate for both spatial heterogeneity and low SNR conditions, but it brings in a new technical challenge: the calculation yields, for a single image, a relatively large number of spatial correlation functions calculated on relatively short spatial intervals.

The fast analysis of a large number of spectra is an issue common to many other spatially resolved spectroscopies. A versatile method of analysis that provides an unbiased, fit-free quantification of spectral properties at each pixel of an image is the so-called phasor approach, originally developed for the identification of components in fluorescence-lifetime imaging microscopy (23) and extensively applied to detection by fluorescence-lifetime imaging microscopy of Förster resonance energy transfer (24, 25, 26, 27, 28). The phasor analysis has been extended to spectral fingerprinting (29, 30, 31), fluorescence correlation spectroscopy (32), and superresolution microscopy (33). This approach is chosen here for the analysis of local spatial correlation functions as a fast and unbiased alternative to the fitting procedure.

In the following, we describe a fast and fit-free algorithm based on the phasor analysis of local ICS (PLICS), capable of mapping the heterogeneity of spatial correlation functions. In the limit of a low density of particles, the algorithm maps structural information from the elements contained in a heterogeneous system. The same information is used to segment the image to retrieve multiple global correlation functions associated with the identified subspecies and calculate the number of elements for each subspecies. We apply the method to quantify the spatial and temporal heterogeneity in the size and number of intracellular vesicles in live cells.

Materials and Methods

PLICS

PLICS algorithm

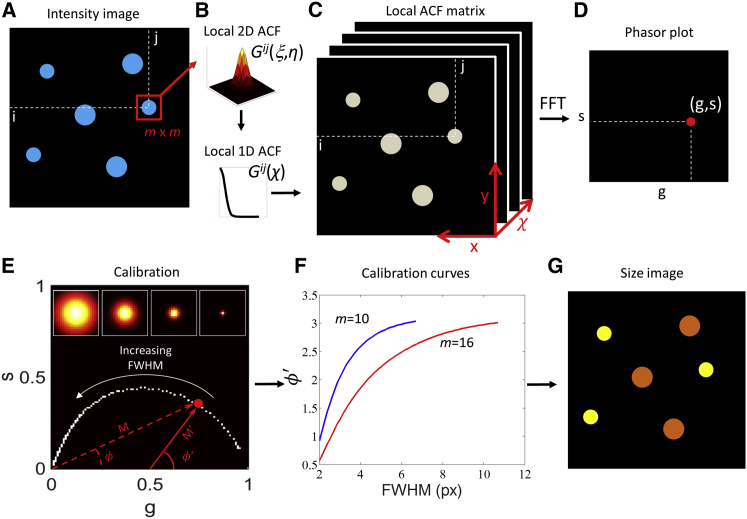
The PLICS algorithm has been implemented in Matlab (The Mathworks, Natick, MA). The workflow of the PLICS algorithm is shown schematically in Fig. 1. Let us assume we have the image of a heterogeneous sample (i.e., two or more populations of particles with different size), as shown in Fig. 1 A. Instead of considering the whole image as in conventional ICS, we use a smaller m × m mask centered on the pixel (i,j) and shift it throughout the entire image, computing, for each of the m × m subimages, its 2D ACF G^ij(ξ,η) (Fig. 1 B, top, local 2D ACF):

$$G^{ij}\left(\xi ,\eta \right)={\langle I\left(x,y\right)I\left(x+\xi ,y+\eta \right)\rangle }_{\left(i,j\right)}.$$ (5)

Each of the local 2D ACFs is computed via a 2D fast Fourier transform (FFT) algorithm. The normalized version of the local 2D ACF Ĝ^ij(ξ,η) is calculated by

$${\hat{G}}^{ij}\left(\xi ,\eta \right)=\frac{{\langle I\left(x,y\right)I\left(x+\xi ,y+\eta \right)\rangle }_{\left(i,j\right)}}{{\langle I\left(x,y\right)\rangle }_{\left(i,j\right)}^2}-1.$$ (6)

If the local 2D ACFs G^ij(ξ,η) are circularly symmetric, we convert them into local 1D ACFs G^ij(χ) (Fig. 1 B, bottom). This is done by performing an angular mean on the local 2D ACF over 60 orientations covering the angle of π radians. To increment the sampling of the function for the angular mean, the local 2D ACF is subject to a fivefold oversampling (via a Fourier transform interpolation) before averaging and then is downsampled back. If the local 2D ACFs are not symmetric, the 1D analysis can be applied to one or more selected orientations of the 2D ACF. This can be useful in the case of nonspherical organelles (e.g., mitochondria) or when the 2D ACF is expected to be asymmetric (34) (Fig. S1 in the Supporting Material).

Figure 1.

(A–F) Schematic workflow of the PLICS method. A small m × m region around each pixel (i,j) of an intensity image (A) is used to calculate a local 2D spatial correlation function (B, top) and its angular mean (B, bottom), which is stored along the third dimension in the corresponding (i,j) position of the local ACF matrix (C). (D) The phasor coordinates (g,s) are obtained by performing an FFT along the third dimension of the local ACF matrix in the (i,j) point (C). (E) Phasor plot obtained by a collection of calibration structures, examples of which are shown in the inset, from which mask-specific calibration curves are obtained (F) and used to construct a size image (G). To see this figure in color, go online.

We then construct a 3D matrix (Fig. 1 C) that stores, in the third dimension, the 1D function G^ij(χ) obtained by analyzing the m × m subimage centered in the (i,j) pixel. By means of an FFT along the third dimension we obtain, for each pixel of the image, the two phasor coordinates (g,s), defined as

$$\begin{array}{l}g\left(i,j\right)=\underset{0}{\overset{L}{\int }}{G}^{ij}\left(\chi \right)\text{cos}\left(2\pi \chi /L\right)dt/\underset{0}{\overset{L}{\int }}{G}^{ij}\left(\chi \right)d\chi \\ s\left(i,j\right)=\underset{0}{\overset{L}{\int }}{G}^{ij}\left(\chi \right)\text{sin}\left(2\pi \chi /L\right)dt/\underset{0}{\overset{L}{\int }}{G}^{ij}\left(\chi \right)d\chi ,\end{array}$$ (7)

where L is the period of the FFT, corresponding to m/2. The coordinates (g,s) can be plotted in a 2D histogram, the phasor plot (Fig. 1 D). The corresponding polar coordinates (M,ϕ) are called modulation and phase. The position of the phasor contains unbiased information about the local correlation function G^ij(χ).

The G^ij(ξ,η) and Ĝ^ij(ξ,η) functions are calculated from small m × m subimages, and when the subimage contains only one or few particles, the shape of the corresponding G^ij(χ) and Ĝ^ij(χ) functions are deformed by the presence of particles at the border (Fig. S2). As a result, the average phase value is dependent on the number of particles in the subimage (Fig. S3). For practical purposes, we consider here two limiting cases of application of the algorithm: 1) a low-density limit, when there is only one particle in the subimage, and 2) a high-density limit, when there are many particles in the subimage.

PLICS in the limit of a low density of particles

If the density of particles is low, we can choose the size, m, of the subimage in such a way that it contains no more than one particle. In this case, the width of the local ACF is directly related to the width of the single particle. A calibration for any given size m × m of the subimage is performed by generating a series of simulated m × m images of Gaussian spots, centered on the images, using their full width at half-maximum (FWHM) as the reference parameter (Fig. 1 E). In this case, we use the function G^ij(ξ,η) (Eq. 5) instead of the function Ĝ^ij(ξ,η), because only in the former case does the phasor show significant variations when the size of the particle approaches the size of the subimage (Fig. S4, A–C). The local correlation functions are analyzed excluding the G^ij(0,0) value, which contains the noise correlation. The specific trajectory described by the phasor as a function of the FWHM is not affected by increasing noise (Fig. S4, A, D, and E), but it does depend on the value of m (Fig. S5).

To exploit, through a single parameter, the variations in both phase and modulation, we define ϕ′ as the phase with respect to the shifted center of reference of coordinates (1/2,0). The shifted phase, ϕ′, is calculated by using the relation: tanϕ′ = s/(g − 1/2) (Fig. 1, E and F). The steepness of the calibration function determines the sensitivity by which a given value of size can be measured, and for values of size FWHM_max > ∼2/3m, the sensitivity is poor (Fig. 1 F). Accordingly, calibration curves were obtained with FWHM values in pixels (px) ranging from 2 to 2/3m, with steps of 0.1, and interpolating with a hyperbolic tangent function, the parameters of which are stored so that by inversion of the curve, one can obtain the absolute size value. If the point spread function (PSF) of the microscope is known, the calibration can also be performed by simulating objects of varying size convoluted with the PSF of the microscope, so that the true size of the objects can be recovered directly from ϕ′ (Fig. S6). Finally, the value of size is assigned to each pixel, resulting in an image pseudocolored according to the size of the particles (Fig. 1 G).

Note that the calibration is strictly valid for an isolated particle; thus, when another particle is close enough to modify the local correlation function, the recovered size deviates from its correct value (Fig. S7). The minimum separation, s_min, between two particles for which the size deviates by <10% from its correct value is a function of both FWHM and m. We estimate that s_min ≈ 0.7FWHM + 0.4m (Fig. S7). As a rule of thumb, for particles of size D, the separation between the particles must be larger than s_min ≈ 1.5D.

Image processing, image segmentation, and calculation of the filtered global functions

In the limit of a low density of particles, we perform two image processing operations.

The first operation, performed on the raw image before calculation of the local ACFs, is a subtraction of the background level, estimated by a moving median filter (filter size, 41 × 41 px, unless otherwise stated; after subtraction, any negative value is set to zero). Background subtraction is required, because the presence of background affects the value of modulation of the G^ij(ξ,η) function (Fig. S8 A).

The second operation, performed after calculation of the local ACFs, reassigns the same value of size to all the pixels belonging to the same particle. To this aim, the value of size obtained when the particle is at the center of the subimage (value of size associated with the brightest-intensity pixel) is assigned also to the nearby pixels. This is performed assigning to every pixel the same (g,s) coordinates computed in the brightest-intensity pixel of a circular area of diameter m + 1 around the pixel (Fig. S8 B).

The size histogram is computed from the size image by counting the occurrences of the pixels with the same value of size and dividing the number of occurrences by the square of this value, so that the histogram is not biased toward structures of larger area. To calculate the number of elements sorted by size, we perform a segmentation of the image based on user-defined size ranges. All the pixels of the size image with values inside the user-defined size range are assigned the value 1, otherwise 0. This logic mask is multiplied to the intensity image to obtain a population-specific thresholded image. Then the global ACF, Ĝ_k(ξ,η), of this image (filtered global ACF) is computed and fitted with a 2D Gaussian function, the amplitude, ĝ_k(0,0), and standard deviation, ${\sigma }_k$, of which are used to retrieve the number of structures of the specific population,

$$N_k={\hat{g}}_k{\left(\mathrm{0,0}\right)}^{-1}\frac{XY}{\pi \times \left(2{\sigma }_k^2\right)},$$ (8)

where XY is the total area of the image (16). The total number is obtained by simply adding the contributions of the single populations. The 2D Gaussian fitting is performed via a custom least-mean-squares (LMS) fitting function.

PLICS in the limit of a high density of particles

If the subimage contains many particles (for instance, >∼5 particles of FWHM = 3 px for a size of m = 12 of the subimage, according to Fig. S3), the phase and modulation of the function Ĝ^ij(χ) can be used to describe the local image correlation functions (Fig. S3). For each pixel (i,j), the values of g and s are calculated from Eq. 7 by using the functions Ĝ^ij(χ) instead of the functions G^ij(χ). The resulting g and s image are smoothed by a moving average filter (filter size, 2m + 1). Then, the phase and modulation are calculated as ϕ = tan⁻¹(s/g) and M = (g²+s²)^−1/2, respectively, and associated with each pixel.

In this case, the phase and modulation parameters, ϕ and M, associated with the local ACF are not representative of a single particle but only of a given location in space. For this reason, we do not perform a calibration to convert these parameters into a size value and we do not perform any reassignment.

Simulations

All simulations were performed in Matlab (The Mathworks). Every image is created by adding a user-defined number of structures (e.g., Gaussian-shaped elements with a certain FWHM), either noise affected or not, in a random position (unless stated otherwise). Poisson noise-affected Gaussian structures were simulated by creating a Gaussian-shaped probability distribution of given FWHM and by randomly adding a number, N, of photons to the image according to this distribution. SNR in this case was quantified as a photon density per element (SNR = N/FWHM², N being the number of photons per structure).

Microscopy

Fluorescent beads

A mixture of 100 nm (diluted 1:10,000 from stock solution) and 500 nm (diluted 1:100 from stock solution) yellow-green fluorescent beads (FluoSpheres carboxylate-modified microspheres, Thermofisher Scientific, Waltham, MA) was deposited on a polylysine-coated coverglass and imaged by a Nikon spinning-disk confocal microscope, based on the combination of a Yokogawa CSU-X1 confocal scanning unit and a Nikon Ti-E inverted microscope. A Nikon Plan Apo λ 100× oil objective, NA 1.45, was used for all measurements. The pixel size was set to 110 nm. PLICS analysis was performed with threshold = 1000 and m = 16. The image was segmented into a population with size <450 nm and a population with size >450 nm. Filtered ACFs were computed on the segmented images.

Live-cell fluorescence imaging

HeLa cells were plated on a LabTek eight-well chamber and let grow overnight. Cells were stained with 10 μg/mL pHrodo Green dextran (pHrodo Green dextran, molecular weight 10,000, Thermofisher Scientific) and left incubating for 20 min at 37°C, then washed twice in live-cell imaging solution (LCIS; Thermofisher Scientific) and resuspended in LCIS. For time-resolved measurements, cells were stained with 10 μg/mL pHrodo Green dextran and imaged without any washing step, i.e., leaving the fluorophore diluted in the buffer (LCIS). The samples were imaged by the Nikon confocal spinning-disk microscope equipped with a temperature-controlled stage kept at 37°C, using a Nikon Plan Apo λ 100× oil objective, NA 1.45, setting the pixel size to 110 nm or 160 nm. PLICS analysis was performed with threshold = 0.4B, B being the average background level before subtraction, and m = 10.

For time-resolved experiments, rectangular regions of interest (ROIs) were selected inside the cell far from the plasma membrane (Fig. S9). For each ROI, the number of vesicles of a given size was calculated. For cumulative results (n = 7 cells), the number of vesicles associated to a given population was calculated as the sum of the vesicles counted on each ROI. The error was estimated as equal to the square root of the calculated number, according to Poisson statistics. The dynamics of the number of vesicles, N_k, of population k as a function of time was fitted to the piecewise linear equation,

$$N_k\left(t\right)=\{\begin{array}{ccc}0& \text{if}& t\le t_k\\ N_{k,\max }\frac{t-t_k}{\Delta t_k}& \text{if}& t_k<t<t_k+\Delta t_k\\ N_{k,\max }& \text{if}& t\ge t_k+\Delta t_k\end{array}.$$ (9)

Results

PLICS maps the size of particles in a heterogeneous system

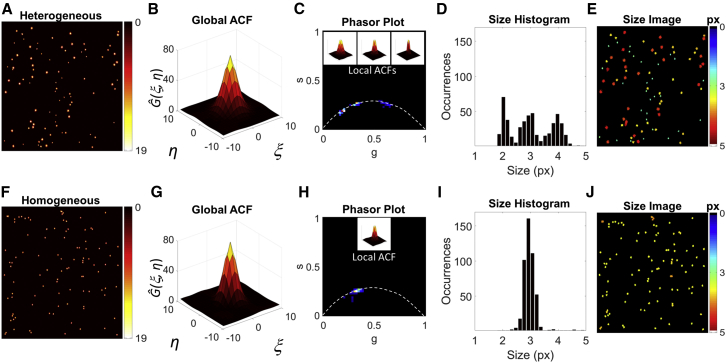
The whole PLICS workflow has been tested on simulated images to compare its performance with respect to global ICS analysis. In the simulations reported in Fig. 2, we compare a polydisperse (Fig. 2 A) versus a monodisperse (Fig. 2 F) sample of particles at low density. Conventional ICS analysis leads to similar global ACFs (Fig. 2, B and G) reflecting the average size of particles in the image. The recovery of the properties of the single species of the heterogeneous sample from the global ACF can be challenging and generally requires an assumption about the number or the brightness of the species. The phasor plot of local ACFs (Fig. 2 C), instead, provides an immediate, unbiased fingerprint of the heterogeneity of the polydisperse sample compared to the phasor plot of the monodisperse sample (Fig. 2 H). In the phasor space (Fig. 2, C and H), it is possible to discriminate three separate species in the polydisperse sample, whereas only a single species is visible in the monodisperse sample, as expected. In the insets of Fig. 2, C and H, are also reported representative local ACFs corresponding to the single populations: comparing them to the global ACF, we can appreciate how much the single-species contribution is hidden in the average. By using the calibration curve, we’re able to transform the information encoded in the phasor coordinates into size information, leading to a size histogram (Fig. 2, D and I) and a size image (Fig. 2, E and J). From this analysis, we can evaluate the mean size and the standard deviation of each single population and their spatial distribution. Note that for particles that cannot be considered isolated, the measured size deviates from its correct value (Fig. 2 J).

Figure 2.

Analysis of polydisperse (A–E) and monodisperse (F–J) randomly distributed Gaussians with SNR = 10. The monodisperse sample consists of 100 elements with FWHM = 3 px, whereas the polydisperse sample consists of 33 elements with FWHM = 2 px, 33 with FWHM = 3 px and 34 with FWHM = 4 px. (B and G) Global ACFs computed on the intensity images (A) and (F), respectively. (C and H) Phasor plots of (A) and (F) compared with the m = 10 calibration curve (white dashed line), with examples of local ACFs shown in the insets. (D and I) Size histograms obtained from the size images (E and J) of (A) and (F), respectively. To see this figure in color, go online.

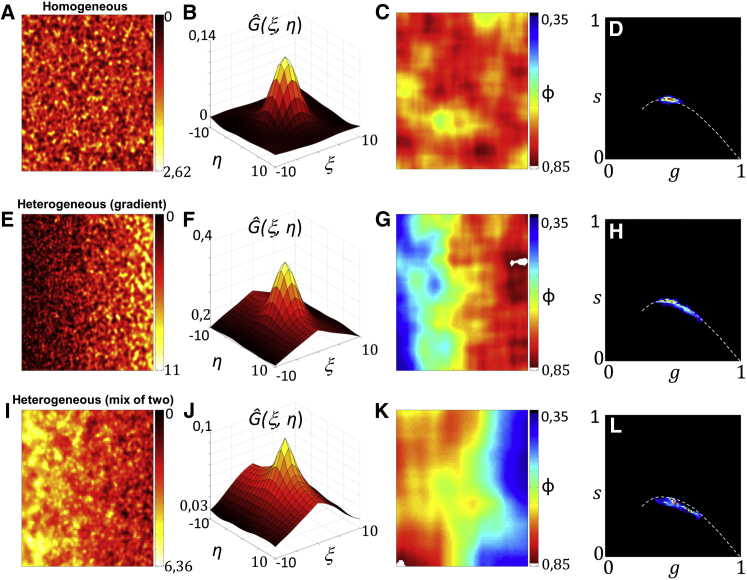
Also in the limit of a high density of particles, the PLICS analysis can be used to visualize the spatial heterogeneity of the correlation functions (Fig. 3). However, in this case, the differences in the local image correlation functions (Fig. 3, G and K) should not be interpreted as variations in the size of single particles.

Figure 3.

PLICS analysis at a high density of monodisperse (A–D) and polydisperse (E–L) particles. The monodisperse sample consists of 10,000 particles with FWHM = 4 px. The polydisperse sample in (E) consists of 10,000 elements with FWHM ranging from 2 to 5 px distributed so that their FWHM increases from left to right according to a linear gradient. The polydisperse sample in (I) consists of 10,000 elements with FWHM equal to either 2 or 5 px distributed so that the density of structures with FWHM = 5 px decreases from left to right, whereas the density of structures with FWHM = 2 px increases from left to right. Shown are the intensity images (A, E, and I), the global ACFs (B, F, and J), the phase images (C, G, and K), and the phasor plots (D, H, and L). The PLICS analysis is performed with m = 16. The dashed white line in the phasor plot is a guide to the eye. To see this figure in color, go online.

For instance, assume that the FWHM of the particles in the image increases from left to right according to a linear gradient (Fig. 3 E): since each subimage contains only particles of approximately the same size, the phase map (Fig. 3 G) indicates that particles of different size are located in different positions in the image. On the other hand, consider now a combination of large and small particles distributed so that the ratio between small and large particles increases from left to right (Fig. 3 I): since each subimage may contain particles of different size, the phase map (Fig. 3 K) indicates only that the average size changes according to location but provides no hint as to the fact that the sample is a combination of two pure species. Nevertheless, a comparison between the phasor plots (Fig. 3, H and L) shows that the local ACF of the sample, which is a mix of two sizes, follows a different trajectory with respect to the sample that has a gradient of size, in agreement with the rules of phasors (23). This suggests that discrimination between the two cases is possible, although further studies are required to confirm this possibility.

PLICS provides a global number of particles sorted by size

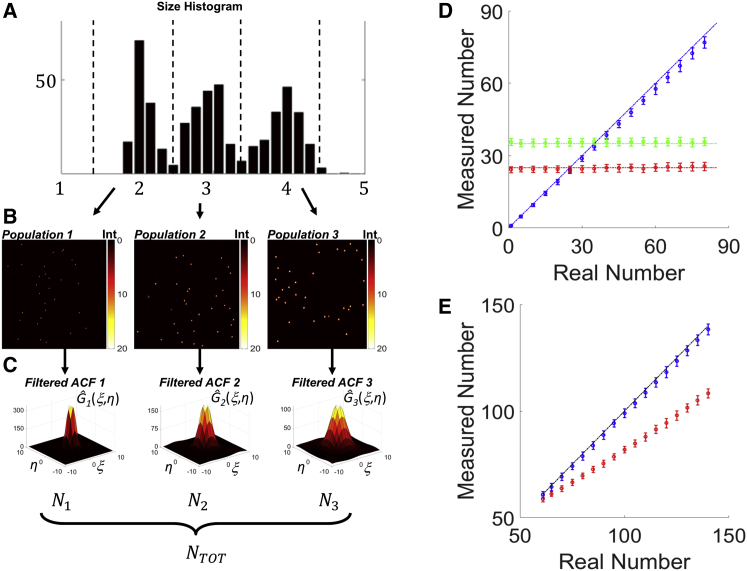
A powerful feature of every ICS-based analysis is the measurement of the number of particles in a system. For a system that is heterogeneous in size, it would be of interest to know the number of particles for each separate subspecies. The PLICS approach provides a way to highlight whether size heterogeneity is present in the system and to measure, at least in the limit of low density, the characteristic sizes of separate subspecies, otherwise hidden in the average properties of the global ACF. Now, consider that the size histogram obtained from the PLICS analysis (Fig. 4 A) can be used to define multiple subspecies and produce a segmentation of the image according to size. With this operation, we can obtain three separate images (Fig. 4 B), each containing only one population of interest. Performing ICS analysis on these images using the global correlation function defined in Eq. 2, we calculate the filtered global ACFs, Ĝ_k(ξ,η) (Fig. 4 C), whose amplitude is inversely proportional to the number of elements in each population. Note that here we use the term filtered to indicate that the new correlation functions are calculated with the purpose of separating the species of a heterogeneous system (35).

Figure 4.

(A) Size histogram of a polydisperse sample of particles, SNR = 10, where the black dotted lines visually show the segmentation performed (1.5 px < size₁ < 2.5 px, 2.5 px < size₂ < 3.5 px, 3.5 px < size₃ < 4.5 px) to obtain the segmented images in (B), shown from the smaller (population 1) to the larger (population 3). (C) Filtered ACFs corresponding to the segmented populations, from which the number of elements of each population has been retrieved (N₁, N₂, and N₃). (D) Retrieved number of a single population (circles) shown as the mean value of a set of 100 realizations, the error bar being the standard deviation; populations 1–3 correspond to blue, red, and green circles, respectively, and the dash-dotted lines show the actual number for each population; populations 2 and 3 were simulated with a constant number (25 and 35, respectively), whereas the population 1 number was varied from 1 to 80. (E) Retrieved total number (blue circles) compared with traditional ICS analysis (red circles) of the same samples in (D). To see this figure in color, go online.

To demonstrate that even the number of a small population could be successfully retrieved by this procedure, we simulated a polydisperse sample with two fixed populations (N₂ = 25 and N₃ = 35 elements) and one population with a variable number of elements (N₁ = 1 ÷ 80 elements). Fig. 4 D shows the number of elements recovered for each population as a function of N₁. The results of the analysis are consistent with the simulated values, with the exception of a small deviation toward larger values of N₁ due to an increasing fraction of particles that appear to be merged to other nearby particles. It is noteworthy that the total number of elements of the heterogeneous system can be calculated as the sum of the numbers of elements of each subspecies (Fig. 4, C and E). This analysis provides a better estimation of the total number of elements with respect to what can be obtained from a single global ACF, which returns an underestimated number (Fig. 4 E).

In the limit of high density, the phase map (Fig. 3, C, G, and K) can be used to assess whether the system is spatially heterogeneous, but can’t be used to perform a particle-based segmentation that separates the different subspecies. In this case, the map can be used to define subregions of analysis that (at least in our algorithm) need to be rectangular (Fig. S10).

Experimental validation of PLICS on polydisperse fluorescent beads

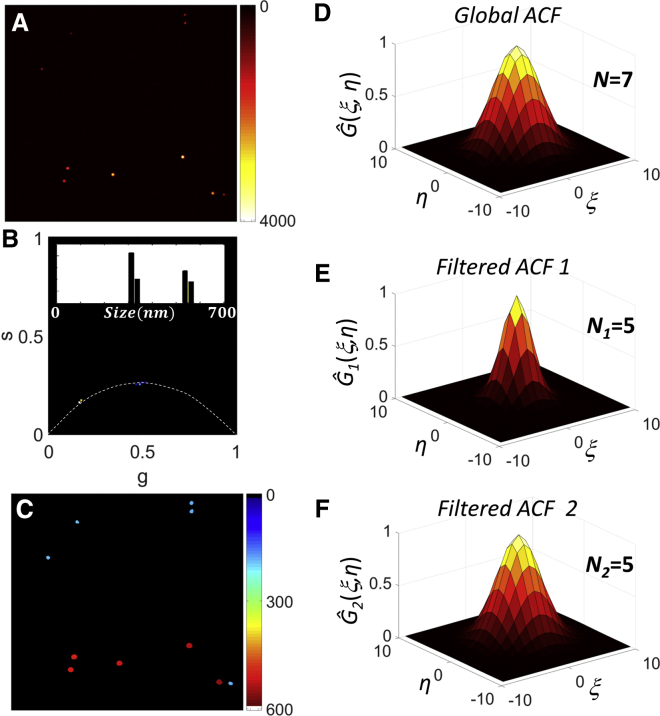
The above-described PLICS analysis has been validated experimentally on a sample of mixed fluorescent spheres (nominal diameter, d₁ = 100 nm and d₂ = 500 nm) imaged on a confocal microscope (Fig. 5 A). The PLICS analysis shows that two well-separated populations are visible in the phasor plot (Fig. 5 B) and in the size image (Fig. 5 C). The absolute values of size here should be interpreted as the size of the particles convolved with the PSF of the confocal microscope.

Figure 5.

(A–C) Background-corrected image of a mixture of 100 nm and 500 nm fluorescent beads (A), associated PLICS phasor plot (B), and size image (C). (D) Global ACF Ĝ(ξ,η) of the background-corrected image. (E and F) Normalized filtered global ACFs Ĝ₁(ξ,η) and Ĝ₂(ξ,η) obtained after segmentation of the image with PLICS in population 1 (size <450 nm) and population 2 (size >450 nm). To see this figure in color, go online.

The segmentation of the image into two species yields two filtered ACFs (Fig. 5, E and F) from which the correct number of beads, sorted by size, is recovered (N₁ = 5, N₂ = 5). In contrast, the total number obtained from the global ACF (Fig. 5 D) is an underestimated value (N = 7). It is worthy of note that since the 100-nm beads are dimmer than the 500-nm beads, their contribution to the global ACF (Fig. 5 D), according to Eq. 4, can be significantly small compared to that of the brighter 500-nm particles; in fact, we can hardly note any difference between the global ACF and the filtered ACF associated with the larger beads (Fig. 5, D and F, respectively).

PLICS maps the size of intracellular vesicles in live cells

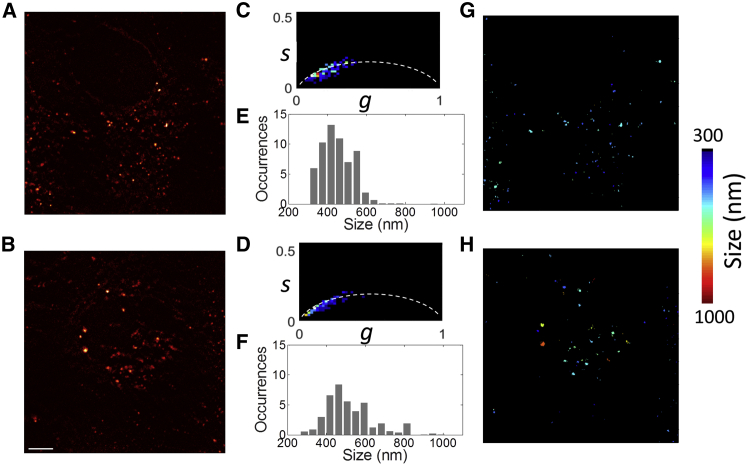
We then validated our method on confocal images of live HeLa cells stained with pHrodo Green dextran, a pH-sensitive probe that selectively stains the intracellular vesicles formed after endocytosis of the dye (Fig. 6, A and B; Fig. S11) (36). The phasor plot of the local ACFs shows a broad distribution along the reference trajectory (Fig. 6, C and D). It is worth noting that if background were not subtracted from the image, the experimental phasors would not lie along the reference trajectory. Indeed, addition of a spatially uncorrelated background causes a decrease in the modulation, M, of the phasor (see Fig. S8). The phasor plot can be used to investigate the size distribution associated with different areas of the specimen (Fig. 6, C and D; Fig. S11). For instance, for the two areas shown in Fig. 6, A and B, one can tell from the phasor plots that in the second area, there are some larger vesicles than in the first one.

Figure 6.

PLICS analysis of intracellular vesicles in confluent HeLa cells stained with pHrodo Green dextran. Shown are the raw intensity images (A and B), the corresponding PLICS phasor plots (C and D), the size histograms (E and F), and the size images (G and H). Scale bar, 5 μm. To see this figure in color, go online.

Converting the phasor coordinates to absolute size, one can map the size of the vesicles in the images (Fig. 6, G and H) and build the associated histograms (Fig. 6, E and F). The mean values of size obtained from PLICS are <FWHM_PLICS> = 459 nm and 514 nm for the first and second regions, respectively, whereas the corresponding values of size estimated from conventional ICS analysis are FWHM_ICS = 357 nm and 439 nm, respectively. Most of the vesicles in Fig. 6 A have an apparent size between 350 nm and 550 nm, whereas in Fig. 6 B the distribution is broader and a significant fraction of vesicles have size >550 nm. This difference can be due to heterogeneity in behavior from cell to cell or, more simply, to the fact that we are limiting the analysis to single optical sections, and we cannot exclude the possibility that vesicles of different size might be located on different focal planes. We checked that our fit-free method provides absolute values of size that are comparable to what can be achieved by performing a local 2D Gaussian fit of the images of the vesicles (Fig. S12).

PLICS detects size-dependent dynamics of internalized vesicles

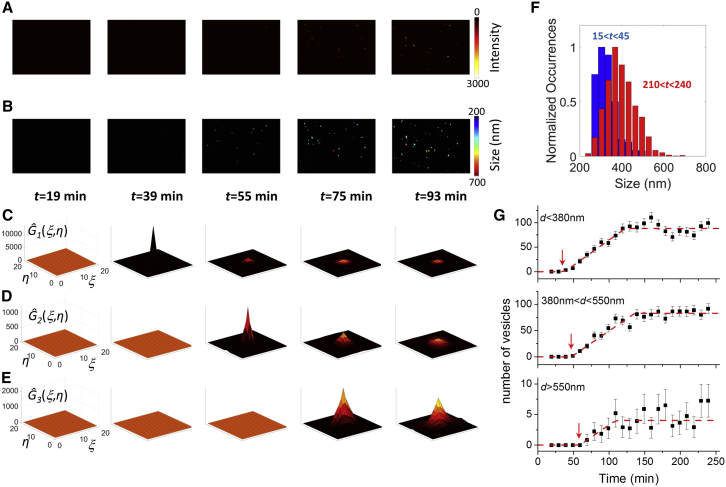
We monitored, finally, the size distribution of the vesicles as a function of the time elapsed from incubation with the dye (Fig. 7, A and B). We started observing the cells 15 min after loading the extracellular medium with the dye and followed the time course of the internalization for as long as 4 h. Intracellular vesicles start appearing at an incubation time of about half an hour and their number increases with time (Fig. 7 A). A comparison of the normalized size distribution at early (15 < t < 45 min) versus late incubation times (210 < t < 240 min) shows that there is an increase in the average size of the vesicles (Fig. 7 F). We then defined three populations of vesicles (small, medium, and large) based on their size (d₁ < 380 nm, 380 < d₂ < 550 nm, and 550 < d₃ < 1100 nm, respectively) and counted the number of vesicles for each population from the filtered global ACFs as a function of time (Fig. 7, C–E). Decreasing values of ĝ₁(0,0), ĝ₂(0,0), and ĝ₃(0,0) indicate an increasing number of vesicles for each population as a function of time (Fig. 7, C–E). On average (n = 7 cells), the medium vesicles (d₂) appear with a 9 min delay with respect to the appearance of small vesicles (d₁), whereas the large vesicles (d₃) appear with a 12 min delay after the appearance of medium vesicles (d₂) (Fig. 7 G). After appearance of the vesicles, their number grows until it reaches a constant value (Fig. 7 G).

Figure 7.

(A and B) Intensity and size images from a time sequence capturing the endocytosis process in a HeLa cell, corresponding to minutes 19, 39, 55, 75, and 93 after incubation with the dye pHrodo Green dextran. (C–E) The filtered global ACFs associated with smaller (d₁ < 380 nm), medium (380 nm < d₂ < 550 nm), and larger (d₃ > 550 nm) vesicles and calculated for the same time frames. (F) Size histograms calculated for all the cells (n = 7) and for the temporal intervals 15 min < t < 45 min (blue) and 210 min < t < 240 min (red). (G) Average time course (n = 7) of the number of small, medium, and large vesicles. Each set of data has been fitted to a piecewise linear function to determine the time, t_k, at which the vesicles of the kth population start to appear (t₁ = 38 min, t₂ = 47 min, t₃ = 59 min; Δt₁ = 85 min, Δt₂ = 89 min, Δt₃ = 50 min). To see this figure in color, go online.

In the conditions of this experiment, since free dye is always available in the extracellular medium, the equilibrium is reached when the amount of dye internalized is equal to the amount of dye that is degraded or expelled from the intracellular vesicles. The dye will fluoresce only inside vesicles with acidic pH. Even if our classification of the vesicles is based only on size and the three populations do not necessarily correspond to functionally different elements of the endosomal compartment, it is worth noting that our observations are in keeping with morphological changes associated with the endosome maturation program (1, 37, 38). Indeed, according to previous studies, primary endocytic vesicles fuse to early endosomes in ∼10 min (38), whereas cargos typically show up in late endosomes 5–15 min later than in early endosomes (1). The timescale of these transitions is consistent with the time delays that we observed between the appearance of small, medium, and large vesicles. Moreover, it is generally assumed that primary endocytic vesicles have smaller size (<200 nm) with respect to early and late endosomes (size in the range 200–1000 nm) and that endosomes grow in size during maturation (38). However, further studies with more specific markers are required to assign a functional role to each type of vesicle.

Discussion

We have described a method based on the analysis of local spatial correlation functions. If a system is spatially heterogeneous, from the point of view of the local correlation functions, this analysis has the double potential of 1) mapping its spatial heterogeneity, and 2) leading to a more accurate ICS analysis. Technically, since the local correlation functions are calculated on relatively small subimages, particles at the subimage border cause density-dependent deformations of the shape of the correlation function. Accordingly, we have defined two limits of operation, namely, a low and a high particle density limit.

In the low-density limit, each subimage contains only one particle; thus, the spatial heterogeneity of the correlation functions corresponds to the heterogeneity in the size of single particles. In this specific case, we can sort the particles based on their size and perform image segmentation before global ICS analysis. The ICS analysis with filtered global ACFs is more accurate, because these functions describe more uniform populations. However, it should be noted that in the low-density limit, similar results could be obtained by single-particle localization algorithms (39). Indeed, our algorithm (in the low-density limit) can be considered as a method aimed at quantifying the morphology of single particles. In our method, the size of particles is obtained by using a predetermined, model-dependent, calibration function to convert an FFT-derived parameter into a distance, in analogy to other nonfitting algorithms (36, 39, 40, 41, 42, 43).

We have applied this method to sparse intracellular vesicles, measuring and mapping the size of the vesicles and counting the number of vesicles sorted by size. Compared to other organelles, the circularly symmetric vesicles represent only a simpler case. However, a generalization to asymmetric particles is possible and will be relevant for the characterization of other types of organelles (e.g., mitochondria) or macromolecular structures (e.g., chromatin) that cannot be approximated as circularly symmetric structures.

The main limitation, in terms of density, is given by the fact that particles of size D need to be farther apart than s_min ≈ 1.5D. When there are few particles in the subimage (between the low- and high-density limits), the analysis of local ACFs is less straightforward, and it will be useful to take into account other parameters, such as the intensity, that can be related to the absolute number of particles (44). Another limitation of our approach is that we are performing the analysis only on 2D optical sections. The size of out-of-focus particles can appear larger due to broadening of the PSF along the optical axis. However, the out-of-focus particles have lower intensity and can be excluded from the analysis by proper thresholding. In general, a more accurate analysis should be performed on a full 3D stack of optical sections, as in 3D particle-tracking algorithms (44).

In the high-density limit, the spatial variations of the correlation functions can be used to compare different locations of the sample and to determine whether the sample is spatially heterogeneous (Fig. 3). In this case, the spatial heterogeneity of the correlation functions (evident, for instance, in Fig. 3, G and K) should not be confused with the heterogeneity of particle size (evident, for instance, in Fig. 2 E). The phase map can be used to quantify the variations of the local ACFs across different areas of the sample. The map can also be used as a reference to restrict the analysis to rectangular subregions. Further studies are needed, however, to determine whether this approach could be effective in mapping spatial heterogeneities related to molecular diffusion and transport detected by ICS (34).

Conclusions

The method described here is based on the pixel-by-pixel analysis of local spatial correlation functions. The advantage of such an approach is more evident when the system under study is heterogeneous, and a prior characterization of its spatial heterogeneity can lead to a better description of the properties of the system. The phasor analysis is used here conveniently as an unbiased, fit-free tool to characterize a large number of correlation functions. After characterization of spatial heterogeneity, a filtered global ICS analysis is introduced to retrieve the number of elements. In this sense, PLICS should not be seen as an alternative to ICS but rather as a prescreening and prefiltering analysis that, in our opinion, can make ICS analysis of heterogeneous systems more robust and quantitative.

Potentially, this idea can be extended to other types of correlation spectroscopy performed on heterogeneous systems. The strength of correlation spectroscopy is that the averaging process of many noisy events yields characteristic parameters (i.e., size, transit time, concentrations, etc.) of the ensemble. However, if we could segment a heterogeneous ensemble into two or more populations before averaging, we will get average parameters that are characteristic for each population. A separation into monodisperse populations is possible if fluctuations can be separated, at least to some extent, in space or in time. For instance, in the specific example described in this article, where the spatial fluctuations are represented by fluorescent vesicles, this condition means that two vesicles do not occupy exactly the same position in the image. In general, any increase in the spatial and temporal resolution of the detection system will increase the capability of observing heterogeneity in spatial or temporal fluctuations (45). Now, with superresolution microscopies becoming more and more compatible with live-cell experiments, we expect PLICS to be increasingly used as a prescreening tool to assess heterogeneity in correlation spectroscopy assays.

Author Contributions

L.L. and A.D. designed research. L.S. and L.L. performed research and wrote software. L.S., E.G., A.D., and L.L. analyzed results. L.L. and L.S. wrote the manuscript. E.G. and A.D. assisted in the project and supported manuscript writing.

Editor: Paul Wiseman.