Abstract
The cell cortex is a key structure for the regulation of cell shape and tissue organization. To reach a better understanding of the mechanics and dynamics of the cortex, we study here HeLa cells in mitosis as a simple model system. In our assay, single rounded cells are dynamically compressed between two parallel plates. Our measurements indicate that the cortical layer is the dominant mechanical element in mitosis as opposed to the cytoplasmic interior. To characterize the time-dependent rheological response, we extract a complex elastic modulus that characterizes the resistance of the cortex against area dilation. In this way, we present a rheological characterization of the cortical actomyosin network in the linear regime. Furthermore, we investigate the influence of actin cross linkers and the impact of active prestress on rheological behavior. Notably, we find that cell mechanics values in mitosis are captured by a simple rheological model characterized by a single timescale on the order of 10 s, which marks the onset of fluidity in the system.
Introduction
The cell cortex plays a key role in determining cell mechanics, cell shape, and tissue organization (1). The cortical layer is an actin-based filament network linked to the plasma membrane (2). It is dynamically maintained at a thickness that has been estimated to range from 0.05 to 1 μm (2). Many actin-associated proteins organize the network structure and filament length including passive cross linkers and active elements such as myosin motors (2). The cortex is therefore an active material and is mechanically characterized by the cortical tension. This cortical tension results from active contractile stress generated in the cytoskeletal network by motor proteins and filament dynamics (1, 2). The cortex provides a cell with an effective surface tension (2). In contrast to the surface tension of a passive system (3), such as a liquid drop, cell surface tension can be locally regulated by cellular signaling processes (1, 4). This allows the cell to use cortical mechanics to regulate shape and, together with cell adhesion, to guide tissue organization (1). For example, cortical tension can regulate cell shape in a tissue, and drive tissue remodeling processes such as T1 transitions (5, 6) and cell extrusions from an epithelium (7). During mitosis, increasing cell surface tension leads to cell rounding. In this way, cells provide sufficient space for the formation of a mitotic spindle unhindered by complex cell geometry found in tissues (8). Cell rounding is associated with major remodeling of the actomyosin cytoskeleton and an increase in cortical tension that is accompanied by a corresponding increase of hydrostatic pressure (9, 10, 11). Round cells will then divide into two during cytokinesis, and return to interphase.
While there is extensive work on the mechanics of the interphase cortex, we know much less about the mechanics of the mitotic cortex. Therefore, we do not understand how mechanical properties of the cortex change to prepare cells for division. Recently, using a parallel plate assay (12), we have shown that compressed mitotic cells acquire a well-defined shape of minimal surface area (10). This permits tight control of cell geometry during measurements of strain and steady-state active tension. Here, by measuring these quantities, we show that cell mechanics in mitosis is dominated by the cortical layer of the cell. Because we can distinguish the cortex from the cytoplasm, this allows us to measure the time-dependent mechanical response of the cortical layer in vivo.
Materials and Methods
Cell culture
We cultured HeLa Kyoto cells expressing a fluorescent histone construct (H2B-GFP) in DMEM supplemented with 10% (vol/vol) fetal bovine serum, 2 mM GlutaMAX, 100 μg/mL penicillin, 100 μg/mL streptomycin, and 0.5 μg/mL geneticin (all Invitrogen, Carlsbad, CA) at 37°C with 5% CO2. One day before the measurement, 10,000 cells were seeded into a silicon cultivation chamber (0.56 cm2, from a 12-well chamber; Ibidi, Martinsried, Germany) that was placed in a 35-mm cell culture dish (glass bottom Fluorodish FD35-100; World Precision Instruments, Sarasota, FL) such that a confluency of ≈30% is reached at the day of measurement. For atomic force microscopy (AFM) experiments, medium was changed to DMEM (Cat. No. 12800-017; Invitrogen) with 4 mM NaHCO3 buffered with 20 mM HEPES/NaOH at pH 7.2. Where indicated, mitotic cells were detached from cell culture dishes with Trypsin/EDTA and measured on dishes coated with PLL-g-PEG (SuSoS, Dubendorf, Switzerland) that prevents cell adhesion but does not induce significant changes in cell surface tension (13). For PEG-coating, dishes were first plasma-cleaned and then incubated for ≈30 min in 0.1 mg/mL PLL-g-PEG solution and afterwards rinsed with PBS and used up to 24 h afterwards. We used the cytoskeletal drugs blebbistatin (Cat. No. B0560; Sigma-Aldrich, St. Louis, MO), latrunculin A (Cat. no. 428021; Merck, www.merck.com), taxol (Cat. No. T7191; Sigma-Aldrich), or nocodazol (Cat. No. M1404; Sigma-Aldrich), where indicated. Drugs were added to indicated concentrations at least 10 min before the experiment. Mitotic arrest of cells was achieved by addition of S-trityl-l-cysteine (STC; Sigma-Aldrich) 2–8 h before the experiment at a concentration of 2 μM. This allowed conservation of cell mechanical properties during measurement times of up to 30 min for one cell (14). Cells in mitotic arrest were identified by their shape and/or H2B-GFP. Diameters of uncompressed, roundish, mitotic cells typically ranged from 19 to 23 μm. We verified that mechanical properties of cells in mitotic arrest are similar to those of cells in metaphase of mitosis (Fig. S16 in the Supporting Material).
Atomic force microscopy
The experimental setup consisted of an atomic force microscope (Nanowizard I; JPK Instruments, Berlin, Germany) mounted on an Axiovert 200M optical, wide-field microscope (Carl Zeiss, Jena, Germany). For imaging, we used a 20× objective (Plan Apochromat, NA = 0.80; Carl Zeiss) and an AxioCam charge-coupled device camera (Carl Zeiss). During measurements, cell culture dishes were kept in a petri dish heater (JPK Instruments) at 37°C. On every measurement day, the spring constant of the cantilever was calibrated using the thermal noise analysis (built-in software; JPK Instruments). Cantilevers were tipless, 200–350-μm long, 35-μm wide, 2-μm thick, and made of pure silicon (NSC12/tipless/noAl or CSC37/tipless/noAl, from MikroMasch; www.mikromasch.com) with nominal force constants between 0.3 and 0.8 N/m. Cantilevers were modified in either of two ways to correct for the 10° cantilever tilt and allow for axisymmetric confinement. For this purpose, cantilevers were supplemented by wedges consisting of UV-curing adhesive (Norland Optical Adhesive 63; Norland Products, Cranbury, NJ) (12). During measurements, measured force, piezo height, and time were output at a time resolution of 10 Hz (compression steps) or 100 Hz (oscillatory compressions). For AFM compression of detached mitotic cells on PEG-coated dishes, we used the CellHesion module (JPK Instruments), which allowed us to vertically control the AFM cantilever in a 100-μm range (15).
Progressive uniaxial compression of cells
To probe the viscoelastic response of cells, we progressively compressed them with the AFM cantilever. Before cell compression, the AFM cantilever was lowered to the dish bottom near the cell until it came into contact with the surface and then retracted to ≈15 μm above the surface. Thereafter, the free cantilever was moved over the cell. The cantilever was then gradually lowered in steps of 0.5–1 μm at a set speed of 0.5 μm/s interrupted by waiting times of 60–100 s. During these waiting times, the AFM cantilever was held at constant height and the measured force was relaxing. The force acting on the cantilever was continuously recorded. The height of the confined cell was computed as the difference between the height that the cantilever was raised from the dish surface and lowered onto the cell plus the height of spikes at the rim of the wedge (due to imperfections in the manufacturing process (12)) and the force-induced deflection of the cantilever. We estimate a total error of cell height of ≈0.5 μm due to unevenness of the cantilever wedge and vertical movement of the cantilever to a position above the cell. The analysis of experimentally measured ΔF in dependence of ξ is described in detail in Section S2 in the Supporting Material.
Oscillatory compression of cells
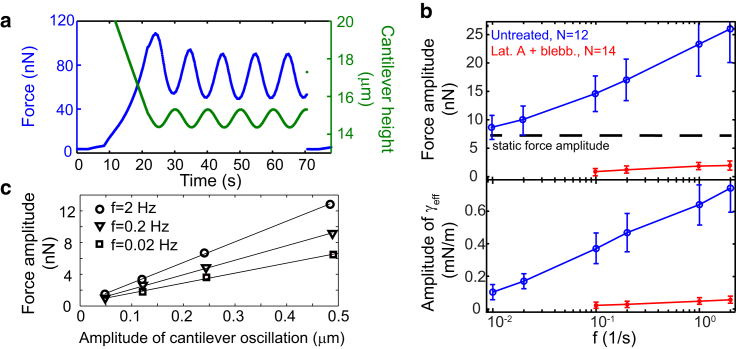
To sample the viscoelastic response of cells at a distinct frequency, we performed oscillatory compressions of cells. To this end, we sandwiched cells between dish bottom and cantilever wedge and carried out oscillatory height modulations of the AFM cantilever with typical oscillation amplitudes of 0.1–0.5 μm in a frequency range of 0.01 and 2 Hz (Supporting Material). During this procedure, the cell was on average kept at a normalized height reduction of 30–40%. Oscillatory cantilever height modulations were generated by a piecewise linear approximation of the sine-function for oscillation periods of 0.5, 1, 5, 10, 50, and 100 s in a piezo height control mode (Supporting Material). If not indicated otherwise, height oscillations were set to an amplitude of 0.5 μm. If force oscillations became large (force minima reaching <50% of the average force value), oscillations were repeated at 0.25-μm amplitude. In this case, the lower-amplitude oscillations were used for stiffness analysis. We also performed cantilever oscillations in the absence of a cell. These blank cantilever oscillations also generated force oscillations. In this case, however, force amplitudes were much smaller (≲0.02 nN). Accordingly, effects of the medium’s viscosity are negligible. Oscillatory force and cantilever height curves were analyzed in the following way: for every data point, effective tension γeff and surface area strain are estimated. An amplitude and a phase angle associated to the oscillatory time variation of effective tension γeff and surface area strain are extracted (Supporting Material). To estimate the value of the complex elastic modulus at a distinct frequency, we determine the phase angles and as well as amplitudes and of effective tension and surface area strain, respectively. The complex elastic modulus at this frequency is then calculated as . In cells treated with a combination of latrunculin A (200 nM) and blebbistatin (10 μM), surface tensions were very low and mitotic cells were not properly rounded if adhered to the cell culture dish. Therefore, rheological measurements were performed on PEG-coated dishes in this condition (Table 1, row 6). Cantilever oscillations were chosen as 0.5 μm by default to achieve an acceptable signal/noise.
Table 1.
Rheological Parameters of Cells In Different Measurement Conditions
| (s) | p-value (for ) | Kh (mN/m) | p-value (for Kh) | (mN/m) | p-value (for ) | ξ | N | |
|---|---|---|---|---|---|---|---|---|
| Control | 13.8 ± 5.2 | 1 | 18 ± 4.6 | 1 | 1.67 | 1 | 0.36 | 9 |
| Blebbistatin 2.5 μM | 24.3 ± 5.8 | 0.002 | 10.3 ± 2.7 | 0.0004 | 0.54 | 3e-4 | 0.38 | 9 |
| Y-27632 5 μM | 31 ± 10.5 | 0.004 | 6.6 ± 2.1 | 0.001 | 0.45 | 0.002 | 0.36 | 6 |
| Control | 12.9 ± 4.1 | 1 | 19.8 ± 8.2 | 1 | 1.9 | 1 | 0.36 | 19 |
| Taxol 100 nM | 8.5 ± 3 | 0.001 | 23.4 ± 11.6 | 0.3 | 2.2 | 0.04 | 0.37 | 20 |
| Control | 11.7 ± 4.3 | 1 | 24.4 ± 9.4 | 1 | 1.88 | 1 | 0.33 | 9 |
| Nocodazol 100 nM | 10 ± 2.8 | 0.33 | 27.3 ± 7.55 | 0.37 | 2.3 | 0.02 | 0.36 | 9 |
| Control, F-Luc (RNAi) | 7.66 ± 3.2 | 1 | 25.7 ± 8.6 | 1 | 1.98 | 1 | 0.4 | 9 |
| MYH9 (RNAi) | 21.8 ± 10.6 | 0.006 | 10.9 ± 2.4 | 0.0015 | 0.68 | 3e-4 | 0.39 | 9 |
| Control, F-Luc (RNAi) | 8.3 ± 1.8 | 1 | 26.5 ± 5.4 | 1 | 2.2 | 1 | 0.35 | 10 |
| ACTN4 (RNAi) | 4.7 ± 2.33 | 0.002 | 22.7 ± 6.5 | 0.11 | 1.7 | 0.02 | 0.36 | 12 |
| Control | 13.2 ± 3.5 | 1 | 20.9 ± 6.3 | 1 | 2.1 | 1 | 0.34 | 12 |
| Latrunculin A 200 nM + blebbistatin 10 μM | 4 ± 1.9 | 1e-5 | 1.3 ± 0.6 | 4e-5 | 0.06 | 1e-23 | 0.39 | 14 |
Parameter values Kh and were fit for each cell measured individually. Shown are average values and SDs. P-values were calculated using a Mann-Whitney test. In addition, mean values of cell surface tension and cell height reduction ξ are indicated. During measurements, cells were adhered to glass-bottom dishes except for measurements corresponding to row 7. There, cells were detached before the measurement and resuspended on PEG-coated dishes to ensure proper cell rounding at very low surface tension (Materials and Methods). Blebbistatin inhibits myosin II; Y-27632 inhibits ROCK, which then affects cortical myosin activity downstream; taxol stabilizes microtubules; nocodazol interferes with microtubule polymerization; and latrunculin A interferes with actin polymerization.
Restoration of myosin activity through photoinactivation of blebbistatin
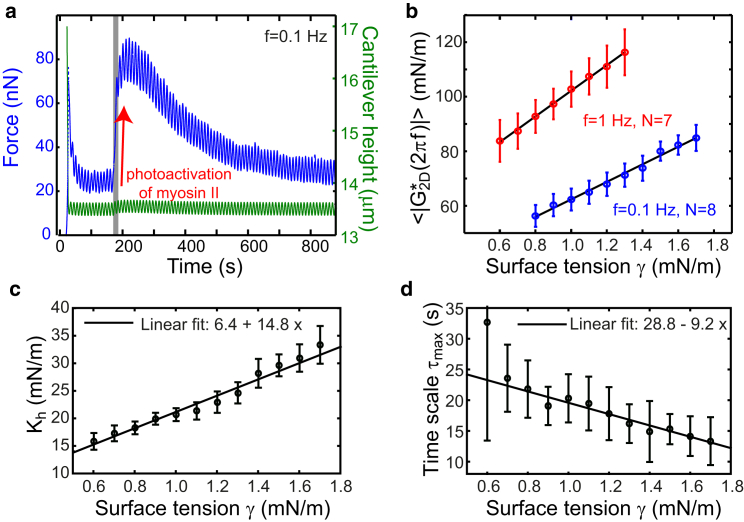
Rheological measurements including (indirect) photoactivation of myosin II in blebbistatin-treated cells were performed on PEG-coated dishes with detached cells. In this way, we could entirely rule out effects of cell shape changes and adhesion during changing cell surface tension. During photoactivation measurements, we performed cantilever height oscillations until force oscillations were in steady state. Then, we exposed the cell for ≈10 s to blue light (GFP excitation, fluorescence lamp). As a consequence, the measured AFM force shoots up and at the same time, oscillation amplitudes increase (see Fig. 6 a). Then, over a time interval of ≈10 min, the average force gradually decreases back to its original value as active blebbistatin reenters the cell (see Fig. 6 a). As this decrease is slow as compared to the sampled oscillation periods (1, 10 s), we expect that oscillations are close to steady state during this time interval. We determined the momentary complex elastic modulus and the average effective tension within moving time windows of two oscillation periods. Oscillation amplitudes were chosen to be very small (0.125 μm) such that the average effective tension could to a good extent be identified with cell surface tension at steady state.
Figure 6.
Mitotic cells stiffen through myosin activity. (a) Restoration of myosin activity during rheological sampling of a mitotic cell treated with blebbistatin (2.5 μM). At time ≈180 s, the cell is exposed to blue light for an exposure time of ≈10 s (gray area), which causes a photoinactivation of blebbistatin (myosin II inhibitor) and thereby restores myosin II activity. This leads to a drastic force increase together with an increase of the force oscillation amplitude. Due to active blebbistatin slowly reentering the cell, average force and oscillation amplitude gradually decrease again over a timescale of ≈10 min. (b) Magnitude of 2D complex elastic modulus in dependence upon momentary cell surface tension measured during the interval of gradual force decrease. Values were averaged over several cells (f = 1 Hz, N = 7 and f = 0.1 Hz, N = 8). Error bars represent SDs. (c and d) Rheological parameters Kh and , dependent upon cell surface tension. Parameters were obtained by fitting averaged values of storage and loss moduli measured at different, binned values of cell surface tension. Error bars are SDs of fit parameters as obtained from bootstrapping using Gaussian random variates (N = 30). Measurements were carried out with detached cells on PEG-coated dishes to avoid potential cell shape changes upon varying cell surface tension. To see this figure in color, go online.
Gene knock-down through RNA interference
To probe the influence of the molecular composition of the cell cortex on the viscoelastic response of cells, we performed gene knock-downs through RNA interference (RNAi). Cells were transfected with esiRNA (Eupheria Biotech, Dresden, Germany) targeting the genes MYH9 and ACTN4 at a concentration of 10 nM (MYH9) and 100 nM (ACTN4), respectively, using the transfection reagent Lipofectamin RNAiMax (Invitrogen). For a control, we used firefly luciferase esiRNA (F-Luc). At day 0, 30,000 cells were seeded into a 24-well plate (Nunc MicroWell Plates with Nunclon; Thermo Fisher Scientific, Waltham, MA). Transfection was carried out at day 1, medium was exchanged at day 2 (without antibiotics), and transfected cells were measured at day 3. Approximately 12 h before measurements, cells were trypsinized, diluted, and transferred onto a glass-bottom petri dish (FD35; World Precision Instruments) to achieve a confluency of 20–40% during AFM measurements.
Estimating cellular shape and volume during AFM measurements
During progressive uniaxial cell compression, a time-lapse of z-stacks was recorded in DIC mode including eight z-planes centered roughly around the cell equator (Δt = 10–20 s and Δz = 1 μm). At each compression level, we chose a time point of the time series, where steady force was reached and selected the z plane with maximal cell diameter and used this as an estimate of equatorial cell radius. It has been shown previously that the shape of mitotic cells during parallel plate confinement is to a very good approximation given by a shape of minimal surface area at negligible adhesion (10). Therefore, the equatorial cell radius Req and cell height h are sufficient parameters to determine cell shape and cell volume (Fig. S9) (10, 16). To calculate cell volume, we used the formula , which can be derived by approximating the profile of the free cell contour by a semicircle. In this way, we estimated cell volume for progressive cell compression levels. In general, we do not find a trend for increasing or decreasing cell volume due to progressive uniaxial cell compression within the uncertainties of our measurement (≈2% error; see Fig. S10). Therefore, we averaged volume values of one cell measured at the first four compression levels and used this average volume as estimated cell volume. Cells that were sampled through oscillatory uniaxial compression were imaged during slow cantilever oscillations (f = 0.01 or 0.02 Hz) and the average equatorial radius during oscillations was determined. The average radius together with average cantilever height during oscillations was used to estimate cell volume as described above. Anticipating shapes of minimal cell surface area in steady state of uniaxial cell compression, we could calculate the area of contact between cell and cantilever wedge (or dish bottom) and the mean curvature H of the free cell surface for each compression level (Fig. S9). To determine the contact radius , we used the approximative formula , described in Fischer-Friedrich et al. (10). Together with measured AFM forces, this allowed us to estimate cell surface tension in steady state (10).
Calculations of the uniaxial compression of elastic model cells
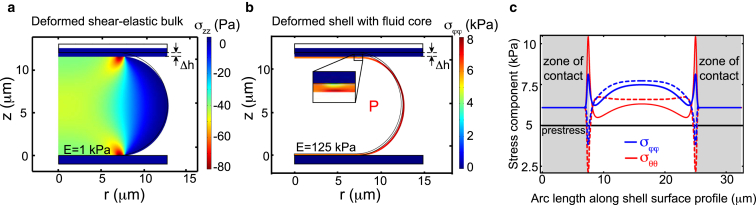
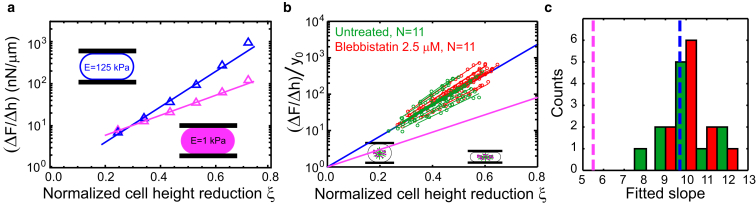
To distinguish between the scenario of a mechanically dominant cell interior or cell cortex, we performed calculations of elastic deformations in idealized model cells. We calculated the elastic deformation of model cells in two different scenarios with the aid of Comsol Multiphysics (https://www.comsol.com; see the Supporting Material for details). In the first scenario, which represents a mechanically dominant cytoplasm, the model cell was represented by an elastic body of revolution (E = 1000 Pa, ν = 0.49) generated by a rectangle and an adjacent semicircle (see black wire-frame in Fig. 2 a). In the second scenario, which represents a mechanically dominant cortical layer, the model cell was represented by an elastic shell (E = 125 kPa, ν = 0.49) whose shape was defined by an outer contour of minimal surface area and a thickness of nm (10). Furthermore, we assigned a uniform, constant mechanical prestress that mimics active tension in the cortex due to the presence of myosin motors. The prestress is a constant, isotropic in-plane stress in the shell that was set to 5000 Pa corresponding to a surface tension of = 1 mN/m. We calculated the force increase ΔF due to the creation of elastic stresses after a uniaxial compression by Δh resulting from a set piezo displacement of 0.5 μm. The total cell volume for both scenarios was V = 5000 μm and was kept constant during the deformation. In the case of a shell, volume conservation was realized by the implementation of an internal pressure that was adjusted in the process of compression. In our calculations, objects are initially free of elastic stresses and only after the performance of the compression step are elastic stresses present. Calculations were carried out with elastic reference shapes with varying cell height h corresponding to different values of cell height reduction , where . We find that the functional dependence of is close to linear (see Fig. 3 a). Linear slopes fitted in the ξ-interval [0.2, 0.6] differ for the two scenarios: while the elastic bulk shows a slope of ≈5.5, the elastic shell displays a slope of ≈9.7 (see Fig. 3 a). Simply speaking, the larger slope of for the case of the shell originates from surface area stretch (ΔA/A) increasing more strongly than bulk strain (≈Δh/h) for increasingly oblate equilibrium shapes. These distinct trends allow us to clearly discriminate between the two scenarios of a bulk- or a shell-dominated mechanics. To compare theoretical results with experimental data, we plotted for each cell measured and fit a linear slope (see Fig. 3 b). Indeed, measured are captured well by a linear dependence and show average slopes of 10.1 ± 1.2 for untreated, mitotic cells (see Fig. 3, b and c, green, 0.5 μm piezo displacement, Δt = 1 s, N = 11). We also measured cells treated with low doses of blebbistatin (2.5 μM), which leads to a reduction of cell surface tension by inhibition of myosin II. Again, we performed iterative cell compression steps on those cells. There, follows on average a slope of 10.1 ± 0.8 (see Fig. 3, b and c, red, N = 11). Comparing slopes as predicted from computer simulations (slope of ≈5.5 for elastic bulk and slope of ≈9.7 for elastic shell) with experimentally derived slopes, we concluded that the experimental data are significantly closer to the scenario of a compressed shell (see Fig. 3 c).
Figure 2.
Finite element simulations of uniaxial compression of elastic model cells (side view, Δh = 0.5 μm). (a) First model cell consisting of a uniform, shear-elastic bulk (E = 1 kPa) with undeformed shape given by a body of revolution generated by a semicircle displaced orthogonally from the axis of revolution (black wire-frame, volume: 5000 μm3). The deformed configuration is shown as a colored area. Color-codes for the magnitude-of-stress component σzz. (b) Second model cell constituted by a shear-elastic shell enclosing a constant volume (E =125 kPa, Poisson ratio ν = 0.49, thickness 200 nm) and with a constant in-plane prestress (5 kPa) corresponding to a constant active tension of ≈1 mN/m. This active tension is balanced by an internal pressure P. The shape before deformation is indicated by a black wire-frame and corresponds to a shape of minimal surface area at a given volume of 5000 μm3. The colored area shows the deformed shell. Color-codes for the value of stress component σφφ, where φ is the azimuthal angle. As the problem is axisymmetric, only one-half of the cell is shown corresponding to azimuthal angle φ = 0. (c) Stress components σφφ, and σθθ, in the compressed shell along the contour of the inner (solid) and outer (dashed) surface of the shell (starting from the center of the contact area and continuing up to the equator). While φ denotes the azimuthal angle, θ parameterizes the direction orthogonal to φ in the tangent plane of the shell surface. Shown is the overall stress (prestress + elastic stress). To see this figure in color, go online.
Figure 3.
Behavior of the cellular force response to compression steps for different cell compression levels in model cells and experiments. (a) Calculated, normalized force increase ΔF due to elastic stresses in model cells of different initial reference shapes as a function of normalized cell height reduction ξ = 1 – h/(2R), where h is the initial cell height and for cell volume V (Fig. 2, shear-elastic bulk: magenta, elastic shell: blue, Δh = 0.5 μm). Every data point was calculated for an elastic object with V = 5000 μm3, which corresponds to a typical volume of a mitotic HeLa cell. (b) Comparison of normalized force increase from measurements and theory. Every cell was measured at different cell heights giving rise to 5–10 measured values ΔF(ξ) per cell (circles). Experimental data points from one cell are fit linearly (untreated cells: green, N = 11; cells treated with 2.5 μM blebbistatin, red, N = 11, 0.5 μm piezo displacement). The lines in blue and magenta represent the linear fit presented in (a). All curves were normalized by division through their y intercept y0 as estimated from a linear fit. (c) Histogram of fit slopes of the measured curves for untreated cells (green) and blebbistatin-treated cells (red). Dashed lines indicate the slopes as predicted by FEM simulations for the scenario of an elastic shell with active tension (blue line) or the scenario of an elastic bulk (magenta). All measured cells were mitotically arrested by addition of STC (2 μM). To see this figure in color, go online.
Results
Rheology of thin active films
We first discuss the mechanics of a thin active film as a model for the cell cortex. The cortex is a dynamic active gel. While myosin and cortical cross-linker proteins turn over on timescales on the order of 1–10 s, actin filaments in the mitotic cortex turn over on the timescale of roughly 1 min (2, 17). In the steady state, actomyosin contractility generates an in-plane contractile tension, the cortical tension denoted . Under dynamic area changes, this film tension becomes a dynamic quantity. The rheology of the film under uniform area dilation is characterized to linear order as
| (1) |
where is the area strain, is a reference area, and the dot denotes a time derivative. The relaxation modulus G2D(t) describes the time-dependent response, including memory effects and viscoelastic material properties (18). Equation 1 describes a relaxation process by which the film tension relaxes to the steady-state value . The relaxation modulus G(t) results in general from a superposition of many collective relaxation modes with a range of relaxation times τ, and can thus be written as (18)
| (2) |
Here, the relaxation spectrum characterizes the relative weight of modes with relaxation time τ. The function characterizes the mechanical properties of the material. In the absence of detailed knowledge of the internal relaxation processes, we use a simple choice of , which corresponds to a relaxation spectrum with constant amplitude up to a maximal time , which is the longest relaxation time (Fig. S1 a). In short, we choose = Kh for τ ≤ and = 0 for τ > . With this choice, the relaxation modulus is given by
| (3) |
where is called the exponential integral (see the Supporting Material). The complex elastic modulus can be decomposed into a real and an imaginary part as with
| (4) |
| (5) |
This complex elastic modulus characterizes the frequency-dependent response of the active film to area dilation. The real-part is a two-dimensional (2D) storage modulus that accounts for the in-phase elastic response. The imaginary part is a 2D loss modulus that accounts for a viscous response. This dissipative part of the response is phase shifted to the applied oscillatory stress by π/2. Alternatively, the complex modulus can also be written as , where the phase φ describes the lag between stress and strain during oscillatory forcing of the material. For viscoelastic materials, this phase shift typically ranges between zero and π/2. If the material is solidlike, the phase shift is small and close to zero. Viscous behavior corresponds to a phase shift close to π/2. Equations 4 and 5 provide a simple model to discuss the rheology of the cortical layer based on a characteristic timescale and a complex elastic modulus.
Note that the general form of the relaxation modulus given by Eq. 3 is model-independent. A particular choice of the relaxation spectrum corresponds to a rheological model. For example, the Maxwell model corresponds to the choice , where τ0 is the Maxwell time and K is an elastic modulus. Our choice of the relaxation spectrum giving rise to the moduli (3, 4, 5) captures the essential features of the experimental data using only two parameters. Note that our model is fundamentally different from the Maxwell model as it captures a broad spectrum of relaxation processes. Power laws are often used to fit experimental data. Power laws also imply the existence of a broad relaxation spectrum. However, in the presence of a maximal relaxation time of the system, the power law must be cut off (Section S1). In the cortex, a maximal relaxation time exists because of filament turnover. As discussed in Results, a power-law relaxation spectrum without cutoff does not provide a good fit to the data.
Cell compression between two parallel plates
To experimentally characterize the mechanics of the cell cortex, we probed the mechanical response of HeLa cells in mitotic arrest utilizing AFM together with wide-field imaging. Cells were chemically arrested in mitosis by addition of STC, an inhibitor of kinesin Eg5. In this way, arrested cells were adopting a rounded shape for several hours. During our measurements, these rounded cells were confined between the cell culture dish and an AFM cantilever that was supplemented with a wedge (10, 12) (Fig. 1 a). To characterize the confined cell shape during our measurements, we introduce the variable normalized cell height reduction ξ = 1−h/(2R), which quantifies how much the perturbed cell height h deviates from that of a sphere of equal volume (, where V is the measured cell volume; see Materials and Methods). This variable takes the value 0 if the cell shape is spherical and 1 if the cell is squeezed entirely to the dish bottom. After confining a cell with the cantilever, we waited until a steady state was reached with a constant force exerted on the cantilever. This steady-state force can be attributed to the presence of a cell surface tension , where is the radius of the cell contact area on the plates and H is the mean curvature of the cell surface (10, 16). While is largely constant independent of the confinement height of the cell, the steady state force increases for increasing ξ (10). We estimated the cell volume at increasing levels of cell height reduction and did not observe volume changes (within the accuracy of our measurements), suggesting that the cell volume is constant during the experiments (Fig. S10).
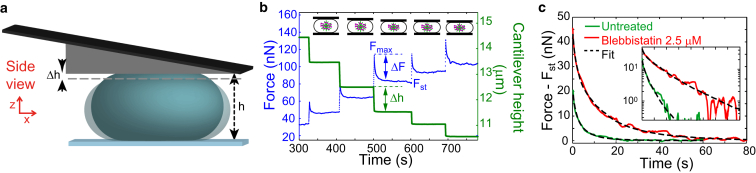
Figure 1.
Stepwise uniaxial compression of a mitotic cell. (a) Schematic of a compressed cell (blue) confined between the dish bottom and a wedged AFM cantilever. In a compression step, the cantilever is lowered by a height interval Δh. (b) Measured compression force and cantilever height during stepwise uniaxial cell compression. (c) Force relaxation after a step of uniaxial cell compression (normalized cell confinement) for an untreated cell (green) and a cell treated with the myosin II inhibiting drug blebbistatin (2.5 μM, red). The steady-state value has been subtracted. (Dashed lines) Fit of the rheological model (untreated: ξ = 0.47, = 11.5 s, Kh = 12.7 mN/m, and = 130 nN; blebbistatin-treated: ξ = 0.55, = 35 s, Kh = 10.3 mN/m, and = 40 nN). (Inset) Same data as in (c) in a semi-log plot. Before measurements, cells were arrested in mitosis by addition of S-trityl-l-cysteine (2 μM). To see this figure in color, go online.
Using the AFM-based assay, we performed step strain experiments by uniaxially compressing the cell in a series of small steps Δh (Fig. 1, a and b). Upon each compression step, we observed a rise in force F up to a peak value Fmax. After the step was completed, the force relaxed to a new steady-state value that corresponds to the new cell height (Fig. 1 b). We thus denote the force difference ΔF = Fmax – as transient force increase (Fig. 1 b). An example of the force relaxation upon a compression step is shown in Fig. 1 c (solid lines), together with a fit of the model given by Eq. 3 (for details, see the Supporting Material). The inset shows a semilogarithmic plot of the same data. The observed force relaxation is similar to previous reports (11) and indicates a viscoelastic response of the cell. From the fact that tension relaxes to a value set by the steady cortical tension, we conclude that elastic stresses relax completely after a finite relaxation time.
Viscoelastic cell stiffness is dominated by the cortical layer
The AFM measurements show that we can characterize the time-dependent mechanical properties of the cell. We next wanted to understand the contribution of the cortical layer to these mechanical properties. For this purpose, we performed calculations of the uniaxial compression of two types of elastic model cells. The first model cell was constituted by an incompressible shear-elastic bulk (Fig. 2 a). This corresponds to the extreme case of a cell with an elastic cytoplasm that dominates the mechanical properties. The second model cell was constituted by an elastic shell enclosing an incompressible bulk (Fig. 2 b). This corresponds to the extreme case of an elastic cortical layer that dominates cell mechanics. This elastic picture, although simplified compared to the cell, allows us to characterize the differences of cortical and cytoplasmic contributions to cell mechanics.
Calculations were performed using linear elasticity theory in terms of finite element simulations (Materials and Methods and see the Supporting Material). For both cell models, we started from a stress-free reference shape with reduced height h = 2R(1−ξ). We deformed each model cell through a step of uniaxial compression by Δh = 0.5 μm and calculated the transient force increase ΔF due to elastic stresses. The two scenarios show different behaviors of ΔF as a function of the normalized cell height reduction ξ (Fig. 3 a). Therefore, the simple alternatives of bulk- or shell-dominated mechanics can be clearly discriminated from the slope of log(ΔF/Δh) upon compression.
In contrast to the ideal elastic model cell, actual cells are viscoelastic and their effective stiffness is timescale-dependent. However, for step strain experiments, a direct analogy can be drawn between an elastic and a viscoelastic system if the strain is applied in a fixed time interval and therefore a particular range of timescales of the system is probed (Section S3). We therefore examined whether experimentally measured ΔF, which is the transient force increase due to the presence of elastic stresses, shows a dependence on normalized cell height reduction that corresponds to either of the two elastic model cells. We plotted ΔF/Δh versus ξ in a semilogarithmic plot comparing the obtained slopes to those obtained from computer simulations (Fig. 3 b). Using histograms of the experimental slopes, we conclude that the experimental data are close to the scenario of a compressed shell (Fig. 3 c and Materials and Methods). This suggests that the cortical layer is the dominant mechanical element in the mitotic cell. Thus, the mechanical cell response shown in Fig. 1 provides information about the rheology of the cell cortex.
Oscillatory forcing of the cell cortex
We next performed a careful rheological analysis of the cortical layer in mitosis using cell compression. A cortical layer is a complex and interlocking set of mechanical elements that responds under uniaxial compression at different timescales. To distinguish the mechanical behavior at different timescales, we performed experiments in which the cell height was oscillated at different frequencies (Fig. 4 a). These height modulations give rise to an oscillatory force response of the cell with a phase difference between the cantilever height oscillation and the cellular force response. We observed that force oscillation amplitudes increase for higher frequencies at constant height amplitude (Fig. 4 b). This implies that cell stiffness is larger at shorter timescales consistent with the observed larger forces at shorter times in Fig. 1 b. Force oscillations were close to a sinusoidal shape and scaled linearly with the amplitude of cantilever height oscillations (Fig. 4, a and c; Fig. S12). Therefore, we conclude this to be in the regime of linear viscoelastic behavior. Note that when the cortex was disintegrated by cytoskeletal drugs, we observed strongly reduced force oscillation amplitudes (Fig. 4 b, red data), consistent with the finding that the cortex dominates cell mechanics.
Figure 4.
Rheological characterization of the mitotic cortex through oscillatory cell compression. (a) Exemplary readout of cantilever height and AFM force during rheological cell probing. The AFM cantilever is lowered onto the cell and sinusoidal cell height oscillations are imposed (green curve). Steady force oscillations emerge after a transient phase (blue curve). (b, Top) Force oscillation amplitudes (blue curve) depend on frequency. For slow oscillation frequencies, force amplitudes approach the value expected from purely geometrical changes (dashed line) at constant cell surface tension. Exposing cells to a combination of the actin-depolymerizing drug latrunculin A (200 nM) and the myosin II-inhibiting drug blebbistatin (2.5 μM), force oscillation amplitudes (red curve) are strongly reduced. (b, Bottom) Associated oscillation amplitudes of effective tension = F/(Acon2H). Cantilever oscillations amplitudes were set to 0.5 μm. Error bars indicate SDs. (c) Force amplitudes increase linearly with cantilever oscillation amplitudes in the measured frequency range. To see this figure in color, go online.
For a rheological analysis, we identified strain and stress variables in our experiments. The results of the previous section indicated that the cellular viscoelastic response is dominated by the cortical layer. We therefore chose the strain variable to be the area strain of the total cell surface area (see Section S4). The relevant stress is the instantaneous cortical tension. To estimate this tension, we used an effective tension γeff given by the normalized AFM force . In steady state, the effective tension equals the cell surface tension . Force amplitudes approach a nonvanishing value for small frequencies. However, amplitudes of effective tension approach zero in this limit (Fig. 4 b, lower panel).
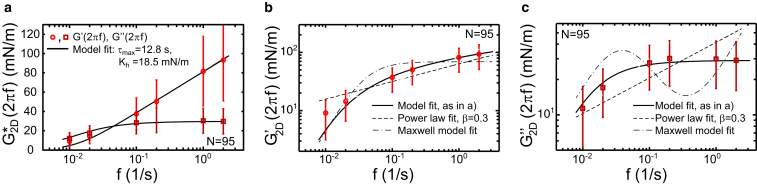
Defining stress and strain as described above, we could deduce a complex elastic modulus of the 2D cell cortex. Measured cortex elastic moduli for untreated cells are shown in Fig. 5 together with a fit of the model defined in Eqs. 4 and 5. For untreated cells in mitotic arrest, we obtained from this fit the parameters and Kh = 18 ± 8 mN/m (N = 95), where errors indicate SDs. In the log-log plots shown in Fig. 5, b and c, fits of a Maxwell model and of a power law to the experimental data are also shown. As expected, the Maxwell model does not correctly account for the data. Furthermore, our rheological model provides a better fit of the data than a power law.
Figure 5.
Two-dimensional, complex elastic modulus obtained from rheological sampling of mitotic cells. (a) Averaged storage (circles) and loss modulus (squares) in dependence upon frequency (N = 95 cells). To calculate elastic moduli, effective tension ( = F/(Acon2H)) was identified with stress, while estimated area strain of overall cell surface area was identified with strain. Storage and loss modulus were fit simultaneously assuming a constant relaxation spectrum of constant magnitude Kh up to a cutoff time . Obtained fit parameters were Kh = 18.5 mN/m and = 12.8 s (solid black lines). (b and c) Averaged storage and loss modulus in a log-log representation (same data as in a) and associated model fits: our model (solid black line as in a); power law (dashed line); and Maxwell model with viscous element (dash-dotted line). For the power-law fit, fit functions were with fitted parameter values A = 36.4 mN/m, B = 23.6 mN/m, and β = 0.3. For the Maxwell-model fit, fit functions were and with fitted parameters k = 69.22 mN/m, τ = 4.16 s, and η = 3.25 mN s/m. Error bars indicate SDs. To see this figure in color, go online.
We tested whether measured values of the complex modulus depend on the degree of normalized cell height reduction ξ. We found that the magnitude of decreases for increasing ξ (Fig. S5 and Section S7). Therefore, to investigate the effect of perturbations on the stiffness of cells, it is important to perform measurements at similar normalized cell height reduction ξ.
When oscillatory cell forcing was applied in the same way to rounded interphase cells, we obtained qualitatively similar rheological data which were still captured by our model (Fig. S17). However, cortex stiffness values as reflected by Kh were roughly one order of magnitude smaller (Kh = 1 mN/m and = 8 s). A similar relative increase in stiffness from interphase to mitosis was reported earlier from AFM indentation experiments on Drosophila S2R+ cells (19).
So far, we have presented 2D complex elastic moduli of the cell cortex in units of mN/m for mitotic cells. To compare our results with previous measurements that showed three-dimensional (3D) complex elastic moduli of cells, we also performed an alternative analysis of our data calculating effective 3D Young’s moduli using normalized cell height as strain and defining stress as σ = F/A, where F is the force and A is the cell cross-sectional area (Fig. S8, a and b). From this analysis, we obtain effective frequency-dependent cell elastic moduli in the range of 100–1500 Pa for mitotic cells. For interphase cells, we obtain values in the range 10–500 Pa that are comparable to effective cell elastic moduli reported earlier for rounded interphase cells (20, 21). Note, however, that effective 3D cell elastic moduli are not appropriate to describe 2D cortical mechanics. Interestingly, these effective 3D cell elastic moduli as a function of frequency resemble a power law more closely than the 2D moduli describing cortical rheology (compare Fig. S8, a and b to Fig. 5, b and c). The reason for the altered shape of the dynamic moduli as a function of frequency originates in the different choice of the stress variables in the definitions of elastic moduli. In the case of effective 3D moduli, the stress variable is the scaled force, while in the case of 2D moduli, it is the cortical tension. Time-dependent force and cortical tension are not just proportional to each other. They are phase-shifted because of the coupling of the time-dependent cell geometrical changes with the active cortical tension in the force balance (see Section S9 for details). Therefore, elastic moduli derived from force or tension oscillations, respectively, show a different frequency-dependence.
Modulation of rheological properties by molecular perturbations
Having set up this method to study time-dependent cortex rheology during mitosis, we wanted to examine the influence of different molecular perturbations in the cellular system. To this end, we used cytoskeletal drugs and gene knock-down by RNA interference. For each condition, we determined the parameters and Kh by fitting the rheological model to the frequency-dependent storage and loss moduli for each cell.
We found that perturbations of the cortex-associated molecular motor myosin II had a clear influence on cortex rheology. After addition of the myosin II perturbing drugs blebbistatin (selective inhibitor of non-muscle myosin II) and Y-27632 (selective inhibitor of ROCK, which regulates myosin II activity (11, 22)), and after knock-down of myosin II, storage and loss moduli decreased (Fig. S13). The associated phase shifts also decreased. Correspondingly, the cutoff time increased and the spectrum amplitude Kh decreased (Table 1, rows 1 and 4; Fig. S13). These results indicate that reduction of myosin II activity makes the cell cortex more solidlike but less stiff.
To further examine the effect of myosin activity on cortical rheology, we used photoinactivation of the myosin II inhibitor blebbistatin under conditions were myosin was initially inhibited by blebbistatin (2.5–5 μM). Because blebbistatin is photo-inactivatable by blue light (23), myosin II activity could be restored by blue light exposure. During oscillatory cell compression, the average force increased rapidly upon illumination by blue light (Fig. 6 a). The amplitude of force oscillations also increased. When illumination was switched off after ∼10 s, the average force gradually relaxed to its original value after ∼10 min as active blebbistatin reentered the cell (Fig. 6 a). In this time interval, we determined rheological properties of a cell while cell surface tension changed gradually because of myosin reinhibition (Materials and Methods). We found that the magnitude of the complex elastic modulus and the phase shift φ between stress and strain decreased roughly linear together with the declining cell surface tension (Fig. 6 b; Fig. S15). This indicates a more fluidlike behavior for higher values of active tension. Using values of measured at f = 0.1 and 1 Hz, we estimated parameter values Kh and as a function of cell surface tension . While Kh increases roughly linearly for increasing , the cutoff timescale decreases (Fig. 6, c and d).
To investigate the possible influence of microtubules in the system, we studied the effect of taxol, which stabilizes microtubules and nocodazol, which depolymerizes them. In the presence of either drug, the cell surface tension is slightly increased, suggesting that the activity of myosin is enhanced in the absence of dynamic microtubules consistent with earlier findings (9, 24). Furthermore, addition of taxol (100 nM) tends to reduce values of storage and loss moduli at low frequencies while phase shifts increase. Correspondingly, is also reduced (Table 1, rows 2 and 3; Fig. S14).
We also examined the influence of the actin cross-linker α-actinin-4 (ACTN4) on cortical mechanics. Just like actin, α-actinin-4 is mainly localized to the cell cortex during mitosis (Fig. S6 d) (25). Knock-down of α-actinin-4 through RNA interference leads to a reduction of steady-state tension in both chemically arrested mitotic cells (Fig. S6, a and b) as well as in cells left to transition through mitosis (Fig. S6). A change of cortical architecture as a consequence of knock-down of α-actinin-4 is also reflected by a reduced cortical localization of myosin, and to a lesser extent of actin (Fig. S6 c). Oscillatory measurements of ACTN4 knock-down cells show that storage and loss moduli are reduced while phase shifts increase. This indicates a fluidization of the cortex due to α-actinin-4 knock-down. Correspondingly, estimated values of and Kh are reduced as compared to control cells (Table 1, row 5; Fig. S13).
Finally, we studied cells in the presence of the actin-depolymerizing drug latrunculin A (200 nM) in combination with the myosin II inhibitor blebbistatin (10 μM). In this condition, we find strongly reduced storage and loss moduli, which is also reflected by a value of Kh that is reduced by approximately an order of magnitude. In addition, the characteristic timescale is reduced from ≈13 s in control cells to 4 s (Table 1, row 6; Fig. S14).
Discussion
In this article, we have probed the mechanics of Hela cells and determined the 2D rheology of the cell cortex in mitotic arrest. To this end, we have performed dynamic uniaxial cell compression with a parallel plate assay. Parallel plate manipulation is an established method to probe cell mechanical properties of adherent interphase cells via microplates (26, 27, 28). We apply this method to mitotic cells using AFM. High cell surface tension in mitosis (10) together with AFM measurement precision allowed us to control cell shape accurately. Our measurements confirm earlier findings that the cortex dominates cell mechanics (Fig. 3) (10, 29, 30, 31, 32, 33). Based on this finding, we determine the frequency-dependent storage and loss moduli of the 2D cell cortex using the dynamic force response of whole cells. Cortical tension arises as the combination of a time-independent active tension due to actomyosin contractility and a dynamic part characterized by a 2D time-dependent relaxation modulus (Eq. 1). We measure a corresponding storage modulus mN/m for frequency f = 1 Hz, which is comparable to the area expansion moduli measured for MDCK II cells by AFM indentation (34) and approximately a factor-of-five smaller than area expansion moduli measured for preswollen red blood cells by micropipette aspiration (35). We can estimate a 3D shear elastic modulus of the cortical layer on the order of 100 kPa for f = 1 Hz, using d ≈ 200 nm for the cortical thickness (36) and a Poisson ratio ν = 0.5, corresponding to an incompressible material. Comparable moduli have been reported for actin-rich structures such as muscle fibers or actin stress fibers (37, 38). We have also analyzed our data calculating effective 3D elastic moduli of the entire cell. We obtain a storage modulus of ∼1300 Pa during mitotic arrest at f = 1 Hz. For interphase cells, we find ≈300 Pa (Fig. S8, a and b). These effective cell moduli are consistent with earlier measurements determining cell elasticity (20, 21). Interestingly, this effective cell modulus is generated mainly by the rheology of the cell cortex, as we show in this work.
Our measurement of dynamic storage and loss moduli allow us to discuss frequency-dependent material properties of the cell cortex. At frequencies <0.02 Hz, the loss modulus dominates and the cortical response becomes fluidlike. This suggests that the cortex behaves like a viscous fluid at slow timescales. This emergence of fluidity might be due to the turnover of actin cross linkers and actin filaments, which leads to the relaxation of elastic stresses at long times (2). Because of this fluidlike behavior, the cortex flows in response to contractility gradients (39, 40). Such cortical flows occur, for example, during cell division, particularly when the division is asymmetric, or during the formation of a contractile ring (39, 41).
Our data suggest the existence of a longest relaxation time , which might be related to cortex turnover. Indeed, a simple rheological model with a constant relaxation spectrum and a cutoff timescale fits the rheological data well (Fig. 5). We compared this fit to fits of a Maxwell model and of a power law. The Maxwell model with only a single relaxation time does not fit the data. The power law does not capture the maximal relaxation time that corresponds to cortical turnover. As a consequence, it provides a poorer fit as compared to our model. This can be seen most clearly when fit to the loss modulus data (Fig. 5 c). However, when using the power law to fit the data, we obtain an exponent ≈0.3, similar to reported values (42, 43).
The actin network is organized by a large number of associated proteins. However, it has been difficult to distinguish the roles of these different proteins for rheological properties of the mitotic cell cortex. In our assay, knock-down of myosin II and α-actinin both reduce the magnitude of the elastic modulus of the cortical layer, as suggested by previous work (44, 45, 46, 47, 48, 49, 50, 51, 52). However, our oscillation experiments show that myosin II tends to fluidize the cortex, while α-actinin tends to solidify it. The solidifying role of α-actinin has been extensively studied in the in vitro actin networks and in vivo (46, 47, 51). In terms of our rheological model, α-actinin knock-down reduces the characteristic timescale , suggesting enhanced cortical turnover under this condition. This is consistent with the observation that α-actinin overexpression inhibits actin turnover during cell division (53). Previous studies have reported both a fluidization or a solidification of actin networks through myosin activity. Myosin II has been shown to fluidize non-cross-linked networks (54) while cross-linked actin networks were reported to solidify when myosin was added (50). Several in vivo measurements have suggested a solidifying role of myosin for adherent cells (45, 55), but a fluidizing effect for suspended cells (20) and myoblasts (52). Here, we observed a solidification when myosin II is inhibited, suggesting that myosin activity in the cortex modulates rheological properties and increases fluidity. This resembles the observed fluidization of cellular material properties when exposed to large external prestress (43, 56). We speculate that the fluidization by myosin in mitotic HeLa cells observed here could stem from enhanced actin turnover in the cortical layer resulting from increased active tension. This is supported by the observation that actin turnover is augmented by myosin activity during cytokinesis of mammalian cells (57).
Despite extensive theoretical work that suggests that the best way to think about the cortex is as an active thin film, it has been difficult to test these ideas in vivo. By introducing uniaxial compression of cells and complementing this with a simple rheological model, our work provides a characterization of the time-dependent mechanical properties of the mitotic cortex, confirming that it behaves like an active fluid film on longer timescales. Modulation of the properties of this film drives cell morphology and tissue reorganization.
Author Contributions
E.F.-F. and C.J.C. performed research and analyzed the data; Y.T. contributed new reagents and analytic tools; E.F.-F., D.J.M., A.A.H., and F.J. designed the research; and E.F.-F., Y.T., C.J.C., D.J.M., A.A.H., and F.J. wrote the article.
Acknowledgments
We thank Benjamin Friedrich, Guillaume Salbreux, Alexander Mietke, Louise Jawerth, and Stefan Münster for helpful discussions on cell mechanics and Jochen Guck and Moritz Kreysing for kind access to Comsol Multiphysics software. Furthermore, we thank Martin Stewart for advice on trans-mitotic AFM measurements and discussions about the consequences of impaired cortex integrity, Subramanian Ramanathan and Jonne Helenius for advice on quantification of cortical components, and the E. Paluch laboratory for contributing the Lifeact-mCherry expressing HeLa cell line.
This work was supported by the Eidgenössische Technische Hochschule Zürich (research grant No. ETH-05 11-2).
Editor: Cecile Sykes.
Footnotes
Supporting Materials and Methods and 17 figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30441-6.
Contributor Information
Anthony A. Hyman, Email: hyman@mpi-cbg.de.
Frank Jülicher, Email: julicher@pks.mpg.de.
Supporting Material
References
- 1.Lecuit T., Lenne P.-F. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat. Rev. Mol. Cell Biol. 2007;8:633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- 2.Salbreux G., Charras G., Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 2012;22:536–545. doi: 10.1016/j.tcb.2012.07.001. [DOI] [PubMed] [Google Scholar]
- 3.Hyman A.A., Weber C.A., Jülicher F. Liquid-liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 2014;30:39–58. doi: 10.1146/annurev-cellbio-100913-013325. [DOI] [PubMed] [Google Scholar]
- 4.Fehon R.G., McClatchey A.I., Bretscher A. Organizing the cell cortex: the role of ERM proteins. Nat. Rev. Mol. Cell Biol. 2010;11:276–287. doi: 10.1038/nrm2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Umetsu D., Aigouy B., Dahmann C. Local increases in mechanical tension shape compartment boundaries by biasing cell intercalations. Curr. Biol. 2014;24:1798–1805. doi: 10.1016/j.cub.2014.06.052. [DOI] [PubMed] [Google Scholar]
- 6.Rauzi M., Verant P., Lenne P.-F. Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat. Cell Biol. 2008;10:1401–1410. doi: 10.1038/ncb1798. [DOI] [PubMed] [Google Scholar]
- 7.Eisenhoffer G.T., Loftus P.D., Rosenblatt J. Crowding induces live cell extrusion to maintain homeostatic cell numbers in epithelia. Nature. 2012;484:546–549. doi: 10.1038/nature10999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Théry M., Jiménez-Dalmaroni A., Jülicher F. Experimental and theoretical study of mitotic spindle orientation. Nature. 2007;447:493–496. doi: 10.1038/nature05786. [DOI] [PubMed] [Google Scholar]
- 9.Stewart M.P., Helenius J., Hyman A.A. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469:226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- 10.Fischer-Friedrich E., Hyman A.A., Helenius J. Quantification of surface tension and internal pressure generated by single mitotic cells. Sci. Rep. 2014;4:6213. doi: 10.1038/srep06213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ramanathan S.P., Helenius J., Müller D.J. Cdk1-dependent mitotic enrichment of cortical myosin II promotes cell rounding against confinement. Nat. Cell Biol. 2015;17:148–159. doi: 10.1038/ncb3098. [DOI] [PubMed] [Google Scholar]
- 12.Stewart M.P., Hodel A.W., Helenius J. Wedged AFM-cantilevers for parallel plate cell mechanics. Methods. 2013;60:186–194. doi: 10.1016/j.ymeth.2013.02.015. [DOI] [PubMed] [Google Scholar]
- 13.Schubert R., Strohmeyer N., Müller D.J. Assay for characterizing the recovery of vertebrate cells for adhesion measurements by single-cell force spectroscopy. FEBS Lett. 2014;588:3639–3648. doi: 10.1016/j.febslet.2014.06.012. [DOI] [PubMed] [Google Scholar]
- 14.Skoufias D.A., DeBonis S., Kozielski F. S-trityl-l-cysteine is a reversible, tight binding inhibitor of the human kinesin Eg5 that specifically blocks mitotic progression. J. Biol. Chem. 2006;281:17559–17569. doi: 10.1074/jbc.M511735200. [DOI] [PubMed] [Google Scholar]
- 15.Puech P.-H., Poole K., Müller D.J. A new technical approach to quantify cell-cell adhesion forces by AFM. Ultramicroscopy. 2006;106:637–644. doi: 10.1016/j.ultramic.2005.08.003. [DOI] [PubMed] [Google Scholar]
- 16.Yoneda M. Tension at the surface of sea-urchin egg: a critical examination of Cole’s experiment. J. Exp. Biol. 1964;41:893–906. doi: 10.1242/jeb.41.4.893. [DOI] [PubMed] [Google Scholar]
- 17.Clark, A. G. 2013. Thickness, Dynamics and Mechanics of the Actomyosin Cortex. Ph.D. thesis. Technische Universitaet Dresden, Dresden, Germany.
- 18.Phan-Thien N. Springer Science & Business Media; Berlin, Germany: 2012. Understanding Viscoelasticity: An Introduction to Rheology. [Google Scholar]
- 19.Kunda P., Pelling A.E., Baum B. Moesin controls cortical rigidity, cell rounding, and spindle morphogenesis during mitosis. Curr. Biol. 2008;18:91–101. doi: 10.1016/j.cub.2007.12.051. [DOI] [PubMed] [Google Scholar]
- 20.Chan C.J., Ekpenyong A.E., Lautenschläger F. Myosin II activity softens cells in suspension. Biophys. J. 2015;108:1856–1869. doi: 10.1016/j.bpj.2015.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rosenbluth M.J., Lam W.A., Fletcher D.A. Force microscopy of nonadherent cells: a comparison of leukemia cell deformability. Biophys. J. 2006;90:2994–3003. doi: 10.1529/biophysj.105.067496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Straight A.F., Cheung A., Mitchison T.J. Dissecting temporal and spatial control of cytokinesis with a myosin II inhibitor. Science. 2003;299:1743–1747. doi: 10.1126/science.1081412. [DOI] [PubMed] [Google Scholar]
- 23.Sakamoto T., Limouze J., Sellers J.R. Blebbistatin, a myosin II inhibitor, is photoinactivated by blue light. Biochemistry. 2005;44:584–588. doi: 10.1021/bi0483357. [DOI] [PubMed] [Google Scholar]
- 24.Mandato C.A., Benink H.A., Bement W.M. Microtubule-actomyosin interactions in cortical flow and cytokinesis. Cell Motil. Cytoskeleton. 2000;45:87–92. doi: 10.1002/(SICI)1097-0169(200002)45:2<87::AID-CM1>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- 25.Hutchins J.R., Toyoda Y., Peters J.M. Systematic analysis of human protein complexes identifies chromosome segregation proteins. Science. 2010;328:593–599. doi: 10.1126/science.1181348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Thoumine O., Ott A. Time scale dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J. Cell Sci. 1997;110:2109–2116. doi: 10.1242/jcs.110.17.2109. [DOI] [PubMed] [Google Scholar]
- 27.Desprat N., Richert A., Asnacios A. Creep function of a single living cell. Biophys. J. 2005;88:2224–2233. doi: 10.1529/biophysj.104.050278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fernández P., Pullarkat P.A., Ott A. A master relation defines the nonlinear viscoelasticity of single fibroblasts. Biophys. J. 2006;90:3796–3805. doi: 10.1529/biophysj.105.072215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ananthakrishnan R., Guck J., Käs J. Quantifying the contribution of actin networks to the elastic strength of fibroblasts. J. Theor. Biol. 2006;242:502–516. doi: 10.1016/j.jtbi.2006.03.021. [DOI] [PubMed] [Google Scholar]
- 30.Yeung A., Evans E. Cortical shell-liquid core model for passive flow of liquid-like spherical cells into micropipets. Biophys. J. 1989;56:139–149. doi: 10.1016/S0006-3495(89)82659-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hochmuth R.M. Micropipette aspiration of living cells. J. Biomech. 2000;33:15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- 32.Monteiro E., Yvonnet J., Asnacios A. Analyzing the interplay between single cell rheology and force generation through large deformation finite element models. Biomech. Model. Mechanobiol. 2011;10:813–830. doi: 10.1007/s10237-010-0276-9. [DOI] [PubMed] [Google Scholar]
- 33.Nawaz S., Sánchez P., Schaap I.A. Cell visco-elasticity measured with AFM and optical trapping at sub-micrometer deformations. PLoS One. 2012;7:e45297. doi: 10.1371/journal.pone.0045297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pietuch A., Brückner B.R., Janshoff A. Elastic properties of cells in the context of confluent cell monolayers: impact of tension and surface area regulation. Soft Matter. 2013;9:11490. [Google Scholar]
- 35.Evans E.A., Waugh R., Melnik L. Elastic area compressibility modulus of red cell membrane. Biophys. J. 1976;16:585–595. doi: 10.1016/S0006-3495(76)85713-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Clark A.G., Dierkes K., Paluch E.K. Monitoring actin cortex thickness in live cells. Biophys. J. 2013;105:570–580. doi: 10.1016/j.bpj.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ogneva I.V., Lebedev D.V., Shenkman B.S. Transversal stiffness and Young’s modulus of single fibers from rat soleus muscle probed by atomic force microscopy. Biophys. J. 2010;98:418–424. doi: 10.1016/j.bpj.2009.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hofmann U.G., Rotsch C., Radmacher M. Investigating the cytoskeleton of chicken cardiocytes with the atomic force microscope. J. Struct. Biol. 1997;119:84–91. doi: 10.1006/jsbi.1997.3868. [DOI] [PubMed] [Google Scholar]
- 39.Mayer M., Depken M., Grill S.W. Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows. Nature. 2010;467:617–621. doi: 10.1038/nature09376. [DOI] [PubMed] [Google Scholar]
- 40.Salbreux G., Prost J., Joanny J.F. Hydrodynamics of cellular cortical flows and the formation of contractile rings. Phys. Rev. Lett. 2009;103:058102. doi: 10.1103/PhysRevLett.103.058102. [DOI] [PubMed] [Google Scholar]
- 41.Cao L.G., Wang Y.L. Mechanism of the formation of contractile ring in dividing cultured animal cells. II. Cortical movement of microinjected actin filaments. J. Cell Biol. 1990;111:1905–1911. doi: 10.1083/jcb.111.5.1905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pullarkat P.A., Fernández P.A., Ott A. Rheological properties of the eukaryotic cell cytoskeleton. Phys. Rep. 2007;449:29–53. [Google Scholar]
- 43.Kollmansberger P., Mierke C.T., Fabry B. Nonlinear viscoelasticity of adherent cells is controlled by cytoskeletal tension. Soft Matter. 2011;7:3127. [Google Scholar]
- 44.Wang N., Tolić-Nørrelykke I.M., Stamenović D. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. Am. J. Physiol. Cell Physiol. 2002;282:C606–C616. doi: 10.1152/ajpcell.00269.2001. [DOI] [PubMed] [Google Scholar]
- 45.Stamenović D., Suki B., Fredberg J.J. Rheology of airway smooth muscle cells is associated with cytoskeletal contractile stress. J. Appl. Physiol. 2004;96:1600–1605. doi: 10.1152/japplphysiol.00595.2003. [DOI] [PubMed] [Google Scholar]
- 46.Tseng Y., Wirtz D. Mechanics and multiple-particle tracking microheterogeneity of α-actinin-cross-linked actin filament networks. Biophys. J. 2001;81:1643–1656. doi: 10.1016/S0006-3495(01)75818-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tseng Y., Kole T.P., Wirtz D. Micromechanical mapping of live cells by multiple-particle-tracking microrheology. Biophys. J. 2002;83:3162–3176. doi: 10.1016/S0006-3495(02)75319-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sen S., Dong M., Kumar S. Isoform-specific contributions of α-actinin to glioma cell mechanobiology. PLoS One. 2009;4:e8427. doi: 10.1371/journal.pone.0008427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gardel M.L., Shin J.H., Weitz D.A. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 50.Koenderink G.H., Dogic Z., Weitz D.A. An active biopolymer network controlled by molecular motors. Proc. Natl. Acad. Sci. USA. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ward S.M.V., Weins A., Weitz D.A. Dynamic viscoelasticity of actin cross-linked with wild-type and disease-causing mutant α-actinin-4. Biophys. J. 2008;95:4915–4923. doi: 10.1529/biophysj.108.131722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Balland M., Richert A., Gallet F. The dissipative contribution of myosin II in the cytoskeleton dynamics of myoblasts. Eur. Biophys. J. 2005;34:255–261. doi: 10.1007/s00249-004-0447-7. [DOI] [PubMed] [Google Scholar]
- 53.Mukhina S., Wang Y.L., Murata-Hori M. α-actinin is required for tightly regulated remodeling of the actin cortical network during cytokinesis. Dev. Cell. 2007;13:554–565. doi: 10.1016/j.devcel.2007.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Humphrey D., Duggan C., Käs J. Active fluidization of polymer networks through molecular motors. Nature. 2002;416:413–416. doi: 10.1038/416413a. [DOI] [PubMed] [Google Scholar]
- 55.Fabry B., Maksym G.N., Fredberg J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 56.Bursac P., Lenormand G., Fredberg J.J. Cytoskeletal remodelling and slow dynamics in the living cell. Nat. Mater. 2005;4:557–561. doi: 10.1038/nmat1404. [DOI] [PubMed] [Google Scholar]
- 57.Murthy K., Wadsworth P. Myosin-II-dependent localization and dynamics of F-actin during cytokinesis. Curr. Biol. 2005;15:724–731. doi: 10.1016/j.cub.2005.02.055. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.