Mechanical Regulation of Three-Dimensional Epithelial Fold Pattern Formation in the Mouse Oviduct

Abstract

Epithelia exhibit various three-dimensional morphologies linked to organ function in animals. However, the mechanisms of three-dimensional morphogenesis remain elusive. The luminal epithelium of the mouse oviduct forms well-aligned straight folds along the longitudinal direction of the tubes. Disruption of the Celsr1 gene, a planar cell polarity-related gene, causes ectopically branched folds. Here, we evaluated the mechanical contributions of the epithelium to the fold pattern formation. In the mutant oviduct, the epithelium was more intricate along the longitudinal direction than in the wild-type, suggesting a higher ratio of the longitudinal length of the epithelial layer to that of the surrounding smooth muscle (SM) layer (L-Epi/SM ratio). Our mathematical modeling and computational simulations suggested that the L-Epi/SM ratio could explain the differences in fold branching between the two genotypes. Longitudinal epithelial tensions were increased in well-aligned folds compared with those in disorganized folds both in the simulations and in experimental estimations. Artificially increasing the epithelial tensions suppressed the branching in simulations, suggesting that the epithelial tensions can regulate fold patterning. The epithelial tensions could be explained by the combination of line tensions along the epithelial cell-cell boundaries with the polarized cell arrays observed in vivo. These results suggest that the fold pattern is associated with the polarized cell array through the longitudinal epithelial tension. Further simulations indicated that the L-Epi/SM ratio could contribute to fold pattern diversity, suggesting that the L-Epi/SM ratio is a critical parameter in the fold patterning in tubular organs.

Introduction

The formation of three-dimensional (3D) structures, which provide structural bases for tissue/organ functions, is a fundamental process in developmental biology. Various 3D epithelial structures, such as folds and villi, are found in the lumens of animal tubular organs. Multiple folds (or ridges) along the longitudinal direction of the tubes are a common structure observed in the airways, esophagus, oviducts, etc. (1, 2, 3, 4, 5). On the other hand, folds along the circumferential direction (circular folds) are observed in the small intestines ((6); http://plaza.umin.ac.jp/∼web-hist/secret.html). Villi are observed in the gut, where longitudinal folds are transiently formed during the developmental process (7, 8, 9). The mechanical bases for the morphogenesis of such folds in some organs have been well studied. In the gut, airways, and esophagus, the growth of the epithelia and the mesenchymal layers, with the geometric constraints imposed by the surrounding smooth muscle (SM) layers, is important for fold formation, probably through provoking mechanical stresses to the epithelia (2, 5, 7, 8, 10). In the presence of these combined stresses and constraints, the folds are formed through buckling by active constriction of microfilaments in the epithelium of the gut (9). The circumferential constriction of the smooth muscle layer is involved in the fold geometry in the airways (1, 5). In the context of physics, compression of soft elastic solids leads to the formation of various shapes of sulci of the surfaces, where compressive stresses can be induced by the constrained growth/swelling of the solids (11). The mechanical bases for fold formation and for relatively simple fold patterning have been well studied, as described above. Mechanisms underlying complicated fold-pattern formation, such as that observed in the gut, however, are still an issue to be addressed (7).

The oviduct, or fallopian tube, is an organ where fertilization occurs, and the fertilized eggs are conveyed to the uterus in mammals. Longitudinally well-aligned folds are formed in the luminal epithelium, especially around the ampulla and the infundibulum, the most upstream region of the oviduct (Fig. S1 A in the Supporting Material) (3). A few folds are generated in the initial stage of oviduct development, and the number of folds is increased as the radius of the oviduct is expanded during postnatal development (3). Recently, we reported that the randomization of the direction and ectopic branching of the folds are observed in mutant mice deficient for the Celsr1 gene, whose product is a homolog of Flamingo in Drosophila (12), a seven-pass transmembrane cadherin controlling planar cell polarity (PCP) (13). The ectopic branches are observed from the early stage of oviduct development. The mechanisms for generating or for suppressing such complicated fold branching have not been studied well in either the oviducts or other tubular organs.

Cell-shape transformation is one of the primary regulators of morphogenesis/organogenesis (14), although it remains a challenge to understand how tissues/organs are shaped in the context of cellular mechanics, especially in large organs, including mammalian tubular organs. Some mechanisms for cell-shape transformation during morphogenesis have been discovered. Accumulation of nonmuscle myosin II on specific cell-cell boundaries in epithelia can modulate cell shape and cell junctional rearrangement, resulting in various tissue morphogenesis (15, 16). Cell shape can also be passively elongated by external forces provided from surrounding tissues (17). In the oviducts, the epithelial cell shapes are disorganized in the Celsr1 mutant: the cells are elongated along the longitudinal direction of the tubes in the wild-type, whereas the elongation is compromised and the orientation of elongation is randomized in the mutant (13). The polarization of cell shape is cell-intrinsically regulated, not by extrinsic cues from the surrounding environment (13). However, the role of the polarized cell shapes in the fold-pattern formation is not well understood.

In this study, we focused on the fold-pattern formation in mouse oviducts and investigated mechanical determinants for the fold shapes by using mathematical modeling and measurement of epithelial and cellular mechanics.

Materials and Methods

Animals

Celsr1 mutant mice have been described previously (18). Celsr1^−/− mice were obtained by crossing Celsr1^+/− mice, and the Celsr1^+/+ littermates were used as wild-type controls. Wild-type female mice (Slc:ICR, Japan SLC, Hamamatsu, Japan) were purchased and used for ovulation analysis (Fig. S1). Animal care and experiments were conducted in accordance with the Guidelines of Animal Experiment of the National Institutes of Natural Sciences. The experiments employed in this study were approved by the Institutional Animal Care and Use Committee of the National Institutes of Natural Sciences. The animals were kept in a light- and temperature-controlled room with a 12-h light/dark cycle at 22 ± 1°C.

R26-VMA mice were generated using an R26 targeting vector (19). cDNA encoding Venus was fused with cDNA encoding the actin-binding region of mouse moesin and inserted into the Rosa26 exon1. ES cells with insertion of this DNA into the Rosa26 locus were selected, and chimeric mice were produced. Homozygous R26-VMA mice were maintained and used for further crossing with Celsr1^+/− animals. For R26-VMA knock-in mice, the primers used to detect the VMA allele were forward primer Phil1 (5′-AAAGTCGCTCTGAGTTGTTAT-3′) and reverse primer pA1 (5′-AAGGGGGAGGATTGGGAAGACA-3′), to yield a PCR product of 497 bp. The primers for the wild-type allele were forward primer Phil1 and reverse primer Phil3 (5′-GGAGCGGGAGAAATGGATATG-3′), to yield a PCR product of 607 bp. LATaq or MightyAmp (TaKaRa, Japan) were used for the genotyping PCR experiments.

Measurement of C-Epi/SM and L-Epi/SM ratios

The cross sections of the oviducts were prepared as cryosections by a cryostat (Microm HM-500M, Carl Zeiss, Oberkochen, Germany), stained with Hoechst 33258 (Molecular Probes, Eugene, OR) and Texas Red-X phalloidin (catalog no. T7471, Molecular Probes). Folds in the longitudinally opened samples, or epithelial and smooth muscle layers in the cross-section samples, were manually traced and their lengths were measured using ImageJ software. See the Supporting Material for details.

Laser ablation experiments

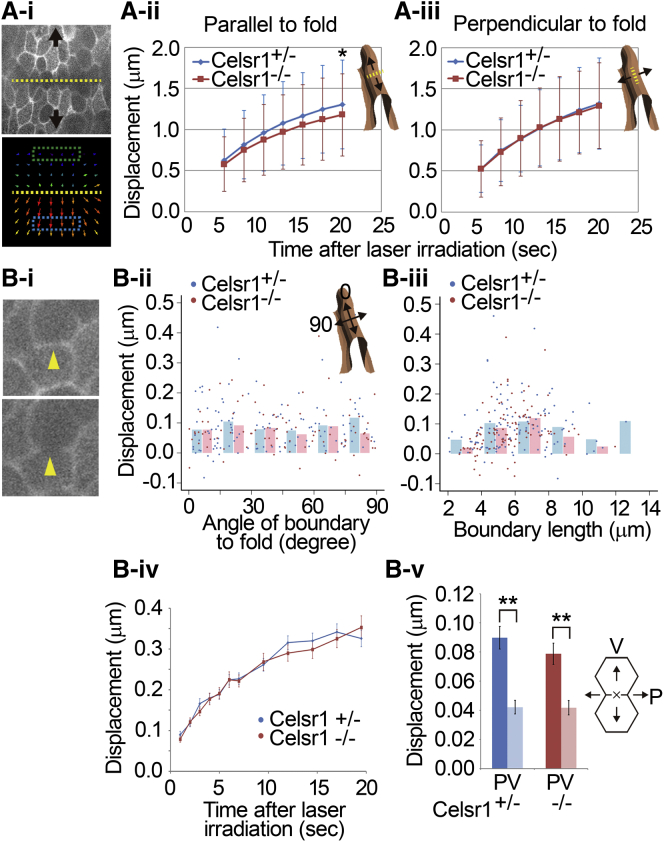
Laser irradiations were applied to the longitudinally opened oviduct using MicroPoint Galvo (Andor, Belfast, United Kingdom). Displacements were measured by particle image velocimetry (PIV) with an ImageJ plugin. See the Supporting Material for details. A statistical test was performed 20 s after irradiation (see Fig. 4 Aii) using the one-sided Student’s t-test. Statistical tests were performed using the two-sided Student’s paired t-test (see Fig. 4 Bv).

Figure 4.

Estimation of mechanical tensions in vivo. (A) Measurement of epithelial tensions. (i) An apical surface of the epithelium visualized by VMA (Venus fused with the actin binding domain of Moesin) (upper) and a PIV analysis used to measure the displacements of neighboring regions after laser irradiation (bottom). Yellow lines indicate the laser irradiation position. Blue and green regions represent the positions measured in PIV. (ii and iii) Displacements after laser irradiation. Laser irradiation directions were perpendicular (ii) or parallel (iii) to the folds, and the displacements parallel or perpendicular to the folds, respectively, were measured. A schematic illustration of a fold with the direction of the displacement is shown for each panel. ^∗p = 0.029 by the Student’s t-test; n = 112 (Celsr1^+/−) and 131 (Celsr1^−/−) for (ii) and n = 57 (Celsr1^+/−) and 54 (Celsr1^−/−) for (iii). Bars indicate the mean ± SD. (B) Measurement of cell boundary tensions. (i) An apical surface of the epithelium visualized by VMA before and after laser irradiation. Arrows indicate laser irradiation points. (ii and iii) Relationship between the displacements and the angle of the cell boundary to the folds (ii) or the cell boundary length (iii). Displacements at 1 s after laser irradiation are shown. The binning data for every 15° (ii) or every 2 μm (iii) are also shown (blue bars, Celsr1; red bars, Celsr1^−/−). (iv) Time courses of the displacements for all measurements shown in (ii) or (iii). (v) Displacements parallel (P) or vertical (V) to the cell boundaries. Displacements at 1 s after laser irradiation are shown. Schematic illustration of cells and the laser irradiation point (black cross) are shown with the P and V directions at right. n = 117 from seven oviducts for Celsr1^+/− and n = 111 from eight oviducts for Celsr1^−/−. Bars indicate the mean ± SE; ^∗∗p < 0.0001 by Student’s t-test. To see this figure in color, go online.

Polarized cell array analyses

In Fig. 5 A, cell boundaries crossing the yellow lines (see Fig. 5 Ai) were manually traced and then the angles of each boundary were measured by ImageJ. Both the number and angles of boundaries were used for the estimation of epithelial tension.

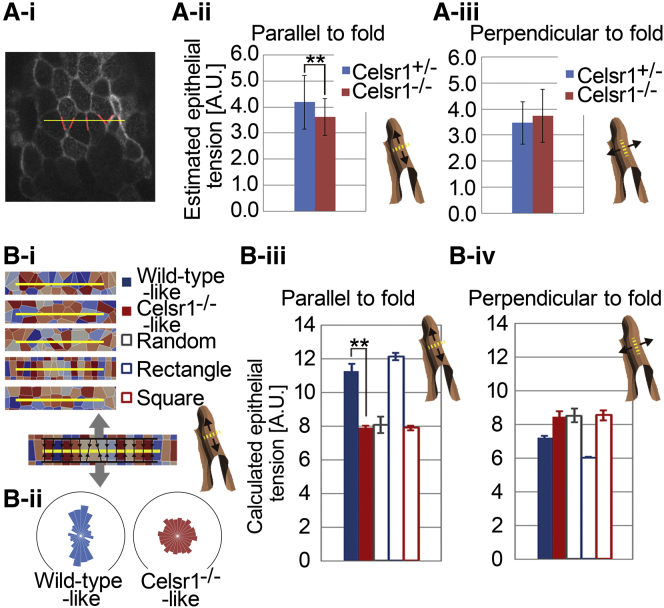
Figure 5.

Combinational effect of cell boundary tensions with polarized cell arrays. (A) Estimation of epithelial tensions from in vivo images. (i) An apical surface of the epithelium visualized by VMA. The image sets used were the same as those in the laser ablation experiments (Fig. 4A). Yellow lines indicate the estimated positions corresponding to the laser irradiation line in Fig. 4A. Red lines indicate cell boundaries crossing the yellow line, used for estimation of epithelial tensions. (ii and iii) Estimated epithelial tensions along the direction parallel (ii) or perpendicular (iii) to the folds in in vivo images. A schematic illustration of a fold with the direction of the tensions is shown for each histogram. ^∗∗p < 0.0001 by Student’s t-test. n = 104 (Celsr1^+/−) and 126 (Celsr1^−/−) (ii), and n = 54 (Celsr1^+/−) and 52 (Celsr1^−/−) (iii). Bars represent the mean ± SD. (B) Calculation of epithelial tensions from in silico images. (i) Voronoi diagrams resembling the wild-type and mutant epithelial cell arrays along with three other artificial diagrams. A schematic illustration of the calculation of epithelial tensions is shown at bottom left. Gray arrows indicate the direction of epithelial tension, Yellow lines the calculation positions, and black arrows the cell boundaries used for the calculation. A schematic illustration of a fold with the direction of the tensions is shown at bottom right. (ii) Distributions of major angles of the cells in the Voronoi diagrams. The averages of cell longest/shortest diameter ratios for each diagram were 1.83 (left) and 1.56 (right), equivalent to our previous report in vivo (13). (iii and iv) Calculated epithelial tensions parallel (iii) or perpendicular (iv) to the folds in the diagrams. ^∗∗p < 0.0001 by Student’s t-test; n = 5 (wild-type-like), 5 (Celsr1^−/−-like), 5 (random), 3 (rectangular), and 3 (square). Bars indicate the mean ± SD. Details of the methods are described in the Supporting Material. To see this figure in color, go online.

In Fig. 5 B, a Voronoi diagram was drawn for ∼400 seeds scattered in a defined square. The scattering patterns were quasirandomly modified to obtain polygonal/cell arrays with desired geometric properties (see the Supporting Material for details). The calculation of epithelial tensions was performed in a similar way to in Fig. 5 A.

Statistical tests were performed (see Fig. 5 Aii and Biii) using one-sided Student’s t-tests.

Results

Basic structure of the mouse oviduct

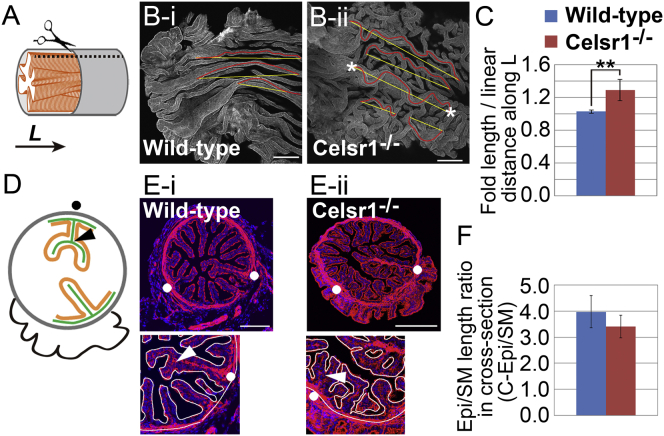
In longitudinally opened infundibulum regions of the oviducts (Fig. 1 A), epithelial folds are longitudinally well aligned in wild-type mice (Fig. 1 Bi), whereas directionally randomized folds with ectopic branches are observed in the Celsr1-deficient mice (Fig. 1 Bii) (13). Our previous mosaic analysis indicated that the mutant cell clones in the epithelium generated ectopic branches even though the smooth muscle layer was composed of wild-type cells, suggesting that the properties of the epithelia, but not of the smooth muscle layers, significantly contribute to fold-pattern formation in the oviducts (13). To investigate the basic structure of the epithelial layer and the folds in the mouse oviducts, we first analyzed the cross sections of the infundibular regions of the oviducts (Figs. 1, D and E, and S2 B). In the wild-type mice, ∼20 folds per cross section were observed that were largely composed of an epithelial layer with a thin mesenchymal layer, as reported previously (Fig. 1 Ei) (3). The epithelial and mesenchymal layers are surrounded by a relatively thick smooth muscle layer. In the Celsr1 mutant mice, the thicknesses of the three layers were essentially similar to those in the wild-type (Fig. 1 Eii), suggesting that the fold shapes in the mutants are generated by the same simple-layered structure as in the wild-type, but not by thickening of any specific layers. The thin mesenchymal layer of the oviduct contrasts with other tubular organs, such as airways and the gut, where substantially thicker mesenchymal layers are formed (1, 7). In addition, radial branches of the folds were observed in cross sections, as reported previously (Fig. 1, D and E) (3), and this seems to be a characteristic pattern in the oviducts. The perimeter of the epithelium was three- to fourfold larger than that of the smooth muscle layer at the adult stage (Fig. 1 F). This ratio was termed the C-Epi/SM (circumferential epithelium/smooth muscle) ratio.

Figure 1.

Characteristics of mouse oviduct structures. (A) Schematic illustration of the oviduct, with a longitudinal broken line to open the oviduct. An epithelium (Epi; orange) and an SM layer (gray) are shown. L, longitudinal direction. (B, i and ii) Folds in the longitudinally opened oviduct, with lines to measure the curvilinear fold lengths (red lines) and the linear distances along the longitudinal direction (yellow lines) between two positions (asterisks) on a fold (details are shown in Fig. S2 A and described in the Supporting Material text). The specimens were stained by phalloidin, and maximal-intensity projections of confocal images are shown. Scale bars, 100 μm. The original images are adapted from Shi et al (13). (C) Ratio of the fold length to the linear distance along the longitudinal direction. ^∗∗p < 0.0001 using Student’s t-test. n = 12 specimens from four oviducts (wild-type) and n = 16 specimens from five oviducts (Celsr1^−/−); mean ± SD. (D) Schematic illustration of a cross section of the oviduct. The Epi (orange), SM (gray), and mesenchymal layers (green) are shown with a radial branch (arrowhead, branch point; solid circle, fold with a branch). Overhung regions from the end of the oviduct are shown in black. (E, i and ii) Folds in the cross section of the oviducts (top) and magnified views with white lines tracing the Epi and SM (bottom). Several examples of radial branches (arrowheads and/or solid circles) are shown. Other examples of cross-sectional images are shown in Fig. S2B. Scale bars, 100 μm. (F) Ratio of the length of Epi to that of SM in the cross sections. n = 7 from four oviducts (wild-type) and n = 12 from four oviducts (Celsr1^−/−); mean ± SD. To see this figure in color, go online.

Next, we focused on the ratio of the length of the epithelium to that of the smooth muscle layer along the longitudinal direction, termed the L-Epi/SM ratio. The fact that the folds in the wild-type were longitudinally straight suggested that the L-Epi/SM ratio was ∼1.0, whereas the L-Epi/SM ratio in the mutant was expected to be >1.0. In other words, the length of the epithelium per unit length of the smooth muscle layers was expected to be increased in the mutant. We roughly estimated the L-Epi/SM ratios as follows. Curvilinear fold length and a linear distance between two positions on a fold were measured, where we selected the two positions that were almost aligned along the longitudinal direction on the same fold (Figs. 1 B and S2 A). The ratio of the curvilinear fold length to the linear distance along the longitudinal direction was 1.03 and 1.29 in the wild-type and mutant mice, respectively (Fig. 1 C). These values may roughly correspond to the L-Epi/SM ratio in the case that the epithelia are unfolded into a flat sheet (Fig. S2 A and Measurement of C-Epi/SM and L-Epi/SM ratios in the Supporting Material).

Construction of a mathematical model

Mechanical features of tissues play central roles in the morphogenesis of various tissues (7, 20). In the oviduct, fold shapes are significantly changed through ovulation, which is accompanied by an increase in the radius of the tube (Fig. S1; Movie S1), suggesting that fold shapes are mechanically regulated. We tested, using mathematical simulations, whether the fold patterns could be explained by the L- and C-Epi/SM ratios with the combination of epithelial and/or cellular mechanics. From our observations of the cross section, we constructed a minimal model that included two layers corresponding to the epithelial and surrounding smooth muscle layers, respectively (Fig. 2 A, i and ii). We neglected the mesenchymal layer, because it was substantially thin (Fig. 1 E). The epithelial layer was assumed to be a thin elastic sheet with mechanically uniform properties. A biological two-dimensional (2D) sheet or membrane has been often modeled on the basis of a finite-element method (FEM) (7, 21), a thin shell/plate theory (22, 23), or discretized elements (nodes) forming a triangular or square spring network (24, 25, 26, 27). Here, we constructed a spring-network model where elastic properties of the sheet against stretch/compression, bending, and shear deformations can be modeled by defining the mechanical potentials of each spring. Each spring in the network may qualitatively reflect the mechanical properties of the epithelium. We did not intend the springs to reflect any specific biological structures such as cells, cytoskeletons, etc. Although triangular networks have been more widely utilized, we chose a square network, because the anisotropic mechanical properties of the sheet could be intuitively introduced as described later. The elastic sheet was modeled as an array of square grids, which was set to be a rectangle when the sheet was unfolded into a flat sheet (Figs. 2 A, iii and iv, and S3 D; Appendix A). We assumed that the smooth muscle layer was relatively stiff compared to the single-cell-layer epithelial sheet, and thus, the smooth muscle layer was introduced as a cylindrical geometric constraint (Figs. 2 Ai and S3 D; Appendix A). The 2D square grid array was embedded in the three-dimensional (3D) cylindrical constraint, and we performed simulations under the case where the C-Epi/SM ratio was ∼3.0 and the L-Epi/SM ratio was ∼1.0–1.3, which reflects the in vivo ratios, and then stable shapes were numerically calculated (Appendix B).

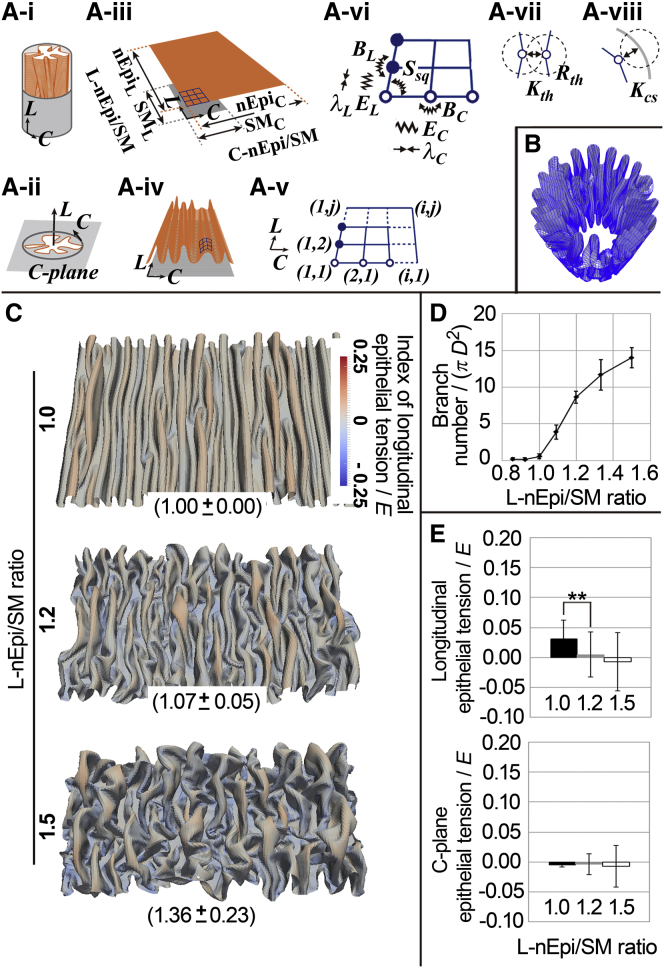
Figure 2.

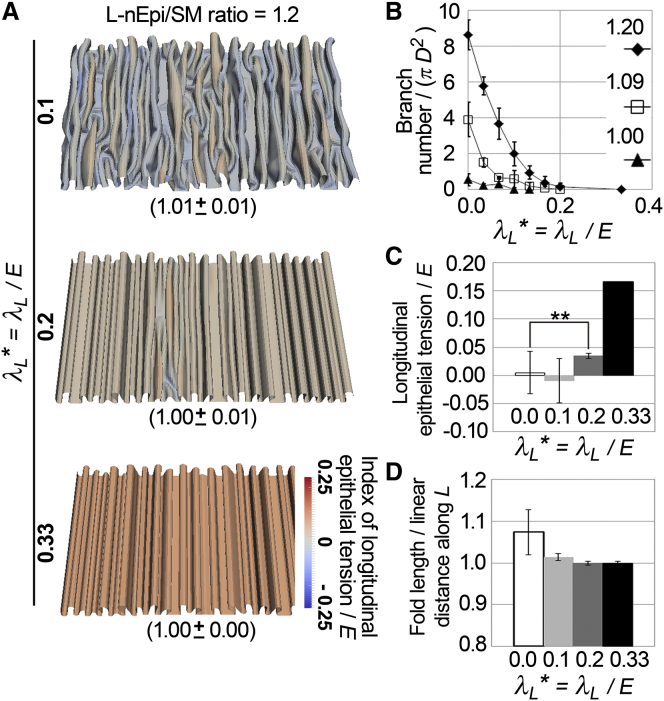
Mathematical modeling and simulations. (A) 2D-sheet model embedded in a 3D cylinder. (i) an epithelium (Epi; orange) and an SM layer (gray). Longitudinal (L) and circumferential (C) directions are shown. (ii) Cross-sectional view. The C-plane is a plane perpendicular to the L direction. (iii) Schematic images of two-dimensionally spread Epi and SM with discrete elements (nodes and crossing points of blue grids). The definitions of nEpi_L, nEpi_C, SM_L, and SM_C are shown. L-nEpi/SM and C-nEpi/SM correspond to the ratios nEpi_L/SM_L and nEpi_C/SM_C, respectively. Note that neither grid corresponds to a cell. Natural lengths of Epi and SM are shown along the L and C directions. (iv) Schematic images of deformed grids during simulations in a longitudinally opened view. (v) A magnified view of the grid shown in (A iii). The numbers of the nodes along the L and C directions are j and i, respectively. (vi) The nodes are shown with mechanical components. Elastic springs (E_L and E_C), bending springs (B_L and B_C), a bending spring for shear deformation (S_sq), which was defined for all corners of the grids, and the active constrictive force (λ_L and λ_C) are shown. (vii) The effect of the thickness of the epithelium (R_th) with the coefficient of the repulsion (K_th) is described. (viii) the effect of the surrounding constraint with the coefficient of the repulsion (K_cs) is described. Details are described in Appendix A. (B) A simulation result of the 2D sheet model. The elastic sheet is shown and the surrounding constraint is hidden. (C) Effect of the L-nEpi/SM ratio. Longitudinally opened views of the simulation results are shown. Ratios of fold length to linear distance measured along the L direction are shown (parentheses; n = 10, mean ± SD). The longitudinal components of the forces from the elastic springs of the four edges were averaged, and the resultant is shown as an index of dimensionless epithelial tension for each grid according to the color code. E is the standard value of E_L and E_C. The calculation of the index is described in the Supporting Material. (D) Number of the branches under each condition. D is the diameter of the cylindrical constraint. Bars represent the mean ± SD for n=4. (E) Dimensionless epithelial tensions for each grid edge along the L direction and perpendicular to the L direction (C-plane). E is the standard value of E_L and E_C. Note that grid edges around the top of the folds were selected for measurement. ^∗∗p < 0.0001 for the Student’s t-test for n = 3930 (L-nEpi/SM = 1.0), 1779 (L-nEpi/SM = 1.2), 891 (L-nEpi/SM = 1.5) edges (top) and 3939 (L-nEpi/SM = 1.0), 4288 (L-nEpi/SM = 1.2), and 4505 (L-nEpi/SM = 1.5) edges (bottom). Bars indicate the mean ± SD. To see this figure in color, go online.

The mechanical potential energy of the whole system, U_tot3, was defined as below.

$$U_{\text{tot}3}=U_{\text{sp}}+U_{\text{b}}+U_{\text{sq}}+U_{\text{th}}+U_{\text{cs}}.$$ (1)

U_sp is the potential energy of elasticity of the sheet (Fig. 2 Avi; Appendix A). U_sp is the sum of a potential energy (u_sp) of an elastic spring defined between two adjacent nodes along the longitudinal and circumferential directions (Fig. 2 A, v and vi). u_sp was defined as

$$u_{\text{sp}}=\frac{1}{2}{E}_{\text{L}\text{or}\text{C}}{\left(\frac{l}{l_0}-1\right)}^2{l}_0,$$ (2)

where E_L and E_C are the coefficients of the springs along the longitudinal and the circumferential directions, respectively (Fig. 2 Avi); l is the length of each spring, and l₀ is the natural length of each spring; U_b is the potential energy of bending elasticity of the sheet (Fig. 2 Avi; Appendix A). U_sq is the potential energy of bending elasticity to resist shear deformation of the grids, by which each grid favors maintenance of a square shape (Fig. 2 Avi; Appendix A). The effect of the thickness (or volume) of the sheet is introduced as the potential energy, U_th (Fig. 2 Avii; Appendix A), which simultaneously provides a self-avoiding effect (24). U_cs is the potential energy derived from the surrounding constraint (Fig. 2 Aviii; Appendix A). To model the self-avoiding effect or the surrounding constraint, we defined U_th or U_cs so as to provide a repulsive force when different regions of the sheet closely approach each other or when a region of the sheet closely approaches the surrounding constraint, respectively. Details of each potential energy other than U_sp are described in Appendix A. The surrounding constraint is assumed to be undeformable, and thus, its position is fixed throughout the simulations. The longitudinal boundaries of both the elastic sheet and the surrounding constraint are set to be periodic, and the surrounding constraint defines the boundary positions (Appendix A).

To achieve a situation of the C-Epi/SM ratio ∼3.0, the sum of l₀ of the circumferential springs in a single row of the grid array was set to be 3.0 times larger than the circumferential length of the surrounding circular constraint (Appendix B). Here, we call the ratio of the sum of l₀ to the circumferential length of the constraint the C-nEpi/SM (circumferential natural epithelium/smooth muscle) ratio. Similarly, to achieve a situation described by the L-Epi/SM ratio ∼1.0–1.3, the sum of l₀ of the longitudinal springs in a single column of the grid array was set to be 1.0–1.3 larger than the longitudinal length of the constraint. The ratio is called the L-nEpi/SM ratio. Under these conditions, stable states were obtained after a relaxation process in the simulations See Fig. S3 and Appendices A and B for details about the model and simulation processes.

We examined whether the sheet modeled here showed typical elastic behaviors against stretch/compression, shear, and bending deformations (Fig. S3, E–N). The forces exerted by the sheet were almost linear against the deformations, though slight anisotropies were observed. Furthermore, by searching for stable shapes, our model can generate some fold patterns that were also reproduced in previous studies using FEM or an analytical approach (7, 8), suggesting that our model is applicable for investigating fold-pattern formation (Appendix C). Thus, we applied this model to investigate fold-pattern formation.

3D simulation

Before analyzing fold morphologies in a 3D situation, we performed simulations in a cross-sectional situation (Fig. S3, A and B). The simulations successfully generated multiple folds and sometimes radial branches (Fig. S3 B).

To test whether the mechanics-based model can reproduce the longitudinal fold pattern observed in the wild-type oviduct in a 3D situation, simulations were performed under the condition where the C-nEpi/SM or L-nEpi/SM ratio was set to be 3.0 or 1.0, respectively. The ratio L-nEpi/SM = 1.0 corresponds to strain ε along the longitudinal direction, which can be defined by (SM_L − nEpi_L)/nEpi_L = (1/(L-nEpi/SM) − 1) = 0.0. The simulations successfully generated longitudinally well-aligned folds with few longitudinal branches (Fig. 2, B, C (top), and D), which recapitulated the wild-type situation. These results are consistent with the idea that the fold patterns in the oviducts are mechanically determined. A similar mechanism may be involved in the fold patterning in the gut, where the longitudinal folds are generated by circumferential constriction of the surrounding smooth muscle layer (7), which can modulate the C-nEpi/SM ratio.

Then, we investigated the effect of the L-nEpi/SM ratio on fold-pattern formation. In the gut, compression of the luminal epithelium along the longitudinal direction, which should increase the L-Epi/SM ratio, leads to a zigzag pattern of folds but not a branching pattern (7). We examined whether the L-nEpi/SM ratio could explain the branching patterns of the folds observed in the Celsr1-deficient oviducts. When larger L-nEpi/SM ratios were given in simulations, folds were severely randomized in their direction, and ectopic branches were generated (Figs. 2 C (middle and bottom) and D, and S3 R). Similar to our treatment in Fig. 1 A, we measured the ratios of fold length to linear distance (given in parentheses in Fig. 2 C). The equivalence of the ratio to the in vivo value in the mutant mice (1.29) resulted from L-nEpi/SM = 1.2–1.5. These conditions were large enough to cause severe ectopic branching, suggesting that the difference between the L-Epi/SM ratios of the wild-type and mutant mice is sufficient to explain the difference in their fold morphologies. Interestingly, the complicated fold patterns were reproduced without directly considering the developmental processes in our simulations. Our results suggest that the L-nEpi/SM ratio in the mature oviducts is effective for determining fold-pattern formation.

Regarding other parameters, the C-nEpi/SM ratio did not significantly affect branching of folds, at least under the conditions where C-nEpi/SM = 3.0–4.0 (data not shown). Other mechanical parameters, such as E_L, E_C, B_L, B_C, S_sp, K_th, and K_cs, described in Fig. 2 A, had minor effects on branching compared to the L-nEpi/SM ratio (Fig. S4, A–C; Parameter Values Used in Simulations in the Supporting Material). In addition, the effects of anisotropic elastic properties were analyzed by giving different values between E_L and E_C or between B_L and B_C. However, no significant changes in branching were detected (data not shown). We also tried to measure experimentally the elastic properties of the epithelium in the oviducts, but we failed to isolate the thin epithelial sheet due to its fragility. Despite the difficulties in experimental measurements, our simulations suggested that the generation of the branching pattern does not significantly depend on the elastic properties of the epithelium but does depend on the L-Epi/SM ratio. Details of parameter setting in the simulations are described elsewhere (see Parameter Values Used in Simulations and Comparison of Epithelial Mechanical Parameters with Realistic Values in the Supporting Material).

Relationship between epithelial tension and fold morphology

The simulations above also showed differences in the mechanical states between the low- and high-L-nEpi/SM conditions: the low-L-nEpi/SM condition (ratio of 1.0) led to larger epithelial tensions along the longitudinal direction in the upper region of the folds (Fig. 2 E, top), but did not significantly change epithelial tensions perpendicular to the longitudinal direction (i.e., in the C-plane (Figs. 2 Aii and E, bottom). We hypothesized that the longitudinal epithelial tension was associated with the fold morphology. To examine this hypothesis, we artificially modulated the epithelial tension by introducing a constrictive force acting between two adjacent nodes (Fig. 2 Avi; Appendix A). The biological interpretation of this force is described in the Discussion. The potential energy between the two nodes was defined as

$$u_{\text{t}}=\lambda l,$$ (3)

where λ corresponds to the constrictive force. To modulate the longitudinal epithelial tensions, the constrictive force was applied to each edge of the grids parallel to the longitudinal direction (λ_L). In other words, λ was set to be anisotropic. Then, simulations were performed under higher L-nEpi/SM-ratio conditions (L-nEpi/SM =1.2). Under larger λ_L conditions, the folds were well-aligned and ectopic branching was suppressed (Figs. 3, A and B, and S4 D). Simultaneously, the longitudinal epithelial tensions were increased (Fig. 3 C). In addition, introducing λ decreased the ratio of fold length to linear distance (Fig. 3 D), suggesting that λ could modulate the L-Epi/SM ratio. By contrast, the application of a larger λ to each edge of the grids along the direction perpendicular to the longitudinal direction did not significantly affect the branching, although the number of the folds was decreased (Fig. S4 E). These results suggest that the increased longitudinal epithelial tension is associated with the suppression of fold branching in our theoretical framework.

Figure 3.

Relationship between epithelial tension and fold morphology in simulations. (A) Effect of longitudinal constrictive force, λ_L, on fold morphology. Simulation results are shown in a manner similar to that presented in Fig. 2C. The meanings of the colors and the parentheses are essentially the same as in Fig. 2C, except that constrictive forces are also included for the calculation of the index of dimensionless epithelial tension (see the Supporting Material). λ_L^∗, dimensionless λ_L; E, standard value of E_L and E_C. (B) Number of branches under each condition. D is the diameter of the cylindrical constraint. Bars represent the mean ± SD of n = 4,. (C) Dimensionless epithelial tension along the L direction for each grid edge. ^∗∗p < 0.0001 by Student’s t-test; n = 1779 (λ_L^∗ = 0.0), 3804 (λ_L^∗ = 0.1), 2237 (λ_L^∗ = 0.2), and 2141 (λ_L^∗ = 0.33) edges; bars represent the mean ± SD. (D) Ratios of fold length to linear distance along the L direction under various conditions of λ_L from Fig. 2C, middle, for λ_L = 0.0 and from Fig. 3A for λ_L = 0.1, 0.2, and 0.33. To see this figure in color, go online.

We compared the values of the epithelial tensions and λ with realistic values. If we assumed that the Young’s modulus of the epithelium is 10²–10³ Pa (7, 28, 29), the diameter of the oviduct, D, is 300 μm (Fig. 1 E), and the thickness of the epithelium is 10 μm (Fig. 1 E), E, which is the standard value of E_L and E_C (Appendix A), was estimated to be 7.1–71 nN (Comparison of Epithelial Mechanical Parameters with Realistic Values in the Supporting Material). Therefore, the epithelial tension/E = 0.05 in Fig. 2 E and λ_L^∗ = 0.2 in Fig. 3 correspond to 0.35–3.5 nN and 1.4–14 nN, respectively. Consequently, epithelial tension derived from the former and the latter per unit length of the epithelium are 0.050–0.50 nN/μm, and 0.20–2.0 nN/μm, respectively (Supporting Material). Since mechanical forces in cellular processes are around the nanonewton order in general (29, 30), our estimations are reasonable.

Estimation of epithelial tension in vivo

If the fold patterns are mechanically determined, epithelial tensions are expected to be affected. Then, we tested whether or not epithelial tensions in vivo were increased in the wild-type compared to the mutant. By using laser-ablation experiments in the mouse oviducts, we estimated epithelial tensions. A line spanning several cell diameters on the epithelium of longitudinally opened oviducts was exposed to a laser, and the displacements of the adjacent regions of the epithelium were measured (Fig. 4 Ai). We carried out the experiment around the upper region of each fold. In general, initial retraction velocities after ablations are considered to be proportional to the forces exerted on the ablated sites (31, 32). Since the displacements immediately after the laser irradiations were too small in the epithelia (∼4 pixels or ∼0.5 μm at 5 s after the irradiations) even if a high-magnification objective lens was used, we compared the time courses of the displacements. When the ablation lines were perpendicular to the folds, the displacements parallel to the folds were larger in the Celsr1 heterozygotes (+/−), which were used as controls comparable to the wild-type, than in the homozygous (−/−) mutants, although the differences were slight (Fig. 4 Aii). In addition, when the ablation lines were parallel to the folds, the displacements perpendicular to the folds in the Celsr1^+/− were comparable to those in the Celsr1^−/− mice (Fig. 4 Aiii). These observations suggest that the longitudinal epithelial tension in the Celsr1^+/− mice increased and that the fold-branching patterns are mechanically determined. Moreover, these observations qualitatively agreed with the results from the mathematical simulations.

Estimation of line tension along cell-cell boundaries in epithelium

Anisotropic epithelial tensions can be regulated by line tensions along apical cell-cell boundaries (cell boundary tensions) (33). To examine the relationship between the epithelial tensions and the cell boundary tensions in the oviducts, we performed laser-ablation experiments on the cell boundaries (Figs. 4 Bi and S5). When cell boundaries parallel to the folds were ablated, no significant differences in displacement between the Celsr1^+/− and ^−/− mutants were detected (Fig. 4 Bii, angle = ∼0.0), suggesting that the cell boundary tensions alone could not explain the differences in epithelial tension along the direction parallel to the folds, shown in Fig. 4 Aii.

Further analyses showed that the displacements were not correlated with the angle of the cell boundary to the fold direction, nor with cell boundary length (Fig. 4 B, ii and iii), and that the displacements of all measurements were not significantly different between the two genotypes (Fig. 4 Biv). Thus, the cell boundary tensions were spatially uniform and comparable between the two genotypes. We also compared the cell boundary tensions with apical surface tensions in the epithelia. When a cell boundary was ablated, the displacement along the direction parallel or vertical to the boundary would reflect the cell boundary tension or the apical surface tension, respectively (Fig. 4 Bv, right). The parallel displacements were ∼2-fold larger than the vertical displacements in the two genotypes (Fig. 4 Bv). This result suggested that the cell boundary tensions could be the major component of the epithelial tensions.

Combinational effect of cell boundary tensions with polarized cell arrays

Epithelial tensions can be influenced not only by cell boundary tensions but also by cell shape (33). Although the cell boundary tensions were not significantly different between Celsr1^+/− and ^−/− mutants, as shown in Fig. 4 B, the entire impact of the cell boundary tensions on the epithelial tensions along the direction parallel to the folds could be larger in the Celsr1^+/− than in the Celsr1^−/− mutant, because the cell shapes and their arrays in the epithelia are different (13). To evaluate the combinational effect of the cell boundary tensions with the polarized cellular geometric patterns on the epithelial tensions, we estimated epithelial tensions using cell arrays in vivo under a setting in which cell boundary tensions were the sole components of the epithelial tensions (Fig. 5 Ai; Mathematical Analyses of Epithelial Tension Using Cell Arrays in the Supporting Material). When cell boundary tensions were assumed to be uniform (equal to 1.0), the estimated epithelial tensions in the Celsr1^+/− cell arrays were slightly increased along the direction parallel to the folds compared with those in the Celsr1^−/− (Fig. 5 Aii), whereas the epithelial tensions were comparable between the two genotypes along the direction perpendicular to the folds (Fig. 5 Aiii).

We mathematically tested whether the polarized cell arrays affected epithelial tensions. Cellular geometric patterns resembling the wild-type or the mutant situations were generated by drawing Voronoi diagrams, a mathematical technique for dividing space into polygons/cells (Mathematical Analyses of Epithelial Tension Using Cell Arrays in the Supporting Material). The patterns showed similarities to the in vivo situations in two geometric features, cell elongation and its direction (Figs. 5 B, i and ii, and S6) (13). Apical cell areas were equivalent among the patterns, reflecting the in vivo situations (data not shown). Similar to Fig. 5 A, the epithelial tensions in the patterns were calculated under the setting where cell boundary tensions were the sole components and were also uniform (equal to 1.0). Wild-type-like patterns exhibited larger epithelial tensions along the direction parallel to the folds compared to Celsr1^−/−-like patterns (Fig. 5 Biii). This difference seemed to be similar to the difference between the patterns with aligned rectangles and squares (Figs. 5 Biii and S6), suggesting that the difference would largely depend on the increased number of cell boundaries crossing a unit length of a perpendicular line (Fig. 5 Bi, yellow lines). In addition, only a relatively slight difference in epithelial tensions along the direction perpendicular to the folds was detected between the two patterns (Fig. 5 Biv). These calculations suggested that the combinational effect of the cell boundary tensions with the polarized cell arrays increased epithelial tensions along the direction parallel to the folds and to the longitudinal direction in the wild-type.

Fold-pattern diversity conferred by L-nEpi/SM and C-nEpi/SM ratios

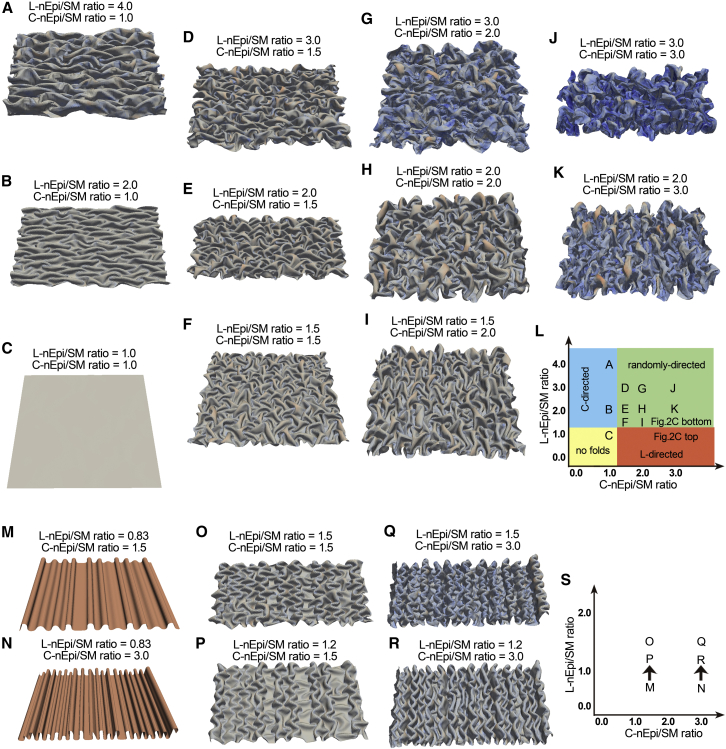
Our results indicated that the L-nEpi/SM ratio together with the C-nEpi/SM ratio can be critical for fold-pattern formation. Isotropic or anisotropic compression of a film on a plane substrate can generate wrinkle patterns with stripes, labyrinths, herringbones, etc (34). We further evaluated the ability of our theoretical framework to explain various fold patterns in tubular organs. The combination of the two ratios could generate circumferential (C-directed) folds (Fig. 6, A and B; Appendix B), which may resemble the circular folds observed in the small intestines (6), and short folds with randomized directions (Fig. 6, D–K; Appendix B). The effect of initial conditions of the simulations was also analyzed. Even under the same L-nEpi/SM ratio condition as in Fig. 2 C (L-nEpi/SM = 1.2 or 1.5), a different initial condition led to zigzag patterns (Fig. 6, O–R) similar to those observed during gut development (7, 8). In Fig. 2 C, the elastic sheet was initially set as a smooth cylinder, but in Fig. 6, O–R, it was initially set as a cylinder with longitudinally well-aligned folds (Fig. 6, M and N; Appendix B). Initial conditions may reflect developmental processes, at least in part. A previous report showed that, by taking the developmental processes of the gut into consideration, a zigzag pattern can be generated in a mathematical simulation (7). Consistent with this, our results suggest that developmental processes can be a considerable factor in morphological outcomes of folds. The fold patterns generated under the various L- and C-Epi/SM ratios are summarized in Fig. 6, L and S: longitudinally (L-directed) well-aligned folds (Fig. 2 C, top), L-directed folds with branches (Fig. 2 C, middle and bottom), L-directed folds with zigzags (Fig. 6, O–R), C-directed folds (Fig. 6, A and B), and randomly directed folds with branches (Fig. 6, D–K). These results suggest that the regulation of the L-Epi/SM and C-Epi/SM ratios plays a central role in fold-pattern formation in various tubular organs.

Figure 6.

Fold pattern diversity conferred by L-nEpi/SM and C-nEpi/SM ratios. (A–K) C-directed fold, randomly-directed fold, and no fold patterns under the L-nEpi/SM and C-nEpi/SM conditions presented. An L-directed fold pattern is shown in Fig. 2C, top. (L) Phase diagram of (A)–(K). (M–R) Zigzag fold patterns (O–R) under the L-nEpi/SM and C-nEpi/SM conditions presented, generated from initial conditions with longitudinally aligned fold patterns (M and N). (O) and (P) were generated from (M), and (Q) and (R) were generated from (N), as described in (S). See Appendix B for the simulation processes. (S) Phase diagram of (O)–(R). To see this figure in color, go online.

Discussion

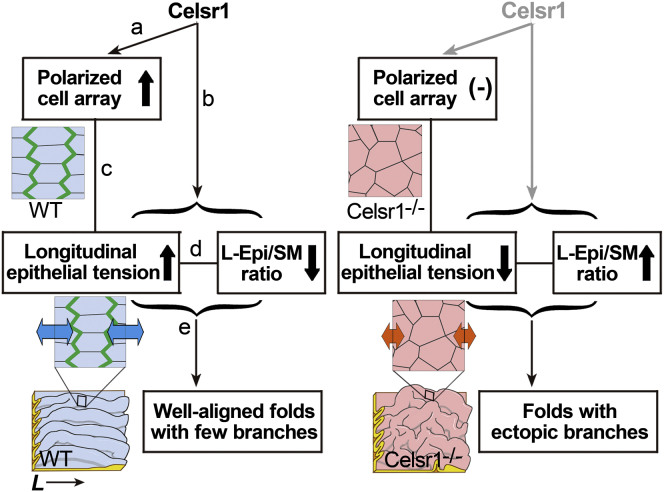
In this report, we investigated the mechanisms for epithelial fold-pattern formation and the relevance of the polarized cell arrays to the fold patterns in mouse oviducts. Our computational simulations suggest that the L-Epi/SM ratio is critical for generating well-aligned folds by suppressing branching (Fig. 7, d and e). Increased longitudinal epithelial tensions were detected in well-aligned folds both in the simulations and in the wild-type oviducts. The polarized cell arrays were associated with the fold patterns through epithelial tensions (Fig. 7, c–e). Together with the length of the epithelium relative to that of the smooth muscle layer (L-Epi/SM), these results suggest that cell polarization is mechanically involved in fold-pattern formation.

Figure 7.

Roles of Celsr1 in fold-pattern formation. Summary of the roles of Celsr1 in fold-pattern formation showing their relationships to cell-shape polarization, epithelial tension, and L-Epi/SM ratio. Cartoons of epithelial cell sheets are shown, with Celsr1 proteins (green) localized and epithelial tension indicated (blue and orange arrows), in wild-type (WT) and Celsr1^−/− situations. The L-Epi/SM ratio and the longitudinal epithelial tension are mutually dependent. Fold shapes are also illustrated. See the main text. To see this figure in color, go online.

Mechanism of fold-pattern formation

Generating well-aligned fold patterns in the oviducts is thought to be important for reproduction, as the Celsr1 mutant female mice are defective in egg transportation and are infertile (13). In general, fold patterns can be affected by various mechanisms. The constriction of the smooth muscle layer affects the fold patterns in the gut (7). However, our previous mosaic analysis indicated that the Celsr1 mutant cell clones in the epithelium formed ectopic branches although the smooth muscle layer was composed of wild-type cells, suggesting that the properties of the epithelia, but not of the smooth muscle layers, significantly contribute to the fold-pattern formation in the oviducts (13). Thicknesses of epithelial and mesenchymal layers can affect the differences in fold patterns in normal and asthmatic airways (1). However, we could not detect any obvious differences in thickness between the wild-type and mutant oviducts (Fig. 1 E). The elastic properties of the epithelium are potential modulators of the fold patterns. However, our simulations suggested that the elastic properties are not as effective on fold branching as the L-Epi/SM ratio (Fig. S4, A–C). In contrast, by considering the L-Epi/SM ratio, the fold patterns in the oviducts were clearly reproduced in our simulations, where the L-Epi/SM ratios were comparable to the experimentally estimated values (Figs. 1 and 2). Our simulations may also present a fold pattern similar to that in oviducts in vivo with an increased radius through ovulation (Appendix D; Figs. S1 B and S3 Q).

We also investigated whether the epithelium and the oviduct store elastic energy in vivo. If this is the case, surgical perturbations would induce changes in the morphologies of the epithelium and the oviduct. When we circumferentially cut the isolated oviduct, we failed to quantitatively measure the changes in the lengths of the epithelial and smooth muscle layers due to peristaltic movements of the oviduct. On the other hand, when the isolated oviduct was opened along the longitudinal direction, the tube tended to twist outward along the circumferential direction and become planar (data not shown). This phenomenon suggests that the inner structures push the outer structures along the circumferential direction. We also isolated the epithelium using a combination of surgical operations with a treatment of EDTA. The isolated epithelium tended to be unfolded (data not shown), although the epithelium was not intact due to EDTA, which inhibits cell-cell adhesion. These observations may suggest that the epithelium is in a stressed state.

Although we do not rule out the possibility that unidentified factors modulate the fold patterns, we favor the idea that the fold branching and its suppression are predominantly determined by the L-Epi/SM ratio in combination with epithelial mechanics.

Regulation of the L-Epi/SM ratio

How can the difference between the L-Epi/SM ratios of the wild-type and mutant mice be generated (Fig.7, b)? The characteristic fold patterns in the wild-type and mutant mice are observed from the early to the mature stages of oviduct development, during which the oviducts become markedly enlarged (13). Therefore, the L-Epi/SM ratio should be regulated throughout the developmental processes. Although cell proliferation rate, cell division orientation, and apical surface area of each cell in the epithelia are expected to modulate the lengths of the epithelia, these three properties in the mutant mice were comparable to those in the wild-type ((13); data not shown). The mosaic analyses revealed that the polarized cell arrays are regulated in a cell-intrinsic manner (Fig. 7, a) (13), and not significantly by the surrounding environment, such as by external forces that substantially modulate cell shape in other systems (17). Since the intrinsic elongation of the cell itself should lead to the expansion of the epithelium along the elongation direction (35), the longitudinal elongation of the cells in the oviducts would increase, not decrease, the L-Epi/SM ratio. In contrast, a tissue such as the notochord can become shrunk along the cell elongation direction during convergent extension accompanied by cell junctional rearrangements (36). Thus, to explain the decreased L-Epi/SM ratio in the oviducts of the wild-type, we speculate that cell junctional rearrangements and/or directed cellular movements in the epithelia would occur, although we have not yet detected them due to technical difficulties in live imaging or clonal analyses after partial labeling of cells, etc. Cell extrusion under high compression also could be involved not only in the maintenance of mechanical homeostasis (37) but in regulation of the L-Epi/SM ratio. Mechanical force is another candidate for regulation of the L-Epi/SM ratio, as discussed below.

Role of mechanical force in fold-pattern formation

Mechanical forces on cell boundaries can induce cell junctional rearrangements and changes in epithelial length (38). The PCP factors are known to be localized at specific cell boundaries and to regulate the distributions of cytoskeletal proteins relating to cellular mechanical forces (39). Actually, in developing chicken embryos, Celsr1 regulates the accumulation of nonmuscle myosin IIs and filamentous actins to specific cell boundaries, which contributes to morphological changes during neural-tube closure (16). However, in the mouse oviducts, although substantial localizations of nonmuscle myosin IIs, filamentous-actins, E-cadherins, and α-catenins were observed in cell boundaries, we could not find any biased accumulations of them (Fig. S7). In addition, these findings are consistent with our laser ablation experiments (Fig. 4 B).

On the other hand, we found that the polarized cell arrays are associated with the fold patterns through epithelial tension. In the mosaic oviducts with wild-type and Celsr1-deficient cells, the straightness of the folds was correlated with the extent of overall cell polarization in the folds (13). In general, cells can be elongated by external forces provided from surrounding tissues during morphogenesis. In such cases, the lengths of the cell boundaries along the direction of cell elongations are also increased and the cell boundary tensions are simultaneously elevated (17). However, our laser ablation experiments suggested no significant correlation between cell boundary tension and length (Fig. 4 Biii). Furthermore, the polarized cell elongation is cell-intrinsically regulated (Fig. 7, a) and precedes the developmental time point when the morphological defects in the mutant folds are observed (13). These facts imply that although the mechanisms underlying polarized cell elongation are largely unknown, cell shape polarization plays an important role in fold-pattern formation.

What is the role of cell shape polarization? One possibility is that cell shape polarization provides longitudinal active epithelial tension. As shown in Fig. 3, longitudinal constrictive force between two nodes can suppress fold branching by reducing the effective L-Epi/SM ratio. The constrictive forces may be interpreted to correspond to epithelial tension actively regulated by constriction of actomyosin networks. Another possibility is that cell shape polarization is required to maintain states with longitudinally increased epithelial tension where the tensions may be passively provided (Fig. 7, c). Taken together with our previous report, this study supports the hypothesis that longitudinal epithelial tension is not just a consequence of factors in the external environment but is maintained and/or regulated by the polarized cell arrays to form a well-aligned fold pattern.

Fold-pattern diversity conferred by L- and C-Epi/SM ratios

Our theoretical framework demonstrates the significance of the L- and C-Epi/SM ratios for various complicated fold-pattern formations. These results imply that regulation of epithelial length would be important for morphogenesis in tubular organs as well as in the oviducts. The study presented here raises the possibility that epithelial length in tubular organs is maintained in a direction-dependent manner (the longitudinal versus the circumferential direction), which could be regulated by the PCP pathway at least in the oviducts (Fig. 7, b).

Mathematical models for investigation of fold-pattern formation

To investigate the fold-pattern formation in the oviducts, we used a model based on a spring network. FEMs (7, 21) and thin-shell/plate theories (22, 23) have also been applied to biological sheets. FEMs and the thin-shell/plate theories can strictly include mechanical properties of biological materials, which are experimentally measured, and thus, quantitatively faithful simulations can be performed. In the case of the oviducts, we could not experimentally measure the mechanical properties of the epithelium, because it is technically quite difficult to isolate the intact epithelium due to its fragility. Although we think that our model can qualitatively explain the fold-pattern formation in the oviducts, for a more quantitative understanding, analyses using FEM or a thin-shell/plate theory in combination with experimental measurements of mechanical properties of the epithelia will be useful.

Conclusion

We have established that the length of the epithelium relative to that of the supporting structure, such as the smooth muscle layer along both the longitudinal and circumferential directions, is critical for generating well-aligned folds and also for various complicated fold patterns observed in tubular organs. We also propose a novel, to our knowledge, PCP-pathway-mediated regulation of the epithelial tensions conferred by polarized cell elongation and suggest that the tensions are responsible for the formation of the well-aligned fold pattern by suppressing branching. Taken together, the regulation of the two layers and the cell polarization cooperatively regulate the fold-pattern formation. We linked cell shape with morphological pattern formation in organs via the mechanics of cell sheets. Such multiscale approaches to morphogenesis have been recently featured (40). Our strategy can be useful for a cellular-level understanding of morphogenesis in large tissues/organs, especially in mammals.

Author Contributions

H.K., D.S., T.U., and T.F. designed the study and wrote the manuscript. H.K. carried out the computational analyses. D.S. and H.K. performed the experiments and analyses. M.S. and N.U. supported the laser ablation experiments.

Editor: Ruth Baker.

Appendix A: Construction of Model for Fold-Pattern Formation

The epithelial layer was assumed to be an elastic sheet. The smooth muscle layer was introduced as a circular or cylindrical constraint surrounding the elastic sheet in a cross-sectional model or as a 2D sheet in a 3D cylinder model, respectively. The elastic sheet was modeled as a single layer-sheet that was discretized and represented as discrete elements (nodes).

Cross-sectional model

In the cross-sectional model, nodes were defined along the circumferential direction (Fig. S3 A). The mechanical potential energy of the whole system, U_tot2, in the cross-sectional-model was defined as

$$U_{\text{tot}2}=U_{\text{sp}}+U_{\text{b}}+U_{\text{th}}+U_{\text{cs}}.$$ (4)

Between any two adjacent nodes, an elastic spring with coefficient E was defined. The potential energy of each spring is defined as

$$u_{\text{sp}}=\frac{1}{2}E{\left(\frac{l}{l_0}-1\right)}^2{l}_0,$$ (5)

where l is the length of each spring and l₀ is the natural length of each spring.

In general, the bending energy of the unit length of an elastic filament may be written as $u_{\text{cv}}=(1/2)B_{\text{cv}}{\left(\text{CV}-{\text{CV}}_0\right)}^2,$ where B_cv is the bending modulus and CV and CV₀ are the curvature and the spontaneous curvature, respectively. In our model, a bending spring with coefficient B was assumed for each node, and the potential energy of each bending spring is defined as

$$u_{\text{b}}=\frac{1}{2}B{\left\{\frac{\text{tan}\left(\frac{\pi -\theta }{2}\right)-\text{tan}\left(\frac{\pi -{\theta }_0}{2}\right)}{l_0}\right\}}^2{l}_0,$$ (6)

where θ is the angle between the lines connecting the node with the adjacent two nodes, and θ₀ is the preferred angle of the bending spring. θ₀ was set to be π.

For the effect of the thickness of the sheet, we assumed that each node has a volume with radius R_th⁰ corresponding to the thickness. To model this effect, a repulsive force was defined to be exerted when the distance between two nodes residing in different regions of the sheet from each other was <R_th⁰. In other words, this effect is equivalent to that of excluded volume for self-avoidance (24). The potential energy was modeled in a manner similar to that used for modeling springs:

$$\begin{array}{cc}{u}_{\text{th}}=\frac{1}{2}{K}_{\text{th}}{\left(l_{\text{th}}-R_{\text{th}}\right)}^2& \left(l_{\text{th}}<R_{\text{th}}\right)\\ =0& \left(l_{\text{th}}\ge R_{\text{th}}\right)\end{array},$$ (7)

where R_th corresponds to R_th⁰, K_th is the coefficient of the repulsive force, and l_th is the distance between the nodes. In contrast to the interaction between the two nodes in different regions of the sheet, in the case where two nodes are close along the lateral direction on the sheet, R_th was defined to be smaller than the distance along the lateral direction between the two nodes in the stress-free state. Otherwise, the repulsive force becomes essentially always exerted between the neighboring two nodes. If the distance was smaller than 2 × R_th⁰, R_th was set to be 0.5-fold of the distance in the stress-free state. In addition, we did not consider friction between the surfaces of the sheet.

For the effect of the surrounding circular constraint, the radius of the inner boundary of the constraint was defined as R_cs, which was fixed throughout the simulations. In other words, the position of the constraint was not deformable. To model this effect, a repulsive force was defined to be exerted when the nodes of the elastic sheet penetrated into the boundary. The potential energy was modeled in a manner similar to springs:

$$\begin{array}{cc}{u}_{\text{cs}}=\frac{1}{2}{K}_{\text{cs}}{\left(l_{\text{cs}}-R_{\text{cs}}\right)}^2& \left(l_{\text{cs}}>R_{\text{cs}}\right)\\ =0& \left(l_{\text{cs}}\le R_{\text{cs}}\right)\end{array},$$ (8)

where K_cs is the coefficient of the repulsive force and l_cs is the distance of the node from the cross-sectional center of the surrounding circular constraint. We did not consider friction between the surface of the sheet and the surrounding constraint.

The sum of lower-case u_xx in the whole system for each potential is the corresponding upper-case U_xx in Eqs. 1, 4, and 9, shown later.

2D sheet in 3D cylinder model

The elastic sheet was assumed to be cylindrical; it will be a rectangle if the sheet is two-dimensionally spread (Figs. 2 Aiii and S3 D). The discrete elements (nodes) were arranged to form a square grid pattern in the initial conditions of the simulations (Figs. 2 Aiii and S3 D). Each edge of the grids orients along the circumferential or longitudinal direction in the initial conditions, and we defined each edge as the circumferentially or longitudinally directed edge, respectively (Fig. 2 Av). These initial definitions were maintained throughout the simulations, even if the circumferentially-directed edge became oriented along the longitudinal direction during the simulations and vice versa. Note that each grid does not correspond to a cell. The top and bottom boundaries in the longitudinal direction of the surrounding cylindrical constraint and the elastic sheet were continuously connected to each other, leading to a periodic boundary. The longitudinal boundary positions of the epithelium were given by the surrounding constraint.

The potential energy of the whole system, U_tot3, previously described in Eq. 1, is rewritten with the potential derived from the constrictive force (Eq. 3):

$$U_{\text{tot}3}=U_{\text{sp}}+U_{\text{b}}+U_{\text{sq}}+U_{\text{th}}+U_{\text{cs}}+U_{\text{t}},$$ (9)

where U_sq and U_t are the potentials derived from the bending springs for shear deformation of the grids or from active constrictive force, respectively. U_th and U_cs are the same as in the cross-sectional-model. U_sp and U_b are also essentially the same as those in the cross-sectional model, but the springs and the bending springs are defined not only along the circumferentially directed edges but also along the longitudinally directed edges (Fig. 2 Avi). The coefficient along the circumferentially or longitudinally directed edge is expressed as E_C or E_L, respectively. The coefficient of the bending spring along the circumferentially or the longitudinally directed edge is expressed as B_C or B_L, respectively.

The potential energy of the bending spring for shear deformation was defined in a similar way to the other two types of bending springs:

$$u_{\text{sq}}=\frac{1}{2}{S}_{\text{sq}}{\left\{\frac{\text{tan}\left(\frac{\pi -\theta }{2}\right)-\text{tan}\left(\frac{\pi -{\theta }_0}{2}\right)}{l_0}\right\}}^2{l}_0,$$ (10)

where S_sq is the coefficient of the springs and θ₀ is set to be π/2.

The potential energy from the constrictive force between the two nodes was previously described in Eq. 3. λ was also defined along the circumferentially (λ_C) and longitudinally (λ_L) directed edges. In this formulation, since the circumferentially and longitudinally directed edges were defined according to the initial directions of the edges, the circumferentially directed edges could become oriented along the longitudinal direction during the simulations, and vice versa, as described previously. In a biological context, this force may be interpreted to be an active epithelial tension caused by active constriction of actomyosin networks, etc.

The quantities above were normalized by E and the diameter of the surrounding cylindrical constraint, D, and corresponding dimensionless quantities were defined as B^∗ ≡ B/(ED²), B_C^∗ ≡ B_C/(E D²), B_L^∗ ≡ B_L/(ED²), E_C^∗ ≡ E_C/E, E_L^∗ ≡ E_L/E, K_th^∗ ≡ K_thD/E, K_cs^∗ ≡ K_csD/E, S_sq^∗ ≡ S_sq/(ED²), λ_C^∗ ≡ λ_C/E, λ_L^∗ ≡ λ_L/E, l^∗ ≡ l/D, l₀^∗ ≡ l₀/D, l_th^∗ ≡ l_th/D, R_th^0∗ ≡ R_th⁰/D, R_th^∗ ≡ R_th/D, l_cs^∗ ≡ l_cs/D, and R_cs^∗ ≡ R_cs/D. Epithelial tensions and forces were also normalized by E (Figs. 2, C and E, 3, A and C, 6, S3, G, K, N, R, and Q, and S4). Widths and curvatures were also normalized by D (Fig. S3, G, K, and N).

Appendix B: Simulation Processes of Fold-Pattern Formation

To numerically search for stable states under the defined potential energy with given L-nEpi/SM and C-nEpi/SM values, we performed simulations including a relaxation process. Simulations were performed where the nodes follow the equation of motion:

$$\mu \frac{d{r}_i}{dt}=-\nabla U_{\text{tot}2\text{or}\text{tot}3},$$ (11)

where r_i (i = 1,…,N) are the positional vectors of N nodes, μ is the coefficient of viscosity, t is time, and ∇ is a vector differential operator. In a general simulation of cellular-scale dynamics, μ may be derived from frictions provided by the surrounding biological structures, including cells and tissues (41). However, in our study, since we focused on the stable structures and not the temporal dynamics of the morphological changes, μ, although biologically meaningless, was introduced for computational reasons. Dimensionless quantities were defined as t^∗ ≡ tE/(Dμ), r_i^∗ ≡ r_i/D, and ∇^∗ ≡ D∇. Speeds of nodes were also normalized by E and μ (Fig. S3 P).

We focused on stable states. Since the C-Epi/SM ratio is 3–4 in mature mice, our simulation was set to satisfy this situation. In the cross-sectional simulations, the sum of the natural lengths of the elastic springs (Nl₀) was set to be 3.0 times larger than the circumferential length of the surrounding constraint (πD), and a relaxation process was performed to obtain stable states. For technical reasons, the initial condition was set so that all nodes were placed along the inner boundary of the surrounding constraint, and the sum of the natural lengths was equal to the circumferential length of the surrounding constraint. Then, during the simulation processes, the natural lengths were gradually increased by 3.0-fold and a relaxation process was implemented. Note that these processes, including the process before the relaxation, are not intended to describe the in vivo developmental process. In the 3D simulations, except for that described in Fig. 6, the natural lengths of the elastic springs were increased by 3.0-fold not only along the circumferential but also along the longitudinal direction.

To satisfy the target value of the L-nEpi/SM ratio, we regulated the longitudinal length of the surrounding constraint. In the initial condition, the longitudinal length of the surrounding constraint was set to be equal to the length of the epithelium, the sum of the natural lengths of the elastic springs of the longitudinally directed edges (L-nEpi/SM ratio = 1.0). Then, as the natural lengths of the elastic springs were increased by 3.0-fold, the longitudinal length of the surrounding constraint was also increased. If the increase of longitudinal length of the surrounding constraint was set to be 3.0- or 2.5-fold, we could simulate a situation where L-nEpi/SM =1.0 (3.0/3.0) or 1.2 (3.0/2.5), respectively. Note again that these processes were not intended to describe the in vivo developmental process but to achieve the target L-nEpi/SM ratio. In addition, actual longitudinal lengths of the epithelia and the smooth muscle layers were meaningless in our simulations, but the lengths of the epithelia per unit length of the smooth muscle layers were meaningful.

For the generation of various patterns in Fig. 6, A–K, essentially the same procedures as above were applied, except that the increase rate of the natural lengths of the elastic springs was set to be different (Table S2).

For the generation of zigzag patterns in Fig. 6, O–R, the initial conditions were different from those in the other simulations: sheets with well-aligned folds, which were generated beforehand under the condition where the L-nEpi/SM and C-nEpi/SM ratios were set to be the values described in Fig. 6, M and N, were used as the initial condition. Then, the L-nEpi/SM ratio was gradually increased by decreasing the longitudinal length of the surrounding constraints, and a relaxation process was implemented. Detailed parameter values are shown in Table S2.

In the actual simulations, for technical reasons, we introduced a fluctuation of the movement of the nodes. Otherwise, folds were not formed; the nodes almost never moved from the initial condition, probably because the simulations were trapped in energetic local-minimum states. The initial condition itself was a local-minimum state. To escape from the local-minimum states, the fluctuation force was included before the relaxation process, as follows:

$$\mu \frac{d{r}_i}{dt}=-\nabla U_{\text{tot}2\text{or}\text{tot}3}+\xi \left(t\right),$$ (12)

where ξ(t) is the fluctuation, resulting in the formation of folds. The dimensionless quantity was defined as: ξ(t)^∗ ≡ ξ(t)/E. ξ(t)^∗ was given by uniform random numbers of ∼0.0–2.0, and the spatial direction was also randomly provided. In our simulations, the fluctuation was introduced for technical reasons, as described above. However, it is possible that the fluctuation might mimic some nonuniformities of mechanical properties or geometries of the epithelial sheet in vivo, which should be required for the generation of folds. Such nonuniformities could be caused by local cell proliferation, etc.

The simulations were performed using the Euler method with a time step, Δt. The force derived from ξ(t) was set to be Δtξ(t). The simulations were programmed in C.

In the general condition of the simulations, except for some simulations described later, the simulations were run for 120 dimensionless time units corresponding to 400,000 iterations, where the time step for each iteration (Δt) is 0.01. A gradual increase of the natural lengths of the elastic springs and changes in the longitudinal length of the surrounding constraint were included over 0–60 dimensionless time units, and the relaxation process was implemented over 60–120 dimensionless time units. In the fourth fold patterns shown in Fig. S4, A–C, the time schedules were the same as described above, but Δt was 0.005, 0.0025, and 0.005, respectively, during 0–60 dimensionless time units, and 0.005, 0.01, and 0.005, respectively, during 60–120 dimensionless time units. In Fig. 6, M and N, the relaxation process was implemented over 60–180 dimensionless time units. In Fig. 6, O–R, the changes in the longitudinal length of the surrounding constraint were included over 0–30 dimensionless time units, and the relaxation process was implemented over 30–90 dimensionless time units.

The number of nodes (i and j for the circumferential and longitudinal directions, respectively; Fig. 2 Av) and the increases in the natural lengths of the elastic springs were set so that the final natural lengths become the same among all simulations (Table S1). In the general conditions, except in Fig. 6, i and j are 400 and 100, respectively. The total number of the elastic springs is 80,000 (400 × 100 × 2). The natural lengths were increased by 3.0-fold. The changes in longitudinal lengths of the surrounding constraint were set to be 3.0-fold (Fig. 2 C, top), 2.5-fold (Figs. 2 C, middle, 3, and S4), and 2.0-fold (Fig. 2 C, bottom), respectively. These parameters in Fig. 6 are shown in Table S2.

The basic behaviors of the simulations and parameter values are described in Appendix D and Fig. S3, P and Q, and in Parameter Values Used in Simulations in the Supporting Material and Tables S1 and S2.

Appendix C: Basic Properties of the Model

We expected that the springs (E, E_{L and C}), bending springs (B, B_{L and C}), and bending springs for shear (S_sq) in our model qualitatively reflect the mechanical properties of the epithelial sheet, such as the Young’s modulus, bending modulus, and shear modulus. To evaluate basic properties of our model, we analyzed the responses of the model to stretch/compression, shear, and bending deformations (Fig. S3, E–N). In these analyses, neither the effect of the thickness of the sheet (Eq. 7) nor the effect of the surrounding circular constraint (Eq. 8) was introduced. In Fig. S3, E–N, the values of the parameters E_L, E_C, B_L, and B_C were set to be the same as in the first simulation condition in Table S1. The values of S_sq are shown in Fig. S3, E–N. The natural length of the springs was also set to be the same as in Table S1.

For stretch/compression, a grid array was stretched or compressed along the grid lines (Fig. S3 E) or along the oblique direction to the grid lines (Fig. S3 F). The positions on the two black lines were provided, and simulations were then performed until a stable state was reached. Finally, total forces exerted by the grid array on the black lines (bold arrows) were measured. As shown in Fig. S3 G, in the case of the stretch/compression along the grid lines, the forces were linearly changed against the ratio of the length to the initial length of the grid array. In the case of the stretch/compression along the oblique direction, the forces were almost linearly changed, although a slight nonlinearity was observed. We found that S_sq influenced the responses along the oblique direction. When S_sq^∗ was set to be 8.0, the response along the oblique direction was similar to that along the grid lines; the response along the grid lines was never affected by S_sq. We also measured the widths at the middle position of the grid arrays (Fig. S3, E and F, arrowheads). The stretch/compression along the grid lines did not induce changes in the widths (Fig. S3 H). On the other hand, the stretch/compression along the oblique direction induced changes in the case where S_sq^∗ = 24.0 and 2.4. However, the changes were not essentially induced in the case where S_sq^∗ = 8.0. E_{L and C} substantially affected the responses, whereas B_{L and C} did not (data not shown). S_sq did not affect the responses along the grid lines, as described above (data not shown).

For shear deformation, a grid array was sheared along the grid lines (Fig. S3 I) or along the oblique direction to the grid lines (Fig. S3 J). Analysis procedures were essentially similar to those in the case of stretch/compression. The relationship between the forces and deformations defined by θ was analyzed (Fig. S3 K, left). In both cases, the forces were linearly changed against θ. The forces were ∼2-fold larger along the grid lines than along the oblique direction. S_sq affected the responses. When S_sq^∗ was set to be 8.0, the response along the oblique direction was similar to that along the grid lines. E_{L and C} also substantially affected the responses, whereas B_{L and C} did not (data not shown).

For bending deformation, a grid array was bent along the grid lines (Fig. S3 L) or along the oblique direction to the grid lines (Fig. S3 M). Analysis procedures were essentially similar to those in the case of stretch/compression. The relationship between the forces and curvatures was analyzed (Fig. S3 N, left). In the case of the bending deformation along the grid lines, the forces were linearly changed against curvatures (Fig. S3 N, right). In the case of the bending deformation along the oblique direction, the forces were almost linearly changed, although a slight nonlinearity was observed (Fig. S3 N, right). The forces were 1- to 2-fold higher along the grid lines than along the oblique direction. B_{L and C} substantially affected the responses, whereas E_{L and C} did not (data not shown). S_sq had a slight influence on the responses along the oblique direction, but not along the grid lines (Fig. S3 N).

From these analyses, we think that these springs (E, E_{L and C}, B, B_{L and C}, and S_sq) reflect some aspects of the mechanical properties of the epithelial sheet.

As shown above, the grid array exhibited almost linear responses of the forces against the three types of deformation. In each type of deformation, although the values of the forces depended on the directions of the deformations, the differences in the values were no more than 2.0-fold. When we calculated the average force exerted by a single node, the differences became ∼1.4-fold (2.0/√2). As shown in Fig. S4, A–C, it seemed that a 2.0- or 1.4-fold change in B_{L and C}, S_sq, or E_{L and C} did not cause significant differences in the fold patterns. In addition, a 2.0-fold change in either B_L or B_C, or E_L or E_C, was not effective on the fold patterns (data not shown). Furthermore, when the grid array was obliquely placed in the surrounding cylinder, similar simulation results to those in Fig. 2 C were obtained (data not shown). Thus, we think that the anisotropies observed in Fig. S3, E–N, do not significantly influence the qualitative results of the fold patterns. Importantly, our model successfully reproduced a well-aligned fold pattern (Fig. 2 C, top) and zigzag patterns (Fig. 6, O–R), both of which have been described in previous studies using an FEM (7) or an analytical approach (8), suggesting that our model is qualitatively consistent with the previous models.

Appendix D: Basic Behaviors of Simulations

We analyzed whether the basic parameters, including Δt, the natural lengths of the elastic springs, and ξ(t), affected the outcomes of simulations or not, and how the simulation time period affected the outcomes.

In the conditions in Fig. 2 C, we confirmed that significant differences were visually almost undetectable over the range of Δt = 0.005–0.02 (data not shown). The natural lengths of the elastic springs were modified by altering the number of the nodes along the circumferential direction (i). The number i is 400 in Fig. 2 C. Essentially similar results were obtained when the number was set to be 300–600, whereas values <300 resulted in the surfaces of the sheets not being visually smooth and the fold shapes not being correctly recognized (data not shown). Thus, the number should be >300 for proper simulations. The number of the folds varied under smaller values of ξ(t) in the cross-sectional model (data not shown). Thus, the magnitude of ξ(t) was set to be large enough to avoid the variability (the maximal value of ξ(t)^∗ is 2.0 in general conditions). On the other hand, in the 2D sheet in the 3D cylinder model, significant differences were visually almost undetectable over the range of the maximal value of ξ(t)^∗ = 0.0–6.0 (data not shown).

We assessed the simulation time period for obtaining stable states in our simulations. Dimensionless speeds of nodes were analyzed under the same simulation conditions as in Fig. 2 C (Fig. S3 P). The average speeds were markedly decreased when the simulations entered into the relaxation processes (dimensionless time = 60), and they gradually decreased after that. Although the average speeds were continuously decreased, only slight changes were visually detected (Fig. S3 Q), as far as the simulation periods from Fig. 2 C were prolonged (dimensionless time = 120) by twofold (dimensionless time = 240). Thus, we considered that the simulations nearly reached stable states. However, we cannot rule out the possibility that the states will significantly change during much longer time periods. However, because of our limited computational resources, it is not technically realistic to prolong the simulation time period.

In addition, during the formation of the folds in our simulations, we observed that the interval between the neighboring folds seemed to be wide (Fig. S3 Q, dimensionless time = 15). This phenomenon may be similar to the in vivo situation of the oviduct swollen through ovulation (Fig. S1 B), although the radius of the tube in the simulations was fixed. Our model may be useful in analyzing the morphological changes in the folds induced through ovulation.

Supporting Citations

References (42, 43, 44, 45, 46) appear in the Supporting Material.

Supporting Material

Movie S1. Morphological Change during the Puncturing

Changes in ampullar morphologies of a superovulated oviduct during and after the puncturing. See also Fig. S1. Time stamp indicates min:sec.