The Limiting Speed of the Bacterial Flagellar Motor

Abstract

Recent experiments on the bacterial flagellar motor have shown that the structure of this nanomachine, which drives locomotion in a wide range of bacterial species, is more dynamic than previously believed. Specifically, the number of active torque-generating complexes (stators) was shown to vary across applied loads. This finding brings under scrutiny the experimental evidence reporting that limiting (zero-torque) speed is independent of the number of active stators. In this study, we propose that, contrary to previous assumptions, the maximum speed of the motor increases as additional stators are recruited. This result arises from our assumption that stators disengage from the motor for a significant portion of their mechanochemical cycles at low loads. We show that this assumption is consistent with current experimental evidence in chimeric motors, as well as with the requirement that a processive motor driving a large load via an elastic linkage must have a high duty ratio.

Introduction

The bacterial flagellar motor (BFM) drives swimming in a wide variety of bacterial species, making it crucial for several fundamental biological processes, including chemotaxis and community formation (1, 2, 3, 4). Accordingly, gaining a mechanistic understanding of this motor’s function has been a fundamental challenge in biophysics.

Because of its complexity and localization to the membrane, atomic structures of the entire motor are not yet available. Still, relatively detailed models have been developed using a combination of partial crystal structures (5, 6, 7), cross-linking and mutagenesis (8, 9, 10), and electron microscopic and cryoelectron tomography images (11, 12) (Fig. 1). Additionally, the relative ease with which the output of a single motor can be measured in real time, by observing rotation of a large bead attached to the motor with light microscopy, has made it one of the best studied of all large biological molecular machines.

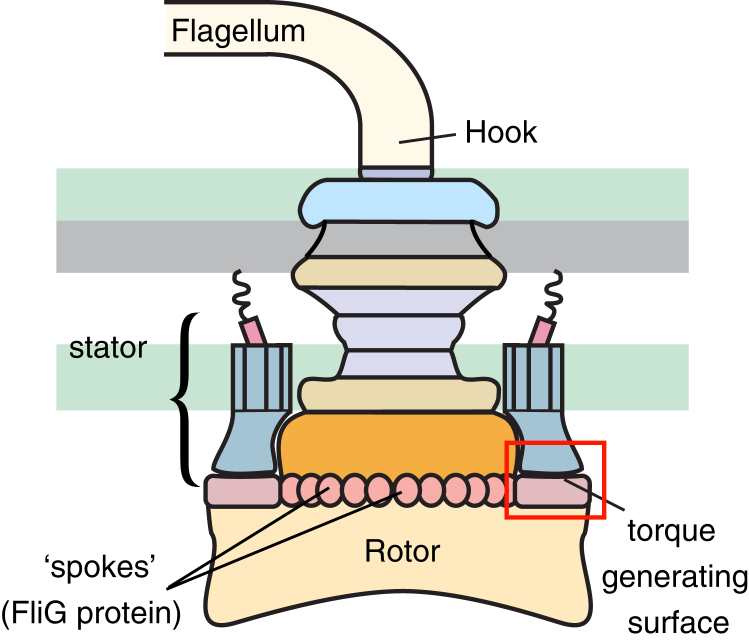
Figure 1.

The bacterial flagellar motor consists of a series of large concentric rings that attach to a flagellar filament via a flexible hook. An active motor can have between 1 and 11 torque-generating stator complexes. Stators interact with protein “spokes” (FliG) along the rotor’s edge to drive motor rotation. To see this figure in color, go online.

Arguably the most important physical probe into the dynamics of a molecular motor is its torque-speed relationship. For the BFM, this curve was shown to have two distinct regimes, separated by a “knee” (Fig. 2). This characteristic feature of the BFM was long held as the first “checkpoint” for any theoretical model of the motor. However, recent experiments showed that the number of torque-generating complexes (stators) in the motor is load-dependent—that is, published torque-speed curves most likely contain measurements from motors with different numbers of docked stators (13, 14). Specifically, at high loads (low speeds) a motor can have up to 11 docked stators, whereas at low loads (high speeds) motors typically operate with only one stator (though we note that the experiments in (13) reported that ∼25% of motors likely had two stators).

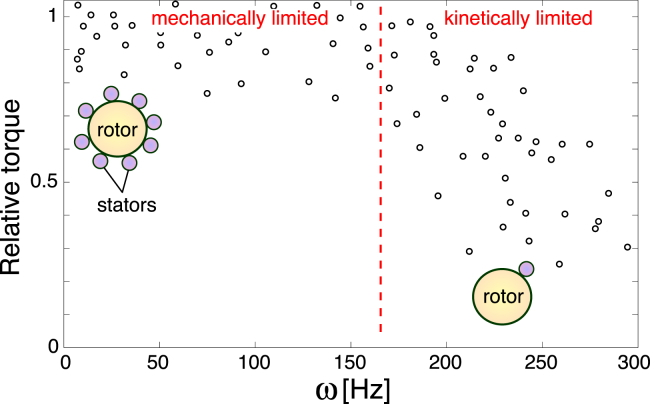
Figure 2.

Recent experiments have shown that the number of torque-generating complexes (stators) is not constant across applied loads. Therefore, it is likely that most measured torque-speed curves were generated using motors with varying numbers of stators: points in the high-load regime correspond to motors with up to 11 stators and points at low loads (within the kinetically limited regime) to motors with only one. Red dashed line separates the mechanically limited and kinetically limited regimes; we focus on the latter. Data shown is from (46); however, we note that another experiment in this same article presents data that seems to be collected from a motor with a constant number of stators. To see this figure in color, go online.

Before continuing, we first clarify some of our terminology. We consider the “low load” regime (also referred to as “high speed,” “maximum speed,” or “zero torque” throughout) to be when the drag coefficient of the load is on the same order of magnitude or lower than the internal friction (i.e., the drag of the rotor). Importantly, we point out that due to experimental constraints, several results originally considered to be “low load” measurements were conducted using loads outside of this regime; these will be noted as they appear in our text.

The recent experimental findings (13, 14) shed doubt on several fundamental results about the dynamics of the BFM, including, importantly, its behavior at low loads. A seminal set of experiments, termed “resurrection” experiments, studied the dependence of motor speed on the number of stators at various external loads (15, 16, 17). In these experiments, paralyzed cells were allowed to begin rotating slowly, and discrete increases in speed were interpreted as the addition of torque-generating complexes. Surprisingly, whereas up to 11 increases of near-equal size were observed at high loads, only a single such “jump” was observed at low loads.

These results quickly led to a series of reworked theoretical models, all of which required that the limiting speed of the motor be independent of the number of stators (18, 19, 20). However, it is likely that low-load measurements were never performed on motors with more than one stator, leaving open the question of how the BFM behaves in the zero-torque (high-speed) limit.

We recently presented a model of flagellar motors with a single stator, in which a steric interaction driven by a conformational change in the stator is implicated as the motor’s torque-generating mechanism (21). In this study, we extend this model to motors with multiple-docked stators and predict that the limiting speed of the BFM increases with the number of active stators.

This result arises from the fact that the stator is not in contact with the rotor in between steps, or “power strokes” (i.e., the duty ratio of the motor is less than 1). We note that although models with high duty ratios also can reproduce current experiments, evidence of a conformational change in stator structure has been reported (see, e.g., (22)). Generic models involving such a conformation will share this property, because such mechanisms likely require stators to “reset” between steps.

In the following, we first give an overview of our model for single-stator motors and then discuss its extension to motors with multiple-docked stators. We then discuss the implication of such a model for motors operating at low load: in particular, challenging the widely held belief that the motor speed near the zero-torque limit is independent of the number of docked stators.

We argue that these mechanisms affect the motor’s duty ratio only at low loads. In this way, our model, and others in this category, are compatible with evidence that the BFM must have a high duty ratio to be processive at high loads. Experiments testing this hypothesis, if successful, would be the first, to our knowledge, to explicitly quantify this relationship in the low-load regime.

Materials and Methods

Our model implicates a steric interaction between the stator and rotor in torque generation (21). Briefly, stators drive motor rotation by stepping along protein “spokes” around the periphery of the rotor, a large ring that connects to the flagellar filament via a flexible hook. This interaction is analogous to parents pushing on the handles of a merry-go-round on the playground for their children’s amusement. An overview of our proposed mechanism is given in Fig. 3.

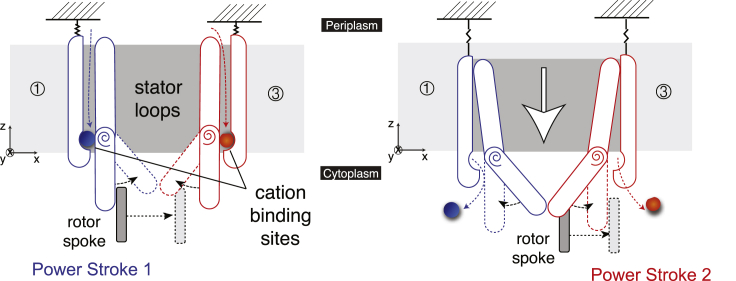
Figure 3.

Overview of our proposed torque-generating mechanism. Cation binding induces a strain in the stator, which causes the loops to bend. This results in the first half of the power stroke (here, by Loop 1), and sets up the second loop (here, Loop 3) to perform its half of the power stroke. Subsequently, the cations are released into the cytoplasm. This occurs because our proposed motion also has a vertical component—the loops lower themselves out of the membrane. This release then reverses the strain and causes the loops to restraighten. This results in the second half of the power stroke. We note that this image depicts a two-dimensional projection of a three-dimensional motion: stator motion is not constrained to the plane of the page. To see this figure in color, go online.

Individual steps are initiated by proton arrivals at ion-binding sites within the stator complex. The gate-controlled diffusion of protons through the BFM’s stator, and its link to motor rotation, was recently explored (23). During the power stroke, conformational changes in the stator apply a steric force onto the spokes of the rotor wheel, rotating it a discrete step length d. Details of the stator potential curves are provided in the Supporting Material and in reference (21).

The motion of the stator and rotor are described by the following Langevin equations:

$${\zeta }_S\frac{d{\varphi }_S}{dt}=\underset{\begin{array}{c}\text{Torque}\text{from}\\ \text{Proline}\text{hinge}\end{array}}{\underbrace{F_p{\ell }_p}}-\underset{\begin{array}{c}\text{Reaction}\\ \text{from}\text{rotor}\end{array}}{\underbrace{{\tau }_{\text{reaction}}}}+\underset{\text{Thermal}\text{fluctuations}}{\underbrace{\sqrt{2k_{B}T{\zeta }_S}{f}_n\left(t\right)}}$$

$${\zeta }_R\frac{d{\theta }_R}{dt}=\underset{\begin{array}{c}\text{Torque}\\ \text{from}\text{stator}\end{array}}{\underbrace{{\tau }_{\text{contact}}}}-\underset{\begin{array}{c}\text{Spring}\text{connection}\\ \text{to}\text{load}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\text{fluctuations}}{\underbrace{\sqrt{2k_{B}T{\zeta }_R}{f}_n\left(t\right)}},$$

where the final term in each equation is the stochastic Brownian force, with $k_{B}T$ being the Boltzmann constant multiplying temperature and $f_n\left(t\right)$ denoting uncorrelated white noise.

Stators apply no force ($F_p$ = 0) to the rotor between power strokes. This results in negligible applied $\left({\tau }_{\text{contact}}\right)$ and reaction torque $\left({\tau }_{\text{reaction}}\right)$ when the stator and rotor are not in contact with each other. The values of these torques are calculated as the gradients of the interaction potential between the stator and the rotor; details on these calculations are provided in the Supporting Material. All other model parameters are described in Table 1. Because the BFM lives at low Reynolds number, the rotor also exhibits no productive movement when the stator is disengaged between steps.

Table 1.

Model Parameters with Units, Values, and Reference

Parameter	Definition	Units	Values	References
$F_p$	Proline hinge force	pN	20	(1)
${\ell }_P$	Length of proline hinge	nm	7	(44)
${\zeta }_S$	Stator drag coefficient	pN-nm-s-rad−1	0.002	fit
${\zeta }_R$	Rotor drag coefficient	pN-nm-s-rad−1	0.02	(1)
${\zeta }_L$	Load drag coefficient	pN-nm-s-rad−1	0.005–10	(45)
κ	Hook spring constant	pN-nm-rad−1	150	(40)
N	Number of stators	-	1–11	(45)
${\tau }_{\text{contact}}$	Contact torque on rotor	pN-nm	–	–
${\tau }_{\text{reaction}}$	Reaction torque on stator	pN-nm	–	–
${\varphi }_S$	Stator angular position	rad	–	–
${\theta }_R$	Rotor angular position	rad	–	–
${\theta }_L$	Load angular position	rad	–	–

We assumed that there are 26 spokes along the edge of the rotor ((24), although see, e.g., (7, 25)). A “perfect” power stroke is defined as a step of length $d=\left(2\pi /26\right)$ rad, leaving the stator in contact with the neighboring spoke. These steps are observed through the rotation of a small bead (the load) attached to the flagellar hook. The dynamics of the load are described by a third Langevin equation:

$${\zeta }_L\frac{d{\theta }_L}{dt}=\underset{\begin{array}{c}\text{Spring}\text{connection}\\ \text{to}\text{rotor}\end{array}}{\underbrace{\kappa \left({\theta }_R-{\theta }_L\right)}}+\underset{\text{Thermal}\text{fluctuations}}{\underbrace{\sqrt{2k_{B}T{\zeta }_L}{f}_n\left(t\right)}}.$$

When the connection between the rotor and the bead is soft (κ is small), discrete motor steps “blur” into a seemingly continuous trajectory. Experimentally, steps have been directly observed by slowing the motor down to a speed of ∼10 Hz (24).

In a motor with multiple stators, the mechanics of each stator follows the equations corresponding to that of a single stator. At any given time, docked stators can be “engaged” (i.e., actively performing a power stroke) or “disengaged” (in between power strokes). The total contact torque on the rotor is given by the following:

$${\tau }_{\text{contact}}=\sum _{i=1}^N{\tau }_{\text{contact}}^i,$$

where N is the total number of docked stators, and each stator i applies a contact torque ${\tau }_{\text{contact}}^i$ on the rotor. Recall that a disengaged stator (i.e., one in the waiting state between successive power strokes) is not applying directional torque to the rotor, and so ${\tau }_{\text{contact}}^i=0$.

We have assumed that each stator is independently “activated” with rates corresponding to cation “hopping on” and “hopping off” events. Because cation arrivals are Poisson processes (i.e., waiting times between arrivals are distributed exponentially) (26, 27), the “next arrival” in a motor with N stators occurs at a rate $N\times k_{\text{on}}$, where $k_{\text{on}}$ is the rate of arrival for a single stator.

Simulations of Langevin dynamics were written in Python 2.7. Further details on the implementation and interaction potentials used in simulations are provided in the Supporting Material. Simulation trajectories showing steps for motors with one and seven engaged stators operating at low load are shown in Fig. 4, a and b. (All code is available at http://ocf.berkeley.edu/∼jnirody).

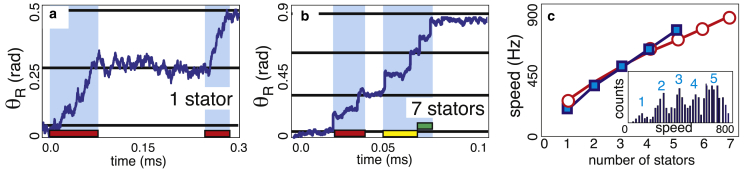
Figure 4.

Simulated trajectories are shown for motors with (a) one and (b) seven engaged stators, with ${\zeta }_L=0.005$ pN-nm-s-rad⁻¹. Horizontal black lines denote the distance between “perfect” steps ($\ell =\left(2\pi /26\right)$ rad). Colored bars at the bottom of the plots mark the duration of individual stator steps (in the shown trace, steps for three out of the seven engaged stators are shown). In the multistator motor trajectory (b), steps for each stator are differently colored. In accordance with published temporal resolutions (47, 48), we consider two steps distinguishable if the end of the first step and the start of the second step are separated by 10 μs. These are shaded in blue; for multistator motors, steps may overlap or be too close together to be observed. (c) Motor speed at low loads increases with the number of stators. An experimentally measured speed distribution at low loads is shown in the inset (data from (28)). Gaussian fits to the major peaks give mean speeds (blue squares) in good agreement with simulation predictions (open red circles). To see this figure in color, go online.

Results

Motor speed at low loads increases with number of stators

From simulations, we predict that the maximum speed of the motor is dependent on the number of engaged torque generating complexes (Fig. 4 c, open red markers). In their recent paper, Lo et al. computed torque-speed curves for a chimeric sodium-driven motor (28). Low-load measurements on these motors were performed using a 100 nm-diameter gold bead (Fig. 4 c, inset).

This data was collected from motors with 1–5 active stators (Fig. 4 c, blue markers). The authors focused on single-stator motor dynamics, leaving open the implications of their data for how the zero-torque speed depends on stator number. The existence of multiple discrete peaks at low load strongly supports the idea that the maximum speed is dependent on the number of stators, at least in chimeric motors. We note that such peaks have not been observed in wild-type motors (17), which may be due to different recruitment in proton-driven and chimeric motors (e.g., wild-type motors fail to recruit multiple stator units at very low loads). Further experiments designed with all the current knowledge in mind will be needed to resolve the exciting questions that arise from these conflicts.

Ryu and coauthors reported a set of general conditions that must be met for the limiting speed to be independent of stator number (29). First, the rate at which steps are initiated must be independent of the relative position of the rotor and the stator. This position is dependent on both the external load and the actions of any other engaged stators. Therefore, the “decision” of a stator to step should be ignorant of both these factors. Second, stators must engage the rotor for the majority of their cycle (i.e., the BFM’s duty ratio DR ≈ 1). Resurrection experiments reporting that the speed at low loads was independent of stator number soon followed (17), which seemed to lend strong support to both of the proposed requirements. We note that, although the experiments in (17) were performed in what we have considered to be near-zero load, the measurements performed in (29) that were referred to as “low load” were actually made at significantly higher loads.

Because we assume that stators are disengaged with (i.e., not applying any directional torque to) the rotor between successive power strokes, our model contains a violation of the second condition. In particular, unlike most proposed mechanisms (but see (30)), we assume motor rotation and ion flow can be loosely coupled: an ion passage may not always result in appreciable rotation of the rotor. The stator’s motion, however, is tightly coupled to ion flow—that is, an ion passage is both necessary and sufficient for the initiation of a stator’s power stroke. Therefore, loose coupling in our model does not arise from some form of ion leakage (30, 31, 32, 33, 34), but because stator steps are rarely “perfect” in multiple-stator motors. If steps overlap, a portion of the second stroke is “wasted” because the rotor is pushed out of the later-firing stator’s reach.

These properties seem contrary to current assumptions that stators in the BFM must have a high duty ratio. However, we show that our prediction that DR < 1 at low loads arises from fundamental differences in motor dynamics between the high- and low-load regimes. In this way, we argue that our proposed mechanism is compatible with experimental evidence for a high duty ratio at high loads (Fig. 5 a).

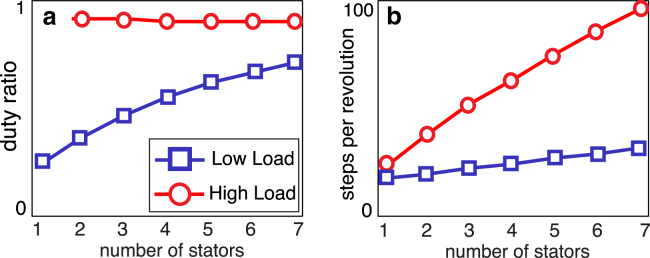
Figure 5.

Comparison of motor dynamics at low (${\zeta }_L=0.005$ pN-nm-s-rad⁻¹, shown as blue squares) and high (${\zeta }_L=0.5$ pN-nm-s-rad⁻¹, shown as red circles) loads. (a) Decrease in the average time between steps with increasing stator number results in an increase in duty ratio in the low-load regime. In contrast, at high loads, each stator step takes a considerable amount of time ($T_m$ is high), and the duty ratio is high even for single-stator motors. (b) As stators are recruited to fast-rotating motors (i.e., at low load), the number of independent stator steps per motor revolution $\left(n_{\text{steps}}\right)$ increases sublinearly from 26 steps/revolution for single-stator motors. At high loads, as predicted in (37), the steps per revolution is proportional to the number of stators. Note that $n_{\text{steps}}$ is the number of independent stepping events, and does not depend on experimental resolution. To see this figure in color, go online.

Kinetically limited stators have low duty ratios

A stator initiates a step when protons arrive at a specified binding site within the complex. The mechanochemical cycle of the stator has two phases: moving and waiting, characterized by timescales $T_m$ and $T_w$, respectively (18). If $T_S$ is the time that a stator engages the rotor during a complete cycle $\left(T_m+T_w\right)$, a single-stator motor has duty ratio $DR=T_S/\left(T_m+T_w\right)$.

The waiting time between strokes $T_w$ depends on the rate of proton arrivals at a binding site. These arrivals are Poissonian with rate $k_{\text{on}}=k_0\text{exp}\left[\lambda \Delta G_{\text{ij}}/k_{B}T\right]$. Here, $\Delta G_{\text{ij}}$ is the thermodynamic contribution of the ion motive force and $k_{B}T$ is Boltzmann’s constant multiplied by temperature (19, 35). For simplicity, we choose $\lambda =0.5$ as done in previous studies (35). The parameter $k_0$ is a function of the pH of the external periplasm; lower pH corresponds to higher proton concentration and thus a speedier arrival at the site. At room temperature and pH 7.0, $\langle T_w\rangle =1/k_{\text{on}}=0.2$ ms for single-stator motors (18, 20).

The average moving time is estimated through the relation $\omega \approx \ell /\left(\langle T_m\rangle +\langle T_w\rangle \right)$ (18). The average motor speed ω is also related to the load drag coefficient ${\zeta }_L$ by ${\zeta }_L\omega \approx \tau$, where $\tau$ is the motor torque (1, 36). In our simulations, the motor is limited by proton arrivals at very low loads ($\langle T_m\rangle \approx 0.01$ ms), whereas at high loads, $\langle T_m\rangle \approx 10$ ms surpasses $\langle T_w\rangle$. These values are consistent with previous studies (18, 20).

Because we predict that motor rotation is driven by steric forces, a stator must be in contact with the rotor for a large part of a productive power stroke $\left(T_S/T_m\approx 1\right)$. Previous models of torque-generation have similarly considered the mechanochemical cycle of the BFM to consist of moving and waiting phases (18, 20). However, our model is unique in assuming that stators disengage from the rotor between subsequent power strokes. This results in DR < 1 for single-stator motors at low loads, as the waiting time is no longer negligible compared with the moving time in this regime (Fig. 5 a, blue squares). The waiting time may even surpass $\langle T_m\rangle$, as shown in Fig. 4, a and b.

The waiting time until a proton binds to any one of N independently stepping stators is exponentially distributed with rate $N\times k_{\text{on}}$. Therefore, $\langle T_w\rangle$ is shortened as additional stators are recruited. The subsequent increase in duty ratio (Fig. 5 a, blue squares) results in an increase in limiting speed with the number of stators.

High duty ratios at high loads

Here, we address the assertion that the duty ratio of the BFM must be very high. Two common arguments in the literature are based on 1) the observation that the number of steps per revolution $n_{\text{steps}}$ increases as additional torque-generating complexes were recruited (37, 38), and 2) a calculation determining that a motor with a low duty ratio cannot be processive due to “unwinding” of the tether connection between the rotor and load (1). The application of these arguments, based on high-load measurements, to the low-load regime has been possible because of the lack of a proposed physical mechanism for BFM rotation. Such a mechanism is now provided in our model (21). To this end, we show these arguments can be consolidated with our proposed mechanism, as well as with the prediction that DR < 1 at low loads.

Samuel and Berg used fluctuation analysis to determine that the number of steps per revolution was proportional to stator number (37, 38). In the absence of a specific physical mechanism, this result was interpreted to mean that a motor decreases its elementary step size as it recruits stators. This in turn implied a motor with a high duty ratio, in which each stator acts with the N – 1 others to rotate a fixed distance d (29).

In our model, this holds in the high-load regime, where these measurements were made. Though stators disengage between strokes, the duty ratio of the motor is very high because the time spent within a power stroke is far greater than the pauses between subsequent strokes $\left(DR=T_s/\left(T_m+T_w\right)\approx T_s/T_m\approx 1\right)$ (Fig. 5 b, red circles). Furthermore, the rotor is likely always in contact with at least one stator as the steps of individual stators almost certainly overlap. This accounts for the observed proportional increase in $n_{\text{steps}}$ with the number of active stators (Fig. 5 b, red circles).

Note that stator steps still may overlap at low loads (high speeds), though they are less likely to do so because $T_m$ is shorter than at high loads. Our simulations predict that similar analyses in this regime will detect a sublinear increase in $n_{\text{steps}}$ with stator number (Fig. 5 b, blue squares).

The second argument was posed by Berg, who posited that if the BFM did not have a duty ratio of close to unity, it could not be processive (1). The reasoning behind this is as follows. Consider an experiment where a cell is tethered to a surface by the hook of its flagella and is spun about by the rotation of the motor at its base. The cell body is large in comparison with the flagellar motor, and accordingly the viscous drag on it is much larger than that on the BFM’s rotor. Therefore, if there are no stators to prevent it, the wound tether between the surface and the cell will unwind exponentially: $\theta ={\theta }_0\text{exp}\left(-\alpha t\right)$, where ${\theta }_0$ is the initial twist and α is the torsional spring constant divided by the rotational drag coefficient of the rotor. A simple calculation showed that unless a motor had a duty ratio of very close to unity, this tether would unwind too quickly for the stator units to keep up.

We note that concrete evidence is still lacking that slowly rotating tethered motors do not “lose” steps to the tether connection unwinding. Support for tightly coupled mechanisms came from reports that the number of ions per revolution was directly proportional to motor speed (39). However, it was later shown that a loosely coupled mechanism also produced a linear relationship with the same slope, but nonzero intercept (34). Regardless, our model construction and parameter choice is such that the unwinding of the tether does not overwhelm the stator in our simulations (see Supporting Material) (21). A final resolution may be reached using experiments that measure how the ion flux at stall (zero speed) differs between single- and multistator motors.

At low loads, however, the relative drags of the bead and the rotor are comparable. As we approach the zero-torque limit, the rotor drag may surpass that of the load (18, 20). For example, we estimated the drag coefficient for the low-load measurement in (28) to be ${\zeta }_L\approx 0.005$ pN-nm-s-rad⁻¹, which is lower than ${\zeta }_R\approx 0.02$ pN-nm-s-rad⁻¹ (1). In this case, the bead will move forward as the tether connection unwinds.

More generally, the characteristic timescale of the load’s motion is given by its frictional drag coefficient divided by the spring constant: $t_L={\zeta }_L/\kappa$. A single-stator motor should have a comparably long power stroke. Note that this is not necessary for a multistator motor: steps from different stators may overlap, extending the period during which at least one complex is present.

To illustrate, we consider the second-smallest bead used by Lo et al. (28). Estimating ${\zeta }_L=0.04$ pN-nm-s-rad⁻¹ and choosing a spring constant $\kappa =150$ pN-nm-rad⁻¹ at the lower edge of the measured range (40), the characteristic timescale of the load is $t_L={\zeta }_L/\kappa \approx 0.27$ ms. A single-stator motor with this load rotated at ≈110 Hz (28). Recall that motor speed $\omega \approx \ell /\left(\langle T_m\rangle +\langle T_w\rangle \right)$, where the step size $\ell =\left(1/26\right)$ revolution and $\langle T_w\rangle \approx 0.2$ ms. Then $\langle T_m\rangle \approx \left(1/26\right)/110-2$ e-4 $\approx 0.15$ ms, and the load is able to (at least partially) catch up to the rotor.

Discussion

The dynamics of the BFM across applied loads have been of great interest since a two-regime torque-speed curve was proposed several decades ago. Recent experiments reporting that the number of stators in a motor varies across loads have opened some interesting questions, and reopened several more.

For instance, the zero-torque speed has been assumed to be independent of the number of docked stators based on the results of early resurrection experiments (15, 16, 17). Theoretical models after these results were reported have all been constructed to reproduce this behavior at low loads. However, recent experiments strongly suggest that these experiments were never performed on motors with more than a single stator (13), making revisiting this long-held assumption timely.

We note that ∼25% of the zero-load motors measured in (13) were interpreted to have two, instead of one, stators. However, it was noted by the authors that motors that were interpreted to have two stators likely had flagella that were incompletely sheared, which may have resulted in an increased load for these motors. Furthermore, this result was reached using a relatively small number of data points, making a statistically significant conclusion difficult to reach. The idea that the stator number varies with load is quite new, and further experiments on the low-load behavior of this motor performed with this knowledge are needed for conclusive evidence in any direction.

In opposition to current assumptions, our simulations predict that the zero-torque speed of the BFM increases with stator number. We note that there was an earlier model that predicted that the motor’s speed at low load was not universal (35). However, the mechanism suggested in (35) was a tightly coupled one that predicted that this speed would decrease with an increasing number of stators. Experiments by Lo et al. (28) (shown in Fig. 4 c) seem to support the opposite trend in chimeric motors, as predicted by our model. However, as such peaks have not been observed in wild-type motors, further experiments at low load are required to make any definitive conclusions. As we mentioned previously, tightly coupled mechanisms can be differentiated from ours by an experiment testing the intercept of the relationship between the number of ions per revolution and motor speed (34).

Our prediction arises from our assumption that stators detach from the motor when they pause between steps. This assumption is common to most models in which a conformational change in the stator drives motor rotation. This results in a low duty ratio for motors at low load, where the waiting time between steps is at least on the order of the time spent in a power stroke. Because the power stroke duration is much longer at high loads, the duty ratio in this regime is not affected by this unbound state. In this way, our mechanism is consistent with evidence that processive motors at high load must have a high duty ratio.

It is important to note that we do not propose that there exists no top speed to the motor at low loads: the moving time $T_m$ at zero-torque still takes some, albeit not much, time. The limiting speed of the motor at low loads will occur when the duty ratio of the motor approaches 1 (i.e., when the waiting time between subsequent power strokes $T_w$ no longer significantly decreases with the recruitment of additional stators). Our simulations suggest, however, that this top speed might not be reached by motors with close to the maximum number of observed stators (Fig. 4 c), let alone by single-stator motors.

Recently, Lo et al. presented evidence of increasing zero-torque speed with stator number in chimeric, sodium-driven motors (28). However, this result was not fully explored as the authors focused on understanding single-stator motor dynamics. Further experiments, especially on wild-type motors, would directly test the hypothesis presented here. Although previous experiments have clarified other aspects of low-load motor behavior (41, 42, 43), the explicit characterization of the dependence of the limiting speed on the number of stator units deserves a more-focused study.

The discovery that stator recruitment in the flagellar motor is dynamic and load-dependent forces us to go back and reconsider many things that were considered common knowledge in the field. We certainly do not claim that the current published data on the wild-type H⁺ motor support or validate our model (though there is support in the sodium-driven motor). However, in light of the evidence found in this study, we do claim that further experiments are required to reach any definitive conclusions.

We hope this work has emphasized that even questions long believed to be closed must be periodically critically examined when new information arises. We strongly hope that our proposal of this model will reinvigorate the question of how the flagellar motor’s low-load speed depends on stator number, and, in particular, will provide the momentum for experiments conducted with all the current knowledge taken into account.

Author Contributions

J.A.N., R.M.B., and G.O. designed research; J.A.N. performed research and analyzed data; J.A.N., R.M.B, and G.O. wrote the article.

Editor: Sean Sun