Systems Physiology of the Airways in Health and Obstructive Pulmonary Disease

Abstract

Fresh air entering the mouth and nose is brought to the blood-gas barrier in the lungs by a repetitively branching network of airways. Provided the individual airway branches remain patent, this airway tree achieves an enormous amplification in cross-sectional area from the trachea to the terminal bronchioles. Obstructive lung diseases such as asthma occur when airway patency becomes compromised. Understanding the pathophysiology of these obstructive disease thus begins with a consideration of the factors that determine the calibre of an individual airway, which include the force balance between the inward elastic recoil of the airway wall, the outward tethering forces of its parenchymal attachments, and any additional forces due to contraction of airway smooth muscle. Other factors may also contribute significantly to airway narrowing, such as thickening of the airway wall and accumulation of secretions in the lumen. Airway obstruction becomes particularly severe when these various factors occur in concert. However, the effect of airway abnormalities on lung function cannot be fully understood only in terms of what happens to a single airway because narrowing throughout the airway tree is invariably heterogeneous and interdependent. Obstructive lung pathologies thus manifest as emergent phenomena arising from the way in which the airway tree behaves a system. These emergent phenomena are studied with clinical measurements of lung function made by spirometry, and by mechanical impedance measured with the forced oscillation technique. Anatomically-based computational models are linking these measurements to underlying anatomic structure in systems physiology terms.

Introduction

The pulmonary airways exist to deal with a fundamental problem that developed when the animal kingdom grew to include members significantly larger than single-cell organisms. With increasing size comes a decrease in the ratio of body surface area to volume and a commensurate decrease in the capacity of direct diffusion of oxygen through the body surface to meet metabolic demands. Diffusion through the body surface is insufficient to support life in mammals. Nature’s answer to this problem is the cardiopulmonary system, which has the express purpose of bringing air and blood together in close proximity either side of a gas-permeable barrier that is large enough and thin enough to afford the necessary diffusive fluxes of oxygen and carbon dioxide. The particular job of the pulmonary airways is to bring fresh air to the alveolar side of this barrier through an enormous geometric transformation in cross-sectional area achieved via multiple sequential airway branching. In the human lung this begins at the trachea, with a cross-section comparable to that of a garden hose, and ends after roughly 23 bifurcations in the distal reaches of the lung where the combined alveolar surface area is comparable to that of a tennis court. A branching structure of comparable complexity achieves a corresponding amplification of surface area on the vascular side of the blood-gas barrier.

The pulmonary airway tree is a system of exquisite structural complexity (Figure 1) that functions in the dynamic environment imposed by respiration and ongoing environmental threats. This structure is a crucial determinant of function, and by the same token function is intimately reflective of structure. The systems physiology of the airways is thus embodied in the link between airway structure and function, a link that is both biological and physical. Indeed, airway physiology has long attracted the attention of physicists, engineers and mathematicians because of the opportunities it presents for the interesting application of quantitative methods. Accordingly, our understanding of the systems physiology of the airways is now infused with sophisticated mathematical and computational models that link structure to function. In this review we examine some of these models and explore how they have helped explain the pathophysiology of lung disease.

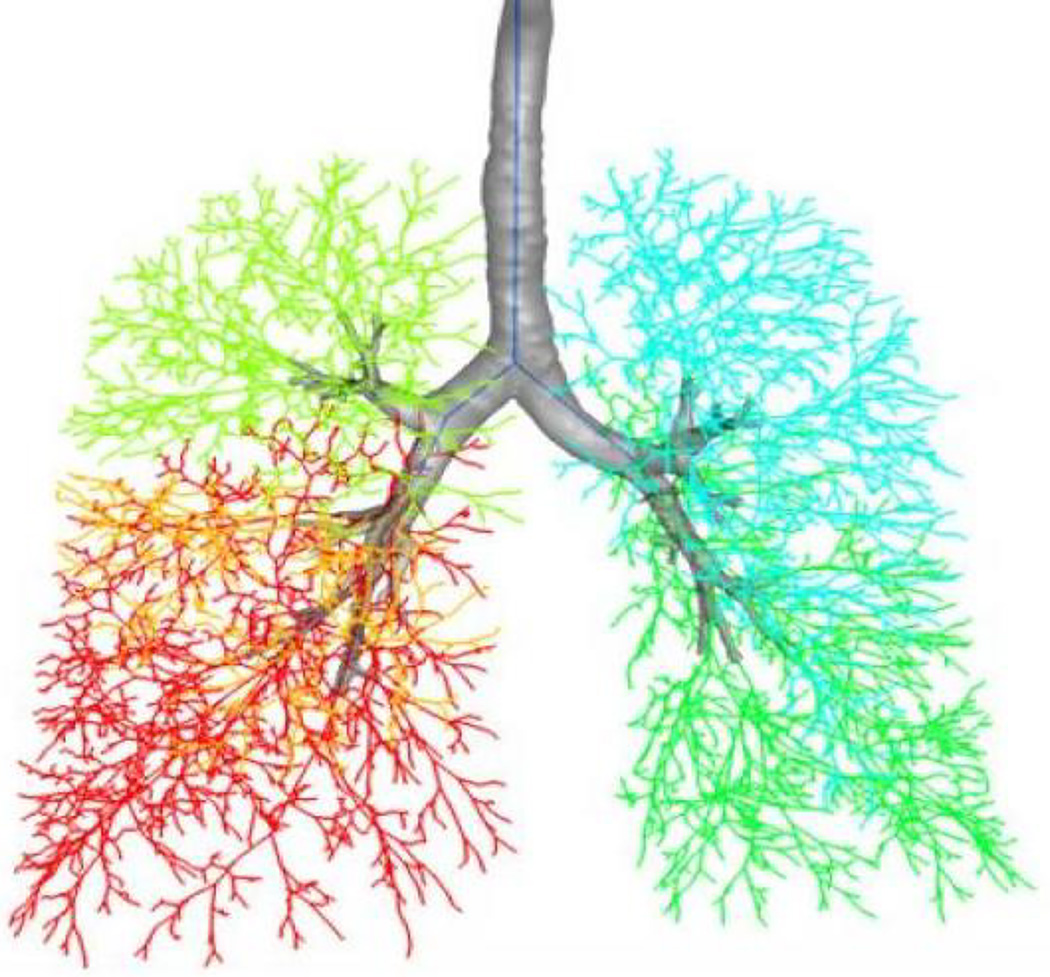
Figure 1.

A space-filling model of the human airway tree created from a 3D computed tomography image from a human subject². The 5 different lung lobes are shown in different colors. (Reproduced with permission of Springer.)

THE BIOPHYSICS OF THE AIRWAY

Airway function

While the tree-like structure of the pulmonary airways is a necessary condition for the lung’s vital function in making mammalian life possible, it also creates conditions that lie at the heart of the most important common lung diseases. The airways must remain patent if air is to flow freely along them at the required rates. Loss of airway patency makes breathing difficult, if not impossible, and is the seminal feature of the obstructive lung diseases exemplified by asthma, bronchitis and emphysema. Also, the conduit function of the airways is not limited to oxygen and carbon dioxide; harmful bacteria and viruses as well as environmental particles and pollutants can easily enter the airways where they threaten the delicate distal structures involved in gas exchange. Elaborate mechanisms have evolved to mitigate against such assaults, but even these defences are sometimes breached. When these defence mechanisms fail to function properly, as in individuals with cystic fibrosis or in habitual smokers, chronic lung infections often result with potentially fatal consequences.

Physics of air flow through the airways

The ability of a branch of the airway tree to transmit gas flow is a function of its dimensions, essentially its length and diameter. Of course, a real airway is not perfectly cylindrical, and its dimensions change continually as a consequence of the physical forces acting on the airway walls and due to secretions that are continually collecting and being cleared from the lumen. These dimensional changes manifest within the timescale of a single breath and are hard to predict precisely from one moment to the next. Attempting to account for the details of airway geometry down to the last detail is generally not worth the time and effort involved for most applications. In some cases, however, it is necessary to know the exact details of flow through the airway tree, such as when trying to understand how inhaled aerosols deposit on the airway walls. In these cases it has proven useful to use computational fluid dynamics to solve for the flow field in anatomically accurate models of the airway tree, which may now be obtained for the larger branches using x-ray tomographic imaging^{9, 10}.

Such details, however, are unnecessary for most applications in which the cylindrical approximation suffices. During quiet breathing, airflow through most branches of the airway tree is laminar and steady so the Poiseuille formula¹¹ provides a useful approximation to the resistance, R, of a branch of length l and radius r:

$$R=\frac{8\mu l}{\pi r^4}$$ (1)

where μ is gas viscosity. The increased flows of during exercise can lead to significant turbulent developing in the proximal airways, but the effect of this on resistance can be approximate quite well by empirical adjustments to the above formula¹². The overall resistance of the entire airway tree can then be calculated by adding the resistances of each branch using the standard electrical formula for the addition of parallel and serial resistors, as the case may be¹¹.

It is clear from Eq. 1 that the most potent geometric determinant of R is r, so a measurement of the resistance of the airway tree, which is a reflection of function, provides a direct link to the caliber of the airways, which is a reflection of structure. Indeed, the most potent determinant of air function is the caliber of the lumen, so obstructive lung diseases in which the lumen becomes compromised constitute one of the most important classes of pulmonary pathology. Accordingly, it is of central importance to understand the factors that determine airway caliber.

Airway wall stiffness

Airway caliber is largely a result of a balance between the forces that tend to collapse the airway and those that tend to keep it open. Of these, there are two important passive components, the elastic recoil of the airway wall itself and the outward tethering forces exerted on the wall by the parenchymal tissue in which it is embedded. To a first approximation the airway wall can be viewed in cross section as a thin ring of elastic material that has an equilibrium radius above which it tends to recoil inward and below which it springs outward. This allows the transmural pressure, P_tm, across the airway wall to be related to its elastic hoop stress, F_el, by the Laplace relationship¹¹

$$P_{\mathit{\text{tm}}}=\frac{F_{\mathit{\text{el}}}}{2r}$$ (2)

Of course, the airway wall actually has a finite thickness so it is possible for the outer reaches of the wall to be in extension while the inner portions are in compression¹³, which has potentially important implications for differential mechanotransduction of cells at different radial positions, but finite element modeling suggests that the average hoop stress approximates an equivalent thin-walled approximation¹⁴.

The pressure-area relationship of the airway wall in cross section defines how its F_el varies with r. This relationship is almost certainly dependent on the airway generation; the large proximal airways with their cartilaginous components are substantially stiffer than the much smaller and more delicate peripheral airways, so many modelers have used the generation-specific pressure-area relationships proposed by Lambert et al.¹⁵. These relationships nevertheless remain somewhat speculative due to the difficulty of measuring them in situ, especially for the smaller airways. Equally speculative is the role that remodeling plays in altering airway stiffness¹⁶. A simpler expression proposed by Thorpe and Bates¹⁷ is obtained if one assumes that a fraction k of the airway wall is completely rigid while the remainder has the same stiffness as the parenchyma.

It seems reasonable to suppose that an inflamed and thickened airway might be stiffer than normal, while an airway subjected to the ravages of proteases might be less stiff. Some contrived experimental preparations have provided evidence of this¹⁸, but the matter remains controversial¹⁶ and allergic inflammation in mice showed no evidence of a change in wall stiffness¹⁹. Regardless, modeling studies have also clearly shown that the normal stiffness of the airway wall plays an important role in the balance of forces that determine airway caliber^{4, 20}.

Airway-parenchymal interdependence

The individual airways of the airway tree, with exception of its most proximal branches, are embedded in the lung parenchyma. The outsides of the walls of these intrapulmonary airways are thus attached to alveolar tissue that is under tension. Indeed, the alveolar attachments to an airway are responsible for transmitting transpulmonary pressure (P_tp) across the airway wall²¹. Accordingly, the parenchyma exerts an outward tethering force on the airways that increases as lung volume (and hence P_tp) increases. Furthermore, the recoil properties of an airway and its surrounding parenchyma are not usually perfectly matched; the airway wall is typically stiffer. This means that the inward pull exerted by an airway on its surrounding parenchyma is greater than would pertain if the airway were simply replaced with parenchyma. The result is that airway radius is less by a fractional amount Δr relative to what it would be if the airway wall behaved exactly like the parenchyma. This causes some degree of local distortion in the parenchyma immediately adjacent to the airway, which gives rise to an additional component to the outward tethering force. When the airways constrict, as for example occurs during an attack of asthma, the local parenchymal distortion and its associated forces around the airway wall increase commensurately. Lai-Fook was the first to investigate this effect in detail²², and showed that, for homogeneous parenchyma, the transmural pressure across an airway wall is approximate by P_tp plus a distortional term proportional to the product of Δr and P_tp. That is,

$$P_{\mathit{\text{tm}}}\propto P_{\mathit{\text{tp}}}(1+\mathrm{\Delta }r)$$ (3)

In other words, the forces due to local parenchymal distortion are proportional to the stress in the tissue (i.e. P_tp). This is a consequence of the shear modulus of lung tissue increasing with P_tp, a phenomenon that has been predicted theoretically²² and shown experimentally²³.

An important feature of the parenchymal distortion around a contracting airway is that it does not propagate far away from the wall - only about as far as the inner parenchymal boundary is pulled in^{22, 24}. This means that the distortional forces produced by an airway can only influence other airways in close proximity, within about 2 airway radii distance²⁵. On the other hand, the tissue distortion caused by narrowing of the entire airway tree has been predicted theoretically to cause an increase in lung elastic recoil²⁶, and has been demonstrated experimentally²⁷.

Dynamic flow limitation

When flow through the airways is modest, one can invoke relatively simple physical principles to link structure to function in a useful way. If flow is laminar, for example, a measurement of resistance can be linked to airway length and diameter via the Poiseuille formula (Eq. 1). Of course, the airway tree is not a single uniform conduit, and flow is not perfectly laminar, steady and full developed everywhere, so the Poiseuille formula merely relates the resistance of the airways to an equivalent ideal conduit. Nevertheless, the functional dependencies of resistance on airway length and diameter still pertain in a general sense, which means, for example, that airway resistance is exquisitely sensitive to the airway radius.

Almost all clinical lung function testing, however, is based on measuring the flow that exits the lungs during a forced expiration, and this reflects a very different set of physical phenomena than those considered above. The concept of airway resistance is based on the notion that flow along the airways will increase in proportion to the pleural pressure generated by the expiratory muscles. However, expiratory flow becomes independent of pressure once pleural pressure exceeds a certain threshold that is readily attained by anyone except young children (below about 5 years of age) and adults who are not physically incapacitated in some way. There are several mechanisms that can give rise to this phenomenon of expiratory flow limitation. For example, since the intra-pulmonary airways are not completely rigid, they will start to collapse if the pressure on their outside walls increases sufficiently. This collapse occurs downstream of so-called equal pressure points in the airways at which lateral air pressure equals pleural pressure²⁸. The location of the equal pressure points is determined by lung elastic recoil pressure, which itself depends on lung volume, and so these points move distally as lung volume falls. Proximal to the equal pressure points, where pleural pressure can cause the airways to narrow, further increases in pressure are cancelled out in their effects on flow by further airway narrowing. Flow limitation has also been ascribed, however, to the finite speed of movement of elastic waves travelling along the airway walls, and equivalently to the progressively reduced lateral pressures caused by the Bernoulli effect acting on compliant airway walls¹¹.

The maximal expiratory flow is thus a function of both airway caliber (via its effects on airflow speed) and airway wall collapsibility. The latter is determined by both the intrinsic properties of the airway wall and the outward force of parenchymal tethering, which itself Is determined by the elastic recoil pressure of the lung, as discussed above. Recoil pressure decreases with decreasing lung volume, which causes maximal expiratory flow to be a decreasing function of volume²⁸. The shape of the expiratory flow-volume curve is thus sensitive to changes in the physical properties of the airways (Figure 2). Unfortunately, it is exceedingly difficult to interpret changes in the maximal expiratory flow-volume relationship in terms of structural changes in the lung, although some sophisticated modeling efforts have been attempted with some success^{15, 29}. This makes spirometry highly sensitive to mechanical abnormalities in the lung, but at the time very non-specific about what these abnormalities might be or where in the airways they are located.

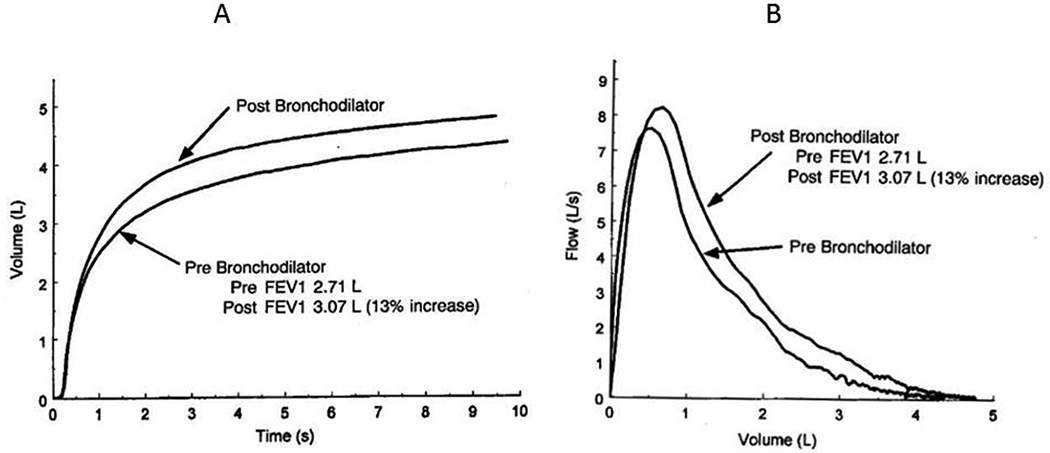
Figure 2.

Examples of clinical data obtained by spirometry¹. A) Volume versus time during a maximal forced expiration show the beneficial effects of a bronchodilator in increasing FVC. B) Expiratory flow-volume curves showing that FEV1 is also increased by a bronchodilator.

Airway smooth muscle

The caliber of an airway is not only determined by the balance of elastic recoil forces exerted by the airway wall and its surrounding parenchyma. In addition, virtually all airways in the human lung are subject to the influence of airway smooth muscle (ASM). In the trachea the ASM is confined to a strip that runs along its anterial aspect, while it is wound around the remainder of the conducting airways. Debate continues as to the evolutionary advantages of ASM³⁰, but there is little doubt about its downside. ASM contraction decreases the airway lumen and is the seminal event behind an asthma attack. Accordingly, the balance of forces that determines airway caliber must include consideration of the active force, F_act, of ASM contraction (Figure 3A), so that Eq. 2 becomes

$$P_{\mathit{\text{tm}}}=\frac{F_{\mathit{\text{el}}}+F_{\mathit{\text{act}}}}{2r}$$ (4)

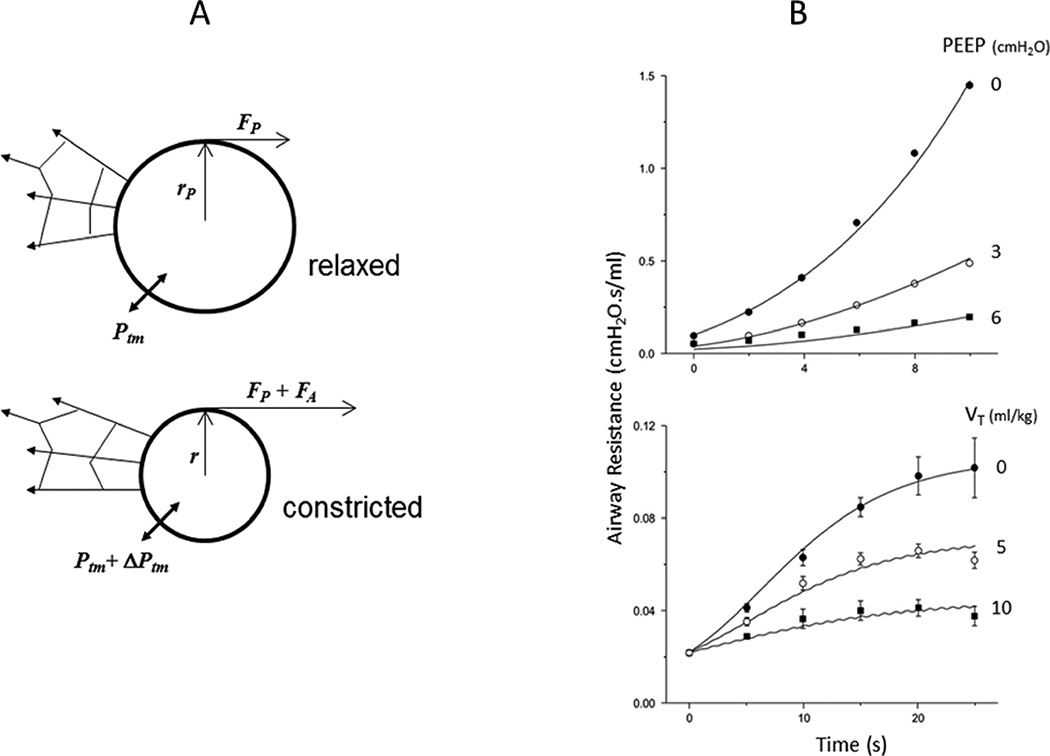
Figure 3.

A) Schematic in cross-section of an elastic airway of passive radius r_p embedded in elastic parenchyma. F_p is the passive hoop stress in the (thin) airway wall⁴. P_tm is the transmural pressure across the airway wall mediated by its parenchymal attachments. B) With the addition of F_A to the hoop stress from active ASM contraction, the airway narrows to a radius r and the transmural pressure increases by ΔP_tm⁴. (Reproduced from with permission from the American Physiological Society.)

Equating this to the value of P_tm determined by the forces of airway-parenchymal interdependence discussed above, and assuming that the compliance of the parenchyma is independent of P_tp, yields an expression for F_act as a function of r. By assuming that F_act is related to ASM contraction velocity via the single-valued hyperbolic Hill equation³¹, Bates and Lauzon⁴ derived an expression for the rate of change of r as function of r and P_tp. They showed that despite having only 4 free parameters this model gives an accurate descriptions of the time course of changes in airway resistance in mice following a bolus injection of the ASM agonist methacholine, including the way this time course is affected by the value of P_tp (Figure 3B).

Nevertheless, numerous in vitro studies have shown that the force-length behavior of activated strips of ASM includes phenomena that the Hill equation cannot account for. Perhaps most significantly, the active force generated in isometrically contracted ASM strips decreases precipitously when the strips are suddenly stretched⁵ (Figure 4A). Similarly, when the strips are length-oscillated about a fixed mean length the peak force is virtually independent of the oscillation amplitude⁸ (Figure 4B). The only reasonable way to account for these observations is that changing the length of the muscle affects the kinetics of cross-bridge cycling. That is, myosin heads become less efficient at attaching to their respective actin binding sites such that the number of heads that are bound at any given time decreases with the rate of length change. This phenomenon is well known in skeletal muscle and is classically explained in terms of the Huxley model³² that explicitly accounts for the dynamics of cross-bridge attachment and detachment as a function of the relative movement of opposing actin and myosin fibers and the degree to which an attached cross-bridge is mechanically stretched. The Huxley model has been adapted to the description of ASM³³ through the inclusion of a 4-state cross-bridge binding scenario³⁴ that accounts for the formation of so-called latch-bridges, a form of slow cycling cross bridge that has been proposed to maintain contractile force at a much reduced energy cost compared to normal cross-bridges. This suggests that ASM force generation in situ should depend on its rate of change of length and its length history imposed by respiratory variations in lung volume. The importance of these effects in vivo remains uncertain, although there is no doubt that stretching ASM in situ by taking a deep breath is an effective way to increase the caliber of constricted airways³⁵.

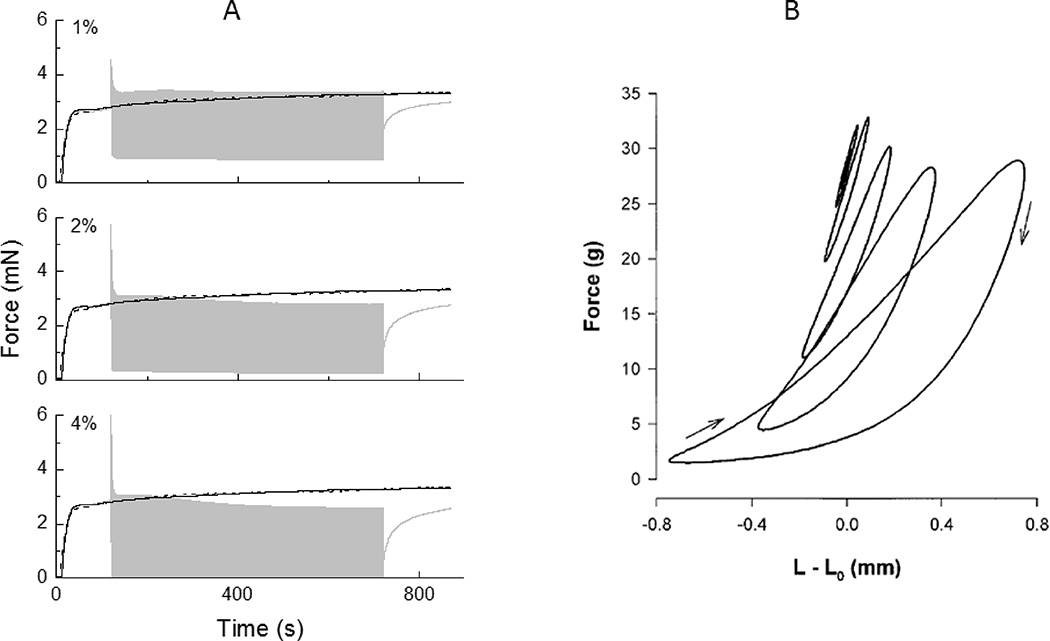
Figure 4.

A) Active force in a strip of ASM produced under isometric conditions (black curve) and when 1%, 2% and 4% length oscillations are imposed beginning at 120 s (gray curve)⁵. Note the immediate and rapid decrement in peak force that occurs when the oscillations commence. (Reproduced with permission of the American Physiological Society.) B) Steady-state force-length loops from activated strips of ASM during length (L) oscillation of various magnitudes about a fixed mean length of L₀⁸. Note that the peak force in each loop is virtually independent of amplitude. (Reprinted with permission of the American Thoracic Society. Copyright © 2016 American Thoracic Society. The American Journal of Respiratory and Critical Care Medicine is an official journal of the American Thoracic Society.)

Sufficiently vigorous stretches applied to a contracted strip of ASM will result in a subsequently impaired ability to generate force that is more profound and longer lasting than can be accounted for in terms of cross-bridge binding kinetics, and which thus appears to be due to some kind of temporary disruption of the contractile machinery within the ASM cell⁵. This has been modeled as reflecting a transient strain-dependent decrement in the total number of cross-bridges available to bind³⁶. There is some evidence of this phenomenon occurring in vivo³⁷ but it requires the imposition of a large increase in lung volume while the ASM is in the process of actively contracting, so its relevance to everyday life remains uncertain.

Another aspect of ASM behavior observed in vivo that is not shared by skeletal muscle is plasticity in its force generating capacity as a function of length^{38, 39}. Skeletal muscle has well defined force-length characteristics that can be understood in terms of the degree of overlap of its actin and myosin filaments. Strips of ASM also exhibit length dependent variations in the maximum active force it can generate, but these variations do not bear a fixed relationship to the length of the strip but rather can adapt to the length that the strip was at prior to being activated. This behavior is presume to reflect the labile nature of the contractile proteins within ASM and their attachments points to the cytoskeleton. Indeed, activation of ASM does not just induce cross-bridge cycling, it also affects the degree of assembly of the contractile filaments themselves^{40, 41}. This gives the ASM cell an ability to adapt is force-generating machinery (Figure 5) to suit the particular configuration in which it finds itself, in contradistinction to skeletal muscle in which the contractile machinery is confined to a very orderly and permanent arrangement.

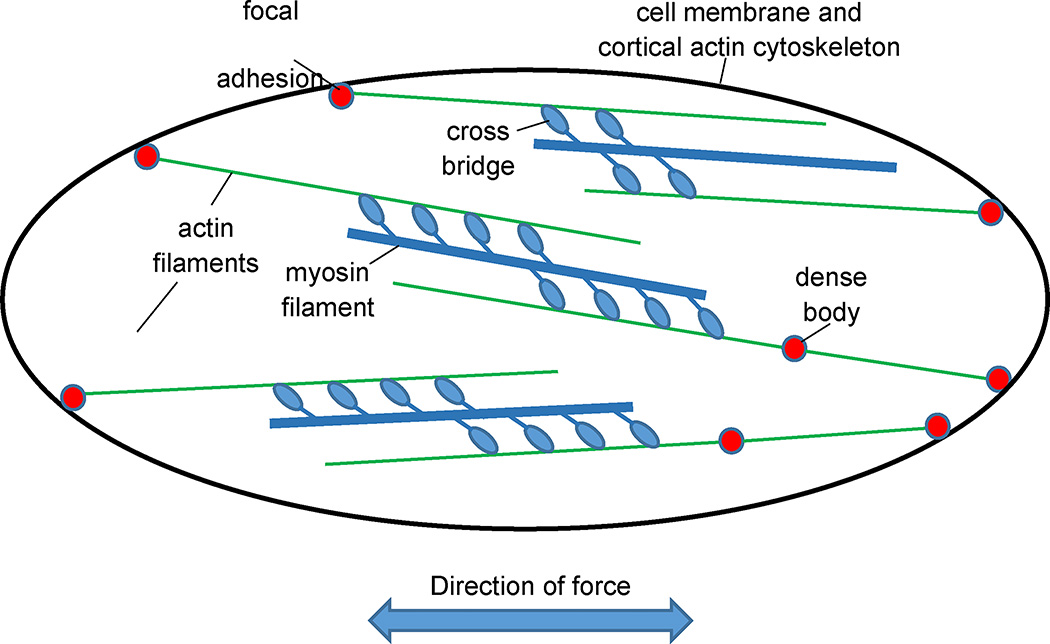
Figure 5.

Schematic of ASM structure depicting a random assembly and intermingling of actin and myosin filaments, the labile connection of actin filaments to the cell cytoskeleton at focal adhesions via dense bodies, and the net direction of force transmission that results from the vector sum of the individual actin-myosin force vectors.

EMERGENT BEHAVIOR OF THE AIRWAY TREE

Lung impedance

So far, we have examined the key factors that determine the caliber of a single branch of the airway tree. However, there are tens of thousands of branches in the human airway tree, all of which have the potential for unique behavior. The overall behavior of the airway tree as a system may thus bear no relationship to the ways in which its individual branches behave. When this happens we say that the overall behavior is emergent.

The overall behavior of the airway tree is reflected in measurements of the mechanical input impedance of the lungs as determined by the so-called forced oscillation technique^{11, 42}. Here, small-amplitude oscillations in flow (V̇) encompassing a range of frequency (f) are applied to the lung via the airway opening (the mouth in a conscious human subject, the tracheal opening in an intubated patient or anesthetized experimental animal model) while the pressure oscillations (P) generated by the flow are measured. Under the assumption that the lung behaviors like a linear dynamic system, V̇ and P then determine impedance in the frequency domain according to

$$Z(f)=\frac{P(f)}{\dot{V}(f)}=R(f)+iX(f)$$ (5)

where the argument f indicates the Fourier transform of the corresponding function of time, and i is the positive square root of −1. Z(f) is a complex function of f, meaning that is has both a real part, R(f), and an imaginary part, X(f).

Mathematical and computational models of impedance

The physiological interpretation of the quantities in Eq. 5 rests of the invocation of a particular model of lung mechanical function. At the simplest level we can imagine the lung as behaving like an elastic compartment (representing the alveolar parenchyma) attached to the end of a single flow-resistive conduit (representing the airway tree). The impedance of this model is^{11, 42}

$$Z(f)=R_{\mathit{\text{aw}}}-\frac{i{E}_{\mathit{\text{tis}}}}{2\pi f}$$ (6)

where R_aw is the resistance of the airway conduit and E_tis is the elastic constant (elastance) of the parenchymal tissue. Because of this simple formula the real part of lung impedance is always called resistance even if the observed behavior is obviously more complicated than that of the single-compartment model. The imaginary part of impedance is called reactance.

Understanding emergent behavior in the airway tree develops from an investigation of how Z(f) behaves as a function of f in more complicated models of the lung. An obvious extension of the single-compartment model, for example, is a model of two compartments to represent in the simples possible terms the fact that the lung exhibits regional variations in its mechanical properties. The two compartment can be arranged in parallel to represent the possibility that the airways leading to different lung regions have different calibers or that the tissue served by these airways have different elastic properties⁴³. Alternatively, the two compartments can be arranged in series where the proximal compartment represents the fact that the airways are not infinitely stiff but in fact can be distended to some degree⁴⁴. Both these models predict that R_aw decreases monotonically as f rather than being constant as predicted by the single-compartment model (Eq. 7). At the same time they predict that E_tis increases with f. Another physiologically plausible model that makes the same predictions is a single airway serving a compartment that is viscoelastic⁴⁵, meaning it exhibits both resistive and elastic characteristics instead of being purely elastic. Determining which of these models best represents a particular lung cannot, in fact, be done purely on the basis of Z(f) alone, but rather requires additional experimental data from measurement sites other than that at which Z(f) is determined (i.e., other than the airway opening). Measurements with the alveolar capsule technique for measuring alveolar pressure directly, for example, have shown that the viscoelastic model is most appropriate for normal dog lungs⁴⁶.

The frequency dependence of resistance and elastance and its interpretation in terms of these candidate two-compartment models became a topic of interest decades ago^43–45, and set the scene for modeling studies that continue to this day and that involve much more anatomically detailed and accurate models of lung mechanics that must be implemented computationally. For example, using standard formula for the addition of impedances in parallel and series, it is possible to calculate the impedance of an entire lung starting with the individual impedances of each branch of the airway tree together with the impedances of the terminal tissue units. Models of this nature can serve as virtual laboratories for numerical experimentation, the results of which can be compared to the results of actual laboratory experiments. This can be invaluable for testing the plausibility of hypothesis about what may have occurred in the real lung to produce the observed impedance data. For example, asthmatic subjects have been classified into two groups based on the nature of their impedance spectra⁶, and forward modeling has led to the conclusion that bronchoconstriction in one group is characterized by narrowing of distal airways that causes shunting of the applied flow oscillations into the central airways while the other responds with a more uniform constriction of both proximal and distal airways^{6, 47} (Figure 6). Anatomically-based forward modelling has also allowed the identification of plausible scenarios of airway narrowing that can potentially account for changes in impedance that have been measured experimentally in human asthmatics⁴⁸.

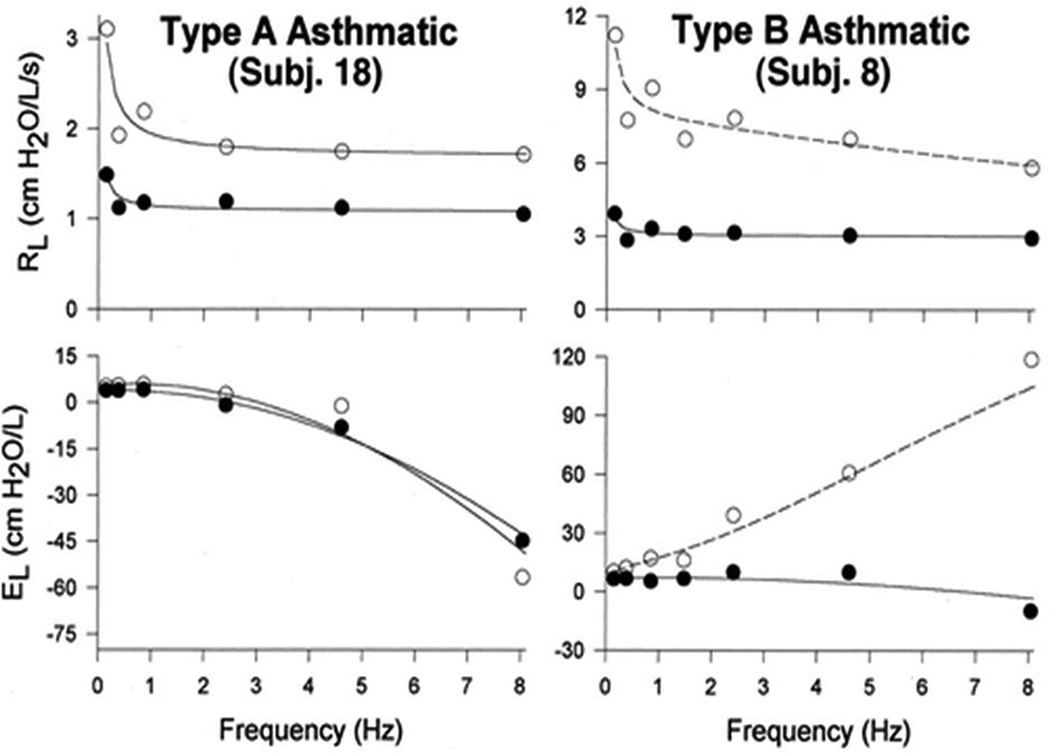
Figure 6.

Example lung impedance spectra from a Type A asthmatic (left) and a Type B asthmatic (right)⁶. Both types of asthmatics have elevated lung resistance (R_L) at all frequencies (open circles) that is reduced by the bronchodilator albuterol (closed circles). Bronchodilation has little effect on, lung elastance (E_L) in Type A asthmatics, but in Type B asthmatics there is a substantial change indicative of a reduction in the amount of central airway shunting. That is, prior to albuterol the distal airways are significantly constricted so that the oscillations in flow that are applied to the lung to measure impedance become progressively more confined to the central airways as oscillation frequency increases. The albuterol relieves the distal airway constriction so that the flow can move past them and into the alveolar regions of the lung. The result is a major reduction in the apparent stiffness of the system as a whole. (Reprinted with permission of the American Thoracic Society. Copyright © 2016 American Thoracic Society. The American Journal of Respiratory and Critical Care Medicine is an official journal of the American Thoracic Society.)

Self-organizing patterns of airway constriction

Heterogeneous patterns of bronchoconstriction throughout the lung do not have to be independent events that occur for reasons related only to local conditions. There is evidence that these patterns can self-organize over characteristic length scales as a result of interactions between different regions mediated by the airways feeding them⁷. This gives rise to emergent behavior that depends in a fundamental way on the branching structure of the airway tree, and that thus determines overall lung mechanical function⁷ (Figure 7). An interesting aspect of this behaviour is the transient exchange of air between alveolar regions that find themselves at different pressures as a result of topographic differences in mechanical function. This phenomenon, known as pendelluft, was first alluded to more than 50 years ago relative to a highly simplistic two-compartment model of the lung⁴³, but has been recently been placed on a quantitative footing in an anatomically-based branching airway tree model⁴⁹. The existence of regional heterogeneities through the lung as a result of heterogeneous airway narrowing has thus been accepted for a long time. Recently, the highly patchy nature of ventilation in disease has been dramatically confirmed in magnetic resonance images of hyperpolarized helium gas following its inspiration into the lungs³ (Figure 8).

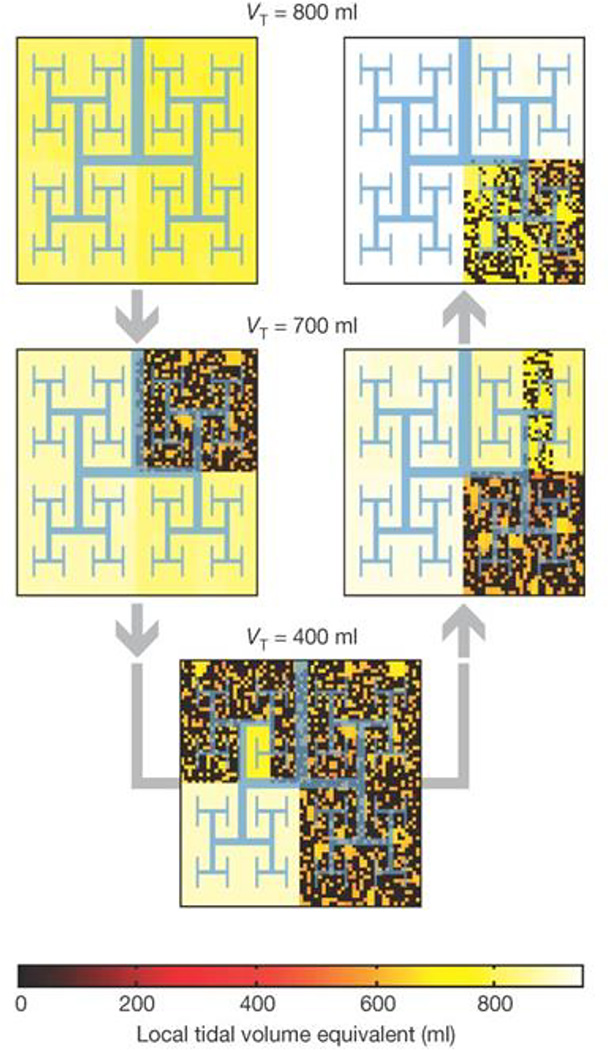
Figure 7.

A fractal model of a bifurcating airway tree that begins being relatively uniformly ventilated (yellow color at top left). As bronchoconstriction proceeds and then dissipates (shown by the direction of the gray arrows) a self-organized pattern of airway narrowing persists. Similar patterns were observed experimentally using positron emission tomography. tomography⁷. (Reprinted by permission from Macmillan Publishers Ltd.)

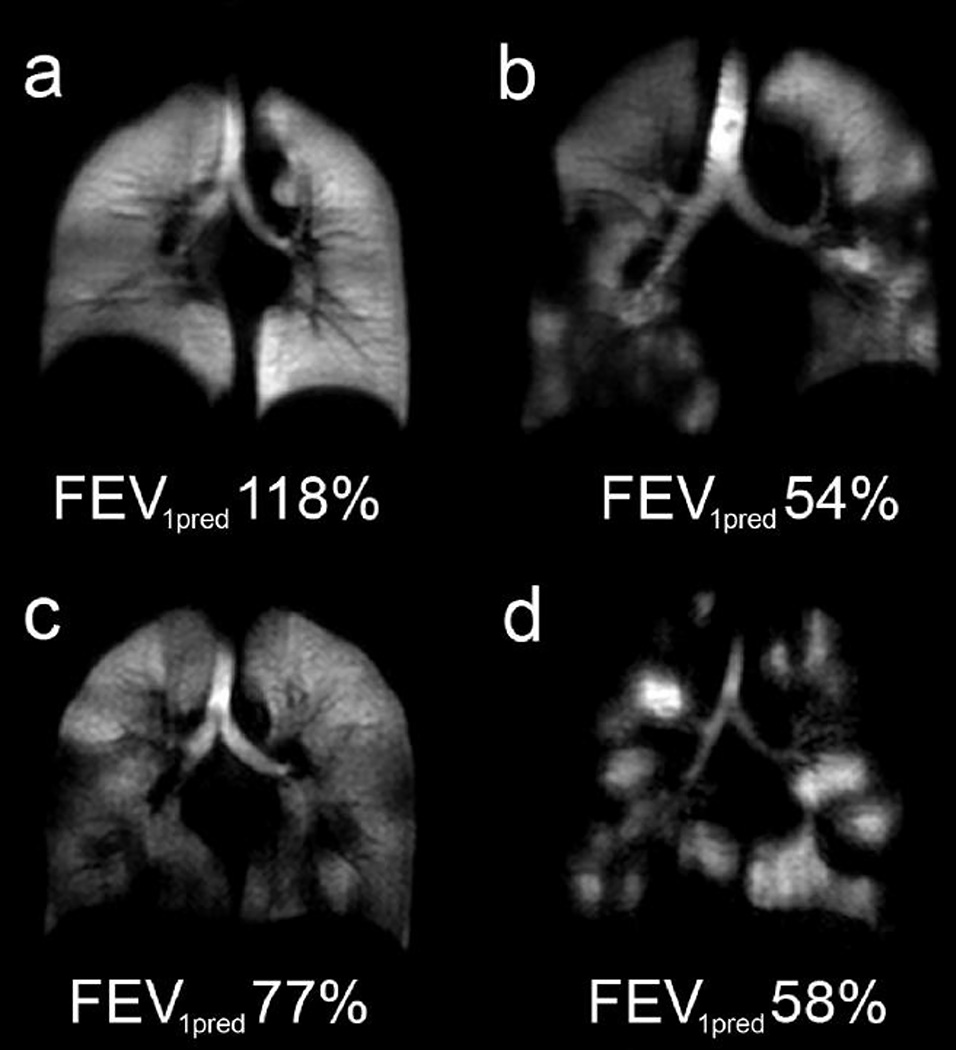
Figure 8.

Coronal slice images of hyperpolarized helium in the lung obtained by magnetic resonance imaging: a) healthy subject, b) subject with chronic obstructive pulmonary disease (COOPD), c) asthmatic subject, and d) subject with cystic fibrosis. The values of FEV1 (percent predicted) are indicated on each panel. (Reprinted by permission from Wiley.)

AIRWAYS HYPERRESPONSIVENESS (AHR)

AHR and asthma

There are a variety of lung diseases that are classed as “obstructive” because they involve an impairment in a patient’s ability to move air along the conducting airways due to narrowing or outright blockage of these passages. The archetypical examples of an obstructive lung disease is asthma, a common and sometimes extremely debilitating condition that is typically experienced as a feeling of chest tightness associated with difficulty breathing. Clinically, asthma is defined as a syndrome inclusive of certain symptomatic features, key among which is an excessive decrement in lung function following airway challenge with standard doses of bronchial agonist¹. The agonist is usually methacholine inhaled as an aerosol, and lung function is invariably assessed by spirometry which involves having the subject exhale as forcibly as possible following a maximal inspiration¹. The diagnostic parameters extracted from this maneuver are the volume of air exhaled in the first (FEV₁) and the total volume exhaled which is known as the forced vital capacity (FVC), both of which are typically depressed in asthmatic subjects.

FEV₁ and FVC are sensitive indicators of abnormalities in lung function, and they can be measured using simple equipment in an outpatient setting. However, FEV₁ in particular is not easily interpreted in mechanistic terms because the physical phenomena that determine it are complex and highly nonlinear. Also, they cannot be measured in individuals unable to perform forced expiratory maneuvers on command, such as very young children and some infirmed adults. For these reasons the measurement of impedance with the forced oscillation technique has been gaining increasing acceptance as a clinical means of assessing lung function^{42, 50, 51}; impedance can be measured without the need for specialized breathing maneuvers, and it can be related, in principle, to lung structure on the basis of physiologically meaningful mathematical models of the lung^{11, 42}.

Long term treatment with inhaled corticosteroids can bring baseline lung function back into the normal range in many asthmatic individuals¹. The widespread success of this form of maintenance therapy leads strong support to the notion that airway inflammation is a central feature of asthma, at least in its most common allergic form¹. Those asthmatics with persistent airway narrowing usually gain relief by inhaling β₂-adrenergic receptor agonists that relax ASM¹, particularly during an asthma attack when symptoms suddenly worsen and such bronchodilator drugs serve as vital rescue therapies.

Biophysical determinants of AHR

When viewed from the perspective of a single airway, the pathophysiology of AHR boils down to a matter of force-balance and geometry. When the ASM that surrounds an airway is stimulated to contract, the extent to which it shortens is critically determined by the forces that oppose it. These forces are comprised of two key components, the outward tethering forces exerted on the parenchyma by its parenchymal attachments²¹ and the stiffness of the airway wall itself^{13, 18, 20}. For a given degree of ASM shortening, however, the degree of narrowing of the actual airway lumen depends both on how the ASM cells are aligned relative to the airway circumference⁵² and on the thickness of the airway wall material lying inside the ASM cells^{53, 54}. Variations in all of these factors has the potential to affect airways responsiveness⁵⁵.

A particularly potent determinant of AHR is airway-parenchymal interdependence because the forces transmitted between the airway wall and its alveolar attachments are so easily and dramatically altered by changes in lung volume^{19, 37, 56}. This is why a deep lung inflation is so effective at reversing established bronchoconstriction, at least in normal subjects³⁵. Similarly, the chronically depressed lung volumes associated with obesity have been postulated as pathogenic for some forms of obese asthma^{57, 58}. However, a physical thickening of the airway wall due to inflammation of the mucosa, as well as accumulation of airways secretions, has been shown the potentially explain AHR entirely in an allergic mouse model of AHR⁵⁴.

The most intuitively obvious potential modulator of airways responsiveness, of course, is the ASM itself⁵⁹. If asthmatic ASM is stronger than normal, or can be activated under conditions in which normal ASM remains quiescent, then AHR would immediately follow. However, although asthmatics have been shown to have increased amounts of ASM in their airways⁶⁰, this could either be a cause of asthma or simply a consequence. Furthermore, the intrinsic contractility of asthmatic ASM does not appear to be any greater than that of normal ASM⁶¹. Accordingly, while there is no doubt that contraction of ASM is the seminal event behind an attack of asthma, it remains very unclear whether or not asthma involves an actual abnormality of the ASM itself⁵⁹, or whether the AHR of asthma is merely normal ASM operating within an abnormal environment⁵⁴.

To complicate matters further, a measurement of AHR can be strongly influenced by how efficiently the challenging agent is delivered to the ASM. A tacit assumption behind all airway challenge testing is that the dose of agonist delivered to a subject is an accurate reflection of the dose which actually reaches its site of action. In fact, increases in the permeability of the barriers presented by both the epithelium for an inhaled aerosol^{62, 63} and the epithelium for an injected agonist¹⁹ can lead to marked increases in the amount of agonist that reaches the ASM, and thus on the airway responsiveness that is measured.

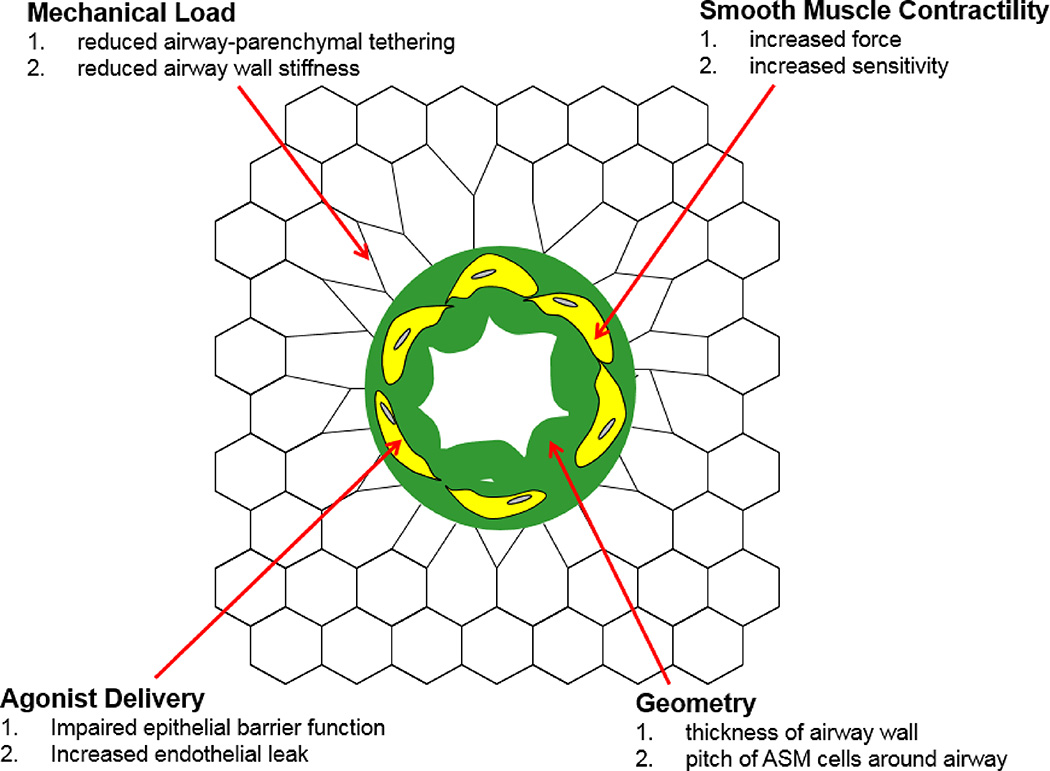
The multi-factorial nature of AHR (Figure 9) makes it a challenging phenomenon to study and understand, yet such understanding is crucial because the various potentially causative factors discussed above have very different therapeutic implications. Also, it is quite likely that different asthmatic individuals have different constellations of factors responsible for their AHR⁶⁴, which would require a personalized approach to therapy. While teasing these factors apart in the animal laboratory may be feasible because of the availability of invasive methods of investigation, methodological limitations make this much more challenging in human subjects.

Figure 9.

Airway narrowing caused by contraction of ASM cells (yellow) that thickens and buckles the airway wall (green) and pulls inward on the attached alveolar walls causing local distortion of the parenchyma (black network). The extent to which the area of the airway lumen (white region) decreases, and hence airway resistance increases, depends on the various factors listed.

Anatomically accurate forward models have been particularly valuable for helping us understanding how AHD can arise from the topographically distributed effects of various mechanisms within. Bronchoconstriction is invariably a heterogeneous process, with some airway narrowing more than others and the parenchymal being differentially affected by secretions. It is impossible to resolve all these details uniquely from measurements of impedance because there are always many physiologically plausible models that can potentially explain a given set of impedance data no matter how accurate the data might be. Consequently, the inverse models that are fit to impedance data must be simple, containing few degrees of freedom and only a handful of adjustable parameters¹¹. Forward models are useful for testing whether, for example, a given degree of airway narrowing at a certain level in the airway tree could possibly account for experimental observations^{6, 48}. It is not possible to prove for certain that an intervention applied to a forward model is what actually transpired in reality because one never knows if some other model manipulation might have produced a similar result. Experiments with forward models thus tend to be most useful when they produce results that are at odds with experiment because then one knows that the forward model is missing something important. This provides an opportunity to learn what might be missing, leading the way to possible confirmation via novel experimental investigation.

Forward modeling has contributed substantially to our understanding of structure-function relationships in the lung in recent years. For example, it has shown that increases in airway secretions and wall thickness, rather than increased ASM shortening⁵⁴, likely explains the AHR seen in allergically inflamed mice, but that in human lungs wall thickening on its own is probably not a potent mechanism for AHR⁶⁵. On the other hand, when wall thickening is combined with increased ASM shortening the result can be a substantial degree of AHR⁶⁶.

The role of animal models

In addition to mathematical and computational models, research into airway disease has relied heavily on the use of another form of model – the animal model of lung disease. Here, some aspect of the pathophysiology of a particular disease is recapitulated in an animal through an appropriate intervention, allowing the resulting phenotype to be investigated via invasive methods that could never ethically be applied in human subjects⁶⁷. The major challenge with animal models, however, is ensuring that they recapitulate the disease in question in a usefully realistic manner, and this is often not the case. Allergic mouse models, for example, have been a mainstay of asthma research, but although they exhibit AHR they actually represent the response of a normal organism reacting to a foreign protein⁶⁸. In fact, the inflammatory response that is elicited in these models is transient because of immunologic tolerance, in contrast to human allergic asthma that can last for years if not a lifetime, so determining how to develop animal models that truly recapitulate the fundamental immunologic abnormalities of allergic asthma remains an ongoing quest⁶⁹. The recent use of complex environmental antigens such as house dust mite⁷⁰ may improve matters in this regard. Mouse models recapitulating features of COPD can be produced by exposure to cigarette smoke for several months⁷¹, but again this is far from the duration experienced by human patients with the disease. The search for improved animal models of lung disease will thus continue to be an important research focus.

Conclusion

Advancing the field of airway systems physiology in health and disease continues to be largely a matter of linking structure to function with every increasing precision in order to identify those factors critical for normal lung function, and to phenotype abnormal function in a patient-specific manner. Computational modelling plays a crucial role in this endeavour because of the highly quantitative manner in which lung function can be assessed. Although different airway diseases tend to be characterized by particular types of abnormality (asthma by airway constriction, COPD by loss of small airways, cystic fibrosis by excessive and abnormal mucus, etc.), there is enormous overlap between them. Furthermore, within a single disease there is often huge phenotypic variability that presumably reflects different constellations of pathophysiologic mechanism, such as in asthma where a major research goal is to determine how to group patients into appropriate sub-classes based on underlying pathophysiology⁶⁴. Hopefully this endeavour will be facilitated through increased use of the forced oscillation method to measure impedance in asthmatic patients, since this is anticipated to provide an increased capacity to link structure to function compared to conventional spirometry⁵¹. This may help, for example, to settle once and for all the question of whether ASM is the key culprit behind some forms of asthma, or whether the AHR observed in patients is the result of essentially normal ASM contracting within an inflamed and mechanically abnormal organ⁷². Also, as medical imaging modalities, particularly x-ray computed tomography, continue to improve in speed and resolution, anatomically-accurate computational models of increasing sophistication will continue to improve our understanding of the link between structure and function in the lung. This will make it increasingly possible to develop personalized therapies based around the anatomic and functional characteristics of individual patients.