Abstract
Background and aims
Low and high endothelial shear stress (ESS) is associated with coronary atherosclerosis progression and high-risk plaque features. Coronary ESS is currently assessed via computational fluid dynamic (CFD) simulation in the lumen geometry determined from invasive imaging such as intravascular ultrasound and optical coherence tomography. This process typically omits side branches of the target vessel in the CFD model as invasive imaging of those vessels is not clinically-indicated. The purpose of this study was to determine the extent to which this simplification affects the determination of those regions of the coronary endothelium subjected to pathologic ESS.
Methods
We determined the diagnostic accuracy of ESS profiling without side branches to detect pathologic ESS in the major coronary arteries of 5 hearts imaged ex vivo with CT angiography. ESS of the three major coronary arteries was calculated both without (test model), and with (reference model) inclusion of all side branches >1.5 mm in diameter, using previously-validated CFD approaches. Diagnostic test characteristics (accuracy, sensitivity, specificity and negative and positive predictive value [NPV/PPV]) with respect to the reference model were assessed for both the entire length as well as only the proximal portion of each major coronary artery, where the majority of high-risk plaques occur.
Results
Using the model without side branches overall accuracy, sensitivity, specificity, NPV and PPV were 83.4%, 54.0%, 96%, 95.9% and 55.1%, respectively to detect low ESS, and 87.0%, 67.7%, 90.7%, 93.7% and 57.5%, respectively to detect high ESS. When considering only the proximal arteries, test characteristics differed for low and high ESS, with low sensitivity (67.7%) and high specificity (90.7%) to detect low ESS, and low sensitivity (44.7%) and high specificity (95.5%) to detect high ESS.
Conclusions
The exclusion of side branches in ESS vascular profiling studies greatly reduces the ability to detect regions of the major coronary arteries subjected to pathologic ESS. Single-conduit models can in general only be used to rule out pathologic ESS.
Keywords: endothelial shear stress, coronary computed tomography, computational fluid dynamics, side branches
Introduction
Atherosclerotic plaque progression is influenced by biological, mechanical and blood rheological factors [1]. Endothelial shear stress (ESS) is a local rheological factor that influences the pathophysiology of coronary plaque formation and progression [2]. Low ESS is an independent predictor of increased plaque burden, plaque progression and luminal narrowing in both animals [3-5] and humans [6, 7]. Conversely, high ESS has been associated with plaque transition to an unstable phenotype [6] and with high risk plaque characteristics [8]. Autopsy [9] and clinical [10] studies have also shown that the majority of high-risk plaques occur in the proximal portions of the major coronary arteries [11-13].
In vivo estimation of ESS requires computational fluid dynamic (CFD) simulation in a three-dimensional (3D) model of the coronary lumen. Most coronary ESS studies have reconstructed the 3D coronary lumen from two or more invasive catheter angiography (ICA) projections to extract the vessel course, and either intravascular ultrasound (IVUS) or optical coherence tomography (OCT) data to extract the lumen contour around this course [14, 15]. The majority of studies thus focus on an individual “target” coronary artery segment where IVUS or OCT are clinically indicated, commonly omitting side branches in that segment [4, 7, 16]. Despite lower spatial resolution, volumetric CT has also been used to model the coronary lumen for ESS calculation [17-22]. With CT angiography, the entirety of the coronary tree lumen, including side branches can be modeled [23].
Inclusion or exclusion of side branches in a CFD model alters the blood flow characteristics (and thus ESS values) calculated. A number of reports have illustrated this in both the left and the right coronary circulation [19, 24], including a recent study that fused OCT of the target coronary segment with a simplified model of the side branches reconstructed from two ICA projections [25]. These studies have either reported a qualitative difference, or an average difference in ESS values between models with and without side branches. The implication of these differences in terms of our ability to detect those regions of the major coronary arteries that are subjected to pathologic (low or high) ESS nonetheless remains unknown.
We systematically assessed the effect of excluding side branches for modeling coronary ESS in the arterial unit (short, e.g., 3 mm-long segments) typically used in clinical studies correlating ESS with plaque progression and characteristics. We report the diagnostic accuracy of ESS vascular profiling when excluding side branches to identify low and high ESS in both the left and right coronary circulation of 5 hearts imaged ex vivo with CT. Given that high-risk plaques tend to occur in the proximal segments of the major coronary arteries, a sub-analysis was additionally performed specifically in those segments.
Materials and methods
Data acquisition
The study was approved by the Institutional Review Board. CTA data was obtained for 5 intact hearts excised from organ donors with coronary artery disease using a standardized clinical coronary CTA protocol. Details on specimen procurement, preparation and imaging have been previously described [26, 27]. Briefly, CTA was performed by filling coronaries with a mixture of low-viscosity methylcellulose (Methocel; DOW Chemical Company, Midland, MI) containing 3% iodinated contrast agent (Isovue 370, Bracco Diagnostics, Princeton, NY) to achieve an intraluminal attenuation of ~250-350 HU, resembling that of in vivo CTA. Each heart was immersed in canola oil and scanned on a 64-detector row CT scanner (GE Discovery CT750 HD; GE Healthcare, Milwaukee, WI, USA). CT scan parameters included 0.625 mm section thickness, 0.39 mm in-plane resolution, 0.35 sec gantry rotation time, 120 kV tube voltage, and 625 mA tube current. Ex vivo imaging was deemed ideal for this study as the lack of motion and surrounding tissues enabled consistent, high-contrast visualization of small side branches using a clinical CT scanner and imaging protocol.
3D reconstruction and computational fluid dynamics
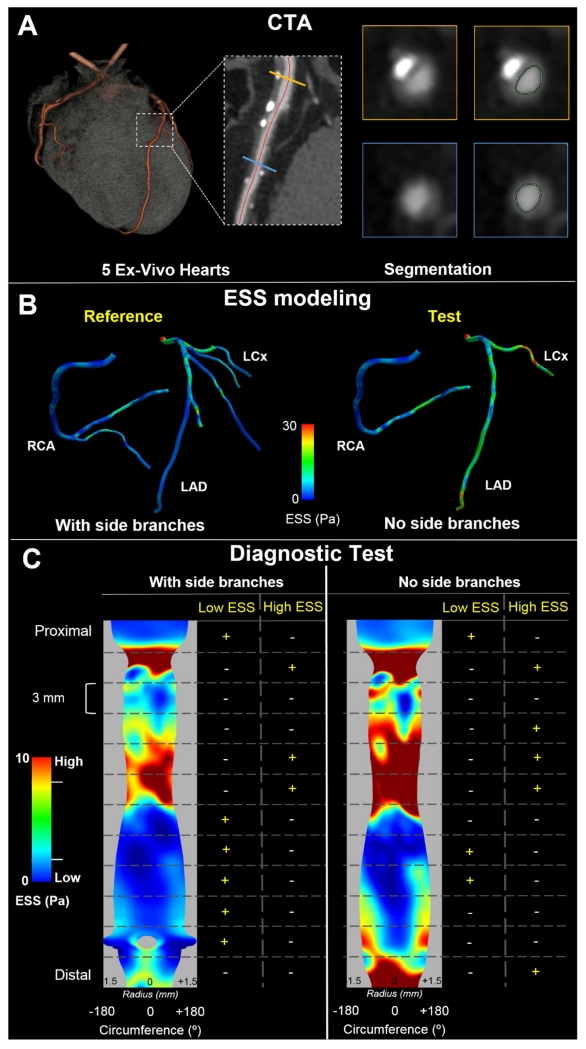
Forty-four coronary branches with >1.5 mm diameter were semi-automatically segmented (Toshiba Cardiac Analysis Package, Toshiba Medical Systems Corporation, Tochigi-ken, Japan) from the 5 hearts (Figure 1A). Two models of the 3D luminal surface of each left and right coronary tree were generated from the segmented cross-sectional lumen profiles; one model included all segmented vessels of each coronary tree (henceforth referred to as the “reference standard model”), and one model excluded all side branches so that only the three major coronary arteries were present in the model (henceforth referred to as the “test model”). The 3D lumen surfaces were converted to a standard tessellation language (STL) model using a purpose-developed algorithm in Matlab (Mathworks, Natick, MA, USA) for CFD calculations.
Fig. 1. Study design and methodology.
(A) 5 ex-vivo hearts were scanned with computed tomography angiography (CTA) and coronary arteries were segmented. First, the arterial centerline was semi-automatically delineated followed by semi-automated segmentation of the axial cross-sections of the lumen (inset shows two representative examples of axial lumen segmentation in the locations marked with the orange and yellow lines, respectively). (B) ESS calculation in the two models used: the entire right and left arterial tree (with side branches >1 mm; reference standard) on the left and omitting side branches (no side branches; test model) on the right. (C) Methodology used to examine the diagnostic test characteristics of the test model to detect regions of pathologic ESS. In a representative example of the mid portion of an RCA, the ESS distribution was reshaped into a 2D map and divided into 3 mm-long sections. For both the reference and the test model, a binary outcome variable was assigned to each 3 mm-long section depending on whether it was categorized as low ESS, and a second binary outcome variable was assigned based on whether it was categorized as high ESS. Branch is denoted as grey void in the reference model.
Unstructured tetrahedral computational meshes of the volumes enclosed by each STL model were generated in ICEM (version 15.0, ANSYS, Canonsburg, PA). The meshes were generated using a 0.2 mm internal element size and 3 prismatic layers with initial layer height of 20 μm and exponential growth factor of 1.2 to capture near wall effects. The internal tetrahedral mesh was subsequently converted to a polyhedral mesh to optimize convergence time. These choices were based on the results of a mesh independence study in one specimen, employing up to 9×106 mesh elements (0.1 mm element size), for which the ESS solution differed by <2% compared to the final parameters used and including the conversion to polyhedral elements.
The incompressible Navier-Stokes equations were solved for steady laminar flow using Fluent (version 15.0, ANSYS, Canonsburg, PA). Blood was considered a non-Newtonian fluid with a constant density of 1058 kg/m3. Effective kinematic viscosity as a function of shear rate was calculated with a power law model with a consistency index k=0.0163 and power-law index η=0.71 obtained from the empirical model developed by Hussain et al. [28] for a hematocrit of 45 %. Total inlet flow rate was calculated based on myocardial mass [29] assuming myocardium rest requirements at a rate of 0.8 ml/min/gram [30] and was applied as a constant (“plug”) inlet velocity profile [24, 31]. Murray’s law [32] was used to determine the relative flow distribution at each coronary bifurcation.
ESS analysis
For each artery, the calculated ESS (Figure 1B) was reshaped into a 2D map with longitudinal arterial location in the x-axis and angle about the arterial centerline on the y-axis. For display, the y-extent of the maps was further shaped by the vessel radius at each longitudinal location, and side branches were depicted as voids (Figure 1C). In keeping with ESS profiling clinical study designs [7, 33], each artery was divided into 3 mm-long sections wherein ESS was averaged. Based on the findings of studies using this design [6, 7, 34], we categorized ESS in each 3-mm section of the reference model as low if it was < 1Pa, and as high if it was > 3 Pa. A binary outcome variable was then assigned to each 3 mm-long section depending on whether it was categorized as low ESS, and a second binary outcome variable was assigned based on whether it was categorized as high ESS (Figure 1C). Since the models without branches involve inherently higher velocities in the major coronary arteries, low and high ESS cutoff values were adjusted to < 1.4 Pa and > 4.8 Pa respectively for the test model in order to maintain the same number of pathologic ESS sections as determined in the reference standard model.
Statistical analyses were performed in GraphPad Prism (GraphPad Software, La Jolla, CA,) and Medcalc (MedCalc Software bvba, Ostend, Belgium). Accuracy, sensitivity, specificity, negative (NPV) and positive predictive value (PPV) of the test model without side branches to detect low and high ESS sections identified by the reference standard were calculated for the three major coronary arteries. The analysis was repeated for only the proximal portions of the arteries, defined as the first 50 mm for the left anterior descending artery (LAD) and for the right coronary artery (RCA) [11] and to the location of the first obtuse marginal origin for the left circumflex artery (LCx) [11, 35].
Results
The average arterial length analyzed was 138.7±27.1 mm for the LAD (range: 108.4-171.1 mm), 72.6±16.3 mm for the LCx (range: 47.9-91.6 mm), and 147.1±42.0 mm for the RCA (range: 101.3-199.6 mm). A total of 606 3 mm-long sections were analyzed in those arteries, of which 210 were in the proximal portions. The mean difference in calculated ESS values within the 3 mm-long sections between the reference and the test model was −2.20±3.52 Pa (range: −34.9 to 1.04 Pa) for the entire arterial length, and −0.68±1.08 Pa (range: −6.31 to 1.01 Pa) for the proximal arteries. Using “point-wise” ESS values, with points defined as the ESS in an patch of endothelium of 0.5° circumferential and 0.25 mm longitudinal length, the mean difference was −2.26±3.94 Pa (range: −56.59 to 8.56 Pa) for the entire arterial length, and −0.79±1.31 Pa (range: −13.83 to 7.96 Pa) for the proximal arteries.
Diagnostic accuracy to identify low ESS
ESS profiling using the test model without side branches had accuracy, sensitivity, specificity, NPV and PPV of 83.4%, 54.0%, 96.0%, 95.9% and 55.1% respectively to detect low ESS regions (Table 1), with 27 of 50 sections that had low ESS, and 534 of 557 sections that did not have low ESS correctly identified. Specificity was high for each coronary individually, being lowest for the LCx (95.3%), while sensitivity ranged from very low (26.7%) to high (100%). Considering only the proximal portions of each artery, accuracy, sensitivity, specificity, NPV and PPV were 87%, 67.7%, 90.7%, 93.7% and 57.5% (Table 2). The test model was able to identify 23 of 34 sections with low ESS, and 165 of 176 sections without low ESS. Specificity per vessel was somewhat lower compared to that for the full arterial length but remained high for each artery, being lowest in the proximal LCx. Sensitivity was slightly increased compared to the full artery results for all three arteries, being lowest in the proximal LAD (39.0%).
Table 1. Diagnostic tests evaluating the test model (without side branches) ESS estimates versus the reference standard (i.e. using the entire coronary tree) ESS estimates.
| Arteries | Low ESS | ||||
|---|---|---|---|---|---|
| Sensitivity (CI) | Specificity (CI) | NPV (CI) | PPV (CI) | Accuracy | |
| All | 54.0 (39.3-68.2) | 96.0 (94.1-97.5) | 95.9 (93.9-97.4) | 55.1 (40.2-69.3) | 83.4 |
| LAD | 26.7 (12.3-45.9) | 96.6 (93.1-98.6) | 90.0 (85.2-93.6) | 53.3 (26.6-78.7) | 87.6 |
| LCx | 94.1 (71.3-99.9) | 95.3 (89.4-98.5) | 99.0 (94.7-99.9) | 76.2 (52.8-91.8) | 95.2 |
| RCA | 100 (29.2-100) | 95.9 (92.6-98.0) | 100 (98.4-100) | 23.1 (5.00-100) | 96.0 |
Test outcomes to detect low ESS regions in the entire length of the coronaries are depicted. All values in percentages [%]; CI: 95% confidence interval, NPV: negative predictive value, PPV: positive predictive value.
Table 2. Diagnostic tests evaluating the test model (without side branches) ESS estimates versus the reference standard (i.e. using the entire coronary tree) ESS estimates.
| Arteries | Low ESS | ||||
|---|---|---|---|---|---|
| Proximal | Sensitivity (CI) | Specificity (CI) | NPV (CI) | PPV (CI) | Accuracy |
| All | 67.7 (49.5-82.6) | 90.7 (85.5-94.5) | 93.7 (89.1-96.8) | 57.5 (40.9-73.0) | 87.0 |
| LAD | 39.0 (17.3-64.3) | 92.5 (83.4-97.5) | 84.9 (74.6-92.2) | 58.3 (27.7-84.8) | 81.2 |
| LCx | 100 (76.8-100) | 84.4 (67.2-94.7) | 100 (87.2-100) | 73.7 (48.8-90.9) | 89.1 |
| RCA | 100 (15.8-100) | 91.6 (83.4-96.5) | 100 (95.3-100) | 22.2 (2.81-60.0) | 91.8 |
Test outcomes to detect low ESS regions in the proximal portions of the coronaries are depicted. All values in percentages [%]; CI: 95% confidence interval, NPV: negative predictive value, PPV: positive predictive value.
Diagnostic accuracy to identify high ESS
Accuracy, sensitivity, specificity, NPV and PPV were 81.2%, 73.9%, 85.9%, 85.7% and 74.3%, respectively to detect high ESS compared to the reference standard model (Table 3), with 336 of 392 sections that did not have high ESS and 159 of 215 sections that had high ESS correctly identified. Similarly to the test characteristics for low ESS, specificity was high for each coronary individually, being lowest for the LAD (81.8%), and sensitivity again ranged from very low to high (22.2-83.5%). Considering only the proximal arteries, accuracy, sensitivity, specificity, NPV and PPV were 86.6%, 44.7%, 95.5%, 89.0% and 68.0% (Table 4), with the test model correctly identifying 117 of 132 coronary sections that did not have a high ESS but only 15 of 91 sections that had high ESS. Unlike the case for low ESS detection, specificity was increased when considering only the proximal portions of the arteries compared to the full arterial length, being high in all arteries (>89.3%). However, sensitivity was greatly reduced in each vessel, being highest in the proximal RCA (41.7%).
Table 3. Diagnostic tests evaluating the test model (without side branches) ESS estimates versus the reference standard (i.e. using the entire coronary tree) ESS estimates.
| Arteries | High ESS | ||||
|---|---|---|---|---|---|
| Sensitivity (CI) | Specificity (CI) | NPV (CI) | PPV (CI) | Accuracy | |
| All | 73.9 (67.6-79.7) | 85.9 (82.1-89.2) | 85.7 (81.9-89.0) | 74.3 (67.9-80.0) | 81.2 |
| LAD | 83.5 (74.3-90.5) | 81.8 (74.5-87.8) | 88.6 (82.0-93.5) | 74.5 (64.9-82.6) | 82.5 |
| LCx | 22.2 (2.81-60.0) | 85.2 (77.4-91.2) | 93.3 (86.8-97.3) | 10.5 (1.30-33.1) | 80.7 |
| RCA | 70.4 (61.2-78.6) | 91.0 (84.8-95.3) | 78.1 (70.7-84.3) | 87.1 (78.6-93.2) | 81.5 |
Test outcomes to detect high ESS regions in the entire length of the coronaries are depicted. All values in percentages [%]; CI: 95% confidence interval, NPV: negative predictive value, PPV: positive predictive value.
Table 4. Diagnostic tests evaluating the test model (without side branches) ESS estimates versus the reference standard (i.e. using the entire coronary tree) ESS estimates.
| Arteries | High ESS | ||||
|---|---|---|---|---|---|
| Proximal | Sensitivity (CI) | Specificity (CI) | NPV (CI) | PPV (CI) | Accuracy |
| All | 44.7 (28.6-61.7) | 95.5 (91.4-98.0) | 89.0 (83.7-93.1) | 68.0 (46.5-85.1) | 86.6 |
| LAD | 30.0 (6.7-65.3) | 89.3 (80.1-95.3) | 90.5 (81.5-96.1) | 27.3 ( 6.0-61.0) | 82.4 |
| LCx | 0 (0-84.2) | 97.7 (88.0-100) | 95.6 (84.9-99.5) | 0 (0-97.5) | 93.5 |
| RCA | 53.9 (33.4-73.4) | 100 (94.0-100) | 83.1 (72.3-91.0) | 100 (76.8-91.0) | 85.9 |
Test outcomes to detect high ESS regions in the proximal portions of the coronaries are depicted. All values in percentages [%]; CI: 95% confidence interval, NPV: negative predictive value, PPV: positive predictive value.
Discussion
ESS has been implicated in atherosclerosis development and progression [6] and is correlated with high risk plaque characteristics [8]. Key to its estimation is the coronary artery lumen 3D model. Using previously validated ESS methods [20, 21, 36] and high-resolution, motion-free CTA images of intact human hearts scanned ex vivo we were able to meticulously characterize the effect of coronary tree models with versus without side branches to identify coronary regions subjected to pathologic ESS. Our results highlight the strengths and pitfalls of using a simplified arterial model that is often necessitated in clinical studies of ESS [7, 16, 31, 37]. Specifically, a simplified model excluding side branches, as has been universally adopted in clinical trials of ESS, has low positive predictive value to identify pathologic ESS regions but may be useful to exclude them.
Accurate generation of the entire 3D coronary tree lumen required to compute ESS from ICA, the modality most-often used to reconstruct the coronary lumen geometry for ESS calculation, is difficult because projections from different angles would be required for each coronary branch that is to be reconstructed depending on its particular 3D orientation. Radiation and contrast concerns thus render this approach impractical in a clinical setting. A number of research studies have sought to assess the effect of this simplification. The largest study to date by Li et al. compared ESS in “target” segments of the major coronary arteries calculated with versus without side branches. In that study geometrically simplified branches were reconstructed to the extent possible using the two angiographic projections selected to optimally visualize the major coronary artery [25]. ESS was overall lower by 4.64 Pa when including the side branches, with the difference ranging from −60.71 to 7.47 Pa. The present study confirms this result and further extends it by determining the extent to which such “point-wise” differences affect diagnostic accuracy to detect those segments of the major coronary arteries that are subjected to low and high ESS in the 3 mm-long arterial unit used to interpret ESS in clinical studies.
The effects on the diagnostic performance to detect low and high pathologic ESS values when excluding side branches are significant in this unit and should be recognized in the interpretation of ESS vascular profiling studies. Over the entire length of the major coronary arteries, exclusion of side branches leads to low PPV to detect those endothelial regions subjected to either low or high ESS. This suggests that the single conduit model is insufficient for studies that aim to compare plaque progression with pathologic ESS. The simplified model does however have high NPV, suggesting that it could in theory be used to exclude arterial segments at risk of ESS-modulated plaque progression, a trait that could be useful for clinical management algorithms. This result remains relevant even when considering only the proximal portions of the arteries, where omission of side branches in ESS calculation provides similarly high NPV (and similarly low PPV) compared to the entire arterial length.
In contrast to ICA-based techniques to estimate coronary ESS, most advanced visualization software tools for CT interpretation include the ability to extract a 3D representation of the entire coronary tree. CTA has inherently lower spatial resolution than invasive imaging. A further limitation of coronary CTA is motion artifact, as the heart is imaged in mid-diastole over 80-250 ms using modern CT hardware, although this was not an issue in our ex vivo study. In this study, despite the lower resolution, CTA data enabled us to fully delineate the 3D lumen geometry of the major arteries and any side branches in order to accurately and thoroughly evaluate ESS profiling differences in models with versus without side branches. Nonetheless, given new technologies being developed by CT manufacturers, including coronary motion correction [38] and low-radiation dose iterative image reconstruction algorithms [39] that can potentially facilitate higher resolution imaging, the CTA-based technique used here may become an attractive technique for non-invasive in vivo ESS vascular profiling in the future.
There are certain limitations that should be considered when interpreting our results. First, we used a steady state rather than a pulsatile flow simulation, although prior studies report little difference compared to the time-averaged ESS that is analyzed in pulsatile simulations [24]. Furthermore, we used estimated values for the total resting coronary flow in keeping with current CFD-based clinical algorithms[29]. This is a typical assumption even for in vivo studies however, as coronary flow measurements e.g., by Doppler sonography are not usually available [31]. Regarding the accuracy of the reconstructed coronary geometry, beyond the relatively lower resolution of CTA compared to invasive imaging, we acknowledge that the ex vivo pressures generated through the process of filling the coronary arteries with the contrast mixture was not monitored and could have led to alteration of the lumen geometry compared to that in vivo. Nonetheless, this would have largely equally affected both the reference standard and test models, and thus the findings of the comparison are unlikely to differ under more accurate physiologic conditions.
In conclusion, there is mounting evidence that the identification of pathologic ESS may provide prognostic information regarding coronary atherosclerotic plaque progression and high-risk plaque formation. Clinical research and potential future application in patient management will necessarily be based on identification of regions of pathologic ESS as opposed to point-by-point ESS interpretation. The effect of exclusion of side branches must be carefully considered when interpreting studies that correlate pathology with the presence of endothelial regions subjected to pathologic ESS. In general, models without side branches can only be used to rule out low ESS.
Highlights.
Coronary CTA enables evaluation of ESS with or without including side branches of the major coronary arteries.
ESS calculated omitting side branches has good negative predictive value for pathologic ESS over the entirety of the major coronary arteries.
In the proximal coronary arteries, where the majority of high-risk plaques tend to occur, single conduit models can be used to rule out pathologic ESS.
Acknowledgments
Financial support
Dr. Mitsouras receives grant support from the National Institutes of Health, National Institute of Biomedical Imaging and Bioengineering grant number K01-EB015868, Toshiba America Medical Systems, and Vital Images, A Toshiba Medical Systems Group Company. Drs Chatzizisis and Antoniadis received support from the Behrakis Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest
The authors declared they do not have anything to disclose regarding conflict of interest with respect to this manuscript.
References
- 1.Kwak BR, et al. Biomechanical factors in atherosclerosis: mechanisms and clinical implications. European Heart Journal. 2014;35(43):3013–3020. doi: 10.1093/eurheartj/ehu353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chatzizisis YS, et al. Role of endothelial shear stress in the natural history of coronary atherosclerosis and vascular remodeling: molecular, cellular, and vascular behavior. J Am Coll Cardiol. 2007;49(25):2379–93. doi: 10.1016/j.jacc.2007.02.059. [DOI] [PubMed] [Google Scholar]
- 3.Chatzizisis YS, et al. Augmented expression and activity of extracellular matrix-degrading enzymes in regions of low endothelial shear stress colocalize with coronary atheromata with thin fibrous caps in pigs. Circulation. 2011;123(6):621–30. doi: 10.1161/CIRCULATIONAHA.110.970038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chatzizisis YS, et al. Prediction of the localization of high-risk coronary atherosclerotic plaques on the basis of low endothelial shear stress: an intravascular ultrasound and histopathology natural history study. Circulation. 2008;117(8):993–1002. doi: 10.1161/CIRCULATIONAHA.107.695254. [DOI] [PubMed] [Google Scholar]
- 5.Koskinas KC, et al. Thin-capped atheromata with reduced collagen content in pigs develop in coronary arterial regions exposed to persistently low endothelial shear stress. Arterioscler Thromb Vasc Biol. 2013;33(7):1494–504. doi: 10.1161/ATVBAHA.112.300827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Samady H, et al. Coronary Artery Wall Shear Stress Is Associated With Progression and Transformation of Atherosclerotic Plaque and Arterial Remodeling in Patients With Coronary Artery Disease. Circulation. 2011;124(7):779–788. doi: 10.1161/CIRCULATIONAHA.111.021824. [DOI] [PubMed] [Google Scholar]
- 7.Stone PH, et al. Prediction of progression of coronary artery disease and clinical outcomes using vascular profiling of endothelial shear stress and arterial plaque characteristics: the PREDICTION Study. Circulation. 2012;126(2):172–81. doi: 10.1161/CIRCULATIONAHA.112.096438. [DOI] [PubMed] [Google Scholar]
- 8.Wentzel JJ, et al. In vivo assessment of the relationship between shear stress and necrotic core in early and advanced coronary artery disease. EuroIntervention. 2013;9(8):989–995. doi: 10.4244/EIJV9I8A165. [DOI] [PubMed] [Google Scholar]
- 9.Cheruvu PK, et al. Frequency and Distribution of Thin-Cap Fibroatheroma and Ruptured Plaques in Human Coronary Arteries: A Pathologic Study. Journal of the American College of Cardiology. 2007;50(10):940–949. doi: 10.1016/j.jacc.2007.04.086. [DOI] [PubMed] [Google Scholar]
- 10.Hong MK, et al. The site of plaque rupture in native coronary arteries: a three-vessel intravascular ultrasound analysis. J Am Coll Cardiol. 2005;46(2):261–5. doi: 10.1016/j.jacc.2005.03.067. [DOI] [PubMed] [Google Scholar]
- 11.Kolodgie FD, et al. The thin-cap fibroatheroma: a type of vulnerable plaque: The major precursor lesion to acute coronary syndromes. Current Opinion in Cardiology. 2001;16(5):285–292. doi: 10.1097/00001573-200109000-00006. [DOI] [PubMed] [Google Scholar]
- 12.Virmani R, et al. Pathology of the Vulnerable Plaque. Journal of the American College of Cardiology. 2006;47(8, Supplement):C13–C18. doi: 10.1016/j.jacc.2005.10.065. [DOI] [PubMed] [Google Scholar]
- 13.Yahagi K, et al. Pathophysiology of native coronary, vein graft, and in-stent atherosclerosis. Nat Rev Cardiol. 2016;13(2):79–98. doi: 10.1038/nrcardio.2015.164. [DOI] [PubMed] [Google Scholar]
- 14.Toutouzas K, et al. Accurate and reproducible reconstruction of coronary arteries and endothelial shear stress calculation using 3D OCT: Comparative study to 3D IVUS and 3D QCA. Atherosclerosis. 240(2):510–519. doi: 10.1016/j.atherosclerosis.2015.04.011. [DOI] [PubMed] [Google Scholar]
- 15.Antoniadis AP, et al. Geometrically correct three-dimensional optical coherence tomography: first self-expanding bifurcation stent evaluation. Eur Heart J. 2013;34(34):2715. doi: 10.1093/eurheartj/eht226. [DOI] [PubMed] [Google Scholar]
- 16.Stone PH, et al. Regions of low endothelial shear stress are the sites where coronary plaque progresses and vascular remodelling occurs in humans: an in vivo serial study. Eur Heart J. 2007;28(6):705–10. doi: 10.1093/eurheartj/ehl575. [DOI] [PubMed] [Google Scholar]
- 17.Chaichana T, Sun Z, Jewkes J. Computation of hemodynamics in the left coronary artery with variable angulations. J Biomech. 2011;44(10):1869–78. doi: 10.1016/j.jbiomech.2011.04.033. [DOI] [PubMed] [Google Scholar]
- 18.Chaichana T, Sun Z, Jewkes J. Hemodynamic impacts of various types of stenosis in the left coronary artery bifurcation: a patient-specific analysis. Phys Med. 2013;29(5):447–52. doi: 10.1016/j.ejmp.2013.02.001. [DOI] [PubMed] [Google Scholar]
- 19.Molony DS, et al. An assessment of intra-patient variability on observed relationships between wall shear stress and plaque progression in coronary arteries. Biomed Eng Online. 2015;14(Suppl 1):S2. doi: 10.1186/1475-925X-14-S1-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ramkumar PG, et al. New advances in cardiac computed tomography. Current Opinion in Cardiology. 2009;24(6):596–603. doi: 10.1097/HCO.0b013e3283319b84. [DOI] [PubMed] [Google Scholar]
- 21.Rybicki F, et al. Prediction of coronary artery plaque progression and potential rupture from 320-detector row prospectively ECG-gated single heart beat CT angiography: Lattice Boltzmann evaluation of endothelial shear stress. The International Journal of Cardiovascular Imaging. 2009;25(2):289–299. [Google Scholar]
- 22.Melchionna S, et al. Endothelial shear stress from large-scale blood flow simulations. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 2011;369(1944):2354–2361. doi: 10.1098/rsta.2011.0042. [DOI] [PubMed] [Google Scholar]
- 23.Gijsen FJ, et al. 3D reconstruction techniques of human coronary bifurcations for shear stress computations. J Biomech. 2014;47(1):39–43. doi: 10.1016/j.jbiomech.2013.10.021. [DOI] [PubMed] [Google Scholar]
- 24.Wellnhofer E, et al. Flow simulation studies in coronary arteries--impact of side-branches. Atherosclerosis. 2010;213(2):475–81. doi: 10.1016/j.atherosclerosis.2010.09.007. [DOI] [PubMed] [Google Scholar]
- 25.Li Y, et al. Impact of Side Branch Modeling on Computation of Endothelial Shear Stress in Coronary Artery Disease: Coronary Tree Reconstruction by Fusion of 3D Angiography and OCT. Journal of the American College of Cardiology. 2015;66(2):125–135. doi: 10.1016/j.jacc.2015.05.008. [DOI] [PubMed] [Google Scholar]
- 26.Maurovich-Horvat P, et al. Differentiation of Early from Advanced Coronary Atherosclerotic Lesions: Systematic Comparison of CT, Intravascular US, and Optical Frequency Domain Imaging with Histopathologic Examination in ex Vivo Human Hearts. Radiology. 2012;265(2):393–401. doi: 10.1148/radiol.12111891. [DOI] [PubMed] [Google Scholar]
- 27.Schlett CL, et al. How to assess non-calcified plaque in CT angiography: delineation methods affect diagnostic accuracy of low-attenuation plaque by CT for lipid-core plaque in histology. European Heart Journal - Cardiovascular Imaging. 2013;14(11):1099–1105. doi: 10.1093/ehjci/jet030. [DOI] [PubMed] [Google Scholar]
- 28.Hussain M, Kar S, Puniyani R. Relationship between power law coefficients and major blood constituents affecting the whole blood viscosity. Journal of Biosciences. 1999;24(3):329–337. [Google Scholar]
- 29.Taylor CA, Fonte TA, Min JK. Computational Fluid Dynamics Applied to Cardiac Computed Tomography for Noninvasive Quantification of Fractional Flow Reserve: Scientific Basis. Journal of the American College of Cardiology. 2013;61(22):2233–2241. doi: 10.1016/j.jacc.2012.11.083. [DOI] [PubMed] [Google Scholar]
- 30.Canty JM., Jr . Coronary Blood Flow and Myocardial Ischemia. In: Bonow R, et al., editors. Braunwald’s Heart Disease, A Textbook of Cardiovascular Medicine. Elsevier; 2012. pp. 1049–1074. [Google Scholar]
- 31.Eshtehardi P, et al. Association of coronary wall shear stress with atherosclerotic plaque burden, composition, and distribution in patients with coronary artery disease. J Am Heart Assoc. 2012;1(4):e002543. doi: 10.1161/JAHA.112.002543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Murray CD. The Physiological Principle of Minimum Work: I. The Vascular System and the Cost of Blood Volume. Proceedings of the National Academy of Sciences of the United States of America. 1926;12(3):207–214. doi: 10.1073/pnas.12.3.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Vergallo R, et al. Endothelial shear stress and coronary plaque characteristics in humans: combined frequency-domain optical coherence tomography and computational fluid dynamics study. Circ Cardiovasc Imaging. 2014;7(6):905–11. doi: 10.1161/CIRCIMAGING.114.001932. [DOI] [PubMed] [Google Scholar]
- 34.Wentzel JJ, et al. Endothelial shear stress in the evolution of coronary atherosclerotic plaque and vascular remodelling: current understanding and remaining questions. Cardiovasc Res. 2012;96(2):234–43. doi: 10.1093/cvr/cvs217. [DOI] [PubMed] [Google Scholar]
- 35.Burke AP, et al. Healed plaque ruptures and sudden coronary death: evidence that subclinical rupture has a role in plaque progression. Circulation. 2001;103(7):934–40. doi: 10.1161/01.cir.103.7.934. [DOI] [PubMed] [Google Scholar]
- 36.Borkin M, et al. Evaluation of Artery Visualizations for Heart Disease Diagnosis. Visualization and Computer Graphics, IEEE Transactions on. 2011;17(12):2479–2488. doi: 10.1109/TVCG.2011.192. [DOI] [PubMed] [Google Scholar]
- 37.Papafaklis MI, et al. Anatomically correct three-dimensional coronary artery reconstruction using frequency domain optical coherence tomographic and angiographic data: head-to-head comparison with intravascular ultrasound for endothelial shear stress assessment in humans. EuroIntervention: journal of EuroPCR in collaboration with the Working Group on Interventional Cardiology of the European Society of Cardiology. 2014 doi: 10.4244/EIJY14M06_11. [DOI] [PubMed] [Google Scholar]
- 38.Andreini D, et al. Intra-Cycle Motion Correction in Coronary CT Angiography. Current Cardiovascular Imaging Reports. 2014;7(8):1–7. [Google Scholar]
- 39.Leipsic J, et al. Adaptive Statistical Iterative Reconstruction: Assessment of Image Noise and Image Quality in Coronary CT Angiography. American Journal of Roentgenology. 2010;195(3):649–654. doi: 10.2214/AJR.10.4285. [DOI] [PubMed] [Google Scholar]