Chunk Formation in Immediate Memory and How It Relates to Data Compression

Abstract

This paper attempts to evaluate the capacity of immediate memory to cope with new situations in relation to the compressibility of information likely to allow the formation of chunks. We constructed a task in which untrained participants had to immediately recall sequences of stimuli with possible associations between them. Compressibility of information was used to measure the chunkability of each sequence on a single trial. Compressibility refers to the recoding of information in a more compact representation. Although compressibility has almost exclusively been used to study long-term memory, our theory suggests that a compression process relying on redundancies within the structure of the list materials can occur very rapidly in immediate memory. The results indicated a span of about three items when the list had no structure, but increased linearly as structure was added. The amount of information retained in immediate memory was maximal for the most compressible sequences, particularly when information was ordered in a way that facilitated the compression process. We discuss the role of immediate memory in the rapid formation of chunks made up of new associations that did not already exist in long-term memory, and we conclude that immediate memory is the starting place for the reorganization of information.

Individuals have a tendency to make information easier to retain by recoding it into chunks (e.g., Cowan, Chen, & Rouder, 2004). The process of chunking simplifies memorization by taking advantage of knowledge to reduce the quantity of information to be retained (Miller, 1956). As a key learning mechanism, chunking (or grouping) has had considerable impact on the study of expertise (e.g., Chase & Simon, 1973; Ericsson, Chase, & Faloon, 1980; Hu & Ericsson, 2012), immediate recall (e.g., Chen & Cowan, 2005; Farrell, Wise, & Lelièvre, 2011), and memory development (e.g., Cowan et al., 2010; Gilchrist, Cowan, & Naveh-Benjamin, 2009).

For chunking to benefit memory, people need to be able to retrieve the chunks they stored. One way people retrieve chunks is via long-term memory processes (French, Addyman, & Mareschal, 2011; Gobet et al., 2001; Guida, Gobet, Tardieu, & Nicolas, 2012; Reder, Liu, Keinath, & Popov, in press). Consider the letter string IBMCIAFBI. As Miller discussed, this letter string can be easily simplified to form three chunks if one uses long-term memory to recall the U.S. agencies (Miller, 1956) whose acronyms are IBM, CIA, and FBI.

Previous work on chunking has focused on how long-term memory aids chunk creation. However, immediate memory might also play a fundamental role in the creation of chunks. People may form chunks in immediate memory by rapidly encoding patterns before any consolidation in long-term memory occurs. For example, it is easy to remember the letter string AQAQAQ using a simple rule of repetition (e.g., AQ three times). This type of simplification does not necessarily depend on the use of long-term memory to recall past knowledge that relates items to each other². Instead, this process depends on the apprehension of regularities inherent to the stimulus at hand, i.e., compression.

This idea that immediate memory might play a fundamental role in the creation of chunks has generally been overlooked. Some previous findings are consistent with the proposal that chunks can increase memory capacity (Brady, Konkle, & Alvarez, 2009; Feigenson & Halberda, 2008). However, these studies have mostly focused on how long-term-memory representations contribute to encoding in immediate memory. In contrast, our goal is to provide a principled quantitative approach to how immediate memory relates to the formation of chunks. Getting a larger picture of chunking as a process originating in immediate memory needs a precise conceptualization, and the concept of compressibility could help in doing so.

We propose a two-factor theory of the formation of chunks in immediate memory. The first factor is compressibility (i.e., the idea that a more compact representation can be used to recode information in a lossless fashion³). Compressibility could predict chunking because it measures the degree to which the material is patterned, and hence the degree to which the material can be simplified. Memory for compressible sequences should be superior to memory for non-compressible sequences (the same way that studies in the domain of categorization have shown that compressible material is better learned over the long term; see Feldman, 2000).

The second factor is the order of the information to memorize. Presentation order might influence the ease with which patterns or regularities in the stimuli can be discovered, and compression algorithms typically depend on this kind of information. A presentation order that aligns with the process of simplifying the material may increase the likelihood that chunking occurs. In contrast, presentation orders that do not aid in the discovery of regularities, might result in failure to chunk compressible materials, causing them to be remembered in a way similar to non-compressible materials. Presentation order should therefore interact with compressibility. As a simple example, one can compress the set “2, 3, 4, 5, 6” with the rule, “all numbers between 2 and 6”, whereas with the series “2, 4, 6, 3, 5”, that same rule might not be noticed by the participant, so compression might not take place.

This two-factor theory is adapted from the domain of categorization, which has provided a framework for studying category formation in long-term memory, with explanations based on the compressibility of descriptions (Bradmetz & Mathy, 2008; Feldman, 2000, 2003; Goodwin & Johnson-Laird, 2013; Lafond, Lacouture, & Mineau, 2007; Vigo, 2006) using different types of presentation orders (based on rules, similarity, or dissimilarity; see Elio & Anderson, 1981, 1984; Gagné, 1950; Mathy & Feldman, 2009; Medin & Bettger, 1994). This framework nicely accounts for a wide range of categorization performance in long-term memory, but could in principle provide similar predictions for immediate memory. Our theory is that a compression model (e.g., Feldman, 2000) can be adapted to immediate memory. The rationale is that elementary structures, i.e., the redundancies that make a structure compressible, are simple enough to be used rapidly in immediate memory to cope with new situations.

We conducted an experiment to test the proposal outlined above, namely, that chunk formation occurs in immediate memory to optimize capacity before any consolidation process in long-term memory occurs. Our prediction is that immediate-memory span is proportional to stimulus compressibility, but only when the order of the information allows the participant to spontaneously detect redundancies such as pairs of similar features.

In the Discussion, we provide ample evidence that there are two major classes of concurrent models that cannot provide correct predictions for our results. The first class is Interference-based models of short-term memory, which predict poorer performance when participants see sequences containing similar features, whereas our model predicts that participants can take advantage of these similarities to compress information. The second class includes the minimal description length (MDL) approaches to long-term memory, which rely on the repetition of trials, and as such, offer no predictions about the compression process at play in our task.

Method

Two key aspects were investigated in the present experiment: compressibility of a sequence and presentation order within a sequence. These two factors were studied using categorizable multidimensional objects, with discrete features, such as small green spiral, large green spiral, small red square. The sequences used could not conform to already-learned chunks. Although the features themselves are part of basic knowledge, we are reasonably confident, for instance, that none of our participants had the exact sequence of items “a small green spiral followed by a large purple pentagon and a small yellow pentagon” in long-term memory before starting our experiment. The procedure used a serial recall task, which allowed to study the incremental encoding of chunks. The duration of the display of the memory items and the number of memory items were two other manipulated factors we thought would help us look into the incremental encoding of the chunks.

Participants

Sixty-seven students enrolled at the University of Franche-Comt, M = 22 years old (sd = 2.7), volunteered to participate in the experiment.

Stimuli

Our stimuli could vary according to three dimensions: shape, size and color. A combination of two shapes, colors, and sizes makes a set of eight different objects. There were eight different values for the shape dimension and the color dimension (Fig. 1a). However, we restricted the size dimension to two values (large vs. small, or 280 × 280 pixels vs. 140 × 140 pixels). Shape, size and color are typically used by category learning researchers to build canonical stimulus sets because these dimensions can be easily and clearly partitioned.

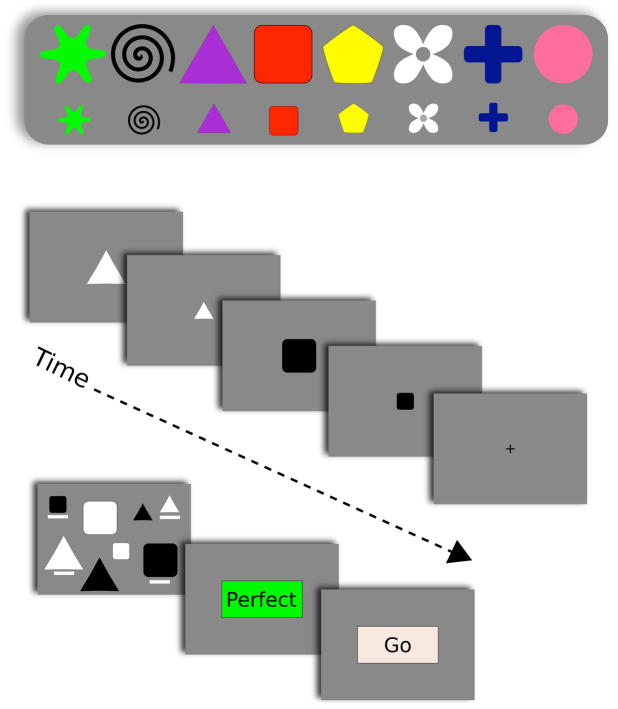
Figure 1.

Screen shots showing a sample of possible stimuli (top panel), a to-be-recalled patterned sequence of stimuli (middle panel), and an example of a response screen that asked the participant to recognize the previous stimuli and to order them by clicking on a mouse (bottom panel).

For a given sequence, the program randomly chose two out of eight shapes and two out of eight colors (see Fig. 1, top panel), in order to create a set of eight objects. For example, if the values “triangle”, “square”, “white”, and “black” were drawn, the program generated 2 × 2 × 2 = 8 stimuli by combining three features for each stimulus (e.g., small white triangle, large white triangle,, large black square). These values allowed for 1568 possible sets of eight objects, so that the probability of a participant coming across two identical sets during the experiment would be very low. The stimuli were presented against a gray background.

Categories

We selected different categories of objects, which were to be displayed and recalled serially. An example is the sequence □ ■ ▫ ▪ ▵ ▴, which can be represented by six individual exemplars (i.e., large white square, large black square, small white square, small black square, small white triangle, and small black triangle). Following Feldman (2000), this sequence can be redescribed accurately by a shorter logical rule provided that order does not matter (‘squares or small’, using inclusive disjunction, or ‘not[large and triangle]’ using conjunction, which by de Morgan’s law are equivalent). Another example is the sequence ▪ ▴ ▫ ▵ (‘small black square, small black triangle, small white square, small white triangle’), which can be simplified by abstracting the feature common to the four objects: “small”. Hence, the information for this category is even more compressible and does not require much mental effort to be retained. The to-be-recalled categories of stimuli were chosen on the basis of the exhaustive list of the 21 categories shown in the Appendix.

Ordering of the categories in the sequences

Our measure of complexity only serves here to predict the chunkability of the category set, not the memorization of the sequence. Controlled presentation orders were thus used to manipulate category compressibility. This second manipulation consisted of ordering the objects according to three main types of orders previously developed in the categorization research: rule, similarity, and dissimilarity.

In the Rule condition (Fig. 2), the objects were grouped by clusters (sub-categories). The differences were minimal within the clusters, but more marked between clusters (whenever clusters could be found). A minimal degree of similarity between clusters contributes to greater discrimination of the clusters into distinguishable units, thus favoring the discovery of a logical rule. Figure 2 shows the example of an organized sequence in the Rule condition. The shortest rule for describing the set of objects is “square or small”. In Figure 2, the first cluster is made up of the large white square (first item) and the large black square (second item), which differ by only one feature. The small white square (third item) that follows the large black square (second item) marks a separation between the first and second clusters because the two contiguous items differ by two features. In the Rule condition, such leap can facilitate the identification of clusters and therefore might induce the formation of chunks based on the clusters (see Fig. 2, bottom, which shows two leaps as a function of time, one after the second item and the other after the fourth item). In this condition, the participants should have the best recall performance, particularly if they attempt to form small groups of objects by compressing information locally⁴.

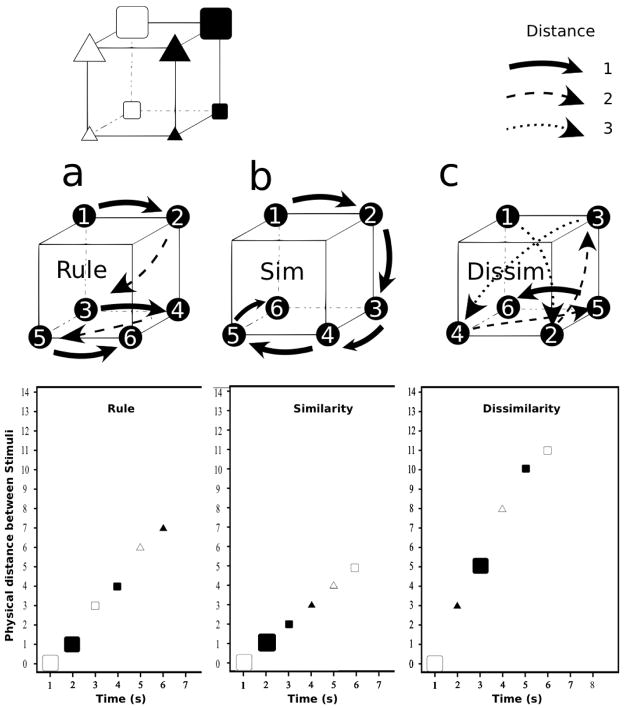
Figure 2.

Example of three sequences from the category structure “square or small”, representing six items (top left cube). Note. The six items are replaced by black numbered circles on each of the three cubes to simulate their sequencing. In each of the three cubes, the presentation order is indicated by the numbers from one to six and by the arrows. The distance between two consecutive objects is described by the type of arrow: solid (one edge, or one feature difference), dashed (two edges), or dotted (three edges). In the Rule condition, the objects are presented in three clusters, within which the solid arrows are parallel and go in the same direction. The regularity of the rule is related to two factors: the separation of the clusters (dashed arrows) and the similarity between the objects in the same cluster (solid arrows), both of which facilitate the formation of small groups. In the Similarity condition, the inter-stimulus distance is minimal. All the objects are linked to each other by solid arrows, which can potentially make a unique chunk of six objects. In the Dissimilarity condition, the sequence is characterized by a maximal inter-stimulus distance. The three plots at the bottom show the distances between the stimuli as a function of presentation time (1 second per item). For instance, the first plot shows two distance leaps in the Rule condition, which can facilitate the identification of three chunks. The leaps are more numerous, larger, and less regular in the Dissimilarity condition, while there are no leaps at all in the Similarity condition.

In the Similarity condition (Fig. 2), a sequence was chosen to favor a minimal overall (i.e., for the entire sequence) inter-stimulus distance. The objects were then presented as a string following the principle that there was maximal similarity between two successively presented objects. Figure 2 shows an example of a similarity order for the same category of objects. Notice that adopting a similarity-based grouping process for this sequence would result in retaining a single long chunk of six items.

Finally, in the Dissimilarity condition (Fig. 2), the set of objects was chosen so as to favor a maximal total inter-stimulus distance. Each object presented minimal similarity with the preceding one. This condition deliberately disorganizes the presentation to make the associations between stimuli more difficult, and should hinder the chunking process. Using a dissimilarity-based strategy would result in retaining several separate small chunks of independent items. Consequently, recall performance should be lower than in the other two conditions. Figure 2 shows an ordered sequence in the dissimilarity condition using the same example as above.

The 21 categories of objects shown in Fig. 5 in the Appendix were transformed into 51 sequences, according to these three presentation orders. The number 51 results from the fact that the order of six categories could not be manipulated. This was the case for four categories made up of one or two objects (once the first object is drawn, only the second object remains), and for two categories, for which the distances are identical between any two objects in a pair (this is the case for the category in the left column of Fig. 5, in which FC (Feldman’s measure of complexity) = 8 and FC = 10)⁵. These six categories were coded “order condition = None”. The Rule, Similarity and Dissimilarity conditions were applied to the 15 remaining categories. Each participant saw all 51 sequences (3 × 15 + 6).

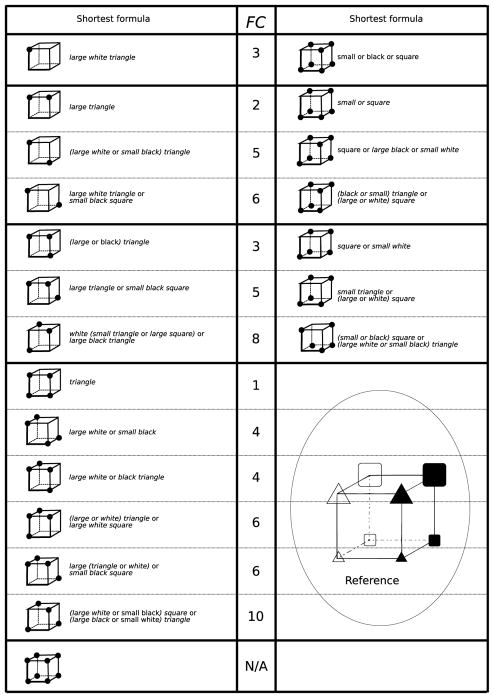
Figure 5.

Feldman’s (2000) minimization of Boolean complexity. Note. Column FC indicates Feldman’s (2000) measure of logical compressibility for each of the categories in the left or right column.

Procedure

For each participant, the 51 sequences were presented in random order to avoid ascending list length or complexity. We established six possible rotations for each category structure that corresponded to six possible ways to place the objects on the diagram while keeping the same structure. One rotation (among the six) was randomly drawn for each sequence presented so as to multiply the possible combinations in dimensional terms (shapes, sizes and colors). Thus, the participant never knew in advance which dimension would be the most relevant for the categorization process. For the experiment as a whole, 3417 sequences/trials (51 × 67 participants) were presented.

Serial report was investigated using a procedure similar to that used in the visual STM serial report task (Avons & Mason, 1999; Smyth, Hay, Hitch, & Horton, 2005), except that the stimuli were mixed with distractors on the response screen. Depending on the sequence, one to eight stimuli were displayed serially in the center of the screen (see Fig. 1, middle panel) at intervals of one second (41 participants) or two seconds (26 participants) per stimulus, depending on the condition⁶. During the recall phase (see Fig. 1, bottom panel), the original set of eight stimuli was displayed randomly on the screen. The stimuli were underlined (using a white line) when the user clicked on them. After the user validated his/her answer with the space bar, a feedback screen indicated if the recall was correct (i.e., both item memory and order memory had to be correct), and then a screen with a GO window appeared and the user moved on to the following sequence by pressing on the space bar. The experiment lasted an average of 25 minutes.

Results

The analyses were conducted on correct (1) or incorrect (0) serial-recall scores for each trial (a response was scored correct when both the items and the positions were correctly recalled), and for the average recall score across conditions (proportion correct). The data was first aggregated for a given variable, e.g., ‘presentation time’, in order to run a separate univariate ANOVA for each dependent variable (e.g., the mean proportion correct for all trials pooled).

Summary of the expected results

(1) Recall performance should depend on sequence length to the extent that longer sequences require a representation with more chunks. (2) A higher compressibility of information (i.e., lower FC within sequences of the same length) should result in better recall because higher compressibility enables better recoding of the entire set of items. (3) A greater degree of regularity in the presentation order (rule-based, followed by similarity-based, followed by dissimilarity-based) should favor the compression of the available regularities into newly formed chunks. (4) For the less important factor, display duration, we expected better recall performance for the longer duration.

Proportion correct

Regarding the 2 s vs. 1 s conditions, a preliminary between-subject analysis on proportion correct (averaged across trials) showed that stimulus duration was significant (t(65) = −2.5, p = .014, η² = .09), with respective means equal to .33 (sd = .11) and .27 (sd = .08). However, because recall was only slightly higher in the 2 s condition, with a rather small size effect, we chose not to keep the 1 s vs. 2 s factor as a moderator in the subsequent analyses.

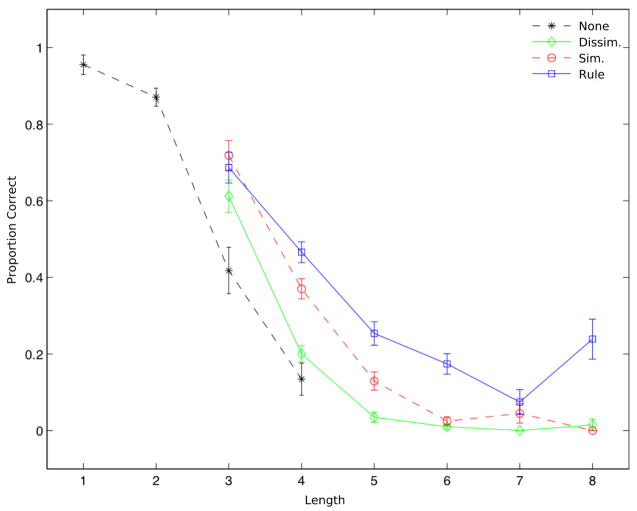
Figure 3 shows the mean proportion of correct responses as a function of the length of the sequence presented, by the type of presentation order. Overall, a nonlinear regression (using an s-shaped sigmoid function of the form a − 1/(1 + exp(− b × x + c)) of the mean points on this figure (along the x-axis) showed that 78% of the performance variance was explained by sequence length (R² = .78). Regardless of order, the memory-span estimate at a threshold of 50% correct responses was 3.5 objects. When the length of the sequence increased from three to four objects, mean performance dropped from .64 to .33. It also diminished by half again as much between four and five items to recall (from .33 to .14). This impressive drop resulted in performance at the lower end of Cowan’s (2001) memory-span estimate of 3–5 items, and is similar to other more specific estimates of 3–4 items (Broadbent, 1975; Chen & Cowan, 2009; Luck & Vogel, 1997).

Figure 3.

Proportion of correct sequences recalled as a function of the sequence length (number of objects), for each presentation order. Note. The error bars show ±1 standard error.

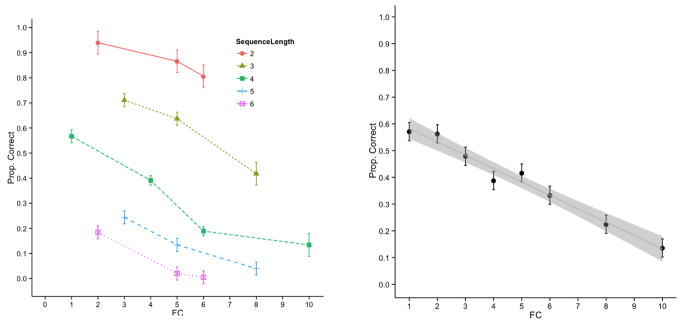
However, a multiple linear regression analysis on mean proportion correct showed that each of the three factors contributed significantly to the drop in performance. The percentages of variance explained were as follows: sequence length (β_ir_{Y i} = 67%), compressibility/FC (β_ir_{Y i} = 9%, which included eight unique values, that is 1, 2, 3, 4, 5, 6, 8, 10), presentation order⁷ (β_ir_{Y i} = 12%), and presentation time (β_ir_{Y i} = 1%), totaling 89%, F(6, 89) = 110, p < .001, R² = .89. The effects of length and presentation order on performance are clearly visible in Figure 3, whereas the effect of compressibility is shown in Figure 4. Regarding the effect of FC, a partial correlation analysis showed that at a constant sequence length, compressibility and correct proportion were negatively correlated (r = −.28, p < .001). Indeed, the more complex the sequence, the lower the performance (see Fig. 4, left). The ANOVA with repeated measures, with FC as a within-subject factor and proportion correct as the dependent variable yielded a significant effect of FC for most sequence lengths: F(2, 132) = 2.9, p = .054, ${\eta }_p^2=.04$ for two-object sequences; F(2, 132) = 11.5, p < .001, ${\eta }_p^2=.15$ for three-object sequences; F(3, 198) = 45.6, p < .001, ${\eta }_p^2=.41$ for four-object sequences; F(2, 132) = 18.8, p < .001, ${\eta }_p^2=.22$ for five-object sequences; and F(2, 132) = 45.1, p < .001, ${\eta }_p^2=.41$ for six-object sequences. Figure 4 shows the linear trend that we obtained using data collapsed across participants, complexity, and sequence length.

Figure 4.

Proportion of correct sequences recalled as a function of Feldman’s Complexity (FC), across each sequence length (left plot) and collapsed (right plot). Note. The analysis shown in the right plot is based on the 3217 trials, to include the entire variance. The error bars show ± one standard error.

The proportions of correct recall for the Rule, Similarity, and Dissimilarity orders were respectively, .35 (sd = .16), .25 (sd = .13), and .16 (sd = .09). The ANOVA with repeated measures yielded a significant effect, F(2, 132) = 80, p < .001, ${\eta }_p^2=.55$. We also observed significant differences between the Rule and Similarity conditions, t(66) = 6.8, p < .001, and between the Similarity and Dissimilarity conditions, t(66) = 7.8, p < .001, even after Bonferroni correction.

At lengths 3 and 4 (the conditions for which the four types of orders applied), the reason for the lower score in the None order is linked to the complexity of the heterogeneous categories, for which FC = 8 and FC = 10. In these conditions, the proportions of correct recall for the Rule, Similarity, Dissimilarity, and None orders were respectively, .52 (sd = .03), .47 (sd = .03), .32 (sd = .02), and .28 (sd = .04). The ANOVA with repeated measures yielded a significant effect, F(3, 198) = 25, p < .001, ${\eta }_p^2=.28$. We also observed significant differences between the Rule and Similarity conditions, t(66) = 2.11, p = .04, and between the Similarity and Dissimilarity conditions, t(66) = 6.7, p < .001, but the difference between the Dissimilarity and None conditions was not significant. At lengths 3 and 4, the only pair left significant after Bonferroni correction was Similarity-Dissimilarity.

A repeated-measures ANOVA was run on presentation order (with the rule-based, similarity, and dissimilarity levels) and FC (with levels 1, 2, 3, 4, 5, 6, and 8; note that the value 10 could not interact with presentation order, and also, the N/A value could not be included to test a linear trend). Feldman’s complexity significantly affected the mean proportion correct, F(6, 396) = 76, p < .001, ${\eta }_p^2=.54$, and we found a linear trend for this factor, F(1, 66) = 235, p < .001, ${\eta }_p^2=.78$. We also found a significant interaction between the two factors, F(12, 792) = 8.5, p < .001, ${\eta }_p^2=.11$, which tended to show that the Rule-order benefited the participants more when FC was low.

Transitional error probabilities

Transitional error probabilities (N. F. Johnson, 1969a, 1969b) can provide further evidence as to whether the participants actually used the available chunks. Without such an analysis, there is no clear evidence of what chunks were adopted during the task. Based on the Johnson’s analyses, one can explore the relationship between performance on two adjacent items when they can be assumed to fall within the same chunk, rather than on opposite sides of a chunk boundary. For instance, the sequence ▫ ▪ ■ □ could be chunked into ▫ ▪ and ■ □ using a logical rule. This sequence thus contains two potential within-chunk transitions (e.g., ▫ to ▪ and ■ to □) and a single between-chunk transition (▪ to ■). The prediction was that within-chunk transitions would more often be made correctly than between-chunk transitions would, under the assumption that participants use the available chunks and store them under the same memory code.

For all adjacent items, a transition was scored correct when the second element was recalled, provided the first item had been correctly recalled. A transition error was counted whenever the second element was not recalled but the first item had been correctly recalled. If the participant’s response was ▫ ▪ ■, the analysis indicated that there was only one out of two correct within-chunk transitions and that the single between-chunk transition was correctly made. A transition was not counted when the first item of an adjacent pair was not recalled.

The results reported in Table 1 show that a greater proportion of transitions were correctly made within chunks than between chunks, and that this difference was particularly great for the rule-based presentation order. Another expected result was that recall decreased more for within-chunk pairs than for between-chunk pairs across all orders. The reason is that rule- and similarity-based orders are assumed to facilitate chunk encoding more. Table 1 shows this interaction between presentation order and the two types of pairs. A repeated-measures ANOVA using order (rule-based, similarity-based, dissimilarity-based) and type of pair (within-chunk vs. between-chunk) as two within-subject factors confirmed this interaction, F(2, 132) = 7.2, p =< .001, ${\eta }_p^2=.10$, as well as a main effect of these two factors (F(2, 132) = 158, p =< .001, ${\eta }_p^2=.71$, and F(1, 66) = 326, p =< .001, ${\eta }_p^2=.83$, respectively).

Table 1.

Average proportion (all participants pooled) of adjacent two-stimulus sequences recalled, as a function of presentation order and pair type.

Type of pair	Rule-based	Similarity-based	Dissimilarity-based
Within-chunk	.56 (.14)	.45 (.13)	.29 (.11)
Between-chunk	.43 (.15)	.35 (.13)	.21 (.09)

Note. Parentheses indicate SDs.

Note that the above analyses argue in favor of the idea that chunk identification was rule-based. To better account for the formation of chunks in the rule-based order and the similarity-based order, a more precise and neutral description of how chunks might be incrementally encoded during the task is presented below

Incremental encoding of chunks of varying lengths using strict position scoring

Finally, we look at how much information participants may have encoded irrespective of whether or not the response was perfectly recalled. To evaluate the actual number of items encoded, we present a microanalytical characterization of how chunks can be encoded incrementally during the task. First, we identified the chunks that could theoretically be formed by binding two or more adjacent objects based on their similarity. This new analysis is more neutral than the previous ones in that it does not favor the rule-based process. We posited that the probability of forming a chunk was maximal when two adjacent objects differed by only one feature. Each study sequence was decomposed into chunks when at least two adjacent objects were considered similar. A chunk could, however, contain three objects if the third object also differed by only one feature from the second object, and so on, when more than three objects could be strung together. Put differently, a new chunk was formed whenever an object differed by at least two features from the preceding object. A single-object chunk was formed whenever there was no way of grouping two objects together. Using this method, chunk size therefore ranged between one object long and eight objects long.

For instance, the following study sequence ▫ ▪ ■ ▴ ▲ □ was split as follows to form a new chunked sequence: ▫ ▪ ■ — ▴ ▲ — □, using three chunks of varying lengths (3, 2, 1, respectively) and totaling six encoded objects. The ratio of six objects to three chunks (i.e., two objects per chunk on average) indicates the compression achieved by the recoding process.

To find the number of chunks that the participants encoded, their response sequences were split using the same encoding process before being aligned to the chunked study sequence. A partial-credit scoring system was used to get the sum of the chunks correctly recalled in their correct positions. For instance, had the participant recalled ▫ ▪ ■ ▴ □, this response sequence was split into ▫ ▪ ■ — ▴ — □ before being aligned to the chunked study sequence ▫ ▪ ■ — ▴ ▲ —□. The alignment would only score the first and third chunks as correctly recalled in their correct positions. The dissimilarity-order condition was removed from this analysis because, by construction, it generally contained one-object chunks. Across all sequence lengths, the theoretical average of to-be-encoded chunks in the rule-based order was 2.9 vs. 1.5 in the similarity-based order. Conversely, the number of objects that could be unpacked from one chunk had a theoretical average that was greater in the similarity-based condition (4.0) than in the rule-based condition (1.7). By construction, the similarity-based condition favored longer chunks (and consequently fewer chunks), whereas the rule-based condition rarely offered the opportunity to form chunks made of more than two objects.

The results indicated a larger number of chunks encoded in the rule-based order (M = 1.28, sd = .42) than in the similarity-based order (M = .45, sd = .20), after averaging the participants’ performance across sequence lengths (t(66) = 20.2, p =< .001, ${\eta }_p^2=.86$). The participants recalled an average of 2.27 objects in the rule-based order versus 1.13 objects in the similarity-based order, and this difference reached the same significance level. The ratio between these two counts indicates that the participants encoded an average of 2.27/1.28 = 1.77 objects per chunk in the rule-based order and 1.13/.45 = 2.5 objects in the similarity-based order. This difference was also significant after averaging participants’ performance across sequence lengths (t(66) = 13.7, p =< .001, ${\eta }_p^2=.74$). In comparison to the theoretical number of objects that could be encoded in chunks in the rule-based condition (1.7, as indicated above), the participants could potentially encode these chunks perfectly (1.77 objects per chunk), while retaining fewer chunks than available (1.28 instead of 2.9). Information was therefore correctly encoded into in chunks but the number of chunks was subject to a capacity limit.

Incremental encoding of chunks of varying lengths, regardless of position

We used a less stringent free-position scoring system that counted a chunk as correctly recalled no matter where it was in the response sequence. We then determined the number of objects that could be unpacked from the recalled chunks. Using this method, the number of objects unpacked from the chunks found in the participants’ responses was significantly greater in the rule-based condition (M = 2.99, sd = .65) than it was when strict position scoring was used (M = 2.27, sd = .74), t(66) = 18.4, p =< .001, ${\eta }_p^2=.84$, and as such, a more plausible estimation of the expected 4±1 span was attained. Recall in the similarity-based condition was also slightly greater, increasing from 1.13 to 1.34 (t(66) = 12.4, p =< .001, ${\eta }_p^2=.70$).

Incremental encoding of chunks corresponding to pairs of items in the similarity-based condition

We carried out a final test to see whether participants in the similarity-based condition encoded smaller chunks than those available, using an encoding process similar to the one induced in the rule-based condition (i.e., encoding objects by pairs). For instance, the sequence ▫ ▪ ■ □ is potentially a single four-object chunk since none of the transitions between adjacent objects involves more than one feature. Because such a long chunk is probably more difficult to encode than two smaller two-object chunks, we separated these long chains by pairing the objects, as follows: ▫ ▪ and ■ □. This method was less strict for scoring participants’ performance. For instance, based on the ▫ ▪ ■ □ study sequence, a ▫ ▪ chunk would be identified in ▫ ▪ ■ (the participant’s response sequence), whereas no chunk would be credited to the participant if ▫ ▪ ■ □ was coded as the only available chunk in the study sequence. In comparison to the first method for identifying the chunks in the sequences, the number of objects recalled in the similarity condition increased from 1.13 to 2.07 using strict-position scoring (t(66) = 24, p =< .001, ${\eta }_p^2=.90$), and from 1.34 to 2.5 using free-position scoring (t(66) = 31.1, p =< .001, ${\eta }_p^2=.94$). This method could not, however, affect the rule-based condition much, because, by construction, none of the chunks could include more than two objects in this condition.

Overall, the number of objects recalled was greater in the rule-based condition, meaning that the participants were more inclined to encode a greater number of smaller chunks than a smaller number of chunks made of a longer chain of similar objects (even though the long chain could be split into several contiguous pairs).

To come back to the analysis of the transitional error probabilities (now that we know that the analysis does no longer favors the identification of chunks that are rule-based), we again divided the frequency of correct transitions by the total number of times that the first item was correctly recalled for a given pair of adjacent items. We then averaged the frequencies of the within-chunk and between-chunk transitions across participants in order to run a repeated-measures ANOVA using order (rule-based vs. similarity-based) and type of pair (within-chunk vs. between-chunk) as within-subject factors. This analysis showed that a greater number of transitions were correctly made (in comparison to Table 1) for the within-chunk transitions (p = .64) than for the between-chunk transitions (p = .48), F(1, 66) = 245, p =< .001, ${\eta }_p^2=.80$, and that more transitions were correctly made in the rule-based condition (p = .60) than in the similarity-based condition (p = .52), F(1, 66) = 31, p =< .001, ${\eta }_p^2=.32$, with no interaction between the two factors. Overall, there were 2178 correct transitions versus 1260 transitional errors in the within-chunk condition, but only 1432 correct transitions versus 1685 transitional errors in the between-chunk condition, corresponding to an odds ratio of 1.4.

Discussion

We explored the ability of untrained participants to increase their immediate memory by parsing sequences of objects into newly-formed chunks. The main reason for exploring chunk formation in immediate memory is that a chunk is too often thought of solely as a product of an already-formed long-term representation. Showing that recoding can occur very rapidly in immediate memory is a different undertaking. This idea may seem merely intuitive, but no other model can give a precise quantitative account of how information is apprehended to determine exactly what patterns can be extracted rapidly to increase memory capacity. Chunking demands a more principled explanation than one simply saying that individuals demonstrate chunking when they group items together while performing a memory task. The chunking memory-span task presented in this study provides a way to explore the formation of a chunk in immediate memory, without relying on chunking that has become familiar via repeated exposure.

Our theory was that a compressibility metric could estimate the opportunities available to participants for immediate recoding of the to-be-recalled material. A first result showed a capacity of about three objects for the most noncompressible sets of objects, at a 50% threshold (see Fig. 3, which corresponds to the lower limit of the 4 ± 1 estimate; Cowan, 2001). This result is consistent with the literature (e.g., Broadbent, 1975; Chen & Cowan, 2009), despite Cowan’s slightly higher estimate (2001). However, in line with our prediction, this capacity limitation is overcome whenever a form of relational information can be computed, that is, when compressible sets of objects are used. The proportion of sequences retained increased with compressibility, particularly when presentation order facilitated the recoding of the sequences (up to about four objects at a 50% threshold; see Fig. 3 for the rule-based order). Overall, this finding showed a minimal span of about three objects that increased monotonically as a function of sequence compressibility.

More refined analyses showed that the objects were most often chunked into pairs, in an incremental fashion. The results also showed that recoding occurred more often in the rule-based order (which favors short, well-clustered logical chunks of two objects) than in the similarity-based order (which favors longer chunks of very similar objects). The dissimilarity condition was less likely to induce chunking because it tended to cluster the objects individually. However, it is more difficult to tell exactly what a chunk or rule is in immediate memory. More specifically, because our method targets a process that occurs before any consolidation process, there is no clear-cut empirical measure of the presence of chunks or rules. Beyond that, however, by calculating the transition-error probabilities and analyzing how chunks were incrementally encoded, we do provide clues as to the nature of the chunks formed.

Chunking in the present study probably emerged in immediate memory thanks to the identification of elementary structures of repetition in the input stream. This is why the present study goes beyond those that have used digit sequences to study chunking (Bor & Owen, 2007; Mathy & Feldman, 2012), insofar as regular digit sequences such as 123 may already have been represented in the participants’ long-term memory (see Jones & Macken, 2015). Also, the chunking memory referred to in our tasks does not correspond exactly to Potter’s (1993, 2012) notion of conceptual short-term memory. In her theory, short-term memory operates by allowing meaningful patterns stored in long-term memory to be unconsciously identified in short-term memory. Our results are closer to those of a previous study in which untrained participants could improve memorization of a set of spatially-grouped objects organized into smaller units by using hierarchically nested levels (Feigenson & Halberda, 2008).

However, we have not lost sight of the fact that some individual strategies devoted to describing the sequences can escape predictions. For instance, we took the risk that some verbal processes usually shown to be critical to short-term memorization (Burgess & Hitch, 1999; Baddeley, Thomson, & Buchanan, 1975; Estes, 1973; Zhang & Simon, 1985) are left uncontrolled in our study because the items can be recoded verbally. Still, we intentionally let the participants recode (verbally or otherwise) our visual-based material because we thought that implementation of articulatory suppression could also affect attention and subsequent encoding of regularities. It was our goal to let the participants encode the objects freely.

The next sections evaluate competing theoretical accounts of the compression effects we found. We will discuss in detail the under estimated role of immediate memory in the formation of chunks and why the compressibility of information is a good theory to capture grouping effects. We begin with the idea that although interference-based models can easily account for forgetting, they cannot account for the potential chunking processes at play in our data. Indeed, the non-distinctiveness of the stimuli can paradoxically be both detrimental to retaining similar items (when it is considered to produce an interference-based forgetting process) and beneficial to grouping (in our study, when it produces a chunking process).

Interference-based models and local distinctiveness account

We believe that short-term memory models based on the stimulus distinctiveness do not explain our presentation-order effects. These models contend that similar items interfere with each other (Lewandowsky, Duncan, & Brown, 2004; Nairne, 1990, 2002; Oberauer & Kliegl, 2006). At best, these models predict no difference between presentation orders, because the overall similarity of items is identical in our three orders. At worst, these models incorrectly predict poorer performance in the similar condition than in the dissimilar condition because of the possible negative effect of similarity between adjacent items.

In contrast to both of these predictions, we correctly predicted better performance in the similarity-based order than in the dissimilarity-based order because the particular kind of similarity we presented allowed for easier compression of the material based on feature continuity between adjacent items. This result supports a more general finding that similarity can be either beneficial or detrimental to memory (Gupta, Lipinski, & Aktunc, 2005; Hunt & McDaniel, 1993; J. S. Johnson, Spencer, Luck, & Schöner, 2009; Lin & Luck, 2009; Nairne & Kelley, 1999). Moreover, we correctly predicted the best performance when the materials lent themselves directly to explicit rules of transition. The similarity condition did have longer potential chains of similarity between contiguous items, but the basis of the similarity kept shifting, so participants were generally unable to use those contiguities as consistently as they could in the rule-based condition. The logical content of our task might explain why an associative process based on similarity occurred less often in our data than a rule-based process did (Sloman, 1996).

For instance, the SIMPLE model (Brown, Neath, & Chater, 2007) suggests that the retrieval of items in memory is a discrimination process at all periods of time (short-term and long-term). In SIMPLE, items may be hard to retrieve when their temporal distance is short, for the same reason that similar items are hard to identify. SIMPLE usually captures the idea that items are more discriminable when they occupy isolated locations on the temporal dimension. Here in our study, it was adapted to capture the idea that items are more discriminable when they are both physically and temporally isolated. The following equation derived from context models (Nosofsky, 1984, 1986) is simple enough to discriminate the effect of our three presentation orders:

$$d_{ij}=\sum _{a=1}^n\mid x_{ia}-x_{ja}\mid$$ (1)

The preceding equation can be used to evaluate both the physical distance and the temporal distance between two items in a pair. For instance, let d_ij = 2 when a ■ is presented one second after a □ (in this case, the total distance is: one feature + one second = 2 differences). The following exponential decay function can be used to relate stimulus similarity to psychological distance (Nosofsky, 1986; Shepard, 1987):

$${\eta }_{ij}=e^{-d_{ij}}$$ (2)

Finally, SIMPLE assumes that the discriminability D_i of a memory trace is inversely proportional to its summed similarity to the n memory traces:

$$D_i=\frac{1}{{\sum }_j^n{\eta }_{ij}}$$ (3)

The probability of recalling item i in its correct temporal position is simply its discriminability.

It appears that our results cannot be modelled by SIMPLE, in which performance may be accounted for by an interference process that would favor the dissimilarity-based order. Looking at Fig. 2, our simulation showed that the overall discriminability (Σ D_i) of the six items in the rule-based order was 3.90 (.69, .64, .62, .62, .64, .69 for the respective six items respectively, summing to 3.9), versus 3.27 for the similarity-based order and 4.79 for the dissimilarity-based order, when only the items’ physical dimension was taken into account. Adding the temporal dimension did not change this ranking and we simply obtained larger overall discriminability values: 5.09, 4.80, and 5.50, respectively. In this interference-based model, the dissimilarity-based order is predicted to produce maximal local distinctiveness (hence better recall), whereas the similarity-based order is predicted to produce maximal interference in memory and subsequently a negative effect on memorization. The rule-based model has an intermediate status in the model, although our results clearly showed its superiority. SIMPLE cannot account for how chunking operates in immediate memory with the present data (even if the predictions are reversed to consider similarity as beneficial, the rule-based order still has an intermediate status).

Compressibility of information

In the present study, recall performance was significantly enhanced for compressible sequences as compared to less compressible ones. Brady et al. (2009) introduced statistical regularities in some sequences of visually presented stimuli in order to study the effect of redundancy on memorization. The authors reported that the observers recalled more information when the stimuli exhibited regularities. They explained this advantage by the fact that several items associated in memory formed a single chunk, leaving more room in memory for storing other stimuli. A compression process using statistical regularities (Brady et al., 2009) can be perfectly modeled with a minimum description length (MDL) type of approach (Rissanen, 1978). MDL is based on an algorithmic notion of compressibility that seems more versatile than Feldman’s (2000). However, the MDL approach seems to offer no advantage for recoding a single short sequence such as the ones used in the current study. A simple example is the difficulty applying MDL to a short sequence such as 12349876. In this case, its recoding into a = 1234 and b = 9876 does not lead to any compression (i.e., the length of the representation “a = 1234 and b = 9876, ab” is greater than the original sequence, because the redescription process needs to be taken into account), whereas it can be clearly useful for a sequence that is slightly longer, such as 123123123123123123123, for which we can use a shorter representation a = 123, aaaaaaa (the a = 123 part corresponds to what is written in the lookup table, and aaaaaaa corresponds to the recoded sequence, but combined, it is shorter than the original string). The same advantage for a = 123 occurs if 123 is repeated many times in the long-term mixed in with other sequences (e.g., 123, 4, 123, 123, 5, 6, 2, 1, 123, 123, 123, etc.). We concentrate here on a practical version of MDL. However, MDL is ideally an algorithmic approach to compression that does not have to rely on frequently repeated patterns, and as such, it is not impossible that MDL could recode a small individual sequence like 12349876 based on a particular appropriate programming language.

We agree with Brady, Konkle, and Alvarez’s (2009) suggestion that chunking can be used as an approximation of an algorithm of psychological compression. However, our results go beyond that earlier work by showing that a short amount of time is sufficient to allow a compression process to occur on the fly. Our interpretation is that compression can be efficient if it makes use of primitive repetition structures, which can be detected and used rapidly in immediate memory. As such, Feldman’s model of compressibility is more suited than MDL for capturing the recoding of single short sequences like the ones in the current study. For instance, for the set ■ ▫ ○ ●, compressibility is very limited and requires a more extensive description in working memory than a more compressible set. When almost no compression is possible, the representation must contain almost as many features as in the original list of objects.

A last point concerns the relationship between compressibility and presentation order. When the members of a compressible set (e.g., one where FC = 1, such as △ ▴ ▵ ▲) are unordered, their memorization can be facilitated by using the rule “triangles”. However, the memorization of the ordered objects △ ▴ ▵ ▲ requires a longer description than “triangles”. Therefore, a compressible category that is not ordered in a regular way can be as difficult to memorize as a noncompressible one. This is noticeable in Fig. 3 in which the mean data point for FC = 10 (this data point is represented by the black curve where length = 4) is very close to the mean data point for the green dissimilarity curve. However, when no compressibility is allowed in the first place, order does not matter anymore.

Conclusion

One common idea is that working memory simply uses pointers to retrieve chunks in long-term memory, and that chunks are only consolidated pieces of information stored in long-term memory. We believe that we observed a chunking process that seems to result from the temporary creation of new representations. Recall performance in the current study was as small as about three items, but the total increased when the sequential order of the items was favorable to the formation of new chunks, i.e., compression of the sequence based on rules discovered within it. One potential strong conclusion is that these variations in performance mean that chunking processes can operate during short-term memorization. It follows from this conclusion that chunks must not be considered solely as permanent groupings of information in long-term memory. It is possible that our participants spontaneously compressed information without much mediation of long-term memory chunks, since it is probable that none of our participants had ever encountered the particular sequences of objects seen in our experiment.

The experiment presented in this paper allows us to draw the conclusion that information can be compressed in a few seconds in immediate memory by capitalizing on the regularities within the materials presented. Our research challenges us to consider that the notion of compression in immediate memory is central to defining grouping, chunking, and probably learning.

Appendix

Notes on Feldman’s (2000) compressibility metric

To use Feldman’s (2000) compressibility metric, the stimuli must be split into categories. Categories (or simply groups of stimuli) from 1 to 8 stimuli were drawn from the initial set of 8 stimuli. The k chosen stimuli represented the class of to-be-recalled stimuli, while the 8 – k remaining objects represented the opposite class that did not have to be recalled after stimulus presentation but were shown in the recall screen. Using all of the eight stimuli in the procedure was thought to preserve the complexity metric on which the present study was based. Had the participants been only requested to reconstruct the order of the chosen stimuli (e.g., ▫ followed by ▪) without contrasting them to the opposite category, the participant would only have to encode the color feature to succeed (e.g., using a “white first” representation of the sequence). For instance, to follow the metric that was first thought to account for categorization processes, the ▫ ▪ sequence, needs to be contrasted to the opposite class (i.e, ▵ ▴ □ ■ △ ▲) by the participants. In this respect, the minimal representation of the category is “small squares”, and the right order (“white first”) applies specifically to the “small squares” category. The minimal representation (“small squares”) that inter-relates the individual stimuli is the compressibility of the category because it is shorter than “small white square or small black square”. The minimal representation that includes order information is “small squares, white first”. Note that it is principally because participants need to remember a sequence in the correct order that the task goes beyond what a categorization task would require.

Figure 5 gives Feldman’s (2000) measure of complexity (FC) for each category, which was used as a measure of compressibility. This measure indicates the number of features in the shortest logical formula allowing one to describe the stimuli, which are indicated by a black dot. The black dots positioned on the cubes illustrate the relationship between the objects that could be used by the participants to associate the stimuli to be recalled in our experiment. Each of the stimuli selected for a category were presented sequentially and their location remained constant in the middle of the screen, so no reference was made during the experiment to the spatial organization shown in this figure (this was done here to bring out the similarity structure between objects for the reader). For instance, the eighth cell on the left indicates that four triangles were used to construct the memory list (see bottom right cube above ‘Reference’ for retrieving the stimuli to which the black dots in the eighth cell on the left are pointing). The “triangle” category representation would be sufficient for free recall of the list.

FC is indicated in the middle column because the FC numbers for a given line fit both the category structures on the left and those on the right. Note that FC is not confounded with sequence length for sequences equal to 2, 3, 4, 5, or 6 objects. However, for the categories made of 1, 7, or 8 objects, no variations in complexity could be manipulated. When a set was composed of eight objects, categorization was no longer involved. In this particular case, the shortest formula was trivial (“all objects”) and it was associated with a ‘Not Applicable’ (N/A) FC value.