Semantic interpretation of robust imaging features for Fuhrman grading of renal carcinoma

Abstract

Pattern recognition in tissue biopsy images can assist in clinical diagnosis and identify relevant image characteristics linked with various biological characteristics. Although previous work suggests several informative imaging features for pattern recognition, there exists a semantic gap between characteristics of these features and pathologists’ interpretation of histopathological images. To address this challenge, we develop a clinical decision support system for automated Fuhrman grading of renal carcinoma biopsy images. We extract 1316 color, shape, texture and topology features and develop one vs. all models for four Fuhrman grades. Our models are highly accurate with 90.4% accuracy in a four-class prediction. Predictivity analysis suggests good generalization of the model development methodology through robustness to dataset sampling in cross-validation. We provide a semantic interpretation for the imaging features used in these models by linking features to pathologists’ grading criteria. Our study identifies novel imaging features that are semantically linked to Fuhrman grading criteria.

SECTION I. Introduction

Pathological analysis of tissues is an important step for cancer diagnosis and treatment. Traditionally, pathologists examine specimens under microscopes and make judgments based on deviations in cellular structures, change in the distribution of cells across the tissue, and clinical information about the patients being treated. However, this process is time-consuming, subjective and inconsistent due to inter-and intra-observer variations [1]. Therefore, computer-aided histological image classification systems are highly desirable to provide efficient, quantitative, and reliable information for cancer diagnosis and treatment planning. The computer-based detection and analysis of cancer tissue represents a challenging, yet unsolved task because of the large volume of patient data and their complexity [2]. The goal of predictive modeling is to construct models that make sound, reliable predictions and help physicians improve their prognosis, diagnosis or treatment planning procedures. However, there are many challenges facing computer-based decision making in clinical medicine. One important challenge is a semantic gap, the lack of biological interpretation of quantitative image features [3]. Because of the semantic gap, decision support systems act as a black box for pathologists and are more susceptible to errors. The purpose of our work is to develop an accurate computer-based decision support system for renal carcinoma grading and identify important image features contributing to high grading accuracy. We discuss relationships of these image features with underlying biological features. With this work, we hope to reduce the semantic gap between pathologists’ knowledge and informative image features.

SECTION II. Background

The grading schema of renal cell carcinoma is based on the microscopic morphology of a hematoxylin and eosin (H&E) stained neoplasm. The most widely used schema is a nuclear grading system described in 1982 by Fuhrman et al. [4]. Pathological samples are classified by their disease stage, tumor size, cell arrangement, cell type, and nuclear grade. Four nuclear grades (1–4) are defined in order of increasing nuclear size, irregularity, and prominence (Fig. 1).

Figure 1.

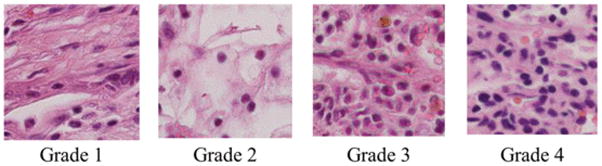
Representative histology images for each fuhrman grade

Nucleoli and other morphological features are important grade indicators, occurring in 94% of malignant cases [5]. Size and shape features capture these differences in nuclear and cellular structure and support discrimination between tissue cell subtypes [6]. Topological features have been shown to support accurate grade classification [5], [7]. Texture features contain information about the spatial distribution of gray tones related to tissue structure and markers in cytoplasm and nuclei. The gray-level co-occurrence matrix (GLCM) encodes properties of this distribution. The gray level run-length matrix (GLRL) captures texture features from contiguous, directional sequences of similar gray level intensities [8]. Local binary pattern (LBP) is a rotation-invariant feature useful for texture classification characterizing spatial structure and contrast [9].

In this study, we have extracted a combination of color, shape, texture, and topology features. Our goal is to identify robust, informative features for Fuhrman grading and link them to pathologists’ interpretation. Similar previous work discussed biological interpretation of statistically significant feature subsets for one vs. one Fuhrman grading models [10]. Compared to previous work, we use a different dataset, a different set of imaging features, and different prediction model design. Using one vs. all Fuhrman grade models, we are able to isolate not only feature subsets but also individual features useful for distinguishing a particular Fuhrman grade from others. Though extracting fewer features overall, our approach extracts all combinations of texture, color and shape features with all segmented regions, while prior work considers only a targeted subset of feature type and region combinations. Consequently, we identify new features semantically linked to Fuhrman grading classification.

SECTION III. Methods

A. Data

Our dataset consists of 160 RGB images of H&E stained renal carcinoma tissue samples. These images are manually curated 2048×2048, 24-bit RGB sections of whole-slide images. Three carcinoma subtypes are represented in the dataset: clear cell (47%), papillary (33%), and chromophobe (20%). Expert pathological labeling of the dataset yielded 13% grade 1,31% grade 2,39% grade 3, and 17% grade 4 using the Fuhrman grading criteria.

B. Feature Extraction

Images are first segmented via the segmentation classifier described in [11] into nuclear, red blood cells, cytoplasm, and background regions. Red blood cell regions are discarded, and morphological cleaning is applied to the three remaining regions. To remove small regions from cytoplasm and background, which may be spurious or contribute to noise in extracted features, regions having a radius smaller than 2 pixels are removed via morphological opening with a disk. Connected components comprised of fewer than 20 pixels are then removed. This cleaning is not applied to nuclear regions, where small components may be individual nuclei. From each image and binary segmentation, we extract 1316 color, texture, shape, and topological features for each image.

Color features include 16-bin histograms and intensity distribution properties for the grayscale image and each color channel, color channel intensity differences, red ratio [12], and each of these features repeated for each region of interest, totaling 704 features. For these and all other features, distribution properties are extracted as eight summary statistics: mean, median, standard deviation, skewness, kurtosis, minimum, maximum, and inter-quartile range [10].

We extract 22 Haralick features from the GLCM, 44 GRLR features, and 18 LBP features for the entire image and each region of interest [8], [9]. The image is quantized into 8 discrete levels prior to GLCM and GLRL feature extraction. In total, we extract 339 texture features.

To quantify whole image shape features, the total area, number of distinct objects, and total perimeter are extracted for each region of interest. Each individual segmented object is also analyzed to reveal information typically related to the nuclear and cytoplasmic structures. Statistical distribution properties of each region of interest are extracted for the area, convex hull area, eccentricity, Euler number, axis lengths, orientation, and solidarity of each connected component, yielding 225 shape features.

Topological features are extracted based on the centroids of connected components segmented as nuclei. We measure distribution statistics of region area, edge length, and region perimeter of the Voronoi diagram and area and edge length of Delaunay triangulation, as well as the edge lengths of the minimal spanning tree of the triangulation graph [7]. This yields 48 topological features.

C. Model Development

Model selection and evaluation is performed through nested cross-validation consisting of 10 iterations of 3 folds in both inner and outer cross-validation. Dataset sampling in both the outer and inner folds is stratified by grade to preserve proportional representation of each grade. Binary one-versus-all classifiers are developed in each inner fold for each grade. Within each inner fold features are ranked for each grade, then a grid search is performed over all (hyper)parameters jointly. Winning parameters are selected according to the maximal mean accuracy of each unique parameter tuple within the inner cross-validation. This winning parameter tuple is used for model training in the corresponding outer cross-validation fold. Multiclass classification is aggregated from the selected binary classifiers by labeling each testing set pattern with the grade whose corresponding binary classifier has the maximal positive class probability (with random tie breaking) [13]. This process is repeated for each outer cross-validation fold independently.

Features are ranked by minimum redundancy maximum relevancy (mRMR) feature selection [14], using mutual information difference as the kernel. mRMR is a supervised, sequential feature ranking process whose object is, for each sequential feature, to select the remaining feature that maximizes the mutual information (joint probability density) with the target labeling while minimizing the mutual information between the new features and all features already selected. The number of features selected for model training is a parameter of grid search rather than chosen by heuristic during ranking. Prior to ranking, features are z-scored, then discretized into half-standard score width bins. Features are also z-scored, but not discretized, for model development.

Radial-basis kernel support vector machines (RBF SVM) are the classification algorithm for all models presented in this work [15]. The misclassification penalty hyperparameter, C, and radial basis function width, γ, are optimized jointly with a number of selected model features via grid search. Parameter search for γ is conducted in {2–16,2–145…,2–1}, C in {20,215,…,212}, and number of selected features in {1, 2,. …,1016,1018,…,103}. In all, we consider 4653 parameter combinations and develop 17.2 million models.

SECTION IV. Results and Discussion

A. Grade Classification

Our model selection methodology resulted in an outer cross-validation accuracy of 90.43±4.43∘ %, as shown in the confusion matrix in Fig. 2. Recall is best for grade 2 and worst for grades 1 and 4. For grades 1, 2, and 3, most confusion occurs between neighboring grades, which is expected given the progressive, ordinal nature of the Fuhrman schema. However, for grade 4, most mislabeling (8%) occurs as grade 1, despite the marked dissimilarity of grade 1 and grade 4 tissue. Overall, most mislabeling occurs from a true lower grade to a predicted higher grade, which may be desirable from a clinical standpoint as the risk of underestimating the severity of illness is typically greater than that of overestimating it.

Figure 2.

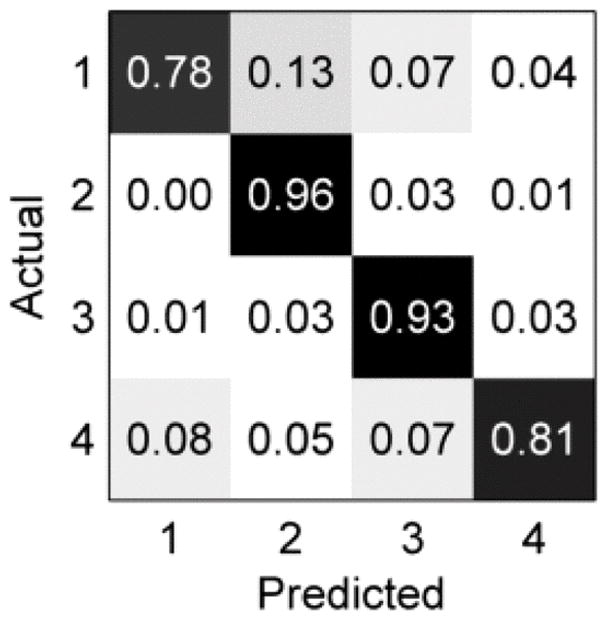
Confusion matrix of grade labeling on outer cross-validation

To evaluate the robustness of our model, Fig. 3 gives an analysis of the predictivity of selected model parameters, i.e., the correlation of model performance in internal and external validation. Although aggregate grade classification variance in outer validation is greater than in internal validation, 70% of outer folds have higher accuracy than the mean inner accuracy and 43% exceed the maximum inner accuracy. In a multiclass setting with high dimensional patterns, the 50% increase in training images in outer folds may increase model accuracy more than bias towards the selected inner CV parameters decreases it. This low bias and the low predictivity dispersion jointly indicate model parameters do not overfit inner cross-validation data.

Figure 3.

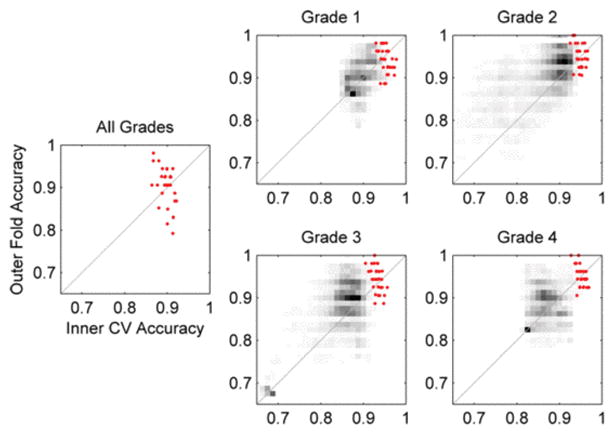
Predictivity analysis of selected models (red points) and all models in the parameter grid search (grayscale density)

The distribution of predictivity of all model parameters in Fig. 3 reflects the accuracy and relative difficulty of each grade classification task in Fig. 2. Selected binary models for all four grades have greater predictivity than nearly all other model parameters (grayscale density). For grade 2 many model parameterizations yield classifiers accurate in both internal and external validation, resulting from a large region of high accuracy in parameter space. In contrast, grade 4 has few parameterizations yielding accurate classifiers in either internal or external validation, with dense regions in Fig. 3 oriented perpendicular to the line perfect predictive correlation indicating high bias-variance tradeoff. Therefore, selecting models with both high internal accuracy and high predictivity is more difficulty for grade 4.

B. Informative Features and Semantic Interpretation

The ranking frequency of the four feature categories aggregated across all inner cross-validation iterations is shown in Fig. 4, which summarizes the relative contribution of different feature types to each grading task. Frequency is normalized by the prevalence of each feature type so that relative performance can be assessed. First color features, then shape features are prevalent at the best ranks for all grades. Since the Fuhrman schema defines grade by nuclear morphology and density, the high ranking of shape and color features suggests that these features can capture cytoplasmic prevalence and nuclear density. Texture, which has previously been suggested to be more pertinent to tissue classification where cytoplasm properties are important indicators, is ranked lower on average than the other three categories. Following the first few ranks dominated by color and shape features, topology is highly ranked in grades 1 and 4. This suggests that topology features can capture sparse cell density in grade 1 and dense nucleation in grade 4.

Figure 4.

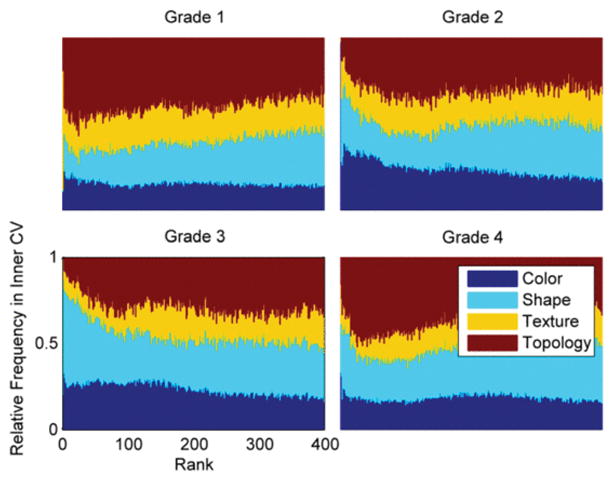
Ranking frequency of color, shape, texture, and topology features

The 5 most frequently selected and best ranked features for each grade in outer cross-validation, in Table 1, suggest features that are most consistent with the Fuhrman schema. In the Fuhrman schema, increasing nuclear size is the primary grade indicator. Table 1 suggests that minimum nuclear major axis length and median nuclear area, which contribute to accurate classification at both extremes of disease progression in grade 1 and grade 4, can capture nuclear size and elongation. The top ranked feature in grade 4, the lowest bin of the red channel histogram, may increase when nuclei are numerous and dense and little cytoplasm is present.

Table I.

Most selected features

	Feature	Type	Frequency
Grade 1	Background Red Histogram 240–255	Color	100%
	Nuclear Major Axis Length (Minimum)	Shape	100%
	Grayscale LBP (14/18)	Texture	100%
	Background Red Histogram 224–239	Color	97%
	Red Histogram 240–255	Color	93%
Grade 2	Red-Blue Channel Difference (Skewness)	Color	100%
	Red Ratio (Mean)	Color	100%
	Red-Green Channel Difference (Mean)	Color	97%
	Nuclear Red Ratio (Median)	Color	90%
	Cytoplasm Red Histogram 112–127	Color	87%
Grade 3	Blue Histogram 192–207	Color	100%
	Nuclear Eccentricity (Inter-Quartile Range)	Shape	100%
	Nuclear Eccentricity (Std. Dev.)	Shape	100%
	Background Eccentricity (Mean)	Shape	100%
	Cytoplasm Red Ratio (Kurtosis)	Color	100%
Grade 4	Red Histogram 0–15	Color	100%
	Nuclear Area (Median)	Shape	100%
	Grayscale Histogram 0–15	Color	100%
	Nuclear Convex Hull Area (Median)	Shape	100%
	Nuclear Major Axis Length (Minimum)	Shape	100%

Likewise, red-blue channel difference skewness is likely to associate with nuclear/cytoplasmic ratios, relating to increasing cell density in grade 2. Selected features also agree well with existing literature. For example, markedly increased nuclear/cytoplasmic ratios and nuclear eccentricity are useful in the separation of low-grade transitional cell carcinoma from benign urothelium [16]. Eccentric nuclei also indicate malignant rhabdoid tumors [17]. Feature type and region combinations not considered in previous work are also highly selected. Notably, regional color features appear for three grades in Table 1. Color properties of nuclear regions may indicate the presence nucleoli, which appear in higher Fuhrman grade samples. The red channel in cytoplasm regions can relate to cell density. In summary, Table 1 lists key image features affected by increasing nuclear size, irregularity, and prominence. Frequent selection of these feature subsets makes them an efficient choice for semantic interpretation of features that most impact the models. Categorical analyses like Fig. 4 can provide broad insight for the remaining features where specific interpretation is impractical.

SECTION V. Conclusion

The models developed by our methodology can classify renal carcinoma images into one of four Fuhrman grades with 90.4% accuracy. Predictivity analysis shows this methodology to be robust to sampling effects and selection set bias, indicating likely generalizability to other datasets in future work. Fuhrman grading criteria mainly depend on progressive growth and deformation of nuclei in carcinoma. Leveraging this fact, we summarize which parsimonious set of image features can best capture these nuclear characteristics. Some of the emerging features explicitly capture shape properties, while others only implicitly relate to pathologists’ judgments, e.g., LPB features and color properties. We report only top 5 features but in fact many more may be used in some complex decision models. In future we will further analyze the model performance with small interpretable feature sets and suggest more granular image feature types that best capture pathologists’ judgments. Using such imaging features will result not only in robust but interpretable decision support systems.