Multivariate Hypergeometric Similarity Measure

Abstract

We propose a similarity measure based on the multivariate hypergeometric distribution for the pairwise comparison of images and data vectors. The formulation and performance of the proposed measure are compared with other similarity measures using synthetic data. A method of piecewise approximation is also implemented to facilitate application of the proposed measure to large samples. Example applications of the proposed similarity measure are presented using mass spectrometry imaging data and gene expression microarray data. Results from synthetic and biological data indicate that the proposed measure is capable of providing meaningful discrimination between samples, and that it can be a useful tool for identifying potentially related samples in large-scale biological data sets.

Introduction

Similarity measures are an important tool in the analysis of a wide range of biomedical data, with applications such as the comparison of peptide sequences [1] and gene expression data [2], as well as in text mining [3] and in image analysis [4], [5]. An important application of similarity measures is in the detection of new and potentially significant patterns in large-scale biological data sets [2], [5], [6]. For example, if a particular gene is known to be associated with a disease, other genes potentially related to the disease may be detected by identifying highly similar patterns of expression. In this respect, similarity measures can be used to provide a shortlist of targets for further research.

Different similarity measures exhibit considerable variation in properties and performance [7], [8]. For example, many common measures do not have a probabilistic framework, although this is a useful property in terms of the interpretation of assigned similarity scores [9]. In this paper, we propose a similarity measure with a probabilistic interpretation, utilizing the multivariate hypergeometric distribution and the Fisher-Freeman-Halton test. Previously, we developed a similarity measure utilizing the hypergeometric distribution and Fisher’s exact test [10]; this measure was restricted to two-class data, i.e., the comparison of binary images and data vectors. However, many types of biological data are not inherently binary in nature, and the process of binarization can discard useful information. Here, we extend our earlier result to present a general similarity measure that accommodates the comparison of nonbinary, “multiclass” data.

After defining the proposed multivariate hypergeometric similarity measure, we describe several tests using synthetic and biological data to investigate its performance. First, its patterns of sample ranking are compared with those of cosine similarity, Pearson correlation and mutual information, three similarity measures which are used in the analysis of many types of biomedical data [2], [3], [4], [5], [11]. Next, we test and implement a method of approximation that facilitates the application of the proposed similarity measure to large samples.

We then consider example applications on biological data sets: first, on mass spectrometry imaging (MSI) data, and second, on gene expression microarray data. MSI is a technique in which mass spectra are acquired over the surface of a sample, such as a tissue slice, to generate a 3D (x,y : spatial, z : spectral) data set as shown in Fig. 1. MSI has numerous biomedical applications, including the study of cancer and neurodegenerative diseases, and pharmaceutical-related research [12], [13]. MSI generates large-scale data sets; the spectral dimension may contain thousands of m/z(mass-to-charge ratio) values. Depending on the data acquisition modality, each m/z value can be interpreted as a molecule or molecular fragment [13]. The data set can be interpreted as a collection of images, each describing the presence and abundance of a single m/z value at every (x, y) point over the sample surface. Spatial comparison of these images can be useful for identifying patterns among m/z values. For example, a single tissue sample may contain healthy, diseased, and marginal regions. Certain m/z values may be spatially localized in particular regions [12]. It may be informative to identify other m/z values expressed predominantly within a region of interest [14], or with similar spatial distributions as an m/z value of interest.

Fig. 1.

Description of 3D data structure of MSI data sets, and three example m/z images.

In this paper, the performance of the proposed similarity measure on biological data is assessed by applying it to an MSI data set to identify m/z images with similar spatial characteristics, and by applying it to a gene expression microarray data set to identify genes with similar expression patterns. Results from synthetic and biological data indicate that the proposed multivariate hypergeometric similarity measure is capable of providing meaningful discrimination among samples, and can be a useful tool for identifying potentially related samples in large-scale biological data sets.

Methods

2.1 Definition of Similarity Measure

Consider an image containing N pixels (or a data vector containing N samples), with all intensities quantized into n bins, where N and n are positive integers. When comparing two such images, there are n₂ possible types of overlap between spatially corresponding pixels. These overlaps can be represented as an n×n contingency table, as shown in Fig. 2. Each class k_ij, for indices i=1,…,n and j=1,…,n, represents the number of spatially corresponding pixels which are in bin i in the first (“reference”) image and in bin j in the second (“query”) image. The terminology is used in the sense that a given image would be selected as a “reference” and other images in a data set would be compared, or “queried” against it to find images similar to the reference. The margins of the contingency table are fixed for a given pair of images: for each row i, Σ_nj=1k_ij=r_i, the number of pixels in bin i in the reference image, and similarly for each column j, Σ_ni=1k_ij=q_j, the number of pixels in bin j in the query image. By definition, Σ_ijk_ij=N. The probability of observing a particular distribution of overlaps k_ij, i.e., the probability of observing a given contingency table, can be represented as the product of probability mass functions of the multivariate hypergeometric distribution. Considering only the first column of an n×ncontingency table with row marginal totals r_i, the column sum is q₁=k₁₁+k₂₁+⋯k_n1. Each component k_i1 is “drawn” from its row sum r_i. Since each draw is independent, the probability of observing a particular distribution of pixels is given as

$$\frac{\left(\begin{array}{c}{r}_1\\ k_{11}\end{array}\right)\left(\begin{array}{c}{r}_2\\ k_{21}\end{array}\right)\cdots \left(\begin{array}{c}{r}_n\\ k_{\mathrm{n}1}\end{array}\right)}{\left(\begin{array}{c}N\\ q_1\end{array}\right)}.$$

Fig. 2.

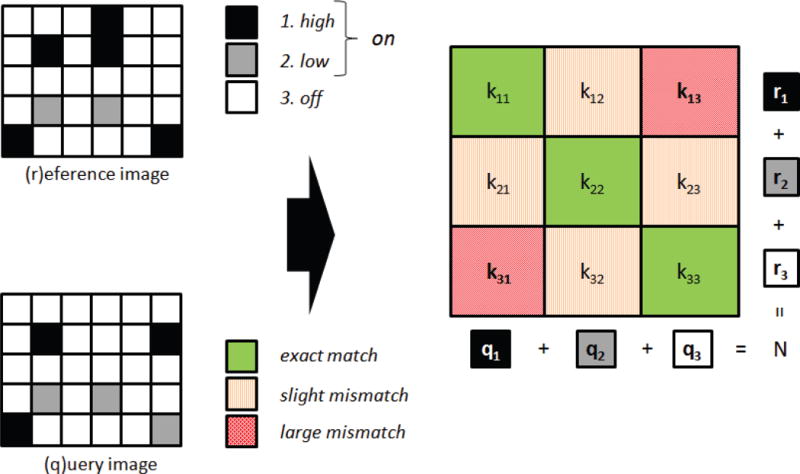
An image pair (reference and query images) with pixel intensities binned into three levels is represented as a 3×3 contingency table with fixed marginal totals.

This quantity is a probability mass function of the multivariate hypergeometric distribution. The probability of observing the second column is described similarly, but accounts for the pixels already assigned in the previous column:

$$\frac{\left(\begin{array}{c}{r}_1-k_{11}\\ k_{12}\end{array}\right)\left(\begin{array}{c}{r}_2-k_{21}\\ k_{22}\end{array}\right)\cdots \left(\begin{array}{c}{r}_n-k_{n1}\\ k_{n2}\end{array}\right)}{\left(\begin{array}{c}N-q_1\\ q_2\end{array}\right)}.$$

The same pattern is followed through the (n−1)th column. Because the row and column sums are fixed, the configuration of the nth column is determined by the preceding columns. Since the configuration of the available pixels in each column (aside from the nth column) is independent of the other columns, the probability p of the complete n×n contingency table is given by the product of the column probabilities. This quantity, shown in (1), is known as the probability for k -variate contingency tables [15], [16]. Here, q=[q1,q2,…,qn], r=[r1,r2,…,rn], and k=[k11,k12,…,knn]:

$$p\left(q,r,k\right)=\frac{{\displaystyle {\prod }_{i=1}^n{r}_i!}\times {\displaystyle {\prod }_{j=1}^n{q}_j!}}{N!\times {\displaystyle {\prod }_{ij}{k}_{ij}!}}.$$ (1)

In our previous work focusing on binary data, we defined a similarity measure based on the hypergeometric distribution; the probability mass function of this distribution gives the probability of a 2×2 contingency table [10]. The similarity measure was defined as the difference between the lower and upper tails of the hypergeometric distribution defined by the marginal totals r and q. The values of r and q are a function of the particular reference image and query image being compared. The tails were defined with respect to the observed overlap, which was defined as the number of spatially corresponding pixels which are “on” in both images, i.e., k₁₁ in this terminology. To extend this approach from the two classes in binary data to n classes, we utilize the probability mass function of the n×n contingency table.

The statistical significance of a contingency table is evaluated by performing Fisher’s exact test (in the binary case) or the Fisher-Freeman-Halton test (in the general case)[15], [17]. In both cases, the isomarginal family of tables (i.e., those tables having the same fixed margins r and q as the original table representing the reference and query image pair) is first generated, and the probability of each table is calculated. In the binary case, the hypergeometric distribution describes the isomarginal family. For each table in the isomarginal family, the value of a chosen statistic S(k) is compared to that of the original table. With respect to S(k), tables in the isomarginal family may be more extreme than the original table in two directions. The set of tables which are “more extremely large” have a larger than or equal value of the statistic, while the set of tables which are “more extremely small” have a smaller than or equal value of the statistic. The significance of a table in a particular direction is found by summing the probabilities of all tables within the respective set.

In the binary case, the choice of the statistic S(k) is straightforward because due to the fixed margins, there is only one degree of freedom. S(k)=k₁₁ completely defines the table, and is reasonable because more similar images will have greater numbers of overlapping pixels. In the general case, however, there are n₂−2n+1 degrees of freedom, and for n>2, the choice of a statistic is not obvious. Here, we choose a vector of statistics—the set of diagonal elements of the n×n table—as S(k), as shown in (2). These diagonal elements represent the exact matches— the spatially corresponding pixels in the reference and query images which are in the same class. While S(k) may be defined in many alternative ways, we propose (2) as a reasonable choice for multiclass data because images which are more similar will have a greater number of each of the n types of exact matches:

$$\mathrm{S}(\mathrm{k})=[{\mathrm{k}}_{11},{\mathrm{k}}_{22},\dots ,{\mathrm{k}}_{\mathrm{nn}}]$$ (2)

For each table in the isomarginal family, we perform an index-wise comparison of each diagonal element to the corresponding diagonal element in the original table. In other words, we compare each element in S(k) with the corresponding element in S₀, which is the instance of S(k) observed for the original table. If each diagonal element in the table is greater than or equal to its corresponding element in S₀, the table is assigned to set G, the set of “more extremely large” tables with respect to all elements of S(k). If each diagonal element is less than or equal to its corresponding element in S₀, the table is assigned to set L, the set of “more extremely small” tables. Equation (3) defines the proposed multivariate hypergeometric similarity measure h:

$$h={\displaystyle \sum _{L}p\left(q,r,k\right)}-{\displaystyle \sum _{G}p\left(q,r,k\right)}.$$ (3)

2.2 Similarity Measure Comparison

The sample rankings obtained from the proposed measure are compared with those from cosine similarity, Pearson correlation, and mutual information. Cosine similarity and Pearson correlation are defined for vectors V₁ and V₂ in (4) and (5), respectively. Mutual information is defined in (6), where x_i and y_j are the elements of V₁ and V₂, respectively:

$$\frac{V_1\cdot V_2}{\Vert V_1\Vert \Vert V_2\Vert },$$ (4)

$$\frac{\left(V_1-\overline{V_1}\right)\cdot \left(V_2-\overline{V_2}\right)}{\Vert V_1-\overline{V_1}\Vert \Vert V_2-\overline{V_2}\Vert },$$ (5)

$$-{\displaystyle \sum _i^{n}p(x_i)}{\log }_2\left(p(x_i)\right)-{\displaystyle \sum _j^{n}p(y_j)}{\log }_2\left(p(y_j)\right)+{\displaystyle \sum _i^n{\displaystyle \sum _j^{n}p(x_i,y_j)}{\log }_2\left(p(x_i,y_j)\right)}.$$ (6)

2.3. Synthetic Data

First, the performance of the multivariate hypergeometric similarity measure is evaluated on synthetic data. While the proposed similarity measure is defined for any n≥2 classes, these synthetic experiments are performed using only three classes to clearly illustrate the method. Two synthetic data sets are used for this comparison. The first consists of the three-class isomarginal family defined by marginal totals (r₁,r₂,r₃,q₁,q₂,q₃)=(5,5,5,5,5,5) and N=15. The second consists of all three-class tables with N=5.

2.4 Piecewise Approximation

Testing the significance of n×n contingency tables obtained from biomedical data, such as MSI data, poses a challenge due to data size. As the numbers of pixels in the images, and hence the marginal totals, increase, generating the isomarginal family of tables to perform the Fisher-Freeman-Halton test becomes demanding. The number of possible tables increases factorially as the numbers of rows, columns, or total pixels increase [18], [19]. As an analytical example, the number of three-class contingency tables where all rows and columns sum to r is given by _(r+22)+3_(r+34) [20], [21]. When faced with a very large number of tables to enumerate in the isomarginal family, approximate solutions can be found through Monte Carlo testing [17]. However, in practice, this may demand a very large numbers of permutations to achieve satisfactory separation of similarity rankings.

Here, we propose a piecewise method of approximation, in which the two images or data vectors to be compared are divided into a number of smaller subsections. The motivating idea is that similar samples will also have similar corresponding subsections. For each pair of reference and query subsections, an n×n contingency table is constructed and the multivariate hypergeometric similarity measure is calculated. The overall similarity of the image pair is computed as a function of the similarities of all subsections. Fig. 3 illustrates this process.

Fig. 3.

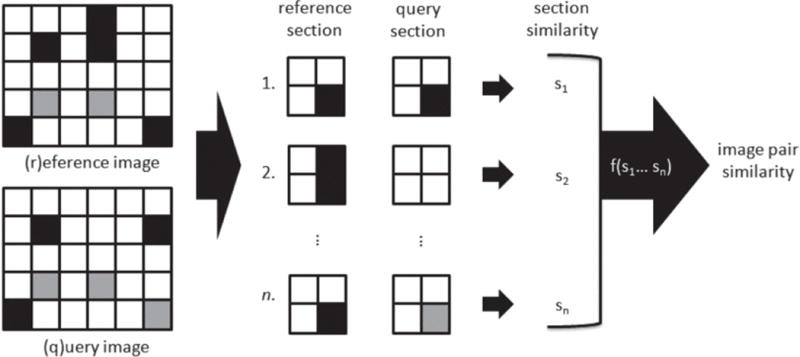
Overview of piecewise approximation process: subsection (1) corresponds to the top-left4×4 blocks of the reference and query images; (2) to the 4×4 blocks to the immediate right of (1); and (n) to the bottomright 4×4 blocks. The similarity is calculated for each spatially corresponding reference and query section, and the overall similarity of the reference and query is calculated as a function of the subsection scores.

Piecewise approximation requires choices in how images or data vectors are separated into subsections (e.g., different subsection sizes) and how the similarity scores for the subsections are combined to obtain an overall similarity score for the image pair (e.g., different functions). Alternative choices are examined here through experiments on synthetic and biomedical data. First, the previously described synthetic data set (for N=15) is used to examine whether there is a pattern between subsection size and the extent of difference observed between the piecewise approximation rankings and the exact rankings. In this test, the rankings for each sample obtained by using subsections of sizes 3, 4, and 5 pixels are compared with the ranking calculated using the whole sample. To avoid the comparison of single-pixel sections, if the sample is not evenly divisible at a particular increment size, the remainder pixels are added to the previous subsection to create one subsection larger than the others. In the same experiment, the effect of permuting the reference and query samples which correspond to a single n×n table is considered. While a given pair of samples yields a single n×n table, mapping a given table back to the sample space yields nonunique indexing of spatially corresponding pixels. This type of indexing difference would not affect the similarity score of a given reference and query pair if the whole sample is utilized. However, when piecewise approximation is employed, different subsections may contain different proportions of the pixels for each type of overlap k_ij. To examine how this may affect results, the “randperm” function in MATLAB was used to generate a permutation of the sample indices, which was applied to both the reference and query samples before they were divided into subsections. This was repeated 10, 000 times. The purpose of this step is to confirm that overall sample rankings in the synthetic data set are not an artifact of arbitrary methods of generating synthetic samples from tables and subsectioning samples. For each subsection size, the sample ranking results shown are the mean across all permutations. Next, biomedical data was used to empirically compare alternative functions for aggregating the subsection similarity scores into an overall score for the image pair.

2.5 Experimental Data

The experimental MSI data used in this study is from a mouse model of Tay-Sachs/Sandhoff disease [22]. The image corresponding to m/z 889.6 (located at index 783 within the data set) was selected as the reference image due to its distinctive spatial pattern. The MSI data set has a spectral dimension of 4, 438 m/z values, each corresponding to an m/z image, and all of these images were tested as query images against the reference image of m/z 889.6. The three-class case was used for this experiment: pixel intensities in the data set were binned into “high” (≥thresholdx), “low” (0< and <x), and “zero” (=0) classes. The threshold x was arbitrarily selected as the 50th percentile of the mean spectrum of the data set. The piecewise approximation approach was used with a primary subsection size of 4×4, chosen after testing several sizes in an effort to balance section size and computational time. The proposed similarity measure score was calculated for each subsection. Several functions for combining subsection scores into an aggregate image pair score were then compared by qualitatively evaluating the images which were ranked by each as highly similar to the reference. Finally, the top m/z images selected by the proposed similarity measure using three classes were compared to the three-class results for cosine similarity, Pearson correlation and mutual information.

The gene expression data used in this study consists of 230 breast cancer samples. The raw Affymetrix *.CEL files were downloaded from the Gene Expression Omnibus (GEO) website (accession: GSE20194). The Affymetrix Expression console software was used to compute log2 normalized gene expression values. Clinical information available on GEO was used to label each sample within the data set as estrogen receptor (ER) positive or negative, and the 141 ER+ samples were used for further analysis. The three-class case was also used for this experiment: gene-specific, percentile-based threshold pairs (x, y) were used to bin each gene expression value into the “high” (>y), “medium” (x< and ≤y) or “low” (≤x) class. Results from several alternative threshold pairs were compared. Probe “205225_at,” for the estrogen receptor gene (ESR1), was used as the reference sample.

Results

This section describes four sets of results. First, the performance of the proposed multivariate hypergeometric similarity measure is compared with the other similarity measures using synthetic data. Second, the effects of subsection size and combination functions on the piecewise approximation method are investigated using synthetic and experimental MSI data. Third, the performance of the proposed similarity measure on experimental MSI data is evaluated. Fourth, its performance is evaluated on experimental gene expression data.

In the first set of results, the rankings of samples in synthetic data sets by the four similarity measures are compared in Figs. 4 and 5. Each sample (horizontal bar) represents a single table, with the green, yellow, and red segments representing the number of exact matches (k₁₁+k₂₂+k₃₃), slight mismatches (k₁₂+k₂₁+k₂₃+k₃₂), and large mismatches (k₁₃+k₃₁), respectively. In Fig. 4, there are 231 tables represented; these tables comprise the isomarginal family defined by marginal totals (r₁,r₂,r₃,q₁, q₂,q₃)=(5,5,5,5,5,5). All four similarity measures agree in that the highest score is assigned to the table with the largest number of exact matches. None of the similarity measures are monotonic with respect to the number of exact matches, but rankings from the proposed similarity measure are much closer to this trend than rankings from cosine similarity and Pearson correlation. Cosine similarity and Pearson correlation more closely sort by the number of large mismatches. For a single isomarginal family, the magnitudes and means of the two vectors are constant. The rankings of cosine similarity and Pearson correlation therefore depend on the value of the dot product, and the minimum dot product is observed when the number of large mismatches is maximized. The proposed similarity measure does not provide such distinction between slight and large mismatches, but it does provide a probabilistic interpretation which cosine similarity and Pearson correlation do not: the samples associated with extreme scores are the most “surprising” patterns of overlap observed. Mutual information assigns higher scores to cases where most pixels are concentrated in a few classes, but does not differentiate among the classes. For example, the tables with [k₁₁,k₂₂,k₃₃]=[5,5,5] (i.e., all exact matches) and [k₃₁,k₂₂,k₁₃]=[5,5,5] (i.e., many large mismatches) both receive equally high scores; as a result, the mutual information results do not show any trend with respect to exact matches, slight mismatches or large mismatches. In contrast, [k₁₁,k₂₂,k₃₃]=[5,5,5] is ranked highly by the proposed similarity measure, while [k₃₁,k₂₂,k₁₃]=[5,5,5] receives a much lower score.

Fig. 4.

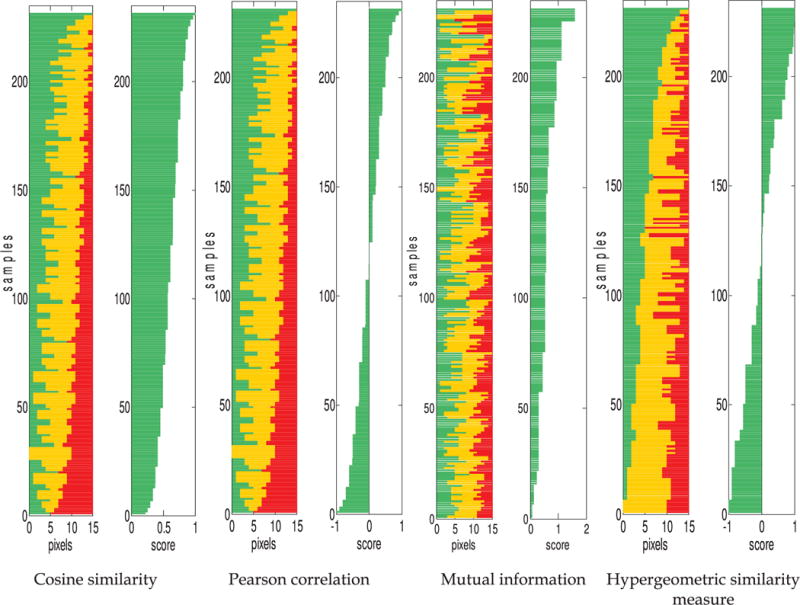
Comparison of sample rankings by the four similarity measures for the synthetic data set comprising the isomarginal family given by (r₁,r₂,r₃,q₁,q₂,q₃)=(5,5,5,5,5,5). Each sample (horizontal bar) represents a certain number of exact matches, slight mismatches, and large mismatches (corresponding to [green, yellow, and red], or [medium, light, and dark] in grayscale). The length of each color segment corresponds to the number of that type of match in the sample. For each similarity measure, the similarity score corresponding to each sample is shown on the right.

Fig. 5.

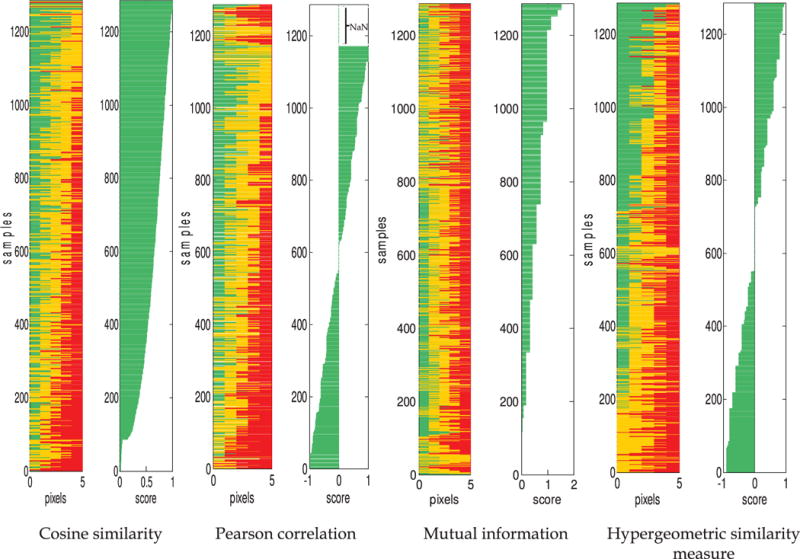
Comparison of sample rankings by the four similarity measures for the synthetic data set containing all tables for N=5. Each sample (horizontal bar) contains a certain number of exact matches, slight mismatches, and large mismatches (corresponding to [green, yellow, and red], or [medium, light, and dark] in grayscale). The length of each color segment corresponds to the number of that type of match in the sample. For each similarity measure, the similarity score for each sample is shown on the right.

Fig. 5 considers the rankings of the 1, 287 tables generated by considering every possible combination of marginal totals such that (r₁+r₂+r₃=5) and (q₁+q₂+ q₃=5). Again, all four similarity measures agree in that the highest score is assigned to the table with the largest number of exact matches, but the proposed similarity measure more consistently assigns lower scores to tables with fewer exact matches. The rankings in this set of all tables for N=5 illustrate additional probabilistic aspects of the proposed similarity measure. For example, the proposed measure can distinguish between instances of overlap with different distribution magnitudes. It assigns identical scores to the set of tables with [k₁₁,k₂₂,k₃₃ ] as [3,1,1],[1,3,1], and [1,1,3], and a different identical score to the other possible set of tables describing only exact overlap, with [k₁₁,k₂₂,k₃₃ ] as [2,2,1],[2,1,2], and [1,2,2]. Pearson correlation and cosine similarity do not distinguish between these two sets of tables. Mutual information distinguishes the two sets of tables, but again does not distinguish between cases of exact matches and many large mismatches; for example, the cases where [k₁₁,k₂₂,k₃₃]=[3,1,1] and [k₃₁,k₂₂,k₁₃]=[3,1,1] are assigned the same score, and[k₁₁,k₂₂,k₃₃]=[2,2,1] and [k₃₁,k₂₂,k₁₃]=[2,1,2] are assigned the same score. For a second example, in the proposed measure, all tables which have marginal totals such that only one n×n table is possible are mapped to a score of zero. If only one set of overlaps k_ij can be observed for a particular pair of images or data vectors, then the overlap which is observed can be considered inherently “unsurprising.” In contrast, this set of tables is undefined for Pearson correlation (i.e., these tables are assigned the value NaN, as shown at the top of the Pearson correlation plot in Fig. 5). Cosine similarity does not group these tables together or otherwise distinguish them.

In the second set of results, the effects of subsection size on the piecewise approximation result are described in Fig. 6. The 231 samples in the synthetic data set shown in Fig. 4 are plotted in order of increasing exact score. The piecewise approximation scores for each sample, across increments of sizes 3, 4, and 5, are compared. For all three subsection sizes, the mean score from 10, 000 permutations of the reference and query vectors is shown. Overall, the piecewise approximation scores follow the trend of the exact score, but there are notable deviations. In such cases, samples are ranked higher or lower as an artifact of the piecewise sectioning process. Interestingly, these cases tend to correspond across all of the subsection sizes; if a sample is scored much higher or lower than its adjacent samples by the piecewise method, the same jump or dip in score is observed across all three subsection sizes. However, the magnitudes of the piecewise scores indicate that, as expected, larger sections give scores closer to the exact result.

Fig. 6.

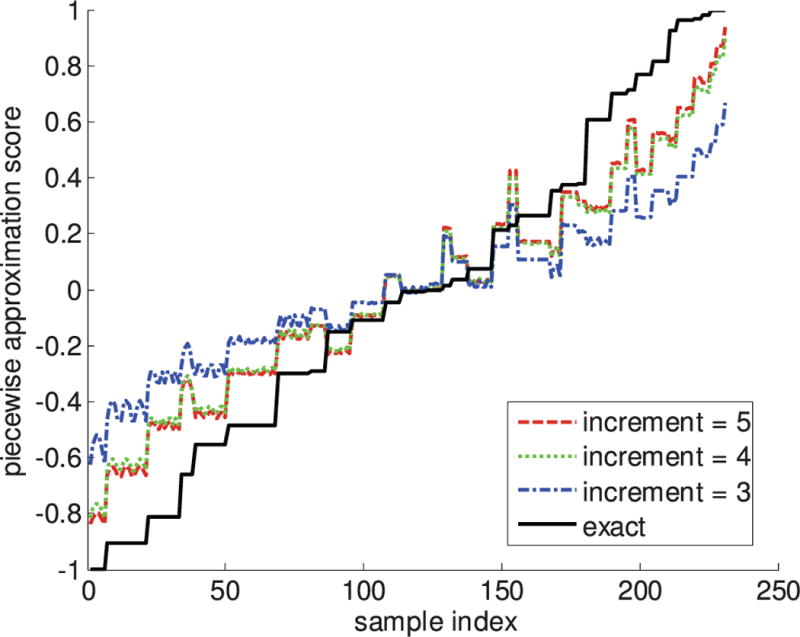
The mean rankings of synthetic samples using piecewise approximation at different subsection sizes (size 3: blue dash-dot line; size 4: green dotted line; and size 5: red dashed line) compared to rankings from using the whole sample (black, solid line).

Next, different statistics for combining the similarity scores of sections into a single overall score for the sample pair are compared empirically, using MSI data with a subsection size of 4×4 pixels for piecewise approximation. Fig. 7 shows the image pair similarity scores for each of the 4, 438 m/z values, computed as the mean, median, mode, variance, skewness, or kurtosis of all of their subsection scores. The x-axis of these plots, showing indices 1 through 4, 438, represents the query m/z images; each is associated with a single score (dot) on the y -axis. This score is obtained by evaluating the specified function (e.g., the mean) over the set of subsection scores obtained for that query image when it was compared to the reference image. To interpret these results, it is necessary to consider that the reference m/z image corresponds to index 783. Since the most similar image in the data set to the reference image should be the reference image itself, a well-performing function should assign the most extreme score to this index. This result is observed for the mean, median, variance, and kurtosis. During previous study of this data set, 47 of the 4, 438 images were observed to be qualitatively very similar to the reference m/z image, and those images were observed to be associated with indices relatively close to the reference index [10]. In contrast, lower indices were associated with noisy images (an artifact of MALDI MSI data acquisition), and higher indices with sparse images. A well-performing function would, therefore, exhibit a peak centered at the reference index of 783. The mean and kurtosis both show this feature by assigning extreme (higher and lower than most others, respectively) scores to indices close to the reference index.

Fig. 7.

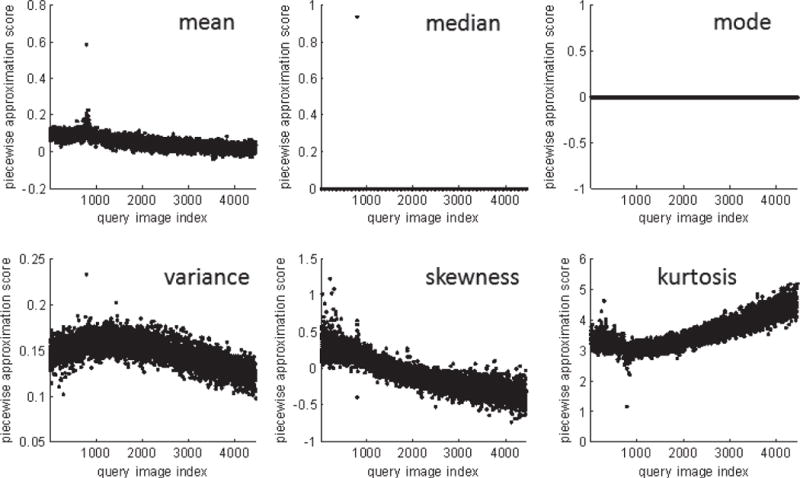
Empirical comparison of alternative functions for combining subsection similarity scores into an overall similarity score through piecewise approximation. Each dot on the scatter plot represents one query image (m/z value); 4, 438 are in the data set. The value (image pair score) of the dot represents the similarity score assigned to the query image based on the specified function of its subsection scores. For example, in the “mean” plot, the image pair score of each query image is the average similarity score of its subsections.

In the third set of results, these findings are applied to experimental MSI data. The 12m/z images selected by each measure as most similar to the reference image are shown in Fig. 8. All measures agree that the reference itself is the most similar (selection 1:m/z 889.6). Notably, the proposed similarity measure gives results which are qualitatively very similar to the reference m/z image. The Pearson correlation and mutual information results for three classes also closely resemble the reference m/z image, while the cosine similarity results for three classes include several noisy images without a clearly discernible pattern. Interestingly, the top 12 results selected by the proposed similarity measure using the mean and kurtosis as combination functions are not identical. Moreover, neither set of results overlaps completely with the results from Pearson correlation, cosine similarity, and mutual information. For example, the proposed similarity measure, using the mean as the combination function, selects m/z908.9, which none of the others select. Similarly, m/z 894.5, another unique selection, is picked by the proposed similarity measure when using the kurtosis as the combination function. Examining the top n results is common when applying a similarity measure to a data set, and these observations indicate that applying the proposed multivariate hypergeometric similarity measure can yield relevant and potentially useful results.

Fig. 8.

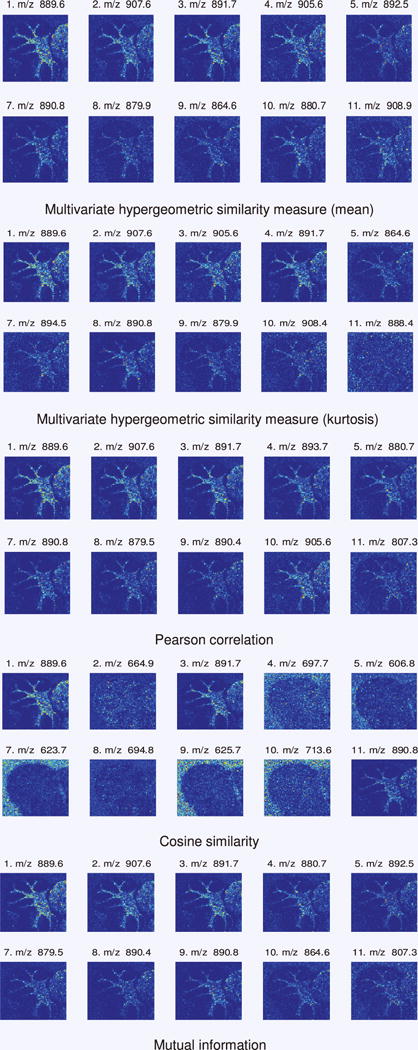
The 12 most similar m/z images, as ranked by the four similarity measures. The multivariate hypergeometric similarity measure results are shown with the mean and kurtosis as combination functions.

In the fourth set of results, Tables 1, 2, and 3 show the top 20 gene rankings for each of the similarity measures for a single ESR1 reference probe across three alternative percentile-based thresholds. First, in all cases, the reference probe “205225_at” is selected as the most similar, as it should be. Second, the multivariate hypergeometric similarity measure (using the mean as a combination function) identifies some of the other ESR1 probes as highly similar to the reference, but highlights the other probes to a lesser extent than the other three measures. Third, this set of results shows that the multivariate hypergeometric similarity measure is successful in identifying genes which are known to be associated with breast cancer, such as BCL2 and FOXA1 in Table 3. Fourth, notably, the proposed similarity measure highlights several genes—WWP1 [23] and NME5 [24] in Table 1, PGRMC2 [25] and HPN [26] in Table 2—which have recently been shown to be relevant in breast cancer, but which are not included in the top rankings of the other three similarity measures.

TABLE 1.

Top 20 Rankings by Similarity Measures, Using Percentiles [0, 25] as Thresholds

	Multivariate hypergeometric similarity measure		Pearson correlation		Cosine similarity		Mutual intormation
Rank	Probe	Gene	Probe	Gene	Probe	Gene	Probe	Gene
1	205225_at	ESR1	205225_at	ESR1	205225_at	ESR1	205225_at	ESR1
2	215552_s_at	ESR1	215552_s_at	ESR1	215552_s_at	ESR1	215552_s_at	ESR1
3	212960_at	TBC1D9	205253_at	PBX1	2052S3_at	PBX1	211235_s_at	ESR1
4	212637_s_at	WWP1	209603_at	GATA3	209603_at	GATA3	205253_at	PBX1
5	219717_at	DCAF16	218186_at	RAB25	218186_at	RAB25	209603_at	GATA3
6	217190_x_at	ESR1	211235_s_at	ESR1	211235_s_at	ESR1	218186_at	RAB25
7	218394_at	ROGDI	204508_s_at	CA12	200711_s_at	SKP1	212446_s_at	LASS6
8	203928_x_at	MAPT	200711_s_at	SKP1	203963_at	CA12	203928_x_at	MAPT
9	204242_s_at	ACOX3	203963_at	CA12	204508_s_at	CA12	200711_s_at	SKP1
10	209064_x_at	PAIP1	215867_x_at	CA12	215867_x_at	CA12	203963_at	CA12
11	212638_s_at	WWP1	217190_x_at	ESR1	217190_x_at	ESR1	204508_s_at	CA12
12	204045_at	TCEAL1	212446_s_at	LASS6	212446_s_at	LASS6	215867_x_at	CA12
13	203359_s_at	MYCBP	203928_x_at	MAPT	203928_x_at	MAPT	217190_x_at	ESR1
14	202596_at	ENSA	209759_s_at	DC1	204798_at	MYB	209064_x_at	PAIP1
15	218524_at	E4F1	212956_at	TBC1D9	209602_s_at	GATA3	209730_at	SEMA3F
16	211233_x_at	ESR1	218086_at	NPDC1	209604_s_at	GATA3	211778_s_at	OVOL2
17	221934_s_at	DALRD3	218195_at	C6orf211	209681_at	SLC19A2	208865_at	CSNK1A1
18	201353_s_at	BAZ2A	204798_at	MYB	209759_s_at	DCI	211234_x_at	ESR1
19	206197_at	NME5	210735_s_at	CA12	210735_s_at	CA12	202596_at	ENSA
20	200719_at	SKP1	212099_at	RHOB	212099_at	RHOB	208614_s_at	FLNB

TABLE 2.

Top 20 Rankings by Similarity Measures, Using Percentiles [25, 75] as Thresholds

	Multivariate hypergeometric similarity measure		Pearson correlation		Cosine similarity		Mutual information
Rank	Probe	Gene	Probe	Gene	Probe	Gene	Probe	Gene
1	205225_at	ESR1	205225_at	ESR1	205225_at	ESR1	205225_at	ESR1
2	211234_x_at	ESR1	215552_s_at	ESR1	215552_s_at	ESR1	215552_s_at	ESR1
3	203359_s_at	MYCBP	211235_s_at	ESR1	211235_s_at	ESR1	211235_s_at	ESR1
4	215552_s_at	ESR1	211234_x_at	ESR1	211234_x_at	ESR1	211234_x_at	ESR1
5	218259_at	MKL2	211233_x_at	ESR1	211233_x_at	ESR1	211233_x_at	ESR1
6	212960_at	TBC1D9	204798_at	MYB	204798_at	MYB	204798_at	MYB
7	204798_at	MYB	204667_at	FOXA1	204667_at	FOXA1	217190_x_at	ESR1
8	209739_s_at	PNPLA4	217190_x_at	ESR1	217190_x_at	ESR1	204667_at	FOXA1
9	201701_s_at	PGRMC2	218437_s_at	LZTFL1	218437_s_at	LZTFL1	209603_at	GATA3
10	205597_at	SLC44A4	215014_at	KCND3	215014_at	KCND3	205253_at	PBX1
11	206869_at	CHAD	209681_at	SLC19A2	209681_at	SLC19A2	211596_s_at	LRIG1
12	203928_x_at	MAPT	208613_s_at	FLNB	208613_s_at	FLNB	203072_at	MYO1E
13	205140_at	FPGT	209603_at	GATA3	203359_s_at	MYCBP	201426_s_at	VIM
14	212956_at	TBC1D9	203359_s_at	MYCBP	208716_s_at	TMCO1	203359_s_at	MYCBP
15	213648_at	EXOSC7	208716_s_at	TMCO1	209603_at	GATA3	218259_at	MKL2
16	204242_s_at	ACOX3	218259_at	MKL2	218259_at	MKL2	209681_at	SLC19A2
17	204934_s_at	HPN	205158_at	RNASE4	205158_at	RNASE4	218437_s_at	LZTFL1
18	211233_x_at	ESR1	209696_at	FBP1	202454_s_at	ERBB3	208613_s_at	FLNB
19	200776_s_at	BZW1	202454_s_at	ERBB3	209696_at	FBP1	215014_at	KCND3
20	203420_at	FAM8A1	217770_at	PIGT	217770_at	PIGT	204508_s_at	CA12

TABLE 3.

Top 20 Rankings by Similarity Measures, Using Percentiles [50, 100] as Thresholds

	Multivariate hypergeometric similarity measure		Pearson correlation		Cosine similarity		Mutual information
Rank	Probe	Gene	Probe	Gene	Probe	Gene	Probe	Gene
1	205225_at	ESR1	205225_at	ESR1	205225_at	ESR1	205225_at	ESR1
2	215552_s_at	ESR1	215552_s_at	ESR1	215552_s_at	ESR1	215552_s_at	ESR1
3	211235_s_at	ESR1	211235_s_at	ESR1	211235_s_at	ESR1	211235_s_at	ESR1
4	200711_s_at	SKP1	204667_at	FOXA1	204667_at	FOXA1	204667_at	FOXA1
5	215014_at	KCND3	211234_x_at	ESR1	211234_x_at	ESR1	211234_x_at	ESR1
6	211234_x_at	ESR1	218437_s_at	LZTFL1	218094_s_at	DBNDD2 SYS1/SYS1-DBNDD2	218094_s_at	DBNDD2/SYS1/SYS1-DBNDD2
7	204667_at	FOXA1	218094_s_at	DBNDD2/SYS1/SYS1-DBNDD2	218437_s_at	LZTFL1	218437_s_at	LZTFL1
8	21052_s_at	TIC39A	200711_s_at	SKP1	200711_s_at	SKP1	206571_s_at	MAP4K4
9	218035_s_at	RBM47	211233_x_at	ESR1	202088_at	SLC39A6	200711_s_at	SKP1
10	203928_x_at	MAPT	202088_at	SLC39A6	202089_s_at	SLC39A6	202088_at	SLC39A6
11	41660_at	CELSR1	202089_s_at	SLC39A6	211233_x_at	ESR1	202089_s_at	SLC39A6
12	217190_x_at	ESR1	204798_at	MYB	201169_s_at	BHLHE40	211233_x_at	ESR1
13	208810_at	DNAJB6/TMEM135	208336_s_at	TECR	204798_at	MYB	219155_at	PITPNC1
14	208336_s_at	TECR	210652_s_at	TIC39A	205186_at	DNALI1	219506_at	C1orf54
15	201845_s_at	RYBP	217860_at	NDUFA10	208336_s_at	TECR	219806_s_at	C11orf75
16	204798_at	MYB	205186_at	DNALI1	209604_s_at	GATA3	201169_s_at	BHLHE40
17	218094_s_at	DBNDD2/SYS1/SYS1-DBNDD2	209604_s_at	GATA3	210652_s_at	TTC39A	204798_at	MYB
18	201826_s_at	SCCPDH	222125_s_at	P4HTM	217860_at	NDUFA10	205186_at	DNALI1
19	206401_s_at	MAPT	201169_s_at	BHLHE40	222125_s_at	P4HTM	208336_s_at	TECR
20	203685_at	BCL2	218026_at	CCDC56	200946_x_at	GLUD1	209604_s_at	GATA3

These results also emphasize the value of integrating multiple forms of analysis to leverage complementary findings. For example, recent investigations have examined the role of MAPT [27] and GATA3 [28] in breast cancer; while MAPT appears in the top rankings of all four similarity measures in Table 1, GATA3 appears in the rankings of the other three similarity measures, but not in those of the multivariate hypergeometric similarity measure. Additionally, the benefits of examining a single data set across alternative thresholds can be clearly observed through the notably different gene lists for each measure in Tables 1, 2, and 3. In addition, parallel assessments with different probes for the same gene are also important. For example, the top 20 rankings by the multivariate hypergeometric similarity measure for ESR1 probe “211235_s_at” in the same data set (rankings not shown) highlight several other genes—IGF1R [29], [30],GMPR2 [31], FGFR3 [32]—which have recently been shown to be relevant in breast cancer. Again, these observations indicate that applying the proposed multivariate hypergeometric similarity measure can yield relevant and potentially useful results.

Discussion

In this paper, we propose a multivariate hypergeometric similarity measure for the pairwise comparison of images and data vectors featuring any positive integer number of intensity levels. This is an extension of our previous work on a hypergeometric similarity measure, which was restricted to binary data. Using synthetic data sets, we compared the proposed measure to Pearson correlation, cosine similarity and mutual information in terms of sample rankings, and identified several favorable properties of the proposed measure. Next, we developed a method of piecewise approximation to facilitate the application of this approach to large data sets. Piecewise approximation was tested at several different subsection sizes on synthetic data, and was observed to follow the trend of the exact score. Then, biological MSI data was used to empirically assess functions for combining subsection similarity scores found through piecewise approximation. The proposed similarity measure was demonstrated to be effective in identifying qualitatively similar images in MSI data and breast cancer-related genes in microarray data. For both data types, it made relevant selections which were not identified by other similarity measures in their top selections.

While the current results of this study are encouraging, they also highlight several avenues for further research on the proposed similarity measure. For instance, this approach is defined for any positive integer number of classes, but the results in this study have considered only three classes. Three classes were chosen both for simplicity in examining similarity measure properties and to highlight the difference between the binary case and the multiclass case. Future work will assess the effect of increasing the number of classes. However, as previously noted, the generation of the isomarginal family becomes increasingly demanding as the number of classes increases [18], [19],[20], [21]. Additionally, alternative definitions of the statistic S (k) will be explored. Here, we chose S (k) as the set of diagonal elements of the contingency table. However, it may be desirable to include sub- and superdiagonal terms when larger numbers of classes are considered. The selection of the appropriate number of classes—and of appropriate thresholds for separating classes—is another issue of interest; in this study, the thresholds between classes for the MSI and gene expression data sets were arbitrarily selected. From the perspective of practical biomedical applications, choices of thresholds for a particular data set may be based on examination of descriptive data statistics, or by applying selected tests as a preliminary step [33]. The selection of functions for aggregating subsection scores obtained from piecewise approximation is another area for further study. Six statistics were tested in this study, and many additional functions could be tested. Interestingly, the set of top selections for MSI data using the mean and kurtosis were not identical, indicating that it may be useful to consider which combination functions may be complimentary.

A notable constraint is that the molecular identities of the m/z values are not known for the MSI data set investigated here; future testing on labeled (MS/MS) data will enable biological interpretation of similarity measure performances for MSI data, similar to what was done for the microarray data. In addition, only one MSI and one microarray data set have been investigated here; implementation on multiple data sets will provide another key measure of performance. Finally, this paper focuses on the application to MSI and gene expression data, but the proposed similarity measure could also be applied to other types of biological data. Future work will also examine the performance of the proposed multivariate hypergeometric similarity measure for detecting patterns in other types of large-scale biological data sets, with which other similarity measures like mutual information, cosine similarity, and Pearson correlation are currently used.