Domain Adaptation for Alzheimer’s Disease Diagnostics

Abstract

With the increasing prevalence of Alzheimer’s disease, research focuses on the early computer-aided diagnosis of dementia with the goal to understand the disease process, determine risk and preserving factors, and explore preventive therapies. By now, large amounts of data from multi-site studies have been made available for developing, training, and evaluating automated classifiers. Yet, their translation to the clinic remains challenging, in part due to their limited generalizability across different datasets. In this work, we describe a compact classification approach that mitigates overfitting by regularizing the multinomial regression with the mixed ℓ₁/ℓ₂ norm. We combine volume, thickness, and anatomical shape features from MRI scans to characterize neuroanatomy for the three-class classification of Alzheimer’s disease, mild cognitive impairment and healthy controls. We demonstrate high classification accuracy via independent evaluation within the scope of the CADDementia challenge. We, furthermore, demonstrate that variations between source and target datasets can substantially influence classification accuracy. The main contribution of this work addresses this problem by proposing an approach for supervised domain adaptation based on instance weighting. Integration of this method into our classifier allows us to assess different strategies for domain adaptation. Our results demonstrate (i) that training on only the target training set yields better results than the naïve combination (union) of source and target training sets, and (ii) that domain adaptation with instance weighting yields the best classification results, especially if only a small training component of the target dataset is available. These insights imply that successful deployment of systems for computer-aided diagnostics to the clinic depends not only on accurate classifiers that avoid overfitting, but also on a dedicated domain adaptation strategy.

1. Introduction

Alzheimer’s disease (AD) is the most common form of dementia with incidence rates further increasing in the future due to increasing life expectancy. Early and accurate diagnosis of AD is a key objective as it can help patients to access supportive therapies earlier allowing them to maintain independence for longer (Paquerault, 2012). When treatment options that directly interfere with disease pathways finally become available, intervention will likely be most effective in early preclinical or presymptomatic disease stages. Furthermore, early identification of high-risk individuals can already support selection into promising drug trials, inform patient stratification, as well as aid the identification of risk and preserving factors. Magnetic resonance imaging (MRI) is an important tool for AD diagnosis because the atrophy measured in MRI correlates with neuron loss and can indicate the onset of the impairment in close temporal proximity (Jack et al., 2013). Computer-aided diagnosis of dementia based on MRI is an active research field as indicated by 50 articles reviewed on this topic by Falahati et al. (2014). The deployment of automated system for diagnosis of AD in the clinic promises several advantages: (i) the improvement of diagnosis in places with limited neuroradiological know-how, (ii) a faster diagnosis without compromising accuracy by avoiding lengthy specialist investigations, and (iii) a more objective diagnostic assessment based increasingly on quantitative information in contrast to traditionally more subjective diagnostic impression (Klöppel et al., 2012). Computational diagnostics promise to be particularly useful for screening purposes to identify individuals with preclinical disease.

Large, multi-center datasets are available for studying Alzheimer’s disease and for supporting the training of complex classification models. A challenge for such models is generalizability, i.e., the ability to transfer a model that is trained on one dataset to another dataset while retaining high prediction accuracy. In an attempt to provide an objective assessment of state-of-the-art methods for AD classification, the CADDementia challenge has been organized recently (Bron et al., 2015). The task was to differentiate between patients with Alzheimer’s disease, mild cognitive impairment (MCI), and healthy controls (CN) based on T1-weighted MRI data. Classification accuracy of a variety of submissions was evaluated on an independent test dataset with hidden diagnosis. Intriguingly, the study showed that all participating groups overestimated the accuracy of their method. One of the main reasons for the overestimation may be overfitting to the training data. Neuroimaging applications are susceptible to overfitting due to a potentially large number of features extracted from images and a restricted number of samples available for training. Overfitting is further aggravated by complex classification models with many degrees-of-freedom that easily fine-tune to a specific population but overestimate the performance on the general population (Adaszewski et al., 2013; Mwangi et al., 2014). In our classifier we employ methods that mitigate overfitting by (i) using sparsity constraints to estimate a compact model and by (ii) choosing a linear classification model based on multinomial regression to further limit the number of free parameters. Yet, in spite of these efforts, the bias towards overestimating performance on the training set still prevails, indicating that overfitting may not solely be responsible. Here, we identify another cause for reduced classification accuracy on the final test set: the differences in the distribution between training and test data.

The main contributions of this work are twofold: We introduce a compact classifier for Alzheimer’s disease that incorporates shape information and evaluate its performance on an independent test setting. We further demonstrate that variations in source and target datasets have a large impact on classification accuracy and present a novel algorithm for domain adaptation that re-weights samples from the source dataset.

1.1. Computer-Aided Diagnosis of Dementia

Predicting or classifying dementia based on structural MRI is an active field of research. Cuingnet et al. (2011) compare several approaches for the discrimination of AD and MCI patients using the cortical thickness, the hippocampus and voxel-based methods. Falahati et al. (2014) review the literature for the classification of individuals with dementia. The extensive list of articles discussed in the review illustrates the wide interest in the research field. In this work, we introduce an algorithm for AD classification that is based on BrainPrint (Wachinger et al., 2015) for quantifying brain morphology, which naturally extends the region of interest (ROI)-based volume and thickness analysis with shape information (Reuter et al., 2006). Anatomical shape features contribute valuable information to the characterization of brain structures, which are only coarsely represented by their volume. Finding representative and descriptive features is crucial for automatic classification as it is well known in pattern recognition that the prediction accuracy is primarily driven by the representation (Dickinson, 2009).

Both of the review articles mentioned above refer to a total of only three publications that employ shape information, indicating that shape is not commonly used. Most previous work that includes shape analysis, typically focus on a single structure, predominantly the hippocampus. More precisely, Gerardin et al. (2009) approximate the hippocampal shape by a series of spherical harmonics. Ferrarini et al. (2009) use permutation tests to extract surface locations that are significantly different among patients with AD and controls. Costafreda et al. (2011) incorporate shape information by deriving thickness measurements of the hippocampus from a medical representation. Shen et al. (2012) use statistical shape models to detect hippocampal shape changes. Bates et al. (2011) investigated spectral signatures for AD classification, with a focus on right hippocampus, right thalamus and right putamen. Other structures of interest for shape analysis were the cortex and ventricles: Kim et al. (2014) use multi-resolution shape features with non-Euclidean wavelets for the analysis of cortical thickness, King et al. (2010) analyze the fractal dimension of the cortical ribbon, and Gutman et al. (2013) model surface changes of the ventricles in a longitudinal setup with a medial representation. In contrast to all these studies, we incorporate an ensemble of both cortical and subcortical structures. This extensive characterization of brain anatomy is promising in diagnosing Alzheimer’s disease, which is associated with widespread atrophy across the entire brain.

1.2. Domain Adaptation

As described above, differences between source and target datasets can significantly reduce classification accuracy. In traditional cross-validation, where a single dataset is split into subsets, such variations are negligible, as the subsets tend to represent the data well. However, when an independent dataset is used for testing, differences in the distributions can have a dramatic impact on the classification accuracy. Such problems are studied in domain adaptation (Pan and Yang, 2010), where the model is learned on a source dataset and then transferred to a target dataset with different properties. In fact, we believe that domain adaptation is crucial for the translation of computer-aided diagnostic methods to the clinic, where the source dataset usually consists of large, possibly multi-center, data and the target dataset is the (limited) data acquired at the specific hospital, where the system is deployed. There are clearly several factors that can contribute to variations between source and target datasets arising from location and selection biases.

Here, we assume a supervised domain adaptation scenario, where a subset of the target dataset is available for training, replicating the situation that a small, local dataset from the clinic is available to support training. Based on this small target training set we weight samples from the source dataset to match distributional properties of the target dataset. The proposed instance weighting presents a general framework, where naïve strategies for combining source and target training data (e.g. the union or selecting one vs. the other) can be derived by setting the weights to appropriate constants. We measure a variation in classification accuracy of more than 20% across strategies, highlighting the importance of domain adaptation. Domain adaptation with instance weighting has previously been described in the machine learning literature (Bickel et al., 2007; Jiang and Zhai, 2007). An unsupervised domain adaptation strategy for AD classification was used by Moradi et al. (2014). This strategy applies discriminative clustering on the source and target domain, where a feature weighting is learned by optimizing the mutual information (Shi and Sha, 2012). In contrast, we use a supervised domain adaptation strategy and do not weight features but instances. Further related are approaches that assume a semi-supervised classification setting (Zhao et al., 2014; Adeli-Mosabbeb et al., 2015), yet they operate on the same domain.

Domain adaptation has previously been successfully used in medical image analysis. van Opbroek et al. (2015) proposed transfer learning for image segmentation across scanners and image protocols with support vector machines and AdaBoost. Heimann et al. (2013) used domain adaptation for the localization of ultrasound transducers in X-ray images with probabilistic boosting trees. Schlegl et al. (2014) applied domain adaptation for lung tissue classification with convolutional neural networks.

2. Methods

In this section, we introduce our approach to AD classification with domain adaptation. The classification task is to predict the diagnostic label y of an individual based on image and non-image data summarized in the vector x. First, we introduce the multinomial classifier used for the prediction. We then derive our approach to multinomial regression with domain adaptation, and finally describe the extraction of image-based features from MRI scans with a focus on shape features from the BrainPrint.

2.1. Elastic-Net Multinomial Regression for Alzheimer’s Classification

We employ multinomial regression with a generalized linear model for the classification of subjects in three diagnostic groups (controls, MCI, and AD). The high-dimensional characterization of an individual may cause overfitting on the training dataset. We therefore select a subset of the features to establish a compact model. The elastic-net regularizes multinomial regression: During the estimation of a model for predicting diagnostic label y from observation x it identifies the most predictive variables (Friedman et al., 2010). The categorical response variable y has K = 3 levels with AD, MCI, and CN. We use the multi-logit model, which is a generalization of linear logistic regression to the multi-class situation. The conditional probability for label ℓ is

$$p(y=\ell \mid \mathbf{x})=\frac{e^{{\beta }_{0\ell }+{\mathbf{x}}^{\top }{\beta }_{\ell }}}{{\sum }_{k=1}^K{e}^{{\beta }_{0k}+{\mathbf{x}}^{\top }{\beta }_k}}$$ (1)

with regression coefficients β. The model is fitted by regularized maximum multinomial likelihood with a penalty on the regression coefficients R(β)

$$\underset{{\{{\beta }_{0\ell },{\beta }_{\ell }\}}_1^K\in {ℝ}^{K(p+1)}}{max}\left[\frac{1}{N}\sum _{i=1}^{N}logp(y_i\mid {\mathbf{x}}_i)-\kappa \sum _{\ell =1}^K{R}_{\alpha }({\beta }_{\ell })\right]$$ (2)

with N the number of training samples. The parameter κ balances the data fit term with the penalty term.

The regularizer in elastic-net combines lasso ℓ ₁ and ridge-regression ℓ₂ penalties, modulated by the parameter α

$$R_{\alpha }(\beta )=(1-\alpha )\frac{1}{2}{\Vert \beta \Vert }_2^2+\alpha {\Vert \beta \Vert }_1.$$ (3)

For correlated predictors, ridge-regression shrinks their coefficients and allows them to borrow strength from each other. In contrast, lasso will tend to pick one and ignore the rest. Increasing α from 0 to 1 will monotonically increase the sparsity of the solution until the lasso solution is reached. In a comparison of methods for model selection (Wachinger et al., 2014), we obtained the best results for the elastic-net, when compared to manual selection or the stepwise selection with the Akaike information criterion.

2.2. Domain Adaptation for AD Classification

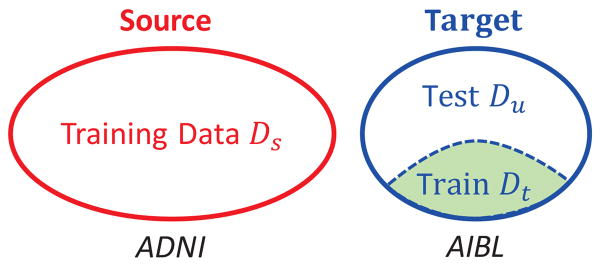
Domain adaptation distinguishes between a source domain and a target domain (Quionero-Candela et al., 2009; Pan and Yang, 2010; Margolis, 2011). The setup for supervised domain adaptation is schematically illustrated in Fig. 1. The source domain is the training domain with labeled data $D_s={\{({\mathbf{x}}_i^s,y_i^s)\}}_{i=1}^{N_s}$, while the target domain is the test domain with only a fraction of labeled data. The labeled data in the target domain is denoted as $D_t={\{({\mathbf{x}}_i^t,y_i^t)\}}_{i=1}^{N_t}$ and the unlabeled data in the target domain as $D_u={\{({\mathbf{x}}_i^u,y_i^u)\}}_{i=1}^{N_u}$. As common in supervised domain adaptation, we assume N_s ≫ N_t and further that the training subset in the target domain is representative of the entire target dataset.

Figure 1.

Supervised domain adaptation with source (red) and target (blue) domains, where a part of the target data (green) is available for training. In the experiments, we use the ADNI data as source data and AIBL data as target data.

For the formulation of the problem, we consider supervised learning as empirical risk minimization. Abstractly, the optimal model θ^* in the model family Θ is inferred by minimizing the loss function L

$${\theta }^{\ast }=\underset{\theta \in \mathrm{\Theta }}{argmin}\sum _{(\mathbf{x},y)\in \mathcal{X}\times \mathcal{Y}}p(\mathbf{x},y)·L(\mathbf{x},y,\theta )$$ (4)

with the joint distribution over observations and labels p(x, y), the input space 𝒳 and label set 𝒴. In this work, we use the negative log-likelihood function from the multi-logit model (first term in Eq. (2)) as loss function, but the formulation is of general nature and therefore also extends to other loss functions. Since the joint distribution p(x, y) is unknown, we use the empirical approximation with the training data ${\{({\mathbf{x}}_i,y_i)\}}_{i=1}^N$

$$\widehat{\theta }=\underset{\theta \in \mathrm{\Theta }}{argmin}\sum _{i=1}^{N}L({\mathbf{x}}_i,y_i,\theta ).$$ (5)

This setup considers a single dataset. For domain adaptation, we want to infer the model with minimal loss on the target dataset D_t, while the source training sample D_s is randomly sampled from the source distribution p_s. In domain adaptation with instance weighting, this problem is addressed by re-weighting the elements of the source training dataset. The weight is dependent on the probability of source samples in the target domain, which can be derived as follows

$${\theta }_t^{\ast }=\underset{\theta \in \mathrm{\Theta }}{argmin}\sum _{(\mathbf{x},y)\in \mathcal{X}\times \mathcal{Y}}{p}_t(\mathbf{x},y)·L(\mathbf{x},y,\theta )$$ (6)

$$=\underset{\theta \in \mathrm{\Theta }}{argmin}\sum _{(\mathbf{x},y)\in \mathcal{X}\times \mathcal{Y}}\frac{p_t(\mathbf{x},y)}{p_s(\mathbf{x},y)}{p}_s(\mathbf{x},y)·L(\mathbf{x},y,\theta )$$ (7)

$$\approx \underset{\theta \in \mathrm{\Theta }}{argmin}\sum _{i=1}^{N_s}\frac{p_t({\mathbf{x}}_i^s,y_i^s)}{p_s({\mathbf{x}}_i^s,y_i^s)}·L({\mathbf{x}}_i^s,y_i^s,\theta ).$$ (8)

Considering further that training data is also available from the target domain, the model estimation is

$${\theta }_t^{\ast }=\underset{\theta \in \mathrm{\Theta }}{argmin}\sum _{i=1}^{N_s}\frac{p_t({\mathbf{x}}_i^s,y_i^s)}{p_s({\mathbf{x}}_i^s,y_i^s)}·L({\mathbf{x}}_i^s,y_i^s,\theta )+\sum _{i=1}^{N_t}L({\mathbf{x}}_i^t,y_i^t,\theta ).$$ (9)

The ratio

$$w_i=\frac{p_t({\mathbf{x}}_i^s,y_i^s)}{p_s({\mathbf{x}}_i^s,y_i^s)}$$ (10)

is the weighting factor for the sample ( ${\mathbf{x}}_i^s,y_i^s$). It evaluates the probability of the source data sample ( ${\mathbf{x}}_i^s,y_i^s$) under the target distribution p_t, normalized by the probability under the the source distribution. The challenging part is the estimation of the probability of the source data under the target distribution $p_t({\mathbf{x}}_i^s,y_i^s)$. For supervised domain adaptation, we have training data in the target domain D_t, which we will use for estimating the target distribution. Fig. 2 illustrates source and target datasets. The probability density functions highlight the different distribution of both datasets. The weight emphasizes points that lie in high density regions of the target domain and low density regions of the source domain, in the figure these are the red dots towards the right. With this re-weighting of the source domain, we infer a model that is better adapted to the target domain and consequently yields higher classification accuracy.

Figure 2.

Schematic illustration of data points (subjects) from the source (blue) and target (red) domain (top). Marginal distributions of the source p_s and target p_t domain (center) show the variation between both domains. With instance weighting by the term w = p_t/p_s (bottom), red source data points on right are assigned higher weights in the estimation of the regression coefficients, while source data points on the left are assigned lower weights.

In contrast to covariate shift that only considers variations in the marginal distributions of the observations p_s(x) ≠ p_t(x) (Shimodaira, 2000) and class imbalance that only considers variations in the marginal distributions of the labels p_s(y) ≠ p_t(y) (Japkowicz and Stephen, 2002), we consider variations in the joint distribution p_s(x, y) ≠ p_t(x, y). To facilitate the estimation, we use the factorization p(x, y) = p(x)p(y), which implies the assumption of independence. The factorization is continued on the multivariate variable x, yielding a product of univariate densities. An alternative would be the direct estimation of the high-dimensional joint density, however, a reliable estimation would require the number of samples to grow exponentially with the number of dimensions. Given the limited number of elements in the target training dataset, a reliable estimation in higher dimensions seems not feasible. In this work, we select diagnostic information, age, sex, and the number APOE4 allele for instance weighting, because they capture important characteristics about an individual. The distributions are estimated with histogramming for discrete variables and kernel density estimation for continuous variables.

The integration of instance weighting for domain adaptation in the multinomial regression in Eq.(2) results in

$$\underset{{\{{\beta }_{0\ell },{\beta }_{\ell }\}}_1^K\in {ℝ}^{K(p+1)}}{max}\left[\sum _{i=1}^{N_s}{w}_{i}logp(y_i^s\mid {\mathbf{x}}_i^s)+\sum _{i=1}^{N_t}logp(y_i^t\mid {\mathbf{x}}_i^t)-\kappa \sum _{\ell =1}^K{P}_{\alpha }({\beta }_{\ell })\right],$$ (11)

where the regression coefficients β correspond to the model parameters θ and training samples in the log-likelihood function are weighted. The weights w_i are defined in Eq.(10) for training samples of the source dataset. Samples from the target training dataset have constant weight one. For solving the optimization problem in Eq.(11), a coordinate descent scheme is used (Friedman et al., 2010). In nested loops over the parameter κ and the classes, partial quadratic approximations to the log-likelihood are computed, where regression coefficients only vary for a single class at a time. Coordinate descent is then used to solve the penalized weighted least-squares problem.

In addition to setting the weights according to the equation for instance weighting, we can enforce different domain adaptation strategies by setting the weights to a constant, w_i = c. The strategies differ in the data used for training:

1. c ≫ 1: only the source training dataset D_s,

2. c = 0: only the target training dataset D_t,

3. c = 1: the union of both training sets D_s ∪ D_t.

Selecting either one of the datasets or combining both are straightforward approaches that do not take the challenges of domain adaptation into account. We show in the results’ section that the chosen strategy substantially influences the classification result.

2.3. Image-Based Features for Classification

As mentioned above, the selection of descriptive features for the classifier is essential for the performance. For the extraction of image-based features, we process the scans with FreeSurfer (Dale and Sereno, 1993; Dale et al., 1999; Fischl et al., 1999a,b, 2002). FreeSurfer automatically segments cortical and subcortical structures in the image. Based on the segmentation, we use the thickness of 70 cortical regions and the volume 39 brain structures. Next to volume and thickness, we use shape features that are derived from the BrainPrint, further explained in Section 2.3.1. The shape features include 14 lateral shape differences and 44 PCA shape variations. The total number of image features for the classification is 167. According to the recent analysis of the normalization of variables for AD classification (Westman et al., 2013), we normalize volumetric measures by the intracranial volume (ICV) but do not normalize cortical thickness measures. Age residualization with linear regression was performed for each feature to remove the confounding effect of age in the analysis. After ICV normalization and age residualization, age and gender was not used in multinomial regression.

2.3.1. The Brain Descriptor BrainPrint

We create surface and volumetric meshes from cortical and subcortical segmentations. Based on these meshes, we compute compact shape representations for all structures, constituting the BrainPrint (Wachinger et al., 2015). The shapeDNA (Reuter et al., 2006) is used as shape descriptor, which performed among the best in a comparison of methods for non-rigid 3D shape retrieval (Lian et al., 2012). The Laplace-Beltrami spectrum is computed on the intrinsic geometry of the object to form the shapeDNA. Considering the Laplace-Beltrami operator Δ, one obtains the spectrum by solving the Laplacian eigenvalue problem (Helmholtz equation)

$$\mathrm{\Delta }f=-\lambda f.$$ (12)

The solution consists of eigenvalue λ_i ∈ ℝ and eigenfunction f_i pairs, sorted by eigenvalues, 0 ≤ λ₁ ≤ λ₂ ≤ … (a positive diverging sequence). The first l non-zero eigenvalues computed using the finite element methods, form the shapeDNA: λ = (λ₁, …, λ_l). To achieve scale independence, we normalize the eigenvalues, ${\lambda }^{\prime }={\text{vol}}^{\frac{2}{D}}\lambda$, where vol is the Riemannian volume of the D-dimensional manifold (Reuter et al., 2006), i.e., the surface area for 2D manifolds. Fig. 3 illustrates the first three eigenfunctions of the left white matter surface. The eigenfunctions show natural vibrations of the shape when oscillating at a frequency specified by the square root of the eigenvalue. We also map the same eigenfunctions on the inflated surface to highlight the characteristics of the eigenfunctions, not obscured by the complex cortical folding patterns.

Figure 3.

Left white matter surface and first three non-constant eigenfunctions of the Laplace-Beltrami operator calculated on the surface, where shape features are derived from natural frequencies of eigenfunctions. Top: Eigenfunctions shown with color gradient. Bottom: Inflated white matter surface with eigenfunctions shown as level sets. The main directions of variation are anterior-posterior, superior-inferior, and lateral-medial, respectively.

The eigenvalues are isometry invariant with respect to the Riemannian manifold, meaning that length-preserving deformations will not change the spectrum. Isometry invariance includes rigid body motion and therefore permits the comparison of shapes across subjects by directly comparing the shapeDNA. A second property is that the spectrum continuously changes with topology-preserving deformations of the boundary of the object. These properties make the shapeDNA well suited for comparing shapes, as initial alignment of the shapes can be completely avoided.

We compute the spectra for all cortical and subcortical structures on the 2D boundary surfaces (triangle meshes (Reuter et al., 2009; Niethammer et al., 2007)) and additionally for cortical structures (white and pial surfaces in both hemispheres) also on the full 3D solid (tetrahedra meshes (Reuter et al., 2007)), forming the BrainPrint Λ = (λ₁, …, λ_η). The BrainPrint contains 36 subcortical structures and 8 descriptors for cortical structures (left/right, white/gray matter, 2D/3D), yielding η = 44.

2.3.2. Features from BrainPrint

Depending on the number of eigenvalues l computed, we can easily end up with thousands of values in the Brain-Print, which may make the approach more susceptible to overfitting. To decrease the number of variables and increase robustness, we (i) use a 1D asymmetry measure (the distance of BrainPrint across hemispheres), and (ii) employ principal component analysis. An important aspect of the BrainPrint is that the eigenvalues form an increasing sequence with the variance increasing as well. Depending on the distance measure, this can cause higher eigenvalues to dominate the similarity measure between two shapes, although these components do not necessarily contain the most important geometric information. To account for these issues we normalize the BrainPrint and employ appropriate distance computations as described next.

Asymmtery

As a first shape feature, we measure the asymmetry of lateralized brain structures in BrainPrint. Since shapeDNA is invariant to mirroring, we directly compute the Mahalanobis distance between the descriptors of a lateralized brain structure s

$$d_s={\Vert {\mathit{\lambda }}_s^{\text{left}}-{\mathit{\lambda }}_s^{\text{right}}\Vert }_{{\mathrm{\sum }}_s},$$ (13)

with Σ_s the covariance matrix across all subjects for structure s. The lateralized structures that we use are white matter and pial surfaces with triangular and tetrahedral meshes, as well as triangular meshes for cerebellum white matter and gray matter, striatum, lateral ventricles, hippocampus, amygdala, thalamus, caudate, putamen, and accumbens.

Alternative distance functions that have been proposed for shapeDNA are the Euclidean distance (or any p-norm), Hausdorff distances, the Euclidean distance on re-weighted eigenvalues λ̂_i = λ_i/i (Reuter et al., 2006; Reuter, 2006), and the weighted spectral distance (Konukoglu et al., 2013). The weighted distances (latter two approaches) are motivated by the need to reduce the impact of higher eigenvalues on the distance. The linear re-weighting is based upon the observation that the eigenvalues demonstrate a linear growth pattern (Weyl’s law) and therefore yields an approximately equal contribution of each eigenvalue. The weighted spectral distance is similar to a division by the squared eigenvalue number and therefore functions like a low-pass filter. Here, we use the Mahalanobis distance because it accounts for the covariance pattern in the data and supports an equal contribution of all eigenvalues in the sequence.

Principal Component Analysis

We derive a second set of features from BrainPrint by computing principal components for each of the 44 brain structures. Projecting the shapeDNA on the principal component retains most of the variance in the dataset, while reducing the dimensionality. Problematic in this regard is once again that higher eigenvalues show most variance, so that they will dominate the identification of the principal component. We have experimented with (i) linear re-weighting, λ̂_i =λ_i/i, and (ii) the normalization of each eigenvalue to unit variance across the dataset. Evaluation of both approaches yielded similar results, so that we employ the simpler linear re-weighting.

Software

shapeDNA and the BrainPrint software is available at http://reuter.mit.edu/software/ and https://github.com/reuter-lab/BrainPrint. We integrated the domain adaptation in the glmnet¹ package in the statistical computing environment R.

2.4. Data

We use data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu), the Australian Imaging Biomarkers and Lifestyle Study of Aging (AIBL, Ellis et al. (2009)), and the CADDementia challenge (Bron et al., 2015). Table 1 summarizes the datasets used for the dementia prediction. All datasets were processed with FreeSurfer.

Table 1.

Demographic, diagnostic, and genetic information of datasets used in this study.

	Subjects	Diagnosis			Gender		Age quantiles			APOE4
		CN	MCI	AD	Male	Female	1st	2nd	3rd	0	1	2
ADNI	751	213	364	174	437(58%)	314(42%)	71.1	75.3	79.8	383	287	81
AIBL	215	142	39	34	114(53%)	101(47%)	67.5	73.0	79.0	107	90	18
CADDementia-Train	30	12	9	9	17(57%)	13(43%)	59.3	65.0	68.0	-	-	-
CADDementia-Test	354	-	-	-	213(60%)	141(40%)	59.0	64.0	71.0	-	-	-

For the CADDementia data, we only have access to the diagnostic information for the 30 subjects in the training dataset. For the larger test dataset with 354 subjects, only the scans with gender and age information is provided. The CADDementia data is composed of imaging data from three medical centers: VU University Medical Center, Amsterdam, the Netherlands; Erasmus MC, Rotterdam, the Netherlands; University of Porto / Hospital de Sao Joao, Porto, Portugal.

AIBL study methodology has been reported previously (Ellis et al., 2009) and AIBL data was collected by the AIBL study group. The study was launched in 2006 and focuses on the early detection of AD, towards lifestyle interventions. The data is collected at two centers (40% subjects from Perth in Western Australia, 60% from Melbourne, Victoria).

The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private-partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The follow up duration of each group is specified in the protocol for ADNI. For up-to-date information, see www.adni-info.org.

3. Results

3.1. CADDementia Challenge

For an independent evaluation of the AD classification method, we report results of our method from the CADDementia challenge (Bron et al., 2015). The task of the challenge was to differentiate between patients with Alzheimer’s disease, mild cognitive impairment, and healthy controls given T1-weighted MRI data. Within the scope of the challenge, 384 multi-center scans were released, where for 30 of the 384 scans the diagnosis was also provided. In addition to the 30 scans also other data, e.g., from ADNI could be used for training. The prediction results for the 354 test cases were submitted to the challenge organizers for the evaluation.

Based on a comparison in (Wachinger et al., 2014), we selected l = 40 eigenvalues. We set α = 1 and the parameter κ in the elastic-net that balances the data fit and penalty term with cross-validation. Fig. 4 shows the cross-validation results, where the lowest multinomial deviance of the model is roughly for κ = exp(−3.5). The figure also shows the number of selected features on top, where smaller κ yields the selection of more features and larger κ yields the selection of fewer features. We merged the 751 ADNI subjects with the 30 CADDementia training subjects for the training, which corresponds to strategy III. Fig. 5 shows the receiver operating characteristic curve for the prediction on the CADDementia test data. Table 2 lists the prediction accuracy together with the true positive fraction across the different diagnostic categories and the area under the curve. The table also shows the confidence interval, which is computed using bootstrapping on the test set (1000 resamples) (Bron et al., 2015). Table 3 shows the classification results as confusion matrix. With these results, the proposed classifier was ranked on the second place after the algorithms of Soerensen in the challenge².

Figure 4.

Multinomial deviance of elastic-net computed with cross-validation for different parameters κ (bottom) and the corresponding number of features (top). The plot shows the mean deviance together with upper and lower standard deviation.

Figure 5.

Receiver operating characteristic (ROC) curve for the classification in control (CN), mild cognitive impairment (MCI), and Alzheimer’s disease (AD) on the CADDementia test data. The plot was created by the challenge organizers.

Table 2.

Classification results on the CADDemetia test data, reported values are in %, confidence intervals are shown in parenthesis. (TPF = true positive fraction, AUC = area under the receiver operating characteristic curve).

Accuracy	TPF-CN	TPF-MCI	TPF-AD	AUC
59.0 (54.0 – 63.6)	72.1 (63.4 – 79.2)	51.6 (43.5 – 61.3)	51.5 (41.5 – 61.2)	77.0 (73.6 – 80.3)

Table 3.

Confusion matrix for the classification results on the CAD-Dementia test data. Rows represent the predicted diagnostic classes, columns represent the true classes. Table entries were computed by the challenge organizers.

		True
		CN	MCI	AD
Pred.	CN	93	44	6
	MCI	36	63	44
	AD	0	15	53

The results show that MCI is the most difficult class to predict. The trained elastic-net classifier selected 9 volume, 15 thickness, and 17 shape features (3 asymmetry, 14 principal components). Notable is the age difference between the challenge and ADNI data. The first quantile of ADNI is higher than the third quantile of the challenge data meaning that 75% of ADNI cases are older than 75% of challenge cases. This mismatch may have a detrimental effect on classification accuracy.

3.2. Domain Adaptation

For the evaluation of the domain adaptation strategies in Sec. 2.2, we use the AIBL data as independent target dataset, because the diagnostic information of the CADDementia-Test dataset has not been disclosed by the organizers in order to allow continuation of the challenge. To obtain the target training data D_t, we randomly sample a subset of the AIBL data. The remaining AIBL data serves as test data D_u. We vary the subset size between 0% and 30% of the original dataset and set α = 0.7. Further, the number of apolipoprotein-E-ε4 (APOE4) allele is added to the variables because it is available for both ADNI and AIBL.

Fig. 6 depicts the three-class prediction accuracy on the AIBL test data for the domain adaptation strategies. The plot shows the mean accuracy and standard error over randomly sampling subsets 50 times from AIBL. The lowest accuracy is achieved with strategy I, where the classifier was only trained on the source data (ADNI). The low accuracy stems from the variations across the two datasets. When merging the ADNI data with training data from the target domain (strategy III), we see an accuracy improvement of about 5%. The accuracy increases about 10% when more data from the target dataset becomes available for training, i.e. when employing 30% instead of only 5% of the target data.

Figure 6.

Results for the domain adaptation with ADNI (source) and AIBL (target) data. In addition to the proposed domain adaptation with instance weighting, we evaluate four strategies that use either one of the datasets (I and II), merge both (III), and combine both with c = 0.5. Discs show mean classification accuracy over 50 samples and bars indicate standard error. We vary the size of the training dataset from AIBL (x-axis), where the remaining AIBL data is used for testing.

Surprisingly, only using the small fraction of the target training data for the estimation of the classifier (strategy II) yields a steep improvement in classification accuracy relative to the combination with the source training data (strategy III). Since these datasets are fairly small for low fractions, we note a larger variance of the results, as shown by the standard error. The consistently higher accuracies for strategy II in comparison to strategy III suggest that the common approach to simply merge source and target training set is is suboptimal. The larger source dataset dominates the smaller one and prevents optimal adaptation to the target data. As an intermediary between strategy II and strategy III, we use the weighting with a constant weight of c = 0.5. This strategy decreases the influence of all the source samples by half and therefore emphasizes the target samples. As expected, the accuracy of this strategy lies between using only target data and the union of source and target data.

The highest classification accuracy in this comparison is achieved for the proposed domain adaptation with instance weighting. The improvement is most prominent for small training fractions of the target data (5%), which is probably the most realistic scenario for the deployment in the hospital. As mentioned previously, we use diagnostic information, age, sex, and the number APOE4 allele for instance weighting. Note, that the standard error for instance weighting is lower than for strategy II (only AIBL), because we also include the ADNI data, making the classification more robust. Increasing the amount of target data available for training above 30% reported in Fig. 6 yields a further increase in classification accuracy for all strategies, where strategy II and instance weighting have a similar accuracy after about 60%. Fig. 7 illustrates the receiver operating characteristic curve for the prediction on the AIBL test data with weighting and 30% of target data available for training. As for the previous results on the CADDementia, the lowest accuracy is for the MCI class.

Figure 7.

Receiver operating characteristic (ROC) curve for the classification in control (CN), mild cognitive impairment (MCI), and Alzheimer’s disease (AD) on the AIBL test data for the weighting strategy with 30% training data.

Fig. 8 illustrates the distribution of weights w_i for instance weighting the source dataset. There is one mode at about 1.0, which causes an equal weighting of source and target samples. The mode with highest frequency is at about 0.3, which decreases the impact of source samples on the estimation. The third mode is at about 1.9 and therefore roughly doubles the weight of such samples. We see from the distribution that only a small subset of the source data receives high weights and that the impact of the majority of elements is reduced.

Figure 8.

Histogram of weights w_i for weighting source samples. Weights above 1.0 increase the importance of elements in the inference and weights below 1.0 decrease the importance.

To illustrate the variation in the selected features across strategies and the fraction of training data, we report the Bhattacharyya coefficient in Table 4. For each strategy and selected fraction, we computed the probability of features being selected across 50 runs. The Bhattacharyya coefficient is a measure for the amount of overlap, where higher values signify more overlap. For the computation, we selected the weighting strategy with 30% training data as reference. The table shows that there is only a slight variation in the selected features for varying the percentage of training data. The features selected with strategy II are more similar to the weighting than the features selected with strategy III, which is similar to the reported classification accuracy. The features that have been selected most frequently across the 50 runs for different subsets of the AIBL dataset are: hippocampus volume/shape, ventricle volume/shape, amygdala shape, entorhinal thickness, parahippocampal thickness, and middletemporal thickness. These features are mainly consistent with previously reported structures associated to Alzheimer’s disease.

Table 4.

Bhattacharyya coefficients to express the overlap between selected features for different strategies and the size of the target training data. The weighting strategy with 30% target data is used as reference. Higher values indicate a more similar selection of features than for the reference.

	Fraction of AIBL training data
	0.05	0.10	0.15	0.20	0.25	0.30
Strategy II	0.76	0.81	0.82	0.83	0.83	0.82
Strategy III	0.57	0.60	0.58	0.58	0.59	0.58
Weighting	0.94	0.98	0.98	0.99	0.99	1.00

4. Discussion

In this work, we present an approach for computer-aided diagnostics of Alzheimer’s disease. Our classifier combines volume, thickness, and shape features to obtain an accurate characterization of brain morphology. In particular, the use of neuroanatomical shape descriptors based on the spectrum of the Laplace-Beltrami operator for AD classification is novel. Inclusion of shape information shows great promise, as demonstrated by the high ranking of our approach on the independent test dataset within the scope of the CADDementia challenge. To reduce susceptibility to overfitting, we limit complexity by choosing a linear model. We further construct a compact model by setting sparsity constraints with the mixed ℓ₁/ℓ₂ norm. This automatic model selection approach is advantageous in comparison to manual selection and stepwise refinement as evaluated previously using the Akaike information criterion. Despite these efforts, our results show strong remaining variations in the classification accuracy on the target dataset that are likely not attributed to overfitting. Instead, we demonstrate that differences in source and target data have a substantial impact on classification accuracy, indicating the need for dedicated domain adaptation approaches in computer-aided diagnosis.

To address this challenge, we present an approach to domain adaptation based on instance weighting and its integration into the multinomial elastic-net classification. Samples in the source training dataset are weighted according to the ratio of the target and source probabilities. For estimating the target probability, we assume that a subset of the target data is available for training, yielding a supervised approach to domain adaptation. In our experiments, we selected random subsets from the target dataset for training. In the clinical use, best results are to be expected if the target training data is representative of the full target dataset. The weighting can be based on several characteristics of the subject, where we include the diagnostic information, age, sex, and APOE4. This could be extended to additional variables, also including image features. Next to single image features, brain distance functions between subjects could be used as proposed by Gerber et al. (2010) for manifold learning. Low-dimensional embeddings have shown that major variations stem from age and sex differences, so that it needs to be further investigated if brain distances add additional value over directly using age and sex. The proposed instance weighting presents a general framework to domain adaptation, where we derived naïve approaches for combining source and target data by setting the weights to different constants, yielding the selection of either the source, or the target data, or the union of both.

Our results demonstrate that the simple union of source and target data, which we used in the CADDementia challenge, is not the optimal strategy for obtaining a high classification accuracy. Due to the much larger cardinality of the source dataset, the impact of the valuable target training data is lost. Surprisingly, the classifier yields better results when employing only the target training dataset and ignoring the source dataset completely, even if only 5% of the target data is available for training. Optimal results are achieved for the proposed domain adaptation with instance weighting, where source and target training data are combined but the importance of each source sample is weighted based on the target and source distributions.

As an alternative strategy to instance weighting, we could select source elements with the highest weights and therefore extract a subset of the source dataset that is most similar to the target training data. Such an approach would require an additional threshold parameter to define the cut-off on the weights. The selection of a subset of the source data that matches covariates on the target training data is related to propensity score matching (Rosenbaum and Rubin, 1983).

With respect to classifier performance, we achieve the lowest classification accuracy for the MCI group. This is not surprising as it can be questioned whether MCI forms a separate diagnostic entity. Some of the individuals in this group convert to AD, while others remain stable. MCI is a clinically heterogeneous group of individuals with varying patterns of brain atrophy (Misra et al., 2009). The results of other challenge participants (Bron et al., 2015) demonstrate a similar low performance for this group. In this work, we considered Alzheimer’s diagnostics by classifying AD, MCI, and CN subjects. Another important topic is Alzheimer’s prognosis, by predicting if and when a subject converts to AD. The early identification of individuals with an elevated risk for developing dementia is of great value for treatments. For predicting the conversion, we face a similar domain adaptation challenge as for the classification, so that the presented strategies may also be of great interest, which remains to be shown in the future.

The algorithm from Sørensen et al. (2014) achieved the highest accuracy in the CADDementia challenge. There are certain similarities to our algorithm; FreeSurfer volume and thickness measurements are used. But also several differences: manual feature selection was used, texture features were integrated, shape features based on surface landmarks were computed, and regularized linear discriminant analysis was used. Further, the training for the challenge was performed on ADNI and AIBL data. Since there are numerous differences between our approach and the one from Sørensen et al. (2014), it is difficult to ascertain what drives the variations in classification accuracy.

Our results provide valuable insights for the optimal implementation of computer-aided diagnosis approaches:

1. Simply relying on large datasets for training is not sufficient for obtaining a classifier that generalizes well. This is due to the large impact of the data distribution on the estimation of model parameters, since the loss minimization is driven by high density areas.

2. Large source datasets are, however, beneficial in supporting the target training set for model estimation. Since large datasets capture a wider portion of the population, it is likely that they also contain instances that are similar to the target samples. These instances can be identified by domain adaptation and emphasized in the model estimation.

3. Availability of training data from the target domain is essential for tailoring the model to each target, e.g., an individual hospital. The benefit of supervised domain adaptation is most pronounced for small training fractions of the target data (5%), which may the most realistic scenario when translating a model to the clinic.

5. Conclusions

We highlight the importance of domain adaptation for the classification of Alzheimer’s disease and present an approach based on instance weighting. We introduce a classifier based on volume, thickness, and shape features, where the BrainPrint is used for the shape representation. A compact model is estimated by regularization of the regression coefficients with the mixed ℓ₁/ℓ₂ norm. This classifier is evaluated on the independent dataset of the CADDementia challenge and used for testing different strategies for domain adaptation. Our results demonstrate that using only data from either the source or target domain, or the union of both, are sub-optimal strategies. We achieved the best results with instance weighting, which compensates for differences in source and target distributions.

Highlights.

• Domain adaptation strategies for the computer-aided diagnosis of AD

• Integration of instance weighting in multinomial regression with elastic-net regularization

• Classification of AD with shape features derived from the BrainPrint

• Evaluation on ADNI, AIBL and data from the CADDementia challenge

• Domain adaptation is crucial for the translation to target data