Multi-scale Modeling in Clinical Oncology: Opportunities and Barriers to Success

Abstract

Hierarchical processes spanning several orders of magnitude of both space and time underlie nearly all cancers. Multi-scale statistical, mathematical, and computational modeling methods are central to designing, implementing and assessing treatment strategies that account for these hierarchies. The basic science underlying these modeling efforts is maturing into a new discipline that is close to influencing and facilitating clinical successes. The purpose of this review is to capture the state-of-the-art as well as the key barriers to success for multi-scale modeling in clinical oncology. We begin with a summary of the long-envisioned promise of multi-scale modeling in clinical oncology, including the synthesis of disparate data types into models that reveal underlying mechanisms and allow for experimental testing of hypotheses. We then evaluate the mathematical techniques employed most widely and present several examples illustrating their application as well as the current gap between pre-clinical and clinical applications. We conclude with a discussion of what we view to be the key challenges and opportunities for multi-scale modeling in clinical oncology.

Introduction

Cancer involves spatial scales ranging from RNA to gene networks to patients to entire populations, and mathematical modeling has provided valuable insights at each level. Successes include uncovering the impact of genetic regulatory circuits on spatial dynamics at cell and tissue levels¹, identifying molecular targets for therapeutic interventions^2,3, establishing tumor angiogenesis as a therapeutic target^4–6, and uncovering the potential of cancer immunology⁷. Cancer also involves diverse temporal scales ranging from gene expression and receptor-ligand interactions (minutes to hours) to tumor growth and metastasis (months to years). Multi-scale modeling that transforms diagnosis and treatment by bridging these diverse spatio-temporal scales has long been pursued, and is now maturing to the point where it shows strong promise for solving critical problems in biology in general⁸, and clinical oncology in particular.

The review begins with an overview of the role that multi-scale modeling can play in oncology, before discussing several of the common mathematical techniques used to attack those problems. The overarching goal of these models is to make a prediction which can then be tested against experiment (either in silico, in vitro, or in vivo) which can lead to model improvement and, eventually, clinical application. We then examine the various areas that are currently barriers to success in applying the methods of multi-scale modeling to clinical oncology. This review is designed for members of the cancer biology and oncology communities who are interested in learning more about multi-scale modeling, as well as those in the modeling community who have recently become interested in using their skills to study cancer.

The role of multi-scale modeling in cancer

Dissecting the multiscale character of cancer to identify therapeutic targets

The long-envisioned promise of multi-scale modeling in clinical oncology revolves around quantification of the hierarchical disease process and the multi-scale feedback structures that enable genetic abnormalities to manifest at the levels of tissues, organs, and systems (see Figure 1 for an overview and Figure 2 for a specific example). A goal of multi-scale modeling is to identify how perturbations at each level can affect the system as a whole, and then to exploit this to attack cancers. Well-known genetic mutations can initiate oncogenesis as these genes translate to the scale of molecular processes, which in turn translate to cellular behavior. These molecular processes can be seen as functional consequences of genetic abnormalities, and involve changes in cell signaling, receptor status activation, genetic regulation, cellular movement and interactions with the extracellular milieu. A key role of multi-scale modeling at this level has been developing knowledge of how “normal” molecular control structures function and, by contrast, how genetic abnormalities produce dysfunction.

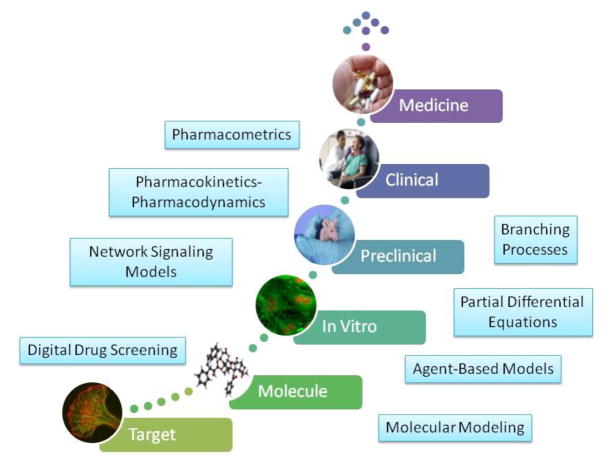
Figure 1.

The continuum of multi-scale components of cancer pharmacological therapy, and the role of each of the modeling techniques described in the text. The process starts with discovery and characterization of a target, followed by drug lead optimization and extensive in vitro and pre-clinical testing. A new medicine will also require successful testing in the clinical setting. Public domain image credits (bottom to top): NCI Center for Cancer Research (Luana Scheffer, Stephen Lockett, Jairaj Acharya); Wikimedia Commons; NCI Center for Cancer Research (Thomas Ried); National Cancer Institute (Leidos Biomedical Research, Inc.); National Cancer Institute (Rhoda Baer); photo courtesy photos-public-domain.com.

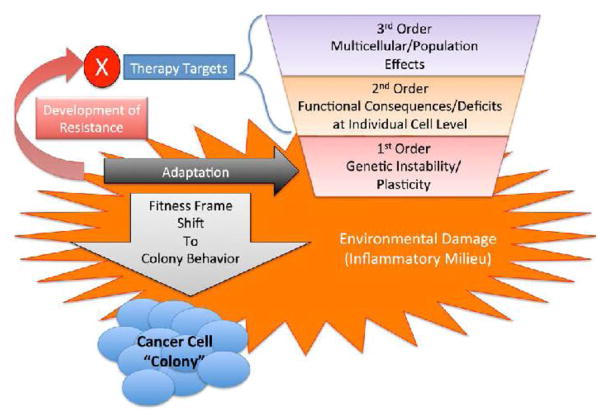
Figure 2.

Proposed Generative Hierarchies for Cancer and the Effect of Inflammation. A depiction of an example of the multi-scale effects of inflammation on the development and subsequent behavior of a tumor, incorporating evolutionary and selection effects across the scales from DNA to cellular populations. This paradigm posits that increased and accumulating genetic damage in an inflammatory milieu leads to a progressive loss of the cellular and molecular control structures that govern stable multi-cellular organization. The loss of these control structures in the tumor leads a more “colony-like” behavior, where the genetic plasticity of the increasingly disordered tumor cells provides a potential selection benefit when subjected to therapeutic interventions, akin to how microbial colonies utilize genetic heterogeneity as an adaptive strategy (as seen in antibiotic resistance). The incorporation of these concepts into a multi-scale computational model allows the exploration of various fundamental processes and behaviors involved in this hypothesis. Reprinted with permission from ref. 81.

At the cellular level, tumors are complex, non-clonal cell populations with their own internal dynamics arising from multi-scale interactions between mutated and normal cells exposed to an abnormal signaling environment. This manifests inappropriately in contextual cell-cell interaction, and is both a byproduct and further enhancer of intra-tumor heterogeneity⁹; cells housing mutations can “hijack” healthy neighbors into propagating a tumor. This in turn fosters selection within tumor cell populations, bringing evolutionary and ecological factors into the behavior of cancers, and defines the context by which tumors interact with their surrounding host tissue. Multiscale models hold the potential to reveal therapeutic targets arising from the ways that cells interact with their neighbors and with their physical environment during these processes.

At the tissue level, all tumors start to develop within normal tissue, and therefore have access to an “interaction space” at the border with the host that presents a potential area for “hijacking” normal processes and cellular populations. This interaction space not only directly affects the growth and selection within the tumor, but also selects for tumor processes best able to release cells into the blood stream and initiate the process of metastasis. The modeling of interactions across the cell, tumor and tissue hierarchy therefore holds the potential for unlocking additional therapeutic targets.

The progression of a tumor from a local to a system-level phenomenon represents another key point in the control of cancer, and motivates a desire to individualize the representation of tumor characteristics to better determine the specific factors involved in a particular tumor’s progression. Personalized tumor modeling might integrate genetic profiling of the primary tumor cells or tumor stem cells with the set of possible behavioral trajectories in a multi-cellular tumor that is actively interacting with its host. These latter characteristics might be represented by tumor-level properties determined by different modalities, such as histology or imaging, which would provide calibration targets for the lower-level mechanisms incorporated into such a model, and then be used to project multiple possible outcomes based on other personal factors, such as health status or interventions.

Finally, at the patient population level, the ability to potentially “simulate” an individual tumor provides a pathway to the generation of computer-generated populations of cancer patients. These simulated populations would provide a more sophisticated accounting for mechanisms than traditional population modeling. They would be key to represent and explain the observed “rarity” of cancer events, thereby accounting for stochastic processes involved in mutational events and allowing the generation of finer grained data sets for identification of subtler patterns in the pre-cancerous and early stage conditions. Ultimately, these models would form the basis of in silico clinical trials for potential therapeutic regimens, and provide another potential pathway for the design and development of cancer therapeutics.

Characterizing drug targets

Molecular targets that are cancer drivers are ultimately part of a mechanistic cascade¹⁰. Antitumor effects can be caused by many pharmacological interventions, both direct (e.g., kinase inhibition¹¹) or indirect (e.g., immune-mediated therapy¹²). Given the broad landscape of potential pharmacological agents, modeling and simulation has a fundamental role in facilitating the investigation of potential targets. Systems pharmacology¹³ is an emerging and powerful tool in the quantitative modeler’s toolbox for guiding the early stages of discovery¹⁴, especially when tool compounds are unavailable and information is sparse about target properties such as abundance in target tissues and turnover¹⁵. Pharmacokinetic-pharmacodynamic (PK-PD) models incorporate compartmental¹⁶, or physiologically-based¹⁷, models of drug distribution and empirical or semi-mechanistic models of drug action¹⁸. They are most suited for investigating the effects of drugs on molecular targets when tool molecules are available to probe disease pathways. At the other end of the scale, pharmacometric¹⁹ models, which incorporate statistical and mechanistic features of the patient population being studied, can be used to quantify the effects of a particular treatment on populations. The statistical technique of mixed effects modeling can be applied to find explanatory variables (covariates) and, eventually, correlates of clinically significant endpoints such as overall or progression-free survival²⁰. All of these modeling approaches ultimately characterize drug targets across the spectrum²¹ of target qualification (cell and tissue), pharmacology (nonclinical models and humans) and disease effect (populations).

Adverse side-effects and lack of efficacy are the two major sources of attrition in the field of drug design²². Substantial efforts have been devoted to addressing this challenge, and modeling approaches have been playing increasingly important roles in addressing the lack of efficacy and undesired off-targets effects^22,23. Recent advances in structural bioinformatics have enabled the reliable prediction of drug off-target binding sites across the proteome²⁴. Large-scale network models have also been widely applied to predict the functional effects of various therapeutics²². These two approaches have been integrated to provide a framework for assessing drug responses in silico²⁵. A recent effort incorporated signaling pathway information for evaluating side effects on primary human hepatocytes, and obtained insightful results with clinical implications²⁶. Collectively, the traditional experiment-based screening strategy to reduce drug off-target effects is becoming time- and resource-consuming, while a variety of recently developed computational models have begun to make significant contributions to rational drug design. In addition, many computational tools based on ordinary differential equations (ODEs) systems have been widely used to model and predict the effects of therapeutics on intracellular signaling pathways^27–30. These model tools were developed based on protein-protein interaction networks with applications on exploring optimal therapeutic strategies. Collectively, ODE-based models with perturbations can be used to explore in silico candidate conditions, screen out critical factors, and guide biological experiments, by investigating drug combination effects with well-known evaluation indexes such as Loewe additivity³¹ and Bliss independence³². Finally, agent-based modeling techniques can be used to integrate multiple biological scales together, especially including intracellular signaling pathways^33–35.

Computing the design of anticancer drugs

It is increasingly clear that there must be an extension from the “rational discovery” of potential drug candidates, often based on molecular-level assumptions of effect, to a “rational design” process, that moves beyond target identification towards characterizing the larger scale consequences of interfering with a particular target gene. This necessarily incorporates recognition of the multi-scale nature of cancer, where there are higher-order properties that involve accounting for the behavior of multi-cellular populations within a tumor, as well as the interactions of that tumor with its host environment. Given this understanding, in any attempt to recognize the potential downstream consequences of a molecular level intervention (as is the case with many anti-cancer drugs), it is critical to account for compensatory processes that remain in either the tumor or adjacent host tissue. Quantitative models that can contextualize the multi-scale processes involved in the development and behavior of cancer have an important role to play in this line of investigation³⁶.

Digital screening of anticancer drugs

Traditional drug discovery relies upon high-throughput screening using a library that contains millions of compounds selected for and then screened for efficacy against a target of interest. While this approach has been successfully used to discover many effective anticancer drugs, it can be enhanced through digital drug screening, a powerful drug discovery technology in the post genomic era. In addition to advances in chemoinformatics³⁷ and the deciphering of the human genome, there has been an enormous increase in the types of chemical compounds, biological and physiological systems, and diseases that have been digitized, stored and archived in publically accessible databases, such as PubChem, ChemSpider and ChEBI³⁸. These databases offer a platform for releasing and publishing experimental data on chemical compounds and their associated structure and functional data. They also offer user-driven search engines that allow users to define and search a particular drug molecule or a class of chemical compounds³⁷.

Conversely, while large sets of biological and medical data are frequently generated, the validation and further standardization of these data remains a significant challenge. One of the difficulties is the poor reproducibility and reliability of these biological and clinical data due to the intrinsic complexity of biological systems and hard-to-access human samples. The development of bioartificial tissue and organ-on-a-chip³⁹ systems could help accumulate more clinically relevant biological and physiological data for digital screening of anticancer drugs. The digitalization of cancer diagnoses offers another opportunity to deposit clinical oncology data into publically available databases. Some of these databases (e.g., Therapeutic Targets Database⁴⁰ and PharmGKB⁴¹) are available today for drug screening.

Another critical element of digital drug screening is provided by computational models that link the data to a specific cancer target. Such models must be multi-scale and target-driven due to the multiple spatial and temporal scales at which the motivating biological and clinical data are collected. Algorithms also need to be developed to predict whether compounds (including proteins or peptides) can be translated into anticancer drugs. For example, BioMap^® (human primary cell phenotypic profiling services developed by DiscoveRx Co.) consists of primary human cell-based assay systems, a database of reference compound profiles, and computational data mining and analysis tools. A system (ChemScore) that uses reactivity based fingerprints of compounds as filters has been developed to determine a reactant-like and a product-like score for virtual drug screening⁴².

Taken together, the combination of available databases and computational models offers unprecedented opportunities to build computational models for drug screening, thereby enabling a fundamental shift from traditional high-throughput screening to data-driven screening of potential anticancer drugs.

Optimizing dosage, drug combinatorics, scheduling, and safety

The classical “maximal tolerated dose” (MTD) approach currently used in early Phase 1 clinical trials of anticancer drugs can be irrelevant in many situations⁴³. For example, some compounds simply do not present a toxicity profile appropriate for reaching the MTD in a dose finding phase. For other compounds with a well-identified MTD, the upper-limit dose may not be appropriate when the compound is given in combination with other therapeutics⁴⁴. Efficacy and toxicity are central issues in design of patient-specific chemotherapy regimens, but do not lend themselves well to trial-and-error approaches. A broad range of coupled in vitro and numerical modeling techniques are becoming available that offer much promise for rapid efficacy and toxicity screening^45,46. Cellular and tumor-level responses may be deduced from the responses of bioartificial tissues, organ-on-a-chip systems, and murine systems in typical screening procedures. These systems also show promise for assessing toxicity of drug regimens. A particularly promising avenue is screening of compounds on bioartificial tissues whose cells are derived from a patient’s own induced pluripotent stem cells⁴⁷.

A critical challenge in the development of anti-cancer drugs is the optimization of the delivery strategy including the proper dosing, timing, and scheduling of drug administration⁴⁸. Optimally selecting treatments for a particular cancer subtype, particularly treatments that involve combination therapy, is an extraordinary challenge, for the number of potentially relevant adjustable parameters is too large to adequately investigate in clinical trials. Multi-scale simulation can play a pivotal role in addressing this problem by anticipating potential synergies between compounds’ mechanisms of action, thus providing a rational method for selecting a dose that would improve efficacy without affecting safety. Progress has already been made using bioinformatics algorithms⁴⁹; however, applications of multi-scale modeling to solving this very important clinical problem remain to be fully explored.

Assessing intervention, prevention, and cancer screening strategies

Multi-scale frameworks that explicitly model clinical outcomes in terms of underlying biological processes, in conjunction with the physical and physiological characteristics of the instrumentation used for screening or drug delivery, are likely to suggest improvements that cannot be gleaned from traditional natural history models of cancer development and drug response. Such traditional models typically ignore important biological processes and time scales in the formation of cancer and its precursors. In contrast, multi-scale models are appropriate for providing a more comprehensive understanding of the underlying mechanistic processes, as well as the spatio-temporal characteristics of cancer screening and surveillance protocols (e.g., using high-resolution imaging, or biopsies). An illustrative example of this reasoning is presented in Figure 3⁵⁰. Although regular biopsy-based surveillance is the standard-of-care for most Barrett’s Esophagus (BE) patients who have not progressed to dysplasia or cancer, it is not clear whether screening under current guidelines is clinically optimal and cost-effective. Curtius et al. describe a computational cell-level multiscale model for the neoplastic progression of Barrett’s metaplasia to esophageal adenocarcinoma allowing for variation in segment length, presence of dysplastic cells in the crypt-structured epithelium and their potential detection by biopsy⁵⁰. Thus, multi-scale-based screening models can potentially be used to better understand the clinical performance (sensitivity/specificity) of various screening methods and the sources that limit their clinical utility.

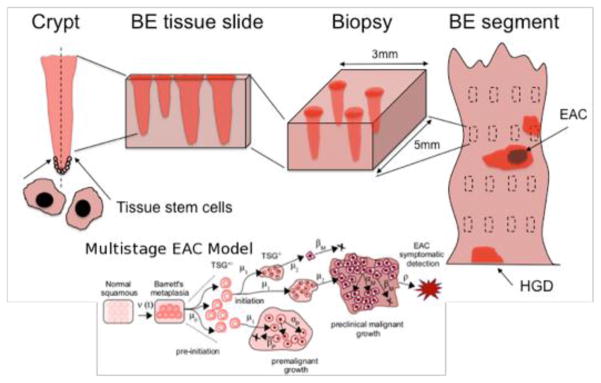
Figure 3.

The Multi-scale nature of screening in Barrett’s esophagus (BE). The standard screening protocol for BE involves scales from stem cells in the crypt (left) to the BE cylindrical segment of the esophagus depicted (right) with rectangles representing biopsy samples taken during endoscopy. The BE segment may have dysplasia and/or malignant tissue patches that may be missed. During histological preparation, portions of each biopsy are sliced by microtome and placed on slides for pathologic assessment. A diagnosis is made by microscopic interpretation of crypt and cellular architecture, reflecting the most severe tissue grade found from all slides. Given the multi-scale nature of the problem, it is natural that a multi-scale-based screening model would have great clinical utility. (EAC = Esophageal Adenocarcinoma; HGD = High Grade Dysplsia.)

State-of-the-art multi-scale approaches to cancer

Multi-scale network signaling models

Advances in mechanistic modeling of signaling networks present opportunities for better understanding of therapeutic targets, designing therapeutic regimens (including combination therapies), as well as the de novo design of drugs. Models of growth factor signaling networks, such as vascular endothelial growth factor (VEGF) and epidermal growth factor (EGF), have been particularly well developed. The VEGF models describe molecular-detailed kinetic interactions between different splice isoforms of VEGF and their cognate receptors VEGFR1 and VEGFR2 and co-receptors neuropilins-1 and -2. The models comprise the blood, normal, and tumor compartments and they also take into account VEGF binding to the extracellular matrix, and soluble factors such as soluble VEGFR1^51,52. Molecular-detailed intracellular signaling models that include receptor dimerization, internalization, recycling, and degradation can potentially be used for simulating intracellular drug targeting with, for example tyrosine kinase inhibitors⁵³. The kinetic receptor-ligand interaction model has been extended to describe the pharmacokinetics and pharmacodynamics (PK/PD) of VEGF-neutralizing anti-angiogenic drugs including the antibody bevacizumab⁵², and aflibercept⁵¹, a fusion of specific domains of VEGFR1 and VEGFR2. They were compared with extensive available clinical data. The difference between these molecular-detailed PK/PD models and more conventional models is in the mechanistic level of detail with which the molecular interactions are represented. Therefore, the model predicts the amounts not only of the drug in the compartments, but also the detailed distribution of the different ligands (e.g., those bound to the cell-surface receptors, extracellular matrix, and free in the interstitium)⁴. For the EGF system a molecular-detailed approach has been used to design and optimize an antibody for cancer applications^54,55.

Pharmacometrics and nonlinear mixed effects models

A popular definition of pharmacometrics is “the science of developing and applying mathematical and statistical methods to: a) characterize, understand, and predict a drug’s PK and PD behavior, b) quantify uncertainty of information about that behavior, and c) rationalize data-driven decision making in the drug development process and pharmacotherapy”⁵⁶. In practice, pharmacometrics often employs nonlinear mixed effects modeling techniques⁵⁷ that combine structural models (algebraic or differential equations) that are nonlinear in their parameters with nested variability in the clinical observations (i.e., variation among and within patients) and trial execution components (i.e., patient adherence and dropout rate). There have been many applications of nonlinear mixed effects models to clinical oncology PK/PD^58,59. In general, nonlinear mixed effects modeling of PK and PD benefited from the early availability of computer software^60,61 and frequent application to situations where other techniques would have been difficult to deploy, such as clinical studies. Since this class of models is informed by data, mechanistic detail is a function of available information, which can be limited in clinical oncology. However useful, nonlinear mixed effects are not the only tool that can be used to understand dose-exposure-response relationships in vivo. It is through the combination and use of multiple, “fit for purpose” modeling approaches, depending on the appropriate biological scale, that we can hope to understand cancer etiology and pharmacotherapy³⁶.

Partial differential equations

For handling clinical data that have spatial dimensions as independent variables (i.e., data that do not depend solely on time), mathematical models based on partial differential equations (PDEs) may be more appropriate than those based on ordinary differential equations (ODEs), which are more amenable to the applications described in the previous two sections. For example, medical images which are composed of rectangular, spatially-resolved voxels describing the shape, location, and texture of the tumor in addition to underlying physiological, cellular, and molecular processes⁶², cannot be readily handled by ODE models. More generally, PDE models are appropriate when the available data is multidimensional⁶³. Most spatial models describe the movement of cancer cells through reaction-diffusion⁶⁴ or advection⁶⁵ terms. The applications are numerous, ranging from monitoring the evolution of slowly evolving tumors such as lung metastases⁶⁶ to defining surgery or irradiation margins^67,68, and improving the insight offered by images⁶⁹. (See Figure 4). PDE models have also been used to evaluate the spatio-temporal distribution of metastases over time⁷⁰, as well as mutations and resistance to treatment⁷¹. However, most applications require being able to recover the parameters of the model from clinical data in order to perform patient-specific simulations or predict patient-specific outcome.

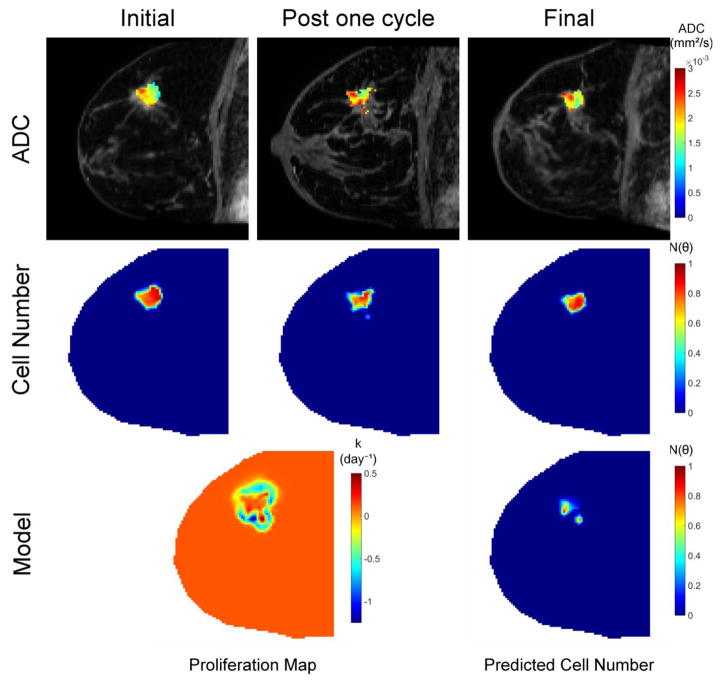
Figure 4.

This illustrative example uses serial diffusion weighted magnetic resonance imaging data to estimate tumor cellularity before and after the first cycle of neoadjuvant therapy. The top row indicates the apparent diffusion coefficient (ADC) obtained from diffusion weighted MRI data at three time points during therapy. Given the known relationship between ADC values and cellularity, this data is then converted to tumor cell number (middle row). The cell number data from the initial and post one cycle time points are then fit to a biomechanical model of tumor growth to estimate patient-specific parameters of tumor cell proliferation and migration. The model, calibrated with the patient-specific parameters determined from the fitting procedure, is then run forward in time to predict residual tumor burden at the conclusion of neoadjuvant therapy. Model predicted cell number can be compared to cell number imaging observations at the final time point in order to assess predictive performance. Details are presented in ref. 69.

It is important to note that PDE models are (relatively) computationally expensive to solve. Classical optimization techniques can often be too expensive to be realistically used. More advanced techniques relying on reduced-order models⁷² or exploiting the features of the solution to a model⁷³, may prove more successful for assimilating clinical data.

Spatially discrete/cellular agent models

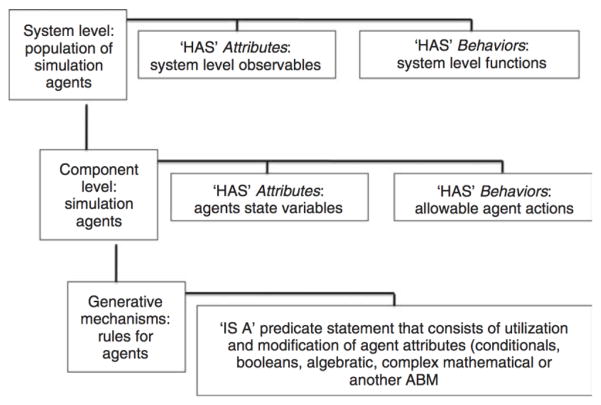
One class of biological computational modeling that has recently increased in popularity is that of spatially discrete, cell-as-agent models. Methods in this category are agent-based models (ABMs), individual based models (IBMs), cellular automata, and cellular Potts Models. For simplicity’s sake, these methods will be globally described as agent-based modeling, and can be generally described as discrete event, object oriented, rule based, and often spatially explicit methods for dynamic computer modeling that represent systems as a series of interacting components⁷⁴. ABMs are programs that generate populations of discrete computational objects (or agents) that correspond to the component-level at which the reference system is being examined. These computational agents are organized into agent classes representing groupings of agents of a similar type defined by shared properties and characteristics. Agents are governed by agent rules; i.e., instructions that allow the agent to be treated as an input-output object. Individual agents incorporate the properties and rule-structures of their parent agent class, but are able to manifest diverging behavior based on local inputs. ABMs intrinsically cross scales of biological organization, utilizing behavioral rules (scale 1) to determine individual agent behavior (scale 2), and then aggregating individuals into population dynamics of the global system (scale 3). When applied to biological systems, cells form a natural agent level within this organizational structure. Subcellular components (e.g., genes, enzymes, receptors, and structural elements) are represented as state variables for the cellular agents. Their behavior and interactions (e.g., gene transcription, intracellular signaling, protein synthesis) can be represented by a wide range of mathematical and computational formulations. Individual cellular agents interact with each other by manipulating state variables of their neighbors or their shared environment. Figure 5 depicts an ontological description of an agent-based model, with an emphasis on its generality that can be tailored to specific modeling tasks. Given this framework, ABMs have been extensively used to study tumor growth and behavior^74–77.

Figure 5.

A schematic of an Agent-based modeling format (ABM). The structure of an ABM intrinsically incorporates at least three representational scales of the system being modeled. For most biomedical ABMs, cells are used for the middle level representation (the agent level). Figure reprinted with permission from Elsevier Ltd.

Multi-scale, agent based modeling has been used to generate high-fidelity replications of tumor structure. The spatial representation of ABMs allows them to generate “realistic” tumor structures incorporating multiple cell types and capturing cancer heterogeneity⁷⁸. This permits a detailed investigation of the multi-scale consequences of genetic or molecular perturbations, and offers the promise of potentially personalizing models based on histological features⁷⁹. ABMs also allow examination of fundamental processes involved in oncogenesis by facilitating a parsimonious approach that provides insight into fundamental processes involved in tumor growth and development⁸⁰. ABMs can also provide linkages to the role of general biological processes, like inflammation, in the development and progression of cancer⁸¹.

As with all modeling methods, agent-based modeling is not without its limitations. Most of these stem from the fact that ABMs do not have a common formal description, which limits the ability to subject them to formal analysis. Their “similarity” to biological systems, particularly in terms of the heterogeneity and non-linearities in their behavior, makes formal, comprehensive exploration of their parameter space difficult and only able to be accomplished using very large sets of simulations. Additionally, ABMs are relatively computationally expensive and difficult to distribute across modern, distributed computing architectures, with the result that very often biomedical ABMs are treated more akin to experimental objects where their use is dependent upon finding some subset of parameters that can provide “realistic” behavior. Despite this limitation, however, ABMs can serve a very useful purpose that can bridge between biological objects/knowledge and more formal mathematical representations.

Branching processes

Disruption of normal cell proliferation and differentiation is the sine qua non of the malignant state. However, numerous experimental and clinical studies provide evidence that the proliferation and differentiation kinetics in normal and premalignant cells are also of critical importance in the carcinogenic process. This notion was further enforced by analytic findings from mathematical modeling of cancer incidence patterns⁸². A prototype branching process model of cancer is the two-stage clonal expansion (TSCE) model⁸³. Initially, this model was formulated with stochastic clonal expansions of both normal and intermediate (or premalignant) stem cells. However, due to the typically very large (and highly regulated) size of the normal tissue stem cell pool, the version most frequently used assumes a deterministic number of normal tissue stem cells. The basic TSCE model is characterized by two rate-limiting events in normal tissue stem cells (premalignant tumor initiation and malignant transformation) together with a stochastic growth process of premalignant cells that can undergo malignant transformation. Various extensions of this model have been put forward (multistage clonal expansion (MSCE) models) to better explain cancer incidence patterns in registries and cohort studies⁸⁴. The availability of analytical tools and likelihood expressions for population-level clinical observations (e.g., cancer incidence, prevalence of a precursor such as colonic adenoma or dysplasia in Barrett’s esophagus patients) greatly facilitates likelihood-based parameter estimation via gradient methods or Markov-Chain Monte Carlo techniques. An example of a ‘mathematical bridge’ that connects the cellular-level with the tissue-level is the filtered Poisson process.

Homogenization approaches

Linear homogenization approaches comprise the simplest techniques for estimating parameters describing cell health and function from measurements conducted on a tissue construct. From the perspective of screening for safety, the desired outcomes are parameters describing electrophysiological and mechanical functioning of individual cells. From the perspective of screening for efficacy, cancer culture models such as the Xu model⁸⁵ exist, and the challenge is determining how chemotherapy agents affect the tumor periphery and factors promoting malignancy. Models estimating tissue and cellular mechanics from multiple loadings of tumor models are capable of estimating these changes⁸⁶, and for estimating effects on cells, protein structures, and networks⁸⁷. Although techniques are preclinical at present, the capacity to test chemotherapy regimens on both heart tissue equivalents from a patient’s own transdifferentiated cells and tumor equivalents from a patient’s own tumor cells shows much promise. Ongoing challenges relate to refinement of electrophysiological and mechanical models to account for local variations within tissues, and to include nonlinear phenomena.

Hybrid models

Multi-scale hybrid models combine different modeling methodologies; e.g., intracellular signaling described by ODEs combined with 3D distributions of oxygen, growth factors and cells described by PDEs, or oxygen and growth factor distributions described by PDEs combined with discrete cell dynamics represented by agent-based modeling. In principle, hybrid models could include all types of models. The advantage of hybrid modeling is that different parts of the system can be described using the methodologies most appropriate for the biological question to be answered, and with a spatial and temporal resolution that makes the problem tractable.

Anderson presented a hybrid model describing the invasion of a solid tumor into healthy tissue that is governed by tumor cells, extracellular matrix, matrix-degrading enzymes and oxygen⁸⁸. In his formulation, the tumor cells themselves are considered as discrete objects, while the remaining three entities are considered continuous variables. His results indicated that cell–cell interactions drive the early stages of development, but it is the loss of cell–cell interaction (due to mutation) that increases the importance of cell-matrix interactions which drive tumor invasion. Many have built on Anderson’s approach. For example, Jiang et al have extended Anderson’s approach to systematically investigate tumor cell invasion within a generalized diffusion framework⁸⁹. The authors found that tumor cells can migrate by a host of diffusion modes and these predictions were supported by patterns seen both in vitro and in standard-of-care images obtained in the clinical setting. In particular, they found that in the case of invasion and metastases, tumor cells display both superdiffusion and ballistic diffusion.

Barriers to and opportunities for progress

Technical/methodological issues

Mathematical complexity

As seen in fields ranging from atomistics to astrophysics, a tradeoff exists between mathematical and computational complexity in modeling oncological problems, especially when the problem involves a large number of interacting components (cell-types), non-linear signaling between components (feedback loops), and stochastic behavior (noise). A main challenge in developing useful multi-scale models is therefore the choice of mathematical abstraction (continuum, discrete, lattice) and choice of relevant (rate-limiting) processes, which may operate at different time and length scales. However, these scales may not be known a priori and the appropriate choice may require preliminary studies and/or additional bio-mechanistic information. A case in point is the problem of emerging resistance to therapy in heterogeneous tumors, specifically whether or not the ‘resistance conferring’ alterations are preexisting, a result of the tumor and its microenviroment being under selection pressure caused by the drug, or simply due to the hypermutability or genomic instability of the tumor⁹⁰. Each of these causes requires a distinct mathematical description. For example, the size fluctuations of preexisting mutants may well be captured by a Luria-Delbrück type of distribution, which allows for mutational jackpots, while a drug-induced response is unlikely to do so given the much shorter time scale of treatment^91–92.

Mathematical complexity in oncologic applications of multi-scale modeling arises in the formulation of the dynamics of bulk behavior and description of underlying constituent processes in the forms described above⁹³. It is important to note that only in exceptional cases (and often only with many simplifying assumptions) are closed form solutions available and parameter identifiability issues addressed. Further adding to the mathematical complexity is the stochastic nature of many cell-level and sub-cellular processes⁹⁴. Although the implementation and mathematical treatment of the stochastic process may be complex, a considerable advantage is that it often lends itself to likelihood-based methods for parameter estimation and hypothesis testing.

Linking models with clinically available data

It is important to acknowledge that while the multi-scale cancer modeling community is rich in models from the nanoscale to the macroscale, many models are framed in terms of parameters and variables that are extraordinarily difficult to obtain in the clinical setting. This a fundamental challenge facing the validation and clinical application of multi-scale modeling. This is particularly true for cases in which electrophysiological, transport, and mechanical factors of cells and a pericellular region are of interest. For the case of the screening of anti-cancer agents, the key difficulties are measuring in the mesoscale range, characterizing the pericellular region, and sampling a sufficient number of cells to overcome the high cell-to-cell variability so inherent to three dimensional culture. These challenges result in modeling approaches that require many (often heuristic) assumptions on model parameters. Consequently, application of such models to make clinically relevant predictions can be quite limited. More specifically, the field of multi-scale modeling in cancer has largely been developed independent of the data types that are typically available in the clinical setting. The community needs to acknowledge that it is not simply enough to test a myriad of modeling approaches in silico by systematically varying parameters, coupling constants, etc. Rather, to be of clinical relevance, the community needs to build multi-scale models that can be initialized and constrained with patient specific data that is readily available in the clinical setting⁹⁵. Only by proceeding along this route will we be able to test hypotheses about patients that directly testable. One area that is underexplored in making progress is the utility of medical imaging data^67,69,96.

The medical imaging technologies of magnetic resonance imaging, x-ray computed tomography, positron emission tomography, single-photon emission computed tomography, and ultrasound can quantify, at multiple time points and in 3D, tumor characteristics at the physiological, cellular, and molecular levels⁶². Furthermore, the images themselves present a natural gridding (i.e., the image pixel or voxel) that enables direct application of finite difference and finite element methods. While using such data in statistical and informatics driven approaches has launched the fields of radioomics and radiogenomics^97,98, such data are only beginning to be incorporated into mechanism-based, predictive models of tumor initiation, growth, invasion, and response to treatment.

Mathematical models of tissue health and function

There is a pressing need for multi-scale modeling techniques that enable the use of in vitro tissue surrogates and organ-on-a-chip models for safety and efficacy screening of chemotherapy agents. Although well-established methods exist for applying integrated multi-scale modeling and experiment to assess subtle, drug-induced changes to the health and function of cells within simple bioartificial tissue constructs⁴⁶, advances are required to account for such tissues and organ-on-a-chip systems with heterogeneous cell populations. With these models in place, the potential to, for example, test a library of anti-cancer agents on bioartificial tissues mimicking a patient’s own tissues may one day become possible, enabling rapid optimization for both efficacy against a patient’s malignant cells and for tolerance by a patient’s healthy cells through quantitative evaluation of changes to cell function.

Institutional issues

Intrinsic to trans-disciplinary endeavors, from medicine to management, are the challenges of reconciling both different views of the world, and the different rhetorical frameworks that are used to reflect those views⁹⁹. Cancer modeling, in its earliest days, involved little communication between modelers and clinicians¹⁰⁰. Although efforts to reconcile pathophysiology with principles from the physical sciences have progressed a great deal since the 19^th century courtroom battles over the topic of model validation¹⁰¹, many cancers remain too complex for identification of abstractions that can approximate natural laws, and validation remains a central challenge¹⁰². However, dynamic computational models representing sets of mechanistic hypotheses can stand in for formal mathematical theories for a defined context and for a constrained use¹⁰³. Within this context the importance of the choice of computational methods is lessened; sufficiently strong hypothesis structures should perform equally well when instantiated in a multiplicity of modeling methods. This is the principle of cross platform validation¹⁰³.

High quality, validated implementations are crucial to establishing the trustworthiness of a particular computational model, and accounting for the relative strengths, weaknesses, and representational capabilities of the different methods is essential. There also needs to be some means by which the appropriate use-context of a particular model is explicitly defined and determined, in order to avoid the misapplication and misinterpretation of a particular model. Dating back to the earliest multiphysics codes and standards (e.g., the American Society of Mechanical Engineering boiler codes¹⁰⁴), these issues have been common to the general use of models and simulations, and have been pragmatically addressed through the establishment of guidelines and standards for model credibility, testing, and reporting in a domain specific fashion. However, for multiscale modeling of cancer, this process is in its infancy. Notable efforts to advance this include, for example, the Committee on Credible Practice in Modeling and Simulation in Healthcare¹⁰⁵, and the EFPIA MID3 Workgroup which recently published a white paper on good practices in model-informed drug discovery and development¹⁰⁶. We view such collaborative efforts as important, as the field continues to advance towards systematically using model-aided design and testing in the regulatory arena (for testing of drugs and devices) and for personalized/precision decision support.

Conclusion

No shortage of powerful—and promising—computational techniques exists for use in the multi-scale modeling of cancer and cancer treatments. What is lacking, however, is access to relevant clinical data and practical modeling approaches to incorporating such data into relevant models. This will allow modelers, experimentalists, and oncologists to effectively close the “build-test-refine cycle” by directly testing the predictive power of a particular model and then improving upon it to the point where it can, ultimately, be applied to clinical problems. We also need a more rigorous understanding of the key components that go into the growth and response to treatment of individual tumor subtypes. Both of these issues are exacerbated by the social constructs in academia. In practice, future progress in clinically relevant multi-scale modeling in oncology requires interdisciplinary collaborations between clinicians, experimentalists (biologists, physiologists, biophysicists, bioengineers, etc.), and mathematical and computational modelers. Although this truth is clearly recognized at the level of the funding agencies, the difficulty in developing such collaborations is generally underappreciated. However, a corollary of successfully working across multiple disciplines is the education and training of a future generation of students and postdocs who are accomplished at both the bench and computer, thereby allowing them to explore and integrate their data into clinically useful models. We believe this is happening as we speak, and that such integration of disciplines through multi-scale modeling will bring great value to clinical oncology.

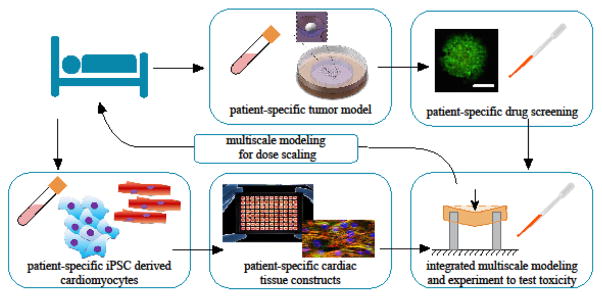
Figure 6.

Patient-specific drug and cardiotoxicity systems are available, but require integrated multi-scale modeling and experiment to apply. Tumor cells can be multiplied in systems like the Xu system (ref. 85) for patient-specific drug screening. Commercial systems exist for testing patient-specific cardiotoxicity on tissue constructs derived from induced pluripotent stem cells (iPSCs); for example. Multi-scale models are required to derive metrics of cellular health from measurements of the mechanical function of tissue constructs, and for scaling dosages. Image credits: Top center and top right: ref. 71; bottom left and bottom center: Invivosciences, LLC. All images used with permission.