Accuracy of automated classification of major depressive disorder as a function of symptom severity

Abstract

Background

Growing evidence documents the potential of machine learning for developing brain based diagnostic methods for major depressive disorder (MDD). As symptom severity may influence brain activity, we investigated whether the severity of MDD affected the accuracies of machine learned MDD-vs-Control diagnostic classifiers.

Methods

Forty-five medication-free patients with DSM-IV defined MDD and 19 healthy controls participated in the study. Based on depression severity as determined by the Hamilton Rating Scale for Depression (HRSD), MDD patients were sorted into three groups: mild to moderate depression (HRSD 14–19), severe depression (HRSD 20–23), and very severe depression (HRSD ≥ 24). We collected functional magnetic resonance imaging (fMRI) data during both resting-state and an emotional-face matching task. Patients in each of the three severity groups were compared against controls in separate analyses, using either the resting-state or task-based fMRI data. We use each of these six datasets with linear support vector machine (SVM) binary classifiers for identifying individuals as patients or controls.

Results

The resting-state fMRI data showed statistically significant classification accuracy only for the very severe depression group (accuracy 66%, p = 0.012 corrected), while mild to moderate (accuracy 58%, p = 1.0 corrected) and severe depression (accuracy 52%, p = 1.0 corrected) were only at chance. With task-based fMRI data, the automated classifier performed at chance in all three severity groups.

Conclusions

Binary linear SVM classifiers achieved significant classification of very severe depression with resting-state fMRI, but the contribution of brain measurements may have limited potential in differentiating patients with less severe depression from healthy controls.

Highlights

• •SVM binary classifiers achieved significant classification of very severe depression with resting state fMRI data.
• •Prefrontal, anterior cingulate and insula were the most discriminative brain regions.
• •No significant classification could be achieved for less severe MDD with resting state data.
• •With emotional task data, SVM classifier performed at chance for all MDD severity groups.

1. Introduction

Major depressive disorder (MDD) is a complex brain disorder associated with dysregulation of distributed neuronal networks involving several cortical and limbic regions. This position is based on evidence from the neuroimaging literature that has documented distinct structural and functional alterations in patients with MDD compared to healthy controls (Mayberg, 2003, Drevets et al., 2008, Price and Drevets, 2012). However, these group-level inferences have had minimal impact on clinical translation at the individual patient level – that is, they do not directly lead to a way to determine whether a specific subject has MDD or not. Recently, machine learning techniques have been applied to neuroimaging data to draw inferences for individual subjects, with the potential for improving patient-specific clinical diagnostic and treatment decisions (Orru et al., 2012, Kloppel et al., 2012). Current diagnosis of mental disorders is based on diagnostic criteria drawn from self-reported clinical symptoms without any objective biomarkers. This has led to the search, in recent years, for a diagnostic system that can use objective measurements from a subject's brain to validate and improve the accuracy of psychiatric diagnosis.

In the last decade, several neuroimaging studies have examined the classification accuracy of machine learned classifiers in differentiating patients with MDD from healthy controls. One major focus has been the application of machine learning techniques to magnetic resonance imaging (MRI) data, including both structural and function MRI (fMRI) data. Machine learning is a sub-area of artificial intelligence that applies statistical methods to training data, such as high dimensional neuroimaging data, to find patterns that can distinguish patients from healthy controls. Authors reported classification accuracy for MDD ranging from 67 to 90% using structural MRI data (Costafreda et al., 2009, Gong et al., 2011, Mwangi et al., 2012a), 94% using resting-state fMRI data (Zeng et al., 2012, Zeng et al., 2014), 67–86% using task-related fMRI data (Fu et al., 2008, Marquand et al., 2008, Hahn et al., 2011) and 76.3% using combined structural and functional MRI data (Nouretdinov et al., 2011). High accuracy prediction is clinically important, as MDD is heterogeneous in symptom profile and prone to clinician bias with poor inter-rater reliability (Regier et al., 2013). The identification of MDD subtypes based on neural abnormalities or brain imaging methods might improve classification accuracy, facilitate new drug discovery and move toward stratified medicine.

Depression subtypes defined by symptom severity have several clinical implications for the treatment and prognosis. For example, baseline symptom severity is associated with drug-placebo differences in randomized control trials (Kirsch et al., 2008) and antidepressants are recommended as the choice of treatment for severe depression whereas psychosocial interventions as the choice of treatment for mild-moderate subthreshold depression (NICE guidelines CG90, 2009). Additionally, epidemiological studies have shown the association of symptom severity with functional impairment, co-morbidity and increased risk of mortality (Kessler et al., 2003, Kessler et al., 2005, Rutledge et al., 2006). In machine learning approaches, severity-related brain abnormalities have been shown to offer good discriminating potential in the classification of MDD and healthy controls. In emotional task fMRI data, Mourao-Miranda et al. (2011) found significant correlations between the distance of participants' feature vectors from the separating hyperplane of a trained support vector machine, and those participants' severity scores from the Hamilton Rating Scale for Depression (HRSD) (Hamilton, 1960), which suggests a relationship between depression severity and test predictions (Mourao-Miranda et al., 2011). Similarly, another study using structural MRI data reported a strong relationship between the fitted SVM weights and ratings of illness severity (Mwangi et al., 2012b). These findings suggest that fitted machine learned classifiers may capture patterns of brain abnormality in functional and structural neuroimaging data related to MDD severity. A model derived from a machine learned classifier may constitute an objective biomarker for depression severity. To date, no previous study has examined how the performance of machine learning algorithms in differentiating MDD vs. health may differ as a function of MDD symptom severity. This research question has important clinical implications in the context of whether machine learning approaches using fMRI data can yield comparable accuracy in the classification of MDD at various levels of severity.

We examined the accuracy of two-class machine learning classification of three distinct groups of MDD patients, with different levels of symptom severity based on the HRSD Scores, versus healthy controls. The three groups of MDD with severity gradation were: mild to moderate depression (HRSD score 14–19), severe depression (HRSD 20–23), and very severe depression (HRSD ≥ 24). (While there is no consensus on cutoff scores on the HRSD for identifying MDD severity subtypes, these severity ranges are consistent with several published recommendations (Zimmerman et al., 2013, Rush et al., 2008, DeRubeis et al., 1999)). We expected that the classifiers would achieve higher accuracy for the patient groups with very severe depression compared to those with severe depression or mild-moderate depression. For each range of severity, we also considered two types of fMRI data – from either resting-state or from an emotional-face matching task – hence, we examined classifier performance for 3 × 2 different situations.

2. Materials & methods

2.1. Participants

Ethics approval was obtained from the local review board. All participants were fluent in English and gave informed, written consent to participate in the study. Forty-five patients meeting DSM-IV criteria for MDD (Association AP, 2000) according to the Structured Clinical Interview for DSM-IV Axis 1 Disorders (First et al., 2002a), were recruited through advertisements. (See Table 1 for participant demographics). Patients included 29 females and 16 males, all right-handed, in the age range of 19–58 years (mean 37 ± 11 SD). The Edinburgh Handedness Inventory was used to assess handedness (Oldfield, 1971). The severity of depressive and anxiety symptoms was assessed using the clinician-administered, 17-item Hamilton Rating Scale for Depression (Hamilton, 1960), the Montgomery Asberg Depression Rating Scale (MADRS) (Montgomery and Asberg, 1979), and the Hamilton Anxiety Rating Scale (HAM-A) (Hamilton, 1959). Patients were also rated for disease severity using the Clinical Global Impression (CGI) scale (Guy, 1976), which allows clinicians to provide a severity rating based on their clinical experience. Patients were included in the study if they met the following inclusion criteria: (1) acute episode of MDD of unipolar subtype and a score of 14 or higher on the HRSD, and (2) free of psychotropic medication for a minimum of three weeks at time of recruitment. Exclusion criteria were: (1) Axis I disorders such as bipolar disorder, anxiety disorder, or psychosis, (2) history of substance abuse within six months of study participation, (3) borderline personality disorder, (4) medical or neurological disorders, (5) severe suicidal symptoms, (6) failure to respond to three trials of antidepressant medication, or (7) contraindications for MRI (metal implants, pregnancy, etc.). Patients were divided into three MDD severity groups based their HRSD scores. The mild-moderate group (HRSD 14–19) included 12 patients. The severe group (HRSD 20–23) included 18 patients. The very severe group (HRSD 24 +) included 15 patients.

Table 1.

Characteristics of three MDD patient groups and healthy controls.

Characteristic	All MDD patients	Mild-moderate MDD	Severe MDD	Very severe MDD	Healthy controls	p-Value (patients vs. controls)	p-Value (3 MDD groups omnibus comparison)
n	45	12	18	15	19
Sex (% female)	64%	42%	67%	80%	58%	0.31	0.09
Age (years)	37 ± 11	33 ± 11	38 ± 10	37 ± 11	33 ± 10	0.18	0.39
Age of onset (years)	24 ± 10	19 ± 5	26 ± 10	27 ± 11	–	–	0.10
Illness duration (years)	12 ± 8	14 ± 11	13 ± 7	10 ± 7	–	–	0.50
Duration of current episode (months)	59 ± 66	42 ± 54	72 ± 73	57 ± 69	–	–	0.48
HRSD score	22 ± 4	17 ± 1	21 ± 1	26 ± 2	3 ± 3	10− 27	10− 15
HAM-A score	24 ± 5	19 ± 4	24 ± 3	27 ± 5	–	–	10− 6
CGI score	4.1 ± 0.9	3.1 ± 0.2	4.1 ± 0.2	5.1 ± 0.4	–	–	0.001
MADRS scores	26 ± 6	20 ± 4	25 ± 4	31 ± 4			0.001

Age, Age of onset, Illness duration, Duration of current episode, HRSD score, HAM-A score, and CGI score rows show mean values ± standard deviations. First p-value column shows p-values for tests comparing all patients vs. controls (t-test or proportion test as appropriate). Second p-value column shows p-values from omnibus tests comparing the three patient groups (F-test or chi-squared test as appropriate).

Nineteen healthy controls, matched for gender (11 females, 8 males) and age (20–52 years, mean 33 +/ 10 SD), were also recruited for the study through advertisements. These participants were screened using the Structured Clinical Interview for DSM–IV Axis I Disorders, non-patient version, to ensure they did not have previous or current Axis I psychiatric disorders (First et al., 2002b) nor any family history of Axis I disorders, as determined by self-report. The control's HRSD scores ranged from 0 to 7. The demographics of the MDD patients and healthy controls are summarized in Table 1.

2.2. MRI data acquisition

MR images were collected using a 3 Tesla General Electric MR scanner (Signa VHi; General Electric Healthcare, Waukesha, WI, USA) equipped with an eight-channel, phased-array head coil. For each participant, two resting-state fMRI scans of 220 s in duration were acquired using a single-shot gradient-recalled echo, echo planar imaging sequence (110 volumes, repeat time (TR) 2000 ms, echo time (TE) 30 ms, flip angle 65°, field of view (FOV) 240 × 240 mm squared, matrix size 64 × 64, in-plane resolution 3.75 mm, 30 axial slices, 4 mm slice thickness). For the resting-state collection, participants were required to remain in the MRI scanner with their eyes open and fixated on a black crosshair at the center of a projection screen. The participants were instructed to relax, not think about anything in particular, and not to fall asleep. In addition, four emotional face task fMRI scans were collected per scanning session (for each subject), lasting 300 s each (150 volumes, TR 2000 ms, TE 30 ms, flip angle 65°, FOV 240 × 240 mm squared, matrix size 64 × 64, in-plane resolution 3.75 mm, 30 axial slices, slice thickness 4 mm). A T1-weighted structural MRI (TR 9.2 ms, TE minimum, flip angle 20°, FOV 256 × 256 mm squared, matrix size 512 × 512, in-plane resolution 0.5 mm, 176 sagittal slices, slice thickness 1 mm) was also acquired for anatomical registration of the fMRI data.

2.3. fMRI emotional-face matching task paradigm

While undergoing fMRI brain imaging, participants viewed triads either of faces or of control geometrical designs during a series of trials (Hariri et al., 2002). Each face had one of four emotional expressions: angry, fearful, happy, or sad. For each face triad, participants used a button box to indicate which of two target faces depicted the same emotion as the source face. Similarly, for control condition, participants responded with button press to indicate which of two geometrical designs matched with source geometrical design. Each fMRI run included 60 trials (12 for each of the four assessed emotions and the control condition). The order of presentation was randomized and each individual trial lasted 5 s (images: 3 s; inter-trial interval: 2 s). Stimulus onset asynchrony between successive trials was jittered (5 s or more in random increments of 0.5 s) to preserve fMRI signal variance (Burock et al., 1998). Previous work has shown that this emotional face matching task compared to control condition engages affective processing mechanisms, and reliably activates the amygdala and other relevant prefrontal and cingulate regions (First et al., 2002b).

2.4. Pre-processing

We considered two fMRI datasets, each involving all of the subjects, both control and MDD: one for resting-state, and another for the emotional face task. Each dataset was preprocessed using SPM8 (Wellcome Trust Centre for Neuroimaging, London, UK) and in-house code written in MATLAB (The MathWorks, Inc., Natick, MA, USA). The preprocessing steps for fMRI data included: (1) 6 parameter rigid body motion correction of fMRI volumes in SPM8, (2) non-linear spatial warping to MNI EPI template at 4 × 4 × 4 mm cubed resolution (43 × 51 × 37 voxels grid) in SPM8, and (3) 8 mm full width at half maximum (FWHM) Gaussian spatial smoothing of fMRI volumes in SPM8. The pre-processed registered fMRI data were masked to exclude voxels outside the brain using a hand-built mask. This mask retained 26,904 voxels (1,513,406 mm³) out of the 81,141 voxels in the interpolated fMRI volume space.

2.5. Dataset notation

To facilitate description of our analysis, we define a simple notation. We performed six analyses, using resting-state fMRI data or emotional face task fMRI data from one of the three patient severity groups (mild-moderate MDD, severe MDD, and very-severe MDD) as well as controls. We will use the phrase “dataset S” to refer to the dataset used in a given analysis. Therefore, dataset S consisted of either resting-state or emotional face task fMRI data from the patients in a given severity group as well as controls.

2.6. Overview of machine learning approach

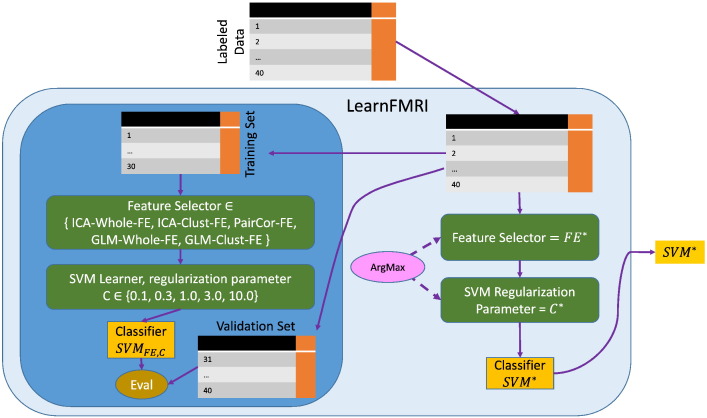
We ran six analyses, each testing the ability of machine learning to produce classifiers that could effectively differentiate between healthy controls and MDD patients from one of the three MDD severity groups, using either resting-state fMRI or emotional face task fMRI data. For each, we ran the LearnFMRI process, which selected one out of five different feature extraction algorithms as well as the regularization parameter value for the linear SVM learning algorithm (all described below). LearnFMRI then ran this particular choice of algorithm and regularization parameter value on all of the training data to produce a classifier, which could then be used to diagnose a future subject; see Fig. 1.

Fig. 1.

Illustration of the LearnFMRI machine learning algorithm. The learning algorithm takes as input a dataset of labeled data, then performs several steps. As shown in the dark blue bubble on the left, it first partitions the data into a Training Set (“1 … 30”) and a validation set (“31 … 40”), and then uses the Training Set to select the Feature Extractor and select the SVM regularization parameter, based on their performance on the Validation Set. (This actually involves 4 iterations, with 4 different internal [Training Set, Validation Set] splits - not shown here.) As shown on the right in the pale blue bubble, after identifying the optimal Feature Selector (FE*) and regularization parameter C, LearnFMRI then runs FE* on the entire set of labeled data (“1 … 40”), then runs the SVM learner with regularization parameter C* on the resulting set of features (over the data), to produce the classifier SVM*, which is returned. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We now provide a detailed explanation of the LearnFMRI procedure. To reduce the dimensionality of the fMRI data, our LearnFMRI system selects one of five different feature extraction algorithms for each of the 6 datasets S (each hand-coded in MATLAB): (1) independent components analysis (ICA) whole brain map feature extraction, ICA-Whole-FE; (2) ICA significant cluster feature extraction, ICA-Clust-FE; (3) pair-wise correlation feature extraction, PairCor-FE; (4) general linear model (GLM) analysis whole brain map feature extraction, GLM-Whole-FE; and (5) GLM significant cluster feature extraction, GLM-Clust-FE. (LearnFMRI considered only ICA-Whole-FE, ICA-Clust-FE and PairCor-FE for resting-state fMRI data, and all five for task-based datasets.) Feature extraction algorithms ICA-Clust-FE and GLM-Clust-FE used statistical testing between patients and controls to extract features (voxel clusters) that were significantly different between the groups. To reduce the potential for overfitting, it performed statistical comparisons only between patients and controls in training sets (see Classifier performance section below). Therefore, different sets of participants (i.e. only the training set participants) contributed to these statistical tests in different folds of the nested cross-validation described below. Statistical maps differed between folds. These differences are illustrated in Supplementary Fig. 1. The ICA-Whole-FE, PairCor-FE and GLM-Whole-FE algorithms did not use statistical testing between patients and controls to generate features. Details of feature extraction algorithms are provided below.

For each task, LearnFMRI also tested the linear support vector machine (SVM) learning algorithm with regularization parameter values 0.1, 0.3, 1.0, 3.0, or 10.0 and selected the best-performing parameter value.

Testing multiple combinations of feature extraction and classifier algorithms on the test data and then presenting only the algorithms that perform best on that data may create a substantial danger of overfitting, where an algorithm works well because it is matching the specific pattern of noise that happens to be present in the dataset tested. This good performance does not generalize to new data with different noise patterns. (Note that this overfitting is in terms of the choice of algorithm; this is still a problem even when cross-validation is used to protect against overfitting in terms of the algorithms' learned weight values.) LearnFMRI therefore used internal cross-validation to protect against overfitting with respect to (1) the choice of feature extraction algorithm, (2) the extracted features (feature extraction used the patient/control labels), (3) the choice of regularization parameter value for the linear SVM learning algorithm and (4) the weights chosen by the linear SVM learning algorithm.

Our LearnFMRI system is summarized in Fig. 1. Given the set of labeled training data for each dataset S, LearnFMRI considers each combination of feature extractor and regularization parameter and returns the best-performing choice of feature extraction algorithm as well as a linear SVM classifier trained using the best regularization parameter value. To estimate the generalization performance of the chosen feature extraction algorithm and trained linear SVM classifier, we used a five-fold cross-validation process, repeated ten times, with different random partitioning of participants into the five folds. Note that different cross-validation folds found different best combinations of feature extraction/regularization parameter. This cross-validation process estimates the accuracy not of a single machine learned classifier but of the entire process of selecting the feature extraction algorithm and regularization parameter value and training the linear SVM classifier.

2.7. Feature extraction preliminaries – cluster growing algorithm

The ICA-Clust-FE and GLM-Clust-FE feature extraction algorithms each identify significant clusters in statistical parametric maps (details provided below). Each uses the following automated region-growing algorithm to identify clusters: Given a 3D statistical parametric map, (t-map generated by comparing patients vs. controls in terms of ICA maps values or GLM beta weight values), the cluster-growing algorithm grows a cluster around each positive or negative statistical peak (local extremum) in the map. Specifically, it uses each peak voxel as a seed of the cluster, and then adds neighboring, statistically significant voxels to the growing cluster one-at-a-time, until the algorithm encounters either non-significant neighbor voxels or significant voxels that have already been added to another growing cluster. If two statistical peaks are too close together (within 10 mm of each other), the less-significant peak is not used as a cluster seed. This prevents large “hills” of significant voxels that happen to have two or more peaks that are close together from being divided into multiple smaller clusters.

2.8. Independent components analysis (ICA) feature extraction – ICA-Whole-FE, ICA-Clust-FE

Our ICA feature extraction algorithms, ICA-Whole-FE and ICA-Clust-FE, are both based on the ICA procedure of Erhardt et al. (2011). Briefly, 15 ICA “connectivity maps” are computed. ICA-Whole-FE simply combines a given participant's ICA map values into one long feature vector for that participant. ICA-Clust-FE extracts significant voxel clusters by comparing patients vs. controls for each of the 15 ICA maps. Note that ICA-Whole-FE does not use the participant labels (patient or control), whereas ICA-Clust-FE does use the labels. We applied ICA-Whole-FE or ICA-Clust-FE to resting-state or task-based fMRI data separately. Details of the algorithms are provided in Appendix A.

2.9. Pair-wise correlation feature extraction – PairCor-FE

The Harvard-Oxford atlas includes 26 prefrontal regions involved in executive control and/or emotion regulation (see Table 2); Previous literature suggest that changes in these regions have been associated with major depressive disorder (Fitzgerald et al., 2008). PairCor-FE defined each participant's feature vector as the 325 pair-wise correlations among those regions' time courses, and al computed these correlation features separately for either the resting-state or task-based fMRI data, as follows. All fMRI data runs for the participant were concatenated along the time axis (two runs for resting-state data, four runs for task-based data). The mean fMRI activation time course was computed for each region (mean across voxels in the region). The Pearson correlation coefficient was computed for each pair of time courses among all 325 pairs of different regions; this 325-tuple of correlation values was the feature vector for the participant, which were used by the classifier; see the Machine learning algorithm – LearnFMRI section below.

Table 2.

Region information for pair-wise correlation features.

#	Name	X	Y	Z	Volume
1	Left Frontal Pole	− 26	54	8	55,697
2	Right Frontal Pole	25	53	9	64,809
3	Left Insular Cortex	− 37	2	1	10,648
4	Right Insular Cortex	36	4	1	10,801
5	Left Superior Frontal Gyrus	− 15	20	57	23,412
6	Right Superior Frontal Gyrus	14	19	58	21,309
7	Left Middle Frontal Gyrus	− 39	19	43	23,430
8	Right Middle Frontal Gyrus	38	20	44	22,069
9	Left Inferior Frontal Gyrus pars triangularis	− 51	29	10	5197
10	Right Inferior Frontal Gyrus pars triangularis	51	29	9	4306
11	Left Inferior Frontal Gyrus pars opercularis	− 52	16	16	6170
12	Right Inferior Frontal Gyrus pars opercularis	51	16	17	5504
13	Left Precentral Gyrus	− 34	− 11	50	35,587
14	Right Precentral Gyrus	34	− 10	51	34,191
49	Left Frontal Medial Cortex	− 6	44	− 17	3641
50	Right Frontal Medial Cortex	4	44	− 18	4045
53	Left Subcallosal Cortex	− 6	21	− 14	4434
54	Right Subcallosal Cortex	4	22	− 14	4423
55	Left Paracingulate Gyrus	− 7	38	22	11,677
56	Right Paracingulate Gyrus	6	38	23	11,322
57	Left Cingulate Gyrus anterior division	− 5	19	25	10,022
58	Right Cingulate Gyrus anterior division	4	20	25	10,649
65	Left Frontal Orbital Cortex	− 31	25	− 16	13,538
66	Right Frontal Orbital Cortex	28	24	− 15	11,619
81	Left Frontal Operculum Cortex	− 41	19	6	2819
82	Right Frontal Operculum Cortex	40	20	6	2494

Regions used in pair-wise correlation feature extraction. Regions are from the Harvard-Oxford atlas. # denotes region numbering from the atlas. X, Y, Z denote region centroid coordinates in mm. Volume is in mm^3.

2.10. GLM analysis feature extraction for task-based data – GLM-Whole-FE, GLM-Clust-FE

The GLM-Whole-FE and GLM-Clust-FE feature extraction algorithms were used with emotional-face task fMRI data only. Both involve the standard General Linear Model (GLM) analysis, based on the following statistical contrasts:

• •localizer contrast (sum of all five trial types),
• •emotional faces - geometric stimuli,
• •positive - negative emotional faces (happy - other emotional faces), and
• •negative faces - geometric stimuli (where negative faces included angry, fearful, and sad faces).

GLM-Whole-FE combines the four (first-level) contrast maps for a given participant into one long feature vector for that participant. GLM-Clust-FE compares contrast maps in terms of patients vs. controls and extracts significant clusters for each map. See Appendix B for details.

2.11. Base-learner: linear SVM

Our LearnFMRI learning algorithm uses the linear support vector machine (SVM) learning algorithm to create trained linear SVM classifiers. We used the LIBSVM implementation of the linear SVM learning algorithm and classifier, along with in-house MATLAB code for all data manipulation, cross-validation book-keeping, and accuracy computations.

2.12. Machine learning algorithm – LearnFMRI

Given a labeled training dataset, LearnFMRI will produce a classifier that can accurately classify novel participants. As shown in Fig. 1, LearnFMRI first selects one feature extraction algorithm (which is one of ICA-Whole-FE, ICA-Clust-FE, PairCor-FE, GLM-Whole-FE or GLM-Clust-FE) as well as the linear SVM regularization parameter C ∈ {0.1, 0.3, 1.0, 3.0, 10.0}. LearnFMRI uses an internal cross-validation to find the appropriate feature selection and regularization parameter; see Fig. 1. This involves trying each specific feature selector and regularization parameter on a portion of the training data and evaluating the performance on the remaining subset. (This is repeated four times; see “Illustration” section below.) After finding the best choice of feature selector and regularization parameter, LearnFMRI then uses these “settings” to train the classifier, using all of the training data. It then returns that resulting trained classifier.

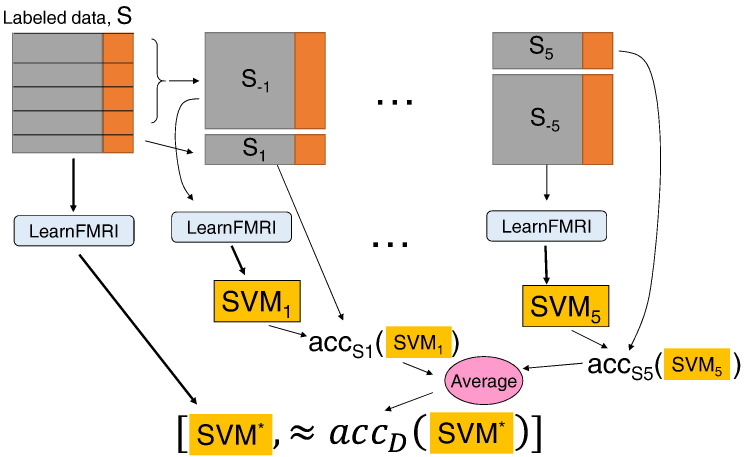
2.13. Classifier performance

For each dataset S, our goal is a single classifier (SVM*) that can accurately diagnose novel participants – that is, participants who were not in the training set. To estimate the expected out-of-sample (generalization) accuracy of this classifier SVM* – the result of running LearnFMRI on all of the training data from a given dataset S – we used five-fold cross-validation; see Fig. 2. For each of the five folds, approximately one fifth of the participants was held out as a test set, with the remaining four-fifths comprising the training set. Test and training sets were balanced as closely as possible for proportions of patients versus controls. Five-fold cross-validation was repeated ten times with different random assignments of participants to the five folds. Note that this cross-validation ran the entire LearnFMRI learning algorithm for each fold, which in turn used internal cross-validation steps inside it – i.e. nested cross-validation inside the outer five-fold cross validation. The use of nested cross-validation was important for protecting against overfitting in the selection of the feature extraction algorithm, cluster selection from statistical testing (patients vs. controls), and choice of regularization parameter for the linear SVM base-learner.

Fig. 2.

Illustration of the five-fold cross-validation procedure for evaluating the performance of running LearnFMRI on the labeled data S. This process first runs LearnFMRI on all of S, to produce the classifier SVM* – see left path. It then does 5 times more work, solely to estimate the actual performance of SVM* – i.e. how well SVM* will perform on unseen data, from the underlying distribution D. We denote the accuracy of SVM* on the underlying distribution D as acc_D(SVM*). This process divides S into 5 partitions. The procedure then runs LearnFMRI on 4/5 of the data (S₁) to produce a classifier SVM₁. It then evaluates this SVM₁ on the remaining data (S _− 1) – i.e. on the data that was not used to train SVM₁. This produces the accuracy number acc_S1(SVM₁). It does this 4 more times, on 4 other partitions [S _− i, S_i] of S, to produce 4 other estimates. We then use the average of these five {acc_Si(SVM_i)} values as our estimate of SVM*'s accuracy.

Notice each of 5 “cross-validation” steps also requires running LearnFMRI, which note (from Fig. 1) has its own internal (4 fold) cross-validation steps, to find the best feature extractor and base learner. Hence, this involves “in fold” feature selection, etc.

We quantified the performance of these classifiers using multiple measures: accuracy, sensitivity, specificity, balanced accuracy, positive predictive value, and negative predictive value (all measures were based on cross-validation). As described above, there were six analyses: mild-moderate MDD (respectively, severe MDD or very severe MDD) patients vs. controls, using either resting-state or task-based fMRI data. For each of these analyses, each of the participants used in that analysis was present in the (outer) test set in precisely one iteration of outer cross-validation, on each of the ten repetitions (see above). Thus, each participant's data underwent ten classification attempts. For each participant, we computed the proportion of correct classification attempts. Accuracy was computed as the mean proportion of correct classification attempts across all participants. Sensitivity was computed as the mean proportion of correct classification attempts for patients (true positives), and specificity was computed as the mean proportion of correct classification attempts for controls (true negatives). Balanced accuracy was computed as the mean of sensitivity and specificity. Positive predictive value (and negative predictive value, respectively) was computed as the proportion correct among positive (respectively, negative) predictions.

For each of the six analyses, mean accuracy values were compared against chance accuracy using one-tailed bootstrap statistical tests on participants' proportion of correct classification attempts values. Chance accuracy was derived from randomly guessing the participant class (patient/control) weighted by the relative proportions of patients and controls in the given analysis. Specifically, let r = proportion of patients = #patients / (#patients + #controls), which is in the range [0,1]. Then random accuracy = r² + (1 − r)², which is in the range [0,1]. Chance accuracy values ranged from 50 to 53% depending on the numbers of patients and controls used in each analysis. The alpha-value (false positive rate under the null hypothesis of chance accuracy) was set a 0.05. Multiple comparison correction was performed using the Bonferroni method (i.e. multiplying the individual p-values by the number of tests; 6 in this case).

2.14. Illustration of the overall learning + evaluation process

We provide a detailed illustration, for a given run of five-fold cross-validation (i.e. set of all five iterations of five-fold cross-validation). See Fig. 2. Here, we first divided the participants into five folds, approximately balanced for proportion of patients and controls. On the i-th iteration of outer cross-validation, we held out the i-th fold as the test set (i.e. outer test set). All participants not in fold i were used as the training set for that iteration (i.e. outer training set input to the learning algorithm LearnFMRI). LearnFMRI then computed accuracy scores for each combination of feature extraction algorithm and regularization parameter. To do so, the learning algorithm employed a four-fold cross validation (inner cross-validation) analysis for each possible combination. For a given combination, on the j-th iteration of inner cross-validation, we held out the j-th fold as the inner test set. All participants not in folds j or i were used as the inner training set for that inner iteration. Statistical comparisons between patients and controls during feature extraction were performed only on participants from the inner training set. The resulting statistical differences were used to extract features for the inner test set participants without using those participants' labels (patient versus control). The classifier was trained on the inner training participants (those not in either fold j or i) and tested on the inner test participants (in fold j). Accuracy results were averaged over the four inner cross-validation folds. In this way, (inner) cross-validated accuracy scores were computed for each combination of feature extraction and regularization parameter. LearnFMRI then chose the best combination, defined as that combination yielding the highest accuracy (proportion of correctly classified participants) over the four-fold inner cross-validation tests. That best combination specified the feature extraction algorithm and regularization parameter, which were then applied to all the participants in the outer training set (i.e. all participants not in fold i), resulting in a trained linear SVM classifier. The choice of feature extraction method and the trained classifier are the output of the learning algorithm. Their performance was then tested on participants in the outer test set (i.e. participants in fold i).

2.15. Visualization of machine learning analysis

To gain insight into the automated diagnosis process, we analyzed the classifier weights for various fMRI-based features. The linear SVM learning algorithm produces a “weight” for each feature, which recall corresponds to a value extracted from one voxel or region or the correlations between two regions (see descriptions of feature extraction algorithms above). The weights for this classifier are presented in the Discriminating brain regions section of the Results.

To visualize which brain regions a classifier used, we created a weight map by weighting each relevant region by the absolute value of its appropriate weight value. We did this only for the analysis of patients with very-severe MDD vs. controls using resting-state fMRI data, as this was the only analysis that performed significantly above chance.

3. Results

3.1. Demographics

There were no significant differences between healthy controls and MDD patients in sex or age (Table 1). There were no significant differences among the three patient groups (mild-moderate MDD, severe MDD, and very-severe MDD) in terms of sex, age, age of MDD onset, illness duration, or duration of current MDD episode (Table 1). As expected, there were group differences in HRSD scores between patients and controls and among the three patient groups. There were also significant differences in MADRS scores, HAM-A scores, CGI scores among the three patient groups, which is consistent with severity categories defined by HRSD scores.

3.2. Classification results

Based on ten repetitions of five-fold cross-validation, classification using resting-state fMRI data comparing MDD patients with very severe depression vs. controls achieved a sensitivity of 59%, specificity of 72% and accuracy of 66% (Table 3). This accuracy value was significantly above chance (p = 0.012, Bonferroni corrected for the 6 tests). Classification analyses using resting-state fMRI data with patients in the mild-moderate and severe depression groups did not achieve accuracies significantly above chance (Table 3). Interestingly, accuracies were not significantly above chance for classification using the emotional face task fMRI data for any of the three patient groups (Table 3).

Table 3.

Classification performance.

MDD patient subgroup	Accuracy	Chance accuracy	p-Value (uncorrected)	p-Value (corrected)	Sensitivity	Specificity	Balanced accuracy	Positive predictive value	Negative predictive value
Resting state fMRI data
Mild-moderate	58%	53%	0.23		8%	89%	49%	32%	61%
Severe	52%	50%	0.36		44%	59%	52%	51%	53%
Very severe	66%	51%	0.002	0.012	59%	72%	66%	62%	69%
Task-based fMRI data
Mild-moderate	55%	53%	0.35		10%	84%	47%	28%	60%
Severe	45%	50%	0.91		44%	45%	45%	43%	46%
Very severe	51%	51%	0.49		21%	56%	48%	40%	54%

Results for two-class classification of patients vs. controls for three patient groups using two different fMRI datasets. p-Values are for bootstrap tests of accuracy against chance accuracy derived from guessing the class (see main text).

3.3. Discriminating brain regions

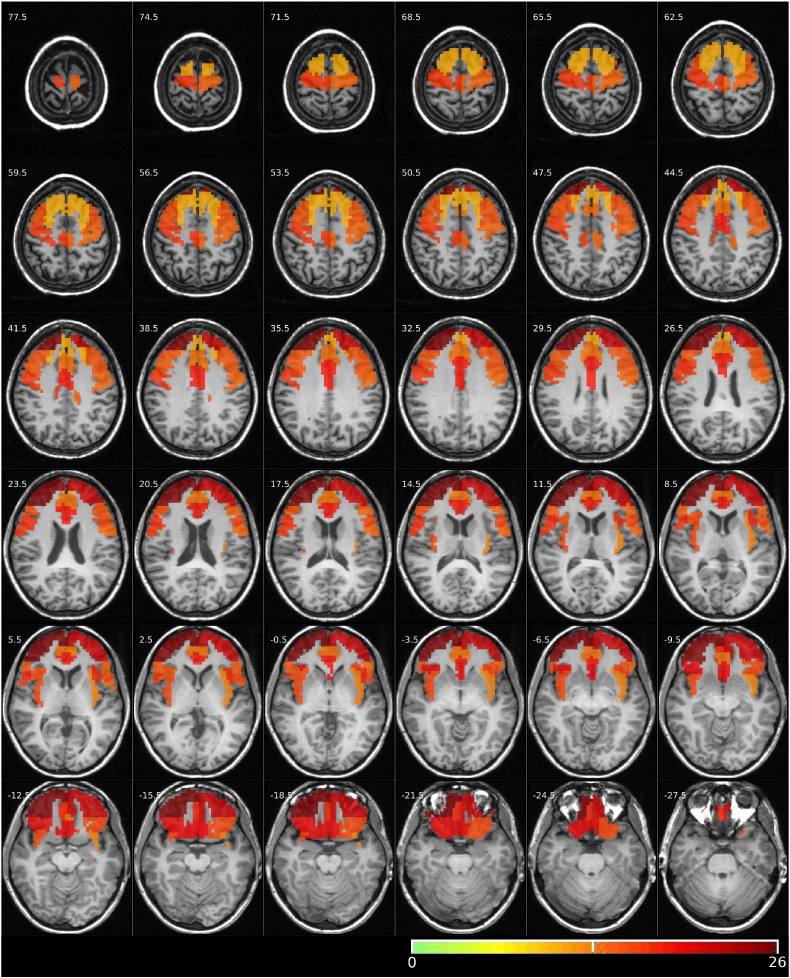
We applied LearnFMRI to resting-state fMRI data from all patients with very-severe MDD and healthy controls to derive one model. In this case, the learning algorithm selected pair-wise correlation feature extraction and the SVM regularization parameter value of C = 0.1. The regions considered for pair-wise correlation features come from the Harvard-Oxford atlas and are listed in Table 2. Fig. 3 shows these regions, colour-coded based on the learned classifier weights and superimposed on one participant's anatomical scan. Table 4 shows the learned weights from the trained linear SVM classifier for all 325 pair-wise correlation features from the analysis of very severe depression vs. healthy controls using resting-state fMRI data. (There are subtleties in interpreting weight values from trained classifiers. See Haufe et al. (2014) for discussion.

Fig. 3.

Regions used to classify participants as having very-severe MDD or being healthy controls are shown in colour, superimposed on one participant's anatomical scan. Neurological convention is used (left side of brain on left of image). Slice z-coordinate in mm in MNI atlas space given in upper left. Yellow regions are less-heavily weighted, while red regions are more-heavily weights. Weights were derived from applying the learning algorithm LearnFMRI to all patients in the very-severe MDD group as well as all healthy controls. LearnFMRI selected the pair-wise correlation feature extraction algorithm and the logistic classifier. The pair-wise correlation feature extraction algorithm computed the correlations among 325 pairs of regions, from the list of 26 regions in Table 2. The trained logistic classifier assigned a weight to each correlation feature. Note that a given region thus participated in 25 different features. The colours in the figure denote the total absolute weight each region was assigned. That is, the colour of a given region was the sum of the absolute values of the weights for the 25 pairs that included that given region. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 4.

Learned weights for pair-wise correlation features.

Region	Left Frontal Pole	Right Frontal Pole	Left Insular Cortex	Right Insular Cortex	Left Superior Frontal Gyrus	Right Superior Frontal Gyrus	Left Middle Frontal Gyrus	Right Middle Frontal Gyrus	Left Inferior Frontal Gyrus pars triangularis	Right Inferior Frontal Gyrus pars triangularis	Left Inferior Frontal Gyrus pars opercularis	Right Inferior Frontal Gyrus pars opercularis	Left Precentral Gyrus	Right Precentral Gyrus	Left Frontal Medial Cortex	Right Frontal Medial Cortex	Left Subcallosal Cortex	Right Subcallosal Cortex	Left Paracingulate Gyrus	Right Paracingulate Gyrus	Left Cingulate Gyrus anterior division	Right Cingulate Gyrus anterior division	Left Frontal Orbital Cortex	Right Frontal Orbital Cortex	Left Frontal Operculum Cortex	Right Frontal Operculum Cortex
Left Frontal Pole
Right Frontal Pole	1.63
Left Insular Cortex	1.49	2.42
Right Insular Cortex	1.73	1.91	1.06
Left Superior Frontal Gyrus	1.16	2.02	− 1.53	− 1.34
Right Superior Frontal Gyrus	0.74	2.07	− 0.9	− 0.36	− 0.79
Left Middle Frontal Gyrus	1.83	2.2	− 1.55	− 1.1	− 0.28	− 0.11
Right Middle Frontal Gyrus	2	1.52	0.69	0.24	− 0.7	0.69	− 0.08
Left Inferior Frontal Gyrus pars triangularis	0.52	2.56	− 0.29	0.4	− 0.01	− 1.55	− 1.86	− 0.9
Right Inferior Frontal Gyrus pars triangularis	− 0.22	0.15	1.18	1.33	− 1.82	− 2.5	− 2.5	− 3.3	0.61
Left Inferior Frontal Gyrus pars opercularis	0.25	1.99	− 1.74	− 1.2	− 0.3	− 1.81	− 2.2	− 1.46	0.93	0.3
Right Inferior Frontal Gyrus pars opercularis	2.5	2.33	1.78	1.62	1.2	1.47	− 0.52	− 0.13	2.47	0.16	− 0.44
Left Precentral Gyrus	2.29	3.52	0.02	0.17	0.65	0.77	0.99	2.13	− 0.41	0.51	− 0.66	1.23
Right Precentral Gyrus	3.35	3.15	1.43	1.23	0.52	0.81	1.5	1.5	1.36	0.06	0.91	0.36	0.74
Left Frontal Medial Cortex	− 0.57	− 1.51	− 0.97	− 2.25	− 1	− 0.22	− 0.27	− 0.48	− 2.93	− 1.45	− 1.94	− 2.1	0.04	0
Right Frontal Medial Cortex	0.87	1.13	− 1	− 2.16	− 1.05	0.08	0.08	0.29	− 1.97	− 1.13	− 2.01	− 1.47	0.73	0.69	− 0.71
Left Subcallosal Cortex	2.4	1.62	− 0.68	− 4.05	0.48	0.98	1.92	1.15	− 1.67	− 2.26	− 0.7	− 1.13	1.82	1.38	1.27	− 0.67
Right Subcallosal Cortex	3.49	3.26	− 0.03	− 2.86	1.09	1.69	2	2.32	− 1.39	− 1.74	− 1.02	− 0.74	2.5	1.93	2	− 0.15	− 1.06
Left Paracingulate Gyrus	2.3	1.58	− 0.74	0.15	− 0.11	− 0.06	0.33	1.22	− 0.28	− 0.7	− 1	1.86	1.9	1.97	− 2.41	− 2.96	− 0.57	− 0.04
Right Paracingulate Gyrus	3.31	1.99	− 0.16	0.87	0.02	0.53	0.63	1.59	− 0.15	− 0.71	− 1.14	1.83	2.17	1.85	− 2.95	− 2.99	− 0.29	0.14	− 0.28
Left Cingulate Gyrus anterior division	0.89	1.46	− 1.67	0.84	− 0.51	− 0.52	− 0.86	1.21	− 1.13	0.63	− 2.21	2.22	0.9	1.59	− 4.4	− 3.91	− 1.9	− 1.67	− 0.91	− 0.72
Right Cingulate Gyrus anterior division	2.27	2.36	− 1.43	1.07	− 0.29	− 0.21	− 0.89	1.02	− 0.31	0.41	− 1.64	2.26	1.04	1.31	− 4.26	− 3.62	− 1.62	− 1.58	− 1.25	− 0.91	0.33
Left Frontal Orbital Cortex	2.74	3.54	− 1.3	− 1.54	− 0.51	− 0.22	− 0.94	0.64	− 0.83	− 0.36	− 1.55	0.98	0.56	1.49	1.03	0.09	− 2.62	− 1.19	− 0.59	0.01	− 2.21	− 2.45
Right Frontal Orbital Cortex	1.39	0.35	− 0.32	− 0.64	− 2.35	− 1.75	− 3.04	− 2.35	− 1.4	− 2.33	− 1.92	− 0.55	− 0.75	− 0.44	− 2.88	− 2.57	− 3.38	− 1.92	− 1.73	− 1.25	− 1.68	− 2.22	1.28
Left Frontal Operculum Cortex	1.58	3.71	− 1.18	1.07	− 0.57	− 0.25	− 1.27	1.55	1.24	3.17	− 0.59	2.75	0.94	2.77	− 1.36	− 0.44	− 1.04	− 1.12	− 1.08	− 0.34	− 0.8	− 0.64	− 2.16	− 0.41
Right Frontal Operculum Cortex	1.43	2.38	0.43	0.43	− 0.84	0.07	− 1.57	− 0.54	1.98	0.63	− 1.15	0.93	0.54	0.61	− 2.31	− 2.08	− 2.13	− 2.5	0.3	0.47	1.37	1.01	− 0.74	− 1.77	2.48

Learned weights from the trained logistic classifier for 325 pair-wise correlation features from analysis of very severe MDD patients vs. healthy controls using resting state fMRI data. A weight is shown for each pair of non-identical regions, each of which contributed one element (one correlation value) to the feature vector. Offset weight was 6.18. Patients and controls were labeled + 1 and − 1, respectively. Weights with absolute value ≥ 0.8 are highlighted in bold font. Notes that interpretation of learned classified weights, as shown here, must be done with caution. See Haufe et al. (2014) for discussion.

4. Discussion

In this study, we evaluated the performance of two-class automated classification (healthy controls vs. patients) for three groups of patients with MDD: mild-moderate MDD, severe MDD, and very-severe MDD. The main finding is that using pattern analysis of resting-state fMRI activity, the accuracy of learned classifier was significantly better than chance at classifying very severe depression versus healthy controls. However, the performance of the classifiers for distinguishing healthy versus mild-moderate depression and healthy versus severe depression, were only at the chance level. Another important finding is that fMRI activation patterns evoked by the emotional face processing task failed to show significant classification performance, for any of the MDD severity groups. Given the small sample size, our results should be considered as preliminary.

The finding of higher classification accuracy for very severe depression is consistent with previous machine learning studies that showed significant correlations between prediction scores and symptom severity scores using structural and functional data. The classification accuracy of 66% for very severe depression is comparable to that of previous studies using working memory neural correlates and structural data (Costafreda et al., 2009, Fu et al., 2008). However, contrary to our results, those previous studies, using similar supervised SVM learners, could significantly distinguish controls from MDD with moderate severity (mean HRSD: 21–22) (Costafreda et al., 2009, Fu et al., 2008, Marquand et al., 2008). The inconsistencies in results could be partly explained by variations in methodology and MRI data, as we used resting-state fMRI data whereas those previous studies used structural MRI and emotional recognition task-dependent fMRI data. Given the lower accuracies for the classification of less severe depression groups, our results suggest that less severe forms of MDD may be heterogeneous and is likely to capture mild forms of depressive states such as dysthymia and anxiety or personality weighted conditions. As less severe forms of depression may be associated with mild brain abnormalities, it might be harder for the learning algorithm to find a meaningful boundary between these groups and controls in a small dataset. We may need larger sample to improve the power and enable the classifiers to distinguish these groups from healthy controls. Considering that the need for machine learning methods in the diagnosis of milder depression would be greater in clinical practice than that of more severe form of depression, the poor accuracy in the classification of milder depression by machine learning methods shown in this study may limit its use as a tool in the early detection of milder or subthreshold depression. However, results based on small sample size precludes any conclusions on clinical utility. In addition, although our current classifier yielded significant classification for very severe depression, the clinical utility of this current system may be limited by its modest specificity (72%). Again, this needs to be tested in larger and independent samples.

The brain regions that contributed to the classification of very severe depression included the various prefrontal and limbic regions listed in Table 2. These regions have been reported to have abnormal structure and function in group-level analyses between patients with MDD and healthy control (Mayberg, 2003, Drevets et al., 2008, Fitzgerald et al., 2008). Moreover, the resting-state functional connectivity between prefrontal, insula and anterior cingulate regions was found to be positively correlated with severity of depression in univariate analysis (Avery et al., 2014, Horn et al., 2010), which is consistent with our findings, and suggests the greater contribution of these networks in the classification of very severe depression from healthy controls.

Although previous fMRI studies using univariate analysis showed significant correlation between severity of depressive symptoms and alteration in regional brain activity due to emotional tasks or stimuli, our results failed to show significant accuracy in distinguishing healthy controls from depression patients, grouped at three levels of severity. Of course, this may be due to the different objectives, as univariate correlations (at the class level) are neither sufficient nor necessary for effective classification performance. In addition, this behavior could be due to low reliability of the task or poor variance of task-related activation between the three depression groups and the control group. Alternatively, this may be due to the small sample sizes here, coupled with the complexity of the emotional task. Although this is the first study to use an emotional-face matching task in fMRI machine learning analysis, several studies used this paradigm to elicit responses in neural regions and circuits implicated in emotional processing (Frodl et al., 2011, Frodl et al., 2009). Previously published fMRI machine learning studies (Fu et al., 2008, Nouretdinov et al., 2011) used an emotional face recognition task that is more cognitively/perceptually demanding than the emotional face matching task used here. In conclusion, our findings suggest that the pattern of resting-state fMRI BOLD signals produced better classification of severe MDD than the fMRI patterns evoked by the emotional face matching task.

The reasons for the better performance of the classifier using resting-state data than task related data remains speculative and could be related to the abnormalities of the default mode network (DMN) in MDD. DMN refers to spontaneously organized brain activities from a network of brain regions including anterior cingulate cortex, medial prefrontal cortex, posterior cingulate cortex, precuneus, and inferior parietal lobule (Raichle et al., 2001), which is activated during rest and deactivated during active tasks (Raichle et al., 2001). Previous studies of MDD showed increased resting-state functional connectivity of the DMN areas especially in anterior cingulate and medial prefrontal regions (Sheline et al., 2010) and decreased functional connectivity in bilateral prefrontal areas of DMN during emotional processing tasks (Shi et al., 2015). Furthermore, higher levels of rumination about depressive symptoms was found to be correlated with higher DMN dominance (Hamilton et al., 2011) and severe depressive symptoms (Kuehner and Weber, 1999). It is therefore possible that the increased levels of rumination and associated increased DMN activity during the resting stage may have contributed for the greater performance of the classifier for very severe depression, whereas the lack of activation in DMN due to reduction in rumination during the engagement with the task may partly explain the poor performance of the classifier with task related data.

4.1. Methodological issues

As mentioned above, a major limitation of the study is the small sample size, which might have influenced our results. Although previous machine learning studies in MDD achieved higher accuracies using small datasets (Fu et al., 2008, Marquand et al., 2008, Nouretdinov et al., 2011), yet larger studies in two independent samples are needed to develop and test predictive models that are sufficiently stable to use in clinical practice. Recent machine learning studies using structural MRI have recommended participant groups with 130 participants or more per group to learn an effective classification for schizophrenia versus healthy controls (Nieuwenhuis et al., 2012). However, there are no clear guidelines on required sample sizes for machine learning studies using resting and task-related fMRI data in patients with MDD. Additionally, owing to our unbalanced sample between MDD (N = 45) and healthy controls (N = 19), we did not examine the accuracy of classification of MDD as a single group vs. healthy controls. Another major methodological issue is the categorization of MDD severity groups based on HDRS scores. As mentioned previously, there is no consensus on the validity of cutoffs on HDRS for defining the severity categories. The American Psychiatric Association (APA) Handbook of Psychiatric Measures recommended the following thresholds to define grades of severity on HRSD: mild to moderate ≤ 18, severe 19–22, very severe ≥ 23 (Rush et al., 2008). In contrast, others have used 20 as the cutoff to distinguish severe depression from mild to moderate (DeRubeis et al., 1999) and 24 or 25 as the cutoff to distinguish severe from very-severe depression (Knesevich et al., 1977, Montgomery and Lecrubier, 1999). As there is very limited empirical research in this area, we used other severity measures such as MADRS and CGI scores to corroborate the severity categories defined by HDRS (see Table 1). A third potential issue is that we used linear SVM classifiers. We focused on this algorithm because it offers the advantage that one can examine the learned weights and attempt to interpret how the classifier is using the input features to produce a classification prediction. It is possible that other machine learning classifiers such as the non-linear radial basis function (RBF) SVM will yield better accuracy in this context. Unfortunately, it is difficult to provide a simple, straightforward interpretation of how algorithms such as RBF SVM produce predictions for a given individual. This difficulty of interpretation presents a barrier to deployment in the clinic, as medical practitioners place a high degree of importance on being able to interpret and evaluate the predictions of any automated clinical decision-making system.

5. Conclusions

Resting-state brain activity provides a statistically significant classification of healthy controls vs. patients with very severe MDD (HRSD scores ≥ 24) but not for less severe depression. Moreover, even the classification accuracy that our approach achieved for very severe MDD is not sufficient from a clinical perspective. The negative results of our study help to focus the future efforts of our community, on considering larger sample sizes. We anticipate this may lead to better results that may provide clinically meaningful classification results for MDD based on severity.

The following are the supplementary data related to this article.

Supplementary Fig. 1

For the ICA-Clust-FE feature extraction and GLM-Clust-FE feature extraction, significant clusters were identified by comparing patients vs. controls for various ICA components or GLM contrasts (see main text for details). These label-dependent statistical comparisons were done using only training set data, never test set data, which is important to avoid overfitting. However, this means that different voxels were selected for the ICA and GLM analysis feature extraction depending on exactly which participants comprised the training set in each fold of five-fold cross-validation. Note also that the five-fold cross-validation process was repeated ten times (for both the resting-state fMRI data and for the task-base fMRI data, for each of the three MDD severity groups). Selected clusters differed over each of the five folds of cross-validation in each of the ten repetitions. This figure provides an illustration of how consistently voxels were selected in ICA-Clust-FE and GLM-Clust-FE feature selection. The ICA-Clust-FE and GLM-Clust-FE analysis feature extraction algorithms actually selected entire clusters of significant difference, but we show statistics for individual voxels here because this is more straight-forward. The histograms show results for ICA-Clust-FE feature extraction with resting-state fMRI data (left), ICA-Clust-FE feature extraction with task-based fMRI data (middle), and GLM-Clust-FE feature extraction with task-based fMRI data (right). The x-axis denotes how consistently a given voxel was selected (i.e. was part of a significant cluster that was selected), and the y-axis denotes the proportion of voxels (out of the total of all voxels that were selected at least once). For example, in the left panel, the bar at x-position 0.18 has height 0.124. This means that, out of all voxels that were selected at least once, some members of that voxel population were selected in about 0.18 (i.e. 18%) of equivalent statistical maps (“equivalent” explained below), and such voxels comprised 0.124 (i.e. 12.4%) of the total population of voxels that were selected at least once. The x-axis values were defined across sets of “equivalent” statistical maps. For example, the ICA analysis computed 15 ICA components. Note that such components are often called “functional connectivity maps”, but we will refer to them as functional connectivity volumes, to avoid using re-using the term “map”, which we are already using to refer to statistical maps comparing patients vs. controls in terms of some underlying value at every voxel. Note also that the set of 15 functional connectivity volumes was different for resting-state and task-based fMRI data (understandably), and they were also different depending on which MDD severity group was being analyzed (i.e. which set of MDD patients were included in the ICA analysis). Then clusters of significant voxels were selected by comparing patients vs. controls for each of these 15 functional connectivity volumes. It would be a logical error to compare whether a given voxel was selected consistently across the 15 functional connectivity volumes because the 15 functional connectivity volumes were different and each contributed separate feature elements to the ICA feature vector. It only makes sense to compare whether a given voxel was selected consistently from the same functional connectivity volume. Thus, we defined “equivalent” statistical maps as maps generated by comparing patients vs. controls using the same functional connectivity volume (or, for the GLM analysis features, the same statistical contrast computed using a given set of participants).

Supplementary material.