Photonic topological insulator with broken time-reversal symmetry

Significance

Topological insulators are first discovered in electronic systems. A key factor is the Kramers doublet for the spin-1/2 electrons under fermionic time-reversal symmetry ${\mathit{T}}_{\mathit{f}}^2=-1$. Unlike electrons, photons are massless bosons with spin-1. Therefore, the Kramers degeneracy theorem cannot readily apply to photons under the bosonic time-reversal symmetry. So far, there has been no coherent physical explanation for the symmetry protection mechanism behind the photonic topological insulator. Here, we design a photonic topological insulator that violates the bosonic time-reversal symmetry but complies with a fermionic-like pseudo time-reversal symmetry. The analyses and results, through comprehensive investigations on the properties of edge states, validate that the topological edge states are, in fact, protected by the fermionic-like pseudo time-reversal symmetry T_p (${\mathit{T}}_{\mathit{p}}^2=-1$).

Abstract

A topological insulator is a material with an insulating interior but time-reversal symmetry-protected conducting edge states. Since its prediction and discovery almost a decade ago, such a symmetry-protected topological phase has been explored beyond electronic systems in the realm of photonics. Electrons are spin-1/2 particles, whereas photons are spin-1 particles. The distinct spin difference between these two kinds of particles means that their corresponding symmetry is fundamentally different. It is well understood that an electronic topological insulator is protected by the electron’s spin-1/2 (fermionic) time-reversal symmetry ${\mathit{T}}_{\mathit{f}}^2=-1$. However, the same protection does not exist under normal circumstances for a photonic topological insulator, due to photon’s spin-1 (bosonic) time-reversal symmetry ${\mathit{T}}_{\mathit{b}}^2=1$. In this work, we report a design of photonic topological insulator using the Tellegen magnetoelectric coupling as the photonic pseudospin orbit interaction for left and right circularly polarized helical spin states. The Tellegen magnetoelectric coupling breaks bosonic time-reversal symmetry but instead gives rise to a conserved artificial fermionic-like-pseudo time-reversal symmetry, T_p (${\mathit{T}}_{\mathit{p}}^2=-1$), due to the electromagnetic duality. Surprisingly, we find that, in this system, the helical edge states are, in fact, protected by this fermionic-like pseudo time-reversal symmetry T_p rather than by the bosonic time-reversal symmetry T_b. This remarkable finding is expected to pave a new path to understanding the symmetry protection mechanism for topological phases of other fundamental particles and to searching for novel implementations for topological insulators.

Topological description of electronic phase has now become a new paradigm in the classification of condensed matters (1–10). Electronic topological insulators (TIs) are time-reversal symmetry (TRS) protected topological phase, exhibiting gapless edge/surface states in their bulk bandgap due to strong spin−orbit coupling (11, 12). This intriguing classification of the topologically protected phase has been applied to study other systems as well, for example, photonic systems. The photonic analog of the integer quantum Hall effect has been proposed and extensively studied with a single transverse electric (TE) polarization state (13, 14) or magnetic field (TM) polarization state (15, 16) in gyrotropic photonic crystals with broken TRS in the presence of an external magnetic bias; the fractional quantum Hall effect has also been investigated in a correlated photonic system (17). To date, to design photonic TIs (PTIs) with TRS, several models have been reported (18–26) using a pair of degenerate photonic states, e.g., hybrid TE+TM/TE − TM states (21, 22, 24) or pseudospins represented by clockwise/counterclockwise helical energy flow states (19, 20, 23), where the degenerate states “see” opposite effective magnetic gauge fields. Additionally, the photonic Floquet TIs have also been explored with a helix photonic structure under a broken spatial inversion symmetry (18). However, the robustness of these topological phases has not been fully investigated and validated against a comprehensive set of TRS invariant impurities (18–27). According to the topological theory developed for condensed matters, having a Kramers doublet is the key to constructing a TI. It is well known that the spin quantum number of photons is different from that of electrons. Hence, they belong to two different classes of particles, boson and fermion, and have different TRS operators: $T_b={\tau }_{z}K$ for photons ($T_b^2=1$) and $T_f=i{\tau }_{y}K$ for electrons ($T_f^2=-1$). Here, ${\tau }_z=diag\left\{1,-1\right\}$ and ${\tau }_y=\left[0,-i;i,0\right]$ are the z and y components, respectively, of a Pauli matrix, and K is the complex conjugation. Kramers degeneracy theorem states that there cannot exist any Kramers doublet for photons under $T_b$. Therefore, the bosonic TRS $T_b$ is highly unlikely to be the TRS requirement for the PTIs, and thus the underlying symmetry protection mechanism requires further investigation. Consequently, the robustness of those previously reported photonic topological states may be questionable and could be readily jeopardized by certain impurities (26, 28).

In this work, we explore this mysterious symmetry protection issue in a Tellegen photonic crystal medium (29), where the Tellegen magnetoelectric coupling can be realized in piezoelectric (PE) and piezomagnetic (PM) superlattice constituents (30, 31). The presence of Tellegen magnetoelectric coupling enables a photonic pseudospin−orbital coupling effect, which breaks the bosonic TRS but, at the same time, creates a fermionic-like pseudo TRS due to the electromagnetic duality. Consequently, two pseudospin states that are helical states represented by left and right circular polarizations (or any two desired modes/polarization states) can be carefully designed and matched to form Kramers degeneracy under the fermionic-like pseudo TRS. In addition, we show that a pair of degenerate gapless edge states for the Kramers doublet, i.e., left and right circular polarizations, exists in the bulk bandgap of the Tellegen photonic crystal. Such edge states exhibit pseudospin-dependent transportation, which characterizes a type of PTI with broken bosonic TRS in the presence of inherent magnetoelectric coupling (32). Our further analysis shows that this PTI is protected by the fermionic-like pseudo TRS $T_p$ ($T_p^2=-1$), and thus the gapless edge states are robust against $T_p$-invariant impurities rather than $T_b$-invariant impurities.

Models

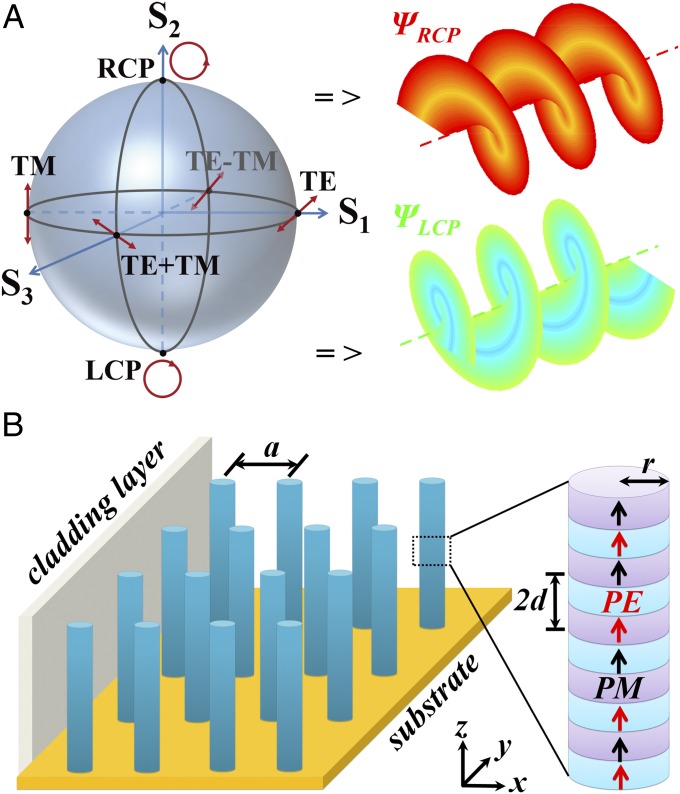
Previous studies on polarization degeneracy-based PTIs mainly focus on a pair of linearly polarized states, e.g., TE/TM states (22) and TE+TM/TE − TM states (21, 24) as shown in a Poincaré sphere (Fig. 1A, Left). There also exists another important pair of polarization states, left circular polarization (LCP: positive helix)/right circular polarization (RCP: negative helix). These two states are commonly used to mimic the electronic spin states (Fig. 1A, Right), due to their opposite helicity−orbital couplings. Herein, they are referred as ${\psi }_{LCP}$ and ${\psi }_{RCP}$ (33)

$$\left[\begin{array}{c}{\psi }_{LCP}\\ {\psi }_{RCP}\end{array}\right]=\left[\begin{array}{cc}1& i\\ i& 1\end{array}\right]\left[\begin{array}{c}{E}_z\\ H_z\end{array}\right].$$ [1]

These photonic polarization states do not generally form a Kramers doublet under $T_b$, because $T_b{\psi }_{LCP}={\psi }_{LCP}^{\ast }$ and $T_b{\psi }_{RCP}=-{\psi }_{RCP}^{\ast }$. It is therefore necessary to identify a different symmetry operator, under which Kramers degeneracy required for constructing TIs can be fulfilled. From the electromagnetic duality, it is not difficult to image that an interchange operator ${\tau }_x=\left[\mathrm{0,1};\mathrm{1,0}\right]$ (the x component of a Pauli matrix) should also be taken into account during the time-reversal operation because of the magnetoelectric interaction $E_z\leftrightarrow H_z$ in our model. A new pseudo TRS operator thus becomes $T_p=T_b{\tau }_x={\tau }_{z}K{\tau }_x=i{\tau }_{y}K$. Surprisingly, this symmetry operator $T_p$ has the same form as the fermionic TRS operator $T_f$, under which ${\psi }_{LCP}$ and ${\psi }_{RCP}$ become a photonic Kramers doublet, opening the door to building a PTI.

Fig. 1.

Schematic of SLPC. (A) (Left) The polarization on the Poincaré sphere, where the three Stokes parameters are S₁=|E_y|²-|E_x|², S₂ = 2|E_x||E_y|sinδ, and S₃ = 2|E_x||E_y|cosδ, and δ is the phase difference between the x and y axis field components. (Right) LCP and RCP photonic states (helicity−orbital coupling). (B) A 2D square lattice SLPC consisting of stacked PE and PM superlattice constituents in vacuum background. The positive domain and stacking direction of PE (red arrows) and PM (black arrows) media are along the z axis. Lattice constants of photonic crystal and PE/PM superlattice are $a$ and $2d$, respectively. The radius of cylinder is $r=0.11a$. LCP and RCP edge states propagate in x−y plane at the boundary (with a separation distance of $0.5a$) between SLPC and cladding layer.

Clearly, the key to realizing a photonic Kramers doublet in our system is to implement the required magnetoelectric coupling. Here we construct a quasi-2D superlattice photonic crystal (SLPC) consisting of arrayed meta-atoms (34, 35): superlattices with alternating PE/PM layers with the periodicity at a deep subwavelength scale along the z direction (Fig. 1B). To realize the pseudospin degenerate states, the point groups of PE and PM materials are chosen to be 622 and 6 mm (or 422 and 4 mm) with nonzero PE coefficient $e_{14}$ and PM coefficient $m_{15}$, respectively. For simplicity, the impedance matching condition is assumed. The values for the density, elastic coefficient, and PM coefficient used in our study are based on the BaTiO₃−CoFe₂O₄ superlattice (30, 31) (SI Appendix, Part A). The effective bianisotropic constitutive relation for these deep-subwavelength superlattices can be described as

$$\mathbf{D}=\overleftrightarrow{\epsilon }\mathbf{E}+\overleftrightarrow{\xi }\mathbf{H},\mathbf{B}=\overleftrightarrow{\zeta }\mathbf{E}+\overleftrightarrow{\mu }\mathbf{H}$$ [2]

where $\overleftrightarrow{\epsilon }=diag\left\{{\epsilon }_{xx},{\epsilon }_{xx},{\epsilon }_{zz}\right\}$, $\overleftrightarrow{\mu }=diag\left\{{\mu }_{xx},{\mu }_{xx},{\mu }_{zz}\right\}$, $\overleftrightarrow{\xi }={\overleftrightarrow{\zeta }}^T$, ${\xi }_{xy}=-{\xi }_{yx}=-A_1{e}_{14}{m}_{15}$, $A_1=2/\left[d^2\rho \left({\omega }^2-{\omega }_T^2+i{\gamma }_T\omega \right)\right]$, and ${\omega }_T=\pi /d\times \sqrt{C_{44}/\rho }$ for the transverse vibration frequency (details in SI Appendix, Part A). The elastic coefficient is $C_{IJ}$ with the damping coefficient ${\gamma }_T$, and ρ is the material density. In a lossless case (${\gamma }_T=0$), $\overleftrightarrow{\xi }={\overleftrightarrow{\zeta }}^{†}$ (superscript dagger denotes the complex conjugate transpose), and it only has real tensor elements, forming the so-called Tellegen media (29), in which the magnetoelectric coupling effect (off-diagonal terms) breaks the TRS and reciprocity ($\overleftrightarrow{\xi }\ne -{\overleftrightarrow{\zeta }}^T$) (32, 36). It is also worth noting that the broken TRS is originated from the polariton induced by the coupling between the elastic vibration of the superlattice and incident electromagnetic waves. The coupling strength in this case is much larger than that in multiferroic materials (37). This approach for generating magnetoelectric coupling is fundamentally different from the previously proposed $T_b$-invariant chiral medium with purely imaginary magnetoelectric parameters (21). Therefore, the Hamiltonian of our designed SLPC for LCP and RCP states can be derived as

$$\mathrm{\mathscr{H}}\left[\begin{array}{c}{\psi }_{LCP}\\ {\psi }_{RCP}\end{array}\right]=\left[\begin{array}{cc}{\mathrm{\mathscr{H}}}_0-i{\mathrm{\mathscr{H}}}_1& 0\\ 0& {\mathrm{\mathscr{H}}}_0+i{\mathrm{\mathscr{H}}}_1\end{array}\right]\left[\begin{array}{c}{\psi }_{LCP}\\ {\psi }_{RCP}\end{array}\right]=0$$ [3]

where ${\mathrm{\mathscr{H}}}_0=k_0^2{\epsilon }_{zz}+{\partial }_x\frac{1}{{\mu }_{\left|\right|}}{\partial }_x+{\partial }_y\frac{1}{{\mu }_{\left|\right|}}{\partial }_y$, ${\mathrm{\mathscr{H}}}_1={\partial }_x\kappa {\partial }_y-{\partial }_y\kappa {\partial }_x$, ${\mu }_{\left|\right|}=\left({\mu }_{xx}{\epsilon }_{xx}-{\xi }_{xy}^2\right)/{\epsilon }_{xx}$, $\kappa =-{\xi }_{xy}/\left({\mu }_{xx}{\epsilon }_{xx}-{\xi }_{xy}^2\right)$ 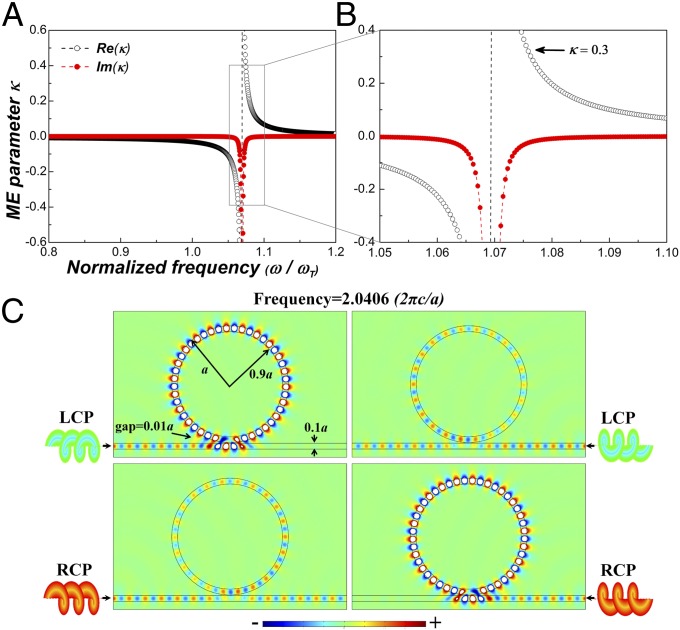is a pseudospin−orbital coupling parameter. This coupling parameter exhibits a polariton dispersion relation near the resonant frequency ${\omega }_T$ (Fig. 2 A and B). The $\pm i{\mathrm{\mathscr{H}}}_1$ operator indicates the pseudospin−orbital coupling and the resulting opposite effective gauge fields for LCP and RCP states, which can further lead to the nonreciprocal transmission of the LCP/RCP polarization states, forming an isolator that is free of external magnetics, as shown in Fig. 2C. In contrast to conventional isolators, such an isolator exhibits a clear pseudospin-dependent transmission manifested by the opposite transmission direction of the LCP and RCP states. This unique one-way transmission property can be further leveraged to construct PTIs.

Fig. 2.

Pseudospin−orbit coupling parameter $\kappa$. (A) Dispersion of $\kappa$, where open and solid circles represent the real and imaginary parts, respectively. (B) Zoom-in view of the rectangular frequency area around frequency of interest. (C) Pseudospin-dependent nonreciprocal transmission of LCP/RCP state in an airborne ring resonator constructed with Tellegen media with material parameters $\epsilon =2.5$, $\mu =2.5$, and $\kappa =0$ for the straight bus waveguide and $\epsilon =2.5$, $\mu =2.5$, and $\kappa =0.3$ for circular waveguide. Colorbar represents the field strength.

Results and Discussion

Gapless Edge State.

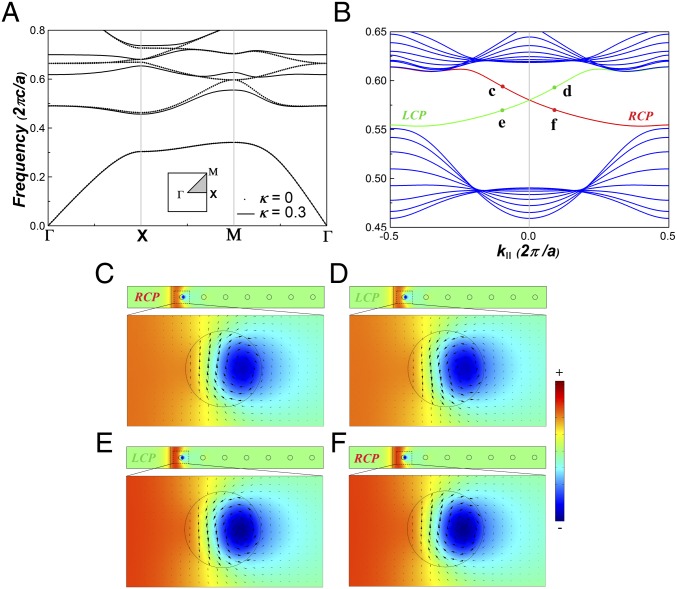
In this work, the thickness of each PE and PM layer is set to be d = 500 nm; the transverse vibration frequency is ${\omega }_T=18.05\hspace{0.17em}\text{GHz}$. The lattice constant of the SLPC is set to be a = 9 mm. The material property PE/PM superlattice inside the SLPC at frequency of $1.076{\omega }_T$ (19.42 GHz) are $\kappa =0.3$ obtained from Fig. 2, ${\mu }_{\left|\right|}={\epsilon }_{\left|\right|}=2.5$, and ${\mu }_{zz}={\epsilon }_{zz}=14.2$. Without considering pseudospin−orbital coupling, i.e., $\kappa =0$, the band structure of the SLPC (Fig. 3A) clearly shows band crossing at M point of the Brillouin zone for the second and third bulk bands. However, after introducing pseudospin−orbital coupling, e.g., $\kappa =0.3$, the degeneracy at M point is lifted, creating a bandgap for the bulk states with their normalized frequency ranging from 0.55 to 0.61 (corresponding to wavelengths from 1.82a to 1.64a, i.e., 16.38 mm to 14.76 mm). In the bandgap, there exist gapless helical edge states for LCP and RCP states (Fig. 3B), which exhibit pseudospin-dependent edge state transportation. Because LCP and RCP states experience opposite effective gauge fields, their power flux transportation behavior is completely reversed, i.e., counterclockwise for LCP and clockwise for RCP (Fig. 3 C–F).

Fig. 3.

Topological edge states in SLPC. (A) Bandstructures without pseudospin coupling effect (dotted lines, $\kappa =0$) and with pseudospin coupling effect (solid lines, $\kappa =0.3$). (B) The projected bandstructures with $\kappa =0.3$, where bulk states are denoted by blue lines and gapless LCP and RCP edge states are denoted by green and red lines, respectively. (C−F) The Bloch field distributions of supercell configuration corresponding to points c (C), d (D), e (E), and f (F) marked in B. Zoom-in view shows the opposite rotating power flux near the boundary represented by black arrows. Colorbar represents the field strength.

Robustness of Pseudospin-Dependent Transportation.

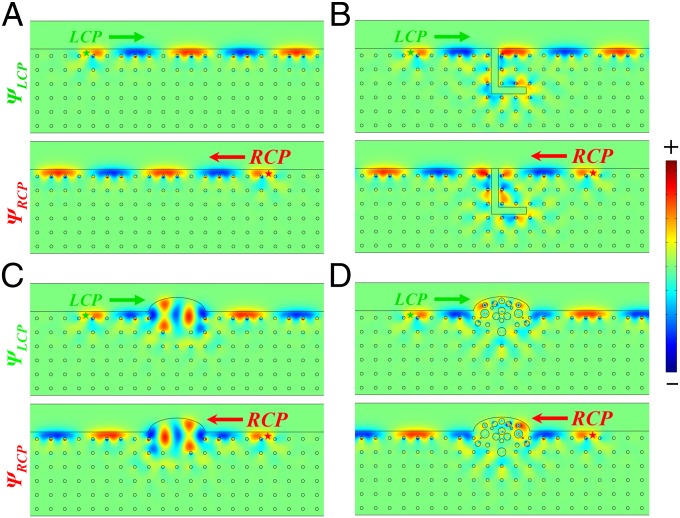
The robustness for the edge states transportation is studied in various SLPC configurations (Fig. 4). Without any defects, the pseudospin-dependent transportation is obvious (Fig. 4A), because the LCP (RCP) source only excites one-way clockwise (counterclockwise) light transportation (SI Appendix, Part B). This one-way robust transportation is then verified and confirmed against three different types of geometric defects, an L-shaped slab obstacle, a cavity obstacle, and a strongly disordered domain inside the cavity as shown in Fig. 4 B–D. Note that the impact of propagation loss can be safely omitted in the above analysis (SI Appendix, Part C), because the frequency of operation is far away from the resonance condition of the superlattice (as shown in Fig. 2A).

Fig. 4.

Field distribution of backscattering immune pseudospin-dependent transportation. (A) LCP (Top) and RCP (Bottom) light propagation without structural defects. (B−D) Robustness for LCP (Top) and RCP (Bottom) light against different types of defects: (B) an L-shape slab obstacle (index of refraction, –i) with thickness 0.5a, (C) a cavity obstacle, and (D) a strongly disordered domain in the cavity. Operating frequency is 0.6($2\pi c/a$). LCP and RCP point excitation sources are indicated by green and red stars, respectively. Colorbar represents the field strength.

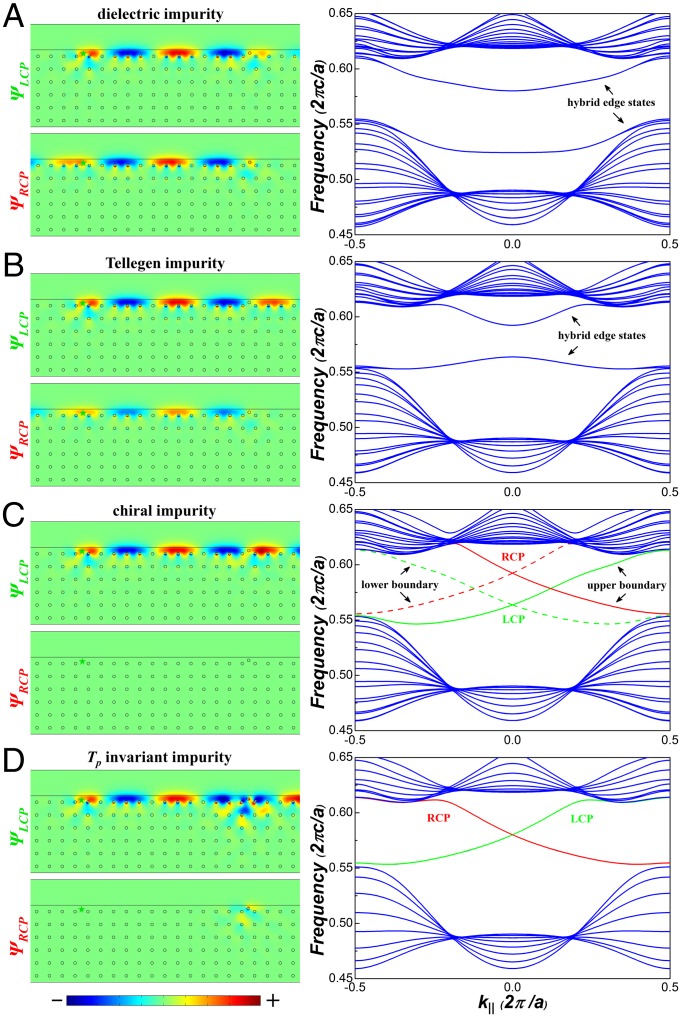
Next, the robustness of such photonic pseudospin-dependent transportation is further checked against a comprehensive set of impurities with optical properties satisfying all possible combination of $T_b$ and $T_p$ symmetries, i.e., (i) a uniaxial dielectric impurity that is $T_b$-invariant but not $T_p$-invariant; (ii) a Tellegen impurity that is neither $T_b$-invariant nor $T_p$-invariant; (iii) a chiral impurity that is $T_b$-invariant but not $T_p$-invariant; and (iv) a chiral impurity that is both $T_b$- and $T_p$-invariant. In cases i and ii, the LCP state can be backscattered into the RCP state by impurities (Fig. 5 A and B, Left). Such findings imply that the pseudospin-dependent transportation is not robust if impurities’ $T_p$ symmetry is broken, regardless of their $T_b$ status. This conclusion is also consistent with the projected band structure (Fig. 5 A and B, Right), which indicates the emergence of a bandgap from an initially gapless band structure. In case iii, the eigen equation of the chiral medium can be treated as a superposition of two orthogonal LCP and RCP eigen states with different Bloch wave vectors. Although the impurity cannot backscatter the RCP state (Fig. 5C, Left), the LCP and RCP edge states decouple, and both states exhibit an independent integer photonic quantum Hall effect (Fig. 5C, Right). In case iv, the RCP state can be excited at the impurity site as shown in Fig. 5D, Left. However, the excited RCP state is localized in the vicinity of the impurity site and no RCP state is backscattered because $T_p$-invariant impurity is a polarization degenerate medium for TE+TM and TE − TM hybrid states. With LCP state incidence, this state decouples into these two degenerate hybrid states inside the impurity, and it reemerges as LCP light after transmitting through it. The destructive interference between two backscattering paths for the RCP light eliminates backscattering, leading to robust one-way transmission. This unique transportation characteristic can be further confirmed by examining the corresponding projected band structure. As shown in Fig. 5D, Right, the edge states remain gapless, and such a system still supports pseudospin-dependent transportation. The above analysis strongly indicates that LCP and RCP eigen states can only be considered as a pair of pseudospin states under the fermionic-like pseudo TRS $T_p$ operator, i.e., $T_p{\psi }_{LCP}={\psi }_{RCP}^{\ast }$ and $T_p{\psi }_{RCP}=-{\psi }_{LCP}^{\ast }$. The Hamiltonian of our SLPC shown in Eq. 3 commutes with $T_p$ : $T_p\mathrm{\mathscr{H}}{T}_p^{-1}=\mathrm{\mathscr{H}}$ but does not commute with $T_b$ : $T_b\mathrm{\mathscr{H}}{T}_b^{-1}\ne \mathrm{\mathscr{H}}$, confirming our proposed Tellegen system is a bosonic TRS broken system. It is thus evident that our proposed PTI is protected by the fermionic-like pseudo TRS $T_p$ rather than by the bosonic TRS $T_b$.

Fig. 5.

(Left) Robustness against four types of impurities: (A) uniaxial dielectric impurity (${\epsilon }_{zz}=4$), (B) Tellegen impurity (${\xi }_{zz}={\zeta }_{zz}=1$), (C) chiral impurity (${\xi }_{zz}=-{\zeta }_{zz}=i$), and (D) chiral impurity with $T_p$ invariance (${\xi }_{xy}=-{\xi }_{yx}={\zeta }_{xy}=-{\zeta }_{yx}=0.3i$; other parameters are the same as superlattice) remaining invariant under $T_p$ operation. LCP point excitation source (green stars) is at a frequency of 0.6($2\pi c/a$). A cylindrical impurity with radius $r=0.11a$ is placed near the boundary. (Right) The corresponding projected bandstructures. Colorbar represents the field strength.

Note that, in our proposed PTI, a unity normalized impedance ($\eta =\sqrt{\mu /\epsilon }=1$) is assumed. Therefore, strictly speaking, backscattering immune propagation is only applicable to impurity with an equally valued relative permeability and permittivity (e.g., vacuum). A slight mismatch between the relative permeability and permittivity may be overcome by using sufficiently large pseudospin−orbital (helicity−orbital) coupling $\kappa$ (refer to Eq. 3 for details). For a large mismatch, two elliptical polarized eigen states ${\phi }_{LCP}=E_z+i\eta H_z,\begin{array}{c}\end{array}{\phi }_{RCP}=i{E}_z+\eta H_z,$ shall be chosen instead of LCP and RCP to construct a $T_p$ protected PTI.

Topological Values.

It should be noticed that each energy band in Fig. 3A is doubly degenerate for LCP and RCP states experiencing opposite gauge fields. Thus, although the total Chern number is zero in our broken TRS system, the spin Chern number for LCP and RCP is +1 and −1, respectively (38). Therefore, in such a system, the photonic quantum spin Hall effect (or PTI) rather than the photonic quantum Hall effect is expected. On the other hand, because the pseudo TRS $T_p$ extracted from our system has the same mathematic form as the fermionic TRS $T_f$, the $Z_2$ invariant of our PTI can be characterized under the constructed pseudo TRS $T_p$. Based on the inversion symmetry of our model (39), the $Z_2$ invariant can be determined by the quantity equation, ${\delta }_i={\displaystyle \prod _{m=1}^N{\xi }_{2m}\left({\mathrm{\Gamma }}_i\right)}$, where ${\xi }_{2m}\left({\mathrm{\Gamma }}_i\right)$ is the parity eigenvalue of the 2mth occupied energy band at four $T_p$-invariant momenta ${\mathrm{\Gamma }}_i$ in the Brillouin zone. The $Z_2$ invariant $v=\mathrm{0,1}$, which distinguishes different quantum spin Hall phases, is governed by the product of all of the ${\delta }_i$: ${(-1)}^v={\displaystyle \prod _i{\delta }_i}$. The quantity equation can be further simplified as ${\delta }_i=\xi \left({\mathrm{\Gamma }}_i\right)$, in which $\xi \left({\mathrm{\Gamma }}_i\right)$ is the parity eigenvalue of lower energy band at ${\mathrm{\Gamma }}_i$. Because our system is of $T_p$ invariance, the eigen states in reciprocal space are degenerate at ${\mathrm{\Gamma }}_i$. It is thus straightforward to demonstrate that the Bloch field distribution at (0, 0) in reciprocal space has even parity with a parity eigenvalue of 1 whereas the Bloch field distributions at three other high-symmetry points have odd parity with parity eigenvalues of −1. With ${(-1)}^{\nu }=-1$ used to determine the $Z_2$ invariant, the $Z_2$ invariant can be readily derived: $\nu =1$, showing a nontrivial topological state supported in our system (SI Appendix, Part D).

Conclusions

In summary, we study the topological property of a Tellegen photonic crystal, which has broken bosonic TRS due to Tellegen magnetoelectric coupling. Such a coupling leads to the interchange of electric field and magnetic field of an eigen state and thus gives rise to an artificial fermionic pseudo TRS $T_p$ symmetry. This symmetry is found to be responsible for the formation of a Kramers doublet in our photonic system. The robustness of the one-way pseudospin-dependent transportations, in this case, is protected by this artificial fermionic pseudo TRS $T_p$ instead of by the bosonic TRS $T_b$. Our concept of $T_p$ symmetry-protected photonic topological phase is by no means limited only to the particular case we considered here. It may be easily applied to identify more PTIs by following the steps outlined below. For step 1, construct two degenerate photonic states that satisfy Kramers degeneracy under an artificial fermionic $T_p$ operator; in step 2, retrieve a proper material constitutive relation by substituting a Kramers doublet and PTI’s Hamiltonian for Maxwell equations; and, in step 3, find appropriate materials or design metamaterials to fulfill the required constitutive relation. We believe that our findings may expand the scope of PTIs and pave a new and viable way to classify PTIs, which can overcome the limitation based on the traditional bosonic TRS. Our results may even inspire researchers to exploit photonic topological states in unconventional systems, for instance, non-Hermitian synthetic parity-time symmetric metamaterials with balanced gain/loss modulation (40) or a purely dissipation-driven system (41). Analogously, the concept of this $T_p$ symmetry-protected PTI may also be applied to other classic waves, such as sound (42) and mechanic modes (43, 44).

Materials and Methods

Theoretical Model.

A full description of the mathematic derivation and parameters of PE and PM superlattice to obtain the effect constitutive relation can be found in SI Appendix, Part A. It should be noticed that a key factor to realizing the pseudospin degenerate states for LCP and RCP is the point groups of PE and PM materials, which are chosen to be 622 and 6 mm in this work to realize off-diagonal magnetoelectric coupling. The loss of such a superlattice can be safely omitted because the operating frequency is far away from the resonance frequency. Furthermore, we also derived the theoretical model of SLPC via the tight-binding approximation approach as shown in SI Appendix, Part D.

Numerical Method.

Numerical investigations in this work are conducted using a hybrid RF mode of commercial FEM software (COMSOL Multiphysics). The parameters used in numerical investigations are based on the effective constitutive relation of PE and PM superlattice.