How is it possible that some individuals struggle to calculate a tip, whereas others find solutions to complex, ancient mathematical problems? Although some have argued that language provides the basis for high-level mathematical expertise, others have contended that such mathematical abilities are linked to nonverbal processes that underpin the processing of magnitude and space. In PNAS, Amalric and Dehaene (1) report data that significantly advance our understanding of the origins of high-level mathematical abilities.
Following his death, Albert Einstein’s brain was extracted, perfused, dissected, and photographed. This evidence offered scientists the unprecedented opportunity to search for the unique features in the brain of one of the most influential scientists of the 20th century. Initial investigations purported to have unearthed evidence for structural uniqueness in Einstein’s parietal cortex (2). However, the methodologies used to study the structure of Einstein’s brain have been subject to substantial criticism (3).
More recently, neuroscientists have used noninvasive neuroimaging methods, such as functional magnetic resonance imaging (fMRI), to study brains of mathematical experts. Such studies have revealed both structural (4) and functional differences (5) between the brains of expert mathematicians compared with nonmathematicians. However, none of the existing studies on the brains of mathematical experts have delved deeply to explore the specific functional origins of the exceptional abilities of these individuals.
Mathematical Expertise Is Not Grounded in Brain Systems for Language
Amalric and Dehaene (1) report a detailed investigation into the neuronal origins and consequences of mathematical expertise. Specifically, using fMRI, they studied 15 expert mathematicians and 15 nonmathematicians with comparable academic qualifications. In the MRI scanner, participants listened to mathematical and nonmathematical statements and had to decide whether the statements were true, false, or meaningless. More specifically, participants listened to the spoken statements, followed by a period in which they were asked to reflect on the sentences before indicating their judgment via a button press. Whereas the nonmathematical statements referred to general knowledge of nature and history, the mathematical statements referred to domains of higher level mathematics: geometry, analysis, algebra, and topology.
The contrast of brain activation measured during the reflection on mathematical statements vs. activation associated with reflecting on nonmathematical statements revealed a network of regions located in the dorsal parietal and frontal cortex. This cortical network was found to be highly similar for all four domains of mathematics examined. Importantly, the same brain network was revealed in the expert mathematicians when contrasting the brain activation associated with meaningful compared with meaningless mathematical statements. Furthermore, this network was not activated when computing the same contrasts for the group of nonmathematicians, and a direct comparison of the groups revealed that parietal and frontal activation during reflection on mathematical statements was only present in the group of expert mathematicians.
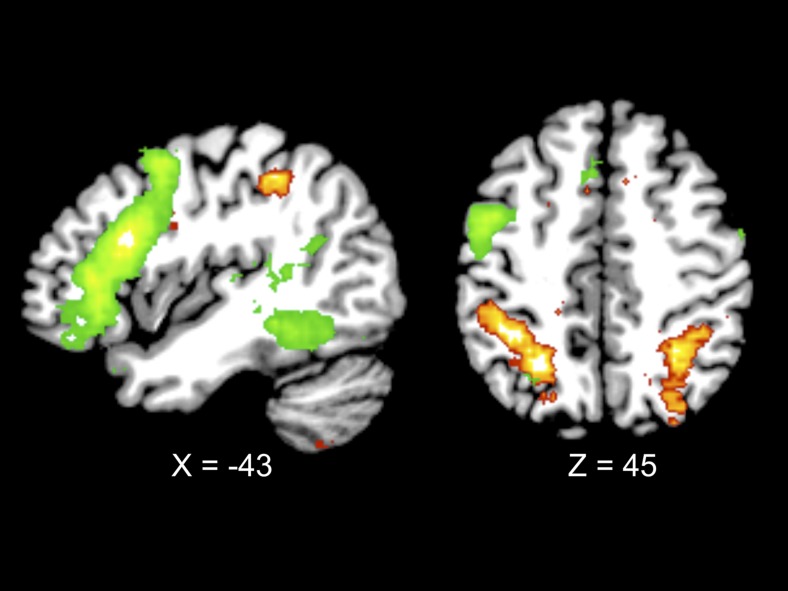
Notably, the brain regions found to be engaged by expert mathematicians during the reflection on mathematical statements lie outside areas typically associated with language. This dissociation between mathematics and language in the brain is consistent with previous findings in nonmathematicians. Consider the results in Fig. 1. What is displayed in this figure are the results of a reverse-inference meta-analysis conducted using Neurosynth (6). The brain activation displayed in orange corresponds to regions that are reported more frequently when an article mentions the term “numerical” in the abstract (taken from 89 studies) compared with articles that do not mention the term numerical. The brain activity in green reflects the same for the term “language” (885 studies). This analysis provides support for the finding that the processing of numerical information is (largely) anatomically distinct from the brain circuitry that is thought to underpin linguistic functions. Critically, the data of Amalric and Dehaene (1) go significantly beyond what was already known by demonstrating that mathematical experts did not recruit language circuits of the brain while reflecting on higher level mathematical statements that did not contain numbers.
Fig. 1.
Results of Neurosynth (neurosynth.org/) reverse-inference meta-analysis analysis for the terms numerical and language. Brain areas associated with numerical processing are shown in red to yellow colors, and regions associated with language are displayed in green colors. Results support the conclusion of Amalric and Dehaene (1) that neural circuits underlying numerical and complex mathematical processing are largely distinct from neural circuits engaged during language.
Hurford famously stated: “without language, no numeracy” (ref. 7, p. 305). Amalric and Dehaene’s findings (1) suggest otherwise. Notwithstanding, it is possible that language may have played a role in the initial acquisition of mathematical expertise or that such a relationship exists at the level of functional connectivity with language areas of the brain rather than through their direct recruitment.
Beyond Language
By showing that expert mathematicians do not recruit brain areas associated with language when engaged in mathematical thinking, Amalric and Dehaene (1) refute the hypothesis that higher level mathematical abilities are grounded in language systems of the brain. However, their findings go even further. Specifically, through the use of cutting-edge neuroimaging analyses, they show that the brain activity associated with reflecting on mathematical statements is both overlapping and correlated with brain activation associated with simple calculation and even the visual processing of Arabic numerals. These findings reveal a connection between the neural circuits engaged during elementary numerical processing and higher level mathematics. By doing so, the data speak against the notion that basic number concepts have little to do with advanced mathematics and instead suggest a deep connection between rudimentary symbolic number processing and advanced mathematics. It remains to be investigated whether this connection also extends to nonsymbolic (e.g., comparison of dot arrays) brain representations of numbers that humans share with other species (8). A connection between symbolic numbers and mathematical expertise in the brain does not necessarily imply that the same is true for nonsymbolic number processing (9).
What Amalric and Dehaene’s findings (1) leave open is exactly how the connection between basic and higher level mathematics is constructed during the process of acquiring mathematical expertise. How exactly are the neural mechanisms underpinning elementary numerical processing bootstrapped or recycled (10) to give rise to mathematical expertise? The authors speculate that beyond the role played by fundamental brain representations of symbolic numbers as a basis for constructing mathematical expertise, the process of acquiring such expertise must involve the integration of spatial, ordinal, and logical concepts. Future studies that build on the findings reported by Amalric and Dehaene (1) should unpack these processes and investigate them more directly by probing the neural correlates of the development of mathematical expertise by, for example, examining the neural consequences of training high-level mathematical abilities. Future investigations should also consider the role of visuospatial skills. Recent evidence has revealed that visuospatial skills fully explain
By showing that expert mathematicians do not recruit brain areas associated with language when engaged in mathematical thinking, Amalric and Dehaene refute the hypothesis that higher level mathematical abilities are grounded in language systems of the brain.
the relationship between basic numerical skills and advanced mathematical abilities (11).
Amalric and Dehaene (1) thoroughly address potential alternative explanations of their data. It is well established that the frontoparietal brain regions found to be engaged by expert mathematicians are associated with numerous cognitive processes that are not specific to mathematics, such as working memory, attention, and task difficulty (12). Might the data therefore reflect differences in the recruitment of these domain-general networks? Amalric and Dehaene (1) report several convincing results to show that the greater activation of networks in the frontoparietal cortex of mathematicians during the reflection on mathematical compared with nonmathematical statements cannot be reduced to differences in the relative difficulty in processing these statements. Nevertheless, it is possible that the mathematical experts attended differently to the mathematical statements because they are particularly salient to them. Put differently, expertise may change the way in which attention is directed to information relevant to the domain of expertise. To investigate this possibility further, it would be valuable to compare the brain activation of expert mathematicians reflecting on mathematical statements with the brain activation of experts in a nonmathematical domain listening to statements relevant to their subject of expertise. Such an investigation would help to dissociate effects of expertise on domain-general brain networks of attention from expertise effects on domain-specific information-processing systems in the brain.
Expertise and Brain Plasticity
In an influential neuropsychological model of number processing, Dehaene and Cohen (13) predicted the existence of a visual number form area (VNFA) in the ventral visual cortex. Although functional neuroimaging studies were unable to support this prediction for many years (14), recent studies (15) using electrocorticography as well as novel methods for high-resolution fMRI (16) have revealed regions in the bilateral inferior temporal gyri that respond significantly more to numerical symbols compared with letters and other nonnumerical symbols. Amalric and Dehaene (1) replicate these findings by showing number-specific activation in the bilateral ventral visual cortex in both groups. Moreover, their findings suggest potential expertise-related plasticity in the functional organization of the ventral visual pathway. Specifically, they found greater response in the mathematical experts to written mathematical formulas in the left inferior temporal gyrus as well a small enhancement of activity in the left, but not the right, VNFA in response to numerals.
Against the background of previous studies suggesting that the acquisition of reading not only leads to changes in the response of the ventral visual stream to words but also affects responses to other categories such as faces (17), Amalric and Dehaene (1) investigated expertise-related effects in the responses to faces, tools, and bodies. Surprisingly, expert mathematicians exhibited reduced activation to faces in the right inferior temporal cortex as well as enhancement in response to tools in the left lateral occipital cortex. These data may suggest that expertise leads to plastic changes in the cortical processing of mathematical formulas and digits, which, in turn, affect the functional organization of other visual categories. Importantly, as Amalric and Dehaene (1) acknowledge, such correlational data cannot be used to infer causality. Although it is possible that the acquisition of mathematical expertise leads to such plastic changes, it is equally plausible that genetic differences between expert mathematicians and nonmathematicians affect the organization of the ventral visual stream. Additional training studies are needed to evaluate the direct effect of high-level mathematical training on the organization of visual categories in the ventral stream. Furthermore, the functional consequences of differences in the ventral stream organization need to be investigated. For example, does a reduced response to faces translate into poorer face-processing skills among expert mathematicians?
Amalric and Dehaene (1) report data on the functional organization of the brains of mathematical experts that will undoubtedly lead to many follow-up studies. By doing so, we will better understand the complex mechanisms that allow some to understand a level of mathematical complexity that is elusive to the majority of humankind.
Acknowledgments
The author is supported by operating grants from the Natural Sciences and Engineering Council of Canada (NSERC), the Canadian Institutes of Health Research, the Canada Research Chairs Program, and an E. W. R. Steacie Memorial Fellowship from the NSERC.
Footnotes
The author declares no conflict of interest.
See companion article on page 4909.
References
- 1.Amalric M, Dehaene S. Origins of the brain networks for advanced mathematics in expert mathematicians. Proc Natl Acad Sci USA. 2016;113:4909–4917. doi: 10.1073/pnas.1603205113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Witelson SF, Kigar DL, Harvey T. The exceptional brain of Albert Einstein. Lancet. 1999;353(9170):2149–2153. doi: 10.1016/S0140-6736(98)10327-6. [DOI] [PubMed] [Google Scholar]
- 3.Hines T. Neuromythology of Einstein’s brain. Brain Cogn. 2014;88:21–25. doi: 10.1016/j.bandc.2014.04.004. [DOI] [PubMed] [Google Scholar]
- 4.Aydin K, et al. Increased gray matter density in the parietal cortex of mathematicians: A voxel-based morphometry study. AJNR Am J Neuroradiol. 2007;28(10):1859–1864. doi: 10.3174/ajnr.A0696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pesenti M, et al. Mental calculation in a prodigy is sustained by right prefrontal and medial temporal areas. Nat Neurosci. 2001;4(1):103–107. doi: 10.1038/82831. [DOI] [PubMed] [Google Scholar]
- 6.Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD. Large-scale automated synthesis of human functional neuroimaging data. Nat Methods. 2011;8(8):665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hurford J. Language and Number: The Emergence of a Cognitive System. Blackwell; Oxford: 1987. [Google Scholar]
- 8.Cantlon JF. Math, monkeys, and the developing brain. Proc Natl Acad Sci USA. 2012;109(Suppl 1):10725–10732. doi: 10.1073/pnas.1201893109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leibovich T, Ansari D. The symbol-grounding problem in numerical cognition: A review of theory, evidence, and outstanding questions. Can J Exp Psychol. 2016;70(1):12–23. doi: 10.1037/cep0000070. [DOI] [PubMed] [Google Scholar]
- 10.Dehaene S, Cohen L. Cultural recycling of cortical maps. Neuron. 2007;56(2):384–398. doi: 10.1016/j.neuron.2007.10.004. [DOI] [PubMed] [Google Scholar]
- 11.Sella F, Sader E, Lolliot S, Cohen Kadosh R. Basic and Advanced Numerical Performances Relate to Mathematical Expertise but Are Fully Mediated by Visuospatial Skills. J Exp Psychol Learn Mem Cogn. 2016 doi: 10.1037/xlm0000249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fedorenko E, Duncan J, Kanwisher N. Broad domain generality in focal regions of frontal and parietal cortex. Proc Natl Acad Sci USA. 2013;110(41):16616–16621. doi: 10.1073/pnas.1315235110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dehaene S, Cohen L. Towards an anatomical and functional model of number processing. Mathematical Cognition. 1995;1:83–120. [Google Scholar]
- 14.Price GR, Ansari D. Symbol processing in the left angular gyrus: Evidence from passive perception of digits. Neuroimage. 2011;57(3):1205–1211. doi: 10.1016/j.neuroimage.2011.05.035. [DOI] [PubMed] [Google Scholar]
- 15.Shum J, et al. A brain area for visual numerals. J Neurosci. 2013;33(16):6709–6715. doi: 10.1523/JNEUROSCI.4558-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grotheer M, Herrmann K-H, Kovács G. Neuroimaging Evidence of a Bilateral Representation for Visually Presented Numbers. J Neurosci. 2016;36(1):88–97. doi: 10.1523/JNEUROSCI.2129-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dehaene S, et al. How learning to read changes the cortical networks for vision and language. Science. 330(6009):1359–1364. doi: 10.1126/science.1194140. [DOI] [PubMed] [Google Scholar]