Cortical subnetwork dynamics during human language tasks

Abstract

Language tasks require the coordinated activation of multiple subnetworks—groups of related cortical interactions involved in specific components of task processing. Although electrocorticography (ECoG) has sufficient temporal and spatial resolution to capture the dynamics of event-related interactions between cortical sites, it is difficult to decompose these complex spatiotemporal patterns into functionally discrete subnetworks without explicit knowledge of each subnetwork’s timing. We hypothesized that subnetworks corresponding to distinct components of task-related processing could be identified as groups of interactions with co-varying strengths. In this study, five subjects implanted with ECoG grids over language areas performed word repetition and picture naming. We estimated the interaction strength between each pair of electrodes during each task using a time-varying dynamic Bayesian network (tvDBN) model constructed from the power of high gamma (70–110 Hz) activity, a surrogate for population firing rates. We then reduced the dimensionality of this model using principal component analysis (PCA) to identify groups of interactions with co-varying strengths, which we term functional network components (FNCs). This data-driven technique estimates both the weight of each interaction’s contribution to a particular subnetwork, and the temporal profile of each subnetwork’s activation during the task. We found FNCs with temporal and anatomical features consistent with articulatory preparation in both tasks, and with auditory and visual processing in the word repetition and picture naming tasks, respectively. These FNCs were highly consistent between subjects with similar electrode placement, and were robust enough to be characterized in single trials. Furthermore, the interaction patterns uncovered by FNC analysis correlated well with recent literature suggesting important functional-anatomical distinctions between processing external and self-produced speech. Our results demonstrate that subnetwork decomposition of event-related cortical interactions is a powerful paradigm for interpreting the rich dynamics of large-scale, distributed cortical networks during human cognitive tasks.

1. Introduction

Converging evidence from lesion analysis, stimulation mapping, and functional neuroimaging has shown that the topography of human language cortex is widely distributed over large-scale networks in the temporal, parietal, and frontal lobes (Broca, 1865; Ojemann et al., 1989; Indefrey and Levelt, 2000; Hickok and Poeppel, 2004; Indefrey and Levelt, 2004). Nevertheless, it is difficult to map the dynamics of interactions between these regions during specific language tasks with current methodologies. Diffusion tensor imaging (DTI) has facilitated detailed estimation of the anatomical connections between language areas (Glasser and Rilling, 2008). The presence of physical connections, however, provides limited information about how those connections are utilized over the course of a task. Functional magnetic resonance imaging (fMRI) has uncovered robust correlations between the metabolic activities of distant brain regions in the absence of a task, providing insight into the functional network architecture of the brain’s resting state (Biswal et al., 1995). However, the slow time scale of these metabolic interactions—on the order of hundreds of milliseconds—and the low temporal resolution of fMRI acquisition make it ill-suited for probing the rich dynamics of event-related cortical interactions during relatively fast activities like object recognition or speech.

Electrocorticography (ECoG) has become a powerful tool for characterizing the dynamics of cortical activation during cognitive tasks with high temporal resolution, on the order of tens of milliseconds. In particular, activity in the high gamma band (> 70 Hz) has been shown to reflect changes in cortical population firing rates (Manning et al., 2009; Ray et al., 2008; Miller, 2010), even in single trials (Flinker et al., 2010). These features make ECoG an ideal modality to capture the event-related interaction (ERI) between cortical sites during language processing. Although ERI can be characterized with ECoG using a variety of methods—for example, changes in measures of correlated activity (Friston et al., 1994; Friston, 2011), or parameters from an imposed model of system dynamics (Winterhalder et al., 2005)—these estimates are inherently high-dimensional regardless of the method used, as every site-site pair produces a new signal depicting the strength of that pair’s interaction over time; hence, a set of n ECoG recordings yields n² − n ERI time series. When each interaction between cortical sites is considered as an independently modulating signal, this high dimensionality presents a considerable challenge for visualization and interpretation of ECoG ERI results.

Recent studies of the neurobiology of language have provided converging evidence for discrete subnetworks of cortex responsible for distinct stages of task computation (Indefrey and Levelt, 2004; Indefrey, 2011; Hickok and Poeppel, 2007). Given this framework, a method capable of parcellating the large array of ERI signals into groups of functionally related interactions would dramatically aid the interpretability of interaction data. Rather than visualizing the strength of each site-site interaction at every point in time, one may see ERI as the activity of a small number of subnetworks, each possessing two complementary representations: (1) a static spatial architecture showing which site-site interactions are implicated in that subnetwork, and (2) a temporal profile of the subnetwork’s aggregate activation during a particular task. Such a decomposition might help elucidate the functional roles of individual sites in task completion. For example, sites that participate in multiple subnetworks might be identified as “bridge” or “connector” nodes, responsible for passing information between stages of task processing (Bullmore and Sporns, 2009).

Previous studies using ERI estimates found that many of the interactions between ECoG sites tend to modulate together over the course of a task (Korzeniewska et al., 2008, 2011; Benz et al., 2012a). We therefore hypothesized that subnetworks corresponding to distinct computational stages could be identified as groups of interactions with similarly timed task-related activation, which we term “function al network components” (FNCs). Here we present a simple method for computing these FNCs based on principal component analysis, a common dimensionality reduction technique that finds weighted combinations of input signals that account for the greatest input variance. We show that this data-driven method yields subnetwork estimates that are spatially and temporally consistent with current models of the neurophysiology of human language, are consistent between individuals with similar coverage, and are robust enough to be observed in single trials.

2. Material and methods

2.1. Study participation and data collection

In this study, we examined 5 subjects with drug-resistant epilepsy undergoing ECoG monitoring for seizure localization prior to resection surgery, whose electrode placement was determined solely by clinical necessity. Subjects were selected for inclusion in this study if their implants covered perisylvian and basal temporal cortices. All subjects provided informed consent before testing began in accordance with our experimental protocol, as approved by the Johns Hopkins Institutional Review Board. The locations of these electrodes relative to the subject’s anatomy were determined by co-registering a post-operative computed tomography scan with a pre-operative magnetic resonance imaging (MRI) scan using the BioImage suite (Duncan et al., 2004; Papademetris et al., 2005). Figure 1 shows these co-registered locations on volumetric MRI reconstructions for all 5 subjects, while Table 1 summarizes the subjects’ demographic information.

Figure 1.

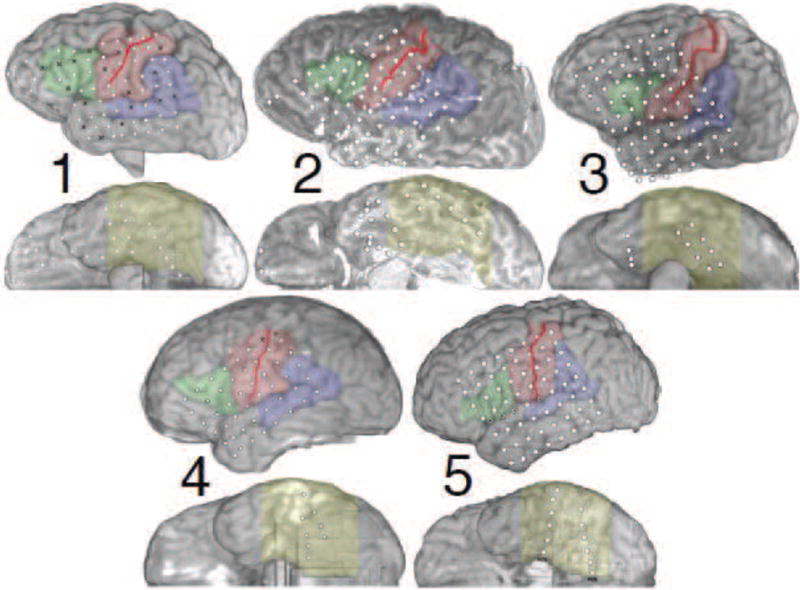
(Two columns.) Overview of the ECoG coverage for all five subjects. Dots indicate locations of electrodes; black Xs mark channels that were determined to have poor signal quality by a clinical neurophysiologist, and were excluded from analysis. The solid red line indicates the location of the central sulcus, while the colored regions denote broad functional-anatomical regions of interest: Wernicke’s area (blue) including posterior superior temporal gyrus (pSTG), angular gyrus, and supramarginal gyrus; visual association regions in ventral occipital-temporal cortex (VOTC, yellow), including inferior temporal, fusiform, and parahippocampal gyri; sensorimotor cortex (SMC, red) including precentral and postcentral gyri; and Broca’s area (green) including pars triangularis and pars opercularis. The “floating” electrodes for subject 3 were in fact located on the basal surface of the temporal pole, and were moved slightly for visual clarity.

Table 1.

Summary of subject demographics. Language dominance was assessed for each subject using the Wada test.

Subject	Age (years)	Age of seizure onset (years)	Gender	Language dominance	HG-active electrodes*	Recording system
1	55	45	Male	Left	21	NeuroPort
2	55	19	Female	Left	34	NeuroPort
3	47	8	Male	Left	24	Stellate
4	23	13	Female	Left	32	Stellate
5	13	15 months	Female	Bilateral	41	Nihon Kohden

^*i.e., the number of electrodes that showed statistically significant high gamma modulation in either task, auditory word repetition or picture naming.

2.1.1. Data acquisition

ECoG signals were recorded using standard 2.3 mm diameter platinum-iridium electrodes with 1 cm center-to-center spacing (Adtech; Racine, WI) placed subdurally. These recordings were referenced to a single intracranial electrode to minimize extracranial sources of artifacts. The raw ECoG signals were recorded using a Stellate (Stellate Systems Inc.; Montréal, Canada), Nihon Kohden (Nihon Kohden Corporation; Tokyo, Japan) or NeuroPort (BlackRock Microsystems; Salt Lake City, UT) system as indicated in Table 1, which amplified and sampled the data at 1–30 kHz and applied analog anti-aliasing filters. Channels with excessive noise were identified visually by a clinical neurophysiologist and excluded from further analysis. Recordings of non-excluded ECoG channels for all subjects were then downsampled to 1 kHz offline, and were re-referenced to their common average to remove common mode noise artifacts and avoid spatial bias from the reference electrode.

2.1.2. Experimental design

Each subject performed two language-oriented tasks: picture naming and auditory word repetition. In the picture naming task, subjects were seated approximately 1 m from an LCD monitor, which presented visual stimuli in a random sequence from a collection of 100 distinct color pictures of objects on a grey background, in two blocks of 50 trials each, using E-Prime (Psychology Software Tools; Sharpsburg, PA). The depicted objects, which were matched for usage frequency in English, spanned a broad array of object categories, including tools, food items, animals, plants, body parts, structures, building parts, common household items, clothing, vehicles, jewelry, and instruments. Each picture was presented for one second, after which the subject would respond verbally with the name of the object. The inter-stimulus interval was selected at random from 6.5–8.2 s for each trial, in order to mitigate anticipatory artifacts. All 100 trials were considered in this analysis; for subject 1, this included 8 trials without a verbal response to the stimulus, as activiton patterns during non-response trials can provide an additional facet to distinguish cue- and response-related stages of processing.

In the word repetition task, subjects were played auditory word stimuli in a random sequence over standard commercial speakers (subject 3) or insert headphones via a high-end psychoacoustics workstation (all other subjects; model Z6A, Tucker-Davis Technologies; Alachua, FL); the word stimuli were identical to those used in, e.g., (Crone et al., 2001). Subjects were instructed to repeat the presented word verbally, after which a randomly chosen delay was applied, with the total inter - stimulus interval ranging from 7 – 8 s. Similar to the visual task, the stimuli were all unique, to avoid effects of repetition priming (Rodriguez Merzagora et al., 2014), and all trials were analyzed, leaving 58 (subject 3, due to time constraints, including 6 without a verbal response) or 116 (all other subjects) trials for analysis.

To later align the ECoG recordings with experimental cues, the stimulus onset and response onset times were marked in each trial for both tasks. We detected the onset of visual stimuli during picture naming by recording the thresholded output of a photodiode mounted on the computer monitor presenting stimuli. In each trial, the photodiode detected a reduction in luminance that occurred when a small black square appeared at the bottom left corner of the screen during presentation of the visual stimulus. This signal was passed into the same amplifier system as the ECoG data for trial alignment. We similarly measured the onset of acoustic stimuli during word repetition by transmitting a trigger pulse synchronized with the onset of the auditory stimuli to the recording system. In both tasks, a microphone was placed in front of the subject to record synchronized audio of verbal responses through the recording system’s analog input; these recordings were used to manually determine the response onset time for each trial.

2.2. Data analysis

Our analysis paradigm progressed in three broad stages: first, extraction of high gamma spectral features from the recorded ECoG data; second, computation of event-related cortical interactions from these features; and finally, estimation of subnetworks from these spatiotemporal interaction patterns. An overview of this pipeline is given in Supplementary Figure 1.

2.2.1. Spectral feature estimation

The common average–referenced ECoG signals were processed with a zero - phase finite impulse response bandpass filter with cutoffs at 70 Hz and 110 Hz to isolate high gamma activity and avoid line noise harmonics at 60 Hz and 120 Hz. These data were then separated into individual trials aligned to experimental cue onset, spanning from 1 s pre- to 3 s post-stimulus. The pre - cue window, used in constructing a base line null distribution for later statistical testing, was chosen to be as long as possible while avoiding any contamination from post - response activity in the previous trial. The relatively long post - cue analysis window was chosen to capture a large proportion of subjects’ responses, the latencies of which were particularly variable in subjects 1 and 3 (see Figure 4). It is notable that, in light of the multiple hypothesis correction used in later statistical testing, lengthening the analysis window could have also lowered the ensuing critical p - value thresholds, resulting in more conservative significance criteria for all time points. All trials were initially extracted with an additional 0.5 s of buffer data on either side to prevent edge effects at later stages of processing.

Figure 4.

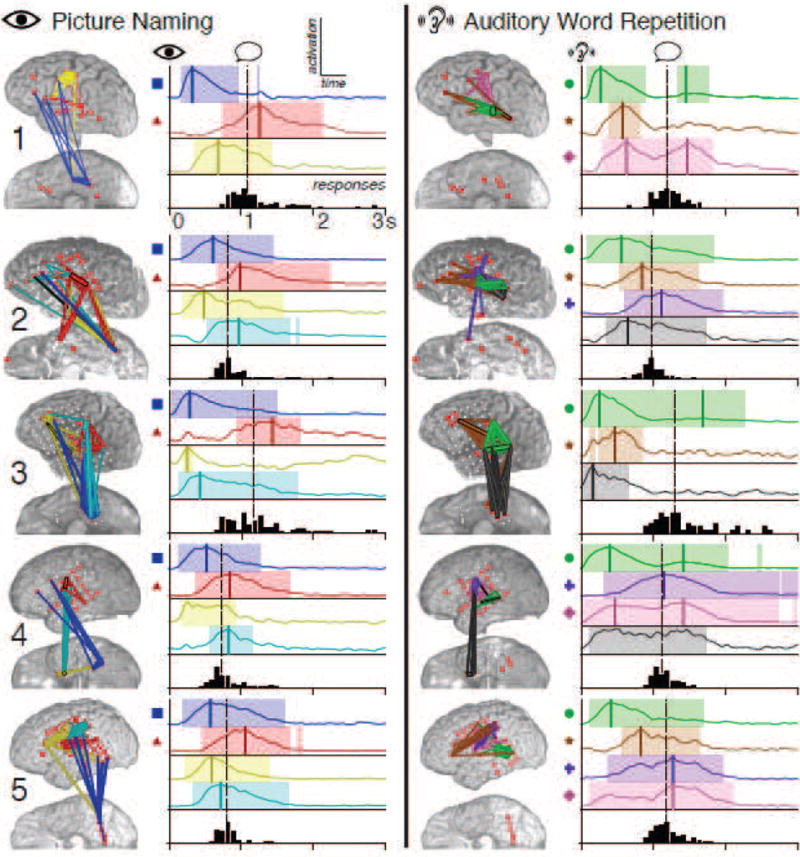
(Two-column.) FNCs for all subjects during picture naming (left) and auditory word repetition (right). For each subject and task, the spatial distribution of FNCs is shown on the subject’s anatomy. Each FNC is identified by unique coloration, with thicker edges representing stronger contributions to the FNC. The adjacent plots show the cue-locked temporal profiles of activation for these FNCs during each task, with the same color coding. The colored bands indicate periods when each FNC was significantly modulated relative to baseline fluctuations, corrected to maintain an FDR of < 0.05. Vertical colored lines have been manually inserted to highlight clearly discernible peaks in activation. Symbols next to the plots denote common spatial-temporal profiles referenced in the text. The black bars below each plot are histograms of observed subject response times, with the median response time indicated by the vertical dotted line.

We then computed time-varying spectra for each trial in 128 ms overlapping windows with 16 ms spacing using the multi-taper windowing method—which resolves the statistical inconsistency of the classical Fourier transform spectral estimator (Thomson, 1982; Babadi and Brown, 2014)—with 5 tapers, as implemented in the open source Chronux toolbox (Bokil et al., 2010). As the noise distribution of spectral power was observed to be lognormal, consistent with previous efforts (Gasser et al., 1982), these spectra were log-transformed and averaged over frequencies from 70–110 Hz to produce a single high gamma activity time series for each channel. Each channel’s data was then normalized using the mean and standard deviation of the aggregate baseline data for that channel, to ensure zero-centering and consistent scaling of the baseline activity distribution.

2.2.2. Feature subset selection

For global interaction methods like the one used in this study, inclusion of features that do not carry meaningful information can substantially degrade estimates for the rest of the network, as the method tries to fit its interaction model to noise. We therefore decided to select a subset of the available ECoG electrodes to use for event-related interaction analysis in each subject.

To select this subset, we first examined which of the recorded channels had significant changes in post-stimulus high gamma band activity. We evaluated this in each channel by performing a t-test between the distribution of high gamma activity across trials for each time bin and that channel’s aggregate baseline distribution, correcting for a familywise error rate of 0.05 using the Bonferroni procedure (i.e., thresholding at p < 0.05/T, where T is the number of time points in the analysis window). Channels with at least one 16 ms time bin showing significant modulation at this level were labeled as “high gamma–active” during that task; the interaction montage selected for each subject was the union of the sets of high gamma–active channels for the two tasks. The interaction montages for the subjects in this study had between 21 and 41 (mean 30) channels, as shown in Table 1.

2.2.3. Estimation of event-related interaction

We used the time-varying dynamic Bayesian network (tvDBN) framework (Song et al., 2009) as a model for estimating interactions between sites. This model makes the assumption that the current system state is a linear, time-varying function of the state at a previous time point, at some fixed delay d. We treated the n baseline-normalized high gamma power time series, x_i[t], as our state vector:

$$\mathbf{x}[t]:={\left[x_1[t]x_2[t]\cdots x_n[t]\right]}^T\in {ℝ}^n$$

The tvDBN framework’s model of the time series’ dynamics was then, in matrix form,

$$\mathbf{x}[t]=\mathbf{A}[t]\mathbf{x}[t-d]+\epsilon [t],\epsilon [t]\stackrel{\text{iid}}{~}\mathcal{N}(\mathbf{0},{\sigma }_{\epsilon }^2{\mathbf{I}}_n)$$

where the Gaussian ε[t] error terms encompass observation noise and nonlinear behavior. This is similar in principle to a first-order multivariate autoregressive model, where the coefficients A are allowed to vary with time.

The time-varying matrix A[t] is interpreted as the instantaneous interaction strength of the system at time t, where the coefficient A_ij is the influence from the jth channel at time t − d to the ith channel at time t. In the tvDBN model, this matrix is estimated row-wise at each time point using regression. Because the number of interaction coefficients being estimated generally exceeds the number of available data points, this problem by itself would be vastly underdetermined. To alleviate this, the tvDBN model makes some assumptions about the structure of the interaction matrices A[t]. First, and most important, the model imposes continuity of the underlying interaction matrix—that is, A[t] is assumed to vary relatively “smoothly” over time. This assumption allows us to estimate A[t] using data from time points near t, by weighting the observations using a kernel function ϕ. Second, self-interactions are excluded from the model, so that the diagonal elements of A[t] are all set to zero. Finally, the model incorporates a regularization penalty to avoid overfitting, given the low-data nature of the problem. Applying these considerations, and letting $D_i=\{\mathbf{a}\in {ℝ}^{1\times n}|a_i=0\}$ denote the space of row vectors with 0 in the ith position, we arrive at the following optimization problem for estimating each row i of A[t]:

$${\widehat{\mathbf{A}}}_i[t]=\underset{{\mathbf{A}}_i[t]\in D_i}{\text{arg}min}\left[{\displaystyle \sum _{\tau =1}^T\varphi (\tau ,t)}{(x_i[\tau ]-{\mathbf{A}}_i[t]\mathbf{x}[\tau -d])}^2+\lambda {({\Vert {\mathbf{A}}_i[t]\Vert }_2)}^2\right]$$

where T is the total length of the signals, λ controls the degree of regularization imposed, and ║ · ║₂ indicates the L² vector norm. This is a weighted ridge regression problem, which we solved for each row at each time point using the standard closed-form solution (Phillips, 1962; Tikhonov, 1963). The original presentation of tvDBN in (Song et al., 2009) used the L¹ norm for the regularization term, allowing their implementation to directly control the degree of sparseness (i.e., the number of nonzero elements) of the resultant A[t] matrices, as estimated using LASSO (Tibshirani, 1996). We opted instead to use the L² variant, as solving this problem is considerably more computationally efficient than LASSO. This method does not directly impose sparseness, but instead reduces the potential for overfitting by penalizing solutions with large norms, and hence encouraging most fitted coefficients to be small. Specifically, L² regularization is equivalent to imposing a zero-mean Gaussian prior on the regressed estimates of A[t], with variance controlled by λ.

Consistent with prior studies using tvDBN in ECoG (Benz et al., 2012b), we used a regularization parameter λ of 100, and a Gaussian kernel for weighting observations:

$$\varphi (\tau ,t)=\frac{k_h(t-\tau )}{{\displaystyle {\sum }_{i=1}^T{k}_h(t-i)}}$$

$$k_h(x)=\text{exp}\left(\frac{-x^2}{h}\right)$$

with a kernel width parameter h of 5 and a prediction lag d of 1 sample. To improve computation time, we truncated the kernel to a total width of 4h samples, as the kernel weights become very small far from the center, and have negligible impact on the regression output.

Our selected prediction lag d of a single sample corresponds to a delay of 16 ms in the transfer of high gamma information between cortical sites. It is unlikely that this single choice reflects the relative timing of all causal influences between cortical regions, and a more comprehensive model would incorporate state information from multiple lags to maximize descriptive power; however, we opted to use the first-order tvDBN model to preserve interpretability of the regressed parameters, and to ensure stable fitting of model coefficients in single trials, as outlined in the Discussion. Also, while the tvDBN model is manifestly directional in theory, and while prior work has shown that this method produces accurate interaction estimates, we observed that these parameter choices resulted in A[t] matrices that were nearly symmetric. Although our choice of h was informed by prior successful decoding work, it is possible that this kernel was too broad, and as a result smeared the directionality of information flow. To avoid confusion and prevent misinterpretation of these results, in all depictions of tvDBN estimates in this study, we have symmetrized the interaction matrices and omitted any indication of directionality; i.e., for a tvDBN coefficient matrix A[t], the results here depict

$${\mathbf{A}}_{\text{symmetric}}[t]=\frac{1}{2}\left(\mathbf{A}[t]+{\mathbf{A}}^T[t]\right)$$

Finally, it is important to acknowledge that in the scheme presented here, as is standard for offline analysis, both the window for spectral estimation and the kernel for interaction estimation were non-causal. Hence, while the computed activity is “centered” in time (making features like time of peak activation unbiased), the smoothing induced by the windows may have caused the computed activity to attain statistical significance up to 150 ms before any physiological activity took place, since activity on the “future” edge of the window could appear at the window’s center.

We approximated the distribution of tvDBN interaction coefficients during the baseline period (1 s prior to cue onset) as a Gaussian, and estimated the mean and variance of this aggregate baseline distribution for each channel pair. We normalized the tvDBN data for each pair relative to that pair’s baseline mean and standard deviation, to ensure zero-centering and consistent scaling of the baseline interaction distributions. We then modeled the interaction strength for each channel pair at each time point as Gaussians, and estimated the mean and variance of each of these distributions, giving us an estimate of the event-related interaction (ERI) between sites over the course of each task. To assess the statistical significance of ERI, we performed a t-test between each interaction’s pre-cue baseline distribution and the same interaction’s distribution in each time bin. To account for multiple comparisons, we determined the threshold for significant ERI by correcting for a false discovery rate (FDR) of 0.05 across time points for each site - site pair using the Benjamini-Hochberg (BH) protocol (Benjamini and Hochberg, 1995).

2.2.4. Subnetwork identification

To identify groups of interactions with similarly timed modulation, we concatenated the post-stimulus ERI data for all trials, and performed principal component analysis (PCA) on this aggregate ERI dataset (Hotelling, 1933). PCA iteratively identifies linear combinations of input signals, called principal components (PCs), that account for maximal amounts of input variance. This procedure results in a decomposition of the input signals with two complementary representations: spatial “loading” vectors, which show the contribution of each input signal to each PC; and temporal “score” time series, which show the modulation of each PC obtained by applying the loadings to the original data.

PCA, in its pursuit to explain the most variance, tends to collapse groups of signals that are highly anticorrelated by assigning the groups opposite - signed weights. This property was undesirable in the context of the present study, where the aim was to characterize groups of related interactions implicated in specific stages of task processing; indeed, any pair of processing stages with distinct temporal envelopes will naturally have activation signatures that are anticorrelated. In such a setting, PCA maximizes parsimony at the potential expense of physical meaning. To ameliorate this, we constructed two “signed PCs” from each computed PC: one from the positive weights with the negative weights set to zero, and the other from the absolute value of the negative weights with the positive weights set to zero. These signed PCs isolated the portions of the raw PC that positively co-varied. A concrete example of this behavior is shown in Figure 2 while the raw PC (orange in C) captures more variance than either of its signed constituents (green and blue), sign separation better elucidates the apparent subnetwork structure.

Figure 2.

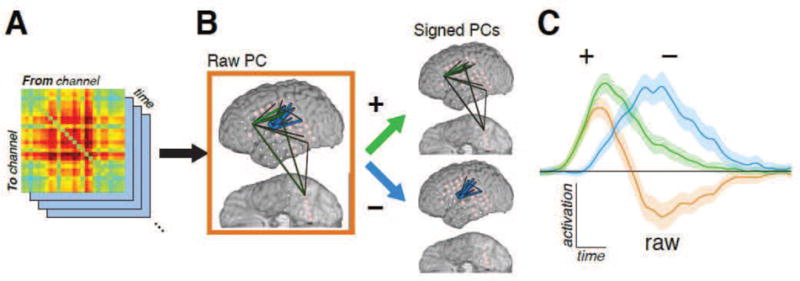
(Two columns.) Schematic of decomposition of dynamic interaction into signed PCs/FNCs. A: Interaction coefficients A[t] estimated using the tvDBN model form a 3-dimensional array, with the network’s state at each time point represented by an adjacency matrix of interaction strengths from each site to each other site. Equivalently, each channel-channel interaction is seen as an independent signal modulating over time. B: This 3D array is decomposed into PCs, with each PC defined by its loading vector—that is, its spatial distribution among the channel-channel interactions. These PCs are then further decomposed into “signed PCs” by treating the positive loadings and the absolute value of the negative loadings as two separate components. C: When the linear combination of features from the loadings is applied to the original interaction data, the result is a score signal for each signed PC. These scores are averaged across trials to assess both which signed PCs are significantly modulated, as well as the temporal profile of that modulation. Signed PCs that exhibit significant event-related modulation are denoted FNCs. The traces here show the mean and FDR-corrected 95% confidence interval for each depicted component’s modulation during the picture naming task compared to baseline; hence, significance is attained when the colored band does not overlap the horizontal line. The score of the original, un-signed PC (orange) is, by linearity, the score of its positive-weight PC (green) minus that of its negative-weight PC (blue); as this example shows, while the raw PC maximizes the captured variance by combining subnetworks with highly anticorrelated activation, it masks the underlying subnetwork structure.

It is important to recognize that “signed PCs” do not possess many of the desirable linear algebraic properties of their unsigned counterparts. First, being a transformation from ℝⁿ to ℝ²ⁿ there is no well-defined inverse mapping from signed PC–space back to interaction-space; as such, the common practice of back-transforming calculations done in PC-space must be avoided when working with signed PCs. Second, the signed PCs are not orthonormal; this, for example, makes it impossible to generalize the familiar notion of “explained variance” to signed PCs.

Although PCA can in theory extract as many PCs as there are input signals (and hence, twice as many signed PCs), in the case of ECoG interaction data, the vast majority of these PCs have an incredibly low signal-to-noise ratio, and hence do not carry discernible task-related information. To determine which signed PCs modulated significantly during the tasks, we used the same statistical paradigm described above for determining the significance of ERI, but replaced the tvDBN interaction data with the signed PC score time series. Once again, the threshold for significant modulation was determined by correcting for an FDR of 0.05 across time points for each signed PC using the BH protocol. For simplicity, we call signed PCs of ERI with significant activation during a task functional network components (FNCs). These FNCs provide estimates of the spatial (PC loadings) and temporal (PC scores) profiles of the activated subnetworks. In each of the subjects tested, we found only 3 to 7 activated FNCs per task, a dramatic reduction from the 420 to 1640 computed ERI signals.

“Mixing”—where one computed FNC had a strong spatial and temporal similarity to another FNC, or combination of FNCs—was evident in several of the examined subjects, owing to the loss of orthonormality in the signed PCs alluded to above. For clarity, we have attempted to omit duplicates of mixed FNCs. Groups exhibiting mixing were found by analyzing the Pearson’s r correlation between the weights of each pair of FNCs; pairs with r > 0.25 were considered mixed. All of the mixed FNCs fell into one of two categories: either one FNC was spatially a strict subset of another FNC, or an FNC was a combination of two other FNCs. In the former case, the “subset” FNC was not considered; in the latter, the two constituent FNCs were kept while the mixture was excluded from further analysis. An example of the combination case is shown in Figure 3; as the underlying behavior is captured by the constituent FNCs, the mixed combination does not lend much interpretational benefit. Removing mixed FNCs left the examined subjects with 3 to 4 remaining unmixed FNCs per task.

Figure 3.

(One-column.) Example of two-FNC mixing from subject 3, during auditory word repetition. A: The spatial composition of the mixed FNC (right) is a combination of the most prominent interactions from each of the constituent FNCs. B: As a result, its temporal profile (green) is, broadly, the sum of the profiles of the two constituents. Based on our selection criteria, the summed (right) FNC would be excluded from analysis.

The essence of subnetwork decomposition lies in utilizing the covariance structure of ERI time series to form a more concise representation that separates the spatial and temporal facets of interaction dynamics. While PCA provides an apt first demonstration of this premise, it is important to note that there are a wide array of techniques available to supply such a decomposition, some of which may be more appropriate than PCA in certain contexts. For example, while the time-varying dynamic Bayesian network model used in this report can yield negative values, many interaction measures—e.g., spectral coherence—are constrained to be strictly non-negative. When working with such measures, the family of methods known collectively as nonnegative matrix factorization (NMF) may provide a more suitable decomposition than PCA (Lee and Seung, 1999, 2001). As its name suggests, the NMF analogues of PC loadings (spatial weights) and scores (temporal activation profiles) are guaranteed to be non-negative, obviating the need for any sign-separation procedure.

2.2.5. Identification of significantly involved interactions

To approximate the null distribution of FNC weights, we imposed the null condition—i.e., we removed the covariance between interactions’ temporal profiles—by shuffling the ERI data across time independently for each channel pair. This procedure was repeated 500 times; in each iteration, we performed PCA on the result, and added the absolute values of the loadings for the 4 highest-variance PCs to the aggregate null distribution, as all of the observed activated FNCs were derived from the top 4 PCs of ERI. This null distribution was approximated by a Gaussian, and an interaction was considered significantly involved in an FNC if the absolute value of its FNC loading was above the 95th percentile of this distribution. FNCs which were so widely distributed as to have no significantly involved interactions were excluded from further analysis.

It is important to note that the unit normalization of the coefficients for each PC places important constraints on the distribution of FNC spatial weights. In particular, FNCs involving widely distributed networks will necessarily have lower spatial weights than FNCs involving a small number of interactions. Hence, while the spatial profile of an FNC shows the relative contributions of individual site-site interactions within that particular FNC, it does not provide a means of comparing the strengths of interactions across FNCs.

3. Results

3.1. Subtask specificity of FNCs

All of the subjects in this study exhibited three or four unmixed FNCs in each task. Figure 4 summarizes the spatial and temporal profiles of all observed FNCs for each subject and task; Supplementary Figure 2 provides a more detailed view of the anatomical composition of selected FNCs from all subjects in isolation.

Several of the observed FNCs showed marked anatomical and temporal similarities across subjects. As shown in the left column of Figure 4, during the picture naming task, all subjects exhibited an FNC that included interactions within ventral occipital-temporal cortex (VOTC, including fusiform gyrus), and between VOTC and perisylvian cortices, including sensorimotor cortex (SMC) and Broca’s area (blue edges in anatomical plots, left; blue temporal plots accompanied by squares, right). As expected given VOTC’s known role in visual processing (Moore and Price, 1999; Allison et al., 1999), these FNCs were active shortly after cue presentation, becoming significant at 50–150 ms and peaking in activation at 200–600 ms. In all subjects, an additional FNC was present with interactions between posterior superior temporal gyrus (pSTG) or supramarginal gyrus (SMG) and either sensorimotor cortex, Broca’s area, or both (red; traces accompanied by triangles). These FNCs attained peak activation after the median latency of the subject’s spoken response, consistent with the involvement of pSTG and SMG, which have been shown to participate in the perception of speech (Celsis et al., 1999; Dehaene-Lambertz et al., 2005).

In auditory word repetition (right column of Figure 4), all subjects displayed an FNC consisting primarily of interactions within pSTG, with activity very early after cue onset (green; traces accompanied by circles). While these intra-pSTG FNCs attained absolute peak activation at 150–500 ms, all showed activity late in the task as well, with those from subjects 1, 3, and 4 attaining a second, much smaller peak after the median response latency. This temporal pattern—including both post-cue and post-response modulation—is again expected given pSTG’s known role in speech perception. Four of the five subjects exhibited an FNC during word repetition incorporating interactions between pSTG and Broca’s area (brown in subjects 1, 2, 3, and 5; traces accompanied by stars). These FNCs attained peak activation at an intermediate stage of the task—after the peak of that subject’s intra-pSTG FNC, but before the median response time. Subjects 2, 4, and 5 had an FNC primarily composed of interactions within sensorimotor cortex (purple; traces accompanied by crosses). These FNCs showed activity centered around the median response latency, consistent with sensorimotor involvement. An additional FNC was seen in three subjects involving interactions between SMC and Wernicke’s area (pink in subjects 1, 4, and 5; traces accompanied by diamonds). As in the case of the primarily intra-pSTG FNCs (green) described above, these SMC-Wernicke FNCs showed activation across both task epochs, with those from subjects 1 and 4 exhibiting a similar double-peaked pattern. However, unlike the intra-pSTG FNCs, which showed much stronger activation during the post-cue period, these FNCs were equally active in both epochs (subjects 1 and 4) or more active during the post-response period (subject 5).

Figure 5 provides a more detailed look at the FNCs from subject 1. In the picture naming task, subject 1 exhibited both of the common FNC spatial-temporal patterns described above: an early post-cue FNC consisting of intra-VOTC and VOTC–Broca’s area interactions (brain 1 with blue network edges in A; blue traces in B), and a later FNC incorporating interactions between sensorimotor cortex and pSTG peaking after the median verbal response time (brain 3; red). An additional FNC with primarily Broca’s area–SMC interactions (brain 2; yellow) peaked in activation at an intermediate latency. In word repetition, three common FNC patterns were evident as well: an intra-pSTG FNC with large post-cue and small post-response peaks (brain 4 with green network edges in C; green traces in B); an FNC linking pSTG and Broca’s area with intermediate timing (brain 5; brown); and a third FNC incorporating mostly SMC–pSTG interactions with post-cue and post-response activity of equal magnitude (brain 6; pink).

Figure 5.

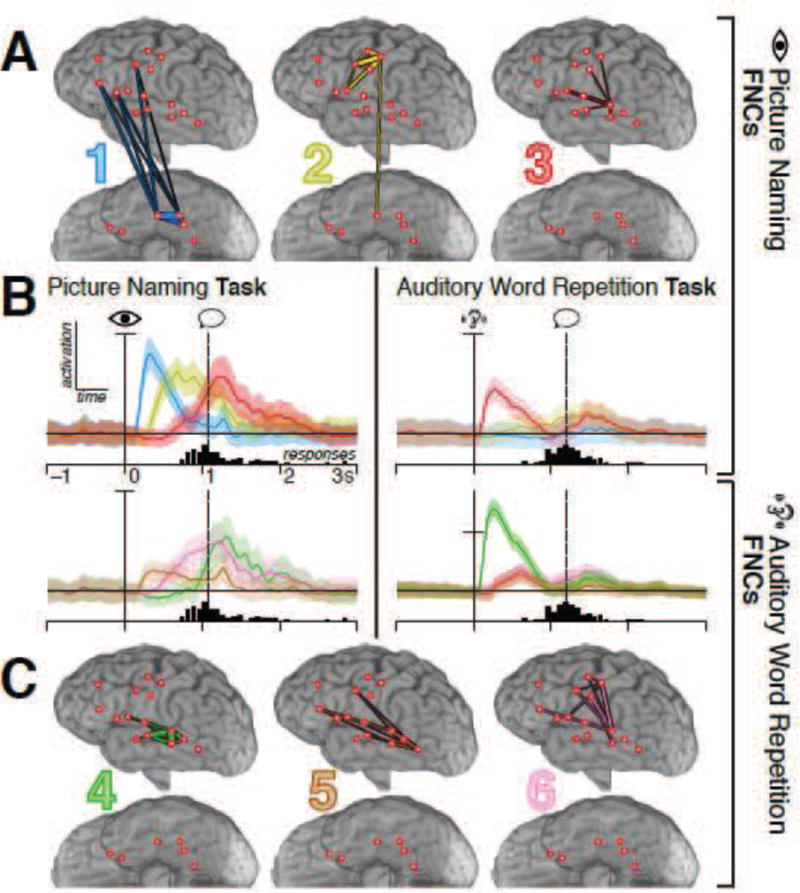
(Two-column.) Spatial and temporal profiles of FNCs for subject 1. A and C show interactions with significant contributions to each FNC estimated from the picture naming (A) or auditory repetition (C) task, with thicker edges corresponding to stronger contributions. B displays the FNCs’ peri-task activation from 1 s before to 3 s after cue presentation, obtained by applying the spatial loadings depicted in A and C to the interaction data from each task. The color of each trace corresponds to the color indicated on that FNC’s spatial profile in A or C, and all traces are normalized to the standard error of each FNC’s own baseline distribution. Rows correspond to the tasks from which the FNC loadings were computed, while columns correspond to the task the FNC loadings were applied to; hence, for example, the top-right plot shows how the FNCs extracted from the picture naming task modulated during the word repetition task. The vertical solid line denotes the time of cue onset; the histogram below each plot shows the distribution of response times for that task, with the vertical dotted line marking the median response time. Colored bands around each trace show the confidence intervals of the difference between each FNC’s modulation and baseline fluctuations of that FNC, corrected for an FDR of 0.05—hence, significance occurs when the band does not overlap the horizontal line (i.e., difference ≠ 0). Vertical scaling is the same for all plots except for the bottom-right, in which the vertical axis has been compressed to accommodate the dramatic peak of the green FNC, as shown by the tick on the ordinate axis.

3.2. Robustness of FNC activation in single trials

The robust aggregate profile of FNC activation was echoed in the modulation of FNCs in single trials. In all of the tested subjects, each FNC displayed a characteristic timing profile relative to cue and/or response onset that was consistent across trials; these single-trial profiles are shown for selected FNCs from all subjects in Supplementary Figure 3. The timing of each FNC’s activation in individual trials fell into one of three broad categories: locked to cue, locked to response, or bimodal with peaks locked to both cue and response. FNCs that were structurally similar across subjects showed largely similar patterns of activation in single trials. For example, the FNCs from picture naming involving interactions with VOTC (blue in Figure 4 and Supplementary Figure 2) showed a consistent burst of activation locked to stimulus presentation (blue in Supplementary Figure 3). In contrast, FNCs from picture naming that primarily included interactions between pSTG and SMC (red in Figure 4 and Supplementary Figure 2) exhibited strong coupling in all subjects to the epoch directly after response onset, with a more or less fixed duration of activation. The two distinct timing patterns seen for FNCs from word repetition incorporating pSTG–Broca’s area interactions (brown in Supplementary Figure 3) appeared to reflect the degree to which the FNCs also incorporated Broca-SMC interactions (brown in Supplementary Figure 2).

The rasters in Figure 6, displaying the modulation of subject 1’s FNCs in single trials, give a representative demonstration of the different temporal profiles described above, and provide more detailed insight into the task-related dynamics of FNC activation. The first FNC from picture naming (blue, top-left), which involved intra-VOTC and VOTC–Broca’s area interactions (anatomy in Figure 5, top-left), was clearly time-locked to cue presentation, and stayed active for a fixed duration of ~600 ms regardless of response latency. The yellow FNC from picture naming, which spanned SMC and Broca’s area (top-middle), was also time-locked to the cue, beginning 100–200 ms after the VOTC-involved FNC became active; however, rather than having a fixed duration of activation, this FNC exhibited activity until roughly 300 ms after response onset in each trial. The red FNC from picture naming, incorporating interactions between Broca’s area, SMC, and pSTG (top-right), showed strong coupling to response onset, and remained active throughout the duration of the subject’s response. It is interesting to note that in trials where the subject did not respond (bottom of the rasters), the blue VOTC-Broca FNC showed consistent activation, the yellow SMC-Broca FNC showed discernible but diminished activation, and the red pSTG-involved FNC showed little to no activation.

Figure 6.

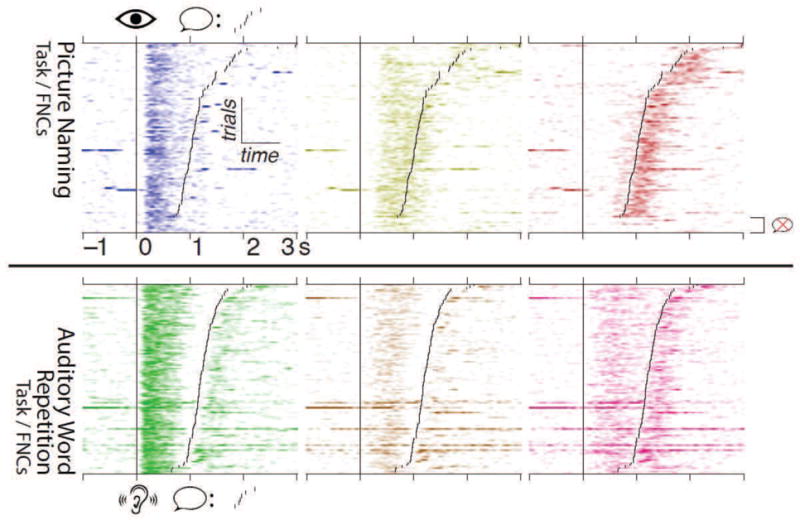
(Two-column.) Single-trial modulation of FNCs for subject 1, from 1 s pre- to 3 s post-stimulus onset. The top row shows results for FNCs computed from picture naming during the picture naming task, while the bottom row shows FNCs computed from word repetition during the word repetition task. The coloration of each plot corresponds to the color for each FNC shown in Figure 5, with darker colors corresponding to stronger activation. Trials are aligned to cue onset (vertical line), and have been sorted according to the subject’s response time (smaller black lines); trials in which the subject didn’t respond are grouped at the bottom. Each FNC exhibits a clear cue- and/or response-aligned pattern of modulation.

During auditory word repetition, the green FNC, incorporating primarily intra-pSTG interactions (anatomy in Figure 5, bottom-left), showed a bimodal activation pattern, with peaks occurring after both cue and response onsets (Figure 6, bottom-left), the former being considerably stronger than the latter in all trials. The brown FNC, spanning pSTG and Broca’s area (bottommiddle), became active primarily in the epoch between the green intra-pSTG FNC’s activation and the subject’s response onset. The pink FNC, spanning SMC, pSTG, and Broca’s area (bottomright), showed two bursts of activity: one after the green intra-pSTG FNC’s activation (leading into the subject’s response), and one starting at response onset and continuing for ~500 ms. Interestingly, while the green intra-pSTG FNC’s bursts of activation were delayed by ~100 ms relative to the onset of the auditory cue or the subject’s spoken response, the FNCs incorporating SMC-Pstg interactions from both word repetition (pink) and picture naming (red) showed response-related activation considerably earlier, with the latter becoming active up to 200 ms pre-response in some trials.

4. Discussion

4.1. FNCs identify subnetworks for different stages of task-related processing

Our hypothesis—that functional network components identify groups of related cortical interactions involved in particular stages of task-related processing—is supported by the high degree of consistency between the spatial-temporal profiles of FNCs and current neurobiological models of speech production. As detailed in Section 3.1, during the picture naming task, all subjects exhibited an FNC consisting of interactions within ventral occipital-temporal cortex, as well as between VOTC and Broca’s area and/or sensorimotor cortex (blue/squares in Figure 4 and Supplementary Figure 2); these FNCs showed early cue-locked activation, exemplified in individual trials in Figure 6 and Supplementary Figure 3 (blue). This profile is expected given the involvement of VOTC, which is known to play a role in visual object processing (Moore and Price, 1999; Allison et al., 1999); the prominent VOTC-Broca interactions may indicate that Broca’s area incorporates the results of this processing during lexical retrieval (Flinker et al., 2015). All subjects also had an FNC during picture naming with interactions between posterior superior temporal gyrus or supramarginal gyrus and either sensorimotor cortex, Broca’s area, or both (red/triangles in Figure 4 and Supplementary Figure 2), with timing strongly aligned to verbal response onset (red in Figure 6 and Supplementary Figure 3). This alignment is consistent with pSTG’s role in auditory processing of speech (Price et al., 1992; Steinschneider et al., 2011; Leonard and Chang, 2014).

Auditory word repetition evoked its own set of robust FNC spatial-temporal profiles. The most prominent of these, seen in all subjects, primarily included interactions within pSTG (green/circles in Figure 4 and Supplementary Figure 2), with strong cue-aligned and weaker response-aligned activation (green in Figure 6 and Supplementary Figure 3). Again, this activation profile is consistent with pSTG’s likely role in processing both the external speech stimuli and the subjects’ spoken responses; the large disparity in activation observed between cue-related and response-related activity may reflect suppression of high gamma activity during self-generated speech (Flinker et al., 2010). Four subjects exhibited FNCs with pSTG–Broca’s area interactions (brown/stars in Figure 4 and Supplementary Figure 2) with intermediate timing, becoming active after the green intra-pSTG FNCs (e.g., Figure 6 and Supplementary Figure 3, brown). These FNCs correlate well with the predicted flow of information from phonological networks in pSTG and posterior middle temporal gyrus (pMTG) to networks for syllabification (Indefrey, 2011) or formation of articulatory codes (Hickok and Poeppel, 2007; Flinker et al., 2015) in Broca’s area. Three subjects had FNCs consisting primarily of intra-SMC interactions (purple/crosses in Figure 4 and Supplementary Figure 2); as expected, these FNCs show activation centered around response onset, consistent with articulatory execution.

Four subjects also exhibited FNCs including prominent SMC-pSTG and/or SMC-SMG interactions (pink/diamonds in Figure 4 and Supplementary Figure 6). These FNCs showed both post-cue and post-response activity like the green intra-pSTG FNCs, as exemplified in Figure 6 and Supplementary Figure 3 (pink); however, rather than being suppressed during the post-response period, these FNCs showed equal or greater activation for self-produced speech. This difference in subnetwork dynamics—between intra-pSTG FNCs that are preferential for the external speech cue, and FNCs with SMC–Wernicke’s area interactions with stronger activation during the subject’s own verbal response—is consistent with recent studies suggesting functional distinctions between processing external and self-generated speech (Towle et al., 2008; Chang et al., 2013; Kort et al., 2014). The inclusion of SMC-Wernicke interactions in these FNCs, as well as in the red response-aligned FNCs from picture naming, is consistent with previous studies in nonhuman primates showing motor-sensory interactions during vocalization (Eliades and Wang, 2003); these interactions may reflect auditory feedback for motor control (Houde and Chang, 2015) and/or feedforward motor inputs for auditory state prediction (Hickok, 2012). Interestingly, subject 5’s SMC-Wernicke FNCs (red and pink in Figure 4) involved distinct sites superior to those implicated in her cue-preferential intra-pSTG FNC (green); this correlates well with predictions of a spatially distinct “sensorimotor interface” for speech (Hickok et al., 2003; Hickok and Poeppel, 2007; Hickok et al., 2009).

To further test the validity of the estimated subnetworks and their interpretation, we examined the activation of FNCs during tasks for which they were not directly computed by applying the FNC loadings from one task to the event-related interaction data from the other task; the results of this procedure applied to subject 1 can be seen in the top-right and bottom-left plots of Figure 5. Remarkably, FNCs computed from one task showed robust profiles of activation when applied to the other task, providing more evidence for their roles in task processing. For example, in subject 1, the early VOTC-involved FNC from picture naming (brain 1 in A; blue traces in B) showed no significant modulation during the auditory repetition task, suggesting that that FNC’s activity was specific to visual processing. As another example, subject 1’s intra-pSTG FNC from word repetition (brain 4 in C; green traces in B) showed similar activation during the picture naming task to subject 1’s post-response FNC from picture naming (brain 3 in A; red traces in B), though the green intra-pSTG FNC attained significance and peak activation slightly later. Subject 1’s pSTG–Broca’s area FNC from word repetition (brain 5 in C; brown traces in B) showed slight intermediate activation during picture naming, perhaps reflecting access to phonology that was overshadowed in the FNC computation by the dependence of lexical retrieval on visual object processing.

Taken as a whole, these results support our original hypothesis: groups of cortico-cortical interactions with strong temporal covariance—as captured by FNC analysis—are indicative of discrete functional subnetworks, and may provide important insights into the dynamics of large-scale cortical networks during cognitive tasks.

4.2. FNCs can be estimated in a computationally efficient manner with single-trial robustness

There are a wide array of tools available for characterizing cortical interplay, spanning the gamut of complexity and interpretability (Winterhalder et al., 2005). In recent studies of interaction dynamics in ECoG, multivariate parametric methods—including partial directed coherence (Baccalá and Sameshima, 2001), the directed transfer function (Kamiński et al., 2001), and event related causality (Korzeniewska et al., 2008)—have come to the fore. The theoretical basis for these methods lies in determining the degree to which one signal “Granger-causes” another—that is, whether information about one signal in the past improves a predictive model of the other signal in the present (Granger, 1988). To this end, these methods approximate ECoG signal dynamics as a multivariate autoregressive (MVAR) model of some specified order p,

$$\mathbf{x}[t]={\displaystyle \sum _{k=1}^p{\mathbf{A}}_k}\mathbf{x}[t-k]+\text{noise}$$

where the A_k matrices encode interactions between channels, and are used to make various inferences about the system, depending on the metric.

Cortical interactions are not static, however; hence, to be truly descriptive about interaction dynamics, a new MVAR model must be fit in each short time window. As this window is made shorter to provide higher time resolution, less data are available to inform the fitted model coefficients. As a result, for modest model order, montage size, and time resolution, the fit becomes unreliable unless the data are aggregated across trials, which is undesirable in many circumstances. As an alternative, the tvDBN model used in this study—which has shown great promise as an ECoG interaction estimator in motor tasks (Benz et al., 2012b)—ameliorates the data-volume problem through simplification: it reduces the complexity of the input data being analyzed by considering only power in the high gamma band, and reduces the complexity of the model by restricting to a first-order MVAR model, which can be robustly evaluated in single trials when subjected to regularization and smoothness conditions as described above. In this way, tvDBN can be seen as a local linear approximation of the multivariate high-gamma envelope dynamics.

PCA signal decomposition is relatively fast on modern hardware; hence, the FNC analysis method introduced here can be readily generalized to other interaction estimation methods. Combined with the relative computational ease of multi-taper spectral estimation and tvDBN interaction estimation, the entire pipeline demonstrated in this report is suitable for online implementation; indeed, even the PCA step need only be run once during a model “training” session, making online use of FNCs a simple linear weighting of interaction features. Our results have shown that FNCs demonstrate robust and informative activation in single trials. As such, FNC analysis on tvDBN ERI estimates is an ideal candidate for use in real-time applications such as control of a brain-machine interface.

4.3. Potential extensions of FNC analysis

Direct cortical stimulation in epilepsy surgery patients has shown that the topography of language cortex is highly variable across individuals, and that even within consistent language areas—e.g., pSTG and posterior inferior frontal gyrus in the dominant hemisphere—there are mosaics of cortical patches in which direct cortical stimulation interferes with language tasks (Ojemann, 2003). To minimize the cognitive side-effects of resection surgery, it is necessary to map the cortical sites crucial for language in each patient. Until recently, this was done exclusively with electrocortical stimulation mapping (ESM); however, important practical limitations of this method (Lesser et al., 1984, 1985; Blume et al., 2004; Pouratian et al., 2004; Hamberger, 2007) have motivated the development of passive ECoG recording and analysis techniques, which measure task-related high gamma responses, as a potential alternative (Lachaux et al., 2007; Miller et al., 2007; Schalk et al., 2008; Cheung and Chang, 2012; Qian et al., 2013). Although mapping of high gamma activation has shown promise, its adoption for routine clinical use has been inhibited by inconsistencies with ESM results (Wu et al., 2010; Cervenka et al., 2011; Ruescher et al., 2013; Bauer et al., 2013) and by methodological difficulties in comparing the post-operative outcomes of resections guided by ESM to those guided by activation-based mapping. Our current study was motivated by the hypothesis that the spatial-temporal profile of task-related cortical interactions provides additional insights into the the relative importance of individual sites for task processing.

FNC analysis may lend several interpretational benefits over ESM or maps of activation at individual sites. First, the participation of sites in particular FNCs provides information about which stages of task processing those sites are involved with. Given the variation in the functional anatomy of language, this information could lend more insight into the specific kinds of deficits risked by lesioning that site than the strength of the site’s task-related activation alone. Second, the location of a site within the FNC architecture may be indicative of that site’s importance in task processing relative to other activated sites. For instance, nodes with high centrality in an FNC may be seen as local “hubs” for a particular processing stage (Bullmore and Sporns, 2009; Newman et al., 2015); hence, resecting such central sites may be more likely to cause cognitive damage specific to that FNC’s processing role, while resecting sites that are more peripheral in the FNC could potentially carry a reduced risk of deficits. Similarly, sites that participate in multiple FNCs may facilitate communication between subnetworks, serving as the “bridge” or “connector” between computation stages; such sites, when resected, might also lead to a specific pattern of impairment. This sort of graph-theoretic analysis of cortical interaction data derived from ECoG has already shown great promise in the characterization of epileptogenic networks (Burns et al., 2012; Ortega et al., 2008; Wilke et al., 2011), and may prove equally informative when applied to task-related network structures like FNCs.

Network structure analysis has great potential outside of the clinic as well: a considerable amount of recent effort in neuroimaging has gone into characterizing the structure of cortical connections, in terms of both physical tracts (DTI) and correlated resting-state metabolic activity (fMRI) (van den Heuvel and Sporns, 2011; Collin et al., 2013). Indeed, the “rich club” nodes of such import to connectomics are presumed to lie at the intersection of network hubs (centers of local processing) and bridges (gateways of information flow). However, the poor time resolution of functional neuroimaging techniques hinders their utility in probing the dynamic exchanges of information that take place during a task. FNC analysis performed on ECoG high gamma activity has the potential to expand upon these noninvasive methods by not only identifying important network loci like hubs and bridges, but also by illuminating the temporal profile of their interactions over the course of a specific activity. Although beyond the scope of the present study, such a characterization of these loci would be an insightful application of the methods introduced here.

5. Conclusions

Mapping the event-related interactions between cortical sites during language tasks, such as picture naming and word repetition, holds great promise for expanding our understanding of the neurophysiology underlying these complex human behaviors. The difficulties of visualizing, analyzing, and interpreting the high volume of data inherent in these interactions can be mitigated by the theoretical framework of subnetwork decomposition, which seeks to identify groups of related interactions that can be treated as a cohesive functional unit. The approach presented in this report, functional network component analysis, is a simple yet informative first step toward this vision in mapping of the dynamics of task-related cortical interactions in the human brain with ECoG. FNCs capture both the strong interaction phenomena common to subjects with broadly similar anatomical coverage, as well as the more nuanced patterns of interactions specific to each subject’s electrode placement and cortical organization. This first demonstration suggests that FNC analysis—and, more generally, the subnetwork decomposition paradigm—may be a powerful tool for investigating the rich dynamics of large-scale, distributed cortical networks recruited during a wide range of human cognitive tasks.

Highlights.

• A method to identify functional subnetworks from ECoG connectivity is proposed.

• Subnetworks simplify connectivity dynamics by grouping co-varying connections.

• Subnetworks observed during language tasks are consistent with current models.