Toward Determining ATPase Mechanism in ABC Transporters: Development of the Reaction Path–Force Matching QM/MM Method

Abstract

Adenosine triphosphate (ATP)-binding cassette (ABC) transporters are ubiquitous ATP-dependent membrane proteins involved in translocations of a wide variety of substrates across cellular membranes. To understand the chemomechanical coupling mechanism as well as functional asymmetry in these systems, a quantitative description of how ABC transporters hydrolyze ATP is needed. Complementary to experimental approaches, computer simulations based on combined quantum mechanical and molecular mechanical (QM/MM) potentials have provided new insights into the catalytic mechanism in ABC transporters. Quantitatively reliable determination of the free energy requirement for enzymatic ATP hydrolysis, however, requires substantial statistical sampling on QM/MM potential. A case study shows that brute force sampling of ab initio QM/MM (AI/MM) potential energy surfaces is computationally impractical for enzyme simulations of ABC transporters. On the other hand, existing semiempirical QM/MM (SE/MM) methods, although affordable for free energy sampling, are unreliable for studying ATP hydrolysis. To close this gap, a multiscale QM/MM approach named reaction path–force matching (RP–FM) has been developed. In RP–FM, specific reaction parameters for a selected SE method are optimized against AI reference data along reaction paths by employing the force matching technique. The feasibility of the method is demonstrated for a proton transfer reaction in the gas phase and in solution. The RP–FM method may offer a general tool for simulating complex enzyme systems such as ABC transporters.

1. INTRODUCTION

Found in organisms of all three kingdoms of life, adenosine triphosphate (ATP)-binding cassette (ABC) transporters represent a family of molecular motor proteins that enable translocations of various substrates, including small organic/inorganic molecules, ions, lipids, peptides, and toxins, across the cell membranes, at the expense of ATP hydrolysis (Davidson, Dassa, Orelle, & Chen, 2008; Hollenstein, Dawson, & Locher, 2007; Schneider & Hunke, 1998). ABC transporters are biomedically important because mutations in these systems can cause an array of human diseases and clinical problems (Borst & Oude Elferink, 2002). All ABC transporters share a common architecture of two basic building blocks: a dimeric transmembrane domain (TMD) composed of transmembrane helices and a pair of intracellular nucleotide-binding domains (NBDs), which is a highly conserved motor ATPase that energizes the transport (Oswald, Holland, & Schmitt, 2006). Forming a channel for substrate passage, the TMD exists at least two distinct states, termed the inward- and outward-facing conformations (Rees, Johnson, & Lewinson, 2009). Despite the general knowledge that the TMD cycles between the inward- and outward-facing conformations as a result of ATP binding and hydrolysis in the NBDs (Newstead et al., 2009), the precise mechanism of ATP hydrolysis in ABC transporters as well as the extent to which enzyme catalysis is coupled to conformational dynamics during substrate translocation have largely remained unknown (Davidson et al., 2008).

One intriguing question staying controversial is how many ATP molecules are hydrolyzed per translocation cycle. Although the dimeric arrangement of NBDs appears to imply that two ATP molecules are consumed, a great body of experimental evidence suggests that the two NBDs have intrinsic functional asymmetry and may be catalytically nonequivalent. If both sites are able to hydrolyze ATP, are their actions of catalysis concerted or sequential? Answers to these questions can provide important insights into understanding the sequence of events that controls conformational coupling between TMD and NBD. A quantitative model to describe the hydrolysis process also offers an important step toward understanding how enzyme catalysis in ABC transporters is coupled to protein dynamics especially when NBDs undergo large conformational changes.

Given the mechanistic complexity of ABC transporters, which are large-sized enzymes that involve multiple active sites, multiscale computer simulations based on the combined quantum mechanical and molecular mechanical (QM/MM) approach are especially useful to complement experiments by providing a unique molecular-level understanding of enzyme mechanism that synthesizes structural, dynamic, and energetic information. In this chapter, we discuss progress and challenges in QM/MM simulations of ABC transporters, which have also led to our recent development of a new multiscale approach aimed at overcoming the limitations found in the existing methods.

To highlight the problem-driven nature of this development, we organize our discussion by first describing the biological questions we seek to answer (Section 2), followed by a brief summary of our QM/MM simulations of ATP hydrolysis in a representative ABC transporter (Section 3). In Section 4, we discuss challenges in those simulations and limitations in the existing computational methods. The newly developed Reaction Path–Force Matching (RP–FM) method is presented in Section 5. Concluding remarks are provided in Section 6.

2. BIOLOGICAL QUESTIONS

2.1 Overview

Based on the direction of translocation, the ABC-transporter family can be divided into two functional categories: importers and exporters (Davidson et al., 2008). To illustrate a typical transport cycle, below we use the maltose transporter (an importer) as an example.

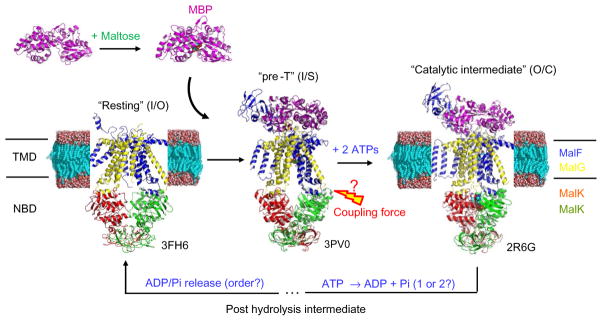
The maltose transporter is responsible for uptake of maltose in bacteria. Its TMD (MalFG) and NBDs (MalK2) are organized as separate polypeptide chains and assembled into a membrane-bound complex. The maltose transport cycle is regulated under a peripheral maltose-binding protein (MBP) (Davidson & Chen, 2004). Crystal structures of isolated NBDs showed that MalK2 can adopt at least three distinct NBD conformations, referred to as the open, semiopen, and closed states (Chen, Lu, Lin, Davidson, & Quiocho, 2003). These NBD conformations were also observed in crystal structures of intact maltose transporter captured at various stages of its working cycle (Fig. 1), including an inward-facing “resting state” (Khare, Oldham, Orelle, Davidson, & Chen, 2009), an outward-facing “catalytic intermediate” (Oldham, Khare, Quiocho, Davidson, & Chen, 2007), and a pretranslocation state (denoted “pre-T”) (Oldham & Chen, 2011). In the resting state structure, NBD is found in the open conformation and interacts with MalFG that faces the cytosolic side of the membrane. The inward- to outward-facing conformational change of TMD during the “pre-T” to “catalytic intermediate” transition is primarily driven by MalK2 dimer closure upon ATP binding. After hydrolysis and product release, the system returns to the resting state, and the motor cycle is reset.

Fig. 1.

Crystal structures captured for key intermediate states in the working cycle of maltose transporter. The TMD/NBD conformations are given in parentheses (TMD: I or O, for inward- or outward-facing conformations; NBD: O, S, or C, for open, semiopen, or closed conformations).

Key questions to be answered for ABC transporters include how TMD and NBD are mechanically coupled and to what extent enzyme catalysis is coupled to conformation transitions of NBD. For a thorough understanding of the chemomechanical coupling mechanism in ABC transporters, catalysis needs to be examined as a function of conformational change. As the first step, we focus on the ATP hydrolysis mechanism in a single-state conformation, ie, the closed conformer of NBD, which is believed to be catalytically more active than the open and semiopen conformers. Specifically, we seek to answer the following questions.

2.2 How Many ATPs Are Hydrolyzed?

One fundamental question regarding the mechanisms of action in ABC transporters is how many ATP molecules are hydrolyzed per translocation cycle. At first glance, the fact that most functional NBDs in bacterial ABC transporters are homodimers seems to suggest that two copies of ATP need to be hydrolyzed to provide the chemical free energy for substrate translocation. Contrary to this intuition, direct measurements of ATP/substrate ratio in ABC transporters, however, have given greatly diverging results ranging from 1 to 25 (Davidson et al., 2008), indicating that a definitive answer to this question is perhaps difficult to obtain experimentally.

A great body of evidence has implied that the two NBDs in ABC transporters are functionally nonequivalent for ATP hydrolysis. In many eukaryotic exporters, such as the transporter associated with antigen processing (Procko, Ferrin-O’Connell, Ng, & Gaudet, 2006), the multidrug resistance protein P-glycoprotein (Urbatsch, Sankaran, Weber, & Senior, 1995), and the cystic fibrosis transmembrane conductance regulator (Atwell et al., 2010), NBDs are heterodimeric in that only one of the two NBD active sites contains all essential residues required for catalysis, suggesting that only one ATP is hydrolyzed. Interestingly, evidence for functional asymmetry has also been reported for ABC transporters that contain homodimeric NBDs. For example, vanadate-trapping experiments showed that the hydrolysis product is found in only one subunit of the NBD homodimer in maltose transporter (Sharma & Davidson, 2000). Intriguingly, mutation to a single NBD active site has been shown to abolish ATPase and transport activities in histidine permease (Nikaido & Ames, 1999; Shyamala, Baichwal, Beall, & Ames, 1991), maltose transporter (Davidson & Sharma, 1997), and vitamin B12 transporter (Tal, Ovcharenko, & Lewinson, 2013). Recent crystal structures of NBDs of HlyB, a bacterial exporter, suggested that the two NBDs, although identical in sequence, may release their hydrolysis products differently (Zaitseva et al., 2006). For the exporter MJ0796, it was found that disabling ATP hydrolysis in a single active site leaves dimer dissociation essentially unchanged (Zoghbi & Altenberg, 2013). Finally, computer simulations of dimeric NBDs of maltose transporter suggested that hydrolysis in a single site can trigger dimer interface opening (Wen & Tajkhorshid, 2008).

Quantitative characterization of such functional asymmetry, especially in terms of catalytic activity in the dimeric NBD sites, may also help resolve mechanistic controversy existing for ABC transporters. Catalytically asymmetric dimer would enhance the chance that only one ATP is hydrolyzed at a time, an essential element in the alternating catalysis mechanism (Senior, Al-Shawi, & Urbatsch, 1995). Without significant catalytic nonequivalence, the transporter would more likely operate under the processive clamp model (Janas et al., 2003), which requires both ATP molecules to be hydrolyzed before NBD dimer dissociation.

2.3 What Is the Precise ATP Hydrolysis Mechanism?

The first step to determine whether the two NBD sites are equivalent in catalysis is to obtain a quantitative description of their ATP hydrolysis mechanism. The observation that NBDs across the ABC-transporter family share a highly conserved active site architecture suggests that they hydrolyze ATP by a common mechanism. Below we use the bacterial exporter HlyB as an example to describe the enzyme mechanistic questions we seek to answer by computation.

Haemolysin B (HlyB) is the inner membrane component of the type I protein secretion apparatus that transports the 107 kDa pore-forming toxin haemolysin A out of Gram-negative bacterial cells (Holland, Schmitt, & Young, 2005). It is well established that HlyB functions as an ABC transporter, consisting of two cytosolic NBDs and two TMDs. As the molecular motor component of the transporter, HlyB-NBD works as an ATPase that catalyzes ATP hydrolysis at a rate constant of k_cat =0.2 s⁻¹ (Zaitseva, Jenewein, Jumpertz, Holland, & Schmitt, 2005), corresponding to a rate acceleration of more than six orders of magnitude compared to the solution phase reaction (k=8×10⁻⁸ s⁻¹) (Khan & Mohan, 1973).

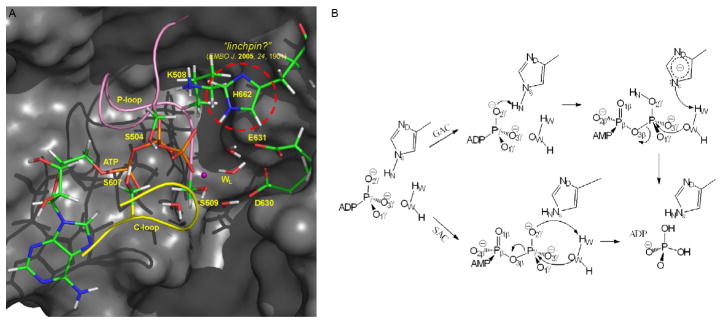
Despite a wealth of information accumulated from sequence analyses (Geourjon et al., 2001) as well as from biochemical and structural characterizations (Zaitseva, Holland, & Schmitt, 2004; Zaitseva, Jenewein, Jumpertz, et al., 2005; Zaitseva, Jenewein, Wiedenmann, et al., 2005; Zaitseva et al., 2006), the precise mechanism of ATP hydrolysis in HlyB remains unavailable. Like many members of ABC transporters, HlyB has a pair of NBD active sites that contain a collection of highly conserved sequence motifs (Fig. 2A), including the Walker A motif (or P-loop: GXXXXGKST, for phosphate tail binding) and the Walker B motif (ϕϕϕϕD, for Mg²⁺ binding), the signature-loop (or C-loop: LSGGQ, from the opposite subunit), a conserved Glu (E631, immediately following the Walker B motif ), and the H-loop that contains a His (H662) (Zaitseva, Jenewein, Jumpertz, et al., 2005). The functional HylB-NBD dimer adopts a “head-to-tail” arrangement such that each of the two ATP molecules bound at the dimer interface is sandwiched between the P-loop of one subunit and the C-loop of the other subunit.

Fig. 2.

(A) Active site of HlyB-NBD. In the “mechanical linchpin” proposal, H662 holds active site residues at their catalytically competent configurations. (B) Proposed enzyme mechanisms for ATP hydrolysis in ABC transporters. In the GAC mechanism, H662 serves as a “chemical linchpin” that explicitly participates in catalysis by providing proton relay. By contrast, in the SAC mechanism, a proton is directly transferred from the catalytic water to the γ-phosphate of ATP.

2.4 Is H-Loop His a “Chemical Linchpin”?

Unlike the relatively well-defined role of the Walker motifs, the role of the H-loop His (H662 in HlyB) in catalysis has remained elusive. The H-loop His is located in the switch II region of HlyB-NBD (Schmitt, Benabdelhak, Blight, Holland, & Stubbs, 2003). Sequence and structural comparisons of ABC transporters and helicases have suggested that the H-loop His may act as a sensor for the γ-phosphate in ATP (Geourjon et al., 2001), therefore reminiscent of the conserved Gln in RecA (Story & Steitz, 1992). Mutagenesis studies showed that the mutation of this H-loop His to Ala (H662A) reduces the ATPase activity of the NBD in HlyB to background levels (<0.1% residual ATPase activity) (Zaitseva et al., 2004; Zaitseva, Jenewein, Jumpertz, et al., 2005). The hydrogen bonding interactions between the H-loop and the P-loop within the same NBD as well as the D-loop (SALD) in the opposite NBD suggest roles of H662 in ATP binding and in conformational signaling across the NBD dimer interface (Zaitseva, Jenewein, Jumpertz, et al., 2005). Based on a crystal structure of ATP/Mg²⁺ bound dimeric NBDs of HlyB that contains Ala mutation at the position of H662, Schmitt and coworkers proposed that H662 and E631 form a catalytic dyad, in which the H662 acts as a “linchpin” (Fig. 2A) that holds other active site residues at their catalytically competent configurations (Zaitseva, Jenewein, Jumpertz, et al., 2005).

One key question we asked is whether the H-loop His can explicitly participate in the enzyme mechanism, by acting as a “chemical linchpin” (Zhou, Ojeda-May, & Pu, 2013). Specifically, two different hydrolysis mechanisms may exist (Fig. 2B). In the first mechanism, which is referred to as the general acid catalysis (GAC) mechanism, the H662 initially serves as a general acid by donating its proton at the N_ε position to the γ-phosphate of ATP and subsequently accepts a proton from the lytic water. The second mechanism utilizes substrate-assisted catalysis (SAC) (Zaitseva, Jenewein, Jumpertz, et al., 2005). The two mechanisms differ in the role of the H-loop H662 residue: in the GAC mechanism H662 explicitly participates in catalysis through proton relay, whereas in the SAC mechanism a direct proton transfer takes place in the presence of a spectator H662.

To provide quantitative answers to the questions concerning ATP hydrolysis in ABC transporters, free energy requirements need to be examined for various catalytic mechanisms in different active sites. To date, the majority of work done in simulating ABC transporters is based on classical mechanical force fields (Jones, O’Mara, & George, 2009; Li, Wen, Moradi, & Tajkhorshid, 2015; Moradi & Tajkhorshid, 2013; Oloo, Kandt, O’Mara, & Tieleman, 2006; Weng, Fan, & Wang, 2010). Classical mechanical simulations, however, are not suitable for studying enzyme mechanisms in ABC transporters due to involvement of bond rearrangements during catalysis. Combined QM/MM (Gao & Thompson, 1998; Warshel & Levitt, 1976) methods provide an especially appealing approach in closing this gap. In QM/MM treatment of enzymes, a small-sized reactive subsystem containing active site molecules is described by QM, and the rest of the system, including nonreactive protein fragments and bulk solvent, is modeled by efficient MM force fields. Despite the popularity of the method, QM/MM had not been applied to simulating any ABC-transporter system only until recently by our group.

3. QM/MM SIMULATIONS OF THE ABC-TRANSPORTER HlyB

3.1 QM/MM Potential Energy Study of ATP Hydrolysis in HlyB

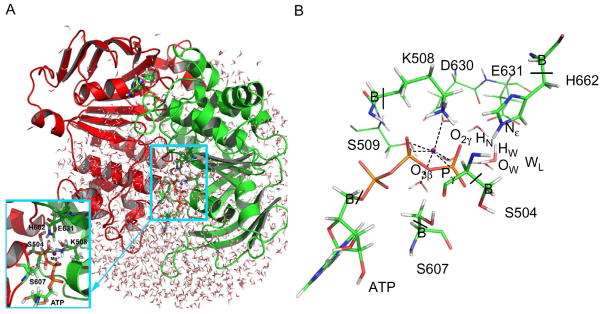
In our recent study (Zhou et al., 2013), we have examined both the GAC and SAC mechanisms (see Fig. 2B for definition) for ATP hydrolysis in HlyB-NBD by QM/MM potential energy calculations. The computer model was constructed based on two crystal structures of E. coli HlyB (PDB: 1XEF and 2FGK). The HlyB-NBD dimer was solvated in a water sphere with a radius of 30.4 Å (Fig. 3A). The selected active site is partitioned into two regions (see Fig. 3B). The QM region, described by the semiempirical AM1 (Dewar, Zoebisch, Healy, & Stewart, 1985) Hamiltonian, consists of the three phosphate groups of ATP, side chains of S504, K508, and H662, the side chain of S607 in the opposite monomer, the lytic water, and five boundary carbon atoms that are treated by the generalized hybrid orbital (GHO) method (Gao, Amara, Alhambra, & Field, 1998; Pu, Gao, & Truhlar, 2004) (Fig. 3B). The MM region, described by the CHARMM22 (MacKerell et al., 1998) force field with CMAP corrections (MacKerell, Feig, & Brooks, 2004), contains the rest of the system. The CHARMM program (Brooks et al., 2009) was employed for both the system setup and QM/MM energy calculations.

Fig. 3.

(A) Simulation setup for studying ATP hydrolysis mechanism in HlyB. (B) QM/MM partition of the active site of HlyB (“B” refers to QM boundary atoms treated by the GHO method). Reproduced from Zhou, Y., Ojeda-May, P., & Pu, J. (2013). H-loop histidine catalyzes ATP hydrolysis in the E. coli ABC-transporter HlyB. Physical Chemistry Chemical Physics, 15, 15811, doi: 10.1039/C3CP50965F with permission from the PCCP Owner Societies.

3.2 GAC Mechanism Identified as the Operative Mechanism

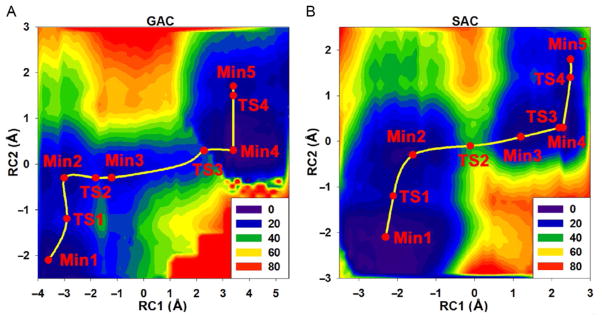
In the same study (Zhou et al., 2013), we obtained two-dimensional (2D) QM/MM potential energy surfaces (PESs) for both the GAC and SAC mechanisms (Fig. 4). For the GAC mechanism (Fig. 4A), RC1 represents a proton relay reaction coordinate (RC) involving the H-loop residue H662. For the SAC mechanism (Fig. 4B), RC1 describes a direct proton transfer (RC1=O_W–H_W – H_W–O_2γ). The phosphoryl transfer reaction coordinate RC2 in both mechanisms is the difference between the O_3β–P_γ and P_γ–O_w bond distances. Based on the reaction pathways identified on these 2D QM/MM PESs, we found that the highest barrier in the GAC mechanism is only 22.1 kcal/mol (GAC:TS3). By contrast, the SAC mechanism gives a substantially higher barrier of 32.1 kcal/mol (SAC:TS2). These results suggest that the GAC mechanism, which involves H-loop assisted proton relay, is energetically more favorable than the direct proton transfer pathway in the SAC mechanism.

Fig. 4.

2D potential energy surfaces (AM1/CHARMM) of ATP hydrolysis catalyzed by HlyB-NBD: (A) the GAC and (B) the SAC mechanisms. The highest barrier found in the GAC mechanism (22.1 kcal/mol; GAC:TS3) is substantially lower than that in the SAC mechanism (32.1 kcal/mol; SAC:TS2). Reproduced from Zhou, Y., Ojeda-May, P., & Pu, J. (2013). H-loop histidine catalyzes ATP hydrolysis in the E. coli ABC-transporter HlyB. Physical Chemistry Chemical Physics, 15, 15811, doi: 10.1039/C3CP50965F with permission from the PCCP Owner Societies.

3.3 QM/MM Minimum Free Energy Path Study of HlyB Using the String Method

To incorporate entropic effects, we have recently obtained QM/MM free energy profiles for both the GAC and SAC mechanisms (Zhou, Ojeda-May, Nagaraju, & Pu, 2016). By employing the finite temperature string method (Maragliano, Fischer, Vanden-Eijnden, & Ciccotti, 2006), we represented minimum free energy paths (MFEPs) by discrete images that connect the reactant and product states based on a set of collective variables (CVs) (Zhou et al., 2016). After mean forces of the free energy with respect to the CVs were determined from restrained QM/MM molecular dynamics (MD) simulations, steepest descent dynamics was carried out to minimize the free energy path. To prevent images along the path from falling into the nearest minima, the reparametrization step was performed to evenly distribute the images along the path (Maragliano et al., 2006). The minimization/reparametrization cycles were repeated until the string paths converge. This QM/MM MFEP study confirmed our earlier conclusion based on QM/MM PESs. We found that the overall free energy of activation for the SAC mechanism is about 10 kcal/mol higher than that for the GAC mechanism (Zhou et al., 2016), supporting our “chemical linchpin” proposal (Zhou et al., 2013).

4. COMPUTATIONAL CHALLENGES

While our exploratory QM/MM simulations provided valuable new insights into the enzyme mechanism in ABC transporters, the computational accuracy needed for characterizing functional asymmetry in dimeric NBDs remains to be achieved. As we explain below, quantitatively reliable QM/MM free energy simulations of enzymatic ATP hydrolysis have posed a grand challenge to existing methods in computational enzymology. Consequently, development of new cost-effective QM/MM approach is highly desirable.

4.1 Quantum Mechanics and Statistical Sampling: Can One Avoid the Other?

Hydrolysis of ATP (or guanosine triphosphate, GTP) is an important subject that has been investigated extensively by computation in the past for many non-ABC transporter systems [see a recent review by Warshel and coworkers (Kamerlin, Sharma, Prasad, & Warshel, 2013) and references therein]. Reliable free energy simulations of enzymatic ATP hydrolysis, however, require sufficient statistical sampling on an accurate QM PES. Such a requirement makes combined QM/MM (Gao & Thompson, 1998; Warshel & Levitt, 1976) an attractive approach, with which the enzyme active site can be treated by QM, and the rest of the protein plus bulk solvents by efficient MM.

In terms of sampling the configuration space, although PES scans can be used to quickly explore the major features of the reaction mechanism, such potential energy information is often considered unreliable due to the lack of entropic contributions and has been associated with various pitfalls in enzyme simulations (Klahn, Braun-Sand, Rosta, & Warshel, 2005). Reliable results can be obtained by sampling the system, often along a few selected RCs, using MD simulations, based on which proper ensemble averages can be made. For reaction mechanism studies, this can be done by using umbrella sampling (Torrier & Valleau, 1974) or MFEP techniques, such as the finite temperature string method (E, Ren, & Vanden-Eijnden, 2005; Maragliano et al., 2006).

For the choice of the QM method in QM/MM, although ab initio molecular orbital (Hehre, Radom, Schleyer, & Pople, 1986) methods and density function theory (DFT) (Parr & Yang, 1994), here collectively referred to as ab initio QM (AI) methods, are considered more accurate and reliable, the computational costs associated with AI/MM calculations preclude these simulations to be performed with sufficient statistical sampling. Even aided with extended Lagrangian (EL) techniques, such as Car-Parrinello (Car & Parrinello, 1985) and density matrix propagation (Schlegel et al., 2002) MD, which eliminate self-consistent iterations of solving the Schrödinger equation, directly sampling AI/MM PESs for extended period of time (eg, ns and beyond), as conventionally done in pure molecular mechanical simulations, remains practically infeasible.

By contrast, semiempirical QM (SE) methods (Thiel, 2014) are several orders of magnitude more efficient than AI methods. Their efficiency stems from the use of simplified electronic integrals under the neglect of diatomic differential overlap approximation (Pople, Santry, & Segal, 1965) as well as the use of minimal basis sets. In spite of being considered less reliable, SE methods have been widely used in combined QM/MM simulations, with which moderate sampling of the reactive systems becomes feasible. For example, one- or two-dimensional potential of mean force (PMF) free energy profiles can be routinely obtained through umbrella sampling simulations at SE/MM levels (Garcia-Viloca, Truhlar, & Gao, 2003; Poulsen, Garcia-Viloca, Gao, & Truhlar, 2003).

When both accuracy and efficiency are demanded, one is facing with a dilemma of choosing between them. Ideally, one would like to conduct umbrella sampling or MFEP simulations on an AI/MM surface for its reliability. However, such a combination is often computationally prohibitive. To illustrate the magnitude of this challenge, we tabulate in Table 1 the computational costs for QM/MM simulations of ATP hydrolysis in HlyB by using various methods. For simulating HlyB-mediated ATP hydrolysis, both proton transfer and phosphoryl transfer RCs are needed; explicit inclusion of more than two RCs becomes impractical in umbrella sampling simulations, but can be done by using the string method, which optimizes MFEPs on the basis of multidimensional CVs (Maragliano et al., 2006; Rosta, Nowotny, Yang, & Hummer, 2011).

Table 1.

Computational Costs for Various Combinations of QM/MM and Sampling Methods Based on Stochastic Boundary Simulations of ATP Hydrolysis in the HlyB System, Which Consists of ~60 QM Atoms and ~13,600 MM Atoms

QM Method in QM/MM	Ncpu	SPEa	MD (200 ps)b	2D-PES scanc	2D-USd	String MFEPe
AM1f	1	0.9 s	2 days	1 days	10 days	10 days
AM1/d-PhoTf	1	1.5 s	3.5 days	2.5 days	17.5 days	18 days
HF/6–31Gg	16	1.5 m	202 days	125 days	2.7 years	2.7 years
B3LYP/6–31+G (d,p)g	16	7.0 m	2.7 years	1.6 years	13.5 years	13.5 years

^aSPE denotes single-point energy.

^b200,000 time steps.

^cPotential energy scan for ~5,000 configurations.

^dUS denotes umbrella sampling; 400 windows in parallel, each with 500 ps sampling.

^eMinimum free energy paths (MFEP) using the string method; 25 images in parallel, each with 20 ps sampling for mean force evaluation; 50 cycles of string path optimizations.

^fSE(-SRP)/MM methods.

^gAI/MM methods, for which b–e (numbers in bold) are rough estimates, based on their SPE costs and ratios of the costs of these calculations in AM1 with respect to the corresponding AM1 SPE cost.

From Table 1, we can see that attempts of using AI/MM methods to simulate ATP hydrolysis in a typical ABC-transporter system are infeasible with commonly available computing resources. Although employing the EL techniques (Car & Parrinello, 1985; Schlegel et al., 2002) can alleviate the problem, these techniques unlikely resolve the computational dilemma outlined earlier; the speedup of using ELMD would become less significant when smaller integration steps are used to maintain adiabatic separation between the electronic and nuclear degrees of freedom. To break even, parallel AI/MM MD simulations need to be accelerated by about three orders of magnitude.

Ideally, however, one would like to perform sampling at the cost of SE/MM methods (which take ~10 days to complete the free energy profile for the HlyB system; see Table 1) to achieve the accuracy of AI/MM. In practice, this goal can be realized, at least in part, by improving SE with specific reaction parameters (SRPs) (Gonzalez-Lafont, Truong, & Truhlar, 1991). Optimization of SRPs for an SE method typically involves one or more of the following steps: (a) construct a training set of gas-phase molecular models that mimic the actual reactive systems; (b) obtain benchmark data, such as reaction energies, barrier heights, proton affinities, vibrational frequencies, atomic charges, dipole moments, geometries, etc., from AI calculations (or from experiments if AI is inaccurate), based on the geometries of stationary species, such as separate reactants/products, reactant/product complexes, and transition states, optimized at the corresponding AI level; (c) adjust selected parameters in the SE method such that the resulting SE-SRP method satisfactorily reproduces the AI results; and finally (d) apply the SE-SRP method to gas-phase or condensed-phase dynamics simulations.

The case study presented here led us to conclude that the practical solution to meet the competing demands for accuracy and efficiency in enzyme simulations of ABC transporters is to use SE(-SRP)/MM methods in conjunction with MFEP samplings. However, as we will show below, the existing SE(-SRP) methods have their own limitations.

4.2 Existing SE(-SRP) Methods Are Not Reliable for Simulating ATP Hydrolysis

The standard parametrizations of popular SE methods, such as AM1, are generally considered unreliable for studying phosphoryl transfer reactions, owing to the empirical nature of its Gaussian treatment of core–core repulsion and the lack of d-orbital description (Lopez & York, 2003). Artificial stabilization of pentacovalent phosphorane intermediates has been reported when AM1 was used to study model reactions for RNA catalysis (Lopez & York, 2003; Nam, Cui, Gao, & York, 2007). There are several SE-SRP methods aimed at improved performance for biological phosphoryl transfers, by including d-orbitals and/or specific parametrizations. Examples of such SE-SRP methods include MNDO+G-SRP (Arantes & Loos, 2006) and AM1/d-PhoT (Nam et al., 2007). Most of these methods were optimized with a training set of data primarily composed of monophosphate esters, which are considerably different from biological phosphate anhydrides, such as ATP. Data in Table 2 provide a glimpse of the challenge of using these existing SE(-SRP) methods to study ATP hydrolysis, based on the reaction energy of hydrolyzing methyl triphosphate (MTP), which serves as a reasonable model for ATP hydrolysis:

Table 2.

Reaction Energy of MTP Hydrolysis from SE(-SRP) and AI Methods^a

Method	ΔE (H2O Attack)	ΔE (OH− Attack)
AM1	−168.1	−103.2
MNDO+G-SRP	−144.1	−89.7
AM1/d-PhoT	−152.4	−90.7
DFTb	−168.0	−103.5
DFT+PCM solvation	−8.6	−25.1

^aSE method: AM1; SE-SRP methods: MNDO+G-SRP and AM1/d-PhoT; AI method: DFT (see footnote b); reaction energies (ΔE) are in kcal/mol and calculated in the gas phase (except data in the last row) without Mg²⁺.

^bB3LYP/6–31+G(d,p).

Table 2 shows that when SE or SE-SRP methods optimized for other chemical situations are used to study ATP hydrolysis, extra care needs to be taken. Both AM1/d-PhoT and MNDO+G-SRP display large errors (15–25 kcal/mol) in reaction energies compared to the DFT benchmark results. Although AM1 seems to agree with the DFT method for the reaction energy of MTP hydrolysis, the agreement relies more on fortuitous error cancelation in AM1, rather than indicating that AM1 is reliable.

5. A MULTISCALE QM/MM METHOD: RP–FM

The analyses in Section 4 suggest that although SE/MM should be chosen over AI/MM for sampling efficiency, currently available SE methods, including those special-purpose SE-SRP methods obtained using the traditional gas-phase fitting procedures, are unlikely to provide the accuracy and reliability needed for determining the ATPase mechanism in ABC transporters. To address this challenge, we recently introduced a new multiscale strategy for reparametrizing SE-SRP within the framework of QM/MM free energy simulations. The new method enables iterative refinements of a selected SE method by fitting accurate forces from AI/MM calculations along reaction paths. Because reaction paths are always sampled at efficient SE-SRP/MM levels, direct sampling of the expensive AI/MM surface is avoided.

5.1 Overall Strategy

The stationary-point-based gas-phase SE-SRP fitting procedure outlined in Section 4.1 may suffer from several limitations. First, only a very limited amount AI data are used for SRP fitting. Second, transferability of SRPs relies on the hope that the gas-phase model systems closely resemble the condensed-phase systems. Third, gas-phase properties may be over-represented in acquiring SRPs. For MTP hydrolysis, the gas-phase reaction energy is −168.0 kcal/mol (Table 2), in comparison with a reaction free energy of −8.6 kcal/mol in solution [based on PCM solvation (Miertus, Scrocco, & Tomasi, 1981)]. This difference highlights the importance of taking solvation free energy changes into account when fitting SRPs for this reaction. In addition, conformations of molecules can change significantly from the gas phase to condensed phases. For example, the β- and γ-phosphates in GTP tend to adopt a staggered configuration in the gas phase and in water but are often found in the eclipsed configuration when bound in enzyme active sites especially when Mg²⁺ is present (Rudack, Xia, Schlitter, Kotting, & Gerwert, 2012).

Due to these reasons, more robust SE-SRP fitting is expected when condensed-phase samples are taken into account. Given that directly sampling AI/MM PESs in condensed phases is such a formidable task, an alternative strategy is to parametrize SE-SRPs based on condensed-phase reaction-path configurations sampled at efficient SE/MM levels (Zhou & Pu, 2014). In addition, we employed the force matching technique (Arkin-Ojo, Song, & Wang, 2008; Csanyi, Albaret, Payne, & De Vita, 2004; Doemer, Maurer, Campomanes, Tavernelli, & Rothlisberger, 2014; Ercolessi & Adams, 1994; Izvekov, Parrinello, Burnham, & Voth, 2004; Izvekov & Voth, 2005; Knight, Maupin, Izvekov, & Voth, 2010; Laio, Bernard, Chiarotti, Scandolo, & Tosatti, 2000; Maurer, Laio, Hugosson, Colombo, & Rothlisberger, 2007) pioneered by Voth and coworkers (Izvekov et al., 2004; Izvekov & Voth, 2005; Knight et al., 2010) for SRP optimization, so that the resulting SE-SRP method reproduces the atomic forces computed at a selected target AI/MM level. Because of the combined use of reaction path (RP) and force matching (FM) techniques in our approach, we named this method as Reaction Path–Force Matching (RP–FM) (Zhou & Pu, 2014).

The RP–FM method can be viewed as repetition of a two-stage process. In the RP stage, an ensemble of configurations along a specific reaction path are collected using SE/MM simulations; examples of such reaction paths include minimum energy paths (MEPs) [or paths along the intrinsic reaction coordinate (IRC) (Fukui, 1981)] and MFEPs obtained by the string method (E et al., 2005; Maragliano et al., 2006). In the subsequent FM stage, the SE-SRP method is calibrated against the target AI/MM method through force matching. Once the AI/MM forces on the selected atoms are reproduced, the resulting SE-SRP method is used to resample the configuration space to obtain a new pool of reaction-path configurations for the next iteration of force matching. The cycle of “reaction-path configuration sampling” (predictor) and “force matching” (corrector) is repeated iteratively until convergence is established.

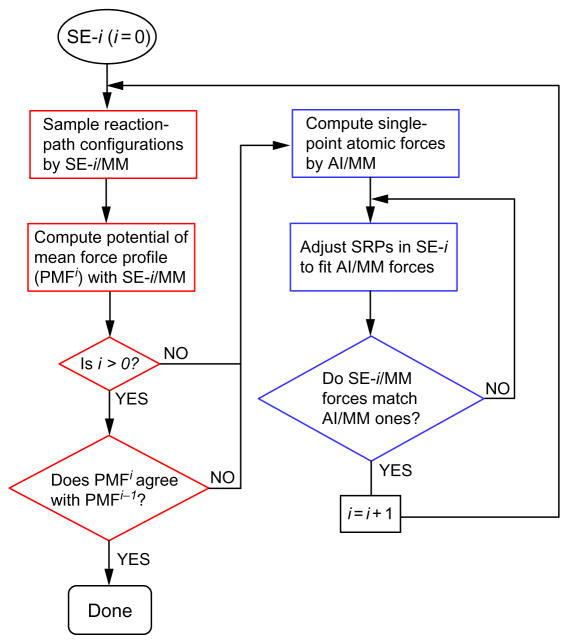
5.2 Generic Procedure

A generic procedure for implementing RP–FM within the QM/MM framework is illustrated in Fig. 5. In this flowchart, the steps associated with the RP and FM stages are grouped in the red and blue boxes, respectively. For convenience, we define the union of a RP stage and the FM stage that immediately follows as a single RP–FM cycle, based on which iterations are carried out. For the initial SE method, referred to as SE-0, we assign a token iteration, ie, “iteration 0.” For each time a single RP–FM cycle is completed, the iteration number is increased by 1. As a convention, the SE-SRP method obtained at the end of the ith RP–FM iteration is labeled as SE-i, which will be used to update the reaction-path configurations in the next iteration. In our notation, we define the reaction path sampled consistently on the SE-i/MM PES as the SE-i path. Following the same convention, we label the PMF profile determined from the SE-i/MM simulations as PMFi, which can be used to monitor convergence.

Fig. 5.

Flowchart of a generic procedure for implementing RP–FM. Reprinted with permission from Zhou, Y., & Pu, J. (2014). Reaction path-force matching: A new strategy of fitting specific reaction parameters for semiempirical methods in combined QM/MM simulations. Journal of Chemical Theory and Computation, 10, 3038–3054. Copyright (2014) American Chemical Society.

5.3 Case Study: Proton Transfer

In a proof-of-concept study (Zhou & Pu, 2014), we have demonstrated the feasibility of the RP–FM method for a proton transfer reaction between ammonium (NH₄ ⁺) and ammonia (NH₃). The Hartree–Fock (HF) (Roothaan, 1951) and PM3 (Stewart, 1989) methods were selected as the target AI and SE levels, respectively. The PM3 method has been shown to overestimate the barrier height for this reaction by ~9 kcal/mol compared to HF/3–21G (Mo & Gao, 2000).

5.3.1 QM/MM Setup and Computer Programs

For a QM/MM treatment of the system, the solute molecules are treated by QM (nine QM atoms) at either the PM3 or HF/3–21G level and a box (40 Å in size) of solvent molecules are represented by the modified TIP3P model (Brooks et al., 1983). The MNDO97 (Thiel, 1998) package incorporated in the CHARMM (Brooks et al., 2009) program was used for PM3 (-SRP)/MM calculations. The Q-Chem (Shao et al., 2006) program combined with CHARMM was used for AI/MM single point force calculations. For force matching, a local code of microgenetic algorithm (μGA) (Carroll, 1998) was employed to minimize the mean force deviation between the SE-SRP/MM and target AI/MM levels; a total of 21 SE parameters in PM3 were adjusted for N and H (Zhou & Pu, 2014).

5.3.2 RP-FM Based On Gas-Phase Reaction Path

For testing purpose, the RP–FM method was first employed to parametrize PM3 along a gas-phase reaction path (Zhou & Pu, 2014). In this case, we chose to fit AI (HF/3–21G) forces along MEP; this represents the “zero-temperature” version of the algorithm. The MEP was determined approximately based on a RC defined as RC=r(N⁺–H)−r(N–H). Restrained geometry optimizations were carried out to scan the PES along RC in the range of 0.0–0.8 Å, resulting in an MEP of nine configurations. Fig. 6A shows the potential energies along MEPs optimized during five RP–FM iterations. The HF single point energy (SPE) profile calculated based on the PM3-n path (ie, HF/3–21G // PM3-n) are also shown for comparison; these “double-slash” profiles are labeled “HF-n.”

Fig. 6.

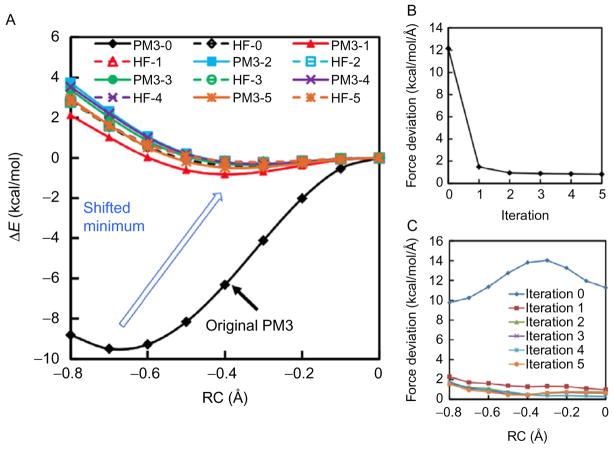
Gas-phase RP–FM applied to proton transfer between ammonium and ammonia: (A) Energy profiles along MEPs of PM3-SRPs optimized using the RP–FM procedure against atomic forces obtained at the HF/3–21 level; (B) Average force deviations between PM3-SRPs and HF/3–21G over RP–FM iterations; and (C) Force deviations decomposed to individual configurations along MEP. Reprinted with permission from Zhou, Y., & Pu, J. (2014). Reaction path-force matching: A new strategy of fitting specific reaction parameters for semiempirical methods in combined QM/MM simulations. Journal of Chemical Theory and Computation, 10, 3038–3054. Copyright (2014) American Chemical Society.

It can be seen from Fig. 6A that the reaction barrier height given by the original PM3 (PM3-0) is 9.5 kcal/mol, which is substantially higher than the barrier of 0.2 kcal/mol given by the corresponding HF/3–21 energy profile (HF-0). After the first RP–FM iteration, the new PM3 energy profile (PM3-1) is in a closer agreement with the associated HF SPE profile (HF-1). Such agreements are steadily improved over RP–FM iterations. After five iterations, the optimized PM3-SRP energy files (PM3-5) and the energy profile at the target level (HF-5) are almost identical. The RP–FM procedure also successfully shifts the product complex minimum from RC=0.7 Å, located on the original PM3 path, to RC=0.3 Å as determined on the HF/3–21 path. As a result, both height and shape of the HF/3–21G barrier are reproduced at the optimized PM3-SRP level.

The force deviations between the SE-SRP and AI levels are displayed in Fig. 6B. The original PM3 yields an average force deviation of 12 kcal/mol/Å per Cartesian coordinate; the deviation is successfully reduced to ~2 kcal/mol/Å after the first round of force matching and stabilizes at <1 kcal/mol/Å during the rest of RP–FM iterations.

Decompositions of the force deviations to individual configurations are shown in Fig. 6C. Our first observation is that the deviations between the PM3 and HF/3–21G forces vary along the MEP. For the PM3-0 method, the transition state (TS) configuration (RC=0.0 Å) gives a force deviation of 11.3 kcal/mol/Å per Cartesian coordinate, which is slightly higher than that of 10.3 kcal/mol/Å at the reactant configuration (RC=−0.7 Å); a maximal force deviation of 14.0 kcal/mol/Å is found at a nonstationary structure (RC=−0.3 Å). After RP–FM optimization, excellent agreements were obtained between the PM3-SRP and HF/3–21G forces on all configurations; force deviations were reduced to <1.5 kcal/mol/Å throughout the MEP.

5.3.3 RP–FM for Solution-Phase Proton Transfer

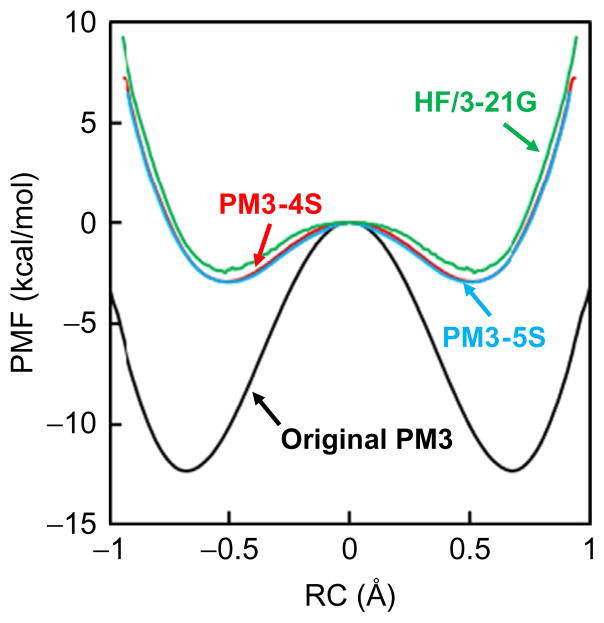
We have also applied the RP–FM method for the same proton transfer in solution (Zhou & Pu, 2014). Umbrella sampling (Torrier & Valleau, 1974) simulations were used to sample along the reaction path on the PM3-SRP/MM PES; seven umbrella windows were placed between the reactant and the transition state. PMF profiles were determined by the weighted histogram analysis method (Kumar, Bouzida, Swendsen, Kollman, & Rosenberg, 1992). For each window, 10 configurations were randomly selected over 200 ps of PM3-SRP/MM MD simulations, resulting in 70 configurations that correspond to 1,890 Cartesian force components for force matching. The PMFs obtained from solution-phase RP–FM, referred to as PM3-iS, are shown in Fig. 7, where the PMF determined separately at the HF/3–21G level (with shorter sampling of 10 ps/window) is also shown for comparison. One can see from Fig. 7 that although initially the original PM3 PMF differs substantially from the HF/3–21G PMF, the RP–FM optimization dramatically improves the agreement between the two levels. At the end of the fifth RP–FM iteration, PMFs obtained for PM3-5S and HF become essentially identical.

Fig. 7.

PMFs of solution-phase proton transfer between ammonium and ammonia obtained from PM3-SRPs/MM and benchmark HF/3–21G/MM simulations; PM3-SRP methods were optimized by RP–FM in solution to reproduce atomic forces at the HF/3–21 level.

5.4 Relation to Other Methods

Before we conclude, we discuss the differences between RP–FM and other related methods. The FM technique has been employed in the QM/MM context by others (Arkin-Ojo et al., 2008; Csanyi et al., 2004; Maurer et al., 2007). These investigations, however, focused on using QM/MM as a target level to fit MM force fields or empirical potentials. By contrast, RP–FM is designed to simulate chemical and enzymatic reactions involving bond rearrangements, for which classical potentials cannot be used. The RP–FM method, in spirit similar to the pioneering work of Voth and coworkers (Knight et al., 2010), matches forces between a tailored reactive potential and a reference QM potential. In the force-matched multistate empirical valence bond (FM-MS-EVB) method developed by Voth and coworkers, the reactivity of the tailored potential is introduced through a reactive force field (Knight et al., 2010). In our RP–FM approach, the SE potential being tailored is instead an electronic structure-based QM potential. A “reactive” scheme is employed in RP–FM so that forces at the two QM levels are matched along reaction paths. The combined use of QM/MM methods in both the tailored and reference potentials and force fitting along reaction paths makes RP–FM a distinctive approach that enables multiscale “reactive” force matching.

The RP–FM method also differs from the “learn-on-the-fly” (LOTF) approach (Csanyi et al., 2004) in that the tailored potentials in the LOTF approach are empirical functions made “reactive” by employing time-dependent parameters, whereas in RP–FM we parametrize a true QM potential using semiglobal force fitting along reaction path. The LOTF method has been demonstrated for simulating diffusion of point defects on solid surfaces, whereas RP–FM has a focus on simulating solution-phase and enzymatic reactions.

The iterative nature of fitting the force and resampling the PES in our work resembles the spirit of the optimal potential (OP) method (Laio et al., 2000) in solid-phase simulations and that of the adaptive force matching method developed by Wang and coworkers (Arkin-Ojo et al., 2008). A similar adaptive potential refining procedure has also been employed in the “paradynamics” method pioneered by Warshel and coworkers (Plotnikov, Kamerlin, & Warshel, 2011; Plotnikov & Warshel, 2012), in which EVB potentials in conjunction with Gaussian-type corrections are parametrized against QM/MM data in the free energy perturbation framework.

6. CONCLUDING REMARKS

In this chapter, we have discussed recent progress in QM/MM simulations of ATPase mechanism in ABC transporters and how the challenges in these simulations fertilize the development of the multiscale RP–FM method. As a paradigm molecular motor system, ABC transporter may have evolved to couple ATP hydrolysis with conformational dynamics through functional asymmetry encoded in its dimeric active sites. Although our exploratory QM/MM simulations have provided exciting new insights into the related enzyme mechanism, conducting such simulations in a quantitatively reliable manner to achieve the ab initio QM/MM accuracy has remained a challenging task. The RP–FM method has been developed to offer a multiscale solution to the challenge. We have successfully demonstrated the effectiveness of this approach in modeling a proton transfer reaction in the gas phase and in solution. To achieve the ultimate goal of determining ATPase mechanism in ABC transporters by RP–FM, the next step is to validate the method on more complex reactions such as solution-phase ATP hydrolysis and a number of well-characterized enzymatic reactions; these investigations are underway.

As we have discussed in this chapter, the RP–FM strategy aims at resolving the dilemma of choosing between accuracy and efficiency in QM/MM simulations, which is a long-standing challenge in computational enzymology. Therefore, development of the RP–FM method is expected to provide not only a feasible way to characterize ATP hydrolysis in ABC transporters but also a general tool for chemical and enzyme simulations in condensed phases.