Integrated PK-PD and Agent-Based Modeling in Oncology

Abstract

Mathematical modeling has become a valuable tool that strives to complement conventional biomedical research modalities in order to predict experimental outcome, generate new medical hypotheses, and optimize clinical therapies. Two specific approaches, pharmacokinetic-pharmacodynamic (PK-PD) modeling, and agent-based modeling (ABM), have been widely applied in cancer research. While they have made important contributions on their own (e.g., PK-PD in examining chemotherapy drug efficacy and resistance, and ABM in describing and predicting tumor growth and metastasis), only a few groups have started to combine both approaches together in an effort to gain more insights into the details of drug dynamics and the resulting impact on tumor growth. In this review, we focus our discussion on some of the most recent modeling studies building on a combined PK-PD and ABM approach that have generated experimentally testable hypotheses. Some future directions are also discussed.

Introduction

Mathematical modeling and computer simulation has increasingly gained popularity as a toolset for studying the mechanisms underlying carcinogenesis [1]. It has a wide range of applications that include predicting chemotherapeutic drug delivery, discovering potential drug targets, and simulating tumor growth and progression behaviors, among many others [2–4]. In particular, mathematical models allow scientists to gain insights into factors not easily observed in wet lab experiments, such as how cell-cell interactions influence the phenotypic transitions of neighboring cells on the individual cell level instead of a cell population level, as often observed in vitro. Many modeling approaches have been investigated and developed over the past two decades within the field of cancer research, including pharmacokinetic-pharmacodynamic (PK-PD) modeling [5–7], agent-based modeling (ABM) [8–13], hybrid modeling [14,15], and multiscale modeling [16]. Each approach has advantages and disadvantages, and the correct method must be chosen to gain the insight the modeler is searching for (see [17–19] for a detailed discussion on these topics). As modeling approaches become more advanced, hybrid models containing more than one approach have emerged, allowing for increasingly intricate descriptions of tumor cells and their environment.

PK-PD modeling is comprised of pharmacokinetics (PK), the study of the body’s effect on drug molecules, and pharmacodynamics (PD), the effect of drug molecules on the body. This modeling approach has become increasingly important especially in preclinical trials to support drug discovery and determine optimal dosing strategies. Thus far, the majority of current PK-PD models consists of systems of ordinary differential equations that describe the temporal response of a population (or multiple populations) of tumor and normal cells to a given therapeutic drug [5–7,20,21]. However, cancer is widely known as a heterogeneous entity (with regions of hypoxia, necrosis, quiescence, and proliferation) whose growth depends also on the changing microenvironment (such as oxygen, glucose, and pH gradients) and irregular vasculature structure [22]. Drug resistance sometimes occurs due to limited penetration of effective quantities of chemotherapeutic drugs deep into the tumor, caused by the fact that drug transport is mainly restricted to diffusion [23]. This implies that not only “time” but also “space” factors should be taken into account when investigating drug effects on the tumor. In this perspective, the PK-PD approach coupled with spatiotemporal tumor modeling is potentially more suitable for exploring drug dynamics and the resulting impact on tumor growth.

In this paper, we present a review of recent advances in PK-PD modeling integrated with a particular discrete-based modeling approach, i.e., ABM. As further discussed below, this integrated concept can provide modelers with advanced approaches to generate more complete models, which may provide new, additional insights into the details of the cancer system being investigated.

Modeling Methods

Agent-based modeling

ABM has been widely accepted as a useful tool in a variety of cancer research fields [11,12,24–35], as it offers many advantages over other methods in understanding cancer initiation, progression, and invasion mechanisms (for excellent reviews please see [1,17,19]). In particular, it is straightforward to use an ABM to examine the role of diversity in cell populations as well as within each individual cell and to determine the relationship of tumor behaviors between scales. In an ABM (and its variant, cellular automata [36]), each cell is often represented as an agent with unique properties and its own spatial coordinates [8,30,37]. Agents are subject to experimentally-inspired, computationally-coded rules that they must follow, such as two agents may not occupy the same space. Other rules determine agent behaviors and decisions, including if agents will replicate, enter quiescence, experience apoptosis or necrosis, undergo mitosis, or transition into a cancerous phenotype. Modeling each agent individually allows for inclusion of details at the cellular level, such as cell-cell interactions and autocrine and paracrine signaling events. Agents are often simulated in a background environment, where they glean information about their surroundings (including both cellular and environmental elements). An agent will then be able to determine its phenotype for the next step using a variety of computational techniques, ranging from neural network approaches [38], to random phenotypic transitions based on a determined distribution and the agent’s internal and external states [28], and even to include Monte Carlo techniques [39,40], all of which can be conducted in either two or three dimensions in space. Whenever possible, the agents’ decisions are based on experimentally measured data, whether in vitro or in vivo. For example, the concentration or total uptake of a chemotherapy drug necessary to kill a cancer cell can be measured in vitro; the agents query the surrounding environment to detect the local drug concentration: if it is above the known lethal concentration based on experimental results, it enters apoptosis/necrosis. Information such as local oxygen, nutrient, and therapeutic drug concentration are often solved over the large scale background using numerical methods, including, e.g., finite difference [41], alternating direction implicit [42], or finite element methods [43–45]. The combination of different spatiotemporal scales in a model often results in a hybrid model, where multiple modeling techniques (such as discrete and continuum) are combined into one model.

Two methods of spatial representation for agents are commonly used: agents may be placed on a grid (i.e., grid-based), or allowed to move freely (i.e., grid-free), without the restriction of grid alignment [46]. Grid-based models only allow agents to occupy certain places on the grid, such as intersections of grid lines, whereas grid-free models permit agents to move and proliferate in any direction (as determined by the model’s rules), as long as there is sufficient space for the cell. In general, grid-free models allow for more accurate representations of physical cell packing, but may come at a cost of requiring longer simulation times for cells to achieve confluence [46]. These costs, however, are often outweighed by their benefits, including allowing modelers to generate more correct descriptions of physical phenomena. When a cell undergoes mitosis, it results in two smaller daughter cells with reduced radii relative to the parent cell (initially because each daughter is roughly half the volume of the mother, but also to reflect the increase in packing pressure that corresponds to higher cell density). Cells in a grid-based model are uniformly distributed, making the size disparity difficult to describe while maintaining physical contact between agents. In models where mechanical effects, cell-cell adhesion, and crowding are important, off-grid models may therefore be a better choice [47]. However, for grid-based models, these limitations can be overcome by refining the mesh such that it is much smaller than the radius of an agent, without introducing a major computational cost, due to the highly computationally efficient nature of regular meshes [48].

ABM has also been successfully implemented by many research groups to examine the nature of tumor heterogeneity. Diversity in the tumor environment is linked to heterogeneity in the cellular states across the tumor, and ABM provides a convenient method to link this tumor heterogeneity to cellular response. Moreover, ABM is uniquely suited to modeling cellular-level cancer contributors [17], such as genetic mutation, epithelial to mesenchymal transition, cell-cell signaling (including interactions between heterogeneous cells), and individual cellular sensitivity to drug treatment. For example, an ABM work has shown that low genetic mutation rates often lead to tumor homogeneity and angiogenesis lowers competition between tumor cells [49]. Heterogeneous distribution of key signaling molecules may result in heterogeneous cellular states as well. Epidermal growth factor receptor (EGFR) heterogeneity in the tumor environment has been shown to have an impact on growth patterns, with higher EGFR receptor density even leading to transition from a proliferative to metastatic phenotype [50]. This indicates that tumor heterogeneity is a key contributor towards transition to and selection for more aggressive phenotypes, warranting the need for current and future study in this area.

A high degree of usability and widespread applicability of ABM has resulted in the development of a number of dedicated ABM software packages. Commercial software packages include AnyLogic and Matlab, while some of the more popular free packages include NetLogo, MASON, Java Swarm, Objective-C Swarm, and Repast (see [51] for a review). Other modelers prefer to code their own ABM, which is often necessary for implementation of multiscale models, as the computations for all scales considered can be included in one programing language. The many possible packages allow for versatility in implementing an ABM, where each modeler may choose the approach they are most comfortable with.

Pharmacokinetic-pharmacodynamic modeling

As stated before, PK focuses on determining concentration profiles and the fate of drug molecules in the body, while PD examines modifications in the body caused by the drug, which in the case of chemotherapy is desirably cancer cell death and inhibition of tumor growth. Employed heavily in the pharmaceutical industry, the rationale for PK-PD modelling is to quantify dose-response relationships, and subsequently describe and predict the time-course effect resulting from a drug dose [52]. PK-PD modeling often uses a translational approach to combine drug-specific and system-specific pathological, physiological, and pharmacological behavior to gain a more complete description of system response. Properties of model variables are described using a series of ordinary or partial differential equations (ODEs or PDEs), and rate constants are quantified based on experimentally measured values whenever possible. While PK-PD refers specifically to drug molecules, the equations for describing the movement of other small molecules in the body (e.g., oxygen and glucose) and the body’s response to them can be described using similar (if not the same) equations.

Recently, PK-PD techniques have been expanded to describe the mechanistic behaviors of new types of anticancer therapies, such as antibody-drug conjugate molecules. These antibody-drug conjugates likely have more complex behaviors than more traditional drug molecules; PK-PD modeling is being used to unlock these mechanisms. These new approaches have successfully described trastuzumab emtansine (an antibody-drug conjugate (ADC)) efficacy, tumor conjugation, and tumor catabolism in HER2-oxerexpressing BT474EEI murine xenografts [53]. PK-PD modeling of ADCs has been shown to be effective for clinical applications as well, and was even able to predict responses to brentuximab-vedotin in Hodkin’s lymphoma patients [54]. Another group has developed a semi-mechanistic PK-PD model that accurately described therapeutic inhibition of cyclin-dependent kinases 4 and 6 (CDK4/6, which play important functions in cell cycle regulations pathways) by LY2835219 (a potentially antineoplastic CDK4/6 inhibitor) and resultant cell-cycle arrest in murine colo-205 human colorectal xenografts, while also correctly predicting therapeutic efficacy in human melanoma A375 murine xenografts [55]. PK-PD modeling techniques are progressing to describe more complicated drug molecules and molecular signaling pathways, as well as including cell-cycle specific parameters and biomarkers. The PK-PD modeling field is actively growing in exciting directions, including hybridization with other modeling techniques, including ABM. For more information on the clinical directions of PK-PD modeling, the reader is referred to [56].

There is a distinct difference between system-specific and drug-specific mathematical descriptions [57]. In PK-PD modeling, transitional states of drug molecules are determined by using known rate constants (when possible), while rate constants that are not known or not easily determined via experimental means can be tuned through trial and error until they accurately recreate in the model behavior observed in vivo or in vitro. An example of this is drug diffusion from the blood. At the time of bolus drug injection, all drug is in the blood, and the system quickly responds to remove drug from the blood through renal excretion, biliary excretion, and hepatic update, rapidly lowering drug concentration in the blood. For example, high dose range bolus delivery of MTX has a half-life of only 2–3 hours [58]. The total concentration of the compound cannot exceed the amount injected into the system, as a drug molecule could be in the blood, or in the surrounding tissue, but not at both compartments at the same time. Efflux rates from the blood into the tumor are represented by a rate term in the PK-PD equations, and as time progresses during the initial drug treatment period and in the case of continuous drug infusion periods, more chemotherapeutic drug will move from the blood to the tumor. Other rates such as active drug uptake are also modeled, and the series of linked equations in PK-PD models can quickly become very complicated as more factors are included in the model (for an example, the reader is referred to [59]).

The techniques of PK-PD modeling have been successfully implemented to study chemotherapy treatment effects on tumor. The well-known Norton-Simon hypothesis, i.e. that increasing the dose intensity may optimize the treatment effects by reducing tumor regrowth between chemotherapy cycles, was generated by a PK-PD model [60,61], and it was successfully validated in clinical trials later on [62]. More recent examples include prediction of chemotherapy drug efficacy using a murine model, which was later modified to human conditions [6], and a study on the effectiveness of 6-mercaptopurine treatment on acute lymphoblastic leukemia [63] based on a series of ordinary differential equations (ODEs) adapted from Mackey’s work [64]. Both models were calibrated to rate constants reported in the literature and to patient data. PK-PD has also been used to study drug interactions [21] and the effect of immune-stimulatory agents [65], which can often be additive (but may also lead to unintended interactions) as some chemotherapy drugs may stimulate the immune system as well [66]. Although PK-PD modeling is often accomplished through algorithms generated and programmed by the modeler, commercially available software such as ACSLXTREME (AEGIS Technologies) [67] and SAAMII [68] have emerged as modeling options as well, offering a diverse toolset for modelers to choose from.

Integrated ABM and PK-PD modeling

As modeling techniques move forward, hybrid multiscale approaches have emerged that combine attributes from multiple methods and spanning scales from whole tissues to cells, and even down into the molecular and atomic range [17,69]. PK-PD modeling provides information on the larger scale, while ABM functions on the cellular scale. Thus, these two approaches hybridize well (Fig. 1), with the PK-PD model providing information to agents in the ABM and agents contributing to and/or changing the parameters in the PK-PD component.

Figure 1.

Schematic of how PK-PD and ABM approaches can be integrated in order to provide more information than using any approach alone in modeling cancer treatment. Briefly, PK-PD models provide information that can be transformed into computationally-coded rules or thresholds which, in turn, can be used to define how cancer cells change their phenotypes and how drug and cells interact, etc. in an ABM. The ABM can then be used to simulate the time- and space-dependent tumor response to drug treatment and drug dynamics (e.g., drug concentration profile).

Commonly, PK-PD methods are used to model factors such as oxygen, nutrient, and chemotherapy drug influx into a tissue (although O₂ is not a drug, the equations are similar and the numerical methods of solution are the same, i.e. both O₂ and drug move through tissue by way of diffusion); these values are then passed on to the ABM. Agents use this information to make behavioral decisions, based on rules imposed by the modeler. In the case of cancer modeling, the PK portion of a hybrid model is often responsible for computing the chemotherapy drug concentration profile, which is transferred to the agents in the ABM. Each individual agent then decides if it will undergo necrosis by comparing the local drug concentration to a programed threshold for drug-induced cancer cell death from the PD portion of the model. Agents may be able to alter their response to the PD model, however; for example, cells may be able to evolve a more drug resistant phenotype. In this way, feedback between the different scale representations and mathematical solutions in these hybrid models allows computational biologists to achieve a more accurate description of tumor response to drug treatment and drug dynamics in both spatial and temporal domains.

Major Hybrid Modeling Work

Discrete tumor modeling

A hybrid PK-PD ABM method was used to investigate the behavior of the bioreductive drug Tirapazamine [70]. Bioreductive drugs are targeted to the under-oxygenated region of the tumor through activation by specific reductases associated with hypoxia [71]. This complex model implements a neural network method adapted from Gerlee and Anderson [38] in 2D to describe a tumor in both proliferation and drug exposure stages. The agent-based tumor growth model includes cellular proliferation, death, quiescence, extra-cellular matrix (ECM) degradation, cell movement, and cell-cell adhesion. The PK-PD system consists of a series of PDEs describing drug concentration profile, nutrient distribution and consumption, and hydrogen ion production. The modelers found that even though bioreductive drugs specifically target the hypoxic region of the tumor, they do not diffuse far enough into the tumor to kill the entire hypoxic region. In their simulations, the chemotherapeutic drug was allowed to diffuse into the tumor via blood from the entire tumor perimeter, but concentrations are reduced towards the center of the tumor due to diffusion limits, hindering drug-induced tumor kill in that region. This is consistent with results from a series of recent mechanistic models of chemotherapy drug transport based on diffusion theory, which identified a direct correlation between blood availability of the drug and its efficacy of killing tumor cells [72–77]. This hybrid approach offers advantages over the separate modeling techniques: PK-PD modeling does not represent the movement of each individual cell, individual cell-cell adhesion and communication (i.e. paracrine signaling), nor does it track each cell’s influence on ECM (i.e. local ECM degradation), while ABM does not track quantities such as large-scale distribution of chemotherapy drug and signaling molecules (i.e. endocrine signaling). Combining both allowed modelers to determine that the drug was not able to reach the inner edge of the hypoxic region, partially due to consumption by agents as it diffused into the tumor. Thus, this hybrid model provided a more complete picture of the tumor environment than either modeling approach alone.

Leukemia treatment using cytosine arabinoside (Ara-C) in acute myeloid leukemia, with consideration of effects from circadian rhythm, was investigated in silico using hybrid PK-PD and ABM [42]. In the ABM, cells are modeled as elastic spheres in 2D and are allowed to move off-grid. Pharmacokinetics of the Ara-C uptake and phosphorylation into its active form are described in detail using a system of equations that combines several Michaelis-Menten terms to determine the amount of active drug in tumor cells. Ara-C acts by replacing natural nucleotides during DNA replication, preventing subsequent replication [78], which is taken to have a constant rate, so the pharmacodynamics are described using a linear equation. This work showed that the time dosage schedule plays a critical role in cell killing effectiveness, which was related to a resonance effect based on cell cycle length. Moreover, proper coordination between cell cycle length, stage and drug dose delivery can both improve cancer cell number reduction and patient tolerance. This in silico description of leukemia proved to be incomplete, however, as the modelers found that, when compared to published clinical results of chemotherapy in patients [79], the number of leukemia cells in the model was lower than measured in the clinic. The authors attributed this to the fact that their model only included one type of cell, while, in reality, leukemia affects more than one type; the addition of the other types of cells to the model would likely increase the number of leukemia cells at the end of the simulation. In this way, the addition of agents to a PK-PD model resulted in findings that might have gone unnoticed without knowing the exact number of agents at every time step, leading the authors towards a more complete and accurate understanding of leukemia than would have been achieved with either modeling approach implemented separately.

The efficacy of angiogenesis inhibitors (AI), vascular disruption agents (VDA), and cytotoxic chemotherapy agents was investigated in glioblastoma multiforme [80]. A hybrid PK-PD ABM method was implemented using a Voronoi tessellation (a method of dividing the plane into cells such that the area of each cell contains all the points that are closer to the agent within it than to any other agent) to generate a distribution of agents, each representing a physical cluster of cells (7 glial cells per cluster). Within the agents, a series of uniform, parallel, straight blood vessels was generated using a modified Krogh cylinder model. The PK-PD portion of the model was implemented using a series of PDE algorithms previously described in [81]. It was found that AI restricted tumor size, and this effect was enhanced when AI was combined with a cytotoxic chemotherapy agent. VDA also helped to reduce the tumor size, but all treatments tested were insufficient to kill the rumor. The modelers observed good agreement between their simulated AI inhibitor treatment and clinical data [82], and the VDA treatment agreed with preclinical observations on VDA antitumor effects; but even so, the combination of both treatments could not kill the tumor. Tumors are a biologically complex environment, and as mentioned above, destruction or lack of vasculature can result in large portions of hypoxic or necrotic regions relative to the biologically active tumor region. By tracking each individual agent’s response to the PK-PD portion of the simulation, the modeler was able to identify and track these regions exactly, and to identify which part of the simulated tumor would not be killed by vasculature destruction, which would have been more difficult without the addition of agents to the PK-PD model. Although these anti-angiogenesis agents were unable to kill the whole tumor in the simulations, they do suggest promising approaches to restrict tumor growth, which the author suggests may be better than attempting to kill the tumor in some cases, based on the work by Gatenby et al. [83,84].

Tumor resistance to the chemotherapy agent cisplatin was studied in silico by simulating the consequence of cisplatin resistance on tumor control [39] based on findings from an in vitro study by Sorenson et al. [85]. Tumors were simulated as ABMs, starting with a single cell and growing until the simulating tumor contained 10⁵ agents. PK in the model simulated drug delivery, including bolus drug administration once a day for two weeks at a defined “clinical dose” concentration that resulted in 80% cellular arrest in the G2 phase. PD in the model included cellular response to drug, cellular phenotype alteration to increase drug resistance, and phenotype alteration to have a decreased tendency towards entering apoptosis in response to drug exposure. The authors found that, in the case of cisplatin, the quiescent cells are not killed efficiently (cisplatin crosslinks DNA, inhibiting mitosis; so cell division is required for cisplatin to kill cancer cells), indicating that a method of inducing the cells to move forward in the cell cycle would increase the efficacy of tumor kill. It was also found that drug resistance is cumulative, resulting in increased resistance to treatment efficacy. Inclusion of ABM with the PK-PD model allowed the modelers to track how drug resistance in some cells was imparted into daughter cells, as well as keep track of the quiescent cells that were not susceptible to cisplatin. Additionally, a relationship between the percent of cycling cells and decrease in population was examined. These findings await further validation using experimental data.

A larger scale collaboration between individuals at eight institutions has led to the development of the ContraCancrum project, a multi-scale modeling effort intended to translate cancer modeling into the clinical setting [41]. The project is capable of simulating both cancer growth and response to therapy, and consists of three main parts: an ABM component, a molecular simulation component that describes both intra and extra-cellular regions, and a continuum reaction-diffusion model for the macroscale, which is solved using both explicit and implicit finite difference methods over a discretized mesh. The continuum model comprised of ODEs and PDEs is used to describe tumor growth, while the discrete ABM component is used to examine response to treatments, and provides modelers with spatiotemporal predictive information about the cellular mitotic potential, information that would not be readily available without representation of each agent individually. At each time step in the simulation, the PK-PD system is solved, in addition to computations related to metabolism, mechanics, and cytokinetics. Using clinical data, the modelers were able to compare their model results with clinically observed cancer behavior. More importantly, the interconnectivity of the ContraCancrum project allows for collaboration between modelers and doctors with patient data and imaging data, attempting to provide an approach for integrating models into the clinical setting in order to help design individualized treatment plans.

Continuum tumor modeling coupled with discrete angiogenesis modeling

In some cases, a full hybrid PK-PD ABM model is not the best choice for a model design. It may not be necessary to represent the entire tumor growth model with agents, especially when information about each agent is not known. In this case, models can be designed to be computationally more efficient by only modeling the regions of interests with agents, while representing the rest of the regions less granularly, i.e. as a continuum; note, however, that this may come at a cost of potentially missing some key information regarding cell-cell and cell-matrix interactions that occur outside those regions of interest. Lowengrub’s group has been using this technique to study tumor response to chemotherapy drug administration. We only introduce two of their most recent developments here.

A model for studying angiogenesis by modeling the tumor as a continuum and newly growing vasculature using ABM was designed to understand how interstitial fluid pressure (IFP) affects delivery of nutrients and other small molecules to the tumor environment [86]. The model expands on previous work [25,87–89], where the continuum model includes cell-ECM interaction, ECM degradation, cell-cell interactions, and tumor cell proliferation, migration and necrosis. Angiogenesis was simulated as an ABM, which includes blood flow and vasculature network remodeling (branching, endothelial cell proliferation, and branch sprouting). ABM is especially well-suited for vasculature modeling, because modelers must keep track of the location of all new endothelium, a task which is inherently built into ABM. Representing endothelial cells as agents offers the additional ability to model interactions between agents (in this example, modelers took into account ECM distribution and Notch signaling between endothelial cells), hence providing a more complete description of endothelial development.

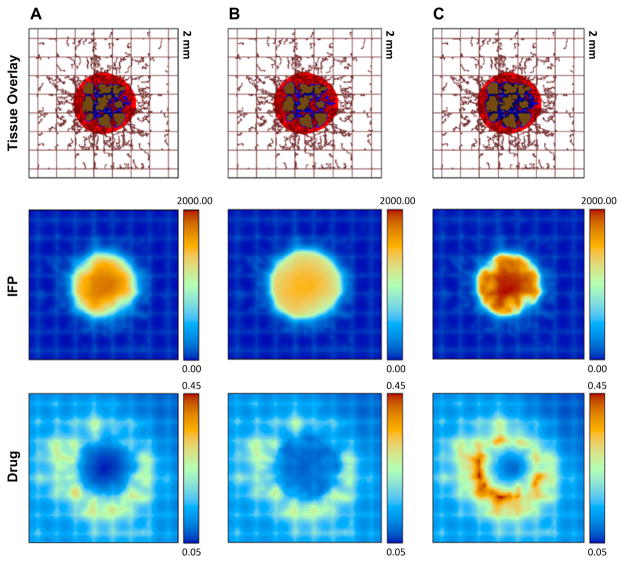
The continuum and ABM models were coupled by (1) oxygen flow from the vasculature to the tumor, and (2) tumor angiogenesis factors for stimulating vasculature proliferation delivery to the ABM. The PK-PD model was represented by parabolic and elliptic PDEs, which were solved by backward Euler and centered finite difference methods. They found that elevated IFP led to a reduction in blood and lymph vessel radius, which limited the amount of new blood that could enter the tumor, resulting in decreased oxygen and small molecule delivery and increased hypoxia in the tumor. The model was then further modified to determine if the high IFP would also reduce therapeutic drug efflux into the tumor (also see Fig. 2) [90]. They found that the IFP profile in larger tumors is more homogeneous, but as the tumor shrinks in response to chemotherapy the IFP becomes non-uniform, slowing chemotherapeutic efficacy at later stages. Changes in blood and lymphatic vessel radial distributions [91] were also found to have effects on drug delivery. Dynamic changes to vasculature diameter are easily accomplished with ABM, as the location of each agent is simply shifted to a new position, making agents a natural choice for representation in this application. Using information the hybrid modeling approach made readily available, the authors conclude that optimization of both the vasculature conditions and IFP are ideal for optimum drug delivery to the tumor microenvironment, which is consistent with prior work on relevant topics [92,93]. In summary, with this combined spatiotemporal tumor growth and PK-PD modeling platform, a variety of tumor and microenvironmental properties relevant to drug delivery can be readily investigated in detail. For example, the effect of different types of drugs (implicating different drug-cell binding kinetics) and their dose and dosing schedules, either used alone or in combination, can be simulated in the heterogeneous tumor environment with the integrated model.

Figure 2.

Examination of the interactions of chemotherapy drug delivery with heterogeneous tumor dynamics at approximately day 18 of the rescaled, simulated treatment. (A): control; (B): interstitial fluid pressure (IFP) with elevated tumor interstitial hydraulic conductivity; (C): IFP with elevated tumor vascular hydraulic conductivity. The IFP with elevated tumor interstitial hydraulic conductivity (B) decreases the drug concentration in and near the tumor. The IFP with elevated tumor vascular hydraulic conductivity (C) is larger than that of control due to excessive fluid extravasation, but the drug distribution is more heterogeneous compared to the control. Tissue Overlay display: tumor with viable tissue in red, hypoxic in blue, and necrotic in brown, with the pre-existing vasculature (brown rectangular gridlines) and neovasculature (irregular brown lines); IFP display: scale-bar, pressure in Pa; and Drug display: non-dimensional unit. Reproduced with permission from [90].

Discussion

We have presented a review of some of the major accomplishments achieved in the past few years using an integrated hybrid PK-PD ABM modeling approach. The examples included here are by no means inclusive, and have partially been selected because a special focus here is on PK-PD modeling of cancer. However, it should be noted that models for simulating cancer therapy typically implement a PK-PD concept, even when the term “PK-PD” is not specifically mentioned. Commonly, the PK component of the model, i.e. diffusion of nutrient, oxygen, drug, and other small molecules from the vasculature into the tumor is computed using some variation of Fick’s laws, employing diffusion or reaction-diffusion equations. These models must also address the PD aspect of modeling as well, as they need a method of computing how agents react to the surrounding conditions.

The complexity of cancer has made the use of mathematical modeling an active area of research. Although much has already been accomplished with PK-PD modeling, the future will see improvements and increases in complexity to allow even more information to be obtained from this approach. However, increased model complexity requires more data to describe the various processes involved. As such, when increasing the complexity of a model, modelers need to recognize the problem of over-fitting the model to data [94]. A large number of models developed so far occur in 2D, which is suitable for many applications without being too computationally intensive. However, improvements in computational speed and the emergence of graphics processing unit based technology [95,96] have reduced limitations of computational ability, opening the way for more complex models. This is already occurring in the form of 3D modeling, as seen in the ContraCancrum project described above, and even as hybrid PK-PD ABM with finite element solutions of the PDEs [97]. Three dimensional modeling opens up the way for full-tissue models, which may comprise whole organs or even organ systems. In fact, whole body PK-PD models are emerging [59], and it is likely whole body hybrid models will follow.

Overall, as models become more sophisticated, the gap between theoretical modeling and clinical applications will likely become smaller. The reader is referred to [69] for further discussion on clinically relevant ABM work. We are hopeful that modeling will ultimately provide a valuable tool for clinicians to designing individualized treatment plans in an effort to increase treatment efficacy and improve patient survival rates. However, challenges exist, as with any cancer modeling approach, and they start with data access, which is essential to advance this field [98]. For instance, sharing curated, consented patient data, needed to build more realistic and clinically more useful models, can be technically difficult and time consuming if multiple institutions are involved. Moreover, clinicians can be skeptical of the power of mathematical modeling, despite its scientific basis, strict adhesion to physical laws, inclusion of experimentally measured values (when known), and validation against in vivo data. Fortunately, this has started to change in recent years, as modelers continue to successfully compute behaviors and predict outcomes seen in the clinical setting [94,99].