Abstract
It is often assumed that it is unlikely that the same insertion or deletion (indel) event occurred at the same position in two independent evolutionary lineages, and thus, indel-based inference of phylogeny should be less subject to homoplasy compared with standard inference which is based on substitution events. Indeed, indels were successfully used to solve debated evolutionary relationships among various taxonomical groups. However, indels are never directly observed but rather inferred from the alignment and thus indel-based inference may be sensitive to alignment errors. It is hypothesized that phylogenetic reconstruction would be more accurate if it relied only on a subset of reliable indels instead of the entire indel data. Here, we developed a method to quantify the reliability of indel characters by measuring how often they appear in a set of alternative multiple sequence alignments. Our approach is based on the assumption that indels that are consistently present in most alternative alignments are more reliable compared with indels that appear only in a small subset of these alignments. Using simulated and empirical data, we studied the impact of filtering and weighting indels by their reliability scores on the accuracy of indel-based phylogenetic reconstruction. The new method is available as a web-server at http://guidance.tau.ac.il/RELINDEL/.
Keywords: phylogeny, indel analysis, multiple sequence alignment, alignment reliability
Introduction
Classic sequence-based phylogenetic methods are restricted to substitution events. Gapped positions are either discarded or treated as missing data. However, insertion and deletion (indel) events contain valuable phylogenetic information, and indeed many studies have previously utilized this information to resolve debated evolutionary relationships (see, e.g., Simmons and Ochoterena 2000; Belinky et al. 2010; Nagy et al. 2012; Luan et al. 2013, and references therein). The motivation for considering indel characters originates from the assumption that an insertion or deletion event is unlikely to occur twice at exactly the same position in two independent lineages. Thus, indel characters are expected to be less homoplasious and hence provide unambiguous phylogenetic signal compared with substitutions-based phylogenetic reconstruction (Rokas and Holland 2000). However, it was previously shown that indel characters may be homoplasious and may also be subject to the long-branch attraction artifact (e.g., Bapteste and Philippe 2002; Belinky et al. 2010).
The first step in reconstructing phylogenetic trees from indel data is to code indels as discrete characters. Various methods for coding indels as binary data were previously developed, among which the Simple Indel Coding (SIC) method was shown to be superior to other coding methods in parsimony reconstruction (Simmons and Ochoterena 2000; Simmons et al. 2007). The SIC methodology uses as input a given multiple sequence alignment (MSA), and transforms it to a matrix of 0/1, in which one and zero represent the presence and absence of a homologous gap, respectively. Indel-coding methods such as SIC implicitly assume that the provided input MSA is “true” and ignore uncertainty in the MSA reconstruction. However, it is evident that often different alignment algorithms provide different MSAs for the same sequence data, which in turn results in different sets of inferred indels. Furthermore, alignment programs usually output only one top-scoring MSA among many co-optimal or suboptimal MSAs. Consequently, both variability in the underlying assumptions among alignment programs and uncertainty stemming from ignoring co-optimal alignment solutions within each program may lead to different indel matrices.
The problem of MSA reliability is well known and was shown to affect downstream analyses (Jordan and Goldman 2012; Privman et al. 2012; Blackburne and Whelan 2013; Levy Karin et al. 2014). This motivated the development of several methods aimed to remove unreliable MSA positions (Castresana 2000; Landan and Graur 2008; Penn, Privman, Landan, et al. 2010; Wu et al. 2012). However, these methods cannot be directly applied to indel data as the removal of unreliable columns (or blocks of columns) may result in indels that were created artificially by the concatenation of positions that are not in proximity to each other (e.g., two independent indels may be concatenated if the region connecting them is removed).
Previous approaches were developed for the identification of reliable indels. The approach proposed by McCrow (2009) is to quantify the reliability of indels by comparing the score of an alignment in which a given indel is present versus the score of the optimal alignment in which it is absent. The main shortcoming of this approach is that its scoring is computed based on pairwise alignments. The valuable information which is part of the multiple-alignment algorithm is not accounted for when quantifying indel reliability. Furthermore, the method highly depends on a set of arbitrary parameters. Unfortunately, this program is unavailable and we thus could not compare it with the methodology we present here. The recently developed web-server SeqFIRE (Ajawatanawong et al. 2012) also enables extracting reliable indels from an input MSA by searching for indels that reside between highly conserved sequence columns. However, there is no quantification of indel reliability (i.e., an indel can only be classified as either reliable or not, instead of having a score reflecting its degree of reliability).
In this article, we present the RELINDEL (RELiable INDELs) method that explicitly quantifies the reliability of indels. We first show that different alignment algorithms can lead to extreme differences in the resulting set of inferred indels. We also show that treating all indels as reliable may lead to erroneous inference of phylogenetic trees. We then describe our method for quantifying indel reliability. Using both real and simulated data, we next study the impact of weighting and filtering unreliable indels on the accuracy of tree reconstruction.
Materials and Methods
Data Sets Construction
We retrieved a large sample of 4,818 coding DNA sequences obtained from version 6 of the OrthoMam database (Ranwez et al. 2007). We chose all genes for which orthologous sequences exist for all the ten species analyzed: Nine primate species (Homo, Pan, Gorilla, Pongo, Macaca, Callithrix, Tarsius, Otolemur, and Microcebus) and a tree shrew (Tupaia), which is used as an outgroup. All DNA sequences were translated into amino acids, replacing ambiguous nucleotide characters with “X” in the amino acid sequence.
Simulation Study
Simulations were conducted to assess the ability to correctly detect erroneously inferred indel characters. For that purpose, we simulated “genes” using ROSE (Stoye et al. 1998) with root length of 348 amino acids along trees with 16 taxa. Two trees were considered, one symmetric and one asymmetric. In each simulation, eight simulated genes were concatenated. All parameters used for the simulations (including tree topologies and branch lengths) were taken from Talavera and Castresana (2007). This simulation procedure was repeated 100 times for each of the two trees.
Alignments
Unaligned sequences (either simulated or real data sets) were given as input to RELINDEL. RELINDEL then aligned each gene using three popular alignment programs: 1) PRANK version v.100311 with the +F argument (Loytynoja and Goldman 2008), 2) MAFFT version 6.710b with the L-INS-i mode (Katoh et al. 2002; Katoh and Toh 2008), and 3) CLUSTALW version 2.0.10 with default parameters (Larkin et al. 2007).
Indel Coding
Indels inferred from each MSA were coded as binary characters using the SIC scheme (Simmons and Ochoterena 2000). Specifically, we have reimplemented the SIC methodology in C++. This source code is freely available as part of our web-server (http://guidance.tau.ac.il/RELINDEL). In the SIC scheme, an MSA is reduced to a 0/1 matrix. Each column in the 0/1 matrix corresponds to a single indel character, which may reflect either an insertion or a deletion of one or more amino acids. Overlapping and nested gaps are considered to reflect different events, and are thus coded separately following the methodology of Simmons and Ochoterena (2000). Here, we do not code gaps that reside at either the 5′- or the 3′-end of input sequences as it is impossible to distinguish genuine gaps from gaps reflecting incomplete sequencing.
Indel-Reliability Score
Indel reliability was assessed for each gene using RELINDEL, providing for each indel a score between 0 and 1 (as described in the Results section). Indel filtering was also performed with the SeqFire program, with default parameters.
Robinson–Foulds Distances and Receiver Operating Characteristic Analysis
Robinson–Foulds (RF) distances (Robinson and Foulds 1981) between trees were computed using PAUP* v4.0b10 (Swofford 2003). To evaluate the performance of RELINDEL, receiver operating characteristic (ROC) curves were computed using the ROCR package (Sing et al. 2005).
Indel-Based Tree Reconstruction
Maximum parsimony reconstructions from the binary indel matrix were performed using PAUP* v4.0b10 (Swofford 2003). Tree searches were performed under the branch-and-bound algorithm and bootstrap supports were computed using 100 replicates under the same algorithm. To test whether the known primate tree (Perelman et al. 2011) and the inferred tree are significantly different, we used the Templeton test (Templeton 1983) as implemented in PAUP*.
Software
Our program is implemented in C++ and is freely available under the GNU license. It can be used either as a web-server (http://guidance.tau.ac.il/RELINDEL) or as a standalone application that can be downloaded from the web-server.
Results
Indel-Based Inference Heavily Depends on the Alignment Method
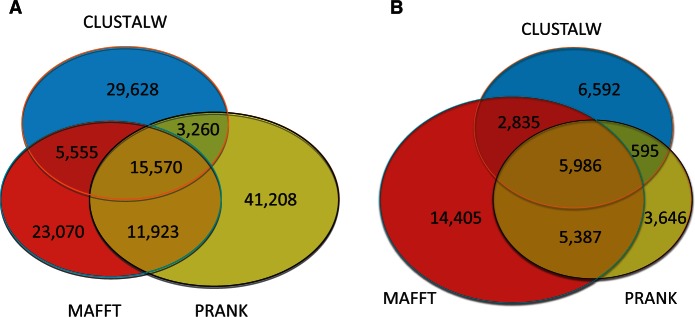
We first tested the degree of agreement between various MSA algorithms regarding the placement of indels. We compared indels obtained from a large set of 4,818 genes which were aligned using MAFFT, PRANK, or CLUSTALW. These alignment methods were chosen as representatives of progressive alignment methodologies. Specifically, MAFFT was demonstrated to be highly accurate and computationally efficient over several benchmark data sets (Blackshields et al. 2006; Nuin et al. 2006; Thompson et al. 2011). PRANK (Loytynoja and Goldman 2008), unlike traditional progressive alignment methods, uses evolutionary information to more accurately infer the placement of gaps. CLUSTALW was chosen as it is the oldest and most cited alignment method (Van Noorden et al. 2014). As previously reported (Loytynoja and Goldman 2008), PRANK alignments are characterized by significantly more indels compared with either MAFFT or CLUSTALW: 71,961 indels were inferred using PRANK compared with 56,118 indels with MAFFT and 54,011 indels with CLUSTALW. As shown in figure 1A, although the total number of indels is similar between MAFFT and CLUSTALW, approximately 60% of the MAFFT indels do not correspond to CLUSTALW indels, and vice versa. The three alignment algorithms inferred a total of 130,212 different indels, out of which the three alignment methods agreed only on 15,570 (11.96%) indels. Thus, the methodology used to align the input sequences has a very strong effect on indel placement, and hence may strongly impact indel-based phylogenetic inference.
Fig. 1.—
The agreement regarding indel characters derived from three common MSA algorithms: MAFFT, PRANK, and CLUSTALW (A) using all indels and (B) using the most reliable indel characters identified by RELINDEL.
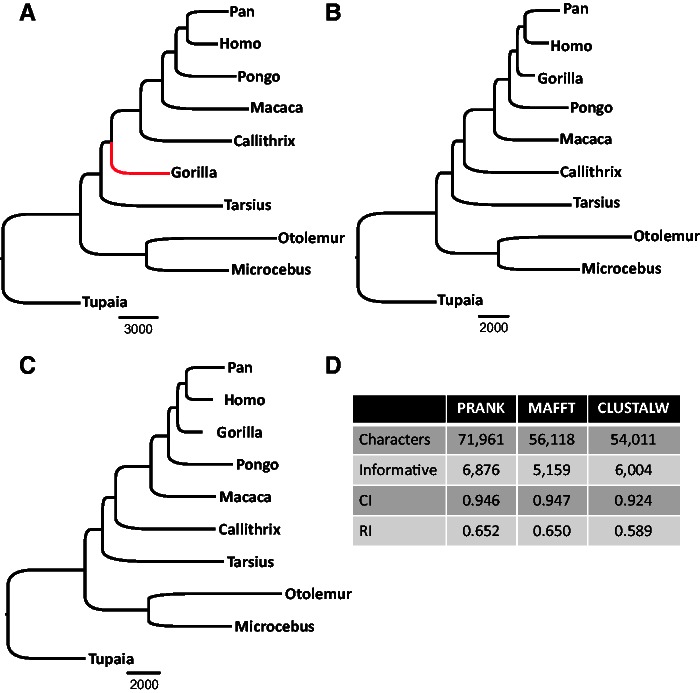
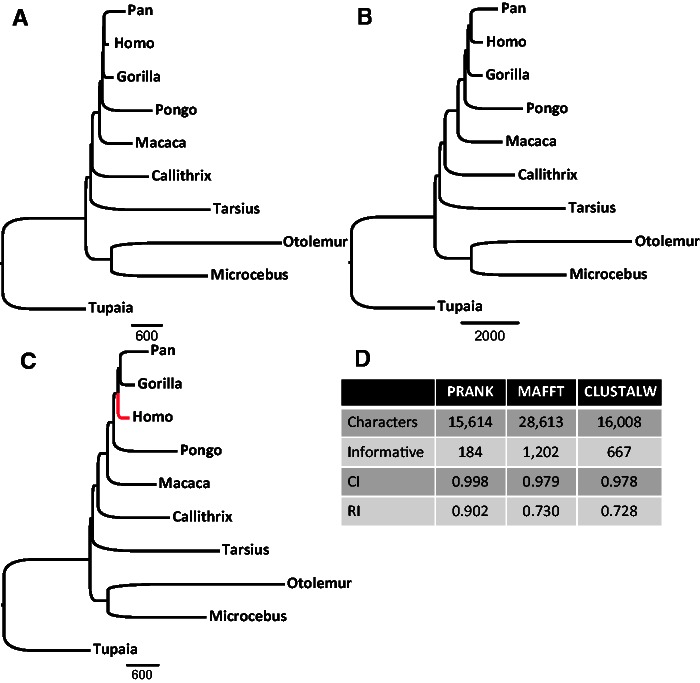
To test whether the above differences in indel placement among the alignment algorithms affect indel-based phylogenetic reconstruction, the entire set of indels obtained from each alignment method was used as input for a parsimony-based tree reconstruction. As the phylogenetic relationships among the species from which the sequences were sampled are considered to be known (Perelman et al. 2011), we compared the inferred tree with the established species tree (see Materials and Methods). Although the phylogenies inferred based on the indels produced by MAFFT and CLUSTALW were in agreement with the known primate phylogeny, the tree inferred based on indels produced by PRANK was significantly different (P < 0.0001, Templeton test) (fig. 2). In the PRANK phylogeny, the gorilla was misplaced at the base of the Simiiformes. These differences in phylogenetic trees, inferred when using different alignment methods, support the hypothesis that indel-based phylogeny may be sensitive to the MSA algorithm used. Surprisingly, the bootstrap supports for all splits in the three obtained phylogenies were 100%. The high support for erroneous splits in the PRANK tree suggests that unreliable indels may bias indel-based tree inference. This, together with the observed differences in indel placement among MSA algorithms, motivated us to develop a method to quantitatively assess the reliability of each indel character and to test the impact of removing unreliable indel characters on indel-based tree inference.
Fig. 2.—
Phylogenetic trees reconstructed using all indel characters coded from MSAs produced by (A) PRANK, (B) MAFFT, and (C) CLUSTALW. When using indels derived from the PRANK MSAs, the obtained tree significantly differed from the accepted primate tree. The red branch shows the misplacement of Gorilla in the PRANK-based inference. Additional statistical information is provided in panel (D) (Informative, number of informative characters; CI, consistence index; RI, retention index).
Quantifying Indel Reliability
Our approach to quantify the reliability of each indel character is based on the assumption that an indel is reliable only if it exists in several possible alternative alignments inferred from the same input sequences. To this end, we use the fact that changing the input parameters of alignment programs (e.g., the guide tree, the gap penalties, and the cost matrices) often results in differences in the inferred alignments. We term MSAs resulting from such changes in input parameters “alternative MSAs.” In the indel-reliability approach developed here, the alternative MSAs are generated by using different guide-trees as input to the (progressive) alignment methods. The various input trees used for constructing the alternative MSAs (100 is the default) are obtained by bootstrapping the original MSAs and reconstructing neighbor-joining trees from these bootstrapped MSAs. We have previously shown that such a bootstrapping method for obtaining alternative MSAs is highly successful in identifying reliable versus nonreliable alignment regions (Penn, Privman, Ashkenazy, et al. 2010; Penn, Privman, Landan, et al. 2010; Hall 2011; Privman et al. 2012). In the methodology developed here, termed RELINDEL, indels shared among many such alternative alignments are considered more reliable than indels shared only by a small subset of these alternative alignments. RELINDEL is implemented as a user friendly web-server and is freely available at http://guidance.tau.ac.il/RELINDEL.
To quantify the reliability of an indel in a given base alignment (the standard MSA which was obtained from the alignment program), we code all indels in it using the SIC scheme (Simmons and Ochoterena 2000). We next code all the indels in the (100) alternative MSAs. An indel character in the base alignment and an indel character in an alternative alignment are considered to be identical if they are of the same length and have the same sequence-relative locations for all species in both alignments. An indel character in the base alignment is defined as reliable (with a perfect score of 1) if it is shared with all alternative MSAs. Otherwise, its reliability score is defined as the fraction of alternative alignments in which it is found.
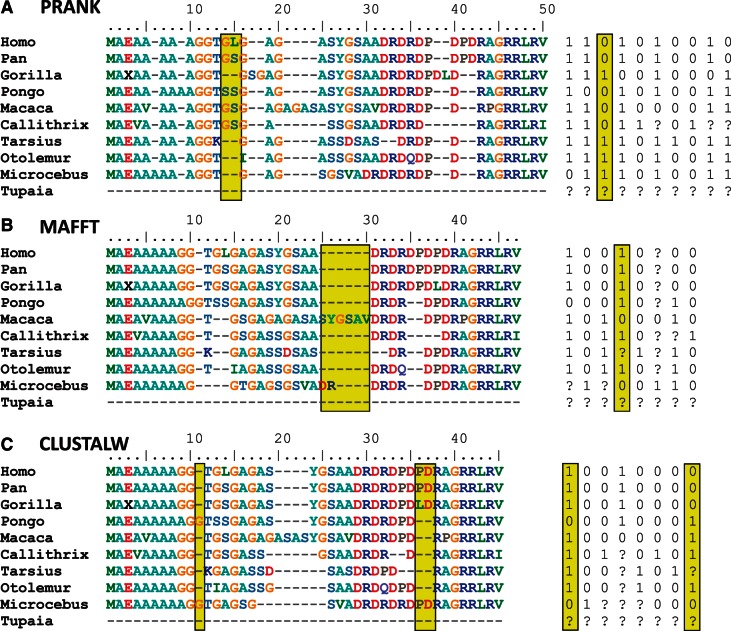
The MSAs shown in figure 3 demonstrate how the same region can be differently aligned by the three alignment methods and lead to different coding matrices. Indel characters that support a different tree from the “true” primate tree are homoplasious. The alignment of CLUSTALW for this region resulted in two homoplasious indels, which are absent from the alignment produced by MAFFT or PRANK. Indeed, our RELINDEL method identified these indels as unreliable and gave them both a score of 0.01. PRANK inferred a different homoplasious indel (with a score of 0), which is absent from the alignments of MAFFT and CLUSTALW. Notably, this unreliable PRANK indel supports the erroneous tree, in which the gorilla is misplaced to be at the base of the Simiiformes (which is the tree inferred when all PRANK indels are used). Figure 3 also exemplifies that PRANK alignments are characterized by more indels compared with MAFFT and CLUSTALW alignments. Finally, a homoplasious and unreliable indel (a score of 0) is also inferred using MAFFT, which is absent in the other two alignments.
Fig. 3.—
MSAs and corresponding indel character matrices for the first 40 amino acids of the human AGPS gene (ENSG00000018510) as inferred by (A) PRANK, (B) MAFFT, and (C) CLUSTALW. Homoplasious indels, which conflict the accepted primate tree, are boxed in yellow. The three alignment methods highly disagree on the placement of these indels. RELINDEL identifies these indels as highly unreliable (see text).
The Impact of Filtering Unreliable Indel Characters
We tested the hypothesis that the differences in indel assignments among MSA algorithms are mainly due to unreliable indel characters and that their filtering will produce more accurate trees. First, we choose to retain only the most reliable indels (i.e., those having a score of 1). This resulted in 28,613 reliable indel characters when using MAFFT (50.99% out of the original 56,118 MAFFT indel characters), 15,614 indel characters when using PRANK (21.7% out of the original 71,961 indels), and 16,088 indel characters when using CLUSTALW (29.79% out of the original 54,011 indels). Figure 1B summarizes these results. The fact that more than 75% of the PRANK indels were considered unreliable may explain why the tree inferred using the entire set of PRANK indels was erroneous.
We next analyzed the reliability of phylogenetically informative indels. Phylogenetically informative indels are those that can support one evolutionary scenario over the other (as a counter example, a gap which is only present in one sequence is noninformative). The filtering scheme removes a large portion of the phylogenetically informative characters in all three alignment methods: In MAFFT, only 23.3% of the informative indels were retained (1,202 indels out of 5,159). In PRANK, only 2.67% of the informative indels were retained (184 indels out of 6,876) and in CLUSTALW, 11.11% (667 out of 6,004 indels). Moreover, informative indels tend to be less reliable compared with noninformative ones (P < 10−100 for all three MSA methodologies, chi-square test). These results suggest that many phylogenetically informative indels are unreliable and may bias phylogenetic inference.
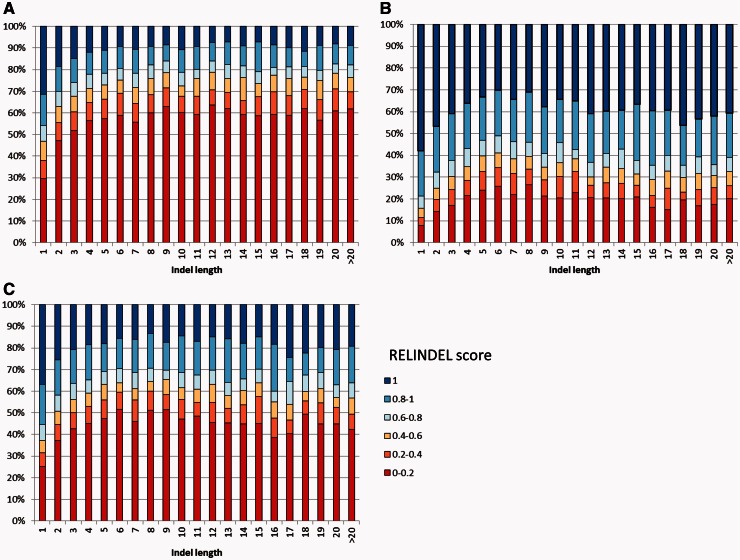
We also compared the reliability as a function of indel length. Indel-reliability scores for the different alignment methods as a function of indel length are shown in figure 4. This analysis clearly shows that unreliable indels are common regardless of indel lengths, although very short indels (one amino acid long) are on average more reliable compared with longer indels.
Fig. 4.—
Distribution of the indel-reliability scores for (A) PRANK, (B) MAFFT, and (C) CLUSTALW as a function of indel length.
The degree of agreement between different alignment methods is measured by the percentage of total indels not supported by any other method, for example, indels inferred only by PRANK. After the filtering of unreliable indels this percentage decreased for PRANK (from 57.26% to 23.34%) and for CLUSTALW (from 54.85% to 41.18%), and increased for MAFFT (from 41.11% to 50.34%) (fig. 1B). The total agreement between the three alignment methods (i.e., the total number of indels shared by all three methods out of the total number of different indels in the three methods combined) also slightly increased from 11.96% to 15.14%. These results further show that a large number of indel characters considered “reliable” according to one alignment method are not inferred as such by the other alignment methods. Nevertheless, the removal of phylogenetic noise by the indel filtering may suffice to accurately reconstruct indel-based trees.
To test the impact of filtering unreliable indels on phylogenetic inference, only the most reliable indels were used to reconstruct the phylogeny based on each of the three MSA methodologies. Filtering-out unreliable indels using RELINDEL resulted in a PRANK tree that is in agreement with the known primate phylogeny (fig. 5). After filtering, the MAFFT tree is still in agreement with the known phylogeny. In contrast, in the CLUSTALW tree, the positions of Homo and Gorilla are inverted, with a bootstrap support of 82% (however, the tree is not significantly different from the known primates phylogeny; P = 0.3532, Templeton test). Notably, using only reliable indels improved the Consistency Index (CI) values for all alignment methods: From 0.946 to 0.998, from 0.947 to 0.979 and from 0.924 to 0.978 for PRANK, MAFFT and CLUSTALW, respectively (figs. 2D and 5D).
Fig. 5.—
Phylogenetic trees reconstructed using the most reliable indels characters coded from MSAs produced by (A) PRANK, (B) MAFFT, and (C) CLUSTALW and filtered by the RELINDEL method. The correct primate phylogeny was reconstructed when using indels derived from both PRANK and MAFFT. Homo is misplaced in the tree reconstructed based on CLUSTALW MSAs (the erroneous branch is marked in red). Additional statistical information is provided in panel (D) (Informative, number of informative characters; CI, consistence index; RI, retention index).
The misplacement of Homo in the CLUSTALW tree after RELINDEL filtering together with the significant increase in the CI score suggests that extensive filtering may, for some data sets, increase reliability but altogether decrease the total phylogenetic signal. To avoid such cases, we tested an alternative approach, in which instead of removing an unreliable indel we use its reliability score as a weight within the tree reconstruction step.
The Impact of Weighting Indels by Their RELINDEL Score
We tested whether the indel-reliability scores computed by RELINDEL can be used as weights to reduce the impact of unreliable indels on the tree reconstruction while avoiding the risk of filtering too much data. Thus, we used all indels extracted for each alignment method and their corresponding weights to reconstruct the phylogeny. Using the weighted indels, all inferred phylogenies for the different alignment methods (PRANK, MAFFT, and CLUSTALW) were in agreement with the known phylogeny. The bootstrap support values were 91–100 for PRANK, 85–100 for MAFFT, and 77–100 for CLUSTALW. The CI values were higher than in the case where all indels were used without weighting and slightly lower than in the case where only the most reliable indels were used: 0.986, 0.965 and 0.963 for PRANK, MAFFT and CLUSTALW, respectively. The results suggest that weighting indels by their reliability score can balance between the need to remove unreliable indels that might impede accurate indel-based inference of phylogenies and the need to maintain sufficient phylogenetic signal.
Simulation Study
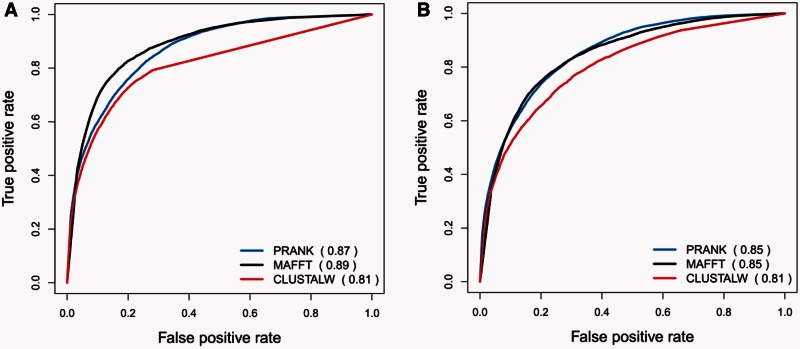
Simulations offer the possibility to evaluate the performance of our indel-reliability method. Specifically, we tested whether RELINDEL can detect indels that are misplaced by the alignment programs. Figure 6 summarizes the ability to correctly identify erroneous indel characters for the three alignment methods (PRANK, MAFFT, and CLUSTALW), as quantified using ROC. The area under the ROC curve (AUC) measures the total performance. An AUC value of 1.0 suggests perfect identification, whereas a random assignment should give, on average, an AUC of 0.5. RELINDEL obtained AUC values that ranged from 0.81 to 0.89 (fig. 6). These results suggest that RELINDEL is relatively accurate in detecting misplaced indels. We thus next tested, again based on simulations, the utility of using RELINDEL to better reconstruct indel-based phylogenetic trees.
Fig. 6.—
ROC curves, quantifying the ability of RELINDEL to accurately detect reliable indels based on simulated data. The AUC is given in parenthesis next to each alignment algorithm. ROC curves for simulations with (A) symmetric tree and (B) asymmetric tree.
We first tested the impact of filtering all unreliable indels identified by RELINDEL on tree inference. As the vast majority of informative indels were filtered out, we were only left with scant data, which were not enough to reliably reconstruct trees (data not shown). Next, we compared the effect of weighting indels by their RELINDEL score with the effect of filtering indels by the SeqFire methodology (Ajawatanawong et al. 2012). Specifically, we compared four alternatives: 1) Using all indels; 2) filtering all unreliable indels according to the program SeqFire, retaining all reliable indels (SeqFire all); 3) SeqFire filtering, retaining only simple indels, that is, nonoverlapping fixed-length indels (SeqFire simple); and 4) weighting indels according to their RELINDEL reliability scores. The effect of these alternatives on tree reconstruction accuracy, as measured by the average RF distance (Robinson and Foulds 1981) between the inferred tree and the simulated tree, is summarized in table 1.
Table 1.
The Impact of Indel Filtering Using SeqFire and Weighting Using RELINDEL on the Accuracy of Phylogenetic Inference
| Alignment Method | Indels Reliability Method | Asymmetric Tree |
Symmetric Tree |
||||
|---|---|---|---|---|---|---|---|
| Average Number of Informative Indel Sites | Average RF | P (one-sided Wilcoxon test) | Average Number of Informative Indel Sites | Average RF | P (one-sided Wilcoxon test) | ||
| PRANK | All indels | 232.29 (±17.81) | 7.73 (±2.14) | 400.53 (±20.79) | 1.57 (±1.80) | ||
| RELINDEL | 232.29 (±17.81) | 6.01 (±2.66) | 1.05e-07 | 400.53 (±20.79) | 1.14 (±1.68) | 0.02507 | |
| SeqFire all | 228.49 (±17.63) | 7.66 (±2.13) | 0.2067 | 394.84 (±20.70) | 1.55 (±1.83) | 0.242 | |
| SeqFire simple | 9.13 (±3.06) | 11.77 (±2.22) | 1 | 10.56 (±3.15) | 9.42 (±2.54) | 1 | |
| MAFFT | All indels | 191.44 (±11.81) | 8.49 (±3.20) | 263.4 (±13.86) | 4.62 (±3.27) | ||
| RELINDEL | 191.44 (±11.81) | 7.25 (±3.22) | 4.35e-4 | 263.4 (±13.86) | 4.94 (±3.41) | 0.7875 | |
| SeqFire all | 188.6 (±11.84) | 8.49 (±3.21) | 0.5115 | 259.27 (±13.97) | 4.48 (±3.16) | 0.06314 | |
| SeqFire simple | 14.81 (±3.65) | 12.32 (±2.73) | 1 | 14.87 (±3.70) | 12.07 (±2.87) | 1 | |
| CLUSTALW | All indels | 251.77 (±14.45) | 11.10 (±3.22) | 331.67 (±17.61) | 5.55 (±2.13) | ||
| RELINDEL | 251.77 (±14.45) | 11.83 (±4.02) | 0.9156 | 331.67 (±17.61) | 9.94 (±3.32) | 1 | |
| SeqFire all | 249.34 (±14.28) | 11.10 (±3.15) | 0.5579 | 327.13 (±17.95) | 5.53 (±2.16) | 0.3116 | |
| SeqFire simple | 19.53 (±4.28) | 13.69 (±3.04) | 1 | 15.32 (±3.51) | 10.77 (±2.71) | 1 | |
| TRUE MSA | 212.58 (±12.96) | 1.38 (±1.44) | 346.82 (±17.83) | 0.34 (±0.82) | |||
Note.—True MSA reports the accuracy when the correct simulated MSA was used as input to code indels. In bold are statistically significant differences in RF distance comparing either RELINDEL, SeqFire all or SeqFire simple from the distance obtained without filtering (All indels). Results are based on 100 simulated data sets.
When the true MSA was given as input to the tree reconstruction program, the average RF distance was 1.38 for the asymmetric tree (table 1). In contrast, when inferred alignments were given as input and all indels were retained, the accuracy substantially decreased: The most accurate alignment program was PRANK, with RF distance (without filtering) of 7.73, compared with RF distance of 8.49 for MAFFT and 11.1 for CLUSTALW. Similar results were obtained for the symmetric tree. These results demonstrate that many erroneously indels are created by alignment programs, resulting in reduced accuracy when used as data for tree inference.
In all cases, filtering with the SeqFire program, retaining only simple indels, resulted in statistically significant loss of accuracy. This is because, in this option, too many informative indel characters are filtered out, leaving not enough data for accurate tree reconstruction (average number of informative indels smaller than 20 for all three MSA programs; table 1). Filtering with the SeqFire (using the SeqFire all option) had comparable RF distance to the option of no filtering, for all alignment programs, for both symmetric and asymmetric trees. Weighting indels according to RELINDEL improved tree reconstruction accuracy for PRANK for both trees and for MAFFT for the asymmetric tree (table 1; P < 0.026, Wilcoxon test). In only one case, it significantly decreased accuracy (for the symmetric tree, with CLUSTALW as the alignment program). These results suggest that at least for the more accurate alignment programs MAFFT and PRANK, filtering does not reduce accuracy (SeqFire all) and weighting by RELINDEL can even be beneficial.
Discussion
Accurate inference of indels is important for better understanding the mutation and selective forces shaping the evolution of genes and genomes. For example, accurate indel inference is essential for quantifying the prevalence of indel events in evolution (e.g., Taylor et al. 2004), elucidating indels as an evolutionary mechanism for adaptation (e.g., McLean et al. 2011), and reconstructing phylogenetic relationships from indel characters (Lloyd and Calder 1991; Rokas and Holland 2000; Bapteste and Philippe 2002; Belinky et al. 2010). Currently available state-of-the-art alignment methods have low level of agreement with respect to indel placement, suggesting that a significant part of inferred indels are unreliable. Although future advances in sequence alignment methodologies may alleviate error rates in indel inference, alignment uncertainty is inevitable due to the stochastic nature of sequence evolution. Nevertheless, some indels are inferred with more certainty than others. In this work, we provide means to quantify this uncertainty and show that our novel methodology can substantially increase the fraction of correctly inferred indels for three common alignment algorithms. Our results further suggest that using only a subset of reliable indels may increase the accuracy of phylogenetic reconstruction on both real and simulated data.
Although our methodology preferentially filters out erroneously placed indels, a fraction of correctly placed indels is also inevitably filtered out. This filtering results in a huge loss of data used for phylogenetic inference (e.g., 76.7% of informative indel characters were filtered out when using the MSA generated using MAFFT). This loss of data, in turn, may render phylogenetic inference more difficult. Thus, there is a signal-to-noise tradeoff, in which filtering removes both noise and phylogenetic signal. When fully sequenced genomes are available (as is the case in our biological example), data are in surplus, and the cost of data filtering is low. However, when a small data set is analyzed, the approach suggested here to weight indels according to their reliability is more appropriate.
Accounting for indel reliability had different impact in simulations versus the empirical data set analysis. For example, although RELINDEL applied to MAFFT MSAs improved tree reconstruction accuracy, the correct tree was inferred both with and without filtering for the empirical primate data. This difference probably reflects the higher divergence of the simulated sequences compared with the primate sequences, suggesting that RELINDEL is especially important when reconstructing deep phylogenetic relationships or when studying fast-evolving genes or organisms. Notably, our simulations are likely oversimplified. They do not account for many scenarios that can potentially bias indel-based tree reconstruction. For example, in real data, incomplete lineage sorting can obscure the phylogenetic signal and is expected to affect indel-based tree reconstruction as well. Notably, when the indel matrix is constructed by combining indels from multiple genes, and the fraction of genes experiencing incomplete lineage sorting is small, incomplete lineage sorting should not bias the inferred tree. Another example of possible bias is when an alternative exon is not recognized as an exon in two distant species, leading to a false inference of perfectly reliable erroneous indels in these two species. To avoid these cases, it is advisable to test whether long indels match exon boundaries when analyzing genomic sequences. Furthermore, wrong inference of orthology relationships or sequence contaminations may lead to many homoplasious indels. In fact, RELINDEL could, in theory, be used to detect such cases in phylogenomics analyses by searching for genes with a significant excess of homoplasious indels relative to the remaining genes. Finally, small scale duplications of genomic regions can also lead to false indel identification. Clearly, careful data quality assurance is critical for real sequence analysis and RELINDEL can help detect genomic alignments of low quality.
The methodology developed here is modular and can be divided into two. First, a set of plausible alignments is generated. Second, the reliability of each indel character is inferred based on its frequency in this set. Regarding the first step, the set of alignments we generate is based on a bootstrap-like approach and can be achieved when using any progressive alignment methodology. However, our method can get as input a set of plausible alignments generated using other methods, such as HoT (Landan and Graur 2008), or alignments sampled using Bayesian procedures (Redelings and Suchard 2005; Novak et al. 2008; Miklos et al. 2009; Satija et al. 2009).
Bayesian approaches (Redelings and Suchard 2005; Novak et al. 2008; Miklos et al. 2009; Satija et al. 2009) allow joint inference of evolutionary trees and alignments using models that account for indels and substitutions simultaneously. However, such methods are computationally very demanding, and are thus inapplicable for analyzing large scale genomic data. As a result, most phylogenetic analyses today discard indel data or treat indels as missing data, potentially losing valuable information.
In this study, we focused on employing reliable indels for indel-based phylogenetic reconstruction. However, inferring reliable indels can be valuable also for structure prediction and loop modeling (Adhikari et al. 2012). In addition, once reliable indels are inferred they can be used to predict functional changes between organisms. For example, indels in noncoding regions can change the regulation network by altering transcription factor binding sites (Wray et al. 2003; Oren et al. 2014).
Reconstructing reliable phylogenies remains a main challenge in molecular evolution studies with many unresolved ancient speciation events, such as early metazoan evolutionary history (Philippe et al. 2011). Indels data were shown to be a valuable source for phylogenetic signal toward resolving these challenging speciation events and complementing the phylogenetic signal derived from substitutions, gene content, gene order, and morphological characters (Simmons and Ochoterena 2000; De Bie et al. 2006; Lin and Moret 2011; Lin et al. 2012). The methodology proposed in this study should set new standards for phylogenetic reconstructions from indel data and should facilitate research aimed at solving some of the most debated questions regarding the tree of life.
Acknowledgments
The authors thank Eli Levy Karin and Itamar Sela for critically reading the manuscript and two anonymous reviewers for their helpful comments. This study was supported by grants from the Israel Science Foundation (1092/13 to T.P. and 663/10 to D.H.). H.A. is a fellow of the Edmond J. Safra Center for Bioinformatics at Tel-Aviv University.
Literature Cited
- Adhikari AN, et al. Modeling large regions in proteins: applications to loops, termini, and folding. Protein Sci. 2012;21:107–121. doi: 10.1002/pro.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ajawatanawong P, Atkinson GC, Watson-Haigh NS, Mackenzie B, Baldauf SL. SeqFIRE: a web application for automated extraction of indel regions and conserved blocks from protein multiple sequence alignments. Nucleic Acids Res. 2012;40:W340–W347. doi: 10.1093/nar/gks561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bapteste E, Philippe H. The potential value of indels as phylogenetic markers: position of trichomonads as a case study. Mol Biol Evol. 2002;19:972–977. doi: 10.1093/oxfordjournals.molbev.a004156. [DOI] [PubMed] [Google Scholar]
- Belinky F, Cohen O, Huchon D. Large-scale parsimony analysis of metazoan indels in protein-coding genes. Mol Biol Evol. 2010;27:441–451. doi: 10.1093/molbev/msp263. [DOI] [PubMed] [Google Scholar]
- Blackburne BP, Whelan S. Class of multiple sequence alignment algorithm affects genomic analysis. Mol Biol Evol. 2013;30:642–653. doi: 10.1093/molbev/mss256. [DOI] [PubMed] [Google Scholar]
- Blackshields G, Wallace IM, Larkin M, Higgins DG. Analysis and comparison of benchmarks for multiple sequence alignment. In Silico Biol. 2006;6:321–339. [PubMed] [Google Scholar]
- Castresana J. Selection of conserved blocks from multiple alignments for their use in phylogenetic analysis. Mol Biol Evol. 2000;17:540–552. doi: 10.1093/oxfordjournals.molbev.a026334. [DOI] [PubMed] [Google Scholar]
- De Bie T, Cristianini N, Demuth JP, Hahn MW. CAFE: a computational tool for the study of gene family evolution. Bioinformatics. 2006;22:1269–1271. doi: 10.1093/bioinformatics/btl097. [DOI] [PubMed] [Google Scholar]
- Hall BG. Phylogenetic trees made easy: a how-to manual. 4th ed. Sunderland (MA): Sinauer; 2011. Advanced alignment with GUIDANCE; pp. 117–190. [Google Scholar]
- Jordan G, Goldman N. The effects of alignment error and alignment filtering on the sitewise detection of positive selection. Mol Biol Evol. 2012;29:1125–1139. doi: 10.1093/molbev/msr272. [DOI] [PubMed] [Google Scholar]
- Katoh K, Misawa K, Kuma K, Miyata T. MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002;30:3059–3066. doi: 10.1093/nar/gkf436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katoh K, Toh H. Recent developments in the MAFFT multiple sequence alignment program. Brief Bioinform. 2008;9:286–298. doi: 10.1093/bib/bbn013. [DOI] [PubMed] [Google Scholar]
- Landan G, Graur D. Local reliability measures from sets of co-optimal multiple sequence alignments. Pac Symp Biocomput. 2008;13:15–24. [PubMed] [Google Scholar]
- Larkin MA, et al. Clustal W and Clustal X version 2.0. Bioinformatics. 2007;23:2947–2948. doi: 10.1093/bioinformatics/btm404. [DOI] [PubMed] [Google Scholar]
- Levy Karin E, Susko E, Pupko T. Alignment errors strongly impact likelihood-based tests for comparing topologies. Mol Biol Evol. 2014;31:3057–3067. doi: 10.1093/molbev/msu231. [DOI] [PubMed] [Google Scholar]
- Lin Y, Moret BM. A new genomic evolutionary model for rearrangements, duplications, and losses that applies across eukaryotes and prokaryotes. J Comput Biol. 2011;18:1055–1064. doi: 10.1089/cmb.2011.0098. [DOI] [PubMed] [Google Scholar]
- Lin Y, Rajan V, Moret BM. TIBA: a tool for phylogeny inference from rearrangement data with bootstrap analysis. Bioinformatics. 2012;28:3324–3325. doi: 10.1093/bioinformatics/bts603. [DOI] [PubMed] [Google Scholar]
- Lloyd DG, Calder VL. Multi-residue gaps, a class of molecular characters with exceptional reliability for phylogenetic analyses. J Evol Biol. 1991;4:9–21. [Google Scholar]
- Loytynoja A, Goldman N. Phylogeny-aware gap placement prevents errors in sequence alignment and evolutionary analysis. Science. 2008;320:1632–1635. doi: 10.1126/science.1158395. [DOI] [PubMed] [Google Scholar]
- Luan PT, Ryder OA, Davis H, Zhang YP, Yu L. Incorporating indels as phylogenetic characters: impact for interfamilial relationships within Arctoidea (Mammalia: Carnivora) Mol Phylogenet Evol. 2013;66:748–756. doi: 10.1016/j.ympev.2012.10.023. [DOI] [PubMed] [Google Scholar]
- McCrow JP. Alignment of phylogenetically unambiguous indels in Shewanella. J Comput Biol. 2009;16:1517–1528. doi: 10.1089/cmb.2009.0188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean CY, et al. Human-specific loss of regulatory DNA and the evolution of human-specific traits. Nature. 2011;471:216–219. doi: 10.1038/nature09774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miklos I, Novak A, Satija R, Lyngso R, Hein J. Stochastic models of sequence evolution including insertion-deletion events. Stat Methods Med Res. 2009;18:453–485. doi: 10.1177/0962280208099500. [DOI] [PubMed] [Google Scholar]
- Nagy LG, et al. Re-mind the gap! insertion - deletion data reveal neglected phylogenetic potential of the nuclear ribosomal Internal Transcribed Spacer (ITS) of Fungi. PLoS One. 2012;7:e49794. doi: 10.1371/journal.pone.0049794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak A, Miklos I, Lyngso R, Hein J. StatAlign: an extendable software package for joint Bayesian estimation of alignments and evolutionary trees. Bioinformatics. 2008;24:2403–2404. doi: 10.1093/bioinformatics/btn457. [DOI] [PubMed] [Google Scholar]
- Nuin PA, Wang Z, Tillier ER. The accuracy of several multiple sequence alignment programs for proteins. BMC Bioinformatics. 2006;7:471. doi: 10.1186/1471-2105-7-471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oren Y, et al. Transfer of noncoding DNA drives regulatory rewiring in bacteria. Proc Natl Acad Sci U S A. 2014;111:16112–16117. doi: 10.1073/pnas.1413272111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penn O, Privman E, Ashkenazy H, et al. GUIDANCE: a web server for assessing alignment confidence scores. Nucleic Acids Res. 2010;38:W23–W28. doi: 10.1093/nar/gkq443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penn O, Privman E, Landan G, Graur D, Pupko T. An alignment confidence score capturing robustness to guide tree uncertainty. Mol Biol Evol. 2010;27:1759–1767. doi: 10.1093/molbev/msq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perelman P, et al. A molecular phylogeny of living primates. PLoS Genet. 2011;7:e1001342. doi: 10.1371/journal.pgen.1001342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippe H, et al. Resolving difficult phylogenetic questions: why more sequences are not enough. PLoS Biol. 2011;9:e1000602. doi: 10.1371/journal.pbio.1000602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Privman E, Penn O, Pupko T. Improving the performance of positive selection inference by filtering unreliable alignment regions. Mol Biol Evol. 2012;29:1–5. doi: 10.1093/molbev/msr177. [DOI] [PubMed] [Google Scholar]
- Ranwez V, et al. OrthoMaM: a database of orthologous genomic markers for placental mammal phylogenetics. BMC Evol Biol. 2007;7:241. doi: 10.1186/1471-2148-7-241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redelings BD, Suchard MA. Joint Bayesian estimation of alignment and phylogeny. Syst Biol. 2005;54:401–418. doi: 10.1080/10635150590947041. [DOI] [PubMed] [Google Scholar]
- Robinson D, Foulds LR. Comparison of phylogenetic trees. Math Biosci. 1981;53:131–147. [Google Scholar]
- Rokas A, Holland PW. Rare genomic changes as a tool for phylogenetics. Trends Ecol Evol. 2000;15:454–459. doi: 10.1016/s0169-5347(00)01967-4. [DOI] [PubMed] [Google Scholar]
- Satija R, Novak A, Miklos I, Lyngso R, Hein J. BigFoot: Bayesian alignment and phylogenetic footprinting with MCMC. BMC Evol Biol. 2009;9:217. doi: 10.1186/1471-2148-9-217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons MP, Muller K, Norton AP. The relative performance of indel-coding methods in simulations. Mol Phylogenet Evol. 2007;44:724–740. doi: 10.1016/j.ympev.2007.04.001. [DOI] [PubMed] [Google Scholar]
- Simmons MP, Ochoterena H. Gaps as characters in sequence-based phylogenetic analyses. Syst Biol. 2000;49:369–381. [PubMed] [Google Scholar]
- Sing T, Sander O, Beerenwinkel N, Lengauer T. ROCR: visualizing classifier performance in R. Bioinformatics. 2005;21:3940–3941. doi: 10.1093/bioinformatics/bti623. [DOI] [PubMed] [Google Scholar]
- Stoye J, Evers D, Meyer F. Rose: generating sequence families. Bioinformatics. 1998;14:157–163. doi: 10.1093/bioinformatics/14.2.157. [DOI] [PubMed] [Google Scholar]
- Swofford D. 2003. PAUP* phylogenetic analysis using parsimony (*and other methods) Version 4.0b10. Sunderland (MA): Sinauer Associates. [Google Scholar]
- Talavera G, Castresana J. Improvement of phylogenies after removing divergent and ambiguously aligned blocks from protein sequence alignments. Syst Biol. 2007;56:564–577. doi: 10.1080/10635150701472164. [DOI] [PubMed] [Google Scholar]
- Taylor MS, Ponting CP, Copley RR. Occurrence and consequences of coding sequence insertions and deletions in Mammalian genomes. Genome Res. 2004;14:555–566. doi: 10.1101/gr.1977804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Templeton AR. Phylogenetic inference from restriction endonuclease cleavage site maps with particular reference to the evolution of humans and the apes. Evolution. 1983;37:221–244. doi: 10.1111/j.1558-5646.1983.tb05533.x. [DOI] [PubMed] [Google Scholar]
- Thompson JD, Linard B, Lecompte O, Poch O. A comprehensive benchmark study of multiple sequence alignment methods: current challenges and future perspectives. PLoS One. 2011;6:e18093. doi: 10.1371/journal.pone.0018093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Noorden R, Maher B, Nuzzo R. The top 100 papers. Nature. 2014;514:550–553. doi: 10.1038/514550a. [DOI] [PubMed] [Google Scholar]
- Wray GA, et al. The evolution of transcriptional regulation in eukaryotes. Mol Biol Evol. 2003;20:1377–1419. doi: 10.1093/molbev/msg140. [DOI] [PubMed] [Google Scholar]
- Wu M, Chatterji S, Eisen JA. Accounting for alignment uncertainty in phylogenomics. PLoS One. 2012;7:e30288. doi: 10.1371/journal.pone.0030288. [DOI] [PMC free article] [PubMed] [Google Scholar]