Rewiring of Genetic Networks in Response to Modification of Genetic Background

Abstract

Genome-scale genetic interaction networks are progressively contributing to map the molecular circuitry that determines cellular behavior. To what extent this mapping changes in response to different environmental or genetic conditions is, however, largely unknown. Here, we assembled a genetic network using an in silico model of metabolism in yeast to explicitly ask how separate genetic backgrounds alter network structure. Backgrounds defined by single deletions of metabolically active enzymes induce strong rewiring when the deletion corresponds to a catabolic gene, evidencing a broad redistribution of fluxes to alternative pathways. We also show how change is more pronounced in interactions linking genes in distinct functional modules and in those connections that present weak epistasis. These patterns reflect overall the distributed robustness of catabolism. In a second class of genetic backgrounds, in which a number of neutral mutations accumulate, we dominantly observe modifications in the negative interactions that together with an increase in the number of essential genes indicate a global reduction in buffering. Notably, neutral trajectories that originate considerable changes in the wild-type network comprise mutations that diminished the environmental plasticity of the corresponding metabolism, what emphasizes a mechanistic integration of genetic and environmental buffering. More generally, our work demonstrates how the specific mechanistic causes of robustness influence the architecture of multiconditional genetic interaction maps.

Introduction

Gene action is commonly determined by its interactions with other genes. This includes not only genes known to be associated to the action under study but also those whose association is less expected or their biochemical properties still unknown. Both classes of interactions can now be effectively mapped at a large scale by following two complementary strategies.

The first one relies on the progress of experimental tools to produce genetic perturbations in large numbers and to automatically quantify their effects (Baryshnikova et al. 2013, growth being typically the primary phenotypic readout but see, for instance, Jonikas et al. 2009). These tools are now providing initial genetic landscapes of cells (e.g., Roguev et al. 2008; Costanzo et al. 2010). A second approach benefits from the advance of computational methods capable to predict phenotypes. Metabolic flux balance models are particularly useful in this regard, as they incorporate genomic information (of metabolism) into an in silico framework that can estimate cell growth under specific conditions (Reed et al. 2006). Notably, flux balance predictions have been confirmed experimentally (e.g., Snitkin et al. 2008). Single mutant fitness and their corresponding genetic interactions can also be produced in this framework (Szappanos et al. 2011).

These strategies are currently being combined to better interpret the molecular underpinnings of genetic interactions (i.e., epistasis), both negative and positive. Negative epistasis (observed when the fitness defect of a double mutant is lower than that expected from single mutant values) indicates redundancy that can reveal as functional associations between some pathways and/or complexes (e.g., the presence of negative epistasis between the urmylation pathway and the elongator complex in yeast suggested that both jointly modify certain transfer RNAs, Costanzo et al. 2010) or as the buffering of alternative metabolic routes (e.g., leading to the synthesis of the same component, Papp et al. 2004). Positive genetic interactions, in contrast, are commonly observed between genes that constitute a multiprotein complex or metabolic pathway, that is, genes being part of the same functional unit (St Onge et al. 2007): A mutation in one of its constituents can inactivate this unit what reduces the effect of other perturbations in additional components.

Large-scale approaches lead as well to the identification of system-level patterns, when the interactions are represented as genetic networks. For instance, the network presentation of high-throughput data of Caenorhabditis elegans and Saccharomyces cerevisiae clearly identified the presence of genetic hubs that are mostly associated to chromatin regulation (Lehner et al. 2006; Costanzo et al. 2010). Another feature, revealed for the first time with flux balance modeling, is monochromaticity; the specific distribution of epistasis types in the interactions within/between functional modules (Segrè et al. 2005). This characteristic was later confirmed by metabolic experiments (Szappanos et al. 2011) and high-throughput data (Costanzo et al. 2010), in which a specific distribution of epistasis strengths was additionally identified (Poyatos 2011).

All previous properties implicitly suggest a stable architecture of genetic networks, a view that was partially influenced by the constant conditions in which interactions were examined. However, recent studies are emphasizing that this stability should not be necessarily the case. Genetic interactions and, more broadly, genetic networks were shown to change depending on the particular context where fitness is evaluated (You and Yin 2002; Harrison et al. 2007; St Onge et al. 2007; Bandyopadhyay et al. 2010; Guénolé et al. 2013). Rewiring is further confirmed by means of comparative analysis across organisms (Dixon et al. 2008; Roguev et al. 2008; Frost et al. 2012; Ryan et al. 2012). Moreover, the “instability” of these networks should not come as a surprise; earlier works already discussed the influence of context (environmental and genetic) on the phenotypic effect of mutations and their interactions (e.g., Chandler et al. 2013; Chari and Dworkin 2013), a phenomenon that can directly influence evolutionary dynamics (Greenspan 2009; Chou et al. 2011; Khan et al. 2011). To what extent genetic networks are context dependent is nevertheless mostly unknown.

Here, we ask how the structure of a genetic network reorganizes in response to changes in gene background. To this aim, we mapped genetic interactions between metabolic genes by using a computational model of metabolism in S. cerevisiae. The advantage of this approach (beyond avoiding experimental complexity) is that it enables the interpretation of the phenotype (i.e., fitness) as an univocal consequence of the structure of the metabolic reaction network underneath. We consider two broad (genetic) background classes. The first class corresponds to single gene deletions of each of the enzymes that are active (i.e., showed nonzero flux) in wild-type (WT) conditions. We characterized which type of backgrounds originate stronger network change and in which kind of interactions this variation is more pronounced. The rewiring patterns found stress the different organization of biosynthetic and catabolic routes and how this impacts their capacity to compensate change. A second class presents neutral backgrounds that are generated by a trajectory of accumulated neutral mutations. This helps us to appreciate how cryptic variability modifies buffering in genetic networks and how the new network structures associate to differential environmental plasticity. We additionally corroborate some of these patterns with inspection of experimental data.

Materials and Methods

Genotypes and Simulations

We considered the iND750 genome-scale model as the WT genotype (Duarte et al. 2004). This model incorporates all the necessary complexity of S. cerevisiae’s metabolism (e.g., it is fully compartmentalized), has been empirically corroborated, and also reduces the computational load associated to the background analysis. We studied two types of genotype derived from this model. Single deletion genotypes were obtained by deleting each gene present in the model individually. Neutral deletion trajectories were obtained by successively deleting genes that have no effect on phenotype (Pál et al. 2006, i.e., optimal growth does not change) until reaching 100 deleted genes. All optimizations were performed using flux balance analysis (FBA) (Price et al. 2004). WT growth conditions correspond to glucose minimal medium and aerobiosis (glucose: 18.5 mmol gr⁻¹ h⁻¹, unlimited O₂). Fluxes through all reactions in the solution of a given genotype were normalized by the amount of biomass produced. This enables the comparison of different solutions with distinct growth rates.

Generation and Processing of Genetic Networks

Optimal growth of all single and double deletion mutants, encompassing all nonessential genes in a given genotype, was computed using FBA (Price et al. 2004). The mutant/WT growth ratios obtained were used to compute the epistasis (ϵ) that incorporated a multiplicative model and posterior scaling (Segrè et al. 2005); interactions with $|\mathrm{ϵ}|<$ 0.01 were not considered. An additional processing was applied to the networks to simplify functional redundancies that are noninformative and do not contribute to the system-level analysis discussed in the article. Namely, we identified all sets of genes coding for exactly the same reactions and excluded all but one from each set for further analysis. This simplifies positive interactions associated to subunits of the same complex (e.g., mitochondrial ATP synthase has 15 essential subunits in the model, which results in $\left(\begin{array}{c}15\\ 2\end{array}\right)$ = 105 positive epistatic interactions) and also negative interactions that exist between equivalent gene duplicates coding for fitness contributing reactions. This data set reduction was applied in all our analyses, unless otherwise specified.

Types of Genetic Interactions

We classified genetic interactions in four groups according to the underlying functional structure. Synthetic lethal (SL) interactions, $\mathrm{ϵ}=-1$, involve two unique alternatives for an essential function. Strong positive (SP) ones, ϵ = 1, imply an absolute functional dependence, for instance, like the one found in genes that act sequentially in a parallel pathway. Two additional classes, weak positive (WP, $0.01<\mathrm{ϵ}<1$) and weak negative (WN, $-1<\mathrm{ϵ}<-0.01$) were defined. WN interactions appear when there exists an additional less efficient solution to the two main functional alternatives represented by the WN-interacting genes. This multiplicity of alternatives with different efficiency usually reflects that (qualitatively) different ways to perform a specific function. WP interactions emerge when the fitness contribution of the interacting genes is only partially overlapping, that is, if one of the genes is deleted, the other still contributes (although to a lower extent) to fitness. This could be interpreted as a form of “multifunctionality.” Note that, as positive interactions appear only among fitness contributing but nonessential genes, this implicitly reflects the presence of a less efficient and qualitatively different alternative.

Advantages of FBA

FBA was considered a suitable tool for this study due to several reasons—beyond the obvious advantage of avoiding the complications of producing the very large number of required genotypes experimentally. First, it simplifies several layers of biological complexity (e.g., gene expression or enzymatic activity regulation) by means of optimality assumptions in a relatively realistic way (Price et al. 2004). Although this could lead to some artifacts, they do not modify in any case the general conclusions of our analysis (see also supplementary material, Supplementary Material online). Second, the model enables a straightforward interpretation of the phenotype as an univocal consequence of the structure of the underlying metabolic reaction network. We can thus imagine the in silico model as a biological “organism” per se that can provide broad conceptual guidelines for a comprehensive interpretation of the rewiring of genetic networks associated to real biological systems (not necessarily restricted to metabolism).

Pleiotropy

We computed the pleiotropy of each nonessential and fitness contributing gene in the WT genotype following Szappanos et al. (2011). The method basically consists in optimizing for the production of a given biomass constituent individually (instead of using the entire biomass reaction) in presence and absence of a given gene. The number of affected constituents represents a rigorous measure of pleiotropy for that specific metabolic gene.

Rewiring and Metabolic Modules

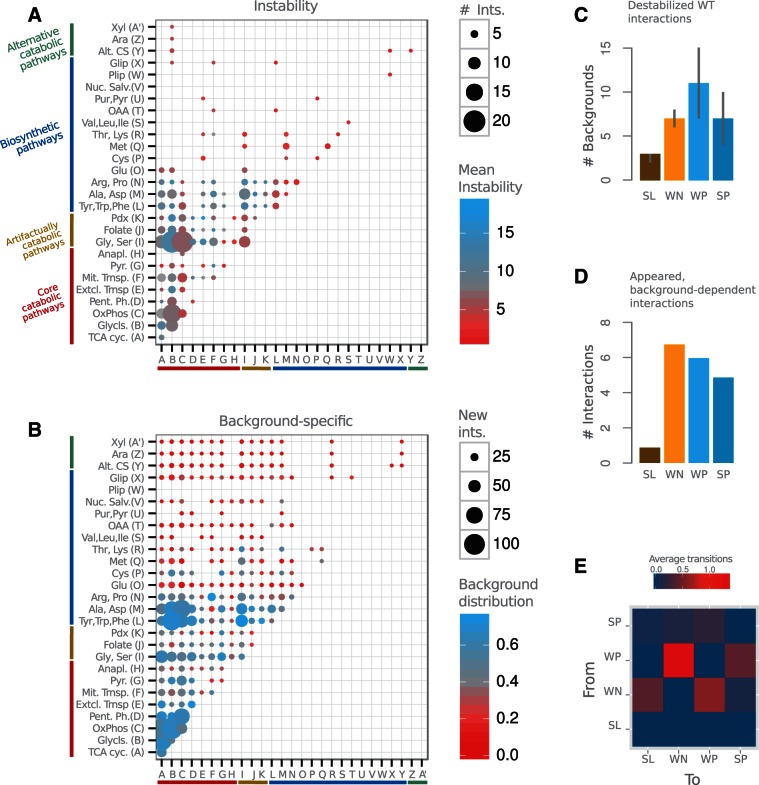
Background dispersion was quantified in figure 2B as normalized Shannon entropy $S_{\text{MP}}$ (MP denotes “module pair”). This is defined as $S_{\text{MP}}=-{\displaystyle {\sum }_{i=1}^n{k}_i}\log k_i/\log N$, with n being the number of backgrounds with new interactions between the two modules, and k_i the number of interactions appearing in the background i (divided by the total number of interactions considering all backgrounds). This was normalized by $\log N$, where N is the total number of analyzed backgrounds where any new interaction appears between any two modules (N = 37). The figure illustrates how catabolic modules are characterized by appearance of many different new interactions in different backgrounds. Conversely, much fewer interactions appear among biosynthetic modules, these being generally much more background specific. The notation of the modules in the figure can be found in supplementary table S6, Supplementary Material online.

Fig. 2.—

Catabolic and biosynthetic modules exhibit distinctive genetic rewiring. (A) Number of interactions of the WT network between the corresponding metabolic annotation modules (dot size) and associated average instability (dot color; measured for each interaction as the number of backgrounds where it disappears, changes sign, or strength). Catabolic modules show higher instability than biosynthetic ones. (B) New interactions (i.e., absent in WT network) between modules (dot size) and their distribution among backgrounds (dot color; distribution quantified as normalized Shannon entropy, see Materials and Methods). Catabolic modules are characterized by the emergence of many new interactions in different backgrounds. Fewer new interactions appear among biosynthetic modules, these being generally more background specific. (C) Instability of interactions, measured as the number of backgrounds in which they disappear, as a function of sign and strength (median with upper and lower quartiles). Weak interactions are more unstable than strong ones of the same sign, and positive interactions are more unstable than negative. (D) Average number of new interactions appearing in each background as a function of strength and sign. WN interactions appear dominant on average. (E) Expected number of transitions between interaction types in an average background. WP to WN conversions are the most recurrent ones. Interaction classes are SL, WN, WP, and SP, see Materials and Methods.

Random Environments

One thousand random environments were generated in which each of 107 organic nutrients was assigned a probability of being present from an exponential distribution (with mean = 0.1, Wang and Zhang 2009). After defining the particular set of nutrients, their dosage was randomly obtained by applying an uniform distribution between 0 and 20 mmol gr⁻¹ h⁻¹. All environments considered were aerobic (i.e., unconstrained O₂ availability).

Stability of Interactions in Response to Environmental Change

Data on instability of interactions in response to environmental change (yeast cells growing in rich media and in the presence of three distinct DNA damaging agents: Methyl methanesulfonate, camptothecin, and zeocin) were obtained from Guénolé et al. (2013). We considered as not significant epistasis those values below 2 and above −2.5 (following the original reference). We defined SP interactions as those in the upper quartile among positive ones and similarly for negative ones. The instability of each category in figure 7A was quantified as the average number of treatments where the interaction changes or disappears (out of three). We quantified the functional similarity of the genes constituting an interaction as the ratio between the number of shared functional classes (i.e., biological process annotations as in Guénolé et al. [2013]) and the minimal number of classes that one of the genes of the pair presents. If this score was more than 0.1 then genes were considered functionally “close” and “distant” otherwise. In addition, we considered an interaction “stable” if it remained within the same category (sign, strength) in all conditions and unstable otherwise (fig. 7B).

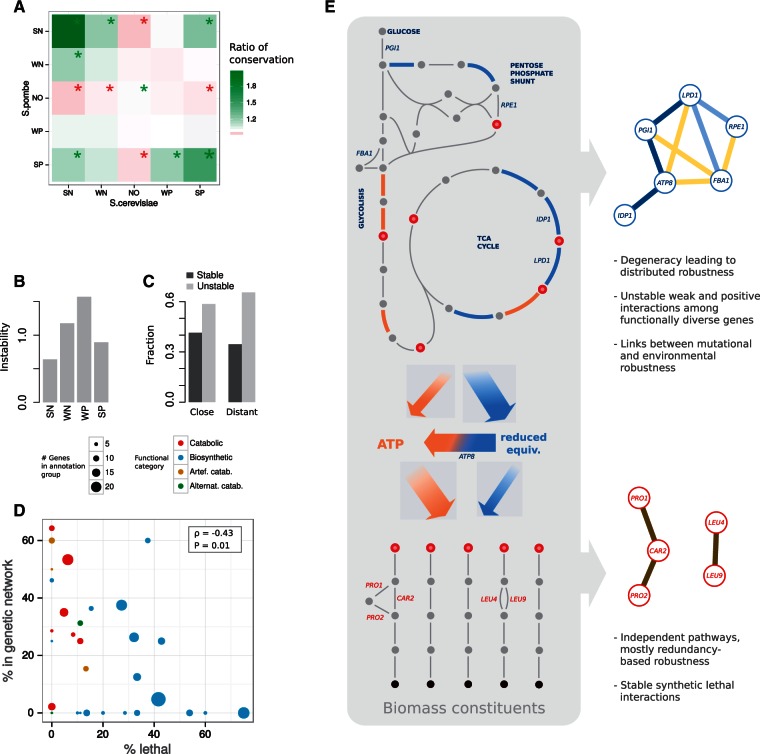
Fig. 7.—

Robustness influences rewiring patterns. (A) We identified interactions between a subset of genes, which are one-to-one orthologs between Saccharomyces cerevisiae and Schizosaccharomyces pombe using data from Ryan et al. (2012) and classified them by strength (SN [WN] denotes those that belong to the upper 30 [lower 70] percentile of all negative interactions, SP and WP are similarly defined, and NO denotes absence of interaction). Box colors represent ratios between the number of times that a transition is observed and its corresponding expected value (obtained by random permutation, 10,000 times; stars indicate significance with $P<{10}^{-4}$). (B) Relative instability of each interaction type after environmental change (interactions were experimentally characterized in yeast growing in rich media and in three different environments, Guénolé et al. 2013, Materials and Methods). This pattern is qualitatively similar to the one predicted in response to modifications of genetic background (fig. 2C). (C) We observe a higher proportion of unstable interactions among those genes functionally distant (${\chi }^2$ test, P = 0.003, see Materials and Methods). (D) Robustness and genetic landscape clearly distinguish catabolic from biosynthetic modules. Each dot represents a metabolic module with size and color indicating number of genes in the module and functional category, respectively. We show percentage of essential genes in each module (as a proxy of robustness; horizontal axis) and number of (nonessential) genes that are nodes in the WT genetic network (as a proxy of genetic landscape; vertical axis). We further confirmed this signal with experimental data (see Materials and Methods). (E) The architecture of catabolism and biosynthesis (left) determines the resulting genetic network and its stability (right). We show in blue the reactions producing NAD(P)H and in orange those producing ATP; metabolites (dots) that constitute biosynthetic precursors are highlighted in red. Some representative genes and their corresponding genetic interactions are included (color code of genetic interactions as previous figures).

Robustness and Genetic Landscape Clearly Distinguish Catabolic from Biosynthetic Modules

We downloaded from http://www-sequence.stanford.edu/group/yeast_deletion_project/deletions3.html a list of yeast essential genes and used the genetic interaction data of yeast metabolism from Szappanos et al. (2011). For each module, we computed the ratio between the number of essential and the number of epistatic genes that we term θ. Average θ for catabolic and biosynthetic modules is $\langle \theta \rangle$ = 0.18 and 0.94, respectively (Wilcoxon–Mann–Whitney test P = 0.01), what broadly confirms the predictions of the in silico model (fig. 7C).

Results

Rearrangement of the Catabolic Repertoire Determines Genetic Rewiring

We began analyzing the rewiring observed in genetic backgrounds defined by deletions of single genes that are metabolically active in WT conditions (see Materials and Methods). These deletions normally result in the blockade of some (nonessential) reactions and the corresponding reconfiguration of metabolic fluxes (Papp et al. 2004; Blank et al. 2005). How is this readjustment contributing to genetic rewiring?

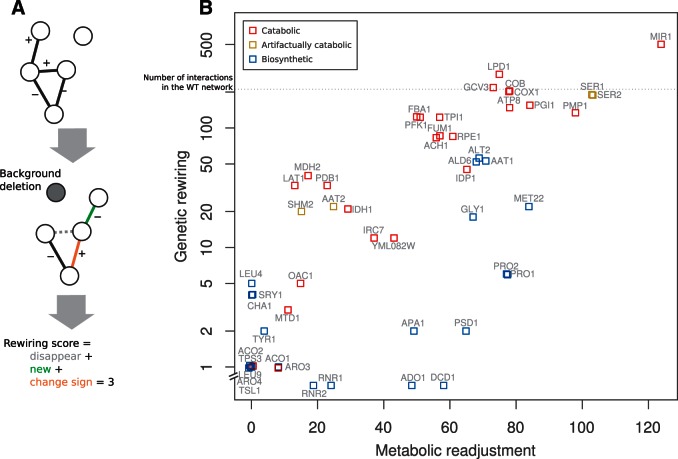
To understand this correspondence, we quantified the number of modified interactions with respect to the WT genetic network as a simple rewiring score (fig. 1A) and also counted the quantity of altered fluxes as measure of the underlying metabolic readjustment. Figure 1B shows the strong relation between these two scores (Spearman’s $\rho =0.72,P<{10}^{-8}$). We subsequently partitioned the metabolic measure into a qualitative and quantitative component (i.e., active fluxes that become inactive or vice versa and changes in relative flux through already active reactions, respectively). Qualitative changes predict the strength of genetic rewiring (multiple linear regression $P<{10}^{-8}$), whereas quantitative ones do not (P = 0.97). Thus, genetic rewiring denotes a redistribution of metabolic fluxes to alternative reactions and pathways.

Fig. 1.—

Genetic rewiring correlates with the underlying metabolic readjustment. (A) Cartoon that illustrates the kind of alterations in the genetic network that contributes to the rewiring score: new interactions + interactions that changed sign + disappeared links (excluding those of the gene acting as background). (B) Association between genetic rewiring and metabolic readjustment (as number of reactions that modified their relative flux) in response to deletions in active genes, that is, backgrounds; there exists 207 interactions in the WT network, we show this number as a dashed line to give a reference for the amount of rewiring. There are as well 277 active fluxes in the corresponding metabolism (coordinates incorporate some noise to help visualization, and the y axis logarithmic scale is broken to locate backgrounds with no genetic rewiring). Note that catabolic genes exhibit much stronger rewiring than biosynthetic ones, regardless of the strength of metabolic readjustment (some genes are artifactually catabolic in the model, see supplementary material, Supplementary Material online).

We then explored if the perturbation of any specific metabolic function leads to particularly strong rewiring. If backgrounds linked to a given function result in strong rewiring, this should be detectable as variation on its associated metabolites. We found that rewiring is predicted by the variation of several metabolites whose production and homeostasis is tightly connected to catabolism (e.g., phosphate, redox equivalents, quinones, or intermediaries from glycolysis or TCA cycle, supplementary table S1, Supplementary Material online). Indeed, backgrounds corresponding to catabolic functions display stronger rewiring than those related to biosynthetic functions (fig. 1B). Note also that the strong genetic rewiring produced by some apparently biosynthetic genes (e.g., SER1, SER2, or SHM2) revealed upon detailed inspection an artifactually catabolic role of these genes (e.g., ATP synthesis, supplementary table S2, Supplementary Material online) that validates a general catabolic underpinning of network rewiring.

Rewiring Is Pronounced between Functional Modules and in Weak Genetic Interactions

We next examined the association of rewiring with the underlying metabolic organization and the type of genetic interaction. We initially computed the instability of each WT interaction by simply counting the number of backgrounds in which it changes (from a total of 100). Interactions tend to be conserved with instability being stronger for those constituted by genes belonging to different metabolic annotation groups (mean instability within same group = 5.1, mean between groups = 7.8, $P=3.4\times {10}^{-5}$). New interactions exhibit as well a tendency to connect different modules (90% of cases) compared with the WT links (78%, Fisher’s test $P<{10}^{-7}$). This pattern resembles recent reports that detected stronger instability in interactions established between (rather than within) functional modules but in response to environmental change (Harrison et al. 2007; Bandyopadhyay et al. 2010).

Figure 2A explicitly illustrates the concentration of genetic interactions in catabolic modules (supplementary table S3, Supplementary Material online) and their high relative instability. Conversely, biosynthetic modules exhibit fewer and more stable links. Catabolic modules are characterized in addition by the appearance of new interactions in different backgrounds. In contrast, new links arise less frequently between biosynthetic modules and in a more background-specific manner (fig. 2B).

Moreover, the strength and sign of the interaction influences as well its instability. We observed weak interactions to be more unstable for each epistasis type (fig. 2C). Although this could be associated to the fact that weak links tend to appear between module (Fisher’s test, P < 0.0002) both being weak and between-module independently correlate to instability (supplementary fig. S1 and table S4, Supplementary Material online). Within new interactions, we also noticed that WN are the dominant class (fig. 2D) and the ones that take part of most sign changes (which usually occur between WN and WP, fig. 2E).

The Structure of Rewiring Evidences the Intertwined Organization of Catabolism

Deletion of catabolic genes originates therefore a strong rewiring of genetic interactions (fig. 1). That these genes exhibit large connectivity (genetic hubs correspond almost uniquely to catabolic genes, supplementary fig. S2, Supplementary Material online) and that this connectivity is dominantly constituted by weak interactions (i.e., nodes with weak average epistasis $|\mathrm{ϵ}|<0.5$ present a mean of ∼8 connections, while those with strong average epistasis, $|\mathrm{ϵ}|>0.5$, present ∼3, Wilcoxon test P = 0.003) suggest that the response to a change in (catabolic) backgrounds is very much linked to the rewiring of hubs—recall the stronger instability of weak links between catabolic modules, figure 2—what ultimately indicates the intertwined organization of catabolism (fig. 3).

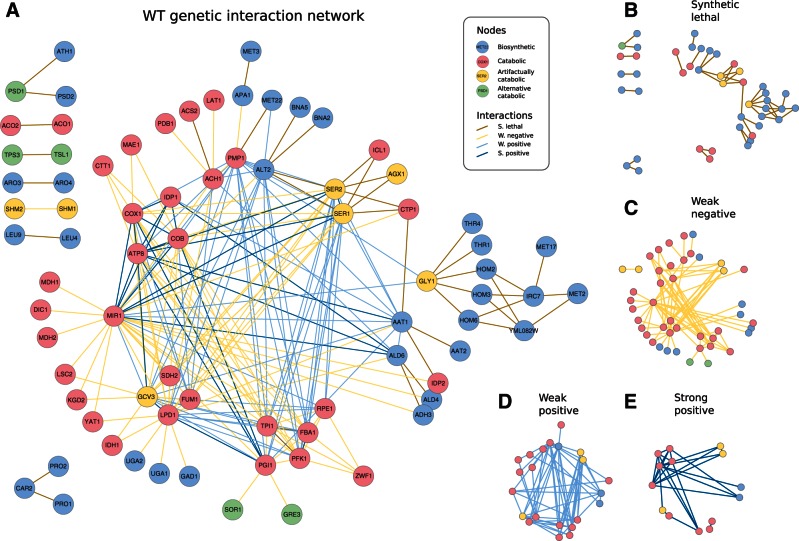
Fig. 3.—

The topology of the WT genetic network reflects the intertwined organization of catabolism. (A) WT genetic network with nodes colored by function and interactions by class. (B–E) Decomposition of the network into the four interaction classes. Note the association between these types and metabolic function (i.e., SL links broadly corresponding to biosynthetic genes and the rest—WN, WP, and SP—to catabolic) that we additionally corroborated with experimental data of epistasis between metabolic gene pairs Szappanos et al. 2011 (supplementary fig. S24, Supplementary Material online). The distribution of weak interactions emphasizes the intertwined organization of the catabolic core (some genes appear as artifactually catabolic in the model, see discussion in supplementary material, Supplementary Material online). Moreover, SL links appear in the “periphery” of this core (full details of each SL cluster in supplementary figs. S27–S33, Supplementary Material online).

This organization is effectively described by the action of a number of versatile genes capable to contribute to fitness in different ways (by altering their function) and to partially buffer each other’s action (fig. 3C–E). The abundance of WP interactions emphasizes the different means to contribute to fitness. For example, although glycolysis (e.g., genes such as TPI1 and FBA1) and the TCA cycle (LPD1 and FUM1) work in coordination to supply reduced equivalents to oxidative phosphorylation, they can also readjust their metabolic role when one of the subsystems is compromised (what causes WP links between TPI1 and LPD1 or FBA1 and FUM1; fig. 3D). Moreover, WN interactions indicate distributed buffering (Wagner 2005) among sets of genes that can implement a particular metabolic action with different degree of efficiency (fig. 3C). An example corresponds to MIR1 that negatively interacts with a group of genes that jointly represent a metabolic alternative for mitochondrial phosphate import (supplementary figs. S3–S5, Supplementary Material online). These include not only genes that contribute to the phosphate import strictly speaking but also many that reduce the redox imbalances generated by this alternative mechanism (as a result of malate being antiported out of mitochondria in exchange for phosphate), with far reaching consequences regarding the whole set of fluxes through catabolic pathways.

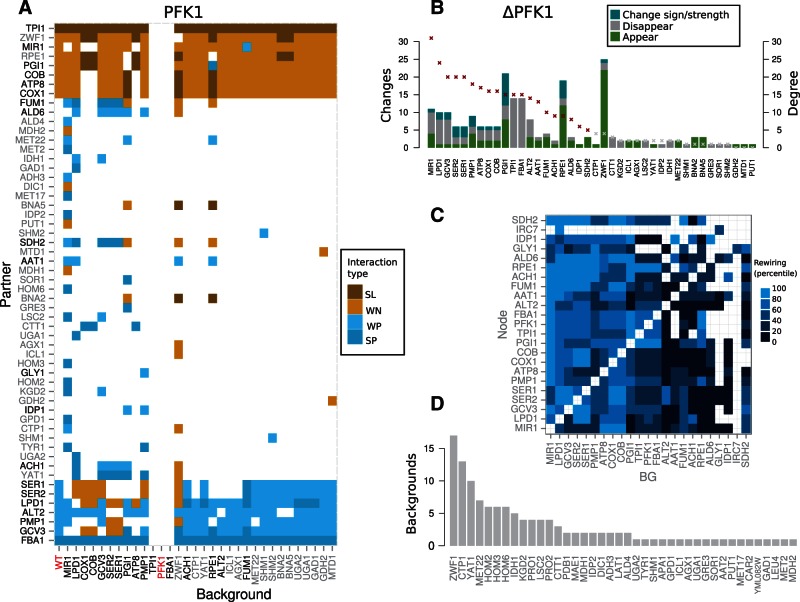
In figure 4A, we showed in detail an example of the rewiring experienced by a hub (PFK1) in different backgrounds (supplementary figs. S6–S14, Supplementary Material online, for rest of hubs). Despite the instability of their interactions, hubs tend to exhibit a remarkable connectivity conservation (supplementary fig. S15, Supplementary Material online). We further display the rewiring caused by PFK1 acting as background (fig. 4B) and how hubs principally rewire their interactions in response to the deletion of other hubs (fig. 4C); this demonstrates the functionally intertwined architecture of catabolism. Notably, we detected a number of genes that acquire the role of genetic hubs in some specific contexts and that frequently corresponds again to catabolic functions (fig. 4D).

Fig. 4.—

Rewiring of hubs. (A) Map of the genetic rewiring of interactions between hub PFK1 and its partners (vertical) in all backgrounds where rewiring of this hub is observed (horizontal). First column corresponds to the WT. Names of backgrounds and partners that are also genetic hubs are highlighted in black. PFK1 shows no connectivity in gene contexts ΔFBA1 that presents an SP link with PFK1, and ΔTPI1, that presents an SL link (i.e., PFK1 becomes essential in these backgrounds). Interaction classes denoted as figure 2. (B) Rewiring experienced by genes in a ΔPFK1 background (color coding illustrates the different types of rewiring). Note that most of the rewiring in this background is observed in hubs (gene connectivity, i.e., degree, also shown)—most specially, in those that are functionally related, e.g., PGI1, TPI1, FBA1—and pentose phosphate genes that assume initial glucose processing after PFK1 deletion. (C) Rewiring of hubs in response to hub deletions. Each rewiring score was normalized by the connectivity of the specific hub in the WT network. The map represents the percentiles of these normalized scores (with percentiles [20, 40, 60, 80, and 100] corresponding to values of [0.22, 0.40, 0.66, 0.96, and 5.6]; a value of 1 means that the number of rewired interactions equals WT connectivity; empty spaces correspond to absence of rewiring). The only hub with a purely biosynthetic function (IRC7) is the one deviating most for this general pattern. (D) List of genes acting as condition-dependent hubs, and number of backgrounds in which they exhibit such large connectivity; many of these genes are related to catabolism.

Genetic Rewiring in Neutral Backgrounds Indicates Reduction in Buffering

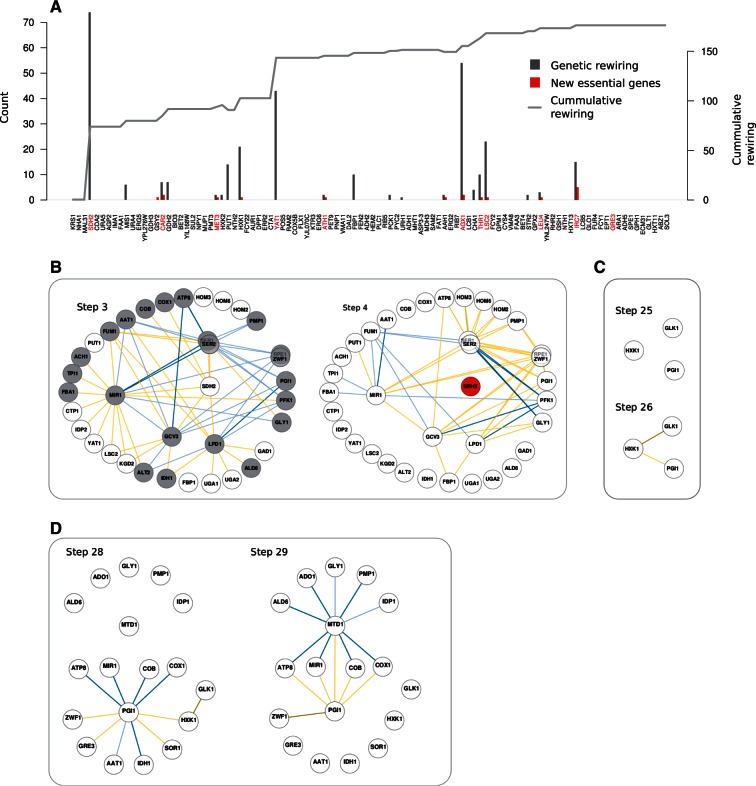
We now introduce a second class of genetic backgrounds in which a set of neutral gene deletions accumulate (see Materials and Methods and fig. 5A for a case trajectory). How does the network rewire in response to these backgrounds? We answer this question by discussing first which genes appear in neutral backgrounds and how their mutation modifies the network.

Fig. 5.—

Detailed view of a neutral deletion trajectory. (A) Genes were consecutively removed (from left to right; nodes of the WT network in red) what accumulates network rewiring (curve). Bars depict “local” change or rewiring score and number of essential genes (both with respect to the previous step). Many deletions do not affect network topology but some few ones produce strong rewiring. The appearance of essential genes is concomitant with variable amounts of genetic rewiring. (B–D) The subnetworks that get to be modified before and after several critical steps of the trajectory. Deletion of SDH2 (B) reveals second-order alternatives to the action of this gene in the “buffering ladder” (as new negative interactions). Several genes additionally undergo changes in their functional role that are reflected in modification of their interaction signs and, notably, in the emergence of new positive interactions. In (C), after the deletion of one of the three alternatives for hexokinase (HXK2), the other two constitute an SL link (HXK1 and GLK1). HXK1 is also able to phosphorylate fructose, and this underlies a supplementary WN interaction with PGI1. Finally, in (D), deletion of HXK1 further rewires PGI1 interactions (e.g., the WN link with pentose phosphate pathway gene ZWF1 becomes SL, as the only alternative for initial glucose processing) and induces several positive links at a relatively distant part of catabolism, for example, MTD1, involved in the artifactual glycine fermentative pathway (color code of genetic interactions as previous figures).

Note that a subset of these deletions could correspond to nodes of the WT network. This implies genes that are part of negative interactions and broadly causes the emergence of novel buffering connections (in terms of new interactions or change of sign of WT links). This is observed for instance in the deletion of SDH2 in figure 5A, a gene that acts as buffer in WT conditions of GCV3, LPD1, etc. (fig. 5B). SDH2 deletion uncovers secondary buffering mechanisms (e.g., by FBP1 or GLY1). Changes of sign in WT links are observed as well; for example, interactions with MIR1 or ZWF1. These changes are typically exhibited by catabolic genes in which different pathways often contribute to fitness either feeding one another linearly (e.g., to ultimately supply redox power to oxidative phosphorylation) or serving as substitutes to each other (e.g., as direct mechanisms of ATP synthesis). In some cases, the new buffering mechanisms can additionally modify how active genes contribute to fitness by removing, or adding, positive interactions to the network (e.g., ALT2–GCV3 link in fig. 5B). Note also how genes that become nodes in one step of the trajectory can produce relatively strong rewiring when they undergo subsequent deletion (e.g., FBP1 that turns into a node after SDH2 mutation to be deleted in a later step, fig. 5A).

Other genes that arise in neutral backgrounds (not being network nodes) can reduce too buffering alternatives. This can be exemplified, for instance, with the deletions of MIS1 or HXK1/HXK2 in figure 5A. The latter is especially illustrative, as three different genes are capable of performing the glucose phosphorylation reaction: HXK1, HXK2, and GLK1. HXK2 is deleted first, and the two remaining ones then exhibit an SL link (fig. 5C). When HXK1 is later deleted, GLK1 becomes essential. However, HXK2 and HXK1, but not GLK1, are capable to perform additional functions as hexokinases, such as fructose or mannose activation. Although not essential, reduction of these functions induces many new catabolic constraints that uncover new genetic interactions: Negative ones, between glycolysis and respiration, and positive ones, between respiration and folate pathway genes (fig. 5D).

Similar analyses of a group of 200 alternative neutral backgrounds contribute to distinguish common patterns of change. First, the corresponding networks exhibit a smaller number of nodes (196 out of 200 contain less nodes than WT). This signal relates of course to the deletion of negatively interacting nodes (supplementary fig. S16, Supplementary Material online) that points to modifications of buffering mechanisms. Second, networks tend to exhibit more epistatic interactions per node (166 out of 200 present larger average epistasis), a pattern again related to negative interactions (supplementary fig. S16, Supplementary Material online). Third, the negative component of the network undergoes a significantly stronger rewiring than the positive one (supplementary fig. S17, Supplementary Material online). This suggests overall that previously hidden phenotypic effects unveiled as a result of the global reduction in buffering mechanisms. This is further evidenced by an increase in the number of essential genes, which is observed in 93.5% (187/200) of genotypes and occurs concomitantly with rewiring of the network.

Catabolic Perturbations Associate Network Instability to Diminished Environmental Plasticity

One could expect that not all accumulated deletions in the neutral backgrounds impair metabolism in the same way, and thus different backgrounds could cause contrasting metabolic plasticity. This can be detected by generating diverse random environments (Wang and Zhang 2009, Materials and Methods) in which fitness is computed. The resulting growth measures did reveal the cryptic variability linked to the neutral trajectories (fig. 6A).

Fig. 6.—

Genetic rewiring patterns predict loss of environmental plasticity in response to neutral backgrounds. (A) Environmental plasticity exhibited by 4,000 different metabolisms originated from the WT after following a neutral deletion trajectory. Plasticity is scored as the median of the fitnesses (growth ratio) of each genotype in 1,000 randomly generated environments (growth ratio, in a given environment, is the division between growth rate of a particular metabolism to the WT growth rate). We highlight in red the groups with HG and LG. (B) Fraction of conserved interactions by type and LG or HG genotypes. (C) Distribution of the number of essential genes in the HG and LG groups. (D) We performed a bootstrapping analysis to check for enrichment/depletion of each metabolic gene in the LG or HG trajectories. Genes significantly enriched (or depleted) in the HG genotype, LG genotype, or both were correspondingly colored in blue, yellow, and green (P < 0.01, after multiple testing). Inset. Percentage of genes with genetic interactions in the WT network in these significant groups. Interaction classes denoted as figure 2.

To relate this variability to specific rewiring patterns (in WT conditions), we assembled the genetic networks of the 100 genotypes with the highest (and lowest) median growth (HG and LG, respectively; note that these are the 200 networks considered as a whole before). Those networks corresponding to LG genotypes display a significantly stronger rewiring (fig. 6B and supplementary fig. S18, Supplementary Material online) and are considerably smaller both in number of nodes and edges (supplementary fig. S19, Supplementary Material online). In addition, interactions associated to catabolic pathways were considerably less conserved in LG genotypes (supplementary fig. S20, Supplementary Material online).

Although the number of new interactions did not differ between LG and HG (mean = 60.6 and 61.0, respectively, P = 0.96, see also supplementary fig. S21A, Supplementary Material online), a subset of them appeared more frequently in LG genotypes—notably, negative ones between pentose phosphate pathway (ZWF1 and RPE1) and other catabolic genes (e.g., PGI1, MIR1, or LPD1, supplementary fig. S21B and S21C, Supplementary Material online). Sign and/or strength change was also considerably stronger in LG genotypes (mean = 24.3 interactions/genotype) when compared with HG (mean = 13.4 interactions/genotype, $P=6.7\times {10}^{-14}$, supplementary fig. S21D and S21E, Supplementary Material online). As a result of the stronger rewiring, LG networks exhibited higher negative-to-positive interaction ratios than HG ones (mean = 1.65 vs. 1.53, Wilcoxon’s test P = 0.0005). The number of essential genes was higher as well (fig. 6C), including several crucial catabolic components (e.g., ATP8, FBA1, PGI1, supplementary fig. S22, Supplementary Material online).

These results evidence that the loss of catabolic buffering mechanisms underlies both genetic network rewiring and reduction of environmental plasticity in LG genotypes. Namely, carbon sources other than glucose usually require only few transformation steps before being incorporated into the core catabolic pathways, for example, at different steps of glycolysis or TCA cycle. Some other sources are alternatively transformed into glucose by means of gluconeogenesis. Core catabolic pathways are used then with relative independence of the external carbon source. However, they can be used differently: Some branches that are optimal in one environment can be suboptimal in another (where they can nevertheless serve as an alternative to the optimal one). This is further corroborated by the differential distribution of deletions between LG and HG genotypes (fig. 6D). LG genotypes are enriched in 26 specific deletions that can be grouped in 1) genes important for the initial processing of different carbon sources (e.g., PNP1, XYL2, XKS1, GAL1, etc), 2) gluconeogenesis (e.g., PCK1), and 3) key catabolic genes, such as SDH2, KGD1, or LSC1. Although neutral in glucose minimal medium, they constitute buffering mechanisms for deletions in other catabolic genes (evidenced also by their multiple negative interactions) but importantly can take over their role under different carbon sources.

Discussion

Different genetic backgrounds can modify the observed phenotype of the interactions between mutations and consequently rewire genetic networks. Here, we systematically examined how backgrounds impact networks by using an in silico model of yeast metabolism (Reed et al. 2006, Materials and Methods).

We first analyzed to what extent strong genetic rewiring is necessarily coupled to strong metabolic readjustments. To this aim, we introduced a class of backgrounds defined by single deletions of active enzymes (i.e., that exhibit nonzero flux in WT conditions). As simple score to measure metabolic reorganization, we counted the number of reactions with a change of flux upon deletion. We found a relatively large number of backgrounds that exhibit substantial readjustment. However, only those that involved a switch to alternative metabolic pathways appeared coupled to strong genetic rewiring (fig. 1). These backgrounds correspond to a set of catabolic genes that act as genetic hubs (fig. 1 and supplementary fig. S2, Supplementary Material online). Interestingly, we also noticed strong genetic rewiring in genes that (artifactually) act as catabolic in the in silico yeast (see supplementary material, Supplementary Material online), which further confirms the linkage of metabolic readjustment and strong rewiring through catabolism.

In fact, most of the genetic instability is observed in the densely connected subnetwork associated to central catabolic functions, which is mainly composed of positive and weak interactions between different functional modules (figs. 2 and 3). In this way, the structure of the WT network is already representing the functional associations that are more sensitive to background change. In addition, most of the background-specific (i.e., not observed in the WT) interactions and hubs are as well related to catabolism and enriched by intermodule WN epistasis (figs. 2B and 4D).

The strong correlation between rewiring and perturbation of currency metabolite balances (supplementary table S1, Supplementary Material online) greatly helps to understand these patterns. The existence of multiple NADH/NADPH and ATP producing enzymes in catabolic pathways enables them as potential substitutes to each other, that is, as regulators of currency metabolite homeostasis (Fuhrer and Sauer 2009). But these mechanisms are not equivalent biochemically and consequently not equally optimal (see supplementary figs. S3–S5 for an example, Supplementary Material online). Catabolism exhibits then a functional degeneracy in which qualitatively different catabolic configurations lead to similar but not identically efficient solutions (Wagner 2005). This explains many of the phenotypic features corresponding to catabolic genes. In particular, it causes catabolic genes to be typically nonessential but often fitness contributing. Degeneracy explains too the pervasiveness of weak and unstable interactions, which reflects either fitness contributions that are partially shared (WP) or deficient buffering (WN). Notably, background-dependent interactions tend to be weak as well. In sum, the distributed nature of catabolic processing determines the transient and context-dependent functional associations that define its epistasis network.

Biosynthetic pathways exhibit in contrast a much different architecture. They usually display relatively isolated and linear configurations, each of them containing very specific metabolites that simply act as intermediates for the synthesis of a particular compound. This limits the buffering possibilities compared with catabolism what is manifested in the enrichment of essential genes and also in a genetic landscape dominated by redundancy-based SL interactions (fig. 3, supplementary figs. S27–S33, Supplementary Material online). These SL interactions form smaller (peripheral) clusters and exhibit a marked stability that only becomes disrupted when one of the partners is deleted or becomes essential (figs. 2–4).

These findings are consistent with several evidences from previous experimental studies on the rewiring of genetic interactions between two distantly related yeasts (S. cerevisiae and Schizosaccharomyces pombe; studies not always linked to metabolism). For instance, SL pairs and interactions within functional modules were found considerably conserved, whereas interactions between modules remodeled (Dixon et al. 2008; Roguev et al. 2008)—both signals confirming what we observed. The change of epistasis sign that we detected in catabolic nodes could also indicate a sort of functional repurposing (Frost et al. 2012). Moreover, using data from (Ryan et al. 2012), we corroborated our predictions that weak interactions are more unstable than strong ones (4.9% vs. 8.7% of conservation, respectively, ${\chi }^2$ test, $P<2.2\times {10}^{-16}$), as well as of positive interactions (0.8% conserved) compared with negative ones (5.4%, ${\chi }^2$ test, $P<2.2\times {10}^{-16}$, fig. 7A). Additionally, we observed that interactions associated to central metabolic pathways tend to be more unstable (39.4% of pairs not conserved) than those associated to the rest of metabolism (29.0% not conserved, ${\chi }^2$ test, $P<2.2\times {10}^{-16}$, metabolic classification according to Kanehisa et al. [2014]). Finally, we also recognized an association between interaction type and metabolic function (as we found in silico) in a set of genetic interactions recently measured experimentally between metabolic genes (supplementary fig. S24, Supplementary Material online) (Szappanos et al. 2011).

Likewise, our analysis clarifies the linkage among fitness contribution, pleiotropy, and network connectivity (node degree) (Szappanos et al. 2011). That a particular gene is nonessential but contributes to fitness implies the existence of a number of inefficient distributed buffering mechanisms (Papp et al. 2004) of the type observed in catabolism. Pleiotropy is in addition strongly related to catabolism due to the participation of currency metabolites in all biosynthetic routes of biomass constituents. Pleiotropy is thus present in catabolic genes and absent in biosynthetic ones (supplementary table S5, Supplementary Material online), and its correlation with fitness contribution and node degree could in the end denote the distributed robustness of the catabolic subsystem. As expected, both pleiotropy and fitness contribution anticipate rewiring (supplementary fig. S23, Supplementary Material online).

We examined a second class of backgrounds that are rather defined by (the accumulation of) neutral deletions (fig. 5) (Deutscher et al. 2006; Pál et al. 2006). These trajectories generally originated metabolisms with a higher incidence of essential genes and smaller but more densely connected genetic networks (supplementary fig. S16, Supplementary Material online). This denotes overall a global reduction in buffering (supplementary fig. S19, Supplementary Material online). Neutral backgrounds also modify environmental plasticity (i.e., capacity for robust growth in a range of environments) in divergent ways (fig. 6A–C and supplementary figs. S20 and S21, Supplementary Material online). Notably, genetic networks associated to more limited plasticity present strongest genetic rewiring that it is mainly observed in interactions between genes associated to catabolic function (fig. 6D). The mechanistic explanation is that, after usually few initial specific processing steps, all contrasting carbon sources enter the common catabolic core (glycolysis, TCA cycle, and respiration). Mutations that are neutral in glucose minimal medium (affecting less efficient catabolic routes) can nevertheless represent the most efficient catabolic processing alternatives in other carbon sources.

The connection between environmental and genetic robustness (Meiklejohn and Hartl 2002) would further predict that the patterns identified in response to the alteration of genetic background could be similarly recognized in reaction to environmental change. To test this hypothesis, we characterized rewiring of a recently assembled (yeast) genetic network after several DNA-damaging treatments (Guénolé et al. 2013). Conservation of the untreated network is well predicted by our model, with weak interactions being more unstable than strong, and positive more unstable than negative (fig. 7B, compare with fig. 2C). Interactions among genes that are functionally related were also more stable (fig. 7C). Moreover, treatment-specific links occur between functionally different genes (92% when compared with 87% in the untreated network, ${\chi }^2$ test, $P=3\times {10}^{-15}$) and are more often weak (supplementary fig. S25, Supplementary Material online).

In summary, we showed how distinct functional structures within the metabolic system, that is, biosynthesis and catabolism, determine both the architecture of the network and its rewiring (fig. 7C and D), an interpretation that is naturally coupled to the two main sources of robustness, that is, redundancies and distributed compensation (Wagner 2005). These predictions are based on global features of metabolism, what overcomes the limitations associated to FBA modeling (that sometimes generates artifacts due, for instance, to its latent optimality assumptions, Szappanos et al. 2011, but that nevertheless can provide useful conceptual guidelines to the associated biology, Wagner 2005). Differential network mapping should thus consider the specific mechanistic causes of robustness in the system under study to accurately interpret the dynamic rewiring of genetic networks in health and disease (Ideker and Krogan 2012; Furlong 2013).

Supplementary Material

Supplementary tables S1–S6 and figures S1–S33 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).