Nanoscale radiation transport and clinical beam modeling for gold nanoparticle dose enhanced radiotherapy (GNPT) using X-rays

Abstract

We review radiation transport and clinical beam modelling for gold nanoparticle dose-enhanced radiotherapy using X-rays. We focus on the nanoscale radiation transport and its relation to macroscopic dosimetry for monoenergetic and clinical beams. Among other aspects, we discuss Monte Carlo and deterministic methods and their applications to predicting dose enhancement using various metrics.

INTRODUCTION

The main purpose of using gold nanoparticles (GNPs) in radiotherapy is to enhance ionizing energy deposition at nanometre to micrometre distances from nanoparticles^1,2 and through this to increase the tumour control probability and decrease the normal tissue complication probability (NTCP). The ultimate goal of radiation transport computations for GNP dose-enhanced radiation therapy (GNPT) is to estimate the overall impact of various physical and clinical factors on the tumour control probability and NTCP. However, because of the multiscale dose deposition patterns and their complex relation to radiobiological factors, the computations require simplifying assumptions. These assumptions are often helpful to build our knowledge piece by piece and it is an acceptable approach provided that the simplifications are carefully considered in practice.

In the present review, we summarise the major challenges encountered in radiation transport and modeling of clinical beams for GNPT. The challenges are both conceptual and computational and can be grouped into several central interdependent categories: (A) multiscale computational problem for a single GNP, (B) X-ray interaction with clusters of GNPs vs a single GNPs homogeneously distributed gold atoms in tissue, (C) distribution of GNPs and clusters of GNPs with respect to cellular and molecular targets, (D) spectral content (aka quality) of clinical beam at a given location in a patient occupied by GNPs, (E) decrease of X-ray flux and hardening of the beam by macroscopic GNP regions, (F) modification of clinical radiation fields or beamlines to achieve maximum dose enhancement, (G) modification of nanoparticle size, shape and structure to optimize dose enhancement, (H) imaging of macroscopic concentrations vs single GNPs, (I) the usage of GNPs in other than X-ray beams (proton, electron), (J) the usage of other than GNPs or contrast agents. We focus mostly on the radiation transport at nanoscales and macroscales and discuss other topics such as radiobiology, the factual biodistribution of GNPs, or clinical beam aspects only to the extent in which they are related to the radiation transport problem and to patterns of energy deposition at various scales. We will limit our discussion from (A) to (F).

For convenience, we arrange the literature according to the following order: general radiation transport aspects relevant for nanoscale simulations,^3–22 macroscopic dose enhancement in contrast agents and dose perturbation at high-Z material interfaces,^23–45 radiation transport for nanoscopic dose enhancement of GNP,^46–58 radiobiological and clinical aspects of GNPT,^59–67 application of Monte Carlo (MC) simulations to cellular environment,^68–70 modification of linear accelerator spectra to maximize dose enhancement⁷¹ and GNPT using other than X-ray therapeutic beams (proton, electron).^72–75

The problem of disparate scales

The presence of high atomic number (high-Z) nanoparticles irradiated by photons gives rise to dose enhancement in the surrounding medium owing to secondary electrons leaking from the nanoparticles. In high-Z materials, in the energy range below about 500 keV, photoelectric absorption dominates the photon interaction processes. Many but not all of the resulting photoelectrons and Auger electrons escape from the nanoparticle and deposit their energy in the close vicinity of the nanoparticle, usually within a few microns. The distribution of the energy deposition density peaks near the surface of the nanoparticle, and within the order of 100 nm, it precipitously drops by nearly an order of magnitude.

One of the most significant complicating factors in the computation of nanoscale energy deposition is the substantially different length scale of photon vs electron interactions. While photon cross-sections strongly depend on energy and material type, electron cross-sections do not exhibit the same dependence. For example, at 100 keV the photon cross-section for gold is nearly 600 times greater than that of water and its energy dependence is proportional to E^−2.5 (below K-edge). In contrast, electron cross-sections show a difference of only a factor of 5–50 over a wide range of energies from 1 keV to 100 keV. While the relative differences between electron cross-sections of different materials are small, the absolute cross-sections are orders of magnitude greater than in the case of photons. Consequently, the mean free path of 100 keV photons in gold is about 100 µm while that of electrons of the same energy is approximately 50 nm. This means that while in 100 µm the intensity of photons incident on gold is reduced by only a factor of approximately 2/3, even the most energetic electrons born in the gold due to photon interactions can be stopped in about one tenth of that distance.

Thus, when photons are incident on a 2-nm gold sphere, <0.01% of them will undergo interaction. It becomes obvious that as the size of the GNP is increased, there is a third order increase in the photon interaction rate, while there is a concomitant decrease in the number of escaping electrons per interaction. Therefore, in MC computations large GNP sizes improve the photon interaction simulations while they deteriorate the efficiency of electron transport simulation, as many electrons do not reach the surface of the GNP while they still demand CPU time. Small GNP sizes suffer the reverse effect: there are too few photon interactions in the GNP volume but the resulting secondary electrons mostly escape.

MC computation, despite its preponderance in the research literature, may not be the best simulation approach in the nanoscale. Except for those that aim to resolve the track structure, most MC computer codes employ the condensed history electron transport method and apply an energy cut-off of 1 keV or 10 keV. This translates to electron ranges of approximately 8 nm in gold and 37 nm in water at best, limiting the spatial resolution of the simulation to these scales. However, while this spatial resolution is not needed between the phantom surface and the location of the macroscopic GNP-laden regions, it may be too coarse to adequately capture the variation of dose at the nanoparticle and molecular scales. Although track-structure MC computations can, in principle, provide adequate spatial resolution, they are vastly inefficient for practical computational domains of interest. In such relatively simple geometries as spherical and cylindrical symmetry, deterministic computational methods often offer superior performance at these spatial scales. Therefore, investigators use various methods, depending on the end point of their simulation, often combining them and segment the simulation to different spatial scales.

Monte Carlo vs deterministic radiation transport simulations

Boltzmann transport equation

Radiation transport simulations numerically solve Boltzmann's linear transport equation. For dose computations in a general case, coupled electron–photon transport must be considered. In charged particle equilibrium (CPE), the transport of secondary electrons can be often neglected, which is equivalent to the assumption that the electrons deposit their energy locally. This simplification permits relatively short computer running times at the expense that the simulation cannot predict the spatial distribution of energy deposition at the interface of high-Z and low-Z materials, that is near the GNP.

Monte Carlo and deterministic methods

Boltzmann's transport equation can be numerically solved by deterministic or stochastic methods. The deterministic approach explicitly solves the problem in the entire phase-space using a finite-differencing technique (such as discrete ordinates) and gives the solution for the mean response of the system.^3,19 In this method, the spatial domain is divided into meshes, the energy is divided into groups and the angular domain is divided into discrete directions. By contrast, the stochastic approach (aka MC method) samples the probability distribution of each particle interaction and simulates the particle trajectory, including progenies, which is known as history. Many histories are run and their response contributions are scored at discrete tally volumes or surfaces. The mean response and their statistical uncertainty are computed from the central limit theorem.

A significant advantage of the MC method is that, at least in theory, it can accurately follow each particle through complex geometries. Unlike the deterministic approach, the response tally is not restricted to the particle flux but it can include other information, such as energy deposition spectrum, pulse height distribution and stopping power. The main limitation of the MC method is the presence of statistical errors, which makes it very inefficient in particle-deprived regions, such as small dose volumes (e.g. GNP) or in deep penetrations. Typically, owing to finite computational speed and memory, simulation of a realistic number of particle histories is not feasible or practical. Variance reduction techniques are used to decrease the number of histories required to achieve low statistical uncertainty. However, caution must be exercised with these non-analogue techniques, as they can introduce non-physical tally scores, and great experience is needed for their reliable use.

The advantage of the deterministic approach is its superior speed of computation, often by many orders of magnitude over that of MC simulations, and that it does not entail statistical uncertainties even at very high spatial and energy resolutions. However, the accuracy of the deterministic method depends on the precision of the discretization. Unlike the MC, this method cannot resolve the position, energy and angle of each particle at every interaction, but it is confined into discrete spatial meshes, energy groups and angular directions. The requirement of using predefined spatial elements in sufficient resolution invariably results in a large number of phase space variables that increase the I/O time of the computation. Furthermore, in using the discrete-ordinates method for the angular discretization, the linear Boltzmann transport equation is solved along a finite number of angles selected from a predefined angular quadrature set. Although for a large number of angles, the discrete-ordinates solution can provide as good a result as MC and for a weakly scattering medium (e.g. water), a numerical “build-up” of the particle flux occurs along discrete angles, which results in non-physical oscillations or ray effects. For example, a simulation artefact of spatial oscillations in the energy deposition may occur owing to directional undersampling and/or too few energy groups (Figure 4c).

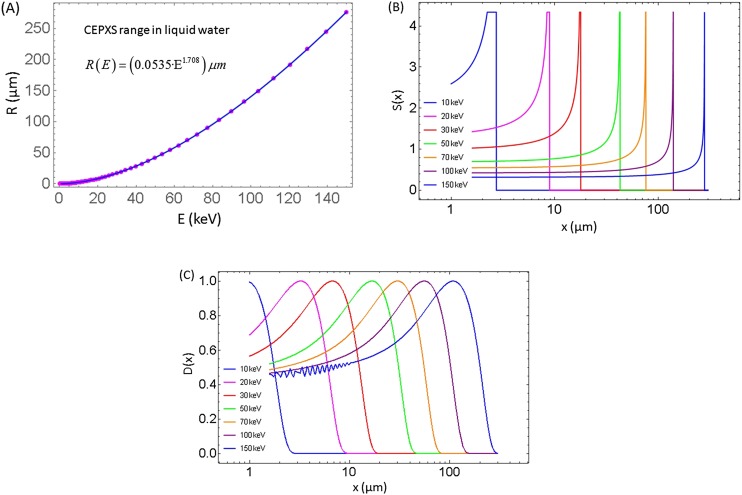
Figure 4.

(a) Range of electrons in water R (E) based on CEPXS simulation.¹⁹ Additional range-energy relation can be found in the study by Meesungnoen et al.¹⁰ (b) The resulting stopping power S (x) using an approximate computational model (without range or energy straggling) based on electron range data shown in (a) for various monoenergetic electron beams. Singularities in the stopping powers are truncated for display purposes. (c) Normalized dose D (x) for monoenergetic plane-parallel electron beams in watercomputed using CEPXS/ONEDANT. Numerical oscillations are intentionally shown for the 10 keV case. This is an example of artefacts in deterministic results due to suboptimal parameters (here, too few energy groups).

On the other hand, the statistical error in MC estimation depends not only on the number of histories but also on the number of particles in a given region of interest. In contrast, the uncertainty in deterministic computations does not depend on the initial number of particles or the number of particles in a given region. Furthermore, with decreasing size of the scoring voxel, MC fluctuations increase. Deterministic methods do not use scoring within voxels but rather evaluate physical quantities at specific coordinates and mesh points.

Modeling of geometry of the medium is a problem in all numerical methods. Even though it is often assumed that MC can be used to simulate any geometry, the medium has to be divided into cells or voxels and material properties have to be ascribed to each voxel. In MC, electron transport through interfaces of different materials with substantially disparate atomic numbers results in boundary crossing artefacts if the condensed history step size is too large compared with the range of the energy gradient at the interfaces. Deterministic methods do not suffer from this problem and furthermore can compute energy deposition at arbitrary distances from the interfaces without noise. The threshold energy and step size parameters play an important role in nanoscale simulations as they can alter the microscopic pattern of energy deposition.

Track structure vs continuous slowing down approximation

MC methods that explicitly simulate the electron track structure [as opposed to using condensed history or the continuous slowing down approximation (CSDA)] are often used in spatial domains at the nanoscale. They can potentially provide the best type of simulation, but they suffer from their own limitations. Because most electron interactions are elastic, resulting in only a directional change, or inelastic with little energy loss, a very large number of interactions must be sampled in each history, leading to impractical or even prohibitive computation times. Therefore, track-structure MC simulations are reserved for specialized cases.

The mean free path of photons in tissue for clinically relevant energies is up to about 40 g cm⁻², which means that the photons interact only a few times in the patient.⁴ Therefore, for typical radiotherapy planning problems 10⁸–10⁹ photon histories are usually sufficient and the event-by-event random-walk photon transport is a feasible mode of simulation. In contrast, the range of electrons is relatively short and before slowing down completely an energetic electron undergoes 10⁵–10⁶ interactions. Using event-by-event history is an inefficient way to simulate this high number of interactions. A numerical simplification, which is employed by most production MC codes, is to “condense” the changes in energy and angle of those electrons that undergo multiple interactions via elastic and inelastic scattering. Based on the CSDA approximation, which assumes all electrons of the same energy will have the same range, electron steps of predefined energy loss are pre-calculated. At each step, substeps are introduced at which the particle direction is resampled using the Goudsmit–Saunderson distribution.

Multiple interaction theories, such as the condensed history electron transport, can accelerate the computations but suffer from the shortcoming that they tend to break down in spatial scales of an electron mean free path, or in scales that have only a few interactions. This is the scale of GNPs.

Deterministic methods for electron transport solve the Boltzmann-Fokker-Planck equation or the Boltzmann-CSD operator equation. Here, the linear Boltzmann transport equation is augmented with the Fokker–Planck terms and with the continuous slowing down (CSD) operator in energy. The Boltzmann terms model the large-angle and large energy-loss scattering, while the Fokker–Planck terms model the small-angle and small energy-loss scattering. In the restricted CSD method, inelastic interactions (both collisional and radiative) are divided into two classes: catastrophic interactions that result in large energy losses and soft interactions that result in small energy losses. Catastrophic interactions are represented by macroscopic cross-sections for which a multigroup treatment of energy is practical. But the cumulative effect of many soft interactions can be approximated by the continuous energy loss of an electron. The restricted CSD operator method does not suffer from the same problems as the condensed history MC method. But it suffers from artificial or numerical energy-loss straggling. Because in the CSD approximation there is no physical energy-loss straggling, in the restricted CSD model soft inelastic interactions should not exhibit energy-loss straggling; yet an apparent straggling occurs when a CSD operator is used which is not of sufficiently high order.

Nanoscopic track structure

Nanoscale patterns of ionization are important for the evaluation of the formation of clustered damage to DNA or other molecular targets. Track-structure MC codes have been used to determine, among others, DNA fragment yields, DNA fragment size distributions, DNA break points in genes, and to confirm the correct chromosome structures between competing models.⁵ Commonly used track-structure codes are KURBUC, PITS, PARTRAC, NOREC, PENELOPE and GEANT4-DNA,^11,12,15 while LEPTS¹³ and TRAX¹⁴ are less widespread. Other ad hoc or approximate models of track-structure energy distribution are also used.^16–18 Note that not all of these computer models can directly simulate non-aqueous media. The track-structure physics in molecular applications using event-by-event interactions with molecules faces different challenges than the track-average approaches.

At low energies, the event-by-event track-structure simulation codes have to rely on theoretical, semi-empirical or scaling methods for their evaluation, because the exact double differential cross-sections for electrons (energy and angle) are not available from experiments.^5,21 This is especially so in solids, in which measured data to verify theories are often missing. Uncertainties in cross-sections result in errors in spatial ionization patterns, although the total energy deposited may be correctly simulated. Moreover, while the stopping power or energy loss per unit path length along the average track is known, the energy lost per unit stochastic track length is not well characterized. Because the stopping power cannot adequately describe radiobiochemistry effects along the particle tracks, several other concepts have been introduced, such as spurs, blobs, short tracks or radial models.^6–8 Electron interaction physics below about 100 eV is not well understood and it could impact the DNA damage computations. For very low-energy electrons, it has been even considered whether the Heisenberg uncertainty might be violated by the simulation code.⁵ Since the radiobiochemical effects (e.g., DNA strand breaks) occur in molecules suspended in condensed matter (mostly aqueous or histone structures), but quantum mechanical models in such media are not available, liquid–water cross-sections are often assumed.

Normally, the Bethe theory is employed to derive the electron stopping power. However, for low electron energies in high-Z materials, this stopping power can become negative, which is physically meaningless. Therefore, under this condition an adjustment in Bethe's theory must be made. Because this adjustment is different for each material and each energy region, this is not implemented in all MC codes. In some cases, most notably in deterministic approaches, when there are accurate extensions available to Bethe's theory,⁹ the restricted stopping power is used for high-Z materials. For example, in CEPXS, below 10 keV a power-series extrapolation is applied to the Bethe stopping power for each element. On the other hand, below 100 eV, the TRAX event-based MC code uses an implementation of the partial wave analysis, interfaced with the screened Rutherford cross-section and the Born approximation at higher energies.⁷²

In tissue or in cellular media (water) inelastic electron interactions become dominant between about 50 eV and 200 eV. Because this corresponds to a mean free path of 100 nm and smaller, this energy range represents an especially important regime for nanoparticle dose enhancement computations. Here, experimental electron cross-sections are rarely available, although recent results for water vapour by Muñoz et al,²² which have been implemented in the LEPTS track-structure electron MC code,¹³ fill an important gap. For liquid water, the availability of measured electron cross-sections in the low-energy range is even scarcer. Hence, most calculations rely on theoretical or semi-empirical models that often do not agree well. For example, Emfietzoglou et al²¹ examined the effect of various theoretical extrapolation methods to optical data on the inelastic electron cross-sections up to 10 keV and found that below 200 eV, substantial discrepancies exist among 6 different models (often several 100%) while above 200 eV, they tend to agree within 10%.

The uncertainties due to cross-sections or quantum mechanical effects in complex condensed media are not the only ones that impact track-structure simulations. Additional group of uncertainties consist of user-defined parameters such as the region of interest and general topology of the media and sources of radiation, the type of DNA damage, electron cut-off energy and the threshold energy for creation of strand breaks.^11,12

It has to be noted that the most suitable method to assess the radiobiochemical effects (e.g., the formation of radiolysis products and DNA strand breaks) due to the stochastic energy deposition pattern along the track of electrons leaking from GNP is the event-by-event track-structure simulation. However, for computation of interaction of X-rays with GNP in a homogeneous medium photon-only or condensed history MC methods are sufficient. Most GNP-related MC studies were, in fact, performed with these methods, and event-by-event studies for GNPT that would focus on radiation biochemistry, including strand breaks, are lacking.

Finally, we emphasize that MC and deterministic methods are two tools in the armament of radiation transport simulation techniques, neither of which can be declared as the “gold standard”. For correct results, a careful selection of the best computational method for the task at hand is of paramount importance. Owing to the recent proliferation of various MC computer codes, they have become user friendly and in simple macroscopic cases even a novice can successfully run them. The same cannot be said of deterministic codes, which still require considerable expertise to use.

Dose at various scales with respect to the gold nanoparticle geometry

Dose is defined as energy deposited in a unit mass. In MC simulation, scoring of energy distribution depends on the voxel size and shape (e.g., cubic, rectangular, cylindrical, spherical). When the scale of the problem geometry is significantly different from the scale of the scoring geometry, a potential ambiguity arises as to what dose means at various scales and geometries (Figures 1 and 2). This is a particular important difficulty in GNPT applications, for which a high degree of charged particle disequilibrium (CPDE) dominates the region where most of the energy deposition occurs. In typical medical physics MC simulations (e.g., treatment planning), millimetre to centimetre rectangular scoring volumes are used. This is inadequate for the purpose of resolving the dose deposition pattern as a function of distance from the GNP. However, it is adequate to estimate the average dose in macroscopic regions containing GNPs. Furthermore, for macroscopic average dose computation it may be sufficient to consider a uniform equivalent mixture of tissue (or water) and gold atoms instead of GNPs, as the internal structure of the radiation transport medium is almost irrelevant in this case. Not so for microscopic computations, in which case the domain of interest has to be modelled as a structured medium with a given number of GNPs in specific locations, and the energy must be scored in a geometry conforming to the geometry of the GNPs. Moreover, for the analysis of radiobiological effects secondary to GNP dose enhancement, microscopic simulation is mandatory. Finally, interpretation of energy deposition patterns for more than one GNP (e.g., GNP clusters) is not straightforward because of a complex three-dimensional heterogeneity of dose, with its macroscopic parallel in the form of brachytherapy dose distribution with “singularities” around the brachytherapy seeds.

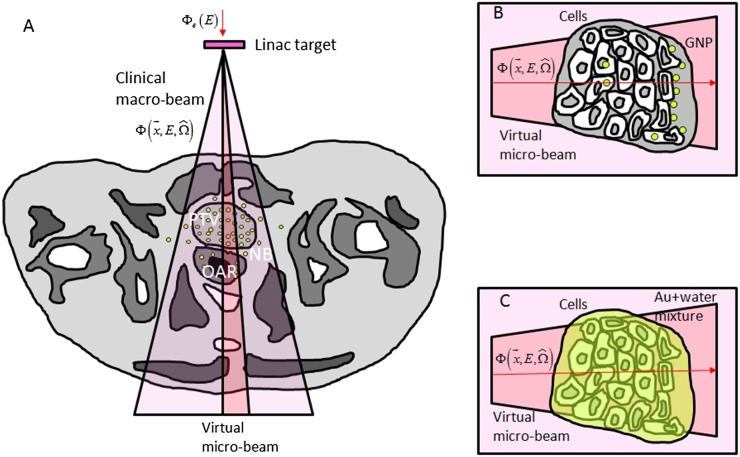
Figure 1.

Macroscopic and microscopic representation of radiation fields. Interaction of clinical beam (e.g., linear accelerator) with gold nanoparticles (GNPs) depends on the specific beam quality represented by the photon flux (a). Beam quality depends on irradiation technique, location and linear accelerator energy and target type. Microbeam interaction with GNPs (b) and with equivalent uniform mixture of gold atoms in water (c).

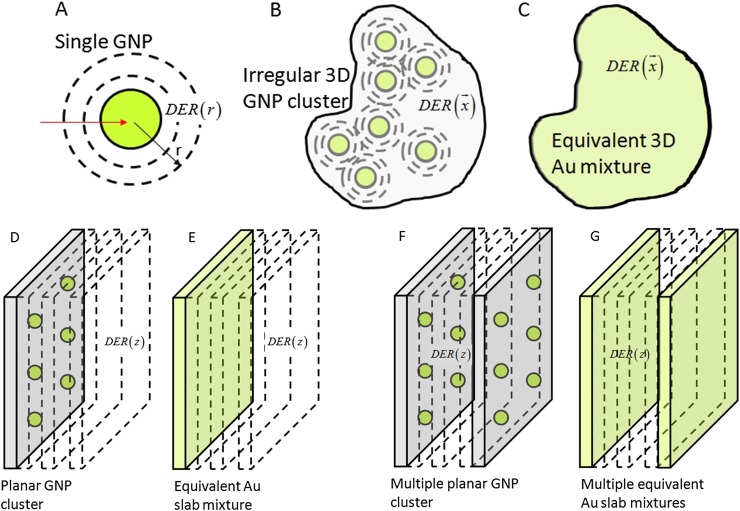
Figure 2.

Gold nanoparticle (GNP) geometry and scoring geometry approaches: single GNP (a), arbitrary three-dimensional (3D) GNP cluster (b), equivalent 3D mixture (c), planar cluster (d), equivalent Au slab mixture (e), multiple planar GNP clusters (f) equivalent planar mixtures (g).

As an initial simplifying strategy, a regular array of GNPs in a planar cluster can be considered. Computation of the average dose as a function of distance from the plane (Figure 2) is equivalent to averaging of dose over the in-plane coordinates. For 3D distribution of GNPs, one can assume multiple planar GNP clusters with a certain concentration of GNPs within each plane and a certain distance between the planar clusters. Thus, the effective macroscopic concentration of GNP is determined by the in-plane concentration and distance between the planes. This geometry with only two parameters has certain advantages over regular rectangular arrays of GNPs. For such multiple planar clusters, the simulation geometry (medium and scoring) problem is converted to a 1D problem.^51–53 This is so by noting that the average in-plane dose as a function of distance from a planar cluster is similar (though not identical, as explained later) to the dose for multiple thin slabs with uniform equivalent mixtures of gold and water. Using thin slab mixtures of gold and water simplifies the geometry and improves the MC statistics.

Dose enhancement and other metrics

Dose enhancement

Dose enhancement can be described by several metrics. One of them is the dose enhancement ratio (DER), which is defined as the ratio of doses in water medium with and without GNP for the same irradiation conditions:^46–58

$$DER\left(\overrightarrow{x}\right)=D_{GNP}\left(\overrightarrow{x}\right)/D_w\left(\overrightarrow{x}\right)$$ (1)

where dose $D\left(\overrightarrow{x}\right)$ is assumed to be computed with sufficient spatial resolution, implying a few nanometre size voxels in MC simulations or a comparable spatial mesh in deterministic computations. A similar DER can be defined for macroscopic regions or for mass-equivalent mixtures of gold with water for a specific concentration of GNP in water:

$$DE{R}_{macro}\left(\overrightarrow{x}\right)={\displaystyle {\int }_{V\left(\overrightarrow{x}\right)}{D}_{GNP}\left(\overrightarrow{x}\mathrm{\text{'}}\right)d^{3}x\mathrm{\text{'}}}/{\displaystyle {\int }_{V\left(\overrightarrow{x}\right)}{D}_w\left(\overrightarrow{x}\mathrm{\text{'}}\right)d^{3}x\mathrm{\text{'}}}$$ (2)

where the integration (scoring) volume V($\overrightarrow{x}$) is centred at $\overrightarrow{x}$, which is measured in hundreds of micrometre to millimetre rather than nanometre. It is assumed that the volume size is much larger than the range of Auger electrons (range of Auger electrons due to a gold K-shell vacancy in liquid water is from a fraction of nm to about 100 µm). Other clinically and radiobiologically relevant metrics are introduced in the following section.

Other metrics

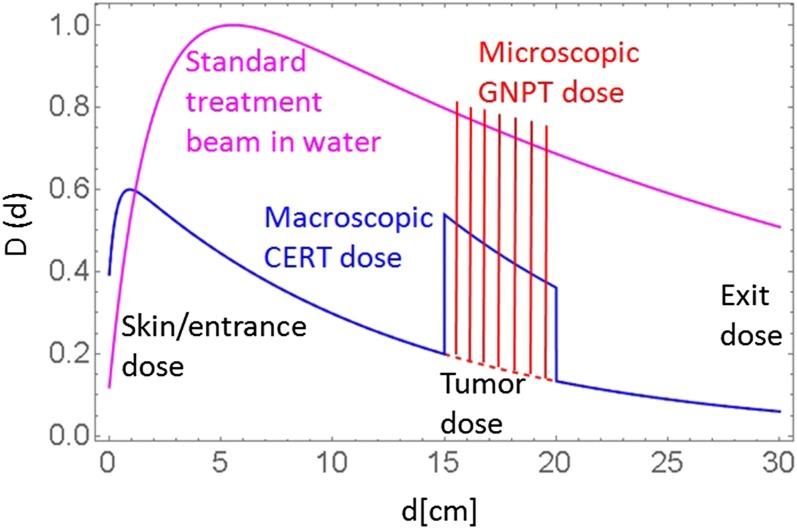
Both macroscopic and microscopic DER metrics, as defined by Equation (1) and (2), respectively, are useful in describing the efficacy of GNPT when applied to small regions containing GNPs. However, when applied to macroscopic regions in a patient, these metrics miss a few important treatment aspects. From treatment planning perspective, dose to tumour must always be compared with dose in other areas of the body. Additional metrics to consider are tumour-to-entrance (skin), tumour-to-maximum and tumour-to-exit doses. These additional metrics are shown in Figure 3. It is clear that both macroscopic [contrast-enhanced RT (CERT) type] and microscopic (GNPT type) types should be used to access tumour-to-entrance or tumour-to-exit metrics and compared with the standard treatment fields in tissue without GNP.

Figure 3.

Schematic diagram of depth dose curves for three types of treatment beams [with and without gold nanoparticle (GNP)]: standard beam dose in pure water (magenta), macroscopic contrast-enhanced RT (CERT)-type dose in water with a macroscopic GNP region (blue) and microscopic gnp dose-enhanced radiotherapy (GNPT)-type dose in the same tumour region (red). Standard beam is normalized to d_max. GNPT beam is normalized such that the local dose maxima in the enhanced dose distribution have similar values to the uniform dose for the standard beam in the tumour region. For colour image see online.

Other categories of metrics have also been used to describe GNP-induced dose enhancement. For instance, the number of nanoparticles per tumour cell needed to double the (macroscopic) dose, or equivalently, the milligrams of GNP per gram of tumour required to double the dose.⁴⁸ There is a direct relation between the concentration of GNPs in water (tumour) or their number per cell and DER (for a given GNP size and size of tumour cell). The concentration of GNP of size (2s) can be defined as the number of GNPs per cell (N_GNP) times GNP mass, divided by the mass of the cell:

$$c=\frac{N_{GNP}\mathrm{\cdot }{m}_{GNP}}{m_{cell}}=N_{GNP}\frac{V_{GNP}\mathrm{\cdot }{\mathit{\rho }}_{Au}}{V_{cell}\mathrm{\cdot }{\mathit{\rho }}_{cell}}=N_{GNP}\frac{\frac{4}{3}\mathit{\pi }\mathrm{\cdot }{s}^3\mathrm{\cdot }{\mathit{\rho }}_{Au}}{V_{cell}\mathrm{\cdot }{\mathit{\rho }}_{cell}}$$ (3)

The required number of GNPs to double the dose is obtained from N_GNP: DER_macro(c) = 2 condition. The underlying assumption is that each targeted cell has the same number of GNPs and they are distributed similarly within the cells or at their surfaces. However, in reality this may not be true. Furthermore, the above concentration of GNPs per given cell may be different (larger) from the macroscopic gold concentration, which is defined as the total mass of GNPs in macroscopic tissue to the mass of the tissue:

$$c_{macro}=\frac{N_{GNP,tissue}\mathrm{\cdot }{m}_{GNP}}{m_{tissue}}\mathrm{\le }c$$ (4)

This condition is true if the GNPs are distributed evenly among the targeted cells (cancer cells or endothelial cells) and are not in the non-targeted cells (normal cells).

In addition to the absorbed dose, radiobiological metrics are also used to assess the equivalent outcomes of GNP-related dose enhancement. For instance, cell survival, S, can be measured as a function of dose and it may be fit using the linear-quadratic (LQ) model. Similarly, relative biological effectiveness (RBE) can be defined as an empirical dose ratio. Both quantities can be also computationally estimated employing the LQ model and radiation transport simulations. The LQ model is a semi-empirical way to represent the dose dependence of cell survival. Even though there is no clear consensus about the mechanistic interpretation of the LQ model,^66,67 it is the most widely used model to characterize experimental cell survival data and the outcomes of clinical radiotherapy. For example, the LQ model neglects the bystander effect and many other effects related to clustered molecular damage.⁶ Although both RBE and S quantities can be used for heterogonous dose distributions, conceptually, the LQ model depends on a macroscopic variable (dose averaged over many cells or even tissue) and it does not explicitly account for dose variations at the cellular and sub-cellular levels. However, the dose around a GNP or a GNP cluster is extremely non-uniform owing to CPDE, and in the nanometre scale, the conventional definition of dose starts to break down owing to the stochastic energy deposition structure of low-energy electrons leaking from the GNP.

The uniform dose required by the LQ model can be computed as the effective (average) dose deposited using the CSD approximation or event-by-event MC simulations. This approach was adopted for GNP⁴⁹ using a mathematical framework similar to the one used in the local effect model (LEM). The LEM is widely used in proton and heavy ion radiotherapy. However, because there are significant differences between the patterns of energy deposition in GNPT compared with proton therapy, any application of LEM to GNPT has to consider those differences.

On one side, because the secondary electrons leaking from GNPs have relatively high linear energy transfer (LET) and their aggregate ionization density is somewhat similar to those of heavy ions and their secondaries, the mathematical framework of LEM is conducive to applying it to the concept to GNPT, with appropriate adjustments. However, the meaning and the interpretation of the thus extended LEM applied to GNPT may not always be the same as that of the standard LEM. The most notable reasons are the differences in linear energy transfer and track structures of heavy charged particles vs GNP-induced dose enhancement (cylindrical vs spherical geometry and size of the enhanced ionization regions). Additionally, GNPs are likely to have uneven spatial distribution with respect to cancer (or endothelial) cells, and since GNPs are the main sources of secondary electrons in the surrounding medium, the variability of the number of GNPs per cell and variability in their distances with respect to cellular targets may create additional variance in the cell survival of a larger population of cells. The latter may lead to stochastic effects, which may impact the response of tumour.

For this reason, another mathematical approach was developed based on the LQ model, which explicitly accounts for the possibility of cell-to-cell variations in stochastic quantities such as the number of GNPs per cell and their relative distances to the cellular targets.⁵⁹ In this approach, denoted as GNP-LQ to distinguish it from the extended LEM,⁶⁵ instead of the spatially averaged dose (or dose squared), a stochastic formulation is derived based on mixed Poisson distributions. The mathematical formulae of GNP-LQ differ from the average dose approach in the order of integration and may result in significantly different responses for the same level of external radiation and the same average concentration of GNPs, depending on the actual distribution of the nanoparticles among the population of cell. These differences may be important for predicting and understanding the biological outcomes of GNPT.

Specifically, the LQ formula $S=e^{-\left(\mathit{\alpha }\mathrm{\cdot }D+\mathit{\beta }\mathrm{\cdot }{D}^2\right)}$ of cell survival inherently assumes a uniform dose distribution and by itself cannot be used to accurately evaluate the cell survival in the presence of GNPs. Theoretical estimation of the RBE metric, $RBE=D_{ref}/D_{new}$, faces a similar problem of how to interpret the nanoscopic heterogeneous dose for the new type of radiation (GNPT) vs the reference radiation (X-rays without GNP). In the case of GNPT, an equivalent uniform dose (EUD), D_EUD, could be computed based on an accurate stochastic model and used for theoretical estimation of cell survival or RBE and compared with the experimental results. The GNP-LQ model accounts for the extreme dose heterogeneity that the cell experiences in the presence of GNPs by integrating the cell survival over the stochastic variable space^49,59 rather than taking an average dose:

$$\begin{array}{l}{S}_{GNP-LQ}={\displaystyle \underset{V_{cell}}{\int }\exp \left[-\left(\mathit{\alpha }\mathrm{\cdot }{D}_{GNP}\left(\overrightarrow{x}\right)+\mathit{\beta }\mathrm{\cdot }{D}_{GNP}{\left(\overrightarrow{x}\right)}^2\right)\right]}dV\\ S_0=\exp \left[-{\displaystyle \underset{V_{cell}}{\int }\left(\mathit{\alpha }\mathrm{\cdot }{D}_{GNP}\left(\overrightarrow{x}\right)+\mathit{\beta }\mathrm{\cdot }{D}_{GNP}{\left(\overrightarrow{x}\right)}^2\right)dV}\right]\\ S_{GNP-LQ}\mathrm{\ge }{S}_0\end{array}$$ (5)

In the above definitions, the integration is over the volume of the cells or of some of their compartments (e.g., nucleus, a chromosome or a DNA segment). As noted, the difference between S₀ and S_GNP-LQ mainly lies in the way the stochastic variables are evaluated. The advantage of GNP-LQ approach in GNPT is that it permits the evaluation of the effective cell survival and the effective cell inactivation enhancement for a heterogeneous distribution of GNPs among the population of cells (which is not the same as the distribution of GNPs for an average cell). This is a clinically important radiobiological aspect because the number of GNPs per cell, N_GNP, and their relative distances to the cellular targets (represented by the integration volume V_cell) are stochastic variables for a population of cells. It has to be noted that the mathematical framework of GNP-LQ could also be used in combination with other cell survival models than the LQ, for instance radiochemical models,⁶⁴ and that the computation of energy deposition may require MC simulation using specific cell geometry.^68–70 Finally, it has to be underlined that GNP-LQ applied to GNPT may not be directly applicable to proton/ion RT and discussing this issue is beyond the scope of this review.

Once cell survival is computed according to, Equation (5) the RBE can be theoretically computed by using the EUD concept, D_EUD:

$$\begin{array}{l}{D}_{EUD}:\exp \left[-\left(\alpha \cdot D_{EUD}+\beta \cdot D_{EUD}^2\right)\right]=S_{GNP-LQ}\\ RBE:=\frac{D_{ref}}{D_{EUD}}\end{array}$$ (6)

Note, while D_EUD has analogous meaning to the macroscopic EUD used in the case of heterogeneous organ doses, its exact computation is different. Nanoscopic radiation transport simulations are crucial for the proper estimation of cell survival integrals Equation (5) and for the evaluation of RBE Equation (6). In particular, when using a MC method track-structure simulations may be required to evaluate the true stochastic impact on cell survival.

It is important to recognize that currently available radiobiology models for GNPT must be refined and verified experimentally. This requires the publication of more rigorous information about the irradiation setup and distribution of GNPs in the scientific literature.

Macroscopic dose enhancement and dose at high-Z interfaces

Macroscopic perturbations in particle scattering and in energy deposition patterns due to the presence of high-Z materials in irradiated tissues has been traditionally of great interest in radiation therapy and in medical imaging. Perturbations due to heterogeneities (bony anatomy, prosthetic or dental implants, spinal or other supportive structures, pacemaker etc.) are sharpest at the interfaces of low- and high-Z materials. The presence of high-Z materials decrease the X-ray flux and harden the spectrum downstream.²⁵ Perturbations at the interfaces of bulk high-Z materials have been studied by numerous authors. From the perspective of GNPT a few studies, which focused on dose perturbation at the interfaces due to CPDE are worthwhile mentioning.^23–29 Similarly, imaging contrast agents result in flux suppression and beam hardening but the changes are gradual and no sharp interface effects are observed. New contrast agents are continually under development^43–45 and are of potential use not only in imaging but also in radiotherapy. CERT has been studied by various authors mostly from MC computational and treatment planning standpoints.^30–40

In CERT studies, macroscopic dose enhancement and beam attenuation are computed based on hypothetical planning CT with and without the contrast. Because contrast uptake is typically passive (via tumour microvasculature), endothelial cells are more likely to experience higher dose enhancement than the tumour cells, which are farther away from the microvessels with the contrast. Furthermore, the concentration of contrast agent is also likely to vary from one microscopic region to another and thus results in heterogeneity of X-ray absorption. However, these aspects have not been studied and only the macroscopic energy deposition described by Equation (2) has been considered in CERT literature. CT contrast agents are typically iodine-based and made in the form of small molecules thus differ in mass and atomic number from GNP whose mass/Z are much larger. For this reason nanoscale heterogeneity of dose is expected to be much larger for GNP than for CERT.

Potential usage of other than GNPs or molecular contrast agents is appealing by observing that many high-Z elements have similar photoelectric cross-section dependence on energy and somewhat similar dose enhancement compared to gold.⁵⁸ In this respect, gadolinium contrast agent was proposed for microbeam radiotherapy (MRT).^41,42 Gadolinium, by virtue of its greater atomic number (Z = 64) than iodine (Z = 53) has dosimetric properties closer to those of gold (Z = 79). While the distances between microbeams in MRT are between 25 µm and 75 µm, these distances are much larger than the mean range of Auger electrons or photoelectrons (≤2 µm), which significantly contribute to DER. Thus, the main advantages of Gd contrast agent for MRT have been considered to be the average enhancement over tenths of micrometre region sizes.

The multiscale radiation transport problem for gold nanoparticle radiotheraphy

Two-stage approach

Computation of macroscopic enhancement for clinical beams is readily achieved by direct simulation of the clinical beam in patient/phantom CT with and without GNP uptake. However, simulation of the macroscopic clinical X-ray beam and its interaction with GNPs at the nanoscale is at its core a multiscale problem since nanoscopic resolution of the phase space far away from the nanoparticles is neither necessary nor practical. A two-stage approach can be adopted to rescale the macroscopic clinical beam to the microscopic world (Figure 1).^48,49,51,52

In the first stage, a macroscopic region of interest (macro-ROI) of the clinical beam phase space in a given region inside the patient is selected. The phase space contains all particles and their energies and directions. Typical clinical field sizes range from a few millimetres [stereotactic radiosurgery or stereotactic body radiotherapy] to 30 cm. The spectra of clinical beams change with depth, off-axis distance and in- vs out-of-field locations. MacroROI beam size must be such that it correctly represents the “quality” of the beam at a particular position in the patient for a given irradiation technique. Next, from this portion of the phase space a microbeam is formed. The microbeam phase space is equivalent to the macroscopic portion of the clinical beam of interest (macroROI) but in higher spatial resolution. This can be achieved by rescaling the macroROI. In the case of MC computations, caution is needed with respect to the noise in the original phase space of the macroROI. If the macroROI phase space is noisy, the noise will propagate to the microbeam and finally will affect the computation of the dose enhancement. The transition from macroscopic to microscopic phase space is somewhat less problematic in deterministic computations, but it requires considerations of mesh size changes in logarithmic steps, which increase the memory and input/output requirements of the computations.

In the second stage, the micro-beam is propagated to a microscopic region containing the GNP or the GNP cluster. Selection of the size of the microbeam and its distance to the GNP region (microROI) are crucial for adequate computation of dose distribution for a given clinical beam quality. Propagation of the microbeam even by small micrometre distances in water can result in loss of lateral CPE. Lateral CPDE of microbeam finds its analogy in narrow beam dosimetry of stereotactic radiosurgery/SBIR, but in the former case, it can be more pronounced because of the smaller dimensions. Generally, the larger the distance to the GNP region and the larger the secondary electron ranges, the wider the microbeam should be to provide lateral CPE. Alternatively, one can adopt reflective boundaries to make the microbeam effectively infinite. Often, in MC simulations the first and second stage computations require different runs. In contrast, using deterministic methods they are within the same computation stream.

Depending on the spectrum of the X-ray source and the energy of electrons, the micro-beam size and distance to GNP must be selected. One can try to select them by trial and error. In addition, the electron range in water may serve as a reference. Range of electrons in liquid water based on CEPXS¹⁹ simulation is shown in Figure 4 and can be parameterized as $R\left(E\right)=a\mathrm{\cdot }{E}^b=0.0535\mathrm{\cdot }{\text{E}}^{1\text{.}71}\mathit{\mu }m$ for energy E in keV units and range R (E) in micrometre. Thus, for instance, for 150 keV there may be some electrons, which travel as far as 260 µm. These electrons can scatter on atomic electrons and produce delta rays, which can cause lateral dose deposition outside of the initial microbeam area.

In MC simulations, another important aspect for GNP is the boundary crossing across the tissue (water) and gold. The condensed history electron step size must be sufficiently small to avoid artefacts in energy deposition owing to the boundary crossing problem. Performing simulation with the same boundaries but in pure water medium may be necessary to decide if the step size is sufficiently small. Artefacts due to boundary crossing will appear as deviations from the uniform dose distribution across the boundaries⁵¹ and they can cause large errors in DER. In the case of deterministic computations, a gradual decrease (increase) in mesh size at the water/GNP (GNP/water) surface transition may be needed.

A very important consideration in both MC and deterministic computations is the particle energy cut-off. The cut-off energy is the energy of the particle at which the computations are terminated and the residual particle energy is deposited at the site of interaction rather then transported to other regions. If the cut-off energy is too high, artefacts in energy deposition will occur, affecting the shape of the dose deposition patterns.

Gold nanoparticle slab model

A simplified simulation approach can be adopted for GNP clusters that stretch over planar or quasiplanar sheets (e.g., adhere to the surface of the microvessels or endothelial cells) (Figure 2). For such geometry, the average DER as a function of the distance from the cluster $DER\left(x\right):=<DER>\left(x\right)$ is of interest rather than the in-plane heterogeneous dose distribution DER (x, y, z).⁵³ Henceforth, adoption of slab model is a viable option for the simulation geometry. Furthermore, the planar cluster of GNPs could be substituted with a nanometre thin slab containing a uniform mixture of water and gold atoms. The mixture has concentration equivalent to the relative mass of GNP cluster compared with the total mass of water in the thin slab. The slab thickness is the same as the size of GNPs in the cluster (e.g. 2–100 nm). The nanoslab mixture model is not exactly identical to the planar cluster model in terms of electron leakage. Average escape probability of electrons from a mixture of gold atoms with water is higher than probability of escape from individual GNPs. In GNP slab model, the microbeam is not necessary, and it is possible to use macroscopic clinical beams directly. The GNP slab area can be made sufficiently large to cover the whole cross-section of the macroscopic clinical beam (macroROI) and be simulated without loss of accuracy or need for rescaling.

Homogenized or atomic gold nanoparticle mixture approach

Interaction of X-rays with GNPs can also be determined in an approximate fashion employing a heuristic homogenized interaction or an “atomic” GNP model.⁴⁶ In this model, a macroscopic clinical beam interacts with a gold atom using analytical calculation. The resulting electrons are then transported using MC simulation. The initial analytical interaction with gold atom is tracked and energy scored in nanometre thick shells around the site of interaction. As a result, point dose kernel is determined for a gold atom. Finally, this dose kernel is rescaled to account for a given mass of GNP or concentration of GNPs. Dose kernel is convolved with arbitrary concentration to compute a DER map. However, in this approach the self-absorption of photo and Auger electrons inside GNP is ignored and therefore the dose kernel is independent of GNP size. Furthermore, several assumptions and corrections are required to rescale the problem from gold atom to an average GNP making this approach undesirable and leading to potential errors.

Approximate computations

Dose enhancement computations can also be carried out based on electron range tables.^60–62 In this approximate approach, it is assumed that the electron range as a function of energy can be employed to derive a stopping power as a function of distance from the GNP. In this approach, a surrogate of dose is computed assuming that the energy lost by electrons leaking from GNP is immediately deposited at the same location. Figure 4a,b shows the electron range R(E) as a function of energy in keV in water and the resulting stopping power as a function of penetration depth $S\left(x\right):=S\left[E\left(x\right)\right]=\left(-\frac{dE}{dx}\right)$, in which E (x) is the residual average energy of the electron at depth x. Stopping power is plotted for various initial energies of electron 10–150 keV. Figure 4c shows the dose for the same energies simulated with CEPXS/ONEDANT in water. Dose in water D(x) in Figure 4c has a maximum which occurs at shallower depths than the peaks in the stopping power profiles S(x) in Figure 4b. This is due to the scatter of the primary electrons and due to secondary electrons, which travel some distance from the interaction site before they deposit their energy. Therefore, even though computations of S(x) can be carried out with nanometre spatial resolution, they are not adequate to determine the nanoscale energy deposition D(x) around the GNP, while providing order-of-magnitude estimate of the cumulative deposited energy around GNP. This method is convenient when used to compare average DERs for various competing spectra.

Green's function method

Full simulation of GNP dose enhancement for various clinical spectra at various locations within the macroscopic beam one by one is inefficient and often practically impossible for more than a few cases. For this reason, an alternative method based on a Green's function approach can be used to speed the computations for multivariate clinical beams.⁵³ In this method, nanoscale dose is simulated for various monoenergetic X-ray beams using exact radiation transport, and dose kernels (Green's functions) are determined with fine spatial resolution for each energy. Dose enhancement for arbitrary spectra is computed as a convolution of the monoenergetic dose kernels with the spectra. Once computed (with great effort), dose kernels provide a fast computational method for arbitrary spectra with high spatial accuracy. This method is suitable for comparison of various clinical spectra and provides accurate spatial accuracy for DER (x).

Nanoscale dose enhancement

One-dimensional metrics

Dose distribution in the vicinity of a single GNP is almost spherically symmetric. Therefore, in most cases scoring energy deposition in concentric shells is a good approximation. Thus, the problem can be simplified to 1D geometry. Although the photoelectron emission has a directional distribution, owing to the presence of Auger electrons, the dose distribution about a planar sheet of nanometre thickness is also almost symmetrical in the upstream vs downstream directions.^51,52 Thus, the average dose between both directions is an acceptable metric. Furthermore, although it is possible for a single GNP, it would be difficult to track the asymmetry and its orientation with respect to the direction of X-rays for GNP clusters. Thus, for practical purposes one-dimensional (1D) DER metrics [DER(r), r = radius or DER(x), x = distance from the plane] could be used for a single GNP or a planar cluster.

Auger vs photoelectron

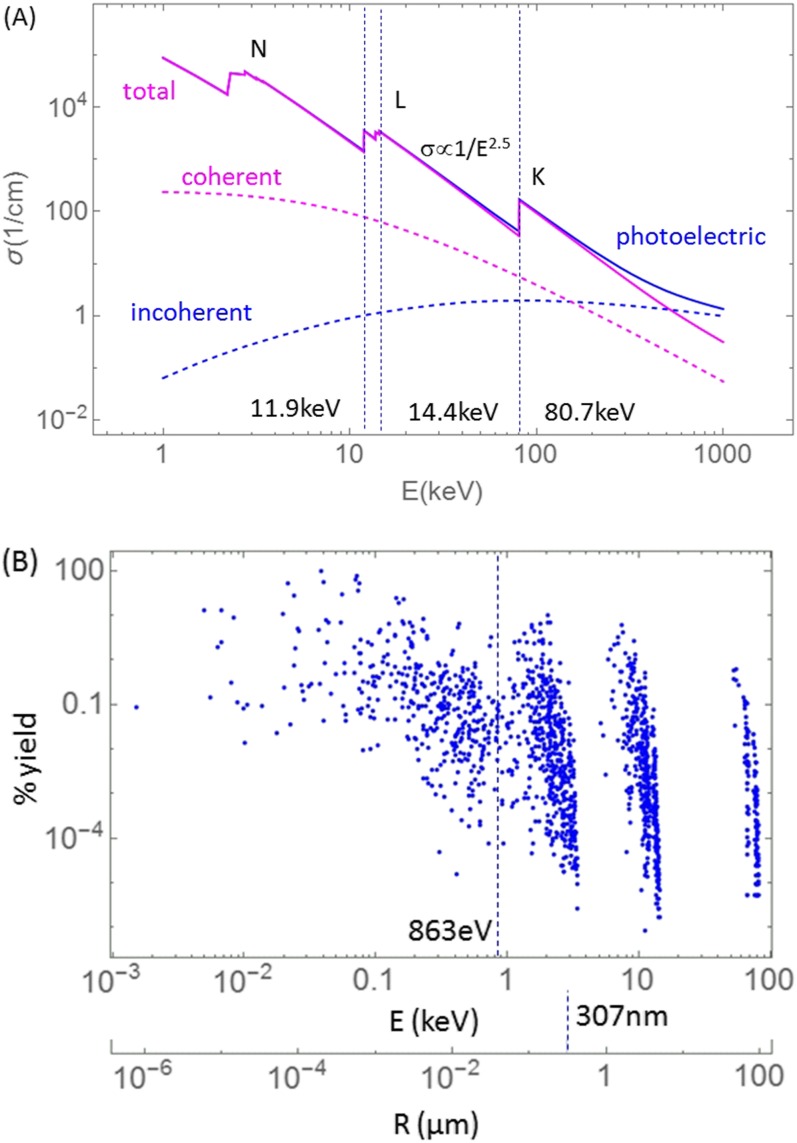
X-ray interaction with GNP for low energies (keV range) is predominantly via photoabsorption, followed by X-ray fluorescence and Auger cascade (Figure 5). Compton interactions and coherent scattering in gold are infrequent between 1 and 500 keV (Figure 5a) and can be neglected in computing the dose enhancement at micrometre distances from GNP. Auger electrons have energies ranging from a few electronvolts to about 80 keV (Figure 5b), with the average energy of about 863 eV. The ranges of Auger electrons in water are as high as 95 µm but on the average only about 307 nm (Figure 5b lower axis). While the photoelectron ranges depend on the X-ray energy and shell from which they are ejected, they are larger than for Auger electrons (Figure 6a,b).

Figure 5.

(a) Cross-sections (photoelectric, coherent, Compton, total attenuation coefficients) in gold expressed as a function of incident X-ray energy. (b) Auger electron yield per K-shell vacancy²⁰ from gold as a function of electron energy and as a function of Auger electron range in water. Electron range in water is computed artificially setting the binding energy to zero and assuming there is no attenuation of electron energy in the GNP. Average range of about 307 nm and average energy of about 863 eV are shown as vertical lines.

Figure 6.

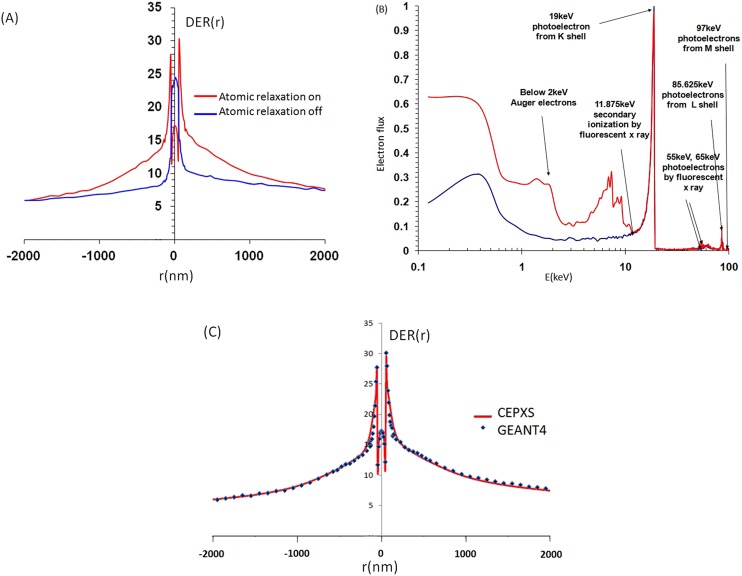
(a) Comparison of GEANT4 simulations of radiation transport with atomic relaxation enabled/disabled. (b) Resulting electron spectra with some of the characteristic features identified. (c) DER (r) for a spherical GNP shell of radius 2 cm computed in GEANT4 vs an equivalent slab in CEPXS/ONEDANT for 100 keV. Shell thickness was 100 nm and its macroscopic radius 2 cm. Data are adapted from.^51,52

Computed DER values depend on simulation geometry (including GNP, macro-ROI and micro-beam), different MC parameters (step size, cut-off energy, material parameters, voxel size, binning geometry) as well as on the model of GNP (single, cluster, slab, average or homogenized) used to simulate or compute DER. Although, uncertainties in simulation are model dependent and parameter dependent, it is possible to achieve relatively good agreement between different methods (Figure 6c). Figure 6c shows an example of DER(r) and electron spectra for 100 keV X-ray at depth of 2 cm for an infinite geometry using GEANT4 compared with CEPXS/ONEDANT in an equivalent slab geometry.

Disabling atomic relaxation has a strong effect on DER in the first 1 µm from GNP (Figure 6a,b). Atomic relaxation gives rise to fluorescent X-rays and Auger electrons. The significant peaks and features are identified in Figure 6b for 100 keV X-ray beam. Incident photons at 100 keV produce photoelectrons with energies (100 keV—binding energy). K-shell gives a peak of about 19 keV, L-shell of about 87 keV and M-shell of about 97 keV photoelectrons. For smaller energies, there is a notable increase in the number of secondary electrons below about 11 keV, corresponding to Auger electrons as well as the presence of secondary ionization by fluorescence X-rays. Electrons with energy E < approximately 2 keV are mostly Auger electrons. The increased number of electrons between 2 and 11 keV is due to the secondary ionization of M-shells by X-ray fluorescence. Small peaks related to fluorescent X-rays are found at approximately 55 and 65 keV. The peak at 55 keV corresponds to L-shells ionized by Kα1 and Kα2 fluorescence X-ray. The 65 keV peak is related to M-shells ionized by Kα1 and Kα2.

Gold nanoparticle size

As noted, dose enhancement depends not only on X-ray energy but also on GNP size. If attenuation of photoelectrons and Auger electrons inside the GNP is neglected then DER would be proportional to the size of GNP. However, in reality electron leakage is limited by self-attenuation in the bulk GNP, especially for GNP sizes >10 nm.^48,49,63 For this reason, smaller size GNPs are more efficient in converting X-ray energy to short-range dose in water. Because the electron leakage is a surface phenomenon, the total energy deposited in a shell outside of the GNP per incident X-ray does not increase exactly linearly with the GNP volume.^48,49,63 Thus, hollow GNPs could be used instead of bulk GNPs to avoid the self-attenuation while maximizing the region where dose enhancement can occur. Hollow GNPs also reduce the attenuation of X-rays through the GNP-laden region.

Energy dependence

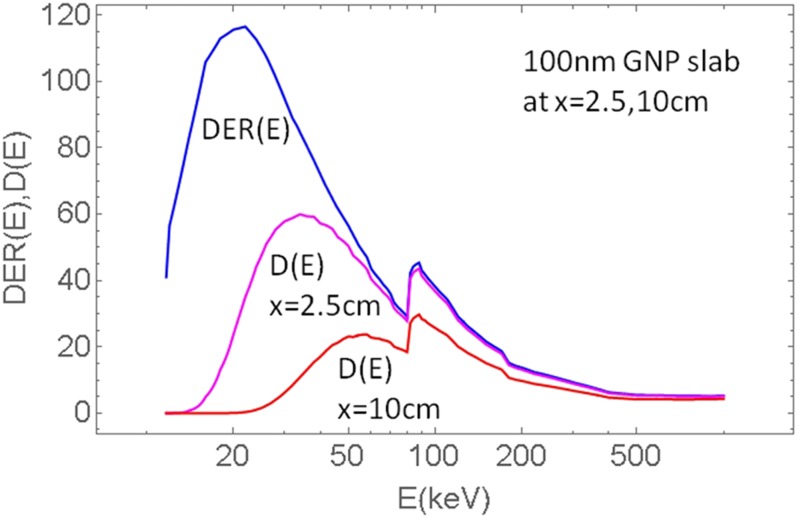
The dependence of dose enhancement on the energy of X-rays is primarily determined by the photoabsorption cross-section and secondarily by the self-attenuation of electron leakage in the GNP, and therefore by the GNP size as well. Photoabsorption in gold below the K-shell, in the 15–80 keV range, is dependent on energy as σ∝E^−2.5. However, in the range 11.9–14.4 keV there are a few L-shell edges. At about 11.9 keV, there is about a factor of 2.4 drop in the cross-section and for lower energies the proportionality to E^−2.5 remains. Externally incident X-rays of energies below the L-shell are of little practical use in GNPT because their penetration depth is very small and such photons are unlikely to reach even marginally deep seated tumours (a few cm). For these reasons, the highest dose enhancement for clinical keV beams would be achieved above the L-shell energy (>15 keV). However, attenuation in water must also be included. Figure 7 shows dose enhancement DER(E) on the surface of 100 nm GNP slab located at 2 cm in water compared to dose D(E) for the same GNP slab located at 2 cm and 10 cm depths. It is seen that owing to attenuation of X-ray flux in water the X-ray energies below 20 keV are not very useful at larger depths (>>1 cm). While X-rays between 15–20 keV are associated with large DER, in external beams their contribution to the total energy is small compared with higher X-ray energies. In summary, self-attenuation of electron flux within the bulk GNP and attenuation of X-ray flux in water are the limiting factors to utilization of X-rays below about 20 keV in most clinical applications utilizing external beams. However, energies below 20 keV may be useful in brachytherapy applications as the radioactive sources are closer to the tumour or are inside the tumour.

Figure 7.

Dose enhancement on the surface of 100 nm GNP slab DER (E)=DER (x = surface, E) and dose resulting from DER and attenuation in water D (x, E):=DER (E)·PDD (x, E) at various depths x = 2.5, 10 cm.

Dose enhancement depends not only on the spectrum but also on the phase space of the microbeam. For instance, using a phase space vs a parallel plane beam with equivalent spectrum may result in many-fold differences in the computed dose enhancements (DER for plane parallel plane >> DER using true phase space parameters).⁵²

Optimal X-ray sources

The optimal usage of GNP is for shallow tumours and X-ray sources with strong 20–100 keV spectral content. Brachytherapy applications are ideal from this perspective. Using GNP with megavoltage linear accelerator X-rays is much less effective because above 500 keV most of the interactions with gold occur via Compton scatter and pair production (above the threshold 1.02 MeV), which results in energy deposition millimetre to centimetre away from the GNP. However, it has been pointed out that even with MV beams there are clinical situations for which enhancement can be increased several-fold compared to standard open beams at the centre of the field.^53,55 Namely, for split-field IMRT and for flattening filter free (FFF) beam lines. Furthermore, new MV beamlines with significantly softer spectra may further increase DER of MV beams, such as low-Z and low-energy targets.⁷¹ MC radiation transport is very useful in designing new beam lines optimized for GNPT as well as for CBCT imaging.

It has been demonstrated that DER outside of the MV beam is higher than inside the field due to the lack of direct X-rays and presence of scattered X-rays with lower energy. Large IMRT fields are typically split to deliver dose using smaller IMRT subfields. For this reason, tumour receives a significant portion of out-of-field dose including phantom scatter and MLC scatter. Split IMRT fields increase DER accordingly and the increase depends on the total monitor units used to irradiate tumour with prescribed dose. This effect is especially pronounced for FFF beamlines, which have softer spectrum compared with standard linear accelerators with flattening filter, which hardens the beam. New low energy target beamlines with energies down to 2.5 MV and beryllium or diamond targets can additionally increase the enhancement by additional factor of about 2.⁷¹

Studies

Simulation of radiation transport and energy deposition as well as the associated radiobiological quantities have been performed in various ways^46–58 using a plethora of radiation transport codes, simulation beams GNP geometries, GNP sizes and concentrations, X-ray sources and energies, as well as normalization schemes and metrics. Table 1 summarizes the literature on simulations using nanoscale MC and deterministic radiation transport. At the present stage of GNPT studies, there is no established systematic methodology or nomenclature. For this reason, simulations are performed sometimes for very different conditions, and results are expressed by using various metrics. As a result, enhancement values range from close to 1 to about 1000 and they are very difficult to compare with each other.

Table 1.

Dose enhancement ratio (DER) values for various clinical spectra and clinical beams

Reference	X-ray sources	Macro codes	Micro codes	Radiation transport microbeam model	GNP model	GNP size/concentration	Metrics	Values
Jones et al46	Yb-169 I-125 Pd-103 Ir-192 50 kVp 6 MV	EGSnrc	NOREC	NOREC Track structure in water EGSnrc condensed history; interaction with Au atoms Scoring in 100 nm thick shells Dose kernel for Au atoms	Au atom rescaled to single GNP or rescaled to GNP concentration	2D distribution based on microscope image	Max DER	MaxDER ∼100–200 ∼500–600 ∼800–1000 ∼50–90 ∼200–500 ∼8–10
Van den Huevel et al47	10–200 keV monoenergetic 110 kVp	MCNPX	MCNPX	Slab geometry Parallel-plane wide beam	1 mm thick slab with a mixture of Au + water	0,1,2,…,10% concentration of Au atoms	SSB(E) DSB(E) DER(E) DER/skin dose	DER ∼4–20 Linearly decreasing with energy Max at 20 keV
Leung et al50	50 kVp 250 kVp Cob 60 6 MV	GEANT4	GEANT4	Microbeam width = GNP size 1 mm distance to GNP Parallel microbeam Scoring in shells	Single GNP	2, 50, 100 nm	Interaction enhancement ratio (IER) with Au	IER∼2000 ∼300 ∼10 ∼15
Lechtman et al48	300 kVp 6 MV Ir 192 Yb 169 I125 Pd103	MCNP5	Penelope	Event-by-event history Using rescaled number of photoabsorption interactions from MCNP Microbeam width = GNP size Scoring in shells	Single GNP	1.9, 5, 30, 100 nm	mg g−1 or number of GNPs per cell (NGNP) required to double the dose Electron flux vs range	NGNP∼103–108 ∼105–1011 ∼104–109 ∼103–108 ∼103–108 ∼103–108
McMahon et al49	20–150 kVp 6 MV 15 MV	GEANT4	GEANT4-DNA	Track-structure single GNP at the centre of 200 μm cube	Single GNP	2–50 nm	RBE Local effect model (LEM)	RBE∼1.2–2.2
Zygmanski et al59	keV–MeV	MC	MC	Event-by-event and CSDA-track structure with short step size required High spatial resolution required	Single GNP and GNP clusters Compartment model of cell with sub-units Number of GNPs per cell and distance to cellular target	Any size	RBE LEM-related model GNP-LQ DER (EUD)	Change in DER from a few percentage to a couple-fold
Douglass et al68	80 kVp 6 MV	GEANT4	GENT4-DNA	Random cell model with 840 cells 9–13 µm in size	Cell with cytoplasm, membrane, nucleus	400 nm Au cluster region 300 nm Au layer	DER (energy) DER (cellular target)	DER∼1–10
Tsiamas et al55	6 MV standard 6 MV FFF	EGSnrc	CEPXS/ONEDANT	Deterministic transport with restricted CSD operator (CSDA based clinical phase spaces) Green's function dose kernels Numerous clinical beams: off-axis, inside/out-of-field, IMRT/split-IMRT/open beam, depth, field size	Parallel-plane dense GNP cluster	10, 100 nm	DER (depth) DER (off-axis location) DER (field size) DER (IMRT) DER (clinical beam spectrum)	DER∼2–16
Zygmanski et al52	20–100 keV 50 kVp	GEANT4	GEANT4 CEPXS/ONEDANT	GEANT: condensed history electron MC with short step size CEPXS: restricted CSD operator Parallel spectral and phase-space microbeams Various microbeam beam widths and distances to GNP Angular dependence of DER	Single GNP Cluster of GNPs in rectangular array Sparse/dense clusters Multiple planar clusters (3D)	10, 100 nm 100 nm–5 µm cluster size 50 nm–5 µm distances	DER (energy, distance, angle)	DER∼1–100
Tsiamas et al53	2.5–6.5 MV	EGSnrc	CEPXS/ONEDANT	Deterministic transport with restricted CSD operator (CSDA-based clinical phase spaces) Beryllium, diamond, tungsten linear accelerator targets Different target thicknesses	Parallel-plane dense GNP cluster			DER∼5–11
Kirkby and Ghasroddashti56	90, 125, 200, 300 kVp 6 MV standard 6 MV FFF Co-60	SpeckCalc EGSnrc Other	Penelope	Event-by-event track structure	Membrane, mitochondria Number of GNPs per mitochondrion	13 nm 10–6000/per mitochondrion	DER(energy, number of GNPS)	DER∼1–8

DER, dose enhancement ratio; DSB, double strand break; EUD, equivalent uniform dose; GNP, gold nanoparticle; IER, interaction enhancement ratio; LEM, local effect model; LQ, linear–quadratic model; RBE, relative biological effectiveness; MC, Monte Carlo; SSB, single strand break.

The highest DER values can be obtained only using photons as incident particles. This is due to the large photoelectric cross-sections relative to interaction cross-sections using other incident particles. Although very high DER values of up to about 1000 were reported in some of the literature, we believe such high DERs are not attainable in clinical applications and is only possible in extreme irradiation conditions and geometries, which cannot be realized except on a computer. In realistic irradiation scenarios, DER values greater than 100 are only attainable for densely packed single-layer GNP clusters. Thus, for single or clustered GNPs the upper limit for DER can be safely placed to be about 100 or not much greater. Second, for smaller GNP sizes (e.g. 10 nm) and sparsely packed GNP clusters the average DER would be much less than 100, however, the actual number depends on the spacing between the individual GNPs in the cluster. DER depends on the incident photon energy as well.

The highest DER is obtained for energy of about 20 keV (DER ≈ 100–160), but photons possessing such low energy have very poor penetration in tissue, thus their utility is restricted mainly to brachytherapy applications. In the case of external beam radiotherapy only a minor fraction of the incident beam has this low energy, and even scattered X-rays do not normally attain this energy. For example, the most likely energy of a 6 MV beam is in the vicinity of 1 MeV. At this energy, the photoelectric cross-section of gold is much smaller resulting in commensurately smaller DER. But the overall effective DER for a spectral 6 MV linear accelerator beam is even lower than this, in the range 1–20, depending on the nanoparticle size and depth in tissue, position within the field (inside or outside of the field) as well as the beamline type (FFF vs standard linear accelerator) and irradiation technique (IMRT vs open fields).

For external radiotherapy, the tumour-to-dmax dose is equally or more important parameter than the DER, as explained in Figures 3 and 7. Presumably, if one would use GNP contrast clinically, one would start with a standard treatment plan and keep the standard doses to skin and normal organs and tissue at the same levels as without GNPs, while attempting to increase the tumour dose as the benefit of GNPs. Thus using a rough calculus, the standard prescription dose would have to be multiplied by DER. However, this operation would have to be done for the photon energy spectrum that occurs in a specific voxel (tumour or normal tissue). Thus, for some energies at which the DER(E) is otherwise large, their dose contribution may be small owing to attenuation.

Clinical beams are known to vary in quality. For instance, the spectrum at a given point in the patient depends on the depth and off-axis location, field size, MLC transmission and scatter, inside or out-of field location, anatomy and other irradiation details.^53,55 For instance, it has been shown that split IMRT fields, which contain a relatively large proportion of out-of-field dose, gives rise to significantly larger DER than the non-split beams. For these reasons, DER may vary substantially and has to be computed for the specific type of irradiation technique, field size and location inside patient.

Another point is that the DER can be specified at various distances from the GNP: near the surface of GNP, at 1 µm or other distances, and as an average over a range of distance, depending on the type of cellular target considered. There are several possible cellular targets, among them the DNA, cell membrane and endothelial cells of tumour vasculature. If the GNPs are used to enhance the dose to the DNA and the GNPs are actually situated on or in the near vicinity of the DNA, then the DER determined at or near the GNP surface is a good figure of merit. But if GNPs are near the tumour endothelial cells, then the average DER within the endothelial cell (about 2 µm in radius) is a better parameter.

Finally, if the GNPs are unevenly distributed among cellular targets, which is likely to occur, then those targets that have more GNPs will be inactivated with higher probability (and potentially “overkilled”), while others that have fewer GNPs will have higher chances to survive. If the overall tumour control can be regarded as a relative number of stochastically independent tumour cells killed, then according to the generalized LEM model the tumour control will be compromised.

The above considerations show that with GNPT not only the macroscopic dosimetric properties but also the microscopic distribution of GNPs or GNP clusters are important. Thus, the computational challenge of GNPT is manifold: the precise fluxes (electron and photon) must be known in a given macroscopic voxel, and similarly the distribution of the number of GNPs and their proximity to cellular targets must be known there as well. Only then the computational goal can be defined and achieved. This also has implications for experimental work with GNP dose enhancement (cell survival or tumour control studies).

Conclusions

In summary the challenges of radiation transport computations for GNPT include the following themes.

Multiscale Monte Carlo problem for a single gold nanoparticle

Properly coupled MC simulations at two very dissimilar scales accounting for both the macroscopic clinical X-ray beam properties and properties of microbeam interacting with a single or an “averaged” nanoparticle (interactions averaged over gold atoms or GNPs and rescaled). This includes effects due to:

• rescaling the phase space from macroscale to microscale followed by using the microbeam phase space to interact with the a single GNP

• the occurrence of CPDE due to the presence of high-Z (GNP)/low-Z (water) interfaces, as well as lateral CPDE of the microbeam itself

• the boundary crossing problem (crossing GNP-water boundary in discrete steps) and selection of step size

• cut-off energies (termination of transport at certain energies) and

• variance reduction techniques in the MC simulation.

X-ray interaction with clusters of gold nanoparticles vs a single gold nanoparticle vs uniformly mixed gold atoms

Computation of energy deposition for specific distributions of nanoparticles in a cluster of GNPs vs average dosimetric quantities. Various cluster configurations must be considered:

• dense or sparse, regular or irregular arrangements of GNPs in a given cluster (e.g., planar cluster, rectangular or random array)

• geometry of clusters (e.g., multiple planar clusters)

• macroscopic concentrations of GNPs or GNP clusters

• homogenized mixtures of gold atoms with water.

Distribution of gold nanoparticles and clusters of gold nanoparticles with respect to cellular targets

Interpretation of extremely heterogeneous energy deposition for specific distribution of the nanoparticles with respect to the cellular and molecular targets. This must account for:

• stochastic radiobiological effect due to a stochastic parameters: number of GNPs per cellular target and their distance to the target

• discrimination between various possible targets such as: cell nucleus/DNA, cell membrane, tumour cell, endothelial cell of the microvasculature and their respective geometries

• stochastic mathematical framework for evaluation of radiobiological effect (e.g. GNP-LQ).

Spectral content (“quality”) of clinical beam at a given location occupied by gold nanoparticles

Sensitivity of enhancement to the specific energy and angular distribution of clinical X-ray beam in the region occupied by GNPs. This implies:

• dependence of energy deposition on the specific clinical irradiation technique and beam parameters

• location of the irradiated GNP with respect to the treatment field and distance to the patient surface

• true phase space content of the micro-beam.

Decrease of X-ray flux and hardening of the beam by macroscopic gold nanoparticle regions

The impact of macroscopic GNP-laden volumes on the beam flux and quality and therefore on dose enhancement. This must account for:

• attenuation of X-ray flux and its hardening in the GNP laid regions

• scatter of X-rays to the neighbouring regions.

Modification of clinical beams to achieve maximum dose enhancement

Various techniques can be explored to optimize the X-ray spectra:

• softening of X-ray spectrum by using low-Z linear accelerator targets, and removing flattening filter

• or by using low MV linear accelerator beams (2.5–4 MV)

• or by using kVp beams (X-ray tube or brachytherapy sources).

In addition, there are other important areas, which are not discussed in detail in the present review article owing to space limitations, but which will have to be investigated before clinical implementations of nanoparticle or contrast based radiation therapy. These are briefly summarized.

Modification of nanoparticle size, shape and structure

Owing to the differences of transport of various types of nanoparticles in the bloodstream and their uptake by the cellular targets as well as their potential toxicity, there are various options for GNP design. The following must be optimized:

• size (e.g. 2–100 nm)

• shape (spherical, rod, disk, full, hollow, layered structures)

• physicochemical composition of GNP surface impacting the uptake, toxicity and imaging of GNPs in addition to dose enhancement.

Imaging of macroscopic concentrations and single gold nanoparticles

The role of radiation transport computations in developing imaging techniques for GNP uptake at two scales (macro and nanoscopic).

The usage of gold nanoparticle in other than X-ray beams

• GNPT based on proton and heavy ions therapies or electron beams.^72–75

The usage of other than gold nanoparticle or contrast agents

• While gold has high photoelectric cross-section, other materials may be of interest as well and moreover may be beneficial from the perspective of cross-section dependence on energy.⁵⁸

There are several caveats of GNP radiotherapy (GNPT), which may not be completely valid in reality. First of all that the nanoparticles accumulate primarily in the tumour microvasculature (passive agents) or in the tumour cells (active agents) and that normal tissues, organs or cells have negligible concentrations of nanoparticles and therefore their direct impact on NTCP is negligible. Second, often there is an unspoken assumption that the distribution of nanoparticles can be “homogenized” at the cellular scale, which leads to an “average” nanoparticle model. The “average” GNP model is still a nanoscopic model and has to be differentiated from the macroscopic mixture model used for contrast agents, such as CT contrast (iodine), but in this model the dosimetric parameters of specific GNPs are averaged. Third, it is also often assumed that stochastic nature of energy deposition and stochastic nature of nanoparticle distribution are not decisive for the estimation of the true radiobiological outcome. None of these assumptions may be completely valid in reality. More work is needed to evaluate dose enhancement effects at computational radiobiological level.