R-U policy frontiers for health data de-identification

Abstract

Objective The Health Insurance Portability and Accountability Act Privacy Rule enables healthcare organizations to share de-identified data via two routes. They can either 1) show re-identification risk is small (e.g., via a formal model, such as k-anonymity) with respect to an anticipated recipient or 2) apply a rule-based policy (i.e., Safe Harbor) that enumerates attributes to be altered (e.g., dates to years). The latter is often invoked because it is interpretable, but it fails to tailor protections to the capabilities of the recipient. The paper shows rule-based policies can be mapped to a utility (U) and re-identification risk (R) space, which can be searched for a collection, or frontier, of policies that systematically trade off between these goals.

Methods We extend an algorithm to efficiently compose an R-U frontier using a lattice of policy options. Risk is proportional to the number of patients to which a record corresponds, while utility is proportional to similarity of the original and de-identified distribution. We allow our method to search 20 000 rule-based policies (out of 2⁷⁰⁰) and compare the resulting frontier with k-anonymous solutions and Safe Harbor using the demographics of 10 U.S. states.

Results The results demonstrate the rule-based frontier 1) consists, on average, of 5000 policies, 2% of which enable better utility with less risk than Safe Harbor and 2) the policies cover a broader spectrum of utility and risk than k-anonymity frontiers.

Conclusions R-U frontiers of de-identification policies can be discovered efficiently, allowing healthcare organizations to tailor protections to anticipated needs and trustworthiness of recipients.

INTRODUCTION

In the age of big data, healthcare organizations will accumulate a substantial quantity of detailed personal data.^1,2 These large-scale resources can support the development of novel healthcare applications and innovative services.^3,4 For instance, the data in electronic medical record systems can enable predictive modeling,^5,6 novel association studies,^7–9 as well as the discovery of personalized treatment regimens.^10,11 At the same time, there are many requests to share patient-level data to support information reuse (e.g.,¹²), learning health systems (e.g.,¹³), transparency (e.g.,^14,15), and to adhere to federal grant policies (e.g.,¹⁶). In other words, there is a belief that sharing data derived from the clinical domain provides utility (U) to society. While publication can enable broad access, there is a risk (R) of violating the privacy rights of the patients to whom the data corresponds.^17–20

The myriad definitions of privacy²¹ are evolving in the context of big data,^22,23 and it should be clear that the goal of this paper is not to suggest which is best, but rather to provide technical mechanisms to support a certain definition that continues to receive a substantial amount of attention. Specifically, various laws state that data are sufficiently protected when it is “difficult” to ascertain an individual’s identity.²⁴ For example, the European Union’s Data Protection Directive refers to such data as “anonymized”²⁵ and the U.S. Health Insurance Portability and Accountability Act (HIPAA) calls that data “de-identified”²⁶ (the convention we use henceforth). In so doing, these laws aim to prevent identity disclosure, which transpires when a recipient of the data links it with some resource containing explicit identifiers (e.g., a voter registration list^27,28).

To achieve de-identification, laws often provide publishers with several options. First, they may invoke a set of rules, or a policy, to transform data into a de-identified state. The Safe Harbor model defined by HIPAA is a clear example of such a policy, which specifies 18 rules, including suppression of explicit identifiers (e.g., personal names) and generalization of “quasi-identifiers” which could enable linkage (e.g., dates of events, such as birth, are replaced with time periods no more specific than one year and ages over 89 years-old are recoded as 90+). Yet, the rigidity of such rule-based policies is not ideal for sharing every data set, such as studies with the elderly (e.g., dementia patients).²⁹

Thus, the law enables publishers to use an alternative, which permits data to be shared in any format, provided the risk of re-identification is appropriately measured and mitigated. Various formal anonymization models (i.e., k-anonymity³⁰) have been proposed to ensure that a certain mathematical property of the dataset holds true. However, these models tend to be overly rigid for a number of practical purposes. Notably, HIPAA states that publishers can ensure the “risk is very small that the information could be used, alone or in combination with other reasonably available information, by an anticipated recipient to identify an individual who is a subject of the information.”²⁶ This implies that risk is proportional to the trustworthiness of the recipient and suggests there are many different policies that could be invoked to de-identify the data. For example, if health data are published on the Internet, via a Centers for Medicare and Medicaid Services dataset, the threat is high because the recipients are unknown and the system is completely open. As such, a data manager could select a policy that heavily favors risk mitigation over utility. By contrast, if health data are published to a more trusted party (e.g., a health services researcher with strong information security practices who agrees to sign a data use agreement), then the threat is much lower and one could apply a policy that favors utility over risk.

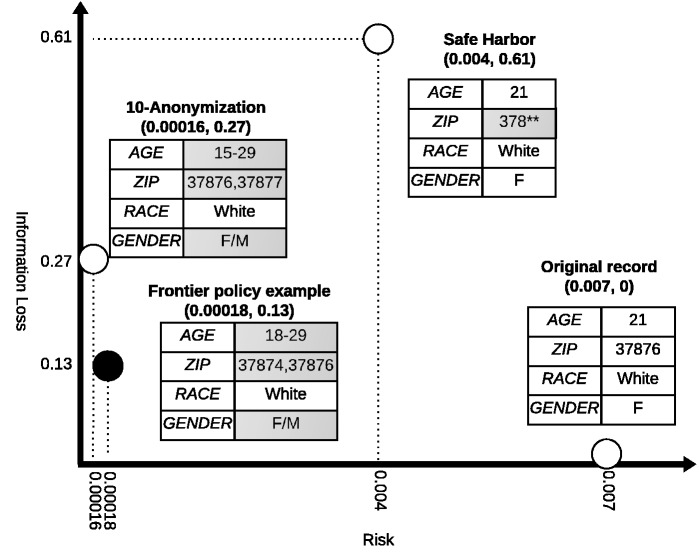
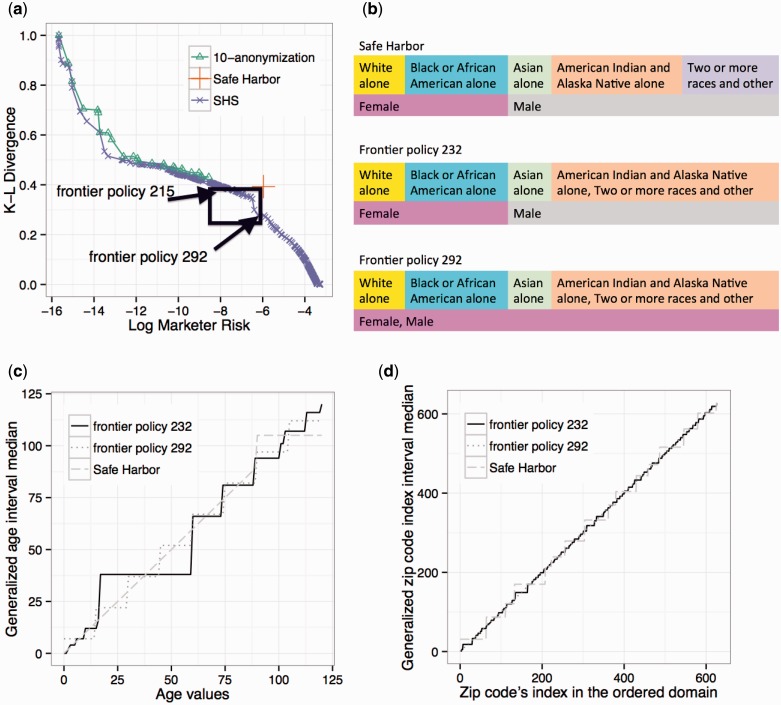
This paper shows that an efficient and effective mechanism can be applied to discover rule-based de-identification policy alternatives for patient-level datasets. To do so, we extend an algorithm³¹ designed to search a collection of de-identification policies that compose a frontier that optimally balances risk (R) and utility (U). We show this approach allows for guidance, interpretation, and justification of rule-based policies, as opposed to relying on a predefined standard in terms of the re-identification risk and data utility or formal models. As a concrete example, Figure 1 depicts how a record from a dataset investigated in our experimental analysis is transformed by one of the frontier policies in comparison with its Safe Harbor and 10-anonymous (i.e., the record is part of a group of no less than 10 records with the same values) versions. In this example, R is defined as inversely proportional to the size of this demographic group defined by the record in a population set, while U is in terms of an information loss metric which represents the discrepancy between the probability density of the record in the original dataset and the transformed dataset. Safe Harbor transforms this record into a group with a large set of ZIP code areas, while 10-anonymization and a policy on the R-U frontier transform it into two different age groups and small ZIP code groups. Based on the population size in these different groups, the record transformed via the frontier policy has slightly higher risk than its 10-anonymous counterpart, while Safe Harbor has the highest risk. On the other hand, the record in the dataset transformed via a frontier policy has lower information loss than its counterparts of both Safe Harbor and 10-anonymous.

Figure 1:

De-identification of a record in the Adult-TN dataset and the corresponding risk and utility (in terms of information loss). De-identification is performed according to Safe Harbor, 10-anonymization, and a de-identification policy on the R-U frontier.

To demonstrate the effectiveness of this approach, we apply it to demographic data from the U.S. Census Bureau (i.e., the “Adult” dataset)³² in combination with geographic information from nine states with medical facilities involved in the Electronic Medical Records and Genomics (eMERGE)³³ network, as well as the state of Hawaii, which has a unique demographic distribution. The results show the de-identification frontier can recommend policies with less risk and more utility than Safe Harbor and cover a broader spectrum of utility and risk than formal protection models in the form of k-anonymity.³⁰

BACKGROUND AND RELATED RESEARCH

A re-identification occurs when a data recipient matches a published record with the identifiers (e.g., personal name) of the corresponding individual. This is often accomplished by a quasi-identifier (e.g., gender, date of birth, and residential 5-digit ZIP code).³⁴ While various methods have been developed for mitigating re-identification risk while preserving data utility in the area of privacy-preserving data publishing,³⁵ in this section, we focus on two topics in this area which are highly related to our work: 1) disclosure control, with particular attention to generalization and suppression strategies and 2) R-U frontier analysis.

Disclosure Control

De-identification policies are rules that guide the processing of the quasi-identifiers to reduce re-identification risk. Many operations can be applied to process quasi-identifiers in medical records, such as generalization, suppression, and randomization.³⁶ Safe Harbor focuses on a certain set of rules for generalization and, thus, to directly relate our method, we represent the policy space as the set of possible generalizations. Focusing on the protection of only quasi-identifiers has certain vulnerabilities (e.g., homogeneity attacks where most, or all, patients have the same diagnosis,^37,38), but it is often used in practice.^39,40,41

Generalization has been invoked by many formal privacy protection models, such as k-anonymity,³⁰ which itself is a specific case of de-identification (where each record must to be equivalent to least k − 1 other records over the set of quasi-identifiers). As a result, a significant number of variations on the generalization space have been proposed.⁴² In this work, we focus on two in particular because they have the strongest relationship with solutions deemed to be useful by the medical research community.⁴⁰ The first is full-domain generalization⁴³ which relies upon a domain generalization hierarchy (DGH) for each quasi-identifier (e.g., age intervals of 1 year, then 5 years, then 10 years, etc.) where the policy space is the cross-product of the level set of each DGH. The second is full-subtree generalization,⁴⁴ which extends the policy space to allow for arbitrary partitions of a quasi-identifier’s domain. It should be recognized that such a space is large and searching for the optimal solution (even for the restricted case of k-anonymity) is NP-hard.⁴⁵ As such, heuristic-driven strategies,⁴⁶ including genetic algorithms⁴⁴ and cost-bounding on subsections of the lattice,⁴⁷ have been invoked.

R-U Frontier of Data Publishing

The notion of an R-U analysis was proposed to support disclosure control decision making. First, the R-U confidentiality map⁴⁸ was introduced to characterize the tradeoff between the level of perturbation (e.g., randomization) applied to a dataset and its predictive accuracy. This concept was then utilized to design algorithms to search for a frontier of k-anonymization solutions with minimum utility loss over a range of k.^49,50 The frontier method has further been extended for set-valued data anonymization, where a record contains more than one value per attribute; for example, a set of diagnosis codes.⁵¹

The policy space was structured as a lattice of binary strings.^44,52 However, the algorithm proposed to search the space considered utility only from a syntactic (e.g., level in the DGH), as opposed to a semantic (e.g., the difference between the distribution of the original and de-identified datasets), perspective. Moreover, the algorithm only searched for policies with risk no worse than HIPAA Safe Harbor and, thus, does not guarantee composition of an R-U frontier. This problem is extended into R-U frontier discovery by introducing a semantic utility loss measure which captures the amount of distortion introduced to the dataset by the de-identification process, and proposed a heuristic algorithm based on a random walk to search the policy lattice.³¹ Yet, as the experiments in the Supplementary Appendix show, the random process is limited in its ability to compose a high-performing frontier in an efficient manner.

METHODS

De-identification Policy Frontier Search Framework

The Sublattice Heuristic Search (SHS) algorithm³¹ was introduced to search a lattice of policies for a frontier in the R-U space. Formally, a frontier is a set of policies that are not strictly dominated by other policies. Intuitively, a policy p_A strictly dominates a policy p_B when both risk and utility loss values of p_A are no greater than the corresponding values of p_B and at least one value is strictly less that of p_B.

SHS is composed mainly of two functions: i) initialize and ii) improve. Figure 2 provides an illustration of how SHS searches for a frontier. Basic versions for these functions in the SHS algorithm relied heavily on randomized processes. For this investigation, we devised functions that used more intelligent heuristics based on patient demographics for frontier composition. Here, we briefly review the basic functions and the new heuristics with the full details in the Supplementary Appendix online. We report on an empirical comparison to prove the improved performance of the heuristics in the results.

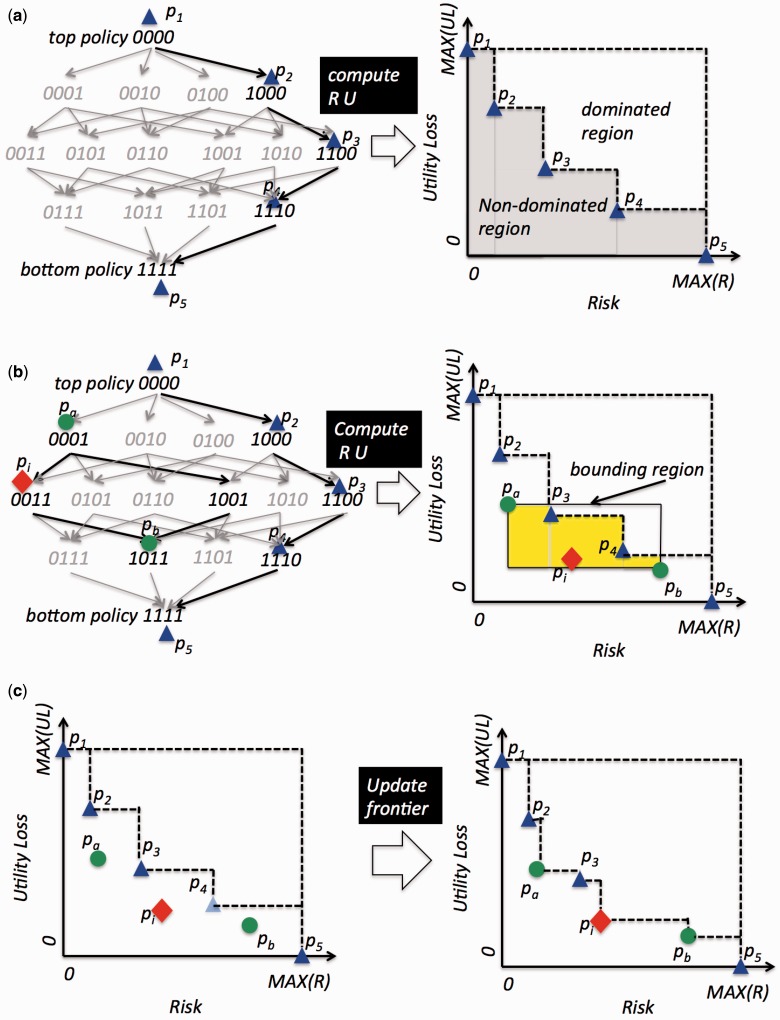
Figure 2:

An example of a policy lattice for five quasi-identifying values and an illustration of the main functions of the SHS algorithm. (a) depicts a random path initialization of the frontier composed of five policies (p₁, p₂, p₃, p₄, and p₅). (b) depicts a sublattice structure sublattice (p_a, p_b) in the policy space and its corresponding bounding region in the R-U space, the yellow area of which is not dominated by the frontier. The proportion of the yellow area is used as the heuristic of the probability that a randomly selected policy in the sublattice can update current frontier. (c) depicts the updates to the frontier: p_a, p_b, and p_i from the sublattice (p_a, p_b) will be on the frontier while policy p₄ is removed.

SHS Initialization: In the basic algorithm, the frontier is initialized by selecting a random path from the most general to the most specific policy in the lattice. An example of random path initialization (or RandPath) is illustrated in Figure 2 (a), where p₁, p₂, p₃, p₄, and p₅ are selected. As an extension, we developed the full domain initialization (FullDom) strategy. FullDom samples a full-domain generalization space to compose the initial frontier and refines it through interpolation. A balanced DGH for each attribute is built in a top-down fashion. Starting from the most generalized value (i.e., generalize every value to the entire domain; e.g., age as [0–120]), in each level, the construction process splits each generalized interval into two equal size intervals. For example, if a level in the age DGH generalizes to 10-year bins, then its immediate children generalize into 5-year bins. This policy space thus corresponds to a cross-product of the level set of the DGH of each attribute. It covers a more diverse set of policies than a random path because i) the full-domain space contains policies from different paths while the random path does not and ii) the full-domain space tends to sample a policy that is multiple levels away from the previous one while a random path samples a child of a previous one.

SHS Improvement: Following initialization, SHS iteratively selects a sublattice to improve the frontier. A sublattice is a subgraph in the lattice containing all policies between a top and a bottom policy (where the latter is a descendent of the former). Figure 2 (b) provides an illustration of such a structure. Assuming the re-identification risk and utility functions are monotonic over the order defined by the policy lattice, the R-U mappings of policies in a sublattice are contained within a bounding region in the R-U space as the rectangle in Figure 2 (b). The basic algorithm relied on a random sublattice generation (RandSub) strategy to iteratively select a sublattice. For each sublattice, RandSub computes the proportion of the bounding region not dominated by the frontier (Figure 2 (b), yellow area), to estimate the probability that a randomly selected policy could improve the frontier. When the computed value is below a predefined threshold, the algorithm skips this sublattice. Otherwise, it searches a random path in an effort to improve the frontier. As illustrated in Figure 2 (c), the newly searched policies (i.e., p_a, p_i, and p_b) will be on the new frontier, while policy p₄ in the old frontier is dominated and is removed from further consideration.

To mitigate randomization effects, we introduce a sublattice chain generation (SubChain) strategy for the SHS improvement function. SubChain generates a sequence of sublattices between the most generalized and the most specific policies of the lattice by using the bottom policy of the sublattice in the current iteration as the top policy of the sublattice in the following iteration. To limit convergence to local optima, SubChain randomly restarts from the most generalized policy when the chain reaches the most specific policy in the lattice. This strategy is based upon the expectation that when a sublattice updates the current frontier, the top and bottom policies are likely to be useful starting points for the subsequent sublattice.

RESULTS

Materials

We evaluated the R-U frontier discovery process using two publicly available datasets. The first is the Adult dataset,³² which consists of 32 561 records without missing values. For comparison with Safe Harbor, we restrict the quasi-identifiers to the demographics of {Age, Gender, Race}. To enable a comparison with respect to geography, we combine the available demographics data from Adult with state-level demographic information obtained from the US Census Bureau’s 2010 Census Tables PCT12A-G⁵³ to provide each tuple with a 5-digit ZIP code. To mitigate the bias that can be introduced through analysis over a single population, we simulated the Adult dataset for 10 US states: Illinois (IL), Hawaii (HI), Massachusetts (MA), Minnesota (MN), New York (NY), Ohio (OH), Pennsylvania (PA), Tennessee (TN), Washington (WA), and Wisconsin (WI). Following the strategy set forth in a previous study,⁵² the Census data of the corresponding states are used as the population statistics to compute the re-identification risk of these synthesized datasets.

All of these states, with the exception of HI, correspond to regions that contain academic medical centers participating in the eMERGE network.³³ These centers are collecting and sharing de-identified data on patients to the public and are actively using the Safe Harbor de-identification policy, but are open to alternatives.²⁹ HI is selected as an additional state because of its unique demographic distribution (e.g., it has the highest percentage of Asians and the lowest percentage of whites in the United States).

To provide analysis on nonsynthetic data, we also conducted experiments on the North Carolina voter registration (NCVR) database,⁵⁴ which contains 6 150 562 records without missing values, each record consists of 18 fields. For this study, we restricted the dataset to a set of four quasi-identifying attributes {Age, Race, Gender, 5-Digit ZIP Code}. We use the entire dataset as the population and randomly sample datasets to publish.

The policy lattice, based on the selected quasi-identifier, contains on the order of 2⁷⁰⁰ policies, which would take a significant length of time to search exhaustively.

Experimental Design

Our experiments were split into two primary sections. First, we evaluated the performance of the frontier initialization and improvement strategies by comparing the resulting frontiers after searching the same quantity of policies. We used the area under the frontier in the R-U space, denoted as AU, as the criteria of the frontier given the orientation of risk and utility loss. We reported the results after every 1000 policies while searching the first 5000 policies. Second, we compared the R-U tradeoffs made by the policies on the frontier discovered by the best SHS configuration to those of two related methods i) a rule-based single policy in the form of HIPAA Safe Harbor and ii) a popular k-anonymization algorithm. In this setting, we allowed SHS to search 20 000 policies.

The details of the generalization rules defined by Safe Harbor (which is a policy in the lattice) are provided in the Supplementary Appendix online. For k-anonymization, we utilized the Incognito⁵⁵ algorithm to find solutions on the frontier for k = 5 and 10, which are commonly adopted protection levels.⁵⁶ We utilized Incognito because it generates all k-anonymous solutions from which the set of nondominated solutions can be selected to create a frontier, which is not the case in many other methods and would lead to an incomplete frontier.

To compute risk, we adopted the marketer risk-based disclosure measure⁵² using the Census data as population statistics, which is based on the distinguishability metric.⁵⁷ Informally, this means that the recipient of the data attacks every record in the dataset and risk is proportional to the average likelihood of successfully re-identifying a record to the population from which it was derived. We used the Kullback–Leibler divergence to measure the utility loss incurred by a generalized dataset with respect to its original form. Informally, the Kullback–Leibler divergence is the difference between the probability distributions of the quasi-identifying values in the original and de-identified datasets. The mathematical definitions for the risk and utility computation can be found in the Supplementary Appendix.

The algorithms were implemented in Python and all experiments were run on an Ubuntu server with 24 Intel(R) Xeon(R) CPUs at 2.4 GHz and 64 GB of RAM. Further details of the parameterization of the algorithms are documented in the Supplementary Appendix.

Performance of SHS strategies

We assessed the performance of SHS using the Adult dataset with TN ZIP codes and a randomly sampled set of 100 000 records from NCVR. We herein report on the average performance of the algorithms over 20 complete runs for each dataset.

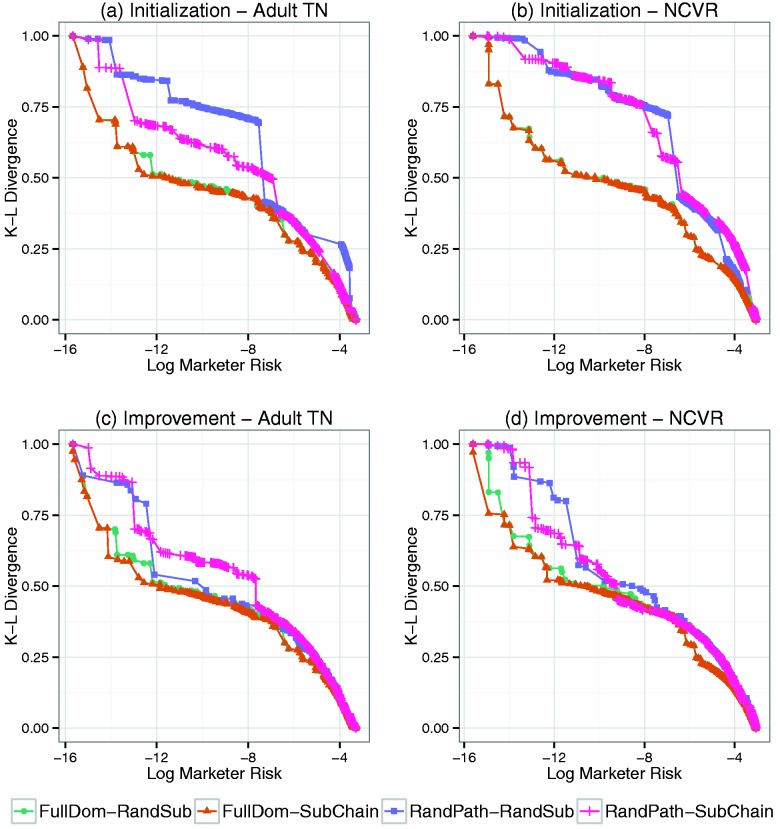
Figure 3 provides snapshots of the R-U frontiers after initialization and the end of the improvement search. The snapshots correspond to a single run of each algorithm (though other 19 runs were similar). Figure 3 (a) and (b) show the FullDom-RandSub and FullDom-SubChain frontiers are closer to the origin than the RandPath-RandSub and RandPath-SubChain frontiers after the initialization process, which implies they have less risk and more utility.

Figure 3:

Snapshots of the R-U frontiers discovered via a single run of the Sublattice Heuristic Search (SHS) algorithm. The initialized frontier for the (a) Adult-TN and (c) North Carolina Voter Registration (NCVR) datasets are based on 1000 policies. The improved frontier for (b) Adult-TN and (d) NCVR datasets are based on an additional 4000 policies.

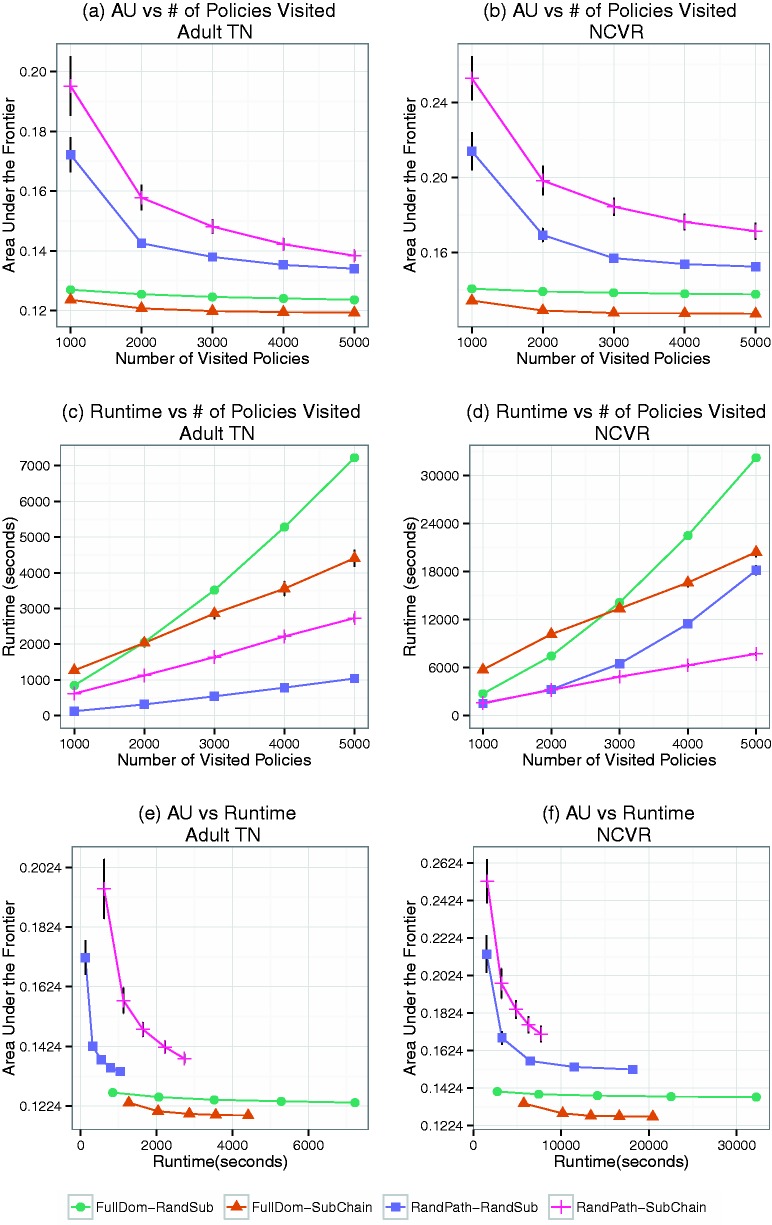
Figure 4 (a) and (b) provides the average and standard deviation the AU of the initial frontiers using different strategies after visiting 1000 polices (i.e., initialization). For orientation, after initialization in the Adult dataset, the average AU of FullDom-RandSub and FullDom-SubChain is 0.127 and 0.124, respectively. By contrast, RandPath-RandSub and RandPath-SubChain exhibited an average AU of 0.172 and 0.195, respectively. The result strongly suggests that FullDom is the dominant initialization strategy.

Figure 4:

Effectiveness versus efficiency for the Sublattice Heuristic Search (SHS) algorithm. The average (±standard deviation) of the area under the frontier (AU) for the frontiers as a function of the number of policies visited is shown for (a) Adult-TN and (b) North Carolina Voter Registration (NCVR). The average (± standard deviation) of the runtime as a function of the number of policies visited is shown for (c) Adult-TN and (d) NCVR. The average (± standard deviation) of the AU for the frontiers as a function of the runtime is shown for (e) Adult-TN and (f) NCVR.

To compare the frontier improvement strategies, Figure 3 (c) and (d) show samples of the frontiers after 5000 policies visited and the average AU of them is reported in Figure 4 (a) and (b). These results show that when the initialization approach is FullDom, SubChain converges to a better frontier than RandSub. For instance, for the NCVR final frontier, the average AU of FullDom-SubChain is 0.127, while FullDom-RandSub is 0.138. By contrast, when RandPath is the initialization process, RandSub outperforms SubChain. For instance, for the NCVR final frontier, the average is 0.171 for RandPath-SubChain and 0.152 for RandPath-RandSub. The result indicates that the SubChain strategy is more efficient in improving a frontier that is closer to the optimal frontier, since FullDom results in a significantly better initial frontier than the RandPath algorithm.

The running time of the algorithms is shown in Figure 4 (c) and (d). It should be noted that the running time is significantly longer for the NCVR dataset than the Adult dataset because the former is approximately 3 times larger in sample size. The result shows that, given the same search budget, initialization via RandPath is faster than FullDom. One possible reason for this is an artifact of our implementation. Our code was optimized to reduce repetition in the risk and utility computations.³¹ And RandPath tends to search policies on the same path, whereas FullDom tends to have more distinct routes. However, even though RandPath initialization is faster than FullDom, Figure 4 (e) and (f) illustrates that FullDom still converges to a better frontier in less time.

These results suggest that FullDom initialization in combination with SubChain sublattice generalization is the best strategy for the SHS algorithm. As such, the remainder of our experiments uses the FullDom-SubChain procedure.

Frontier Case Studies

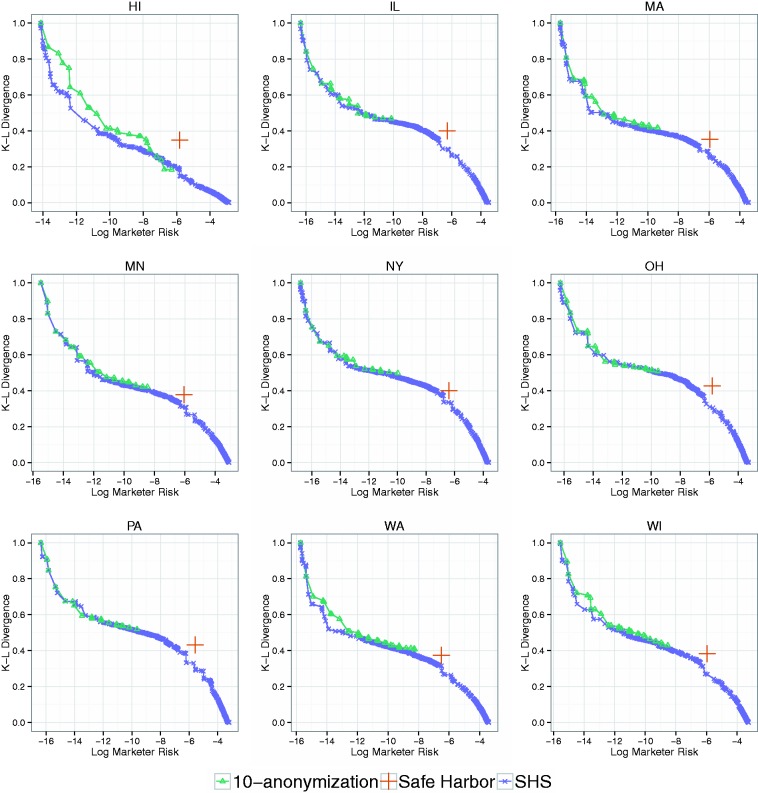
The frontier for SHS and 10-anonymization (the result for 5-anonymization (in the Supplementary Appendix)) is similar for Adult-TN is depicted in Figure 5 (a), while results for the other states are in Figure 6. Notably, the results indicate that a region of the frontier discovered by SHS dominates the Safe Harbor policy in all states. Moreover, the frontier region that dominates Safe Harbor results in both greater utility and risk than the results of 10-anonymization.

Figure 5:

Results from the case study for the Adult-TN dataset. (a) A comparison of the 10-anonymization frontier, Safe Harbor policy, and the Sublattice Heuristic Search (SHS) frontier in the R-U space. The policies between the 215th and the 292nd on the SHS frontier (in the rectangle) dominate Safe Harbor. (b)–(d) provide a comparison of Safe Harbor and two dominating policies −232 and 292. (b) A comparison of the generalization rules for race and gender attributes. (c) A comparison of the age generalization rule. The x-axis corresponds to the original age, while the y-axis corresponds to the median of the generalized age interval. (d) A comparison of the ZIP generalization rule. The x-axis corresponds to the original ZIP, while the y-axis corresponds to the median of the ZIP interval. The ZIP codes are represented as an ordinal index, the translation for which can be found in the Supplementary Appendix online.

Figure 6:

A comparison of the 10-anonymization frontier, the Safe Harbor policy, and the the Sublattice Heuristic Search (SHS) frontier in the R-U space for the Adult dataset simulated over nine U.S. states.

For illustration, two policies that dominate Safe Harbor (i.e., less risk and better utility) are highlighted in Figure 5. The discovered policies exhibit notable differences from Safe Harbor. For instance, both policies generalize race and ages below 90 to larger groups than Safe Harbor (as illustrated in Figure 5 (c)), but retain more specific geographic information (as illustrated in Figure 5 (d)). Additionally, the second policy generalizes gender to (Male or Female).

Policies on the Frontier

Table 1 reports the number of policies on each frontier. The SHS frontier contains an average of 4700 policies while the k-anonymity frontier contains an average of 33 and 26 policies when k = 5 and 10, respectively. This is because SHS can search a significantly larger space than the Incognito k-anonymization algorithm, due to the construction of their respective lattices. Even though the number of policies in the SHS frontier is large, these policies are ordered by their R-U values, so a data publisher can quickly locate the policies they are interested in.

Table 1:

Number of policies on the frontier for the Adult dataset with ZIP codes simulated based on U.S. census data

State	Number of policies on frontier
	SHS	k = 5	k = 10
HI	4545	28	25
IL	3999	28	21
MA	3510	29	23
MN	5655	34	25
NY	4374	27	20
OH	3257	39	27
PA	4161	29	23
TN	7766	39	27
WA	5296	33	35
WI	5147	42	34
Average	4771	33	26
St. Dev.	1234	5.5	5.03

Policies Dominating Safe Harbor

The ratio of policies on the SHS and k-anonymization frontiers that dominate Safe Harbor is summarized in Table 2. Notice that the SHS frontier contains policies that dominate Safe Harbor in all states. By contrast, 5-anonymization leads to solutions that dominate Safe Harbor for only HI, TN, MN, WA, and WI, while 10-anonymization can only find dominant solution for HI. This is because k-anonymity datasets tend to have more utility loss than does a dataset de-identified through Safe Harbor.

Table 2:

Proportion of policies that dominate Safe Harbor for the Adult dataset with ZIP codes simulated based on 2010 U.S. census data

State	Proportion of frontier dominating Safe Harbor
	SHS	k = 5	k = 10
HI	0.01	0.36	0.28
IL	0.04	0	0
MA	0.01	0	0
MN	0.03	0.09	0
NY	0.001	0	0
OH	0.06	0	0
PA	0.003	0	0
TN	0.01	0.13	0
WA	0.01	0.12	0
WI	0.01	0.10	0
Average	0.018	0.08	0.028
St. Dev.	0.018	0.11	0.084

Frontier Ranges

Table 3 summarizes the result of the comparison of ranges of the k-anonymity frontier and the SHS frontier. The results indicate k-anonymization solutions are constrained in a very small sub-interval of the SHS frontier. This interval tends to have very small risk and large utility loss. Thus, SHS may be particularly useful when the data publisher is interested in solutions with better utility at the cost of an acceptable increase in risk. For instance, in the state of NY, the maximum risk of the 5-anonymization frontier is only 0.003 that of the SHS frontier. On the other hand, the minimum utility loss of the 5-anonymization frontier is between 0.15 and 0.52, while SHS is always at 0. This phenomenon is visualized is in Figure 5 (a), where the 10-anonymization has a much smaller range than that of the SHS frontier. This finding indicates that the SHS frontier can provide solutions in a broader range than the k-anonymity frontier.

Table 3:

Maximum risk values (MAX Risk) and minimum utility loss (MIN Utility Loss) of the frontiers for the Adult dataset with ZIP codes simulated from U.S. census data

State	Max. risk			Min. utility loss
	SHS	k = 5	k = 10	SHS	k = 5	k = 10
HI	0.057	2.6 × 10−3	1.8 × 10−3	0	0.15	0.18
IL	0.031	2.4 × 10−4	4.0 × 10−5	0	0.43	0.47
MA	0.032	3.8 × 10−4	9.0 × 10−5	0	0.36	0.42
MN	0.045	5.2 × 10−4	2.1 × 10−4	0	0.36	0.42
NY	0.027	9.0 × 10−5	4.0 × 10−5	0	0.48	0.50
OH	0.037	2.9 × 10−4	7.0 × 10−5	0	0.45	0.51
PA	0.041	2.9 × 10−4	7.0 × 10−5	0	0.49	0.52
TN	0.037	4.3 × 10−4	1.9 × 10−4	0	0.36	0.43
WA	0.033	4.1 × 10−4	2.6 × 10−4	0	0.35	0.41
WI	0.039	4.6 × 10−4	2.0 × 10−4	0	0.36	0.43
Average	0.038	5.7 × 10−4	3.0 × 10−4	0	0.38	0.43
St. Dev.	0.009	7.1 × 10−4	5.5 × 10−4	0	0.10	0.10

Improvement of the Frontier R-U Tradeoff

The frontier R-U tradeoff improvement made by SHS over k-anonymization is outlined in Table 4. We use the relative difference of AU of the k-anonymization frontier F_k and the SHS frontier F_s to represents the R-U tradeoff improvement rate of the SHS frontier over the k-anonymization frontier: IR = (AU(F_k) − AU(F_s))/(AU(F_s)). A positive value indicates F_s improves upon F_k. We truncate the SHS frontier to be in the same range of the corresponding k-anonymization frontier for a fair comparison.

Table 4:

Frontier R-U tradeoff improvement rate of the SHS over k-anonymization (IR) for the Adult dataset with ZIP codes simulated based on U.S. census data

State	IR
	k = 5	k = 10
HI	0.054	0.050
IL	0.035	0.018
MA	0.058	0.062
MN	0.020	0.049
NY	0.034	0.034
OH	−0.003	0.005
PA	0.018	0.019
TN	0.018	0.050
WA	0.040	0.060
WI	0.026	0.050
Average	0.030	0.040
St. Dev.	0.017	0.019

In 9 out of 10 states (OH being the exception), the SHS frontier dominates the k-anonymization frontier. Recall that a positive value in this table indicates the corresponding k-anonymization frontier is dominated by the SHS frontier.

DISCUSSION

The present study illustrates that the SHS framework is, under many conditions, superior to k-anonymization strategies, as well as existing one-size-fits-all policies often invoked in practice (e.g., HIPAA Safe Harbor). Specifically, we observed that k-anonymity limits a frontier to a very small range with extremely low risk and potentially significant loss in data utility. We emphasize that our empirical analysis was performed over a range of diverse population distributions from 10 U.S. states to mitigate biases in the results. We believe that the SHS strategy has the potential to be a method that overcomes the limitations of a single fixed rule-based policy while being interpretable to health data managers. A healthcare organization, for instance, could present the policy frontier as a “documented method”²⁶ to an Institutional Review Board or legal counsel to justify its selection of a certain degree of protection when sharing data in a de-identified manner.

At the same time, there are several limitations to this work. First, the policy lattice was constructed under the assumption that the set of quasi-identifying attributes is known to the data publisher as a priori. We believe, however, there are several possible ways by which our method could be extended to address this problem. One potential strategy is to construct a policy lattice of the superset of all the possible quasi-identifier sets of attributes and measure re-identification risk as a weighted sum of the risk associated with each potential quasi-identifier. The weight of each quasi-identifier could be dependent on the availability of the corresponding external data resources. An alternative strategy is to construct a policy lattice for every subset with a size no greater than a threshold of the set of all the possible quasi-identifying attributes and search for a policy frontier in each space. Applying the latter would require a strategy to reconcile the de-identification policy associated with attributes that are in the overlapping part of multiple policy spaces (e.g., age, if [Age, Zip, Gender] and [Age, Gender, Race] are both possible quasi-identifiers).

Second, our search strategy does not cover the entire policy space. As such, the frontier is not guaranteed to be optimal. SHS is based on several heuristics and it is possible that more effective approaches could be developed. It may also be possible to develop methods to more systematically and efficiently navigate the space of policies using advanced pruning strategies, such as cost bounding. Moreover, the lattice search process should be amenable to parallel computing techniques as has recently been achieved for k-anonymization⁵⁸ provided an appropriate master program that minimizes reassessment of sections of the lattice can be designed.

Third, our investigation is based on specific measures of risk and utility. In particular, we rely on the marketer risk model, which amortizes the risk over all records in a published dataset. Yet, this is only one way to define risk. The amortization model itself, for instance, can be refined to allow for a discounting function that applies greater weight to individuals in smaller groups. Beyond the risk model, one could also consider worst-case re-identification scenarios, such as prosecutor or journalist attacks (which state that the risk of a dataset is equal to that of the most risky record).³⁹ From the perspective of utility, it is important to recognize that we adopted a generic information loss measure, which was based on the assumption that the specific usage of the dataset is unknown a priori. The data utility function is not necessarily consistent with the usage of the dataset in certain clinical data mining or statistical analysis applications. Nonetheless, if it is known that the dataset will be used in a certain study, then the frontier policy search framework can be customized with an alternative utility function defined by domain experts, provided that the function satisfies the monotonicity requirements of our framework.

Finally, while SHS builds a better frontier than other methods, it can yield a very large number of policies. A data manager would still need to determine which policy is best and it is clear that they could not review every policy on the frontier. As such, a strategy to present the most interesting policy options should be devised.

CONCLUSIONS

Current regulations permit institutions to publish de-identified data according to two conceptual routes: 1) fixed rules-based policies and 2) statistically-informed strategies that appropriately mitigate the risk of re-identification. While formal privacy models such as k-anonymity provide guarantees of protection, they can, at times, be too rigorous, leading to unacceptable levels of data utility in comparison to a rule-based policy. This paper showed, with evaluation over multiple datasets, that a de-identification policy frontier can provide a broader range of options than a well-known k-anonymization algorithm. In most cases, the de-identification frontier dominates 5-anonymization and is always superior to the popular HIPAA Safe Harbor rule-based policy. There are, however, several opportunities to improve the efficiency and selectivity of the SHS method to ensure it is directly usable by health data managers.

FUNDING

This work was supported, in part, by the Australian Research Council grant number [DP110103142], National Science Foundation grant number [CCF0424422], National Institutes of Health grant numbers [U01HG006385, U01HG006378, UL1TR000135, R01HG006844], and National Natural Science Foundation of China grant number [61472148].

COMPETING INTERESTS

None.

CONTRIBUTORS

WX designed the algorithm, performed the study, analyzed the experiment results, and wrote the paper. RH assisted in the experiment design, data analysis, and revised the paper. XD and JL provided insights in the outline of the study, analysis of the results and the refinement of the paper. BM designed and supervised the study, analyzed the data, and revised the paper.