Abstract
The present study explored the method of testing muscle mechanical properties through the linear force-velocity (F–V) relationships obtained from loaded vertical jumps. Specifically, we hypothesised that the F-V relationship parameters depicting the force, power, and velocity of the tested muscles will differ among individuals of different physical fitness. Strength trained, physically active, and sedentary male participants (N=10+10+10; age 20–29 years) were tested on maximum countermovement and squat jumps where manipulation of external loads provided a range of F and V data. The observed F–V relationships of the tested leg muscles were approximately linear and mainly strong (median correlation coefficients ranged from 0.77 to 0.92; all p < 0.05), independently of either the tested group or the jump type. The maximum power revealed higher values in the strength trained than in the physically active and sedentary participants. This difference originated from the differences in F-intercepts, rather than from the V-intercepts. We conclude that the observed parameters could be sensitive enough to detect the differences among both the individuals of different physical fitness and various jump types. The present findings support using loaded vertical jumps and, possibly, other maximum performance multi-joint movements for the assessment of mechanical properties of active muscles.
Keywords: Power, strength, vertical jump, load
INTRODUCTION
It has been known for decades that the force-velocity (F-V) relationship of individual muscles and muscle groups is approximately hyperbolic (Hill, 1938; Kaneko, Fuchimoto, Toji, & Suei, 1983). However, a number of more recent studies have suggested that the F-V relationship of the loaded maximum performance multi-joint movements could be rather linear (Jaric, 2015). Specifically, approximately linear F-V relationships have been obtained from cycling (Driss & Vandewalle, 2013; Nikolaidis, 2012), various vertical jumps (Cuk et al., 2014; Rahmani, Viale, Dalleau, & Lacour, 2001; Samozino, Edouard, et al., 2014a; Samozino, Rejc, Di Prampero, Belli, & Morin, 2012; Sheppard, Cormack, Taylor, McGuigan, & Newton, 2008; Vandewalle, Peres, Heller, Panel, & Monod, 1987), simultaneous leg extensions where leg muscles act through closed kinetic chains (Samozino, Edouard, et al., 2014a; Samozino et al., 2012; Samozino, Rejc, di Prampero, Belli, & Morin, 2014; Yamauchi, Mishima, Nakayama, & Ishii, 2009), or arms and upper body movements (Hintzy, Tordi, Predine, Rouillon, & Belli, 2003; Nikolaidis, 2012; Sreckovic et al., 2015).
If experimentally supported, the linear F-V relationship of multi-joint movements could be of both practical and theoretical importance. For example, a linear regression model applied to the F and V data obtained from maximum performance tasks tested under different external loads gives
where F0 is F-intercept corresponding to the maximum isometric F, while a is the slope that corresponds to F0/V0 [see also (Cuk et al., 2014; Samozino et al., 2012; Vandewalle et al., 1987) for details], V0 corresponds to the V-intercept (i.e., the maximum V at zero F), while the maximum power equals Pmax = (F0V0)/4. Therefore, the loaded maximum performance movements could serve for the development of relatively simple routine tests for the assessment of force, velocity, and power generating capacity of the tested muscles through the linear F-V relationship (Cuk et al., 2014; Driss, Vandewalle, & Monod, 1998; Jaric, 2015; Samozino et al., 2012). Those tests could detect a potential imbalance of the muscle force and velocity generating capacity through the F-V slope a [i.e., the ‘normalised F-V profile’; (Samozino, Edouard, et al., 2014a; Samozino et al., 2012)], evaluate adaptations of the tested muscles to various athletic training and rehabilitation interventions (Cormie, McGuigan, & Newton, 2010a), or assess the bilateral deficit (Samozino, Rejc, et al., 2014).
Having in mind its potential theoretical and practical importance, several studies have evaluated patterns of the F-V relationship in various multi-joint maximum performance tasks, as well as the properties of their parameters. In addition to being fairly linear (see above for details), the concurrent validity of parameters of the F-V relationship (i.e., F0, V0, a and Pmax) regarding the directly measured values could be on average moderate (Cuk et al., 2014; Sreckovic et al., 2015; Yamauchi & Ishii, 2007). Surprisingly, their reliability could be high [(Cuk et al., 2014; Sheppard et al., 2008; Sreckovic et al., 2015); see also (Driss & Vandewalle, 2013) for review], even when F0 and V0 are outcomes of distant extrapolation (Cuk et al., 2014). However, not only have very few studies explored the sensitivity of the F-V relationship parameters when detecting differences among various populations, but they have also revealed inconsistent findings (Jaric, 2015). For example, when individuals of different ages are compared, a higher Pmax in younger individuals could predominantly originate from either a higher V0 (Callahan & Kent-Braun, 2011) or a higher F0 (Yamauchi et al., 2009; Yamauchi, Mishima, Nakayama, & Ishii, 2010), while the differences in the F-V parameters in different muscles in 14 years old boys and girls revealed conflicting outcomes [see (Driss & Vandewalle, 2013) for review]. Finally, none of the cited studies assessed the sensitivity of the relationship’s slope, which could be an important factor in maximising the movement performance (Samozino, Edouard, et al., 2014a; Samozino et al., 2012) nor have they used loaded vertical jumping as experimental model. Regarding the later point, both the countermovement [CMJ; (Limonta & Sacchi, 2010; Sheppard et al., 2008)] and squat jumps [SJ; (Cormie et al., 2010a; Samozino, Edouard, et al., 2014a, 2014b)], or both (Cuk et al., 2014), have been extensively utilised to assess the effects of the load on jumping kinematics and kinetics. Both jumps have also been routinely applied as routine tests of leg muscle power and they are obvious candidates for testing mechanical properties of leg muscles. Finally, their F-V relationship parameters can be markedly different (Cuk et al., 2014). However, it remains unexplored which jump type could be more sensitive to detect the differences among various populations through the assessed F-V relationship.
The main aim of our study was to explore the pattern of the F-V relationship and the differences in the relationship parameters among the 3 groups of participants. We specifically hypothesised that the F-V relationship parameters would be able to distinguish among the groups, particularly regarding Pmax and F0. The expected findings would motivate further development of loaded maximum performance movements into standard tests that could discern among the F, V, and P producing capacities of the tested muscles.
METHODS
Participants
We calculated estimates of the sample size based on the data reported in our previous studies (Cuk et al., 2014; Markovic & Jaric, 2007). The results revealed that the sample sizes of less than ten participants per group appeared to be necessary to detect the effects of load on the tested dependent variables. Therefore, we conservatively recruited three groups of ten healthy male participants that differed regarding their level and type of physical activity. Their anthropometric characteristics and assessed strength variables are presented in Table 1. The first group consisted of strength-trained bodybuilders (StrengthG). Although none of them were professional competitors, they had had at least 3 years of experience in bodybuilding and a minimum of 3 strength-training sessions per week. Three of them were also sport and physical education students, which implied additional types of physical activity (see further text for details). The second group consisted of 10 physically active individuals (ActiveG). They were sport and physical education students who were active through their standard academic curriculum. It included 6–8 activity classes per week that involved both low and high-intensity exercises, but did not include any type of resistance training. More than half of their activities were directly related to sport games (e.g., football, basketball, volleyball, handball) and other types of predominantly fast movements. The third group consisted of sedentary participants (SedentaryG). Their daily physical activity was assessed by the IPAQ questionnaire (Taylor-Piliae et al., 2006), where 3 participants reported a moderate level of physical activity, while the remaining 7 reported a low level of physical activity.
Table 1.
Participants’ anthropometric characteristics and indices of muscle strength (mean ± SD)
| Variable | All (N=30) | StrengthG (N=10) | ActiveG (N=10) | SedentaryG (N=10) |
|---|---|---|---|---|
| Age (y) | 24.4 ±2.3 | 24.4 ± 2.3 | 23.4 ±3.2 | 25.4 ±1.3 |
| Height (cm) | 182.4 ± 6.2 | 182.8 ± 7.6 | 183.2 ± 6.0 | 181.2 ± 6.0 |
| Body mass (kg) | 80.2 ±7.0 | 83.9 ± 6.4 | 79.6 ± 7.3 | 77.0 ± 6.2 |
| BMI (kg/m2) | 24.1 ± 2.1 | 25.3 ± 1.5 | 23.7 ± 1.9 | 23.4 ± 2.3 |
| Muscle mass (kg) | 40.7 ±5.0 | 44.8 ± 3.2 | 41.2 ± 4.2 | 36.1 ± 3.2a,b |
| Body fat (%) | 11.5 ±5.7 | 7.3 ± 2.8 | 10.3 ± 3.1 | 17.1 ± 5.5a,b |
| 1RM squat (kg) | 139.6 ±44.9 | 192.0 ± 15.5 | 129.3 ± 29.5a | 97.4 ± 15.1a,b |
| MVC (N) | 884 ±174 | 1068 ± 105 | 858 ± 103a | 726 ± 96a,b |
BMI, body mass index; 1 RM, 1-repetition maximum; MVC, maximum voluntary contraction force;
Significantly different from StrengthG;
Significantly different from ActiveG (p < 0.05)
None of participants reported any medical problem or recent injuries. They were also instructed to avoid any unusual strenuous activities over the course of the study. All participants gave written informed consent to the experiments, which was in accordance with the Declaration of Helsinki and approved by the University of Belgrade Institutional Review Board.
Experimental procedures
Body height was measured with a standard anthropometer (GPM, Switzerland), while body mass, percent body fat, and muscle mass (standard errors of measurements 0.1 kg, 0.5%, and 0.2 kg, respectively) were assessed using a bioelectric impedance method (In Body 720; USA).
The strength of the leg extensors was assessed through one-repetition maximum squat (1RM squat), and a maximum voluntary contraction of the knee extensors (MVC). 1RM squat testing was performed on a custom made Smith machine, from a semi-squat position (knee angle was set at 90°) and was conducted according to the standard procedure (Markovic & Jaric, 2007; McBride, Triplett-McBride, Davie, & Newton, 1999). The MVC was recorded under isometric conditions over 4–5 s on a Kin-Com isokinetic dynamometer according to the manufacturer recommendation (Chatex Corporation, Chattanooga, TN, USA). A rest period between both the 1RM series and the MVC trials was set to 2–5 min.
Participants were tested on two types of vertical jumps. Regarding the squat jump (SJ), they were instructed to hold their hands on their hips and perform a maximum jump from the knee joint angle fixed at 90°. Visual inspection of the force signal was additionally used to detect a possible counter movement prior to the SJ. Regarding the countermovement jump without the arm swing (CMJ), the participants were instructed to perform an unconstrained maximum vertical jump from a standing upright position that included the initial counter movement, while keeping their hands on their hips.
The jumps were performed on a force plate while a pulley system exerted either loading or unloading forces that corresponded to 10%, 20%, or 30% of their body weight (BW) providing the total weight measured by the force plate (AMTI, USA; sampling frequency 1,000 Hz) between 0.7 and 1.3 BW. The force platform placed beneath the participants’ feet allowed for an accurate adjustment of the applied loading force. The rest period between two consecutive jumping trials was 15–25 s, and about 2 min between different jump types and/or loading magnitudes.
Experimental protocol
Each participant completed 3 sessions separated by 5 to 7 days of rest. Each session was preceded by a standard warm-up procedure (5 min cycling and 5 min of calisthenics and dynamic stretching). The first testing session included anthropometric measurements followed by MVC testing and the familiarisation with the loaded and unloaded jumps. The familiarisation was repeated during the second session preceded by 1RM squat testing, while the third session served for the gathering of data. The participants completed 28 jumps per session (7 loading magnitudes × 2 jump types × 2 trials) and the second trial was taken for further analysis. The sequence of loading magnitudes and jump types were block randomised to avoid the effect of different orders across the groups. Note also that conducting only 2 trials per loading magnitude allowed testing the jumps within a single experimental session without dealing the effect of fatigue.
The pulley device and loading conditions
A pulley system was used to simulate either an increase or a decrease in body weight BW [see (Leontijevic et al., 2012; Markovic, Mirkov, Knezevic, & Jaric, 2013; Pazin, Berjan, Nedeljkovic, Markovic, & Jaric, 2013) for details]. Two long rubber bands (resting length 13.5 m, coefficient of elasticity 21 N/m) were stretched to provide the pulling force of up to 30% of the participants’ body weight, acting either vertically upwards (negative load), or downwards (positive load). The bands were attached at the lateral sides of a belt fixed approximately on the participants’ waist and stretched over a system of low-friction and low-inertia plastic wheels. As a result, the loading method allowed for unconstrained vertical jumps, while the relative change in their stretched length over the course of the tested jumps was up to approximately 4%, yielding a similar change in the loading force (Cuk et al., 2014).
Data processing and analysis
The force plate was mounted on the floor and calibrated according to the manufacturer’s specifications. Custom-designed software (LabVIEW 2010, National Instruments, Austin, TX, USA) was used to record and process the vertical component of the ground reaction force (F). The data were low-pass filtered (a second-order recursive Butterworth filter at a cut-off frequency of 10 Hz) and the velocity of the centre of mass was calculated by integrations of the acceleration signal assessed from F (Fig. 1). Thereafter, the average values of F (calculated from the vertical component of the ground reaction force) and V (calculated for the body’s centre of mass) were calculated from the jump concentric phase.
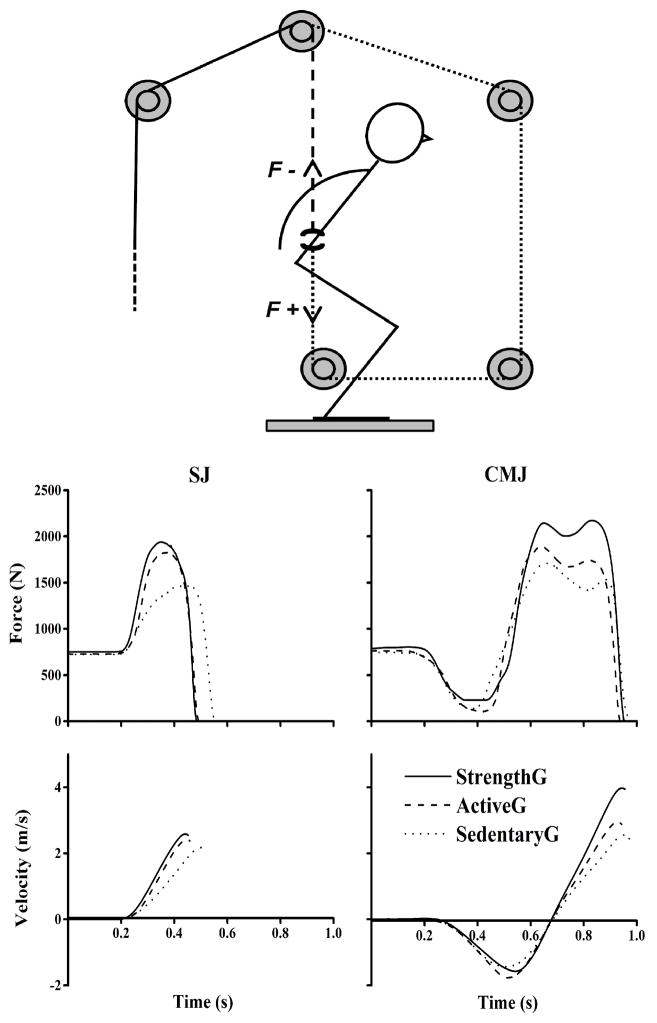
Figure 1.
Illustration of the loading conditions while performing the tested jumps. Rubber bands extended over a series of wheels pulled participants either downward (dotted line) or upward (dashed line) exerting a loading (F+) or unloading force (F−) upon the participant’s belt. The middle and bottom panels show the time series of the ground reaction force (F) and velocity of the centre of mass (V), respectively, obtained from 3 representative participants under 1.0 BW loading condition of SJ and CMJ. The time series are aligned either with respect to jump initiation (SJ) or the instant of transition from the eccentric to concentric jump phase (CMJ).
F-V relationships were assessed from the F and V data obtained from 7 loading magnitudes separately for the SJ and CMJ. Linear regressions (eq.1) were calculated together with the corresponding correlation coefficients (r) for both the individual data sets and from the data averaged across the participants of each group. The regressions were extrapolated to determine the maximum force (F0; the force at zero velocity) and maximum velocity (V0; the velocity at zero force), as well as the slope of the relationship (a = F0/V0). Finally, the maximum power output (Pmax; eq.3) was calculated from F0 and V0.
Statistical analyses
One-way between ANOVA’s was applied to test the age, anthropometric, and strength differences among the three groups. Two-way between-within ANOVA’s was applied on the F-V relationship parameters (i.e., F0, V0, a and Pmax) to assess the differences both among the three groups (StrengthG, ActiveG and SedentaryG) and between the two jump types (SJ and CMJ). To provide normally distributed data, the same ANOVA was also applied on the Fisher Z-transformed r. In case of significant main effects without interactions, T-tests for the independent samples (factor ‘jump type’) were applied to compare the dependent variables obtained from the SJ and CMJ. A Bonferroni post-hoc test was applied to assess significant interactions. Eta squared (η2) was also calculated together with ANOVA’s, where the values of the effect sizes 0.01, 0.06, and above 0.14 were considered small, medium, and large, respectively (Cohen, 1988). Prior to the statistical analyses, initial testing revealed that none of the dependent variables significantly deviated from their normal distribution (Kolmogorov–Smirnov test). Alpha was set to 0.05. All statistical tests were performed using SPSS 16.0 (SPSS Inc, Chicago, IL, USA).
RESULTS
The anthropometric and strength characteristics of the tested participants are presented in Table 1. While no differences in height, body mass, and BMI were recorded among the groups, both StrengthG and ActiveG revealed a higher muscle mass and less body fat than SedentaryG. As expected, StrengthG showed the highest and SedentaryG showed the lowest scores in both the 1RM squat and MVC tests (see Table 1).
Figure 1 illustrates typical force and velocity profiles obtained from individual participants. Note that despite similar body mass, the StrengthG participant exerted the highest ground reaction force and the velocity of the centre of mass, while the same values for the SedentaryG participant were the lowest.
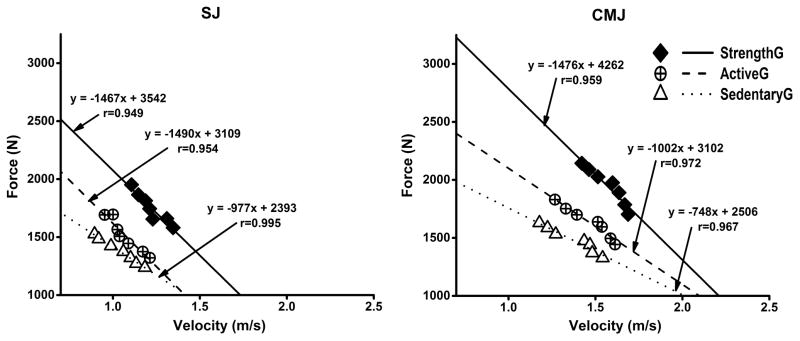
Figure 2 shows the linear regression lines that represent the studied F-V relationships assessed from the averaged across the participants’ data within each group. Note that the correlation coefficients were exceptionally high (r ranged from 0.949 to 0.995) and significant at the level p < 0.01.
Figure 2.
F–V relationships observed from the concentric phase of 2 jumps under seven loading conditions (data averaged across the participants). The linear regression equations are presented together with corresponding correlation coefficients.
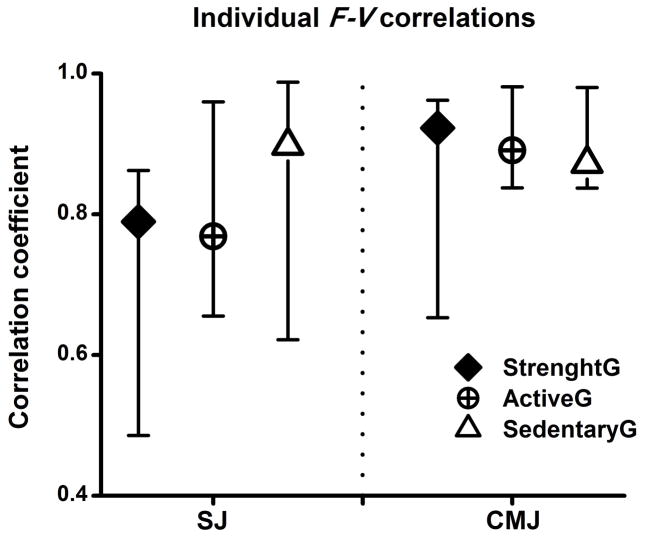
Figure 3 shows median correlation coefficients and their ranges obtained from the linear regression applied on individual sets of F-V data and averaged across the groups. The coefficients ranged from 0.77 to 0.92 depending on the jump type and the group. Two-way ANOVA applied on their Z-transformed values revealed the main effect of jump type [F(1,28)=5.71, η2=0.09, P=0.024], and neither the main effect of group [F(2,27)=2.26, η2=0.06, p=0.12], nor their interaction [F(2,27)=2.62, η2=0.08, p=0.091]. Specifically, the studied relationships were stronger for CMJ than for SJ.
Figure 3.
Median correlation coefficients (with error bars representing ranges) of the linear F-V relationship obtained from 2 jumps and 3 groups of participants.
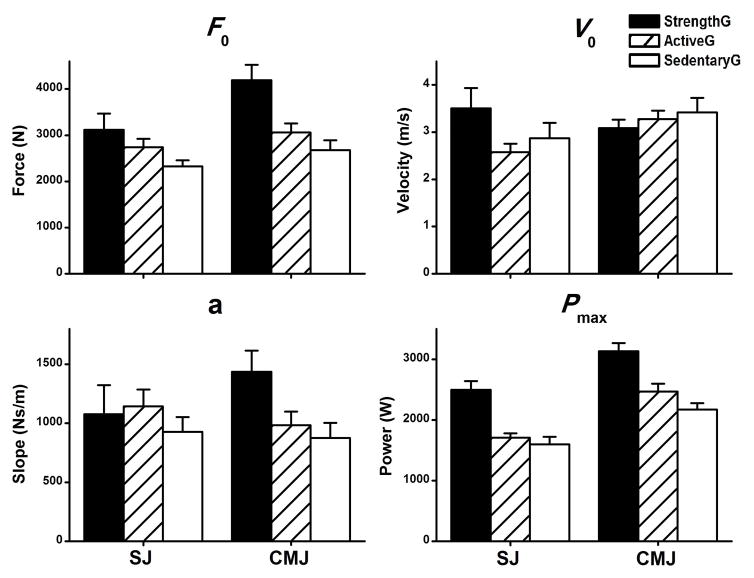
The parameters (i.e., F0, V0, a and Pmax) obtained from individual linear regressions (data averaged within each group) are depicted in Figure 4. Two-way ANOVA’s were applied to assess the main effects of group and jump type. The F-intercept (F0) revealed significant effects of both the group [F(2,27)=10.7, η2=0.25, p<0.01] and jump type [F(1,28)=8.62, η2=0.10, p<0.01], but not their interaction [F(2,27)=1.53, η2 =0.03, p=0.23]. F0 was higher in StrengthG than in both ActiveG and SedentaryG, and it was also higher in CMJ than in SJ. In terms of the V-intercept (V0), there were neither significant main effects of jump type [F(1,28)=1.78, η2=0.02, p=0.19] and group [F(2,27)=0.73, η2=0.03, P=0.49], nor their interaction [F(2,27)=2.79, η2=0.07, p=0.079]. The regression slopes (a) also revealed neither the significant main effects of jump type [F(1,28)=0.13, η2<0.01, p=0.72] and group [F(2,27)=2.48, η2=0.08, p=0.10], nor their interaction [F(2,27)=1.39, η2=0.05, p=0.27]. Finally, the maximum power output (Pmax) revealed significant main effects of group [F(2,27)=25.0, η2=0.40, P<0.01] and jump type [F(1,28)=67.7, η2=0.27, P<0.01], but not their interaction [F(2,27)=0.47, η2<0.01, p=0.63]. StrengthG showed a higher Pmax than both ActiveG and SedentaryG, while the same values were higher in the CMJ than in the SJ.
Figure 4.
Parameters of linear F–V regressions (data averaged across the participants with SE error bars). The individual data sets show force intercepts (F0), velocity intercepts (V0), regression slopes (a), and the maximum power output (Pmax).
DISCUSSION AND IMPLICATIONS
The main aim of our study was to explore the pattern of the F-V relationship and the differences in the relationship parameters among the 3 groups of participants. The obtained F-V relationships were fairly linear and generally strong regardless of either the jump type or the tested group. However, the main finding could be that the obtained F-V relationships were sensitive enough to detect the hypothesised differences among individuals of different levels of physical fitness. Even more important and particularly novel finding could be that the observed differences in Pmax predominantly originate from F0, rather than from V0.
The differences in Pmax are in line with virtually all studies that assessed leg muscle power from individuals of different levels of physical fitness [c.f. (Cormie, McGuigan, & Newton, 2010b; Nuzzo et al., 2010; Pazin, Berjan, Nedeljkovic, Markovic, & Jaric, 2013)]. Therefore, the main finding of the present study could be that the differences in Pmax predominantly originate from prominent differences in F0, while the differences in V0 appear to be rather small. Specifically, our data suggest that more powerful individuals are characterised with a steeper F-V slope that could predominantly originate from differences in strength, but not the velocity. Although this finding is in line with the differences obtained between young and old individuals (Yamauchi et al., 2009, 2010), it implicitly contradicts some recent theoretical models. For example, our finding challenges the macroscopic model of leg extensors suggesting that the optimum F-V profile for maximising vertical jump performance in more powerful individuals should be less steep [i.e., relatively higher V0 than F0 is expected; (Samozino et al., 2012)]. The same finding also contradicts the strength independent behaviour of leg muscles [i.e., body mass provides the optimum load regardless the leg muscle strength; (Jaric & Markovic, 2009, 2013; Suzovic et al., 2013)] which clearly requires the adaptation of F-V profiles towards either force (i.e., F0) or velocity (V0) producing capacities depending on muscle power. Finally, it has been known for decades that the magnitude of the training load can selectively push the muscle F-V relationship towards either a higher F0 or V0 [c.f. (Kaneko et al., 1983)]. Therefore, one could argue that the lack of difference in the V0 observed from the 3 tested groups could originate from a high training load typically used by bodybuilders that increased the F0 (but not V0) in StrengthG, while the differences in the overall power between ActiveG and SedentaryG were too small to reveal differences in the V0. Alternatively, the obtained finding could also be explained by the direction of the tested movement since muscle strength could be more important when acting against gravity than in the movements performed in the horizontal direction (Minetti, 2002; Samozino et al., 2012). Therefore, future comparisons of the strength and speed-trained individuals could reveal whether the observed differences in the tested power based on the differences in the F0 (but not V0) represent an inherent property of human leg muscles or, alternatively, represent the consequence of either the selection of participants, or the selection of the tested movement direction.
Regarding the obtained magnitudes of the obtained F-V parameters per se, although their values can widely vary across the population and tasks (Jaric, 2015), the range of F0 we obtained closely corresponds to the values reported from maximum leg extensions and SJ performed by untrained (Samozino, Rejc, et al., 2014; Yamauchi & Ishii, 2007) and trained males (Cormie et al., 2010a; Rahmani et al., 2001). The same studies revealed a V0 close to the values we obtained from the SJ. Therefore, one could conclude that the present application of both positive and negative loads on the maximum vertical jumps revealed outcomes similar not only to positively loaded SJ, but also to the loaded leg push-offs that typically require elaborate lab equipment [c.f., (Samozino et al., 2012; Yamauchi et al., 2009)]. In addition, both the body size and the directly tested strength of the ActiveG and SedentaryG closely corresponded to the values obtained from non-trained populations [(Cuk et al., 2014; Nuzzo et al., 2010); see also (Jaric, 2015) for review]. Nevertheless, it should also be noted that the magnitude of the observed parameters could markedly differ depending upon the jump type. Not surprisingly, CMJ revealed a higher Pmax than did SJ [c.f., (Cormie et al., 2010b; Cuk et al., 2014; Suzovic et al., 2013)], which resulted from both a higher F0 and a higher V0.
In favour of the concurrent validity of the discussed parameters is the finding that the F0 magnitudes assessed from SJ were only marginally higher than the sum of the body weight plus the added weight lifted in the 1RM squat. Moreover, the differences in F0 among the groups closely reflect the differences in the leg strength directly measured through both the 1RM squat and MVC. Of importance could be that although we applied both the negative and positive load to increase the total loading range, the observed F-V relationship parameters F0 and V0 were still the outcome of a relatively remote extrapolation of experimental data. However, note that a similar extrapolation has been used in a number of other studies that revealed not only comparable values of F-V relationship parameters (see above), but the same parameters were both highly reliable and at least moderately valid [(Cuk et al., 2014; Sheppard et al., 2008; Yamauchi & Ishii, 2007); see also (Jaric, 2015) for review].
From the theoretical perspective, the muscles mechanical properties assessed through the linear F-V relationship could provide valuable insight into the design and function of the muscular system, such as its possible adaptation to maximise its dynamic output when acting against its own body (Jaric & Markovic, 2009, 2013; Suzovic et al., 2013). The main practical implication of the discussed finding is that the present method could be applied in routine testing of the muscle mechanical properties. Namely, the validity of outcomes of standard tests based on multi-joint functional movements (e.g., maximum jumps, stationary biking, push-offs, weight lifts etc.) should be generally questioned since the muscle strength, power, and velocity cannot be distinguished from a single trial. Similarly, the routine tests conducted on isokinetic devices could be criticised for lack of distinguishing among the same muscle properties, as well as for a lack of ecological validity of the tested single-joint movements. Conversely, the applied method based on manipulation of external loads and the linear F-V model proves not only to provide reliable and valid data (Cuk et al., 2014; Sreckovic et al., 2015; Vandewalle et al., 1987), but also to allow for selective assessment of the tested muscular systems regarding its ability to produce a high force, power and velocity output.
CONCLUSION
To conclude, within the present study we found that the F-V relationship parameters could be sensitive enough to detect the differences among individuals of different physical fitness levels. The observed differences in the maximum power (Pmax) in the studied populations appear to be predominantly based on differences in maximum strength (i.e., F0) rather than on differences in maximum velocity (V0). To both advance our knowledge of muscle mechanics and improve the testing methods based on similar methodology, future studies could extend this line of research to both different multi-joint maximum performance tasks and different populations, as well as explore the effects of different loading conditions. Regarding the practical application, the results of the present study contribute to the evidence that the loaded multi-joint maximum performance tasks could be used for routine testing of leg and other muscles regarding their force, velocity, and power producing capacities.
Acknowledgments
The study was supported by NIH under grant R21AR06065, and by the Serbian Research Council under grant 175037.
References
- Callahan DM, Kent-Braun JA. Effect of old age on human skeletal muscle force-velocity and fatigue properties. Journal of Applied Physiology. 2011;111(5):1345–1352. doi: 10.1152/japplphysiol.00367.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2. Hillsdale, NJ: Lawrence Erlbaum Associates; 1988. pp. 273–283. [Google Scholar]
- Cormie P, McGuigan MR, Newton RU. Adaptations in athletic performance after ballistic power versus strength training. Medicine & Science in Sports & Exercise. 2010a;42(8):1582–1598. doi: 10.1249/MSS.0b013e3181d2013a. [DOI] [PubMed] [Google Scholar]
- Cormie P, McGuigan MR, Newton RU. Changes in the eccentric phase contribute to improved stretch-shorten cycle performance after training. Medicine & Science in Sports & Exercise. 2010b;42(9):1731–1744. doi: 10.1249/MSS.0b013e3181d392e8. [DOI] [PubMed] [Google Scholar]
- Cuk I, Markovic M, Nedeljkovic A, Ugarkovic D, Kukolj M, Jaric S. Force-velocity relationship of leg extensors obtained from loaded and unloaded vertical jumps. European Journal of Applied Physiology. 2014;114(8):1703–1714. doi: 10.1007/s00421-014-2901-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driss T, Vandewalle H. The measurement of maximal (anaerobic) power output on a cycle ergometer: a critical review. BioMed Research International. 2013;2013:589361. doi: 10.1155/2013/589361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driss T, Vandewalle H, Monod H. Maximal power and force-velocity relationships during cycling and cranking exercises in volleyball players. Correlation with the vertical jump test. Journal of Sports Medicine and Physical Fitness. 1998;38(4):286–293. [PubMed] [Google Scholar]
- Hill AV. The heat of shortening and the dynamic constants of muscle. Proceedings of The Royal Society of London Series B, Biological Sciences. 1938;126(843):136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- Hintzy F, Tordi N, Predine E, Rouillon JD, Belli A. Force-velocity characteristics of upper limb extension during maximal wheelchair sprinting performed by healthy able-bodied females. Journal of Sports Sciences. 2003;21(11):921–926. doi: 10.1080/0264041031000140392. [DOI] [PubMed] [Google Scholar]
- Jaric S. Force-velocity relationship of muscles performing multi-joint maximum performance tasks. International Journal of Sports Medicine. 2015;36(9):699–704. doi: 10.1055/s-0035-1547283. [DOI] [PubMed] [Google Scholar]
- Jaric S, Markovic G. Leg muscles design: the maximum dynamic output hypothesis. Medicine & Science in Sports & Exercise. 2009;41(4):780–787. doi: 10.1249/MSS.0b013e31818f2bfa. [DOI] [PubMed] [Google Scholar]
- Jaric S, Markovic G. Body mass maximizes power output in human jumping: a strength-independent optimum loading behavior. European Journal of Applied Physiology. 2013;113(12):2913–2923. doi: 10.1007/s00421-013-2707-7. [DOI] [PubMed] [Google Scholar]
- Kaneko M, Fuchimoto T, Toji H, Suei K. Training effect of different loads on the force-velocity relationship and mechanical power output in human muscle. Scandinavian Journal of Medicine and Science in Sports. 1983;5(2):50–55. [Google Scholar]
- Limonta E, Sacchi M. Morphological analysis of force/velocity relationship in dynamic exercise at varying loads. Journal of Strength and Conditioning Research. 2010;24(8):2065–2072. doi: 10.1519/JSC.0b013e3181db23ac. [DOI] [PubMed] [Google Scholar]
- Minetti AE. On the mechanical power of joint extensions as affected by the change in muscle force (or cross-sectional area), ceteris paribus. European Journal of Applied Physiology. 2002;86(4):363–369. doi: 10.1007/s00421-001-0554-4. [DOI] [PubMed] [Google Scholar]
- Nikolaidis PT. Age-and sex-related differences in force-velocity characteristics of upper and lower limbs of competitive adolescent swimmers. Journal of Human Kinetics. 2012;32:87–95. doi: 10.2478/v10078-012-0026-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzzo JL, McBride JM, Dayne AM, Israetel MA, Dumke CL, Triplett NT. Testing of the maximal dynamic output hypothesis in trained and untrained subjects. Journal of Strength and Conditioning Research. 2010;24(5):1269–1276. doi: 10.1519/JSC.0b013e3181d68691. [DOI] [PubMed] [Google Scholar]
- Pazin N, Berjan B, Nedeljkovic A, Markovic G, Jaric S. Power output in vertical jumps: does optimum loading depend on activity profiles? European Journal of Applied Physiology. 2013;113(3):577–589. doi: 10.1007/s00421-012-2464-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahmani A, Viale F, Dalleau G, Lacour JR. Force/velocity and power/velocity relationships in squat exercise. European Journal of Applied Physiology. 2001;84(3):227–232. doi: 10.1007/PL00007956. [DOI] [PubMed] [Google Scholar]
- Samozino P, Edouard P, Sangnier S, Brughelli M, Gimenez P, Morin JB. Force-velocity profile: imbalance determination and effect on lower limb ballistic performance. International Journal of Sports Medicine. 2014a;35(6):505–510. doi: 10.1055/s-0033-1354382. [DOI] [PubMed] [Google Scholar]
- Samozino P, Edouard P, Sangnier S, Brughelli M, Gimenez P, Morin JB. Force-velocity profile: imbalance determination and effect on lower limb ballistic performance. International Journal of Sports Medicine. 2014b;35(6):505–510. doi: 10.1055/s-0033-1354382. [DOI] [PubMed] [Google Scholar]
- Samozino P, Rejc E, Di Prampero PE, Belli A, Morin JB. Optimal force-velocity profile in ballistic movements--altius: citius or fortius? Medicine & Science in Sports & Exercise. 2012;44(2):313–322. doi: 10.1249/MSS.0b013e31822d757a. [DOI] [PubMed] [Google Scholar]
- Samozino P, Rejc E, di Prampero PE, Belli A, Morin JB. Force-velocity properties’ contribution to bilateral deficit during ballistic push-off. Medicine & Science in Sports & Exercise. 2014;46(1):107–114. doi: 10.1249/MSS.0b013e3182a124fb. [DOI] [PubMed] [Google Scholar]
- Sheppard JM, Cormack S, Taylor KL, McGuigan MR, Newton RU. Assessing the force-velocity characteristics of the leg extensors in well-trained athletes: the incremental load power profile. Journal of Strength and Conditioning Research. 2008;22(4):1320–1326. doi: 10.1519/JSC.0b013e31816d671b. [DOI] [PubMed] [Google Scholar]
- Sreckovic S, Cuk I, Djuric S, Nedeljkovic A, Mirkov D, Jaric S. Evaluation of force-velocity and power-velocity relationship of arm muscles. European Journal of Applied Physiology. 2015;115(8):1779–1787. doi: 10.1007/s00421-015-3165-1. [DOI] [PubMed] [Google Scholar]
- Suzovic D, Markovic G, Pasic M, Jaric S. Optimum load in various vertical jumps support the maximum dynamic output hypothesis. International Journal of Sports Medicine. 2013;34(11):1007–1014. doi: 10.1055/s-0033-1337942. [DOI] [PubMed] [Google Scholar]
- Taylor-Piliae RE, Norton LC, Haskell WL, Mahbouda MH, Fair JM, Iribarren C, … Fortmann SP. Validation of a new brief physical activity survey among men and women aged 60–69 years. American Journal of Epidemiology. 2006;164(6):598–606. doi: 10.1093/aje/kwj248. [DOI] [PubMed] [Google Scholar]
- Vandewalle H, Peres G, Heller J, Panel J, Monod H. Force-velocity relationship and maximal power on a cycle ergometer. Correlation with the height of a vertical jump. European Journal of Applied Physiology. 1987;56(6):650–656. doi: 10.1007/BF00424805. [DOI] [PubMed] [Google Scholar]
- Yamauchi J, Ishii N. Relations between force-velocity characteristics of the knee-hip extension movement and vertical jump performance. Journal of Strength and Conditioning Research. 2007;21(3):703–709. doi: 10.1519/R-20516.1. [DOI] [PubMed] [Google Scholar]
- Yamauchi J, Mishima C, Nakayama S, Ishii N. Force-velocity, force-power relationships of bilateral and unilateral leg multi-joint movements in young and elderly women. Journal of Biomechanics. 2009;42(13):2151–2157. doi: 10.1016/j.jbiomech.2009.05.032. [DOI] [PubMed] [Google Scholar]
- Yamauchi J, Mishima C, Nakayama S, Ishii N. Aging-related differences in maximum force, unloaded velocity and power of human leg multi-joint movement. Gerontology. 2010;56(2):167–174. doi: 10.1159/000235814. [DOI] [PubMed] [Google Scholar]