Abstract
A phase gradient angiography (PGA) method is proposed for optical coherence tomography (OCT). This method allows the use of phase information to map the microvasculature in tissue without the correction of bulk motion and laser trigger jitter induced phase artifacts. PGA can also be combined with the amplitude/intensity to improve the performance. Split-spectrum technique can further increase the signal to noise ratio by more than two times. In-vivo imaging of human retinal circulation is shown with a 70 kHz, 840 nm spectral domain OCT system and a 200 kHz, 1050 nm swept source OCT system. Four different OCT angiography methods are compared. The best performance was achieved with split-spectrum amplitude and phase-gradient angiography.
OCIS codes: (110.4500) Optical coherence tomography, (170.3340) Laser Doppler velocimetry, (170.2655) Functional monitoring and imaging, (170.3880) Medical and biological imaging
1. Introduction
Fluorescein angiography (FA), the current standard of care for retinal vasculature imaging, requires intravenous injection of a dye that can cause nausea in 10% of patients and even anaphylaxis or death in rare cases [1]. Optical coherence tomography angiography (OCTA), a recently developed clinical retinal and choroidal imaging technique, can obtain high-quality, high-contrast angiograms quickly without dye contrast. Instead, OCTA detects blood flow by computing the variation of OCT signal between consecutive cross-sectional images (B-frames) taken at the same location. This variation is caused by moving blood cells and provides microvasculature contrast against static retinal tissue. Perhaps the most appealing quality of OCTA for clinical use, OCTA does not require a hardware modification, allowing it to be implemented on most currently available, high scan speed OCT systems.
Several OCTA algorithms have been proposed for both spectral-domain OCT (SD-OCT) and swept source OCT (SS-OCT). These methods compute the variation of OCT signal in terms of amplitude/intensity, phase, or complex values (combination of phase and amplitude) [2–11]. Amplitude/intensity based OCTA algorithms include speckle variance, intensity-based Doppler variance, intensity-based optical microangiography (OMAG), cross-correlation mapping, and split-spectrum amplitude decorrelation angiography (SSADA). These algorithms use variance, decorrelation, cross-correlation, or absolute difference of OCT signal amplitude/intensity between consecutive B-scans to map the microvasculature. The amplitude/intensity based OCTA methods have been shown to be less vulnerable to motion artifacts [3, 12–14]. In contrast, phase and complex OCTA algorithms, such as Doppler variance, phase variance, and OMAG, require the removal or correction of motion artifacts [6, 7, 12, 15]. The removal of bulk motion phase artifact (induced by sample or machine movement) is essential for high quality angiography imaging, especially for in-vivo applications [8, 16]. Additional phase artifacts may also be induced by the laser trigger jitter of SS-OCT systems [17, 18]. Unlike amplitude/intensity based methods, phase and complex OCTA algorithms require either software or hardware methods to reduce these trigger jitter induced phase artifacts.
In this paper, we propose a phase gradient angiography (PGA) for OCTA application. It is capable of mapping retinal microvasculature without the correction of bulk motion and laser trigger jitter induced phase artifacts. Several extensions of our PGA method are also introduced in this paper. We demonstrate that PGA can be combined with amplitude signal to improve performance. Furthermore, the split-spectrum technique can be applied to increase the signal to noise ratio (SNR). Here, split-spectrum phase gradient angiography (SSPGA) and split-spectrum amplitude and phase-gradient angiography (SSAPGA) will be proposed. We then perform a quantitative comparison between PGA, SSADA, SSPGA, and SSAPGA methods applied in-vivo, using a 70 kHz SD-OCT system and a 200 kHz SS-OCT system.
2. Method
The goal of phase OCTA methods is to extract only the phase shift induced by red blood cell (RBC) movement in blood vessel. For in-vivo applications, any relatively small movement between the sample and the OCT system introduces additional phase shifts. This includes sample movement caused by involuntary movement of the participant (such as breathing), environmental vibrations, or accidental movement of the machine by the operator [8, 16, 19]. Additional phase noise is mixed with phase shift signal originating from RBC movement. In the following paragraphs, we analyze the features of the different phase shifts.
For simplicity, we only analyze the B-scans that are acquired at a single location so that our analysis is limited to two dimensions. Three-dimensional analysis can be done by extending the current analysis to all repeated B-scan locations. The complex OCT data signal at lateral, axial location, and time in a B-scan is described as,
| (1) |
where is the signal amplitude and is the phase. Because repeated B-scan protocol is used, the complex OCT data signal for the same location () from the repeated B-scan will be
| (2) |
where is the time interval between the two repeated B-scans. The phase difference at location () between the two repeated B-scans can be calculated directly by subtraction:
| (3) |
However, Eq. (3) may not obtain the actual phase shift induced by RBC movement inside the vessel. Instead, it also includes phase noise and phase artifact originating from sample movement and equipment vibration as described. To separate the phase shift induced by RBC movement from phase artifact and phase noise, we rewrite the above Eq. (3) as
| (4) |
where is the phase induced by RBC movement, is phase artifact and is the phase noise.
In SD-OCT, the main source of is the bulk phase () caused by the participant’s involuntary movement. The bulk phase is typically independent of depth and is only a function of . For SS-OCT system, another source of phase artifact is caused by the mechanical scanning device used for wavelength sweeping. This mechanical instability results in uncertainty with trigger timing so that the starting point of the spectral interferogram acquisition changes from cycle to cycle in wavenumber (k) space [18]. If there is relative k shift of between two acquired interferograms and ,
| (5) |
where is the sampling wavenumber interval, the Fourier transformations of and only differ on the phase term [20]
| (6) |
where means Fourier transform and N is the number of data points in an A-scan. Therefore, in SS-OCT system, an additional depth dependent phase term of may exist. This phase will contribute as another kind of artifact to the phase shift obtained from Eq. (3). Consequently, the phase shift ( may be the sum of actual phase difference () induced by flow, bulk phase () induced by sample movement, and trigger jitter induced depth dependent phase and phase noise:
| (7) |
To eliminate these two kinds of phase artifacts, separate schemes have to be used. Bulk phase term is typically removed with pure numerical methods. Since the blood vessels are usually inside tissue and are relative small, the vessels take fewer axial pixels than non-vessel tissue. Based on this assumption, a simple median/mean value search along the depth direction will find the bulk phase term [8, 21]. By repeating this step for all lateral locations, the bulk phase can be obtained for all the locations. In recent years, histogram based maximum bin searching method has been shown to give better performance and has been adopted by several groups [6–8, 22–24]. Although effective, in regions with relatively large vessels or strong vessel shadows, these methods will fail to generate the correct bulk phase and may require additional correction steps [25].
For SS-OCT system, corrections of phase instability induced by trigger jitter have been demonstrated with hardware and software methods. Hendargo et al. demonstrated a way to reduce the trigger jitter by generating the A-scan trigger signal with a narrow linewidth fiber Brag grating (FBG) [26]. Braaf et al. proposed a method to resample the interference fringe to the exact wavenumber space using a simultaneously recorded calibration interference signal [27]. Choi et al. improved the SS-OCT phase stability by shifting the interferograms with a reference dip produced from a narrow linewidth FBG [28]. Previously, we also proposed a method that aligns the interferograms by minimizing fixed pattern noise intensity [20]. However, these methods either increase the system complexity and cost, or they increase the computation time.
In this paper, we propose a PGA method for OCTA application. By taking the axial gradient of the phase difference in Eq. (7), axial phase gradient can be obtained as
| (8) |
is not dependent on the depth and its axial gradient will be zero. The phase gradient will eliminate the bulk phase. The trigger jitter induced phase is a linear function of depth and its axial gradient will be a constant value: . The constant value, is typically very small. For example, when N = 1024 and = 1, the value is around 6 milliradians per depth pixel. This value is much smaller than the phase noise which is typically produced by galvanometer scanners [29]. The remaining term in Eq. (8) is the axial gradient of the phase shift induced by RBC in the blood vessels. Phase gradient can be used to image the vessels alone. It may also be combined with OCT signal amplitude/intensity to enhance the flow contrast.
Amplitude/intensity OCTA methods based on the difference, variance, or decorrelation of amplitude/intensity signal have been demonstrated [3, 4, 30]. Since decorrelation based algorithm has a normalized value, we will use decorrelation algorithm to combine the phase gradient contrast with amplitude/intensity contrast
| (9) |
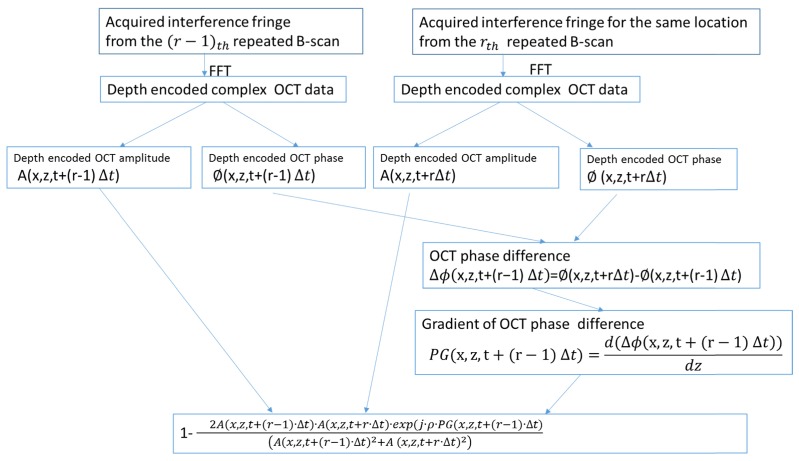
where is the flow contrast, is the number of repetitions at the same B-scan location, where is the weight parameter that controls the contribution from phase gradient contrast and will be used in the following. Figure 1 shows the flow chart used to calculate the flow contrast from the Eq. (9). Depth encoded complex OCT data are obtained through Fourier transform of the acquired fringes. The phase difference between A-scans at the same location in repeated B-scans is obtained. The gradient of the phase difference is calculated and then combined with amplitude to calculate the flow contrast.
Fig. 1.
Procedures to calculate the amplitude combined phase gradient in a Fourier domain OCT system. Depth encoded complex OCT data are obtained from Fourier transform of the acquired fringes (may require addition calibration or dispersion compensation dependent on system used). The phase difference (or phase shift) between A-scans scans at the same location in sequential repeated B-scans is obtained. The axial gradient is calculated from the phase difference. This gradient is then combined with amplitude to calculate the decorrelation and then contrast.
Split spectrum method has been shown to improve the SNR of flow detection [5,31]. After splitting the spectrum into several narrow bands, the data in each narrower bands are processed separately to generate several OCTA images for the same B-scan location. These images are then averaged to achieve a higher SNR image for the specific B-scan location [31]. The following equations will be used for the calculation of SSPGA and SSAPGA:
| (10) |
| (11) |
where M is the number of narrow split spectrum bands.
3. In-vivo results
3.1 Spectral domain OCT system
The algorithm was tested for clinical retinal imaging (Fig. 2) on a healthy human participant using a 70 kHz, 840 nm spectral OCT system (RTVue-XR, Optovue). The imaging protocol consisted of a single volumetric scan covering a 3 × 3 mm area centered at the fovea. In the fast transverse scanning direction, 304 A-scans were sampled to obtain a single B-scan. For flow detection, two sequential B-scans were collected at each location. In the slow transverse scanning direction, 304 locations were sampled. The total imaging time was aproximately 3 seconds.
Fig. 2.
Cross sectinal structure OCT (A) and OCTA images (B-E) from a healthy participant. The PGA shows high background noise (B). The three split-spectrum methods (SSPGA, SSADA and SSAPGA) show very similar results (C-E).
Two different split-spectrum PGA methods (SSPGA, and SSAPGA), each with 11 split-spectrum bands, were used to process the data. In short, the acquired spectrum was split into eleven differenct narrow band spectrums using Gaussian windows with different central wavlengths but the same full width of half maximum value. The 11 narrow band spectrums were processed seperately, with typical SD-OCT data processing procedures. These include numerical interpolaration for wavelength calibration, numerical dispersion compensation, and fast Fourier transform (FFT). The phase term of the complex OCT signal after the FFT was used to obtain the PGA according to Eq. (8). The PGA signals from different bands were averaged to get the SSPGA image according to Eq. (10). The PGA signals were also combined with the ampltiude signal in each band and further averaged according to Eq. (11) to get the SSAPGA image. Results from PGA (non-split-spectrum) and SSADA (11 split bands) were also obtained for comparison. All the OCTA images were thresholded with a value equal to sum of the median OCTA and 3 times standard deviation in the retinal tissue region.
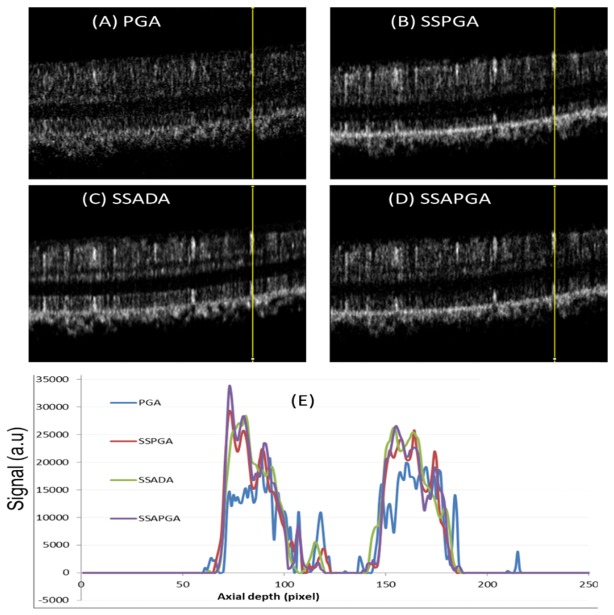
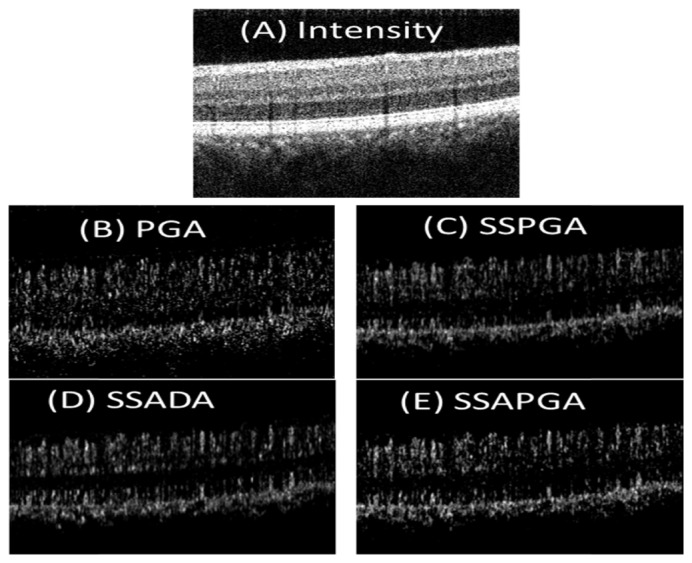
Cross-sectional OCT and OCTA images of a healthy eye are shown in Fig. 2. All the images are processed from the same data set. The images from the three split-spectrum methods (SSPGA, SSADA and SSAPGA) do not show major difference (Fig. 2(B)-2(E)). The PGA method visually shows higher noise, which manifests as random dots in the image (Fig. 2(A)). By averaging 5 adjacent frames of cross-sectional OCTA images (Figs. 3(A)-3(D) ), noise in the OCTA image can be further reduced and single OCTA A-scan profiles (Fig. 3(E)) from different methods can be extracted and compared. Methods using the split-spectrum technique show much more smoothed profiles. This is due to lower noise and worse resolution of the split-spectrum method. PGA method shows overall higher noise. SSADA (Fig. 3(C)) shows more signal at the inner segment-outer segment (IS-OS) junctional layer and retina pigment epithelium (RPE) layer. This may suggest that SSADA suffers more from a vessel projection artifact. It should be noted that the scheme of averaging of 5 adjacent cross-sectional OCTA is only for the prupose of comparing the results from different methods. This scheme is not used for calculating or generating the final en-face OCTA images.
Fig. 3.
Averaged cross-sectional PGA (A), SSPGA (B), SSADA (C) and SSAPGA (D) OCTA images. (E) Axial profiles along the yellow lines in (A)-(D).
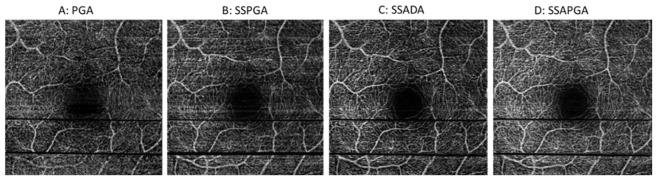
The performances of these methods are also compared in en-face view, which is the prefered way to evalute retinal microvasculatures clinically (Fiq 4). The 3D image data was separated into retinal and choroidal regions with the dividing boundary set at the RPE layer. Figure 4 shows the average intensity projection angiography images for human retinal vasculature from PGA (Fig. 4(A)), SSPGA (Fig. 4(B)), SSADA (Fig. 4(C)) and SSAPGA (Fig. 4(D)). Except a few minor differences, these images show very similar retinal vasculature. Quantatitive analysis is necessary for comparison. Two parameters, the image SNR and image contrast are used here to compare the images. SNR for flow detection was calculated as
| (12) |
The fovea avascular zone was taken as the noise baseline and the other region was taken as the signal [14]. Root mean square (RMS) contrast was used and is defined as the standard deviation of the pixel intensities [32]:
| (13) |
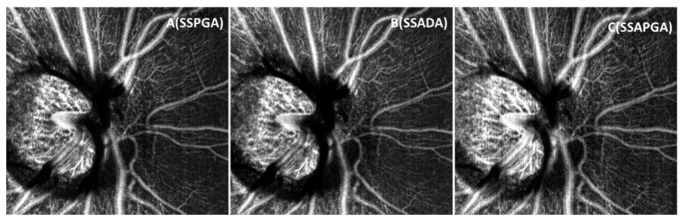
where x,y are the number of pixels in the two dimensional image, are the angiography value for the pixel at the (x,y) location in the image and is the average values of all pixels in the image. Quantatative analysis results are shown in Table 1. PGA image was set as reference. Compared to PGA (Fig. 4(A)), increase of 129.04%, 267.0%, and 355.9% in SNR were found for SSPGA (Fig. 4(B)), SSADA (Fig. 4(C)) and SSAPGA (Fig. 4(D)). Among the three methods, SSAPGA shows best image contrast and SNR and SSPGA shows the worst image contrast and SNR.
Fig. 4.
3 × 3mm OCTA of human retinal circulation from PGA (A) and SSPGA (B), SSADA (C) and SSAPGA (D).
Table 1. Quantatative comparison of different OCTA methods.
| SNR | Improvement | Contrast | Improvement | |
|---|---|---|---|---|
| PGA | 4.06 | – | 37.6 | – |
| SSPGA | 9.3 | 129.04% | 40.54 | 7.8% |
| SSADA | 14.9 | 267.0% | 45.89 | 22.0% |
| SSAPGA | 18.51 | 355.9% | 78.67 | 109.2% |
3.2 Swept source OCT system
A custom-built SS-OCT system was used to test the algorithms. Briefly, the system used a 200 kHz swept laser with a central wavelength of 1050nm and bandwidth of 100nm (Axsun 1050). The system was based on a fiber Mach-Zehnder interferometer. The final interference signal was detected by a balanced detector and digitized by a high speed digitizer (ATS9360, Alazar Technologies). The clock signal provided by the laser was used for data acquisition. There were 1216 data points in a single A-scan. The laser power on the corneal is 1.4 mW with a beam spot size approximately 2 mm. The imaging protocol consisted of a single volumetric scan covering a 3 × 3 mm area of the disk in a healthy human participant. In the fast transverse scanning direction, 600 A-scans were sampled to obtain a single B-scan (100 A-scans for galvonometer flyback). Three sequential B-scans were collected at each location for flow detection. In the slow transverse scanning direction, 500 locations were sampled. The data processing steps are similar to those described in section 3.1 and 11 subbands were used for split-spectrum calculation.
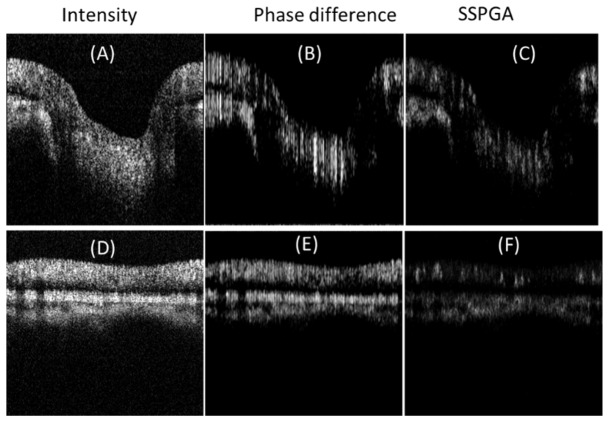
Figure 5 shows the both cross sectional structure OCT and OCTA images from a healthy eye acquired with the SS-OCT system. Due to the phase instability of the SS-OCT system, the phase difference (between repeated B frames) image (Figs. 5(B) and 5(E)) shows strong vertical lines artifacts. By taking the axial gradient of the phase difference, the result show clearer vessel boundaries (Figs. 5(C) and 5(F)). It should be noted that no phase instability correction or bulk phase removal method was used here. The en-face projection OCTA images from SSPGA, SSADA, SSAPGA were also generated for comparision (Fig. 6). The three split-spectrum methods show similar results however, visual comparison shows SSAPGA had the best overall performance.
Fig. 5.
Cross-sectional OCT intensity (A, D) and OCTA images (B, C, E, F) from a healthy eye acquired with a SS-OCT system. Phase difference image (B, E) shows vertical line artifacts due to the depth dependent phase difference induced by the triggering jitter and bulk motion. Axial gradient of the phase difference image shows clear vessel boundaries (C, F).
Fig. 6.
En face projection OCTA of human disc and retinal circulation acquired with a SS-OCT. SSPGA (A), SSADA (B) and SSAPGA (C) are used to process.
4. Flow phantom experiment
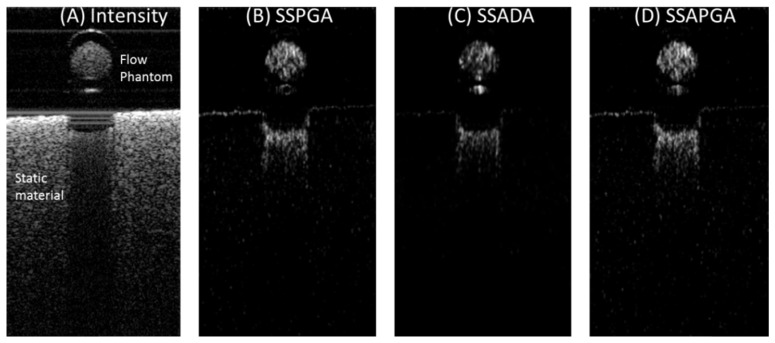
A blood flow phantom experiment was performed to verify the proposed methods. Fresh bovine blood (Animal Technologies, Inc., Tyler, TX) in a syringe was pumped into a plastic flow channel and scanned using the custom SS-OCT system described in section 3.2. A 60D Slit Lamp Lens (Volk Optical Inc., Mentor, OH) was used to focus the light on to the flow channel. The plastic channel had an inner diameter of 0.5 mm. A syringe pump (11 Plus, Harvard Apparatus, Massachusetts) was used to generate an average flow velocity of approximately 2.0 mm/s within the channel. Two sequential B-scans each consisting of 500 A-scans were taken at the same location to detect flow with the OCTA algorithms (SSPGA, SSADA and SSAPGA). The log OCT reflectance and OCTA cross-sectional images of the flow phantom are shown in Fig. 7. The SSPGA (Fig. 7(B)) and SSADA (Fig. 7(C)) images show different details of the flow channel due to different flow contrast mechanisms. The SSAPGA image (Fig. 7(D)) combine both features from SSPGA and SSADA. All the methods were able to detect the flow signal in the channel.
Fig. 7.
Blood flow phantom experiment to verify the proposed methods. OCT intensity image (A) of the flow phantom and OCTA images calculated from two sequential B-scan images at the same location using SSPGA (B), SSADA (C) and SSAPGA (D).
5. Discussion
Phase-resolved technique is one of the earliest methods that has been investigated for OCTA application [22]. However, the correction of artifacts in the application of phase-resolved technique for OCTA may be cumbersome and sometimes unperfected, especially for SS-OCT system [33]. The PGA uses the phase information for OCTA without correction of phase artifacts. The PGA works for both SD-OCT and SS-OCT. Because the phase-resolved OCTA and amplitude-resolved OCTA base their contrasts on different mechanisms, the combination of both phase and amplitude/intensity could improve OCTA performance [34]. The PGA method offers an easy way to use the phase-resolved contrast and it can be combined with the amplitude/intensity –resolved contrast. So the PGA method will be useful for phase-resolved OCTA and for complex value –resolved OCTA. SS-OCT is becoming a preferred system for ultrafast OCT imaging, which is important for OCTA application. Trigger jitter is still an issue for most SS-OCT based OCTA systems. The proposed method here could be an option for those who want to use phase or both phase and amplitude for OCTA imaging.
We have compared a few different OCTA methods, mainly developed by our group. Involving more methods including those developed by other groups will be ideal. This is not done because 1) There are too many methods and each method may have different version of realization. 2) Details for optimizing the specific method may not be found from publication. This may result in un-optimized image results from other method. Fortunately, the comparison of different OCTA methods have been performed by several other research groups [34, 35]. Gorczynska et al. compared three methods: speckle variance, amplitude decorrelation and phase variance and concluded that, “Although differences exist among them, no single universal method can be identified, yet.” The authors also found that each method might have advantages in imaging of specific tissues and split-spectrum increase the image quality for all the methods tested [35]. Our results here show the SSPGA show better performance than PGA. So split-spectrum should be considered for improving the image quality. Gorczynska et al. did not compare OCTA method that use complex (both phase and intensity) signal information. Zhang et al. compared different OCTA methods including OMAG, speckle variance, phase variance, SSADA, and correlation mapping [34]. They found that complex OCTA based methods might provide the best visual result of retinal microvascular networks in terms of image contrast, vessel connectivity, and SNR. The conclusions from Gorczynska et al. and Zhang et al. may suggest that the combining phase and amplitude contrast, together with split-spectrum technique, could give overall better image quality. Our results here show that SSAPGA offers a better image quality than SSADA and SSPGA.
In the split-spectrum method, 11 bands were used. These 11 bands have overlapped spectrum and for each band, a normalized bandwidth of 0.28 was used for the processing. The axial resolution was reduced to ~18 µm for SD-OCT system and to ~20 µm for the SS-OCT system. After the splitting, the axial resolution was similar to the lateral resolution of the systems [31]. With these resolutions, capillaries can be detected with both the SD-OCT and the SS-OCT systems, as can be seen from Figs. 4 and 6.
With a custom Matlab code running one a Dell Precision 7910 workstation with Intel Xeon CPU E5-2620 @2.4GHz and 64GB Memory, the computation time to process a 3D data set acquired with SD-OCT system was measured to be 826 seconds for the SSPGA and 836 seconds for the SSAPGA. For a 3D data set acquired with the SS-OCT system, the computation time was 2023 seconds for SSPGA and 2065 seconds for SSAPGA. The processing time could be greatly reduced by parallel computation techniques, which will be developed in the future.
6. Conclusions
A PGA method was proposed for OCTA imaging. PGA method utilizes the phase information to map the vasculature without requirement of bulk phase removal for SD-OCT system and phase instability correction for SS-OCT. Combining PGA with amplitude can improve OCTA image. Quantitative comparison between PGA, SSPGA, SSADA, and SSAPGA shows that SSAPGA gave better performance in terms of SNR and contrast. Split-spectrum could improve the performance of PGA by more than 2 times.
Financial disclosures
Drs. Yali Jia and David Huang have a significant financial interest in Optovue, Inc., a company that may have a commercial interest in the results of this research and technology. David Huang also has a financial interest in Carl Zeiss Meditec, Inc. These potential conflicts of interest have been reviewed and managed by OHSU. Other authors do not have financial interest in the participant of this article.
Funding
Oregon Health & Science Foundation, National Institutes of Health Grants DP3 DK104397, R01 EY024544, R01 EY023285 and R01 EY018184, unrestricted departmental funding from Research to Prevent Blindness (New York, NY), and P30 EY010572 from the National Institutes of Health (Bethesda, MD).
References and links
- 1.Panel A. A. o. O. R. V., “Preferred Practice Pattern: Diabetic Retinopathy,” in American Academy of Ophthalmology Preferred Practice Patterns, (American Academy of Ophthalmology, San Francisco, CA, 2014), pp. 1–65. [Google Scholar]
- 2.Jia Y., Wang R. K., “Optical micro-angiography images structural and functional cerebral blood perfusion in mice with cranium left intact,” J. Biophotonics 4(1-2), 57–63 (2011). 10.1002/jbio.201000001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mariampillai A., Standish B. A., Moriyama E. H., Khurana M., Munce N. R., Leung M. K., Jiang J., Cable A., Wilson B. C., Vitkin I. A., Yang V. X., “Speckle variance detection of microvasculature using swept-source optical coherence tomography,” Opt. Lett. 33(13), 1530–1532 (2008). 10.1364/OL.33.001530 [DOI] [PubMed] [Google Scholar]
- 4.Liu G., Chou L., Jia W., Qi W., Choi B., Chen Z., “Intensity-based modified Doppler variance algorithm: application to phase instable and phase stable optical coherence tomography systems,” Opt. Express 19(12), 11429–11440 (2011). 10.1364/OE.19.011429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yu L., Chen Z., “Doppler variance imaging for three-dimensional retina and choroid angiography,” J. Biomed. Opt. 15(1), 016029 (2010). 10.1117/1.3302806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim D. Y., Fingler J., Werner J. S., Schwartz D. M., Fraser S. E., Zawadzki R. J., “In vivo volumetric imaging of human retinal circulation with phase-variance optical coherence tomography,” Biomed. Opt. Express 2(6), 1504–1513 (2011). 10.1364/BOE.2.001504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang V. X., Gordon M. L., Mok A., Zhao Y., Chen Z., Cobbold R. S. C., Wilson B. C., Vitkin I. A., “Improved phase-resolved optical Doppler tomography using the Kasai velocity estimator and histogram segmentation,” Opt. Commun. 208(4-6), 209–214 (2002). 10.1016/S0030-4018(02)01501-8 [DOI] [Google Scholar]
- 9.Park B., Pierce M., Cense B., de Boer J., “Real-time multi-functional optical coherence tomography,” Opt. Express 11(7), 782–793 (2003). 10.1364/OE.11.000782 [DOI] [PubMed] [Google Scholar]
- 10.Nam A. S., Chico-Calero I., Vakoc B. J., “Complex differential variance algorithm for optical coherence tomography angiography,” Biomed. Opt. Express 5(11), 3822–3832 (2014). 10.1364/BOE.5.003822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Enfield J., Jonathan E., Leahy M., “In vivo imaging of the microcirculation of the volar forearm using correlation mapping optical coherence tomography (cmOCT),” Biomed. Opt. Express 2(5), 1184–1193 (2011). 10.1364/BOE.2.001184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu G., Lin A. J., Tromberg B. J., Chen Z., “A comparison of Doppler optical coherence tomography methods,” Biomed. Opt. Express 3(10), 2669–2680 (2012). 10.1364/BOE.3.002669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jonathan E., Enfield J., Leahy M. J., “Correlation mapping method for generating microcirculation morphology from optical coherence tomography (OCT) intensity images,” J. Biophotonics 4(9), 583–587 (2011). [DOI] [PubMed] [Google Scholar]
- 14.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang R. K., An L., “Doppler optical micro-angiography for volumetric imaging of vascular perfusion in vivo,” Opt. Express 17(11), 8926–8940 (2009). 10.1364/OE.17.008926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Swanson E. A., Izatt J. A., Hee M. R., Huang D., Lin C. P., Schuman J. S., Puliafito C. A., Fujimoto J. G., “In vivo retinal imaging by optical coherence tomography,” Opt. Lett. 18(21), 1864–1866 (1993). 10.1364/OL.18.001864 [DOI] [PubMed] [Google Scholar]
- 17.Zhang J., Chen Z., “In vivo blood flow imaging by a swept laser source based Fourier domain optical Doppler tomography,” Opt. Express 13(19), 7449–7457 (2005). 10.1364/OPEX.13.007449 [DOI] [PubMed] [Google Scholar]
- 18.Vakoc B., Yun S., de Boer J., Tearney G., Bouma B., “Phase-resolved optical frequency domain imaging,” Opt. Express 13(14), 5483–5493 (2005). 10.1364/OPEX.13.005483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yazdanfar S., Rollins A. M., Izatt J. A., “Imaging and velocimetry of the human retinal circulation with color Doppler optical coherence tomography,” Opt. Lett. 25(19), 1448–1450 (2000). 10.1364/OL.25.001448 [DOI] [PubMed] [Google Scholar]
- 20.Liu G., Tan O., Gao S. S., Pechauer A. D., Lee B., Lu C. D., Fujimoto J. G., Huang D., “Postprocessing algorithms to minimize fixed-pattern artifact and reduce trigger jitter in swept source optical coherence tomography,” Opt. Express 23(8), 9824–9834 (2015). 10.1364/OE.23.009824 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.White B., Pierce M., Nassif N., Cense B., Park B., Tearney G., Bouma B., Chen T., de Boer J., “In vivo dynamic human retinal blood flow imaging using ultra-high-speed spectral domain optical coherence tomography,” Opt. Express 11(25), 3490–3497 (2003). 10.1364/OE.11.003490 [DOI] [PubMed] [Google Scholar]
- 22.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 23.Liu G., Qi W., Yu L., Chen Z., “Real-time bulk-motion-correction free Doppler variance optical coherence tomography for choroidal capillary vasculature imaging,” Opt. Express 19(4), 3657–3666 (2011). 10.1364/OE.19.003657 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.An L., Wang R. K., “In vivo volumetric imaging of vascular perfusion within human retina and choroids with optical micro-angiography,” Opt. Express 16(15), 11438–11452 (2008). 10.1364/OE.16.011438 [DOI] [PubMed] [Google Scholar]
- 25.Rao B., Yu L., Chiang H. K., Zacharias L. C., Kurtz R. M., Kuppermann B. D., Chen Z., “Imaging pulsatile retinal blood flow in human eye,” J. Biomed. Opt. 13(4), 040505 (2008). 10.1117/1.2967986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hendargo H. C., McNabb R. P., Dhalla A.-H., Shepherd N., Izatt J. A., “Doppler velocity detection limitations in spectrometer-based versus swept-source optical coherence tomography,” Biomed. Opt. Express 2(8), 2175–2188 (2011). 10.1364/BOE.2.002175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Braaf B., Vermeer K. A., Sicam V. A. D. P., van Zeeburg E., van Meurs J. C., de Boer J. F., “Phase-stabilized optical frequency domain imaging at 1-µm for the measurement of blood flow in the human choroid,” Opt. Express 19(21), 20886–20903 (2011). 10.1364/OE.19.020886 [DOI] [PubMed] [Google Scholar]
- 28.Choi W., Potsaid B., Jayaraman V., Baumann B., Grulkowski I., Liu J. J., Lu C. D., Cable A. E., Huang D., Duker J. S., Fujimoto J. G., “Phase-sensitive swept-source optical coherence tomography imaging of the human retina with a vertical cavity surface-emitting laser light source,” Opt. Lett. 38(3), 338–340 (2013). 10.1364/OL.38.000338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Braaf B., Vermeer K. A., Vienola K. V., de Boer J. F., “Angiography of the retina and the choroid with phase-resolved OCT using interval-optimized backstitched B-scans,” Opt. Express 20(18), 20516–20534 (2012). 10.1364/OE.20.020516 [DOI] [PubMed] [Google Scholar]
- 30.Blatter C., Klein T., Grajciar B., Schmoll T., Wieser W., Andre R., Huber R., Leitgeb R. A., “Ultrahigh-speed non-invasive widefield angiography,” J. Biomed. Opt. 17(7), 070505 (2012). 10.1117/1.JBO.17.7.070505 [DOI] [PubMed] [Google Scholar]
- 31.Gao S. S., Liu G., Huang D., Jia Y., “Optimization of the split-spectrum amplitude-decorrelation angiography algorithm on a spectral optical coherence tomography system,” Opt. Lett. 40(10), 2305–2308 (2015). 10.1364/OL.40.002305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Peli E., “Contrast in complex images,” J. Opt. Soc. Am. A 7(10), 2032–2040 (1990). 10.1364/JOSAA.7.002032 [DOI] [PubMed] [Google Scholar]
- 33.Liu G., Lin A. J., Tromberg B. J., Chen Z., “A comparison of Doppler optical coherence tomography methods,” Biomed. Opt. Express 3(10), 2669–2680 (2012). 10.1364/BOE.3.002669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang A., Zhang Q., Chen C.-L., Wang R. K., “Methods and algorithms for optical coherence tomography-based angiography: a review and comparison,” J. Biomed. Opt. 20(10), 100901 (2015). 10.1117/1.JBO.20.10.100901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gorczynska I., Migacz J. V., Zawadzki R. J., Capps A. G., Werner J. S., “Comparison of amplitude-decorrelation, speckle-variance and phase-variance OCT angiography methods for imaging the human retina and choroid,” Biomed. Opt. Express 7(3), 911–942 (2016). 10.1364/BOE.7.000911 [DOI] [PMC free article] [PubMed] [Google Scholar]