Mayer waves reduce the accuracy of estimated hemodynamic response functions in functional near-infrared spectroscopy

Abstract

Analysis of cerebral hemodynamics reveals a wide spectrum of oscillations ranging from 0.0095 to 2 Hz. While most of these oscillations can be filtered out during analysis of functional near-infrared spectroscopy (fNIRS) signals when estimating stimulus evoked hemodynamic responses, oscillations around 0.1 Hz are an exception. This is due to the fact that they share a common spectral range with typical stimulus evoked hemodynamic responses from the brain. Here we investigate the effect of hemodynamic oscillations around 0.1 Hz on the estimation of hemodynamic response functions from fNIRS data. Our results show that for an expected response of ~1 µM in oxygenated hemoglobin concentration (HbO), Mayer wave oscillations with an amplitude > ~1 µM at 0.1 Hz reduce the accuracy of the estimated response as quantified by a 3 fold increase in the mean squared error and decrease in correlation (R² below 0.78) when compared to the true HRF. These results indicate that the amplitude of oscillations at 0.1 Hz can serve as an objective metric of the expected HRF estimation accuracy. In addition, we investigated the effect of short separation regression on the recovered HRF, and found that this improves the recovered HRF when large amplitude 0.1 Hz oscillations are present in fNIRS data. We suspect that the development of other filtering strategies may provide even further improvement.

1. Introduction

Analysis of hemodynamics by various techniques including Laser Doppler Flowmetry, video recordings of blood cell velocity and capillary pressure measurements have revealed a broad spectrum of oscillation frequencies ranging from 0.0095 Hz to 2 Hz [1,2]. These oscillations also appear in blood oxygen level-dependent functional magnetic resonance imaging (BOLD fMRI) and functional near-infrared spectroscopy (fNIRS) [3–8]. Six major cardiovascular oscillations have been distinguished in this frequency range: cardiac (~1 Hz), respiratory (~0.3 Hz), one low frequency oscillation (~0.1 Hz) related to myogenic activity of vessels and three very low frequency oscillations (~0.04) related to neurogenic activity of vessels and (~0.01 and ~0.007 Hz) associated with vascular endothelial function [2].

Among these oscillations, low frequency Mayer waves were introduced by Ludwig Traube, Ewald Hering and Siegmund Mayer independently and thus previously called Traube-Hering-Mayer waves. These waves are defined as waves in arterial blood pressure with a frequency around 0.1 Hz [9]. They are spontaneous hemodynamic oscillations in arterial pressure and can be distinguished from heart beat and respiratory cycles because of their frequency [7]. On a related note, the term “vasomotion” and Mayer waves are sometimes used interchangeably. Vasomotion, as opposed to Mayer waves, is defined as the oscillation in the tone of blood vessels, which causes the cross section of the blood vessels to oscillate and gives rise to flowmotion [8,10], this of course does not rule out the possible association between the two physiological phenomena. Note that, the frequency range used in resting state functional connectivity analysis is typically lower than 0.1 Hz (0 and 0.05 Hz) [11].

The sensitivity of NIRS to brain activation is diminished by these physiological fluctuations or “systemic interference” that arises from scalp, skull and brain. These systemic changes may result in false positives by mimicking the brain hemodynamic response, or results in false negatives by attenuating it [12]. Various methods have been proposed in the literature to overcome this problem. It is rather easy to filter out the high frequency components (such as heart rate ~1 Hz) or instrumental noise [13] and very low frequency components (such as oscillations <0.01 Hz). More advanced techniques have been introduced to overcome interference from low frequency oscillations which share a common spectral range with the brain hemodynamic response. Some examples are adaptive average waveform subtraction [14], principal component analysis [15–17], wavelet filtering [18], independent component analysis [19] and use of regressors as filters including short source-detector separation channels that are only sensitive to superficial layers [20] and independent measures of the systemic fluctuations [21,22].

Anecdotally, we have found in our own experience over the last 10 + years that we cannot recover a HRF in approximately 10% of our subjects and that these same subjects tend to have large amplitude Mayer waves. Here, our goal is to quantify the specific effect of Mayer waves on the recovered hemodynamic response function. We aim to provide quantitative evidence in support of using the Mayer wave amplitude as a metric for objectively excluding data from higher level analyses. In addition, given the likelihood that the Mayer waves are producing HbO oscillations superficially in the scalp, we hypothesize that one can benefit from utilizing the short-separation regression method [23] to reduce their impact on the estimation of the HRF. This method uses additional NIRS measurements with short optode separations to measure the systemic hemodynamic fluctuations in the superficial layers. These measurements can then be used as regressors to remove the systemic contamination and recover the brain signal. We explore whether or not short-separation fNIRS measurements of the scalp hemodynamics can be used to filter the oscillations from long-separation measurements of brain activation that are contaminated by the HbO fluctuations in the scalp.

2. Methods

The study was approved by the Institutional Review Board of the Massachusetts General Hospital. Seventeen healthy subjects (male, 28 ± 5 years old) were recruited and a total of 23 sessions were performed. Each subject gave informed written consent prior to the experiments. Subjects with a history of neurological trauma or psychiatric disorders were excluded.

2.1 System and probe

Recordings were obtained using a multichannel functional near-infrared spectrometer operating at 690 and 830 nm wavelengths (TechEn Inc. MA, USA, CW7 System). The head cap contained 15 sources, 15 standard separation detectors, and 16 short separation detectors (Fig. 1). Long separation detectors were positioned 30 mm from adjacent sources and short separation detectors were located 8 millimeters from a single source. The probe covered the motor and somatosensory regions as well as the frontal region. Six minutes of resting state data were recorded during each session while the subjects were seated. Subjects were instructed to keep their head still as much as possible.

Fig. 1.

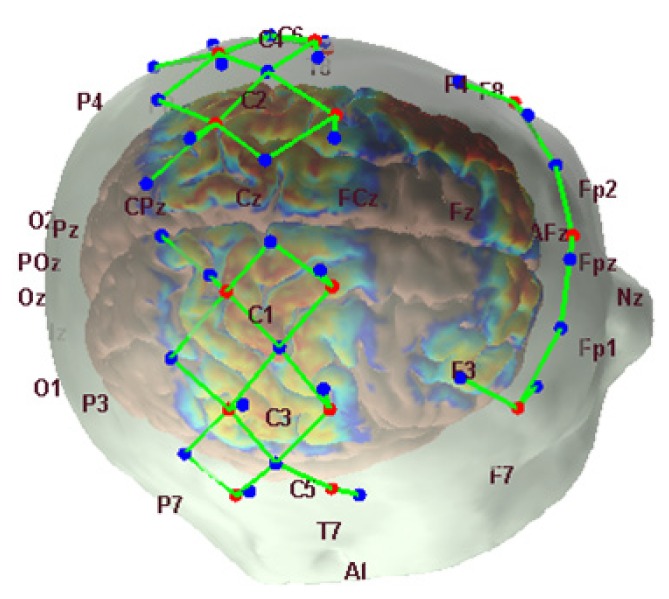
The locations of the detectors (blue dots), the sources (red dots), the channels (green lines) and the sensitivity profile are shown for one subject with 10-20 EEG locations.

2.2 Data analysis

A synthetic hemodynamic response function (HRF) that consisted of a gamma function with a time-to-peak of 6 s and a duration of 15 s was generated by introducing a signal change of 1% from baseline for the 690 nm signal and 2% for the 830 nm signal in the raw NIRS data (case 1) or by introducing a signal change of 0.2% from baseline for the 690 nm signal and 0.4% for 830 nm signal in the raw NIRS data (case 2). These percent signal changes were chosen to produce evoked changes in hemoglobin species comparable to the observed concentration changes in typical NIRS experiments (HbO of 0.7 µM and HbR of 0.24 µM in case 1, and in HbO of 0.14 µM and HbR of 0.048 µM in case 2). This synthetic HRF was then added to the raw signal at long distance channels with an inter-stimulus interval of 20 to 25 sec, which resulted in up to 18 stimuli over the 6 minute data set. We generated 25 such time courses with different randomly generated stimulus vectors for each of the 23 sessions. The channels that had an SNR (mean/std of raw signal) lower than 5 or raw intensity lower than 80 dB were excluded from the analysis.

The raw fNIRS data (resting-state data with added synthetic HRFs) were then analyzed to estimate the evoked hemodynamic response following standard fNIRS analysis procedures. The fNIRS intensity at each wavelength was converted into changes in optical density. Motion artifacts were identified automatically using Homer2 software [24] (https://www.nitrc.org/projects/homer2/), and corrected using the targeted principle component analysis method [25]. The data was then band-pass filtered with a third order Butterworth filter between 0.01 and 0.5 Hz. The changes in optical density were converted to changes in hemoglobin concentrations using the modified Beer-Lambert law using a pathlength factor of 6 [26–28].

The HRF was estimated using a General Linear Model, using a consecutive sequence of Gaussian functions as the temporal basis for the HRF as we have detailed in [23]. Briefly, each Gaussian had a width of 0.5 s and they were spaced every 0.5 s over the regression time range of −2 to 15 seconds. The short separation channel with the highest correlation with a given long separation channel was used as a static estimator and regressed out from that long distance channel while simultaneously estimating the HRF following the procedure described in [23]. This procedure is based on the fact that the long distance channels probe both scalp and brain while the short distance channels probe only the scalp. The short separation regression method assumes that the contamination has a comparable time course at the short and long separations while no assumption is made about the relative amplitudes of concentration changes on long versus short channels.

2.3 Calculation of MSE and correlation

The mean-squared error (MSE) and the coefficient of determination R² (square of Pearson’s correlation coefficient R) between the true HRF and the retrieved HRF were obtained using MATLAB built-in functions (The MathWorks Inc., Natick, MA, USA). To obtain normalized MSE values, we divided each MSE value with the corresponding amplitude of the true HRF.

2.4 Power analysis and statistics

We obtained the power spectra of each HbO concentration time series using the pwelch function in MATLAB with a 80-s Hamming windowing of the data and 50% overlap of successive segments in each segment. The HbO concentration time series was obtained from the raw fNIRS data prior to the addition of an HRF. The raw data was converted to optical density and then to concentration units following the procedure outlined above except no low-pass filter was applied to the data. The amplitude of the desired frequency range was then calculated by taking the square-root of the mean of the power spectrum over that specific frequency range. Frequency ranges used for each physiological oscillation were as follows: cardiac: 1-1.6 Hz, respiration: 0.2-0.33 Hz and Mayer waves: 0.06-0.14 Hz.

Paired t-tests were performed using MATLAB to determine whether there was a significant difference between the MSEs and correlations with low versus high amplitude Mayer waves as well as with and without short separation regression. We have defined the threshold between low and high Mayer wave amplitude as 1 µM, which is approximately the median amplitude of the Mayer wave that we observed in our data (~1 µM). Significance was set at p < 0.05.

We have performed a semi-partial correlation analysis to assess the relative contributions of Mayer waves and respiration on the MSE and correlation obtained for the estimated HRFs.

2.5 Receiver operator characteristic analysis for evaluating accurate estimation of the HRF

We have performed a Receiver Operator Characteristic (ROC) analysis to estimate the true positive and false positive rate for estimation of the HRF with and without short separation regression at low and high Mayer wave powers. ROC curves have been produced using the t-statistic of the HRF estimation as the threshold for detection. This is done by taking the mean of the t-values obtained from each of the 25 different stimulus paradigms.

3. Results

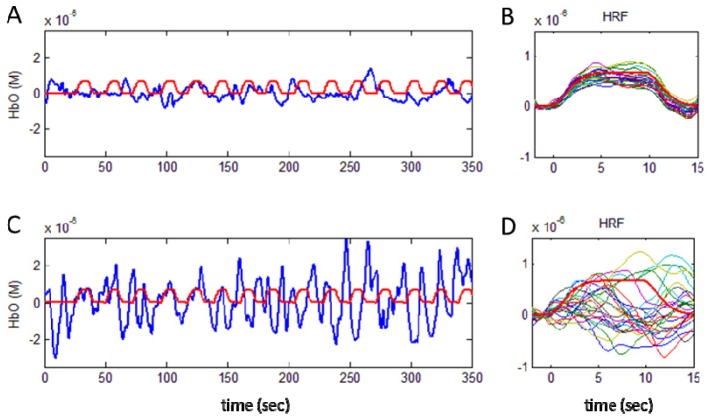
Figure 2 illustrates HbO concentration resting-state time series from two channels from two different subjects: one with low Mayer wave power (top row) and the other with high Mayer wave power (bottom row). The fluctuation in HbO concentration in the raw signal can be compared with the synthetic hemodynamic response functions (HRF) shown in red. In this particular example, the signal with high Mayer wave power is almost five times larger than the synthetic HRF amplitude, which makes HRF estimation difficult.

Fig. 2.

Examples of small and large amplitude Mayer waves in the HbO time course are shown by the blue lines in (A) and (C) respectively. The synthetic HRF is indicated by the red lines. The hemodynamic response function recovered for 25 different stimulus paradigms are shown in (B) and (D) for the small and large amplitude Mayer waves respectively. Note that results are shown for HRF estimation after introducing a signal change of 1% from baseline for the 690 nm and 2% for 830 nm in the raw NIRS data (case 1).

3.1 HRF estimation depends on Mayer wave power in the signal

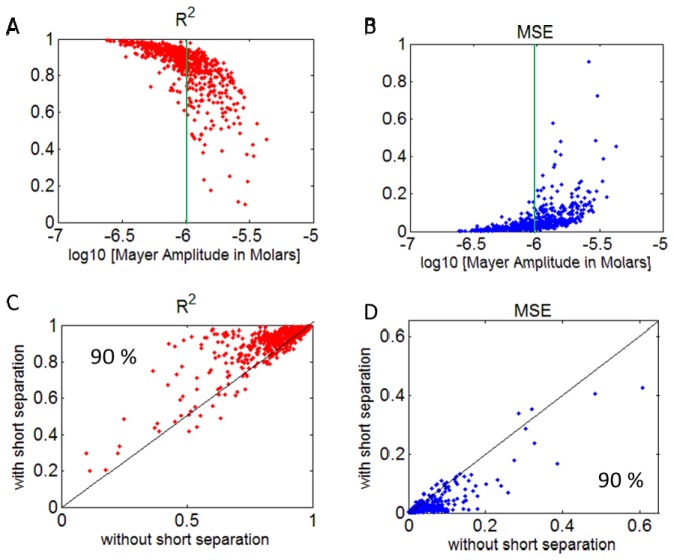
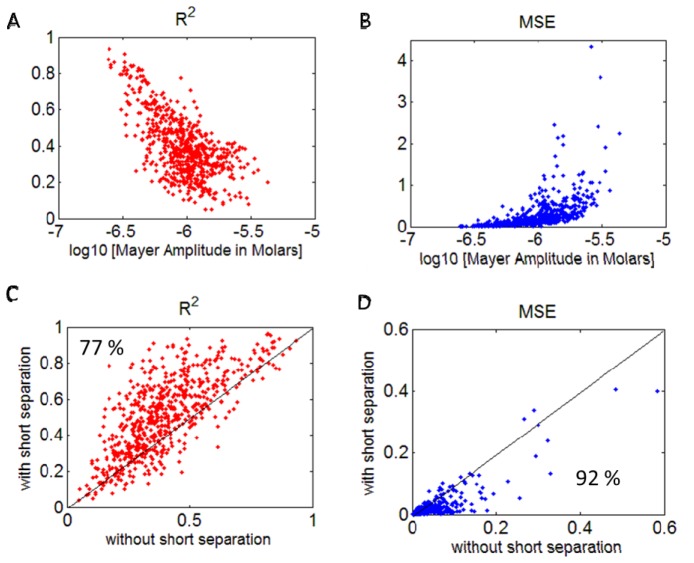
We investigated the effect of Mayer wave power in the fNIRS signal on the estimation of the HRF, by adding a synthetic HRF to the raw NIRS signal and recovering it. We used three metrics to evaluate the efficiency of the HRF estimation: The coefficient of determination (R²), the mean squared error (MSE) and ROC curves. Figures 3 and 4 (top row) show R² and MSE of the recovered HRF versus the Mayer wave power for the various data sets analyzed. Figure 3 shows the results for estimating the HRF that has a true HbO change of 0.7 µM, while Fig. 4 shows the results for a true HbO change of 0.14 µM. The results clearly show that the R² gradually decreases and MSE increases with an increase in Mayer wave power. These results are even more dramatic when the true HbO change is smaller (case 2). Note that the mean squared error when normalized by the true HbO change is four fold higher in case 2 when the true HbO change was reduced by 80%. The statistics for comparison of R² and MSE at low versus high Mayer wave power are shown in Table 1 and confirm the expectation that recovery accuracy of the HRF is significantly reduced with higher Mayer wave power.

Fig. 3.

R² (A) and normalized MSE (B) vs. Mayer wave amplitude (in Molars) in HbO signal for all runs. Comparison of R² (C) and absolute MSE (D) obtained using GLM with and without short separation regression. Percentages in the lower panels indicate the percent of data points above/below the midline indicating that short separation regression improved the estimation. The vertical green line shows the median value for the observed Mayer wave amplitude. Note that results are shown for HRF estimation after introducing a signal change of 1% from baseline for the 690 nm and 2% for 830 nm in the raw NIRS data (case 1).

Fig. 4.

R² (A) and normalized MSE (B) vs. Mayer wave amplitude (in Molars) in HbO signal. Comparison of R² (C) and absolute MSE (D) obtained using GLM with and without short separation regression. Percentages on the lower panels show the percent of data points above or below the midline. Note that results are shown for HRF estimation after introducing a signal change of 0.2% from baseline for the 690 nm and 0.4% for 830 nm producing an evoked HbO change of of 0.14 µM in the NIRS data (case 2).

Table 1. Mean and standard deviation of R² and MSE for the estimation of the HRF for signals with low and high Mayer wave power. P-values obtained from a paired t-test which compares R² and MSE at low and high Mayer wave powers in the HbO signal are also presented. The results are obtained from the estimation without short separation regression.

Mean ± std	Low Mayer power	High Mayer power	p value
R2	0.93 ± 0.05	0.78 ± 0.15	<0.001
MSE	0.02 ± 0.01	0.06 ± 0.07	<0.001

3.1 Short separation regression improves HRF estimation even at high Mayer powers

We investigated the effect of filtering the global physiological fluctuations using short separation regression on the estimation of the HRF. Figures 3 and 4 (bottom row) show the comparison of R² and MSE obtained with and without short separation regression. Both figures indicate that short separation regression improves the estimation of the HRF. Figure 3 shows that for 90% of the cases, short separation regression improved the estimation of the HRF in terms of R² and MSE (Fig. 3, case 1), the improvement was observed in 77% of the cases in terms of R² and 92% of the cases for MSE for case 2 (Fig. 4, case 2). The improvement in HRF estimation with short separation regression is found to be statistically significant (Table 2).

Table 2. Mean and standard deviation of R² and MSE obtained using GLM with and without short separation (SS) regression and p-values obtained when a paired t-test is applied for the comparison of methods for case 1 (Fig. 3) and case 2 (Fig. 4).

	mean ± std	without SS	with SS	p value
CASE 1	R2	0.85 ± 0.13	0.91 ± 0.11	<0.001
	MSE	0.037 ± 0.053	0.02 ± 0.04	<0.001
CASE 2	R2	0.39 ± 0.17	0.50 ± 0.21	<0.001
	MSE	0.036 ± 0.051	0.02 ± 0.04	<0.001

3.2 Receiver operating characteristic (ROC) curve analysis

We have also obtained ROC curves where the true positive rate versus false positive rate is plotted using the t-statistic of the HRF estimation as the threshold for detection (Fig. 5). Our results show that during HRF estimation with HbO, Type I error reduces when using short separation regression in the analysis (Fig. 5, panels B, C and D). The improvement in the ROC curve due to short separation regression is more pronounced for case 2, which has a lower amplitude synthetic HRF (Fig. 5, panels C and D). During HRF estimation with HbR, on the other hand, the short separation regression does not reduce the Type I error except for case 2 at low Mayer wave power. Our results show that, overall, the HRF is better estimated by HbO. The only exception to this is when the HRF is estimated for a lower amplitude synthetic HRF at high Mayer wave power without short separation regression, in which case HbR is a better estimator (Fig. 5, panel D, compare red lines).

Fig. 5.

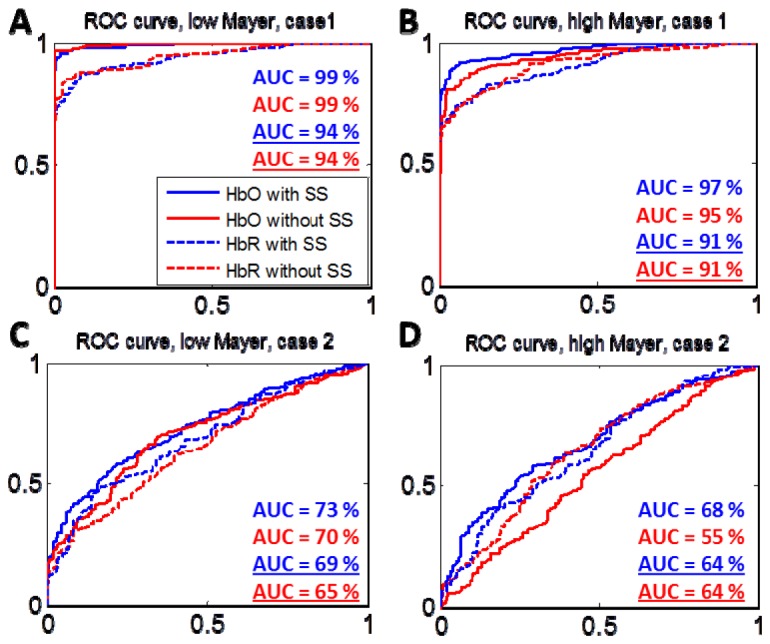
Receiver Operating Characteristic (ROC) Curves obtained for the estimation of the HRF at low and high Mayer wave power with and without short separation regression for case 1 (Panels A and B) and case 2 (Panels C and D). Solid lines are for HbO estimation and dashed lines are for HbR estimation. The AUC for the ROC curves are shown with and without underline for the HbO and HbR estimations respectively.

3.3 Contribution of respiration on results

Respiration is another confounding factor in the estimation of the HRF that is challenging to remove from the data by filtering because of close frequency overlap with the HRF. In order to investigate the relative contribution of Mayer waves and respiration on the estimated HRF, we have performed a semi-partial correlation analysis on the correlation and MSE results. According to this analysis, Mayer wave power alone explains 53% of the variance in correlation, while respiration power alone explains 24% of the variance. Similarly for the MSE, Mayer wave power alone explains 49% of the variance while respiration power alone explains 27%.

3.4 Mayer power is variable across channels within subject

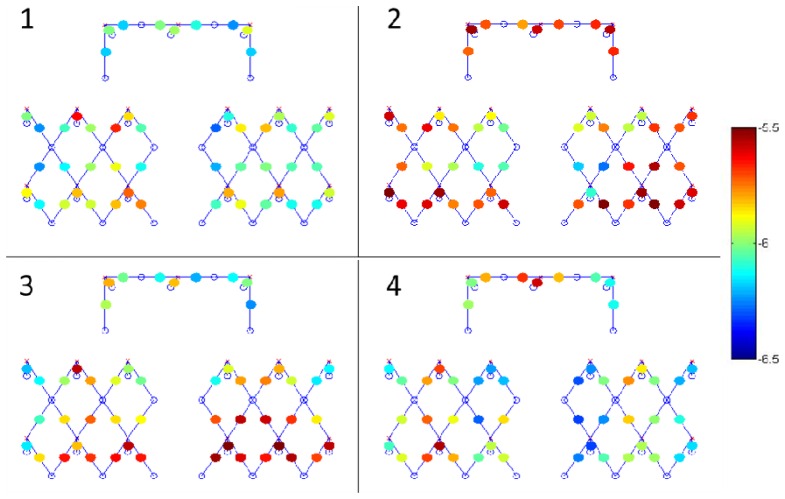
One interesting result that we did not anticipate is that the Mayer wave power exhibited as much variability across channels within a subject as we observed across subjects. We expected the variability across channels within a subject to be less than the variability across subjects. Figure 6 presents the spatial distribution of Mayer wave power in the HbO signal for four different subjects. Table 3 shows the minimum, median and maximum values of the Mayer wave power across channels for each of these four subjects as well as the result for all 23 sessions. When all subjects are considered, the minimum, median and maximum Mayer wave amplitudes were 0.2, 1 and 4.3 µM respectively with a standard deviation of 0.6 µM.

Fig. 6.

Mayer wave power of the HbO signal for each channel shown on the probe layout for four different subjects. Sources (red x’s) and detectors (blue circles) and channels (blue lines) are also shown. The color bar indicates the Mayer wave amplitude in Molar units of log10.

Table 3. Minimum, median and maximum values for the Mayer wave amplitude (shown in µM) of the HbO signal across channels within a subject along with the standard deviation. First four rows correspond to the subject results displayed in Fig. 6. The last row shows the minimum, median, maximum and standard deviation averaged across all subjects.

	Min	Median	Max	Std ( ± )
Subject 1	0.5	1.0	2.5	0.4
Subject 2	0.5	1.9	3.9	0.8
Subject 3	0.6	1.6	3.9	0.8
Subject 4	0.5	1.0	2.5	0.5
All (23 sessions)	0.2	1.0	4.3	0.6

4. Discussion

In this study, we have investigated the effect of Mayer wave power on the estimation of stimulus evoked hemodynamic responses measured with fNIRS. For this, we added a synthetic HRF to real resting state fNIRS recordings. The fNIRS recordings contained physiological oscillations at approximately 0.1 Hz consistent with Mayer waves, with oscillation amplitudes ranging from weak to strong between subjects, and also across channels within individual subjects. By recovering the HRF, we were able to compare the HRF recovered from a signal with weak Mayer waves to that from a signal with strong Mayer waves. Our results support the notion that strong Mayer waves reduce the HRF recovery accuracy. Specifically, our results show that the accuracy diminishes continually with increasing Mayer wave amplitude. As such, it is worth considering the use of Mayer wave amplitude as an objective metric for excluding data from higher level analyses

We further investigated the benefit of using short separation regression to improve the accuracy of the recovered HRF. While long separation channels are sensitive to the brain and superficial layers, short separation channels are generally only sensitive to the superficial layers. By using the short separation measurement as a regressor, we can filter the systemic interference produced by the Mayer waves from the long separation measurements and obtain a better estimate of the evoked HRF in the brain. Our results indicate that short-separation regression produces a statistically significant improvement in the recovery of the estimated HRF (reduction in MSE by 45% (for both case 1 and case 2) and increase in correlation by 7% (case 1) and by 28% (case 2)). This result, among many other studies [29–31], highlights the importance of including short separation channels in the probe design and how it can improve the analysis when there are large amplitude systemic physiology fluctuations present in the fNIRS data.

Our ROC curve analysis shows that, overall, HbO is a better estimator of the HRF than HbR. The only exception to this is when the HRF is estimated for a lower amplitude synthetic HRF at high Mayer wave power when no short separation regression is used in the analysis, in which case HbR is a better estimator. This result can be explained by the well-known fact that the power of physiological fluctuations including Mayer waves, cardiac and respiratory oscillations is much higher in the HbO signal than the HbR signal [32]. Thus, when the amplitude of the Mayer wave is larger, it will impact the estimation of the HbO HRF more than the HbR HRF, unless a filtering strategy is utilized. However, when the Mayer wave amplitude is lower, the HbO HRF estimation is generally more accurate than the HbR HRF estimation as the HbR HRF estimation generally has a lower contrast to noise ratio [33]. None-the-less, this result supports simultaneous use of HbO and HbR when analyzing the HRF in cases where the global physiology cannot be dealt with properly. We also showed that using short separation regression reduces Type I error when using HbO as an HRF estimator but not for HbR. This result is also due to the fact that the HbO signal contains more physiological interference that benefits from short separation regression analysis.

One interesting result we did not anticipate is that there is a large variability in the Mayer wave amplitude not only across subjects but also within a subject across channels, as opposed to our initial expectation of a more uniform Mayer wave amplitude across channels. We believe that this variability across channels is a result of the position of the optodes on the scalp relative to the positions of the major arteries in the scalp. Specifically, if a measurement channel happens to spatially coincide with a larger artery, we expect it will be more sensitive to the Mayer wave associated blood pressure induced variations in HbO. Confirmation of this hypothesis is left for future work. A recent work by Zhang et al. also found regional differences in Mayer wave power across the scalp (measured by short separation channels) [32]. Their group-averaged results from 8 subjects show a 3.5 fold increase in Mayer power in medial regions compared with lateral regions.

Respiratory oscillations also have an effect on accurate estimation of the HRF, since unlike the cardiac and very low frequency oscillations, they cannot be removed using simple filtering without adversely impacting estimation of the HRF. In order to shed light on the relative contribution of Mayer waves and respiration on the estimated HRF, we have performed a semi-partial correlation anaysis on the correlation and MSE results. We found that the Mayer wave power is a good predictor of both MSE and correlation even when the effect of respiration is removed. Moreover, we found that the respiration alone is a relatively poorer predictor. So we conclude that the main contributor in the estimation of the HRF are the Mayer waves. However, since the correlation between these oscillations is significant (R = 0.37), we cannot fully rule out the effect of respiration.

5. Conclusion

In this study, we investigated the effect of hemodynamic oscillations around 0.1 Hz on the estimation of brain activation evoked hemodynamic response functions in fNIRS data. Our results indicate that the amplitude of oscillations at 0.1 Hz can serve as an objective metric of the expected HRF estimation accuracy and that short separation regression significantly improves the recovered HRF when large amplitude 0.1 Hz oscillations are present in the fNIRS data.