Dynamic and rheological properties of soft biological cell suspensions

Abstract

Quantifying dynamic and rheological properties of suspensions of soft biological particles such as vesicles, capsules, and red blood cells (RBCs) is fundamentally important in computational biology and biomedical engineering. In this review, recent studies on dynamic and rheological behavior of soft biological cell suspensions by computer simulations are presented, considering both unbounded and confined shear flow. Furthermore, the hemodynamic and hemorheological characteristics of RBCs in diseases such as malaria and sickle cell anemia are highlighted.

Introduction

Blood is a biological fluid that delivers necessary substances such as nutrients and oxygen throughout the human body and carries away metabolic waste products. Plasma, red blood cells (RBCs), white blood cells (WBCs), and platelets are the four main components of whole human blood. Due to its particulate nature, blood is considered as a complex non-Newtonian fluid exhibiting intriguing dynamic and rheological behavior depending on flow rates, volume fraction of suspending particles especially RBCs, and the vessel geometries.

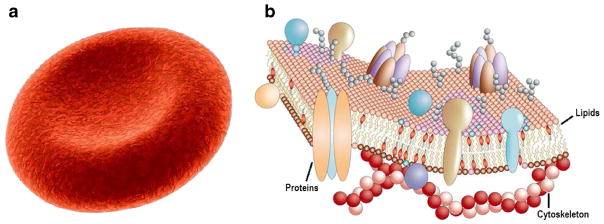
The deformability of an RBC is determined by the geometry, elasticity, and viscosity of its membrane. A healthy RBC has a biconcave shape when not subject to any external stress and is approximately 8.0 μm in diameter and 2.0 μm in thickness (Fig. 1a) (Fung 1993). The membrane of a RBC consists of a lipid bilayer supported by an attached spectrin network that acts as a cytoskeleton (Fig. 1b) (Pietzsch 2004). The resistance of the lipid bilayer to bending elasticity is controlled by the bending rigidity, while the spectrin network’s resistance to shear strain is characterized by the in-plane shear modulus. Experimental and numerical observations of RBC behavior in flow mimicking the microcirculation reveal dramatic deformations and rich dynamics (Abkarian et al. 2007; Dupire et al. 2012). The extreme deformability allows RBC to squeeze without any damage when passing through narrow capillaries in microcirculation. However, this feature of RBCs can be critically affected by genetic or acquired pathological conditions such as malaria (Diez-Silva et al. 2010) and sickle cell anemia (SCA) (Barabino et al. 2010). Thus, as an important component of the blood, RBCs and their mechanical properties play a crucial role in the dynamic and rheological behavior of blood in normal and disease states.

Fig. 1.

Simple representation of a healthy human RBC (a) and its complex membrane structure (b). The equilibrium shape of healthy human RBC is a biconcave disk approximately 8.0 μm in diameter and 2.0 μm in width. Its cell membrane is made of a lipid bilayer reinforced on its inner face by a flexible two-dimensional skeletal protein network. The fluid-mosaic model of the RBC membrane is adapted with permission from Pietzsch (2004)

The other two and important particles in blood, i.e., WBCs and platelets, have much smaller density compared to RBCs. Alterations in blood flow and its rheology have a significant impact on the adhesion and activation mechanisms of platelets and WBCs (Lehoux et al. 2006). WBCs are relatively larger and less deformable particles than RBCs and play a significant role in our immune system. In order to get to the site of inflammation, WBCs typically migrate to the vessel walls and perform a rolling motion. Platelets in their unactivated resting form are nondeformable biconvex discoid structures of 2–3 μm in diameter. Platelets play an important role in hemostasis and thrombus formation at the site of injured endothelium. Since RBCs are more deformable, they migrate toward the vessel center, creating a depletion or cell-free layer (CFL) close to the wall. This phenomenon was first found by Fåhræus and Lindqvist (1931) in capillaries. The less deformable cells such as WBCs and platelets, however, tend to migrate toward the wall. A process called margination, which is essential for the cells to reach to the site of action.

Other types of soft particles that share several intricate mechanical properties of RBCs are vesicles and capsules. Vesicles are viscous liquid drops enclosed by bilayer membranes prepared from compounds such as phospholipids (Ryman and Tyrrell 1979; Lipowsky 1991) and amphiphilic block copolymers (Discher and Eisenberg 2002; Li et al. 2009, 2013a, 2014c), whereas a capsule membrane is made of extensible polymer shell (Pozrikidis, 2003; Barthes-Biesel 2010, 2011). Artificial vesicles and capsules can be used for targeted drug delivery and cell and hemoglobin encapsulation. Both particles reproduce several dynamical behavior known for RBCs under flow. Thus, vesicles and capsules have gained popularity as model systems to study the RBC dynamics and membrane biophysics in general.

Computational modeling and simulations can tackle a broad range of dynamics and rheology problems relevant to blood. Several computational models, including continuum-based fluid-structure interaction models (Rehage et al. 2002; Peskin 2002; Doddi and Bagchi 2009; Zhao et al. 2010; Veerapaneni et al. 2011a; Kumar and Graham 2012a), and particle-based spectrin-level and multiscale models (Boal et al. 1992; Discher et al. 1998; Noguchi and Gompper 2005b; Li et al. 2005, 2007; Pivkin and Karniadakis, 2008; Fedosov et al., 2010; Pan et al., 2010; Peng et al., 2013), have been developed. Continuum-based models treat the cell membrane and embedding fluids as homogeneous materials, using immersed boundary method (IBM) (Peskin 2002; Doddi and Bagchi 2009; Yazdani and Bagchi 2011; Fai et al. 2013), boundary integral method (BIM) (Ramanujan and Pozrikidis 1998; Lac et al. 2004; Zhao et al. 2010; Veerapaneni et al. 2011a), and fictitious domain method (FDM) (Shi et al. 2014; Hao et al. 2015). Particle-based models treat both the fluid and the membrane as particulate materials, using multiparticle collision dynamics (MPCD) (Noguchi and Gompper 2005b; McWhirter et al. 2009), coarse-grained molecular dynamics (CGMD) (Kotsalis et al. 2010; Hanasaki et al. 2010; Li and Lykotrafitis 2012b; 2014a), dissipative particle dynamics (DPD) (Pivkin and Karniadakis 2008; Fedosov et al. 2010; Pan et al. 2010; Peng et al. 2013), Smoothed Dissipative Particle Dynamics (SDPD) (Fedosov et al. 2014a), and smoothed particle hydrodynamics (SPH) (Hosseini and Feng 2012; Wu and Feng 2013). Currently, there is a wide variety of modeling approaches since there is no universal solution for all blood-flow-related problems. Eventually, the cross-fertilization between continuum- and particle-based models leads to practical yet physically and biologically accurate, and computationally efficient methods that can tackle a broad range of dynamics and rheological problems relevant to biological applications. This is a very active research area, see for recent review (Barthes-Biesel 2010, 2011; Li et al. 2013b; Fedosov et al. 2014b; Freund 2014; Winkler et al. 2014). In this article, we overview the applications of both continuum and discrete computational approaches on the modeling of dynamic and rheological properties of healthy and diseased RBCs as well as other soft particles with focus on the most recent contributions.

Dynamics of deformable particles in dilute suspensions

Computational modeling and simulations help in predicting how deformable particles behave in shear flow and provide insights into how viscous flow transforms shapes of these deformable particles and how they distort the surrounding flow. Here, we assume a dilute suspension of isolated particles where particle interactions are negligible. The hydrodynamic stress, Σ^b, for the bulk flow of a Newtonian fluid is given by

$$\mathit{\sigma }=-p\mathbf{I}+\eta (\nabla \mathbf{v}+{(\nabla \mathbf{v})}^{\mathbf{T}}),$$ (1)

where p is the pressure, η is the fluid viscosity, I is the unit tensor, and v is the fluid velocity. The surrounding fluid exerts tractions, Δf, on the membrane that are balanced by the tensions developed in the particle’s membrane

$$\mathrm{\Delta }\mathbf{f}=({\mathit{\sigma }}_{ex}-{\mathit{\sigma }}_{in})·\mathbf{n}={\mathit{f}}^{\kappa }+{\mathit{f}}^{el},$$ (2)

where n is the unit normal vector, f^κ and f^el are the tensions due to the membrane bending and elastic resistances, respectively. It should be mentioned that RBC and vesicle possess an inextensible bilayer membrane, whereas capsules normally do not conserve the area. The membrane tensions can be evaluated using appropriate constitutive laws, the most famous of which are the Helfrich’s bending energy for lipid bilayer (Ou-Yang and Helfrich 1989), Skalak law for elastic and area-conserving cytoskeleton (Skalak et al. 1973), and new-Hookean hyperelastic law for capsules (Dimitrakopoulos 2012). Also note that the RBC membrane more precisely behaves as a viscoelastic material following a power law, and a more complicated viscoelastic tension f^vis can replace f^el in Eq. 2 (Yazdani and Bagchi 2013). Here, we summarize the generic behavior of vesicles, capsules, and RBCs in shear flow. Specifically, we focus on two situations relevant to blood circulation, i.e., uniform shear flow and confined (tube or channel) flow.

Vesicles, capsules, and RBCs in uniform shear flow

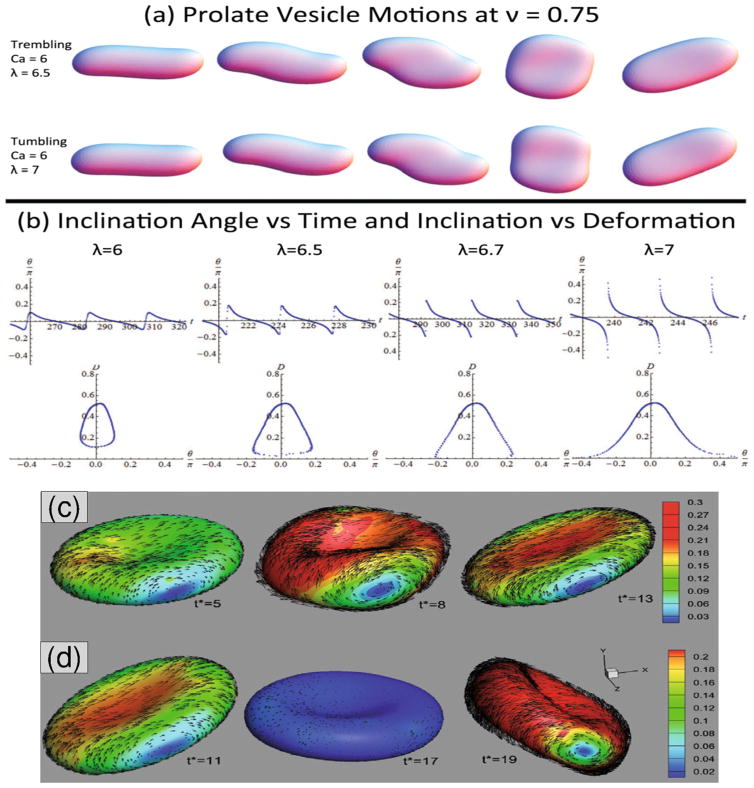
Vesicles, capsules, and RBCs in uniform unbounded shear flow have been observed to exhibit two primary types of dynamics (see Fig. 2): (1) Tank treading (TT) motion (Fischer et al. 1978; Kantsler and Steinberg 2005) where the soft particle deforms into an elongated ellipsoidal shape and its inclination angle θ remains constant with time; (2) Tumbling (TB) motion (Kantsler and Steinberg 2006) where the soft particle undergoes a periodic flipping motion and θ is periodic in time. More complicated intermediate type of dynamics such as vacillating-breathing (VB) (Misbah 2006) also called alternatively trembling (TR) (Deschamps et al. 2009a, b) or swinging (SW) motion (Noguchi and Gompper 2007) have also been observed both numerically and experimentally for these soft particles.

Fig. 2.

Vesicles and RBCs in unbounded shear flow. a Trembling (also known as VB or SW), and tumbling vesicle at slightly higher λ. b Inclination angle vs. time and vs. deformation show the transition from trembling to tumbling as λ increases from 6 to 7. Here, Ca_κ = 6 and reduced volume v = 0.75. Figure is reproduced with permission from (Spann et al. 2014). c Breathing dynamics of an RBC, and d tumbling dynamics. Vectors show the in-plane membrane TT velocities, where the contours present their magnitudes. t* is the dimensionless time defined as γ̇t. Reprinted with permission from Bagchi and Yazdani (2012)

For a vesicle with constant volume V and constant surface area A, its dynamics in shear flow is fully characterized by three parameters: (i) reduced volume, $v=3V/(4\pi R_0^3)$, where $R_0=\sqrt{A/4\pi }$ is the radius of a sphere with the same area, (ii) viscosity ratio, λ = η_in/η_out, between internal and external fluid viscosity, and (iii) Capillary number, $C{a}_{\kappa }=\eta \stackrel{.}{\gamma }{R}_0^3/\kappa$, defined based on the bending stiffness κ and shear rate γ̇. The classic Keller-Skalak theory (Keller and Skalak 1982) predicts only TT and TB motions exist if the vesicle shape is fixed (Kraus et al. 1996; Noguchi and Gompper 2004, 2005a). Allowing the vesicle shape to freely evolve has led to VB motion (Kantsler and Steinberg 2006; Biben et al. 2011; Zhao and Shaqfeh 2011a; Yazdani and Bagchi 2012).

Due to the shear elasticity of their membranes, capsules exhibit very similar dynamics as RBCs in shear flow sharing the same TT-SW-TB dynamics. There are extensive numerical and analytical studies on the dynamics of spherical and nonspherical capsules in shear flow (e.g., Bagchi and Kalluri, 2009; Barthes-Biesel and Rallison, 1981; Pozrikidis, 2003; Sui et al., 2008). A VB-like dynamics similar to vesicles was found for nonspherical capsules in the numerical study (Bagchi and Kalluri 2009), where a large-amplitude oscillation in capsule shape and a strong coupling between the shape deformation and orientation dynamics were observed. The mechanism of the SW motion between vesicles and capsules/RBCs is different (Veerapaneni et al. 2011b): For capsules/RBCs, SW motion arises from a periodic variation in the elastic membrane energy during TT motion. For vesicles, SW motion is due to a periodic vesicle deformation as the TB inclusion pushes on the membrane.

Shear flow dynamics of RBCs is richer than capsules and vesicles due to their unique mechanical properties and biconcave shapes. Several new dynamics such as rolling, kayaking, and hovering were observed both in the experiments and simulations (Dupire et al. 2012; Cordasco and Bagchi 2014). Similar to vesicles and close to the TB-to-TT transition border, breathing-like motion for RBCs in which the membrane major axis oscillates about the flow direction as the shape exhibits large-amplitude deformations was also observed in numerical study (Fig. 2) (Yazdani and Bagchi 2011), whereas experimental observations suggested that the breathing dynamics could not exist for RBCs. More recent numerical studies have shown that the RBC stress-free shape can have considerable effects on its dynamics, stability of TT modes, and transition from TT to TB (Cordasco et al. 2014; Peng et al. 2014, 2015). These studies suggest that RBC’s stress-free shape must be closer to a sphere rather than the biconcave shape confirming the experimental results (Dupire et al. 2012). Furthermore, breathing dynamics were no longer observed if the sphere was chosen as the stress-free shape. In addition, near the TB-to-TT transition, there exists a narrow intermittent region where theory predicts an instability such that TB motion of RBCs can be followed by TT motion and vice versa. This intermittent dynamics were first reported in the numerical simulations of Fedosov et al. (2010). A more recent front-tracking study gives a detailed analysis of the intermittency and synchronous dynamics of RBCs in shear flow as well as their off-shear plane dynamics (Cordasco and Bagchi 2014).

Although there is a number of experimental studies aiming to address the viscoelastic properties of RBC membrane and to measure the membrane viscosity (e.g., Hochmuth et al. 1979; Puig-de-Morales-Marinkovic et al. 2007), there are very few numerical studies incorporating membrane viscosity in their models. Fedosov et al. utilized a worm-like-chain spectrin model with additional dissipative forces to account for the lipid bilayer viscous effects (Fedosov et al. 2010). Comparing the simulated TT frequencies of RBCs with experiments showed that a purely elastic RBC results in an over-prediction of TT frequencies. Similar conclusion was also made in a continuum study of capsule dynamics under the influence of membrane viscosity (Yazdani and Bagchi 2013). They found that increasing the membrane viscosity is equivalent to increasing the viscosity of the internal fluid in regards to TT frequencies and TT-to-TB transitional dynamics.

Vesicles, capsules, and RBCs in bounded flow

Deformable particles suspended in fluid flowing through conduits are often encountered in many biological processes, and in biomedical devices. Examples are the motion of blood cells through blood vessels, flow chambers, and cell separation devices. Simulations of suspensions of blood cells in a tube or a channel mimic many properties of blood flow in vessel in vivo. Here, we summarize some of the simulation studies on the dynamic behavior of these soft particles in tube and channel flow.

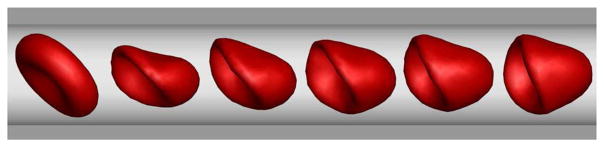
A widely studied flow is the confined Poiseuille flow, in which the dynamic behavior of vesicles, capsules, and RBCs is often considered in both continuum-based simulations (Secomb et al. 2007; Coupier et al. 2008; Danker et al. 2009; Coupier et al. 2012) and particle-based simulations (Noguchi and Gompper 2005b; McWhirter et al. 2009, 2011; Deng et al. 2012). In a Poiseuille flow at low Reynolds numbers, RBCs and vesicles in narrow channels or narrow vessels deform themselves into parachute-like shapes (see Fig. 3). For example, Pan and Wang studied the shape memory ability of the RBC membrane by a spring model (Pan and Wang 2009). They found that the parachute-like shaped RBCs return back to initial biconcave shapes after stopping the flow. A similar phenomenon was simulated by Pivkin and Karniadakis using a multiscale RBC (MS-RBC) model based on DPD (Pivkin and Karniadakis 2008). RBC deformed into the parachute-like shape under the flow condition while it recovered its equilibrium biconcave shape after the fluid returned to rest. McWhirter et al. used MPCD to study the shape changes and clustering of RBCs under flow in cylindrical microcapillary (McWhirter et al. 2011). They found that the RBCs transition from discocyte shape at low velocity to parachute-like shape at high velocity.

Fig. 3.

Sequence of RBC shapes from biconcave to parachute in Poiseuille flow in microtube (unpublished work)

Vesicles have gained popularity as well-defined models to study the RBC dynamics. For example, Noguchi and Gompper have employed MPCD to study the shape transitions of fluid vesicles in capillary flows (Noguchi and Gompper 2005b). Different from the shape transition of RBCs, they found that the fluid vesicle transits its shape from discocyte to prolate ellipsoid with the increase of flow velocity. Danker et al. employed BIM to investigate the effect of viscosity ratio on vesicle migration in a Poiseuille flow (Danker et al. 2009). They predicted the coexistence of two types of shapes: bullet-like and parachute-like shapes. Vesicles and RBCs flowing in microvessels often exhibit parachute-like shapes usually attributed to an increase of hydrodynamic constraint; however, in a recent study, Coupier et al. showed that the presence of a fluid membrane leads to reverse phenomenon (Coupier et al. 2012). They found that the parachute-like to bullet-like shapes crossover depends on the capillary number but not on the confinement.

Variability in deformation of different soft particles is a crucial factor in the variation of their lateral (lift) force and velocities affecting their near-wall dynamics. Lateral migration of capsules is studied numerically in planar Poiseuille flow (Doddi and Bagchi 2008), square duct with a corner (Zhu and Brandt 2014), and in bounded shear flow (Singh et al. 2014). For vesicles, there are experimental and numerical studies addressing different and interesting shape transformations as the vesicles migrate towards the center of microchannel (e.g. Coupier et al. 2008; Danker et al. 2009; Zhao et al. 2011).

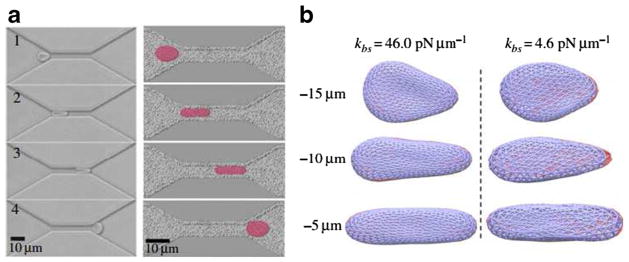
RBCs are highly deformable allowing them to travel through capillaries with diameter smaller than their size. When RBCs flow through capillaries, they undergo drastic deformation by shear stress. Accordingly, microfluidic channels are used to mimic human capillaries and study RBC deformability. It has been found that RBCs undergo a continuous and severe transition from their normal biconcave shapes to ellipsoidal shapes by the elongation of their sizes in the flow direction (longitudinal axis) and shortening of their sizes in the cross-flow direction (transverse axis). Figure 4a shows a qualitative comparison of the simulation results from the two-component RBC model based on the DPD approach (Li et al. 2014b) with experimental measurements (Quinn et al. 2011). The dynamic observations of the deformation of RBC traversal across the microfluidic channel were in accordance with the experimental phenomena. The simulations also demonstrated that the bilayer-cytoskeletal elastic interaction coefficient, k_bs, plays a key role in the RBC traversing narrow microfluidic channel as shown in Fig. 4b. When k_bs is large, there is a strong coupling between the lipid bilayer and the cytoskeleton, i.e., the RBC behaves as if it was an effective membrane. If k_bs is small, the bilayer-cytoskeletal coupling is weak, and the detachment of the lipid bilayer from the cytoskeleton is much more likely to occur.

Fig. 4.

a Shape characteristics of a RBC traversing across microfluidic channels from experimental (left) and simulation (right) data. b Bilayer-cytoskeletal detachment for an RBC traversing the microfluidic channel at different bilayer-cytoskeletal elastic interactions. The lipid bilayer and the cytoskeleton are shown as dark and light grey (red and blue in the online version) triangular networks, respectively, and only half of the triangular network of the lipid bilayer is shown for clarity. Reproduced from Li et al. (2014b), by permission

Dynamics of platelets and WBCs

As mentioned in the previous section, confined blood flow in tubes and channels exhibit an intricate and rich dynamics of its constituents, namely RBCs, platelets, and WBCs. Lateral migration of RBCs leads to the CFL formation adjacent to the vessel wall. Reduced local viscosity in this layer helps reducing the resistance to flow in small vessels, and is critical for blood flow in microcirculation. Furthermore, RBCs tend to push out various solutes from the central region into the CFL (Fig. 5). This process leads to margination of less deformable particles such as platelets and WBCs to the wall, which is essential to their functions.

Fig. 5.

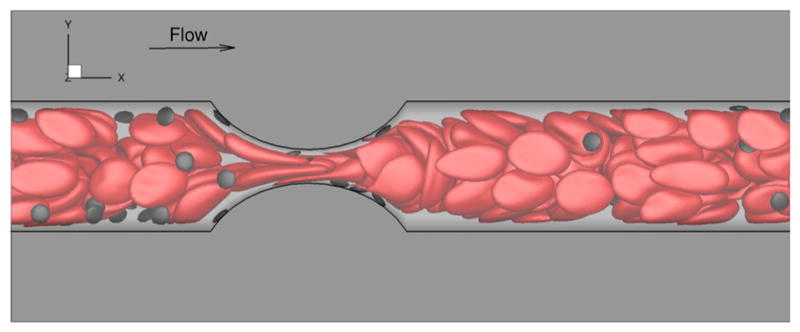
Margination of platelets in whole blood simulation at 35 % H_ct in microchannel with 75 % degree of stenosis. These simulations are based on DPD to model RBCs, platelets, and plasma (unpublished work)

A margination theory for binary suspensions of spherical capsules in a dilute or semi-dilute suspension was proposed in (Kumar and Graham 2012b). The key idea is the balance between wall-induced hydrodynamic migration and shear-induced pair collisions (also known as shear-induced diffusion) of particles. In a similar approach, Narishman et al. developed a low-order, kinetic theory to describe the concentration distribution of deformable particles in wall-bounded Couette flow (Narsimhan et al. 2013).

WBC margination has been studied both experimentally and numerically in detail (Fedosov et al. 2012; Freund 2007; Sun et al. 2003). It is found that besides WBC’s spherical and less deformable shape, several flow parameters contribute significantly to its margination as well. These factors include flow hematocrit (H_ct) level, flow rate, RBC aggregation, and the vessel geometry. Fedosov et al. in a 2D study found that WBC margination becomes weaker as the cells become more deformable, whereas RBC aggregation and higher H_ct proved to enhance WBC margination (Fedosov et al. 2012).

Similar to WBCs, it is extremely crucial for platelets function in hemostasis and thrombosis. An increased concentration of platelets near the walls has been confirmed in in vivo (Woldhuis et al. 1992) and in vitro (Tilles and Eckstein 1987) studies. To describe experimental observations of the margination of platelets, a phenomenological drift-diffusion model for platelet motion in blood flow was developed (Eckstein and Belgacem 1991). The drift-diffusion equation results in a good qualitative description of platelet margination. Here, the drift can be considered to be due to wall-platelet hydrodynamic interactions (although there is no rigorous physical foundations for that), whereas the shear-induced diffusivity of platelets is due to their collisions with RBCs. There is a growing number of numerical studies on platelet margination and its mechanisms (AlMomani et al. 2008; Tokarev et al. 2011; Zhao and Shaqfeh 2011b; Reasor Jr et al. 2013; Vahidkhah et al. 2014; Vahidkhah and Bagchi 2015). Crowl and Fogelson employed a Fokker-Planck approach coupled with 2D numerical simulations to model platelet transport in blood flow (Crowl and Fogelson 2011). The anisotropy, and three-dimensionality in platelet margination as well as their interactions with RBCs necessitate 3D whole blood simulations (Zhao and Shaqfeh 2011b; Reasor Jr et al. 2013; Vahidkhah et al. 2014; Vahidkhah and Bagchi 2015). The effect of particle shapes on its margination has been shown to be substantial in the numerical study of Reasor Jr et al. (2013); they found that spherical particles marginate more effectively than those having ellipsoidal shapes. A recent study of microparticles in blood have shown that the shape of the particles affects their dynamics differently in the margination than the adhesion. While oblate ellipsoidal particles of moderate aspect ratio show the highest near-wall accumulation, very long elongated particles are more likely to form the initial wall contact. Furthermore, the adhesion efficiency of oblate discocyte shapes similar to platelets was proved to be the highest (Vahidkhah and Bagchi 2015).

Dynamics of diseased RBCs

Blood disorders can affect any or all of the three types of blood cells, i.e., RBCs, WBCs, and platelets. Blood disorders can also affect the plasma, i.e., the liquid portion of blood. Numerical simulations have been used for qualitative and quantitative interpretation and predictions of mechanical properties and dynamic behavior of RBCs in malaria and other hematological diseases (Fedosov et al. 2011a; Quinn et al. 2011; Lei and Karniadakis 2013). Below, we highlight some of the research being performed to study the changes in mechanical and dynamic properties of RBCs in malaria and SCA.

Malaria-infected RBCs

Malaria is one of the most severe parasitic diseases. When the malaria parasite is inside an RBC, the cell is stiffer than normal. Thus, blood flow may be significantly affected by altered RBC structural and mechanical properties occurring in malaria. The computational RBC models are ideal tools to study the RBC dynamics in malaria. For example, Imai et al. employed SPH to study the microvascular hemodynamics arising from the malaria infection (Imai et al. 2010, 2011). They examined flow in microtubes and found that the hydrodynamic interaction between healthy RBCs and malaria-infected RBCs causes train formation. Ye et al. used DPD to simulate the flow dynamics of healthy RBCs and malaria-infected RBCs (Ye et al. 2014). They observed a downward inclusion phenomenon where malaria-infected RBCs cannot undergo the dynamic motion at the level higher than that exhibited by the healthy RBCs.

Different cell models have also been employed to study the adhesion dynamics of malaria-infected RBCs under flow. For example, Fedosov and coworkers performed ambitious DPD simulations of the adhesion and flipping dynamics of malaria-infected RBCs (Fedosov et al. 2011a). Their simulation results revealed several types of cell dynamics such as firm adhesion and intermittent slipping. They also modeled the effect of solid parasite inside the malaria-infected RBCs and found that the presence of a rigid body inside the RBC induces higher variances in cell motion and pronounces flipping of the malaria-infected RBC as it tethers to the surface.

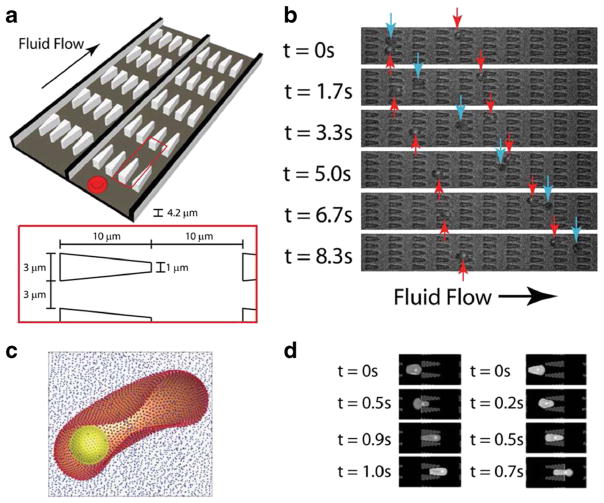
Quantifying the dynamic cell deformability for various stages of malaria-infected RBCs and other types of blood cells is significant. Bow et al. developed a microfluidic device with periodic obstacles to blood flow to characterize the biomechanical properties of malaria-infected RBCs (Fig. 6b) (Bow et al. 2011). They employed the MS-RBC model to translate the experimental measurements into quantitative data describing the mechanical properties of individual RBCs. Their simulations were able to capture the effect of the changes of RBC properties arising from parasitization on the movement of healthy RBCs and malaria-infected RBCs quite accurately (Fig. 6d). Aingaran et al. used finite elements to investigate the deformability properties of malaria-infected RBCs during sexual development (Aingaran et al. 2012). Their simulations suggested that along with deformability variations, the morphological changes of the parasite may play an important role in tissue distribution in vivo. In a recent study, Wu and Feng used SPH to simulate the traverse of malaria-infected RBCs through a converging microfluidic channel (Wu and Feng 2013). They examined the influences of RBC structural and mechanical changes due to malaria infection on the RBC dynamics in microfluidic channels and found that RBC gradually lost its deformability with progression of the malaria infection.

Fig. 6.

a Illustration of the flow cytometer device. b Experimental images of ring-stage infected (red arrows) and uninfected (blue arrows) RBCs in the channels. c The computational RBC model consists of 5000 particles connected with links. The parasite is modeled as a rigid sphere inside the cell. d DPD simulation images of malaria-infected RBCs traveling in channels of converging (left) and diverging (right) pore geometries. Reproduced from Bow et al. (2011), by permission

Most blood test analysis in medical laboratories is often performed on cell-free samples, therefore, blood-plasma separation needs to be achieved. The blood-plasma separation depends on cell deformability. The malaria-infected RBCs lose their deformability and in turn affects blood flow. The motion of RBC flow in bifurcating microfluidic channel was simulated using a low-dimensional RBC (LD-RBC) model (Li et al. 2012d). The separation efficiency of malaria-infected RBCs was found to be lower than those of healthy RBCs.

Dynamic behavior of RBCs in SCA

SCA is an inherited blood disorder exhibiting heterogeneous cell morphology and abnormal rheology, especially under hypoxic conditions (Chien et al. 1970; Kaul and Xue 1991). SCA has been characterized as the first “molecular disease” being linked to an alteration in the molecular structure of hemoglobin. The symptoms of the disease have been traced to the polymerization of sickle hemoglobin upon hypoxic condition, forming long fibers that distort the shapes of RBCs and dramatically alter their mechanical and rheological properties. The affected RBCs become more rigid and sticky compared with normal RBCs, resulting in a difficulty when they flow through small blood vessels and capillaries, hence depriving tissues and organ of oxygen.

Computational modeling and simulations of sickle RBCs and sickle blood are helpful in understanding how sickling occurs and how it affects RBC dynamics and blood vaso-occlusion (Chiang and Frenette 2005). To this end, Dou and Ferrone developed a kinetic model for sickle hemoglobin polymerization to understand domain formation. Their qualitative results showed that the transformation of a single fiber into wheat-sheaf bundles and then to spherulitic domains (Dou and Ferrone 1993). Dynamic simulations of self-assembly of sickle hemoglobin confirmed that chain chirality is the main driver for the formation of sickle hemoglobin fibers (Li et al. 2012c). Different CGMD models have also been introduced to simulate the dynamic behavior such as zipping and unzipping dynamics of sickle hemoglobin fibers (Li and Lykotrafitis 2011; Li et al. 2012a). The simulation results showed that fiber frustration and compression result in partial unzippering of bundles of sickle hemoglobin fibers.

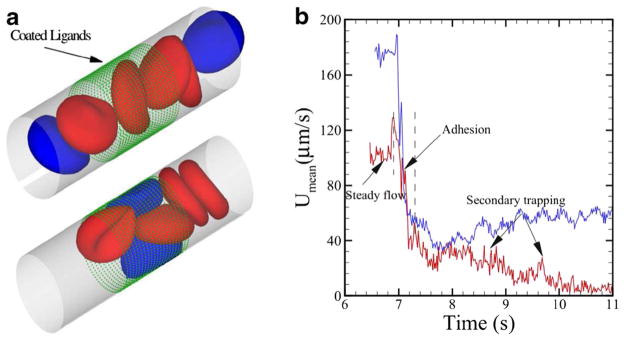
Decreased RBC deformability and increased cell rigidity in SCA have significant implications for microcirculatory flow. Some simulation attempts have been made to understand the dynamic behavior of blood flow in SCA. For example, Dupin et al. studied sickle blood flow through an aperture of diameter less than the size of a single cell (Dupin et al. 2008). Lei and Karniadakis quantified the hemodynamics of blood flow with SCA under various physiological conditions (Lei and Karniadakis 2012). They found that the increase of flow resistance by granular RBCs was greater than the resistance of blood flow with sickle-shaped RBCs. They also applied adhesion dynamics to the effect of SCA and found that blood flow exhibits a transition from steady flow to partial/full occluded state, see Fig. 7. Their simulation results showed that the adhesion interaction between cells and vessel walls plays a profound effect on the hemodynamics of sickle RBCs and addressed the conditions of sickle cell shape, adhesiveness, and elasticity that can cause the occlusion of a small blood vessel (Lei and Karniadakis 2013).

Fig. 7.

a Sickle blood flow with adhesive dynamics. The green dots represent the ligands coated on the vessel wall. The blue cells represent the “active” group of sickle cell exhibiting adhesive interaction with the coated ligands. b Mean velocity of the sickle blood at different stages of the adhesive dynamics. Reproduced from Lei and Karniadakis (2012), by permission

Rheology of vesicles, capsules, and RBCs

While the dynamics of rigid particles in suspension and their rheological behavior have been investigated in depth and well understood, simulating the rheology of deformable particles especially in non-dilute suspensions has become possible only recently. As a consequence of the deformable nature of soft particles, the suspension attains viscoelastic properties and the effective viscosity (η_eff) shows a pronounced dependence on shear rate. In the past decades, computational models have proven to be an important tool in predicting the macroscopic flow properties of a suspension (e.g., shear viscosity, yield stress) from the mesoscopic properties of these soft particles (e.g., deformability, membrane properties, and particle size). Recent progress on the rheology of soft-particle suspensions by computer simulations is reviewed herein.

Rheology of vesicle and capsule suspensions

To quantify the rheology of a suspension in uniform shear flow with the shear rate γ̇, we first evaluate the bulk stress of the suspension. Following Batchelor (Batchelor 1970), the overall force-free suspension stress is split into a contribution of the pressure in the fluid volume, the fluid stress in the absence of particles, and the stress due to the particles

$${\mathit{\sigma }}^b=-P\mathbf{I}+2\eta \mathbf{E}+{\mathit{\sigma }}^{\mathbf{p}},$$ (3)

where P, E, and σ^p are the volume-averaged scalar pressure, strain tensor, and the average particle stress, respectively. Assuming negligible inertia, the particle contribution to the suspension stress can be calculated using the stresslet formulation (Batchelor 1970) and Eq. 2

$${\mathit{\sigma }}^p=\frac{1}{V}\sum _N{\int }_A\left[\frac{1}{2}(\mathrm{\Delta }\mathbf{f}\mathbf{r}+\mathbf{r}\mathrm{\Delta }\mathbf{f})+{\eta }_{\mathit{out}}(\lambda -1)(\mathbf{u}\mathbf{n}+\mathbf{n}\mathbf{u})\right]dA,$$ (4)

where r and u are the position and velocity vectors on the particle’s surface, V is the volume of the fluid, and the summation is carried over all N particles. The effective suspension viscosity can then be computed using the shear component of the stress tensor as η_eff = σ_xy/γ̇, which also gives the intrinsic viscosity due to particle contributions η_I = (η_eff − η_out)/η_out ϕ with ϕ being the suspension volume fraction.

The perturbation theory analysis of nearly-spherical vesicles in a dilute solution (ϕ < ≈ 10 %) predicts ashear-rate-independent suspension rheology at leading order. More importantly, the shear viscosity decreases with λ and attains a minimum at λ_c corresponding to the TB-to-TT transition (Misbah 2006; Danker and Misbah 2007), followed by an increase. This nonmonotonic behavior is in agreement with experiments (Vitkova et al. 2008) in semi-dilute regime as well. Interestingly, in a subsequent study using boundary integral simulation of non-dilute vesicle suspensions, similar nonmonotic behavior for the effective viscosity was observed for volume fractions as high as 20 % (Zhao and Shaqfeh 2013). In the dilute limit, suspensions of deformable particles are shear thinning due to the increased deformation of the suspended phase. Similar to vesicles, numerical simulations of dilute elastic spherical capsules in a tank-treading configuration demonstrate a minimum in the suspension viscosity as λ increases (Bagchi and Kalluri 2010).

Dense suspension of capsules has first been studied in 2D (Breyiannis and Pozrikidis 2000). More recently, rheology and microstructure of suspensions of initially spherical elastic capsules have been studied using a coupled lattice-Boltzmann/finite element (LB/FE) method for volume fractions as high as 40 % (Clausen et al. 2011). A detailed numerical study of suspension of aggregation-free capsules with RBC-like membrane properties was carried out in Gross et al. (2014), where ϕ up to 90 % and reduced shear rates of Ca_s = η_outγ̇R/G_s < 0.1 were considered, with G_s the capsule shear modulus. They found that for the effective viscosity at small capillary numbers, a Newtonian plateau is present at low volume fractions, which goes over into a yield stress regime at high volume fractions; for large capillary numbers, the viscosity is strongly shear-thinning, following a power-law with ${\eta }_{\mathit{eff}}~C{a}_s^{0.5}$. The evidence of yield stress at low shear rates was found even for non-aggregating capsules. Achieving higher shear rates still remains a challenge.

Blood rheology

Blood cells are subjected to intense mechanical stimulation from both blood flow and vessel walls, and their rheological properties are important to their effectiveness in performing their biological functions in micro-circulation. Computational modeling and simulations of blood flow have improved considerably in recent years (Baskurt and Meiselman 2003; Zupancic Valant et al. 2011; Apostolidis and Beris 2014; Fedosov et al. 2014b). For example, dynamic simulations can model how blood flow behaves in microfluidic channels and predict blood viscosity in silico (Fedosov et al. 2011c). Different cell models have also been employed for various qualitative and quantitative interpretations as well as predictions of biomechanical properties of RBCs with hematological diseases. Examples include dynamic cell deformability for various stages of malaria-infected RBCs (Fedosov et al. 2011a) and vaso-occlusion phenomena in SCA (Lei and Karniadakis 2013). Here, we draw attention to the computational hemorheology of blood flow in health and disease.

Rheological behavior of normal blood

At the microcirculatory level, the particulate nature of the blood becomes significant. The rheological properties of RBCs are key factors of the blood flow characteristics in microvessels because of their large hematocrit (H_ct ≈ 45 %) in the whole blood. Blood viscosity has been extensively investigated, and it is generally believed that five factors, namely hematocrit, cell deformability, cell aggregation, plasma viscosity, and temperature, primarily determine the rheological behavior of blood (Baskurt and Meiselman 2003).

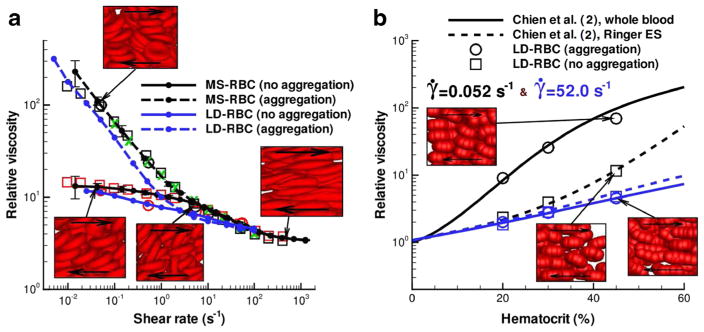
Dynamic simulation can predict the rheological and flow properties of blood flow. Two different RBC models, the MS-RBC model (Pivkin and Karniadakis 2008; Fedosov et al. 2010) and the LD-RBC model (Pan et al. 2010), have been developed and employed to predict rheological properties of blood flow. In particular, the LD-RBC model, which models one RBC as a closed torus-like ring of ten colloidal particles, allows the simulation of blood flow over a wide range of hematocrit levels at computational costs that are considerably below those for the MS-RBC model. Using these two cell models, Fedosov et al. accurately predicted the dependence of blood viscosity on shear rate and hematocrit (Fig. 8) (Fedosov et al. 2011c). The model prediction of blood viscosity was in agreement with experimental measurement (Merrill et al. 1963; Chien et al. 1966; Skalak et al. 1981). Their cell suspension model also captured the effect of aggregation on the viscosity at low shear rates and suggests that cells and molecules other than RBCs have little effect on the viscosity.

Fig. 8.

a Non-Newtonian relative viscosity of blood as a function of shear rate at Hct = 45 % from the MS-RBC model (black lines) and LD-RBC model (blue lines). b Relative viscosity of blood as a function of hematocrit at two different shear rates. Reproduced from Fedosov et al. (2011c), by permission

Under physiological conditions, blood is typically viscoplastic, i.e., it exhibits a yield stress that acts as a minimum threshold for flow to begin. The yield stress is usually calculated by extrapolation of available viscometric data to zero shear rate on the basis of Casson’s equation (Casson 1992):

$${\tau }_{xy}^{1/2}={\tau }_y^{1/2}+{\eta }^{1/2}{\stackrel{.}{\gamma }}^{1/2},$$ (5)

where τ_y is a yield stress and η is the suspension viscosity. In a recent study, Apostolidis and Beris simulated the rheology of blood in steady-state shear flows (Apostolidis and Beris 2014). They showed that the Casson model emerges naturally as the best non-Newtonian model for fitting available shear stress vs shear-rate literature data. In an extension study, they simulated blood flow rheology in transient shear flows (Apostolidis et al. 2015). They found that the modified version of the “Delaware model” (Mujumdar et al. 2002) is capable of predicting the time-dependent shear flow rheology of blood at low and moderate values of shear rate. Fedosov et al. computed shear stress for RBC suspension and extrapolated it to zero shear rate using a polynomial fit in Casson coordinates (Fedosov et al. 2011c). Their simulation results support the hypothesis that whole blood has a non-zero yield stress due to cell aggregation.

Blood rheology in malaria

Malaria-infected RBCs show progressing alteration of their mechanical and adhesive properties as the parasite develops. These changes greatly affect rheological properties of malaria-infected RBCs and lead to obstructions of small capillaries. Numerical simulations have been performed to simulate infected RBCs in malaria (Fedosov et al. 2011b; Peng et al. 2013; Li et al. 2014b). The rheological properties of RBCs in malaria have been studied and compared with those obtained by optical magnetic twisting cytometry (Puig-de-Morales-Marinkovic et al. 2007) and by monitoring membrane fluctuations at room, physiological, and febrile temperatures (Park et al. 2008, 2010). The simulation results matched well with the membrane fluctuations of malaria-infected RBCs, and suggest that the interactions between the lipid bilayer and the cytoskeleton of RBCs play key roles in determination of cell membrane mechanical and rheological properties.

Progression through the stages lead to considerable increase in flow resistance of blood in malaria as found in recent experiments (Dondorp et al. 2004). The DPD computational RBC models have also been employed to predict the bulk viscosity and adhesive dynamics of malaria-infected RBCs (Fedosov et al. 2011a). The simulations quantitatively predicted the increase of blood flow resistance in malaria (see Fig. 9) and demonstrated that adherence of malaria-infected RBCs to the vascular endothelium contribute to the blood flow resistance as well.

Fig. 9.

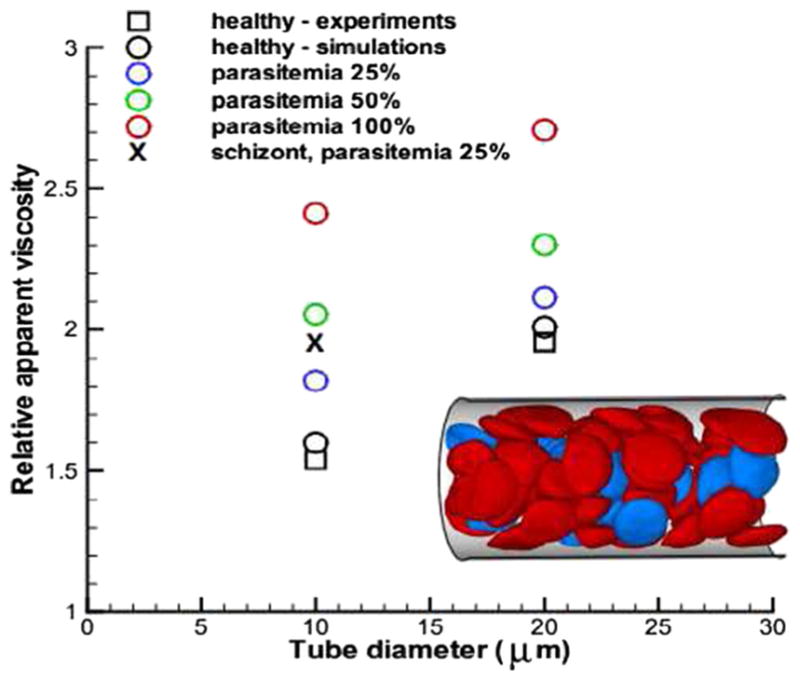
Flow resistance of blood in malaria for various parasitemia levels and tube diameters. Symbol “X” corresponds to the schizont stage with a near-spherical shape. Inset shows a snapshot of healthy (red) and malaria-infected RBCs (blue) in Poiseuille flow in a tube of diameter D = 20 μm. Reproduced from Fedosov et al. (2011a), by permission

Blood rheology in SCA

In SCA, mechanically fragile and poorly deformable RBCs contribute to impaired blood flow and other pathophysiological aspects of the disease. When the flow of blood is relatively slow, cellular reactions that lead to adhesion of sickle RBCs to vascular endothelium, resulting in vaso-occlusion and consequent clinical manifestations such as organ damage, pain, and even death. Computational methods have been used to evaluate rheological properties, to help multi-factorial nature and pathogenesis of vaso-occlusion.

The sickle RBCs has decreased cell deformability and increased cell rigidity, causing abnormal rheology in sickle blood and eventually various complications of SCA. It is known that the deformability of individual sickle RBCs is decreased under fully oxygenation state and deteriorates further under deoxygenation. Previous studies have shown that the viscosity of sickle RBCs or sickle blood are above normal under oxygenation and become further elevated with reductions in oxygen tension (Kaul and Xue 1991). To verify the significant role of cell deformability in determining the rheological property of sickle RBCs, numerical simulations have been performed at different shear modulus values and at different oxygen tensions (Lei and Karniadakis 2012). The blood flow showed that an increase in shear modulus leads to greater viscosity of sickle RBCs and the flow resistance further increase at deoxygenated state.

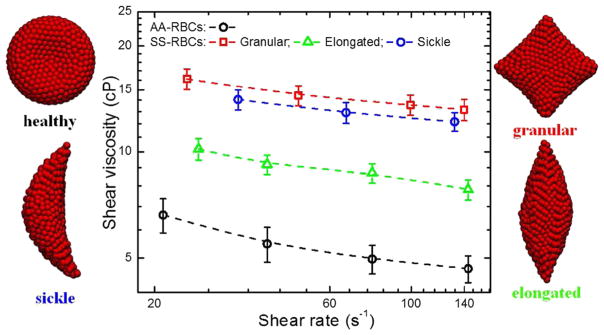
Sickle RBC suspensions exhibit different levels of viscosity for different cell morphologies, which are dependent on the rate of deoxygenation (Kaul and Xue 1991). Gradual deoxygenation is known to result in predominantly elongated- and classic sickle-shaped RBCs, which are intrinsically more rigid and viscous. The increase in viscosity is much greater when deoxygenation is rapid (resulting in less distorted but highly viscous granular-shaped RBCs) than when it is gradual. The MS-RBC model has also been employed to simulate the rheological properties of sickle RBC suspensions. The simulation results confirmed that the sickle RBC suspensions exhibit different viscosity values for different cell shapes: the granular RBC suspension is the most viscous, while the shear viscosity of sickle RBC suspensions containing elongated RBCs shows a dramatic decrease (Fig. 10).

Fig. 10.

Shear viscosity of sickle RBC suspensions with different cell morphology at different shear rate (unpublished work)

Computational models have also been employed to quantify the adhesive and dynamic properties of sickle RBC suspensions in tube flows (Lei and Karniadakis 2012, 2013). Available evidence indicates that adhesive interactions between the sickle RBCs and vascular endothelium play a key role in triggering vaso-occlusion in straight vessels.

Summary and outlook

Computational simulations are playing an increasingly important role in enhancing our understanding of the dynamics and rheology of soft biological cell suspensions and various local processes in blood (e.g., thrombosis, malaria, SCA). In this article, an overview on the current progress in modeling of suspensions of synthetic and biological particles such as vesicles, capsules, and RBCs was given.

Blood flow in microcirculation normally falls in the Stokes regime where the inertia is negligible, hence making boundary integral methods (BIM) a very good candidate to address suspension flows of soft particles. However, the first numerical studies on the dynamics of capsules using boundary element method (with second-order or cubic polynomial basis functions) in linear shear flow suffered the numerical instability at high deformation due to mesh degradation (Ramanujan and Pozrikidis 1998; Lac et al. 2004). Consequently, BIM formulations with higher order representations of the membrane using spherical harmonics were presented that could achieve spectral accuracy (Zhao et al. 2010; Veerapaneni et al. 2011a). More recently, a loop subdivision method was developed in the context of BIM to present smooth and C¹ continuous vesicle shapes with very high deformations (Spann et al. 2014).

Among other continuum solvers, the immersed boundary method (IBM) has become very effective in addressing FSI problems (Peskin 2002; Fai et al. 2013). In this method, a force density is distributed to the Cartesian mesh in the vicinity of the moving boundary (front) in order to account for its effect. The main advantage of IBM is that the front is advected in a fixed Eulerian grid which is not needed to be conformal. There are several numerical extensions of IBM depending on the choice of the structural or fluid formulations. For example, the immersed-boundary/front-tracking method in (Doddi and Bagchi 2009; Yazdani and Bagchi 2011) used a finite element triangulation of the cell’s membrane, while the full Navier-Stokes equation was solved using a projection splitting scheme. In addition, Lattice-Boltzmann method as the fluid solver has been used in several studies (Sui et al. 2008; Clausen et al. 2011). One problem with the IBM is the smoothing of the force density transferred to the fluid which renders the surface diffusive rather being sharp. More recently, fictitious domain methods (FDM) for solving coupled fluid-structure systems has been used (Shi et al. 2014; Hao et al. 2015). In the FDM, the fluid and solid domains are coupled by introducing a Lagrange multiplier over the solid domain. This multiplier acts as a penalty term that imposes the kinematic constraint in the solid domain. It has to be mentioned that modeling fluid-structure interaction at the microscopic level with continuum solvers requires consistent inclusion of thermal fluctuations; to address this issue, a stochastic formulation for IBM has been given (Atzberger et al. 2007).

Particle-based methods (Noguchi and Gompper 2005b; McWhirter et al. 2009; Fedosov et al. 2010), where mesoscopic particle-collision models are employed, provide opportunities to significantly reduce computational expense on a per-cell basis. Being constructed from a CGMD approach, they can naturally include thermal fluctuations. Such formulations are compatible with coarse-grained descriptions of the membrane mechanics (Fedosov et al. 2010) with the advantage of including the membrane viscosity with no additional cost. However, some issues remain open for the particle-based methods. For example, the narrow regions between closely packed cells and consequently the lubrication effect will not be captured accurately unless the particle density is increased significantly. Imposing the no-slip condition on the cell surface is also a challenge. In a more recent study, an alternative Lagrangian formulation for the hydrodynamics and coarse-grained cell membrane based on smoothed dissipative particle dynamics (SDPD) has been presented (Fedosov et al. 2014a).

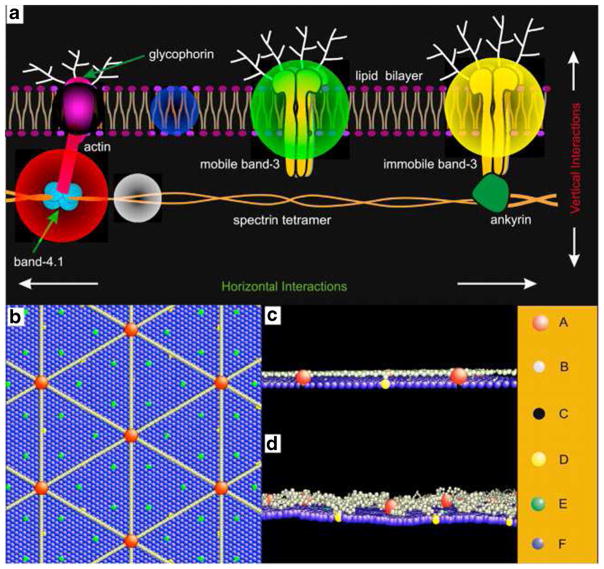
The current computational models of soft biological particles offer unique tools for the qualification and quantification of dynamics and rheological properties of healthy and pathological RBCs under select experimental conditions. However, they do not lend themselves to detailed whole-cell investigations of a wide variety of biophysical problems involving the RBCs, such as the bilayer loss in hereditary spherocytosis due to defective protein attachments and uncoupling between the lipid bilayer and cytoskeleton in sickle cell anemia due to sickle hemoglobin polymerization (Liu et al. 1991). For these reasons, there is a compelling need to develop a more realistic RBC representation, e.g., to endow the spectrin-based RBC models with more accurate structure, e.g., account separately for the lipid bilayer and cytoskeleton but also include explicitly the transmembrane proteins. Recent efforts have been directed towards this approach. For example, Li and Lykotrafitis introduced a two-component RBC membrane model, where the lipid bilayer and cytoskeleton as well as the transmembrane proteins are explicitly represented by coarse-grained particles (Fig. 11) (Li and Lykotrafitis 2012b, 2014a). This detailed membrane model has been successfully applied to study some membrane-related problems in RBCs such as the dynamic behavior of RBC membrane under shear and the diffusion of transmembrane proteins. However, at present, it is computationally inefficient to be used for blood dynamics and rheological studies involving large numbers of RBCs in flow. Recently, a two-component continuum-based whole cell model (Peng et al. 2010) and a two-component particle-based whole cell model (Peng et al. 2013), which treat the lipid bilayer and the cytoskeleton as two distinct components, have been developed. These whole cell models have been used in simulations of blood flow and quantified the existence of bilayer-cytoskeletal slip for RBCs in pathological state. However, they are not yet capable of modeling the interactions between the spectrin filaments and trans-membrane proteins such as the band-3. Thus, a challenge in computational modeling of blood flow which encompass all scales would be to develop hybrid model that integrates both approaches. Such a model would provide a more reliable method and an overall modeling framework to extract dynamic and rheological properties of RBCs.

Fig. 11.

a Schematic of the human RBC membrane. b–d A mesoscale detailed membrane model. b, c show the initial configuration of the cell membrane from the top view (b) and side view (c), and (b) shows the equilibrium configuration of the cell membrane from the side view. The blue sphere represents a lipid particle and the red sphere signifies an actin junctional complex. The gray sphere represents a spectrin particle and the black sphere represents a glycophorin particle. The yellow and green circles correspond to a band-3 complex connected to the spectrin network and a mobile band-3 complex, respectively. Reproduced from Li and Lykotrafitis (2014a), by permission

To sum up, continuum and particle-based methods have proved themselves to become more efficient and mature in dealing with complicated problems of soft particle suspensions. Initially, they were used extensively to study the intricate underlying physics of dilute suspensions, and recently have become ideal tools to study the rheological behavior of dense suspensions in health and disease (e.g., malaria and SCA). The range of applicability of these methods is quite diverse, and they can be used in addressing other types of biological problems involving microscopic deformable cells in moving or quiescent fluid. These problems include but not limited to cell motility and adhesion of other types of eukaryotic cells such as bacteria, dynamics of cancer cells in microvascular networks, whole blood simulations in complex geometries such as aneurysms and stenoses, mechanobiology of cells, and complex multiscale biological processes such as thrombus formation at the injury site.