Myeloma cell dynamics in response to treatment supports a model of hierarchical differentiation and clonal evolution

Abstract

Purpose

Since the pioneering work of Salmon and Durie, quantitative measures of tumor burden in multiple myeloma (MM) have been used to make clinical predictions and model tumor growth. However, such quantitative analyses have not yet been performed on large data sets from trials using modern chemotherapy regimens.

Experimental design

We analyzed a large set of tumor response data from three randomized controlled trials of bortezomib-based chemotherapy regimens (total sample size n=1,469 patients) to establish and validate a novel mathematical model of MM cell dynamics.

Results

Treatment dynamics in newly diagnosed patients were most consistent with a model postulating two tumor cell subpopulations, “progenitor cells” and “differentiated cells”. Differential treatment responses were observed with significant tumoricidal effects on differentiated cells and less clear effects on progenitor cells. We validated this model using a second trial of newly diagnosed patients and a third trial of refractory patients. When applying our model to data of relapsed patients, we found that a hybrid model incorporating both a differentiation hierarchy and clonal evolution best explains the response patterns.

Conclusions

The clinical data, together with mathematical modeling, suggest that bortezomib-based therapy exerts a selection pressure on myeloma cells that can shape the disease phenotype, thereby generating further inter-patient variability. This model may be a useful tool for improving our understanding of disease biology and the response to chemotherapy regimens.

INTRODUCTION

Multiple myeloma (MM) was the first metastatic malignancy for which quantitative measurements of tumor burden became available, allowing for mathematical and statistical approaches to studying this disease (ref. ^1-4). Unlike other cancers for which serial measurements of tumor size are a challenging problem, it was shown in MM that serum levels of myeloma protein (M-protein) is strongly correlated with tumor burden, which allowed for study of the kinetics of this disease (ref. ³). Sullivan and Salmon proposed a mathematical model where tumor growth rate is dependent on the total cell mass (ref. ⁴), and Hokanson et al. compared this model with a constant growth rate model, using two cell populations with differing drug sensitivities, to describe the dynamics of treatment response in MM patients (ref. ¹). Furthermore, Swan and Vincent suggested an optimal dosing strategy based on these models, demonstrating the potential for clinical application of these techniques (ref. ⁵). However, such quantitative analyses have not yet been performed on large data sets from trials using modern chemotherapy regimens.

Therapy with melphalan and prednisone has been the standard of care for elderly patients with newly diagnosed multiple myeloma (MM) for more than 40 years (ref. ^{6, 7}). In 2008, the proteasome inhibitor bortezomib (VELCADE^R) was approved in combination with melphalan and prednisone for treatment of newly diagnosed MM patients not eligible for high-dose chemotherapy, based on the results of the randomized phase III VISTA trial (ref. ⁸) comparing bortezomib-melphalan-prednisone to melphalan-prednisone treatment. Earlier, bortezomib was approved for treatment of relapsed multiple myeloma based on the results of the randomized phase III APEX trial (ref. ^{9, 10}) comparing bortezomib monotherapy to dexamethasone treatment. Although in both phase III studies, bortezomib had been able to induce complete tumor responses and significantly prolong survival (ref. ^10-12), myeloma relapses eventually occurred and the patients could not be considered cured. Recently the randomized phase II MMY-2001 trial investigating the safety and efficacy of the addition of siltuximab to the bortezomib-melphalan-prednisone regimen showed no survival difference associated with the siltuximab addition (ref. ¹³). The dynamics of treatment response in these trials have not previously been studied but such efforts would lead to a better understanding of disease mechanisms, which would in turn help inform treatment strategies. Furthermore, the existence of a differentiation hierarchy of MM cells has been suggested (ref. ¹⁴), but the effects of chemotherapies on different subpopulations in vivo remain largely unexplored. Here we analyzed the treatment response of MM patients and sought to identify a mechanistic model capable of explaining the trial response data in both newly diagnosed (ref. ^{11, 13}) and relapsed MM patients (ref. ^8-10).

METHODS

To develop a model for MM tumor cell dynamics, we utilized data from 682 newly diagnosed MM patients who were treated with first-line melphalan and prednisone with bortezomib (the “VISTA VMP” cohort) or without (the “VISTA MP” cohort) within the randomized phase III VISTA trial (ref. ¹¹) (see SI, “Patient cohorts”). Serum M-protein measurements (g/dl) were analyzed uniformly by a central laboratory and were determined as surrogates for disease burden (ref. ¹⁵). By VISTA trial design, patients were to be treated in both cohorts for a maximum duration of 54 weeks, unless treatment was discontinued earlier due to toxicity or myeloma progression. Of the 682 randomized patients, 299 patients in the VISTA MP cohort and 300 patients in the VISTA VMP cohort were evaluated for their disease kinetics (Figure 1a, SI, “Patient selection” for exclusion criteria). To investigate the treatment effects of melphalan, prednisone, and bortezomib, we first utilized a statistical modeling approach to identify trends within the treatment response data (SI, “Statistical modeling”). We then aimed to design simple mathematical models, developed in a biologically intuitive way, to investigate the treatment dynamics of the disease; similar approaches have previously led to a mechanistic understanding of infectious diseases (ref. ¹⁶). Finally, we validated our model using M-protein data from two independent trials, the MMY-2001 and APEX trials, which include both newly diagnosed (ref. ^{11, 13}) and relapsed MM patients (ref. ^8-10). The SI contains details on all patient cohorts, analyses, and models.

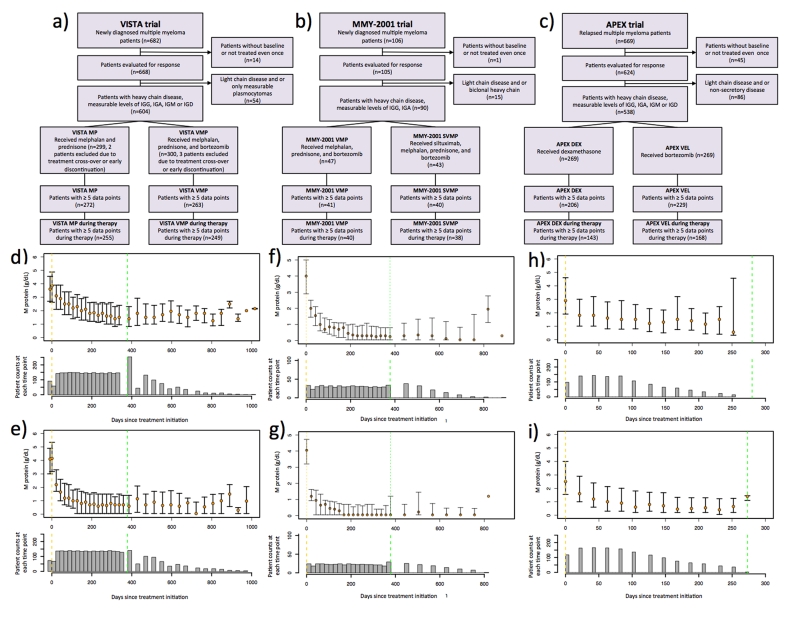
Figure 1. Patient selection criteria and M-protein treatment response in the VISTA and APEX trials.

(a-c) Flowcharts outlining the patient inclusion and exclusion criteria for quantitative analysis of M-protein treatment response. (d-i) Median longitudinal M-protein trajectories for each cohort in the three trials, and the associated numbers of patients at each time point: d): VISTA MP cohort, e): VISTA VMP cohort, f): MMY2001 VMP cohort, g): MMY2001 SVMP cohort, h): APEX DEX cohort and i): APEX VEL cohort. The median M-protein values are indicated by the orange circles, and quartiles are indicated by the whiskers. The numbers of patients at each time point are shown by the histograms. Vertical yellow and green dashed lines indicate treatment initiation and termination times, respectively. For the VISTA and MMY-2001 trials (panels d-g), only patients who completed the entire treatment regimen are included. For the APEX trial (panel h-i), due to the small number of patients who completed the entire treatment regimen, only the M-protein response during treatment is shown.

RESULTS

We analyzed the observed tumor burden trajectories from the three trials in the following order: 1) we applied statistical modeling to determine the trends in longitudinal tumor trajectories from newly diagnosed MM patients in the VISTA trial, 2) we built two biologically sound mathematical models in an attempt to recapitulate the observed trends, 3) we compared our models’ predictions against observed results, and 4) we validated our model with external data from the independent MMY-2001 and APEX trials and expanded our model to explain trends in refractory patients.

Statistical modeling of VISTA trial data

Prior to biology-based mathematical modeling, we first investigated different statistical approaches to identify the shape of the treatment response data, i.e. the statistical model with the best fit to the M-protein data (Figure 1d-e, SI, “Statistical modeling”, Figure S1). We began with the data from the VISTA trial, which demonstrated a clear survival advantage for bortezomib, melphalan, and prednisone (VMP) versus melphalan and prednisone alone (MP) in newly diagnosed elderly patients (ref. ¹¹). When studying the cohort-level patient dynamics of treatment response in both the VISTA MP and VMP cohorts, we identified a 2-phasic exponential model (i.e. a curve with a bend, or turning point, Figure S1) to be the best-fitting statistical model among 1-phasic exponential and 2-phasic exponential models for both cohorts (SI, “Treatment phase model fitting”, Table 1). The summary statistics for the first slopes (β₁), second slopes (β₂) and turning points (τ) when fitting 2-phasic exponential models to all patients in each cohort are shown in Table 2. First, we found that patients in the VISTA VMP cohort had a significantly steeper first slope on average than patients in the VISTA MP cohort (p = 3×10⁻¹⁵ Wilcoxon rank-sum test), corresponding to a faster initial response rate in the VMP cohort. Second, the difference between the cohorts’ second slopes was not statistically significant (p=0.2439 Wilcoxon rank-sum test), and both cohorts were not significantly different from zero (MP p=0.2645 and VMP p=0.08 t-statistics). Third, the difference between the cohorts’ turning points was also not statistically significant (p=0.3852 Wilcoxon rank-sum test).

Table 1. Summary statistics of the treatment response data analysis.

The table displays statistics on the individual patient model fitting as well as whole cohort model fitting for the cohorts for the three trials during treatment. See SI, “Treatment phase model fitting”, for details.

	VISTA MP cohort during treatment (255 patients)		VISTA VMP cohort during treatment (249 patients)
	2-phasic exponential model	Exponential model	2-phasic exponential model	Exponential model
Min* of $R_i^2$	0.089	0	0.174	0.002
1st Quartile* of $R_i^2$	0.678	0.327	0.874	0.374
Median* of $R_i^2$	0.865	0.629	0.929	0.645
Mean* of $R_i^2$	0.787	0.572	0.889	0.577
3rd Quartile* of $R_i^2$	0.938	0.847	0.962	0.813
Max* of $R_i^2$	0.999	0.980	1	0.955
**Final R2	0.902	0.706	0.910	0.642
***Sum of BICs	−1096.8	−978.9	−773.1	−480.5

	MMY-2001 VMP cohort during treatment (40 patients)		MMY-2001 SVMP cohort during treatment (38 patients)
	2-phasic exponential model	Exponential model	2-phasic exponential model	Exponential model
Min* of $R_i^2$	0.684	0.007	0.187	0.003
1st Quartile* of $R_i^2$	0.872	0.444	0.876	0.250
Median* of $R_i^2$	0.926	0.630	0.948	0.399
Mean* of $R_i^2$	0.912	0.573	0.883	0.473
3rd Quartile* of $R_i^2$	0.968	0.731	0.968	0.773
Max* of $R_i^2$	0.999	0.938	1	0.950
**Final R2	0.929	0.640	0.934	0.471
***Sum of BICs	−313.9	−241.5	−309.5	−214.8

	APEX DEX cohort during treatment (143 patients)		APEX VEL cohort during treatment (168 patients)
	2-phasic exponential model	Exponential model	2-phasic exponential model	Exponential model
Min* of $R_i^2$	0.054	0.000	0.228	0.000
1st Quartile* of $R_i^2$	0.716	0.105	0.828	0.195
Median* of $R_i^2$	0.846	0.370	0.937	0.529
Mean* of $R_i^2$	0.799	0.404	0.873	0.498
3rd Quartile* of $R_i^2$	0.944	0.684	0.983	0.777
Max* of $R_i^2$	1.000	0.964	1.000	0.996
**Final R2	0.830	0.496	0.898	0.580
***Sum of BICs	−1402.5	−1201.4	−1729.7	−1376.1

^*the Minimum/1^st Quartile/Median/Mean/3^rd Quartile/Maximum of the $R_i^2$, i = 1, …, N, calculated from the corresponding fitted model for each individual patient, where N is the total number of patients and $R_i^2$ = 1 - SSE_i / SST_i;

^**Final R², calculated as 1 - Σ SSE_i / Σ SST_i, evaluates the overall fit of the corresponding model to the whole time series data with all patients for each cohort;

^***Sum of BICs is the sum of BICs over all subjects for each cohort.

Table 2. Summary statistics of slopes and turning points in the treatment response data.

The table displays the means of the first (β₁) and second (β₂) slopes as well as the turning points (τ) obtained from fitting a bi-phasic model to each cohort.

Cohort (# patients)	First slope, β1 (standard deviation)	Second slope, β2 (standard deviation)	Turning point, τ (standard deviation)
VISTA MP (255)	−0.0067 (0.0094)	−0.0011 (0.0162)	116.20 (87.02)
VISTA VMP (249)	−0.0237 (0.0217)	−0.0016 (0.0145)	106.20 (77.59)
MMY-2001 VMP (40)	−0.0192(0.0153)	0.0004(0.0191)	151.55(80.05)
MMY-2001 SVMP (38)	−0.0530(0.0562)	0.0014(0.0068)	106.61(75.89)
APEX DEX (143)	−0.0169 (0.0151)	0.0037 (0.0175)	67.1 (44.75)
APEX VEL (168)	−0.0285 (0.0243)	0.0034 (0.0132)	70.1 (40.06)

We then performed individual patient analyses to ensure that the observed patterns at the cohort level are representative of sufficiently many individual patients such that we are not focusing only on a small subset of patients. Comparing between patients who displayed 1- versus 2-phasic exponential declines, we found that there was a significantly larger proportion of 2-phasic patients in the VISTA VMP cohort as compared to the VISTA MP cohort (p ≤ 10⁻¹⁶, Fisher’s exact test). Furthermore, 2-phasic patients in the VISTA VMP cohort had a significantly steeper first slope than such patients in the VISTA MP cohort (p = 3×10⁻¹⁵ for all patients with β₁ < 0, Wilcoxon rank-sum test), again indicating a faster initial response rate in the VMP cohort. The difference between cohorts in the second slope was not statistically significant. Finally, 2-phasic patients in the VISTA VMP cohort had a smaller turning point than patients in the VISTA MP cohort, indicating that the time at which the response rate changes was shorter in the VMP cohort than the MP cohort (p = 0.02 for all 2-phasic patients with β₁ < 0 and p = 0.01 for all 2-phasic patients with β₁ < 0 and β₂ < 0, Wilcoxon rank-sum test).

When investigating the relationship between the best-fitting model and MM stage (ISS stage) (ref. ¹⁷), we found that patients with advanced-stage disease in the VISTA MP cohort were significantly more likely to display a 2-phasic rather than a 1-phasic exponential trend after the initiation of therapy (Table S4). For the VISTA VMP cohort, however, there was no significant association between MM stage and the shape of the treatment response curve (Table S4). In both cohorts, there were more deaths of patients with positive second slopes compared to patients with negative second slopes (Table S5). Furthermore, for VISTA VMP patients displaying a 2-phasic M-protein depletion in the treatment phase, the first slope was significantly associated with the time to progression (p = 0.005, Cox model) when controlling for MM stage.

Mathematical modeling of VISTA trial data

The fact that many patients displayed more complex response kinetics than a simple exponential decay of M-protein abundance over time suggests complex intra-patient disease dynamics. We therefore designed biologically sound mathematical models to explain the response dynamics. These models were created to relate the abundance of measurable M-protein to the numbers of different types of MM cells, which are not directly detectable in the clinical trial data, offering an explanation for the observed trial results from a theoretical biology perspective. To validate the model-predicted and observed outcomes, we compared their turning points and the proportion of 1- and 2-phasic patients.

We first postulated a model based on the existence of two genetically independent MM clones. In this “clonal evolution” model, tumor cells evolve independently and there is no differentiation hierarchy within the myeloma cell population (SI, “The clonal evolution model”). We found that there was a significant difference in the numbers of 1- and 2-phasic patients between the observed clinical data in the VISTA trial and the simulated data based on the clonal evolution model (observed 1-phasic patients/total number of patients: 55/249; in one simulation, 1-phasic patients/total number of patients: 113/249; p = 5×10⁻⁸, Fisher’s exact test). Furthermore, the estimated turning points for 2-phasic patients were significantly different between the observed clinical data in the VISTA trial and the simulated data based on the clonal evolution model, 90 ± 69, median 72 days in VISTA data; 186 ± 81, median 169 days in simulated data; p = 2×10⁻¹², two-sample t-test (SI, “The clonal evolution model”). Thus, a clonal evolution model, which considers two genetically different MM clones, was unable to recapitulate the tumor dynamics observed from the VISTA trial data.

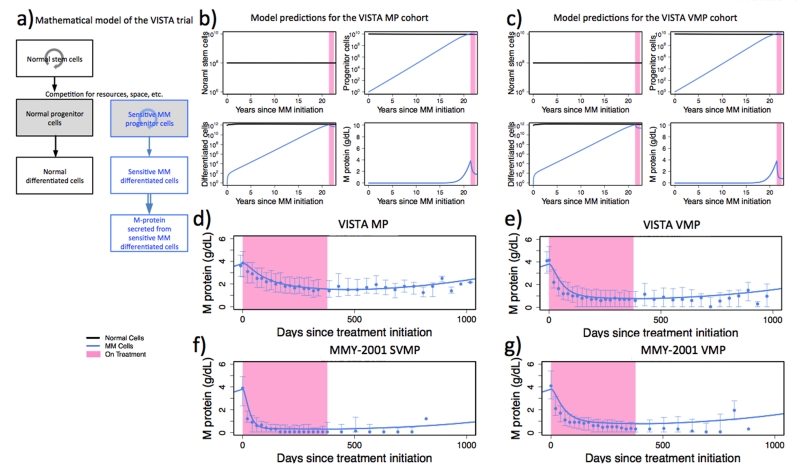
We then designed a second model which describes the differentiation hierarchy of the hematopoietic system; in this hierarchical model, we postulated that myeloma cells in part recapitulate normal differentiation and are composed of two populations: myeloma “progenitor” cells and “differentiated” cells (Figure 2a and SI, “The differentiation hierarchy model”). In the context of this model, normal stem cells reside on top of the hierarchy and give rise to progenitor cells, which in turn produce differentiated cells. In addition to normal cells, the bone marrow of MM patients also includes MM cells. MM progenitors reside on top of the MM hierarchy and give rise to MM differentiated cells, which in turn produce M-protein. MM progenitors produce none or only low amounts of M-protein, which we neglected in the mathematical model. We found good agreement between the VISTA trial data and predictions of the mathematical model (Figure 2d-e and SI, “The differentiation hierarchy model”).

Figure 2. The hierarchical mathematical model accurately predicts the dynamics of M-protein response in the VISTA and MMY-2001 trials.

(a) Illustration of the hierarchical mathematical model. Normal and MM cells are shown in black and blue, respectively. Solid downward arrows indicate the direction in the differentiation hierarchy. Circular arrows indicate cellular regeneration within each differentiation level. Double-lined arrow indicates M-protein production from differentiated MM cells. (b-c) The panels display the model-predicted abundances of normal (black) stem cells, normal (black) and MM (blue) progenitor cells, and normal (black) and MM (blue) differentiated cells over time (years) for the VISTA MP (panel b) and VISTA VMP (panel c) cohorts since the emergence of the first MM cell, as predicted by the mathematical framework (see SI, “The differentiation hierarchy model”). The pink shaded region denotes the time during which patients receive treatment. (d-g) Concordance between observed population-level MM protein trajectories (blue intervals, error bars indicating the observed quartiles) and the MM protein levels predicted by the mathematical model (solid blue lines). The parameter values for the first and second slopes used to generate panels d, e, and f are listed in Table 2. For panel g, the model predicted trajectory is generated using the same first and second slopes as panel e. All ancillary parameters for panels d-g are identical and are listed in SI, “Parameter values for the hierarchical and hybrid models.”

After treatment initiation, the MM cell population declines at the death rate of differentiated MM cells during therapy (equal to the first slope identified in the data, mean −0.0067 for the VISTA MP cohort and −0.0237 for the VISTA VMP cohort) until the latter reach a steady state with MM progenitor cells; from this time onwards, the kinetics display a shallower decrease signifying the depletion of progenitor cells during treatment (equal to the second slope identified in the data, mean −0.0011 for the VISTA MP cohort and −0.0016 for the VISTA VMP cohort). After treatment discontinuation, some patients show a lasting suppression of their M-protein values, while others experience a disease rebound (Figure S7). In the context of the hierarchical model, these patterns are generated by a selective effect of treatment on different MM clones: treatment may select for MM phenotypes with altered growth and differentiation kinetics as compared to the predominant clone present at the time of diagnosis. In patients in whom no rebound occurs by the end of follow-up, the MM clones that remain after treatment are less “fit” (either via a decreased growth rate or an increased death rate) than those present before treatment. Thus, their expansion occurs on a slower time scale, such that the M-protein value slowly increases after treatment cessation but remains below the detection limit. In patients in whom a rebound occurs, resistant cells slowly outcompete sensitive cells and lead to positive M-protein values after variable periods of time, depending on the size of the resistant clone and their growth rate.

Validation of the hierarchical model using additional trial data

We then utilized data from two independent clinical trials to test the hierarchical model’s ability to explain patient responses: the MMY-2001 trial (ref. ¹³) comparing bortezomib-melphalan-prednisone (VMP) vs. siltuximab plus VMP (SVMP) in newly diagnosed MM patients (n=106, Figure 1b); and the APEX trial comparing high-dose dexamethasone (DEX) vs. single agent bortezomib (VEL) in refractory patients (n=669, Figure 1c).

For these two validation data sets, we first performed the same statistical analysis as before to estimate the shapes of the treatment response curves (Figure 1f-i). For both the MMY-2001 and APEX trials, we found that the cohort-level M-protein dynamics during treatment were best explained by the 2-phasic exponential model (Table 1); summary statistics are shown in Table 2. Gratifyingly, we found the first slopes of patients in the VISTA VMP and MMY-2001 VMP cohorts were not significantly different (p=0.2082, t test). For the MMY-2001 trial, we found that there was a statistically significant difference between VMP and SVMP cohorts in terms of the first slopes (p=0.0005, t test). Interestingly, although the addition of siltuximab significantly increased the initial reduction of M-protein levels, it failed to improve progression-free of overall survival (ref. ¹³). In terms of the second slopes, there was no significant difference between MMY-2001 VMP and SVMP cohorts (p=0.7586, t test), and both cohorts were not significantly different from zero (VMP p= 0.8953 and SVMP p=0.2123, t test). For the APEX trial, we found that patients in the VEL cohort had a significantly steeper first slope than patients in the DEX cohort (p = 0.0035 t test). Also, the difference between cohorts in terms of the second slope was not statistically significant (p=0.8635 t test). However, unlike the VISTA and MMY-2001 trials, in the APEX trial the second slopes were significantly positive (DEX p=0.01231 and VMP p=0.001 t-statistics). These increases are consistent with disease progression and likely signify the development of drug-resistant MM cells. In all three trials, patients displayed significant reductions in M-protein levels immediately upon receiving bortezomib-based treatment; however, the long-term effects of these medications varied.

We then aimed to validate the hierarchical model using data from the MMY-2001 and the APEX trials. We found that, for the MMY-2001 trial consisting of newly diagnosed patients, the hierarchical model was able to recapitulate the population-level M-protein trajectories; the MMY-2001 VMP cohort could be recapitulated using the same parameters as for the VISTA VMP cohort (Figure 2g). The correlations between observed mean, median and model predicted values were 0.82 and 0.78, respectively. The SVMP cohort could be recapitulated using slope estimates obtained from the SVMP patient data and keeping all other parameters unchanged (Figure 2f and Table 2).

For the APEX trial, we observed increasing trends in M-protein values already during the treatment phase in many patients; this was not unexpected as the time to myeloma progression is shorter in relapsed MM than in newly diagnosed MM, and therefore for many patients in the APEX trial, this time fell within the trial-specified treatment duration. First, among patients displaying 1-phasic patterns, more patients in the APEX trial had statistically significant positive slopes (β₁>0 and p<0.05; APEX DEX: 4/94 and APEX VEL: 11/83) than in the VISTA trial (VISTA MP: 3/153 and VISTA VMP: 0/55). Second, for patients displaying 2-phasic patterns in the APEX trial, we observed rebounds (β₂>0) in the M-protein values during treatment (Table 2 and Figure S9). Initially, 2-phasic patients in both trials had similar responses to treatment, as shown by the decline in M-protein values immediately after treatment initiation and the similarity in the magnitudes of β₁. However, the long-term treatment response differed between the APEX and VISTA patients. We observed that, among patients who displayed 2-phasic trends, relapsed patients in the APEX trial were more likely to have statistically significant rebounds (β₂ >0 and p<0.05; APEX DEX: 22/49 and APEX VEL: 31/85) than the newly diagnosed patients in the VISTA trial (VISTA MP: 19/102 and VISTA VMP: 27/194). In addition, most rebounding patients in the APEX trial had M-protein rebounds within 100 days after the start of treatment, while still on treatment (median: 74.21 days; mean: 83.20; sd: 41.88 for the rebounding patients in the APEX DEX cohort and median: 68.02 days; mean: 69.14; sd: 27.80 for the rebounding patients in the APEX VEL cohort).

Development of a hybrid mathematical model for MM cell dynamics

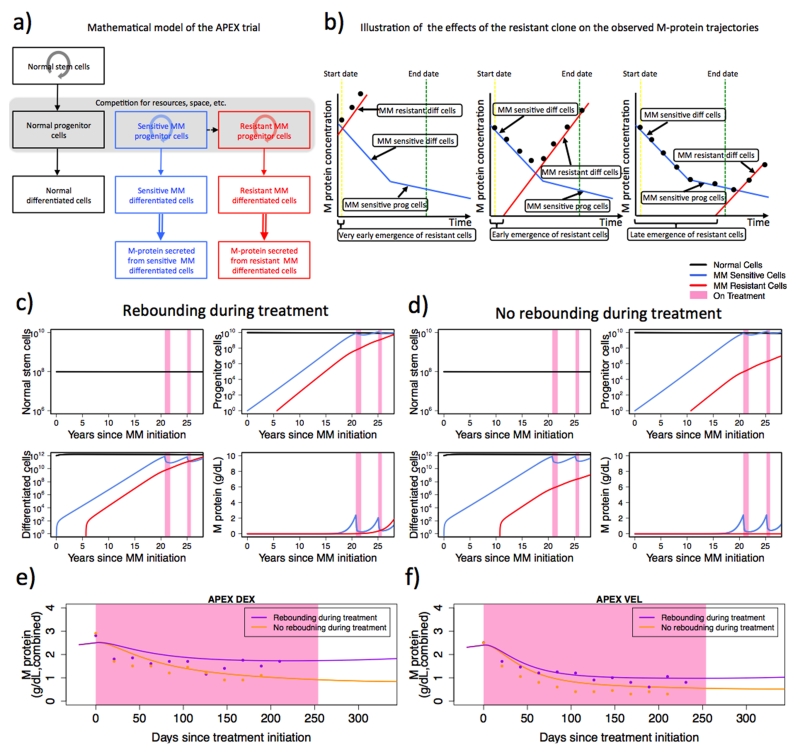
Based on these observations, we attributed the differences in M-protein dynamics between newly diagnosed and relapsed patients to the existence and expansion of a resistant clone in relapsed patients (Figure 3a). A dominant resistant clone existing prior to treatment explains the increasing M-protein values during treatment among 1-phasic patients in the APEX trial; an expanding resistant clone during treatment explains the initial declines followed by increases in M-protein values; and the presence of a small resistant clone explains continuing 2-phasic declines in the remaining patients (Figure 3b-d). Therefore, we extended our mathematical model to take into account resistant clone(s) (Figure 3a, SI, “The hybrid model”). In this extended model, in addition to normal cells and sensitive MM cells, there is a resistant clone that originally arose from the sensitive progenitor MM cells. This resistant clone gives rise to a similar differentiation hierarchy as the sensitive cells. The observed M-protein values are the sum of M-protein values generated from the sensitive and resistant clones; the amount of M-protein secreted by each clone is proportional to the size of the clone and the relative secretion rates, which are considered to be similar. The time at which resistance arises determines the relative proportion of sensitive and resistant cells. In newly diagnosed patients, the M-protein contribution from the resistant cells during treatment is negligible; this is supported by the observation that only a relatively small number of patients (7 and 21% in VISTA VMP and MP cohorts, respectively) experienced increases in M-protein values while on treatment in the VISTA trial. In contrast, in the relapsed patients from the APEX trial, due to prior treatment-induced clonal selection, the M-protein contribution from the resistant clone is sufficiently large and stable in size (between 1% and 10%) to alter the treatment response trajectory, leading to rebounds in a subset of patients while on treatment in the APEX trial (SI, “Rebound dynamics”). Unlike the clonal expansion model, the resistant cells do not need to be substantial in size at the beginning of the first treatment to drive the rebound trajectory; rather, through multiple rounds of treatment-induced selection, the fraction of resistant cells may increase sufficiently much to alter the response trajectory. This hybrid model was able to explain the M-protein dynamics for both newly diagnosed and relapsed myeloma patients in response to chemotherapy (Figure 2d-e and Figure 3e-f). Our model suggests that treatment-induced clonal selection may contribute to the increases of the M-protein levels in the refractory patients while on treatment.

Figure 3. The hybrid mathematical model accurately predicts the dynamics of M-protein response in all three trials.

(a) Illustration of the hybrid mathematical model. Normal, sensitive, and resistant MM cells are shown in black, blue, and red, respectively. The dashed arrow indicates the mutation event that gives rise to the first resistant cell. Solid downward arrows indicate the direction in the differentiation hierarchy. Circular arrows indicate cell regeneration within each differentiation level. Double-lined arrow indicates the production of M-protein from differentiated MM cells. (b) Illustration of effects of the time at which resistance arises on the observed M-protein trajectories. Left: resistance emerges very early; middle: resistance emerges early; right: resistance emerges late. The blue lines denote the contribution to the changes in the observed M-protein values of sensitive MM cells; the red lines denote the contribution to the changes in the observed M-protein values of resistant MM cells; and the black dots represent the observed total M-protein levels from both sensitive and resistant MM cells. Although the sensitive cells’ response to treatment remains identical in all three subpanels, the timing at which resistance arises determines the observed M-protein response. Similar to the VISTA trial, the initial steep decline in M-protein (middle and right subpanels) is attributed to the reduction in the sensitive differentiated MM cells; the shallow decline in M-protein is interpreted as the result of the reduction in the number of sensitive MM progenitor cells. Vertical dashed lines in yellow and green indicate treatment start and end dates. (c-d) The panels display the model-predicted abundances of normal (black) stem cells; normal (black), sensitive MM (blue), and resistant MM (red) progenitor cells; and normal (black), sensitive MM (blue), and resistant MM (red) differentiated cells over time (years) for early (c) vs. late (d) emergence of resistance for the APEX DEX cohort, as predicted by the mathematical framework (see SI, “The hybrid model”). Panels (c) and (d) have identical parameter values except for the time at which resistance arises (for the full set of parameter values, see SI, “Parameter values for the hierarchical and hybrid models”). The time at which resistance arises dictates whether a rebound occurs during the treatment phase. (e-f) M-protein treatment response dichotomized based on rebound status for APEX DEX and VEL cohorts. Rebound during treatment (purple): patients with at least one positive slope during the treatment phase; no rebound during treatment (orange): patients with all negative slope(s) during the treatment phase. Observed median M-protein values (≥10 observations) from each subgroup are shown in dots. Lines show model-predicted M-protein trajectories. Within each cohort, all parameter values are identical, except the time at which resistance arises (for the full set of parameter values, see SI, “Parameter values for the hierarchical and hybrid models,” and Supplementary Table S7).

DISCUSSION

Here, we present a comprehensive quantitative analysis of myeloma cell growth and treatment response based on three large randomized trials (total sample size n=1,469). Our analysis of responses to induction therapy in newly diagnosed patients in the VISTA trial revealed complex but structured kinetic patterns that support a hierarchical two-cell population mathematical model for MM. This model was able to recapitulate the observed two-phasic decline patterns observed in the majority of newly diagnosed patients. Importantly, an alternative clonal selection model of myeloma cell growth did not fit the trial data. The hierarchical model suggests the existence of a MM progenitor cell population that has self-renewal capacity and distinct growth kinetics and gives rise to the differentiated MM cell population. The observation of a significantly larger proportion of 2-phasic patients in the VISTA VMP cohort as compared to the VISTA MP cohort when performing the individual level analysis signifies the potential treatment effect of bortezomib in combination with melphalan and prednisone on increasing the death rate of MM progenitor cells during therapy. Our model of MM progenitors, which are non-secretory and relatively drug-resistant compared to differentiated cells, is supported by experimental evidence (ref. ^18-20).

We used the two additional independent sets of clinical trial data to validate and extend the hierarchical model. All trial data supported the model for disease response to treatment; however, inter-patient variability of disease kinetics was noted to be significant at the time of disease relapse, requiring the adjustment of growth parameters in the model and suggesting that distinct MM progenitor subclones were selected by induction treatment. The existence of clonal selection between myeloma subclones was also supported by the analysis of relapsed or refractory patients in the APEX trial. The varied trajectories of disease relapse observed necessitated the development of a hybrid model with preexisting drug-resistant myeloma cell clones. Importantly, mathematical modeling in myeloma has not been attempted previously on this scale. In addition, statistical analyses reveal different M-protein trajectories even among patients randomly assigned to the same treatment cohorts. Significant association between slopes in M-protein trajectories and survival outcomes have been observed. Hence, M-protein trajectories may have the potential to serve as a key second endpoint for the early detection of disease relapse.

Our approach evaluated myeloma cell behavior unbiased by prior assumptions, by analyzing available patient data without a priori defined patient subgroups. If quantitative data on the effect of patient-specific mutations on cell growth, for example, become available, the model might be further refined. Recent studies (ref. ^21-23) documented pronounced intra-patient genetic heterogeneity in human neoplasias and attributed disease progression and drug resistance to the differential molecular features of the underlying tumor subclones. However, it remains a formal possibility that the functional heterogeneity within a tumor as described by our model will not be genetically determined but rather controlled by microenvironmental or epigenetic factors. Elucidating the pathways that control functional heterogeneity among subclones is experimentally challenging, but mathematical modeling can address these limitations and provide insights into the effects of novel treatments on tumor cell dynamics and how they determine the behavior of human cancers.

A strength of our model is that it is based on in vivo patient data. Our model is agnostic in regards to the identity of progenitor and differentiated myeloma cells and mechanisms of disease resistance. Our analysis is consistent with reports of clonogenic B-cell “MM stem cells” isolated from patient samples (ref. ^{14, 24}). However, experimental data are divided on whether MM progenitor cells are in fact contained within the CD138- cell compartment (ref. ^25-27). Additional surface markers may be needed to identify MM progenitor cells, but alternative biological explanations are also possible. MM progenitors may be a functionally distinct subset of MM cells defined by something other than markers of normal B-cell maturation, e.g. by stromal cell interactions (ref. ^{28, 29}). Alternatively, two-phase response kinetics might be explained by yet undefined drug metabolism induced over time (although published pharmacokinetic data on bortezomib are not consistent with this hypothesis) (ref. ³⁰), or by the induction of immune or other host responses activated after treatment initiation. Mechanisms of disease resistance have been identified in MM, and additional experiments will be required to determine which mechanisms explain in vivo resistance observed in clinical trials. However, our model was examined in clinical trials with a bortezomib-based therapy. The kinetics of tumor growth may be different with immunomodulatory agents such as lenalidomide or pomalidomide when used alone or in combination with proteasome inhibitors. Future studies to examine these kinetics would be interesting to determine whether these agents have similar effects on progenitor cell populations and heterogeneous clonal populations. Another caveat of our study is that measurement of tumor burden in MM is based on M-protein level in the peripheral blood. Our model may not be predictive if the therapeutic agent inhibits secretion of M-protein or induces a cytostatic and not cytotoxic effect on the tumor cells.

The current goal of treatment in MM is to achieve deep complete remissions. Mathematical modeling based on treatment responses can provide an additional method for testing biological hypotheses relevant to disease outcomes in patients with MM. Here, we presented a model based on a large amount of available clinical data, but models such as this one can also be used to improve the design of new clinical trials in myeloma by using treatment effects of specific agents on both differentiated and progenitor cells populations as endpoints (ref. ³¹). Mathematical modeling as suggested here might eventually be useful for investigating the efficacies of novel treatment modalities. For instance, if the effects of an agent on individual myeloma cell populations are known, our mathematical model can help predict how diverse patient populations will respond to treatment. As multiple MM clones are present at diagnosis, the administration of rational combination treatments at relapse may reduce their expansion and therefore lead to deeper and more prolonged remissions, again an area where the model may have utility (ref. ^{32, 33}). Finally, mathematical models are limited by the availability of uniformly collected quantitative patient data. The utility of mathematical models such as this one would be improved by collecting additional quantitative data centrally from future clinical trials.

TRANSLATIONAL RELEVANCE.

Relapse in multiple myeloma patients suggests the existence of progenitor cells responsible for tumor regrowth, but this population has never been confirmed. Here, we used mathematical modeling to show that the combined data from three clinical trials of bortezomib-based chemotherapy is consistent with a differentiation hierarchy where a myeloma progenitor cell population that is relatively resistant to therapy gives rise to a differentiated cell population that is sensitive to therapy. Thus, we conclude that bortezomib-based therapy exerts a selection pressure on myeloma cells, and the administration of rational combination treatments may reduce expansion of resistant clones, leading to more prolonged remissions. Our model could be used to improve future clinical trial design for multiple myeloma by using treatment effects of therapeutic agents on both differentiated and progenitor cells populations in order to predict how patients will respond to treatment.