New Insights into Activity Patterns in Children, Found Using Functional Data Analyses

Abstract

Introduction/Purpose

Continuous monitoring of activity using accelerometers and other wearable devices provides objective, unbiased measurement of physical activity in minute-by-minute or finer resolutions. Accelerometers have already been widely deployed in studies of healthy aging, recovery of function after heart surgery, and other outcomes. While common analyses of accelerometer data focus on single summary variables, such as the total or average activity count, there is growing interest in the determinants of diurnal profiles of activity.

Methods

We use tools from functional data analysis (FDA), an area with an established statistical literature, to treat complete 24-hour diurnal profiles as outcomes in a regression model. We illustrate the use of such models by analyzing data collected in New York City from 420 children participating in a Head Start program. Covariates of interest include season, sex, BMI Z-score, presence of an asthma diagnosis, and mother’s birthplace.

Results

The FDA model finds several meaningful associations between several covariates and diurnal profiles of activity. In some cases, including shifted activity patterns for children of foreign-born mothers and time-specific effects of asthma on activity, these associations exist for covariates that are not associated with average activity count.

Conclusion

FDA provides a useful statistical framework for settings in which the effect of covariates on the timing of activity is of interest. The use of similar models in other applications should be considered, and we make code public to facilitate this process.

1 Introduction

1.1 Motivation

Accelerometers have become an appealing alternative to self-report techniques for studying physical activity in observational studies and clinical trials, largely because of their relative objectivity. During observation periods, the devices measure electrical signals that are a proxy for acceleration (28) (32) (33). “Activity counts” are then devised by summarizing the voltage signals across a short period known as an epoch; while sub-second observations are the focus of a growing literature, one-minute epochs are common. Thus, activity counts provide a quantification of the amount and intensity of activities that result in acceleration of the device. Although the resulting observation of physical activity is imperfect -- depending on device placement, for example, not all activity types will result in measureable acceleration -- these counts are often a useful surrogate measurement of activity. Moreover, because accelerometers can be worn comfortably and unobtrusively for days at a time, they produce around-the-clock observations of many kinds of activity.

Understanding the determinants of diurnal activity profiles is essential for the development of effective physical activity interventions. Children with differing patterns of physical activity may require different interventions to increase their overall level of physical activity (10) (15) (30). The influence of the built environment and neighborhood disadvantage on physical activity may vary by time of day. Features of the built environment may influence the frequency and duration of bouts of moderate or vigorous activity and sedentary time (14). Neighborhood disadvantage may impede physical activity at night but not during the day. Recognizing these activity patterns will allow the tailoring of interventions to promote physical activity to the individual, rather than taking a “one-size-fits-all” approach.

There are several existing approaches for the analysis of accelerometer data. Perhaps the common is to focus on the total or average activity count aggregated over hours or days as a single observed measure of physical activity (3) (13) (31) (32). Such methods provide useful insights into overall activity, but by aggregating remove the ability to examine diurnal profile. Mumford et. al. (21) examine a collection of indices of rythmicity as summary measures of diurnal profile. Like aggregating activity counts, this reduces observed profiles to a collection of pre-defined features that may be hard to interpret or to use as a guide for interventions. Most similarly to our approach, Faurholt-Jepsen et. al. (2) computed activity count averages for each hour of the day separately and conduct statistical analyses within each hour. Doing so provides insight into diurnal profiles, but doesn’t take into account the correlation over time within a subject when estimating effects and performing tests.

In parallel to the rising popularity of accelerometers, the statistical subfield of functional data analysis (FDA) has been under intense methodological and theoretical development. In this context, “functional” refers to the data structure rather than to, say, patient or cognitive function. The key concept in FDA is to treat a completely observed profile, in this case parameterized by time, as a single unit of observation instead of considering each minute of each day as a separate, disconnected data point (23). This framework depends on the notion of temporal structure and ordering, and thus allows the examination of time-specific effects and associations. Although FDA is clearly relevant to many open research questions, it has rarely been described outside the statistical literature.

Our purpose is to articulate the use of regression models with functional responses and scalar predictors for accelerometer studies. The term “functional response” refers to the complete profile recorded by the accelerometer analyzed as as the dependent variable or outcome of interest; the term “scalar predictor” refers to any traditional covariate, such as age or sex, used as a predictor of the activity response. Such models are the subject of an established statistical literature (8) (20) (25) (7). This article presents a re-analysis of an existing dataset using function-on-scalar regression, emphasizing the interpretation of the models and estimated coefficients, to demonstrate the usefulness of FDA for uncovering time-specific associations. An interactive graphic showing the results of our analysis is available online, and to encourage readers to use such models we have made all code used in this application publicly available as supplementary digital content (see http://jeffgoldsmith.com/Downloads/HeadStartCode.zip).

1.2 Dataset and original analysis

Our data have been discussed and analyzed previously, and we provide only an overview here; for more complete details see (26) and (18).

Study participants were recruited from 50 Head Start centers in northern Manhattan, the Bronx, and Brooklyn, in neighborhoods with high rates of pediatric asthma. After obtaining informed consent from the enrolling parent and using a study protocol approved by the Institutional Review Board of the Columbia University Medical Center, we used a survey instrument to collect data on the child’s age, race, sex, asthma symptoms and other medical conditions, birth order and family-related factors, and features of the home environment. Field staff measured the child’s height, weight, and skin-fold thicknesses The staff then attached the accelerometer to the child’s non-dominant wrist with a hospital band. To allow the child to become comfortable with the device before it began recording, staff and programmed it to delay starting data collection until 11:50 pm the first day; it then recorded the child’s physical activity for six days, 24 hours per day, using 1-minute epochs

Rundle et al. (26), analyzed these accelerometer data using standard techniques, with the goal of identifying variables associated with physical activity in children. Multiple linear regression models were used to examine effects of season (warmer months May to September or colder months October to April), child demographics (sex, age, BMI Z-score), mother’s demographics (age, birthplace, occupation), and behavioral variables (>2hr per day of TV, > 1hr per day of video games) on the mean activity count during awake minutes. A primary focus of the study was on the association of asthma symptoms with physical activity.

With minor modifications, we reanalyzed these data using the same approach. The results of our re-analysis, provided in Table 1, are similar to the original findings. Briefly, we find that aggregated activity counts as a single outcome are associated with season, sex, whether the mother works or attends school, and the interaction between season and mother’s work status. Remaining variables, including whether the child watches 2 or more hours of TV per day and mother’s birthplace (United States or elsewhere), were not significantly associated with average counts, nor were asthma symptoms.

Table 1.

Estimated coefficients (“Beta”) and p-values from two analysis strategies. Multiple linear regression (MLR) results are shown in the first columns; function-on-scalar regression (FoSR) results are shown in the second columns. For the FoSR model, estimated effects are the integrated coefficient functions and p-values are global tests of significance for the coefficient function.

	Beta, MLR	P-value, MLR	Beta, FoSR	Global P-value, FoSR
Season (ref: Cold)	−117.565	0	−111.234	0
Sex (ref: Male)	−55.012	0.002	−59.758	0.003
Number of Rooms in the House	8.505	0.097	9.655	0.185
Mother Works/is in School	−52.285	0.003	−46.645	0.006
Mother Born in the US	14.890	0.287	29.369	0.012
>2hr TV per day	−15.999	0.139	−21.609	0.082
>1hr Video Games per day	−9.595	0.439	−15.958	0.068
Child age (in months)	0.895	0.176	1.300	0.042
Child has Asthma	−15.889	0.163	−12.307	0.257
BMI Z-score	1.098	0.787	0.057	0.524
Interaction: Sex by Season	33.588	0.126	30.290	0.17
Interaction: Mother Works by Season	46.812	0.035	43.146	0.125

2 Methods

We now introduce the conceptual framework for a functional data approach to accelerometer data; see (29) for a recent review article of FDA and (23) for a book-length treatment of the area.

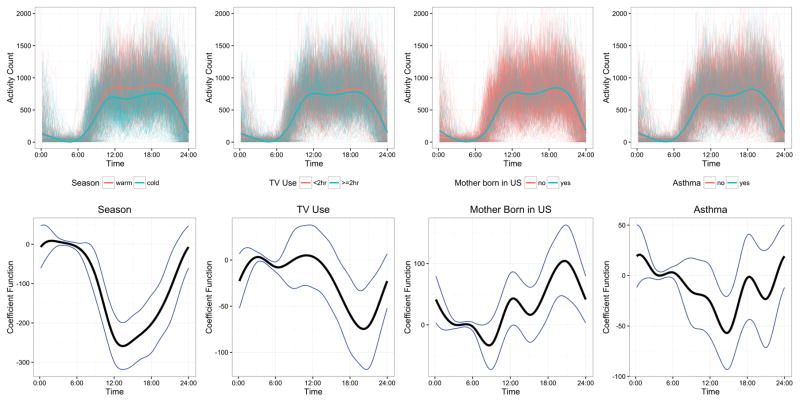
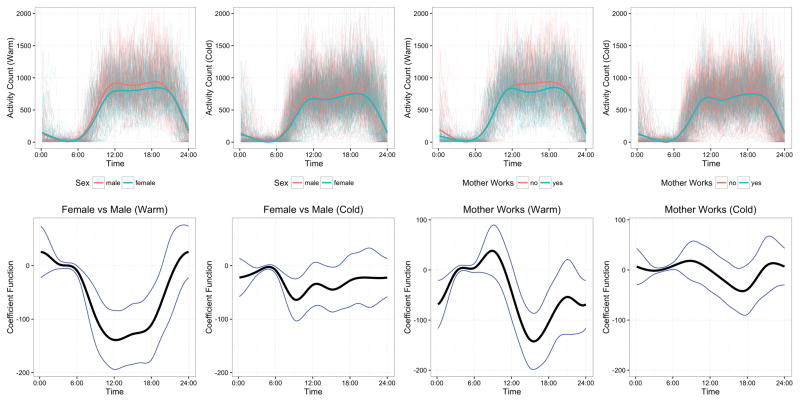
We regard the complete diurnal activity profile for a subject as a single functional data point, which we denote as y_i(t) for child i and time of day t. By including the index t in our unit of observation, the time of day is incorporated into all subsequent analyses. We obtain y_i(t) by averaging, for each t separately, across the six days of observation for each child. Additionally, we aggregate into 10 minute epochs; doing so improves the statistical performance of estimates in our model by making y_i(t) approximately Normally distributed for each t. The profiles y_i(t) are plotted for all children in the top row of Figures 1 and 2.

Figure 1.

Observed accelerometer data for all subjects (faded curves) and group averages (bold curves) are shown in the top panels, colored by covariate value. The bottom row shows estimated coefficient functions in the function-on-scalar regression model (black curves), with pointwise 95% confidence intervals (blue curves), corresponding to the comparison in the top row.

Figure 2.

Observed accelerometer data for all subjects (faded curves) and group averages (bold curves) are shown in the top panels, separately by season and colored by covariate value. The bottom row shows estimated coefficient functions in the function-on-scalar regression model (black curves), with pointwise 95% confidence intervals (blue curves), corresponding to the comparison in the top row.

Our goal is to understand how diurnal profiles differ across covariate levels. As an exploratory analysis, the top row of Figure 1 shows all observed profiles with children separated into groups based on observed covariates, and includes group-specific means as bold curves. Comparisons of group-specific mean curves suggest that covariate effects are often time-specific. For example, children who watch ≥2 hours of TV have lower activity than children who watch <2 hours of TV, but this difference is largely confined to the evening hours. The top row of Figure 2 shows the observed profiles for warm and cold seasons separately; the two left panels children are additionally separated by sex, while in the right two panels children are additionally separated by the mother’s work status. These panels illustrate the possible effect modification of season on the time-specific association between covariates and activity. For example, boys are much more active that girls during the daylight hours in the warm season, but have similar activity levels in the cold season. To better understand these associations, to adjust for possible confounding, and to establish statistical significance, we make use of regression modeling.

Function-on-scalar regression (FoSR) relates functional responses y_i(t) to scalar covariates x_i (e.g. age, sex, asthma diagnosis). As a starting point, the function-on-scalar model that is analogous to simple linear regression is

$${\mathrm{y}}_{\mathrm{i}}(\mathrm{t})={\mathrm{\beta }}_0(\mathrm{t})+{\mathrm{\beta }}_1(\mathrm{t}){\mathrm{x}}_{\mathrm{i}}+{\mathrm{\epsilon }}_{\mathrm{i}}(\mathrm{t}).$$

Details on the estimation of the FoSR model appear in the Appendix (see Document, Supplemental Digital Content 1, Estimation of the Function-on-Scalar Regression model). The coefficients β₀(t) and β₁(t) are interpreted analogously to coefficients in a simple linear regression -- the intercept is the expected response in the reference group, and the slope is the expected difference in response for each one unit difference in the predictor -- with the exception that they, like the outcome, are defined for all time points during the day. Similarly, the error term ε_i(t) indicates the departure of the observed data from its conditional expectation at each time t. Errors ε_i(t) are assumed to be correlated over time t, so that above-average activity in the morning may indicate above-average activity in the afternoon, but are independent across subjects i.

The inclusion of time t in the coefficient β₁(t) suggests that covariate effects at nearby times should be similar. This is incorporated into the model estimation through assumptions on the structure of coefficient functions, most notably that they are “smooth”. While this can be a reasonable assumption, particularly because coefficient functions are average differences across groups, it does limit the sensitivity of the FoSR model to covariate effects that take place over short time periods.

The “simple linear” FoSR model above can be straightforwardly extended to allow other covariate effects. Indeed, the model structures possible for usual multiple linear regression, including categorical predictors and interactions, are available for FoSR. Many of the same caveats apply as well, and overfitting can be a concern. Although degrees-of-freedom are less easily defined for FoSR models, a useful rule of thumb is to compare the number of subjects to the number of coefficient functions as a guide for decisions about model size and complexity.

The test H₀:β_k(t)=0 for all t is a “global” test of the k^th covariate effect; under the null, there is no association between the predictor and outcome at any time. The test H₀:β_k(t)= 0 for a specific t is a “local” test of the k^th covariate effect at a given time; under the null, there is no association between the predictor and outcome at time t. These tests for FoSR models are similar to global F-tests and individual t-tests, respectively, in standard multiple linear regressions, and can be used in the same ways. For example, global tests avoid the issues of multiple comparisons implicit in individual local tests and thus may be preferred in the first stages of analysis. In FoSR models neighboring local tests are highly correlated, making multiple comparisons corrections challenging; as a result, uncorrected local tests are typically presented and should be interpreted with some caution.

The following property helps connect the FoSR model to more common aggregation approaches for accelerometer data. Integrating a curve over t takes the average of that curve: ∫ y_i(t) dt = ȳ_i is the average activity observed for subject i. Analogously, ∫ β₀(t) dt = β̄₀ is the average activity in the reference group, and ∫ β₁(t) dt = β̄₁ is the expected difference in the average activity for each one unit difference in the predictor. These values can be compared to the coefficients estimated in a multiple linear regression for average activity. For data with no non-wear time and a specific FoSR estimation approach, the values will be exactly equal; in general we expect the values differ somewhat, for reasons given in the Appendix (see Document, Supplemental Digital Content 1, Estimation of the Function-on-Scalar Regression model). Thus, the comparison of methods provides an intuitive motivation for the FoSR model and a heuristic check for the validity of FoSR results.

3 Results

We use the FoSR model to study the association between activity trajectories and season, child demographics (sex, age, BMI Z-score), mother’s demographics (age, birthplace, occupation), behavioral variables (>2hr per day of TV, > 1hr per day of video games), and asthma symptoms. We include interactions between season and sex and between season and mother’s birthplace; other interactions were considered, but little evidence supporting season as an effect modifier for other covariates was found.

Examining coefficient functions β(t) illustrates the time-specific effect of covariates over the course of the day. In the bottom row of Figure 1, we show the coefficient functions for season, TV use, mother’s place of birth, and asthma diagnosis. These can be compared to the plots in the top row, which show the observed data for all subjects separated by those covariates. Similarly, the bottom row of Figure 2 shows the coefficient functions for sex and mother’s work status, separately for warm and cold seasons, and can be compared to the observed data in the top row. For each coefficient function, we include 95% confidence intervals to indicate the strength of association at each time. P-values resulting from global hypothesis tests H₀:β_k(t)=0 for all t are given in Table 1.

The coefficient function for season indicates a substantial and consistent drop in activity during daytime hours in the winter months (p-value of global test 0). TV watching has more localized effects: children who watch ≥2 hours of TV are less active than others in the evening but not in the morning or afternoon (p-value of global test 0.082). There is some evidence that season modifies the effect of sex and mother’s work status on diurnal activity profile. In the warm season, boys are more active than girls throughout the daylight hours (p-value of global test 0.003). Also in the warm season, the coefficient function for mother’s work status, a binary variable indicating that the mother works outside the home or is in school, suggests that the mother’s absence has a significant negative effect on activity in the afternoon and early evening, but no effect in the morning or later in the evening (p-value of global test 0.006). For both sex and mother’s work status, effects are smaller and generally non-significant (using local tests) in the cold season.

A primary hypothesis of the original study was that children with asthma have different activity levels than children without asthma. A test of the global hypothesis H₀:β_asthma(t) = 0 for all t in the FoSR model fails to reject the null, and a similar conclusion was reported in (26). However, examining the effect over the daytime hours indicates periods of decreased activity among asthmatic children: the confidence interval for the coefficient function does not include 0 from approximately 12:00 to 16:00, suggesting that children with asthma may be less active than other children in this time window. At many time points during the day asthma is not associated with activity and these times limit the power to reject the global null hypothesis, analogously to a situation often arises in multiple linear regressions when conducting a global test of many coefficients.

To provide context for our results, we also fit a multiple linear regression analysis using average activity counts over the course of the day as the scalar response. Table 1 shows coefficient estimates and p-values for the multiple linear regression in the first two columns; they are comparable to those found in previous analyses of these data (26). The remaining columns show the integrated coefficient functions and the p-values resulting from a test of the gloabl null hypothesis H₀:β(t) = 0 for all t.

A comparison of covariate effects in Table 1 indicates general agreement between the multiple linear regression and the function-on-scalar regression model in terms of the sign and magnitude of coefficients and, in most cases, in the statistical significance of the estimates. For example, both models suggest that girls are significantly less active than boys in the warm season, and that children who watch <2 hours of TV are more active than children who watch ≥2 hours, although this effect is not significant. Some exceptions do exist, as in the magnitude of the coefficient for mother’s birthplace, the reasons for which are described in the Appendix (see Document, Supplemental Digital Content 1, Estimation of the Function-on-Scalar Regression model). We emphasize that the results in Table 1 are intended to provide a frame of reference for the FoSR model rather than to suggest this approach as a replacement for analyses of aggregate outcomes.

One striking result in Table 1 is the difference in the significance, comparing the MLR to the FoSR model, for the effect of mother’s birthplace. We briefly discuss this difference to provide insights into the differences in methods. The multiple linear regression suggests that children of foreign-born mothers and children of mothers born in the United States do not differ in aggregate activity (p-value 0.287), but the function-on-scalar regression models indicate that mother’s birthplace has is indeed associated with children’s physical activity (p-value 0.012). The coefficient function for this effect, in third panel of the bottom row in Figure 1, helps to explain the discrepancy: the children of mothers born in the United States are somewhat less active in the morning and more active in the evening than children of mothers born elsewhere. Because these differences are offsetting in aggregate, the MLR correctly concludes no difference in average activity, while the FoSR correctly concludes that time-specific differences exist. For our goal of understanding the determinants of diurnal profile the second conclusion is more useful, although both are valid.

4 Discussion

Our re-analysis of accelerometer data using function-on-scalar regression has improved our understanding of physical activity in children in several important ways. For predictors that have been previously associated with aggregate activity, the analyses provide information about the specific time course of differences. For instance, a deficit in activity has been previously observed with more time spent watching TV and the mother either working or attending school; in our analysis the time course of this deficit is evident. The results regarding moms who work or attend school suggest that interventions targeting activity opportunities in day care facilities during the summer may lead to substantial increases in activity. The FoSR analyses also identify time-specific associations between diurnal activity profiles and socio-demographic characteristics – the lower afternoon activity of the children of mothers born outside the United States – and between physical activity and health – the dip in activity during the afternoon among children with asthma. Thus our analysis strategy augments standard analyses of total activity counts, and are useful when information about the timing and structure of activity is of interest.

The FoSR analyses show that while children of mothers born in the U.S. and children of mothers born outside the United States have similar total counts of activity, the two groups of children achieve their activity levels on different schedules. While we advocate increasing activity levels among all children regardless of maternal nativity, we hope that more tailored approaches that target times when individual children are less active would provide greater efficacy. Thus, our analyses suggest that interventions to increase total physical activity among children of mothers born outside the United States might focus on activity in the late afternoon or evening. The analyses do not tell us why children of mothers born outside the United States are less active in the afternoon than other children, but the results at least raise a question we would not otherwise know enough to ask. We can then undertake qualitative research studies to understand the causes and use that understanding to formulate effective interventions to increase activity.

The relative drop in activity in the afternoon among children with asthma as compared to children without asthma is of particular interest: prior analyses of total physical activity in this data set showed no difference in activity by asthma status (26). Ground level ozone levels peak in the summer months, in the early afternoon, and ozone exposure is associated with increased emergency department (ED) visits and hospitalizations for asthma a few days after high ozone exposures (12) (27). The dips in activity observed among children with asthma during the early afternoon may reflect mild respiratory function impairment or irritation of the respiratory tract associated with ozone exposure among asthmatics (4) (5) (9) (11). Alternatively, it is possible that pollen levels or other ecological factors play a causal role. FoSR analyses of accelerometer data may be useful for identifying more subtle effects of environmental pollutants on behavior among at-risk children, although obtaining high-quality relevant data is a challenge.

The novel insights presented in this paper were made through the application of recently developed statistical models to our motivating data. Such applications are not uncommon in the functional data analysis literature, with methods developed for both FoSR and several related settings (19) (7) (17) (16) (22) (35). Several barriers to the broader adoption of such methods exist, and one goal of this article is to reduce those barriers by building awareness of functional data approaches and clearly interpreting the results of such analyses. To facilitate similar analyses for other datasets, implementations of FoSR are available in the refund R package on CRAN (1). To help interpret the results of such analyses, interactive graphics for FoSR are available in the refund.shiny R package on CRAN (6) (34). Code used for the analyses in this paper, taking advantage of the preceding resources, is publicly available (see http://jeffgoldsmith.com/Downloads/HeadStartCode.zip).

Lastly, while our focus has been on the determinants of diurnal activity profiles with the goal of tailoring interventions, it is reasonable to imagine that activity levels will affect long-term health outcomes. For such models, the scalar-on-function regression framework, in which functional data are considered predictors of scalar outcomes, may be of use. As in FoSR, these models assume that the associations between the predictor and outcome are time-specific: for example, lower activity in the afternoon may be indicative of poor outcomes, with no association in the morning or evening. Whether such time-specific associations are plausible will depend on the context but can be investigated. There is a rich literature for scalar-on-function regression; see Reiss et. al. (24) for a recent review. More broadly, it may be useful to model bidirectional associations between patterns of activity and health outcomes from a functional data perspective, although doing so will require additional methods development.

Supplementary Material

Supplemental Data File _.doc_ .tif_ pdf_ etc._

Supplementary Digital Content 1: Technical Appendix (.pdf)—Estimation of the Function-on-Scalar Regression model