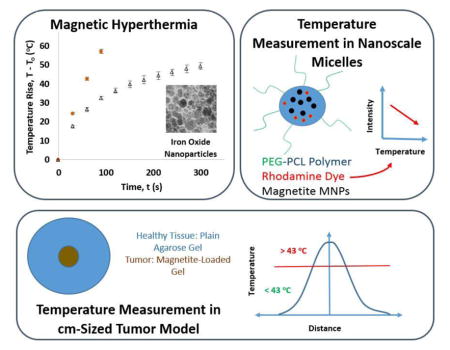
Abstract
Magnetic iron oxide nanoparticles (MNPs) have been developed for magnetic fluid hyperthermia (MFH) cancer therapy, where cancer cells are treated through the heat generated by application of a high frequency magnetic field. This heat has also been proposed as a mechanism to trigger release of chemotherapy agents. In each of these cases, MNPs with optimal heating performance can be used to maximize therapeutic effect while minimizing the required dosage of MNPs. In this study, the heating efficiencies (or specific absorption rate, SAR) of two types of MNPs were evaluated experimentally and then predicted from their magnetic properties. MNPs were also incorporated in the core of poly(ethylene glycol-b-caprolactone) micelles, co-localized with rhodamine B fluorescent dye attached to polycaprolactone to monitor local, nanoscale temperatures during magnetic heating. Despite a relatively high SAR produced by these MNPs, no significant temperature rise beyond that observed in the bulk solution was measured by fluorescence in the core of the magnetic micelles. MNPs were also incorporated into a macro-scale agarose gel system that mimicked a tumor targeted by MNPs and surrounded by healthy tissues. The agarose-based tumor models showed that targeted MNPs can reach hyperthermia temperatures inside a tumor with a sufficient MNP concentration, while causing minimal temperature rise in the healthy tissue surrounding the tumor.
Keywords: hyperthermia, magnetic heating, iron oxide nanoparticles, magnetic field, power generation, specific absorption rate, local nanoparticle temperature, agarose gel tumor model
Graphical Abstract
1. Introduction
The use of magnetic nanoparticles (MNPs) is progressively increasing for theranostics of life-threatening diseases such as cancer [1–8]. With proper design, MNPs can be employed in cancer therapy due to their ability to generate heat when exposed to a high frequency magnetic field. This treatment, known as magnetic fluid hyperthermia (MFH), aims to provide an effective treatment which has minimal side effects when targeted to tumors [1–8]. The ability of these MNPs to generate heat also makes them candidates for use in thermally-triggered nanoscale drug release systems. These systems can then provide dual therapy in forms of MFH and chemotherapy which increases the therapeutic effectiveness compared to either of the treatments administered individually [8]. Recently, many of the MFH systems have been successfully utilized in vivo to cause a reduction in tumor mass, and demonstrate the potential of MFH to treat cancer using animal models [9 – 11]. MFH has also been used to target and reduce cancer stem cell populations in the body to minimize proliferation and metastasis of tumor cells [12, 13]. The efficiency of MFH treatment and the novel therapeutic options facilitated by this therapy depend on the heating efficiency of MNPs used in such treatments; hence it is essential to investigate the phenomenon of heat generation in MNPs under application of alternating magnetic field to develop MNPs that maximize the generation of heat.
Heat generation in superparamagnetic MNPs occurs by two main mechanisms known as Néel relaxation and Brownian relaxation, as described by the linear response theory (LRT) [14–16]. LRT has been used to theoretically calculate the amount of heat generated by MNPs, but it has several limitations and it is essential to note that under most circumstances LRT is valid only when ξ < 1 (Equation 1), and μ 0Hmax ≪ μ 0Hk [16, 17] where:
| Eq. 1 |
Here, μo is the permeability of free space (4π*10−7 T-m/A), Md is domain magnetization of magnetic material used, H is the maximum applied field strength, Vm is the magnetic volume of nanoparticles, k is the Boltzmann constant, T is the absolute temperature, and Hk is the anisotropy field.
Despite the limitations of LRT, it can prove to be useful to calculate power generation in MNPs under certain situations, where the magnetization of the MNP system shows a linear response to applied magnetic field. For the MNPs that fall within the LRT domain, heat is generated by both Brownian and Néel relaxation processes. Brownian relaxation occurs by nanoparticle rotation leading to the motion of MNPs against the viscous forces in the fluid dispersion, while Néel relaxation occurs due to re-orientation of the magnetic moment inside the MNP in response to the alternating magnetic field. These relaxation processes are facilitated by thermal fluctuations as opposed to just the energy provided by an applied alternating magnetic field [16, 18]. Based on the assumption of linear response, Rosensweig [14] has related power generation (P), and thus heat generation, to various field and material parameters (Equation 2):
| Eq.2 |
Here, χo is the magnetic susceptibility of the particles, H is the field strength of the applied magnetic field, f is magnetic field frequency, and τ is the relaxation time for reorientation of magnetic moments in MNPs [14]. Usually Néel relaxation dominates for smaller MNPs, while larger MNPs generate more heat due to Brownian relaxation *14+. Brownian relaxation time (τB) depends on the viscosity (η) of the medium, hydrodynamic volume of MNPs (VH), absolute temperature (T), and the Boltzmann constant (k) (Equation 3):
| Eq. 3 |
Thus, an increase in the viscosity of the medium surrounding the MNPs can increase the Brownian relaxation time and reduce its contribution to magnetic heating. For in vivo applications, the viscosity of protein-containing interstitial fluids, or the rigidity of materials surrounding the MNPs inside a drug delivery vehicle can significantly reduce the temperature rise due to magnetic heating. Experimental validation of this situation has been conducted by researchers, where SAR of MNPs is reduced to 47% of the original value when the iron oxide MNPs dispersed in water are transferred to a rigid silicon-based organic polymer [19]. In addition to these factors, magnetic heating strongly depends on the MNP magnetic properties and magnetic field parameters.
Rosensweig’s equation demonstrates a clear relationship between power generation and magnetic field strength, frequency, and magnetic properties of MNPs (Equation 2), and these relationships have been verified by experimental studies. Several studies have demonstrated that power generation increases with an increase in the field strength applied for MFH [20–25]. Although it is harder to test the effect of frequency at a constant field strength, some studies have shown that MFH at higher frequencies can produce heat quite efficiently [23, 25]. In addition to the ability to tune heating by selecting magnetic field parameters, the magnetic properties of MNPs and the procedures used to synthesize and disperse MNPs can also affect the heating efficiency of MNPs [24, 26, 27]. Additionally, several experimental and theoretical studies have determined the relationship between optimal size for iron-oxide MNPs and their ability to generate heat for use in MFH [21–24, 28–30].
Carrey et al., have provided a clear understanding of the domain of validity of LRT, and other theories based on the Stoner-Wohlfarth (SW) model that can be used to calculate MNP SAR based on MNP magnetic properties as well as the magnitude of the applied magnetic field. For single-domain, randomly oriented ferromagnetic MNPs where μ 0Hmax > 2μ 0Hc (where Hc is the coercivity of MNPs determined from a magnetic hysteresis loop), SW-based theories are used to predict SAR for MNPs [16, 17], which relate power generation by MNPs to the area of the magnetic hysteresis loop (A) and the frequency of the applied magnetic field (f) as follows:
| Eq. 4 |
To compare the power generation or heating efficiency of the MNPs, specific absorption rate (SAR) values are determined from MNP heating profiles to normalize the power generated by MNPs by the mass of MNPs or iron content of MNPs (W/gMNPs or W/gFe ) [23–31]. MNPs with high SAR are largely favored for cancer treatment as the MNP dose can be kept minimum, while also reducing the time required for patient exposure to a magnetic field. SAR is calculated from the magnetic heating data as:
| Eq. 5 |
Here ms is the mass of solution, mnp is the mass of MNPs, cp is the heat capacity of the solution, and (ΔT/Δt) is the initial slope of temperature rise vs. time curve for MNP heating. The SAR value serves as guidance for comparing the heating rates of MNPs with different compositions and concentrations, or different magnetic field settings. SAR values depend strongly on MNP size and other factors discussed previously.
The optimal MNP size and effect of magnetic properties of MNPs on heating efficiency can be predicted by estimating the effective relaxation time (τ, which depends on Néel relaxation time τN, and Brownian relaxation time, τB) of MNPs and magnetic susceptibility (χo) to determine the power generated by MNPs when the MNP core diameter is varied (Equations 1, 6–9).
| Eq. 6 |
| Eq. 7 |
| Eq. 8 |
| Eq. 9 |
For determining the magnitude of relaxation time and susceptibility, values of domain magnetization (Md), magnetic volume (Vm), hydrodynamic volume (VH), effective nanoparticle anisotropy (K), and the volume fraction of MNPs in solution (Φ are required. Since, we investigated MNPs that were predominantly maghemite (γ-Fe2O3) for purposes of predicting SAR [32–34], we utilized anisotropy values for maghemite in nanoparticle form. For superparamagnetic maghemite MNPs, the domain magnetization of single domain superparamagnetic MNPs is equal to the saturation magnetization of MNPs at room temperature (using data from magnetization curves) [35], and the effective anisotropy value ranges from 4.7 kJ/m3 (for bulk maghemite) to 47 kJ/m3 (for nanoscale maghemite) as reported in the literature [14, 36, 37].
For the larger-sized ferromagnetic particles, where μ 0Hmax > 2μ 0Hc and ξ > 1, LRT is no longer valid and SW-based theories are utilized to estimate SAR. In this scenario, the effective anisotropy of these nanoparticles could be calculated by simultaneously solving equations 10 and 11, as described by Shokhufar et al. [17],
| Eq. 10 |
| Eq. 11 |
Where T1 = 0 K, T2 = 298 K, Keff is the effective anisotropy of MNPs, τ0 = 10−10 sec, and f is the measurement frequency assumed to be 5.5*10−4 Hz [17].
After calculating the anisotropy for a particular sized MNP, the coercivity (Hc) can be determined as a function of temperature (T = 298 K) and the frequency of the applied magnetic field using the following equations developed by Garcia-Otero et al. (Equation 12) and modified by Usov et al. (Equations 13, 14) [15–17, 38–39].
| Eq. 12 |
| [39] | Eq. 13 |
| Eq. 14 |
The area, A, of the hysteresis loop was then calculated using equation 15 for randomly oriented nanoparticles,
| Eq. 15 |
Here, α = 0.39 accounts for the reduced squareness of the hysteresis loop for an optimized system with randomly oriented MNP easy axes (the axes where an MNP would tend to orient itself in the absence of any external field) [16]. SAR is then calculated from the area inside the hysteresis loop using Equation 4. The calculations based on LRT and SW-based theories can thus be used to determine the heating efficiency of MNPs and the feasibility of using these nanoparticles for MFH and drug release applications.
Recently MNPs have been used in nano-scale drug release systems such as micelles, liposomes, and dendrimers [8, 40, 41]. Some of these systems are designed to rely on the temperature increase caused by magnetic heating to trigger drug release, but the MNP loading in these systems may not be high enough to cause a substantial temperature rise in the bulk dispersion. For this reason, it was speculated that the local temperature rise (within a few nanometers of the MNP surface) would be much higher than the temperature rise seen on a larger scale.
Techniques involving the use of nanolithography, nano-scale thermocouples, carbon nanotubes, fluorescent dyes, and quantum dots have been used to probe the local temperature of nanoscale objects [42], but these techniques are not optimized for measuring local MNP temperature and have low accuracy in temperature measurement. Recently, techniques have been reported to experimentally verify the temperature rise near the MNP surface when subjected to magnetic heating [43–45]. Riedinger et al. have shown indirectly using fluorophores attached to MNPs through thermally-labile azo bonds that the local temperature within 0.5 nm of the surface of iron oxide MNPs is much higher (ΔT > 45 °C) than the temperature of bulk fluid [43] during application of a 334.5 kHz, 7 – 13.5 kA/m magnetic field. Using this technique with different spacer lengths between the MNP and the fluorophore, the temperature at distances greater than 4 nm to 5 nm away from the MNP surface was observed to be nearly the same as the bulk solution temperature during magnetic heating [43]. Despite the progress in elucidating the temperatures in close proximity of MNPs (< 4 nm), there is not enough evidence to prove that heat generated by individual MNPs in a nano-scale drug-loaded vehicle can cause drug release without a bulk temperature rise (arising from the contribution of multiple MNPs). One such thermally-triggered delivery system was poly (ethylene glycol-b-caprolactone) (PEG-PCL) micelles that would release drugs when the semi-crystalline PCL core of micelle melts around 40 – 45 °C [8].
In our study, SAR for in-house synthesized iron oxide MNPs (predominantly γ-Fe2O3 as verified later by X-ray photoelectron spectroscopy, XPS) and maghemite nanopowder (γ-Fe2O3 as sold by the manufacturer and verified by XPS) was determined experimentally using MFH equipment and later compared to theoretical SAR. SAR values were calculated for dispersions containing uniform-sized MNPs (equal to mean size) and also polydisperse size distributions (based on size histogram) using LRT and SW-based models in their domain of validity when the MNP properties were obtained from hysteresis loops and literature.
To probe the local temperature in the hydrophobic core of PEG-PCL micelles, rhodamine B (RhB) was conjugated to a hydrophobic PCL oligomer (RhB-PCL), and used in the self-assembly of block copolymers to form PEG-PCL micelles. RhB is a hydrophobic dye whose fluorescent intensity drops up to 3.4 % with 1 °C increase in surrounding temperature [46]. Since RhB-PCL and MNPs would be present within close proximity of each other inside the core of micelles (< 50 nm micelle diameter [8]), it was hypothesized that RhB-PCL would show a noticeable change in fluorescent intensity if the temperature rise in the micelle core was much higher than the bulk fluid temperature during magnetic heating. These results would determine parameters needed to trigger melting, predict the mechanism of drug release, and also suggest necessary modifications to micelle design.
To contrast the magnetic heating inside a nano-scale system, MFH was applied to a macro-scale MNP-loaded agarose gel tumor model. This system simulates the temperature rise that would occur inside a tumor loaded with targeted MNPs and surrounded by healthy body tissue or organs. The model consisted of two concentric agarose discs, where the center agarose disc contained MNPs mimicking a tumor targeted with MNPs, with diameters ranging from 0.8 cm to 1.6 cm, and thickness of 0.16 cm. The outer disc of 3.5 cm diameter and thickness of 0.7 cm, contained plain agarose gel that mimicked healthy body tissue. In contrast to the nano-scale micelle setup, the bulk temperature rise was measured in the agarose gel instead of local MNP temperature. The dimensions of the center disc were varied to study the effect of tumor size and the amount of MNPs loaded in the tumor on the capability of this system to reach hyperthermia temperature (at least 43 °C), while also ensuring that the surrounding tissue temperature stays below this limit. Based on comparison of the bulk magnetic heating to local magnetic heating, conclusions could be drawn regarding which mechanism would be essential for cancer hyperthermia treatment.
2. Experimental Section
2.1 Materials
Unless specified, all reagents used for the synthesis of polymers, micelles, and MNPs were purchased from Sigma-Aldrich (St. Louis, MO) at reagent grade or better. Tetrahydrofuran (THF), used for micelle synthesis, was filtered before use by using a 0.2 μm syringe filter. Agarose in pure powder form was obtained for Acros Organics (New Jersey, NY), and Rhodamine B was obtained from ICN Biomedicals, Inc. (Irvine, CA).
Poly(ethylene glycol) (PEG), and ε-caprolactone (PCL) were purified before use in experiments. ε-Caprolactone was freshly distilled from calcium hydride and stored over 4 Å molecular sieves, Poly(ethylene glycol) monomethyl ether (Mn = 2000), was dried at 60 °C in a vacuum oven overnight and the dried polymer was stored in a desiccator. Rhodamine B (RhB) was used as received. Poly(ethylene glycol-b-caprolactone) diblock copolymer (PEG42-PCL19) was prepared by the tin-catalyzed ring-opening polymerization of ε-caprolactone from the alcohol terminus of poly(ethylene glycol) monomethyl ether, (Mn ~ 2,000) as described earlier [4]. NMR was used to determine the average degree of polymerization of the PEG block (42) and PCL block (19) [8].
2.2 MNP Synthesis and Characterization
Two different types of MNPs were investigated: one synthesized in-house (AP003) and one purchased as a nanopowder. AP003 iron oxide MNPs were synthesized by a modified thermal decomposition method suggested by Hyeon et al. [34]. The AP003 MNPs were dispersed in toluene/THF using oleic acid as a surfactant. The nanopowder (obtained from Sigma) was dispersed in DI water and decanted before use, to remove the larger sized MNPs that settled at the bottom of the vial. The crystal structure of nanopowder was stated by the manufacturer to be maghemite, and was confirmed using XPS.
X-ray photoelectron spectroscopy (XPS, Kratos AXIS165 Multitechnique Electron Spectrometer, Manchester, UK) was used to distinguish between magnetite and maghemite crystal structures of the iron oxide nanoparticles. The X-ray photoelectron spectrum for the Fe 2p binding energy region for both nanoparticles was used to determine the presence or absence of the satellite peak as reported in our previous study [23].
Transmission electron microscopy (TEM, FEI Technai F-20, Hillsboro, OR) was used to determine the size of both iron oxide MNPs. The AP003 MNPs were dispersed in hexane, whereas the maghemite nanopowder were dispersed in water. A drop of these dispersion was placed on a holey carbon-coated copper TEM grid (Energy Sciences model HC-400-Cu) and allowed to dry overnight before performing TEM. The accelerating voltage on the TEM was 200 keV. Image J analysis was conducted on TEM images to generate a size histogram and calculate a mean MNP size (Table 1). In addition to TEM, dynamic light scattering (DLS, Malvern ZEN3600, Malvern, Worcestershire, UK) was used to determine the hydrodynamic diameter of maghemite nanopowder MNPs dispersed in water. DLS was also performed on magnetic PEG42-PCL19 micelles, as reported in a previous study that revealed micelles to be 51 nm in diameter [8].
Table 1.
MNP size and magnetic properties
| Nanoparticle | Core Diameter (TEM, nm) | Hydrodynamic Diameter (DLS, nm) | Saturation Magnetization (VSM, emu/g) |
|---|---|---|---|
| Maghemite Nanopowder | 22 ± 10a | 53 ± 17a | 63 |
| AP003 Sample (Predominantly | 7 ± 1a | N/Ab | 46 |
The values are represented as mean nanoparticle size ± standard deviation
DLS could not be performed on AP003 MNPs as they were dispersed in toluene.
Based on XPS and the synthesis procedure used to synthesize these MNPs as described by Hyeon et al. [34]
Vibrating sample magnetometry (VSM, Digital Measurement Systems) was performed on the MNPs to determine saturation magnetization and MNP magnetic susceptibility. The magnetometer was calibrated using a high purity nickel standard. Magnetization curves were obtained over a range of +5000 Oe to -5000 Oe.
2.3 Magnetic coil setup and magnetic heating coil configuration
Magnetic heating was performed using a setup described in our previous study [23]. Briefly, for all magnetic heating experiments except those based on agarose tumor models, 1.2 mL of well-insulated samples (as described below) were placed in a plastic centrifuge tube inside a custom-made 4- turn coil with 4 cm inner diameter, designed to hold 3.5 cm Petri dishes (Induction Atmospheres, Rochester, NY). A 5kW power supply (Ameritherm, Model Novastar 5kW, Scottsville, NY) was used to power the heating station and coils attached to it. A chiller bath (Koolant Koolers, Model JT1000, Kalamazoo, MI) was used to circulate water at 18 °C through the center of the hollow 4 – turn coil. The magnetic heating experiments were conducted using a frequency of 430 kHz, and a field strength of 38.2 kA/m. Temperature measurements during magnetic experiments were conducted by using an infrared camera, which was positioned so that it was not affect by presence of the magnetic field (Model E40, FLIR systems, North Billerica, MA). The IR camera was positioned directly above the opening of insulated sample and the surface temperature of the MNP dispersion was recorded at 30 second intervals.
2.4 Making agarose gel based tumor model
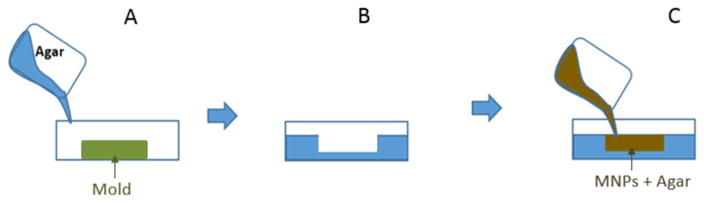
Agarose gel-based tumor models were formed using a disc of MNP-loaded agarose in the center (mimicking a tumor loaded with MNPs) surrounded by a concentric disc of plain agarose gel (mimicking healthy tissues) inside a 3.5 cm Petri dish (Figure 1). The nanopowder loaded 1.5 % (w/v) agarose gel was synthesized by mixing 0.075 g of agarose powder in 5 mL of 4 mg/mL maghemite nanopowder dispersion in DI water heated on a hot plate, and maintaining the mixture slightly below 80 °C. Simultaneously, a plain 1.5 % (w/v) agarose gel was made by dissolving 0.15 g agarose powder in 10 mL of DI water, and desired volume of this mixture was poured over a mold placed inside a 3.5 cm Petri dish such that the height of agarose gel inside the dish was 0.7 cm (Figure 1). Three different diameter (0.8 cm, 1.3 cm, and 1.6 cm) molds, each with a depth of 0.16 cm, were used to produce gels to simulate different tumor dimensions. When the plain agarose gel solidified over the mold, it was separated and flipped over to expose the well in its center. The previously made nanopowder loaded agarose dispersion was then poured into this well to construct a model of a MNP-targeted tumor growing in the center of healthy body tissues or organs. Magnetic heating was conducted on these gels at a field strength of 38.2 kA/m and frequency of 430 kHz for a time period of 10 min, and the temperature profile (on the top surface of agarose gel) across the diameter of the gels was measured at 0, 5, and 10 min intervals using an infrared camera with a resolution of less than 0.5 mm.
Figure 1.
Constructing agarose gel based tumor model: A) Pour plain agarose dissolved in water over mold, B) flip the solidified plain agarose gel, C) pour MNP-containing agarose into the well.
2.5 Method for measuring SAR
Magnetic heating of liquid dispersions was conducted using 1.2 mL of solution contained in a micro-centrifuge tube, placed in the axial and radial center of the magnetic heating coil. MFH was conducted for a duration of 1.5 min to 5 min (based on the sample heating rate) and the initial slope (using the linear portion of the heating curve, which included a minimum of 3 data points) of the time-temperature curve was calculated using 3 replicates for each case. Equation 5 was then used to calculate SAR.
For measuring the SAR of MNPs embedded in agarose gel, 1.2 mL of maghemite nanopowder (4 mg/mL) containing agarose gel samples were used instead of 1.2 mL liquid MNP dispersions at the same concentration. MNP containing agarose gels were formed by mixing 0.075 g agarose gel powder in 5 mL of 4 mg/mL MNP dispersion (in DI water) to make 1.5 % (w/v) MNP-containing agarose gel. The mixture was heated slightly below 80 °C to form a homogenous agarose-nanopowder dispersion. AP003 MNPs could not be used to form gels as they were dispersed in toluene. 1.2 mL of this liquid dispersion was poured into a micro-centrifuge tube and allowed to solidify. This sample was then treated similar to a fluid dispersion, and SAR was calculated as stated above.
2.6 Synthesis of RhB-PCL
A 25 mL round bottom flask was dried at 110 °C. The flask was equipped with magnetic stirring, an oil bath for heating and a dry nitrogen atmosphere. RhB (0.4913 g, 1.03 mmol), ε-caprolactone (2.4051 g, 21.1 mmol) and 2 drops of tin(II) 2-ethylhexanoate (a polymerization catalyst) were added to the reaction flask. The flask was heated to 120 °C with the oil bath and allowed to stir at 120 °C for 48 hours under nitrogen. After 48 hours, the reaction mixture was a viscous, deep purple liquid. The oil bath was removed and the reaction mixture slowly cooled to room temperature. Tetrahydrofuran (12 mL) was added to the flask and the mixture was stirred overnight after which the polymer dissolved. Hexane (~ 9 mL, a non-solvent) was added to the point of imminent precipitation. The solution was placed in the freezer at −30 °C overnight. The next day the product was isolated by suction filtration and rinsed with 90 mL hexane. It was allowed to dry on the vacuum filter to give a purple, semi-crystalline solid RhB-PCL.
2.7 Making MNP and RhB-PCL loaded micelles
Magnetic micelles loaded with RhB-PCL were synthesized to test the local temperature rise near the MNP surfaces. To synthesize these micelles, 50 mg PEG42-PCL19 polymer, and 5 mg RhB-PCL were dissolved in 1 mL of filtered THF (using 0.22 μM syringe filter), while 50 mg AP003 MNPs were dispersed in 2 mL filtered THF with 80 μL oleic acid in a second vial. The MNPs in THF were washed with 1 mL ethanol to remove excess oleic acid, and re-dispersed in 1 mL filtered THF. The contents of these two vials were mixed and added drop-wise to 10 mL of ultrapure water (resistivity of 18.2 MΩ cm) with probe sonication, followed by evaporation of THF overnight. After 24 h, this solution was diluted back to the original 10 mL volume to account for any water that may have evaporated along with THF. Aggregates of MNP-polymer were removed from the micelle solution by centrifuging it at 3000 rpm for 1 hr. These micelles were then dialyzed for 72 hours using a dialysis membrane of 50 kDa MWCO (Spectrum Laboratories, Rancho Dominguez, CA) to filter free RhB-PCL, and water was added to adjust the volume to 10 mL. Finally the micelles were filtered through a 0.45 μm syringe filter to obtain an optically clear micelle solution. A balance between the MNP loading and RhB-PCL loading in the micelles was necessary to obtain a clear reading for RhB fluorescent intensity
2.8 Local and bulk temperature measurement
During magnetic heating, bulk fluid temperatures were measured by IR camera for ferrofluids, or by Optotemp 2000 fiber optic probe (Micromaterials, Tampa, FL) for RhB-PCL magnetic micelle dispersions. Local temperatures in the micelle core were determined by measuring the fluorescent intensity of RhB during water bath or magnetic heating.
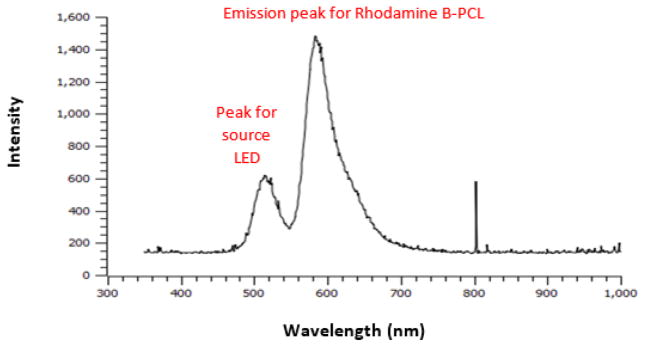
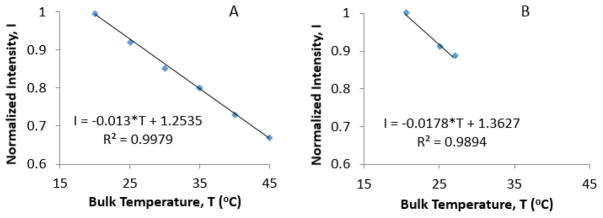
An Ocean Optics (Model USB 650 Red Tide, Dunedin, FL) portable spectrometer was used to measure the fluorescence spectra of micelles. The fluorescence spectrum was collected with a fiber optic probe (Thorlabs, Newton, NJ). The fiber optic probe had a zirconium ferrule at its terminus which allowed it to be placed near the magnetic field coils (a metal ferrule would heat during magnetic field heating experiments). To calibrate the fluorescent intensity over a range of temperatures, aqueous solutions of RhB-PCL magnetic micelles were placed in a heating jacket connected to a circulating water bath (NESLAB RTE-111, Thermo Scientific, Newington, HN). The temperature was adjusted in the range of 20 °C to 45 °C to obtain a calibration curve relating RhB-PCL fluorescent intensity to temperature. A green LED light bulb (~516 nm wavelength) was used to excite RhB-PCL in the micelle cores, resulting in an emission peak at 588 nm (Figure 2). The Optotemp probe was inserted from the top opening of the cuvette to simultaneously collect bulk temperature data. Using the data from the water bath calibration, the fluorescent intensity showed a linear relationship with temperature. For direct comparison of data, the same batch of magnetic micelles was used for both water bath heating and magnetic heating.
Figure 2.
Emission spectra for RhB-PCL inside magnetic micelle core
2.9 Magnetic heating setup for magnetic micelles
Magnetic micelles were heated using the same magnetic coil configuration and field settings as the MFH experiments. Temperature and fluorescence were measured simultaneously during magnetic heating. Inside the magnetic field, the fluorescence signal was obtained at 5, 10, and 15 minute time points, which were used to determine the corresponding local micelle core temperatures. After the micelle dispersion reached a temperature rise of 6.4 °C above room temperature after 15 minutes of exposure to the magnetic field, the rate of magnetic heating dropped to a large extent and no further data were collected. The local temperature calculated from the change in fluorescent intensity of RhB-PCL micelles was compared to the bulk solution temperature, measured by the Optotemp probe.
3. Results and Discussion
3.1 Iron oxide nanoparticle size and crystal structure
AP003 MNPs had a mean diameter and standard deviation of 7 ± 1 nm, and the maghemite nanopowder had a larger mean diameter and standard deviation of 22 ± 10 nm, based on Image J analsysis performed on TEM images for AP003 MNPs (Figure 3A) and maghemite nanopowder (Figure 3B).
Figure 3.
TEM images for A) AP003 MNPs and B) maghemite nanopowder
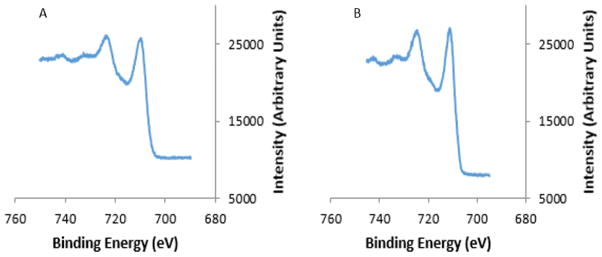
The X-ray photoelectron spectrum for the Fe 2p binding energy region for AP003 MNPs (Figure 4A) shows satellite peaks indicative of a maghemite phase [32, 33]. These satellite peaks were also seen in the spectrum for the commercial maghemite nanopowder (Figure 4B). Hyeon and coworkers have prepared a series of iron oxide nanoparticles having different diameters by the thermal decomposition of iron(III) oleate where X-ray absorption edge spectra and X-ray magnetic circular dichroism spectra showed that the phase composition (γ-Fe2O3)1-x(Fe3O4)x varied with increasing particle diameter from maghemite for 5 nm particles to magnetite for 22 nm particles [34]. The observation from the XPS that the 7 nm diameter AP003 particles were predominantly maghemite is consistent with the results reported by Hyeon and coworkers.
Figure 4.
XPS spectra used to determine the iron oxide structure of (A) AP003 MNPs (B) Maghemite nanopowder
3.2 SAR comparison by experiment and SAR calculations
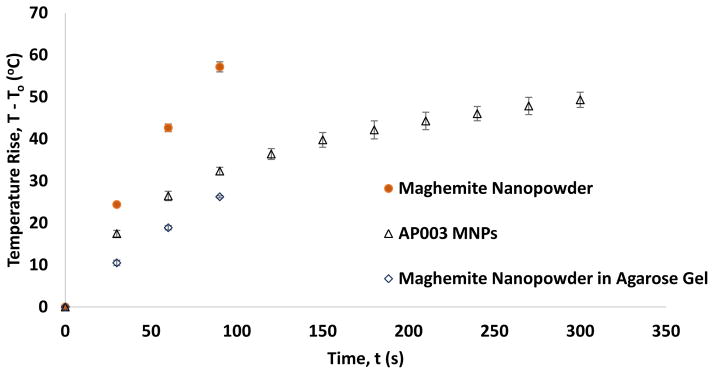
AP003 MNPs dispersed in toluene heated rapidly upon application of a 430 kHz magnetic field (Figure 5). The SAR for AP003 MNPs was found to be 135 W/g MNP or 193 W/g Fe (assuming crystal structure to be predominantly maghemite as per literature and XPS). The SAR for maghemite nanopowder was found to be significantly higher with values of 694 W/g MNP and 993 W/g Fe (assuming the crystal structure to be maghemite as per manufacturer and XPS).
Figure 5.
Normalized magnetic heating of MNPs in a fluid dispersion or embedded in agarose (H = 38.2 kA/m, f = 430 kHz). The concentration of maghemite nanopowder was 4 mg/mL in water and agarose, while concentration of AP003 MNPs was 6 mg/mL in Toluene. Temperature rise data were normalized to discount contributions of non-specific heating that were observed when the pure solvent or agarose gels with no MNPs were exposed to the same magnetic field. Error bars represent standard deviation for three replicates.
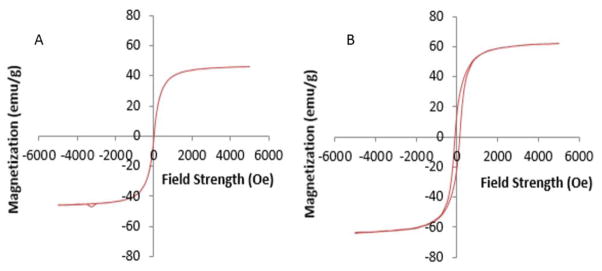
The crystal structure of iron oxides (magnetite vs maghemite) has an effect on MNP SAR for use in hyperthermia treatment [47], but since both MNPs were predominantly maghemite (Figure 4) this should not be a major factor affecting their SAR. VSM curves for the two MNPs studied here differ in that the magnetization curve for the custom synthesized AP003 MNPs displays a closed loop behavior characteristic of superparamagnetic MNPs with a saturation magnetization of 46 emu/g, while the maghemite nanopowder purchased from Sigma have an open loop magnetization curve that signifies a ferromagnetic nature and a saturation magnetization of 63 emu/g (Figure 6, Table 1). Larger MNPs may no longer display a linear response to an applied magnetic field, and in some cases hysteresis in larger MNPs has been suggested to generate a greater amount of heat compared to smaller MNPs [48].
Figure 6.
Magnetization curves for (A) AP003 MNPs and (B) maghemite nanopowder, obtained by vibrating sample magnetometry (VSM).
Aggregation of nanoparticles is a common occurrence in dispersions, and this can impact magnetic heating. For the MNPs investigated here, the maghemite nanopowder had some aggregation (see DLS results in Table 1), likely due to the lack of surface coatings to stabilize the aqueous dispersions. There have been conflicting views on whether aggregation of MNPs increases or decreases magnetic heating [49–53], and varying magnitudes of magnetic interactions occurring in these two MNP systems (maghemite nanopowder and AP003 MNPs) may affect their SAR in complex ways (as discussed later in this paper). The major factors leading to higher SAR values observed for maghemite nanopowder mainly originate from their larger diameter (where LRT may no longer be valid), and their ferromagnetic nature which can influence the processes contributing to heat generation in these MNPs.
For AP003 maghemite MNPs subjected to an AC magnetic field (H = 38.2 kA/m, f = 430 kHz), ξ was slightly less than 1 and the LRT model was used to predict the SAR values. Using the Rosensweig equation (Equation 2), the SAR of AP003 MNPs was predicted to be 10.3 W/g Fe, assuming that all MNPs were 7 nm in size and possessed an effective anisotropy of 47 kJ/m3 (as suggested by Fiorani et al. [37] for 8.7 nm maghemite MNPs). This value was an order of magnitude lower than the experimental SAR value of 193 W/g Fe obtained for AP003 MNPs subjected to this field. However, from size analysis on TEM images it was determined that the AP003 MNPs are polydisperse in size, covering a range from 3 to 11 nm (Figure 3). Thus, estimation of heat generation from these particles was determined by calculating a composite SAR value using the power generated as a function of MNP size over the distribution of diameters The value of SAR calculated after accounting for the polydispersity of these MNPs was equal to 103 W/g Fe, and was closer to the experimental value of SAR determined for this dispersion. Although the LRT model gives an estimate of SAR when ξ is close to 1, it has been described by Carrey et al. that LRT may under-predict SAR by 40 % in this regime [16]. This can lead to a significant difference in experimental and theoretical values of SAR, as observed in our study.
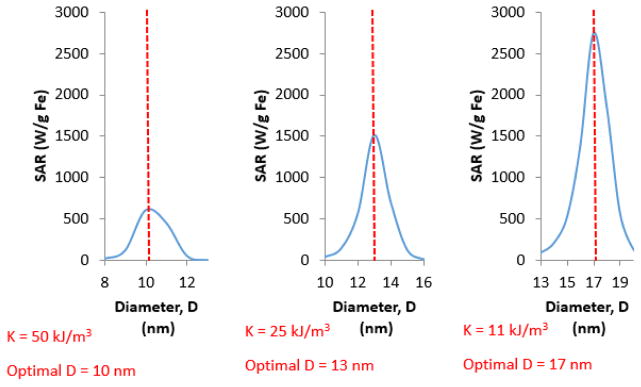
In addition to the factors discussed above, the Rosensweig equation relates power generation to Néel relaxation time, which in turn depends on the anisotropy of MNPs. There is a correlation between optimal size of MNPs for magnetic heating and effective anisotropy of MNPs (Figure 7). MNPs with larger anisotropy usually generate more heat at smaller nanoparticle sizes. To illustrate this, 17 nm MNPs were estimated to have maximum SAR values for an effective anisotropy of 11 kJ/m3 (Figure 7). But, if the effective MNP anisotropy increases to 50 kJ/m3 the optimal size for magnetic heating shifts to 10 nm (Figure 7). Deatsch et al. have described a relation between the optimal size of MNPs and their anisotropy, where a change in MNP anisotropy was observed to have a large impact on heat generation [54]. Changes in anisotropy and particle size can thus be used to tune the maximum possible SAR from application of an AC magnetic field. For example, the estimated SAR values increase from slightly over 1000 W/g Fe at K = 50 kJ/m3 and D = 10 nm, to almost 2000 W/g Fe at K = 11 kJ/m3 and D = 17 nm for maghemite nanoparticles (Figure 7). As such, tailoring the anisotropy of MNPs in relation to MNP size can serve as an effective way to maximize SAR. This result can also suggest that modifying the shape of MNPs can be used as a technique to manipulate effective MNP anisotropy and alter the amount of heat that a dispersion could produce.
Figure 7.
Effect of MNP effective anisotropy (K) on optimal MNP size to maximize power generation. SAR was estimated using Equations 2, 3, 6–9.
Heat generated by applying a magnetic field to the larger-sized maghemite nanopowder was calculated using SW based models for magnetic heating. These MNPs displayed a hysteresis loop (denoting ferromagnetic behavior), and fulfilled the condition μ 0Hmax > μ 0Hk that is essential for use of SW based models. Also, for MNPs with mean diameters around 22 nm, ξ was greater than 1 making LRT invalid for this situation. Thus, SW-based models were appropriate for predicting the effective anisotropy and calculating SAR for these MNPs.
The theoretical SAR for monodisperse maghemite MNPs ranged from 1108 W/g Fe (for 32 nm MNPs with calculated K = 11.7 kJ/m3) to 2300 W/g Fe (for 22 nm MNPs with calculated K = 27.1 kJ/m3) calculated using SW-based equations developed by Garcia-Otero et al. [38]. The SW-based equations described by Usov et al. [16, 17, 38, 39] resulted in a k value of 0.16 (making them valid to predict SAR for these conditions), and the maximum possible calculated SAR ranged from 1365 W/g Fe (for 32 nm MNPs with calculated K = 11.7 kJ/m3) to 2878 W/g Fe (for 22 nm MNPs with calculated K = 27.1 kJ/m3). It can be seen that these predicted SAR values are much larger than the experimental SAR of 993 W/g Fe, but it is important to note that the experimental system is not optimized and the α values for reported experiments have only been as large as 0.3 (instead of α = 0.39 used here in Equation 14)*16+. Additionally, the size distribution of MNPs is not accounted for while calculating this range of SAR values. Since the maghemite nanopowder used in our experiments has a wide size distribution, it is expected that the smaller nanoparticles in the dispersion generate heat due to the relaxation mechanisms as suggested by LRT, while larger particles act as SW MNPs. This is also evident from the calculations where LRT predicts a much lower SAR for nanoparticles with the size and anisotropy range stated above, whereas SW based theories over-predicts the SAR for this dispersion (> 2000 W/g Fe for 22 nm MNPs). To calculate accurate SAR values for this dispersion, the use of both LRT and SW theories is essential. These results show that the LRT and SW models can provide an estimate of SAR for MNP dispersions when their validity is tested based on the magnetic properties of the nanoparticles as well as MNP size and magnetic field parameters. Using the described models only in their domain of validity, can help avoid the error in predicting SAR values as suggested by other researchers [16, 17].
One shortcoming of these theories, when used to predict SAR, is that they neglect the effect of nanoparticle interaction on heat generation that has recently been reported in literature [55, 56]. When MNP solutions are concentrated, as is the case in these studies, the average distance between two nanoparticles greatly decreases, increasing the dipole-dipole interactions between two MNPs. In spherical MNPs with randomly oriented anisotropy axes, these interactions lower the energy barrier between two steady states, decreasing the SAR with increasing MNP concentration [55, 56]. However, when the magnitude of anisotropy decreases, the strength of dipole-dipole interactions increase and the system can switch between two minimum energy states just by the influence of the applied magnetic field; the system may now behave in a more complex manner where its SAR can either increase or decrease based on the MNP size [55]. Most MNPs in the maghemite nanopowder are relatively large in size and have a large effective anisotropy value, suggesting that the presence of MNP interactions in this system would tend to lower its SAR. This is evident when comparing the higher predicted SAR (e.g., > 2000 W/g Fe for 22 nm MNPs with effective anisotropy (K) = 27.1 kJ/m3, at H = 38.2 kA/m and f = 430 kHz where MNPs are assumed to be non-interacting) to lower experimental SAR values (e.g., 993 W/g Fe at the same field strength and frequency) where MNP interactions dominate due to a high MNP concentration used in this experiment.
LRT and SW-based theories can be valuable for predicting the change in SAR based on changes in the magnetic properties and size distribution of nanoparticle dispersions, rather than predicting exact SAR values. One source of error in SAR calculations based on these models occurs as they neglect the effect of MNP interactions on SAR, which could be overcome using computational techniques such as Monte Carlo simulations. Thus, accurately predicting exact SAR values for an experimental system may not be possible, even for monodisperse nanoparticles [17], although the accuracy of calculations would be improved significantly if the MNPs are synthesized using processes that yield dispersions with narrow size distributions and nearly identical magnetic properties. Nevertheless, these theories can be used to gain knowledge about magnetic properties that may be favorable for a specific application, and MNPs with a desired size and anisotropy can then be synthesized to optimize heating at a particular field strength and frequency. Also, if the concentration of dispersions used for the experiments is dilute enough to prevent dipole-dipole interactions between the MNPs, the models that make an assumption of non-interacting MNPs would more accurately predict trends for change in SAR based on MNP properties without the need for complex simulations to account for MNP interactions. Although making dilute solutions would help to predict accurate SAR values, the heat generated per MNP becomes significantly diminished by the heat capacity of the surrounding solution, thus making the temperature increase during heating nearly undetectable.
3.3 Comparison between SAR inside agarose gel and water
By imbedding MNPs in an agarose gel, SAR values decreased compared to the free solution, due to a significant increase in the viscosity of the medium surrounding the MNPs. The SAR for maghemite MNPs dispersed in water was 993 W/g Fe, while the SAR dropped to 449 W/g Fe inside the agarose gel. A similar trend was observed in our previous study [23], and also by other researchers who tested the effect of viscosity on MNP heating efficiency [19]. Rosensweig’s equation also predicts that an increase in viscosity decreases the heating efficiency of MNPs [14]. A possible explanation for this is that the Brownian relaxation time increases as the viscosity of the medium increases, reducing its overall contribution to magnetic heating (Equations 1, 2, and 4). This is an essential factor to consider when administering hyperthermia treatment inside the human body as MNPs would be in contact with viscous fluids and rigid tissues inside the organs. A similar scenario would be encountered when the heating efficiency of MNPs could be reduced when they are imbedded inside a rigid core of nano-scale drug delivery vehicle.
3.4 Local temperatures inside RhB-PCL micelle core
Experiments and calculations show that AP003 MNPs are capable of generating power efficiently when concentrated in solution, however there is a concern whether this amount of power generation would be adequate to cause a measurable rise in temperature inside a dispersed nano-scale system. To determine the local temperature inside nano-sized micelles, the change in fluorescent intensity of RhB-PCL inside the core of magnetic micelles was calibrated using a water bath and compared to change in fluorescent intensity of RhB-PCL caused by exposure of magnetic micelles to high frequency AC magnetic field. When subjected to temperatures controlled by a water bath, there was a 1.3 % decrease in fluorescent intensity at a peak wavelength of 588 nm per 1 °C rise in bulk solution temperature of RhB-PCL magnetic micelles over a range of temperatures from 20 – 45 °C (Figure 8A). Thus, the temperature of the micelles could be determined from the fluorescent intensity measurement. Chen et al. performed a similar experiment where they measured the fluorescent intensity of RhB soaked into a cotton thread by confocal laser scanning microscopy and compared it to temperature rise measured using fiber optic probes [46]. The 1.3 % change in intensity per °C for RhB-PCL magnetic micelles (observed in our experiment) was less than 3.4 % change per °C reported by Chen et al. who used free RhB, unlike the RhB-PCL used in this experiment [46]. The lower sensitivity in our system is likely due to the presence of the polymer micelle surrounding RhB-PCL, and presence of MNPs that could mask the fluorescence signal of the dye.
Figure 8.
Change in fluorescent intensity at 588 nm observed while heating magnetic RhB-micelles using (A) a water bath and (B) magnetic coils (H = 38.2 kA/m, f = 430 kHz). The temperature on the x-axis was measured using a fiber optic probe
The fluorescent intensity of RhB-PCL magnetic micelles inside the magnetic field decreased by 1.8 % per 1 °C temperature rise of in bulk solution (as measured using a fluoroptic probe) (Figure 8B). Thus, the change in normalized intensity was slightly higher inside the magnetic coils than the 1.3 % change in fluorescent intensity per °C observed while causing bulk temperature rise using a water bath. This suggests that the rate of local temperature rise in the vicinity of MNPs, inside the core of polymer micelles, is higher than the rate of temperature rise in the bulk micelle solution.
The fluorescent intensity change was then converted to the local temperature inside the micelle core for the hyperthermia experiment conducted inside the magnetic field (Table 2). The local temperature inside the micelle core when subjected to magnetic field is higher than the bulk fluid temperature, but the error in temperature measurement of ± 1.5 °C using the fluoroptic probe implies that this difference may not be significant (Table 2). Also, during this process the temperature inside the core of micelles did not reach hyperthermia conditions over a period of 20 minutes, suggesting that (1) the distance between the fluorophores and the MNP surfaces was larger than few nanometers [43, 45], and (2) that a greater concentration of MNPs inside the micelles may be necessary to reach temperatures needed to melt the micelle cores.
Table 2.
Bulk fluid temperature for MFH using magnetic micelles and corresponding local temperature inside the micelle core.
| Time (min) | Bulk Fluid Temperature (°C) Inside Magnetic Field (Optotemp probe) | Local Temperature (°C) in Magnetic Field (Spectroscopy) |
|---|---|---|
| 0 | 20.5 ± 1.5a | 20.5 |
| 10 | 25.0 ± 1.5a | 26.3 |
| 15 | 26.9 ± 1.5a | 28.1 |
The Optotemp probe used to measure bulk solution temperature has an error close to ± 1.5 °C.
Precise experimental techniques and maximizing the heat production inside the micelle core can reduce the error in temperature measurement, and help to determine if the difference in local and bulk dispersion temperatures would be significantly different. Few studies have successfully gauged the nano-scale temperature near the surface of a magnetic nanoparticle, but the temperature has been noted to drop just few nanometers away from MNP surface. Reidinger et al. have indirectly measured temperatures within 0.5 nm of a MNP surface, and have observed an increase in temperature as high as 45 °C upon application of a high frequency magnetic field at frequency of 334.5 kHz and field strength in the range of 7.2 – 13.5 kA/m *43+. Similar results have been published by Dias et al., where the temperature at 5.6 nm (ten times more than Riedinger et al.) away from the MNP surface was found to be 6 °C higher than the bulk fluid temperature [43, 45]. Based on these observations, no major difference would be seen in the fluorescent intensity of RhB-PCL, unless the RhB was located within a few nanometers of MNP surfaces. Since the average size of the PEG-PCL micelles is 51 nm [8], there is a possibility that the MNPs and dye molecules may not always be in close proximity of each other, lowering the effective intensity of RhB-PCL recorded through spectroscopy. The marginal rise in % change of fluorescent intensity observed for magnetically heating RhB-PCL magnetic micelles can be attributed to the fraction of RhB molecules that were situated in close proximity of MNPs inside the micelle core. Although there is a possibility of observing high temperatures next to MNP surfaces, the temperature difference between local and bulk temperatures in nano-scale systems becomes negligible at distances of just a few nanometers from the surfaces of MNPs. To probe the local nanoparticle temperature accurately it would be essential to attach the dye molecules directly onto the MNPs loaded inside the micelles.
These results emphasize the need for high MNP loading in micelles that are designed for magnetically triggered drug release applications. During drug delivery applications, the drug molecules may not always be located within few nanometers of MNP surface (inside the micelle core). In such situations high MNP loading in micelles would ensure that both the local temperature inside the micelle core and bulk solution temperature surpasses the hyperthermia temperature of 43 °C. Although the core of magnetic micelles may attain temperatures slightly higher than the bulk solution temperature, the amount of drug released from such micelles could be improved significantly by achieving a high MNP loading such that there is local as well as bulk temperature rise.
3.5 High temperature rise in macro-scale agarose gel
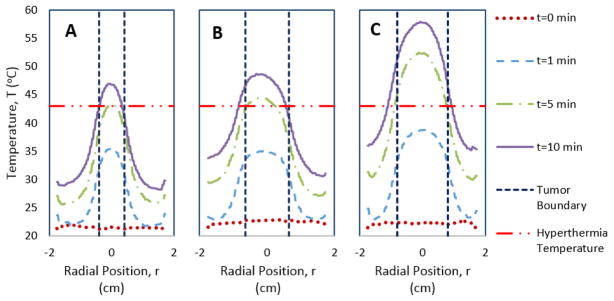
Despite no significant rise in micelle core temperature compared to bulk fluid temperature during magnetic heating, MNPs embedded inside the agarose gel tumor model (with diameters of 0.8 to 1.6 cm) showed a substantial bulk temperature rise. Compared to an agarose gel with no MNPs, those that included maghemite nanopowder easily reached temperatures above the 43 °C limit needed for MFH. For all three MNP embedded tumor diameters (0.8, 1.3, 1.6 cm), the surface temperature in the tumor region reaches well above 43 °C after 10 minutes of applied magnetic field, whereas the temperature further away from the tumor remains below 43 °C (Figure 9). However, the two larger diameter tumor models (with 1.3 cm and 1.6 cm diameters) reach the 43 °C threshold after just 5 minutes, and obtain a temperature profile that shows magnetic heating to be mostly confined to the tumor region. These temperature profiles show that when maghemite MNPs with 993 W/g Fe MNP SAR are loaded in macro-sized systems they can generate sufficient heat in tumor models subjected to magnetic hyperthermia at the stated magnetic field parameters. A potential disadvantage in this system is that the heating of surrounding tissue (modeled by agarose gel with no MNPs) can cause collateral damage to healthy tissue, as is commonly incurred in cancer therapies. Also in all three profiles the peak temperature in the center of the tumor rises to more than 46 °C, which is considered an upper limit for MFH treatment. Exposure to temperature above 46 °C changes the mode of death in tumor cells from apoptosis to necrosis (as has been shown in murine mastocytoma cells [57]), which can cause damage in surrounding healthy tissue. However this temperature rise can be easily adjusting by reducing the applied field strength, frequency, or time course of magnetic heating. The effective MNP concentration can also be manipulated to reduce the amount of MNPs that contribute to bulk temperature rise, and fine-tune the amount of heat generated in the tumor.
Figure 9.
Temperature profiles across the diameter of agarose gel models that depict: A) 0.8 cm tumor B) 1.3 cm tumor C) 1.6 cm tumor
For smaller diameter tumor models, the total amount of heat generated in the tumor volume filled with MNPs decreases as opposed to larger tumors that generate more heat due to larger quantity of accumulated MNPs. Inside the human body, MNPs administered intravenously localize inside the tumor volume due to the enhanced permeation and retention effect [58]. This implies that for small tumors, the total amount of MNPs contributing to heat generation for effective hyperthermia treatment decreases. One possible way to cause higher heat generation with a limited amount of MNPs would be to increase the magnetic field strength or frequency. However, work by Brezovich determined criteria that the product of magnetic field strength and frequency should be maintained below 4.85*108 A/m-s, to minimize patient discomfort [59]. The viable solution in this situation would be to increase the MNP concentration, but this would require efficient delivery and targeting techniques such that most MNPs would be located in the tumor core. Ultimately, bigger tumors may be easier to treat with MFH if bulk MNP heating is the only factor taken into account.
Although our experimental design provides some basic understanding of the effectiveness of MFH in simulated tumors, the effect of blood perfusion is neglected here. Blood perfusion would lead to significant heat loss as compared to the adiabatic conditions assumed in this model and MNPs with high SAR values or larger MNP concentrations would be required to achieve the desired temperature rise in a tumor. Starting with Pennes’ bio-heat transfer equation [60], which includes terms for convective heat transfer (blood perfusion) and point sources of heat (metabolic heating), recent papers have sought to improve predictive capabilities for determining transient temperature profiles in simulated tumors or human tissue. For example, recent studies have included the effect of tumor angiogenesis on bio heat transfer [61] or the effect of temperature on blood perfusion rates to improve model accuracy [62]. Despite simplifications made to observe MNP heat generation in our model, its aim was to contrast the effectiveness of the same set of MNPs at causing temperature rise in nano-scale micelles versus the more conventional form of whole tumor MFH treatment. Additionally, it is essential to note that tumors or systems that could harbor larger amounts of MNPs compared to small tumors (mm-sized), would be easier to treat using MFH when considering just the bulk temperature rise.
Recent experiments have shown that MFH can be utilized to cause cell death without a perceivable rise in bulk temperature [63]. For localized MFH to be effective, some researchers have proposed that MNPs can be internalized inside cells and targeted to specific organelles. A study by Domenech et al. has shown that MNPs can be internalized into the lysosomes of the MDA-MB-231 human breast cell line and cause cell death more effectively than non-targeted MNPs upon application of magnetic field [64]. This can serve as an efficient technique to kill cells as any damage to lysosome membranes could leak harmful fluids into the cytoplasm, leading to cell death. However, in the absence of effective techniques to target and internalize MNPs into tumors, bulk MFH can serve as an effective option to treat cancerous tumors.
The observance of a higher temperature rise in the tumor model compared to MNPs organized in the core of micelles is largely due to the collective heating of numerous MNPs over a larger volume, with a smaller surface area to volume ratio between the MNP-loaded region and the surrounding environment which reduces the effect of conductive and convective heat transfer in the tumor model. This highlights the importance of localizing MNPs within a few nanometers of targeted cells or tissue when deployed in micelles or other systems where nanoscale heat transfer can dissipate heat rapidly and there may not be significant rise in bulk solution temperature. This underscores the importance of work by many researchers to develop MNPs with high SAR to sufficiently generate heat in nano-scale systems where bulk temperature rise may be negligible.
4. Conclusions
The predicted SAR values can help to determine the heating efficiency of MNPs with different size, crystal structure, and magnetic properties. Despite producing a relatively high SAR, iron oxide MNPs appeared to cause a small rise in local temperatures in the micelle core. However, due to high signal to noise ratio of the fiber optic probe, it was not possible to observe a statistically significant temperature rise inside the core of PEG-PCL polymer micelles compared to the bulk solution temperature. When these MNPs were embedded in a macro-scale agarose gel they could generate sufficient heat to cross the lower hyperthermia temperature threshold of 43 °C. Larger tumor models achieved the hyperthermia temperature at a faster rate suggesting that the temperature rise was largely dependent on tumor size, and amount of MNPs harbored by the tumor. It was concluded that hyperthermia could be more effective for treating larger tumors, when the bulk temperature rise is the major factor leading to cell death, but MFH therapy on sub-centimeter sized tumors or individual cells will likely rely on targeting MNPs within a few nanometers of cell membranes or organelles critical to normal cell functions.
Highlights.
Evaluated the use of magnetic iron oxide nanoparticles for cancer hyperthermia
Determined power generation in nanoparticles experimentally and theoretically
Elucidated local temperature in core of polymeric micelles during hyperthermia
Evaluated bulk temperature rise in cm sized tumors during magnetic hyperthermia
Compared the rise in bulk solution temperature to local nanoparticle temperature
Acknowledgments
The authors gratefully acknowledge the support of the National Cancer Institute under NIH grant R21CA141388, and The University of Alabama through funds supporting graduate student tuition and stipends. They also thank Dr. Yuping Bao for use of dynamic light scattering equipment in her lab. This work used instruments in the Central Analytical facility, which is supported by The University of Alabama.
Footnotes
Conflicts of Interest
The authors declare no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Rhythm R. Shah, Email: rrshah@crimson.ua.edu.
Alexander R. Dombrowsky, Email: ardombrowsky@crimson.ua.edu.
Abigail L. Paulson, Email: alpaulson@crimson.ua.edu.
Margaret P. Johnson, Email: mpjohnson1@crimson.ua.edu.
David E. Nikles, Email: dnikles@mint.ua.edu.
Christopher S. Brazel, Email: cbrazel@eng.ua.edu.
References
- 1.Singh A, Sahoo SK. Magnetic nanoparticles: a novel platform for cancer theranostics. Drug discovery today. 2014;19(4):474–481. doi: 10.1016/j.drudis.2013.10.005. [DOI] [PubMed] [Google Scholar]
- 2.Hayashi K, Nakamura M, Miki H, Ozaki S, Abe M, Matsumoto T, Sakamoto W, Yogo T, Ishimura K. Magnetically responsive smart nanoparticles for cancer treatment with a combination of magnetic hyperthermia and remote-control drug release. Theranostics. 2014;4(8):834. doi: 10.7150/thno.9199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kumar S, Daverey A, Khalilzad-Sharghi V, Sahu NK, Kidambi S, Othman SF, Bahadur D. Theranostic fluorescent silica encapsulated magnetic nanoassemblies for in vitro MRI imaging and hyperthermia. RSC Advances. 2015;5(66):53180–53188. [Google Scholar]
- 4.Murase K, Aoki M, Banura N, Nishimoto K, Mimura A, Kuboyabu T, Yabata I. Usefulness of Magnetic Particle Imaging for Predicting the Therapeutic Effect of Magnetic Hyperthermia. Open Journal of Medical Imaging. 2015;5(02):85. [Google Scholar]
- 5.Overgaard J. History and heritage—an introduction. Hyperthermic oncology. 1985;2:8–9. [Google Scholar]
- 6.Streffer C, Van Beuningen D. The biological basis for tumour therapy by hyperthermia and radiation. In Hyperthermia and the Therapy of Malignant Tumors. 1987:24–70. doi: 10.1007/978-3-642-82955-0_2. [DOI] [PubMed] [Google Scholar]
- 7.van der Zee J. Heating the patient: a promising approach? Annals of oncology. 2002;13(8):1173–1184. doi: 10.1093/annonc/mdf280. [DOI] [PubMed] [Google Scholar]
- 8.Glover AL, Bennett JB, Pritchett JS, Nikles SM, Nikles DE, Nikles J, Brazel CS. Magnetic heating of iron oxide nanoparticles and magnetic micelles for cancer therapy. Magnetics, IEEE Transactions on. 2013;49(1):231–235. doi: 10.1109/TMAG.2012.2222359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Xu C, Zheng Y, Gao W, Xu J, Zuo G, Chen Y, Zhao M, Li J, Song J, Zhang N, Wang Z. Magnetic Hyperthermia Ablation of Tumors Using Injectable Fe3O4/Calcium Phosphate Cement. ACS applied materials & interfaces. 2015;7(25):13866–13875. doi: 10.1021/acsami.5b02077. [DOI] [PubMed] [Google Scholar]
- 10.Johannsen M, Thiesen B, Jordan A, Taymoorian K, Gneveckow U, Waldöfner N, Scholz R, Koch M, Lein M, Jung K, Loening SA. Magnetic fluid hyperthermia (MFH) reduces prostate cancer growth in the orthotopic Dunning R3327 rat model. The prostate. 2005;64(3):283–292. doi: 10.1002/pros.20213. [DOI] [PubMed] [Google Scholar]
- 11.Staruch RM, Hynynen K, Chopra R. Hyperthermia-mediated doxorubicin release from thermosensitive liposomes using MR-HIFU: Therapeutic effect in rabbit Vx2 tumours. International Journal of Hyperthermia. 2015;31(2):118–133. doi: 10.3109/02656736.2014.992483. [DOI] [PubMed] [Google Scholar]
- 12.Sadhukha T, Niu L, Wiedmann TS, Panyam J. Effective elimination of cancer stem cells by magnetic hyperthermia. Molecular pharmaceutics. 2013;10(4):1432–1441. doi: 10.1021/mp400015b. [DOI] [PubMed] [Google Scholar]
- 13.de Paula LB, Primo FL, Pinto MR, Morais PC, Tedesco AC. Combination of hyperthermia and photodynamic therapy on mesenchymal stem cell line treated with chloroaluminum phthalocyanine magnetic-nanoemulsion. Journal of Magnetism and Magnetic Materials. 2015;380:372–376. [Google Scholar]
- 14.Rosensweig RE. Heating magnetic fluid with alternating magnetic field. Journal of magnetism and magnetic materials. 2002;252:370–374. [Google Scholar]
- 15.Verde EL, Landi GT, Gomes JDA, Sousa MH, Bakuzis AF. Magnetic hyperthermia investigation of cobalt ferrite nanoparticles: Comparison between experiment, linear response theory, and dynamic hysteresis simulations. Journal of Applied Physics. 2012;111(12):123902. [Google Scholar]
- 16.Carrey J, Mehdaoui B, Respaud M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. Journal of Applied Physics. 2011;109(8):083921. [Google Scholar]
- 17.Shokuhfar A, Afghahi SSS. Size Controlled Synthesis of FeCo Alloy Nanoparticles and Study of the Particle Size and Distribution Effects on Magnetic Properties. Advances in Materials Science and Engineering. 2014;2014 [Google Scholar]
- 18.Mamiya H, Jeyadevan B. Hyperthermic effects of dissipative structures of magnetic nanoparticles in large alternating magnetic fields. Scientific reports. 2011;1 doi: 10.1038/srep00157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen S, Chiang CL, Hsieh S. Simulating physiological conditions to evaluate nanoparticles for magnetic fluid hyperthermia (MFH) therapy applications. Journal of Magnetism and Magnetic Materials. 2010;322(2):247–252. [Google Scholar]
- 20.Bordelon DE, Cornejo C, Grüttner C, Westphal F, DeWeese TL, Ivkov R. Magnetic nanoparticle heating efficiency reveals magneto-structural differences when characterized with wide ranging and high amplitude alternating magnetic fields. Journal of Applied Physics. 2011;109(12):124904. [Google Scholar]
- 21.Murase K, Oonoki J, Takata H, Song R, Angraini A, Ausanai P, Matsushita T. Simulation and experimental studies on magnetic hyperthermia with use of superparamagnetic iron oxide nanoparticles. Radiological physics and technology. 2011;4(2):194–202. doi: 10.1007/s12194-011-0123-4. [DOI] [PubMed] [Google Scholar]
- 22.Gonzales-Weimuller M, Zeisberger M, Krishnan KM. Size-dependant heating rates of iron oxide nanoparticles for magnetic fluid hyperthermia. Journal of Magnetism and Magnetic Materials. 2009;321(13):1947–1950. doi: 10.1016/j.jmmm.2008.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shah RR, Davis TP, Glover AL, Nikles DE, Brazel CS. Impact of magnetic field parameters and iron oxide nanoparticle properties on heat generation for use in magnetic hyperthermia. Journal of magnetism and magnetic materials. 2015;387:96–106. doi: 10.1016/j.jmmm.2015.03.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Salunkhe AB, Khot VM, Pawar SH. Magnetic hyperthermia with magnetic nanoparticles: a status review. Current topics in medicinal chemistry. 2014;14(5):572–594. doi: 10.2174/1568026614666140118203550. [DOI] [PubMed] [Google Scholar]
- 25.Kallumadil M, Tada M, Nakagawa T, Abe M, Southern P, Pankhurst QA. Suitability of commercial colloids for magnetic hyperthermia. Journal of Magnetism and Magnetic Materials. 2009;321(10):1509–1513. [Google Scholar]
- 26.Kolhatkar AG, Jamison AC, Litvinov D, Willson RC, Lee TR. Tuning the magnetic properties of nanoparticles. International journal of molecular sciences. 2013;14(8):15977–16009. doi: 10.3390/ijms140815977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Obaidat IM, Issa B, Haik Y. Magnetic Properties of Magnetic Nanoparticles for Efficient Hyperthermia. Nanomaterials. 2015;5(1):63–89. doi: 10.3390/nano5010063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.De la Presa P, Luengo Y, Multigner M, Costo R, Morales MP, Rivero G, Hernando A. Study of heating efficiency as a function of concentration, size, and applied field in γ-Fe2O3 nanoparticles. The Journal of Physical Chemistry C. 2012;116(48):25602–25610. [Google Scholar]
- 29.Ma M, Wu Y, Zhou J, Sun Y, Zhang Y, Gu N. Size dependence of specific power absorption of Fe 3 O 4 particles in AC magnetic field. Journal of Magnetism and Magnetic Materials. 2004;268(1):33–39. [Google Scholar]
- 30.Fortin JP, Wilhelm C, Servais J, Ménager C, Bacri JC, Gazeau F. Size-sorted anionic iron oxide nanomagnets as colloidal mediators for magnetic hyperthermia. Journal of the American Chemical Society. 2007;129(9):2628–2635. doi: 10.1021/ja067457e. [DOI] [PubMed] [Google Scholar]
- 31.Guardia P, Di Corato R, Lartigue L, Wilhelm C, Espinosa A, Garcia-Hernandez M, Gazeau F, Manna L, Pellegrino T. Water-soluble iron oxide nanocubes with high values of specific absorption rate for cancer cell hyperthermia treatment. ACS nano. 2012;6(4):3080–3091. doi: 10.1021/nn2048137. [DOI] [PubMed] [Google Scholar]
- 32.Mills P, Sullivan JL. A study of the core level electrons in iron and its three oxides by means of X-ray photoelectron spectroscopy. Journal of Physics D: Applied Physics. 1983;16(5):723. [Google Scholar]
- 33.Yamashita T, Hayes P. Analysis of XPS spectra of Fe 2+ and Fe 3+ ions in oxide materials. Applied Surface Science. 2008;254(8):2441–2449. [Google Scholar]
- 34.Park J, An K, Hwang Y, Park JG, Noh HJ, Kim JY, Park JH, Hwang NM, Hyeon T. Ultra-large-scale syntheses of monodisperse nanocrystals. Nature materials. 2004;3(12):891–895. doi: 10.1038/nmat1251. [DOI] [PubMed] [Google Scholar]
- 35.Smilga V, Belousov IM. The Muon Method in Science. Vol. 219. Nova Publishers; 1994. [Google Scholar]
- 36.Guivar JAR, Martínez AI, Anaya AO, Valladares LDLS, Félix LL, Dominguez AB. Structural and Magnetic Properties of Monophasic Maghemite (γ-Fe 2 O 3) Nanocrystalline Powder. Advances in Nanoparticles. 2014;2014 [Google Scholar]
- 37.Fiorani D, Testa AM, Lucari F, D’orazio F, Romero H. Magnetic properties of maghemite nanoparticle systems: surface anisotropy and interparticle interaction effects. Physica B: Condensed Matter. 2002;320(1):122–126. [Google Scholar]
- 38.Garcia-Otero J, Garcia-Bastida AJ, Rivas J. Influence of temperature on the coercive field of non-interacting fine magnetic particles. Journal of magnetism and magnetic materials. 1998;189(3):377–383. [Google Scholar]
- 39.Usov NA, Grebenshchikov YB. Hysteresis loops of an assembly of superparamagnetic nanoparticles with uniaxial anisotropy. Journal of Applied Physics. 2009;106(2):023917. [Google Scholar]
- 40.Kesharwani P, Jain K, Jain NK. Dendrimer as nanocarrier for drug delivery. Progress in Polymer Science. 2014;39(2):268–307. [Google Scholar]
- 41.Lammers T, Kiessling F, Hennink WE, Storm G. Drug targeting to tumors: principles, pitfalls and (pre-) clinical progress. Journal of controlled release. 2012;161(2):175–187. doi: 10.1016/j.jconrel.2011.09.063. [DOI] [PubMed] [Google Scholar]
- 42.Yue Y, Wang X. Nanoscale thermal probing. Nano reviews. 2012;3 doi: 10.3402/nano.v3i0.11586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Riedinger A, Guardia P, Curcio A, Garcia MA, Cingolani R, Manna L, Pellegrino T. Subnanometer local temperature probing and remotely controlled drug release based on azo-functionalized iron oxide nanoparticles. Nano letters. 2013;13(6):2399–2406. doi: 10.1021/nl400188q. [DOI] [PubMed] [Google Scholar]
- 44.Gupta A, Kane RS, Borca-Tasciuc DA. Local temperature measurement in the vicinity of electromagnetically heated magnetite and gold nanoparticles. Journal of Applied Physics. 2010;108(6):064901. [Google Scholar]
- 45.Dias JT, Moros M, del Pino P, Rivera S, Grazú V, de la Fuente JM. DNA as a molecular local thermal probe for the analysis of magnetic hyperthermia. Angewandte Chemie. 2013;125(44):11740–11743. doi: 10.1002/anie.201305835. [DOI] [PubMed] [Google Scholar]
- 46.Chen YY, Wood AW. Application of a temperature-dependent fluorescent dye (Rhodamine B) to the measurement of radiofrequency radiation-induced temperature changes in biological samples. Bioelectromagnetics. 2009;30(7):583–590. doi: 10.1002/bem.20514. [DOI] [PubMed] [Google Scholar]
- 47.Habib AH, Ondeck CL, Chaudhary P, Bockstaller MR, McHenry ME. Evaluation of iron-cobalt/ferrite core-shell nanoparticles for cancer thermotherapy. Journal of Applied Physics. 2008;103(7):07A307. [Google Scholar]
- 48.Hergt R, Dutz S, Zeisberger M. Validity limits of the Néel relaxation model of magnetic nanoparticles for hyperthermia. Nanotechnology. 2010;21(1):015706. doi: 10.1088/0957-4484/21/1/015706. [DOI] [PubMed] [Google Scholar]
- 49.Saville SL, Qi B, Baker J, Stone R, Camley RE, Livesey KL, Ye L, Crawford TM, Mefford OT. The formation of linear aggregates in magnetic hyperthermia: Implications on specific absorption rate and magnetic anisotropy. Journal of colloid and interface science. 2014;424:141–151. doi: 10.1016/j.jcis.2014.03.007. [DOI] [PubMed] [Google Scholar]
- 50.Etheridge ML, Hurley KR, Zhang J, Jeon S, Ring HL, Hogan C, Haynes CL, Garwood M, Bischof JC. Accounting for biological aggregation in heating and imaging of magnetic nanoparticles. Technology. 2014;2(03):214–228. doi: 10.1142/S2339547814500198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cabrera D, Camarero J, Ortega D, Teran FJ. Influence of the aggregation, concentration, and viscosity on the nanomagnetism of iron oxide nanoparticle colloids for magnetic hyperthermia. Journal of Nanoparticle Research. 2015;17(3):1–6. [Google Scholar]
- 52.Martinez-Boubeta C, Simeonidis K, Makridis A, Angelakeris M, Iglesias O, Guardia P, Cabot A, Yedra L, Estradé S, Peiró F, Saghi Z. Learning from nature to improve the heat generation of iron-oxide nanoparticles for magnetic hyperthermia applications. Scientific reports. 2013;3 doi: 10.1038/srep01652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Serantes D, Simeonidis K, Angelakeris M, Chubykalo-Fesenko O, Marciello M, Morales MDP, Baldomir D, Martinez-Boubeta C. Multiplying magnetic hyperthermia response by nanoparticle assembling. The Journal of Physical Chemistry C. 2014;118(11):5927–5934. [Google Scholar]
- 54.Deatsch AE, Evans BA. Heating efficiency in magnetic nanoparticle hyperthermia. Journal of Magnetism and Magnetic Materials. 2014;354:163–172. [Google Scholar]
- 55.Ruta S, Chantrell R, Hovorka O. Unified model of hyperthermia via hysteresis heating in systems of interacting magnetic nanoparticles. Scientific reports. 2015;5 doi: 10.1038/srep09090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hovorka O, Barker J, Friedman G, Chantrell RW. Role of geometrical symmetry in thermally activated processes in clusters of interacting dipolar moments. Physical Review B. 2014;89(10):104410. [Google Scholar]
- 57.Harmon BV, Corder AM, Collins RJ, Gobe GC, Allen J, Allan DJ, Kerr JFR. Cell death induced in a murine mastocytoma by 42–47 C heating in vitro: evidence that the form of death changes from apoptosis to necrosis above a critical heat load. International journal of radiation biology. 1990;58(5):845–858. doi: 10.1080/09553009014552221. [DOI] [PubMed] [Google Scholar]
- 58.Brannon-Peppas L, Blanchette JO. Nanoparticle and targeted systems for cancer therapy. Advanced drug delivery reviews. 2012;64:206–212. doi: 10.1016/j.addr.2004.02.014. [DOI] [PubMed] [Google Scholar]
- 59.Brezovich IA. Low frequency hyperthermia. Medical Physics, Monograph. 1988;16:82–111. [Google Scholar]
- 60.Incropera FP, Lavine AS, Bergman TL, Dewitt DP. Introduction to heat transfer 2007 [Google Scholar]
- 61.Yifat J, Gannot I. 3D discrete angiogenesis dynamic model and stochastic simulation for the assessment of blood perfusion coefficient and impact on heat transfer between nanoparticles and malignant tumors. Microvascular research. 2015;98:197–217. doi: 10.1016/j.mvr.2014.01.006. [DOI] [PubMed] [Google Scholar]
- 62.Reis RF, dos Santos Loureiro F, Lobosco M. 3D numerical simulations on GPUs of hyperthermia with nanoparticles by a nonlinear bioheat model. Journal of Computational and Applied Mathematics 2015 [Google Scholar]
- 63.Creixell M, Bohorquez AC, Torres-Lugo M, Rinaldi C. EGFR-targeted magnetic nanoparticle heaters kill cancer cells without a perceptible temperature rise. ACS nano. 2011;5(9):7124–7129. doi: 10.1021/nn201822b. [DOI] [PubMed] [Google Scholar]
- 64.Domenech M, Marrero-Berrios I, Torres-Lugo M, Rinaldi C. Lysosomal membrane permeabilization by targeted magnetic nanoparticles in alternating magnetic fields. ACS nano. 2013;7(6):5091–5101. doi: 10.1021/nn4007048. [DOI] [PubMed] [Google Scholar]