Thermodynamic control of anvil cloud amount

Significance

Assessing the response of clouds to global warming remains a challenge of climate science. Past research has elucidated what controls the height and temperature of high-level anvil clouds, but the factors that control their horizontal extent remained uncertain. We show that the anvil cloud amount is expected to shrink as the climate warms or when convection becomes more clustered, due to a mechanism rooted in basic energetic and thermodynamic properties of the atmosphere. It is supported by three climate models and consistent with results from a cloud-resolving model and observations. We thus believe that this mechanism is robust and that it adds a new piece to understanding how clouds respond to climate warming.

Abstract

General circulation models show that as the surface temperature increases, the convective anvil clouds shrink. By analyzing radiative–convective equilibrium simulations, we show that this behavior is rooted in basic energetic and thermodynamic properties of the atmosphere: As the climate warms, the clouds rise and remain at nearly the same temperature, but find themselves in a more stable atmosphere; this enhanced stability reduces the convective outflow in the upper troposphere and decreases the anvil cloud fraction. By warming the troposphere and increasing the upper-tropospheric stability, the clustering of deep convection also reduces the convective outflow and the anvil cloud fraction. When clouds are radiatively active, this robust coupling between temperature, high clouds, and circulation exerts a positive feedback on convective aggregation and favors the maintenance of strongly aggregated atmospheric states at high temperatures. This stability iris mechanism likely contributes to the narrowing of rainy areas as the climate warms. Whether or not it influences climate sensitivity requires further investigation.

How do clouds respond to a change in surface temperature? The answer is central to understanding how Earth’s average surface temperature responds to external perturbations. But understanding how clouds change, particularly high clouds, is also crucial for understanding how regional patterns of temperature and rainfall may change with surface warming (1–5).

Compelling physical arguments, with varying degrees of observational support, suggest that cloud changes with warming constitute a net positive feedback on radiative forcing (6). Two main contributors to this positive feedback are an expected reduction of low-level cloud amount (7–10) and a rise of high-level clouds (11, 12). Some arguments have also been advanced for negative feedbacks that would reduce the sensitivity of Earth’s temperature to perturbations, through for instance a greater preponderance of liquid in clouds at warmer temperatures (13) or, for reasons that are unclear, a reduction in the relative area of the wet, vs. dry, tropics with warming (14, 15). The wet tropics are very much associated with the occurrence of precipitating deep convection, whose detrained water condensate gives rise to the formation of high-level clouds referred to as anvils. A natural question thus arises: How does the area of the wet tropics, in particular their high anvil clouds, respond to warming?

A seminal contribution to understanding controls on anvil clouds was the idea of Hartmann and Larson (11) that water vapor acts, through its control on clear-sky radiative cooling, as a thermostatic control of the height at which convective outflow occurs. According to this idea [known as the fixed anvil temperature (FAT) hypothesis] anvil clouds occur at the height where the convective detrainment maximizes. This height can be determined, via mass conservation, from the height of the maximum of the mass convergence in clear-sky nonconvective areas. This mass convergence in turn is determined by the vertical gradient in the clear-sky radiative cooling that emerges when the water vapor specific humidity becomes sufficiently low, as it does at the cold temperatures of the upper troposphere. This connection between temperature, radiative cooling, and convective outflow implies that as the climate warms, the anvil clouds shift upward but experience a range of atmospheric temperatures that remains nearly unchanged or exhibits only a slight warming due to a change in static stability [an idea that has been referred to as the proportionally higher anvil temperature (PHAT) (12)]. FAT, or PHAT, has since been shown to be consistent with highly resolved numerical simulations, as well as with a variety of observational data (e.g., refs. 12, 16, 17, and references therein).

An analysis of global warming simulations from general circulation models (GCMs) and of radiative–convective equilibrium (RCE) simulations from cloud-resolving models (CRMs) suggests that as the surface temperature increases, anvil clouds rise as outlined above for well-understood reasons, but their coverage falls, for reasons that are not well understood (12, 18–21). Despite a poor understanding of changes in anvil cloud coverage (6), a closer analysis of the literature provides a hint that they might be related to the same mechanisms that control cloud height, namely FAT (12, 17, 19). In particular, Zelinka and Hartmann (12, 17) pointed out that an increase in the upper-tropospheric static stability could reduce the upper-level mass convergence in clear-sky areas, which could in turn reduce the anvil cloud coverage. Other studies suggested that factors not directly related to surface temperature such as the Brewer–Dobson circulation (22) or the prescription of the vertical distribution of ozone (17, 19) could also influence the static stability in the region of convective detrainment.

The organization of convection also influences the anvil cloud coverage. Numerical (21, 23, 24) and observational studies (25, 26) show that when convection is more clustered, the free atmosphere is drier and the area covered by anvil clouds is smaller. Because this clustering, or aggregation, is expected to occur more easily at high surface temperatures (27), such a process might affect cloud feedbacks and climate sensitivity (28, 29). However, here again it has remained unclear as to how convective aggregation influences the anvil cloud amount and whether the mechanisms are the same as those that influence anvil clouds with warming, let alone whether contemporary climate models are able to simulate such processes.

In this study, we address these questions by examining the mechanisms that control the anvil cloud amount. A hierarchy of models run in a variety of configurations have been studied, and all show a consistent behavior; nonetheless, we present our ideas mostly through the analysis of idealized experiments run by three independently developed GCMs as these best distill the basic ideas. First, we show that with warming, the models all predict a reduction of the anvil cloud amount, in a manner that is readily attributable to robust changes in the static stability of the upper troposphere. We then show that these changes in static stability are rooted in the same basic energetic and thermodynamical mechanisms that control cloud top height and that similar mechanisms control anvil cloud amount under global warming and under convective aggregation. Finally, we discuss the potential implications of these findings for large-scale circulations and the sensitivity of Earth’s surface temperature to perturbations.

Temperature Dependence of the Anvil Cloud Amount

We investigate controls on anvil cloud amount in three GCMs developed independently at the Institute Pierre-Simon Laplace (IPSL), Max-Planck Institute (MPI), and National Center for Atmospheric Research (NCAR) (Materials and Methods). Our analysis concentrates on simulations of radiative–convective equilibrium states for a large range of prescribed, globally uniform, sea surface temperatures (SSTs). In these simulations the insolation is spatially uniform and a water-covered surface is specified over the global domain. Earth’s rotational parameter is set to zero.

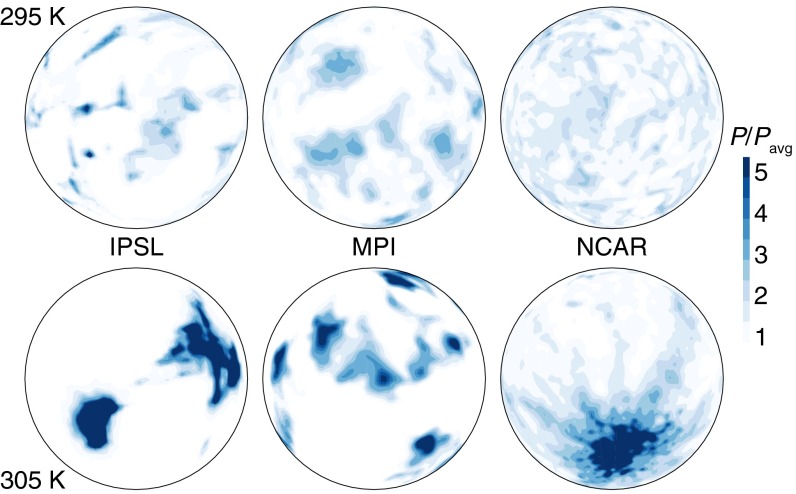
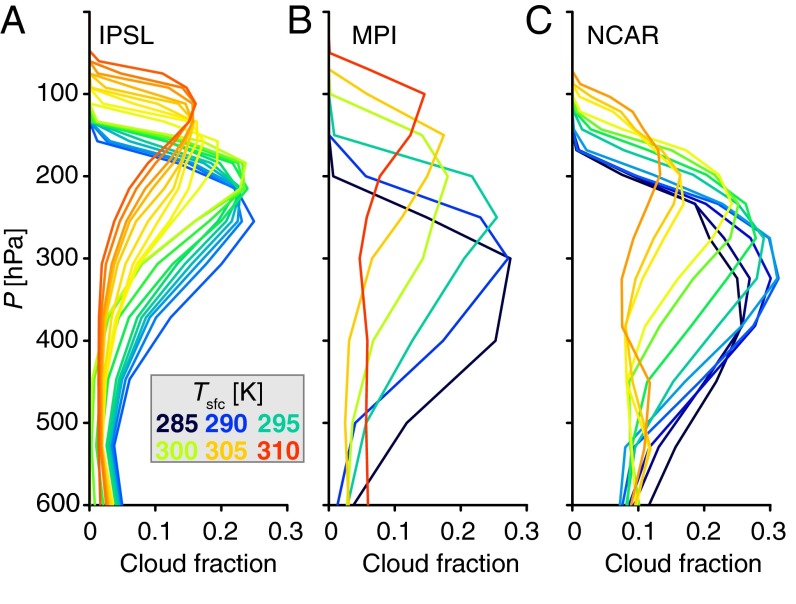
As in CRMs, under certain conditions the GCMs predict that the radiative–convective equilibrium becomes unstable: The convective areas spontaneously self-aggregate; i.e., they evolve into a state with a few isolated clusters of deep convection within a large area of subsidence, and a large-scale circulation arises (30, 31). This “self-aggregation” depends on surface temperature and becomes more pronounced at high SSTs, with a narrowing of rainy areas (Fig. 1). In parallel, as SST is increased, the peak of the globally averaged upper-level cloud fraction (hereafter, anvil cloud fraction) rises (Fig. 2). Consistent with the analysis of simulations in more realistic configurations (12), the rise is such that the anvil cloud temperature follows the temperature at the level of maximum tropospheric mass convergence in the clear-sky atmosphere (PHAT), which is nearly isothermal (cloud top warming is fivefold less than the warming of the upper-tropospheric temperatures at a constant pressure level). As the anvil clouds rise, the anvil cloud fraction falls (Fig. 2). Anvil cloud amount reduces by a factor of 2 or more as temperature increases from 290 K to 310 K. This behavior is robust across the models, despite their very different treatment of physical processes.

Fig. 1.

Monthly precipitation (normalized by its global mean value) predicted by the IPSL, MPI, and NCAR GCMs in RCE simulations forced by an SST of (Top) 295 K and (Bottom) 305 K.

Fig. 2.

Vertical profile of the cloud fraction simulated by (A) IPSL, (B) MPI, and (C) NCAR GCMs for different surface temperatures.

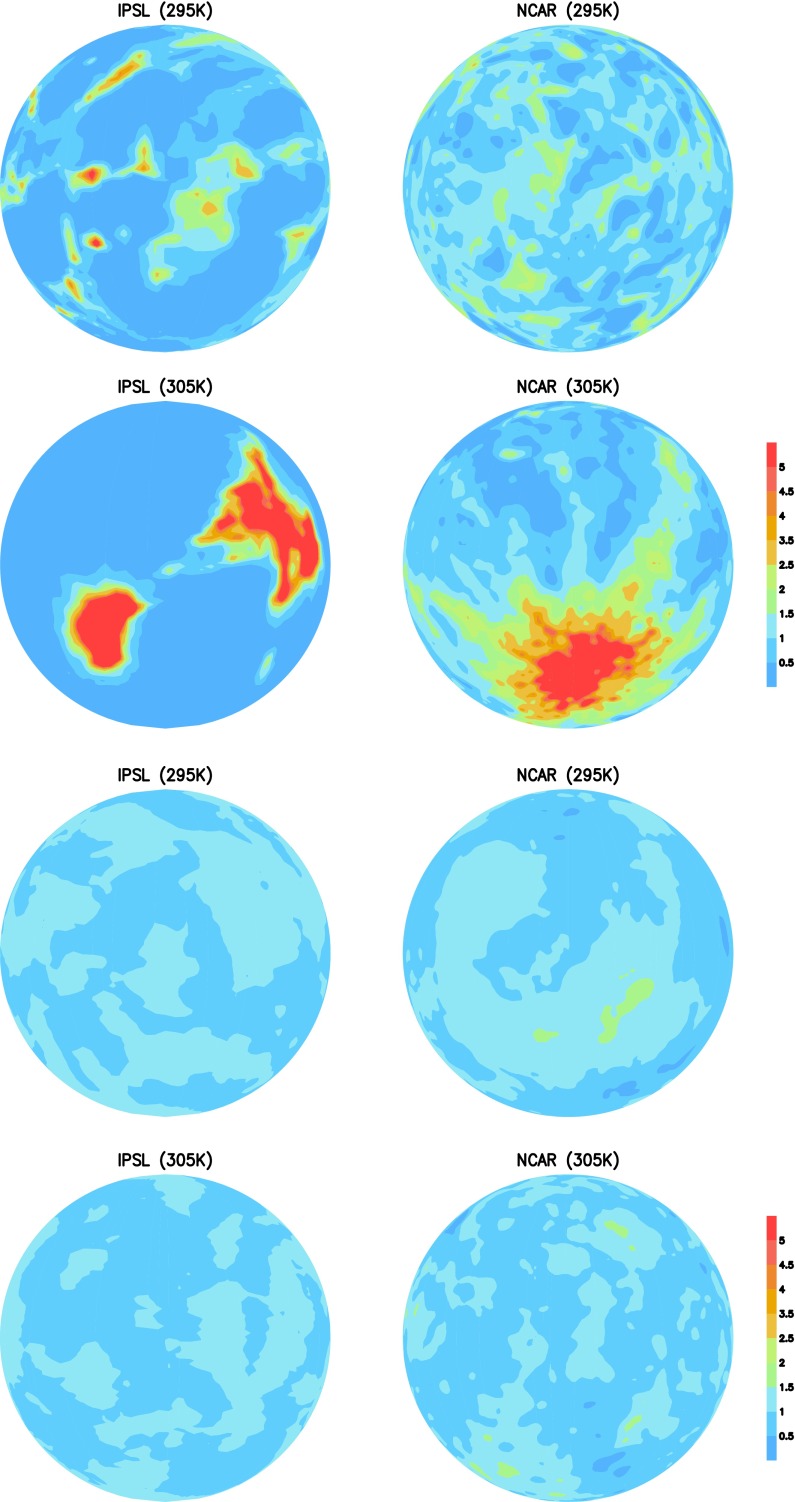
Because the initiation of self-aggregation depends on surface temperature (21, 24, 27, 31), and the clumping of convection is known to be associated with a reduction of the upper-level cloud amount (21, 25), the question arises whether the reduction of the anvil cloud amount with SST shown in Fig. 2 simply reflects the evolution of the anvil cloud fraction with convective aggregation or whether a more fundamental process is at play. We thus perform and analyze an additional ensemble of RCE simulations using the identical experimental protocol, but without cloud-radiative effects (radiative transfer is computed by assuming that clouds are transparent to radiation). In these simulations, the anvil cloud fraction is larger and the atmosphere is colder because of the lack of radiative heating by deep convective clouds, but more importantly, the simulations do not self-aggregate (24, 31, 32) (Fig. S1). Yet, as is shown below, each model still predicts a decrease of the anvil cloud amount as the SST increases. This finding suggests that convective self-aggregation does not constitute the primary cause of the decrease in anvil cloud amount with warming.

Fig. S1.

Monthly precipitation (normalized by its global mean value) predicted by the IPSL and NCAR GCMs in RCE simulations forced by an SST of 295 K or 305 K. Top four panels: with cloud-radiative effects. Bottom four panels: without cloud-radiative effects. In the absence of cloud-radiative effects, these GCMs do not predict any large-scale convective aggregation.

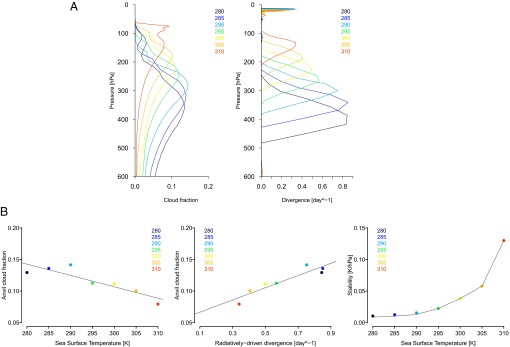
The decrease of the anvil cloud amount with warming also emerges from cloud-resolving model simulations run either in a rotating (20) or in a nonrotating RCE framework (21) (Fig. S2) and when analyzing interannual climate variations through observations (17) and in a variety of realistically configured GCM simulations, including in the absence of convective parameterization (Figs. S3 and S4). Both the consistency and the strength of the response across rather different models, and for a variety of model configurations, suggest that it might be worthwhile to try to understand the ultimate cause of this behavior.

Fig. S2.

CRM simulations: vertical profiles of (Upper Left) cloud fraction and (Upper Right) radiatively driven divergence associated with different SSTs (ranging from 280 K to 310 K), and relationship (Bottom Left) between the anvil cloud amount and SST, (Bottom Center) between the anvil cloud amount and the radiatively driven divergence, and (Bottom Right) between the static stability at the level of maximum divergence (and along the 220 K isotherm, dashed line) and SST derived from nonrotating RCE CRM simulations from Wing and Cronin (21). All quantities are domain averages computed over days 50–75 of each simulation.

Fig. S3.

Interannual variations in full-blown GCMs: relationship between the tropical mean anvil cloud amount and the tropical surface temperature (land + ocean) derived from (Left) IPSL, (Center) MPI, and (Right) NCAR GCMs in AMIP simulations run in a realistic configuration (with rotation, continents, etc.) and forced by observed sea surface temperatures and time-varying radiative forcings (greenhouse gases and aerosols). Each point represents an annual average of tropical mean quantities (30°S–30°N) during 1979–2005.

Fig. S4.

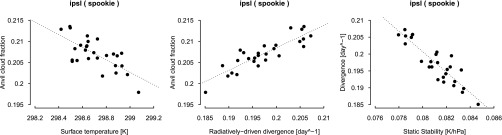
Relationships among anvil cloud fraction, $T_{\text{sfc}}$, $D_{\text{r}},$ and S. Relationships are plotted at the height of anvil clouds, derived from an AMIP simulation run with the IPSL-CM5A-LR GCM in the absence of convective parameterization [so-called SPOOKIE simulation (43)]. Each point represents an annual average of tropical mean quantities (30°S–30°N) during 1979–2005.

Mass and Energy Constraints on Anvil Clouds

Following the analysis applied to anvil cloud changes inferred from observations (17), we investigate the relationship between variations in the anvil cloud amount and variations in the peak of the radiatively driven clear-sky upper-tropospheric mass convergence. Owing to mass conservation, this peak corresponds to the maximum of mass divergence in convective regions and hence we refer to it as $D_{\text{r}}.$ We diagnose $D_{\text{r}}$ from clear-sky radiative cooling, $Q_{\text{r}},$ and the static stability, $S,$ as

$$D_{\text{r}}=\frac{\partial \omega }{\partial P}\hspace{1em}\text{with}\hspace{1em}\omega =-\hspace{0.17em}\frac{{\mathit{Q}}_{\text{r}}}{\mathit{S}}.$$ [1]

Here, ω is the downward large-scale vertical (pressure, P) velocity. In the absence of horizontal temperature gradients or other diabatic sources, the energy balance of the free troposphere is between the clear-sky radiative cooling rate ($Q_{\text{r}}<0$) and the adiabatic warming by subsiding motions ($\omega S$). The static stability can be calculated from the pressure dependence of the potential temperature (θ) profile as

$$S=-\hspace{0.17em}\frac{T}{\theta }\frac{\partial \theta }{\partial P}=\left(\frac{R_{\text{d}}}{c_{p\text{d}}}\right)\frac{T}{P}\hspace{0.17em}\left(1-\gamma \right),$$ [2]

where T is the temperature, γ denotes the ratio of the actual over dry adiabatic temperature lapse rates, and $R_{\text{d}}$ and $c_{\text{d}}$ are the gas constant and isobaric specific heat of dry air.

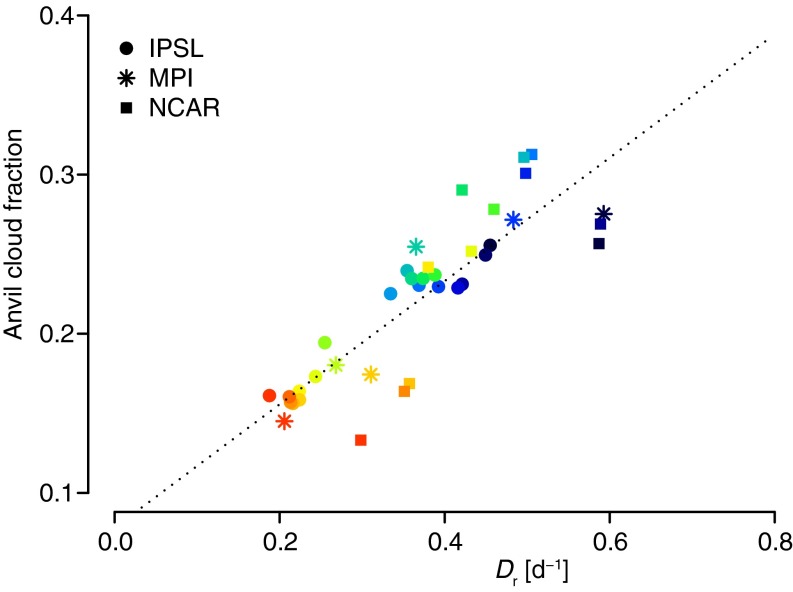
Fig. 3 shows that simulated anvil cloud fractions vary linearly with $D_{\text{r}},$ more or less consistently across models. Consistent with what is found in observations (17), this finding demonstrates that a reduction in the anvil cloud coverage, as surface temperature rises, is associated with a systematic reduction of the convective outflow ($D_{\text{r}}$) in the upper troposphere. A similar relationship emerges from simulations without cloud-radiative effects ($\partial f/\partial D_{\text{r}}=0.40\pm 0.13\hspace{0.17em}\text{d}$ and $0.37\pm 0.14\hspace{0.17em}\text{d}$ in experiments with and without cloud-radiative effects, respectively) (Fig. S5), demonstrating that this behavior is not primarily driven by changes in convective aggregation. GCM simulations suggest that the anvil cloud amount does not fall below about 10–15%. We hypothesize that some limiting process, perhaps related to constraints on the convective area, sets a lower bound on anvil cloud amount, but the details of this merit further investigation. This type of response is evident in a newer version of the MPI model, but the details of this merit further investigation.

Fig. 3.

Relationship between the anvil cloud fraction and the radiatively driven divergence $D_{\text{r}}$ predicted by three GCMs in simulations forced by a range of SSTs (colors ranging from blue to red correspond to increasing SST, and each GCM is associated with a different marker). The dashed line represents the linear regression line across all points.

Fig. S5.

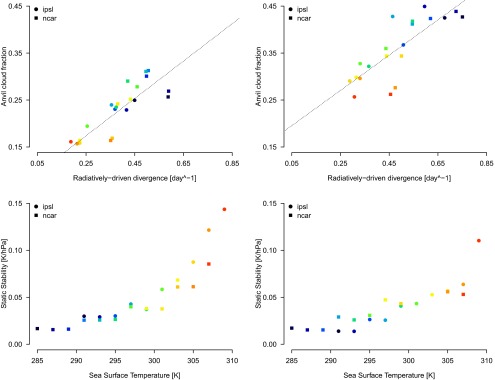
Clouds-on vs. clouds-off: comparison of the relationship (Top) between the anvil cloud amount and the radiatively driven divergence and (Bottom) between the static stability at the level of maximum divergence and SST in IPSL and NCAR GCM simulations run (Left) with and (Right) without cloud-radiative effects. (Top Left) $R^2$ = 0.68, $\partial f/\partial D_r$ = 0.40 $\pm$ 0.13 d; (Top Right) $R^2$ = 0.65, $\partial f/\partial D_r$ = 0.37 $\pm$ 0.14 d.

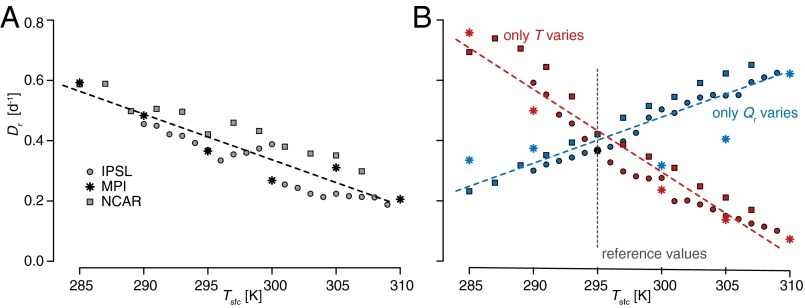
The reduction of $D_{\text{r}}$ with surface warming can largely be attributed to changes in the stability $S.$ This result is illustrated with the help of Fig. 4, which plots $D_{\text{r}}$ assuming only that either $Q_{\text{r}}$ or S is held fixed at the value it attains at a reference SST of 295 K. Because a warmer troposphere is associated with an enhanced radiative cooling, for a given static stability the subsidence increases, and hence changes in $Q_{\text{r}}$ with increasing SST tend to increase $D_{\text{r}}.$ Thus, it is the change in the static stability that is responsible for the reduction of $D_{\text{r}}$ as the SST increases: As the climate warms, anvil clouds rise and remain at nearly the same temperature, but find themselves in a more stable atmosphere (Fig. S5).

Fig. 4.

Relationship between the radiatively driven convective divergence $D_{\text{r}}$ and sea surface temperature for the three GCMs ($\partial D_{\text{r}}/\partial T_{\text{sfc}}=$ −4.1 $\pm$ 0.6%/K). (A) Relationship actually predicted by the models. (B) Relationship diagnosed by assuming that either the temperature profile or the clear-sky radiative cooling profile does not vary with sea surface temperature.

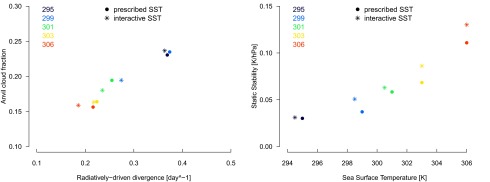
A reduction in anvil cloud fraction and in $D_{\text{r}}$ occurs in all GCMs, irrespective of the presence or not of convective aggregation or cloud-radiative effects (Fig. S5). This analysis also indicates that it is not changes in the relative importance of ozone for the radiative heating that directly influences $D_{\text{r}}.$ To test for an indirect effect of ozone heating on the stability, we have also performed simulations without radiative forcing by ozone, and these show the same behavior (Fig. S6). Similar responses emerge for simulations run with interactive SSTs (Fig. S7) and for simulations using a model that simulates clouds and convection explicitly rather than through parameterizations (CRM simulations of ref. 21) (Fig. S2). Such robust behavior likely results from a simple and basic physical mechanism.

Fig. S6.

Sensitivity to ozone and cloud-radiative effects in the IPSL GCM: comparison of (Top) aggregation vs. SST and of (Middle) the relationship between the anvil cloud amount and the radiatively driven divergence and (Bottom) between static stability at the level of maximum divergence and SST in RCE simulations (Left) with cloud-radiative effects (CRE) and ozone, (Center) with cloud-radiative effects but without ozone, and (Right) without cloud-radiative effects and without ozone. Also reported in Bottom panels are the evolutions of static stability along the 225 K isotherm. The aggregation index is defined as the fractional area of the globe covered by large-scale subsidence (31). A value close to 0.5 corresponds to the absence of aggregation.

Fig. S7.

Prescribed vs. interactive SST: relationship between (Left) the anvil cloud fraction and the radiatively driven divergence and (Right) the static stability at the level of maximum divergence and SST in IPSL GCM simulations forced by prescribed SSTs or by computing the SST interactively, using an ocean mixed layer of 10 m depth and a CO₂ atmospheric concentration set to 0.5, 0.75, 1, 2, or 3 times its present-day value.

Dependence of Stability on Cloud Base Temperature

Indeed, simple thermodynamic arguments show that if the convective outflow happens at a more or less fixed temperature, then the static stability of the outflow depends strongly on the temperature at cloud base. To demonstrate this, we assume that the temperature in the convective atmosphere is determined by a pseudo moist-adiabatic process for a cloud base fixed at 950 hPa. The results of this analysis are robust to the details of the thermodynamic process chosen to define the temperature profile, and they generalize further if processes that this calculation neglects, like radiative heating, do not fundamentally change the relationship between the resultant temperature profile and the pseudoadiabatic one (Fig. 5A).

Fig. 5.

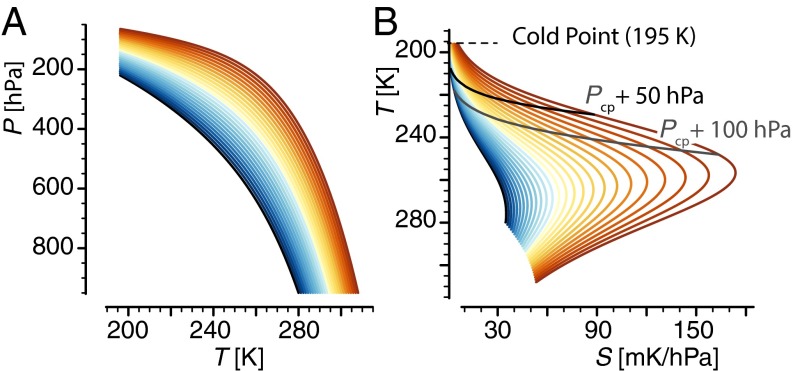
(A) Vertical profile of temperature (plotted as a function of pressure) and (B) static stability (plotted as a function of atmospheric temperature) computed by assuming that the atmosphere follows a moist adiabat starting at 950 hPa and associated with a range of cloud-base temperatures (increasing from blue to red). The dashed lines in B show a constant pressure distance (50 hPa and 100 hPa) from the cold point tropopause. Above these levels, the static stability of the actual atmosphere significantly deviates from a moist adiabatic stratification and increases up to the tropopause, the moist-adiabatic assumption thus representing a lower bound on static stability.

Our calculations indicate that as the temperature at cloud base rises, a given isotherm is associated with a lower pressure and a higher static stability (Fig. 5B). The effect is easy to understand, as it arises in part from the inverse pressure dependence in Eq. 2 and is a simple consequence of the first law of thermodynamics—it takes less work to expand the atmosphere a given amount if the ambient pressure is low.

To understand why a given isotherm is associated with a higher stability as the cloud base warms, assume, as a first approximation, that γ depends only on T. As the cloud base warms, the pressure at which any given temperature is reached, as we move upward with the convection, is lower and hence S is higher. It turns out that γ also depends on $P,$ through its dependence on the saturation specific humidity, which further amplifies the effect. The inverse pressure dependence of S on P (Eq. 2) also explains why the response of the upper-tropospheric stability to changes in cloud base (and hence surface) temperature is strongly nonlinear (with S increasing sharply for surface temperatures above 300 K) and why this feature not only appears in the idealized calculation (Fig. 5B) but also similarly and robustly emerges across the models, irrespective of their particular configuration (e.g., Figs. S2, S5, and S6).

$D_{\text{r}}$ does not exactly maximize at a fixed temperature, but rather shifts to a slightly warmer temperature as cloud base temperatures rise; e.g., following PHAT (12) rather than FAT, this makes the increase of stability with cloud base warming yet stronger. In the extreme case, where the pressure at which $D_{\text{r}}$ maximizes does not decrease with cloud base temperature, but for whatever reasons remains unchanged, then the temperature at this level must also increase, which itself causes S to increase and the magnitude of $D_{\text{r}}$ to decrease. Thus, barring a profound change in the thermodynamic processes that control the temperature profile in the convective region, we expect S to increase with rising temperature at cloud base: either because pressure decreases to keep the detrainment-level temperature constant (FAT) or because the temperature at the detrainment level must increase if the detrainment-level pressure does not decrease.

Anvil Clouds and Tropospheric Temperature

The idea that anvil temperatures might be proportionally higher with cloud base warming (i.e., PHAT) allows for a temperature effect on S. In situations when the detrainment pressure does not change much (either because the tropospheric warming is small, or the models do not resolve small differences in the detrainment pressure because of their coarse vertical resolution in the upper troposphere, or other processes such as mixing compensate for the effect of warming on the detrainment height), then the sensitivity of $S,$ and hence $D_{\text{r}},$ to the convective temperature profile may thus affect the anvil cloud fraction. The aggregation of convection, which is accompanied by a sharp rise in the convecting temperature (even for the same surface temperature) (21, 23, 33) and influences the column humidity and hence the effects of mixing with environmental air, represents one such process.

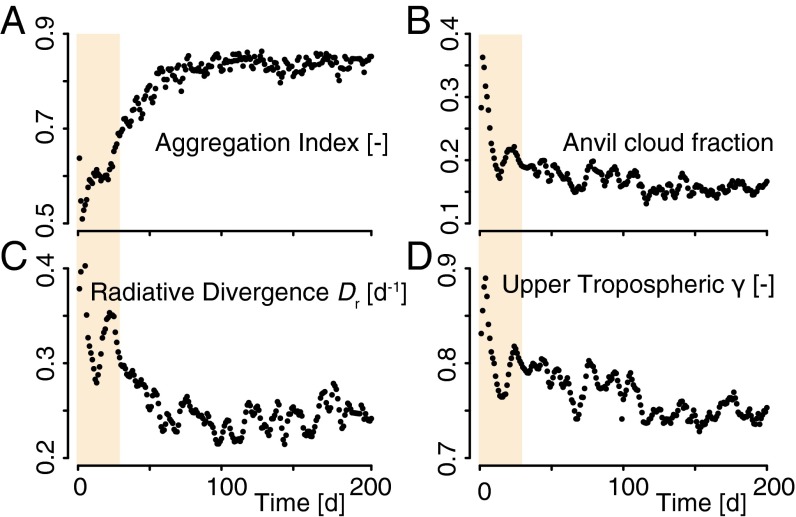
As in CRMs (e.g., ref. 21), in our simulations we find a strong relationship between the evolution of aggregation and the anvil cloud fraction. This finding is illustrated through an analysis of the time evolution of a simulation with the IPSL model for a surface temperature of 305 K (Fig. 6). At this SST, the IPSL model predicts an unstable RCE state and the convective areas spontaneously evolve to an aggregated state (the fractional area of the globe covered by large-scale subsidence, a quantity referred to as the subsiding fraction, is about 0.85 at equilibrium). As the atmosphere transitions to this self-aggregated state (see ref. 31 for a detailed analysis of the origins of this transition), the anvil cloud fraction decreases by roughly a factor of 2, and $D_{\text{r}}$ decreases by a similar amount (Fig. 6). Daily variations of the anvil cloud fraction and $D_{\text{r}}$ and between $D_{\text{r}}$ and the upper-tropospheric γ are strongly correlated (0.87 and 0.80 over the first 100 d, respectively). This result suggests that the evolution of the anvil cloud fraction as convection aggregates is also controlled by the large-scale radiative divergence in the upper troposphere. As convective self-aggregation develops, the convective region becomes associated with a higher humidity in the lower troposphere and an elevated moist adiabat, yielding a warmer free troposphere (23). In this experiment the SST is fixed and the cold point and anvil clouds do not rise much as self-aggregation proceeds. However, as the upper troposphere becomes warmer and more stable, the convective outflow and the anvil cloud fraction are reduced. In comparison, changes in the radiative cooling play much less of a role in the change in $D_{\text{r}}.$ It suggests that convective aggregation can reduce the anvil cloud fraction through its effect on the temperature profile and upper-tropospheric stability, although other microphysical processes such as an increased precipitation efficiency may amplify these effects by reducing the amount of water detrainment associated with a given mass divergence.

Fig. 6.

Daily evolutions of (A) convective self-aggregation, (B) anvil cloud amount, (C) $D_{\text{r}},$ and (D) upper-tropospheric γ predicted by the IPSL GCM in a RCE simulation forced by an SST of 305 K. Shading denotes the timescale (ca. 30 d) for subsidence to turn over the troposphere.

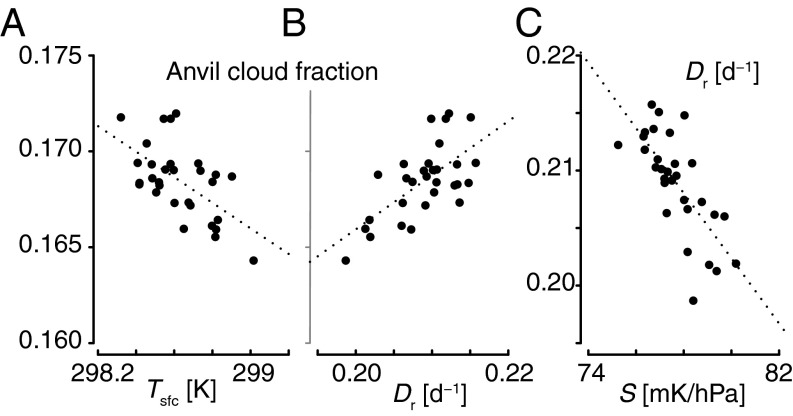
At the interannual timescale under less idealized simulations, even small increases of surface (and then tropospheric) temperature remain strongly correlated with changes in anvil cloud amount over the tropics. This result is illustrated in Fig. 7, which presents the relationship among tropical mean anvil cloud amount, stability, and $D_{\text{r}}$ in the atmospheric model intercomparison project (AMIP) (Materials and Methods) simulation by the IPSL model. AMIP simulations with the NCAR and MPI models appear to show a similar response (Fig. S3), but for those simulations the clear-sky diagnostics were missing.

Fig. 7.

Relationship (A) between anvil cloud amount and surface temperature, (B) between anvil cloud amount and Dr, and (C) between Dr and static stability at the height of anvil clouds derived from interannual climate variations simulated by the real-world GCM equivalent of the IPSL model during 1979–2005. All quantities are annual mean tropical averages (30°S–30°N).

Summary and Discussion

The analysis of nonrotating RCE simulations from three GCMs shows that as the climate warms, the convective anvils rise, to approximately maintain a constant temperature, but their coverage decreases. A nearly isothermal rise is consistent with the fixed anvil temperature hypotheses that relate the anvil cloud height to upper-level mass divergence and then to radiative cooling and atmospheric temperature (11, 12). This thermostatic control of the depth of the troposphere, when combined with the fact that convection maintains the tropospheric temperature profile near a moist adiabat, implies greater stability in the anvil cloud region as the convecting temperature increases. Hence less clear-sky mass divergence is required to balance the vertical gradient in radiative cooling, leading to less anvil cloud. Because convective aggregation increases the variance of subcloud moist static energy and raises the convecting temperature (23), enhanced clustering of convection also tends to be associated with weaker upper-level mass divergence in convective regions and a reduced anvil cloud amount.

Some other studies have also noted that the rise of upper-level clouds with surface warming was not perfectly isothermal but associated with a slight rise of cloud-top temperatures and that it was due to a more stably stratified upper troposphere (12). Different explanations were proposed for this finding, ranging from an influence of the Brewer–Dobson circulation (22) to radiative heating by ozone (19). These factors are unlikely to play a primary role in the simulations analyzed here because the increase of stability and decrease of the anvil cloud fraction occur even in the absence of Brewer–Dobson circulation (absent in the RCE framework) and in simulations without ozone. However, our work does not rule out a role for these processes. It merely suggests that a more basic mechanism controlling upper-tropospheric stability and anvil fraction is at play.

The reduction of the anvil cloud fraction as the climate warms can impact the organization of convection and atmospheric circulations. Indeed, deep convective clouds reduce very strongly the radiative cooling of the atmospheric column in which they are embedded (34) and tend to strengthen large-scale ascents (1, 2). As the surface temperature rises, the convective outflow weakens and the high-cloud amount decreases, which makes the cloud radiative heating increasingly localized and promotes elsewhere the maintenance and extension of clear subsiding areas. The coupling between temperature, anvil cloud amount, and circulation thus feeds back positively on convective aggregation and promotes the narrowing of moist convective areas as the climate warms. Indeed, in all three GCMs, as SST increases the fractional area covered by large-scale ascents (defined as regions where the vertical mean large-scale pressure vertical velocity is negative) is highly correlated to the anvil cloud fraction (0.92, 0.84, and 0.89 in the IPSL, MPI, and NCAR GCMs, respectively), and rainy areas become increasingly concentrated (Fig. 1). It shows that high surface temperatures not only facilitate the initiation of convective aggregation; they also contribute to the maintenance of a stronger aggregation of convection and therefore to the increasing concentration of rainy areas. Such a process may contribute to the tendency of models to narrow large-scale convergence zones in a warmer climate (6) and may explain why cloud-radiative effects in the free troposphere are found to be so critical, both for the growth and maintenance of convective aggregation (21, 24, 27, 31, 32) and for large-scale circulations (3, 5, 35, 36).

The systematic reduction of anvil cloud amount with increasing temperature, as we find here, can be interpreted as an iris effect, whereby more infrared radiation escapes to space as SSTs increase. We call this a stability iris to distinguish it from an iris effect resulting from microphysical mechanisms, as was originally proposed (15). By virtue of its clearer connection to near-surface temperature, through the link between the thermostatic control of anvil cloud top height and properties of the moist adiabat, the stability iris is arguably a more compelling mechanism for the same effect. However, the difference in the underlying mechanism is crucial, because in contrast to the speculation about possible microphysical mechanisms influencing anvil cloud amount, the stability iris effect is robustly represented in Earth system models.

One may thus wonder whether, and how, this mechanism influences climate sensitivity. Unlike the robust rise of the cloud top, which influences only the cloud greenhouse effect, the net radiative effect of the stability iris is more ambiguous. Changes in anvil cloud fraction influence Earth’s radiation budget at the top of the atmosphere in two antagonistic ways (through a cloud greenhouse effect and a cloud albedo effect). Observational studies (17, 25) found that the albedo effect of changes in anvil cloud fraction largely compensates the changes in the greenhouse effect. In climate change simulations, the compensation may well be model dependent, as it will be sensitive to the cloud optical thickness of the simulated upper-level clouds and to the behavior of underlying boundary-layer clouds. Moreover, in a warmer climate, if the precipitation efficiency remains the same, then the detrained condensate will increase. When combined with the decreasing anvil fraction, this result implies denser and brighter anvils that would partly oppose the radiative impact of changes in cloud fraction, more strongly so in the shortwave. This would tip the balance in favor of a reduced greenhouse effect. In addition, because a decrease of the upper-level cloud amount reduces the downward longwave radiation at the top of low-level clouds, the stability iris could increase low-cloud cover (37) or weaken the reduction of the albedo induced by the reduction in high clouds. Both effects could contribute negatively to the net cloud feedback. However, even if this result is the case, the effect is not strong enough to change the sign of the overall cloud feedback, which is, on the whole, positive in the GCMs considered here (6). This positive feedback might simply be because a reduction of anvil clouds exposes more of the climate system to the effects of positive feedbacks from low clouds. This possibility highlights that, as far as climate sensitivity is concerned, benefits from advances in understanding of controls on high clouds may have to await similar advances in understanding of controls on tropical low clouds.

Materials and Methods

The GCMs used here are the atmospheric components of three Earth System Models: IPSL-CM5A-LR [LMDZ5A, with 96 × 95 grid points regularly distributed in longitude and sine of latitude and 39 vertical levels (38)], NCAR-CESM1 [CAM5, used with the spectral element dynamics package implemented on a cubed-sphere grid, run at the ne30 resolution, i.e., $\approx$ 100 km grid spacing and 30 vertical levels (39)], and MPI-ESM-LR [ECHAM-6.1.05, with T63 spectral truncation and 47 levels (40)]. The models are run in the RCE setup, which consists of an ocean-covered Earth with diurnally varying, spatially uniform insolation and no rotation effects (30, 31, 41). The SST is prescribed and globally uniform. A set of simulations is run for a range of SSTs, with and without cloud-radiative effects (in the latter case, clouds are assumed to be transparent to radiation). The models are run for several years and unless stated otherwise, we analyze monthly outputs from the last year to avoid spin-up. Simulations of the present-day climate were run with the same GCMs, but including rotation and a realistic geography, and forced by time-varying SSTs and greenhouse gas concentrations derived from observations [so-called AMIP runs (42)].