Size-dependent forced PEG partitioning into channels: VDAC, OmpC, and α-hemolysin

Significance

With consequences for the selective partitioning of large molecules in cells, polymer partitioning into nanopores is instructive for single-molecule sensing as well as for polymer-assisted transport and packaging. Here we detect and analyze not only passive but also forced size-dependent partitioning of binary mixtures of differently sized PEGs. We probe three structurally different channels exhibiting forced partitioning that can be understood conceptually as well as quantitatively within a “polymers-pushing-polymers” model, allowing good estimates for the size-dependent pore penetration energy differences. Beyond proof of concept, forced partitioning in cells can now be recognized and used as a new tool for molecule-selective transport and active osmotically regulated packaging.

Abstract

Nonideal polymer mixtures of PEGs of different molecular weights partition differently into nanosize protein channels. Here, we assess the validity of the recently proposed theoretical approach of forced partitioning for three structurally different β-barrel channels: voltage-dependent anion channel from outer mitochondrial membrane VDAC, bacterial porin OmpC (outer membrane protein C), and bacterial channel-forming toxin α-hemolysin. Our interpretation is based on the idea that relatively less-penetrating polymers push the more easily penetrating ones into nanosize channels in excess of their bath concentration. Comparison of the theory with experiments is excellent for VDAC. Polymer partitioning data for the other two channels are consistent with theory if additional assumptions regarding the energy penalty of pore penetration are included. The obtained results demonstrate that the general concept of “polymers pushing polymers” is helpful in understanding and quantification of concrete examples of size-dependent forced partitioning of polymers into protein nanopores.

Partitioning of polymers into nanosize cavities has broad relevance (1), generally in biology, where the consequences of molecular crowding are well appreciated but not completely understood (2, 3), and in biotechnology for single-molecule sensing and characterization based on the variation of current through ion-conducting aqueous pores (4–7). The partitioning of nonionic polymers such as PEG into α-hemolysin (aHL) from Staphylococcus aureus has been previously studied and shown to be size-dependent at relatively low salt concentrations (8–13). In a different way, namely, as the amplitude of channel blockage, polymer size dependency has also been observed in single-molecule studies at high salt concentrations (4 M KCl) with aHL (14) and recently with aerolysin from Aeromonas hydrophila (15), and was shown to exhibit pronounced size sensitivity with resolution in the submonomer range.

We studied passive size-dependent partitioning and size discrimination that can be manipulated to force polymers into nanosize pores under strong nonideality, when polymer partitioning is qualitatively modified by polymer–polymer repulsion that allows polymers, which are excluded in dilute solutions, to enter the channel pore (13). This concentration-dependent partitioning was rationalized by an argument that the overlap concentration of the polymer in the pore is higher than that in the bath (16, 17). For polymer mixtures, where one component is used to preferentially push another into a cavity, this phenomenon of forced polymer partitioning was referred to as “polymers pushing polymers” (PPP) (18). Using the osmotic pressure of a polymer solution composed of various sizes of the same type of polymers, these theoretical advances quantified the forced preferential entry of polymers into a nanopore depending on their size and the pore penetration energy penalty. The theoretical analysis (18) was formulated specifically for a binary polymer mixture, where only one component is allowed to penetrate the pore, whereas the other polymer is excluded. An equation of state (EOS) of a polymer mixture (osmotic pressure as a function of composition) is first validated with osmotic measurements for a binary polymer mixture. Then this EOS, together with the observed polymer selectivity of the pore, is used to interpret the polymer partitioning coefficient.

We apply this approach to different β-barrel pores to assess to what extent it can be useful in understanding concrete examples of size-dependent forced polymer partitioning. We performed partitioning measurements of differently sized PEGs into three pores: mitochondrial voltage-dependent anion channel (VDAC), bacterial porin OmpC (outer membrane protein C), and bacterial toxin aHL. In what follows we limit ourselves exclusively to the case of PEG mixtures, composed of “short” (PEG200) and “long” (PEG3400) polymer components.

Osmotic Pressure of PEGs

The osmotic pressure of a binary polymer solution was recently addressed theoretically (18) by generalizing the EOS of a nonideal monodisperse polymer solution (19). We first test experimentally the applicability of this EOS. The ansatz for the osmotic pressure of a binary polymer mixture, $\mathrm{\Pi }\left({\varphi }_s,{\varphi }_b\right)$, as a function of the two monomer fractions has the form

$$\begin{array}{c}\frac{\overline{V}\mathrm{\Pi }\left({\varphi }_s,{\varphi }_b\right)}{kT}=-ln\left(1-{\varphi }_s-{\varphi }_b\right)+\left(1-{\varphi }_s-{\varphi }_b\right)-1-\frac{1}{2}{\left({\varphi }_s+{\varphi }_b\right)}^2\\ +\left(\frac{{\varphi }_s}{N_s}+\frac{{\varphi }_b}{N_b}\right)+\frac{5}{4}\tilde{\alpha }{\left({\varphi }_s+{\varphi }_b\right)}^{9/4}.\end{array}$$ [1]

${\varphi }_s$, ${\varphi }_b$ and $N_s$, $N_b$ are the monomer fractions and segment numbers (i.e., the polymerization index, or the number of the $\left[{\text{CH}}_2-{\text{CH}}_2-\text{O}\right]$ units in the PEG chain) of small (s) and big (b) polymers in a binary mixture. $\overline{V}$ is the molecular volume of water and $\tilde{a}=\alpha {\left(1/2-\chi \right)}^{3/4}$, where χ is the Flory–Huggins parameter and α is defined in ref. 19. In the lowest order in monomer fractions, this general form of osmotic pressure for a binary mixture reduces to the EOS introduced in ref. 20 for a monodisperse polymer solution (${\varphi }_s=0$ or ${\varphi }_b=0$) describing a smooth transition between the Van’t Hoff and the des Cloizeaux regime, formalized by the last two terms of the above equation. The last term arises from concentration fluctuations of the mixture, proportional to the inverse of the cube of the mesh size or correlation length, and the rest of the terms arise from the entropy of mixing and mean field two-body interactions. This EOS and its derivatives describe the thermodynamic equilibrium condition governing the partitioning of the binary polymer mixture components between the pore and the bulk (18).

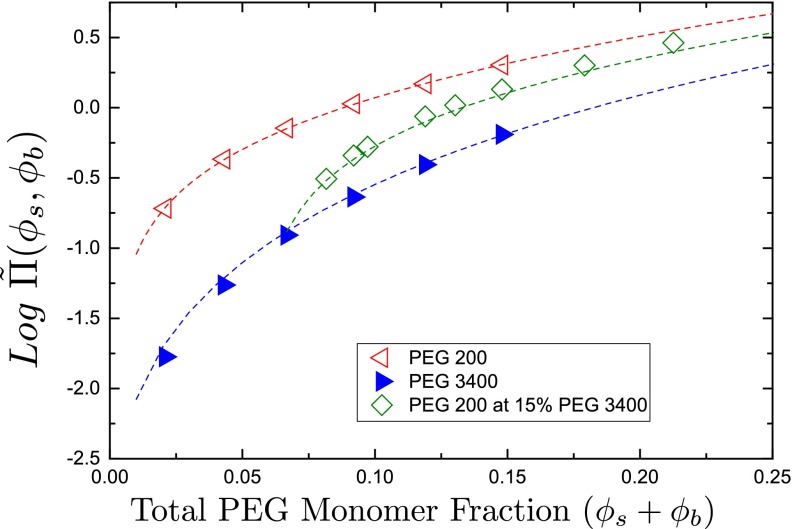
Fig. 1 shows osmotic pressure data and fits to Eq. 1, yielding ${\tilde{\alpha }}_{PEG200}=0.67$, ${\tilde{\alpha }}_{PEG3400}=0.49$ and $N_{PEG200}=6.2$, $N_{PEG3400}=76$. We observe weak dependence of $\tilde{\alpha }$ on N_s, as noted in ref. 21, with shorter chains in general having a higher $\tilde{\alpha }$. The difference between ${\tilde{\alpha }}_{PEG200}$ and ${\tilde{\alpha }}_{PEG3400}$ is much smaller than predicted from the finite-size effects in renormalization group theory (21). A fit to the binary mixtures with a single value of $\tilde{\alpha }$ thus gives a good accuracy of ∼10%. Note that the salt concentration within the relevant range (≤1 M) does not affect the equation of state of PEG (i.e., the fitted value of $\tilde{\alpha }$), nor does it affect the molar volume taken up by PEG. For possible electrolyte effects see Supporting Information.

Fig. 1.

Osmotic pressure of PEGs. Measured osmotic pressures of PEG200 and PEG3400, and their binary mixture, as described in Materials and Methods, are shown as functions of the total polymer monomer fractions. PEG200 and PEG3400 data are fit to Eq. 1; fits are shown as dashed lines. The fit to binary-mixture data were numerically calculated using the $N_s,N_b,\tilde{\alpha }$ parameters obtained from the previous fits.

Effects of PEG on Electrolyte Solution

To infer the amount of polymer partitioned into an ion channel, we need to make assumptions on how the polymer affects the channel conductance. The usual treatment is that the ion channel is a nanosize cylindrical cuvette filled with electrolyte solution, and thus total channel resistance is the integral resistance of the solution in the channel (13). The effect of polymer on channel conductance is then related to the effect of polymer on solution conductivity. We, therefore, first need to understand how polymer affects solution conductivity.

In solutions of small salt concentrations (≤1 M) addition of PEG has two effects: (i) Polymer causes a decrease in solution conductivity and (ii) polymer increases the effective salt concentration in the regions where it is excluded (however, see Supporting Information for a discussion of PEG–cation binding).

PEG Reduces Electrolyte Conductivity

The detailed mechanism of PEG-induced reduction in channel conductance involves multiple effects carefully considered elsewhere (22, 23). For simplicity, here we use an empirical approach developed and verified in a number of studies (e.g., refs. 8–13), which accounts for the major effects in question. PEG was shown to reduce the bulk solution conductivity $\left({\sigma }_0\right)$ by (i) reducing the overall ion concentration by a factor of $\left(1-\mathrm{\Phi }\right)$ and (ii) decreasing ion mobility by a factor of $e^{-k\left(\frac{\mathrm{\Phi }}{1-\mathrm{\Phi }}\right)}$ compared with that in polymer-free solution, with the latter correction termed “microviscosity” (24). Here, $\mathrm{\Phi }$ is the polymer volume fraction and k is a fitting parameter. In terms of polymer weight fraction (c), this empirical result can be expressed as

$$\sigma \left(c\right)={\sigma }_0{e}^{-\frac{k}{\xi }\frac{c}{1-c}}\xi \left(1-c\right)/\left(c+\xi \left(1-c\right)\right),$$ [2]

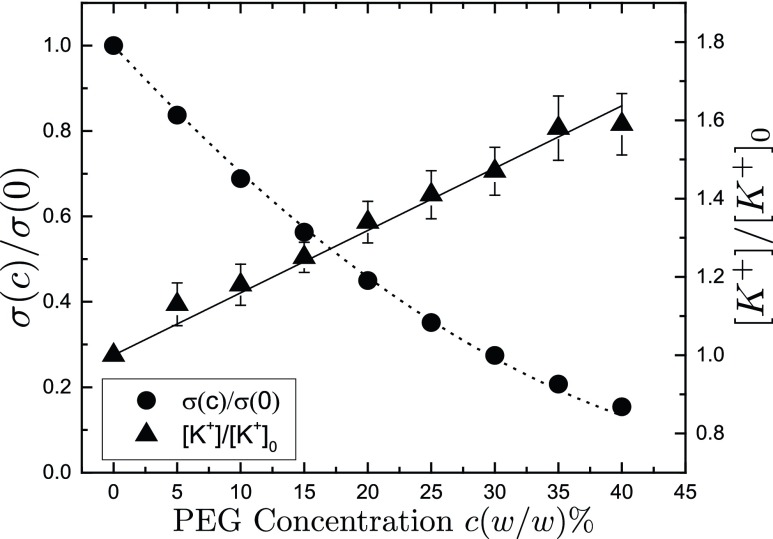
where ξ is the ratio of the partial specific volume of water to that of PEG $\xi ={\overline{v}}_{H_{2}O}/{\overline{v}}_{PEG}\approx 1.13$. Fig. 2 shows our data and a good fit to Eq. 2, yielding $k=2.66$. We observe that the reduction in conductivity depends only on polymer concentration and not on polymer molecular weight.

Fig. 2.

Normalized conductivity and effective ion concentrations of KCl solutions in the presence of PEG. PEG concentrations range from $0\text{\%}$ to $40\text{\%}$ (wt/wt). Dashed line corresponds to a fit to Eq. 2 with fitting parameter $k=2.66$. Ion selective $K^{+}$ electrode measurements are made on 0.5 M KCl electrolyte solutions, where PEG concentrations range from $0\text{\%}$ to $40\text{\%}$ (wt/wt). Solid line corresponds to a fit to Eq. 3 with fitting parameter $\beta =1.54$.

PEG Increases Effective Ion Concentration in Polymer-Excluded Regions

Ion activities in PEG solutions were previously studied in refs. 9 and 25 for NaCl solutions, using ion selective electrodes and ultrafiltration. It has been observed that PEG-free regions in these solutions, such as the interior measuring chamber of an ion-selective electrode, showed increased ion activity. We measured the ion activity of 0.5 M KCl solutions using an ion-selective $K^{+}$ electrode that completely excludes PEG from its measuring chamber. When PEG weight percent is varied from $0\text{\%}$ to $40\text{\%}$ (wt/wt), the effective ion concentration ${\left[K^{+}\right]}_{eff}$ increases empirically with c as

$${\left[K^{+}\right]}_{eff}=\left(1+\beta c\right){\left[K^{+}\right]}_0.$$ [3]

Fig. 2 shows this effect with $\beta =1.54$ for $K^{+}$ ions. The parameter β was seen to be independent of PEG molecular weight. The linearity of this effect allows us to express the increase in effective ion concentration inside the channel cavity, when there is a difference in PEG concentration between the channel cavity and the bathing solution as

$${\left[K^{+}\right]}_{eff}=\left(1+\beta \left(c_o-c_i\right)\right){\left[K^{+}\right]}_0,$$ [4]

where $c_o$ is the PEG concentration in the bath and $c_i$ is the polymer concentration inside the channel.

Effects of PEG on Channel Conductance

Unlike its influence on bulk electrolyte solutions, we expect that the PEG molecular weight will have a significant effect on the channel conductance because the characteristic size of the PEG molecules in solution is comparable to the diameter of the pore. For a number of channels it was shown that PEG200 partitions freely between the channel and the bath, decreasing channel conductance in proportion to the solution conductivity (e.g., refs. 6 and 8–11). In contrast, for large PEG3400 one expects their complete exclusion from the channel interior until their concentration in the bath is comparable to the solution overlap concentration $\left(c_o\sim c^{\text{*}}\right)$ (13).

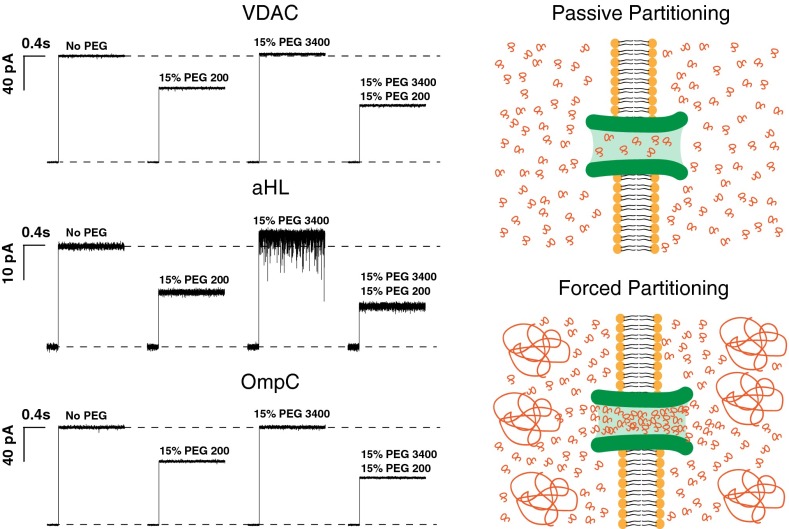
Fig. 3 shows current traces from VDAC, aHL, and OmpC after spontaneous insertion of a single channel into the membrane. It is seen that at a given concentration PEG200 causes a significant drop in channel conductance, whereas PEG3400 causes an apparent increase in channel conductance. We attribute this effect to the increase in effective ion concentration in the channel due to polymer exclusion Eq. 4. When the small PEG is added to the bathing solution in the presence of the large PEG, we see that the channel conductance decreases to a greater extent than if the latter is absent.

Fig. 3.

The effect of differently sized PEGs and their mixtures on channel conductance. Traces labeled “No PEG” show the current jump right after spontaneous channel formation. Addition of 15% (wt/wt) PEG200 causes a significant drop in single channel conductance (VDAC, 30%; aHL, 45%; and OmpC, 35%). Addition of 15% (wt/wt) PEG 3400, which does not penetrate the channel at this concentration, causes an apparent increase in single-channel conductance (VDAC, 2%; aHL, 10%; and OmpC, 2%). Addition of 15% (wt/wt) PEG200 along with 15% (wt/wt) of PEG3400 drops the channel conductance by an extra 15%, due to additional PEG200 partitioning into the pore, as it is“pushed” by PEG3400 molecules in the bathing solution. Current jumps after PEG addition correspond to the moments of transmembrane voltage application of 30 mV.

Although all three channels behave similarly, we need to quantify the amount of PEG inside the channels to determine the partition coefficients. When one measures the conductance of an ion channel, one is actually measuring the conductance of the channel proper, reduced by the access resistance of the channel. Channel access resistance depends on the channel radius and the conductivity of the solution outside the channel. We use the usual form of access resistance (26, 27), where $R_{acc}={\left(4\sigma \left(c\right)r\right)}^{-1}$ is the access resistance at one end of the channel. Other more complex expressions for the access resistance have been shown to be irrelevant in our concentration regime (28). For simplicity, we take channel radii to be symmetrical and write the total channel resistance in the absence of PEG as

$$G_m^{-1}\left(0\right)=G_p^{-1}\left(0\right)+{\left(2\sigma \left(0\right)r\right)}^{-1},$$ [5]

where $G_m$ is the measured conductance, $G_p$ is the channel proper conductance, and r is the channel radius.

Polymer addition to the bathing solution affects both the channel access resistance and the conductance of the channel proper. To determine the amount of polymer partitioned into the channel, we thus need to estimate the channel radius. Using large nonpartitioning PEG3400 is helpful in this respect. Up to the concentration of $15\text{\%}$ (wt/wt) it is excluded from the channel interior. The solution conductivity decreases according to Eq. 2 and the channel proper conductance increases according to Eq. 4 in these regimes. We take the PEG concentration inside the channel as $c_i=0$ and arrive at

$$G_m^{-1}\left(c_o\right)={\left(\left(1+\beta c_o\right)G_p\left(0\right)\right)}^{-1}+{\left(2\sigma \left(c_o\right)r\right)}^{-1}.$$ [6]

Using Eqs. 5 and 6, eliminating $G_p\left(0\right)$, we derive the following expression for the measured channel conductance at a given polymer concentration with β and r as fitting parameters:

$$G_m^{-1}\left(c_o\right)=\left(\frac{2\sigma \left(0\right)r-G_m\left(0\right)}{\left(1+\beta c_o\right)G_m\left(0\right)\left(2\sigma \left(0\right)r\right)}+\frac{1}{2\sigma \left(c_o\right)r}\right).$$ [7]

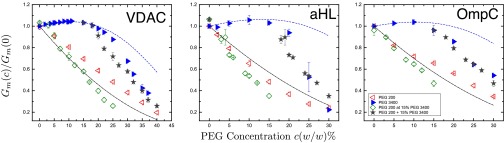
Fig. 4 shows fits of Eq. 7 to the PEG3400 data applied in the range $0\text{\%}-15\text{\%}$ (wt/wt), yielding estimates for the channel radii, the access resistance, and thus the proper channel conductance. The results of the fits are summarized in Table 1. The fits for β are within $10\text{\%}$ of what we obtain from the ion selective electrode measurements.

Fig. 4.

Normalized channel conductance of VDAC, aHL, and OmpC in the presence of different PEGs in 1.0 M KCl. Channel conductance is normalized with respect to the channel conductance measured in polymer-free 1.0 M KCl solution. Blue closed triangles show PEG3400 data. Red open triangles show PEG200 data. Green open diamonds show data for polymer mixtures, where PEG3400 concentration was kept constant at 15% (wt/wt) while PEG200 concentration was varied, in terms of the total PEG200 concentration. Gray stars show the same data in terms of the total polymer concentration. Blue dashed lines are fits to Eq. 7 in the range 0%–15% (wt/wt). Black dot-dashed lines show the expected channel conductance for polymer equipartitioning in accordance with Eq. 8. All channels show an increase in their measured conductance when PEG3400 concentrations are at or below 15% (wt/wt). All channels show an increased partitioning of PEG200 when 15% (wt/wt) PEG3400 is present in the bathing solution.

Table 1.

Derived parameters

Channel	reff, Å∗	Rt, MΩ†	Rp, MΩ†	Racc, MΩ†	β‡
VDAC	$11.1\pm 0.1$	$248\pm 6$	$208\pm 6$	$39.6\pm 0.3$	$1.46\pm 0.01$
aHL	$3.1\pm 0.13$	$1113\pm 11$	$966\pm 5$	$147\pm 6$	$1.48\pm 0.06$
OmpC	$7.9\pm 0.02$	$352\pm 2$	$296\pm 2$	$56.2\pm 0.2$	$1.42\pm 0.05$

^*Effective radius of the channel obtained from access resistance considerations by fitting PEG3400 data to Eq. 5.

^†R_t, R_p, and R_acc are the total, proper, and access resistances of the channels, respectively.

^‡Parameter defining the effective increase in electrolyte concentration, obtained by fitting PEG3400 data to Eq. 5.

Due to its small size, PEG200 is usually assumed to equipartition between the channel and the bathing solution (13). We refrain from adopting that assumption a priori and make an effort to deduce it from our experiments. Using β and r from Eq. 7, we estimate the conductance of the channel proper. In the case of equipartitioning, we expect the channel proper and measured conductance to scale with solution conductivity, $G_p\left(c_i\right)/G_p\left(0\right)=\sigma \left(c_i\right)/\sigma \left(0\right)$, and $c_i=c_o$, yielding the measured channel conductance

$$G_m\left(c_o\right)=G_m\left(0\right)\sigma \left(c_0\right)/\sigma \left(0\right).$$ [8]

Fig. 4 shows the expected channel conductances for equipartitioning polymers. We observe that in the case of aHL, PEG200 indeed behaves like an equipartitioning polymer, whereas it does not seem to equipartition into VDAC. For the case of OmpC PEG200 equipartitions at concentrations below $10\text{\%}$ and is excluded above that concentration.

Partitioning of Polymers into Ion Channels

One can use the relative drop in channel conductance at a given polymer concentration to determine the partition coefficients $p=\varphi \left(I\right)/\varphi \left(O\right)$, where $\varphi \left(I\right)$ and $\varphi \left(O\right)$ are the polymer monomer fractions inside and outside the channel respectively. We determine the polymer weight concentration inside the channel using the most general expression,

$$G_m^{-1}\left(c_o\right)=G_p^{-1}\left(c_o\right)+{\left(2\sigma \left(c_o\right)r\right)}^{-1},$$ [9]

and the channel proper conductance $G_p$ is calculated from

$$G_p\left(c_o\right)/G_p\left(0\right)=\left(1+\beta \left(c_o-c_i\right)\right)\sigma \left(c_i\right)/\sigma \left(0\right).$$ [10]

This equation is then solved numerically to determine the polymer concentration inside the channel. It should be noted that for PEG mixtures we assume that only the small PEG200 partitions into the channel. Thus, $c_o$ is the total polymer concentration outside and $c_i$ is the small polymer concentration inside the channel. Fig. 5 shows the obtained partition coefficients. Once the weight concentration is known, one can easily obtain the monomer fractions.

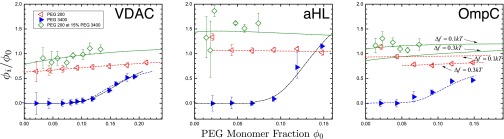
Fig. 5.

Partition coefficients of different PEGs in 1.0 M KCl for VDAC, aHL, and OmpC. Partition coefficients are calculated using Eq. 10. Data points are as indicated in the inset. PEG200 data are fit to Eq. 12 and PEG3400 data are fit to Eq. 13 (dot-dashed line) and the modified Eq. 12 (dashed line) as discussed in the text, with $\mathrm{\Delta }{f}_0$ as the only free parameter. The fitted values are listed in Table 2 and discussed in the text. Fitting to PEG mixture data (short-dashed line) was numerically calculated using Eq. 11 with the $\mathrm{\Delta }{f}_0$ parameter obtained from the PEG200 fit.

To interpret the partition coefficient data, we use the recently suggested theoretical model (18). In this model the partition coefficient p is obtained from the equality of the chemical potential of the penetrating polymer and the solvent in terms of the derivatives of the EOS (Eq. 1), predicting the following dependence on the monomer fractions:

$$\begin{array}{l}ln\left(p\right)+\mathrm{\Delta }f=N_s(ln\left(1-p{\varphi }_s\right)-ln\left(1-{\varphi }_s-{\varphi }_b\right)+\\ +\left(p{\varphi }_s-{\varphi }_s-{\varphi }_b\right)+\frac{9}{4}\tilde{\alpha }\left({\left({\varphi }_s+{\varphi }_b\right)}^{5/4}-{\left(p{\varphi }_s\right)}^{5/4}\right)),\end{array}$$ [11]

where the partition coefficient is defined as $p={\varphi }_s\left(I\right)/{\varphi }_s\left(O\right),$ with ${\varphi }_s\left(I\right)$ and ${\varphi }_s\left(O\right)$ the monomer fractions of the penetrating (small) polymer inside the channel and in the bathing solution, respectively, and ${\varphi }_b$ is the monomer fraction of the big polymer in the bathing solution, with $\tilde{\alpha }$ defined in Eq. 1. $\mathrm{\Delta }f$ is the free energy penalty of pore penetration. For a single type of polymer, this equation reduces to

$$ln\left(p\right)+\mathrm{\Delta }f=N_s\left(ln\frac{1-p{\varphi }_s}{1-{\varphi }_s}+\left(p-1\right){\varphi }_s+\frac{9}{4}\tilde{\alpha }\left(1-p^{5/4}\right){\varphi }_s^{5/4}\right).$$ [12]

We fitted our results to Eq. 12 for PEG200 and PEG3400 using $\mathrm{\Delta }f$ as a free parameter. It seems that PEG3400 partitions more sharply than Eq. 12 predicts. To describe the PEG3400 results, we then use two approaches: (i) We use a modified $\mathrm{\Delta }f$ that varies with polymer concentration and (ii) we use $\mathrm{\Delta }f$ as described in ref. 16, which relies upon different values of polymer overlap concentration for the bath and the pore:

• i)Assuming that $\mathrm{\Delta }f$ has the usual scaling form $\mathrm{\Delta }{f}_0\propto {\left(R_g/R\right)}^{5/3}$, where $R_g$ is the radius of gyration of the polymer and R is the radius of the pore, we surmise that (13) the free energy of confinement decreases with bulk polymer concentration due to a decrease in the radius of gyration of the polymer $R_g/R_{g_0}={\left({\mathrm{\Phi }}_s/{\mathrm{\Phi }}^{\text{∗}}\right)}^{-1/8}$ (29). Thus, we can express the free energy penalty as $\mathrm{\Delta }f={\left({\mathrm{\Phi }}_s/{\mathrm{\Phi }}^{\text{∗}}\right)}^{\left(-5/24\right)}\mathrm{\Delta }{f}_0$, where ${\mathrm{\Phi }}^{\text{∗}}$ is the polymer overlap concentration that depends on polymer monomer number N as ${\mathrm{\Phi }}^{\text{∗}}\sim N^{-4/5}$. Using the free energy penalty of this form, we are then able to successfully fit Eq. 12 to PEG3400 data for VDAC and OmpC.
• ii)Assuming the partitioning model suggested in ref. 16, used for explaining PEG3400 partitioning reported previously (13), we assume that the polymer overlap concentration is different in the bulk solution and in the pore. Using the equation already obtained in ref. 13,

$$ln\left(p\right)+\mathrm{\Delta }f=N_s\left(\frac{9}{5}\tilde{\alpha }\left(1-\frac{\gamma }{\mathrm{\Delta }f}\hspace{0.17em}{p}^{5/4}\right){\varphi }_s^{5/4}\right),$$ [13]

which is a limiting case of Eq. 12 with ${\varphi }_s\ll 1$,

$$ln\left(p\right)+\mathrm{\Delta }f=N_s\left(\frac{9}{4}\tilde{\alpha }\left(1-p^{5/4}\right){\varphi }_s^{5/4}\right).$$ [14]

Here $\gamma /\mathrm{\Delta }f$ is a term that arises due to the difference in overlap concentrations. γ is independent of $N_s$ and ${\varphi }_s$. Using this form of the partition coefficient, we are then able to successfully fit Eq. 13 to the PEG3400 results for aHL.

The $\mathrm{\Delta }{f}_0$ values (Table 2) clearly show a marked difference between PEG200 and PEG3400, irrespective of the details of the two models. The value of $\mathrm{\Delta }{f}_0$ for PEG3400 is significantly larger than that for PEG200. For VDAC both fits are meaningful and lead to $\sim 1.5$ difference in the estimated value of $\mathrm{\Delta }{f}_0$. For aHL acceptable fits can only be obtained if one assumes the validity of model ii, whereas OmpC data correspond to model i. Of the three channels, OmpC has the most unusual behavior for partitioning profile, which could be attributed to the trimeric pore structure and complexities it creates with access resistance (30).

Table 2.

Free energies of confinement $\mathrm{\Delta }{f}_0$

Polymer	VDAC, kT	aHL, kT	OmpC, kT
PEG 200	0.46	−0.1	0.1, 0.3
PEG 3400*	12.2	—	8.5
PEG 3400†	8.0	8.3	—

^*Obtained from fitting to Eq. 12 as described in Fig. 5.

^†Obtained from fitting to Eq. 13 as described in Fig. 5.

Discussion

A cell is a crowded place. As an example, volume concentration of macromolecules in the cytoplasm of Escherichia coli is as high as 30–40% (3, 31), leading to a significant modulation of macromolecular reaction rates and equilibria. The current consensus is that the functional consequences of molecular crowding stem from two phenomena: hard-core repulsions, otherwise referred to as “entropic effects” (32), and soft chemical interactions (3). In the present paper we demonstrate that the entropic effects are generally more subtle than just the hard-core repulsions, because they necessarily include the phenomenon of forced macromolecule partitioning into protein cavities.

We studied partitioning of PEG200 and PEG3400, as well as their binary mixtures, into three structurally different ion-conducting β-barrel pores. We compared our findings with recently developed theories of polymer partitioning into nanopores, be it for monodisperse solutions (16) or binary polymer mixtures (18). We first demonstrate that the proposed EOS (Eq. 1) agrees with our osmotic pressure data and correctly describes the basic physics, so that it can be used to analyze the partitioning of polymers into nanosize pores.

To quantify the partitioning of PEGs into the channels, we first investigated polymer effects on electrolyte solutions. It is found that their presence both decreases solution conductivity and increases the effective ion concentration in PEG free regions, consistent with previous studies (9, 24, 25). In the relevant regime of salt concentrations ($\le 1$ M) we do not observe any neutral vs. polyelectrolyte behavior of PEG (Supporting Information, Effect of Electrolytes). Combining solution conductivity with the channel conductance measured in the presence of PEG3400, we estimated the mean channel radii from access resistance (Table 1). Structural analysis and previous estimates of channel dimensions (33–35) compare favorably with our findings. For VDAC the calculated effective radius of 11 Å is comparable to the radius of 16 Å (35). For the OmpC channel the estimated effective radius is 7.9 Å, vs. the previously estimated ≈10.8 Å (34). Finally, the effective radius of aHL of 3.1 Å is comparable with the radius of the constriction but is much smaller that the radii of the channel entrances (33).

Estimating the channel access resistance was necessary for the determination of channel proper conductance, which was used to obtain the partition coefficients. We then compared these partition coefficients with different theories of partitioning (16, 18). Specifically, we found that the pore penetration by a single type of polymer, either PEG200 or PEG3400, is described accurately by the theory presented in ref. 18, especially for VDAC. It yields $\mathrm{\Delta }{f}_0$ values that are at least an order of magnitude larger for the bigger PEG (∼8–12 kT) compared with the smaller (∼0.5 kT). Assuming a PEG monomer size a ≈ 3.5–7.2 Å (20), the energies of confinement are in agreement with the scaling argument $\left(\mathrm{\Delta }{f}_0/kT=N{\left(a/R\right)}^{5/3}\right)$. Furthermore, if one estimates the concentration at which PEG3400 partitions into the channel by using the blob size argument (17) and that the blob size is described by $d_b=R_{g_0}{\left(\rho /{\rho }^{\text{∗}}\right)}^{-3/4}$ (29), where ρ is the polymer monomer density, we find that for the PEG3400 to reach the blob size of 22 Å the polymer concentration in terms of polymer weight fraction c should reach ≈12% (wt/wt), which is exactly when we start to see PEG3400 partition into VDAC.

The situation with aHL and OmpC is in this respect different. Because of the several implicit assumptions, deviations from the theoretical predictions are expected. Indeed, both approaches (16, 18) imply that (i) channel pores are circular cylinders of a constant radius, (ii) the cylinder lengths are much larger than their radii, and (iii) the entropic interactions considered above are the only interactions between the polymer and the channel. From the available structural data (33–35) it follows that assumptions i and ii could be too strong and may result in oversimplification. In what concerns assumption iii, it is known that, at least in the case of aHL, there are significant pore-PEG attractive interactions that depend on polymer size and salt concentration (4, 36).

Nevertheless, it seems that the PPP theory agrees with the polymer partitioning data presented and polymers that cannot penetrate nanosize pores act as agents pushing the penetrating polymers into the pore to an excess of their bath concentration. VDAC fits best the assumptions of the PPP theory, but the situation is less clear-cut for aHL and OmpC. In the latter cases, one needs to invoke additional assumptions that allow for the variation of the pore penetration energy penalty with polymer concentration. We hope that these findings will lead to more refined theories that take into account structural details of the particular channels.

Materials and Methods

Osmotic Pressures.

Osmotic Pressures of PEGs were measured using a Wescor Vapro 5600 vapor pressure osmometer (Wescor, Inc.). Solutions contained 5% (wt/wt) to 30% (wt/wt) PEGs in increments of 5% (wt/wt) for monodisperse PEG solutions. Binary mixtures contained 15% (wt/wt) PEG3400 and PEG200 was added up to a total concentration of 40% (wt/wt). Solutions were prepared with Millipore-grade deionized water. No electrolytes were used due to the limited range of the osmometer.

Single-Channel Recording.

See Supporting Information for full methods and sample preparation. The single-channel recording apparatus consisted of a two compartment (cis and trans) Teflon chamber (≈3 mL each) separated by a 15-μ Teflon partition with about 100-μm-diameter aperture for membrane formation. Channel current traces are recorded with Ag/AgCl electrodes in agarose bridges containing 2.0 M KCl, the cis side of the chamber being the ground, using the Axopatch 200B (Molecular Devices, LLC) patch-clamp amplifier in V-clamp mode (whole cell β = 1) with a CV-203BU headstage. The output signal was filtered by a Bessel filter at 15 kHz and saved with a sampling frequency of 50 kHz.

Conductivity and Ion Activities.

Conductivity measurements were performed with a Thermo Fisher Scientific 2-Cell conductivity probe (Thermo-Fisher); ion activities were measured with a Thomas Brand Combination K⁺ ion selective electrode (Thomas Scientific). Conductivity measurements were performed on the collected bathing solutions. Ion activities were measured with 0.5 M KCl solutions containing PEG, because 1.0 M KCl is beyond the linear range of the electrodes.

Sample Preparation

aHL from S. aureus, PEGs of average molecular weights PEG200 and PEG3400, and anhydrous pentane and hexadecane were purchased from Sigma Aldrich Chemical Co., Inc. Diphytanoylphosphatidylcholine (DPhPC, 10 mg/mL) in chloroform was purchased from Avanti Polar Lipids. VDAC was isolated from frozen mitochondrial fractions of rat liver that were a generous gift of Marco Colombini, University of Maryland, College Park, MD and purified following the standard methods (37). OmpC was purified from E. coli strain AW741, a generous gift of Dr. Anne Delcour, University of Houston. Cells were grown overnight in LB broth. The cells were harvested by centrifugation, resuspended in 50 mM sodium phosphate buffer, 0.1 M NaCl, 2 mM EDTA, and 5% (wt/vol) sucrose and broken by a French press (two times, 10 MPa). Cell debris was prespun to remove nonbroken cells (6,000 × g, 10 min) and spun down on the ultracentrifuge (100,000 × g, 40 min). OmpC was extracted from the membrane fraction (pellet) by octyl-POE detergent with ultracentrifugation at 100,000 × g in the buffer containing 20 mM sodium phosphate buffer and 3% octyl-POE (pH 7). Buffer solutions were prepared with 18.2 M $\mathrm{\Omega }$⋅cm Millipore-grade water. Stock electrolyte solution contained 1.0 M KCl and 10 mM Hepes at pH 7.4 adjusted with 8.0 N KOH. Bathing solutions containing 0% (wt/wt) up to 40% (wt/wt) PEGs were either made by adding PEGs directly to the stock electrolyte solution (for aHL and OmpC experiments) or by adding incremental amounts of PEG stock solutions (100% PEG200, 50% (wt/wt) PEG3400, 15% (wt/wt) PEG3400, and 50% PEG200) to the bathing solution containing 1.0 M KCl (for VDAC experiments).

Single-Channel Recording

The single-channel recording apparatus consisted of a two-compartment (cis and trans) Teflon chamber (≈3 mL each) separated by a 15-μ Teflon partition with about 100-μm-diameter aperture for membrane formation. Bathing solutions are symmetrically applied to both sides of the chamber (cis and trans). Channel current traces are recorded with Ag/AgCl electrodes in agarose bridges containing 2.0 M KCl, the cis side of the chamber being the virtual ground, using the Axopatch 200B (Molecular Devices, LLC) patch-clamp amplifier in V-clamp mode (whole cell β = 1) with a CV-203BU headstage. The output signal was filtered by a Bessel filter at 15 kHz and saved with a sampling frequency of 50 kHz.

Bilayer lipid membranes were formed from DPhPC using the lipid monolayer opposition technique (38), adding 10 μL of 1 mg/mL of DPhPC in pentane (pentane added after chloroform is fully evaporated under high-purity nitrogen gas) to cis and trans sides of the chamber with the aperture treated with $10\text{\%}$ (vol/vol) hexadecane in pentane. The total capacitance after stable bilayer formation was ≈90 pF.

VDAC, aHL, and OmpC were added to the cis side of the chamber in the bathing solutions at ≈1 pM concentrations from their stock solutions after stable bilayer formation. Solutions were stirred until single channel reconstitution was observed. With aHL and OmpC, channel conductances were measured in the range of −120 mV to 120 mV in steps of $\mathrm{\Delta }V=20$ mV and/or $\mathrm{\Delta }V=5$ mV. The minimum membrane potential was $\pm 20$ mV for aHL and $\pm 5$ mV for OmpC. Three to six single channel events were recorded at PEG concentrations of $0\text{\%}$ to $30\text{\%}$ for each channel. With VDAC, channel conductances were measured in the range of $-40$ mV to $+40$ mV in steps of $\mathrm{\Delta }V=2.5$ mV, minimum membrane potential being $\pm 2.5$ mV. An entire range of PEG concentrations of a single molecular weight, from $0\text{\%}$ to $40\text{\%}$ (wt/wt) was scanned using a single reconstituted channel. Experiments were repeated for three to six single-channel reconstitutions for each PEG type. For all channels the experiment was terminated if a second channel was observed. Unless otherwise stated all channel conductances reported are conductances extrapolated to 0 mV. Bathing solutions were collected for conductivity measurements.

Effect of Electrolytes

At high salt concentrations (2–4 M KCl), much larger than those considered here (≤1 M KCl), neutral PEG is seen to enter into aHL pore preferentially in the direction of the applied electric field, an observation interpreted as due to PEG–cation complexation (refs. 14, 22, 23, 39, and 40 and references therein). These PEG-polyelectrolyte effects are highly ion-specific, being absent in, for instance, LiCl, and beside direct complexation could be due to a variety of causes including the Hofmeister and steric effects at high salt concentrations. However, for conditions relevant for our experiments, no voltage dependence of the on–off rates and consequently no PEG-polyelectrolyte behavior has been detected (40).