Delayed mortality effects cut the malaria transmission potential of insecticide-resistant mosquitoes

Significance

Insecticide resistance poses one of the greatest challenges to the control of malaria and other vector-borne diseases. Quantifying the magnitude of its impact is essential to ensure the sustainability of future control programs. Mosquito vectors are defined as “resistant” when insecticides are no longer able to kill them on contact. However, they may suffer longer-term impairment following insecticide exposure that reduces their ability to transmit disease. We show that even highly resistant strains of the major malaria vector Anopheles gambiae have their life span cut by ∼50% after exposure to long-lasting insecticidal nets (LLINs). These delayed effects are sufficient to reduce their malaria transmission potential by two-thirds and could partially explain why insecticide resistance is not inextricably associated with LLIN failure.

Abstract

Malaria transmission has been substantially reduced across Africa through the distribution of long-lasting insecticidal nets (LLINs). However, the emergence of insecticide resistance within mosquito vectors risks jeopardizing the future efficacy of this control strategy. The severity of this threat is uncertain because the consequences of resistance for mosquito fitness are poorly understood: while resistant mosquitoes are no longer immediately killed upon contact with LLINs, their transmission potential may be curtailed because of longer-term fitness costs that persist beyond the first 24 h after exposure. Here, we used a Bayesian state-space model to quantify the immediate (within 24 h of exposure) and delayed (>24 h after exposure) impact of insecticides on daily survival and malaria transmission potential of moderately and highly resistant laboratory populations of the major African malaria vector Anopheles gambiae. Contact with LLINs reduced the immediate survival of moderately and highly resistant An. gambiae strains by 60–100% and 3–61%, respectively, and delayed mortality impacts occurring beyond the first 24 h after exposure further reduced their overall life spans by nearly one-half. In total, insecticide exposure was predicted to reduce the lifetime malaria transmission potential of insecticide-resistant vectors by two-thirds, with delayed effects accounting for at least one-half of this reduction. The existence of substantial, previously unreported, delayed mortality effects within highly resistant malaria vectors following exposure to insecticides does not diminish the threat of growing resistance, but posits an explanation for the apparent paradox of continued LLIN effectiveness in the presence of high insecticide resistance.

Insecticides are the most widespread and successful strategy to control and eliminate insect pest populations (1–3). However, their extensive use has inevitably triggered intense selection for insecticide resistance (IR) in targeted populations (4, 5). Consequently, resistance to one or more classes of insecticides has now been documented in over 440 insects and mite species (6). Resistance can spread extremely fast after its initial emergence. For example, the frequency of mutations associated with pyrethroid resistance has increased 50- to 1,000-fold in insects such as aphids and mosquitoes in less than a decade (7, 8).

The challenge of IR is particularly acute in the Anopheles mosquitoes that transmit malaria. Malaria remains a leading cause of mortality and morbidity throughout the tropics, where it is estimated to have killed ∼438,000 people in 2015 alone (9). Historically, disease burden has been highest in sub-Saharan Africa, but great progress has been achieved over the past 15 y with the number of malaria cases being halved (9, 10). The widespread use of long-lasting insecticidal nets (LLINs) has been the major contributor to this decline (10). LLINs provide physical protection from mosquito bites to people sleeping under them, but the main reason for their success is that the insecticides in them kill mosquitoes within a few hours of contact. The addition of insecticides to nets can almost double the preventive effect of LLINs (11). Only one class of insecticides, the pyrethroids, has World Health Organization (WHO) approval for use on LLINs (12), and their widespread use has led to the rapid emergence and increase of pyrethroid resistance all across Africa (13). With alternative insecticides for LLINs still several years away from being licensed (14), there is great concern that rapidly increasing IR levels will soon erode and reverse current and future malaria control gains.

The WHO classifies mosquitoes as being IR if the population mortality is <90% in the 24 h following exposure to insecticides in standardized bioassays (15). According to this definition, resistance to at least one class of insecticide has been identified in malaria vectors from 64 countries with ongoing malaria transmission since 2010 (15). Although standardized definitions of resistance are of value for surveillance, the reliability of current metrics for predicting the epidemiological consequences of IR are unclear. Specifically, it is unclear how LLINs maintain high levels of efficacy despite increasing levels of IR. We hypothesize that, although IR mosquitoes are no longer killed upon immediate contact with insecticides, they may still suffer longer-term consequences from exposure that indirectly reduce their disease transmission potential.

Mosquito survival is the most important biological determinant of malaria transmission intensity (16, 17). This is because only mosquitoes that survive at least 9 further days after consuming infected blood [i.e., the minimum time required for the parasite to complete its extrinsic incubation period (18)] are capable of onward transmission. Malaria vector survival rates are typically low in natural populations, with <20% expected to survive long enough to transmit (16, 19). Consequently, even if insecticides have no immediate impact on IR vectors, they could still have a considerable impact on malaria transmission if they reduce the long-term survival of vectors. Additionally, delayed mortality effects of insecticides could effectively slow down the spread of resistance by imposing a cost that prevents resistance genes from going to fixation. Although the potential advantages of slow-acting insecticides have received theoretical consideration (20), there has been little assessment of whether such effects are already acting within natural vector populations. In this study, we test whether reductions in the survival of resistant lines of the major African malaria vector, Anopheles gambiae, following repeated insecticide exposures, are evident beyond the first 24 h after exposure and quantify the associated consequences for their malaria transmission potential. Demonstration of delayed mortality impacts from LLIN exposure in resistant malaria vectors could considerably alter prediction of the epidemiological risk posed by IR (16, 17).

Results

We investigated the immediate (within 24 h) and lifelong impact of insecticide exposure in two IR strains of Anopheles gambiae mosquitoes: (i) Tiassale (TIA) and (ii) Tororo (TOR). Both strains are defined as pyrethroid-resistant according to the WHO definition (15), but the exposure duration required to kill 50% of the TIA is 26 times longer than for the TOR strain, indicating that the levels of IR are substantially higher in the former (21). Cohorts of ∼100 females of each strain were exposed either to a LLIN coated with the pyrethroid deltamethrin (Permanet 2.0; LLIN treatment) or to an untreated bed net (control) in WHO standard cone bioassays (15). Over a series of different experiments, the frequency with which mosquitoes were exposed to these treatments varied: (A) daily exposure for 5 consecutive days; (B) exposure every 4 d, for a maximum of four exposures over 16 d; and (C) exposure and feed, where mosquitoes were exposed every 4–6 d for a maximum of four exposures, and blood fed during exposure (in contrast to other regimes where mosquitoes were fed only sugar water; Methods). These regimes were selected to investigate a range of biologically plausible exposures. Specifically, under natural conditions, An. gambiae is expected to blood feed once every 2–4 d (22). If a blood meal is successfully obtained, the mosquito will refrain from feeding until eggs have been laid (∼4 d). Regime A mimics a mosquito that is repeatedly prevented from biting by the presence of a LLIN (thus contacts LLINs on consecutive nights), whereas regime C corresponds to the scenario where the mosquito is able to bite through the LLIN while simultaneously feeding. Together, these regimes cover the likely maximum (daily) and minimum (every 4 d) exposure that An. gambiae would expect in areas of high LLIN coverage. In all experiments, mosquitoes were first exposed to insecticides when they were 4–5 d old, and then monitored daily to record mortality until no survivors remained (i.e., maximum of 44 d). Each experiment (A, B, and C) was replicated twice per strain, with the exception of the daily-exposure experiment for which there was only one replicate per strain in the control treatment.

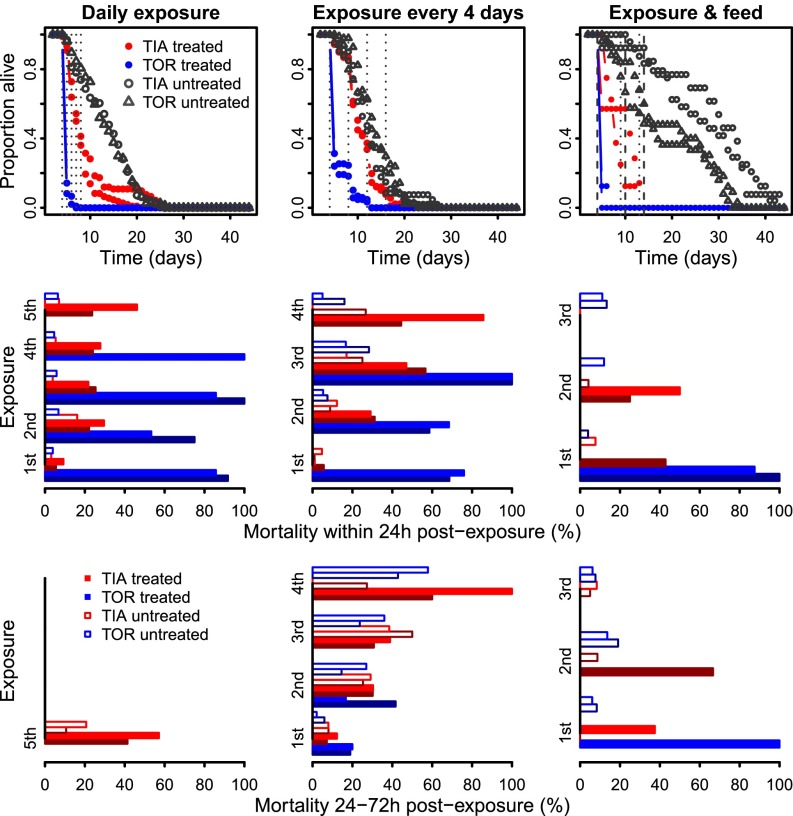
Across all experimental regimes, mosquito survival was lower after exposure to insecticides in comparison with the control treatments (Fig. 1, upper plots, black vs. colored lines). Survival was also higher in the more resistant TIA than TOR strain (red vs. blue lines), but consistent between replicates of the same experimental treatment and strain combination (lines of same color). Overall, mortality rates in the 24 h following exposure to insecticides ranged from 60% to 100% in the TOR strain, and from 3% to 61% in the TIA strain. The 24-h mortality of mosquitoes exposed to untreated nets was <20% in both strains (Fig. 1, middle panels). The mortality rate between 24 and 72 h (within 1 and 4 d) after last exposure of TIA ranged from 7% to 100%, which was higher than that of the controls, which ranged from 2% to 57% (Fig. 1, bottom panels). When present, this delayed mortality was also higher in the TOR strain (20–100%) than in the controls.

Fig. 1.

Experimental data. Top panels show the observed daily survival curves, i.e., the proportion of mosquitoes from day x − 1 alive at day x for each exposure regime (across panels), strain (different colors), and treatment (filled vs. open symbols) combination. Vertical dotted lines correspond to the time of exposure. Middle panels show the immediate mortality rate of each group, i.e., within 24 h of exposure to pyrethroids. Replicates shown with different shades of the same color. Bottom panels show the delayed mortality rate of each group, i.e., 24–72 h after exposure to pyrethroids.

Impact of Immediate and Delayed Effects on Survival.

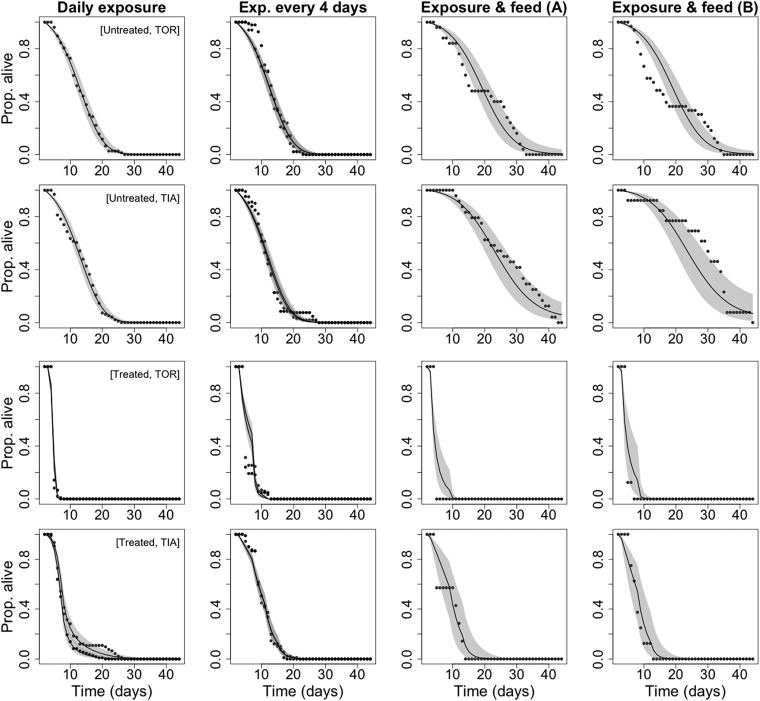
Our aim was to test whether reductions in mosquito survival following insecticide exposure persisted beyond the first 24 h after exposure. To distinguish and quantify these immediate and delayed impacts, we used a Bayesian nonlinear state-space model (SSM) on the cohort data, in which observed daily survival was modeled as a binomial process. Briefly, the model described the daily survival of each strain under the different exposure regimes (A–C) and treatments (exposed or control). Among the candidate models tested (i.e., models with varying covariate combinations; see Methods for further details), the one with the highest degree of support incorporated both immediate and delayed impacts of insecticide exposure, and senescence (i.e., increase in baseline mortality rate with age; see Methods and model fit in Fig. S1). Support for the inclusion of both immediate and delayed impacts of insecticide exposure was particularly strong (Tables S1 and S2).

Fig. S1.

Model fit of the binomial survival model. Comparison of the observed (points) and model-fitted survival curves (lines with shaded 95% credible intervals) of each exposure regime (columns), strain, and treatment group (row).

Table S1.

Candidate binomial survival models and resultant DIC differences relative to the best model (i.e., model K)

Model	Missing parameters	Formulation (Si,j)	ΔDIC
A	Linear senescence	$S_{i,t}={\beta }_0+{\beta }_1{t}^2-{\beta }_{2,x,s}{\displaystyle \sum \left(e^{-{\beta }_{3,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}+u_i$	479.75
B	Quadratic senescence	$S_{i,t}={\beta }_0+{\beta }_{1}t-{\beta }_{2,x,s}{\displaystyle \sum \left(e^{-{\beta }_{3,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}+u_i$	27.33
C	Replicate	$S_{i,t}={\beta }_0+{\beta }_1{t}^2-{\beta }_{2,x,s}{\displaystyle \sum \left(e^{-{\beta }_{3,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}$	485.12
D	Quadratic senescence and replicate	$S_{i,t}={\beta }_0+{\beta }_{1}t-{\beta }_{2,x,s}{\displaystyle \sum \left(e^{-{\beta }_{3,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}$	314.62
E	Linear senescence and delayed effect	$S_{i,t}={\beta }_0+{\beta }_1{t}^2-{\beta }_{2,x,s}+u_i$	863.56
F	Linear senescence, delayed effect and replicate	$S_{i,t}={\beta }_0+{\beta }_1{t}^2-{\beta }_{2,x,s}$	1117.6
G	Quadratic senescence and delayed effect	$S_{i,t}={\beta }_0+{\beta }_{1}t-{\beta }_{2,x,s}+u_i$	535.75
H	Quadratic senescence, delayed effect and replicate	$S_{i,t}={\beta }_0+{\beta }_{1}t-{\beta }_{2,x,s}$	883.83
I	Senescence and replicate	$S_{i,t}={\beta }_0-{\beta }_{2,x,s}{\displaystyle \sum \left(e^{-{\beta }_{3,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}$	639.25
J	Senescence	$S_{i,t}={\beta }_0-{\beta }_{2,x,s}{\displaystyle \sum \left(e^{-{\beta }_{3,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}+u_i$	477.45
K	Full model	$S_{i,t}={\beta }_0+{\beta }_{1}t+{\beta }_2{t}^2-{\beta }_{3,x,s}{\displaystyle \sum \left(e^{-{\beta }_{4,x,s}\mathrm{\Delta }{T}_{i,t}}\right)}+u_i$	0

Table S2.

Median and 95% credible interval of the posterior distributions obtained for the coefficients of the best model K and from the sensitivity analysis model run without regime C

Coefficient	Best model K	Sensitivity model
	Median (95% credible interval)	Median (95% credible interval)
β0 (intercept)	4.403 (3.96, 4.80)	4.659 (4.39, 4.94)
β1 (linear senescence)	−0.234 (−0.27, −0.20)	−0.349 (−0.40, −0.30)
β2 (quadratic senescence)	0.004 (0.002, 0.005)	0.008 (0.006, 0.01)
β3 (immediate mortality)
[x = treated, s = TIA]	0.852 (0.71, 1.00)	0.746 (0.62, 0.89)
[x = treated, s = TOR]	2.827 (2.46, 3.22)	2.549 (2.33, 2.81)
[x = untreated, s = TIA]	0	0
[x = untreated, s = TOR]	0	0
β4 (delayed effects)
[x = treated, s = TIA]	0.17 (0.13, 0.23)	0.251 (0.18, 0.33)
[x = treated, s = TOR]	0.180 (0.14, 0.22)	0.280 (0.16, 0.26)
[x = untreated, s = TIA]	5.60e−11 (2.5e−36, 1.5e−3)	1.43e−9 (5.7e−56, 5.54e−1)
[x = untreated, s = TOR]	4.08e−10 (2.6e−38, 1.27e−2)	5.31e−11 (1.7e−35, 5.6e−3)

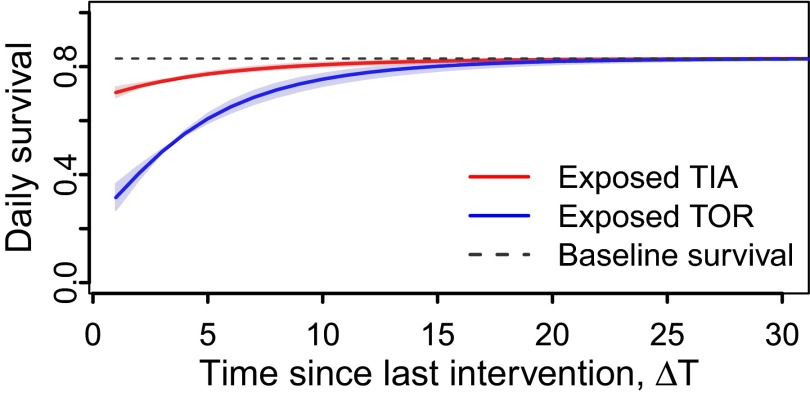
The magnitude of insecticide impacts varied between strains (Fig. 2, blue and red lines). For example, the mean daily survival of the TOR strain was 3.7 times lower in the 24 h following insecticide exposure (at t = 0 in Fig. 2) than in the unexposed control (Table 1), whereas survival in the TIA strain was only 1.2 times lower than the controls over the same period. Similar strain differences were observed in the magnitude of delayed mortality impacts (>24 h after exposure; Fig. 2). Although both strains experienced a permanent reduction in survival >24 h following LLIN exposure (i.e., the preexposure age-independent baseline daily survival levels are never achieved again; Fig. 2, dotted lines); TIA mosquitoes were predicted to require ∼7 d to recover their daily survival rate to 95% of the baseline, whereas TOR mosquitoes required ∼14 d (i.e., Fig. 2). The delayed mortality effects of TIA disappear faster mainly because the initial impact on TOR survival (i.e., immediate mortality) was much greater, which resulted in a longer period of recovery back (asymptotically) to the baseline daily survival (i.e., control daily survival rate; Fig. 2). After exposure to untreated nets, the daily survival of control mosquitoes from either strain was unaffected by long-term residual impact of insecticides, and remained at baseline levels (Fig. 2, dotted line).

Fig. 2.

Estimated impact of delayed effects of exposure to insecticides on mosquito daily survival of moderately (blue) and highly (red) resistant strains. The dotted line corresponds to the baseline daily survival (and controls) of both strains and the shaded area to the 95% credible interval.

Table 1.

EST and CF mean daily mosquito survival

Strain	Regime	Mean daily survival		Proportion alive at day 9
		EST	CF	EST	CF
TIA (exposed)	A	0.80	0.90	0.25	0.77
	B	0.74	0.85	0.60	0.74
	C1	0.70	0.79	0.58	0.69
	C2	0.64	0.74	0.39	0.52
TOR (exposed)	A	0.46	0.88	0.00	0.29
	B	0.43	0.81	0.05	0.42
	C1	0.35	0.66	0.07	0.33
	C2	0.38	0.70	0.02	0.16
TIA (unexposed)	A	0.83	—	0.75	—
	B	0.80	—	0.70	—
	C1	0.96	—	0.95	—
	C2	0.96	—	0.96	—
TOR (unexposed)	A	0.83	—	0.75	—
	B	0.82	—	0.74	—
	C1	0.93	—	0.91	—
	C2	0.93	—	0.91	—

Estimated (EST) and counterfactual (CF) mean daily survival and mean proportion of mosquitoes alive at day 9 after first exposure, for each treatment, strain and exposure regime: A, daily exposure; B, exposure every 4 d; and C1 and C2, exposure with simultaneous blood meal. The dash reflects absence of CF value.

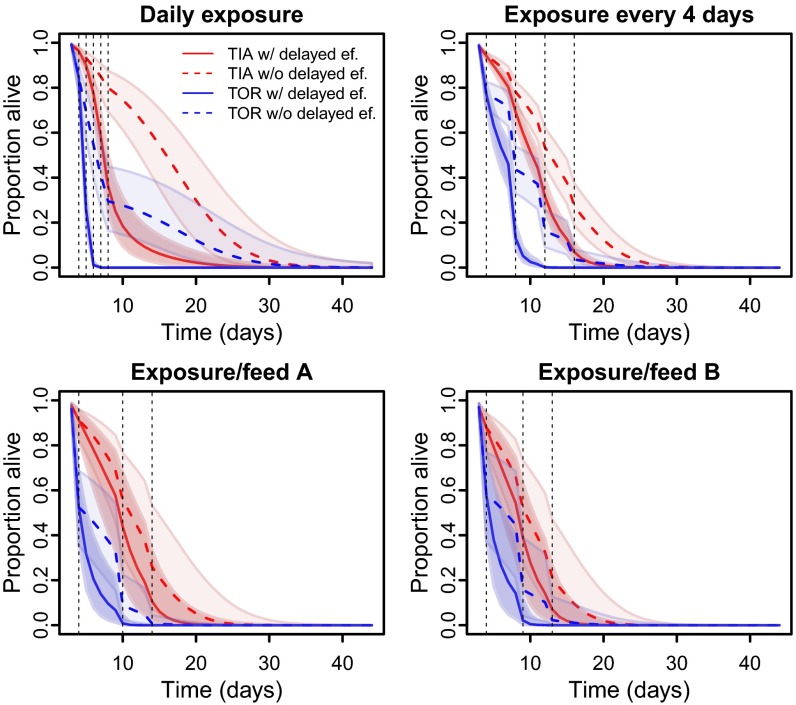
To further investigate the magnitude of delayed mortality impacts of insecticide exposure, we used our model to contrast scenarios in which these effects were present [as estimated in data (EST)] and in which they were removed [counterfactual (CF)]. Comparison of the estimated and counterfactual survival estimates (Fig. 3 and Table 1) indicates that the median life span of TOR mosquitoes is reduced by 17–57% in the presence of delayed mortality impacts relative to when they are absent. The median life span in the TIA strain was also estimated to be reduced by 0–40% (depending on exposure regime) in the presence of delayed mortality impacts of insecticides (Fig. 3 and Table S3). We investigated how these delayed mortality impacts influenced the proportion of mosquitoes surviving for 9 d after first exposure, which is the minimum necessary time for a mosquito to transmit malaria assuming it was infected on first bite (18). The proportion of TIA mosquitoes expected to live at least 9 d following insecticide exposure was predicted to be 25–60% (across different exposure regimes) in the presence of observed levels of delayed mortality, rising to 52–77% when these effects were counterfactually removed (Table 1). These differences were even more pronounced within the TOR strain, where <7% were estimated to survive for 9 d following insecticide exposure when delayed mortality impacts were acting (EST), compared with 16–42% when only immediate impacts were assumed (CF, Table 1).

Fig. 3.

Modeled daily survival curves of An. gambiae after different exposure regimes to LLINs. Full lines represent the curve estimated from fitting the binomial model to the data, and the dotted lines represent the counterfactual curve predicted with no delayed effects. Lines correspond to the median prediction with shaded 95% credible intervals.

Table S3.

EST and CF median life expectancy for each treatment, strain, and exposure regime

Strain	Regime	Median life expectancy
		EST	CF
TIA (exposed)	A	6	10
	B	6	8
	C1	7	7
	C2	6	7
TOR (exposed)	A	4	7
	B	5	6
	C1	4	5
	C2	4	5
TIA (unexposed)	A	8	—
	B	8	—
	C1	14	—
	C2	14	—
TOR (unexposed)	A	8	—
	B	8	—
	C1	12	—
	C2	11	—

Estimated (EST) and counterfactual (CF) median life expectancy for each treatment, strain, and exposure regime: A, daily exposure; B, exposure every 4 d; and C1 and C2, exposure with simultaneous blood meal.

The impact of insecticides also differed between insecticide exposure regimes (within each strain). In both strains, mosquito mean daily survival across their life span was higher in regime A, with consecutive daily exposures, than in the regime B with similar number but more spaced-out exposures (e.g., Table 1). However, a smaller proportion of mosquitoes survived until 9 d after first bite in higher-frequency daily exposure compared with other treatments (e.g., regime A vs. B and C). For example, no TOR mosquitoes were estimated to be alive at day 9 in the daily-exposure regime compared with 2–7% in treatments where exposures were spaced over 4–5 d. Similarly, 25% of TIA mosquitoes were estimated to survive until day 9 under the daily-exposure regime, compared with 39–60% when exposures were spaced out (Table 1). For regime C, the mean daily survival was ∼10% lower in both strains compared with regimes A and B. However, the comparative magnitude of all longevity measures (Table 1) between strains was similar with those of regime B, which had similar exposure frequencies. Despite these differences across regimes, the magnitude of delayed insecticide impact was relatively similar. For example, the counterfactual mean daily survival of the TOR strain was ∼1.9-fold higher than that estimated under each of the three exposure regimes. Similarly, the counterfactual mean daily survival of the TIA strain was ∼1.2-fold across all exposure regimes (Table 1).

Empirically, the delayed effects were higher in regime C (Fig. 1, bottom panels). To guarantee that the detection of delayed effects was not purely driven by this regime in our models, we rerun the model without regime C. The magnitudes of immediate and delayed effects were slightly smaller but still significant in this analysis, and show clear evidence of delayed effects even with the exclusion of regime C. These outputs are shown in Supporting Information (Table S2).

Implications for Malaria Transmission Potential.

Using the observed and counterfactual survival curves, we developed a stochastic individual-based simulation to investigate the potential epidemiological consequences of delayed mortality following insecticide exposure in IR strains of An. gambiae. These impacts were quantified in terms of the number of potentially infectious bites a mosquito would be expected to deliver under scenarios where the mortality effects following exposure to insecticides is of a similar magnitude to that detected in our experimental data. Our simulation predicted the probability distribution of the number of infectious bites that a TIA and TOR mosquito could deliver over its lifetime (assuming it was infected on its first bite). Transmission potential (quantified as the mean of this distribution) was simulated under varying levels of insecticide exposure and biting probabilities (detailed in Methods and Dataset S1). Predictions were obtained both in the presence of immediate and delayed mortality effects following exposure (as observed in our data), and under the counterfactual scenario where these delayed mortality effects were absent.

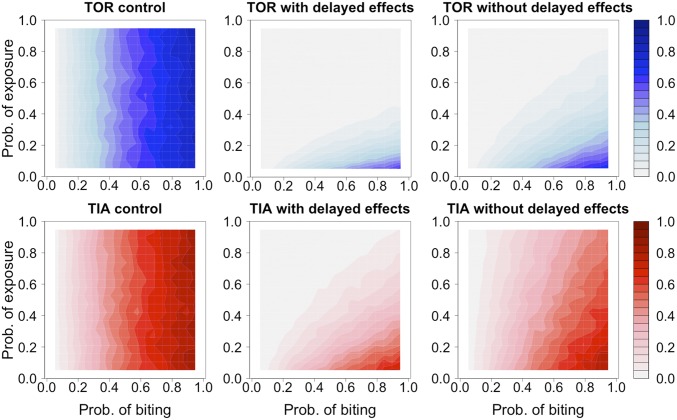
Under the control scenarios (exposure to untreated nets), transmission potential was dependent only on biting probability (Fig. 4, left panels) and was relatively high, with 47% of mosquitoes from both strains having potential to deliver at least one infectious bite (Fig. 4). Exposure to LLINs was estimated to reduce the overall transmission potential of both TIA and TOR strains by 3.3 and 7.8 times, respectively (see reduction of dark blue and red areas across panels in Fig. 4). Notably, there were marked differences between the transmission potential of mosquitoes exposed to insecticides, depending on whether they were assumed to experience immediate mortality impacts, or both immediate and delayed impacts of the magnitude detected in our experiments (Fig. 4). For example, across all combinations of biting and exposure probabilities, the proportion of TIA mosquitoes expected to deliver at least one infectious bite was 33% when only immediate mortality was considered, compared with 14% when delayed impacts were also incorporated. Similarly, for the TOR strain, the proportion of mosquitoes with potential to deliver one infectious bite fell from 12% to 6% when delayed as well as immediate mortality impacts were included. Thus, incorporation of delayed mortality effects from insecticide exposure is expected to significantly curtail the transmission potential of even technically defined “resistant” malaria vectors.

Fig. 4.

Contour plots of the mean number of infectious bites per mosquito of TOR (blue upper panels) and TIA (red bottom panels) strains obtained for mosquitoes exposed to untreated (control) and insecticide-treated nets with and without delayed effects across varying probabilities of biting (x axis) and exposure (y axis).

Discussion

The cumulative impact of LLIN exposure on the survival of even highly resistant An. gambiae mosquitoes was estimated to reduce their expected lifetime transmission by threefold, with delayed effects accounting for at least one-half of this reduction. If delayed mortality effects of similar magnitude occur in natural conditions, estimates of transmission potential of IR mosquitoes should be reduced to ∼50% to what would be assumed if insecticides had no impact on their survival.

To our knowledge, delayed mortality effects of a similar magnitude to ours have not been described in malaria vectors or any other insecticide resistant insect. Although the distinction between immediate and delayed mortality has been discussed for other resistant insects [e.g., lesser grain borer, which infects maize (23)], the magnitude of the effects from exposure to pesticides has not been accurately quantified. To our knowledge, our results are the first clear evidence that delayed mortality effects occur in IR Anopheles sp., and that they are of sufficient magnitude to have important epidemiological implications for the continued control of malaria.

The magnitude of delayed mortality effects varied between the two An. gambiae strains used here. These differential impacts may be reflective of the mechanisms of resistance within these two strains. Physiological resistance to insecticides can arise through target site mutations that interfere with insecticide binding, metabolic resistance in which insecticides are detoxified by the overproduction of enzymes, and penetration resistance in which the mosquito cuticle is altered in a way that inhibits insecticide uptake (13). The TOR strain exhibits target site resistance through the L1014S knockdown resistance (kdr) mutation (24) but has shown no clear evidence for metabolic resistance. In contrast, the TIA strain has both target site resistance arising from a high frequency of 1014F kdr allele and metabolic resistance arising from elevated expression of key P450s (25). It is likely that the long-term impacts of LLIN exposure on mosquito survival were minimized in the TIA strain because of its additional capacity to detoxify residual insecticides. If so, the delayed mortality effects could be a transitory feature arising along the evolutionary pathway from full susceptibility to “complete” resistance (e.g., resistance via multiple mechanisms). For example, delayed mortality impacts may be of most significance in populations where resistance has newly arisen and is conferred by a limited range of target site mutations, but have minimal impact in populations that have developed both multiple resistance mechanisms and compensatory mutations through years of intense selection. Thus, even though delayed mortality impacts of insecticides may be reducing the transmission potential of IR mosquitoes under current conditions, this mitigating effect could become eroded by continued, intense selection for resistance in the future.

Our findings may help explain the apparent paradox of increases in the number of malaria cases averted over time that are attributed to LLINs across Africa (10), even in the face of increasing resistance. If IR was causing widespread failure of LLINs, the impact of LLINS on malaria transmission across Africa would be reduced. The available evidence on how IR influences malaria risk is small and shows some discrepancies. For example, parallel studies in Malawi where Anopheles funestus is moderately resistant variously reported that LLINs appeared to have little impact [i.e., when the endpoint was prevalence (26)] or were still reducing transmission by 30% [i.e., when the endpoint was incidence (27)]. However, recent models suggest that LLINs continue to be responsible for the vast majority of malaria cases averted in Africa over the last decade (10) even with increasing IR. The presence of these delayed mortality effects, which reduce the impact of IR on transmission, may help explain why a widespread, catastrophic impact of IR has not yet been observed. However, because the reduction in malaria transmission potential by mosquitoes exposed to LLINs seems to decrease with increasing intensity of IR (i.e., TOR vs. TIA), our findings also serve as a warning that resistance could eventually reduce the public health benefit of pyrethroid-based LLINs.

Some studies have shown that exposure to insecticides alters the behavior of IR arthropods in a way that could indirectly reduce their fitness [e.g., altered dispersal, reduced neurosensory perception and higher risk of predation (13, 28)]. For example, exposure to neonicotinoid insecticides at sublethal concentration decreases the feeding activity of the grain aphid (23). Similarly, An. gambiae exposed to LLINs seem to temporarily lose the ability to host-seek (29). This study did not test for such additional indirect impacts; however, preliminary data indicate a reduction in the feeding success of exposed IR mosquitoes. In this and other studies (30, 31), it was observed that the legs of mosquitoes can become detached when trying to feed through nets, which would be one mechanism to explain their subsequent reduction in blood feeding. Further work is needed to quantify this phenomenon and other indirect fitness consequences of LLIN exposure in IR mosquitoes to calculate their combined impact on transmission (13). Alternatively, contact with LLINs could prompt behavioral changes that increase the transmission potential of IR mosquitoes, by, for example, changing the time and location of their biting to avoid nets [e.g., “behavioral resistance” (32)]. Furthermore, previous studies have suggested that resistance is associated with changes in the susceptibility of mosquitoes to infection [ranging from an enhancement, reduction, or no change (33–35)]. IR also drives various physiological modifications that may ultimately impact survival and parasite competence (28). For example, resistant Anopheles and other taxa have an increased capacity to tolerate oxidative stress, which in turn reduces long-term survival (36, 37). Thus, although results presented here constitute valuable proof-of-principle on delayed mortality impacts from insecticide exposure, consideration of a wider range of indirect consequences is needed to accurately predict the transmission potential of IR mosquitoes.

A previous study tested for a cumulative impact of low-dose insecticide exposure in Anopheles but found no evidence of higher mosquito mortality following repeated exposures (33). Similarly, our results show no association between the immediate mortality of mosquitoes following exposure, and the number of times they had been previously exposed. However, we also show that mosquitoes’ natural mortality varies with age. Older mosquitoes have been previously shown to be more susceptible to pyrethroids than their younger counterparts (33, 38). Our findings suggest this result may have been driven by changes in the natural mortality of mosquitoes over time (i.e., senescence) rather than increases in susceptibility to insecticide exposure. The ability to estimate additional effects, such as senescence, is one of the advantages of using our modeling approach. The state-space framework used to analyze the survival curves was also critical for the quantification of the nonlinear effect of delayed effects of exposure on mosquito mortality, which would not be possible with more commonly used survival analysis.

Our findings highlight the importance of investigating the impacts of resistance beyond immediate mortality. The existence of previously ignored delayed mortality effects presents a hypothesis for why the presence of pyrethroid resistance in African malaria vectors does not appear to have resulted in widespread reductions in LLIN efficacy (10, 27). However, the present study warns that increasing resistance could erode the ability of LLINs to hold back malaria. As the degree of resistance increases, the magnitude of these delayed mortality impacts may diminish and eventually disappear. This study provides a proof-of-principle for the existence of these delayed mortality effects at a magnitude that could have significant implications for malaria transmission. Ideally, the next step would be to validate these findings in wild populations and assess their relevance to operational control. There are currently several constraints to testing this hypothesis in the field; namely, difficulties in aging and determining the history of insecticide exposure of wild mosquitoes and mark–recapture methods for survival estimation have poor efficiency (39). While technology develops, alternatively, this phenomenon could be investigated under semifield conditions (40) where wild mosquitoes can be exposed to LLINs under realistic but contained conditions. Further empirical studies combined with the modeling framework developed here will be vital for prediction of the impact of insecticide resistance on malaria control.

Methods

Experimental Design.

Two strains of An. gambiae mosquitoes differing in their IR levels were used in this study: TIA, which originates from Southern Cote d’Ivoire, and TOR from Uganda. Details of their resistance profile can be found in ref. 21 and references therein. A fully susceptible strain was not included in this study as all mosquitoes die within 24 h, and hence delayed mortality cannot be measured. Cohorts of ∼100 mosquitoes of each strain were exposed to Permanet 2.0 LLINs containing 50 mg/m² deltamethrin (Vestergaard Frandsen), the standard dose to mimic field exposures, or to an insecticide-free bed net for 3 min using the WHO cone bioassay (15). Details of the experimental design, such as sample sizes and frequency of exposure, are detailed in Table S4. Three alternative exposure regimes were used: (A) daily exposure; (B) exposure every 4 d; and (C) exposure and feed; and two replicates were carried out for each regime and strain combination. The mosquitoes for the replicates were taken from different colony cohorts apart from those in regime A, which were from the same colony cohort (hence only one replicate was available for A). Mortality was recorded daily starting 24 h after the first exposure, and all surviving mosquitoes were held with access to sugar solution ad libitum. For the exposure regime C, mosquitoes were starved of sugar water 12 h before exposure and mosquitoes were aspirated into two containers, one covered with a Permanet 2.0 and the second with an untreated net. Mosquitoes were provided access to a blood meal for 20 min via a volunteer’s arm rested on the netting of each container. Unfed mosquitoes were then counted and discarded. Mortality was recorded daily starting 24 h after the first exposure. At the end of the bioassay, daily mortality was available for a total of 1,497 mosquitoes, from 22 different experimental groups (3 exposure regimes; 2 strains; 2 treatments, i.e., exposed and nonexposed to insecticide; and 2 replicates).

Table S4.

Experimental design of the three exposure regimes used to investigate the long-term survival of An. gambiae after exposure to pyrethroids

Exposure regime	Frequency, d	Exposure days (posteclosion)	Sample size* (exposed TIA)	Sample size* (exposed TOR)	Sample size* (control TIA/TOR)
A	Daily	4, 5, 6, 7, 8	92, 108	97, 105	96/77
B	4	4, 8, 12, 16	89, 91	118, 104	101, 106/184, 96
C.1	∼5	4, 10, 14	50	50	50/50
C.2	∼4	4, 9, 13	50	50	50/50

All regimes were applied to both strains (TIA and TOR) and implemented with two treatments: Permanet 2.0 and untreated netting. Each regime/strain/treatment combination was replicated twice except C.1 and C.2, which were performed once; however, they are considered replicas of each other.

^*Sample size at first exposure.

Bayesian Survival Model.

A Bayesian SSM was constructed to quantify the impact of the different insecticide exposure regimes on An. gambiae survival, and disentangle the impacts of immediate (i.e., within 24 h of exposure) and long-term cumulative mortality. The observed number of mosquitoes alive, N_i,t, in each experimental replicate i (22 in total), at time t, was modeled as a binomial variable: N_i,t ∼ binomial (S_i,t, N_i,t-1); where N_i,t-1 is the total number of mosquitoes alive in group i at time t − 1 and S_i,t, is the probability of daily survival described with a logit link to its nonlinear predictor (${\overline{S}}_{i,t}$):

$${\overline{S}}_{i,t}={\beta }_0+{\beta }_{1}t+{\beta }_2{t}^2-{\beta }_{3,x,s}{E}_{i,t}+u_i.$$ [1]

Here, β₀ corresponds to the intercept, and the coefficients β₁ and β₂ were used to incorporate natural mortality (i.e., senescence) over time (or age, t). The short-term “immediate” impact of exposure to a (treated or untreated) bed net, on mosquito daily survival was represented by the coefficient β₃, which was allowed to have a different value for each treatment x (i.e., exposed or unexposed to insecticides) and strain s (i.e., TIA or TOR) combination. Biologically, β_3,x,s corresponds to the magnitude (in the predictor scale) of the reduction in daily survival occurring after exposure. Exposure is treated as the nonlinear covariate E and was introduced to quantify the postulated delayed effects of insecticide, which was constructed as the superposition of multiple, time-decaying effects corresponding to the multiple exposure regimes:

$$E_{i,t}={\displaystyle \sum }{e}^{-{\beta }_{4,x,s}\mathrm{\Delta }{T}_{i,t}},$$ [2]

where, β₄ quantifies the decay rate of the delayed mosquito mortality risk after exposure, and is specific to each treatment x and strain s; and ΔT, the time since last exposure in each replicate i at time t. The coefficient u was incorporated into the model as a Gaussian random effect that accounts for other unattributed differences between replicates. Further details, including prior distributions and model code (Dataset S1), are provided in Supporting Information.

Model Selection.

An initial set of 11 candidate models representing differing, biologically plausible permutations of our predefined coefficients: i.e., senescence (as a linear or quadratic effect), immediate effects of exposure, delayed effects of exposure, and random effect of replicate, were constructed (Table S1). After assessing convergence, model goodness-of-fit and the deviance information criterion of all candidate models (41), we chose the best model (described in Eq. 1). All models were fit using Monte Carlo Markov chain methods within software JAGS (42) via interface with R (R Development Core Team). Further details can be found in Supporting Information.

Prediction of the Impact of Delayed Effects.

The survival curves S_i,t for each replicate were estimated as a function of the predicted coefficients obtained from Eq. 1. The relative impact of delayed effects was quantified by comparing these survival curves, which incorporated delayed effects of the magnitude detected in experimental results, with “counterfactual” scenarios in which their effect had been removed after model fitting. This was done during the refit of the model by setting the decay rate coefficient of delayed effects (β_4,x,s) to the very high value of 10,000 (i.e., delayed effects do not exist and only immediate mortality can impact mosquito survival).

Transmission Potential (T_p).

A stochastic individual-based simulation was used to investigate the potential epidemiological consequences [i.e., transmission potential (T_p)] of delayed mortality following insecticide exposure in resistant strains of An. gambiae. These impacts were quantified in terms of the number of potentially infectious bites a mosquito would be expected to deliver under scenarios when exposure to insecticides is of a similar magnitude as detected in our experimental data.

We simulated transmission potential for the full range of combinations for the probabilities of biting and exposure, although some of the combinations in this space of scenarios are unlikely (e.g., it is near-impossible that with an exposure probability of 1 implying an intact LLIN, biting probability can ever approach 1). We explored the space of exposure and biting probabilities through 400 distinct combination scenarios (20 × 20 values) and each scenario was simulated 1,500 times to obtain a frequency distribution for the number of infections bites. The simulation used the following assumptions: (i) adult female mosquitoes began their life on day zero, and were given their first opportunity to blood feed on day 2; (ii) all mosquitoes became infected with malaria upon their first blood meal; after feeding, surviving mosquitoes had the opportunity to blood feed again every 3 d; (iii) feeding success was determined as a binomial distribution based on the probability of biting achieved for each draw; (iv) mosquitoes become infectious after an average of 12 d after becoming infected. This incubation period was drawn from a normal distribution with mean 12 and SD of 1.5, which resulted in a range between 9 and 23 d [values known to occur at temperatures between 30 and 20 °C (18)].

Based on these assumptions and the generated probabilities of exposure and biting, a binomial process was simulated to determine when a mosquito was exposed to insecticides and when it was successful at biting, during their lifetime (i.e., from day 1 to day 50). The daily survival of each mosquito was based on the estimated posterior distributions of the SSM implemented to our experimental data (i.e., Eq. 1). For each mosquito of each strain (TIA and TOR) and treatment (exposed to insecticide-treated nets and control), the survival curves (Eq. 1) were reestimated using the exposure over time (i.e., across the 50 d when exposures occurred) obtained from the exposure–biting relationship, and independent draws from the posterior distributions of the coefficients obtained from the SSM for the respective observed and counterfactual (without delayed effects) survival curves. The use of the posterior distributions, as opposed to a mean coefficient, ensured that all uncertainty was correctly propagated through to the estimates of transmission potential. The survival state of a mosquito at day t (alive or dead from day 1 to 50) was also defined through a binomial process with a probability of daily survival.

Finally, the total number of infectious bites expected to be delivered by a mosquito, or transmission potential (T_p) of each mosquito, was obtained as follows:

$$T_p={\displaystyle \sum }_t{S}_t{B}_t{I}_t,$$ [3]

where S_t is the survival state on day t (i.e., alive or dead), B_t is the number of bites on day t, and I_t is the infectious state on day t. The T_p of each mosquito were finally used to generate a heatmap of transmission potential across the varying exposure and biting probabilities, for each strain, with and without delayed effects.

SI Experimental Design

Mosquito adults were maintained in 30 × 30 × 30-cm rearing cages (Bugdorm; Megaview Science) at 27 ± 2 °C, 80 ± 10% relative humidity with a 12-h photoperiod, and fed on 10% sugar solution.

Details of the WHO cone bioassay exposure experiment of insecticide resistance mosquitoes to insecticides are provided below in Table S4.

SI Methods

Bayesian Survival Model.

The observed number of mosquitoes alive, N_i,t, in each experimental replicate i (22 in total), at time t, was modeled as a binomial variable: N_i,t ∼ binomial (S_i,t, N_i,t−1); where N_i,t−1 is the total number of mosquitos alive in group i at time t − 1, and S_i,t is the probability of daily survival described with a logit link to its nonlinear predictor (${\overline{S}}_{i,t}$):

$${\overline{S}}_{i,t}={\beta }_0+{\beta }_{1}t+{\beta }_2{t}^2-{\beta }_{3,x,s}{E}_{i,t}+u_i.$$ [S1]

Here, β₀ represents the intercept for the baseline survival i.e. $[\text{exp}\left({\beta }_0\right)/1+\text{exp}\left({\beta }_0\right)$], at t = 0, and was assigned a prior value from a normal distribution of mean 1 and variance 1. We note that β₀ and the all of the following coefficients are specified in the predictor (i.e., logit) scale. The coefficients β₁ and β₂ were used to incorporate senescence over time; where β₁ corresponds to the coefficient of a linear effect that expresses the hypothesis that senescence operates continuously throughout the life of the mosquitos, and β₂ to the coefficient of a quadratic term in time that allows senescence to accelerate at later stages in life. Senescence is here defined as a consistent change in the baseline mortality rate of mosquitoes through time (or age, t) and is fixed across replicates. These senescence coefficients were assigned a normal prior distribution with mean zero and variance 10⁴.

The short-term or “immediate” impact (within 24 h) of exposure to insecticides (or to an untreated bed net) on mosquito survival was incorporated within the coefficient β_3,x,s for each treatment x and strain s combination. Biologically, β_3,x,s corresponds to the magnitude (in the predictor scale) of the reduction in daily survival occurring in the first day after exposure. Because insecticides either decrease daily mosquito survival, or in the worst scenario have no impact upon it, the prior for β_3,x,s was defined as strictly positive and drawn from a gamma prior distribution with mean 3 and variance 1, which is sufficient to cover the range of all possible effects ranging from 100% mortality to zero impact of insecticides across the maximum period of which mosquito mortality was monitored in these experiments (44 d). The term u was incorporated into the model as a Gaussian random effect that accounts for other unattributed differences between replicates. The variance for u was drawn from a uniform prior distribution in the domain 0–10⁴. Finally, the nonlinear covariate E was introduced to quantify the postulated delayed effects of insecticide exposure. It was constructed as the superposition of multiple delayed (and time-decaying) effects from multiple exposures at different times:

$$E_{i,t}={\displaystyle \sum }{e}^{-{\beta }_{4,x,s}\mathrm{\Delta }{T}_{i,t}},$$ [S2]

where β_4,x,s quantifies the decay rate of the delayed mosquito mortality risk after exposure for each treatment (x) and strain (s) combination, and ΔT_i,t, the time since last exposure in each replicate i at time t. A slow decay rate provides evidence for the existence of delayed mortality arising from exposure to insecticides (e.g., values of β₄ = 0 imply permanent impairment of survival as a result of exposure, whereas β₄ > 10 implies instant recovery to baseline survival rates). As with β₃, the prior for β_4,x,s was defined as strictly positive from a gamma distribution of mean 0.2 and variance 1, which allows for the possibility of no delayed mortality effects (e.g., that mosquitoes still alive 24 h after exposure have the same subsequent daily survival as those that were never exposed) and scenarios where a residual, relative reduction in mosquito daily survival is evident for the rest of their lives (i.e., as evidenced by low decay rate).

This model was fit using JAGS (42) through R (R Development Core Team). JAGS requires starting values for all model parameters to begin, which were here allocated randomly by JAGS. We ran two chains of our model for 10⁵ iterations, discarding the first half to ensure full convergence. The code is provided in Dataset S1.

Model Selection.

An initial set of 11 candidate models representing differing, biologically plausible permutations of our predefined coefficients (i.e., senescence, immediate effects of exposure, delayed effects of exposure, and random replicate effects) were constructed (Table S1). After assessing convergence and model goodness-of-fit of all candidate models, we conducted model selection. Convergence of the posterior distribution was assessed using the Brooks, Gelman, and Rubin diagnostic (43), and visual inspection of the chains and posteriors distributions (i.e., the chains should overlap in parameter space and the posteriors should be roughly normally distributed). Goodness-of-fit of the model was investigated by comparing the data and estimated daily survival curves. Finally, we calculated the deviance information criterion (DIC) (41) for all 11 candidate models and used it to arrive at the model with the best combination between goodness-of-fit and parsimony. The most parsimonious model is typically one with the lowest DIC, and also one with at least two DIC values below that of a simpler model (i.e., with less parameters) (41). Our best model (described in Eq. S1) had a DIC with 27 less units than the next competitor, which differed only in the shape of the senescence term (i.e., linear instead of quadratic).

Prediction of the Impact of Sublethal Effects.

The survival curves S_i,t for each replicate were estimated as a function of the predicted coefficients obtained from the best model as identified through the selection procedure described above in Eq. S1. These estimated survival curves included impacts of senescence, immediate mortality, and delayed effects, as the coefficients associated with these variables were estimated as nonzero. The relative impact of delayed effects was quantified by comparing survival curves that incorporated delayed effects of the magnitude detected in experimental results with “counterfactual” scenarios in which their effect had been removed after model fitting. This was done by setting the decay rate coefficient of delayed effects (β_4,x,s) to the very high value of 10,000 (i.e., delayed effects do not exist and only immediate mortality can impact mosquito survival).

Sensitivity Analysis.

Empirically, the delayed effects were higher in regime C (Fig. 1, bottom panels). To guarantee that the detection of delayed effects was not purely driven by this regime in our models, we rerun the SSM described above without regime C.

SI Results

Comparison of the observed data and the model-fitted survival curves validate the best model (model K from Table S4) as they are consistently very close to one another (Fig. S1).

The estimated parameter values for each variable in the chosen model (Eq. S1) are presented in Table S2. Of particular interest is the effect size of senescence (β₁ and β₂) and delayed-effects parameters (β₄), in which 95% credible intervals of the respective posterior distributions are well below and above zero, respectively, indicating their relevance for the understanding of the impact of insecticides on insecticide-resistant mosquito mortality.