Mechanical signaling coordinates the embryonic heartbeat

Significance

There is a mounting body of evidence that physical forces induce biochemical changes. Here, we suggest that the early embryonic heart provides a striking illustration of the importance of mechanics in living matter. Whereas adult hearts use electrical signaling to coordinate the heartbeat, we propose that embryonic hearts use mechanical signaling. We model the embryonic heart as mechanically excitable tissue, with cardiac myocytes that are triggered to contract under strain. Such contractions exert strains on nearby cells and induce further contraction, thus propagating the signal through the heart. This simple model captures key features observed in the heartbeat of stiffness-modified embryonic hearts that cannot be explained by standard electrochemical signaling and yields predictions that we confirm with experiments.

Abstract

In the beating heart, cardiac myocytes (CMs) contract in a coordinated fashion, generating contractile wave fronts that propagate through the heart with each beat. Coordinating this wave front requires fast and robust signaling mechanisms between CMs. The primary signaling mechanism has long been identified as electrical: gap junctions conduct ions between CMs, triggering membrane depolarization, intracellular calcium release, and actomyosin contraction. In contrast, we propose here that, in the early embryonic heart tube, the signaling mechanism coordinating beats is mechanical rather than electrical. We present a simple biophysical model in which CMs are mechanically excitable inclusions embedded within the extracellular matrix (ECM), modeled as an elastic-fluid biphasic material. Our model predicts strong stiffness dependence in both the heartbeat velocity and strain in isolated hearts, as well as the strain for a hydrogel-cultured CM, in quantitative agreement with recent experiments. We challenge our model with experiments disrupting electrical conduction by perfusing intact adult and embryonic hearts with a gap junction blocker, β-glycyrrhetinic acid (BGA). We find this treatment causes rapid failure in adult hearts but not embryonic hearts—consistent with our hypothesis. Last, our model predicts a minimum matrix stiffness necessary to propagate a mechanically coordinated wave front. The predicted value is in accord with our stiffness measurements at the onset of beating, suggesting that mechanical signaling may initiate the very first heartbeats.

The heart is a prime example of an active system with mechanical behavior—the heartbeat—that is robust and remarkably well coordinated. The fundamental contractile units of the heart are muscle cells called cardiac myocytes (CMs). Individual CMs coordinate their contractions through intercellular signaling, generating contractile wave fronts that propagate through the tissue to pump macroscopic volumes of fluid. When this organization breaks down, tissue-scale contractions cease and blood circulation stops. It has long been understood that this signal is electrical (1): ions pass from one cell to another through gap junctions (2), depolarizing the cell membrane and initiating a process that ultimately releases ${\text{Ca}}^{2+}$ from intracellular stores, driving CM contraction. The potential difference between CMs drives ion transport through gap junctions into the next cell, thus propagating the signal. This electrical signaling cascade is responsible for the contractile wave fronts of the heartbeat in adults and has been assumed to regulate the heartbeat at all stages of development. Here, we propose that the early embryonic heart does not follow this established electrical signaling mechanism, but may instead use mechanical signaling to coordinate and propagate its beat. In our picture, embryonic CMs are mechanically excitable: we postulate that sufficiently high strains trigger intracellular release of ${\text{Ca}}^{2+}$ ions through a molecular mechanism that is not yet determined, leading to contraction. We denote this mechanically driven release of ${\text{Ca}}^{2+}$ ions and subsequent contraction as mechanical activation. This in turn strains neighboring CMs and induces additional contraction, resulting in a coordinating signal that is propagated mechanically rather than electrically.

Although embryonic CMs beat spontaneously (3, 4), they would contract with random phases in the absence of a coordinating signal. A number of studies have shown that embryonic, neonatal, and adult CMs are sensitive to mechanical cues (5–9). Recently, the role of mechanics was explored at the tissue scale through extracellular matrix (ECM) stiffening and softening of isolated avian embryonic hearts (10). The speed and strain of the contractile wave front were found to be strongly dependent upon the tissue stiffness, suggesting that the electrical signaling picture is insufficient for the embryonic heart and that the stiffness of the matrix must be taken into account.

Here, we show that mechanical signaling between CMs can explain stiffness-dependent contractile wave front speed and strain via a nonlinear mechanical “reaction–diffusion” mechanism, in which sufficient strain on a CM causes it to “react” by triggering contraction and stress “diffuses” through the tissue. Few models of CM signaling in the heart include mechanics; of these, most assume instantaneous mechanical signal propagation (11, 12) and therefore do not exhibit strong stiffness dependence. Our model is related to a mechanical version (10, 13) of the fire–diffuse–fire model (14), which also fails to capture key stiffness-dependent features. We model the heart as tissue composed of active and passive components. We treat the active CMs as mechanically excitable inclusions that contract when the local strain exceeds a threshold value. The surrounding ECM is treated as a passive elastic-fluid biphasic material. This simple mechanical signaling model quantitatively captures the stiffness dependence of contractile wave front velocity and strain, as well as the strain of CMs cultured on hydrogels observed in ref. 10.

We challenge the hypothesis underlying our model—that mechanical signaling coordinates the embryonic heart—by blocking gap junctions with 18-β-glycyrrhetinic acid (BGA). We find that embryonic hearts continue to beat, even at BGA concentrations 10-fold higher than those sufficient to stop the adult heartbeat in minutes, confirming our hypothesis. Finally, our model predicts a minimum matrix modulus necessary to support a steady-state mechanical wave front. We show experimentally that this value is consistent with the heart’s stiffness when it first starts to beat. Thus, the heart, the first functional organ in the embryo, begins to beat as soon as mechanical signaling can support propagating wave fronts.

Production of CMs from pluripotent stem cells has generated considerable interest in the factors that govern maturation of these cells to heart tissue (15) particularly for repair of adult heart damage. Mechanical determinants in this process remain poorly understood, although the role of mechanical cues is increasingly recognized in cell differentiation, proliferation, and morphogenesis (16–19). Our results here indicate that mechanics in the developing heart may be necessary to tissue-scale function during stem cell maturation and may have application to heart damage repair.

Physical Model of Cardiac Mechanical Signaling

The myocardium of the embryonic heart is composed primarily of mechanically excitable CMs (that contract when activated) and the surrounding ECM. We treat CMs as elastic inclusions embedded in the ECM, in accord with recent experiments of CMs embedded in 3D hydrogels (20). We ignore direct cell–cell mechanical coupling; experimental evidence indicates that stresses are transmitted primarily through cell–matrix adhesions rather than cell–cell contacts during development (21), likely due to the prevalence of cell–junction remodeling. In addition, collagenase treatment indicates that ECM is the primary component of tissue structural integrity (10). We find that a good approximation (Materials and Methods) is to consider CMs as infinitesimal and arranged in a cubic array, spaced by Δx = 10 μm (Table 1). We consider a 3D mechanical version of fire-diffuse-fire signaling. This requires capturing the physics of (i) activated CMs creating mechanical stress; (ii) stress propagation between CMs; and (iii) activation of quiescent CMs in response to mechanical stress in the ECM.

Table 1.

Parameter symbols, references, and values

Parameter	Symbol	Value (fit/ref.)
Mesh/fluid drag	$\mathrm{\Gamma }$	0.4 mPa⋅s/μm2 (Fit)
E4 myocardium modulus	$E^{\ast }$	1.6 kPa (10)
ECM Poisson ratio	ν	0.4 (26)
Fluid fraction (average)	ϕ	0.8 (50, 51)
Fluid viscosity (water, 25 °C)	η	0.89 mPa⋅s
CM spacing	$\mathrm{\Delta }x$	10 μm (10)
CM modulus	$E^c$	0.75 kPa (fit)
CM eigenstrain magnitude	${\mathit{ϵ}}^{\ast }$	0.2 (6)
CM strain threshold	α	0.11 (fit)
CM Poisson ratio	${\nu }^c$	0.4 (26)
Contraction time (AP duration)	τ	250 ms

How Activated CMs Create Stress.

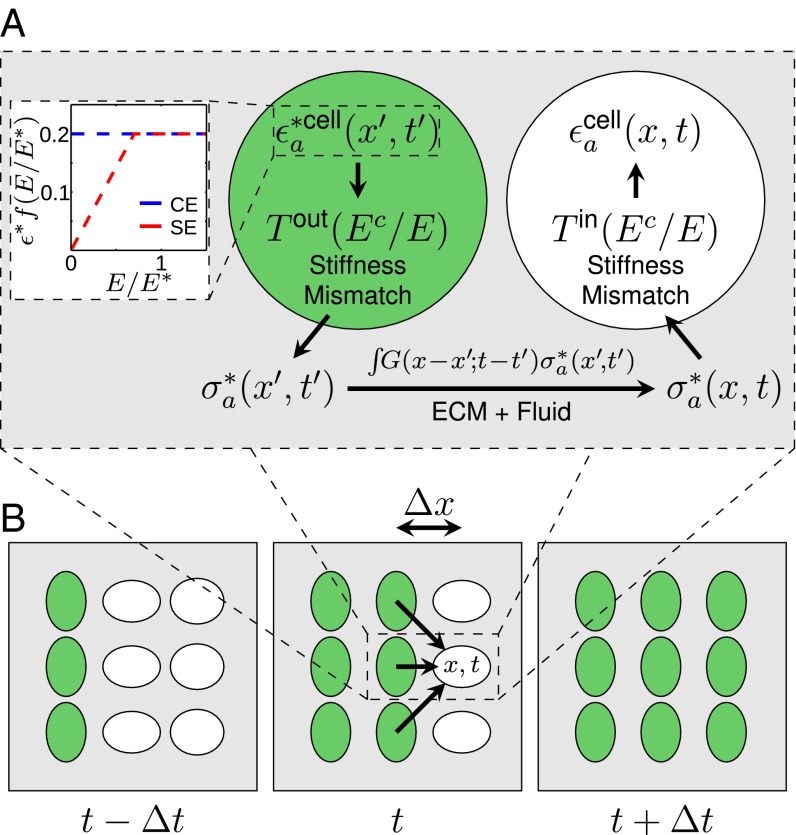
We use two models to characterize the eigenstrain, i.e., the strain of an active inclusion (CM) in the absence of external stresses. In the constant eigenstrain (CE) model, we assume that CMs contract with a fixed eigenstrain independent of ECM stiffness. In the saturating eigenstrain (SE) model, the eigenstrain increases linearly with Young’s modulus E up to a stall stiffness $E_s$, and is independent of E for $E>E_s$ (Fig. 1A, Inset). This behavior is observed for embryonic and neonatal CMs cultured on hydrogels (5, 7, 8, 22) and has been studied theoretically (23).

Fig. 1.

Model for stress propagation in the myocardium. (A, Inset) CE and SE models as a function of ECM Young’s modulus, which determines the strength of contraction (Eq. 1). (Main) The contracting CM (green) acts as a stress source for a quiescent CM (white). An activated cell a contracts with an eigenstrain ${\mathit{ϵ}\ast }_{a,ij}^{\text{cell}}\left(x\prime ,t\prime \right)$, locally inducing a stress ${\sigma \ast }_{a,ij}\left(x\prime ,t\prime \right)$ in the ECM that depends on the relative stiffness between the ECM and CMs. We capture these physics via the tensor $T_{ijkl}^{\text{out}}$ in accordance with the Eshelby theory of elastic inclusions (Supporting Information). This stress propagates according to the ECM response function $G_{ijkl}\left(x-x\prime ,t-t\prime \right)$ (Supporting Information). The matrix stress at $\left(x,t\right)$ due to cell a is ${\sigma }_{a,ij}\left(x,t\right)={\displaystyle \int d^{3}x\prime dt\prime G_{ijkl}\left(x-x\prime ,t-t\prime \right){\sigma \ast }_{a,kl}\left(x\prime ,t\prime \right)}$. This creates ${\mathit{ϵ}}_{a,ij}^{\text{cell}}\left(x,t\right)$, the strain induced in the quiescent CM due to the contraction of a (modified by $T_{ijkl}^{\text{in}}$). (B) Sketch depicting quiescent (white) and activated (green) CMs in a traveling mechanical wave front at subsequent activation times separated by $\mathrm{\Delta }t$. Arrows represent stresses propagated through the ECM (not all shown) to a quiescent CM, which activates when ${\mathit{ϵ}}_{ii}^{\text{cell}}\left(x,t\right)\ge \alpha$.

The two models for the strain exerted by a CM when it contracts are as follows:

$$\begin{array}{c}{\mathit{ϵ}}_{ij}^{\ast }={\mathit{ϵ}}^{\ast }f\left(E/E_s\right)Q_{ij},\\ f_{\text{CE}}\left(E/E_s\right)=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall E\\ f_{\text{SE}}\left(E/E_s\right)=\{\begin{array}{ll}E/E_s\hfill & E<E_s\hfill \\ 1\hfill & E\ge E_s\hfill \end{array},\end{array}$$ [1]

where $Q_{ij}$ is the strain tensor representation of a uniaxial contraction in the x direction (Supporting Information) and ${\mathit{ϵ}}^{\ast }$ is the magnitude of the eigenstrain in the CE model or of the eigenstrain for $E>E_s$ in the SE model. See Fig. 1A, Inset.

The eigenstrain ${\mathit{ϵ}}_{kl}^{\ast }$ from the activated CM induces a stress in the matrix. To properly capture the physical effects of differences in stiffness between CMs and their surrounding ECM, we use Eshelby’s theory of elastic inclusions (24, 25). We compute the tensor $T_{ijkl}^{\text{out}}\left(E\right)$, which relates the CM eigenstrain to the stress it induces in the ECM, shown schematically in Fig. 1A (see Supporting Information for detailed calculations). The resulting ECM stress source due to an activated CM takes the following form:

$${\sigma }_{a,ij}^{\ast }\left(x,t\right)=T_{ijkl}^{\text{out}}{\mathit{ϵ}}_{kl}^{\ast }\mathrm{\Theta }\left(t-t_a\right)\mathrm{\Theta }\left(\tau +t_a-t\right){\delta }^3\left(x-x_a\right),$$ [2]

where $\mathrm{\Theta }\left(t\right)$ is the Heaviside function.

How Stress Propagates Between CMs.

At the cellular length scale and CM contraction velocity scale, the Reynolds number is small ($\sim {10}^{-5}$). We therefore model the ECM as an overdamped, incompressible biphasic material. See Table 1 for parameter values. It is composed of a linear elastic mesh [with Young’s modulus E and Poisson ratio $\nu =0.4$ (10, 26)] and interstitial fluid (of viscosity η similar to water). The fluid and elastic components are coupled through incompressibility and a drag term $\mathrm{\Gamma }$, an effect of matrix permeability to fluid. Similar approaches were used to model collagenous tissue (27) and active gels (28). Using this model, we calculate the response function $G_{ijkl}\left(x,t\right)$ to describe propagation of mechanical stress within the ECM (Supporting Information).

How Quiescent CMs Are Activated Mechanically.

We assume that, when the strain on a quiescent CM exceeds threshold α [${\mathit{ϵ}}_{kk}^{\text{cell}}\left(x_q,t\right)\ge \alpha$], the CM is activated (it contracts). To describe this mathematically, we index noncontracting (quiescent) cells with q and contracting (active) cells with a. Each activated CM contracts for a physiologically relevant amount of time τ before deactivating and becoming refractory. We assume that the refractory timescale is longer than mechanical relaxation, allowing us to ignore backpropagation. Let us consider a CM at $x_a$ that activated at time $t_a$. Then $t_a$ is the moment when this CM’s strain trace first crossed the strain activation threshold ${\mathit{ϵ}}_{kk}^{\text{cell}}\left(x_a,t_a\right)=\alpha$, transforming the originally quiescent CM into an active one. The active CM contracts, creating an eigenstrain ${\mathit{ϵ}}_{kl}^{\ast }$ (Eq. 1) for time $t_a<t<t_a+\tau$, which can be represented as a product of Heaviside functions.

To relate the strain on an embedded quiescent CM q at $\left(x_q,t\right)$ due to local mechanical stress within the ECM, we compute the tensor $T_{ijkl}^{\text{in}}\left(E\right)$ (also shown schematically in Fig. 1A) using elastic inclusion theory (Supporting Information). The strain contribution on q from an activated CM a is then as follows:

$${\mathit{ϵ}}_{a,ij}^{\text{cell}}\left(x_q,t\right)=T_{ijkl}^{\text{in}}{\displaystyle \int G_{klmn}\left(x_q-x\prime ;t-t\prime \right){\sigma }_{a,mn}^{\ast }\left(x\prime ,t\prime \right)},$$ [3]

with ${\sigma }_{a,mn}^{\ast }\left(x\prime ,t\prime \right)$ from Eq. 2. The total strain induced in q is the sum over the contribution from all activated cells ${\mathit{ϵ}}_{ij}^{\text{cell}}\left(x_q,t\right)={\displaystyle {\sum }_a{\mathit{ϵ}}_{a,ij}^{\text{cell}}\left(x_q,t\right)}$.

Results

Mechanical Signaling Model Yields Contractile Wave Fronts.

From the model, we calculate the velocity of the propagating contractile wave front as a function of matrix stiffness as follows. When a CM contracts, it creates a stress field ${\sigma }_{a,ij}^{\ast }$ in the ECM that can induce further contraction by activating quiescent CMs. If the activation process cascades through the tissue, the resulting contraction wave front can attain a comoving steady state ${\mathit{ϵ}}_{ij}\left(x,t\right)={\mathit{ϵ}}_{ij}\left(x-vt\right)$ with velocity v. This is unsurprising because the model is a mechanical analog of nonlinear reaction-diffusion; such systems are well known to exhibit propagating wave front solutions. The activation condition ${\mathit{ϵ}}_{kk}^{\text{cell}}\left(x,t\right)=\alpha$ with a comoving steady state relates the wave front velocity v to the model parameters through an algebraic relation (Supporting Information). Once v is determined, we compute the maximal tissue strain by coarse-grained solution of the waveform (Supporting Information).

Mechanical Signaling Model Fits Experimental Wave Front Velocities with Physiologically Relevant Parameters.

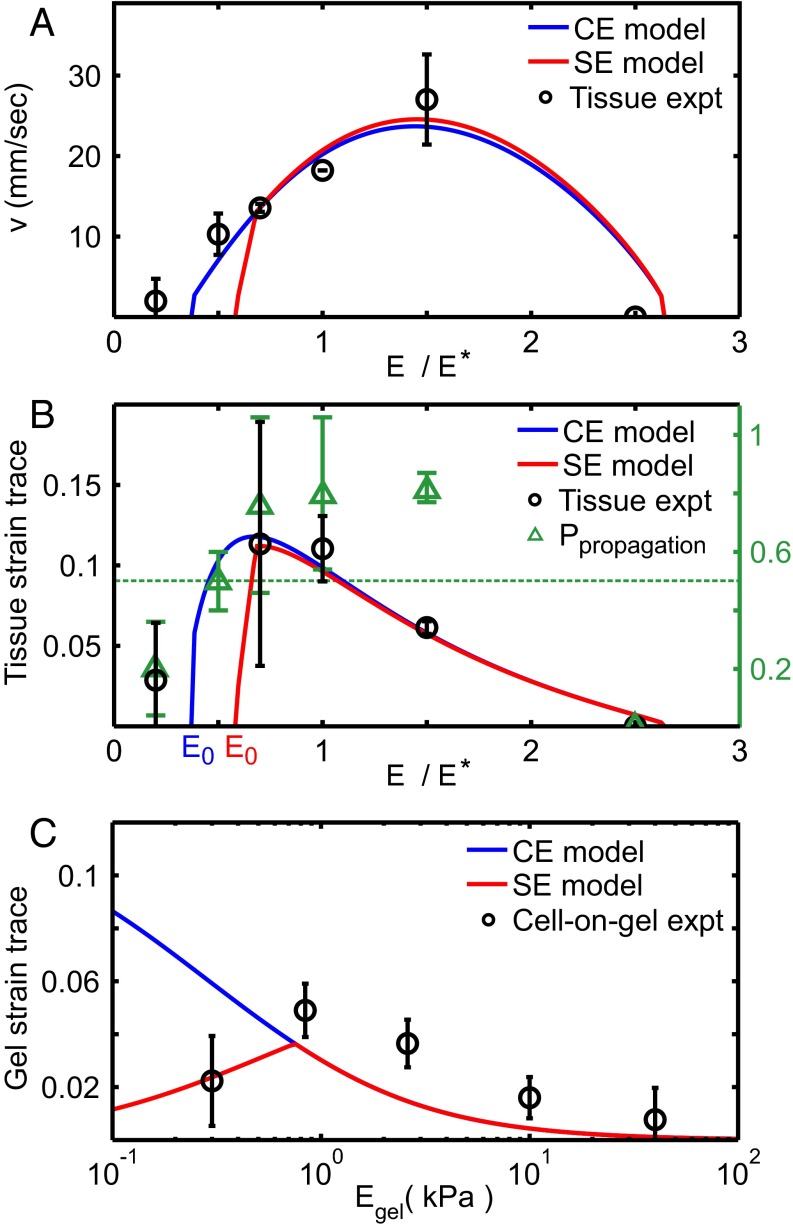
We obtain most of the physiological parameter values from the literature (Table 1). We treat CMs as elastic inclusions with Young’s modulus $E^c$ and with the same Poisson ratio as the surrounding tissue (26) and estimate CM eigenstrain magnitude to be ${\mathit{ϵ}}^{\ast }=0.2$ from intracellular embryonic CM principal strain measurements (6). Stress saturation stiffness is estimated to be the cell modulus $E_s=E^c$ (5, 6). Three model parameters could not be identified from the literature and are fit via nonlinear regression to wave front velocity data from ref. 10. These three parameters are the mesh-fluid drag $\mathrm{\Gamma }$, the CM activation threshold α, and the effective CM Young’s modulus $E^c$. All three fit values (Table 1) fall within physiologically sensible ranges. The resulting velocity is plotted against ventricle contraction velocity data (black circles, from ref. 10) of stiffness-modified embryonic day 4 (E4) hearts in Fig. 2A. No steady-state solution exists below stiffness $E_0$ (which differs between CE and SE models). Physically, $E_0$ arises because when the tissue is too soft, contracting CMs cannot provide enough strain to trigger additional contraction in quiescent CMs. This is consistent with a significantly reduced likelihood of wave front propagation observed in experiment (green triangles in Fig. 2B). Likewise, the wave front velocity vanishes at high tissue stiffness, where the stiffness mismatch between CMs and the surrounding ECM prevents contracting CMs from exerting sufficient strain on the ECM to trigger contraction of quiescent cells.

Fig. 2.

Results from CE (blue) and SE (red) models (Eq. 1) compared with experimental measurements (black) from ref. 10. (A) Best fits (Table 1) of model contractile wave front velocities to experimental data from the embryonic ventricle. (B) Maximal tissue strain as a function of E calculated with no additional fit parameters vs. experimental data (black circles). Green triangles denote likelihood that wave front propagated across the entire ventricle in experiment; for the two lowest $E/E^{\ast }$ data points, the likelihood falls below $50\text{\%}$ (green dotted line), consistent with our models, which predict no stationary solutions below $E_0$. (C) Predicted induced strain trace for a single cell adhered to gel surface (Supporting Information) compared with cell-on-gel data (black circles).

Calculated Wave Front Strain Agrees with Experimental Observations with No Additional Fitting Parameters.

Using the three parameters ($\mathrm{\Gamma },\alpha ,E^c$) fit from wave front velocity data, we independently calculate the tissue strain of the contractile wave front and compare with the measured maximal ventricular strain from ref. 10 (Fig. 2B). Both the CE (blue) and SE (red) models are in excellent quantitative agreement with the observed behavior (black circles) as a function of tissue stiffness, providing strong evidence in favor of our model. Note that the correct optimum stiffness naturally emerges from our model by treating CMs as elastic inclusions (Supporting Information) embedded within a surrounding matrix of variable stiffness. This quantitative agreement is significant and nontrivial, as we can observe from the different values of E corresponding to optimum velocity and optimum strain in experiment and model. Note also that no purely electrochemical model can correctly predict strain as a function of stiffness.

SE Model Is Consistent with Cell-on-Gel Measurements with No Additional Fitting Parameters.

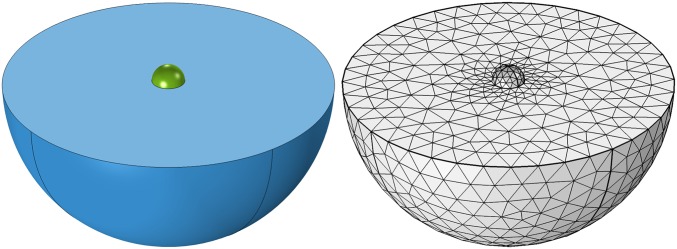
We further test our model by comparing to data for beating E4 CMs cultured on polyacrylamide gel where gel strain at cell edges was measured for varying gel stiffness (10). We calculate the trace of the 2D projected strain by finite-element simulation (Materials and Methods and Fig. S1) using the fit $E^c$ value and comparing to experiment in Fig. 2C. The failure of the CE model on soft gels is expected from cultured CM experiments (7, 8, 22). Remarkably, we find agreement between the SE model with cell-on-gel measurements, demonstrating that we can deduce this single CM behavior as a function of E quantitatively from collective behavior in tissue.

Fig. S1.

Illustration and meshing of COMSOL finite-element–simulated “cell-on-gel” contraction. Active CM (green) contracts while adhered to matrices (blue) of variable stiffness. Chosen mesh is shown in gray. Maximal matrix strain trace is averaged over CM–matrix contact surface and shown in Fig. 2A.

Mechanical Signaling Model Correctly Predicts Appearance of First Heartbeats.

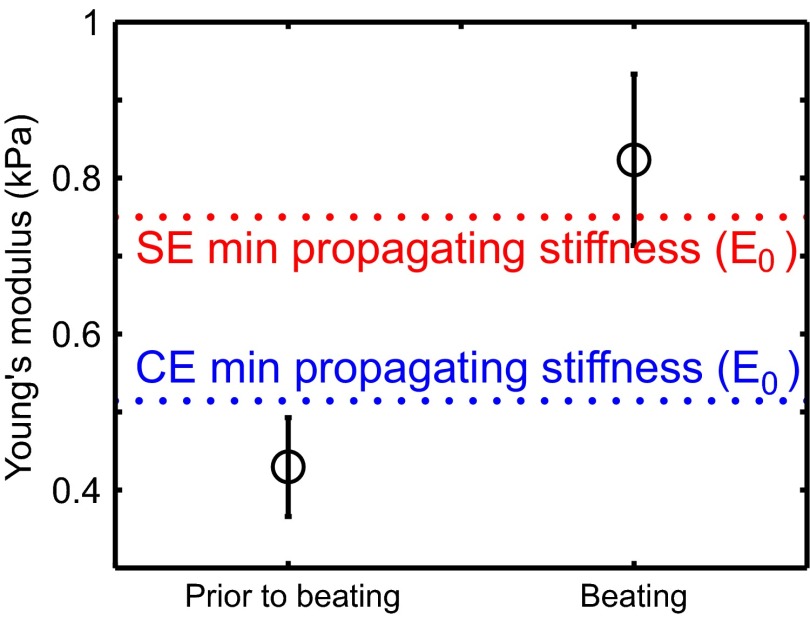
The developing heart stiffens with age due to increased collagen in the ECM (10). CMs begin periodic contractions at about 1.5 d after fertilization (E1.5). At that point, the heart does not beat but “shivers”; this shivering is similar to behavior observed in strain-activated contractile cell aggregates (29), which lack a signaling mechanism to coordinate the phases of the periodically contracting cells. The first fully coordinated beats do not occur until hours after CMs start contracting. Our model predicts that coordinated beats cannot appear until the matrix reaches the minimum stiffness $E_0$ (Fig. 2A). Here, we ask whether the predicted value of $E_0$ coincides with heart stiffness at the onset of beating.

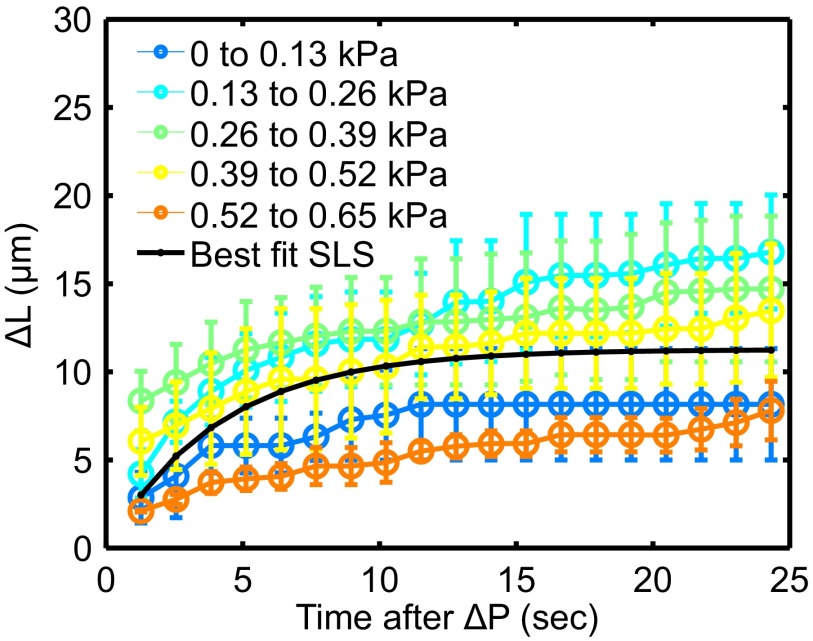
We measure embryonic chick hearts stiffnesses at Hamburger–Hamilton (HH) stages 10 and 11 (E1.5–E2) via micropipette aspiration (Materials and Methods). Early stage 10 does not exhibit fully coordinated beats, whereas stage 11 exhibits full-tissue contraction (Movie S1). At the strains applied, the tissue behaves as a standard linear solid (Fig. S2).

Fig. S2.

Results from ramp-hold experiments performed on explanted HH stage 10–11 avian hearts. Pressure of micropipette applied to the tissue increases with increments of 0.13 kPa every 46 s. Excursion length differences as a function of pressure (indicated colors) and time after a pressure ramp (axis) are plotted. The best-fit standard linear solid (SLS) model is shown in black. For the majority of pressures applied, the heart behaves quantitatively as a linear viscoelastic material.

We sort the measured stiffnesses depending on whether or not the hearts exhibit coordinated contractions (black circles in Fig. 3). The prebeating stiffness is just above that of the undifferentiated embryonic disk (10), suggesting that the first stage of heart development involves some differentiation with little stiffening. The minimum stiffnesses $E_0$ for the CE (blue) and SE (red) models both fall between the measured prebeating and postbeating values. These measurements are consistent with our model prediction and suggest that heartbeats may initially emerge once the tissue becomes stiff enough to support mechanically activated wave fronts.

Fig. 3.

Measurements of heart stiffness before and after the appearance of heartbeats, compared with minimum stiffness necessary to support a mechanically coordinated contraction in our model. Stiffness is measured via micropipette aspiration for six Hamburger–Hamilton (HH) stage 10 and five HH stage 11 hearts, corresponding to E1.5–E2 (Materials and Methods). Dashed lines indicate predicted $E_0$ values for the CE (blue) and SE (red) models, corresponding to the lower-stiffness cutoffs shown in Fig. 2A.

Conduction Interference Experiments Are Consistent with Mechanically Coordinated Heartbeats.

Gap junctions are critical for electrical coordination of adult heartbeats. Our mechanical signaling hypothesis implies that blocking electrical signaling should not impede the embryonic heartbeat. We therefore test our hypothesis by blocking electrical signaling through pharmacological interference of gap junctions.

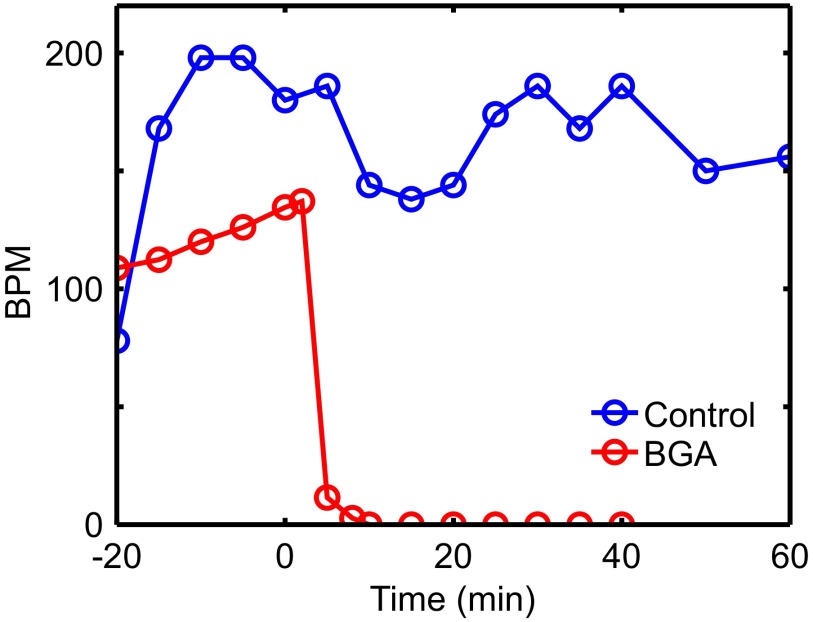
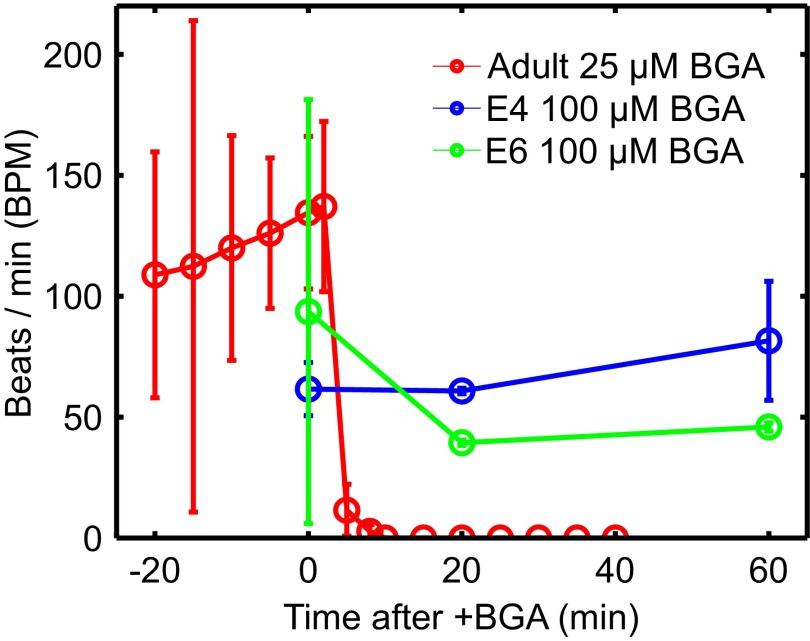
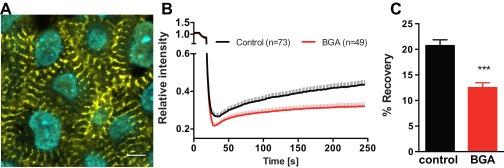
We perfuse isolated adult and embryonic hearts with BGA, a nonspecific gap junction blocker known to inhibit intercellular ion transport between embryonic chick epithelial cells at 10 μM (30) and in rat, frog, mouse, and human systems (31–34). Adult hearts stopped beating within 10 min posttreatment at 25 μM BGA (Fig. S3 and Movie S2). However, the embryonic heartbeat was unaffected for 1 h even at 100 μM BGA (Fig. 4), and was robust even when subjected to 250 μM for an additional hour. We also validated its effect in embryonic hearts via fluorescence recovery after photobleaching (FRAP) experiments and found that BGA treatment reduced intercellular diffusion (Supporting Information, Fig. S4, and Movie S3). Additionally, our protocol successfully perfuses the embryonic heart with other small-molecule drugs such as blebbistatin and mecarbil (Figs. S5 and S6). These experiments demonstrate that embryonic CMs can coordinate their contractions without functional gap junctions needed to support electrical signaling, supporting our hypothesis of mechanically coordinated CMs in the early heart (Materials and Methods).

Fig. S3.

Beats per minute from isolated Langendorff-perfused adult mouse heart control experiment shown with mean beats per minute from three adult hearts treated with 25 μM BGA (from Fig. 4 in main text). Beats-per-minute data were extracted from 20-s intervals of acquired movie. This demonstrates the effectiveness of BGA on adult heartbeat disruption.

Fig. 4.

Conduction interference results for isolated hearts from three murine adults and four chicken embryos. Gap junctions are disrupted by perfusing intact adult (red) and embryonic E4 and E6 (blue and green, respectively) hearts with β-glycyrrhetinic acid (BGA). Heart functionality is quantified by beats per minute (BPM). Adult hearts stop beating after $\sim$10 min at 25 μM BGA (Movie S2). Embryonic hearts perfused at higher 100 μM show little to no effect after an hour. See Fig. S3 for adult heart BPM controls and Fig. S4 for control experiments on embryonic heart BGA perfusion.

Fig. S4.

A displays a representative image of E4 chicken embryonic CMs stained for α-actinin and DNA. Image was taken 4 μm below the surface in the outflow tract of the looping heart. (Scale bar: 5 μm.) As exampled here, CMs in the E4 heart exhibit premature periodic striations, suggesting myofibrillogenesis of CMs. These cells were subjected to testing for effective gap junction interference via FRAP. B shows aggregated results from calcein red-orange FRAP experiments in control and BGA-treated E4 avian hearts. Individual CMs within the tissue were selected and photobleached (see example, Movie S3). Fluorescent intensity recovery was tracked over at 4 min in 49 +BGA CMs and 73 −BGA CMs. Rapid early recovery is likely due to intracellular diffusion and is unaffected by BGA treatment. In contrast, BGA treatment disrupts prolonged recovery, which is likely mediated by intercellular transport through gap junctions. C demonstrates the significantly higher fluorescence recovery after 4 min in control hearts, demonstrating BGA efficacy in disrupting E4 avian heart gap junctions. ***P < 0.001, unpaired Student's t test.

Fig. S5.

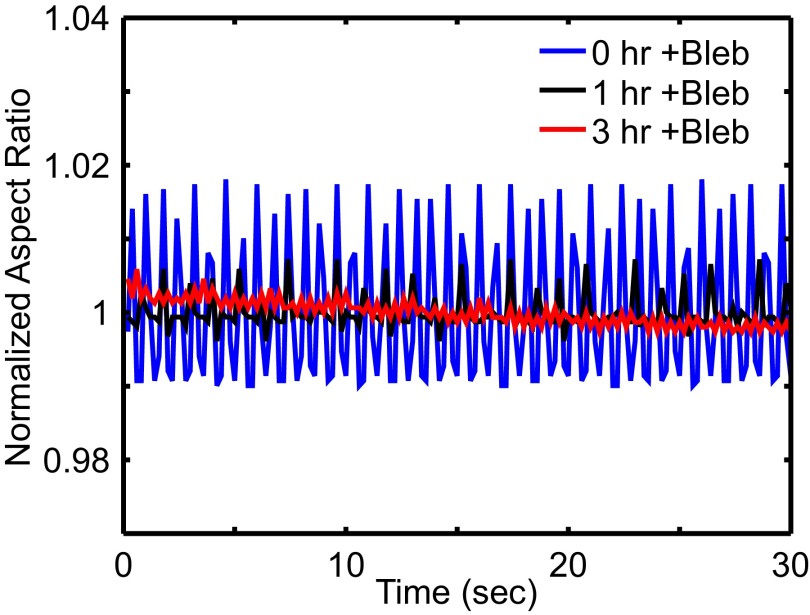
Results from blebbistatin disruption on E4 chick heart. Mean-normalized aspect ratio is recorded over time intervals of 30 s at time points 0, 1, and 3 h after treatment of 20 μM blebbistatin. Significant decreases in beating amplitude and BPM are observed.

Fig. S6.

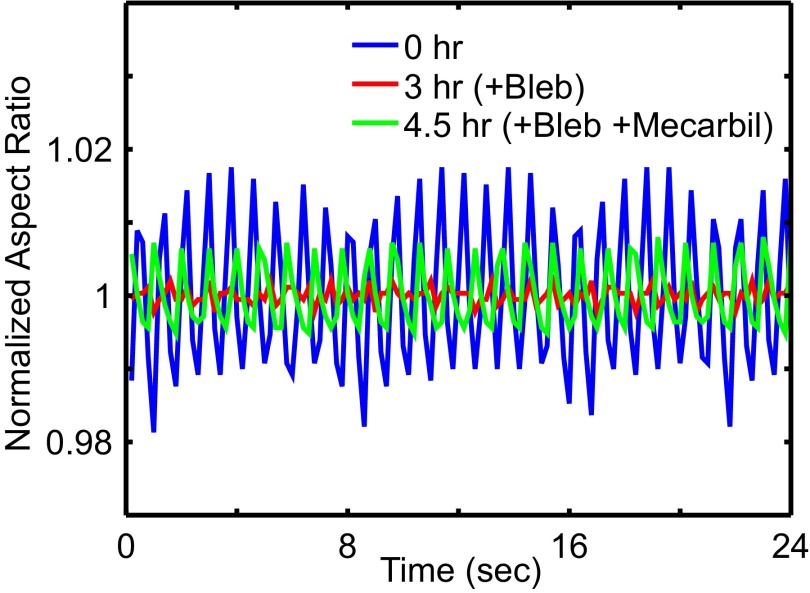
Results from blebbistatin disruption with mecarbil rescue on E4 chick heart. Mean-normalized aspect ratio is recorded over 24-s intervals at time points before drug treatment, postblebbistatin, and postblebbistatin and mecarbil. At $t=0$ h, the heart tube is treated with 20 μM blebbistatin dilution to disrupt actomyosin activity. At $t=3$ h, the blebbistatin solution is removed via aspiration and replaced with 1 μM mecarbil to enhance cardiac myosin activity. We observe rescued beat amplitude and coherence. This also demonstrates effective small-molecule perfusion into isolated embryonic hearts. Additionally, force-enhancing rescue of beats is consistent with a mechanical signaling model.

Discussion

Mechanical Signaling Robustly Explains Strong Dependence of Wave Front Velocity and Strain on Stiffness.

Tissue stiffness is a mechanical property that cells can sense. A strong dependence on tissue stiffness is an indicator of cell response to mechanical cues. Our model combines elasticity with simple mechanical activation of CMs, using a minimum of assumptions and adjustable parameters, and yet captures multiple observed cell- and tissue-scale phenomena quantitatively.

Our model is robust to noise: the predicted strain threshold α requires several nearest-neighbor contractions to trigger activation. As a result, a rogue contraction cannot set off a wave front. Our results are also robust to how we incorporate mechanosensitivity. We considered a model variant in which the CM contracts with a probability $p\left({\mathit{ϵ}}_{kk}\right)$ that increases with strain, and found similar stiffness dependence of the contractile wave front. This stochastic activation model corresponds mathematically to stochastic pulse-coupled oscillator (SPCO) models of neural networks (35), but with an additional spatially dependent phase set by mechanical reaction–diffusion. Synchronized states in SPCO models map onto steady-state wave fronts of our stochastic model.

We note that embryonic CMs spontaneously contract in periodic manner (3, 4). In the beating embryonic heart, the wave front is initiated at the atrial end of the heart tube by CMs that contract at a higher frequency. Our model describes the nonlinear propagating wave front emanating from each contraction of these atrial CMs that activates other CMs. An alternate but equivalent description is to consider the coordination of CMs as nonlinear oscillators coupled through the ECM. Because the ECM has a viscous fluid component as well as an elastic component, this coupling does not lead to synchronization, as typical for phase-coupled biological oscillators (36), but to a propagating wave front.

Mechanical Signaling Is Consistent with Known Mechanosensitivity of CMs.

There is solid evidence that stretch can trigger contraction of CMs. External tissue-scale stretch of the heart triggers arrhythmic beats (37). Healthy adult rat CMs exhibit increased intracellular calcium release events under $8\text{\%}$ strain (38), whereas diseased adult myocytes demonstrate direct mechano-chemotransduction through full intracellular calcium release (9). Mechanical stimulation of the substrate in cultured embryonic chick CMs with $6\text{\%}$ stretch excites quiescent myocytes (39). Mechanical stress exerted by fibroblasts affects the wave front velocity of neonatal rat CMs (40, 41), and neonatal and adult rat CMs cultured in similar conditions exhibit mechanical stimulation and entrainment (42). In some of these experiments, it is known that stretch-induced activation involves cardiac ryanodine receptors (9).

Mechanical vs. Electrical Signaling in the Developing Heart.

There is evidence in the literature that electrical conduction may not be fully functional in the early heart. When whole-tissue contractions first appear, the cardiac conduction system is not yet identifiable (43). Embryonic chick hearts exhibit low levels of the primary cardiovascular gap junction protein, Connexin43 (Cx43), and the small amounts present are distributed uniformly through the cytosol until trabeculation occurs (44, 45). Other studies find that, in posthatch and adult chick, the primary ventricle myocardial gap junction is Cx42. However, Cx42 appears to be absent in working myocytes and cardiac conduction tissues until E9–E11, leading to speculation that CMs may not be electrically coupled by gap junctions during embryogenesis (46). Primary markers of the conduction system do not appear definitively until E9–E15 (47).

In conjunction with our results, such observations suggest that the heart may switch from mechanical to electrical signaling as it matures. We speculate that mechanically coordinated heartbeats may assist in organizing the heart: myocytes seeking to maximize contractile activity will align with each other (48) and cyclic stretch of neonatal rat ventricular myocytes was found to polarize gap junction localization (49). Perhaps current limitations in producing fully mature CMs from stem cells (15) reflect an incomplete understanding of the role of mechanics in heart development.

It is possible that mechanical signaling prevails in early development because it is robust. Electrical coupling requires gap junctions, which may be difficult to maintain as CMs proliferate and rearrange in the rapidly growing heart. Mechanical signals, on the other hand, are inevitably present because CMs must exert stresses on their surroundings when they contract. However, electrical signaling is easier to regulate when the heart develops more complicated structure.

In summary, the highly sophisticated electrical conduction system that precisely regulates the adult heart has been assumed to coordinate every heartbeat, from the first to the last. Here, we use a biophysical theory, bolstered by experiment, to propose that mechanical—not electrical—signaling is responsible for coordinating early heartbeats. If further verified, this idea could transform the way we think about how the heart develops and functions.

Materials and Methods

Model Details.

We solve the matrix response function in three dimensions. We assume a stationary constant-velocity wave front [${\mathit{ϵ}}_{ij}\left(x,t\right)={\mathit{ϵ}}_{ij}\left(x-vt\right)$] within a cubic array of infinitesimal active sites. The infinitesimal approximation was validated through finite element simulation (Supporting Information and Fig. S7). Self-consistency of the activation condition with the time between activation events relates v to model parameters. See Supporting Information.

Fig. S7.

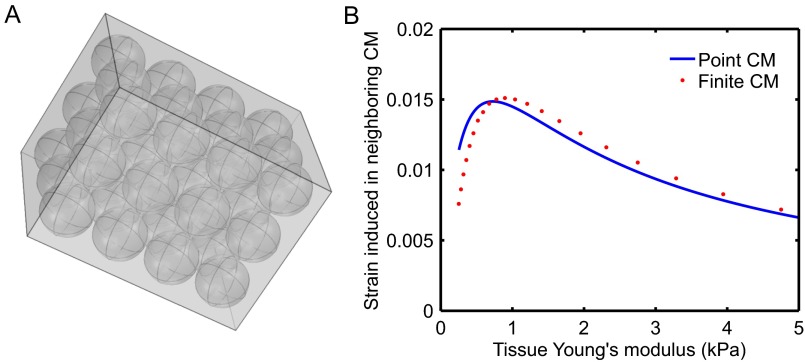
Comparison of mechanical response between point-like and finite-sized CMs. We perform finite-element simulations in COMSOL. We embed 36 elastic inclusions (CMs) within a surrounding elastic matrix, as shown in A. We impose a contractile eigenstrain in one of the centrally located CMs. We plot (B) the maximum strain induced in the neighboring centrally located CM against our analytic result for point-like CMs as a function of effective tissue Young’s modulus. We observe good quantitative agreement between the two models, justifying our approximation of CMs as point-like elastic inclusions.

Numerical Computations and Data Analysis.

Numerical computations were performed in C/C++ and MATLAB. Data analysis and nonlinear least-squares parameter fitting was done in MATLAB with custom subroutines.

Finite-Element Simulation.

Linear elastic finite-element simulations were performed in MATLAB and COMSOL. Cell-on-gel culture was modeled as a hemisphere adhered to a substrate. See Supporting Information and Table S1 for simulation parameters.

Table S1.

Finite-element method simulation parameter description, symbol, and values

Description	Parameter	Value
Hemispherical cell radius	$\mathrm{\Delta }x$	5 μm
Hemispherical substrate radius	R	10Δx
Cell Young’s modulus	$E_c$	0.75 kPa
Force saturation Young’s modulus	$E_s$	$E_c$
Substrate Young’s modulus	E	[0.1–100] kPa
Poisson ratio	ν	0.4
Cell strain amplitude	${\mathit{ϵ}}^{\ast }$	0.2

Myocardium Stiffness Measurements.

Embryonic hearts were isolated as described in ref. 10. Aspiration was performed at room temperature. See Supporting Information.

Conduction Interference: Embryonic Hearts.

Embryonic chick hearts were isolated as in ref. 10 and incubated in heart medium at 37 °C (α-MEM supplemented with 10% (vol/vol) FBS and 1% penn-strep; Gibco; 12571-063) for at least 2 h before drug treatment. Desired concentrations of 18-β-glycyrrhetinic acid (Cayman Chemical; 11845) and blebbistatin (EMD Millipore; 203390) were prepared by diluting in heart culture medium [with or without 10% (vol/vol) FBS] and DMSO, respectively. Isolated hearts were then treated with BGA or blebbistatin by aspirating out the medium and perfusing the hearts in the prepared drug solutions. E4 hearts were imaged using an Olympus I81 microscope and recorded for a minimum of 15 s using a CCD camera at 21 frames per s. E6 hearts were imaged using a Nikon SMZ1500 microscope. Analysis was performed in ImageJ by tracking morphological parameters over 10- to 15-s intervals.

Conduction Interference: Adult Hearts.

Adult (8–12 wk) C57/BL6 mice were anesthetized by induction in an isoflurane chamber, followed by thoracotomy and excision of the heart. Isolated hearts were suspended from a Langendorff perfusion column via cannulation of the aorta and perfused with an oxygenated heart medium at 37 °C. Under control conditions, hearts cannulated via this method generate intrinsic rhythm and maintain rhythmic beating for over 3 h. BGA solution was prepared by dilution in medium and DMSO. After ensuring 20 min of rhythmic beating, the medium was exchanged for BGA-prepped solution. Twenty-second movie acquisitions were acquired every 3–5 min to analyze changes in heart rate over time. Experiments were terminated if the heart stopped beating for more than 10 min. Movie segments from different time points were randomized and analyzed blindly to determine beats per minute from 20-s intervals.

Linearized Biphasic Model

In the linearized biphasic model composed of fluid and elastic mesh, we assume that the fluid and elastic components mutually exclude each other and that the total volume is fixed. Then for an infinitesimal volume element at x, if the fluid volume fraction is ϕ the elastic mesh must occupy $1-\varphi$. As a result, within the volume element at x neither fluid nor mesh network satisfy the regular incompressible condition, because fluid and mesh mutually displace each other. In our model, we take into account the fluid dynamic viscosity, mesh elasticity, fluid–mesh drag coupling, and the total volume (fluid plus mesh) constraint to linear order in the dynamic variables:

$$\begin{array}{c}\mathrm{\Gamma }\left({\dot{u}}_i-v_i\right)=\frac{E}{2\left(1+\nu \right)}\left[{\partial }^2{u}_i+\frac{1}{1-2\nu }{\partial }_i{\partial }_j{u}_j\right]-\left(1-\varphi \right){\partial }_{i}p\\ \mathrm{\Gamma }\left(v_i-{\dot{u}}_i\right)=\eta \left[{\partial }^2{v}_i+\frac{1}{3}{\partial }_i{\partial }_j{v}_j\right]-\varphi {\partial }_{i}p\\ 0=\left(1-\varphi \right){\partial }_i{\dot{u}}_i+\varphi {\partial }_i{v}_i.\end{array}$$ [S1]

Because we are interested primarily in comparing to experimental wave front speeds and tissue strain trace, for brevity we detail only the strain trace and strain rate trace equations here. The fluid and solid (traces of) strain rates and strain are ${\dot{\mathit{ϵ}}}_{f,ii}={\partial }_i{v}_i$, ${\dot{\mathit{ϵ}}}_{s,ii}={\partial }_i{\dot{u}}_i$, and ${\mathit{ϵ}}_{s,ii}={\partial }_i{u}_i$. For physiological values of $\varphi \approx 0.8$ in muscle tissue (Table 1), we solve the equations:

$$\begin{array}{l}\mathrm{\Gamma }\left({\dot{\mathit{ϵ}}}_s-{\dot{\mathit{ϵ}}}_f\right)=\frac{E\left(1-\nu \right)}{\left(1+\nu \right)\left(1-2\nu \right)}{\partial }^2{\mathit{ϵ}}_s-\left(1-\varphi \right){\partial }^{2}p\\ \mathrm{\Gamma }\left({\dot{\mathit{ϵ}}}_f-{\dot{\mathit{ϵ}}}_s\right)=\frac{4}{3}\eta {\partial }^2{\dot{\mathit{ϵ}}}_f-\varphi {\partial }^{2}p\\ {\dot{\mathit{ϵ}}}_f=-{\dot{\mathit{ϵ}}}_s\frac{1-\varphi }{\varphi }.\end{array}$$ [S2]

Then solving in terms of ${\mathit{ϵ}}_s$, we obtain the equation of motion:

$$\left[{\dot{\mathit{ϵ}}}_s-\frac{4{\left(1-\varphi \right)}^2\eta }{3\mathrm{\Gamma }}{\partial }^2{\dot{\mathit{ϵ}}}_s\right]=D{\partial }^2{\mathit{ϵ}}_s,$$ [S3]

where $D={\varphi }^{2}E\left(1-\nu \right)/\left(\mathrm{\Gamma }\left(1+\nu \right)\left(1-2\nu \right)\right)$. We assume that the interstitial fluid viscosity is approximately the viscosity of water at body temperature. Best fits (Results) then indicate that $\mathrm{\Gamma }\approx 45\left(\eta /\mathrm{\Delta }{x}^2\right)$, where $\mathrm{\Delta }x$ the spacing between myocytes. As a result, the fluid–mesh drag $\mathrm{\Gamma }$ is dominant over fluid viscosity at physical length scales of interest, and the second term on the left-hand side in Eq. S3 can be dropped. This result is used throughout the text. For our parameter values, the linearized equations are stable to perturbations at the onset of propagation. In contrast to standard reaction–diffusion models, but consistent with fire–diffuse–fire [14] models, the nonlinear character of transitions between the nonpropagating and propagating phases is a result of threshold activation and as a result is not captured by linear stability analysis.

Induced Strain of Eshelby Inclusions

Here, we detail the stresses induced by CMs, which are treated as spherical Eshelby inclusions (elastic inclusions with elastic constants that may be different from the surrounding matrix). We compute two tensors, $T_{ijkl}^{\text{out}}$ and $T_{ijkl}^{\text{in}}$, which correspond (respectively) to strain induced in the matrix due to an active inclusion, and the strain felt by a passive inclusion due to strain in the matrix (Fig. 1A). Because we model CM sources as infinitesimal, incoming stresses are treated as far-field. Note that we have checked this approximation using finite-element calculations (SI Materials and Methods, CMs-in-Matrix Finite-Element Method Simulations, and Fig. S7), and find that it is quantitatively quite accurate. We also assume that, near an excited inclusion, the matrix responds quickly; this allows us to make use of the static Eshelby tensor.

Suppose a cell, represented as an ellipsoidal inclusion with stiffness tensor $C_{ijkl}$, is embedded in an infinite bulk medium (i.e., the tissue) with the same stiffness tensor. Although we use the general form, in the isotropic case this tensor is determined by just two independent parameters, which we call the Young’s modulus E and Poisson ratio ν in the main text. Suppose the cell contracts uniformly throughout its volume with an eigenstress ${\sigma }_{ij}^{\ast \text{cell}}$. We equivalently represent this contraction strength as an eigenstrain ${\mathit{ϵ}}_{ij}^{\ast \text{cell}}$, related to the stress by ${\sigma }_{ij}^{\ast cell}=C_{ijkl}{\mathit{ϵ}}_{kl}^{\ast \text{cell}}$. This eigenstrain can be thought of as how much the cell would strain if the surroundings exerted no stress on the cell. By Eshelby inclusion theory, the observed strain of an embedded inclusion is related to the eigenstrain by the following:

$${\mathit{ϵ}}_{ij}^{\ast }=S_{ijkl}{\mathit{ϵ}}_{kl}^{\ast \text{cell}},$$ [S4]

where $S_{ijkl}$ is the Eshelby tensor [24]. For a spherical inclusion, this tensor is uniform and given by the following:

$$S_{ijkl}=\frac{1+\nu }{3\left(1-\nu \right)}{|v^1\rangle }_{ijkl}+\frac{2\left(4-5\nu \right)}{15\left(1-\nu \right)}{|v^2\rangle }_{ijkl},$$ [S5]

where ${|v^1\rangle }_{ijkl}$ and ${|v^2\rangle }_{ijkl}$ are defined for convenience as follows:

$$\begin{array}{c}{|v^1\rangle }_{ijkl}=\frac{1}{3}{\delta }_{ij}{\delta }_{kl}\\ {|v^2\rangle }_{ijkl}=\frac{1}{2}\left[{\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}-\frac{2}{3}{\delta }_{ij}{\delta }_{kl}\right].\end{array}$$ [S6]

Stress Locally Induced in Matrix by Eshelby Inclusion.

Now suppose the cell and tissue have different stiffness tensors $C_{ijkl}^c$ and $C_{ijkl}$, respectively. As before, an isotropic medium reduces the independent parameters to E and ν. Assume the cell contracts with a stress ${\sigma }_{ij}^{\ast cell}=C_{ijkl}^c{\mathit{ϵ}}_{kl}^{\ast \text{cell}}$. The total stress inside the cell embedded in the tissue is related to the strain by the following:

$${\sigma }_{ij}^T=C_{ijkl}^c\left({\mathit{ϵ}}_{kl}^{\ast }-{\mathit{ϵ}}_{kl}^{\ast \text{cell}}\right).$$ [S7]

By superposition, we can map this to a problem to the Eshelby tensor for a homogeneous material with an additional strain source [24]. This is done by imposing an effective strain source in the cell ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$ such that we get identical stresses and strains as the inhomogeneous problem. The stress–strain relation then becomes the following:

$${\sigma }_{ij}^T=C_{ijkl}\left({\mathit{ϵ}}_{kl}^{\ast }-{\mathit{ϵ}}_{kl}^{\ast \text{eff}}\right).$$ [S8]

Note that the effective strain source ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$ does not actually exist but is just a mathematical trick to reduce the inhomogeneous inclusion problem to the previously solved homogeneous inclusion problem. Eshelby’s solution now tells us that the strain experienced in the cell embedded in the tissue is as follows:

$${\mathit{ϵ}}_{ij}^{\ast }=S_{ijkl}{\mathit{ϵ}}_{kl}^{\ast \text{eff}},$$ [S9]

with the Eshelby tensor calculated using $C_{ijkl}$. Now we calculate the effective source ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$ by equating Eqs. S7 and S8, to identify the (actual) inhomogeneous case with the (constructed) homogeneous problem:

$$C_{ijkl}^c\left({\mathit{ϵ}}_{kl}^{\ast }-{\mathit{ϵ}}_{kl}^{\ast \text{cell}}\right)=C_{ijkl}\left({\mathit{ϵ}}_{kl}^{\ast }-{\mathit{ϵ}}_{kl}^{\ast \text{eff}}\right).$$ [S10]

Substituting in Eq. S9, we get an equation for ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$,

$$\left[\left(C_{ijkl}^c-C_{ijkl}\right)S_{klmn}+C_{ijmn})\right]{\mathit{ϵ}}_{mn}^{\ast \text{off}}=C_{ijkl}^c{\mathit{ϵ}}_{kl}^{\ast \text{cell}}.$$ [S11]

Solving for ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$ in terms of ${\mathit{ϵ}}_{ij}^{\ast \text{cell}}$, we find ${\mathit{ϵ}}_{ij}^{\ast }$ (via Eq. S9). We can now calculate the stress source in the homogeneous case ${\sigma }_{ij}^{\ast }=C_{ijkl}{\mathit{ϵ}}_{kl}^{\ast }$. We define the tensor $T_{ijkl}^{\text{out}}$ to relate this stress to our cell strain source,

$${\sigma }_{ij}^{\ast }=T_{ijkl}^{\text{out}}{\mathit{ϵ}}_{kl}^{\ast \text{cell}},$$ [S12]

as in Fig. 1A. For a spherical inclusion and isotropic matrix with Young’s moduli $E^c$ and E and Poisson ratios ${\nu }^c$ and ν, respectively,

$$\begin{array}{c}{T}_{ijkl}^{\text{out}}=\left[\frac{\frac{E}{\left(1-2\nu \right)}\frac{\left(1-\nu \right)}{\left(1+\nu \right)}}{1+2\frac{\left(1-2{\nu }^c\right)}{\left(1+\nu \right)}\frac{E}{E^c}}\right]{|v^1\rangle }_{ijkl}+\left[\frac{\frac{15E}{4\left(1+\nu \right)}\frac{\left(1-\nu \right)}{\left(4-5\nu \right)}}{1+\frac{1}{2}\frac{\left(7-5\nu \right)}{\left(4-5\nu \right)}\frac{\left(1+{\nu }^c\right)}{\left(1+\nu \right)}\frac{E}{E^c}}\right]{|v^2\rangle }_{ijkl}\\ =\frac{E}{3\left(1-2\nu \right)}{T}_1^{\text{out}}{|v^1\rangle }_{ijkl}+\frac{E}{2\left(1+\nu \right)}{T}_2^{\text{out}}{|v^2\rangle }_{ijkl},\end{array}$$ [S13]

where $T_1^{\text{out}}$ and $T_2^{\text{out}}$ are dimensionless quantities, with prefactors of the tissue bulk and shear moduli.

Stress Induced in Eshelby Inclusion by Uniform Stress in Matrix.

As in the previous section, we can likewise compute the strain in a cell given some homogeneous stress ${\sigma }_{ij}=C_{ijkl}{\mathit{ϵ}}_{kl}$ throughout the neighborhood of tissue surrounding the inclusion. The primary difference is that this system now exists under a prestress condition without a cell source. As before, cell and tissue stiffness tensors are $C_{ijkl}^c$ and $C_{ijkl}$. The total stress inside the cell is given by the following:

$${\sigma }_{ij}^T=C_{ijkl}^c{\mathit{ϵ}}_{kl}^{\text{cell}}.$$ [S14]

By linearity, the strain in the cell can be broken up into two components: the homogeneous strain in the surrounding tissue ${\mathit{ϵ}}_{ij}$, and the effects of the inclusion’s stiffness mismatch with the tissue ${\mathit{ϵ}}_{ij}^I$,

$${\mathit{ϵ}}_{ij}^{\text{cell}}={\mathit{ϵ}}_{ij}+{\mathit{ϵ}}_{ij}^I.$$ [S15]

As in the previous section, we map this inhomogeneous problem to a homogeneous one with additional cell strain source ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$, but the same total stress and strain:

$${\sigma }_{ij}^T=C_{ijkl}\left({\mathit{ϵ}}_{kl}^{\text{cell}}-{\mathit{ϵ}}_{kl}^{\ast \text{eff}}\right).$$ [S16]

Eshelby’s solution now tells us that the contribution to the strain from the inclusion is as follows:

$${\mathit{ϵ}}_{ij}^I=S_{ijkl}{\mathit{ϵ}}_{kl}^{\ast \text{eff}}.$$ [S17]

Equating Eqs. S14 and S16, and using the relation from Eq. S15,

$$C_{ijkl}^c\left({\mathit{ϵ}}_{kl}+{\mathit{ϵ}}_{kl}^I\right)=C_{ijkl}\left({\mathit{ϵ}}_{kl}+{\mathit{ϵ}}_{kl}^I-{\mathit{ϵ}}_{kl}^{\ast \text{eff}}\right).$$ [S18]

Substituting in Eq. S17, we get an equation for ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$,

$$\left[\left(C_{ijkl}^c-C_{ijkl}\right)S_{klmn}+C_{ijmn})\right]{\mathit{ϵ}}_{mn}^{\ast \text{eff}}=\left(C_{ijkl}-C_{ijkl}^c\right){\mathit{ϵ}}_{kl}.$$ [S19]

Solving for ${\mathit{ϵ}}_{ij}^{\ast \text{eff}}$ in terms of ${\mathit{ϵ}}_{ij}$, we find ${\mathit{ϵ}}_{ij}^I$ via Eq. S17. This gives the cell strain ${\mathit{ϵ}}_{ij}^{\text{cell}}$. Using the relation ${\sigma }_{ij}=C_{ijkl}{\mathit{ϵ}}_{kl}$ for the homogeneous case, we express ${\mathit{ϵ}}_{ij}^{\text{cell}}$ in terms of ${\sigma }_{ij}$. We define $T_{ijkl}^{\text{in}}$ to relate this stress to the strain in the cell as follows:

$${\mathit{ϵ}}_{ij}^{\text{cell}}=T_{ijkl}^{\text{in}}{\sigma }_{kl},$$ [S20]

as in Fig. 1A. For a spherical inclusion and isotropic matrix with Young’s moduli $E^c$ and E and Poisson ratios ${\nu }^c$ and ν,

$$\begin{array}{c}{T}_{ijkl}^{\text{in}}=\frac{3\left(1-2\nu \right)}{E}\left[1+\frac{\frac{\left(1-2{\nu }^c\right)}{\left(1-2\nu \right)}\frac{E}{E^c}-1}{1+2\frac{\left(1-2{\nu }^c\right)}{\left(1+\nu \right)}\frac{E}{E^c}}\right]{|v^1\rangle }_{ijkl}+\frac{2\left(1+\nu \right)}{E}\left[1+\frac{\frac{\left(1+{\nu }^c\right)}{\left(1-\nu \right)}\frac{E}{E^c}-1}{1+\frac{1}{2}\frac{\left(7-5\nu \right)}{\left(4-5\nu \right)}\frac{\left(1+{\nu }^c\right)}{\left(1+\nu \right)}\frac{E}{E^c}}\right]{|v^2\rangle }_{ijkl}\\ =\frac{3\left(1-2\nu \right)}{E}{T}_1^{\text{in}}{|v^1\rangle }_{ijkl}+\frac{2\left(1+\nu \right)}{E}{T}_2^{\text{in}}{|v^2\rangle }_{ijkl},\end{array}$$ [S21]

where $T_1^{\text{in}}$ and $T_2^{\text{in}}$ are dimensionless quantities, with prefactors of the inverse tissue bulk and shear moduli.

Activation Condition

In our model, when CMs contract they generate an eigenstress corresponding to a negative force dipole in the x direction. This assumption is based on the observation that E4 CMs exhibit striations, which polarize contraction, and serves to simplify analysis. An activated CM in our model has an eigenstrain ${\mathit{ϵ}}_{kl}^{\ast }$ and induces a matrix stress ${\sigma }_{ij}^{\ast }$:

$${\mathit{ϵ}}_{kl}^{\ast }={\mathit{ϵ}}^{\ast }\left(\begin{array}{ccc}-1& 0& 0\\ 0& {\nu }^c& 0\\ 0& 0& {\nu }^c\end{array}\right),{\sigma }_{ij}^{\ast }=T_{ijkl}^{\text{out}}{\mathit{ϵ}}_{kl}^{\ast }.$$ [S22]

Given a stress source ${\sigma }_{a,kl}^{\ast }\left(r\prime ,t\prime \right)$ indexed by a in the biphasic medium, the strain trace induced in an included cell at $\left(r,t\right)$ is as follows:

$${\mathit{ϵ}}_{a,ii}^{\text{cell}}\left(r,t\right)=\frac{1-2\nu }{E}{T}_1^{\text{in}}{\displaystyle \int dt\prime d^{3}r\prime G_{iikl}\left(r-r\prime ;t-t\prime \right){\sigma }_{a,kl}^{\text{*}}\left(r\prime ,t\prime \right)},$$ [S23]

for the Green’s function $G_{ijkl}$. Combining Eqs. S12 and 3,

$${\sigma }_{a,ij}^{\ast }\left(r\prime ,t\prime \right)=T_{ijkl}^{\text{out}}{\mathit{ϵ}}_{a,kl}^{\ast }\left(r\prime ,t\prime \right)=T_{ijkl}^{\text{out}}{\mathit{ϵ}}_{kl}^{\ast }\mathrm{\Theta }\left(t-t_a\right)\mathrm{\Theta }\left(\tau +t_a-t\right){\delta }^3\left(x-x_a\right).$$ [S24]

For a quiescent cell at $\left(r,t\right)$ to reach the activation threshold α, we consider all activated CMs (indexed here by a) as contributing to the local strain. This requires the following:

$${\mathit{ϵ}}_{ii}^{\text{cell}}\left(r,t\right)={\displaystyle \sum _a{\mathit{ϵ}}_{a,ii}^{\text{cell}}\left(r,t\right)}=\alpha .$$ [S25]

Consider a steady-state wave front traveling in the x direction through a cubic array of CMs spaced by $\mathrm{\Delta }x$ as in Fig. 1. We label each CM with lattice indices $\left[n^x,n^y,n^z\right]$. Steady state assumes CMs with the same x coordinate activate simultaneously with a constant (but unknown) time interval $\mathrm{\Delta }t$ between activations at neighboring sites $\left(x,y,z\right)$ and $\left(x+\mathrm{\Delta }x,y,z\right)$.

We express the activation positions and times as $r_a={\left[n_a^x,n_a^y,n_a^z\right]}^T\mathrm{\Delta }x$ and $t_a=n_a^x\mathrm{\Delta }t$ where the index $n^x$ is in the propagation direction x. In conjunction with the activation condition (Eq. 3),

$$\begin{array}{c}\frac{E{\displaystyle {\sum }_a{\mathit{ϵ}}_{a,ii}^{\text{cell}}}}{\left(1-2\nu \right)T_1^{\text{in}}}={\displaystyle \sum _a{\displaystyle \int dt\prime d^{3}r\prime G_{iikl}\left(r-r\prime ;t-t\prime \right){\sigma }_{a,kl}^{\ast }\left(r\prime ,t\prime \right)}}\\ ={\displaystyle \sum _{n^x,n^y,n^z}{\displaystyle \int dt\prime G_{iikl}\left(r-\left[\begin{array}{c}{n}^x\\ n^y\\ n^z\end{array}\right]\mathrm{\Delta }x;t-t\prime \right)\left[\mathrm{\Theta }\left(t\prime -n^x\mathrm{\Delta }t\right)-\mathrm{\Theta }\left(t\prime -n^x\mathrm{\Delta }t-\tau \right)\right]T_{klmn}^{\text{out}}{\mathit{ϵ}}_{mn}^{\ast }}},\end{array}$$ [S26]

for $n^x\in \left\{\mathrm{1,2},\dots ,\mathrm{\infty }\right\}$ and $n^y,n^z\in \left\{-\infty ,\dots ,-\mathrm{1,0,1},\dots ,\mathrm{\infty }\right\}$ and the activation eigenstrain ${\mathit{ϵ}}_{mn}^{\ast }$ as defined in main-text Eq. 1. Using the Green’s function $G_{ijkl}\left(r,t\right)$ for Eq. S3, we find that the response to a Heaviside point force dipole $\sim {\delta }^3\left(r\right)\mathrm{\Theta }\left(t\right)$ is as follows:

$$\begin{array}{c}{H}_{iikl}\left(r,t\right)={\displaystyle \int dt\prime G_{iikl}\left(r,t-t\prime \right)\mathrm{\Theta }(t\prime )}=\frac{1}{4\pi \mathrm{\Gamma }D{r}^3}\left[H_1\left(r,t\right){\delta }_{kl}+H_2\left(r,t\right)\frac{r_k{r}_l}{r^2}\right]\mathrm{\Theta }\left(t\right),\\ H_1=\text{erfc}\left(\frac{\text{r}}{\sqrt{4\text{Dt}}}\right)+\frac{2r}{\sqrt{4\pi Dt}}{e}^{-\frac{r^2}{4Dt}}\\ H_2=-3\text{erfc}\left(\frac{\text{r}}{\sqrt{4\text{Dt}}}\right)-\left(\frac{6r}{\sqrt{4\pi Dt}}+\frac{4r^2}{4\pi Dt}\right)e^{-\frac{r^2}{4Dt}},\end{array}$$ [S27]

in the limit where $\mathrm{\Gamma }\gg \eta q^2$. Here, $D={\varphi }^{2}E\left(1-\nu \right)/\left(\mathrm{\Gamma }\left(1+\nu \right)\left(1-2\nu \right)\right)$as before. Combining Eqs. S25–S27, we find a transcendental relation for $\mathrm{\Delta }t$ in terms of CM and ECM parameters:

$$\frac{E\alpha }{1-2\nu }=T_1^{\text{in}}{\displaystyle \sum _a(H_{iikl}(r-r_a;t-t_a)-H_{iikl}\left(r-r_a;t-t_a-\tau \right)T_{klmn}^{\text{out}}{\mathit{ϵ}}_{mn}^{\ast }}.$$ [S28]

We truncate the sum when the estimated relative error $\delta <{10}^{-4}$, which corresponds to $\left|m\right|,\left|n\right|,\left|o\right|<20$ for physiological parameters. We use Newton–Raphson to solve numerically for $\mathrm{\Delta }t$ to obtain the steady-state wave front velocity, $v=\mathrm{\Delta }x/\mathrm{\Delta }t$. The cubic lattice approximation was chosen due to its simple analytic solution. We found that the steady-state wave front behavior depends primarily on average spacing between active sites and not the chosen lattice.

Tissue Strain Calculation

We calculate the wave front strain trace with a coarse-grained, stationary wave back solution. Consider Eq. S3 in the limit $\eta /\left(\mathrm{\Gamma }\mathrm{\Delta }{x}^2\right)\ll 1$. We assume a steady-state traveling wave front $\mathit{ϵ}\left(x,y,z,t\right)=\mathit{ϵ}\left(x-vt,y,z\right)$ with a comoving excitation front with velocity v driven by the activation condition solved above. Because the sites behind the wave front are refractory, there are no other stress sources other than the activation front. The equations of motion then become the following:

$$-v{\partial }_x{\mathit{ϵ}}_{kk}\left(x-vt,y,z\right)=D{\partial }^2{\mathit{ϵ}}_{kk}\left(x-vt,y,z\right)-\frac{{\sigma }_{ij}^{\ast }}{\mathrm{\Gamma }}{\partial }_i{\partial }_j{\displaystyle \sum _a{\delta }^3\left(x-x_a-vt,y-y_a,z-z_a\right),}$$ [S29]

where $D={\varphi }^{2}E\left(1-\nu \right)/\left(\mathrm{\Gamma }\left(1+\nu \right)\left(1-2\nu \right)\right)$; ${\sigma }_{ij}^{\ast }=T_{ijkl}^{\text{out}}{\mathit{ϵ}}_{kl}^{\ast }$, the stress generated in the matrix by each contracting myocyte; and a, the activated sites. Assuming a cubic lattice in the comoving frame, the number of activated sites N in x corresponds to the width of the activated front, $N=v\tau /\mathrm{\Delta }x$. So we take the following:

$${\displaystyle \sum _a}={\displaystyle \sum _{n^x,n^y,n^z}},$$ [S30]

where $n^x\in \left\{1,\dots ,N\right\},n^y,n^z\in \left\{-\infty ,\dots ,\mathrm{\infty }\right\}$. In comoving Fourier space, we find that the strain trace becomes the following:

$${\widetilde{\mathit{ϵ}}}_{kk}={\left(-iv{k}_x-k^{2}D\right)}^{-1}\frac{{\sigma }_{ij}^{\ast }{k}_i{k}_j}{\mathrm{\Gamma }}{\displaystyle \sum _{n^x,n^y,n^z}{e}^{-i\mathrm{\Delta }x\left(k_x{n}^x+k_y{n}^y+k_z{n}^z\right)}}.$$ [S31]

To compute the tissue-scale limit, we coarse-grain the system and consider length scales $1/\left|k\right|\gg \mathrm{\Delta }x$. We can then express the sum over all activated sites as follows:

$${\displaystyle \sum _{n^x,n^y,n^z}{e}^{-i\mathrm{\Delta }x\left(k_x{n}^x+k_y{n}^y+k_z{n}^z\right)}}=\frac{1}{{\left(\mathrm{\Delta }x\right)}^3}\left({\displaystyle \sum _{n^x=0}^N\mathrm{\Delta }x{e}^{-i{n}^x{k}_x\mathrm{\Delta }x}}\right)\left({\displaystyle \sum _{n^y,n^z=-\infty }^{\infty }{\left(\mathrm{\Delta }x\right)}^2{e}^{-i\left(n^y{k}_y+n^z{k}_z\right)\mathrm{\Delta }x}}\right).$$ [S32]

We then replace the sums with integrals. Let us call $x\prime =n^x\mathrm{\Delta }x,y\prime =n^y\mathrm{\Delta }x,z\prime =n^z\mathrm{\Delta }x$, $\mathrm{\Delta }x$ the spacing between myocytes. In the continuum limit:

$$\frac{1}{{\left(\mathrm{\Delta }x\right)}^3}{\displaystyle {\int }_{-v\tau }^{0}dx\prime e^{-i{k}_{x}x\prime }}{\displaystyle {\int }_{-\infty }^{\infty }dy\prime dz\prime e^{-i\left(k_{y}y\prime +k_{z}z\prime \right)}}=\frac{{\left(2\pi \right)}^2}{i{k}_x{\left(\mathrm{\Delta }x\right)}^3}\left[1-e^{i{k}_{x}v\tau }\right]\delta \left(k_y\right)\delta \left(k_z\right).$$ [S33]

Substituting this into Eq. S31, we observe that the infinite number of excitations in y and z only contribute in the infinite wavelength limit $k_y,k_z\to 0$ and these components are trivially integrated out. The inverse transform in $k_x$ is a simple contour integral with poles no higher than second order. Computing this gives the tissue scale response in terms of the individual CM excitation strength:

$${\mathit{ϵ}}_{kk}=\frac{{\sigma }_{xx}^{\ast }}{D\mathrm{\Gamma }{\left(\mathrm{\Delta }x\right)}^3}\times \{\begin{array}{ll}\text{exp}\left(\frac{v}{D}\left(x-vt+v\tau \right)\right)\hfill & x<v\left(t-\tau \right)\hfill \\ 1\hfill & v\left(t-\tau \right)<x<vt\hfill \end{array},$$ [S34]

where ${\sigma }_{xx}^{\ast }/{\left(\mathrm{\Delta }x\right)}^3$ is associated with the microscopic stress exerted by each CM. The coefficient in Eq. S34 is the maximal tissue strain of the contracting wave front. We note that this solution fails for $x>vt$ because for those positions the tissue is not passive: CMs are primed for activation.

β-Glycyrrhetinic Acid Obstructs Intercellular Transport in Embryonic Cardiac Tissue

To verify that β-glycyrrhetinic acid (BGA) properly interferes with gap junctions in embryonic CMs, we performed fluorescence recovery after photobleaching (FRAP) experiments to verify reduced intercellular transport between myocytes. Through α-actinin staining, we first verified that the cells of interest exhibited characteristic striations found in myocytes and myocyte precursors (Fig. S4A). E4 chick hearts were loaded with calcein red-orange AM, a cell tracer. This compound is cleaved as it enters cells, rendering it membrane impermeable. Myocytes are selected within the tissue and bleached down to 20% of the initial intensity. Fluorescence recovery was recorded and analyzed via (software) and ImageJ (Movie S3). Quantitative FRAP results are shown in Fig. S4 B and C. BGA-treated hearts systematically exhibited CMs (n = 49) with significantly reduced fluorescence recovery in rate and intensity compared with control (n = 73), demonstrating that BGA does indeed interfere with gap junctions in E4 avian heart tissue. See SI Materials and Methods.

Small-Molecule Drugs Perfuse Embryonic Hearts

Treating embryonic hearts with blebbistatin, a drug that blocks myosin II activity, disrupts the heartbeat (Fig. S5); the heartbeat is then rescued by mecarbil, a cardiac-myosin force-enhancing drug (Fig. S6). This further indicates that many small-molecule drugs indeed perfuse the tissue given our experimental protocols and serves as a control for pharmacologically disrupted (and rescued) beating.

SI Materials and Methods

Cell-on-Gel Finite-Element Method Simulations.

Finite-element simulations were performed using the Structural Mechanics Module in COMSOL. An isolated hydrogel-cultured cell was modeled as a hemisphere resting with its flat side fully in contact with a substrate. The substrate was also modeled as a hemisphere with the cell placed in the center of its flat surface (Fig. S1). The substrate radius was $10\mathrm{\Delta }x$, large enough such that substrate boundary effects are negligible on cell strain. Both components were modeled as static linear elastic materials. Under cell contraction, the partial strain trace (${\mathit{ϵ}}_{2d}={\mathit{ϵ}}_{xx}+{\mathit{ϵ}}_{yy}$) in the plane of the substrate surface was calculated and averaged over the cell’s contact surface. This procedure was repeated for a range of values for the substrate Young’s modulus. Both the saturating and constant eigenstrain models were used for the contraction strength of the cell. The “fine” option was used for the element mesh size to ensure convergence. See Table S1 for a list of input parameters.

CMs-in-Matrix Finite-Element Method Simulations.

Finite-element simulations were performed using the Structural Mechanics Module in COMSOL. Thirty-six CMs were modeled as linear elastic spherical inclusions arranged in a cubic array and embedded within a surrounding elastic matrix of 30 × 30 × 40 μm³ (Fig. S7A), with all model parameters corresponding to Table S1, except that the CM radius is set to 4.6 μm < 5.0 μm to prevent issues with meshing in the simulation. We then excited one of the centrally located CMs by inducing a contractile eigenstrain and computed the volume-averaged maximal strain induced in the neighboring central CM as a function of effective tissue Young’s modulus. The effective modulus was determined by simulated uniaxial tensile testing on the composite system. The “fine” element mesh size was used to ensure convergence. Note the excellent quantitative agreement between our analytical calculation and the finite-element calculations for finite-sized inclusions; this agreement justifies our approximation of CMs as point-like elastic inclusions.

Myocardial Stiffness Measurements.

White Leghorn chicken eggs (Charles River Laboratories) were incubated at 37 °C until the desired developmental stage was reached and isolated as described in [10]. Embryos were extracted at room temperature (RT) and placed into a Petri dish. The thick albumin was removed using blunt forceps and KimWipes. The embryos were adhered to a Whatman #2 filter paper with an elliptical hole of ∼1 × 2 cm cut in it. The embryos were rinsed in PBS and placed ventral side up. Prewarmed chick heart media (α-MEM supplemented with 10% FBS and 1% penn-strep; Gibco; 12571-063) was added at this point.

The heart was extracted with fine forceps severing above the atrium and below the outflow tract and transferred into a six-well plate. Micropipettes were pulled from glass capillaries (World Precision Instruments) and broken to final inner diameters of 30–100 μm. Pipettes were filled with PBS and attached to water-filled reservoir. Aspiration was performed at RT in either PBS supplemented with 3% BSA or heart culture media. Before each experiment, pipette tips were placed in the solution for $\le$ 20 min to prevent sticking. During aspiration, several pressures were applied in the range of 0–0.8 kPa. Imaging was done using a Nikon TE300 microscope with a 20× air objective and recorded using a Cascade Photometric CCD camera. Image analysis was performed in ImageJ.

BGA FRAP.

Isolated E4 hearts were stained with 0.5 μM CellTrace Calcein Red-Orange, AM (ThermoFisher Scientific; C34851) and Hoechst 33342 in Hepes-buffered α-MEM culture media (Gibco; 12571-063; supplemented with 10% FBS and 1% penn-strep) for 15 min at RT with gentle rocking. Cytochalasin D (Cayman Chemical Company; 11330; 25 μM) was added to minimize contractions and drift during imaging. Calcein and Hoechst 33342 were then washed out three times with culture media supplemented with cytochalasin D. For BGA treatment, embryonic hearts preloaded with calcein were perfused in 100 μM 18-β-glycyrrhetinic acid (BGA) (Cayman Chemical; 11845) for 1 h at RT, with gentle rocking. BGA-treated and untreated control hearts were placed on 35-mm glass bottom dishes (MatTek; P35G-1.5-10-C) with media filling up the center well and capped with a coverslip for FRAP imaging.

Confocal time-lapse images were acquired using a Zeiss 880 laser-scanning confocal microscope equipped with a 40× oil, 1.4 N.A. objective. Zeiss ZEN Black software was configured to acquire images every 2 s for 6 min and photobleaching started after acquiring eight frames and stopped until the intensity dropped to 20% of the original. Average intensity in each bleached region and a nonbleached region were measured by using ImageJ (https://imagej.nih.gov/ij/download.html) with the time series analyzer plugin (https://imagej.nih.gov/ij/plugins/time-series.html). Intensity of the bleached region was normalized to that of the nonbleached region in the same time series to correct overall photobleaching during imaging. Data were analyzed with a custom C++ code, and graphs were plotted in GraphPad Prism version 6.0d (www.graphpad.com).

Immunostaining of Embryonic Hearts.

Isolated E4 hearts were fixed in 4% paraformaldehyde for 15 min at RT on a rocker. Fixed E4 hearts were then washed with PBS three times for 5 min each and permeabilized with 0.1% Triton X in PBS for 30 min. Blocking was performed in 5% BSA and 0.1% Triton X in PBS for 1.5 h at RT. Hearts were immunostained for α-actinin-2 (Abcam; EA-53 mouse monoclonal Ab; 1:200 dilution in blocking solution) and DNA (Hoechst; 33342; 1:1,000) for 3 h at RT with gentle shaking. Primary antibodies were washed out with PBS three times for 15 min each. Secondary antibody (goat anti-mouse IgG Atto565; Hypermol; 2107; 1:500) staining was performed for 1.5 h at RT and the hearts were washed with PBS three times before confocal imaging. Images were acquired using a Zeiss 880 Airyscan confocal with a 40× oil, 1.4 N.A. objective. Image analysis was performed using ZEN Black software for Airyscan processing.