Abstract
Novel techniques for high-throughput steady-state metabolomic profiling yield information about changes of nearly thousands of metabolites. Such metabolomic profiles, when analyzed together with transcriptional profiles, can reveal novel insights about underlying biological processes. While a number of conceptual approaches have been developed for data integration, easily accessible tools for integrated analysis of mammalian steady-state metabolomic and transcriptional data are lacking. Here we present GAM (‘genes and metabolites’): a web-service for integrated network analysis of transcriptional and steady-state metabolomic data focused on identification of the most changing metabolic subnetworks between two conditions of interest. In the web-service, we have pre-assembled metabolic networks for humans, mice, Arabidopsis and yeast and adapted exact solvers for an optimal subgraph search to work in the context of these metabolic networks. The output is the most regulated metabolic subnetwork of size controlled by false discovery rate parameters. The subnetworks are then visualized online and also can be downloaded in Cytoscape format for subsequent processing. The web-service is available at: https://artyomovlab.wustl.edu/shiny/gam/
INTRODUCTION
Integration of metabolomic and transcriptional data has been widely discussed in the context of flux optimization of bacterial production of various metabolites (1,2). Recent developments in high-throughput steady-state metabolomic profiling provide novel opportunities for studying details of metabolic rewiring in mammalian cells, especially in the context of cancer and immune cell metabolism (3,4). Current state-of-the-art methods allow measuring up to thousands of steady-state metabolic signals, yielding robust coverage of 200–400 metabolites. Thus, in a context of metabolic networks, these datasets contribute considerable amount of coverage (for comparison—typical connected component of the mammalian metabolic network contains about 1000–2000 enzymes). Overall, this warrants efficient and accessible tools for integration of steady-state metabolomics data with steady-state mRNA level measurements.
Three major approaches are typically used for metabolomic and transcriptional data integration: (i) flux balance analysis (FBA), (ii) pathway-enrichment and (iii) network analysis. While FBA-based methods have been used successfully in the context of metabolic flux (5), incorporating steady-state metabolomic data into such methods is not straightforward. Yizhak et al. have developed an Integrative Omics-Metabolic Analysis (IOMA) method for such integration, but it has been shown to work only for bacterial-size models (6). Widely used pathway enrichment methods, such as iPEAP and Metaboanalyst (7,8), are directly applicable for integrating steady-state metabolomic and transcriptional data. These methods, however, depend highly on the pre-defined pathways and, thus, lack the power to identify novel pathways and links between the existing pathways. In contrast, network-based methods have a potential advantage of an unbiased identification of novel pathways critical in the specific biological context, particularly when comparing different conditions or activation states (3,4).
Network-based methods were originally developed in the context of protein–protein interactions with the goal to identify regulatory modules of interacting genes based on differential expression (DE) data (9,10). By leveraging connections among the input signals of potentially different type such methods allow integration of different types of data. The connections could be both inferred, for example from the correlational structure of the data (11,12), or be inherent to the data types, such as metabolic networks for integrating transcriptional and metabolomic data. Recently, integration approaches that use of metabolic networks have proven to be powerful in identifying novel regulatory modules in yeast (13), micro-organisms (14) and simple plants (15). In the context of the mammalian systems, the network-based approaches are restricted to the analysis of nearest neighbor interactions, e.g. MetScape (16,17) and lack subnetwork analysis capabilities. In this work, we describe easily accessible tool for identification of the most regulated subnetworks based on DE analysis of steady-state metabolomic and transcriptional data. Such analysis allows to identify reactions and modules that are changing the most when comparing between two conditions, providing a valuable insight for further biological follow-up and hypothesis generation.
Two major aspects have to be addressed in creating such tool: the underlying network structure and the subnetwork search algorithm. In the case of metabolic networks, network structure reflects not only specific connectivity of the metabolites and reactions but also the way such connections are represented. For example, reactions can be represented (and scored) as network nodes reflecting underlying enzymes, or as edges connecting different metabolites. For each representation, different scoring schemes and corresponding formulations of subnetwork search algorithms have to be used. Accordingly, we have implemented a web-service providing three different subnetwork search algorithms. Two of the algorithms (18,19) were adapted from the protein–protein interaction network analysis, the third one was developed by our group. Specifically, in their work (18), Dittrich et al. used a subnetwork scoring scheme for protein–protein interaction networks that could be reduced to a maximum-weight connected subgraph (MWCS) problem. They also developed a practical exact solver and later showed that the approach of reducing to MWCS is robust to different types of noise (20). For a special case when reactions are scored and represented as edges in the network we have also developed an original exact solver for finding the most regulated subnetworks.
MATERIALS AND METHODS
Network analysis pipeline
Overall, GAM (‘genes and metabolites’) networks provided in the web interface are constructed based on KEGG REACTION database, using RPAIR database for the case when reactions/enzymes are represented as edges. The web-service has human, mouse, Arabidopsis and yeast networks configured and ready to use. However, networks for other organisms available in KEGG can be added on request.
The analysis takes as input DE tables for genes and/or metabolites between two conditions of interest containing all expressed genes (whether they are differentially expressed or not). Then the following procedures are carried out for the analysis (Figure 1):
The network is adjusted to contain only reactions with expressed enzymes.
The network is mapped to a simple graph in order to apply the subgraph search algorithm.
Nodes or nodes and edges are scored depending on the chosen network representation to yield a scored global network. Each reaction and metabolite is scored using a scheme adopted from Dittrich et al. (18) so that the reactions and metabolites with low P-value have positive scores and ones with high P-values have negative scores. The number of positive nodes and edges is controlled by false discovery rate parameter (FDR) thresholds.
The most regulated subnetwork is identified. For the scored graph, a problem of finding MWCS is solved using one of the supported solvers. For a node-scored network we support heinz (18) or heinz2 (19) solver. If the nodes-and-edges scoring is used, which might be considered more biologically meaningful, then we use heinz solver or the original solver called gmwcs (see ‘Solving MWCS’ section). This final step produces a module that contains a connected subnetwork of significantly regulated reactions and metabolites while minimizing the number of non-significantly regulated connections.
Post-processing operations are applied. To ease biological interpretation and visualization, we implemented a few of optional post-processing steps that enrich the module with additional nodes and edges such as nearest neighbor metabolites. Final networks are visualized in the web-service and can be downloaded in PDF, XLSX or Cytoscape formats.
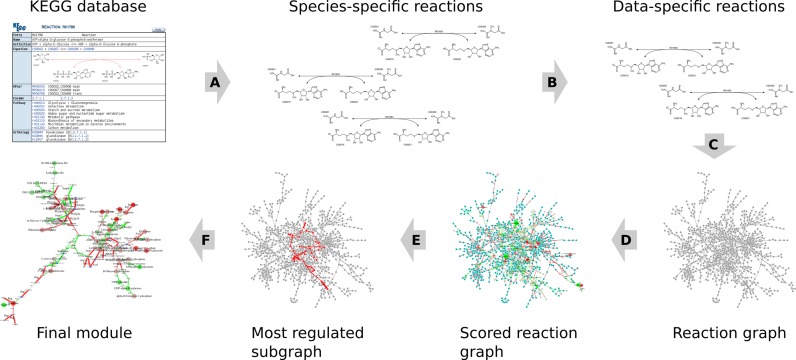
Figure 1.
The GAM workflow. (A) From the KEGG database reactions possible in the selected species are extracted. (B) If the gene DE data are available reactions without expressed enzymes (i.e. present in the input) are removed. (C) Reaction network is mapped to a simple graph. (D) Nodes and/or edges of the graph are scored based on the corresponding P-values and chosen FDR values. (E) The most regulated module is identified using maximum-weight connected subgraph solver. (F) The post-processing options are applied to get the final module.
Implementation details
Internally, GAM consists of three parts: (i) an R-package GAM with the method implementation, (ii) an R-package GAM.db with the required data from KEGG (21) and Metabocards (22) databases and (iii) a web-interface written using R Shiny framework. Additionally, GAM.networks package can be built that contains constructed networks for the supported organisms. We provide all the source codes, so that the analysis can be carried out programmatically, if the KEGG database and solvers are available. Source codes for GAM, GAM.db and GAM.networks packages are available at https://github.com/ctlab/GAM. The web-interface source code is available at https://github.com/ctlab/shinygam.
Constructing the global network
We implemented the following procedure for constructing the network. First, based on KEGG REACTION database, a global reaction-metabolite network is constructed. Next, for purposes of the network analysis, a number of ubiquitous metabolites have to be excluded to avoid biases due to their extreme connectivity (Supplementary Table S1). Furthermore, groups of anomeric metabolites are collapsed into one metabolite (Supplementary Table S2). Next, a reaction-enzyme mapping is extracted from KEGG REACTION database followed by an enzyme-gene-organism mapping from KEGG ENZYME. To avoid redundancy, reactions that are part of a multi-step reaction are excluded from the global network (Supplementary Table S3). By combining information about enzymes, reactions and genes, we construct a many-to-many mapping between reactions and genes encoding corresponding enzymes.
Input files
Before the analysis, files with DE data for genes and/or metabolites have to be uploaded into GAM. Each DE dataset must be in a separate text file (comma-, tab- and space- separated files are supported, archived files are supported too). The first line of each file must contain a header with column names. Files should contain the following columns:
‘ID’: RefSeq mRNA transcript ID, Entrez ID or symbol for genes and HMDB or KEGG ID for metbolites.
‘pval’: DE P-value (non-adjusted).
‘log2FC’: Base 2 logarithm of the fold-change.
The columns in the files can have somewhat different names, in which case GAM will try to guess which one to use by comparing with a set of alternative names for these columns. Raw outputs of limma (23) and DESeq2 (24) tools are supported.
The ‘log2FC’ column is optional, but we recommend providing it if possible. It informs about the directionality of changes, which is later used for assigning corresponding colors in the graph visualization. Any other columns will be copied to a network as node or edge attributes. Example DE data tables are available as Supplementary Tables S4 and 5 and are embedded into the web-service.
Adjusting the global network
For a particular analysis we consider a network only from the reactions with enzymes present in the input data. This allows user to control the ‘expressed universe’ of enzymes by removing reactions without expressed enzymes. We recommend the input data to include about 10 000–15 000 of the most expressed genes, which roughly corresponds to the number of well-expressed genes in an individual cell. If no transcriptional data are provided we consider the complete species-specific network that includes all enzymes for that species.
Mapping to a simple graph
In order to apply subnetwork search algorithms, the network of reactions has to be converted into a simple graph. In the case of metabolic networks, this procedure is non-trivial due to a presence of bimolecular reactions. We implemented two distinct ways for such mapping (Supplementary Figure S1). The first one represents the metabolic flow centric view: it maps metabolites to nodes and reactions to edges that represent interconversions between the metabolites (Supplementary Figure S1B). We also use information from KEGG RPAIR database, so that only substrate-product pairs that represent ‘main’ interconversions in the reaction are connected (Supplementary Figure S1C). The other way is gene-centric, this is preferred mode of analysis when one only has transcriptional data. Here, both metabolites and reactions are mapped to nodes that are connected if the metabolite is involved in the reaction (Supplementary Figure S1D). Connected reactions that share an enzyme are collapsed into one node associated with the corresponding enzyme (Supplementary Figure S1E and F). This reduces redundancy of the network and helps to avoid artificial biases toward differentially regulated enzymes catalyzing multiple topologically close reactions.
Overall, the flow-centric method with only ‘main’ RPAIRs proved to give better interpretable results if metabolomic data are available (see case studies for examples). For other cases use of gene-centric approach is recommended.
Scoring
The method of scoring reactions and metabolites is adopted from Dittrich et al. (18). First, DE P-values between two conditions in consideration are fitted into a β-uniform distribution, where B(a, 1) distribution corresponds to signal component and the uniform distribution corresponds to the noise (Supplementary Figure S2). Then score is calculated as a log-likelihood ratio of a P-value being in the signal component, normalized to an FDR threshold. The procedure is carried out separately for GAM. This results in metabolites and reactions with low p-value having positive scores and ones with high P-values having negative scores. The score for metabolites absent from the data is a free parameter, which by default is equal to the score for P-value of 1. Since sometimes multiple enzymes catalyze one reaction and are encoded by multiple genes, we attribute to the reaction the smallest p-value among the gene corresponding to the reaction. Biologically, this corresponds to anticipating change of the reaction flux even if only one of the enzymes changes significantly.
Selecting FDRs
The FDR values and the score for absent metabolites options control the size of the module. Generally, increasing the FDR value makes adding reactions or metabolites to a module easier and thus expands the size of produced subnetwork. Separate FDR thresholds for metabolites and enzymes allow to control the shift between metabolic or transcriptional signals. We recommend to start from the default-generated values which gives ∼150 positively-scored GAM, a reasonably-sized starting module (‘Autogenerate FDRs’ button). While these default values do not necessarily lead to the best results from the hypothesis generation point of view, they provide a good start for exploring the dataset. Depending on the results thresholds can be tweaked to be more stringent to restrict the module to more significant signals or to be more relaxed to get the broader view on the data.
Solving MWCS
The problem of finding MWCS can have slightly different formulations. There are three of them that we define and that are useful in the context of metabolic networks: simple, generalized and acyclic MWCS. The first, simple MWCS (SMWCS), requires to find a subgraph with the maximal weight for a graph with weighted nodes. This formulation was used by Dittrich et al. in their work (18). It can be shown that for such formulation the optimal solution can always be represented as a tree. In a more general formulation, that we call generalized MWCS (GMWCS), not only nodes, but also edges have weights. If edge weights are allowed to be positive, the optimal solution is not restricted to a tree, but also can be a graph with cycles. Trivial example is a graph with three positive nodes pairwise-connected with three positive edges. Finally, an acyclic MWCS (AMWCS) formulation can be defined where both nodes and edges are weighted but only acyclic subgraphs are considered.
In the web-service there are three MWCS solvers available: heinz, heinz 2 and gmwcs. Heinz is a solver first described in (18) for SMWCS and in (20) for AMWCS. It can be used to solve the edge-weighted problem, but only searches for acyclic solutions. The web-service uses version 1.68 (http://homepages.cwi.nl/∼klau/data/heinz_1.68.tgz). Heinz 2 is described by El-Kebir and Klau in (19). It solves the SMWCS problem where only nodes are scored. Thus, it cannot be used when reactions are mapped to edges and with DE for genes available. Gmwcs is a solver developed by our group for solving the GMWCS formulation, able to find maximum-weighted connected subgraph with weighted edges, not limited to acyclic solutions (in contrast to heinz). It is available at https://github.com/ctlab/gmwcs-solver. The solver uses a reduction of GMWCS instance into an integer linear programming (ILP) problem described in (25) and an heuristic to split instance into smaller problems (Supplementary Figure S3). IBM ILOG CPLEX is used as an ILP solver.
By default, heinz 2 and gmwcs solvers with a time limit of 30 s are used if edge weights are absent or present, respectively, as they show more robust performance of finding good suboptimal solution when the time is limited. Option to use heinz solver is available as the means to faster way to reach a provable optimality (time is limited to 4 min). We suggest using this option for the final version of analysis. Although heinz is limited in searching for acyclic solutions, the result is usually similar to gmwcs, because optimal solutions are almost acyclic (have just a few more edges than is required for connectivity) in practice.
Post-processing
For the ease of interpretation we provide post-processing options which allow to see interconnections that are not required for the connectivity but may be relevant for the interpretation. When reactions are represented as edges and RPAIRs are used, there is a post-processing option ‘Add trans-edges’. It adds edges between metabolites in the module that correspond to ‘trans’ RPAIR type (Supplementary Figure S4A and B). When reactions are represented as nodes there is a post-processing option ‘Add common metabolites’. It adds metabolites that are simultaneously taking part in at least two reactions in the module (Supplementary Figure S4C and D).
RESULTS
Web-service
From the user perspective the analysis implemented in GAM consists of two steps:
Step 1: creating a global network of metabolites and reactions specific to the provided expression data.
Step 2: finding a connected subnetwork (module) that contains the most significant changes.
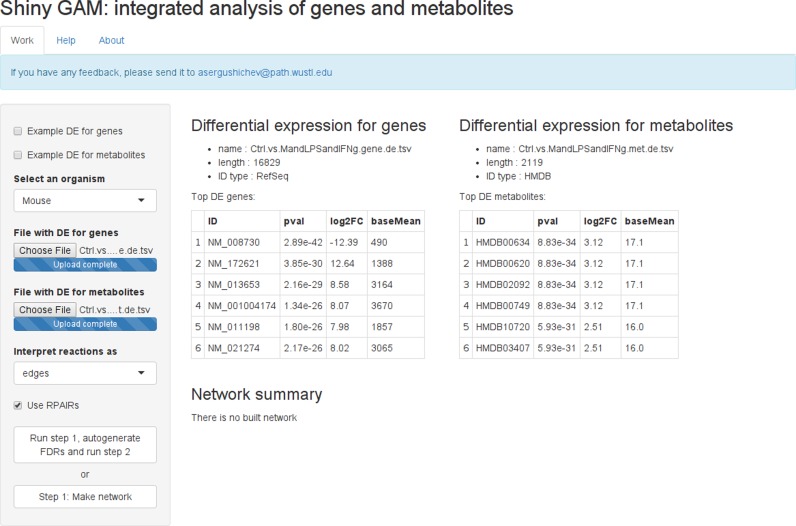
In the first step the user needs to select the organism to use, upload the DE data and select options of mapping network to a graph (see ‘Mapping to a simple graph’ section). Each DE dataset must be in a separate file (see ‘Input files’ section). After the files are uploaded, a file summary is displayed and recommended options for mapping to a graph are automatically selected (Figure 2). Clicking the ‘Step 1: make network’ button will create a data-specific global network suitable for the consecutive subnetwork search.
Figure 2.
Screenshot of the web-service after data uploading. Summary of input differential expression tables is displayed. Supplementary Tables S4 and 5 were used as the input data.
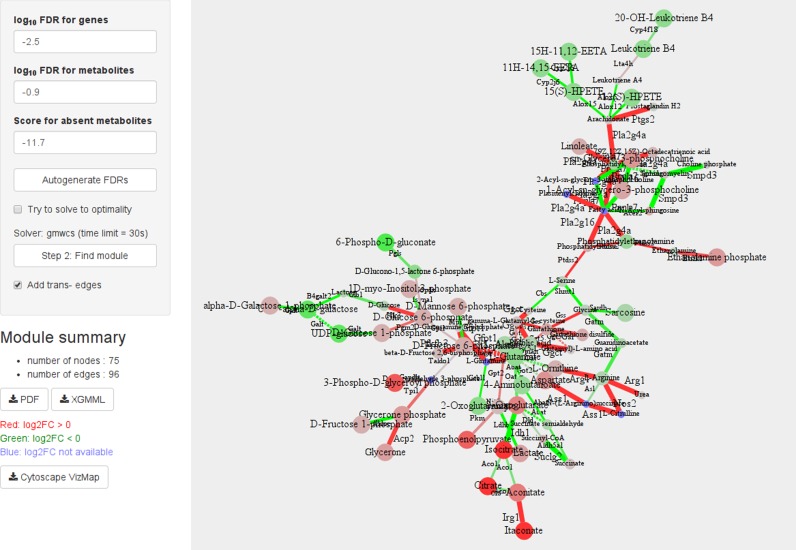
After the network is created, a module that contains the most significantly changed GAM can be found. This requires setting FDRs (see ‘Scoring’ and ‘Selecting FDRs’ sections) and selecting whether the module search should be done to provable optimality. The button ‘Autogenerate FDRs’ generates FDR values so that the resulting module will be about 100–150 reactions. By default, the module search is limited to 30 s so that the service is more interactive compared to optimal solving. The button ‘Find module’ runs an MWCS solving algorithm and displays the result (Figure 3). For convenience, reactions and metabolites in the displayed module have links to the corresponding KEGG entries.
Figure 3.
Screenshot of the web-service after module search. The most regulated module found for the example data for mouse macrophages M0 versus M1 comparison (Supplementary Tables S4 and 5) and default parameter values.
The button ‘Run step 1, autogenerate FDRs and run step 2’ allows a one-click analysis after the data are uploaded with autoselected options.
The module can be downloaded as a PDF, XLSX or XGMML file. The latter can be loaded in Cytoscape for additional processing. Corresponding visual style is available at https://artyomovlab.wustl.edu/publications/supp_materials/GAM/GAM_VizMap.xml.
Case study: mouse macrophage activation
We applied GAM to analyze differences between LPS + IFNg-stimulated (M1) and unstimulated (M0) mouse macrophages based on high-throughput metabolomic and transcriptional data (3) (input data are provided in Supplementary Tables S4 and 5 and as the example dataset in the web-service). We computed the most regulated module using metabolomic and transcriptional data together as well as separately (see Supplementary File S1). Notably, the differences in regulation of the tricarboxylic acid (TCA) cycle and glycolysis are highlighted at the metabolic level, while the differences in the urea cycle and fatty acid synthesis are best seen at the transcriptional level. Yet, it is the integration of the both data types that provides a complete picture of the overall changes in cellular metabolism.
Case study: glucose metabolism in mammary cell lines
We also applied GAM to analyze control versus 2-deoxy-glucose (2DG) treated mammary epithelial cells (MCF10A). The data were acquired from GEO Omnibus GSE59228 (26). The DE table is available in Supplementary Table S6.
2DG treatment blocks glycolysis and results in the same effects as glucose deprivation. The analysis highlighted two major upregulated features: (i) upregulation of glutathione redox control locus and (ii) usage of glutamine via glutaminolysis (Supplementary File S2). Notably, these features have been documented as characteristic for glucose starved cells (27,28). This application illustrates the power of metabolic network based analysis even when only transcriptional data are available.
CONCLUSIONS
GAM is a web-service that facilitates an analysis of the metabolomic and transcriptional profiling data in the context of cellular reaction network. GAM service provides a way for a quick interactive analysis of the data to identify the most regulated metabolic subnetworks. The service supports multiple input formats, including results from widely-used DESeq2 and limma pipelines, provides automatic selection of recommended parameter values and uses a range of MWCS solvers yielding good suboptimal solutions in a time frame of 30 s.
By comparing steady state metabolomics and transcriptional data between two conditions or cell states, GAM allows the identification of critical modules within a global metabolic network. Such regulated modules provide excellent candidates for further biological investigation as evidenced by application of GAM in the contexts of cancer and immune cells (3,4).
Supplementary Material
Acknowledgments
The authors thank Nicole Rockweiler for the useful comments.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Government of Russian Federation [074-U01 to A.A.S., A.A.L.]. Funding for open access charge: start-up fund at the Department of Pathology & Immunology of Washington University in St.Louis.
Conflict of interest statement. E.M.D. declares competing financial interest as a founder and shareholder of General Metabolics. A.K.J. was an employee of Agios Pharmaceuticals when this study was conducted.
REFERENCES
- 1.Lee S.Y., Lee D.-Y., Kim T.Y. Systems biotechnology for strain improvement. Trends Biotechnol. 2005;23:349–358. doi: 10.1016/j.tibtech.2005.05.003. [DOI] [PubMed] [Google Scholar]
- 2.Blazier A.S., Papin J.A. Integration of expression data in genome-scale metabolic network reconstructions. Front. Physiol. 2012;3:299. doi: 10.3389/fphys.2012.00299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jha A.K., Huang S.C.-C., Sergushichev A., Lampropoulou V., Ivanova Y., Loginicheva E., Chmielewski K., Stewart K.M., Ashall J., Everts B., et al. Network integration of parallel metabolic and transcriptional data reveals metabolic modules that regulate macrophage polarization. Immunity. 2015;42:419–430. doi: 10.1016/j.immuni.2015.02.005. [DOI] [PubMed] [Google Scholar]
- 4.Vincent E.E., Sergushichev A., Griss T., Gingras M., Samborska B., Ntimbane T., Coelho P.P., Blagih J., Raissi T.C., Choinière L., et al. Mitochondrial phosphoenolpyruvate carboxykinase regulates metabolic adaptation and enables glucose-independent tumor growth. Mol. Cell. 2015;60:195–207. doi: 10.1016/j.molcel.2015.08.013. [DOI] [PubMed] [Google Scholar]
- 5.Bordbar A., Mo M.L., Nakayasu E.S., Schrimpe-Rutledge A.C., Kim Y.-M., Metz T.O., Jones M.B., Frank B.C., Smith R.D., Peterson S.N., et al. Model-driven multi-omic data analysis elucidates metabolic immunomodulators of macrophage activation. Mol. Syst. Biol. 2012;8:558. doi: 10.1038/msb.2012.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yizhak K., Benyamini T., Liebermeister W., Ruppin E., Shlomi T. Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model. Bioinformatics. 2010;26:i255–i260. doi: 10.1093/bioinformatics/btq183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xia J., Mandal R., Sinelnikov I. V, Broadhurst D., Wishart D.S. MetaboAnalyst 2.0–a comprehensive server for metabolomic data analysis. Nucleic Acids Res. 2012;40:W127–W133. doi: 10.1093/nar/gks374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sun H., Wang H., Zhu R., Tang K., Gong Q., Cui J., Cao Z., Liu Q. iPEAP: integrating multiple omics and genetic data for pathway enrichment analysis. Bioinformatics. 2014;30:737–739. doi: 10.1093/bioinformatics/btt576. [DOI] [PubMed] [Google Scholar]
- 9.Ideker T., Ozier O., Schwikowski B., Siegel A.F. Discovering regulatory and signalling circuits in molecular interaction networks. Bioinformatics. 2002;18(Suppl. 1):S233–S240. doi: 10.1093/bioinformatics/18.suppl_1.s233. [DOI] [PubMed] [Google Scholar]
- 10.Alcaraz N., Pauling J., Batra R., Barbosa E., Junge A., Christensen A.G.L., Azevedo V., Ditzel H.J., Baumbach J. KeyPathwayMiner 4.0: condition-specific pathway analysis by combining multiple omics studies and networks with Cytoscape. BMC Syst. Biol. 2014;8:1–6. doi: 10.1186/s12918-014-0099-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hirai M.Y., Klein M., Fujikawa Y., Yano M., Goodenowe D.B., Yamazaki Y., Kanaya S., Nakamura Y., Kitayama M., Suzuki H., et al. Elucidation of gene-to-gene and metabolite-to-gene networks in arabidopsis by integration of metabolomics and transcriptomics. J. Biol. Chem. 2005;280:25590–25595. doi: 10.1074/jbc.M502332200. [DOI] [PubMed] [Google Scholar]
- 12.Kling T., Johansson P., Sanchez J., Marinescu V.D., Jörnsten R., Nelander S. Efficient exploration of pan-cancer networks by generalized covariance selection and interactive web content. Nucleic Acids Res. 2015;43:e98. doi: 10.1093/nar/gkv413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhu J., Sova P., Xu Q., Dombek K.M., Xu E.Y., Vu H., Tu Z., Brem R.B., Bumgarner R.E., Schadt E.E. Stitching together multiple data dimensions reveals interacting metabolomic and transcriptomic networks that modulate cell regulation. PLoS Biol. 2012;10:e1001301. doi: 10.1371/journal.pbio.1001301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beisser D., Grohme M.A., Kopka J., Frohme M., Schill R.O., Hengherr S., Dandekar T., Klau G.W., Dittrich M., Müller T. Integrated pathway modules using time-course metabolic profiles and EST data from Milnesium tardigradum. BMC Syst. Biol. 2012;6:1–13. doi: 10.1186/1752-0509-6-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Landesfeind M., Kaever A., Feussner K., Thurow C., Gatz C., Feussner I., Meinicke P. Integrative study of Arabidopsis thaliana metabolomic and transcriptomic data with the interactive MarVis-Graph software. PeerJ. 2014;2:e239. doi: 10.7717/peerj.239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Karnovsky A., Weymouth T., Hull T., Tarcea V.G., Scardoni G., Laudanna C., Sartor M.A., Stringer K.A., Jagadish H.V., Burant C., et al. Metscape 2 bioinformatics tool for the analysis and visualization of metabolomics and gene expression data. Bioinformatics. 2012;28:373–380. doi: 10.1093/bioinformatics/btr661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Evans C.R., Karnovsky A., Kovach M.A., Standiford T.J., Burant C.F., Stringer K.A. Untargeted LC-MS metabolomics of bronchoalveolar lavage fluid differentiates acute respiratory distress syndrome from health. J. Proteome Res. 2014;13:640–649. doi: 10.1021/pr4007624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dittrich M.T., Klau G.W., Rosenwald A., Dandekar T., Müller T. Identifying functional modules in protein-protein interaction networks: an integrated exact approach. Bioinformatics. 2008;24:i223–i231. doi: 10.1093/bioinformatics/btn161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.El-Kebir M., Klau G.W. Solving the maximum-weight connected subgraph problem to optimality. 2014. http://arxiv.org/abs/1409.5308 [Google Scholar]
- 20.Beisser D., Brunkhorst S., Dandekar T., Klau G.W., Dittrich M.T., Müller T. Robustness and accuracy of functional modules in integrated network analysis. Bioinformatics. 2012;28:1887–1894. doi: 10.1093/bioinformatics/bts265. [DOI] [PubMed] [Google Scholar]
- 21.Kanehisa M. KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wishart D.S., Tzur D., Knox C., Eisner R., Guo A.C., Young N., Cheng D., Jewell K., Arndt D., Sawhney S., et al. HMDB: the human metabolome database. Nucleic Acids Res. 2007;35:D521–D526. doi: 10.1093/nar/gkl923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ritchie M.E., Phipson B., Wu D., Hu Y., Law C.W., Shi W., Smyth G.K. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015;43:e47. doi: 10.1093/nar/gkv007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Love M.I., Huber W., Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15:1–21. doi: 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Haouari M., Maculan N., Mrad M. Enhanced compact models for the connected subgraph problem and for the shortest path problem in digraphs with negative cycles. Comput. Oper. Res. 2013;40:2485–2492. [Google Scholar]
- 26.Enzo E., Santinon G., Pocaterra A., Aragona M., Bresolin S., Forcato M., Grifoni D., Pession A., Zanconato F., Guzzo G., et al. Aerobic glycolysis tunes YAP/TAZ transcriptional activity. EMBO J. 2015;34:1349–1370. doi: 10.15252/embj.201490379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu Y., Song X.-D., Liu W., Zhang T.-Y., Zuo J. Glucose deprivation induces mitochondrial dysfunction and oxidative stress in PC12 cell line. J. Cell. Mol. Med. 2003;7:49–56. doi: 10.1111/j.1582-4934.2003.tb00202.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Le A., Lane A.N., Hamaker M., Bose S., Gouw A., Barbi J., Tsukamoto T., Rojas C.J., Slusher B.S., Zhang H., et al. Glucose-independent glutamine metabolism via TCA cycling for proliferation and survival in B cells. Cell Metab. 2012;15:110–121. doi: 10.1016/j.cmet.2011.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.