Validation and Comparison of Seven Mortality Prediction Models for Hospitalized Patients With Acute Decompensated Heart Failure

Abstract

Background

Heart failure (HF) inpatient mortality prediction models can help clinicians make treatment decisions and researchers conduct observational studies. Published models have not been validated in external populations, however.

Methods and Results

We compared the performance of seven models that predict inpatient mortality in patients hospitalized with acute decompensated heart failure (ADHF): Four HF-specific mortality prediction models developed from three clinical databases (Acute Decompensated HF National Registry [ADHERE], Enhanced Feedback for Effective Cardiac Treatment [EFFECT] Study, Get with the Guidelines-HF [GWTG-HF] Registry); two administrative HF mortality prediction models (Premier, Premier+); and a model that uses clinical data but is not specific for HF (Laboratory-Based Acute Physiology Score [LAPS2]). Using a multi-hospital electronic health record-derived (EHR) dataset (HealthFacts [Cerner Corp], 2010–2012), we identified patients ≥18 years admitted with HF. Of 13,163 eligible patients, median age was 74 years; half were women; and 27% were black. In-hospital mortality was 4.3%. Model predicted mortality ranges varied: Premier+ (0.8–23.1%), LAPS2 (0.7–19.0%), ADHERE (1.2–17.4%), EFFECT (1.0–12.8%), GWTC-Eapen (1.2–13.8%), and GWTG-Peterson (1.1–12.8%). The LAPS2 and Premier models outperformed the clinical models (c-statistics: LAPS2 0.80 [95% CI: 0.78–0.82], Premier models 0.81 [95% CI: 0.79–0.83]) and 0.76 [95% CI: 0.74–0.78]; clinical models 0.68–0.70).

Conclusions

Four clinically-derived inpatient HF mortality models exhibited similar performance, with c-statistics near 0.70. Three other models, one developed in EHR data and two developed in administrative data, also were predictive, with c-statistics from 0.76–0.80. Because every model performed acceptably, the decision to use a given model should depend on practical concerns and intended use.

Heart failure (HF) is a leading cause of hospital admissions in patients aged 65 years and older.^1,2 Patients hospitalized with acute decompensated heart failure (ADHF) have a high risk of mortality, with 30-day mortality rates approaching 10%.^3,4 Because risk of mortality varies across patient populations, a mortality prediction model that estimates an individual patient’s risk can be a useful aid for making clinical decisions at the bedside. Additionally, researchers performing comparative effectiveness studies of treatments for ADHF need a validated method of risk adjustment to ensure that differences in outcomes are not simply the result of differences in patient case-mix.

Several published mortality prediction models and scoring systems have been developed using clinical data collected for research purposes (e.g., from registries or randomized trials). Each of these was designed with the goal of helping clinicians risk-stratify hospitalized patients with ADHF at the bedside.^5–9 However, none of the models were validated in external populations, some are now more than a decade old, and none have been widely adopted in routine clinical settings. It is also not clear how the models perform relative to each other or relative to other risk adjustment methods. We therefore examined the performance of four published clinical HF inpatient mortality prediction models in a dataset derived from the comprehensive electronic health records (EHRs) of more than 50 U.S. hospitals. We compared clinical model performance to three other models used for risk adjustment, one that uses EHR data and two that use administrative data. Since the administrative and EHR models included many more variables, we hypothesized that they would outperform the clinical models. However, we also hypothesized that we would identify that one or more of the clinical models could be useful for risk stratification at the bedside.

Methods

Data Source and Patient Population

We used HealthFacts (Cerner Corporation), a database that is derived from the EHRs of more than 50 geographically and structurally diverse hospitals throughout the U.S. HealthFacts contains time-stamped pharmacy, laboratory, vital sign (physiologic), and billing information for more than 84 million acute admissions and emergency and ambulatory patient visits.^10–13 We first limited the dataset to hospitals that contributed laboratory and vital signs to the database. We then identified a cohort of patients who were 18 years or older, admitted to an included hospital between 1/1/2010 and 12/31/2012, and had a principal International Classification of Diseases, Ninth Revision (ICD-9-CM) diagnosis of HF or a principal diagnosis of respiratory failure with a secondary diagnosis of HF (ICD-9-CM codes for HF: 402.01, 402.11, 402.91, 404.01, 404.03, 404.11, 404.13, 404.91, 404.93, 428.xx; for respiratory failure: 518.81, 518.82, 518.84). To ensure that patients were treated for ADHF during the hospitalization, we restricted the cohort to patients in whom at least one HF therapy (including loop diuretics, metolazone, inotropes, vasodilators, or intra-aortic balloon pump) was initiated within the first two days of hospitalization. We excluded patients who had a length of stay less than 24 hours, lacked vital signs or laboratory data, and patients that were transferred to or from another acute care facility (because we could not accurately determine the onset or subsequent course of their illness). Healthfacts includes demographics (patient age, gender, marital status, insurance status, and race/ethnicity), and we used these variables for some of the models. For models that included comorbid conditions, we used software provided by the Healthcare Costs and Utilization Project of the Agency for Healthcare Research and Quality to identify comorbidities included in the Elixhauser index.^14,15 Additionally, for the administrative (Premier) models, we used ICD-9-CM codes to identify other acute conditions that are of concern in the setting of heart failure, including atrial fibrillation (427.3), acute myocardial infarction (410.x1, 410.x2), pneumonia (480–487), malnutrition (263, V77.2), and acute kidney injury (580.4, 580.0, 580.81, 580.89, 580.9,584.5, 584.6, 584.7,584.8, 584.9). The Institutional Review Board at Baystate Medical Center granted permission to conduct the study.

Validation Methods by Mortality Prediction Method

For each mortality prediction model, we replicated the methods used by the original authors to calculate the predicted mortality for HF patients in the Healthfacts database. In some cases, due to lack of availability of variables or missing data, we had to slightly modify the original methods. These are described in detail in the sections below (see also the Appendix).

Premier Models (Administrative Models)

Using administrative billing data, we previously developed a model^16,17 that is similar to the heart failure model developed by Krumholz et al. for the Centers for Medicare and Medicaid Services (CMS).¹⁸ We developed this model using data from the cost-accounting systems of 433 hospitals that participated in the Premier, Inc. Data Warehouse (PDW, a voluntary, fee-supported database) between January 1, 2009, and June 30, 2011. PDW contains all elements found in hospital claims derived from the uniform billing 04 form (UB-04). In addition, PDW contains an itemized, date-stamped log of all items and services charged to the patient or insurer, including medications, diagnostic and therapeutic services, and laboratory tests. PDW has been used extensively for research purposes.^19,20 We used a generalized estimating equation logistic regression model (GEE), clustering on hospital, to predict each patient’s in-hospital mortality. We initially included all clinically relevant variables in the model: variables with a well-established association with mortality (such as age), all conditions listed in the Elixhauser comorbidity index,¹⁴ and selected comorbid acute illnesses (described above). Using backward selection, we retained variables in the final model (“The Premier Model”) with p<0.05.

We then developed a second administrative model that includes the variables above plus critical care therapies instituted within the first two hospital days (Tables 1 and 2) as markers of presenting severity (this model is called Premier plus treatments, or Premier+). We added these early treatments (mechanical ventilation, vasopressors, inotropes, pulmonary artery catheters, arterial lines, and/or an intra-aortic balloon pump) as markers of severity of illness at hospital admission. We based our selection of these treatments in the critical care literature, which includes several models (e.g., the Mortality Prediction Model (MPM) and the Sequential Organ Failure Assessment (SOFA) Score)^21,22 that use critical care therapies during the first two hospital days as proxies for presenting severity. We used billing codes to identify medications and ICD-9-CM procedure codes to identify other initial therapies. After demonstrating that both the Premier and the Premier+ models performed well in the PDW dataset in both derivation and internal validation cohorts, we applied the coefficients from the derivation cohort to HealthFacts data.

Table 1.

Variables for Heart Failure Mortality Models

	MORTALITY PREDICTION MODELS
	LAPS223	ADHERE5	EFFECT6	GWTG-HF Peterson8	GWTG- HF Eapen7	Premier16 With Treatment*	Premier16 Without Treatment*
C-statistic	0.80	0.68	0.70	0.69	0.70	0.81	0.76
Demographics
Age (year)	✓	✓	✓	✓	✓	✓	✓
Sex	✓					✓	✓
Race (% Black)				✓	✓	✓	✓
Insurance						✓	✓
Admitted to Emergency Department	✓
Clinical Characteristics
Laboratory Tests
Sodium (mEq/L)	✓		✓	✓	✓
Blood urea nitrogen (BUN) (mg/dL)	✓	✓	✓	✓	✓
Creatinine (mg/dL)	✓				✓
BUN/Creatinine	✓
Albumin (g/dL)	✓
Hematocrit (%)	✓
White blood cell count (WBC) (1000s/mm3)	✓
Arterial pH	✓
Lactate (mM/L)	✓
Arterial PaCO2 (mm Hg)	✓
Arterial PaO2 (mm Hg)	✓
Glucose (mg/dL)	✓
Bilirubin (mg/dL)	✓
Troponin (ng/mL)	✓				✓
Estimated Lactate†	✓
B-type Natriuretic Peptide (BNP) (pg/mL)					✓
Hemoglobin (g/dL)			✓		✓
Vital Signs and Neurologic Score
Temperature (°F)	✓
Heart Rate (beats/min)	✓	✓		✓	✓
Respiratory Rate (breaths/min)	✓		✓		✓
Systolic Blood Pressure (SBP) (mm Hg)	✓	✓	✓	✓	✓
Shock Index	✓
Oxygen Saturation (SpO2) (%)	✓
Glasgow Coma Score	✓
Weight (kg)					✓
Comorbid Conditions
Cerebrovascular Disease (%)			✓			✓	✓
Dementia (%)			✓			✓	✓
Chronic Obstructive Pulmonary Disease (%)			✓	✓		✓	✓
Liver Disease (%)			✓			✓	✓
Cancer (%)			✓	✓		✓	✓

✓ Used in the model for ADHERE, EFFECT, GWTG, LAPS2, or Premier

^*Contains all Elixhauser comorbidities and other acute conditions not listed here; treatment model includes early critical care treatments (e.g. mechanical ventilation, inotropes), see Table 2

^†Formula for Estimated Lactate: (Anion Gap/Bicarbonate) ×100

Table 2.

Characteristics of Patients with Heart Failure in the HealthFacts Dataset

	HealthFacts data N (%)
TOTAL	13,163 (100%)
Demographics
Age, Mean (Median, Q1– Q3)*	71.8 (74, 62–84)
Female*	6,775 (51.5)
Race/Ethnicity*
White	8,605 (65.4)
Black	3,551 (27.0)
Hispanic	339 (2.6)
Other	668 (5.1)
Insurance Payer*
Medicare	7,925 (60.2)
Medicaid	1,044 (7.9)
Private	1,257 (9.6)
Uninsured	495 (3.8)
Other/Unknown	2,442 (18.6)
Clinical Characteristics
Elixhauser Comorbidities*
Valvular Disease	539 (4.1)
Pulmonary Circulation Disease	494 (3.8)
Peripheral Vascular Disease	1,376 (10.5)
Hypertension	8,257 (62.7)
Paralysis	233 (1.8)
Other Neurological Disorders	884 (6.7)
Chronic Pulmonary Disease	4,967 (37.7)
Diabetes	5,567 (42.3)
Renal Failure	5,203 (39.5)
Liver Disease	348 (2.6)
Peptic Ulcer Disease with Bleeding	3 (0.0)
Acquired Immunodeficiency Syndrome (AIDS)	17 (0.1)
Lymphoma	115 (0.9)
Metastatic Cancer	120 (0.9)
Solid Tumor without Metastasis	244 (1.9)
Rheumatoid Arthritis	359 (2.7)
Coagulopathy	784 (6.0)
Obesity	2,495 (19.0)
Weight Loss	538 (4.1)
Fluid and Electrolyte Disorders	3,934 (29.9)
Chronic Blood Loss Anemia	107 (0.8)
Deficiency Anemias	3,804 (28.9)
Alcohol Abuse	335 (2.6)
Drug Abuse	334 (2.5)
Psychoses	306 (2.3)
Depression	1,142 (8.7)
Comorbidity Score	4.6 (4, 3–6)
≤ 2	2,927 (22.2)
3–4	3,722 (28.3)
5–6	3,834 (29.1)
≥ 7	2,680 (20.4)
Additional Acute Comorbidities*
Acute Myocardial Infarction	588 (4.5)
Acute Kidney Injury	2,922 (22.2)
Atrial Fibrillation	4,786 (36.4)
Coronary Artery Disease	6,536 (49.7)
Pneumonia	1,806 (13.7)
Treatment During First 48 Hours†
Non-invasive Ventilation	1,220 (9.3)
Invasive Mechanical Ventilation	865 (6.6)
Vasopressors	386 (2.9)
Inotropes	836 (6.4)
Vasodilators	1,039 (7.9)
Prior Admission
None	9,525 (72.4)
1	2,246 (17.1)
≥ 2	1,392 (10.6)
Outcomes
Mortality	560 (4.3)
Hospital Characteristics
Urban (vs. Rural)	13,136 (99.8)
Teaching	10,414 (79.1)
Geographical Location
Midwest	2,318 (17.6)
North	4,893 (37.2)
South	4,492 (34.1)
West	1,460 (11.1)
Number of Beds
≤199	1,358 (10.3)
200 – 499	8,295 (63.0)
≥ 500	3,510 (26.7)

^*Included in both Premier models

^†Included in the Premier treatment model

Laboratory-Based Acute Physiology Score Model (LAPS2) (EHR model)

The Laboratory Acute Physiology Score (LAPS2) is a validated score that uses physiologic, laboratory, and vital signs data derived from an EHR to predict mortality across conditions common to hospitalized patients, including HF. It uses a 2-stage algorithm that first includes selected variables (age, sex, blood urea nitrogen [BUN], serum creatinine, and serum sodium) to stratify patients into low and high mortality risk groups. Then, in a second stage, vital signs and laboratory values are added to the algorithm (Table 1).^23,24 The LAPS2 algorithm has a validated protocol for selection of the most deranged laboratory value during a timeframe and assigns points based on level of derangement and risk stratum. When lab values are not present within the interval, the algorithm assigns the missing value using points based upon mortality risk group (rather than using imputation).^23,24 Because LAPS2 includes neurologic status checks but HealthFacts does not include these checks, we used the Glasgow Coma Score (GCS) as our marker of neurologic status. Of note, LAPS2 is a score that assesses presenting severity. Thus, it is designed to be used as a variable in a model that includes other patients’ characteristics, such as demographics and comoribidities. We therefore created a mortality prediction model using the LAPS2 score along with age, sex, race, and comorbidities.^23,24 Although we call this model “LAPS2,” we are referring not just to the LAPS2 score but to the entire model that includes the score plus these other variables.

Clinical Models

We next replicated the methods for all included clinical models. Of note, we applied the LAPS2 method for missing data (by assigning points based upon mortality risk group) in all of the clinical models described below.

Acute Decompensated Heart Failure National Registry Model (ADHERE)

The Acute Decompensated Heart Failure National Registry (ADHERE) contains data on patients with ADHF (initially identified using discharge diagnosis) who were admitted to one of 263 centers across the United States from 10/2001 to 2/2003. In 2005, the ADHERE study group created a multivariable model that identified BUN, systolic blood pressure, heart rate, and age as mortality predictors (Table 1).⁵ They validated their model within a subset of the starting cohort but not in an external population. We used the coefficients from their multivariable model to calculate the log odds of mortality in the HealthFacts data, which we then converted into probability of mortality.

Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Model

The Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study included patients hospitalized in 14 hospitals in Ontario, Canada who had a principal discharge diagnosis of heart failure from 4/1999 to 3/2001. In 2003, study authors described a model that predicted mortality at 30 days and one year. This model included age, respiratory rate, systolic blood pressure, BUN, serum sodium, and history of selected comorbid conditions (Table 1).⁶ They validated the model within a subset of the starting cohort. We converted the mortality score for 30-day mortality into a predicted probability of in-hospital mortality.

Get with the Guidelines-Heart Failure (GWTG-HF) Peterson Model

The Get with the Guidelines-Heart Failure (GWTG-HF) Registry is a voluntary quality improvement initiative that collects clinical data on patients admitted to participating hospitals with ADHF (identified by treating clinician’s diagnosis). Peterson et al. identified seven variables for inclusion in the final model: age, race, systolic blood pressure, pulse rate, serum sodium, BUN, and diagnosis of chronic obstructive pulmonary disease (Table 1). They validated the model within a subset of the starting cohort. Because the final published version was a risk score, we used the score in a logistic regression model to predict mortality.

Get With the Guidelines-Heart Failure (GWTG-HF) Eapen Model

Using GWTG-HF data from 2005 to 2009 linked to Medicare claims data, the authors constructed a GEE logistic model to predict 30-day mortality. Covariates included age, race, weight, admission vital signs, and selected admission laboratory values (Table 1). The authors validated the model in a 30% subsample of the original cohort. Following the method recommended in Eapen’s original manuscript,⁷ we used the mean of patients’ age and gender group to impute missing weights. Because model coefficients were not available, we refit the variables used in the final model to HealthFacts data.

Analysis

After defining predicted mortality for each model, we examined discrimination and calibration for each model. We examined calibration by plotting calibration across deciles of predicted mortality and then visually examining and comparing the calibration curves. We examined discrimination using the area under the Receiver Operating Curve (ROC). To compare inpatient mortality prediction across pairs of models, we constructed Bland-Altman plots (a graphical method to plot the difference in paired values versus their average).

Finally, for each included model, we calculated specificity at a set sensitivity of 0.75 (at which we would correctly identify 75% of those who die as predicted to die). We then computed the specificity (the proportion correctly predicted to survive) at this sensitivity.

Results

Population

We included 13,163 eligible patients from 62 hospitals that contributed both vital sign and laboratory data to the HealthFacts database. Median (IQR) age was 74 (62–84) (Table 2). Principal diagnosis was HF in 89% of patients and respiratory failure in 11% of patients. A majority of subjects were women (51%) and white (65%). About one-third of subjects were African American (27%). Most patients were insured under Medicare (60%). Comorbidities were common, including chronic obstructive pulmonary disease (38%) and chronic renal insufficiency (40%), and a substantial proportion of patients had coexisting acute conditions, such as atrial fibrillation (36%), pneumonia (14%), and acute kidney injury (22%). In-hospital mortality was 4.3%.

Discrimination

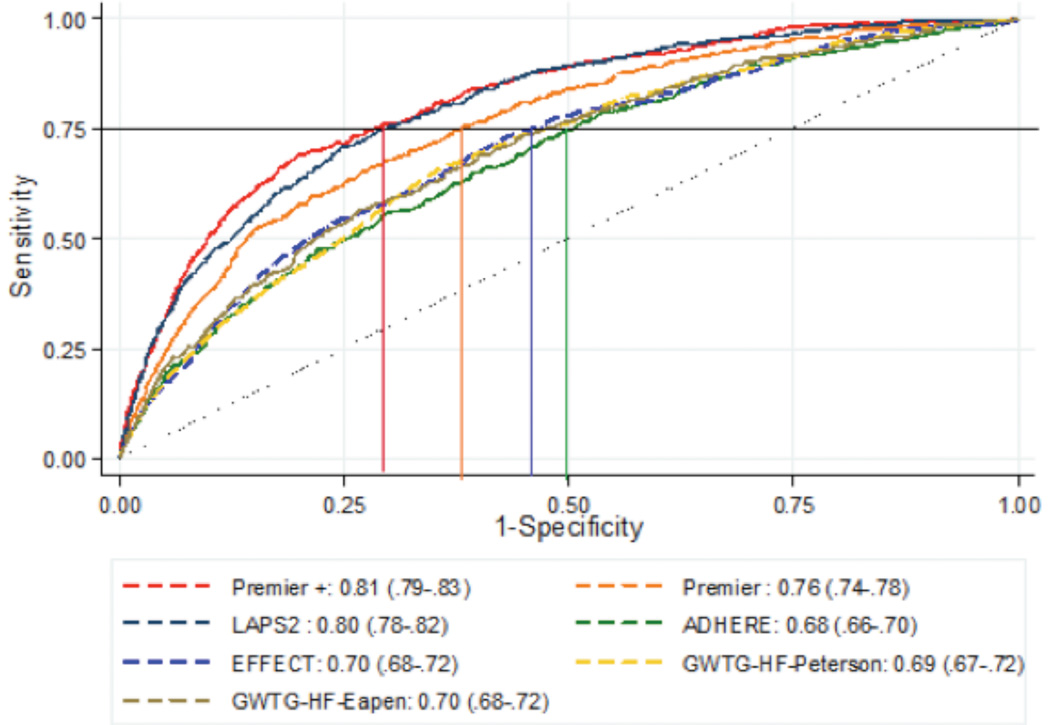
The LAPS2 and the Premier+ models demonstrated the highest discrimination (Figure 1). For each of these two models, c-statistics were predictive (LAPS2 (0.80 [95% CI: 0.78–0.82] and Premier+ 0.81 [95% CI: 0.79–0.83]), demonstrating significantly better discrimination compared to the other models (P<0.001 for both). The clinical models (ADHERE, EFFECT, and the two GWTG models) demonstrated similar discrimination, with c-statistics around 0.70 and with no significant differences among the four models. The Premier model (without treatments) ranked in between with a c-statistic of 0.76 (95% CI: 0.74–0.78), being both statistically better than clinical models and inferior to both the LAPS2 and Premier+.

Figure 1.

Area Under the Receiver Operating Curves for Seven Mortality Prediction Models with Lines Indicating Specificity at Sensitivity of 0.75

Range of Predicted Mortalities

The Premier+ and the LAPS2 models had the broadest range of patient-level predicted mortalities: Premier+ ranged from 0.8 to 23.1% with a mean of 5.1%, and the LAPS2 demonstrated a predicted mortality ranging from 0.7 to 19.0% with a mean of 4.8% (Figure 2). The next broadest range of predicted mortality was the Premier model excluding treatments, with a predicted mortality ranging from 1.0 to 18.2%. The clinical models all had a narrower range of predicted mortalities (ADHERE: 1.2 to 17.4%; EFFECT: 1.0 to 12.8%; GWTC-Eapen: 1.2 to 13.8%; GWTG-Petersen: 1.1 to 12.8%).

Figure 2.

Calibration Curves for Seven Mortality Prediction Models

Calibration

Calibration appeared best for the LAPS2 model, showing close adherence to the line of equality even at high levels of predicted mortality (Figure 2). The Premier+ model appeared to slightly over-predict death at the highest levels of mortality when compared to the LAPS2. The four clinical models performed similarly to the LAPS2 and the Premier models at lower predicted mortalities, but lacked the range to predict mortality among the sickest patients and tended to over-predict mortality among patients at a higher risk for death.

Bland-Altman Plots

Bland-Altman plots are a graphical method to plot the difference of two measurements²⁵ ([y-axis] against predicted mortality from 0 to 100% [x-axis]) (Figure 3). A lack of a discernable trend (i.e., a “cloud” of data within the upper and lower limits) indicates that the two predictive models are in agreement across predicted mortalities. The GWTG models and the EFFECT model were the most similar across the range of predicted values. However, agreement does not necessarily indicate good fit: calibration plots showed that the GWTG and EFFECT models all had a narrow range of predicted mortality and tended to over-predict mortality at the high end. All of the models were similar to each other when the predicted probability of mortality was low (as indicated by symmetry at the far left of each of the boxes). The Premier models and LAPS2 models diverged the most from the clinical models at the higher predicted probabilities of mortality (note asymmetry at the right of the plots). Finally, although discrimination and calibration were similar for all the clinical models, the asymmetry in the Bland-Altman plots suggest that ADHERE outperformed EFFECT and the two GWTGs models at higher predicted mortality.

Figure 3.

Bland-Altman Plots for Seven Mortality Prediction Models

Specificity at a Fixed Sensitivity

Finally, we examined comparative specificity of the models when sensitivity was fixed at 0.75 (Table 3). We found that the Premier+ and LAPS2 models have specificities of about 0.71, meaning about 71% of those predicted to survive using this cutoff did survive, while for the ADHERE model only about 50% of those predicted to survive at this cutoff value actually survived. We also examined this cut-off in relation to the ROC curves (Figure 1) by drawing a line across from the axis depicting sensitivity at 0.75 and then dropping a line to the axis depicting 1-specificity. We found that there were slight differences in model rankings when using this method (vs. examining the c-statistics alone) because some of the curves crossed. However, none of the models that were re-ranked with this method had c-statistics that were significantly different from each other.

Table 3.

Specificity at a Fixed Sensitivity

	ROC area	Specificity when Sensitivity=0.75
Premier +16	0.81	0.72
LAPS223	0.80	0.71
Premier16	0.76	0.63
EFFECT6	0.70	0.55
GWTG-HF-Eapen7	0.70	0.52
GWTG-HF-Peterson8	0.69	0.55
ADHERE5	0.68	0.50

Discussion

Using data derived from more than 60 hospital-based EHRs, we externally validated and compared seven previously published mortality prediction models for hospitalized patients with ADHF. Overall, we demonstrated that each of the models performed relatively well. Discrimination was best for two models, the Premier+ and the LAPS2. The four clinically-based, HF-specific models (ADHERE, EFFECT, and two GWTG models) demonstrated modest to good discrimination, despite the fact that they had many fewer variables than the Premier models or the LAPS2. However, their ranges of predicted mortality were narrower and calibration was not as good as the better performing models, especially among patients at the highest risk for in-hospital death. The Premier model without treatments fell in between the highest performing models and the clinical models in terms of both discrimination and calibration.

These findings must be taken in the context of the original intentions of each model’s designers. As their authors state in their original published manuscripts, EFFECT, ADHERE, and the two GWTG models were designed to stratify patient risk at the bedside.^5–9 Despite the fact that some of these models are now more than a decade old, none have been widely adopted by clinicians. We hypothesize that there are several reasons for this. First, none have previously been validated in an external population. Second, clinicians may make decisions based on whether a patient is “crashing” or on longer term prognosis (e.g., the Seattle Heart Failure Model²⁶). Although these are potential barriers to adoption, other disease processes (e.g., pneumonia) have demonstrated the usefulness of bedside calculators for hospitalized patients (e.g., CURB 65).²⁷ As suggested by Aujesky and Fine, the rationale behind these methods is that prognostication allows physicians to inform patients about the expected outcomes of an acute illness, helps physicians and patients to know the probability of serious adverse events (i.e., severe medical complications or death), and “assists physicians in their initial management decisions, such as determining the most appropriate site of treatment (home vs. hospital), the intensity of hospital management (medical floor vs. intensive care unit), and the intensity of diagnostic testing and/or therapy.”²⁸ If there were a validated, clinical scoring system for ADHF that were easy to use and widely available, it seems logical that patients with ADHF and the physicians treating them might reap these same benefits. This is especially important for patients with ADHF who are cared for by non-cardiologists, who may lack the clinical expertise to identify a patient with ADHF who is at high risk. Consider, for example, a hospitalist or emergency physician at a small rural hospital who is trying to determine whether to admit a patient with ADHF or to transfer that patient to a tertiary facility with a cardiac intensive care unit.

If any of the clinical models are to be widely adopted for real-time clinical use, however, an online calculator (or mobile application) is needed because each of the models contains five to ten variables. To date, however, only the EFFECT score has an online risk calculator.²⁹ Because ADHERE performed best in terms of range of predicted mortality and prediction among sicker patients, an online calculator or mobile application using the ADHERE multivariable model would offer an important contribution to the clinician’s toolkit.

The other three models (LAPS2 and the two Premier models) use complicated statistical methods and therefore present additional obstacles for bedside use. Because the Premier models use diagnosis codes, which are assigned at discharge, they cannot be used to calculate individual patient risk at the time of admission. In contrast, an automated version of the LAPS2 score was built into one health system’s EHR, allowing real-time use.³⁰ If other systems choose to make the same investment, the LAPS2 score could be an important alternative to online risk calculators for clinical models.

Given the observed discrimination of the two Premier and the LAPS2 models and their improved ability to predict mortality in high-risk HF patients, any of these three models could be used to conduct retrospective observational studies that compare treatment outcomes across large patient populations. While it may initially seem surprising that two models derived from hospital billing data outperformed clinical models, the difference is explained by the fact that the Premier and LAPS2 models include many more variables and were developed recently. Improvements in care tend to lead to decreased mortality rates over time,³¹ leading to over-prediction of mortality by older models.³² This may explain why all of the models, with the exception of LAPS2, tended to over-predict mortality.

When clinical data (but not administrative claims) are available for observational studies of ADHF, LAPS2 is the best option, but it includes neurologic data that may not be routinely available. In this case, any of the clinical models could be used. To address the lack of range of predicted mortalities for these models, researchers could create a multivariable model that includes the models’ physiologic and laboratory variables, but also adds demographics and comorbidities.

This study also has some limitations. First, we identified HF patients using a combination of ICD-9-CM codes and initial treatments rather than using clinical criteria. While we believe that, for the most part, the identified cohort was admitted and being treated for ADHF, we could have missed some patients who did not receive HF therapies in the first two days or did not receive an ICD-9-CM diagnosis code indicating that they had HF. Additionally, we used same cohort identification method that we used for the developed of the Premier models. In contrast, the other methods used other cohort identification techniques (LAPS2 was developed in all hospitalized patients; other models used discharge diagnosis codes or a clinician’s working diagnosis). This difference might have advantaged the Premier models. Second, we did not include patients who received a left ventricular assist device (but no other HF treatment) in the first two days of hospitalization. However, we believe that the number of patients in this group is very small and does not represent the majority of patients hospitalized with ADHF. Third, two of the included models (i.e., EFFECT and GTWG-Eapen) were developed for 30-day mortality, but we validated them for inpatient mortality. This could have disadvantaged these models in terms of comparative performance. Fourth, because model coefficients were not always available, we refit some of the models (e.g., GWTG-Eapen) and, for others, merely applied the coefficients (e.g., Premier, ADHERE). This creates a bias towards models that are refit (LAPS2 and Eapen). However, ADHERE was not refit and actually performed best of the clinical models. Fifth, we modified some components of the included models so that we could use them with the HealthFacts database. For example, we used GCS in lieu of “neurologic checks” in computing LAPS2. This decision was based on a recently published validation that reported that GCS performed similarly to other methods of assessing altered mental status.³³ Also, when data were missing, we imputed weight (for the GWTG-Eapen model) as recommended by the original author (Eapen).⁷ When other data were missing, we used a validated algorithm designed by the creators of the LAPS2 score that estimated the missing value based on the patient’s mortality risk.^23,24 Finally, because the dataset was deidentified, we may have, in rare cases, included the same patient on more than one hospitalization.

In conclusion, we have demonstrated that four clinically derived inpatient HF mortality models exhibited similar performance, with c-statistics hovering around 0.70. Two other models, one developed in EHR data and another developed in administrative data, were also predictive of mortality, with c-statistics around 0.80. Because all included models performed well, the decision to use any given model should depend on the model characteristics (e.g., number of variables), practical concerns (e.g., availability of an online calculator or EHR-imbedded calculator), and intended use (observational research vs. bedside risk stratification).

Clinical Perspective.

Heart failure (HF) inpatient mortality prediction models can help physicians to inform patients about the expected outcomes of an acute illness, know the probability of serious adverse events during hospitalization, and make initial management decisions. They are also useful for researchers conducting observational studies. Over the last decade, several mortality prediction models designed to stratify HF patients’ risk during a hospitalization were published, but none has been widely adopted. We compared the performance of seven models that predict inpatient mortality in patients hospitalized with acute decompensated heart failure (ADHF): four models developed from three clinical databases (Acute Decompensated HF National Registry [ADHERE], Enhanced Feedback for Effective Cardiac Treatment [EFFECT] Study, Get with the Guidelines-HF [GWTG-HF] Registry), two administrative HF mortality prediction models (Premier, Premier+), and a model that uses clinical data but is not specific for HF (Laboratory-Based Acute Physiology Score [LAPS2]). We found that all models were predictive, with c-statistics ranging from 0.70–0.80. The decision to use a given model should therefore depend on intended use. To use any model in real-time, an online calculator is helpful so that clinicians can more easily incorporate the numerous variables. Of the clinical models, only EFFECT currently has an online calculator. An automated version of the LAPS2 was built into one health system’s EHR, allowing real-time use. Because the Premier models use discharge diagnosis codes, they cannot be used to calculate risk at the time of admission, but, like any of the models, could be used to conduct retrospective observational studies that compare treatment outcomes.