Genetic parameters for body weight in meat quail

Abstract

The aim of this study was to estimate genetic parameters for BW in meat quail at different ages. A total of 24,382 weight records from 3,652 quail, born between 2009 and 2011, were evaluated. Weekly BW was measured from hatch until 42 d of age. The genetic parameters were estimated by the restricted maximum likelihood method using a multivariate animal model. Heritability of BW ranged from 0.03 to 0.23. Genetic correlations were mainly high and positive. Selection for BW at 28 d of age yielded good indirect genetic progress in BW at 42 d of age.

INTRODUCTION

The production of meat quail has been growing in recent years due mainly to a search for new animal sources of quality. According to the Brazilian Institute of Geography and Statistics (IBGE, 2011), quail production in Brazil has increased by 19.8% since 2010.

With the goal of forming national lineages specific for meat production, it has become necessary to optimize the potential of quail with the goal of improving quality at a low production cost. The assessment of population structure available through genetic parameters is essential to defining selection strategies in breeding programs.

Generally in breeding programs for meat production, growth traits are of great importance, and the relative ease and low cost of measuring them make them the first ones to be worked on. Anthony et al. (1991) reported on the effect of selection for BW prior to sexual maturity on growth curves for three lines of quail. Aggrey and Cheng (1994) estimated heritabilities and genetic correlations for BW at hatch as well as at 7, 14, 21, and 28 d of age and for BW gain (BWG) between 0 and 7, 8 and 14, 15 and 21, and 22 and 28 d of age. Nestor et al. (1996) studied correlated responses in growth and reproduction traits after 30 generations of selection of different lines of quail. Anthony et al. (1996) discussed results from short-term selection for 4 wk BW experiments in quail. However, only a few estimates of heritabilities and genetic correlations for Brazilian quail populations are available (Dionello et al., 2008; Bonafé et al., 2011; Gonçalves et al., 2011) because the breeding programs are still in the initial stages. Therefore, the objective of this work was to estimate genetic parameters for growth traits of a population of meat quail to help develop strategies and decision making for breeding programs.

MATERIALS AND METHODS

Data were obtained from 3,652 female quail from a line (LF1) hatched between 2009 and 2011 that belonged to the Breeding Program at the Quail Department of Animal Science, Federal University of Jequitinhonha and Mucuri Valleys in Diamantina, Minas Gerais, Brazil.

After hatching, the quail were banded with numbered plastic rings, weighed (BW at day zero), sex-determined, and transferred to the boxes. Weighing was performed weekly on a precision balance; BW was obtained at 7, 14, 21, 28, 35, and 42 d of age.

Analyses of data consistency and environmental effects for each trait were performed using the program R (R Development Core Team, 2012). Contemporary groups were formed for all traits based on generation, hatching, and sex and were included as fixed effects in the mixed model used to estimate genetic parameters. The model for BW at day zero included the direct and maternal genetic effects in addition to the common environment provided by the dam. For others traits, the genetic maternal effect was not considered.

The models can be written as:

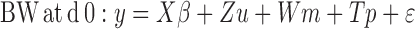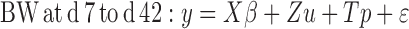Where:

• y = Vector of body weight observations

• X = Incidence matrix relating fixed effects to y

• β = Vector of fixed effects (contemporary groups)

• Z = Incidence matrix of random additive direct effects to y

• u = Vector of random additive direct effects

• W = Incidence matrix relating maternal genetic effects to y

• m = Vector of genetic maternal effects

• T = Incidence matrix relating maternal common environment effects to y

• p = Vector of maternal common environment effects and ε the vector random errors

Estimates of genetic parameters for the traits were obtained by the restricted maximum likelihood method (REML) using multivariate analysis employing the animal model and the software Wombat (Meyer, 2007).

RESULTS AND DISCUSSION

The description of the data after consistency analyses are in Table 1.

Table 1.

Number of observations (N), Mean (M), minimum (Min), maximum (Max), Standard Deviation (SD), Coefficient of Variation (CV), direct heritability (h²_d), maternal heritability (h²_m) and common maternal environment variance ratio (c²) obtained for BW at 0, 7, 14, 21, 28, 35, and 42 d of age.

Traits	N	M (g)	Min (g)	Max (g)	SD	CV	h2d (SE)	h2m (SE)	c2 (SE)
d 0	3255	8.95	6.50	12.70	0.90	10.05	0.03 (0.06)	0.18 (0.06)	0.38 (0.06)
d 7	3205	26.47	10.60	48.90	5.72	21.60	0.17 (0.04)	–	0.11 (0.02)
d 14	3143	61.96	24.80	110.30	13.72	22.14	0.16 (0.04)	–	0.09 (0.02)
d 21	3174	108.92	40.90	182.50	23.23	21.32	0.17 (0.04)	–	0.09 (0.02)
d 28	3141	163.22	56.10	261.40	31.26	19.15	0.20 (0.04)	–	0.06 (0.02)
d 35	3218	211.31	94.50	306.40	32.02	15.15	0.23 (0.04)	–	0.04 (0.02)
d 42	2708	245.50	119.20	367.60	31.96	13.01	0.22 (0.04)	–	0.03 (0.02)

Heritabilities (h²) were moderate for all traits (except for BW at day zero). Heritabilities were lower for BW at 0 to 21 d compared to BW at 28 to 42 d. The heritability for BW at day zero was low (0.03) because most of the influence over this trait is due to common maternal environment (0.38), which is considerably less important for the others traits, thus lowering its value in older ages (Table 1).

The moderate heritability estimates for weights at advanced ages indicate that selection performed on predicted breeding values should yield genetic progress in these traits. The heritabilities estimated for this population tended to increase during the measurement period.

In the present study, the genetic correlations were positive and high, ranging from 0.34 to 0.96 (Table 2). The highest correlations were observed between traits measured at an interval of 7 d, such as between BW at 28 and 35 d and between BW at 35 and 42 d. Weight recordings could therefore be obtained at intervals of 15 d, reducing costs, time, and labor and still allowing good monitoring of animal growth.

Table 2.

Estimates of heritability (diagonal), genetic correlation (above the diagonal), and phenotypic correlation (below the diagonal) obtained for the traits by multivariate analysis.

BW	d 0	d 7	d 14	d 21	d 28	d 35	d 42
d 0	–	0.34 (0.44)	0.52 (0.51)	0.62 (0.55)	0.73 (0.62)	0.77 (0.63)	0.76 (0.64)
d 7	0.29 (0.02)	–	0.93 (0.04)	0.77 (0.08)	0.57 (0.11)	0.38 (0.13)	0.20 (0.15)
d 14	0.22 (0.02)	0.75 (0.01)	–	0.95 (0.03)	0.82 (0.06)	0.66 (0.09)	0.48 (0.13)
d 21	0.21 (0.02)	0.64 (0.01)	0.84 (0.01)	–	0.95 (0.02)	0.83 (0.06)	0.66 (0.10)
d 28	0.18 (0.02)	0.55 (0.01)	0.73 (0.01)	0.88 (0.01)	–	0.96 (0.02)	0.86 (0.05)
d 35	0.19 (0.02)	0.44 (0.02)	0.60 (0.01)	0.75 (0.01)	0.87 (0.01)	–	0.96 (0.03)
d 42	0.17 (0.02)	0.35 (0.02)	0.44 (0.02)	0.55 (0.01)	0.67 (0.01)	0.75 (0.01)	–

*Values in parentheses are the SE of the estimates.

The only relatively low genetic correlation between two adjacent traits was observed between BW at 0 and 7 d (0.34). However, all the genetic correlation involving BW at day zero are associated with high SE, and any conclusions about it would be too risky. In any case, the correlations between BW at day zero and the other measurements were expected to decrease in older ages, as showed in Aggrey and Cheng (1994); Dionello et al. (2008); Bonafé et al. (2011). The results presented here were unexpected because the model used to determine BW at day zero was considerably parameterized, and the data were not abundant, yielding large SE and inconsistent estimates of genetic correlations.

The genetic correlations with BW at 42 d increased with increasing age: 0.20, 0.48, 0.66, 0.86, and 0.96 for BW at 7, 14, 21, 28, and 35 d, respectively. The same trend was reported by Dionello et al. (2008). Selection for BW at 42 d (which is of greater interest) cannot be done adequately using BW at 21 d because the genetic correlation is not sufficiently high (0.66), i.e., selection for this trait may increase the frequency of alleles that are not important for the determination of BW at 42 d. On the other hand, accurate selection for BW at 42 d can be achieved based on BW at 28 d because the 2 traits show a genetic correlation of 0.86, indicating a high degree of pleiotropy. Within this context, genetically favorable individuals for BW at 28 d should also be the most desirable for BW at 42 d.