Significance
Glial cells in the brain actively communicate with neurons through release of transmitter molecules that result in neuronal voltage deflections, thereby playing vital roles in neuronal information processing. Although a significant proportion of information processing in neurons is performed in their dendritic arborization, the impact of gliotransmission on neuronal dendrites has not been mapped. Here, we show that gliotransmission, acting through differentially localized slow receptors, results in strikingly large voltage deflections in neuronal dendrites, with the strength and spread of these deflections critically regulated by dendritic ion channels. Our results add a significantly complex dimension to neuron–glia interactions by demonstrating that neuronal dendrites and their voltage-gated channels play active roles in regulating the impact of such interactions.
Keywords: neuron–astrocyte interaction, NMDA receptors, HCN channels, transient potassium channels, plateau potentials
Abstract
An important consequence of gliotransmission, a signaling mechanism that involves glial release of active transmitter molecules, is its manifestation as N-methyl-d-aspartate receptor (NMDAR)-dependent slow inward currents in neurons. However, the intraneuronal spatial dynamics of these events or the role of active dendrites in regulating their amplitude and spatial spread have remained unexplored. Here, we used somatic and/or dendritic recordings from rat hippocampal pyramidal neurons and demonstrate that a majority of NMDAR-dependent spontaneous slow excitatory potentials (SEP) originate at dendritic locations and are significantly attenuated through their propagation across the neuronal arbor. We substantiated the astrocytic origin of SEPs through paired neuron–astrocyte recordings, where we found that specific infusion of inositol trisphosphate (InsP3) into either distal or proximal astrocytes enhanced the amplitude and frequency of neuronal SEPs. Importantly, SEPs recorded after InsP3 infusion into distal astrocytes exhibited significantly slower kinetics compared with those recorded after proximal infusion. Furthermore, using neuron-specific infusion of pharmacological agents and morphologically realistic conductance-based computational models, we demonstrate that dendritically expressed hyperpolarization-activated cyclic-nucleotide–gated (HCN) and transient potassium channels play critical roles in regulating the strength, kinetics, and compartmentalization of neuronal SEPs. Finally, through the application of subtype-specific receptor blockers during paired neuron–astrocyte recordings, we provide evidence that GluN2B- and GluN2D-containing NMDARs predominantly mediate perisomatic and dendritic SEPs, respectively. Our results unveil an important role for active dendrites in regulating the impact of gliotransmission on neurons and suggest astrocytes as a source of dendritic plateau potentials that have been implicated in localized plasticity and place cell formation.
Gliotransmission, a signaling mechanism that involves glial release of active transmitter molecules, has been implicated in the regulation of several neurophysiological processes that include synaptogenesis, synaptic transmission and plasticity, neuronal excitability, and synchrony (1–3). An important consequence of gliotransmission is its manifestation as slow inward currents (SIC), events that are mediated by neuronal extrasynaptic N-methyl-d-aspartate receptors (NMDAR) and are concomitant to astrocytic calcium elevations (3–8). Although these well-studied events have provided us with important insights into tripartite neuron–astrocyte interactions (1–9), recordings of such SICs have focused predominantly on the soma despite the dendritic localization of a majority of synapses (10). Research over the past two decades has clearly established that dendritic processing critically contributes to neuronal physiology and is best assessed by direct dendritic recordings given the localized nature of such processing (11–15). Importantly, the expression and plasticity of numerous dendritic voltage-gated ion channels (VGIC) and their nontrivial contribution to signal integration have emphasized the need to map neuronal physiology across the somatodendritic arbor (12–18). Juxtaposed against this extensive literature on dendritic physiology, it is surprising that the impact of gliotransmission on neuronal dendrites and the role of dendritic VGICs in regulating this impact have remained unexplored.
Although the role of active dendrites in regulating the impact of synaptic neurotransmission is well established (11–20), direct extrapolation of these results to gliotransmission is impeded by differences between synaptic neurotransmission and extrasynaptic gliotransmission. Specifically, the kinetics of postsynaptic responses to synaptic neurotransmission are much faster compared with the kinetics of such responses to extrasynaptic gliotransmission. As the frequency dependence of passive (14, 21, 22) and active (12, 14, 15, 23, 24) dendritic processing is well established, this difference in kinetics implies that the role of dendrites and their ion channels in altering the impact of gliotransmission could be different from how they alter the impact of neurotransmission. For instance, the spatial spread of the slower gliotransmission could be larger than that of faster neurotransmission as the cable length constant drops significantly with increase in the frequency of the input signal (22), implying a much wider reach of glial-origin signals compared with neurotransmission. Additionally, the density, voltage dependence, and activation/inactivation kinetics of channels in the dendrites confer frequency-dependent processing capabilities, thereby allowing differential processing of slow vs. fast signals (12, 14, 15, 23–26). As several passive and active components and significant interactions among them contribute to such frequency-dependent properties, it is essential to directly assess the role of neuronal dendrites and their ion channels in the strength and spread of the impact of gliotransmission. Finally, as a critical extrasynaptic afferent input that regulates several aspects of neuronal physiology (1–4, 7–9), the extent of the spread of gliotransmitter impact is an important parameter that regulates how these inputs interact and alter synaptic afferents and other ion channels. Specifically, whereas a spatially widespread impact of gliotransmission would imply a lack of distinction between different synaptic afferents and their plasticity, a constriction of the impact of gliotransmission would mean localized computation that involves only adjacent locations within the dendritic structure. Together, despite established differences between the kinetics of neurotransmission and gliotransmission, and despite key differences in the specific physiological roles of gliotransmission that the spatial extent of its impact would imply, a direct and systematic mapping of the impact of gliotransmission on neuronal dendrites is essential but lacking.
To fill these lacunae, we systematically mapped somatodendritic response profiles of slow excitatory potentials (SEP, the voltage counterpart of SIC) mediated by gliotransmitters, using current clamp recordings along the apical dendritic axis and paired neuron–astrocyte recordings in the rat hippocampus. Apart from mapping the spatial dynamics of SEPs, this experimental design allowed us to assess the physiological roles of dendritically expressed channels and receptors in regulating the impact of gliotransmission on neurons. Our results show that dendritic ion channels actively compartmentalize the impact of gliotransmission on neurons to generate localized dendritic plateau potentials and provide evidence for a differential involvement of GluN2B- and GluN2D-containing NMDARs in predominantly regulating perisomatic and distal SEPs, respectively.
Results
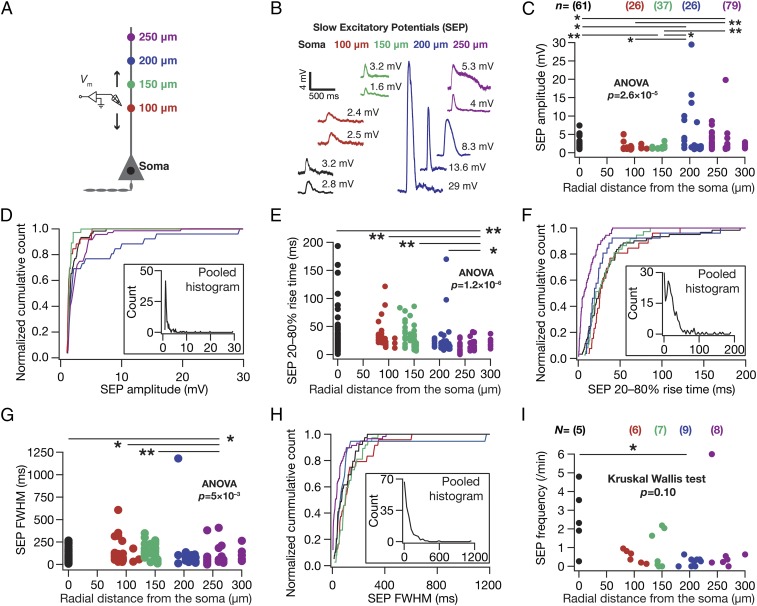
As a first step in assessing the spatial dynamics of astrocyte–neuron interactions at the single-neuron scale, we recorded spontaneous SEPs (sSEP) across the somatoapical trunk (up to ∼300 µm away from the soma) of hippocampal pyramidal neurons (in brain slices from 5- to 11-wk-old rats, under physiological temperatures) with synaptic transmission blocked with tetrodotoxin (TTX) and fast AMPA/kainate receptors blocked with 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) in a magnesium-free extracellular solution. Such systematic mapping would directly address the question of spatial compartmentalization of gliotransmitter impact. Specifically, a spatially compartmentalized spread of sSEPs would reflect as significantly large events around locations of origin with a significant reduction in voltages recorded at other locations. On the other hand, spatially widespread impact of gliotransmission would result in almost equal amplitude signals across the somatodendritic structure. Using direct somatodendritic recordings, we found that dendritic sSEPs were significantly larger in amplitude, with a fourfold increase in the peak amplitudes of sSEPs recorded at distal dendritic locations compared with their perisomatic counterparts (Fig. 1 A–D and Fig. S1E; perisomatic, 7.4 mV; distal dendrites, 29.5 mV). This increase in sSEP amplitude in distal dendritic locations was accompanied by significant reductions in their rise times and widths (Figs. 1 E–H and Fig. S1 F–G), together providing evidence for spatially compartmentalized spread of dendritically originating sSEPs. The frequency of these events was comparable with frequency of SICs reported in the literature (7, 27) and did not vary significantly across the somatodendritic axis (Fig. 1I and Fig. S1H).
Fig. 1.
Spontaneous SEPs recorded at distal dendritic locations were larger in amplitude with faster kinetics than their perisomatic counterparts. (A) Schematic of experimental design used to record sSEPs at various locations along the somato-apical trunk, also providing color codes for B–I. All data presented in Figs. 1–7 were recorded at physiological temperatures, with synaptic transmission and AMPARs blocked with 1 µM TTX and 10 µM CNQX, respectively. For all figures, N represents number of neurons, and n depicts number of SEPs. (B) Representative traces of sSEPs recorded at different locations along the somato-apical trunk. (C) sSEP amplitude as a function of corresponding somato-apical recording location. (D) Normalized cumulative histograms of sSEP amplitudes for different locations (data in C). D, Inset depicts a histogram of pooled sSEP amplitudes across all locations. (E and F) Same as C and D, for 20–80% rise time of sSEPs. (G and H) Same as C and D, for full width at half maximum (FWHM) of sSEPs. (I) sSEP frequency for each neuron plotted as a function of recording location. *P < 0.05, Mann–Whitney test. For C, E, and G, *P < 0.05, **P < 0.005, Student’s t test (Figs. S1–S4).
Fig. S1.
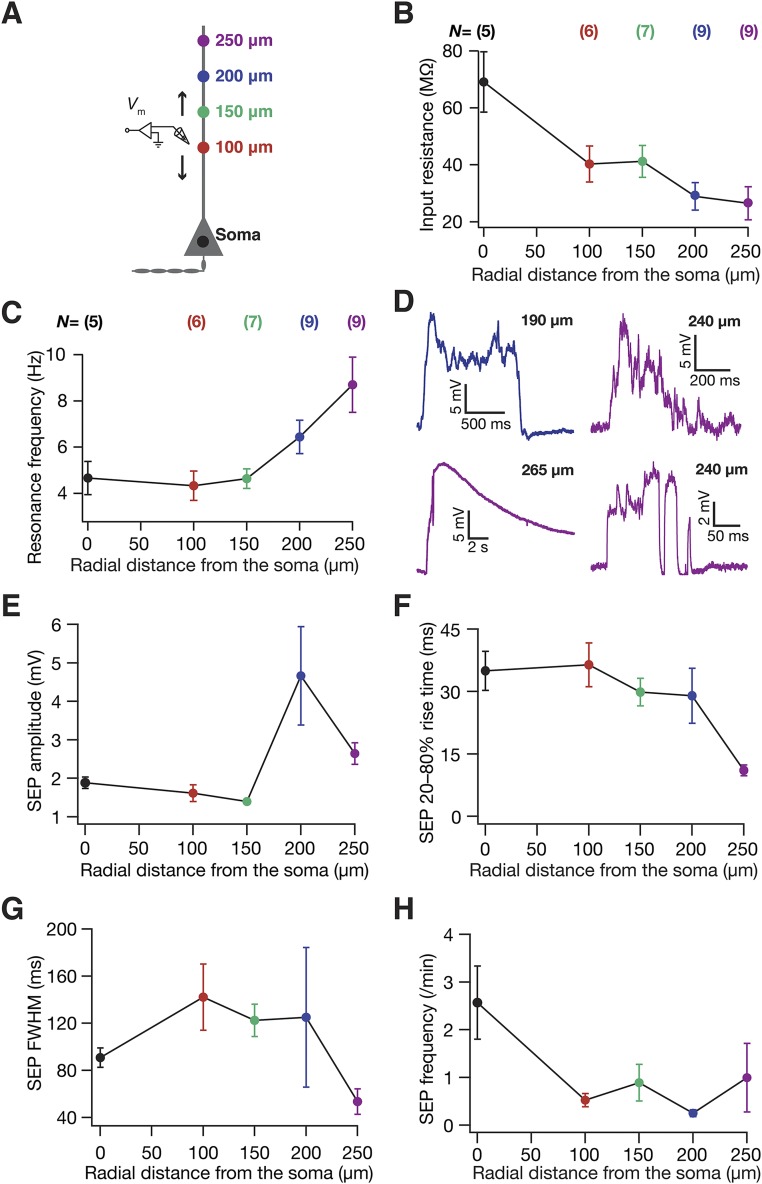
sSEPs and neuronal intrinsic properties exhibited location dependence along the somato-apical trunk. (A) Schematic of experimental setup with color codes representing locations. (B and C) Input resistance (B) and resonance frequency (C) recorded at different locations along the somato-apical trunk in CA1 pyramidal neurons, consistent with previous reports of these measurements (15, 35). (D) Example traces of clustered sSEPs recorded at distal dendritic locations. The incomplete Bottom Left trace with a rise time of 540 ms and a width of ∼9.5 s was not included in the analyses. (E–H) sSEP amplitude (E), 20–80% rise time (F), FWHM (G), and frequency (H), all represented as mean ± SEM, plotted as functions of radial distance from the soma. These plots correspond to data presented in Fig. 1 C, E, G, and I, respectively. N = number of neurons recorded; n = number of SEPs recorded.
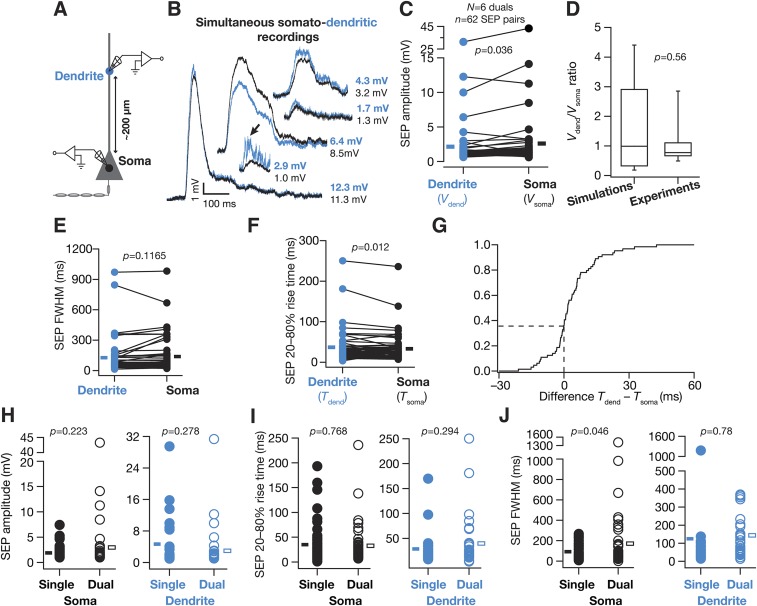
Although these results provide functional evidence that a majority of sSEPs originate at dendritic locations, the somatic and dendritic recordings were not from the same neuron. To alleviate this, we performed dual somato-dendritic recordings from the same neuron with identical recording solutions to those above and recorded sSEPs at both a somatic and a dendritic location on the apical trunk (Fig. S2; ∼200 µm away from the soma). Consistent with our previous conclusion on spatial compartmentalization, the amplitudes of sSEPs simultaneously recorded at somatic and dendritic locations were not equal, but exhibited significant variability in how their amplitudes (Fig. S2 C and D) and kinetics (Fig. S2 E–G) were related. We reasoned that such variability should be expected because of the random point of origin of sSEPs that could span the entire dendritic arbor. For instance, if the point of origin of sSEPs were closer to the somatic electrode (say, proximal obliques or basal dendrites), then the amplitude at the somatic electrode would be higher than at the dendritic electrode. To quantitatively evaluate this, we used our computational model (see below) to simultaneously record simulated SEPs at a dendritic (∼200 µm from the soma) and a somatic location, with the point of origin of the SEPs set to span a large portion of the dendritic arbor. We computed the ratio of dendritic amplitude to the corresponding somatic amplitude for SEPs recorded from our dual experiments and our simulations. We found that the distributions of this ratio were not significantly different between experimentally recorded and simulated SEPs (Fig. S2D), suggesting that the experimentally recorded SEPs originated from a broad span of the dendritic tree. Taken together, our results (Fig. 1 and Fig. S2) provide direct functional evidence that a majority of sSEPs are not of somatic origin, but originate from a broad span of dendritic locations and undergo significant attenuation through their propagation across the neuronal arbor (Fig. 1 and Fig. S2), pointing to compartmentalization of their spatial spread.
Fig. S2.
The distribution of SEP amplitudes recorded simultaneously from somatic and dendritic locations was consistent with simulations where SEPs originated across a large span of the somatodendritic arbor. (A) Schematic of experimental design used for simultaneous recording of sSEPs at the soma and apical dendritic trunk ∼200 µm (194.8 ± 7.7 µm, mean ± SEM; N = 6 simultaneous recordings; n = 62 sSEP pairs) away from the soma, also providing color codes for the other panels. (B) Representative traces of temporally aligned spontaneous SEPs, recorded simultaneously at the soma and the dendrite. It should be noted that the dendritic SEP amplitudes were similar, greater than or less than the somatic SEPs, a manifestation of multiple locations of origin of SEPs along the somatodendritic arbor. Arrow shows a dendritic event consisting of multiple overriding SEPs, which resembles a single event at the soma when subjected to dendritic filtering. (C) Population data of dendritic (Vdend) and somatic (Vsoma) SEP amplitudes obtained from the simultaneous somatic and dendritic recordings. Solid rectangles correspond to population mean values. (D) Distribution (median and quartiles) of the ratio of simultaneously recorded Vdend to Vsoma from the population data shown in C (Experiments). This distribution of voltage ratios was compared with a corresponding distribution from simulations (Simulations; outcomes from Fig. 8 and Fig. S10), showing the ratio between the SEP amplitude at an apical trunk location at 200 µm (to match with experiments) and the corresponding SEP amplitude at the soma. This ratio was computed from simulations (10 epochs) where the receptor (point of origin of the SEP) was randomly located at one of the apical dendritic compartments within 250 µm of radial distance from the soma. To match with experimental analyses, SEPs whose dendritic or somatic amplitudes were greater than 1 mV were retained, leaving the total SEPs at 680. Despite the dendritic origins of these simulated events (mostly in thin obliques, which occupy most of the surface area in CA1 pyramidal neurons), and despite the higher density of dendritic NMDARs in these simulations (Fig. 8), a majority of events (63.2%) recorded in simulations had their dendritic SEP amplitude lower than that of their somatic counterparts, which matched with experimental observations where a majority of events (72.6%) had their Vdend/Vsoma less than 1. Importantly, the distribution of the ratio of Vdend/Vsoma from the simulated events was not significantly different from the Vdend/Vsoma ratio distribution obtained from experiments (Wilcoxon's rank sum test, P = 0.56), suggesting that the SEPs originated from a broad span of the dendritic tree. Finally, although our simulations did not include SEPs with basal dendritic origin, in experiments, SEPs could have originated from basal dendrites with events that have Vdend/Vsoma less than 1 (as recordings were performed from the apical trunk). (E) Population data of FWHM of dendritic and somatic SEPs obtained from the simultaneous somatic and dendritic recordings. Solid rectangles correspond to population mean values. (F) Population data of 20–80% rise time of dendritic (Tdend) and somatic (Tsoma) SEPs obtained from the simultaneous somatic and dendritic recordings. Solid rectangles correspond to population mean values. (G) Normalized cumulative histogram of the difference in the 20–80% rise times of dendritic and somatic spontaneous SEPs recorded simultaneously at both locations. Owing to random somatodendritic origins of SEPs, the difference (Tdend – Tdend) followed a distribution where 37.5% of dendritically recorded SEPs were faster than the somatically recorded SEPs, with the rest assuming an opposite sign. (H and I) Somatic and dendritic SEP amplitudes (H) and rise times (I) were not significantly different from corresponding spontaneous values presented in Fig. 1. (J) Somatic and dendritic FWHM values were comparable to corresponding spontaneous values presented in Fig. 1. For H–J, data from soma and 200-µm spontaneous SEPs from Fig. 1 were respectively compared with somatic and dendritic events (≥1 mV) under simultaneous somatodendritic recordings. Single, spontaneous SEPs recorded from individual somatic or dendritic recordings, presented in Fig. 1; Dual, spontaneous SEPs recorded under the simultaneous somatodendritic recording configuration. Rectangles represent population means. The frequency of sSEPs from Fig. 1 was also not significantly different from that of their counterparts recorded under the simultaneous somatic and dendritic recording configuration (Wilcoxon's rank sum test, P = 0.42).
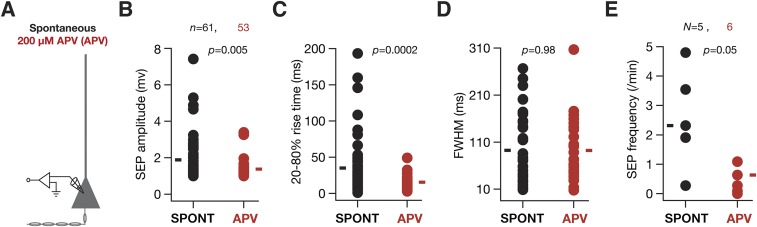
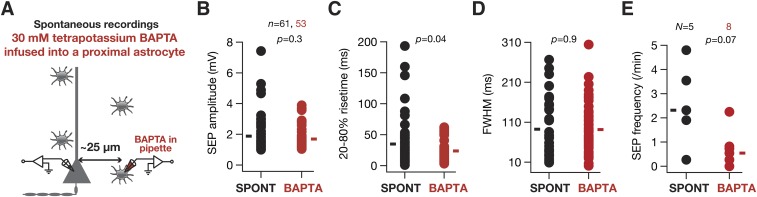
What receptors mediated these sSEPs? Motivated by evidence from the literature that SICs are mediated by NMDA receptors (5–7), we recorded sSEPs in the presence of NMDAR antagonist d,l-2-amino-5-phosphonovaleric acid (d,l APV). Consistent with the literature, we found that these sSEPs were significantly suppressed by APV, in terms of both the amplitude and the frequency of these events (Fig. S3), suggesting that they were mediated by NMDARs. Next, we asked whether these sSEPs were of astrocytic origin by recording neuronal sSEPs after injecting the calcium chelator 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA) (30 mM) into a nearby astrocyte and allowing it to spread into the astrocytic syncytium for ∼1 h (5, 8). Although such astrocytic calcium chelation elicited complete blockade of sSEPs in one of eight neurons and there was strong reduction in the frequency of events in the others, in some neurons sSEP frequency in the presence of astrocytic BAPTA was comparable to sSEPs recorded in the absence of astrocytic BAPTA (Fig. S4). We noted that these results were consistent with the literature on the suppression of spontaneous SICs recorded after the infusion of BAPTA into the astrocytic syncytium (5, 8).
Fig. S3.
Spontaneous SEPs were mediated by NMDA receptors. (A) Schematic of experimental design used to assess the impact of blocking NMDA receptors on somatic sSEPs. The protocol and extracellular/intracellular solutions were similar to somatic recordings in Fig. 1 in all aspects, except for the application of 200 µM d,l APV to the extracellular bath solution. (B–E) Amplitude (B), 20–80% rise time (C), FWHM (D), and frequency of sSEPs (E), recorded in the presence (red) and absence (black) of 200 µM APV. For A–C solid rectangles represent the mean values, and P values correspond to Student’s t test. For D solid rectangles represent the median frequency values, and P value corresponds to Wilcoxon's rank sum test. Note that the blockade of sSEPs was complete in one of the six cells recorded with 200 µM APV, where there was no sSEP during the recording period.
Fig. S4.
Infusion of BAPTA in astrocytes suppressed the frequency of spontaneous SEPs. (A) Schematic representation of experimental design. Whereas spontaneous SEP recordings (SPONT) were obtained without any paired astrocytic recordings, SEPs with astrocytic BAPTA (BAPTA) were recorded 1 h after patching a nearby astrocyte with 30 mM tetrapotassium BAPTA. The protocol and extracellular/intracellular solutions were similar to somatic recordings in Fig. 1. (B–E) Amplitude (B), 20–80% rise time (C), FWHM (D), and frequency of sSEPs (E), recorded after the infusion of astrocytic BAPTA (red) or under baseline conditions (black). For A–C solid rectangles represent the mean values, and P values correspond to Student’s t test. For D solid rectangles represent the median values, and P value corresponds to Wilcoxon's rank sum test. Note that the blockade of sSEPs was complete in one of the eight cells recorded with astrocytic BAPTA infusion, where there was no sSEP during the recording period.
Dendritic Ion Channels Actively Compartmentalize the Impact of Gliotransmission on Neurons.
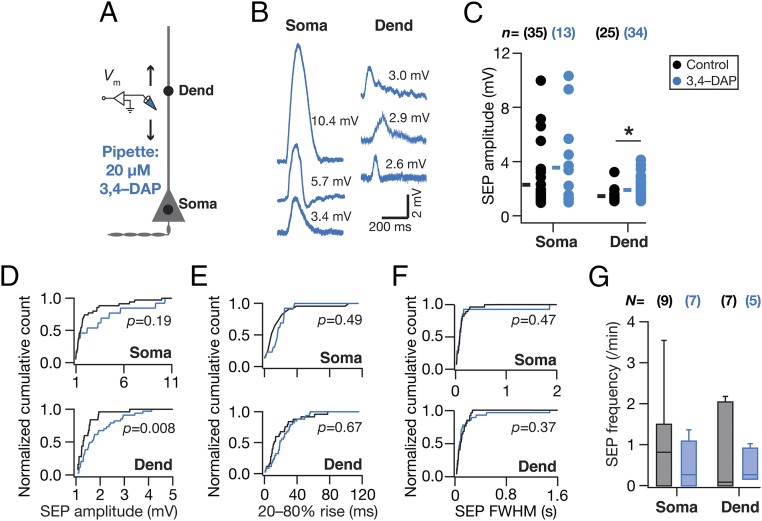
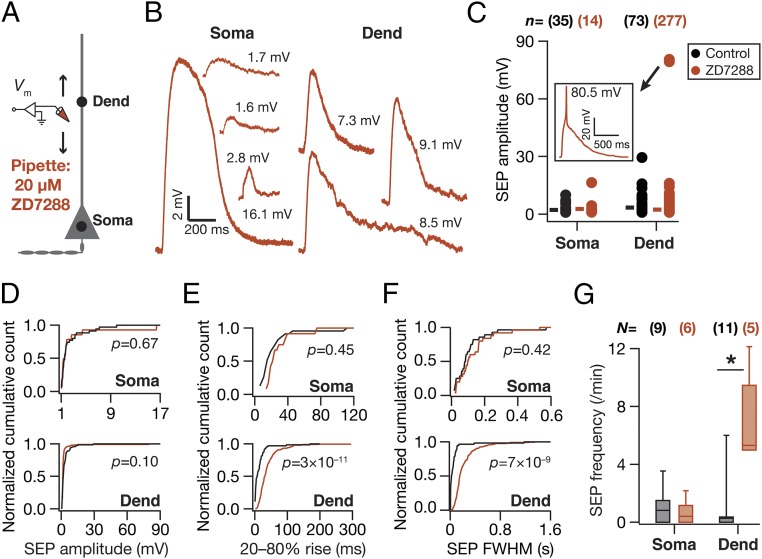
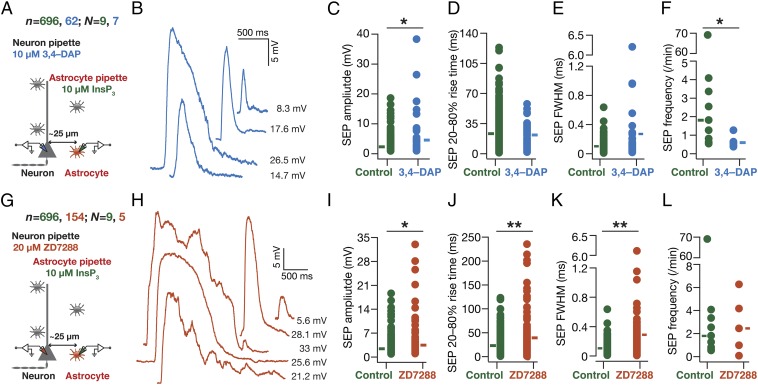
What mediates the attenuation, filtering, and spatiotemporal compartmentalization of these dendritically originating sSEPs? Hippocampal neuronal dendrites are endowed with a variety of VGICs, expressing with diverse subcellular localization profiles, which mediate several intraneuronal functional maps that significantly contribute to neuronal physiology and plasticity (11–14, 16, 17). Do these active dendritic components play a role in regulating the strength, kinetics, and spread of the impact of gliotransmission on neurons? To answer this, we assessed the role of two prominent VGICs that are expressed at higher densities in the dendrites of these neurons: the A-type K+ (KA) and hyperpolarization-activated cyclic-nucleotide–gated nonspecific-cation (HCN) channels. We found that pharmacological blockade of KA channels, confined to the neuron that was being recorded, resulted in a significant increase in sSEP amplitudes at dendritic locations, but not at the soma (Fig. 2 A–D). However, there was no significant impact of KA-channel blockade on the frequency, rise time, and width of somatic or dendritic sSEPs (Fig. 2 E–G). In contrast, pharmacological blockade of HCN channels, confined to the neuron that was being recorded, did not result in significant differences in sSEP amplitudes (Fig. 3 A–D). This was despite the emergence of 2 (of 27; Fig. 3C) sSEPs that resulted in putative dendritic calcium spikes in the presence of HCN channel blockers. Importantly, blocking HCN channels resulted in significant increases in the rise time, duration, and frequency of dendritic, but not somatic, sSEPs (Fig. 3 E–G). Whereas the KA-channel regulation of SEP amplitudes is consistent with their fast kinetics and their ability to regulate synaptic potentials (16), the lack of a significant impact of HCN-channel blockade on SEP amplitudes is consistent with their slow time constants and similar observations on synaptic potentials (17). The positive impact of HCN channels on SEP frequency could be related to the reduced electrotonic distances observed after blockade of these channels (17), implying efficient propagation and improved detectability of propagating SEPs (21, 22). Together, these observations demonstrate that KA and HCN channels critically regulate the amplitude and kinetics of spontaneous SEPs, respectively, and demonstrate that dendritic ion channels actively compartmentalize the impact of gliotransmission on neurons to generate localized excitatory potentials.
Fig. 2.
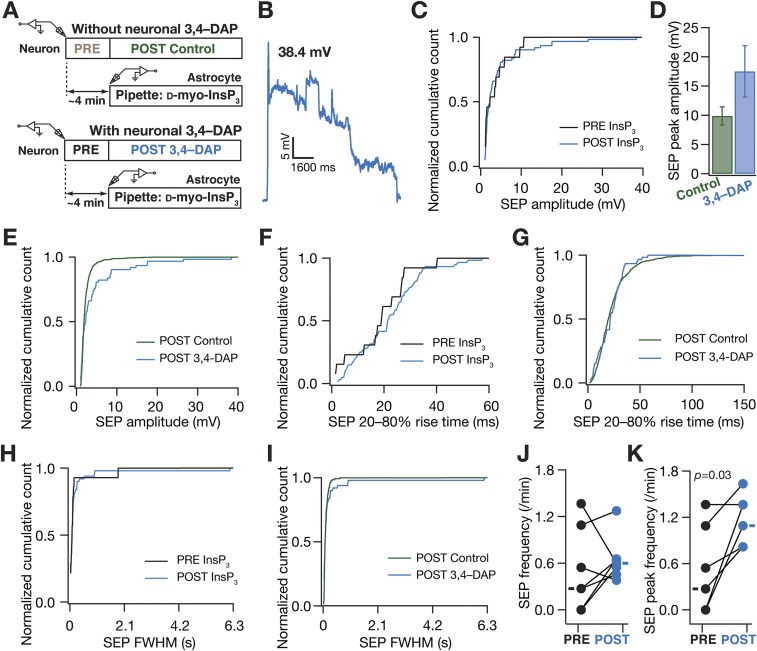
A-type K+ channels preferentially regulated the amplitude of somatodendritic spontaneous SEPs. (A) Schematic of experimental design used to record sSEPs at various locations along the somato-apical trunk with 20 µM 3,4-diamonopyridine (3,4–DAP) in the recording pipette to block KA channels. (B) Representative traces of somatic and dendritic sSEPs after blocking KA channels. (C) sSEP amplitudes (cyan) recorded at somatic and dendritic (distance from soma for control, 153 ± 5.74 µm; 3,4–DAP = 160 ± 4.47 µm, mean± SEM; P = 0.36, Student’s t test) locations with (3,4–DAP) and without (Control) KA-channel blockade. *P < 0.05: Student’s t test. Rectangles represent the mean values. (D–F) Normalized cumulative histograms of sSEP amplitude (D), rise time (E), and FWHM (F) for different locations. P values are for Student’s t test. (G) sSEP frequency at somatic and dendritic locations (median and quartiles) with (3,4–DAP) and without (Control) KA-channel blockade.
Fig. 3.
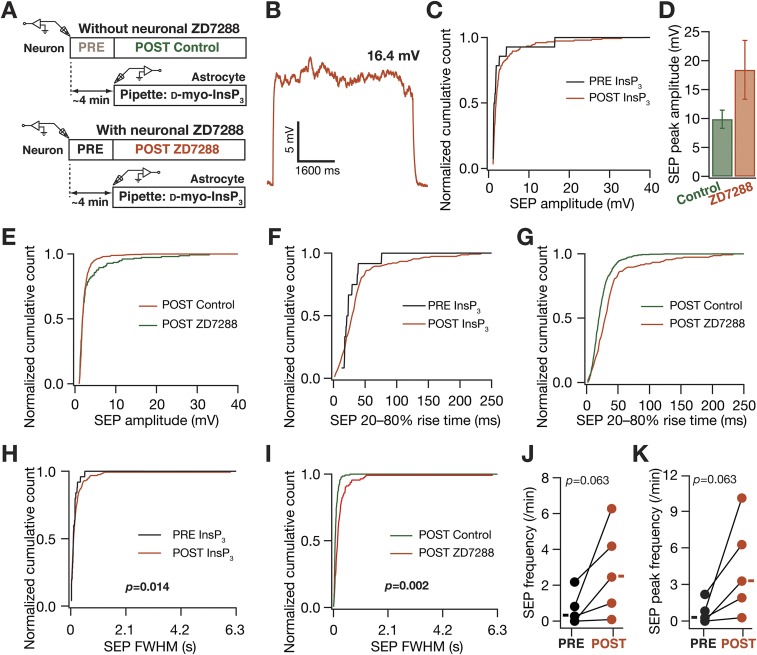
HCN channels preferentially regulated the kinetics of somatodendritic spontaneous SEPs. (A) Schematic of experimental design used to record sSEPs at various locations along the somato-apical trunk with 20 µM 4-Ethylphenylamino-1,2-dimethyl-6-methylaminopyrimidinium chloride (ZD7288) in the recording pipette to block HCN channels. (B) Representative traces of somatic and dendritic sSEPs after blocking HCN channels. (C) sSEP amplitudes (cyan) recorded at somatic and dendritic (distance from soma for Control, 213.5 ± 5.6 µm; ZD7288, 212 ± 9.7 µm) (mean ± SEM; P = 0.9, Student’s t test) locations with (ZD7288) and without (Control) HCN-channel blockade. C, Inset represents a dendritic calcium spike that was induced by the sSEP and rectangles represent the mean values. (D–F) Normalized cumulative histograms of sSEP amplitude (D), rise time (E), and FWHM (F) for different locations. P values are for Student’s t test. (G) sSEP frequency at somatic and dendritic locations (median and quartiles) with (ZD7288) and without (Control) HCN-channel blockade. *P < 0.05, Mann–Whitney test.
Infusion of Inositol Trisphosphate into Proximal or Distal Astrocytes Enhanced the Occurrence and Amplitude of Neuronal SEPs.
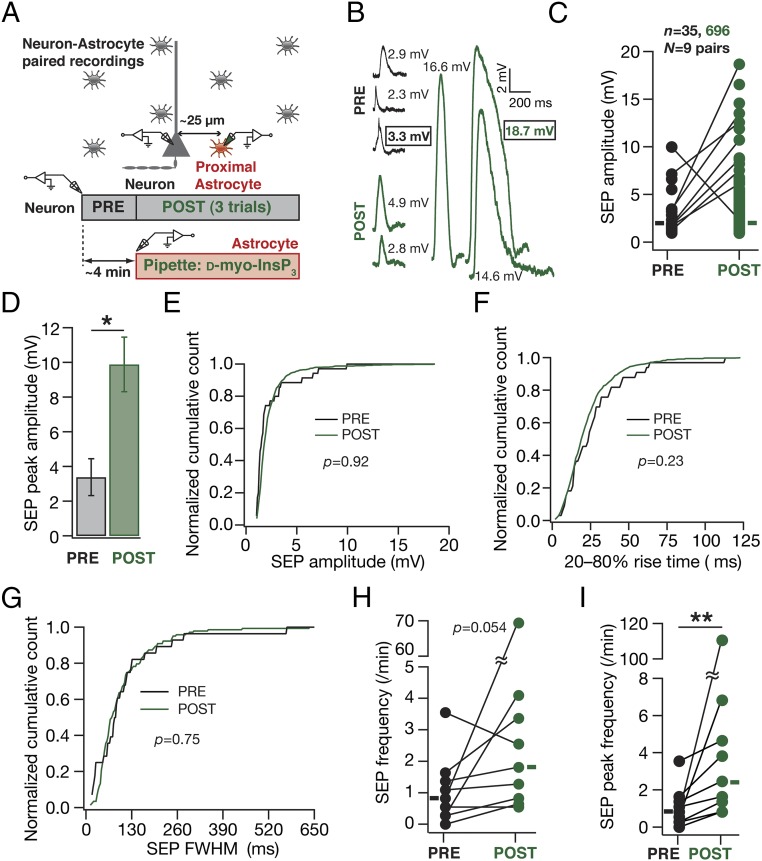
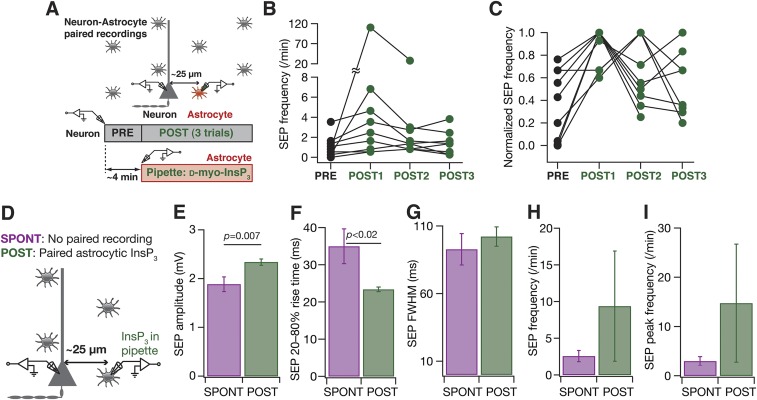
Although these observations provided direct evidence for a critical role for active dendrites in regulating sSEP amplitudes and compartmentalizing their spread, a significant limitation was the lack of evidence establishing astrocytic origin of these sSEPs. To overcome this, we used a well-established technique of inducing targeted gliotransmitter release from astrocytes through direct infusion of d-myo-inositol 1,4,5-trisphosphate (InsP3), an endogenous ligand that activated InsP3 receptors on the endoplasmic reticulum, coupled with paired recordings from a nearby neuron (28). We found that infusion of 10 µM InsP3 into visually identified proximal astrocytes (<50 µm away from a patched neuron) significantly increased the peak amplitude and frequency of InsP3-induced SEPs (iiSEPs) in the neuron, compared with SEPs recorded before astrocytic infusion of InsP3 (Fig. 4 and Fig. S5). This increase was specific to infusion of InsP3 because iiSEP amplitudes were significantly higher than sSEP amplitudes recorded in the absence of paired astrocytic recording (Fig. S5) and because large depolarizations of astrocytes in paired recordings, in the absence of InsP3 in the recording pipette, were ineffective in introducing significant differences in recorded SEPs (Fig. S6). Rise time and duration of iiSEPs were not significantly different from their preinfusion conditions in the same neuron (Fig. 4 E–G).
Fig. 4.
In paired astrocyte–neuron recordings, infusion of InsP3 into a proximal astrocyte enhanced the occurrence and amplitude of neuronal SEPs. (A) Schematic of the experimental design for paired astrocyte–neuron recordings with 10 µM InsP3 in the astrocytic recording pipette. (B) Representative traces from a single neuron recorded before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte. Numbers correspond to SEP amplitudes of adjacent traces, and boxed numbers denote that the adjacent trace exhibited the peak amplitudes recorded during the course of a given experiment (PRE or POST infusion). (C and D) Amplitude (C) and peak amplitude (D) of SEPs recorded before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte. The sticks in C connect the peak amplitudes recorded before and after InsP3 infusion in each of the nine pairs and rectangles represent mean values. The plot in D depicts a mean ± SEM representation of the PRE and POST peak amplitudes in individual cells. *P < 0.05: paired Student’s t test. (E–G) Normalized cumulative histograms of amplitude (E), 20–80% rise time (F), and FWHM (G) for SEPs recorded before (PRE) and after (POST) infusion of 10 µM InsP3 into a nearby astrocyte. P values are for Student’s t test. (H and I) Frequency (H) and peak frequency (I) of SEPs recorded before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte. For H and I rectangles represent the population median values. P values are for a paired Mann–Whitney test with **P < 0.005 (Figs. S5 and S6).
Fig. S5.
Infusion of InsP3 into astrocytes resulted in an increase in SEP amplitude and frequency. (A) Schematic of the experimental design for paired astrocyte–neuron recordings with 10 µM InsP3 in the astrocytic recording pipette. (B) SEP frequency recorded before (PRE) and in three consecutive epochs of ∼4 min (POST1, POST2, and POST3) after infusion of 10 µM InsP3 into a nearby astrocyte. (C) Normalized SEP frequencies for the data presented in B. It should be noted that the POST SEP frequency peaked at different recording epochs in different neurons, and the peak SEP frequency was always higher than the PRE SEP frequency. For B and C, sticks connect frequencies of the same neuron. (D) Schematic representation of experimental design. Whereas spontaneous SEP recordings (SPONT) were obtained without any paired astrocytic recordings, SEPs with astrocytic InsP3 were recorded after (POST) patching a nearby astrocyte with 10 µM d-myo-InsP3 in the recording pipette. SPONT data were derived from spontaneous somatic recordings presented in Fig. 1, and POST data were derived from POST recordings shown in Fig. 4. (E–I) Amplitude (E), 20–80% rise time (F), FWHM duration (G), frequency (H), and peak frequency (I) of spontaneous and astrocytic InsP3-induced SEP recorded at the soma. Data are presented as mean ± SEM, and P values correspond to Student’s t test.
Fig. S6.
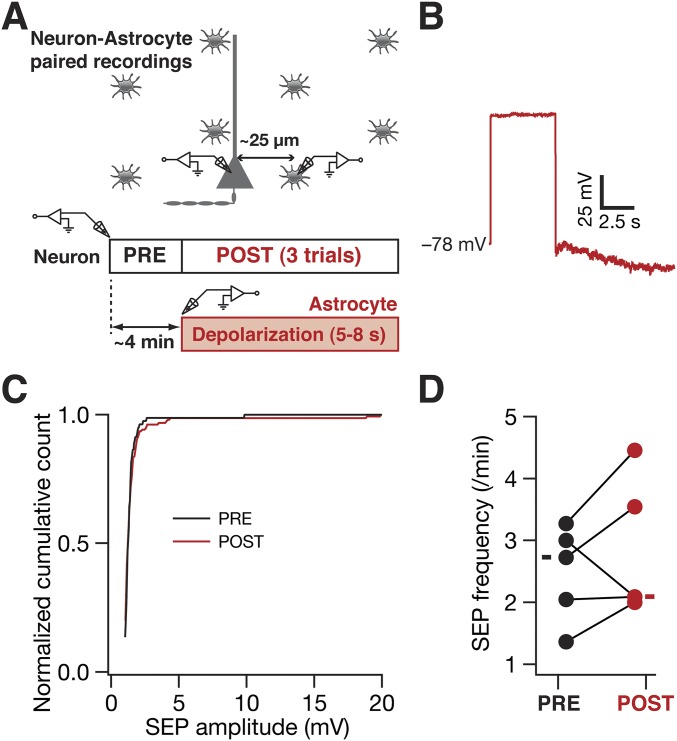
Depolarization of astrocytes did not result in significant changes in either amplitude or frequency of neuronal SEPs. (A) Schematic representation of the experimental design using astrocyte–neuron paired recordings to test the role of astrocytic depolarization in eliciting SEPs in nearby neurons. Astrocytes were recorded in current-clamp mode and were repeatedly depolarized by large current injections (to take the membrane potential beyond 0 mV) for 5–8 s. Neuronal SEPs were recorded during the periods before (PRE) and after (POST) current injections. (B) Representative trace of membrane potential in an astrocyte after current injection for 5 s. (C) Normalized cumulative histograms for the SEPs before (black) and after (red) astrocytic depolarization. PRE n = 81, POST n = 156. (D) SEP frequency before and after astrocytic depolarization recorded from five astrocyte–neuron pairs. For D solid rectangles represent the mean values. For these experiments the extracellular bath solution contained 125 mM NaCl, 3 mM KCl, 1.25 mM NaH2PO4, 25 mM NaHCO3, 2 mM CaCl2, 0 mM MgCl2, 10 mM dextrose (pH 7.3; 300 mOsm) with 1 µM TTX to block synaptic transmission. These results suggest that astrocytic voltage-gated calcium channels do not play a significant role in regulating SEPs in brain slices of adult rats.
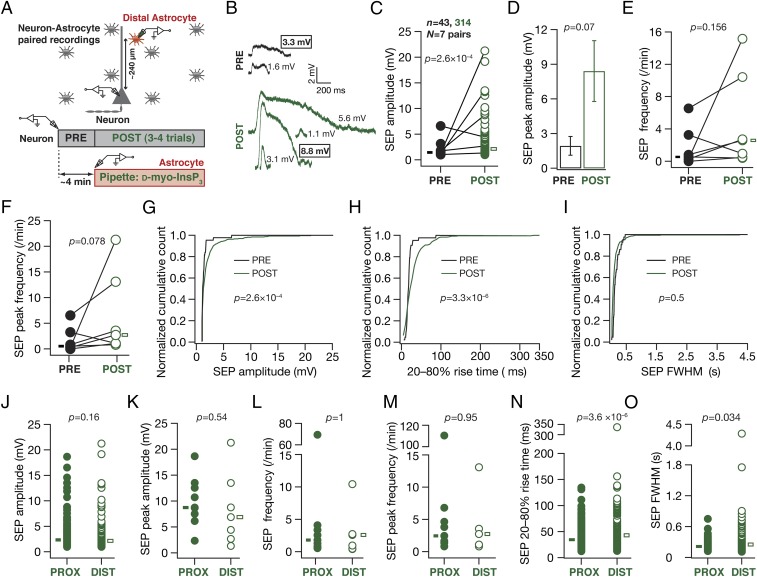
Are there differences in iiSEPs evoked through InsP3 infusion into proximal vs. distal astrocytes? As astrocytic processes are well organized with extents of their influence limited to specific regions of their arbor, we performed paired recordings where distal astrocytes (located at around 240 µm along the apical dendritic arbor) were paired with neuronal soma (Fig. 5). Conforming to our results with paired recordings involving proximal astrocytes (Fig. 4), we found that InsP3 infusion into distal astrocytes increased the amplitude and frequency of SEPs recorded in the neuron (Fig. 5 C–G). However, the rise time distribution of iiSEPs recorded after InsP3 infusion into distal astrocytes was significantly different from corresponding preinfusion distribution in the same neuron (Fig. 5H), consistent with dendritic filtering (22) consequent to predominantly distal origins of these iiSEPs. Concordantly, although the amplitudes (Fig. 5 J and K) and frequencies (Fig. 5 L and M) of iiSEPs recorded after InsP3 infusion into proximal (Fig. 4) vs. distal astrocytes (Fig. 5 C–I) were not significantly different, the rise time (Fig. 5N) and FWHM (Fig. 5O) of iiSEPs recorded after InsP3 infusion into distal astrocytes were significantly higher compared with those recorded after proximal infusion.
Fig. 5.
Infusion of InsP3 into a distal astrocyte enhanced the occurrence and amplitude of neuronal SEPs at the soma, with SEPs exhibiting slower kinetics compared with those recorded with InsP3 infusion into proximal astrocytes. (A) Schematic of the experimental design for paired astrocyte–neuron recordings with 10 µM InsP3 in the recording pipette of astrocytes located at a distance of 200–300 µm (240 ± 16.7 µm, mean ± SEM) from the soma in the apical dendritic region. (B) Representative traces from a single neuron recorded before (PRE) and after (POST) infusion of InsP3 into a distal astrocyte. Numbers correspond to SEP amplitudes of adjacent traces, and boxed numbers denote that the adjacent trace exhibited the peak amplitude recorded during the course of a given experiment (PRE or POST infusion). (C and D) Amplitude (C) and peak amplitude (D) of SEPs recorded before (PRE) and after (POST) infusion of InsP3 into a distal astrocyte. The sticks in C connect the peak amplitudes recorded before and after InsP3 infusion in each of seven pairs. Boxes in C represent the mean SEP amplitudes under PRE (solid, black)- and POST (open, green)-infusion conditions. *P < 0.05: unpaired Student’s t test of all PRE and POST events. The plot in D depicts a mean ± SEM representation of the PRE and POST peak amplitudes in individual cells. *P < 0.05: paired Student’s t test. (E and F) Frequency (E) and peak frequency (F) of SEPs recorded before (PRE) and after (POST) infusion of InsP3 into a distal astrocyte. P values are for a paired Mann–Whitney test. (G–I) Normalized cumulative histograms of amplitude (G), 20–80% rise time (H), and FWHM (I) for SEPs recorded before (PRE) and after (POST) infusion of 10 µM InsP3 into a distal astrocyte. P values are for Student’s t test. (J–O) Amplitudes (J), peak amplitudes (K), frequencies (L), peak frequencies (M), 20–80% rise times (N), and FWHM (O) for SEPs recorded after InsP3 infusion (POST) into proximal (∼25 µm, solid circles; data from Fig. 4) or distal (∼240 µm, open circles) astrocytes. Boxes in J, N, and O represent population mean values, and P values there are for Student’s t test, whereas boxes in K–M represent population medians, and P values there are for Wilcoxon's rank sum test.
Together, these observations established that specific activation of an astrocyte through InsP3 infusion significantly enhanced the occurrence and amplitude of SEPs in nearby neurons, thereby providing clear evidence for the astrocytic origin of SEPs. Importantly, we show that iiSEPs recorded after InsP3 infusion into distal astrocytes exhibited significantly slower kinetics compared with those recorded after proximal infusion. These results unveil a direct link between the location of an activated astrocyte and the point of origin of the associated SEP along the somatodendritic axis, thereby further substantiating the astrocytic origin of SEPs.
Blocking KA or HCN Channels Enhanced SEPs Induced by the Infusion of InsP3 into a Nearby Astrocyte.
Given the specificity of this paired recording process in delineating the astrocytic origin of SEPs, we returned to our question on the role of neuronal VGICs in regulating the impact of gliotransmission on neurons. Consistent with our results on sSEPs (Figs. 2 and 3), we found that blocking KA channels resulted in an increase in the amplitude of iiSEPs, compared with iiSEPs recorded without KA-channel blockade, without significantly altering their rise time or duration (Fig. 6 A–F). Additionally, blocking HCN channels resulted in significant increases in the amplitude, rise time, and duration of iiSEPs compared with the conditions where HCN-channel blockers were absent (Fig. 6 G–L). There were some differences in our results from iiSEPs and sSEPs (e.g., HCN-channel regulation of SEP amplitude or KA-channel regulation of SEP frequency), which could partly be attributed to iiSEPs being larger than sSEPs (Figs. S5, S7, and S8), leading to differential activation of ionic conductances across the somatodendritic arbor. Together, our results from dendritic recordings of spontaneous SEPs (Figs. 2 and 3) and paired neuron–astrocyte recordings of iiSEPs (Fig. 6) clearly demonstrate a critical role for dendritic ion channels in regulating the strength, kinetics, and spread of the impact of gliotransmission on neurons.
Fig. 6.
In paired astrocyte–neuron recordings, A-type K+ and HCN channels regulated neuronal SEPs induced by infusion of InsP3 in astrocytes. (A) Experimental design to record iiSEPs when KA channels were blocked with 20 µM 3,4–DAP in the neuronal recording pipette. (B) Representative iiSEPs after blocking KA channels. (C–F) Amplitude (C), 20–80% rise time (D), FWHM (E), and frequency (F) of iiSEPs recorded with (3,4–DAP) and without (Control) KA-channel blockade. (G–L) Same as (A–F), but with 20 µM ZD7288 in the neuronal pipette to block HCN channels. For C–E and I–K solid rectangles represent mean values whereas for F and L they represent median values. For F, *P < 0.05, Mann–Whitney test; for C and I–K, *P < 0.05, **P < 0.005, Student’s t test (Figs. S7 and S8).
Fig. S7.
A-type K+ channels regulated slow excitatory potentials induced by infusing d-myo-inositol trisphosphate into a nearby astrocyte. (A) Schematic depicting experimental design associated with data presented in this figure. Two sets of experiments (same as Fig. 6), one with and the other without 20 µM 3,4–DAP (A-type K+ channel blocker) in the recording pipette, were performed. Color codes for each dataset are shown and are the same for B–K. (B) Representative trace of a high-amplitude long-duration SEP when A-type K+ channels were blocked. This trace was recorded after infusion of InsP3 into a nearby astrocyte. (C) Normalized cumulative histogram of SEP amplitude before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte, after A-type K+ channels were blocked with 3,4–DAP. (D and E) SEP peak amplitude (D; mean ± SEM) and normalized cumulative histogram of amplitudes of all recorded SEPs (E) plotted for cases where A-type K+ channels were present (Control) or blocked (3,4–DAP), after infusion of InsP3 into a nearby astrocyte. (F) Normalized cumulative histogram of SEP 20–80% rise time, with the experimental configuration described in C. (G) Normalized cumulative histogram of SEP 20–80% rise time, with the experimental configuration described in E. (H) Normalized cumulative histogram of SEP FWHM duration, with the experimental configuration the same as in C. (I) Normalized cumulative histogram of FWHM, with the experimental configuration the same as in E. (J and K) SEP frequency (J) and peak SEP frequency (K) before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte, after A-type K+ channels were blocked with 3,4–DAP. For J and K solid rectangles represent the mean values. The data represented in E, G, and I are the same as in Fig. 6 C, D, and E, respectively. For K, P values correspond to a Mann–Whitney test.
Fig. S8.
Hyperpolarization-activated cyclic-nucleotide–gated nonspecific cationic (HCN) channels regulated slow excitatory potentials induced by infusing d-myo-inositol trisphosphate into a nearby astrocyte. (A) Schematic depicting experimental design associated with data presented in this figure. Two sets of experiments (same as Fig. 6), one with and the other without 20 µM ZD7288 (HCN channel blocker) in the recording pipette, were performed. Color codes for each dataset are shown and are the same for B–K. (B) Representative trace of a high-amplitude long-duration SEP when HCN channels were blocked. This trace was recorded after infusion of InsP3 into a nearby astrocyte. (C) Normalized cumulative histogram of SEP amplitude before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte, after HCN channels were blocked with ZD7288. (D and E) SEP peak amplitude (D; mean ± SEM) and normalized cumulative histogram of amplitudes of all recorded SEPs (E) plotted for cases where HCN channels were present (Control) or blocked (ZD7288), after infusion of InsP3 into a nearby astrocyte. (F) Normalized cumulative histogram of SEP 20–80% rise time, with the experimental configuration described in C. (G) Normalized cumulative histogram of SEP 20–80% rise time, with the experimental configuration described in E. (H) Normalized cumulative histogram of SEP FWHM duration, with the experimental configuration the same as in C. (I) Normalized cumulative histogram of FWHM, with the experimental configuration the same as in E. (J and K) SEP frequency (J) and peak SEP frequency (K) before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte, after HCN channels were blocked with ZD7288. For J and K solid rectangles represent the mean values .The data shown in E, G, and I are the same as in Fig. 6 I, J, and K, respectively. P values correspond to Student’s t test (H and I) and a paired Mann–Whitney test (J and K).
GluN2B- and GluN2D-Containing NMDARs Predominantly Mediate Perisomatic and Dendritic SEPs.
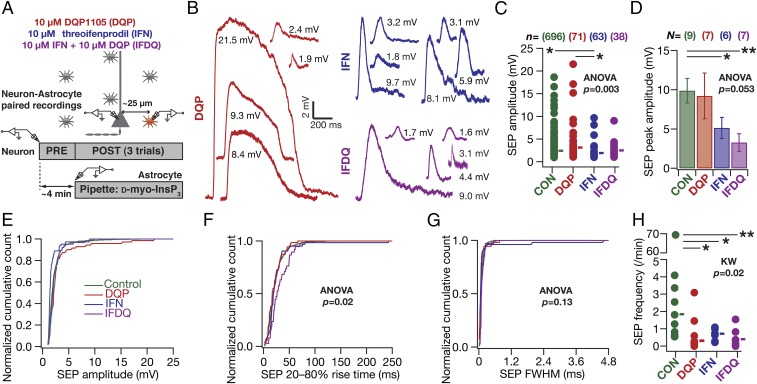
Previous studies in juvenile rodents have demonstrated SICs to be mediated by GluN2B-containing NMDARs (GluN2BR) (7, 27). However, receptor localization studies in the adult CA1 region have shown GluN2BRs to express predominantly at perisomatic locations (29). In the context of our observations that sSEP amplitudes were larger at dendritic locations (Fig. 1), this receptor localization profile constitutes a paradox. In an effort to resolve this, and motivated by the presence of GluN2D-specific NMDARs (GluN2DR) in the CA1 dendritic region (29), we assessed the specific contributions of GluN2BR and GluN2DR to iiSEPs in paired neuron–astrocyte recordings (Fig. 7A). We found that blocking GluN2DR suppressed low-amplitude iiSEPs, whereas blockade of GluN2BR suppressed high-amplitude iiSEPs (Fig. 7 B and C and Fig. S9D). Consequently, whereas blocking of GluN2BR, but not GluN2DR alone, resulted in a significant reduction in the iiSEP amplitude (Fig. 7 D and E), blocking either receptor (independently or together) yielded significant reductions in the iiSEP frequency (Fig. 7H). Together, and in conjunction with previous results (7, 27, 29), these observations provide direct functional evidence that GluN2BR and GluN2DR predominantly mediate perisomatic and dendritic SEPs, respectively.
Fig. 7.
In paired astrocyte–neuron recordings, SEPs were mediated by GluN2B- and GluN2D-containing NMDA receptors. (A) Schematic of experimental design to assess the role of different NMDAR subunits on neuronal SEPs induced by infusion of InsP3 into a nearby astrocyte. The different pharmacological agents added to the artificial cerebral spinal fluid (ACSF), their (nonsaturating) concentrations, and color codes are also listed. (B) Representative iiSEPs recorded in the presence of blockers of different NMDAR subunits. (C and D) Amplitude (C) and peak amplitude (D) of iiSEPs recorded in the presence of blockers of different NMDAR subunits. Solid rectangles in C represent mean values. *P < 0.05, **P < 0.005, Student’s t test. (E–G) Normalized cumulative histogram of iiSEP amplitude (E), 20–80% SEP rise time (F), and FWHM (G) recorded after infusion of InsP3 into a nearby astrocyte, for experiments where specific NMDARs were blocked. For F the rise times for IFDQ were significantly different from Control (P = 0.006) and DQP (P = 0.005) groups with Student’s t test. (H) Frequency of iiSEPs recorded in the presence of blockers of different NMDAR subunits. Solid rectangles are median frequency values. KW, Kruskal–Wallis test. *P < 0.05, **P < 0.005, Mann–Whitney test. There were no iiSEPs in two astrocyte–neuron pairs and one each in the DQP and IFDQ groups (Fig. S9). DQP, 10 μM DQP1105; IFN, 10 μM threo ifenprodil; IFDQ, 10 μM threo ifenprodil + 10 μM DQP1105.
Fig. S9.
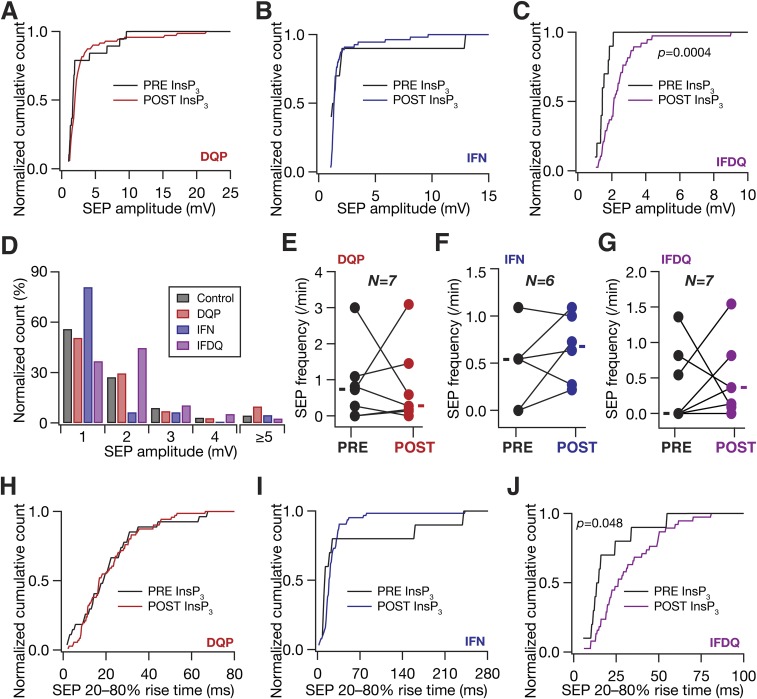
Different NMDA receptor (NMDAR) subtypes contribute to astrocytically originating SEPs in CA1 pyramidal neurons. Schematics depicting experimental design associated with data presented in this figure are the same as same as in Fig. 7. (A–C) Normalized cumulative histograms of SEP amplitude before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte when 10 µM DQP1105 (A; DQP), or 10 µM threo ifenprodil (B; IFN), or both DQP and IFN (C; IFDQ) were added to the extracellular bath solution. (D) Normalized histogram showing the percentage of SEPs in different amplitude ranges under control conditions (Control) and with bath application of either 10 µM DQP1105 (DQP) or 10 µM threo ifenprodil (IFN) or both (IFDQ). The data shown are from Fig. 7C. (E–G) SEP frequency before (PRE) and after (POST) infusion of InsP3 into a nearby astrocyte, after different NMDAR subtypes were blocked with DQP1105 (E), or threo ifenprodil (F), or both (G). Solid rectangles represent population medians. (H–J) Same as A–C, but for 20–80% rise time of SEP. For C and J, P values are for Student’s t test.
Computational Analyses Predicted an Increase in Extrasynaptic NMDAR Density with Increasing Distance from the Soma.
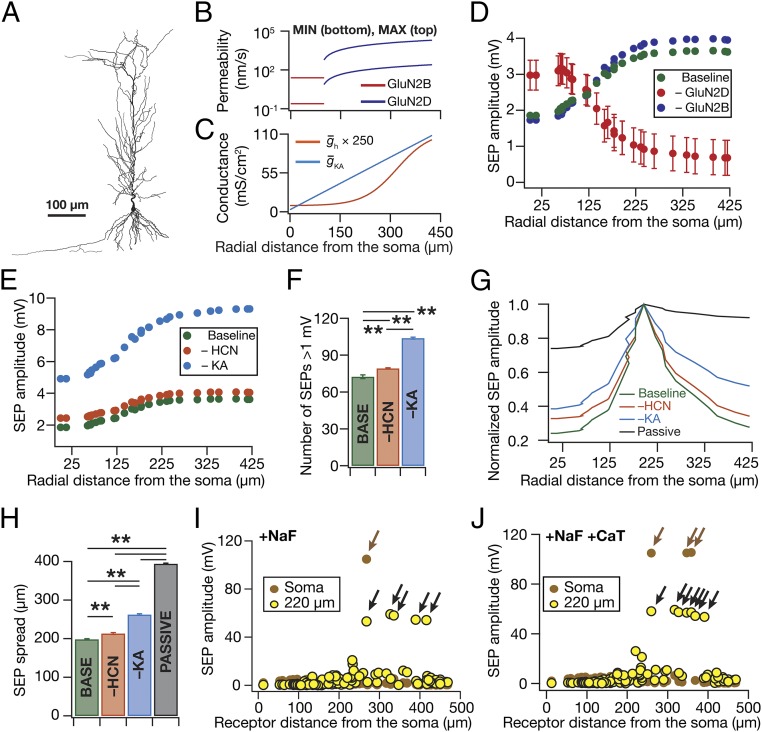
What distribution of NMDARs would result in the emergence of an observed intraneuronal map of SEP amplitudes (Fig. 1) along the somato-apical trunk in the CA1 pyramidal neurons (12)? To address this and to quantitatively assess the role of active dendrites in regulating SEPs, we constructed a morphologically and biophysically realistic multicompartmental model of CA1 pyramidal neurons with various active and passive parameters tuned to replicate experimentally observed measurements along the somato-apical trunk (Fig. 8 A–C and Fig. S10 A–C). We simulated SEPs by incorporation and activation of biophysically realistic models of GluN2B and GluN2D receptors with their distributions set (Fig. 8B) according to previous observations (29). Upon performing simulations in models where receptors were distributed with different somatodendritic gradients, we found that an increase in GluN2DR density with increasing distance from the soma was essential to match the experimentally observed increase in the dendritic SEP amplitudes (Fig. 8E; compare Fig. 1 and Fig. S1E). Importantly, providing quantitative credence to our earlier observations (Figs. 2, 3, and 6), removal of KA or HCN conductances from the model resulted in similar impacts on SEP amplitude (Fig. 8E) and frequency (Fig. 8F), when identical receptors were activated across the somatodendritic structure.
Fig. 8.
Computational simulations replicated experimental findings when a somatodendritic gradient in NMDAR density was introduced and demonstrated a critical role for active dendrites in compartmentalizing the impact of gliotransmission on neurons. (A–C) Neuronal morphology (A) and associated somatodenritic gradients in receptor permeability (B) and channel conductances (C) used in the computational model. Receptor permeability for a given location, for any of the several trials, was chosen randomly from a uniform distribution that spanned the minimum and maximum values represented in this plot (C). (D) Simulated SEP amplitudes in the absence of GluN2B (–GluN2B) and GluN2D (–GluN2D) receptors are plotted along with those in the presence of both receptors (Baseline). (E) Simulated SEP amplitudes in the absence of HCN (–HCN) and KA (–KA) channels are plotted along with those in the presence of both channels (Baseline). (F) Number of simulated SEPs (at ∼260 µm from the soma) with amplitude >1 mV for experiments in E. (G) Normalized SEP amplitudes recorded along the somatoapical trunk, with different channel combinations (Passive implies the absence of both HCN and KA channels), when the SEP was elicited at a distance of 192 µm from the soma. (H) Area under the curve (AUC) for the SEP amplitudes recorded along the somatoapical trunk, under various conditions depicted in the graph, when all of the 119 receptor locations were individually activated to get SEPs across the trunk. **P < 0.005, paired Student’s t test. (I and J) Somatic (brown) and corresponding dendritic (∼220 µm from the soma, yellow) SEP amplitudes recorded when fast sodium channels (NaF) were incorporated into the model without (I) or with (J) T-type calcium (CaT) channels. Black arrows depict localized dendritic spikes and the brown arrow depicts a somatic action potential consequent to successful propagation of the corresponding dendritic spike (Fig. S10).
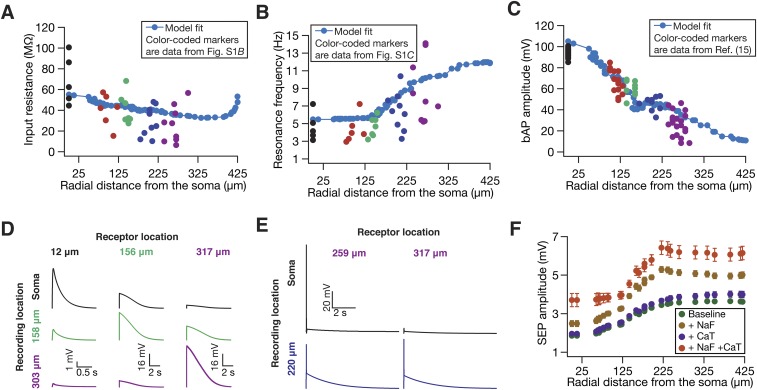
Fig. S10.
The presence of fast sodium and/or transient calcium channels increased SEP amplitude in a biophysically and morphologically realistic model. Experimentally observed somatodendritic maps of input resistance (A), resonance frequency (B), and back-propagating action potentials (C) were replicated in the model. For A–C, model fits are shown in blue, whereas colored markers (color coded with reference to distances shown in Fig. S1A) represent corresponding electrophysiological data from Fig. S1B for A, from Fig. S1C for B, and from ref. 15 (also depicted in ref. 26) for C. Apart from bAP amplitude (C), Rin and fR model fits shown here are also consistent with corresponding electrophysiological data from ref. 15 (also depicted in ref. 26). (D) Traces of simulated SEPs recorded at soma and along the apical dendritic trunk (at specified locations) when either GluN2B- or GluN2D-containing NMDARs were activated at different locations along the apical tree. Permeabilities of receptors in these simulations were set to the maximal permeability value at their respective location given by Fig. 8B. (E) Traces of SEP-induced dendritic spikes, recorded at the radial distance of 220 µm from the soma, in the presence of spiking conductances in the model. E, Left shows an example of a spike that actively propagates to elicit a somatic action potential. E, Right exemplifies a nonpropagating dendritic spike. The locations of receptors whose activation resulted in these dendritic spikes are also indicated. (F) Amplitudes of simulated SEPs under baseline conditions (Fig. 8), with fast sodium channels incorporated into the model (+NaF), with T-type calcium channels (+CaT) incorporated into the model, and with both NaF and CaT channels incorporated (+NaF +CaT).
Computational Analyses Demonstrated a Critical Role for Dendritic Ion Channels in Compartmentalizing the Spread of SEPs.
As the intrinsic (Fig. S10) and SEP properties (Fig. 8 D–F) were matched in the model, we used our computational model to quantify the spatial spread of individual SEPs in the presence and absence of HCN and KA conductances. First, consistent with lower passive attenuation of low-frequency signals (22), we found that SEPs were not significantly attenuated in a passive dendritic structure (Fig. 8G). This lack of attenuation in the passive structure was consistent across all somatodendritic locations and was inferred from the 394-µm average SEP spread for the passive structure (Fig. 8H), which is close to the maximum spread of 425 µm achievable by unattenuated SEPs. However, introduction of either HCN or KA or both channels into the dendritic tree (with distributions specified in Fig. 8C) resulted in significant reductions in the spatial spread of SEPs. These results provide further quantitative evidence that the observed compartmentalization in SEP spread (Fig. 1) was not due to passive attenuation, but was consequent to an active role for dendritically expressed conductances.
Finally, all our experiments required delineating SEPs from synaptic potentials through blockade of synaptic transmission with TTX, which also implied the absence of somatodendritic sodium channels. As experiments without TTX would imply ambiguous results that involve synaptic potentials as well, we used our computational model to assess the role of spike-generating fast sodium (NaF) channels in the regulation of SEPs. Specifically, we incorporated NaF conductances uniformly across the somatodendritic arbor (30) and activated identical receptors across the somatodendritic structure to record the resultant SEPs across the somatoapical trunk. Expectedly, the presence of NaF channels in the somatodendritic arbor increased the SEP amplitude across the trunk, with large-amplitude SEPs resulting in dendritically initiated spikes that rarely propagated to the soma toward the generation of a somatic action potential (Fig. 8I and Fig. S10 E and F). Additionally, incorporation of T-type calcium (CaT) channels into the model, with its density increasing with distance from the soma (30), specifically enhanced SEP amplitude at distal locations compared with their proximal counterparts (Fig. S10F), when receptor distribution was maintained identical to the baseline scenario. Further, incorporation of both NaF and CaT conductances (with their respective somatodendritic distributions) synergistically increased the SEP amplitudes beyond values recorded with their individual presence (Fig. S10F) and resulted in more dendritically initiated spikes, with more numbers of them (compared with the absence of CaT channels; Fig. 8I) propagating to generate a somatic action potential (Fig. 8J).
Discussion
In this study, we unveil an important role for active dendrites in regulating the impact of gliotransmission on neurons and demonstrate that dendritically expressed ion channels actively regulate the amplitude, kinetics, frequency, and spread of slow excitatory potentials resulting from gliotransmission. We arrived at these conclusions through systematic and direct mapping of somatodendritic voltage responses to gliotransmission and through the use of pharmacological agents that were specifically applied only to the neuron under consideration. Whereas this ensured that channels in other cells in the network were not affected, our paired recording technique with specific infusion of InsP3 into astrocytes provided clear lines of evidence that SEPs were consequent to gliotransmission. Importantly, our experiments involving InsP3 infusion into proximal vs. distal astrocytes established a vital link between the location of an activated astrocyte and the point of origin of the associated SEP along the neuronal somatodendritic axis. In conjunction with our somatodendritic and dual recordings of spontaneous SEPs, these results provide direct functional evidence for the dendritic origin of SEPs. Furthermore, our results unveil a functional role for the slower GluN2D-containing NMDARs in mediating the impact of gliotransmission on neurons. Specifically, using paired neuron–astrocyte recordings, we provide direct functional evidence, consistent with previous immunolocalization studies, that GluN2B- and GluN2D-containing NMDARs predominantly mediate SEPs in the perisomatic and distal dendritic locations. Using computational simulations to provide a quantitative corroboration of our experimental observations, we demonstrated that dendritic ion channels actively mediated spatiotemporal compartmentalization of SEPs. Finally, based on these simulations, we argued that SEPs could result in dendritic spikes and offered a testable prediction on a distance-dependent increase in extrasynaptic NMDARs.
Implications for Active Dendritic Regulation of the Impact of Gliotransmission.
Our results provide experimental and quantitative computational evidence pointing to a critical role for active dendrites and their plasticity in structured compartmentalization of SEPs, whereby their spatiotemporal influence is confined to specific dendritic compartments (closer to the point of their origin) without necessarily propagating to distal compartments (including the soma). Such compartmentalization confers upon neurons the ability to distinguish between the activations of different astrocytes, thereby lending specificity to and enhancing the information processing capacity of neuron–astrocyte interactions. Additionally, spatially restricted events of such large amplitudes mediated by NMDARs imply a significant calcium influx into specific compartments, which could translate to localized plasticity in neuronal channels and receptors through downstream signaling components (13, 18, 31).
From a broader perspective, our demonstration of an active role for dendritically expressed ion channels in regulating the impact of gliotransmission calls for a marked rethink of the complexities associated with neuron–glia communication. Specifically, the numbers associated with dendritic ion channel subtypes, their auxiliary subunits, their subcellular localization profiles, and their local or global modulation through neuromodulatory substances or activity-dependent plasticity are staggeringly combinatorial. This additional layer of complexity introduced by the active role of dendritic ion channels in regulating the dynamics of neuron–glia signaling implies a manyfold increase in the complexity of neuronal and network computation of afferent information. Given this enhanced complexity, and given that neuron–glia interactions and any consequent plasticity would be localized to specific segments of the dendritic arbor, it is essential that future studies use direct dendritic recordings in studying neuron–glia signaling rather than focusing only on somatic physiology. Although our focus for this study has been limited to hippocampal pyramidal neurons and to two specific ion channels, the implications of our conclusions extend to other brain regions and dendritically expressed ion channels there. Given the wide diversity of expression profiles and properties of ion channels, future studies could explore the specific roles of active dendrites in regulating neuron–glia interactions in different brain regions.
Finally, and importantly, the amplitude and kinetics of several SEPs strikingly resemble those of plateau potentials (large-amplitude, long-duration depolarizations) recorded in these neurons under in vivo and in vitro conditions (31, 32). Based on this resemblance, we postulate that astrocytically originating SEPs form a substrate for the spontaneous long-duration (hundreds of milliseconds) large-amplitude plateau potentials that have been implicated in the formation of place cells through localized plasticity (32). Specifically, behavioral regimes that lead to synchronous excitation of CA1 microcircuits could induce the release of gliotransmitters, which, through the activation of extrasynaptic NMDARs, could result in the emergence of spatiotemporally localized plateau potentials resulting in localized neuronal plasticity. As processes of single astrocytes contact 300–600 neuronal dendrites overseeing tens of thousands of synapses (2), plateau potentials mediated by gliotransmission form an ideal substrate for their postulated role in binding of information streams (33). Together, we postulate that dendritic SEPs of astrocytic origin constitute a putative cellular mechanism that can integrate network activity with biophysical and biochemical signal processing in a single neuron, thereby playing critical roles in neural coding and homeostasis.
Materials and Methods
Detailed descriptions of the surgical, electrophysiological, data analysis, and computational procedures used in this study are provided in SI Materials and Methods. Briefly, all surgical and electrophysiological procedures were similar to established protocols (15, 34, 35) and were performed in strict compliance with the protocols cleared by the Institute Animal Ethics Committee of the Indian Institute of Science, Bangalore, India. All neuronal and astrocytic recordings were performed under current-clamp configuration at physiological temperatures (33–35 °C) in 350-µm middle near-horizontal hippocampal slices (Bregma, –6.5 mm to –5.1 mm) from 5- to 11-wk-old male Sprague–Dawley rats. All SEPs were recorded at –70 mV. To characterize SEPs, only the events with ≥1 mV were considered for the analysis. Peak SEP amplitude (e.g., Fig. 4D) refers to the ensemble maximum among all SEPs recorded from the same neuron, during a given period of recording (e.g., PRE vs. POST period in Fig. 4D). Statistical analyses were performed using the R computing package (36) and are presented in Dataset S1 (36). Computational modeling procedures were similar to procedures in ref. 26 and involved a biophysically realistic conductance-based multicompartmental model that was constructed within the NEURON simulation environment (37), using a morphological reconstruction of a CA1 pyramidal neuron (n123) taken from the Neuromorpho.org database (38, 39). Passive and active (five different ion channels: Na, KDR, KA, CaT, and HCN) properties of the model neuron were set to match several somatodendritic measurements from CA1 pyramidal neurons (15–17, 26, 30, 40–42). SEPs were modeled by incorporation and activation of GluN2D- and GluN2B-containing NMDA receptors (29, 43–46), with receptor location spanning the somatoapical dendritic tree.
SI Materials and Methods
Electrophysiological Recordings from Neurons and/or Astrocytes.
Ethical approval.
All experiments were performed in strict compliance with the protocols cleared by the Institute Animal Ethics Committee of the Indian Institute of Science, Bangalore, India.
Surgery and brain slice preparation.
Surgical and electrophysiological procedures used in this study were similar to established protocols (15, 34, 35). To elaborate, 5- to 11-wk-old male Sprague–Dawley rats were anesthetized by intraperitoneal injection of a ketamine–xylazine mixture. After onset of deep anesthesia, assessed by cessation of toe-pinch reflex, transcardial perfusion of ice-cold cutting solution was performed, which contained 2.5 mM KCl, 1.25 mM NaH2PO4, 25 mM NaHCO3, 0.5 mM CaCl2, 7 mM MgCl2, 7 mM dextrose, 3 mM sodium pyruvate, and 200 mM sucrose (pH 7.3, ∼300 mOsm) saturated with 95% O2 and 5% CO2 bubbling. Thereafter the brain was removed quickly and 350-µm-thick near horizontal slices were prepared from middle hippocampi (Bregma, –6.5 mm to –5.1 mm), using a vibrating blade microtome (Leica Vibratome), while submerged in ice-cold cutting solution saturated with 95% O2 and 5% CO2 bubbling. The slices were then incubated for 10 min at 34 °C in a chamber containing the holding solution containing 125 mM NaCl, 2.5 mM KCl, 1.25 mM NaH2PO4, 25 mM NaHCO3, 2 mM CaCl2, 2 mM MgCl2, 10 mM dextrose (pH 7.3, ∼300 mOsm) saturated with 95% O2 and 5% CO2 bubbling. Thereafter the slices were kept in a holding chamber at room temperature for at least 45 min before the start of recordings.
Electrophysiology.
For electrophysiological recordings, slices were transferred to the recording chamber and continuously perfused with artificial cerebrospinal fluid (ACSF/extracellular recording solution) at a flow rate of 4 mL/min. All neuronal and astrocytic recordings were performed under current-clamp configuration at physiological temperatures (33–35 °C), achieved through an inline heater that was part of a closed-loop temperature control system (Harvard Apparatus). The ACSF contained 125 mM NaCl, 3 mM KCl, 1.25 mM NaH2PO4, 25 mM NaHCO3, 2 mM CaCl2, 0 mM MgCl2, 10 mM dextrose (pH 7.3; ∼300 mOsm) saturated with 95% O2 and 5% CO2 bubbling. Slices were visualized under a 63× water immersion objective through a Dodt contrast microscope (Carl Zeiss Axioexaminer). Whole-cell current-clamp recordings were performed from visually identified CA1 pyramidal neuron somata and/or dendrites and/or astrocytes, using Dagan BVC-700A amplifiers. Borosilicate glass electrodes with electrode tip resistance between 4 MΩ and 9 MΩ were pulled (P-97 Flaming/Brown micropipette puller; Sutter) from thick glass capillaries (1.5-mm outer diameter and 0.86-mm inner diameter; Sutter) and used for patch-clamp recordings. The pipette solution contained 120 mM K-gluconate, 20 mM KCl, 10 mM Hepes, 4 mM NaCl, 4 mM Mg-ATP, 0.3 mM Na-GTP, and 7 mM K2-phosphocreatine (pH 7.3 adjusted with KOH, osmolarity ∼300 mOsm). The rationale behind the use of current-clamp recordings was twofold: (i) to directly assess the impact of dendritic VGICs on somatodendritic responses to gliotransmission, which would not be possible with voltage-clamp recordings, and (ii) to avoid the well-established errors in recorded data that are consequent to space-clamp issues with voltage-clamp recordings (21, 47, 48). Additionally, in current-clamp recordings the somatodendritic voltages evolve as a direct consequence of the activation of (and interactions among) receptors, channels, and pumps, without an artificial clamping of voltage, thereby recreating conditions that are conducive to assessing the overall physiological impact of gliotransmission.
For paired astrocyte–neuron experiments, both the electrodes were first positioned above the brain slice after a neuronal soma and a nearby astrocyte were visually identified. The neuron was patched first and the astrocyte was patched after baseline responses were recorded from the neuron (Fig. 4A). The intercellular distance between recorded astrocyte–neuron pairs was 19.5 ± 1.7 µm (mean ± SEM, range 4–42 µm). A two-step procedure of identifying and confirming recordings from astrocytes was used for these experiments. First, putative astrocytes were visually identified by their small cell bodies (<10 µm diameter). Occasionally primary branches were also seen originating from the cell body. Second, after patching such cells, their identity was confirmed by their electrophysiological signatures: hyperpolarized membrane potential at rest (usually between –79 to –75 mV) and the absence of any action potential in response to a short pulse of large depolarizing current injection into the cell (2 nA for 2 ms). This depolarizing current always produced an action potential in all of the neurons tested. Additional confirmation of patched astrocytes came from their low input resistance of 1.9 ± 0.3 MΩ (mean ± SEM, n = 7). All experiments were completed within 2–3 h after slicing. During paired recordings data acquisition consisted of four different epochs (one pre- and three postastrocytic patches, Fig. 4A). Each epoch consisted of 11 consecutive trials of 20 s each.
For dual soma–dendrite recordings, both somatic and dendritic electrodes were lowered to a visually identified somatodendritic pair. The soma was patched first with a glass electrode with a resistance 4–7 MΩ, immediately after which the corresponding dendrite (around 200 µm on the apical trunk from the soma) was patched with an electrode of resistance 6–10 MΩ. The pipette solution was identical for both electrodes and was the same as that mentioned above. It was confirmed that both electrodes were patched onto the same neuron by injecting current pulses (depolarizing and hyperpolarizing) through one of them and assessing voltage recordings obtained from both electrodes. Spontaneous SEPs were then recorded through both electrodes and saved for further analysis.
Acquisition of data for single, dual, and paired recordings was performed using custom-written software in the Igor Pro environment (Wavemetrics) with signals sampled at 10 kHz. All SEP recordings were recorded at –70 mV in the neuron, through hyperpolarizing current injection at the single electrodes or at both electrodes (in dual recordings) patched onto the neurons. Series resistance (Rs) was monitored continuously, by examining the voltage response of the patched neurons to a hyperpolarizing current injection of –150 pA, and was compensated online throughout the course of the experiments. Experiments were discarded only if there were temperature fluctuations or if Rs reached >30 MΩ for somatic or >40 MΩ for dendritic recordings. For dual somatodendritic recordings, the cutoff for dendritic series resistance was relaxed to 45 MΩ.
Pharmacology.
To block all synaptic transmission and the contribution of AMPA/kainate receptors to SEPs, a mixture of 10 µM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) and 1 µM tetrodotoxin (TTX) was used in the extracellular recording solution (Allied Scientific). At the beginning of each experiment, we injected brief, large-amplitude (2 nA) depolarizing pulses to check for cessation of action potential generation, thereby assessing whether the blockade of Na+ channels by TTX was complete. Data recordings were started only after the cessation of action potential generation. To block A-type K+ channels specifically in the recorded neuron, without altering activity in other cells, 20 µM 3,4-Diamonopyridine (3,4–DAP; Sigma) was incorporated in the pipette solution used for neuronal patch-clamp recording (49). Although 3,4–DAP blocks transient potassium channels (50), it is known to block delayed rectifier potassium channels as well (49). Similarly, to block HCN channels without altering network activity, 20 µM 4-Ethylphenylamino-1,2-dimethyl-6-methylaminopyrimidinium chloride (ZD7288; Tocris) was incorporated in the pipette solution used for neuronal patch-clamp recording (15, 35).
To block N-methyl-d-aspartate (NMDA) receptors, 200 µM of d,l-2-amino-5-phosphonovaleric acid (APV; Tocris) was added to the extracellular recording solution. To specifically block only GluN2B-containing NMDARs, 10 µM threo ifenprodil hemitartarate (Tocris) was used in the extracellular recording solution, and to specifically block GluN2C/D-containing NMDARs 10 µM 5-(4-Bromophenyl)-3-(1,2-dihydro-6-methyl-2-oxo-4-phenyl-3-quinolinyl)-4,5-dihydro-g-oxo-1H-pyrazole-1-butanoic acid (DQP1105; Tocris) was used in the extracellular recording solution. Although only 80% of the target receptors are blocked at these concentrations of threo ifenprodil and DQP1105 (51, 52), we chose these concentrations to avoid nonspecific blockade of other isoforms of NMDARs. To elicit release of gliotransmitters from the astrocytes, 10 µM d-myo-inositol trisphosphate (Sigma-Aldrich) was incorporated to the pipette solution used for patching astrocytes (28).
In experiments involving chelation of calcium from the astrocytic syncytium, an astrocyte was patched with an intracellular solution containing 30 mM 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid tetrapotassium salt (tetrapotassium BAPTA; Life technologies), 20 mM KCl, 10 mM Hepes, 4 mM NaCl, 4 mM Mg-ATP, 0.3 mM Na-GTP, and 7 mM K2-phosphocreatine (pH 7.3 adjusted with KOH, osmolarity ∼300 mOsm with sucrose). A nearby neuron was patched 1 h after the astrocytic patch was established, to allow for the spread of BAPTA through the astrocytic syncytium, and spontaneous SEPs were recorded from the neuron.
Data representation, analysis, and measurements.
To characterize SEPs, only the events with amplitude ≥1 mV were considered for the analysis. SEP amplitude was calculated as the maximum membrane potential deflection from rest. Peak SEP amplitude (e.g., Fig. 4D) refers to the ensemble maximum among all SEPs recorded from the same neuron, during a given period of recording (e.g., PRE vs. POST period in Fig. 4D). Specifically, if formed a set of SEP amplitudes recorded from a given cell during a given period, then the peak SEP would be defined as the . Rise time was defined as the duration between 20% and 80% of the SEP amplitude during its rising phase. The full-width at half-maximal (FWHM) amplitude duration was defined as the duration for which the rising and decay phase of SEP was above its half-maximal amplitude. Frequency of SEPs was assessed as the ratio between the SEP count and the recording duration.
Recordings to measure neuronal input resistance (Rin) and resonance frequency (fR) were performed at –65 mV and were similar to established procedures (15, 34). Rin was computed by measuring the deflection in the membrane voltage in response –50 pA to +50 pA current injections (for 700 ms) with an increment of 10 pA. Specifically, the steady-state voltage deflection was plotted against the injected current and Rin was defined as the slope of the straight line fitted to this plot. To measure fR, a sinusoidal current of constant amplitude and linearly increasing frequency from 0.5 Hz to 15 Hz in 15 s (chirp stimulus) was injected into the neuron. The impedance amplitude profile was computed by dividing the Fourier transform of voltage response of the neuron to the chirp stimulus by the Fourier transform of injected current (chirp stimulus). The frequency at which this impedance amplitude profile reached its maximum was defined as the fR.
All data analyses were performed using custom-written software in Igor Pro (Wavemetrics), and statistical analyses were performed using the R computing package (36). To represent the variability in the recorded data and to avoid misleading conclusions by using mean or median (53), all recorded data points are plotted (e.g., Fig. 1C) along with their distributions (e.g., Fig. 1D) to enable accurate data representation. Additionally, whenever data were statistically compared using a parametric test, population mean values are appended to the plots, whereas if data were compared using a nonparametric test population, medians are shown. In certain cases, the mean ± SEM representation (for data already presented in the main figures) is also provided as part of the SI figures (e.g., Fig. S1 for Fig. 1). The specific statistical tests performed and their results (including the exact P values) are tabulated in Dataset S1. Whereas SEP amplitudes, rise times, and FWHM values were compared with ANOVA followed by Student’s t test, SEP frequencies (given lower sample sizes) were compared using their nonparametric equivalents: Kruskal–Wallis test followed by Mann–Whitney test.
Morphologically Realistic Conductance-Based Computational Models.
A biophysically realistic conductance-based multicompartmental model was constructed using a morphological reconstruction of a CA1 pyramidal neuron (n123) taken from the Neuromorpho.org database (38, 39). Passive parameters were set as follows: membrane capacitance, Cm = 1 µF/cm2; specific membrane resistance (Rm) and axial resistivity (Ra) for various compartments along the somato-apical trunk were functions of radial distance of the compartment from the soma, x (15, 54–56),
| [S1] |
| [S2] |
where = 125 kΩ.cm2 and = 120 Ω.cm were values at the soma, and = 85 kΩ.cm2 and = 70 Ω.cm were values assigned to the terminal end of the apical trunk (which was ∼425 µm away from the soma for the reconstruction under consideration). This was done to keep the passive local input resistance (Rin) almost constant throughout the trunk (15). The basal dendrites and the axonal compartments had somatic Rm and Ra. The spatial compartmentalization of the model was done using the dλ rule (37), which ensures that each compartment is smaller than 0.1 λ100, where λ100 is the space constant at 100 Hz for the section under consideration. This yielded a total number of 873 spatial compartments in the model.
Active properties.
We incorporated five different types of voltage-gated ion channels into the model, each modeled using the Hodgkin–Huxley formulation: fast Na+ (NaF), delayed rectifier K+ (KDR), A-type K+ (KA), hyperpolarization-activated cyclic-nucleotide–gated nonspecific-cation (HCN), and T-type Ca2+ (CaT) channels. In doing this, the densities and properties of these channels were specified to account for experimental observations in the hippocampal CA1 pyramidal neurons (16, 17, 30, 41). Specifically, the NaF channel density (when present) was uniform (16 mS/cm2) across all somatodendritic compartments (30) and was increased fivefold in the axon initial segment (57). Axonal compartments other than the axonal initial segment were considered passive. To account for slower recovery from inactivation of dendritic Na+ channels an extra inactivation gate was added to model the channel kinetics for dendritic NaF channels (40, 41). The KDR current density was uniform across the somatodendritic axis (16), with the value set at 10 mS/cm2. Channel kinetics and voltage dependence of KA channels were different for the proximal (≤100 µm from the soma) and distal (>100 µm) compartments (16, 41). KA channel density increased linearly (16, 41) as a function of radial distance of the compartments from the soma (Fig. 8C),
| [S3] |
where was the maximal KA conductance at radial distance x µm from the soma, and was the maximal KA conductance value at the soma with the default set as 3.1 mS/cm2. This gradient was set such that the back-propagating action potential amplitude at a trunk location ∼300 µm from the soma was around 30 mV (Fig. S10C) (16, 41, 42). The basal dendritic compartments had the same density of A-type K+ channels as that of the soma.
The density of HCN conductances followed a sigmoidal gradient along the somatodendritic axis to account for experimentally observed distance-dependent reduction in the input resistance and a concurrent increase in the resonance frequency conferred by these channels (Figs. S1G–H and S10B) (15). This gradient had the functional form (Fig. 8C)
| [S4] |
where was the maximal HCN conductance at radial distance x µm from the soma, and was the maximal conductance value for HCN channel at the soma with a default value of 25 µS/cm2. The basal dendritic compartments had somatic The half-maximal activation voltage of HCN channels also varied along the somatodendritic axis (17). Specifically, in the soma, in basal dendrites and in apical dendritic compartments located at radial distance of <100 µm from the soma, the half-maximal activation voltage was –82 mV. From 100 µm to 300 µm on the apical dendritic region this voltage varied linearly from –82 mV to –90 mV as function of radial distance of the dendritic compartment from the soma. Beyond 300 µm it was –90 mV (15, 17).
The density of CaT channel conductance, when present, followed an increasing gradient along the somatodendritic axis to account for higher density of these channels in the distal dendritic region (30). This gradient had the functional form
| [S5] |
where, was the maximal CaT channel conductance at radial distance x µm from the soma, and was the maximal conductance value at the soma with a default value of 50 µS/cm2.
GluN2D- and GluN2B-specific NMDA receptors.
SEPs were modeled by incorporation and activation of GluN2D- and GluN2B-containing NMDA receptors into the model. Specifically, the canonical NMDAR current was modeled as a combination of three different ionic currents: namely Ca2+, Na+, and K+ through these receptors,
| [S6] |
where
| [S7] |
| [S8] |
| [S9] |
where is the maximum permeability of the NMDAR; and PCa = 10.6, PNa = 1, PK = 1, owing to the permeability of the NMDAR to different ions being PCa:PNa:PK = 10.6:1:1 (58, 59). Default concentrations of the three ionic species were [Na]i = 18 mM, [Na]o = 140 mM, [K]i = 140 mM, [K]o = 5 mM, [Ca]i = 100 × 10−6 mM, [Ca]o = 2 mM. This set the equilibrium potential for Na+ at +55 mV and that for K+ at –90 mV. MgB(v) governs the magnesium dependence of the NMDAR current. GluN1/GluN2A and GluN1/GluN2B NMDAR have very similar half-maximal inhibitory effect concentration (IC50) for Mg2+ (44). Accordingly, MgB(v) for GluN2B-containing NMDAR current was (45)
| [S10] |
GluN1/GluN2D NMDAR has fivefold lower sensitivity for Mg2+ compared with the GluN1/GluN2A heteromer (46). Accordingly, the MgB(v) for these receptors was defined as
| [S11] |
with the default value of [Mg]o set at 2 mM. s(t) governed the kinetics of the NMDAR and had the functional form
| [S12] |
where a is a normalization constant, making sure that 0 ≤ s(t) ≤ 1, td is the decay time constant, and τr is rise time, with τr = 5 ms for both GluN2B- and GluN2D-specific NMDARs. τd was set to 280 ms and 1,660 ms for GluN2B- and GluN2D-containing NMDARs, respectively, based on experimental measurements (43). The distribution of these receptors along the somato-apical dendritic axis was based on the findings from immunohistochemical experiments: GluN2B-containing NMDARs are localized in the perisomatic regions of CA1 hippocampal neurons (29, 60), whereas GluN2D-containing NMDARs are expressed in apical and basal dendrites beyond the perisomatic region (29). As a close approximation of these findings we incorporated GluN2B-containing NMDARs in the perisomatic compartments (<100 µm of radial distance from the soma) and GluN2B-containing NMDARs in the dendritic compartments located beyond 100 µm of radial distance from the soma. For each GluN2B-containing NMDAR its maximal permeability value () was assigned randomly from a uniform distribution spanning 2.5 × 10−8–2.5 × 10−6 cm/s (Fig. 8B). GluN2D-containing NMDAR maximal permeability () increased linearly as a function of radial distance from the soma,
| [S13] |
where was the maximum permeability of a GluN2D-containing NMDAR located in a dendritic compartment at a radial distance of x µm from the soma. The value of for a given GluN2D-containing NMDAR was assigned randomly from a uniform distribution within a range of 1.2 × 10−8 cm/s and 1 × 10−6 cm/s (Fig. 8B). These permeability values and receptor density gradients were chosen to match experimentally observed mean SEP amplitudes across the somatodendritic axis (Figs. 1C and 8D and Fig. S1B).
To replicate our experimental protocol, extracellular [Mg2+] was set to 0 and the resting membrane potential of the model neuron was set to –70 mV. A total of 12 GluN2B-containing and 107 GluN2D-containing NMDAR synapses were inserted into the model. These numbers correspond to the number of geometric sections on the apical trunk and the apical obliques that fell into the distance ranges specified above. One epoch of stimulations involved 119 trials, corresponding to the activation of receptors at each of the 119 compartments, with only one receptor activated per trial. The peak voltage response of the neuron to each activation trial was recorded at all locations along the apical trunk as the SEP amplitude at that location. This protocol was repeated for 10 epochs, each with different sets of randomly chosen permeability values (with ranges mentioned as above). The SEP amplitudes at each trunk location for the activation of each of the 119 trials in the 10 epochs were then used to compute the mean and SEM of SEPs recorded at that location (Fig. 8D).
To calculate the spread of SEPs, for each trial, we divided SEP amplitudes along the somato-apical trunk by the maximal SEP amplitude (across all locations along the somato-apical trunk) for that trial and plotted it as a function of distance from the soma (e.g., Fig. 8G). We defined the spread of this SEP as the area under this normalized curve. A nonattenuated SEP would be at unity across all locations, yielding a spread measure of ∼425 µm, the length of the trunk in the chosen morphology, and compartmentalization of the SEP would result in a reduction in this spread in a manner that is reflective of the amount of attenuation incurred by the SEP. We computed the spread for all 119 locations across all 10 epochs and used the population to compute the average spread for a given channel combination (Fig. 8H). The calculation of SEP amplitude, frequency, and spread was performed under different channel combinations to assess the impact of channel expression on these measurements. In doing this, the randomized pairs of permeability–location were maintained for all 119 locations and 10 epochs, to enable direct pairwise comparisons across different channel combinations.
All simulations were performed in the NEURON simulation environment (37) with an integration time constant of 25 µs. The simulation temperature was set to 34 °C and ion channel kinetics were appropriately adjusted according to their experimentally determined Q10 coefficients. Data analysis was performed using custom-built software in the Igor Pro (Wavemetrics) programming environment.
Supplementary Material
Acknowledgments
The authors thank Dr. Daniel Johnston for helpful discussions and thank members of the cellular neurophysiology laboratory for helpful discussions and for comments on a draft of this manuscript. This work was supported by the Human Frontier Science Program (HFSP) Organization (R.N.), the Department of Biotechnology (R.N.), the Department of Science and Technology (R.N.), and the Indian Institute of Science (R.N. and S.A.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. P.G.H. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1522180113/-/DCSupplemental.
References
- 1.Khakh BS, Sofroniew MV. Diversity of astrocyte functions and phenotypes in neural circuits. Nat Neurosci. 2015;18(7):942–952. doi: 10.1038/nn.4043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Halassa MM, Haydon PG. Integrated brain circuits: astrocytic networks modulate neuronal activity and behavior. Annu Rev Physiol. 2010;72:335–355. doi: 10.1146/annurev-physiol-021909-135843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Araque A, et al. Gliotransmitters travel in time and space. Neuron. 2014;81(4):728–739. doi: 10.1016/j.neuron.2014.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Angulo MC, Kozlov AS, Charpak S, Audinat E. Glutamate released from glial cells synchronizes neuronal activity in the hippocampus. J Neurosci. 2004;24(31):6920–6927. doi: 10.1523/JNEUROSCI.0473-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Araque A, Parpura V, Sanzgiri RP, Haydon PG. Glutamate-dependent astrocyte modulation of synaptic transmission between cultured hippocampal neurons. Eur J Neurosci. 1998;10(6):2129–2142. doi: 10.1046/j.1460-9568.1998.00221.x. [DOI] [PubMed] [Google Scholar]
- 6.Araque A, Sanzgiri RP, Parpura V, Haydon PG. Calcium elevation in astrocytes causes an NMDA receptor-dependent increase in the frequency of miniature synaptic currents in cultured hippocampal neurons. J Neurosci. 1998;18(17):6822–6829. doi: 10.1523/JNEUROSCI.18-17-06822.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fellin T, et al. Neuronal synchrony mediated by astrocytic glutamate through activation of extrasynaptic NMDA receptors. Neuron. 2004;43(5):729–743. doi: 10.1016/j.neuron.2004.08.011. [DOI] [PubMed] [Google Scholar]
- 8.Perea G, Araque A. Properties of synaptically evoked astrocyte calcium signal reveal synaptic information processing by astrocytes. J Neurosci. 2005;25(9):2192–2203. doi: 10.1523/JNEUROSCI.3965-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Perea G, Araque A. Astrocytes potentiate transmitter release at single hippocampal synapses. Science. 2007;317(5841):1083–1086. doi: 10.1126/science.1144640. [DOI] [PubMed] [Google Scholar]
- 10.Megías M, Emri Z, Freund TF, Gulyás AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience. 2001;102(3):527–540. doi: 10.1016/s0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
- 11.Johnston D, Narayanan R. Active dendrites: Colorful wings of the mysterious butterflies. Trends Neurosci. 2008;31(6):309–316. doi: 10.1016/j.tins.2008.03.004. [DOI] [PubMed] [Google Scholar]
- 12.Narayanan R, Johnston D. Functional maps within a single neuron. J Neurophysiol. 2012;108(9):2343–2351. doi: 10.1152/jn.00530.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sjöström PJ, Rancz EA, Roth A, Häusser M. Dendritic excitability and synaptic plasticity. Physiol Rev. 2008;88(2):769–840. doi: 10.1152/physrev.00016.2007. [DOI] [PubMed] [Google Scholar]
- 14.Spruston N. Pyramidal neurons: Dendritic structure and synaptic integration. Nat Rev Neurosci. 2008;9(3):206–221. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]
- 15.Narayanan R, Johnston D. Long-term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron. 2007;56(6):1061–1075. doi: 10.1016/j.neuron.2007.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hoffman DA, Magee JC, Colbert CM, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387(6636):869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- 17.Magee JC. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J Neurosci. 1998;18(19):7613–7624. doi: 10.1523/JNEUROSCI.18-19-07613.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452(7186):436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
- 19.Magee JC. Dendritic integration of excitatory synaptic input. Nat Rev Neurosci. 2000;1(3):181–190. doi: 10.1038/35044552. [DOI] [PubMed] [Google Scholar]
- 20.Magee JC, Johnston D. Synaptic activation of voltage-gated channels in the dendrites of hippocampal pyramidal neurons. Science. 1995;268(5208):301–304. doi: 10.1126/science.7716525. [DOI] [PubMed] [Google Scholar]
- 21.Spruston N, Jaffe DB, Johnston D. Dendritic attenuation of synaptic potentials and currents: The role of passive membrane properties. Trends Neurosci. 1994;17(4):161–166. doi: 10.1016/0166-2236(94)90094-9. [DOI] [PubMed] [Google Scholar]
- 22.Rall W. 1977. Core conductor theory and cable properties of neurons. Handbook of Physiology. The Nervous System. Cellular Biology of Neurons, ed Kandel ER (Am Physiol Soc, Bethesda), Vol 1, pp 39–97.
- 23.Narayanan R, Johnston D. The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci. 2008;28(22):5846–5860. doi: 10.1523/JNEUROSCI.0835-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Das A, Narayanan R. Active dendrites regulate spectral selectivity in location-dependent spike initiation dynamics of hippocampal model neurons. J Neurosci. 2014;34(4):1195–1211. doi: 10.1523/JNEUROSCI.3203-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rathour RK, Narayanan R. Inactivating ion channels augment robustness of subthreshold intrinsic response dynamics to parametric variability in hippocampal model neurons. J Physiol. 2012;590(22):5629–5652. doi: 10.1113/jphysiol.2012.239418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rathour RK, Narayanan R. Homeostasis of functional maps in active dendrites emerges in the absence of individual channelostasis. Proc Natl Acad Sci USA. 2014;111(17):E1787–E1796. doi: 10.1073/pnas.1316599111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shigetomi E, Bowser DN, Sofroniew MV, Khakh BS. Two forms of astrocyte calcium excitability have distinct effects on NMDA receptor-mediated slow inward currents in pyramidal neurons. J Neurosci. 2008;28(26):6659–6663. doi: 10.1523/JNEUROSCI.1717-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kang N, Xu J, Xu Q, Nedergaard M, Kang J. Astrocytic glutamate release-induced transient depolarization and epileptiform discharges in hippocampal CA1 pyramidal neurons. J Neurophysiol. 2005;94(6):4121–4130. doi: 10.1152/jn.00448.2005. [DOI] [PubMed] [Google Scholar]
- 29.Thompson CL, Drewery DL, Atkins HD, Stephenson FA, Chazot PL. Immunohistochemical localization of N-methyl-D-aspartate receptor subunits in the adult murine hippocampal formation: Evidence for a unique role of the NR2D subunit. Brain Res Mol Brain Res. 2002;102(1–2):55–61. doi: 10.1016/s0169-328x(02)00183-3. [DOI] [PubMed] [Google Scholar]
- 30.Magee JC, Johnston D. Characterization of single voltage-gated Na+ and Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. J Physiol. 1995;487(1):67–90. doi: 10.1113/jphysiol.1995.sp020862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Takahashi H, Magee JC. Pathway interactions and synaptic plasticity in the dendritic tuft regions of CA1 pyramidal neurons. Neuron. 2009;62(1):102–111. doi: 10.1016/j.neuron.2009.03.007. [DOI] [PubMed] [Google Scholar]
- 32.Bittner KC, et al. Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nat Neurosci. 2015;18(8):1133–1142. doi: 10.1038/nn.4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sheffield ME, Dombeck DA. The binding solution? Nat Neurosci. 2015;18(8):1060–1062. doi: 10.1038/nn.4075. [DOI] [PubMed] [Google Scholar]
- 34.Ashhad S, Johnston D, Narayanan R. Activation of InsP3 receptors is sufficient for inducing graded intrinsic plasticity in rat hippocampal pyramidal neurons. J Neurophysiol. 2015;113(7):2002–2013. doi: 10.1152/jn.00833.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Narayanan R, Dougherty KJ, Johnston D. Calcium store depletion induces persistent perisomatic increases in the functional density of h channels in hippocampal pyramidal neurons. Neuron. 2010;68(5):921–935. doi: 10.1016/j.neuron.2010.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.R Core Team 2013 A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna). Available at www.R-project.org.
- 37.Carnevale NT, Hines ML. 2006. The NEURON Book (Cambridge Univ Press, Cambridge, UK)
- 38.Pyapali GK, Sik A, Penttonen M, Buzsaki G, Turner DA. Dendritic properties of hippocampal CA1 pyramidal neurons in the rat: Intracellular staining in vivo and in vitro. J Comp Neurol. 1998;391(3):335–352. doi: 10.1002/(sici)1096-9861(19980216)391:3<335::aid-cne4>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 39.Ascoli GA, Donohue DE, Halavi M. NeuroMorpho.Org: A central resource for neuronal morphologies. J Neurosci. 2007;27(35):9247–9251. doi: 10.1523/JNEUROSCI.2055-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Colbert CM, Magee JC, Hoffman DA, Johnston D. Slow recovery from inactivation of Na+ channels underlies the activity-dependent attenuation of dendritic action potentials in hippocampal CA1 pyramidal neurons. J Neurosci. 1997;17(17):6512–6521. doi: 10.1523/JNEUROSCI.17-17-06512.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Migliore M, Hoffman DA, Magee JC, Johnston D. Role of an A-type K+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J Comput Neurosci. 1999;7(1):5–15. doi: 10.1023/a:1008906225285. [DOI] [PubMed] [Google Scholar]
- 42.Spruston N, Schiller Y, Stuart G, Sakmann B. Activity-dependent action potential invasion and calcium influx into hippocampal CA1 dendrites. Science. 1995;268(5208):297–300. doi: 10.1126/science.7716524. [DOI] [PubMed] [Google Scholar]
- 43.Vicini S, et al. Functional and pharmacological differences between recombinant N-methyl-D-aspartate receptors. J Neurophysiol. 1998;79(2):555–566. doi: 10.1152/jn.1998.79.2.555. [DOI] [PubMed] [Google Scholar]
- 44.Liu HT, Hollmann MW, Liu WH, Hoenemann CW, Durieux ME. Modulation of NMDA receptor function by ketamine and magnesium: Part I. Anesth Analg. 2001;92(5):1173–1181. doi: 10.1097/00000539-200105000-00019. [DOI] [PubMed] [Google Scholar]
- 45.Jahr CE, Stevens CF. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990;10(9):3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Qian A, Buller AL, Johnson JW. NR2 subunit-dependence of NMDA receptor channel block by external Mg2+ J Physiol. 2005;562(Pt 2):319–331. doi: 10.1113/jphysiol.2004.076737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Spruston N, Jaffe DB, Williams SH, Johnston D. Voltage- and space-clamp errors associated with the measurement of electrotonically remote synaptic events. J Neurophysiol. 1993;70(2):781–802. doi: 10.1152/jn.1993.70.2.781. [DOI] [PubMed] [Google Scholar]
- 48.Williams SR, Mitchell SJ. Direct measurement of somatic voltage clamp errors in central neurons. Nat Neurosci. 2008;11(7):790–798. doi: 10.1038/nn.2137. [DOI] [PubMed] [Google Scholar]
- 49.Kirsch GE, Narahashi T. 3,4-diaminopyridine. A potent new potassium channel blocker. Biophys J. 1978;22(3):507–512. doi: 10.1016/S0006-3495(78)85503-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Thompson S. Aminopyridine block of transient potassium current. J Gen Physiol. 1982;80(1):1–18. doi: 10.1085/jgp.80.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Acker TM, et al. Mechanism for noncompetitive inhibition by novel GluN2C/D N-methyl-D-aspartate receptor subunit-selective modulators. Mol Pharmacol. 2011;80(5):782–795. doi: 10.1124/mol.111.073239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Avenet P, et al. Antagonist properties of the stereoisomers of ifenprodil at NR1A/NR2A and NR1A/NR2B subtypes of the NMDA receptor expressed in Xenopus oocytes. Eur J Pharmacol. 1996;296(2):209–213. doi: 10.1016/0014-2999(95)00700-8. [DOI] [PubMed] [Google Scholar]
- 53.Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci. 2011;14(2):133–138. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Golding NL, Mickus TJ, Katz Y, Kath WL, Spruston N. Factors mediating powerful voltage attenuation along CA1 pyramidal neuron dendrites. J Physiol. 2005;568(Pt 1):69–82. doi: 10.1113/jphysiol.2005.086793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Poirazi P, Brannon T, Mel BW. Pyramidal neuron as two-layer neural network. Neuron. 2003;37(6):989–999. doi: 10.1016/s0896-6273(03)00149-1. [DOI] [PubMed] [Google Scholar]
- 56.Poirazi P, Brannon T, Mel BW. Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron. 2003;37(6):977–987. doi: 10.1016/s0896-6273(03)00148-x. [DOI] [PubMed] [Google Scholar]
- 57.Fleidervish IA, Lasser-Ross N, Gutnick MJ, Ross WN. Na+ imaging reveals little difference in action potential-evoked Na+ influx between axon and soma. Nat Neurosci. 2010;13(7):852–860. doi: 10.1038/nn.2574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Canavier CC. Sodium dynamics underlying burst firing and putative mechanisms for the regulation of the firing pattern in midbrain dopamine neurons: A computational approach. J Comput Neurosci. 1999;6(1):49–69. doi: 10.1023/a:1008809000182. [DOI] [PubMed] [Google Scholar]
- 59.Mayer ML, Westbrook GL. Permeation and block of N-methyl-D-aspartic acid receptor channels by divalent cations in mouse cultured central neurones. J Physiol. 1987;394:501–527. doi: 10.1113/jphysiol.1987.sp016883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Charton JP, Herkert M, Becker CM, Schröder H. Cellular and subcellular localization of the 2B-subunit of the NMDA receptor in the adult rat telencephalon. Brain Res. 1999;816(2):609–617. doi: 10.1016/s0006-8993(98)01243-8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.