Significance
Big data and, in particular, mobile phone data are expected to revolutionize epidemiology, yet their full potential is still untapped. Here, we take a significant step forward by developing an epidemiological model that accounts for the spatiotemporal patterns of human mobility derived by directly tracking properly anonymized mobile phone users. Such data allow us to investigate, with an unprecedented level of detail, the effect that mass gatherings can have on the spreading of waterborne diseases like cholera. Identifying and understanding transmission hotspots opens the way to the implementation of novel disease control strategies.
Keywords: mobile phone call data, cholera epidemics, spatially explicit epidemiological models, waterborne disease
Abstract
The spatiotemporal evolution of human mobility and the related fluctuations of population density are known to be key drivers of the dynamics of infectious disease outbreaks. These factors are particularly relevant in the case of mass gatherings, which may act as hotspots of disease transmission and spread. Understanding these dynamics, however, is usually limited by the lack of accurate data, especially in developing countries. Mobile phone call data provide a new, first-order source of information that allows the tracking of the evolution of mobility fluxes with high resolution in space and time. Here, we analyze a dataset of mobile phone records of ∼150,000 users in Senegal to extract human mobility fluxes and directly incorporate them into a spatially explicit, dynamic epidemiological framework. Our model, which also takes into account other drivers of disease transmission such as rainfall, is applied to the 2005 cholera outbreak in Senegal, which totaled more than 30,000 reported cases. Our findings highlight the major influence that a mass gathering, which took place during the initial phase of the outbreak, had on the course of the epidemic. Such an effect could not be explained by classic, static approaches describing human mobility. Model results also show how concentrated efforts toward disease control in a transmission hotspot could have an important effect on the large-scale progression of an outbreak.
Human mobility is undisputedly one of the main spreading mechanisms of infectious diseases. Understanding the propagation of an epidemic in a population at any spatial scale of analysis inevitably calls for the understanding of the underlying mobility patterns (1–6). Researchers have commonly focused on infectious diseases transmitted through direct contact between persons (e.g., refs. 1–4). The key role of human mobility has only recently been acknowledged also for water-related diseases (where transmission is mediated by water, which influences the habitat’s suitability for the pathogen and/or its possible intermediate hosts), as highlighted by the development and widespread application of spatially explicit epidemiological models (7–10). Such models translate our comprehension of the mechanisms driving disease transmission [such as rainfall (10)] and spread [such as hydrologic transport of pathogens (8, 11) besides human mobility] into a simplified mathematical form. They may be used not only to predict the spatiotemporal pattern of the spread of a disease (12–14) but also to test alternative model implementations (15), or to evaluate the effects of various interventions on disease dynamics (16–18).
To include population movement in epidemiological models, researchers often rely on approaches such as gravity (e.g., ref. 19) or radiation (20) models, where the fluxes between any two sites are expressed as a function of their relative distance and the embedded population distribution. Such models have primarily been developed and tested for countries in the western world, where transportation networks are dense and efficient, supraregional travel is cheap, and regular commuting patterns are predominant. Lack of data has so far frustrated a thorough validation of such models in the developing world, where mobility drivers and patterns may be different than those of western countries. In some applications, the absence of information about mobility fluxes has been circumvented by inferring the parameters of the mobility model directly from epidemiological data (9, 10, 17). This, however, contributes to increasing uncertainty in model identification because many different factors concur in the spreading of an epidemic. Another important shortcoming of current mobility models is their inability to adapt to seasonal and subseasonal changes in mobility patterns.
With the increasing diffusion of mobile phones, which have become very widely used even in developing countries (21, 22), a new source of information about human mobility has emerged. Each time a phone emits or receives a call or text message, the antenna that the cell phone is logged into is registered by the service provider, along with the time of the event (23). It is thus possible to track the movement of cell phone users as they advance from antenna to antenna. Suitably aggregated and properly anonymized to prevent privacy issues (24), a sample of this data can be used to estimate fluxes of people between areas in a region by assigning a set of antennas to each geographical area in the study domain (e.g., based on administrative boundaries). The resolution in time can be as high as the typical frequency of calls allows, whereas the spatial resolution is limited only by the typical distance between two antennas (23). Using mobile phone records of a sufficiently large number of users, one can thus estimate human mobility fluxes with high accuracy, including spatiotemporal variability across a variety of scales (24), and without resorting to any particular model.
A number of recent studies focus on the use of mobile phone data to extract human mobility patterns in developing countries at different scales in space and time (25–27). Others compare the movement patterns extracted from mobile records to traditional data sources such as censuses (28) and surveys (29). Several studies deal with the comparison with human mobility models (21, 30). In the context of infectious disease spread in developing countries, this new source of information enables previously unseen kinds of analyses. Examples are the derivation of magnitude and destination of population fluxes following a sudden outbreak (25, 31), and the quantification of the importance of human mobility and its seasonal variations on the spread of disease in terms of increased outbreak risk in and infectious pressure on connected areas (5, 30, 32–34).
Mass gatherings, such as pilgrimages, sport events, or music festivals, can be critical in the spread of infectious diseases via various transmission routes (35, 36). When it comes to orofecally transmitted diseases, such as shigellosis (37) or cholera (38, 39), insufficient safe drinking water supply and sanitary infrastructure related to overcrowding are often the main causes of local disease outbreaks and subsequent spread by homecoming infected attendees. To model the effect of mass gatherings, one needs to account for the spatiotemporal dynamics of human mobility and the associated short-term fluctuations of population distribution. Mobility models and static data sources, such as censuses or surveys, are therefore unsuitable. Conversely, mobile phone records contain all required information at the desired timescales and thus represent an excellent new data source for epidemiological models.
Here, we study the cholera epidemic that spread throughout Senegal in 2005. A distinctive feature of this outbreak was its sudden flare. It started from the order of magnitude of hundreds of cases per week during the first 3 mo of the year, localized in the region of Diourbel and surroundings, and abruptly jumped to thousands of cases at the end of March, rapidly spreading to 10 out of 11 regions of the country, with over 27,000 reported cases (Table 1). Anecdotal evidence (38, 40, 41) suggests that this first peak was related to a religious pilgrimage, the Grand Magal de Touba (GMdT), that took place in late March when an estimated 3 million pilgrims traveled to Touba in the region of Diourbel. During later stages, the outbreak evolved, showing distinct dynamics in different regions of the country, rainfall and the associated floods being important drivers, especially in the capital city of Dakar (39).
Table 1.
Regions of Senegal (as of 2005) with their population (2005 estimates), total number of reported cases during the epidemic, cumulative incidence, and mobile phone sample size (relative to 2013 population)
| Region | Population, | Cases | Incidence, ‰ | Sample size, ‰ |
| Dakar | 2.62 | 6,573 | 2.51 | 22.64 |
| Diourbel | 1.22 | 11,772 | 9.61 | 4.11 |
| Fatick | 0.64 | 1,928 | 3.00 | 4.63 |
| Kaolack | 1.06 | 1,014 | 0.96 | 5.19 |
| Kolda | 0.89 | 57 | 0.06 | 3.86 |
| Louga | 0.68 | 1,806 | 2.64 | 5.43 |
| Matam | 0.50 | 0 | 0 | 7.12 |
| Saint-Louis | 0.75 | 1,653 | 2.20 | 8.99 |
| Tambacounda | 0.58 | 87 | 0.15 | 6.11 |
| Thiès | 1.28 | 2,515 | 1.97 | 9.60 |
| Ziguinchor | 0.31 | 124 | 0.40 | 9.79 |
Here we develop a spatially explicit, fully mechanistic model for the 2005 Senegal cholera outbreak, based on previous work (10, 14, 42). In addition to human mobility, we take into account rainfall as an important driver of disease transmission (10, 39), and we incorporate the effect of overcrowding by assuming an increase in exposure and contamination rates caused by unusually high density of people, and the related pressure on water and sanitation infrastructures (Materials and Methods). Daily population fluxes between the 123 arrondissements of Senegal (Fig. S1A) are estimated from a dataset of roughly 150,000 randomly selected mobile phone users tracked during the entire year 2013 (Materials and Methods and ref. 43). We specifically aim at testing the role played by human mobility and mass gatherings in the spread of a cholera epidemic, with implications for disease control.
Fig. S1.
Additional data. (A) Population density (people per square kilometer) per arrondissement in Senegal (2010). Regions (according to the 2005 subdivision) are numbered as follows: Dakar (1), Diourbel (2), Fatick (3), Kaolack (4), Kolda (5), Louga (6), Matam (7), Saint-Louis (8), Tambacounda (9), Thiés (10), and Ziguinchor (11). (B) Daily precipitation depth in 2005 averaged over all arrondissements. (C) Evolution of the total number of moving people (i.e., people leaving their home arrondissement) throughout 2005 according to variants I (blue), II (red), and III (green) (Model Selection). The first spike, present in all variants, corresponds to the GMdT. The four spikes present only in variant 3 correspond to the following events (in chronological order): Gamou de Tivaouane, Magal de Porokhane, Magal de Kazu Rajab, and Magal de Darou Mouhty.
Results
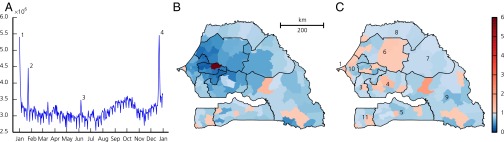
Fig 1 shows the evolution of the estimated number of mobile people (i.e., people having left their home arrondissement on a given day) throughout the year 2013. Seasonal fluctuations, weekly patterns, and sudden peaks can clearly be identified. The latter correspond to mass gatherings, most notably the GMdT [which took place twice in 2013 (Materials and Methods)], and during which the number of people traveling outside their home arrondissement almost doubles with respect to an average day. Fig. 1B shows the estimated fraction of people present in every arrondissement of Senegal during the GMdT. Major differences can be noted with respect to the yearly average (Fig. 1C). People traveled to Touba from all over the country, and the estimated number of people present during the GMdT in the arrondissement where the city is located was nearly 6 times its usual population.
Fig. 1.
(A) Daily evolution of the total number of moving people (i.e., people leaving their home arrondissement) throughout 2013 estimated from mobile phone records. Numbered peaks correspond to the following mass gatherings: GMdT (1 and 4), Gamou de Tivaouane (2), and Magal de Kazu Rajab (3). (B and C) Number of people present in each arrondissement on December 22, 2013, during the GMdT (B) and averaged over the year (C) divided by the number of people living there. Regions (according to the 2005 subdivision; see Supporting Information) are numbered as follows: Dakar (1), Diourbel (2), Fatick (3), Kaolack (4), Kolda (5), Louga (6), Matam (7), Saint-Louis (8), Tambacounda (9), Thiès (10), and Ziguinchor (11).
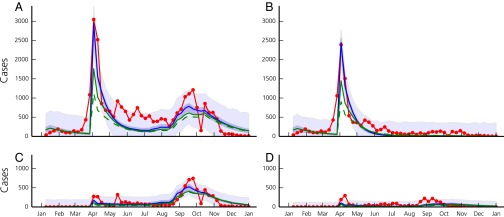
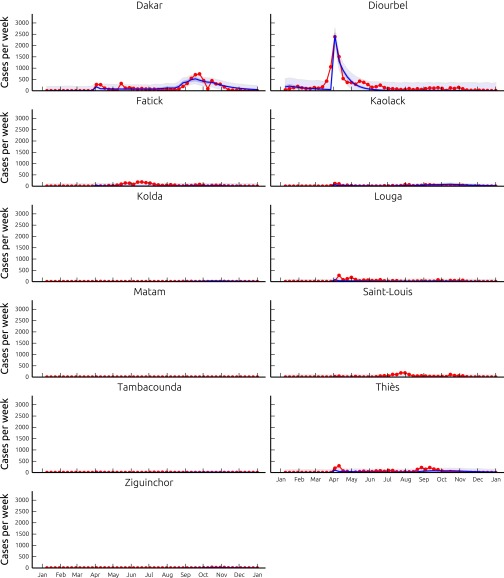
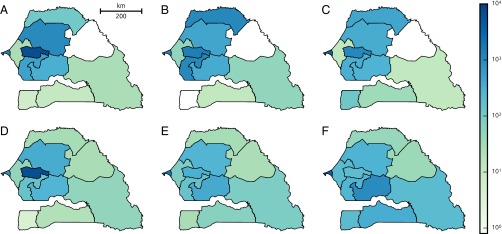
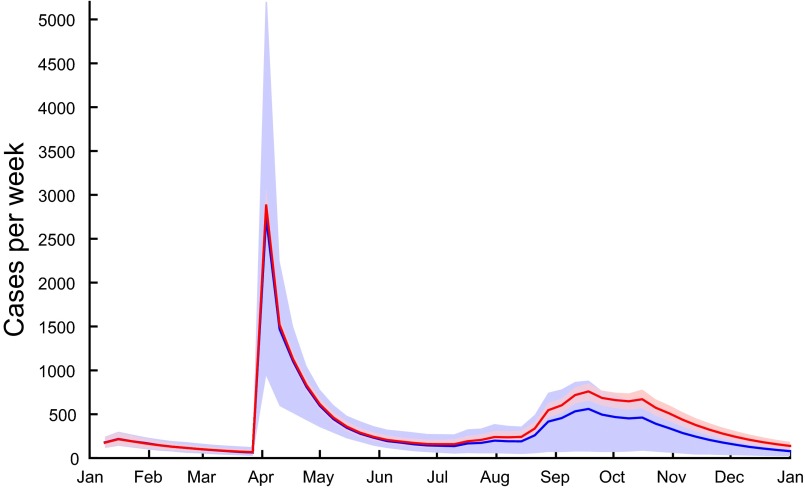
Model results and estimated uncertainties of the best performing model are shown in Fig. 2 (total cases and the regions most severely hit) and Fig. S2 (all regions). The values of the calibrated parameters are reported in Table S1. The model accurately reproduces the important peak of cases in Diourbel coinciding with the GMdT (coefficient of determination between modeled and reported weekly cases in the region of Diourbel) as well as the spread of the disease throughout Senegal by pilgrims returning to their homes. The second peak, most probably related to the rainy season, is also well reproduced ( in the region of Dakar). The overall value of , computed using all data points in all regions, is equal to 0.77. Fig. 3 shows the spatial distribution of cases in the country during the GMdT, and during two other key periods of the outbreak according to the reported cases and to our model.
Fig. 2.
Reported (red line) and modeled number of new cases per week for the entire country of Senegal (A), and for the regions of Diourbel (B), Dakar (C), and Thiès (D). Blue lines correspond to runs of the model (Eqs. 1–4) with the best posterior parameter set. Shaded bands correspond the 2.5–97.5 percentiles of the uncertainty related to parameter estimation (dark blue) and of the total uncertainty assuming Gaussian, homoscedastic error (light blue). Modeled cases under the assumption of a 10% (solid green line) and 20% (dashed green line) reduction in transmission in Touba during the GMdT are also shown.
Fig. S2.
Reported (red line) and modeled (blue line) number of cases per week, resulting from model A run with the best parameter set (Table S1), in the 11 regions of Senegal. Shaded bands show the 2.5–97.5 percentile bounds of the uncertainty related to parameter estimation (dark blue) and of the total uncertainty assuming Gaussian, homoscedastic error (light blue).
Table S1.
Fixed and calibrated parameters of the best performing model (A in Table S2)
| Parameter | Units | Prior | Value | Reference |
| Fixed | ||||
| γ | d−1 | 0.2 | (10) | |
| μ | d−1 | 1/(61×365) | (56) | |
| α | d−1 | 0.004 | (10, 12) | |
| d−1 | 0.2 | (10, 12) | ||
| ρ | d−1 | 1/600 | (52) | |
| β | d−1 | 1 | (10, 11, 57) | |
| Calibrated | ||||
| θ | d−1 | [0, 2] | 0.34 [0.28 0.41] | |
| λ | mm−1 | [0, 1] | 0.049 [0.040 0.061] | |
| σ | – | [0, 0.5] | 0.019 [0.016 0.021] | |
| ω | – | [0, 2] | 0.86 [0.824 0.889] | |
| c | – | [1, 2] | 1.40 [1.375 1.410] | |
| * | – | [1, 500] | 301 [204 416] |
For the calibrated parameters, the 95% confidence intervals of the posterior distribution are also shown.
Initial number of infected in the region of Diourbel equally distributed among arrondissements.
Fig. 3.
Spatial distribution of reported (A−C) and modeled (D−F) cases from March 28 to May 29, the first weeks after the GMdT (A and D), from June 30 to September 4 (B and E), and from September 5 to December 31 (C and F).
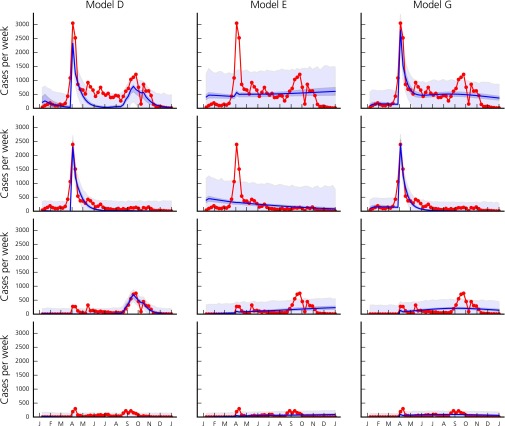
A comparison of different models (Supporting Information and Table S2) shows that the ones including both human mobility fluxes between arrondissements and the effect of overcrowding outperform other models. Including either of the two mechanisms individually, however, is not sufficient to reproduce all features of the epidemic correctly (Fig. S3). In addition, a model adopting a calibrated gravity model performs poorly compared with models using mobile phone data to estimate human mobility. The inclusion of rainfall as a driver of the disease enables our model to capture the autumn peak in addition to the one related to the GMdT (Table S2 and Fig. S3). Finally, it appears that both the correction of bias in mobile phone ownership and the calibration of the initial number of infected in Diourbel improve the model performance.
Table S2.
Comparison of models including different mechanisms (see Model Selection) using the DIC as well as the coefficient of determination R2, computed including weekly case data from all or from one selected region
| Model | Mobility fluxes* | Overcrowding* | Precipitation | Bias correction† | IC‡ | Parameters | Log-likelihood§ | DIC | R2 overall | R2 Dakar | R2 Diourbel | R2 Thiés |
| A | + | + | + | + | c | 6 | −3,256 | 6,533 | 0.77 | 0.72 | 0.78 | 0.20 |
| B | + | + | + | − | c | 5 | −3,328 | 6,669 | 0.71 | 0.68 | 0.69 | 0.41 |
| C | + | + | + | + | d | 5 | −3,279 | 6,573 | 0.75 | 0.73 | 0.75 | 0.04 |
| D | − | + | + | + | a | 6 | −3,308 | 6,631 | 0.72 | 0.71 | 0.75 | −0.47 |
| E | + | − | + | + | c | 5 | −3,595 | 7,204 | 0.25 | 0.10 | 0.08 | −0.02 |
| F | − | − | + | − | a | 4 | −3,641 | 7,295 | 0.12 | 0.60 | −0.19 | 0.31 |
| G | + | + | − | + | c | 5 | −3,302 | 6,615 | 0.73 | 0.22 | 0.81 | 0.13 |
| H¶ | + | + | + | − | c | 7 | −3,459 | 6,943 | 0.54 | −0.50 | 0.73 | −0.50 |
+, Denotes the inclusion of the corresponding mechanism in the model; −, denotes its absence.
Note that human mobility fluxes and overcrowding both depend on human mobility estimates but can be taken into account separately. See Model Selection for more details.
Absence of bias correction with .
Initial number of infected; a, calibrated (all arrondissements); c, calibrated (only Diourbel); and d, fixed (only Diourbel).
Highest log-likelihood value in the posterior sample.
For model H, human mobility has been determined using a gravity model (e.g., ref. 10) instead of deriving it from mobile phone data.
Fig. S3.
Reported (red line) and modeled number of new cases per week for the entire country of Senegal (first row), and for the regions of Diourbel (second row), Dakar (third row), and Thiés (last row) according to models D (first column, not including mobility fluxes), E (second column, not including the overcrowding effect), and G (third column, not including rainfall). Blue lines correspond to model runs with the best posterior parameter set. Shaded bands shown correspond to the 2.5–97.5 percentiles of the uncertainty related to parameter estimation (dark blue) and of the total uncertainty assuming Gaussian, homoscedastic error (light blue).
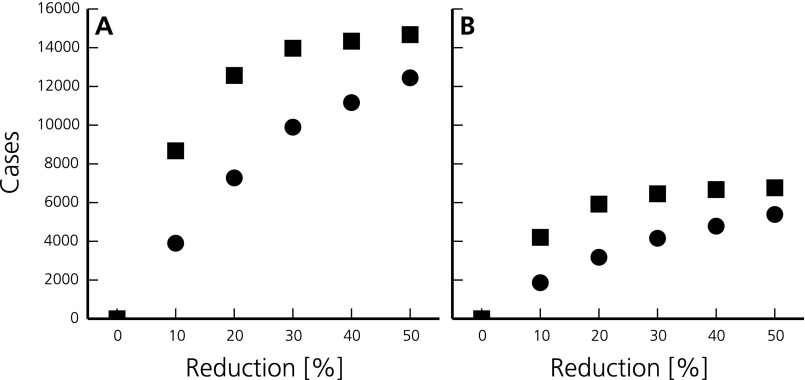
Potential effects of localized interventions in Touba during the GMdT, such as improving sanitation and access to clean drinking water (Materials and Methods), are reported in Fig. 2. Under the assumptions of our model, these actions could have led to considerably lower numbers of new cases during the pilgrimage as well as all over the country during later stages of the outbreak (Supporting Information). For instance, a reduction of the rates of exposure and contamination by 10% (20%) in Touba during the GMdT could have led to a reduction of the total number of cases of 23% (38%) in Diourbel and 18% (34%) in the whole country (Fig. S4 and Table S3).
Fig. S4.
Modeled number of total avoided cases in 2005 overall Senegal (A) and in the region of Diourbel (B) when reducing the rates of exposure to contaminated water and bacterial shedding by a varying percentage in Touba during the GMdT only (10 d, circles) and throughout the year (squares).
Table S3.
Estimated (according to model A) number of cases and percentage of avoided cases in all regions in 2005 when reducing the rates of exposure to contaminated water and bacterial shedding in Touba by 10% or 20% during the GMdT or during the entire year
| Region | Modeled cases | 10% during GMdT | 20% during GMdT | 10% entire year | 20% entire year |
| Dakar | 7,062 | 12 | 21 | 20 | 34 |
| Diourbel | 8,276 | 23 | 38 | 51 | 72 |
| Fatick | 579 | 19 | 41 | 47 | 68 |
| Kaolack | 1,609 | 17 | 41 | 50 | 71 |
| Kolda | 435 | 16 | 47 | 54 | 74 |
| Louga | 940 | 25 | 47 | 53 | 73 |
| Matam | 90 | 28 | 48 | 55 | 74 |
| Saint-Louis | 104 | 28 | 47 | 53 | 69 |
| Tambacounda | 341 | 24 | 47 | 54 | 71 |
| Thiés | 1,802 | 21 | 42 | 45 | 65 |
| Ziguinchor | 229 | 3 | 37 | 46 | 62 |
| Senegal | 21,467 | 18 | 34 | 40 | 59 |
Discussion
The case study of the 2005 Senegal cholera outbreak illustrates the crucial role played by human mobility (and its spatiotemporal variability) in a cholera epidemic whose sudden flare and subsequent spread can be explained by the repercussions of a mass gathering that took place during the initial phase of the outbreak. Indeed, the temporary high density of people in Touba during the pilgrimage and the related pressure on water, sanitation, and health infrastructure are likely to have created favorable conditions for cholera transmission. After the initial peak, homecoming infected pilgrims spread the disease throughout vast parts of the country. No approach to quantify human mobility other than mobile phone data analysis could have provided the required level of detail to capture such phenomena. In addition, the comparison of different models shows that the actual epidemiological dynamic cannot be reproduced accurately without including mobility fluxes and the related effect of overcrowding, nor does the use of a gravity model lead to acceptable results.
The high temporal and spatial resolution of the mobility patterns extracted from mobile phone data allows identification of disease transmission hotspots suggesting intervention strategies to control the evolution of an epidemic, whose expected benefits can be evaluated using epidemiological models. In our case study, concentrated effort to reduce the transmission rate at the mass gathering site, for example, providing safe drinking water or sanitation for a higher number of people, could have had important effects, preventing numerous infections not only locally but throughout the whole country (Supporting Information).
Although our model has a high explanatory power at the whole-country scale and in regions with high cumulative incidence, it does not perform equally well in less affected regions. Although the timing of disease introduction and rainfall-related autumn peaks is well captured in all regions, the simulated temporal evolution of the number of cases deviates from the reported numbers of cases, especially in some of the regions less impacted by the disease. Possible reasons for this include higher influence of demographic stochasticity when the number of infected is low (Supporting Information), but also biased case reporting and/or identification (39) in regions with lower numbers of cases or with low population density (e.g., Matam). Also, one should consider that our likelihood formulation emphasizes peak values because it includes a square error term (Supporting Information).
Even if mobile phone data provide an excellent source of information about human mobility, several downsides still exist. One of them is the strong assumptions (Materials and Methods and ref. 34) made when translating mobile phone records to human mobility patterns, especially considering that they are difficult to validate due to the lack of alternative data sources. Studies comparing different methods and their underlying assumptions would be necessary to determine the sensitivity of the resulting mobility patterns. In addition, a potential source of inaccuracy in the analysis of mobile phone data is the possible presence of a bias in device ownership. A Kenya-based case study (44) has shown that mobile phone owners are more likely to be wealthy, male, and well educated, and that a bias exists between urban and rural populations. Urbanites with higher incomes tend to travel more often and farther, leading to overestimations of frequency and distance of trips (45). In our study, this effect was at least partially addressed by the introduction of a parameter (Materials and Methods) accounting for the underrepresentation of people staying at their home node. The values taken by this parameter during calibration might indeed indicate the presence of a bias, but might also be due to the fact that long-distance human mobility has played a major role in the propagation of the outbreak only during the pilgrimage, whereas local factors, such as precipitation and flooding, might have been more important in later stages. Additional sources of bias could arise from the fact that not all social classes are equally represented among the pilgrims (46), as well as from the uneven coverage of the mobile phone network between different areas of the country.
The reconstruction of the 2005 mobility matrix from that of 2013 (Materials and Methods) is based on the implicit assumption that general mobility patterns on relevant scales did not change significantly between the two years. Although several ways of reconstructing the 2005 mobility matrix have been compared (Supporting Information), their validity cannot be verified, due to the lack of alternative data sources. Among numerous factors that might have influenced mobility patterns is the cholera outbreak itself, which might have led to behavioral change of individuals in 2005, in turn affecting the disease dynamics (3, 42, 47).
In conclusion, we demonstrate that mobile phone records allow for an accurate quantification of spatiotemporal fluctuations in human mobility, whether short term, seasonal, or during rare events such as mass gatherings. The resulting mobility patterns allow for a deeper understanding of epidemiological dynamics. Inclusion in epidemiological models is straightforward and may lead to higher accuracy with respect to other approaches, as human movement patterns can be directly derived from data rather than inferred from models (e.g., gravity or radiation).
Materials and Methods
Mobile Phone Data and Inference of Human Mobility Patterns.
Human mobility has been estimated from a dataset containing the locations of calls and text messages (hereafter calls) made by 146,352 randomly selected users throughout the year 2013 at arrondissement level (Fig. 1 and Table 1). The dataset has been temporarily released by an important Senegalese mobile phone provider, for the D4D-Senegal challenge (43) and can no longer be legally accessed. A record in the dataset consists of an anonymous user identification, a time stamp, and the arrondissement where the call was made. First the home of each user, e.g., the arrondissement where the most calls were made during night hours (1900 to 0700 hours), was determined. Then, for every day t, the quantity was computed as the number of calls made while in arrondissement j by users with home node i divided by the total number of calls made by users with home node i. Under the assumption that the number of phone calls made by a user while in arrondissement j is proportional to the time spent there, the value represents the community-level average fraction of time that users living in arrondissement i spend in arrondissement j during day t. thus represent the fraction of time spent at the home arrondissement (34). The quantity is provided (Datasets S1 and S2) to ensure the reproducibility of the results only. For any other use, a request should be submitted to Orange/Sonatel.
As the Islamic calendar is based on a lunar scheme with 354 d per year, the dates of the pilgrimages change within every Gregorian year. The GMdT, for instance, took place twice in 2013, on January 1 and December 22, whereas, in 2005, it was held just once, on March 29. To develop a model for the 2005 cholera outbreak, it was thus necessary to reconstruct the 2005 mobility matrix accordingly. For the purpose of this study, we averaged the human mobility matrix throughout 2013, excluding only the periods of the two occurrences of the GMdT. We used the resulting mobility matrix for all days in 2005, except for the period of the GMdT (March d), which, in turn, was assigned the mobility of the December 2013 event. Alternative ways of reconstructing the mobility matrix of 2005 from that of 2013, also accounting for seasonal components in the mobility and/or for other pilgrimages, have been tested but were not retained in model selection (Supporting Information, Fig. S1C, and Table S4).
Table S4.
Recalibration of model A using different mobility matrices (Model Selection)
| Mobility matrix | Log-likelihood* | DIC | R2 overall | R2 Dakar | R2 Diourbel | R2 Thiés |
| I | −3,256 | 6,533 | 0.77 | 0.72 | 0.78 | 0.20 |
| II | −3,306 | 6,632 | 0.73 | 0.38 | 0.79 | −0.25 |
| III | −3,267 | 6,559 | 0.76 | 0.74 | 0.77 | 0.15 |
| IV | −3,474 | 6,974 | 0.51 | −0.50 | 0.66 | −0.51 |
| V | −3,579 | 7,229 | 0.30 | −0.49 | 0.32 | −0.51 |
Highest log-likelihood value in the posterior sample.
Spatially Explicit Epidemiological Model.
The spatially explicit epidemiological model used herein builds on previous work (10, 14, 16, 42). The model domain is the country of Senegal, each arrondissement (Fig. S1A, ) being a node i with population (Supporting Information). The population of each node i is subdivided into three compartments, namely susceptibles , infected , and recovered . Every node is considered to have an ambient bacterial concentration of Vibrio cholerae. We thus get the following set of differential equations describing the evolution of state variables (terms and parameters of the equations will be explained hereafter):
| [1] |
| [2] |
| [3] |
| [4] |
where
| [5] |
| [6] |
| [7] |
The population is assumed to be in demographic equilibrium, with per capita birth and natural death rate μ. Equations of different nodes are coupled via the human mobility matrix , which is derived matrix estimated from mobile phone data. To account for a possible underestimation of the number of people staying at their home node due to, e.g., bias in mobile phone ownership (44, 45), we introduce a calibration parameter c that relates the two matrices as follows:
| [8] |
| [9] |
| [10] |
where ensures that rows sum to 1.
Susceptibles living at node i get infected at rate . is the rate at which a person living at node i comes into contact with contaminated water at node j during day t and becomes infected depending on the bacterial concentration through a semisaturation function with parameter K and rate of exposure β. accounts for the effects of the increase in exposure and contamination rate due to the increased population density (overcrowding). This increase is modeled as an exponential function with the exponent composed of parameter ω and the number of people present at the node at time t divided by its actual population. We assume that only a fraction σ of infections are symptomatic. Asymptomatically infected hosts do not significantly contribute to the bacterial load in the environment, nor die of cholera (14, 16, 48), and can thus, for the purpose of the model, be considered recovered immediately. Symptomatically infected people may recover at rate γ or die from cholera-unrelated causes at rate μ or from cholera at rate α, whereas those who recover lose their acquired immunity at rate ρ or die from causes not related to cholera.
Bacteria are shed at rate p by infected present at node i at time t and reach the local environmental compartment, whose size is proportional to the population with a proportionality constant a. The contamination of the environment is increased by local rainfall via parameter λ (10) (Supporting Information), and by overcrowding through the factor . The environmental bacteria population decays with rate . We define . Expressing the system of equations in this term, parameters a and K get absorbed in so that the number of free parameters is reduced by 2.
The model (Eqs. 1–4) was solved numerically. Model outputs are the number of new cases per arrondissement and week, which are upscaled to the regional level for calibration and comparison with reported data (Table 1 and Supporting Information). Six parameters were estimated by using values from the literature, and another six were calibrated (Table S1), including the number of cholera cases present in the region of Diourbel in January 2005 (initial condition). Calibration was done using a method based on Markov chain Monte Carlo (MCMC) (Supporting Information and ref. 49).
To determine relevant processes to be included in the model and to find an appropriate compromise between accuracy and model complexity, hereby preventing overfitting, eight candidate models were compared using the Deviance Information Criterion (DIC) (50). Processes and mechanisms tested for their significance are the coupling of the local models in individual arrondissements through human mobility fluxes, the overcrowding effect, the correction of bias in mobile phone ownership, the inclusion of precipitation, and the calibration of the initial number of infected in Diourbel as a parameter. We also include a model that makes use of a gravity model instead of mobile phone data to determine human mobility. The model presented above (Eqs. 1–4) is selected as the best performing candidate. Descriptions of all other candidate models, as well as results of the model comparison, are reported in Supporting Information. A discrete, stochastic version of the model has also been implemented to verify the validity of the assumption of continuous variables underlying Eqs. 1–4, which proves reasonable (Supporting Information and Fig. S5).
Fig. S5.
Modeled number of new cases per week in the entire country of Senegal according to the continuous (red) and the discrete stochastic (blue) implementations of model A. Red shaded areas correspond to the 2.5–97.5 percentiles of the uncertainty related to the posterior parameter of the continuous model. Blue shaded areas correspond to 2.5–97.5 percentiles over 1,000 model runs using parameter sets drawn from the posterior distribution of the continuous model. Solid lines show the median.
Potential Effects of Local Interventions.
To investigate the potential effects of local interventions, we ran our best fit model with 10% and 20% reduction of the rates of exposure to contaminated water and bacterial shedding. Such reductions are assumed to be concentrated in Touba during the GMdT, and could have been achieved by providing additional drinking water and sanitation facilities to the pilgrims (Supporting Information).
Study Domain and Administrative Subdivision of Senegal
The domain of our study is the country of Senegal, subdivided into 123 arrondissements as of 2013 (Fig. S1). The administrative subdivision of the country changed in 2008; in particular, the number of regions changed from 11 to 14. Epidemiological data refer to the regions as of 2005. To upscale the model output from the 2013 arrondissement scale to that of the epidemiological data, each 2013 arrondissement was assigned to a 2005 region. For 2013 arrondissements belonging to more than one 2005 region, cases were assigned proportionally to the population living in each region.
Data
Mobile Phone Records.
Mobile phone call records belong to a dataset that was released by Orange/Sonatel, an important mobile phone provider in Senegal, for the D4D-Senegal challenge (d4d.orange.com/en, accessed on November 10, 2015) (43). The dataset used herein has been coarse-grained by the provider from antenna to arrondissement level (Study Domain and Administrative Subdivision of Senegal) and contains the arrondissement where 146,352 randomly selected users were located while making calls or sending text messages throughout the year 2013.
Population.
Spatially distributed population estimates for the year 2010 with a resolution of ∼100 m were obtained from AfriPop (www.afripop.org, accessed on November 14, 2014) (51) and spatially aggregated to the 123 arrondissements of Senegal. As the total population of Senegal increased by 15% between 2005 and 2010, an average growth rate per region was computed using official data from the Agence Nationale de la Statistique et de la Démographie (www.ansd.sn, accessed on November 14, 2014), and the population in each arrondissement was adapted accordingly.
Cholera Cases.
Reported cholera case data were obtained from the website of the Senegalese Ministry of Health (39) and from the World Health Organization national office in Dakar.
Precipitation.
Daily remotely acquired precipitation estimates (Climate Prediction Center/Famine Early Warning System Daily Estimates) for the year 2005 with a resolution of ∼0.1° were obtained from the National Oceanic and Atmospheric Administration (www.cpc.ncep.noaa.gov/products/fews/rfe.shtml, accessed on October 14, 2015). They have been spatially averaged over each of the 123 arrondissements.
Initial Conditions
The initial conditions characterize the epidemiological state of the population at the beginning of January 2005. An initial number of cases was assigned to each arrondissement in Diourbel, the region where the first cases were reported, which was either manually fixed (one case per arrondissement) or calibrated (see Parameter Estimation and Table S2). The rest of the population is assumed to be susceptible. We consider that there is no initial immunity, because the last major cholera epidemic in Senegal had occurred in 1996 (38) and thus the period between the two events is much longer than reported immunity duration in endemic settings (52). The initial bacterial concentration is assumed to be in equilibrium with the initial number of infected in absence of mobility: (10, 16).
Parameter Estimation
Although some parameters were assigned using values from the literature (Table S1), others (number depending on the model; Model Selection and Table S2) were calibrated, including the initial number of cases in the region of Diourbel, equally distributed among arrondissements. Model calibration was performed using a parallel implementation of the MCMC method called emcee PT sampler (49), which allows exchange of information among walkers. To explore the largest possible portion of the parameter space, a total of 300 walkers running at three different “temperatures,” which set the probability of accepting jumps to less favorable regions, and starting from the region of a well-performing hand-tuned parameter set were used. We used wide uniform priors (Table S1). The walkers were run up to visual convergence (– iterations), and all but the last iterations were discarded as burn-in.
The models were evaluated against reported numbers of cases in all 11 regions. Weekly cumulative cases were computed from the model using the following equation:
where τ corresponds to the end of the week and is 1 wk. The results were then upscaled from the arrondissement to the regional scale for comparison with reported cases. Model likelihood was computed assuming mutually independent, homoscedastic, and normally distributed residuals (53) across regions.
Model Selection
Processes.
We compared the performance of eight different models with the goal of evaluating the importance of individual processes, namely bias correction, human mobility fluxes, overcrowding, and precipitation. The results are presented in Table S2. We evaluated models that consider mobile phone data to be unbiased () (model B) or with a fixed initial condition (one initial case in each arrondissement of Diourbel, model C). In model D, the mobile phone data are used to determine temporal variations in population distribution due to human mobility, and thus to account for overcrowding, whereas the mobility fluxes between individual arrondissements are not considered. Model E includes mobility fluxes but not the overcrowding. Model F does not take into account human mobility at all. The absence of fluxes in models D and F leads to a de facto uncoupling of the local models, which makes it necessary to calibrate the initial number of cases and equally distribute them among arrondissements. Model G does not take precipitation into account, and Model H adapts the gravity model (see ref. 10 for implementation) instead of mobile phone data to determine human mobility. Fig. S3 shows the modeled cases for models D, E, and G.
Models were compared using the DIC (50, 54) as well as the coefficient of determination. DIC, which allows for the ranking of different models while preventing overfitting, is straightforward to compute from the output of our Bayesian calibration procedure, as it is based on the likelihood values of the posterior distribution. Results show that models including human mobility (to estimate fluxes between arrondissements and/or overcrowding effect) clearly outperform model F, which does not account for those effects. The gravity model does not provide an appropriate description of human mobility for the case of this study. Indeed, model H provides a reasonable fit for the region with the highest number of cases; however, lacking a proper description of spatiotemporal variations of human mobility, it does not correctly capture the spread of the disease to other regions. This also leads to convergence problems and unrealistic posterior parameter values. The overcrowding effect alone leads to a model performing relatively well (model D), which, however, does not correctly reproduce the spread of the epidemic, and which is outcompeted by models accounting also for human mobility fluxes between the arrondissements (models A and B). The bias correction of mobility data leads to a slight improvement in model performance, as does the calibration of the initial number of infected in Diourbel. Interesting insight is provided by the results of model G, implying that the overall results can still be reasonably good without rainfall, but that its addition is necessary to be able to capture the autumn peak in Dakar (among other regions), previously associated with rainfall (39).
Alternative Ways of Reconstructing the Mobility of 2005.
The mobility matrix extracted from the mobile phone records contains information not only about mobility during exceptional events such as the GMdT or other pilgrimages (Fig. 2) but also about seasonal and subseasonal variations of mobility. To exploit this information, and to test if its use leads to improvements in model performance with respect to our baseline mobility matrix presented in Materials and Methods, we compared five alternative mobility matrices by incorporating them into our best performing model (A) and recalibrating the baseline mobility matrix, as presented in the Materials and Methods. For variant I, we averaged the human mobility matrix throughout 2013, excluding only the periods of the two occurrences of the GMdT. We used the resulting mobility matrix for all days in 2005, except for the period of the GMdT ( 3 d), which in turn was assigned the mobility of the GMdT that had taken place in December 2013. The purpose of this mobility matrix is to test if seasonal and subseasonal variations of mobility other than the GMdT should also be considered in our model (instead of assuming constant mobility throughout the year, except from the GMdT). For variant II, we thus first extracted the seasonal signal, defined as the mobility matrix excluding the effect of the GMdT as well as other important and clearly identifiable mobility pulses. We followed the following procedure: (i) exclusion of both editions of the GMdT and replacement by the average mobility of the previous and following weeks; (ii) step i with four other clearly identifiable mobility pulses caused by the following events: Gamou de Tivaouane, Magal de Porokhane, Magal de Kazu Rajab, and Magal de Darou Mouhty; (iii) step i with four irregularities present in the mobility matrix, identified by visual inspection, which might correspond to cell phone network breakdowns or electric power cuts; (iv) application of a 7-d moving average to smooth out the weekly cycle and get a purely seasonal signal, and (v) determination of individual contribution of the GMdT by subtracting the seasonal signal from the original mobility matrix during the period of the event.
The contribution of the GMdT in December 2013 was then added to the seasonal signal during the period of the GMdT 2005 to obtain a mobility matrix for the entire year 2005. Variant III was the same as variant II, except that, in addition to the GMdT, we also added the contribution of four other events (Gamou de Tivaouane, Magal de Porokhane, Magal de Kazu Rajab, and Magal de Darou Mouhty) to the seasonal signal; variant IV was the same as variant I, but without considering the GMdT, e.g., constant mobility throughout the year; and variant V was the same as variant II, but without considering the GMdT, e.g., considering the seasonal variation of mobility only.
Variants IV and V have been included to evaluate if the mobility during the GMdT is essential for our model to perform well. Results of the comparison are shown in Table S4. A comparison of the countrywide number of mobile people every day according to variants I−III is shown in Fig. S1C.
The comparison of model performance under different assumptions about mobility shows that the inclusion of the GMdT in the mobility matrix is crucial for the model to perform well, but that including the baseline seasonality as well as additional but smaller mass gatherings decreases the model’s ability to reproduce the data. This might be due to the fact that the seasonality in 2005 was different from the one in 2013, or that mobility was of high importance only during the GMdT but not during the rest of the year.
Impact of Reduced Transmission During the GMdT
We tested several scenarios to quantify the influence of control measures that could possibly have attenuated the 2005 cholera epidemic. Modeling results suggest Touba as a promising focal point for actions aimed at containing disease spread. Therefore, we focused our attention on interventions localized (in space and/or) time around the GMdT. We assume that by providing additional sanitation facilities and clean drinking water, a reduction of disease transmission through a reduced bacterial shedding rate (parameter θ), also accounting for a reduced contamination of environmental water bodies with fecal matter (16), and through a reduced rate of exposure to contaminated water (parameter β) can be achieved. We run our best performing model reducing both relevant parameters by a varying percentage in Touba either only during the GMdT (10 d) or throughout the year. The resulting numbers of avoided cases are shown in Fig. S4 and Table S4. According to our model, the number of avoided cases increases with the duration of the interventions not only in Diourbel but throughout Senegal. When reducing exposure and contamination only during the GMdT, the number of avoided cases grows less rapidly than when applying the reductions throughout the year, which might be the result of less cases and smaller bacterial population in Touba just before the GMdT.
Effects of Demographic Stochasticity
To investigate the possible effect of demographic stochasticity associated with the discrete nature of the transmission processes, we implemented a discrete stochastic formulation of the model. In particular, we considered all possible discrete events (birth, death, infection, recovery, and immunity loss) and modeled their temporal occurrence using the Gillespie algorithm (55). Bacterial concentration was modeled as a continuous variable. Details on the model implementation can be found in Bertuzzo et al. (14). Fig. S5 compares the results obtained with the continuous and the discrete formulations of model A. For the first half of the year, where the peak related to the pilgrimage occurs, the two formulations produce very similar patterns, with the discrete formulation expectedly exhibiting higher variance among different realizations. During the second half of the year, the number of cases predicted by the discrete model is slightly lower than that according to the continuous one. This difference is due to the fact that, according to the discrete model, the epidemic goes locally extinct during the low phase in some areas, whereas the continuous model predicts a small but positive prevalence of infection instead. With the arrival of rainfall, such areas show a much quicker response in the continuous model than in the discrete one.
The continuous approximation cannot correctly reproduce extinction dynamics. This causes slight discrepancies between the two model formulations. However, the main features of the epidemic remain unaffected by the continuous approximations, and the discrepancies are limited to few areas with a small number of cases. On the other hand, the continuous assumption has significant operational advantages; in particular, it allows the fast simulation of the runs that are needed to calibrate the model and the formal model comparison. Overall, for the specific scope of this study, we deem the continuous approximation reasonable.
Supplementary Material
Acknowledgments
Anonymous mobile phone data were made temporarily available by Orange and Sonatel within the framework of the D4D-Senegal challenge. The authors thank Dr. Malang Coly from the Office of the WHO representation in Dakar for his help in obtaining the cholera case data, and Prof. Renato Casagrandi and Prof. Marino Gatto (Politecnico di Milano) for useful discussions on the analysis of mobile phone data. F.F., E.B., and A.R. acknowledge support from the Swiss National Science Foundation project “Dynamics and controls of large-scale cholera outbreaks” (DYCHO CR23I2 138104).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1522305113/-/DCSupplemental.
References
- 1.Colizza V, Barrat A, Barthélemy M, Vespignani A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc Natl Acad Sci USA. 2006;103(7):2015–2020. doi: 10.1073/pnas.0510525103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Balcan D, et al. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc Natl Acad Sci USA. 2009;106(51):21484–21489. doi: 10.1073/pnas.0906910106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Meloni S, et al. Modeling human mobility responses to the large-scale spreading of infectious diseases. Sci Rep. 2011;1:62. doi: 10.1038/srep00062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bajardi P, et al. Human mobility networks, travel restrictions, and the global spread of 2009 H1N1 pandemic. PLoS One. 2011;6(1):e16591. doi: 10.1371/journal.pone.0016591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wesolowski A, et al. Quantifying the impact of human mobility on malaria. Science. 2012;338(6104):267–270. doi: 10.1126/science.1223467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tizzoni M, et al. On the use of human mobility proxies for modeling epidemics. PLOS Comput Biol. 2014;10(7):e1003716. doi: 10.1371/journal.pcbi.1003716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chao DL, Halloran ME, Longini IM., Jr Vaccination strategies for epidemic cholera in Haiti with implications for the developing world. Proc Natl Acad Sci USA. 2011;108(17):7081–7085. doi: 10.1073/pnas.1102149108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gurarie D, Seto EYW. Connectivity sustains disease transmission in environments with low potential for endemicity: Modelling schistosomiasis with hydrologic and social connectivities. J R Soc Interface. 2009;6(35):495–508. doi: 10.1098/rsif.2008.0265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mari L, et al. Modelling cholera epidemics: The role of waterways, human mobility and sanitation. J R Soc Interface. 2012;9(67):376–388. doi: 10.1098/rsif.2011.0304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rinaldo A, et al. Reassessment of the 2010−2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc Natl Acad Sci USA. 2012;109(17):6602–6607. doi: 10.1073/pnas.1203333109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bertuzzo E, et al. On the space-time evolution of a cholera epidemic. Water Resour Res. 2008;44(1):W01424. [Google Scholar]
- 12.Bertuzzo E, et al. Prediction of the spatial evolution and effects of control measures for the unfolding Haiti cholera outbreak. Geophys Res Lett. 2011;38(6):L06403. [Google Scholar]
- 13.Reiner RC, Jr, et al. Highly localized sensitivity to climate forcing drives endemic cholera in a megacity. Proc Natl Acad Sci USA. 2012;109(6):2033–2036. doi: 10.1073/pnas.1108438109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bertuzzo E, Finger F, Mari L, Gatto M, Rinaldo A. On the probability of extinction of the Haiti cholera epidemic. Stochastic Environ Res Risk Assess. 2014 doi: 10.1007/s00477-014-0906-3. [DOI] [Google Scholar]
- 15.Mari L, et al. On the predictive ability of mechanistic models for the Haitian cholera epidemic. J R Soc Interface. 2015;12(104):20140840. doi: 10.1098/rsif.2014.0840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kühn J, et al. Glucose- but not rice-based oral rehydration therapy enhances the production of virulence determinants in the human pathogen Vibrio cholerae. PLoS Negl Trop Dis. 2014;8(12):e3347. doi: 10.1371/journal.pntd.0003347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tuite AR, et al. Cholera epidemic in Haiti, 2010: Using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann Intern Med. 2011;154(9):593–601. doi: 10.7326/0003-4819-154-9-201105030-00334. [DOI] [PubMed] [Google Scholar]
- 18.Azman AS, et al. Urban cholera transmission hotspots and their implications for reactive vaccination: evidence from Bissau city, Guinea bissau. PLoS Negl Trop Dis. 2012;6(11):e1901. doi: 10.1371/journal.pntd.0001901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Erlander S, Stewart NF. The Gravity Model in Transportation Analysis – Theory and Extensions. VSP Books; Zeist, The Netherlands: 1990. [Google Scholar]
- 20.Simini F, González MC, Maritan A, Barabási A-L. A universal model for mobility and migration patterns. Nature. 2012;484(7392):96–100. doi: 10.1038/nature10856. [DOI] [PubMed] [Google Scholar]
- 21.Palchykov V, Mitrović M, Jo H-H, Saramäki J, Pan RK. Inferring human mobility using communication patterns. Sci Rep. 2014;4:6174. doi: 10.1038/srep06174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wesolowski A, et al. Commentary: Containing the ebola outbreak - the potential and challenge of mobile network data. PLoS Curr. 2014;6:1. doi: 10.1371/currents.outbreaks.0177e7fcf52217b8b634376e2f3efc5e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Candia J, et al. Uncovering individual and collective human dynamics from mobile phone records. J Phys A Math Theor. 2008;41:224015. [Google Scholar]
- 24.de Montjoye Y-A, Hidalgo CA, Verleysen M, Blondel VD. Unique in the crowd: The privacy bounds of human mobility. Sci Rep. 2013;3:1376. doi: 10.1038/srep01376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lu X, Bengtsson L, Holme P. Predictability of population displacement after the 2010 Haiti earthquake. Proc Natl Acad Sci USA. 2012;109(29):11576–11581. doi: 10.1073/pnas.1203882109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lu X, Wetter E, Bharti N, Tatem AJ, Bengtsson L. Approaching the limit of predictability in human mobility. Sci Rep. 2013;3:2923. doi: 10.1038/srep02923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Perkins TA, et al. Theory and data for simulating fine-scale human movement in an urban environment. J R Soc Interface. 2014;11(99):20140642. doi: 10.1098/rsif.2014.0642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wesolowski A, et al. The use of census migration data to approximate human movement patterns across temporal scales. PLoS One. 2013;8(1):e52971. doi: 10.1371/journal.pone.0052971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wesolowski A, et al. Quantifying travel behavior for infectious disease research: A comparison of data from surveys and mobile phones. Sci Rep. 2014;4:5678. doi: 10.1038/srep05678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bengtsson L, et al. Using mobile phone data to predict the spatial spread of cholera. Sci Rep. 2015;5:8923. doi: 10.1038/srep08923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bengtsson L, Lu X, Thorson A, Garfield R, von Schreeb J. Improved response to disasters and outbreaks by tracking population movements with mobile phone network data: A post-earthquake geospatial study in Haiti. PLoS Med. 2011;8(8):e1001083. doi: 10.1371/journal.pmed.1001083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tatem AJ, et al. Integrating rapid risk mapping and mobile phone call record data for strategic malaria elimination planning. Malar J. 2014;13:52. doi: 10.1186/1475-2875-13-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wesolowski A, et al. Quantifying seasonal population fluxes driving rubella transmission dynamics using mobile phone data. Proc Natl Acad Sci USA. 2015;112(35):11114–11119. doi: 10.1073/pnas.1423542112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mari L, et al. Netmob Conference 2015: Data for Development Challenge Senegal. Mass Inst Technol; Cambridge, MA: 2015. Uncovering the impact of human mobility on schistosomiasis via mobile phone data; pp. 71–97. [Google Scholar]
- 35.Abubakar I, et al. Global perspectives for prevention of infectious diseases associated with mass gatherings. Lancet Infect Dis. 2012;12(1):66–74. doi: 10.1016/S1473-3099(11)70246-8. [DOI] [PubMed] [Google Scholar]
- 36.Memish ZA, et al. Mass gathering and globalization of respiratory pathogens during the 2013 Hajj. Clin Microbiol Infect. 2015;21(6):571.e1–571.e8. doi: 10.1016/j.cmi.2015.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wharton M, et al. A large outbreak of antibiotic-resistant shigellosis at a mass gathering. J Infect Dis. 1990;162(6):1324–1328. doi: 10.1093/infdis/162.6.1324. [DOI] [PubMed] [Google Scholar]
- 38.World Health Organization . Cholera Country Profile: Senegal. World Health Org; Geneva: 2008. [Google Scholar]
- 39.de Magny GC, et al. Cholera outbreak in Senegal in 2005: Was climate a factor? PLoS One. 2012;7(8):e44577. doi: 10.1371/journal.pone.0044577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.International Federation of Red Cross and Red Crescent Societies 2007. Senegal: Cholera Final Report (Int Fed Red Cross Red Cresent Soc, Geneva), DREF Bull 05ME020. [DOI] [PubMed]
- 41.Echenberg M. Africa in the Time of Cholera: A History of Pandemics from 1817 to the Present. Cambridge Univ Press; Cambridge, UK: 2011. [Google Scholar]
- 42.Mari L, et al. On the role of human mobility in the spread of cholera epidemics: Towards an epidemiological movement ecology. Ecohydrology. 2012;5(5):531–540. [Google Scholar]
- 43.de Montjoye Y-A, Smoreda Z, Trinquart R, Ziemlicki C, Blondel VD. 2014. D4D-Senegal: The second mobile phone data for development challenge, arXiv:1407:4885.
- 44.Wesolowski A, Eagle N, Noor AM, Snow RW, Buckee CO. Heterogeneous mobile phone ownership and usage patterns in Kenya. PLoS One. 2012;7(4):e35319. doi: 10.1371/journal.pone.0035319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wesolowski A, Eagle N, Noor AM, Snow RW, Buckee CO. The impact of biases in mobile phone ownership on estimates of human mobility. J R Soc Interface. 2013;10(81):20120986. doi: 10.1098/rsif.2012.0986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Boone C. Political Topographies of the African State: Territorial Authority and Institutional Choice. Cambridge Univ Press; Cambridge, UK: 2003. [Google Scholar]
- 47.Funk S, Salathé M, Jansen VAA. Modelling the influence of human behaviour on the spread of infectious diseases: A review. J R Soc Interface. 2010;7(50):1247–1256. doi: 10.1098/rsif.2010.0142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.King AA, Ionides EL, Pascual M, Bouma MJ. Inapparent infections and cholera dynamics. Nature. 2008;454(7206):877–880. doi: 10.1038/nature07084. [DOI] [PubMed] [Google Scholar]
- 49.Foreman-Mackey D, Hogg DW, Lang D, Goodman J. emcee: the MCMC hammer. Publ Astron Soc Pac. 2013;125(925):306–312. [Google Scholar]
- 50.Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A. Bayesian measures of model complexity and fit. J R Stat Soc Ser A Stat Soc. 2002;64(4):583–639. [Google Scholar]
- 51.Linard C, Gilbert M, Snow RW, Noor AM, Tatem AJ. Population distribution, settlement patterns and accessibility across Africa in 2010. PLoS One. 2012;7(2):e31743. doi: 10.1371/journal.pone.0031743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Koelle K, Rodó X, Pascual M, Yunus M, Mostafa G. Refractory periods and climate forcing in cholera dynamics. Nature. 2005;436(7051):696–700. doi: 10.1038/nature03820. [DOI] [PubMed] [Google Scholar]
- 53.Sorooshian S, Dracup JA. Stochastic parameter estimation procedures for hydrologie rainfall-runoff models: Correlated and heteroscedastic error cases. Water Resour Res. 1980;16(2):430–442. [Google Scholar]
- 54.Gelman A, Carlin J, Stern H, Rubin D. Bayesian Data Analysis. 2nd Ed CRC Press; Boca Raton, FL: 2003. [Google Scholar]
- 55.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81(25):2340–2361. [Google Scholar]
- 56.Central Intelligence Agency . The World Factbook 2013-14. Central Intell Agency; Washington, DC: 2013. [Google Scholar]
- 57.Codeço CT. Endemic and epidemic dynamics of cholera: The role of the aquatic reservoir. BMC Infect Dis. 2001;1:1. doi: 10.1186/1471-2334-1-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.