Abstract
Estimation of a parameter of interest from image data represents a task that is commonly carried out in single molecule microscopy data analysis. The determination of the positional coordinates of a molecule from its image, for example, forms the basis of standard applications such as single molecule tracking and localization-based superresolution image reconstruction. Assuming that the estimator used recovers, on average, the true value of the parameter, its accuracy, or standard deviation, is then at best equal to the square root of the Cramér-Rao lower bound. The Cramér-Rao lower bound can therefore be used as a benchmark in the evaluation of the accuracy of an estimator. Additionally, as its value can be computed and assessed for different experimental settings, it is useful as an experimental design tool. This tutorial demonstrates a mathematical framework that has been specifically developed to calculate the Cramér-Rao lower bound for estimation problems in single molecule microscopy and, more broadly, fluorescence microscopy. The material includes a presentation of the photon detection process that underlies all image data, various image data models that describe images acquired with different detector types, and Fisher information expressions that are necessary for the calculation of the lower bound. Throughout the tutorial, examples involving concrete estimation problems are used to illustrate the effects of various factors on the accuracy of parameter estimation, and more generally, to demonstrate the flexibility of the mathematical framework.
1. INTRODUCTION
Single molecule microscopy [1, 2] is a powerful technique that has enabled the study of biological processes at the level of individual molecules using the fluorescence microscope. The technique is achieved through the use of a suitable fluorophore to label the molecule of interest, an appropriate light source to excite the fluorophore, a properly designed microscope system to capture the fluorescence emitted by the fluorophore while minimizing the collection of extraneous light, and a quantum-efficient detector to record the fluorescence. Using experimental setups built to this high-level specification, researchers have gained significant insight into dynamic processes in living cells by observing and analyzing the behavior of individual molecules of interest [3–9].
An important aspect of quantitative data analysis in single molecule microscopy is the estimation of parameters of interest from the acquired images. Perhaps the most prominent of examples is the estimation of the positional coordinates of a molecule of interest [10, 11]. By estimating the position of a moving molecule in each image of a time sequence, the complex motion revealed by the resulting trajectory has contributed to the elucidation of biological processes at the molecular level [3, 4, 7–9]. Estimating the position of a molecule also represents a crucial step in the localization-based superresolution reconstruction of subcellular structures [12–15], since the high-resolution image of a structure is generated from the positional coordinates of individual fluorophores that label the structure.
Regardless of the particular application, it is desirable that the estimator of a given parameter is unbiased, meaning that on average it recovers the true value of the parameter. Moreover, it is desirable that the estimator recovers the true value with high accuracy, in the sense that estimates of the parameter obtained from repeat images of the same scene can be expected to have a distribution about the true value that is characterized by a small standard deviation. Both unbiasedness and accuracy are important [16–18], since analysis based on values returned by a biased and/or inaccurate estimator can lead to misrepresentations of the biological process or structure being investigated [19, 20].
This tutorial deals with the accuracy of parameter estimation in single molecule microscopy, specifically addressing how one can calculate, for a given parameter, a lower bound on the standard deviation with which it can be determined by any unbiased estimator. This lower bound, which is also referred to as the limit of the accuracy [21, 22] with which the parameter can be estimated, is a practically useful quantity in two ways. First, it serves as a benchmark against which the standard deviation of a particular estimator can be evaluated, indicating how much room there might be for improvement. Second, by calculating and assessing its value under different experimental settings, the limit of accuracy can be used to design an experiment that will generate image data from which a parameter of interest can be estimated with the desired standard deviation.
The objective of the tutorial is to demonstrate how the information theory-based mathematical framework developed in [21, 22] can be used to calculate a limit of accuracy. This framework is characterized by its generality, in the sense that as it makes no assumptions about problem-specific details such as the parameters to be estimated, the mathematical description of the image of an object of interest, and the type of detector that is used to capture the image, it can be used with appropriate specifications of such details to calculate limits of accuracy for a wide variety of estimation problems. Originally illustrated with limits of accuracy calculated for the estimation of the positional coordinates of an in-focus molecule that is imaged by a charge-coupled device (CCD) detector [21, 22], the framework has subsequently been utilized, for example, to compute limits of accuracy for the localization of an out-of-focus molecule [8, 23, 24], the determination of the distance separating two molecules [25, 26], and the estimation of parameters from image data produced by an electron-multiplying CCD (EMCCD) detector [27].
The limit of the accuracy for estimating a parameter is given by the square root of the Cramér-Rao lower bound [28, 29] on the variance with which the parameter can be determined by any unbiased estimator. The Cramér-Rao lower bound is a well-known result from estimation theory, and its calculation requires a stochastic description of the data from which the parameter of interest is to be estimated, and the computation of the Fisher information matrix [28, 29] corresponding to the data description. The Fisher information matrix is essentially a quantity that provides a measure of the amount of information that the acquired data contains about the parameter that one wishes to estimate from the data. The greater the amount of information that the data carries about the parameter, the higher the accuracy (i.e., the smaller the standard deviation) with which the parameter can be estimated. The amount of information is determined by considering how the likelihood of observing the acquired data, which is stochastic in nature, changes with the value of the parameter of interest. If the likelihood of the data does not vary significantly with the value of the parameter, then the data contains relatively little information about the parameter. On the other hand, if the likelihood of the data is very sensitive to changes in the value of the parameter, then the data carries a relatively large amount of information about the parameter and will allow it to be estimated with relatively high accuracy. Given the Fisher information matrix, the Cramér-Rao lower bound corresponding to the parameter of interest is obtained through the inverse of the matrix, reflecting the expectation that a larger amount of information about the parameter should result in a smaller bound on the variance with which the parameter can be estimated.
The mathematical framework of [21, 22] essentially provides the foundation for calculating the Fisher information matrix pertaining to image data generated by single molecule microscopy and, more generally, fluorescence microscopy, experiments. Since the introduction of the framework, the use of Fisher information-based limits of accuracy has become prevalent in the field of single molecule microscopy. Different groups have, for example, computed Fisher information-based limits of accuracy for molecule localization involving different point spread functions that describe the image of the molecule [20, 30– 35], for the estimation of the orientation of a fluorescent dipole emitter [33, 35–37], and for the determination of the diffusion coefficient based on the recorded trajectory of a molecule [38, 39]. A method has also been demonstrated that generates information-rich point spread functions via the optimization of limits of the localization accuracy [40].
Note that in the context of the localization of a molecule, another commonly used benchmark for assessing the accuracy of an estimator is described in [41]. This accuracy benchmark does not make use of Fisher information, and is derived based on the least squares minimization of errors. It has been adapted in various ways [42, 43], such as for the localization of a molecule from image data produced by an EMCCD detector. A similar accuracy benchmark [44] has also been derived that takes into account the effect of the diffusional movement of the molecule to be localized. For a comparison of the benchmark of [41] and the Fisher information-based limit of the localization accuracy, see [17].
A limit of accuracy is computed for a specific experimental setting and a specific estimation problem. It is therefore a quantity that depends on a multitude of factors, including the value of the parameter of interest itself (e.g., the value of a molecule’s positional coordinate, or the value of the distance separating two molecules), the number of photons detected from the object of interest, the number of photons detected from a background component, the wavelength of the detected photons, the numerical aperture of the objective lens used to collect the photons, the lateral magnification of the microscopy system, the pixel size of the detector used to capture the image, the type and amount of noise introduced by the detector, and even the size of the pixel array from which the parameter of interest is estimated. Importantly, a limit of accuracy also depends, as alluded to above, on the mathematical description of the image of the object of interest, which should in principle mirror reality as closely as possible. In the case of a single molecule, for example, a point spread function should be used that appropriately models the observed image of the molecule. Its dependence on many details makes the limit of accuracy a valuable tool for experimental design, since one can determine the effect of a particular experimental parameter or a particular attribute of the object of interest by computing the limit of accuracy for different values of the parameter or attribute. At the same time, it makes it a difficult task to fully illustrate the effect of any one experimental parameter or any one object attribute, given that the effect of a parameter or attribute typically has to be considered in combination with the values of the other parameters and attributes. This tutorial will nevertheless attempt to provide a relatively comprehensive view and discussion of the general effects of various parameters and attributes, and in doing so, demonstrate the flexibility of the mathematical framework which enables the investigation of these effects in the context of different estimation problems. With an aim towards accessibility, emphasis will be placed on the usage rather than the more technical aspects of the mathematical framework. For a rigorous treatment of the framework, the reader is referred to [22].
The tutorial is organized as follows. In Section 2, the modeling of the photon detection process that underlies all fluorescence microscopy image data is described. In Section 3, different image data models are presented that correspond to different detector types, including ones that represent the commonly used CCD [45], EMCCD [46, 47], and complementary metal-oxide-semiconductor (CMOS) [48, 49] detectors. In Section 4, Fisher information expressions corresponding to different image data models are presented, and limits of accuracy computed using these expressions are used to illustrate the effects of factors such as the detected photon count, the effective pixel size of the acquired image, and detector noise. In Section 5, the computation of limits of accuracy is extended to the case where a parameter of interest is estimated from data that comprises multiple images. Throughout the tutorial, the commonly encountered estimation problem of single molecule localization is used as the primary example for illustrative purposes.
2. MODELING OF PHOTON DETECTION
Before the limit of the accuracy for estimating a parameter can be calculated, a mathematical description of the acquired image data is needed. Different image data models, both hypothetical and practical, can be obtained based on assumptions made about the nature of the image detector and the noise sources that corrupt the photon signal detected from the object of interest. All image data models, however, are built upon the same description of the underlying process by which photons are detected from the object of interest. Therefore, before delving into the different data models for which limits of accuracy can be calculated, it is necessary to consider this photon detection process.
A. Photon detection as a spatio-temporal random process
The detection of a photon is intrinsically random in terms of both the time and the location on the detector at which the photon is detected. As photon emission by a fluorescent object is typically assumed to follow a Poisson process, the temporal component of the detection of the emitted photons is accordingly assumed to be a Poisson process. The intensity function that characterizes this Poisson process is referred to as the photon detection rate [22], and is given generally by the function of time Λθ (τ), τ ≥ t0, where t0 ∈ ℝ is some arbitrary time point, and θ ∈ Θ is the vector of parameters to be estimated from the resulting image data, with Θ denoting the parameter space. A specific definition of Λθ might, for example, be an exponential decay function that models the photobleaching of the object of interest, or a constant function when the object has relatively high photostability. It is understood that in its definition, Λθ takes into account the loss of photons as determined by the optical efficiency of the imaging setup’s detection system, which comprises the microscope’s detection optics and the image detector. Alternatively, Λθ can be equivalently expressed in terms of the object’s photon emission rate and an explicit optical efficiency parameter [21].
Note that throughout this tutorial, the subscript θ is used to denote the fact that the given function or random variable can in general depend on the vector θ of parameters to be estimated. In the case of a function, this simply means that the function is potentially expressed in terms of parameters that are to be estimated from the image data. For example, in the case where the photon detection rate Λθ is modeled with an exponential decay function, the decay constant might be a parameter of interest that is included in θ. In the case where it is modeled with a constant function, the constant detection rate itself might be a parameter of interest and therefore a component of θ. For the purposes and illustrations in this section and Section 3, a precise definition for θ is not critical so long as it is understood that the given function or random variable depends on θ. A precise definition becomes crucial in the illustrations of Sections 4 and 5, however, as the calculation of limits of accuracy requires that a Fisher information matrix is derived for a specifically defined θ. Note also that in the specific examples of Sections 4 and 5, the subscript θ will be dropped from the notation for functions such as Λθ without further explanation whenever the function does not depend on θ as defined for the given estimation problem.
The spatial component of the photon detection process is specified by a two-dimensional (2D) probability density function that describes the distribution of the location at which a photon emitted by the object of interest is detected. Referred to as a photon distribution profile [22], this density function is given generally by fθ,τ(x, y), (x, y) ∈ ℝ2, θ ∈ Θ, τ ≥ t0, where the dependence on τ denotes that, in general, the spatial density of photon detection varies with time, as in the case of a moving object of interest. To use more accurate language, fθ,τ as given here specifies the distribution at time τ of the location at which a photon is detected only in the case of a detector with an infinitely large detection area. When the detector has a finite detection area, fθ,τ specifies the distribution at time τ of the location at which a photon impacts the detector plane, since in this case, only a photon that falls within the finite detection area is actually detected.
The specific definition of fθ,τ is based on the image of the object of interest as observed using the imaging setup. By the typical approximation of the optical microscope as a laterally shift-invariant system [50], fθ,τ has the form
| (1) |
(x, y) ∈ ℝ2, θ ∈ Θ, τ ≥ t0, where M > 0 is the lateral magnification of the imaging setup, (x0,τ, y0,τ, z0,τ) are the object space positional coordinates of the object at time τ, and qz0 (x, y), (x, y) ∈ ℝ2, z0 ∈ ℝ, is a function that describes, at unit lateral magnification, the image of the object in the detector plane when the object is located at (0, 0, z0) in the object space. The function qz0 is referred to as an image function [22], and has the additional property that it integrates to one over ℝ2. By the assumption of lateral shift invariance, the photon distribution profile is thus a scaled and laterally shifted version of the object’s unmagnified image when the object is laterally located at the origin of the object space coordinate system.
The image function qz0 can in principle be defined for any type of object, typically as the convolution of the object with the point spread function of the microscope. In [51], for example, such a definition is given for the image function of a fluorescent microsphere. For a point-like object such as a single fluorescent protein or dye molecule, the image function is usually given by just the point spread function itself. A typical image function for an in-focus molecule is the Airy pattern from optical diffraction theory [52]. Dropping the subscript z0 from the notation as the in-focus condition confines the molecule to the microscope’s focal plane, the Airy pattern image function can be written as
| (2) |
where J1 is the first order Bessel function of the first kind, na is the numerical aperture of the objective lens, and λ is the wavelength of the photons detected from the molecule. Another commonly used point spread function model for the in-focus scenario is the 2D Gaussian function [16, 41, 53, 54], and the corresponding image function is given by
| (3) |
where σg > 0 is the standard deviation of the component one-dimensional Gaussian function in both the x and y directions.
For the out-of-focus scenario, the image function is given instead by a three-dimensional (3D) point spread function. The image function corresponding to the classical point spread function of Born and Wolf [52], for example, can be written as
| (4) |
(x, y) ∈ ℝ2, z0 ∈ ℝ, where J0 is the zeroth order Bessel function of the first kind, na and λ are as defined in Eq. (2), and n is the refractive index of the objective lens immersion medium.
Note that the temporal and spatial components of the photon detection process are assumed to be mutually independent. Moreover, in the spatial component, the locations at which photons impact the detector plane are assumed to be mutually independent.
B. Superposition of independent photon detection processes
The spatio-temporal random process described in Section 2.A pertains to the detection of photons from a single object of interest. The formalism, however, can be extended in a straightforward manner to include the simultaneous but independent detection of photons from other sources, such as a second object of interest or a background component like the autofluorescence of a cellular sample. Given two independent photon detection processes characterized by the photon detection rates and and photon distribution profiles and , τ ≥ t0, their superposition [22] is simply the photon detection process with photon detection rate
| (5) |
and photon distribution profile
| (6) |
(x, y) ∈ ℝ2, θ ∈ Θ, τ ≥ t0. To give a more specific example for fθ,τ, suppose photons are detected from two in-focus and stationary objects of interest located at (x01, y01) and (x02, y02). Using the expression of Eq. (1) without the dependence on time and z location for both and in Eq. (6), the resulting photon distribution profile for the superposition of the two photon detection processes is given by
| (7) |
(x, y) ∈ ℝ2, θ ∈ Θ, τ ≥ t0, where q1 and q2 are the image functions for the two objects.
3. IMAGE DATA MODELS
Building on the mathematical description of the photon detection process in Section 2, image data models can be obtained that differ in terms of the size of the detector, whether the detector is pixelated, and the types of noise that the detector introduces. The models can also differ in terms of whether a background component exists that introduces additional noise to the acquired data. Many different models are possible by taking different combinations of detector attributes and noise sources. However, they can be subsumed under four main models, namely the fundamental data model, the Poisson data model, the CCD/CMOS data model, and the EMCCD data model. The first two models are hypothetical in nature as they assume the use of detectors that do not exist. As will be seen in Section 4, however, they are extremely useful in that they represent ideal imaging scenarios against which the practical imaging scenarios represented by the CCD/CMOS and EMCCD data models can be compared.
A. Fundamental data model
The fundamental data model describes image data that is acquired under the most ideal of imaging scenarios. It assumes the use of an image detector that has an unpixelated and infinitely large photon detection area. The absence of pixelation means that the location at which a photon is detected is recorded with an arbitrarily high precision, and the infinitely large area ensures that no photon is undetected by virtue of impacting the detector plane at a location outside of the detector. The fundamental data model further assumes that the detector does not introduce noise of any kind, and that there is no background component. Therefore, the photon signal detected from the object(s) of interest is not in any way corrupted by noise.
In the fundamental data model, the data acquired over the time interval [t0, t] consists of the time points of detection {τ1, …, τN0} and the locations of detection {(x1, y1), …, (xN0, yN0)} of the N0 photons that are detected during the interval. As presented in Section 2.A, the time points are distributed according to the Poisson process with intensity function Λθ (τ), τ ≥ t0, θ ∈ Θ, and for k = 1, 2, …, N0, the positional coordinate pair (xk, yk) is a realization of the bivariate random variable distributed according to the spatial density function fθ,τk (x, y), (x, y) ∈ ℝ2, θ ∈ Θ, τ ≥ t0.
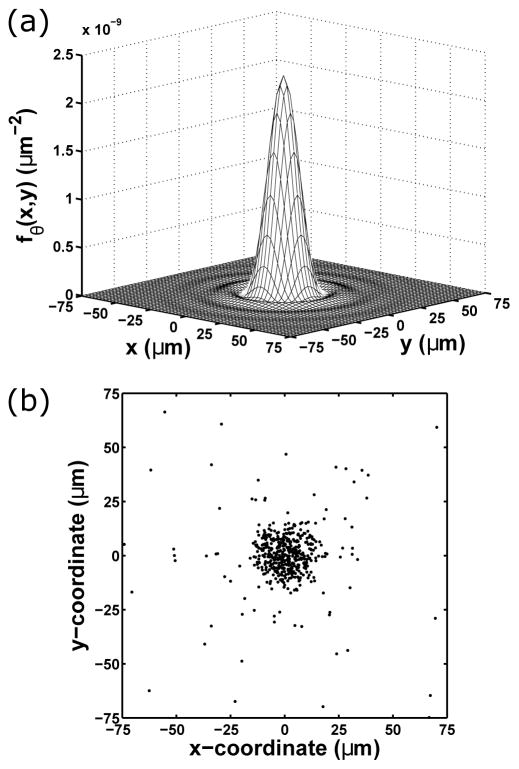
For a concrete example of a fundamental image, consider the relatively simple case in which the positional coordinates of a stationary molecule are to be estimated. In this specific scenario, the time points of photon detection need not be simulated as they do not play a role in the estimation of the molecule’s positional coordinates. Instead, only the number of detected photons, N0, needs to be determined as a realization of the Poisson random variable with mean . The location of each of the N0 photons is then generated as a realization of the bivariate random variable with probability density fθ given by fθ,τ of Eq. (1) without the dependence on time τ. Assuming the molecule to be in-focus and to have an image described by the Airy pattern of Eq. (2), an example of fθ is shown in Fig. 1(a), and an image simulated as described is shown in Fig. 1(b). For the simulation, the photon detection rate is assumed to be a constant function Λθ (τ) = Λ0, τ ≥ t0, where Λ0 is a positive constant.
Fig. 1.
Fundamental data model example. (a) The photon distribution profile fθ for an in-focus and stationary molecule whose image is modeled with the Airy pattern. This profile assumes that the molecule is located at (x0, y0) = (0 nm, 0 nm) in the object space, and that photons of wavelength λ = 520 nm are collected using an objective lens with a numerical aperture of na = 1.4 and a magnification of M = 100. While the profile is defined over the detector plane ℝ2, the plot shows its values over the 150 μm × 150 μm region over which it is centered. (b) A fundamental image simulated according to the profile in (a), with each dot representing the location at which a photon is detected. The simulation assumes a constant photon detection rate of Λ0 = 10000 photons/s and an acquisition time of t − t0 = 0.05 s, such that the mean photon count in an image is Λ0 · (t − t0) = 500. In this particular realization, N0 = 516 photons are detected, of which 492 fall within the 150 μm × 150 μm region shown, over which the image is centered.
The most important property that distinguishes the fundamental data model from the data models that follow is the assumption of an unpixelated detection area that allows the locations of the detected photons to be recorded with arbitrarily high precision. All variations of the fundamental data model will therefore retain this property. A variation can be obtained, for example, by introducing a background component using the superposition property described in Section 2.B, or by imposing a finite photon detection area. Variations of the fundamental data model will be used in Section 4 to help illustrate the different levels of accuracy benchmarking that are possible.
B. Poisson data model
The Poisson data model describes image data that is acquired using an image detector with a pixelated and finite photon detection area. It also allows for the existence of a background component that corrupts the photon signal detected from the object(s) of interest. In these regards, the Poisson data model considers an imaging scenario that is significantly closer to what is encountered in practice than the scenario considered by the fundamental data model. Indeed, due to these realistic assumptions, it has generally been characterized as a practical data model (e.g., [17, 25, 26]). Strictly speaking, however, the Poisson data model is hypothetical, as it makes the impractical assumption that the detector does not introduce noise when reading out the electrons accumulated in its pixels.
Despite its hypothetical nature, the Poisson data model can be a reasonable model in cases where the number of photons detected in each pixel from the object(s) of interest and background component is generally expected to be large compared to the readout noise in the pixel. For examples of experimental data analysis based on the Poisson data model, see [20, 30, 34, 55].
According to the Poisson data model, a K-pixel image acquired over the time interval [t0, t] consists of the numbers of electrons z1, …, zK accumulated in the K pixels during the interval. For k = 1, …, K, the electron count zk in the kth pixel is a realization of the random variable Hθ,k given by
| (8) |
where Sθ,k and Bθ,k are independent Poisson random variables representing quantities resulting from independent processes. The variable Sθ,k represents the number of photoelectrons in the kth pixel that result from the detection of photons from the object(s) of interest, and is distributed with mean
| (9) |
where Ck is the region in the detector plane corresponding to the kth pixel, and Λθ (τ) and fθ,τ are the rate of photon detection and the profile of photon distribution as described in Section 2.A. This expression for the mean photoelectron count in the kth pixel due to the object(s) of interest is intuitively the fraction of the photon distribution profile over the kth pixel scaled by the mean number of photons that impact the detector plane over the acquisition interval. The variable Bθ,k represents the number of electrons in the kth pixel that arise from a background component, which besides sources of spurious photons such as the sample’s autofluorescence, can more generally include sources of spurious electrons such as the detector’s dark current. It is distributed with mean
| (10) |
which is analogous in form to Eq. (9), with , τ ≥ t0, and , (x, y) ∈ ℝ2, τ ≥ t0, denoting the detection rate and distribution profile of photons from the background component. Taking some liberty with terminology for ease of presentation, and are referred to as a photon detection rate and a photon distribution profile despite the fact that Bθ,k can include electrons that do not result from the detection of photons. This is justified because Bθ,k is primarily made up of photoelectrons resulting from the detection of spurious photons, given that spurious electrons that originate from the detector, such as those arising from the dark current, typically represent a negligible portion of the background component. Henceforth, with the understanding that they can consist in small part of spurious electrons, Bθ,k will accordingly be viewed as representing the background photoelectron count in the kth pixel, and βθ,k the mean of the background photoelectron count in the kth pixel.
As Hθ,k of Eq. (8) is the sum of two independent Poisson random variables, it is itself a Poisson random variable, with mean given by
| (11) |
the sum of Eqs. (9) and (10). Note that by applying the result of Section 2.B, Eq. (11) can also be derived from a single detection process consisting of the superposition of the independent processes of object and background photon detection.
The function νθ,k of Eq. (11) is thus the mean of the photoelectron count in the kth pixel. The terminology “photoelectrons” is importantly used to distinguish electrons in a given pixel that are generated by the detection of photons and accumulated in the pixel during the image acquisition interval from electrons in the pixel that arise from the detector’s noise processes. This distinction will help with the clarity of presentation in the remainder of this tutorial. Note also that in this tutorial, each detected photon is assumed, based on the physics of photon-to-electron conversion, to result in the generation of one photoelectron.
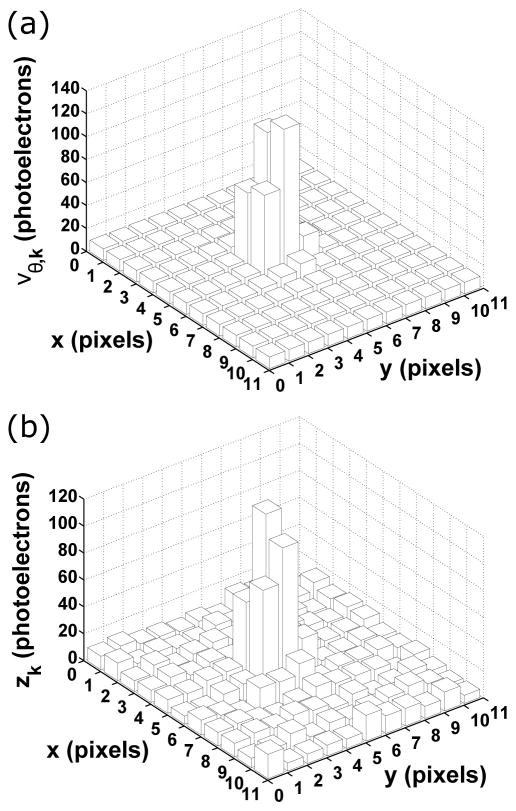
In Fig. 2(a), the mean image of the in-focus and stationary molecule of Fig. 1, computed over an 11×11-pixel region using Eq. (11), is shown. For this mean image, the spatial distribution of the background photons is assumed to be uniform over the 11×11-pixel region, and to not depend on time. Specifically, it is defined as for (x, y) within the 11×11-pixel region with area A, and otherwise. Moreover, the detection rate of the background photons is, as in the case of the molecule’s photon detection rate, assumed to be a constant function. It is defined as , τ ≥ t0, where is a positive constant. Every pixel in the mean image therefore has the same mean background photoelectron count, and Eq. (10) simplifies to , k = 1, …, K, where Apixel denotes the area of a pixel. In Fig. 2(b), a Poisson realization of the mean image is shown, providing an example of an image simulated according to the Poisson data model. The Poisson noise is particularly evident in the fluctuations of the photoelectron counts in the peripheral pixels, whose mean photoelectron counts are in contrast nearly identical, as seen in Fig. 2(a), by virtue of the signal from the molecule being small compared to the uniform background in the outer portions of the 11×11-pixel region.
Fig. 2.
Poisson data model example. (a) The mean pixelated image of the in-focus and stationary molecule of Fig. 1, computed over an 11×11-pixel region with a pixel size of 13 μm × 13 μm and a mean background photoelectron count of βθ,0 = 10 per pixel (obtained as the product of the constant background photon detection rate and the uniform spatial distribution , integrated over each pixel and the acquisition time of t − t0 = 0.05 s). The molecule is located at (x0, y0) = (656.5 nm, 682.5 nm) in the object space, which corresponds to (5.05 pixels, 5.25 pixels) in the image space, assuming (0, 0) in both spaces coincides with the upper left corner of the 11×11-pixel region. In terms of the photoelectron count due to the molecule, the mean image contains 476.15 out of the total of Λ0 · (t − t0) = 500 mean number of photoelectrons distributed over the detector plane. All other relevant parameters are as specified in Fig. 1. (b) A Poisson realization of the mean image in (a). The photoelectron count in each pixel is drawn from the Poisson distribution with mean given by the photoelectron count in the corresponding pixel in (a).
C. CCD/CMOS data model
The CCD/CMOS data model describes image data that is acquired using a CCD or CMOS detector. It builds on the Poisson data model by adding a component that accounts for the noise introduced by the detector when the photoelectrons accumulated in a pixel are read out. This additional component to the acquired data represents the primary noise source associated with a CCD or CMOS detector, and it is typically assumed to be Gaussian distributed. A K-pixel CCD or CMOS image acquired over the time interval [t0, t] therefore comprises the electron counts z1, …, zK, where the count zk in the kth pixel, k = 1, …, K, is a realization of the random variable Hθ,k given by
| (12) |
In Eq. (12), Sθ,k and Bθ,k are the same Poisson random variables from Eq. (8), and Wk is a Gaussian random variable with mean ηk and variance that represents the number of electrons due to the readout process of the detector. The three random variables are mutually independent, as they represent quantities resulting from independent processes. Note that the mean ηk of Wk can be used to model the detector offset for the kth pixel. Also, though in principle Wk can depend on the parameter vector θ, here the assumption is that ηk (the detector offset) and are either known or can be separately determined. For more on the determination of the detector offset and the readout noise variance, see Section 3.E.
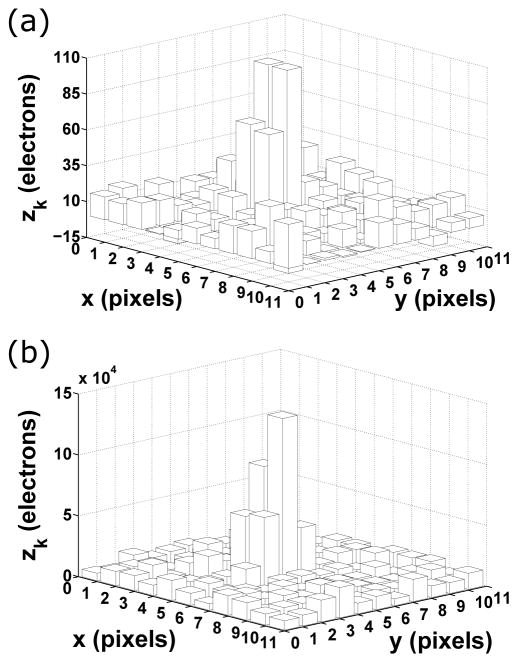
Based on Eq. (12), the electron count zk in the kth pixel of a CCD or CMOS image is just the sum of a realization of a Poisson random variable with mean νθ,k given by Eq. (11) and a realization of a Gaussian random variable with mean ηk and variance . In Fig. 3(a), a CCD realization of the mean image of Fig. 2(a) is shown. This particular realization is generated by simply adding to each pixel of the Poisson realization of Fig. 2(b) a random number drawn from the Gaussian distribution with mean η0 = 0 electrons and standard deviation σ0 = 8 electrons. This image is a CCD realization because the same Gaussian distribution with parameters η0 and σ0 is used to simulate the readout noise in every pixel (i.e., ηk = η0 and σk = σ0, k = 1, …, K), reflecting the fact that all pixels in a CCD detector share the same readout circuitry. To account for the fact that each pixel in a CMOS detector has its own dedicated readout circuitry, a CMOS realization can be obtained by using Gaussian distributions with different mean and standard deviation values to simulate the readout noise in different pixels. For a study that accounts for the pixel-dependent readout noise of a CMOS detector, see [56]. Note that in Fig. 3(a), a view is chosen to ensure that a few negative electron counts can be seen in the image. A negative count is obtained in a pixel whenever the Gaussian readout noise is negative and is greater in magnitude than the Poisson component of the data. In experimental data analysis, this can occur after the typical preprocessing step of detector offset subtraction (which is equivalent to setting η0 to 0 electrons) and subsequent multiplication by the digital count-to-electron count conversion factor (see Section 3.E for more on the modeling of experimental data). Note that a negative electron count is a reflection of the detector’s measurement error when reading out a small number of electrons in a pixel, and does not indicate an actual occurrence of a negative number of electrons.
Fig. 3.
CCD data model and EMCCD data model examples. (a) A CCD realization of the mean image in Fig. 2(a). The electron count in each pixel is the sum of a random number drawn from the Poisson distribution with mean given by the photoelectron count in the corresponding pixel in Fig. 2(a), and a random number drawn from the Gaussian distribution with mean η0 = 0 electrons and standard deviation σ0 = 8 electrons. In this particular realization, the Poisson random numbers are taken directly from the Poisson realization of Fig. 2(b). (b) An EMCCD realization of the mean image in Fig. 2(a). The electron count in each pixel is the sum of a random number drawn from the probability distribution of Eq. (14) with electron multiplication gain g = 950 and νθ,k given by the photoelectron count in the corresponding pixel in Fig. 2(a), and a random number drawn from the Gaussian distribution with mean η0 = 0 electrons and standard deviation σ0 = 24 electrons.
D. EMCCD data model
The EMCCD data model describes image data that is acquired using an EMCCD detector. It is similar to the CCD/CMOS data model in that the data in a given pixel is modeled as the sum of three components corresponding to the three independent processes of object detection, background detection, and detector readout. The difference, however, lies in the fact that the electron counts corresponding to the object(s) of interest and the background component are no longer the Poisson-distributed numbers of photoelectrons resulting directly from their respective detection processes. Instead, they are stochastically amplified versions of those Poisson-distributed photoelectron counts, and are accordingly modeled with random variables having probability distributions that account for the stochastic amplification. This multiplication of the photoelectrons accumulated in a pixel is what distinguishes an EMCCD detector from a CCD detector, and it importantly enables imaging under low-light conditions by rendering the readout noise small in comparison to the augmented electron count.
A K-pixel EMCCD image acquired over the time interval [t0, t] thus consists of the electron counts z1, …, zK, where the count zk in the kth pixel, k = 1, …, K, is a realization of the random variable Hθ,k given by
| (13) |
As in the CCD/CMOS data model of Eq. (12), Wk in Eq. (13) is a Gaussian random variable with mean ηk and variance that models the electron count contributed by the detector’s readout process. The random variables and , on the other hand, respectively represent the results of the stochastic amplification of the photoelectron counts modeled by the Poisson random variables Sθ,k and Bθ,k in Eq. (12). Depending on the model of amplification, different probability distributions can be used to describe and . Assuming, however, that the photoelectrons accumulated in a pixel are multiplied according to a branching process [57] that generates, for each input electron in each multiplication stage, a geometrically distributed number of electrons that includes the input electron itself, the sum random variable has the probability mass function [27]
| (14) |
θ ∈ Θ, where denotes “(l − 1) choose j”, the binomial coefficient indexed by l −1 and j, νθ,k is as defined in Eq. (11) and is the mean of the Poisson random variable Sθ,k + Bθ,k representing the photoelectron count in the kth pixel prior to amplification, and g > 1 is the electron multiplication gain, or more technically, the mean gain of the branching process, defined as the mean number of electrons that result from the multiplication of a single initial electron. Note that Eq. (14) is obtained by treating the sum as a single amplified electron count having originated from the single Poisson-distributed photoelectron count Sθ,k + Bθ,k with mean νθ,k. This is equivalent to considering the amplification separately for the object and background photoelectrons.
According to Eq. (13), the electron count zk in the kth pixel of an EMCCD image is the sum of a realization of a random variable with probability mass function given by Eq. (14) and a realization of a Gaussian random variable with mean ηk and variance . An EMCCD realization of the mean image of Fig. 2(a) generated using this approach is shown in Fig. 3(b). Specifically, to obtain the electron count zk, a random number is drawn from the probability distribution of Eq. (14) with the electron multiplication gain set to a relatively high g = 950 and νθ,k given by the kth pixel of the mean image of Fig. 2(a), and added to a random number drawn from the Gaussian distribution with mean η0 = 0 electrons and standard deviation σ0 = 24 electrons. Here the same Gaussian distribution with parameters η0 and σ0 is used to simulate the readout noise in every pixel because just as in the case of a CCD detector, all pixels in an EMCCD detector share the same readout circuitry. Note that to reflect the typically larger standard deviation for the readout noise of an EMCCD detector, a larger σ0 is used here compared to σ0 used for the CCD realization of Fig. 3(a). Note also that due to the electron multiplication, the electron counts in the EMCCD realization are much larger than those in the CCD realization. In addition, note that in general negative electron counts can also arise in an EMCCD image due to negative Gaussian readout noise. Negative counts are not present in the realization of Fig. 3(b), however, and in fact are unlikely for the particular scenario considered here. This is because the effect of the combination of the high electron multiplication gain of g = 950 and the relatively high background level of βθ,0 = 10 photoelectrons per pixel is such that even a peripheral pixel in an image will likely have an amplified electron count that is larger in magnitude than any potential negative readout noise at the given level of σ0 = 24 electrons.
It is of interest to note that when, as is typically the case, an EMCCD detector is used with a high electron multiplication gain g, the probability distribution, given a single initial electron, of a geometrically amplified electron count is well approximated by an exponential distribution with parameter 1/g. Based on this result, for a large g the probability distribution of Eq. (14) can be replaced by the probability density function [27]
| (15) |
θ ∈ Θ, where I1 is the first order modified Bessel function of the first kind. This density function has frequently been used to model electron multiplication in an EMCCD detector. It is found in [58], for example, in an equivalent form that does not include the jump at u = 0 and does not use the modified Bessel function representation. It is also found in identical form in [59] and [43].
E. Modeling of experimental data
In the pixelated data models of Sections 3.B, 3.C, and 3.D, the pixel values of an image are specified in units of electrons. In practice, however, a typical CCD, CMOS, or EMCCD detector produces image data with pixel values given in units of digital counts. Moreover, the value of each pixel includes a detector offset. Therefore, in order to perform data modeling based on experimentally acquired data, a unit conversion is required and the detector offset needs to be accounted for. The unit conversion is carried out by multiplying the value of each pixel by a digital count-to-electron count conversion factor. This conversion factor can usually be found in the specification sheet of the detector, and it can also be measured using a standard methodology (e.g., [60]) that exploits the linear relationship between the mean and variance of the data acquired in a pixel. Unlike the unit conversion factor which is not accounted for in the data models, the detector offset for the kth pixel can be represented by the mean ηk of the readout noise Gaussian random variable Wk. Both the offset ηk and the readout noise variance for the kth pixel can be determined from dark frames acquired with a minimal exposure time (e.g., [45]). Note that while the same unit conversion factor, detector offset, and readout noise variance are applicable to all the pixels of a CCD or EMCCD image, the fact that each CMOS pixel has its own readout circuitry means that every pixel of a CMOS image has its own values for these three quantities. The same methodologies for determining these quantities, however, apply on a per-pixel basis. For an example of a study in which the per-pixel determination of these quantities is carried out for the analysis of CMOS images, see [56]. Regardless of the detector type, given that the unit conversion factor(s) and the detector offset(s) have been determined for the pixels of an image, a typical way of converting the image to units of electrons consists of removing the appropriate offset from each pixel by subtraction (thereby setting ηk to 0 electrons for each pixel k) and multiplying each resulting pixel value by the appropriate conversion factor.
4. FISHER INFORMATION AND CRAMÉR-RAO LOWER BOUND
The main purpose of the material in Sections 2 and 3 is to provide a mathematical description of the image data from which parameters of interest are to be estimated. The mathematical description of the data is critical, as it allows the determination of how accurately the parameters can be estimated from the data. The description, as seen in Sections 2 and 3, includes models for the detection of photons from the object(s) of interest and a potential background component, a model for the detector used for the image acquisition, and models for the noise sources that corrupt the photon signal detected from the object(s) of interest. The parameters to be estimated can be anything from an object’s positional coordinates to the level of the background noise in the image, so long as they are appropriately incorporated into the description of the data.
According to estimation theory, the limit of the accuracy, in other words the limit to the standard deviation, with which a given parameter can be determined by an unbiased estimator is given by the square root of the Cramér-Rao lower bound on the variance for estimating the parameter. The Cramér-Rao lower bound is in turn given by the main diagonal element, corresponding to the parameter, of the inverse of a square matrix quantity known as the Fisher information matrix. The Fisher information matrix is a function of the parameter, and as it measures the amount of information that the data carries about the parameter, it is calculated based on the mathematical description of the data from which the parameter is to be estimated.
More formally, the Cramér-Rao inequality [28, 29] states that the covariance matrix of any unbiased estimator θ̂ of the vector of parameters θ ∈ Θ, where Θ is the parameter space, is no smaller than the inverse of the Fisher information matrix I(θ). Mathematically, this inequality is given by
| (16) |
where for θ = (θ1, θ2, …, θN) ∈ Θ and θ̂ = (θ̂1, θ̂2, …, θ̂N), where N is a positive integer, both the covariance matrix Cov (θ̂) and the inverse Fisher information matrix I−1(θ) are N×N matrices. While the matrix inequality of Eq. (16) does not imply that each element of Cov (θ̂) is greater than or equal to its corresponding element in I−1(θ), it does imply that each main diagonal element of Cov (θ̂) is greater than or equal to its corresponding element in I−1(θ). This arises from the fact that the matrix Cov(θ̂) − I−1(θ) is positive semidefinite, and importantly means that the variance of the estimate θ̂i of the parameter θi, i = 1, …, N, is bounded from below by the ith main diagonal element of the inverse Fisher information matrix. Mathematically, this can be expressed as
| (17) |
where the subscript ii denotes the ith main diagonal element. It is then straightforward to see that the limit to the standard deviation with which parameter θi can be estimated is given by . Note that the second inequality in Eq. (17) implies that the square root of the inverse of the ith main diagonal element of the Fisher information matrix provides a potentially looser lower bound on the standard deviation of θ̂i.
It is thus clear that the key to determining the limit of the accuracy for the estimation of a parameter lies with the calculation of the Fisher information matrix I(θ). In order to calculate I(θ), the likelihood function for θ, which is just the probability distribution of the data viewed as a function of θ, is needed. Given the data w with probability distribution pθ(w), the Fisher information matrix is given by (e.g., [29])
| (18) |
where T denotes the transpose. As mentioned in Section 1, the calculation of the Fisher information matrix is based on assessing how the likelihood of the observed data is affected by changes in the values of the parameters of interest. Mathematically, this assessment is realized by considering, as seen in Eq. (18), the derivative of the logarithm of the likelihood function with respect to the parameter vector θ. The expectation is taken over all possible values of the data, so that the Fisher information is an indicator of how, on average, the likelihood function changes with θ.
Due to the differences in their mathematical descriptions, the image data models of Section 3 are associated with different probability distributions, and therefore have different expressions for the Fisher information matrix. In the ensuing subsections, relatively high-level expressions for the Fisher information matrix will be given for the image data models, and illustrations will be presented by instantiating the high-level expressions with specific parameter estimation problems.
A. Fundamental data model
For the fundamental data model of Section 3.A, the probability distribution of the acquired data is represented by the sample function density for the spatio-temporal random process characterized by the photon detection rate Λθ (τ), τ ≥ t0, θ ∈ Θ, and the photon distribution profile fθ,τ(x, y), (x, y) ∈ ℝ2, θ ∈ Θ, τ ≥ t0. If a fundamental image realization consisting of N0 photons detected over the acquisition interval [t0, t], where N0 is Poisson-distributed with mean , is denoted by {w1, …,wN0}, where wk = (τk, rk), k = 1, …, N0, represents the time point of detection τk and the location of detection rk = (xk, yk) ∈ ℝ2 of the kth detected photon, then the sample function density is given by
| (19) |
θ ∈ Θ. Using Eq. (19) in place of pθ (w) in Eq. (18), the resulting Fisher information matrix can be expressed as
| (20) |
For details on the derivation of Eqs. (19) and (20), see [61].
Continuing the example from Section 3.A of an in-focus and stationary molecule whose photons are detected at a constant rate of Λθ (τ) = Λ0, τ ≥ t0, and whose photon distribution profile fθ is given by Eq. (1) without the time dependence and with the image function q given by the Airy image function of Eq. (2), suppose the molecule’s positional coordinates (x0, y0) and the photon detection rate Λ0 are to be estimated from a fundamental image acquired over the time interval [t0, t]. Then for θ = (x0, y0,Λ0) ∈ Θ, where Θ = ℝ ×ℝ ×ℝ+, evaluation of Eq. (20) followed by application of Eq. (17) for each parameter yields the limits of accuracy [21, 22]
| (21) |
| (22) |
| (23) |
Several points are of note, all of which are exceptions rather than the general rule, owing to the specifics of this particular localization problem. First, all three limits of accuracy have simple analytical expressions, which would not be the case if, for example, the detector had a finite and rectangular photon detection area. Second, the limits of accuracy δx0 and δy0 for the estimation of x0 and y0, respectively, are identical because the Airy pattern’s circular symmetry, combined with the detector’s infinite and unpixelated photon detection area, produces images that contain exactly the same information about x0 and y0. Third, δx0 and δy0 are not dependent on the magnification M or the coordinates x0 and y0 themselves, a fact that is attributable again to the infinite and unpixelated nature of the detection area. Fourth, δx0 and δy0 have a simple inverse square root dependence on the mean detected photon count Λ0 · (t − t0), a special property that would not generally hold if, for example, a background component had been present.
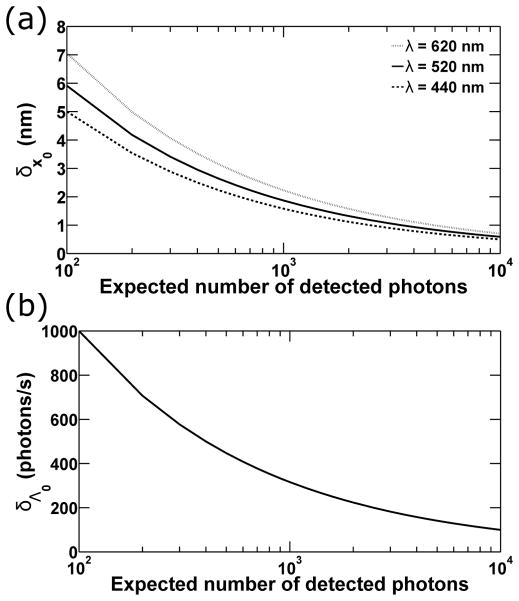
In Fig. 4(a), δx0 of Eq. (21) (which is identical to δy0 of Eq. (22)) is shown, for three different values of the wavelength λ of the photons detected from the molecule, as a function of the expected number of detected photons Λ0 · (t − t0), which ranges from 100 to 10000. For each wavelength, the lower bound on the standard deviation with which x0 or y0 can be estimated is seen to decrease in value, and therefore improve, as the mean detected photon count is increased. This result is expected from the inverse square root dependence on the photon count, but also agrees with the intuition that the accuracy with which any parameter can be estimated should improve as more data is collected. The curves of Fig. 4(a) additionally show that for a given mean photon count, the limit of accuracy improves with decreasing wavelength of the detected photons. This is expected as well, since a shorter wavelength produces a narrower Airy pattern that allows the peak of the pattern, which gives the location of the molecule, to be estimated with better accuracy. Note that based on Eqs. (21) and (22), the same effect can also be obtained by using a larger numerical aperture na.
Fig. 4.
Limits of accuracy under the fundamental data model. (a) The limit of accuracy δx0 for the estimation of the x0 coordinate of an in-focus and stationary molecule from a fundamental image is plotted as a function of the expected number of photons detected in the image. Curves are shown that correspond to the detection of photons of wavelengths λ = 620 nm (dotted), 520 nm (solid), and 440 nm (dashed), which are collected by an objective lens with numerical aperture na = 1.4. The expected photon counts range from 100 to 10000, and are obtained as the product of the constant photon detection rate Λ0 = 10000 photons/s and acquisition times t − t0 ranging from 0.01 s to 1 s. The image of the molecule is described by the Airy image function. (b) The limit of accuracy δΛ0 for the estimation of the photon detection rate Λ0 = 10000 photons/s from a fundamental image is shown as a function of the expected number of photons detected in the image.
To give a specific example, the curve corresponding to λ = 520 nm shows that from a fundamental image like the one shown in Fig. 1(b), which has a mean detected photon count of Λ0 · (t − t0) = 500, the x0 and y0 coordinates of the molecule can each be determined with a standard deviation of no smaller than 2.64 nm. By doubling the expected photon count to 1000, the curve shows that the limit of accuracy is improved to 1.87 nm. If in addition the molecule is changed to one that emits photons of wavelength λ = 440 nm, then the limit of accuracy is improved further to 1.58 nm.
Note that a limit of the accuracy with which a positional coordinate can be estimated, such as δx0 and δy0 in this example, is also referred to as a localization accuracy measure [17, 62].
In Fig. 4(b), δΛ0 of Eq. (23) is also seen, for the specific localization problem considered here, to have an inverse square root dependence on the mean detected photon count. For example, the curve shows that by doubling the acquisition time t − t0 from 0.05 s to 0.1 s, and hence doubling the mean detected photon count Λ0 · (t − t0) from 500 to 1000, the lower bound on the standard deviation with which the photon detection rate of Λ0 = 10000 photons/s can be estimated is improved from 447.2 photons/s to 316.2 photons/s.
It is of interest to note that if the image of the molecule were described by the 2D Gaussian function of Eq. (3) instead of the Airy pattern, simple analytical expressions similar to those of Eqs. (21), (22), and (23) would have been obtained for the limits of accuracy. Specifically, δΛ0 would be identical in expression, and δx0 and δy0 would each be given by [21, 22]. Therefore, in terms of the results obtained with the 2D Gaussian image function, Fig. 4(b) would apply just as well to δΛ0, and the patterns of dependence on the photon count and the width of the image function illustrated in Fig. 4(a) would apply to δx0 and δy0. In the case of the 2D Gaussian image function, a shorter wavelength λ or a larger numerical aperture na would equate to a smaller standard deviation σg, which leads to a narrower 2D Gaussian function.
For another illustration of limits of accuracy under the fundamental data model, consider the estimation of the distance d > 0 separating two like molecules that are both in-focus and stationary. Suppose the rates Λ1 and Λ2 at which the molecules’ photons are detected are constant and equal, such that Λ1(τ) = Λ2(τ) = Λ0, Λ0 > 0, τ ≥ t0. Note that the subscript θ is not used with the photon detection rates as they are assumed to be known in this example and will not be estimated. Further suppose that the molecules lie on the x-axis and are equidistant from the origin (0, 0) of the object space coordinate system. Since the processes corresponding to the detection of photons from the two molecules are independent, their superposition is described by the photon detection rate of Eq. (5), which reduces to Λ(τ) = 2Λ0, τ ≥ t0, and by the photon distribution profile fθ of Eq. (7), which likewise becomes time-independent given the photon detection rates as defined, and has the molecules’ positional coordinates specified by (x01, y01) = (−d/2, 0) and (x02, y02) = (d/2, 0) based on the given geometry. Further assuming the molecules’ image functions q1 and q2 in Eq. (7) to each be given by the Airy pattern of Eq. (2), evaluation of the Fisher information matrix of Eq. (20), with θ = d ∈ ℝ+ and Λ and fθ as described, yields the limit of accuracy [25]
| (24) |
where
where , γ = 2πna/λ, and J2 is the second order Bessel function of the first kind.
For three different wavelengths λ of the detected photons, δd of Eq. (24) is plotted in Fig. 5 as a function of the distance d that separates the two molecules. For each wavelength, the limit of the accuracy with which d can be estimated is seen to improve as the value of d increases, corroborating the expectation that a larger distance should be easier to determine because there is less of an overlap between the images of the two molecules. The curves in Fig. 5 further show that for a given separation distance d, decreasing the wavelength of the detected photons improves the lower bound on the standard deviation with which d can be estimated. This result is again attributable to the narrowing of the Airy pattern when the wavelength is decreased, which reduces the overlap between the patterns corresponding to the two molecules.
Fig. 5.
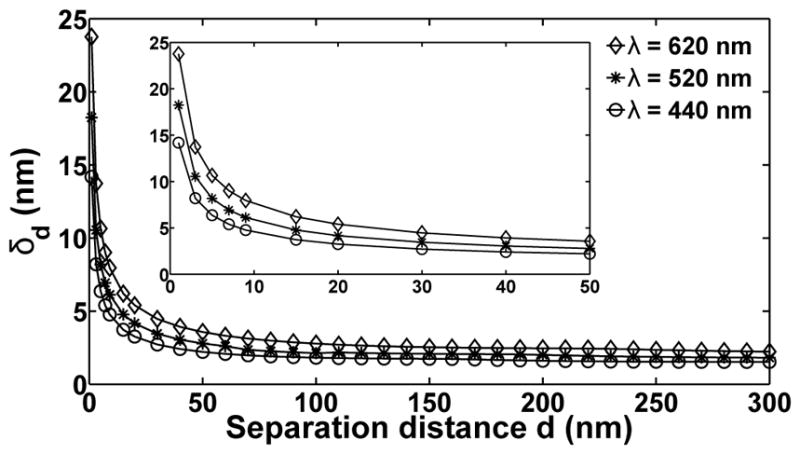
Limit of the accuracy for separation distance estimation under the fundamental data model. The limit of accuracy δd for the estimation, from a fundamental image, of the distance d separating two in-focus and stationary molecules is plotted as a function of the distance d. Curves are shown that correspond to the detection of photons of wavelengths λ = 620 nm (◇), 520 nm (*), and 440 nm (○), which are collected by an objective lens with numerical aperture na = 1.4. Photons are detected from each molecule at a rate of Λ0 = 10000 photons/s over an acquisition time of 0.3 s, such that Λ0 · (t − t0) = 3000 photons are on average detected from each molecule in a given image. The image of each molecule is described by the Airy image function. The inset shows the portion of the curves from d = 1 nm to d = 50 nm.
The limit of accuracy δd importantly shows that, contrary to the Rayleigh criterion [52, 63] which specifies a minimum separation distance below which two point sources are deemed indistinguishable, arbitrarily small distances between two point sources can in fact be determined. With the limit of accuracy, the question becomes one of not whether, but how well two point sources can be resolved, in the sense of how accurately the distance separating them can be determined. For example, whereas the Rayleigh criterion, given by 0.61λ/na, specifies a minimum resolvable distance of 226.57 nm for λ = 520 nm and na = 1.4, the curve corresponding to λ = 520 nm in Fig. 5 shows that a much smaller separation distance of 20 nm can be estimated with a standard deviation of no better than 4.16 nm when Λ0 · (t−t0) = 3000 photons are on average detected from each point source. Moreover, as can be seen from Eq. (24), this limit of accuracy can be improved, as demonstrated in Fig. 4 for the localization problem, by increasing the expected number of detected photons Λ0 · (t − t0).
A limit of accuracy δd for the estimation of a separation distance is also referred to as a resolution measure [25, 26]. More information and results for the scenario of two in-focus molecules considered here, including δd derived under the pixelated data models, can be found in [25]. The resolution measure has also been extended to the more general scenario of two molecules in 3D space [26], where it has been compared with the classical axial analogue [63] of the Rayleigh criterion.
Note that the simple inverse square root dependence of δd of Eq. (24) on the mean number of photons Λ0 · (t − t0) detected from each molecule is something that can be seen from a much higher level. In the distance estimation problem as presented, the photon detection process that underlies the fundamental image is described by a photon detection rate Λ that does not depend on the parameter vector θ, and a photon distribution profile fθ that does not change with time. Given such a photon detection process, the Fisher information matrix of Eq. (20) decouples into the product of integrals
| (25) |
θ ∈ Θ, where the integral over time is just the expected number of detected photons. Therefore, upon inverting the matrix and taking the square root of each main diagonal element, the limit of the accuracy for estimating any given parameter in θ will have as part of its expression, as is seen in Eq. (24) where Λ(τ), τ ≥ t0, is defined as the constant function 2Λ0. It is important to point out that while Eq. (25) corresponds to a common estimation problem formulation, Fisher information matrices corresponding to other problem descriptions can also lead to limits of accuracy with an inverse square root dependence on the mean detected photon count. The Fisher information matrix from which the limits of accuracy of Eqs. (21), (22), and (23) are obtained provides such an example, since its associated problem description involves a photon detection rate Λθ that does depend on θ.
As the fundamental data model embodies the most ideal of imaging conditions, each limit of accuracy in the above examples represents, within the context of the particular estimation problem, the absolute best accuracy with which the given parameter can be determined. Put another way, a limit of accuracy obtained under the fundamental data model importantly marks the point beyond which no further improvement in accuracy is possible for estimating the parameter. It can therefore be used as the ultimate target of comparison to determine how much room there is for improving the accuracy of estimation. Given the practical limitations of an experimental setup, however, a limit of accuracy obtained under the fundamental data model often represents an unrealistic target. Instead, a tighter limit of accuracy that is obtained under a data model that assumes, for example, a pixelated detector with a finite photon detection area will provide a more realistic accuracy benchmark that can be approached in practice. This will be demonstrated in the next subsections, but as alluded to in Section 3.A, variations of the fundamental data model can be obtained that will already yield tighter limits of accuracy that provide more realistic targets. The Fisher information matrix corresponding to variations entailing the addition of a background component or a finite photon detection area for the detector is obtained by a straightforward generalization of Eq. (20) that adds a background component using the superposition property of Section 2.B and restricts the region of integration of photon distribution profiles to the confines of the finite detection area. For an image acquired over the time interval [t0, t], this matrix is given by
| (26) |
θ ∈ Θ, where , τ ≥ t0 and , (x, y) ∈ ℝ2, τ ≥ t0, are the photon detection rate and distribution profile, respectively, of the background component, and C is the finite region within ℝ2 corresponding to the photon detection area of the detector. This expression will be used in the next subsection to calculate limits of accuracy that represent more realistic benchmarks than the limit obtained with Eq. (20).
B. Poisson data model
In a pixelated image, the data in each pixel is obtained independently of the data in all other pixels. Given this typical and well-justified assumption, the probability distribution for the data comprising a K-pixel image is the product of the probability distributions for the data in the K pixels. Denoting the probability distribution for the random variable Hθ,k that models the electron count zk in the kth pixel by pθ,k, k = 1, …, K, the probability distribution pθ for a K-pixel image can be written as
| (27) |
Using Eq. (27) in place of pθ (w) in the general expression of Eq. (18), the Fisher information matrix corresponding to a K-pixel image can be shown to be
| (28) |
θ ∈ Θ, which is easily verified to be the sum of the Fisher information matrices corresponding to the data in the K pixels.
From the examples of Section 4.A, it can be seen that in a typical estimation problem, parameters of interest represented by the vector θ, such as the positional coordinates of an object, the rate at which photons are detected from an object, and the distance separating two objects, are naturally all part of the specification of the detection rate Λθ and distribution profile fθ,τ of the photon detection process. It follows that in the pixelated case, information about θ in the kth pixel of an image is contained in the object-based component Sθ,k of the data in the pixel (see Eq. (8)), whose mean μθ,k is specified in terms of Λθ and fθ,τ. In addition, information about θ is present in the background component Bθ,k of the data in the pixel when one chooses to estimate quantities that parameterize its mean βθ,k. Taken together, information about θ in the kth pixel is contained in the Poisson component Sθ,k + Bθ,k of the data in the pixel, which has mean νθ,k given by Eq. (11). On the other hand, information about θ is typically not contained in the detector-based noise components of the data in the pixel. Even though parameters such as the readout noise mean and variance and the EMCCD detector’s electron multiplication gain can in principle be included in θ, they are usually not included because they can be determined separately from the object-based and background-based parameters. Given this typical form of an estimation problem where, in the kth pixel, θ parameterizes only the mean νθ,k of the Poisson component of the data, the Fisher information matrix of Eq. (28) can be written as
| (29) |
θ ∈ Θ. For k = 1, …, K, this representation importantly expresses the Fisher information matrix corresponding to the data in the kth pixel as a product of two fundamentally different parts. The first part is a matrix of partial derivatives of the mean photoelectron count νθ,k with respect to the parameters in θ. It is a function of the specific estimation problem, as the derivatives depend on the vector θ of the parameters to be estimated, and through νθ,k, on the specification of the photon detection rates and distribution profiles corresponding to the object(s) of interest and a potential background component. Since νθ,k is purely a function of photon detection rates and distribution profiles, the matrix is not dependent in any way on the particular detector or type of detector that is used to capture the image data. Therefore, for a given estimation problem, the matrix is the same regardless of the detector used. This can be seen in the fact that the Poisson image of Fig. 2(b) and the CCD and EMCCD images of Fig. 3 are all realizations based on the same mean image of Fig. 2(a), which is just a pixel array of νθ,k values. (Note that as mentioned in Section 3.B, νθ,k can in fact include, through the mean βθ,k of the background component, spurious electrons that originate from the detector. However, since these spurious electrons are common to, and typically very small in number in all standard detector types, νθ,k can justifiably be considered to be independent of the particular detector and type of detector used.)
In direct contrast, the second part of the product is a scalar expectation term that is not dependent on the specific estimation problem, but is dependent on the particular detector and type of detector used. It depends on the detector through the probability distribution pθ,k of the electron count in the kth pixel, which is a function of parameters specific to a detector such as the mean and variance of the readout noise in the case of a CCD or CMOS detector, and both the mean and variance of the readout noise and the electron multiplication gain in the case of an EMCCD detector. The scalar expectation term does not depend on the specific estimation problem, in the sense that while it is a function of νθ,k, it is dependent only on its value, and not how the value is obtained through the underlying photon detection rates and distribution profiles. In other words, a given value of νθ,k, regardless of how νθ,k or θ is defined, will always produce the same value for the scalar expectation term, provided all other parameters in the term’s expression remain the same.
As will be seen in Section 4.E, the fact that it is not dependent on the specific estimation problem makes the scalar expectation term a useful tool for determining, based solely on the mean photoelectron count in a pixel, the effect that a given detector has on the information content of the pixel. Indeed, the breaking of the overall data description into an estimation problem-dependent portion and a detector noise-dependent portion has also been exploited in a nested expectation maximization algorithm for the localization of closely spaced fluorescence emitters [64].
Since the scalar expectation term of Eq. (29) is the only part of the Fisher information expression that is dependent on the type of detector used, the Fisher information matrices corresponding to images captured with different types of pixelated detectors will differ by this term through the probability distributions that describe the electron counts comprising the images.
In a K-pixel image described by the Poisson data model, which assumes a hypothetical detector that introduces no readout noise, the photoelectron count zk in the kth pixel, k = 1, …, K, is according to Eq. (8) a realization of the Poisson random variable Hθ,k with mean νθ,k. The probability distribution pθ,k for Hθ,k, k = 1, …, K, is thus the Poisson probability mass function
| (30) |
Evaluating the scalar expectation term of Eq. (29) with Eq. (30) yields the Fisher information matrix
| (31) |
By incorporating the realistic assumption of a detector with a finite and pixelated photon detection area and by allowing for the presence of a background component, a limit of accuracy computed under the Poisson data model can be significantly worse than the limit of accuracy computed under the fundamental data model. This is because the conditions assumed by the Poisson data model represent a deterioration of the quality of the acquired image data. The finite detection area means a loss of data in that photons falling outside the detection area are not detected, and the pixelation of the detection area means a loss of precision with which the location of a detected photon is recorded, since the extent to which the location is known is reduced to the pixel within which the photon impacts the detection area. Meanwhile, the presence of a background component naturally results in the corruption of the photon signal detected from the object(s) of interest.
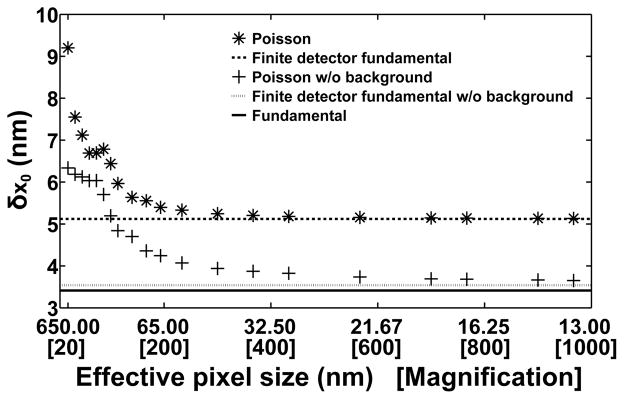
A comparison of limits of accuracy computed under the Poisson and fundamental data models is given in Fig. 6, which again uses the example of the limit of accuracy δx0 for the estimation of an in-focus and stationary molecule’s x0 coordinate. In the figure, δx0 corresponding to the Poisson data model (*), computed using Eq. (31), is seen to improve as the precision of the recording of photon location by the detector is increased by a decrease in the effective pixel size, which is in turn realized by increasing the magnification used for the imaging. The improvement is seen to level off, however, at more than 1.5 nm away from the fundamental data model’s limit of accuracy of δx0= 3.41 nm (solid line). This substantial gap is largely attributable to the presence of background noise that is uniformly distributed over the image. By assuming the absence of this background component (by ignoring βθ,k in Eq. (11) and using νθ,k = μθ,k, k = 1, …, K, in Eq. (31)), δx0 for the Poisson data model (+) can be seen to level off at a vastly improved value that is within a quarter of a nanometer of the target of 3.41 nm. Note that for a given effective pixel size, δx0 for the Poisson data model assuming the absence of background noise represents, as expected, a better accuracy than δx0 for the Poisson data model assuming the presence of background noise.
Fig. 6.
Comparing limits of accuracy corresponding to different data models and variations thereof. (a) The limit of accuracy δx0 for the estimation of the x0 coordinate of an in-focus and stationary molecule from an image is plotted as a function of the effective pixel size for the Poisson data model (*) and the Poisson data model assuming the absence of background noise (+). Also shown are the limits of accuracy corresponding to the finite detection area variation of the fundamental data model (dashed line), the finite detection area variation of the fundamental data model assuming the absence of background noise (dotted line), and the fundamental data model (solid line), which are plotted as horizontal lines as they do not depend on the effective pixel size. For the two cases involving the Poisson data model, the physical pixel size is 13 μm × 13 μm, and the different effective pixel sizes are obtained by varying the lateral magnification from M = 20 to M = 966.67. The image consists of a 15×15-pixel region at M = 100, and a proportionately scaled pixel region at each of the other magnifications. At each magnification, the molecule is positioned such that the center of its image, given by the Airy image function, is located at 0.05 pixels in the x direction and 0.25 pixels in the y direction with respect to the upper left corner of the center pixel of the image. For the two cases involving the finite detection area variation of the fundamental data model, δx0 is computed using the unpixelated equivalent of the M = 100 scenario, though any other scenario can be used to obtain the same result. For all cases, photons are detected from the molecule at a rate of Λ0 = 6000 photons/s over an acquisition time of t − t0 = 0.05 s, such that Λ0 · (t − t0) = 300 photons are on average detected from the molecule over the detector plane (and 289.5 photons are on average detected from the molecule over a given finite-sized image). For the two cases involving a background component, a background detection rate of is assumed, along with a uniform background spatial distribution of fb(x, y) = 1/A μm−2, (x, y) ∈ C, where C is the region in the detector plane corresponding to the image and A is the area of C. For example, for the M = 100 scenario, fb(x, y) = 1/38025 μm−2, such that there is a background level of β0 = 5 photoelectrons per pixel over the 15×15-pixel region. For all cases, it is assumed that photons of wavelength λ = 520 nm are collected by an objective lens with numerical aperture na = 1.4.
Even with the absence of background noise and the use of a small effective pixel size, it is clear from Fig. 6 that δx0 for the Poisson data model still does not quite approach δx0 for the fundamental data model. The remaining small gap is primarily due to the detector’s finite photon detection area under the Poisson data model, and this is illustrated by the fact that δx0 computed for the same finite, but unpixelated photon detection area, and with the assumption of the absence of background noise (dotted line), has a value of 3.54 nm that is greater than δx0 for the fundamental data model. As can be seen, the value of 3.54 nm represents a more realistic target for δx0 corresponding to the Poisson data model assuming the absence of background noise. This value is calculated using the generalized Fisher information matrix of Eq. (26), without the background photon detection rate and distribution profile , and with the region of integration C defined to be the region in the detector plane corresponding to the image. Equation (26) is also used to compute δx0 under the same conditions, but with and defined to specify the uniformly distributed background noise (dashed line) that is accounted for by the Poisson data model that assumes the presence of background noise. The value of δx0 obtained in this case is 5.12 nm, and analogously represents a tighter bound for δx0 corresponding to the Poisson data model assuming the presence of background noise.
Figure 6 thus demonstrates the various levels of accuracy benchmarking that are possible for a given estimation problem by considering the Fisher information for different data models and variations thereof. Importantly, it illustrates that by comparing the limits of accuracy corresponding to different data models and their variations, one can obtain a clear picture of the factors responsible for, and the degrees to which they affect, the distance between a given limit of accuracy and the ultimate target as provided by the fundamental data model.
Note that the limits of accuracy in Fig. 6 are computed for θ = (x0, y0) ∈ ℝ2, and that while not shown, the results for δy0 follow the same patterns as the results for δx0. The above discussion therefore applies equally well to δy0. Note also that in the cases involving a finite photon detection area, δy0 is not identical in value to δx0 because of the asymmetric positioning of the Airy pattern within the image. While they are nearly identical in value when the image is unpixelated or has a fine effective pixelation, they can have very different values when the image has a coarse effective pixelation.
C. CCD/CMOS data model
According to Eq. (12), the electron count zk, k = 1, …, K, in the kth pixel of a K-pixel CCD or CMOS image is a realization of the random variable Hθ,k obtained as the sum of a Poisson random variable with mean νθ,k and a Gaussian random variable with mean ηk and variance . By the independence of the Poisson and Gaussian random variables, the probability distribution pθ,k for Hθ,k, k = 1, …, K, is the convolution of a Poisson distribution and a Gaussian distribution with the given parameters. The result of the convolution is the probability density function [21, 65]
| (32) |
Using Eq. (32) in Eq. (29) gives the Fisher information matrix
| (33) |
θ ∈ Θ, where pθ,k is the density function of Eq. (32).
For the same localization problem considered in Fig. 6, limits of accuracy computed for three different levels of readout noise using the Fisher information matrix of Eq. (33) are shown in Fig. 7(a) as a function of the effective pixel size. These limits of accuracy correspond to the CCD data model, as the same mean and variance are assumed for the readout noise in every pixel of the detector. However, note that while the relatively high readout noise standard deviation of 6 electrons is typical of older but still commonly used CCD detectors, the readout noise standard deviations of 0.5 electrons and 1 electron can be regarded as being representative of idealized versions of very-low-noise CMOS detectors that have readout circuitries with identical noise characteristics for all their pixels. The CCD limits of accuracy are computed for the same conditions used for δx0 for the Poisson data model (with background noise) from Fig. 6, but with added readout noise. Consequently, Fig. 7(a) shows that for a given effective pixel size, they represent accuracies that are strictly worse than the Poisson limit of accuracy reproduced from Fig. 6. For the larger effective pixel sizes, this is seen more clearly in the figure’s inset. More generally, this provides an example of using limits of accuracy computed under the Poisson data model as tight benchmarks for the evaluation of limits of accuracy computed under a practical data model.
Fig. 7.
Comparing limits of accuracy corresponding to the CCD and EMCCD data models. (a) For the CCD data model, the limit of accuracy δx0 for the estimation of the x0 coordinate of an in-focus and stationary molecule from an image is plotted as a function of the effective pixel size. Limits of accuracy are shown for three different levels of readout noise in each pixel, characterized by standard deviations of σ0 = 6 electrons (●), 1 electron (◇), and 0.5 electrons (○). In each case, the mean of the readout noise in each pixel is η0 = 0 electrons. The limit of accuracy for the Poisson data model (with background noise) from Fig. 6 (*) is shown as a reference for comparison, since the CCD limits of accuracy are computed by adding readout noise to the same assumed conditions. All details not mentioned are therefore exactly as given in Fig. 6 for the Poisson data model. The inset provides a clearer view of some data points for five relatively large effective pixel sizes. (b) Zoomed-in version of (a) with the addition of δx0 corresponding to the EMCCD data model with readout noise of mean η0 = 0 electrons and standard deviation σ0 = 48 electrons in each pixel, and an electron multiplication gain of g = 1000.
Figure 7(a) further demonstrates the deteriorative effect of readout noise by showing δx0 corresponding to the CCD data model to worsen, at a given effective pixel size, with increasing values of the readout noise standard deviation. At the larger effective pixel sizes, the pattern can be seen for the small readout noise standard deviations of 1 and 0.5 electrons in the figure’s inset. Also of note is the fact that neither very large nor very small effective pixel sizes are optimal in terms of parameter estimation accuracy when a CCD detector is used. (For a clearer view of the shapes of the curves, see the zoomed-in versions in Fig. 7(b).) When the effective pixel size is large, the number of photoelectrons in each pixel will be relatively large, so that the effect of the readout noise will be minimal. This explains the fact that at the largest effective pixel sizes, the δx0 values for the CCD data models with already low readout noise standard deviations of 1 and 0.5 electrons are nearly equal to the corresponding values of δx0 for the Poisson data model. However, such a scenario will not necessarily yield the best limit of accuracy since large pixels also mean that the locations of the detected photons are recorded with poor precision, and that the resulting pixelated image represents a poorly sampled version of the continuous image described by the underlying photon distribution profiles. On the other hand, a small effective pixel size will also not necessarily yield the best limit of accuracy despite the pixelated image being a finely sampled version of the continuous image. In this scenario, the relatively few photoelectrons in each pixel will mean that the effect of readout noise becomes significant.
For a specific example, consider the CCD data model with the readout noise standard deviation of 6 electrons in Fig. 7. In this case, δx0 attains its lowest value of around 7.94 nm at an effective pixel size of approximately 216.67 nm (60× magnification). At the large effective pixel size of 650 nm (20× magnification), it has a poorer value of 9.86 nm, and at the small effective pixel size of 43.33 nm (300× magnification), it predicts an even worse estimation accuracy of no better than 16.81 nm.
D. EMCCD data model
In a K-pixel EMCCD image, the electron count zk in the kth pixel, k = 1, …, K, is according to Eq. (13) a realization of the random variable Hθ,k obtained as the sum of a random variable with probability mass function given by Eq. (14) and a Gaussian random variable with mean ηk and variance . By the independence of the two summand random variables, the probability distribution pθ,k for Hθ,k, k = 1, …, K, is the convolution of Eq. (14) and a Gaussian distribution with mean ηk and variance . The resulting probability density function is given by [27]
| (34) |
θ ∈ Θ. Evaluation of Eq. (29) using Eq. (34) yields the Fisher information matrix
| (35) |
θ ∈ Θ, where pθ,k is the density function of Eq. (34). This expression applies specifically to the modeling of electron multiplication by a geometrically multiplied branching process, since its derivation makes use of Eq. (14) for the distribution of the amplified electron count in the kth pixel. If Eq. (14) is replaced by the exponential distribution-based density function of Eq. (15) in the convolution with the Gaussian distribution with mean ηk and variance , then the probability distribution pθ,k for Hθ,k, k = 1, …, K, is given by [27]
| (36) |
θ ∈ Θ. Using Eq. (36) in Eq. (29) yields the Fisher information matrix
| (37) |
θ ∈ Θ, where I0 is the zeroth order modified Bessel function of the first kind, and pθ,k is the density function of Eq. (36). Since the probability distribution of Eq. (15) is a good approximation of the probability distribution of Eq. (14) when the electron multiplication gain g is large, Eq. (37) can be expected to yield limits of accuracy that are very similar in value to those obtained with Eq. (35) for large values of g.
Returning to the example of the localization of an in-focus and stationary molecule, Fig. 7(b) adds to Fig. 7(a) by showing δx0 for the EMCCD data model, computed using the Fisher information matrix of Eq. (35) with an electron multiplication gain of g = 1000 and a readout noise standard deviation of σ0 = 48 electrons per pixel. Since the EMCCD limit of accuracy is also calculated for the same conditions used for δx0 for the Poisson data model, but accounts for the effects of electron multiplication and added readout noise, it is, as in the case of the CCD limits of accuracy, strictly worse than the Poisson limit of accuracy for a given effective pixel size.
Compared with the three curves corresponding to the CCD data model, one can see that the EMCCD limit of accuracy is worse at the largest effective pixel sizes. This is expected, since the relatively high numbers of photoelectrons in the large pixels render the stochastic electron multiplication unnecessary, causing it to have the net effect of introducing additional noise to the data. As the effective pixel size is decreased, the EMCCD limit of accuracy can be seen to improve, much like δx0 for the CCD detectors with the low readout noise standard deviations of 1 and 0.5 electrons. Unlike the CCD limits of accuracy, however, it continues to improve at the smallest effective pixel sizes shown, and surpasses even the CCD limit of accuracy computed for the 0.5-electron readout noise standard deviation at a pixel size of around 17 nm. At this small pixel size, only about 2 photons are on average detected in the brightest pixel of the image (largest νθ,k value is 2.03 photoelectrons), and less than 1 photon is on average detected in over 99% of the pixels. This shows that the EMCCD detector is particularly suited for imaging under conditions in which a very small amount of light is expected to impinge on each of its pixels. This unique property of the EMCCD detector forms the basis of the Ultrahigh Accuracy Imaging Modality proposed in [66], and will be treated in more detail in Section 4.E.
It is important to emphasize that the results of Fig. 7(b) are specific to the conditions assumed. In particular, given that an average of 289.5 photons are detected from the molecule in a given image and an average of β0 = 5 background photons per pixel are detected at the 100× magnification, Fig. 7(b) shows that the smallest δx0 values are attained by the CCD detectors with the 1-electron and 0.5-electron readout noise standard deviations at an effective pixel size in the neighborhood of 60 nm. Given sufficiently smaller mean photon counts from the molecule and the background component, however, the EMCCD detector can be expected to attain the overall lowest value of δx0 within the range of effective pixel sizes considered, and to start outperforming the very-low-noise CCD detectors at a larger effective pixel size [66].
E. Noise coefficient
As seen in Sections 4.C and 4.D, limits of accuracy corresponding to the CCD/CMOS and EMCCD data models depend in different ways on the amount of light that is detected in their pixels. Whereas the CCD and CMOS detectors tend to provide superior parameter estimation performance when relatively many photons are detected in each of their pixels, the EMCCD detector tends to yield the best limits of accuracy when the expected photoelectron count in each of its pixels is very small. This difference in dependence on the pixel photoelectron count can be explored using a quantity based on the scalar expectation term in the Fisher information matrix expression of Eq. (29).
For k = 1, …, K, the scalar expectation term corresponding to the kth pixel of a K-pixel image is easily verified to be the Fisher information with respect to the mean νθ,k of the Poisson-distributed photoelectron count due to the photons detected in the kth pixel. Therefore, the larger the value of this scalar term, the greater the amount of information that the data in the kth pixel contains about the mean νθ,k of the photoelectron count in the pixel, and the lower the bound on the standard deviation with which νθ,k can be estimated. As noted in Section 4.B, this term is also the part of the Fisher information expression for the kth pixel that, through its dependence on the probability distribution pθ,k of the data in the kth pixel, accounts for the deteriorative effects of the noise introduced by the particular detector that is used to capture the image. The value of this term therefore importantly provides a detector-dependent measure of the amount of information that the data in the kth pixel contains about νθ,k. More generally, it can be seen from Eq. (29) that this scalar term is a detector-dependent scaling factor for the estimation problem-dependent matrix portion of the Fisher information expression for the kth pixel. Therefore, it is also the case that the larger its value, the greater the amount of information that the data in the kth pixel carries about the vector θ of parameters to be estimated, and accordingly the lower the bound on the standard deviation with which each of those parameters can be determined based on the data in the kth pixel. It follows that for a given level of light νθ,k that impinges on the kth pixel, the scalar expectation term can be calculated for different detector noise settings and detector types to determine, by comparison, the detector and noise settings that yield data in the pixel with the highest information content with respect to θ. Comparisons using the expectation term are based solely on the expected amount of light νθ,k that is detected in the kth pixel, and do not depend on the particular estimation problem since, as noted in Section 4.B, the expectation term depends only on the value of νθ,k, and not on the definition of νθ,k or θ.
To facilitate the use of the scalar expectation term in assessing the information content of the data in the kth pixel, a meaningful point of reference for comparison is taken to be the expectation term 1/νθ,k (see Eq. (31)) corresponding to the Poisson data model. For a given νθ,k, this expectation term has the largest value compared with the expectation terms for the other pixelated data models because the Poisson data model represents the most ideal of the pixelated data models by assuming the absence of detector readout noise and therefore an uncorrupted photoelectron count in the kth pixel. This point of reference is incorporated through the definition of a quantity called the noise coefficient [27]. Denoted by αk, the noise coefficient for the kth pixel of a given detector is quite simply the ratio of the expectation term for the kth pixel of the detector to the expectation term 1/νθ,k for the corresponding pixel of the hypothetical detector assumed by the Poisson data model. It is given by
| (38) |
and note that the Fisher information matrix of Eq. (29) can easily be expressed in terms of this coefficient by substituting the expectation term with αk/νθ,k. The noise coefficient as defined conveniently takes on a minimum value of 0 and a maximum value of 1. It takes on a minimum value of 0 because νθ,k > 0, and because the expectation term, being the expected value of a squared expression, must be greater than or equal to 0. The minimum value of 0 is therefore attained when the expectation term is 0, which occurs in the extreme case in which the data in the kth pixel consists of only the detector’s readout noise, and hence carries no information about θ. The noise coefficient takes on a maximum value of 1 because the expectation term, as noted above, can at most be equal to 1/νθ,k. In other words, a maximum value of 1 is attained for the coefficient when the given detector is the Poisson data model-based reference detector itself, a scenario that represents the opposite extreme wherein the data in the kth pixel consists of only the photoelectron count, uncorrupted by readout noise.
For a practical detector described by the CCD/CMOS data model or the EMCCD data model, the noise coefficient thus takes on a value between 0 and 1. For a given light level νθ,k, a value close to 0, which results from a small expectation term, indicates that the data in the kth pixel is to a large extent corrupted by detector noise, and therefore contains little information about θ. On the other hand, a value close to 1, which results from a large expectation term, indicates that the data in the kth pixel is minimally corrupted by detector noise, and therefore contains close to the same amount of information about θ as the uncorrupted photoelectron count. Using the noise coefficient, comparison of the information content of the data in a pixel is thus reduced to a comparison of values between 0 and 1.
Noise coefficients αk calculated using Eq. (38) with the probability density functions of Eq. (32) and Eq. (34) for the CCD/CMOS and EMCCD data models, respectively, are shown in Fig. 8 as a function of the light level νθ,k. The noise coefficient curves corresponding to CCD detectors with 0.5-electron and 1-electron readout noise standard deviations can both be seen to approach the maximum value of 1 at large values of νθ,k, demonstrating that when enough photons can be detected in a pixel to render the readout noise insignificant, the data in the pixel is minimally corrupted and contains nearly the same amount of information about θ as the uncorrupted photoelectron count assumed by the Poisson data model. On the other hand, these two curves can be seen to approach the minimum value of 0 at values of νθ,k that are significantly less than 1, illustrating that when not enough photons can be detected in a pixel, the CCD detector’s readout noise dominates the data in the pixel to such an extent that the data contains almost no information about θ. A comparison of the two CCD noise coefficient curves also shows that a smaller readout noise standard deviation will, as expected, result in data containing larger amounts of information about θ, particularly over the range of νθ,k values between the convergence of the curves to 0 and the convergence of the curves to 1.
Fig. 8.
Comparing noise coefficients corresponding to the CCD and EMCCD data models. The noise coefficient αk for the kth pixel of an image is plotted as a function of the mean photoelectron count νθ,k in the pixel. Noise coefficients are shown for two EMCCD detectors operated at an electron multiplication gain of g = 1000, with readout noise of standard deviations σ0 = 24 electrons (□) and 48 electrons (+) in each pixel, and for two CCD detectors, with readout noise of standard deviations σ0 = 0.5 electrons (○) and 1 electron (◇) in each pixel. The readout noise mean is η0 = 0 electrons in all cases.
In terms of the EMCCD detector, Fig. 8 shows the noise coefficient curves corresponding to EMCCD detectors with 24-electron and 48-electron readout noise standard deviations and an electron multiplication gain of 1000 to both converge to the value 0.5 at large values of νθ,k. A noise coefficient value of 0.5 represents a halving of the maximum amount of information that the data in the pixel can carry about θ. As shown in [27], this halving of the maximum information content is consistent with the well-known excess noise factor [47, 67, 68] associated with stochastic electron multiplication, based on which it is commonly believed that the standard deviation with which a parameter can be estimated from an EMCCD image is at best the corresponding Poisson limit of accuracy multiplied by . While this is indeed approximately the case when a relatively large number of photons are detected in each pixel of an EMCCD image, there has been a misconception that the penalty applies generally for all EMCCD images. The two EMCCD noise coefficient curves in Fig. 8 thus importantly show that at values of νθ,k less than 1, substantially more than half of the maximum information content is in fact available in the pixel. This means that given an EMCCD image characterized by very low expected photoelectron counts in its pixels, the associated limits of accuracy are penalized, with respect to the corresponding Poisson limits of accuracy, by a factor that is potentially significantly less than and substantially closer to 1. The two EMCCD noise coefficient curves further demonstrate that, for a given light level νθ,k, the information content of the data in the pixel can be pushed closer to the maximum possible by lowering the EMCCD detector’s readout noise standard deviation. In [66], it is also shown that the same result can be realized by increasing the electron multiplication gain.
The noise coefficient curves of Fig. 8 thus corroborate the patterns exhibited by the CCD and EMCCD limits of accuracy in the example of Fig. 7(b). More generally, noise coefficient curves are useful as they allow an assessment, over a range of light levels, of the extent to which the information content of the data in a pixel is affected by a change in the detector type or a detector noise setting.
F. Effect of additional unknown parameters
An important factor that can impact the limit of the accuracy with which a parameter of interest (e.g., a positional coordinate of a molecule) can be estimated is the inclusion of other unknown parameters (e.g., the width of the point spread function that describes the molecule’s image, the rates at which photons are detected from the molecule and the background component) in the vector θ of parameters to be estimated. At best, the limit of the accuracy with which a parameter of interest can be estimated will not be affected by the inclusion of additional unknown parameters. In general, however, it can be expected to worsen, potentially significantly, as a result of the inclusion. Intuitively, this can be explained by the fact that having more unknowns will not contribute additional information about the parameters of interest, and if anything, can only make the overall estimation task more difficult.
Mathematically, the extent to which the limit of the accuracy for the determination of a parameter is deteriorated by the inclusion of other parameters in the estimation is related to the magnitudes of the off-diagonal elements of the Fisher information matrix. If element (i, j) of the matrix is small in magnitude, then the limit of the accuracy for estimating parameter θi can be expected to worsen by a relatively small amount as a result of the inclusion of parameter θj, and vice versa. In the special situation where the Fisher information matrix is diagonal (i.e., all off-diagonal elements are zero), the limit of the accuracy for estimating each parameter in θ is unaffected by the inclusion of the other parameters. This is in fact the case for the example of Section 4.A that considers the simultaneous estimation of a molecule’s positional coordinates and the rate of photon detection from an image described by the fundamental data model. Note that when the Fisher information matrix is diagonal, the second inequality in Eq. (17) becomes an equality, and the limit of the accuracy for estimating parameter θi is easily obtained as the square root of the inverse of the ith main diagonal element of the Fisher information matrix.
For a given problem, it is therefore useful to calculate and compare limits of accuracy corresponding to definitions of θ that include and exclude additional unknown parameters. If the limits of accuracy for estimating the parameters of interest deteriorate significantly with the inclusion of the additional unknown parameters, then one might consider independently estimating the additional unknown parameters and treating them as known parameters in the estimation of the parameters of interest. A critical assumption with this approach, however, is that the independent estimation of the additional unknown parameters is unbiased and very accurate, so that these parameters can effectively be considered as known parameters. For a study on how limits of accuracy are influenced by the inclusion of additional unknown parameters, see [69].
G. Attainment of limit of accuracy
A limit of accuracy is a lower bound on the standard deviation with which a parameter of interest can be determined by any unbiased estimator. Given an unbiased estimator, the question then naturally arises as to whether it can determine a parameter of interest with a standard deviation that equals the limit of accuracy (i.e., whether equality is achieved in Eq. (17) between the variance of the estimate of the parameter and the corresponding element in the inverse Fisher information matrix). This is often a difficult question to answer analytically, and in some cases, it is possible that no unbiased estimator exists whose standard deviation attains the limit. In the context of single molecule microscopy, however, it has been analytically proven [21] that in the special case of a stationary and in-focus molecule whose image is described by the 2D Gaussian function of Eq. (3) and is acquired under the conditions of the fundamental data model, with the exception that the same number of photons is guaranteed to be detected in each repeat image, the maximum likelihood estimator of the molecule’s x0 and y0 positional coordinates does in fact determine those parameters with standard deviations that equal their respective limits of accuracy (which happen to be identical). In terms of pixelated image data, studies using simulated data (e.g., [17, 21, 26, 27, 55]) have shown that in many practical scenarios, the maximum likelihood estimator can determine a parameter of interest with a standard deviation that comes close to the limit of accuracy.
5. EXTENSION TO MULTIPLE IMAGES
A basic assumption that is made throughout the presentation of Sections 4.A through 4.D is that parameters of interest are estimated from data consisting of a single image. The examples given therefore involve limits of accuracy that are calculated for estimation based on a single image. In many situations, however, the data from which parameters are to be determined comprises multiple images. The data can, for example, consist of a time sequence of images that capture the trajectory of a moving object, or comprise a set of images of an object that have been simultaneously acquired from distinct focal planes within a sample. In the former case, Cramér-Rao lower bounds have been derived [70] that predict the accuracies with which parameters such as the starting positional coordinates and the speed of an object moving in a trajectory of known shape can be estimated from an image sequence. In the latter case, limits of accuracy have been calculated [8, 24] to determine how well the axial coordinate z0 of a molecule can be estimated from a set of images acquired using multifocal plane microscopy (MUM) [71, 72] or a modality that implements the same principle of simultaneously imaging different focal planes within a sample [73–75]. Another example relates to the determination of distances of separation, where limits of accuracy have been computed [25, 76] for cases where images in which only one of the two molecules is detected are used, potentially in conjunction with an image in which both molecules are detected, to estimate the distance separating the two molecules.
Provided that the Nim images comprising a set are generated by stochastically independent photon detection processes and detector noise processes, the Fisher information matrix Iset(θ) corresponding to the set of Nim images is given simply by the sum of the Fisher information matrices corresponding to the individual images. Denoting the matrix for the kth image by Ik(θ), k = 1, …, Nim, the matrix Iset(θ) can be written as
| (39) |
Note that this result follows from the same principle that underlies the fact that, by the mutual independence of the data in its component pixels, the Fisher information matrix for a pixelated image is the sum of the Fisher information matrices corresponding to the individual pixels (see Eq. (28)). Indeed, a set of mutually independent pixelated images may be viewed as a single image comprising all the pixels, as the corresponding Fisher information matrix Iset(θ) is effectively a summation of the matrices corresponding to all the pixels in the set.
The use of MUM to overcome the poor depth discrimination of conventional microscopy provides a practical illustration of the calculation of limits of accuracy with which parameters can be estimated from a set of images. The poor depth discrimination capability of a conventional microscopy setup, in which images of an object of interest are captured from a single focal plane, refers to the fact that the closer an object is axially located with respect to the focal plane, the significantly more difficult it becomes to accurately determine its axial coordinate z0. This phenomenon can be appreciated by looking at the limit of accuracy δz0 for the estimation of z0 as a function of z0 itself. An example is shown in Fig. 9, where δz0 is calculated for the case where a CCD detector is used to image an out-of-focus and stationary molecule of interest. In the figure, δz0 corresponding to a conventional microscopy setup is seen to worsen, in severe fashion, as the axial location of the molecule approaches the focal plane at z0 = 0 nm from either above or below. In this example, δz0 is computed for an image acquired over the time interval [t0, t], using the Fisher information matrix of Eq. (33) by assuming a constant rate of detection Λ(τ) = Λ0, τ ≥ t0, of photons from the molecule, and a distribution profile for those photons given by fθ of Eq. (1), without the time dependence and with the image function qz0 given by the Born and Wolf image function of Eq. (4). The parameter vector is given by θ = (x0, y0, z0) ∈ ℝ3, and a time-independent and uniformly distributed background component is assumed.
Fig. 9.
Limits of the axial coordinate estimation accuracy for a conventional microscopy setup and a two-plane MUM setup. The limit of accuracy δz0 for the estimation of the z0 coordinate of an out-of-focus and stationary molecule from a conventional image (*) or a pair of two-plane MUM images (○) is plotted as a function of the coordinate z0. Focal planes 1 and 2 of the MUM setup are denoted by vertical dashed lines, and are located at z0 = 0 nm and z0 = 450 nm, respectively. The value of z0 is specified with respect to focal plane 1, which coincides with the focal plane of the conventional setup. In both setups, an image consists of an 11×11-pixel region, acquired using a CCD detector with a pixel size of 13 μm × 13 μm and readout noise with mean η0 = 0 electrons and standard deviation σ0 = 6 electrons at each pixel. The image of the molecule is described by the Born and Wolf image function. For the conventional setup, the molecule is laterally positioned such that the center of its image is located at 5.05 pixels in the x direction and 5.25 pixels in the y direction. Photons are detected from the molecule at a rate of Λ0 = 10000 photons/s over an acquisition time of t − t0 = 0.1 s, such that Λ0 · (t − t0) = 1000 photons are on average detected from the molecule over the detector plane (and 952.3 photons are on average detected from the molecule over a given image when the molecule is in focus). A background detection rate of is assumed, along with a uniform background spatial distribution of fb(x, y) = 1/20449 μm−2, such that there is a background level of β0 = 20 photoelectrons per pixel over the 11×11-pixel image. Photons of wavelength λ = 520 nm are collected by an objective lens with magnification M = 100 and numerical aperture na = 1.4. The refractive index of the immersion medium is n = 1.518. For the MUM setup, the collected molecule and background photons are split equally between the images corresponding to the two focal planes. Therefore, the photon detection rate is Λ0 = 5000 photons/s per image, and the background detection rate is per image. For the image corresponding to focal plane 1, all other details are as given for the conventional setup. For the image corresponding to focal plane 2, the magnification is M = 98.18, calculated using a formula from [76] for a plane spacing of Δzf = 450 nm and a tube length of 160 mm. The lateral position of the image of the molecule and the background spatial distribution are accordingly adjusted based on this slightly smaller magnification.
Different solutions to the depth discrimination problem have been proposed and demonstrated [71, 77–80], and MUM is one such solution. For a two-plane MUM solution in which a pair of images acquired from two different focal planes are used for the estimation of θ, the Fisher information matrix according to Eq. (39) is given by Iset(θ) = I1(θ) + I2(θ), where I1(θ) and I2(θ) are the Fisher information matrices corresponding to the images captured from focal planes 1 and 2. Assuming an equal splitting of the photons collected by the objective lens between the two images, and taking focal plane 1 to be the focal plane of the conventional setup, I1(θ) is given as described for the Fisher information matrix for the conventional setup, with the rates of photon and background detection reduced by 50%. The expression for I2(θ) is of the same form as I1(θ), but includes two modifications. First, assuming that focal plane 2 is positioned at a distance of Δzf above focal plane 1, the axial coordinate of the molecule with respect to focal plane 2 is given by z0 − Δzf. Second, the lateral magnification associated with focal plane 2 is different from the lateral magnification associated with focal plane 1, and is in this example determined using a geometrical optics-based formula from [76].
Figure 9 shows that δz0 computed using Iset(θ) for a two-plane MUM setup with a plane spacing of Δzf = 450 nm does not exhibit any severe deterioration at either focal plane. In fact, though it is not better than δz0 for the conventional setup at all values of z0, δz0 for the two-plane MUM setup remains relatively constant and small throughout the 1.5-μm axial range shown.
The improvement that a MUM setup offers over a conventional setup is dependent on the number of focal planes used, the spacings between the focal planes, and other experimental parameters. For a Fisher information-based analysis of the effects of these factors on the limit of accuracy δz0 for a MUM setup, see [62].
6. CONCLUSION
By taking into account the multitude of factors that influence the accuracy with which a parameter of interest can be estimated from an image, the information theory-based limit of accuracy represents a particularly useful tool for estimator evaluation and experimental design in single molecule microscopy. This tutorial has demonstrated the use of the mathematical framework introduced in [21, 22] over a decade ago to calculate limits of accuracy for an estimation problem. Specifically, it has described the photon detection process, various image data models, and various Fisher information expressions that constitute the ingredients for the computation of limits of accuracy. Importantly, the tutorial has used specific examples of estimation problems to illustrate the effects that different experimental parameters and object attributes have on the accuracy for estimating a parameter of interest. These examples demonstrate that by calculating and comparing limits of accuracy corresponding to different detector types and different values for parameters such as the expected number of detected photons, the wavelength of the detected photons, the effective pixel size, and the detector readout noise level, one can arrive at appropriate choices of detector, fluorophore, magnification, readout setting, and other aspects of an experimental setup that will yield the desired level of accuracy for the estimation of a parameter of interest from the acquired image data. The material presented in the tutorial represents a bringing together of some major results produced over the last decade or so that have made use of the mathematical framework. These results exemplify the ability of the framework to accommodate the analysis of different estimation problems. As the use of the Fisher information-based limit of accuracy becomes increasingly more common in the field of single molecule microscopy, it is expected that this framework will continue to serve as a useful blueprint for its calculation.
Acknowledgments
Funding. National Institutes of Health (NIH) (R01 GM085575).
Footnotes
OCIS codes: (180.2520) Fluorescence microscopy; (100.2960) Image analysis; (110.3055) Information theoretical analysis; (030.5290) Photon statistics; (000.5490) Probability theory, stochastic processes, and statistics.
References
- 1.Moerner WE, Fromm DP. Methods of single-molecule fluorescence spectroscopy and microscopy. Rev Sci Instrum. 2003;74:3597–3619. [Google Scholar]
- 2.Walter NG, Huang CY, Manzo AJ, Sobhy MA. Do-it-yourself guide: how to use the modern single-molecule toolkit. Nat Methods. 2008;5:475–489. doi: 10.1038/nmeth.1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Smith PR, Morrison IEG, Wilson KM, Fernández N, Cherry RJ. Anomalous diffusion of major histocompatibility complex class I molecules on HeLa cells determined by single particle tracking. Biophys J. 1999;76:3331–3344. doi: 10.1016/S0006-3495(99)77486-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Iino R, Koyama I, Kusumi A. Single molecule imaging of green fluorescent proteins in living cells: E-cadherin forms oligomers on the free cell surface. Biophys J. 2001;80:2667–2677. doi: 10.1016/S0006-3495(01)76236-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ober RJ, Martinez C, Lai X, Zhou J, Ward ES. Exocytosis of IgG as mediated by the receptor, FcRn: an analysis at the single-molecule level. Proc Natl Acad Sci USA. 2004;101:11076–11081. doi: 10.1073/pnas.0402970101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yu J, Xiao J, Ren X, Lao K, Xie XS. Probing gene expression in live cells, one protein molecule at a time. Science. 2006;311:1600–1603. doi: 10.1126/science.1119623. [DOI] [PubMed] [Google Scholar]
- 7.Dange T, Grünwald D, Grünwald A, Peters R, Kubitscheck U. Autonomy and robustness of translocation through the nuclear pore complex: a single-molecule study. J Cell Biol. 2008;183:77–86. doi: 10.1083/jcb.200806173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ram S, Prabhat P, Chao J, Ward ES, Ober RJ. High accuracy 3D quantum dot tracking with multifocal plane microscopy for the study of fast intracellular dynamics in live cells. Biophys J. 2008;95:6025–6043. doi: 10.1529/biophysj.108.140392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thompson MA, Casolari JM, Badieirostami M, Brown PO, Moerner WE. Three-dimensional tracking of single mRNA particles in Saccharomyces cerevisiae using a double-helix point spread function. Proc Natl Acad Sci USA. 2010;107:17864–17871. doi: 10.1073/pnas.1012868107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Deschout H, Cella Zanacchi F, Mlodzianoski M, Diaspro A, Bewersdorf J, Hess ST, Braeckmans K. Precisely and accurately localizing single emitters in fluorescence microscopy. Nat Methods. 2014;11:253–266. doi: 10.1038/nmeth.2843. [DOI] [PubMed] [Google Scholar]
- 11.Small A, Stahlheber S. Fluorophore localization algorithms for super-resolution microscopy. Nat Methods. 2014;11:267–279. doi: 10.1038/nmeth.2844. [DOI] [PubMed] [Google Scholar]
- 12.Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 13.Hess ST, Girirajan TPK, Mason MD. Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys J. 2006;91:4258–4272. doi: 10.1529/biophysj.106.091116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy STORM. Nat Methods. 2006;3:793–795. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Heilemann M, van de Linde S, Schüttpelz M, Kasper R, Seefeldt B, Mukherjee A, Tinnefeld P, Sauer M. Subdiffraction-resolution fluorescence imaging with conventional fluorescent probes. Angew Chem Int Ed. 2008;47:6172–6176. doi: 10.1002/anie.200802376. [DOI] [PubMed] [Google Scholar]
- 16.Cheezum MK, Walker WF, Guilford WH. Quantitative comparison of algorithms for tracking single fluorescent particles. Biophys J. 2001;81:2378–2388. doi: 10.1016/S0006-3495(01)75884-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Abraham AV, Ram S, Chao J, Ward ES, Ober RJ. Quantitative study of single molecule location estimation techniques. Opt Express. 2009;17:23352–23373. doi: 10.1364/OE.17.023352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shen Z, Andersson SB. Bias and precision of the fluoroBancroft algorithm for single particle localization in fluorescence microscopy. IEEE T Signal Proces. 2011;59:4041–4046. [Google Scholar]
- 19.Michalet X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys Rev E. 2010;82:041914. doi: 10.1103/PhysRevE.82.041914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liu S, Kromann EB, Krueger WD, Bewersdorf J, Lidke KA. Three dimensional single molecule localization using a phase retrieved pupil function. Opt Express. 2013;21:29462–29487. doi: 10.1364/OE.21.029462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ober RJ, Ram S, Ward ES. Localization accuracy in single-molecule microscopy. Biophys J. 2004;86:1185–1200. doi: 10.1016/S0006-3495(04)74193-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ram S, Ward ES, Ober RJ. A stochastic analysis of performance limits for optical microscopes. Multidim Syst Sign P. 2006;17:27–57. [Google Scholar]
- 23.Ram S, Ward ES, Ober RJ. How accurately can a single molecule be localized in three dimensions using a fluorescence microscope? Proc SPIE. 2005;5699:426–435. doi: 10.1117/12.587878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ram S, Chao J, Prabhat P, Ward ES, Ober RJ. A novel approach to determining the three-dimensional location of microscopic objects with applications to 3D particle tracking. Proc SPIE. 2007;6443:64430D. [Google Scholar]
- 25.Ram S, Ward ES, Ober RJ. Beyond Rayleigh’s criterion: a resolution measure with application to single-molecule microscopy. Proc Natl Acad Sci USA. 2006;103:4457–4462. doi: 10.1073/pnas.0508047103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chao J, Ram S, Abraham AV, Ward ES, Ober RJ. A resolution measure for three-dimensional microscopy. Opt Commun. 2009;282:1751–1761. doi: 10.1016/j.optcom.2009.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chao J, Ward ES, Ober RJ. Fisher information matrix for branching processes with application to electron-multiplying charge-coupled devices. Multidim Syst Sign P. 2012;23:349–379. doi: 10.1007/s11045-011-0150-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rao CR. Linear Statistical Inference and Its Applications. Wiley; 1965. [Google Scholar]
- 29.Kay SM. Fundamentals of Statistical Signal Processing: Estimation Theory. I. Prentice Hall PTR; 1993. [Google Scholar]
- 30.Aguet F, Van De Ville D, Unser M. A maximum-likelihood formalism for sub-resolution axial localization of fluorescent nanoparticles. Opt Express. 2005;13:10503–10522. doi: 10.1364/opex.13.010503. [DOI] [PubMed] [Google Scholar]
- 31.Holtzer L, Meckel T, Schmidt T. Nanometric three-dimensional tracking of individual quantum dots in cells. Appl Phys Lett. 2007;90:053902. [Google Scholar]
- 32.Pavani SRP, Piestun R. Three dimensional tracking of fluorescent microparticles using a photon-limited double-helix response system. Opt Express. 2008;16:22048–22057. doi: 10.1364/oe.16.022048. [DOI] [PubMed] [Google Scholar]
- 33.Aguet F, Geissbühler S, Märki I, Lasser T, Unser M. Superresolution orientation estimation and localization of fluorescent dipoles using 3-D steerable filters. Opt Express. 2009;17:6829–6848. doi: 10.1364/oe.17.006829. [DOI] [PubMed] [Google Scholar]
- 34.Thompson MA, Lew MD, Badieirostami M, Moerner WE. Localizing and tracking single nanoscale emitters in three dimensions with high spatiotemporal resolution using a double-helix point spread function. Nano Lett. 2010;10:211–218. doi: 10.1021/nl903295p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Stallinga S, Rieger B. Position and orientation estimation of fixed dipole emitters using an effective Hermite point spread function model. Opt Express. 2012;20:5896–5921. doi: 10.1364/OE.20.005896. [DOI] [PubMed] [Google Scholar]
- 36.Foreman MR, Török P. Fundamental limits in single-molecule orientation measurements. New J Phys. 2011;13:093013. [Google Scholar]
- 37.Agrawal A, Quirin S, Grover G, Piestun R. Limits of 3D dipole localization and orientation estimation for single-molecule imaging: towards Green’s tensor engineering. Opt Express. 2012;20:26667–26680. doi: 10.1364/OE.20.026667. [DOI] [PubMed] [Google Scholar]
- 38.Berglund AJ. Statistics of camera-based single-particle tracking. Phys Rev E. 2010;82:011917. doi: 10.1103/PhysRevE.82.011917. [DOI] [PubMed] [Google Scholar]
- 39.Michalet X, Berglund AJ. Optimal diffusion coefficient estimation in single-particle tracking. Phys Rev E. 2012;85:061916. doi: 10.1103/PhysRevE.85.061916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shechtman Y, Sahl SJ, Backer AS, Moerner WE. Optimal point spread function design for 3D imaging. Phys Rev Lett. 2014;113:133902. doi: 10.1103/PhysRevLett.113.133902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Quan T, Zeng S, Huang ZL. Localization capability and limitation of electron-multiplying charge-coupled, scientific complementary metal-oxide semiconductor, and charge-coupled devices for superresolution imaging. J Biomed Opt. 2010;15:066005. doi: 10.1117/1.3505017. [DOI] [PubMed] [Google Scholar]
- 43.Mortensen KI, Churchman LS, Spudich JA, Flyvbjerg H. Optimized localization analysis for single-molecule tracking and superresolution microscopy. Nat Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Deschout H, Neyts K, Braeckmans K. The influence of movement on the localization precision of sub-resolution particles in fluorescence microscopy. J Biophotonics. 2012;5:97–109. doi: 10.1002/jbio.201100078. [DOI] [PubMed] [Google Scholar]
- 45.Janesick JR. Scientific Charge-Coupled Devices. SPIE; 2001. [Google Scholar]
- 46.Hynecek J. Impactron - a new solid state image intensifier. IEEE T Electron Dev. 2001;48:2238–2241. [Google Scholar]
- 47.Hynecek J, Nishiwaki T. Excess noise and other important characteristics of low light level imaging using charge multiplying CCDs. IEEE T Electron Dev. 2003;50:239–245. [Google Scholar]
- 48.Fossum ER. CMOS image sensors: electronic camera-on-a-chip. IEEE T Electron Dev. 1997;44:1689–1698. [Google Scholar]
- 49.Bigas M, Cabruja E, Forest J, Salvi J. Review of CMOS image sensors. Microelectron J. 2006;37:433–451. [Google Scholar]
- 50.Goodman JW. Introduction to Fourier Optics. 2nd ed McGraw-Hill; 1996. [Google Scholar]
- 51.Chao J, Lee T, Ward ES, Ober RJ. Fluorescent microspheres as point sources: a localization study. PLoS ONE. 2015;10:e0134112. doi: 10.1371/journal.pone.0134112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Born M, Wolf E. Principles of Optics. Cambridge University; 1999. [Google Scholar]
- 53.Zhang B, Zerubia J, Olivo-Marin J-C. Gaussian approximations of fluorescence microscope point-spread function models. Appl Opt. 2007;46:1819–1829. doi: 10.1364/ao.46.001819. [DOI] [PubMed] [Google Scholar]
- 54.Stallinga S, Rieger B. Accuracy of the Gaussian point spread function model in 2D localization microscopy. Opt Express. 2010;18:24461– 24476. doi: 10.1364/OE.18.024461. [DOI] [PubMed] [Google Scholar]
- 55.Smith CS, Joseph N, Rieger B, Lidke KA. Fast, single-molecule localization that achieves theoretically minimum uncertainty. Nat Methods. 2010;7:373–375. doi: 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Huang F, Hartwich TMP, Rivera-Molina FE, Lin Y, Duim WC, Long JJ, Uchil PD, Myers JR, Baird MA, Mothes W, Davidson MW, Toomre D, Bewersdorf J. Video-rate nanoscopy using sCMOS camera-specific single-molecule localization algorithms. Nat Methods. 2013;10:653–658. doi: 10.1038/nmeth.2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Harris TE. The Theory of Branching Processes. Prentice-Hall; 1963. [Google Scholar]
- 58.Basden AG, Haniff CA, Mackay CD. Photon counting strategies with low-light-level CCDs. Mon Not R Astron Soc. 2003;345:985–991. [Google Scholar]
- 59.Ulbrich MH, Isacoff EY. Subunit counting in membrane-bound proteins. Nat Methods. 2007;4:319–321. doi: 10.1038/NMETH1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Newberry M. Technical note. Mirametrics, Inc; 1998. Pixel response effects on CCD camera gain calibration. http://www.mirametrics.com/tech_note_ccdgain.htm. [Google Scholar]
- 61.Ram S. PhD thesis. University of Texas; Arlington: 2007. Resolution and localization in single molecule microscopy. [Google Scholar]
- 62.Tahmasbi A, Ram S, Chao J, Abraham AV, Tang FW, Ward ES, Ober RJ. Designing the focal plane spacing for multifocal plane microscopy. Opt Express. 2014;22:16706–16721. doi: 10.1364/OE.22.016706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Inoué S. Foundations of confocal scanned imaging in light microscopy. In: Pawley JB, editor. Handbook of Biological Confocal Microscopy. 3rd ed Springer Science+Business Media, LLC; 2006. pp. 1–19. [Google Scholar]
- 64.Krull A, Steinborn A, Ananthanarayanan V, Ramunno-Johnson D, Petersohn U, Tolić-Nørrelykke IM. A divide and conquer strategy for the maximum likelihood localization of low intensity objects. Opt Express. 2014;22:210–228. doi: 10.1364/OE.22.000210. [DOI] [PubMed] [Google Scholar]
- 65.Snyder DL, Helstrom CW, Lanterman AD, Faisal M, White RL. Compensation for readout noise in CCD images. J Opt Soc Am A. 1995;12:272–283. [Google Scholar]
- 66.Chao J, Ram S, Ward ES, Ober RJ. Ultrahigh accuracy imaging modality for super-localization microscopy. Nat Methods. 2013;10:335–338. doi: 10.1038/nmeth.2396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Matsuo K, Teich MC, Saleh BEA. Noise properties and time response of the staircase avalanche photodiode. IEEE T Electron Dev. 1985;32:2615–2623. [Google Scholar]
- 68.Hollenhorst JN. A theory of multiplication noise. IEEE T Electron Dev. 1990;37:781–788. [Google Scholar]
- 69.Lin Z, Wong Y, Ober RJ. Proceedings of IEEE International Symposium on Circuits and Systems. IEEE; 2013. Influence of prior knowledge on the accuracy limit of parameter estimation in single-molecule fluorescence microscopy; pp. 1304–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wong Y, Chao J, Lin Z, Ober RJ. Effect of time discretization of the imaging process on the accuracy of trajectory estimation in fluorescence microscopy. Opt Express. 2014;22:20396–20420. doi: 10.1364/OE.22.020396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Prabhat P, Ram S, Ward ES, Ober RJ. Simultaneous imaging of different focal planes in fluorescence microscopy for the study of cellular dynamics in three dimensions. IEEE T Nanobiosci. 2004;3:237–242. doi: 10.1109/tnb.2004.837899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Prabhat P, Gan Z, Chao J, Ram S, Vaccaro C, Gibbons S, Ober RJ, Ward ES. Elucidation of intracellular recycling pathways leading to exocytosis of the Fc receptor, FcRn, by using multifocal plane microscopy. Proc Natl Acad Sci USA. 2007;104:5889–5894. doi: 10.1073/pnas.0700337104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Blanchard PM, Greenaway AH. Simultaneous multiplane imaging with a distorted diffraction grating. Appl Opt. 1999;38:6692–6699. doi: 10.1364/ao.38.006692. [DOI] [PubMed] [Google Scholar]
- 74.Abrahamsson S, Chen J, Hajj B, Stallinga S, Katsov AY, Wisniewski J, Mizuguchi G, Soule P, Mueller F, Darzacq CD, Darzacq X, Wu C, Bargmann CI, Agard DA, Dahan M, Gustafsson MGL. Fast multicolor 3D imaging using aberration-corrected multifocus microscopy. Nat Methods. 2013;10:60–63. doi: 10.1038/nmeth.2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Juette MF, Gould TJ, Lessard MD, Mlodzianoski MJ, Nagpure BS, Bennett BT, Hess ST, Bewersdorf J. Three-dimensional sub-100 nm resolution fluorescence microscopy of thick samples. Nat Methods. 2008;5:527–529. doi: 10.1038/nmeth.1211. [DOI] [PubMed] [Google Scholar]
- 76.Chao J, Ram S, Ward ES, Ober RJ. A comparative study of high resolution microscopy imaging modalities using a three-dimensional resolution measure. Opt Express. 2009;17:24377–24402. doi: 10.1364/OE.17.024377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kao HP, Verkman AS. Tracking of single fluorescent particles in three dimensions: use of cylindrical optics to encode particle position. Biophys J. 1994;67:1291–1300. doi: 10.1016/S0006-3495(94)80601-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Speidel M, Jonáš A, Florin EL. Three-dimensional tracking of fluorescent nanoparticles with subnanometer precision by use of off-focus imaging. Opt Lett. 2003;28:69–71. doi: 10.1364/ol.28.000069. [DOI] [PubMed] [Google Scholar]
- 79.Greengard A, Schechner YY, Piestun R. Depth from diffracted rotation. Opt Lett. 2006;31:181–183. doi: 10.1364/ol.31.000181. [DOI] [PubMed] [Google Scholar]
- 80.Sun Y, McKenna JD, Murray JM, Ostap EM, Goldman YE. Parallax: high accuracy three-dimensional single molecule tracking using split images. Nano Lett. 2009;9:2676–2682. doi: 10.1021/nl901129j. [DOI] [PMC free article] [PubMed] [Google Scholar]