Assessing systematic effects of stroke on motorcontrol by using hierarchical function-on-scalar regression

Abstract

This work is concerned with understanding common population-level effects of stroke on motor control while accounting for possible subject-level idiosyncratic effects. Upper extremity motor control for each subject is assessed through repeated planar reaching motions from a central point to eight pre-specified targets arranged on a circle. We observe the kinematic data for hand position as a bivariate function of time for each reach. Our goal is to estimate the bivariate function-on-scalar regression with subject-level random functional effects while accounting for potential correlation in residual curves; covariates of interest are severity of motor impairment and target number. We express fixed effects and random effects using penalized splines, and allow for residual correlation using a Wishart prior distribution. Parameters are jointly estimated in a Bayesian framework, and we implement a computationally efficient approximation algorithm using variational Bayes. Simulations indicate that the proposed method yields accurate estimation and inference, and application results suggest that the effect of stroke on motor control has a systematic component observed across subjects.

1 Introduction

Stroke is the leading cause of long-term disability in the United States, with an incidence of over 795,000 events each year (Go et al., 2013) – a rate that is expected to grow to over one million by 2025 (Broderick, 2004). Disability induced by stroke is manifested in many activities including motor control, speech, 1 and cognitive performance. Between 30–66% of stroke patients have clinically apparent motor deficits involving the upper extremity at 6 months (Kwakkel et al., 2003). Because of this, there is a great need for development of neurorehabilitative therapies to improve arm movements after stroke. One of the challenges in developing and testing therapeutic interventions to promote motor recovery after stroke is that it remains unclear to what extent these motor deficits are idiosyncratic (or subject-specific) rather than common across affected patients, and how these deficits vary according to the severity of motor impairment. A better understanding of these factors would allow for therapies that target the specific motor deficits that are shared by stroke patients, but perhaps to also tailor therapies based on individual characteristics, such as stroke severity.

In this current study we focus on the effects of stroke on motor control, which we define as the ability to make accurate, goal-directed movements. We use a planar reaching task designed to test a fundamental level of motor control (Kitago et al., 2013), and explore the relationship between patients’ performance on this task and the Fugl-Meyer Upper Extremity Motor Assessment (FM-UE, Fugl-Meyer et al. (1974)), a clinical measure of the severity of arm motor impairment, in a population of chronic stroke patients with residual arm paresis. Elderly healthy controls are included as a reference group.

In the reaching task, observations at the subject level are repeated two-dimensional motion trajectories to eight target directions parameterized by time. Our analytical approach for these multilevel bivariate functional data is to jointly model main effects for motor impairment and target direction, subject-level random effects, and residual correlation in a Bayesian function-on-scalar regression.

1.1 Two-dimensional Planar Reaching Data

We now describe the scientific setting and data structure in more detail. Our study population consists of patients who had a first time ischemic or hemorhagic stroke six or more months in the past, and have residual paresis of the affected arm (FM-UE less than the maximum score of 66). Exclusion criteria include multiple stroke events, hemorrhagic stroke, traumatic brain injury, major non-stroke medical illness that alters brain function, orthopedic or neurological condition that interferes with arm function, or inability to give informed consent. Selected patients exhibit moderate to severe motor impairment in the affected arm. Healthy controls with an age distribution similar to that in stroke patients are included as a reference group.

As a measurement of upper extremity motor control, subjects make repeated center-out arm reaching movements to 8 targets in the following experimental design. After subjects are seated to align the shoulder, elbow, and hand in the horizontal plane, the trunk is comfortably secured and the wrist and hand are immobilized with a splint. The forearm is supported on an air-sled system to reduce the effects of friction and gravity, diminishing the impact of strength deficits on motions and isolating motor control. Subjects make reaching movements from a central starting point to eight targets arranged equidistantly on a circle of radius 8cm around the starting point. The center-out reaching movements required can be performed by all but the most severely impaired subjects. Before data acquisition, a short introductory period familiarizes subjects with the experiment configuration. These data were collected as part of baseline assessments for two longitudinal stroke intervention studies (Kitago et al., 2013; Huang et al., 2012) and a study of cerebral blood ow after stroke (unpublished data), which were approved by the Columbia University Medical Center Institutional Review Board.

Kinematic data are recorded for each motion made by each subject. That is, we observe the X and Y coordinate of the hand position for as a function of time giving bivariate functional observations $(P_{ij}^X(t),P_{ij}^Y(t))$ for subjects i and motions j. Our dataset consists of 24 healthy controls, 25 mildly affected stroke patients (FM-UE 44 and above), and 8 severely affected stroke patients (FM-UE <44); all participants make 22 reaching motions with both their dominant and nondominant hands to each of the eight targets, giving 352 motions for each subject and roughly 20,000 overall bivariate functional observations (due to technical errors in recording, some motions are removed from the dataset). Although the data are inherently functional in nature, existing analyses have primarily focused on scalar summaries of observed trajectories including the deviation of endpoint from target, peak velocity, and curvature (Levin, 1996; Lang et al., 2006; Coderre et al., 2010).

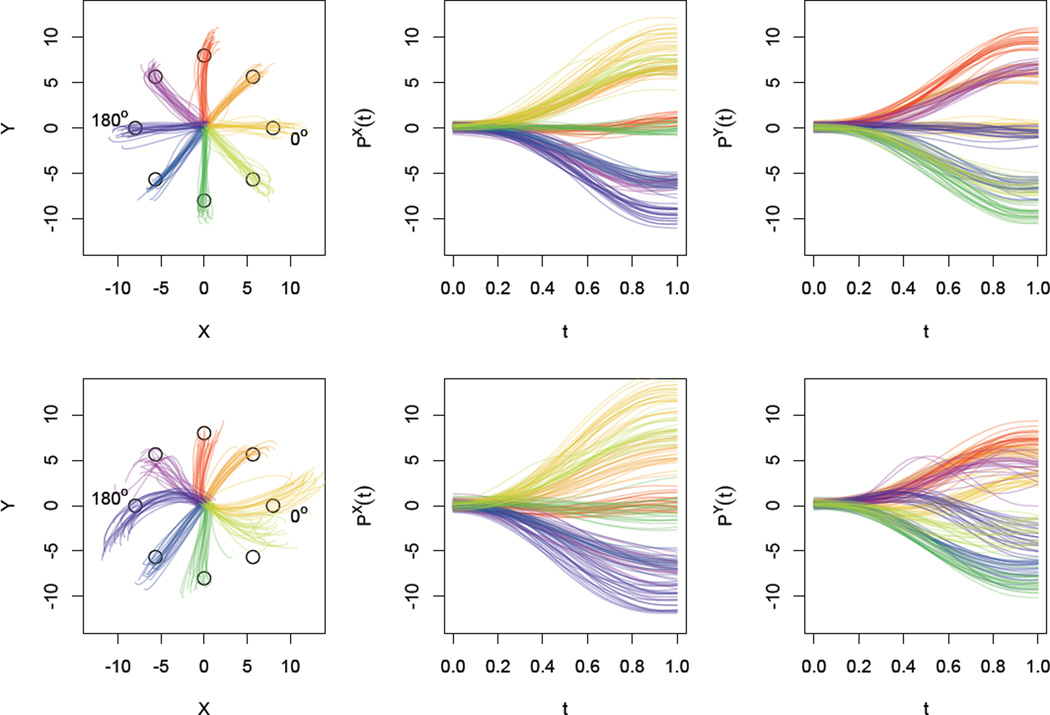
Figure 1 shows the observed data for one healthy control in the top row and one severely affected stroke patient in the bottom row. In the left column are complete trajectories, illustrating the full path of each reaching motion colored according to target. There are clear differences comparing the healthy control and stroke patient, particularly in the average motion made to each target: for instance, for the target at 0° the stroke patient exhibits both overextension and increased curvature with respect to the control subject. The middle and right columns show the constituent functions $P_{ij}^X(t)$ and $P_{ij}^Y(t)$ that make up the kinematic data for each trajectory – we will model these using a combination of population-level fixed effects, subject-level random effects, and curve-level FPCA effects. The stroke patient has unilateral tissue damage due to blockage of the right middle cerebral artery, which results in disrupted motor skill in the dominant arm.

Figure 1.

Observed data for two subjects; the top row shows the dominant hand of a healthy control, and the bottom row shows the affected dominant hand of a severe stroke patient. The left column shows observed kinematic data for all reaches observed in the dominant hand. The middle and right columns show the X- and Y- position separately for all reaches.

Our goal in this analysis is to explore the extent to which the effects of stroke on motor control are shared across subjects or are subject-specific through a regression analysis using a combination of subject-level scalar covariates, such as the Fugl-Meyer measure of impairment severity, as predictors of interest. Evidence for systematic effects of stroke on motor control would indicate that the induced control abnormality is not entirely subject specific, but rather that disrupting the motor cortex or its descending pathways leads to predictable deficits in upper extremity motor control. The data structure necessitates correctly accounting for subject-level effects through the inclusion of random functional intercepts, and accurate inference depends on incorporating residual correlation. Throughout, our outcome is the bivariate kinematic function for hand position over time.

1.2 Statistical Methods

Conceptually, we observe functional data $[P_{ij}^X(t),P_{ij}^Y(t),{\mathit{w}}_i]$ for subjects i = 1, …, I and visits j = 1, … J_i for a total number of observations n = ∑_i J_i. In our application $P_{ij}^X(t),P_{ij}^Y(t)$ are the X and Y position curves indexed by time t ∈ [0, 1] and w_i = [w_i1, …, w_ip] is a length p vector of scalar covariates. We propose the model

$$\{\begin{array}{c}{P}_{ij}^X(t)={\beta }_0^X(t)+{\mathrm{\Sigma }}_{k=1}^p{w}_{ik}{\beta }_k^X(t)+b_i^X(t)+{\epsilon }_{ij}^X(t)\hfill \\ P_{ij}^Y(t)={\beta }_0^Y(t)+{\mathrm{\Sigma }}_{k=1}^p{w}_{ik}{\beta }_k^Y(t)+b_i^Y(t)+{\epsilon }_{ij}^Y(t)\hfill \end{array}$$ (1)

where ${\beta }_k^X(t),{\beta }_k^Y(t)$ are fixed effects associated with scalar covariates, $b_i^X(t),b_i^Y(t)$ are subject-specific random effects, and ${\epsilon }_{ij}^X(t),{\epsilon }_{ij}^Y(t)$ are potentially correlated residual curves. Penalized splines are used to estimate fixed and random effects; although many options are possible, we will use a cubic B-splines basis with a combined zeroth and second derivative penalty throughout. All parameters are modeled in a Bayesian framework that allows the joint modeling of the mean structure (through fixed and random effects) and residual correlation (through the error covariance matrix) in a single Gibbs sampler. Importantly, a variational Bayes algorithm provides a computationally efficient and accurate approximation to the full sampler. Model 1 is analogous to a standard mixed model with subject-level random intercepts; the identifiability of fixed and random effects will depend on the prior specification, hyperparameter selection and sampling framework, which we discuss in Sections 2.1 and 2.3.

In practice, observations are not truly functional but are observed as structured discrete vectors. For notational simplicity, we assume functional observations lie on a dense grid of the domain [0, 1] with D elements, and that this grid is common to all subjects. In our application, trajectories are observed at 120Hz. Although efforts were made to ensure uniform motion times of approximately .5 seconds, motions take different times to complete and we use a linear registration to obtain a common, evenly-space observation grid of length D = 25 prior to analysis. After registration, motions are observed from t = 0 to t = 1 with 0 and 1 indicating the beginning and end of the motion, respectively. Despite being observed as vectors, objects that are functional in nature will be denoted as f(t) where appropriate to emphasize the structure underlying the data.

There is a large body of existing work for the analysis of functional outcome models. We broadly consider two methodological categories, the first of which consists of approaches that seek to estimate each curve in the dataset. Brumback and Rice (1998) posed a function-on-scalar regression in which population-level coefficients and curve-level deviations are modeled using penalized splines; for computational convenience, intercepts and slopes for curve-level effects were treated as fixed effects. Guo (2002) extended this approach by formulating curve-specific deviations as random effects. Due to the difficulty in estimating all curves using penalized splines, these approaches can be computationally intensive for large datasets. Functional principal component methods for cross sectional data (Yao et al., 2005), as well as recent extensions for multilevel (Di et al., 2009), longitudinal (Greven et al., 2010), and spatially correlated data (Staicu et al., 2010), have modeled curve-specific deviations from a population mean using low-dimensional basis functions estimated from the empirical covariance matrix. These methods did not focus on the flexible estimation of the population mean surface; moreover in assessing uncertainty these methods implicitly conditioned on estimated decomposition objects, which can lead to the understatement of total variability (Goldsmith et al., 2013).

Alternatively, one can view individual curves as errors around the population- or subject-level mean of interest. This approach is described in (Ramsay and Silverman, 2005, §13.4), in which fixed effects at the population level are estimated using penalized splines but individual curves are not directly modeled. Reiss et al. (2010) built on this approach by taking advantage of the inherent connection between penalized splines and ridge regression to develop fast methods for leave-one-out cross validation to select tuning parameters. Scheipl et al. (2013) proposed a very flexible class of functional outcome models, allowing cross sectional or multilevel data as well as scalar or functional predictors and estimating effects in a mixed model framework; a robust software implementation of this method is provided in the refund R package (Crainiceanu et al., 2012). A drawback of these approaches is the assumption that error curves consist only of uncorrelated measurement error despite clear correlation in the functional domain. One alternative, proposed by Reiss et al. (2010), is an iterative procedure to estimate the mean structure and then, using this mean, the residual covariance matrix followed by a re-estimation of the mean using generalized least squares. Doing so necessarily increases the computational burden and does not allow joint estimation of the mean and covariance; additionally, coverage properties of this approach have not been presented.

Several Bayesian methods for function-on-scalar regression exist in the literature. Morris et al. (2003) developed wavelet-based functional mixed models (FMMs) assuming residual curves consist of independent measurement errors; Morris and Carroll (2006) extended this to allow correlated residual curves. Both approaches used a discrete wavelet transform (DWT) of the observed data and model coefficients in the wavelet domain using spike-and-slab priors. It was assumed that errors in the wavelet domain are independent, justified heuristically by the whitening property of the DWT. After modeling using MCMC, the inverse DWT provided estimates in the observed space. A penalized spline approach for FMMs was taken in Baladandayuthapani et al. (2007), while Baladandayuthapani et al. (2010) used a piecewise constant basis; in both cases, correlated residual curves are explicitly modeled rather than treated as errors around the mean. For cross-sectional functional data observed sparsely at the subject level, Montagna et al. (2012) developed a Bayesian latent factor model in which predictors are incorporated at the latent factor level; a potentially large number of factors are allowed, and sparsity is induced through a shrinkage prior on the basis coefficients. The computation burden of the Bayesian procedures can be prohibitive for data exploration and model building even for moderate datasets, which has contributed to the slow adoption of Bayesian methods in functional data analysis. As an example, a comparison of the Bayesian penalized spline method in Baladandayuthapani et al. (2007) to an FPCA-based method on simulated data found computation times of five hours versus five seconds (Staicu et al., 2010).

This paper presents several methodological advancements. We develop a Bayesian framework for penalized spline function-on-scalar regression, allowing the joint modeling of population-level fixed effects, subject-level random effects and residual covariance. Dramatic computational improvements compared to the fully Bayesian and, surprisingly, to a frequentist mixed model approaches are obtained through a variational Bayes approximation that is fast and accurate. This algorithm enables model selection and comparison, which for large datasets is infeasible with competing approaches. Novelly in multilevel function-on-scalar regression, we consider bivariate functional data as the outcome of interest. Finally, the size and structure of the motivating dataset – which consists of nearly 20,000 trajectories, nested within subjects and depending on target, impairment severity and affected hand as covariates – is unique in the functional data analysis literature.

The remainder of the paper is organized as follows. We discuss the model formulation and the variational Bayes approximation in Section 2. In Section 3 we conduct simulations designed to mimic the motivating data. Section 4 presents the analysis of the complete dataset. We close with a discussion in Section 5. The web-based supporting materials present the complete Gibbs sampler and variational Bayes algorithm. R implementations of all proposed methods and complete simulation code are publicly available.

2 Methods

We begin by focusing on a simplification of model (1) for univariate functional data in Sections 2.1, 2.2 and 2.3. These Sections develop our methodology for estimating fixed effects, random effects, and residual covariance when a single functional response is observed. Once this is established, we consider the bivariate model in Section 2.4.

2.1 Full Model

For now, assume data are [Y_ij(t),w_i] for subjects i = 1, …, I and visits j = 1, … J_i, giving a total of n = ∑_i J_i functional observations. Univariate functional outcomes Y_ij(t) are observed on a regular grid of length D for all subjects and visits. We pose the outcome model

$${\mathit{y}}_{ij}={\mathit{w}}_i\mathit{\beta }+{\mathit{z}}_{ij}\mathit{b}+{\mathit{\epsilon }}_{ij}\text{ with }{\mathit{\epsilon }}_{ij}~\mathrm{N}[0,\mathrm{\Sigma }]$$ (2)

where y_ij is the 1 × D observed functional outcome; w_i and z_ij are fixed and random effect design vectors of size 1 × p and 1 × I respectively; β and b are fixed and random effect coefficient matrices of size p × D and I × D, respectively; and ε_ij is a 1 × D vector of residual curves distributed N[0, Σ] where Σ is a D × D covariance matrix. Errors ε_ij are conditionally independent given fixed effects and subject-specific random effects, and are iid across subjects and visits.

We express the functional effects in the rows of β and b using a spline expansion. Let Θ denote a D × K_θ cubic B-spline evaluation matrix with K_θ basis functions. Further let B_W and B_Z denote the matrices whose columns are basis coefficients for β and b respectively, so that β = [ΘB_W]^T and b = [ΘB_Z]^T. (This notation is drawn from Ramsay and Silverman (2005, Section 13.4.3) and Reiss et al. (2010); readers should note potential conicts in notation, particularly with Montagna et al. (2012) and references therein.)

Penalization is a commonly-used technique to avoid overfitting and induce smoothness in functional effects. For spline coefficients in the kth column B_W,k of B_W and ith column B_Z,i of B_Z, we assume that $B_{W,k}~\mathrm{N}[0,{\sigma }_{W,k}^2{P}^{-1}]$ and $B_{Z,i}~\mathrm{N}[0,{\sigma }_Z^2{P}^{-1}]$. P is a known penalty matrix shared across fixed and random effects to enforce a common penalty structure. Variances $\{{\sigma }_{W,k}^2\}$ are unique to each coefficient function to allow unique levels of smoothness, and ${\sigma }_Z^2$ is shared across random effects so that they are draws from a common population. Notationally, the “zeroth” column B_W,0 of B_W and the variance ${\sigma }_{W,0}^2$ correspond to the intercept β₀(t). The connection between this prior specification and a quadratic roughness penalty well known; see Ruppert et al. (2003, Ch. 4.9) for a detailed treatment. The choice of penalty matrix P is discussed in Section 2.3. In this penalized spline framework, the number and position of knots is typically unimportant provided that the number is sufficient to model the complexity of the coefficient functions (Ruppert, 2002). Using this specification, model (2) can be expressed as

$${\mathit{y}}_{ij}={\mathit{w}}_i{B}_W^T{\mathrm{\Theta }}^T+{\mathit{z}}_{ij}{B}_Z^T{\mathrm{\Theta }}^T+{\mathit{\epsilon }}_{ij}$$

$${\mathit{\epsilon }}_{ij}~\mathrm{N}[0,\mathrm{\Sigma }]$$

$$B_{Z,i}~\mathrm{N}[0,{\sigma }_Z^2{P}^{-1}]\text{ for }i=1\dots I$$

$$B_{W,k}~\mathrm{N}[0,{\sigma }_{W,k}^2{P}^{-1}]\text{ for }k=0\dots p$$ (3)

which has a form similar to a traditional mixed model.

The variance components $\{{\sigma }_{W,k}^2\},{\sigma }_Z^2$ are assigned inverse-gamma priors, and our model specification is completed using an inverse Wishart prior for the residual covariance matrix Σ. Although these priors are convenient for the development of a straightforward Gibbs sampler and for the derivation of the variational approximation in Section 2.2, they have been criticized by several researchers (Gelman, 2006; Yang and Berger, 1994). Inverse-gamma priors can be sensitive to the choice of hyperparameters a and b, especially for “uninformative” values like a = b = .001 that place a large prior mass near zero, and inverse-Wishart priors may not shrink eigenvalues as expected. In Section 2.3 we suggest using the data to help choose hyperparameters in a reasonable way, but emphasize the need for sensitivity analyses to these choices.

Following Gelfand et al. (1995), we pursue an alternative parameterization of model (3) to improve sampling performance through hierarchical recentering. For a simple example of this idea, consider the (non-functional) model y_ij = μ + b_i + ε_ij with priors for μ and b_i having mean zero; alternatively one could let Y_ij = η_i + ε_ij with the prior for η_i having mean α and the prior for α having mean zero. The latter parameterization often results in better behavior of the posterior chains and increased identifiability of fixed and random effects. For our function-on-scalar regression model, let Y be an n × D matrix of row-stacked functional outcomes, Z be the random effects design matrix, W be the fixed effects matrix constructed by row-stacking the w_i, and ⊗ represent the Kronecker product operator. Using hierarchical recentering, we reparameterize model (3) using

$$Y=Z{B}_Z^T{\mathrm{\Theta }}^T+\epsilon$$

$$\epsilon ~\mathrm{N}[0,\mathrm{\Sigma }\otimes I_n];\mathrm{\Sigma }~\mathrm{I}\mathrm{W}[\nu ,\mathrm{\Psi }]$$

$$B_{Z,i}~\mathrm{N}[B_W{\mathit{w}}_i^T,{\sigma }_Z^2{P}^{-1}]\text{ for }i=1\dots I;{\sigma }_Z^2~\mathrm{I}\mathrm{G}[a_Z,b_Z]$$

$$B_{W,k}~\mathrm{N}[0,{\sigma }_{W,k}^2{P}^{-1}],{\sigma }_{W,k}^2~\mathrm{I}\mathrm{G}[a_{W,k},b_{W,k}]\text{ for }k=1\dots p.$$ (4)

Full conditionals for all model parameters are straightforward to obtain using vector notation and Kronecker products. For matrix M and vector c, let vec (M) be the vector formed by concatenating the columns of M and diag (c) be the matrix with elements of c on the main diagonal and zero elsewhere. Further let “rest” include both the observed data and all parameters not currently under consideration. As an example of the full conditional distributions resulting from model (4), it can be shown that

$$p[\text{vec }(B_W)|\text{rest}]\propto \mathrm{N}[{\mu }_{B_W},{\mathrm{\Sigma }}_{B_W}]$$

where

$${\mathrm{\Sigma }}_{B_W}={(\frac{1}{{\sigma }_Z^2}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)(W\otimes I_{K_{\theta }})+\text{diag }(\frac{1}{{\sigma }_{W,k}^2})\otimes P)}^{-1}$$

and

$${\mu }_{B_W}={\mathrm{\Sigma }}_{B_W}(\frac{1}{{\sigma }_Z^2}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)\text{vec }(B_Z)).$$

Additionally, we have that

$$p[{\sigma }_{W,k}^2|\text{rest}]\propto \mathrm{I}\mathrm{G}[a_{W,k}+\frac{K_{\theta }}{2},b_{W,k}+B_{W,k}^{T}P{B}_{W,k}].$$

Complete derivations of this and all other full conditional distributions are provided in the web-based supplementary materials.

Model (4) contains a large number of parameters, particularly in the spline coefficient matrices B_W and B_Z. Typically the available data for estimation in the n × D outcome matrix Y will dwarf the number of parameters in B_W and B_Z, meaning these can be well-estimated. However, in some cases it may be necessary to use a low-dimensional spline basis or other parametric approach for the estimation of fixed and random effects. This is possible using a simplification of model (4), but it should be noted the choice of parametric form will be an implicit tuning parameter that replaces the explicit penalization implemented above. When the number of observed points per curve D is large the covariance matrix Σ will also be large, and the number of parameters in this matrix could be substantial; again, a modification of model (4) to use a parametric form for Σ is possible and perhaps advisable in this case, although the caveats regarding the introduction of a parametric structure still apply. In our motivating dataset n is large (≈ 20000) while D is modest (50 for bivariate curves), and model (4) is reasonable.

2.2 Variational Bayes

Variational Bayes methods are regularly used in the computer science literature, and to a more limited extent in the statistics literature, to provide approximate solutions to intractable inference problems (Jordan, 2004; Jordan et al., 1999; Titterington, 2004; Ormerod and Wand, 2012). These tools have also been used somewhat rarely in functional data analysis (Goldsmith et al., 2011; McLean et al., 2013; van der Linde, 2008). Here we review variational Bayes only as much as needed to develop an iterative algorithm for approximate Bayesian inference in penalized function-on-scalar regression; for a more detailed overview see Ormerod and Wand (2010) and Bishop (2006, Chapter 10). We emphasize that the variational Bayes approach is not intended to supplant a more complete MCMC sampler, but rather is an appealing computationally efficient approximation that is useful for model building and data exploration.

Let y and ϕ represent respectively the full data and parameter collection. The goal of variational Bayes methods is to approximate the full posterior p(ϕ|y) using q(ϕ), where q is restricted to a class of functions that are more tractable than the full posterior distribution. From the restricted class of functions, we wish to choose the element q* that minimizes the Kullback-Leibler distance from p(ϕ|y). Divergence between p(ϕ|y) and q(ϕ) is measured using $L_q=\int q(\mathit{\varphi })\text{log}\frac{p(\mathit{y},\mathit{\varphi })}{q(\mathit{\varphi })}d\mathit{\varphi }$, the q-specific lower bound on the marginal log-likelihood log p(y); maximizing L_q across the class of candidate functions gives the best possible approximation to the full posterior distribution. To make the approximation tractable, the candidate functions q(ϕ) are products over a partition of ϕ, so that $q(\mathit{\varphi })={\prod }_{l=1}^L{q}_l({\varphi }_l)$, and each q_l is a parametric density function. It can be shown that the optimal $q_l^{*}$ densities are given by

$$q_l^{*}({\varphi }_l)\propto \text{ exp }[E_{{\varphi }_{-l}}\text{ log }p(\mathit{y},\varphi )]\propto \text{ exp }[E_{{\varphi }_{-l}}\text{ log }p({\varphi }_l|\text{rest})]$$

where, again, rest ≡ {y, ϕ₁, …, ϕ_l−1, ϕ_l+1, …, ϕ_L} is the collection of all remaining parameters and the observed data. In practice, one sets initial values for each of the ϕ_l and updates the respective optimal densities iteratively, similarly to a Gibbs sampler, while monitoring the q-specific lower bound L_q for convergence.

For the function-on-scalar regression model shown in Equation (4), we assume

$$q(B_Z,B_W,{\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })=q(B_Z)q(B_W)q({\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })$$

where the functions q are distinguished by their argument rather than by subscript l. The additional factorization

$$q(B_Z,B_W,{\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })=(\prod _{i=1}^{I}q(B_{Z,i}))q(B_W)(\prod _{k=0}^{p}q({\sigma }_{W,k}^2))q({\sigma }_Z^2)q(\mathrm{\Sigma })$$

is induced by the conditional independence properties of the joint distribution (see Bishop (2006, Sec. 10.2.5); a directed acyclic graph of our model appears in Figure A.1). Using this factorization, it can be shown that the optimal density q*(vec (B_W)) for is N [μ_q(BW),Σ_q(BW)], where

$${\mathrm{\Sigma }}_{q(B_W)}=({\mu }_{q(1/{\sigma }_Z^2)}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)(W\otimes I_{K_{\theta }})+\text{diag }({\mu }_{q(1/{\sigma }_{W,k}^2)})\otimes P{)}^{-1}$$

and

$${\mu }_{q(B_W)}={\mathrm{\Sigma }}_{q(B_W)}({\mu }_{q(1/{\sigma }_Z^2)}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)\text{vec }({\mu }_{q(B_Z)})).$$

In the above, the notation μ_q(ϕ) and Σ_q(ϕ) indicate the mean and variance of the density q(ϕ). Thus, the optimal density q*(vec (B_W)) is Normal with mean and variance completely determined by the data and the parameters of the remaining densities. Similar expressions are obtained for all model parameters. Together, these forms suggest an iterative algorithm in which each density is updated in turn using the parameters from the remaining densities; convergence of this algorithm is monitored through L_q, the q-specific lower bound of the marginal log-likelihood. The iterative algorithm and the form for L_q are provided in the web-based supplementary materials.

2.3 Choice of penalty matrix, hyperparameters, and initial values

In both the Gibbs sampler presented in Section 2.1 and in density updates for the variational Bayes algorithm described in 2.2, it is not necessary that the penalty matrix P be of full rank: although this introduces improper priors for the functional effects, the posteriors are proper. However the lower bound L_q, used to monitor convergence of the variational Bayes algorithm, contains a term of the form log(|P⁻¹|), thus requiring P to be full rank. For this reason, we propose to use P = αP₀ + (1 − α)P₂, where P₀ and P₂ are the matrices corresponding to zeroth and second derivative penalties. The P₂ penalty matrix is commonly used in functional data analysis and enforces smoothness in the estimated function, but is noninvertible. The P₀ penalty matrix is the identity matrix, induces general shrinkage and is full rank. Details on the construction of P₀ and P₂ are available in Eilers and Marx (1996). Selecting 0 < α ≤ 1 balances smoothness and shrinkage, and results in a full rank penalty matrix. There is can be some sensitivity to the choice of α, with large values shrinking estimates toward 0; we recommend a relatively small value (α = 0.01 or smaller) in keeping with the tendency to enforce smoothness rather than shrinkage.

We use the following procedure based on model (4) to choose hyperparameters. First, we estimate B_Z using ordinary least squares from the regression $\mathrm{E}[Y]=Z{B}_Z^T{\mathrm{\Theta }}^T$ to obtain $B_Z^{OLS}$. We estimate the error covariance Σ using a functional principal components decomposition of the residuals from this regression to obtain Σ̂ (Yao et al., 2005), and use ν = ∑_i J_i, Ψ = ∑_i J_iΣ̂ as hyperparameters in the prior for Σ. Next, we estimate B_W using weighted least squares from the regression $\mathrm{E}\left[{(B_Z^{OLS})}^T\right]=W{B}_W^T$ with weight matrix P⁻¹ to obtain $B_W^{WLS}$. We choose

$$a_z=\frac{I*K_{\theta }}{2},b_z=\frac{1}{2}\text{tr }\left[{({(B_Z^{OLS})}^T-W{(B_W^{WLS})}^T)}^{T}P\right({(B_Z^{OLS})}^T-W{(B_W^{WLS})}^T\left)\right]$$

and

$$a_{W,k}=\frac{K_{\theta }}{2},b_{W,k}=\frac{1}{2}{(B_{W,k}^{WLS})}^{T}P(B_{W,k}^{WLS})$$

motivated by the form of the full conditionals for these variance components.

This procedure avoids the default “uninformative” choice a_z = b_z = a_W,k = b_W,k = .001, which places a large prior mass near zero for all variance components. Such a choice favors overshrinkage of fixed and random effects toward zero. In our application, we found that using this default tended to result in the incorporation of subject-level random effects into the error variance Σ. Sensitivity to the choice of tuning parameters should be assessed in each application, and weakly informative priors used where possible; see Section 4.2 and the web-based supplementary materials for details of a sensitivity analysis for our application.

Initial values are sampled from a N[0, 100] for spline coefficients and from a Uniform[.1, 10] for variance components. The starting value for Σ is σ²I_D where σ² is Uniform[.1, 10]. For other applications, different starting values may be needed.

2.4 Bivariate data

In the preceding we have focused on a univariate outcome for clarity of exposition while introducing methods. In this section we describe the bivariate outcome model. Only straightforward modifications to the Gibbs sampler and variational Bayes updates given in Sections 2.1 and 2.2, respectively, are needed for this setting. Similar extensions to three or more curves observed over a common domain proceed similarly.

Let Y = [Y₁Y₂] be the concatenation of two outcome matrices Y₁ and Y₂ (in our example, we concatenate the X and Y position curves so that Y = [P^XP^Y]). Next, let $B_W^T=[B_{1,W}^T,B_{2,W}^T]$ so that the columns of B_W concatenate the fixed effect spline coefficients for Y₁ and Y₂. Similarly, let $B_Z^T=[B_{1,Z}^T,B_{2,Z}^T]$ so that the columns of B_Z concatenate the random effect spline coefficients for Y₁ and Y₂. Then $B_Z^T(I_2\otimes {\mathrm{\Theta }}^T)$ contains subject-specific random effects for the overall outcome matrix Y. For spline coefficients in columns B_W,k we assume that $B_{W,k}~\mathrm{N}[0,\text{diag}({\sigma }_{1,W_k}^2,{\sigma }_{2,W_k}^2)\otimes P^{-1}]$, so that fixed effects for Y₁ and Y₂ are penalized separately and assumed independent a priori. A similar specification is used for the columns B_Z,i, and variance components are assigned inverse-gamma priors. Again using a hierarchical formulation, for bivariate data our complete model is

$$Y=Z{B}_Z^T(I_2\otimes {\mathrm{\Theta }}^T)+\epsilon$$

$$\epsilon ~\mathrm{N}[0,\mathrm{\Sigma }\otimes I_n];\mathrm{\Sigma }~\mathrm{I}\mathrm{W}[\nu ,\mathrm{\Psi }]$$

$$B_{Z,i}~\mathrm{N}[B_W{\mathit{w}}_i^T,\text{diag }({\sigma }_{1,Z,}^2,{\sigma }_{2,Z}^2)\otimes P^{-1}]\text{ for }i=1\dots I$$

$${\sigma }_{m,Z}^2~\mathrm{I}\mathrm{G}[a_{m,Z},b_{m,Z}]\text{ for }m=1,2$$

$$B_{W,k}~\mathrm{N}[0,\text{diag }({\sigma }_{1,W_k}^2,{\sigma }_{2,W_k}^2)\otimes P^{-1}]$$

$${\sigma }_{m,W_k}^2~\mathrm{I}\mathrm{G}[a_{m,W_k},b_{,m{W}_k}]\text{ for }m=1,2\text{ and }k=1\dots p.$$ (5)

This model extends the univariate outcome model (4), but the Gibbs sampler and variational Bayes approximations can be directly modified for bivariate data. Similarly, the method for setting initial values and choosing hyperparameters given in Section 2.3 can be adapted to model (5).

This bivariate model is motivated by the data structure, in which X and Y position curves are observed concurrently for all motions – in that sense, the bivariate model is more faithful to the observed data than fitting separate univariate models. A bivariate model also explicitly models correlation in X and Y position error curves. In our application, this correlation may provide insight into sensory or visual feedback in reaching motions, or into the biomechanical processes involved. Nonetheless, it is possible to fit a bivariate model using two separate univariate models, especially if X and Y errors are uncorrelated or if this correlation is not scientifically meaningful.

3 Simulations

We demonstrate the performance of our method using a simulation in which generated data mimic the motivating application; all code needed to reproduce these simulations is available on the first author’s website. Our simulations consider three groups: control subjects’ dominant hand; the affected dominant hand of moderately affected stroke patients; and the affected dominant hand of severely affected stroke patients. We therefore created a three-level categorical predictor with Groups 1, 2, and 3 referring to controls, moderately affected subjects, and severely affected subjects.

Curves are observed on a common grid of length D = 25. Data are generated from the univariate outcome model y_ij = w_iβ + b_i + ε_ij where w_i is a length-3 binary vector indicating group membership for subject i, β is a 3 × D matrix whose rows are group average curves, b_i is a length-D random effect, and ε_ij is a residual vector. For each simulated dataset, the predictors w_i are sampled from a multinomial distribution with probabilities set to the proportions of each group in the motivating data, random effects b_i are drawn from a N [0, Σ^b] and residuals ε_ij are drawn from a N[0,Σ^ε].

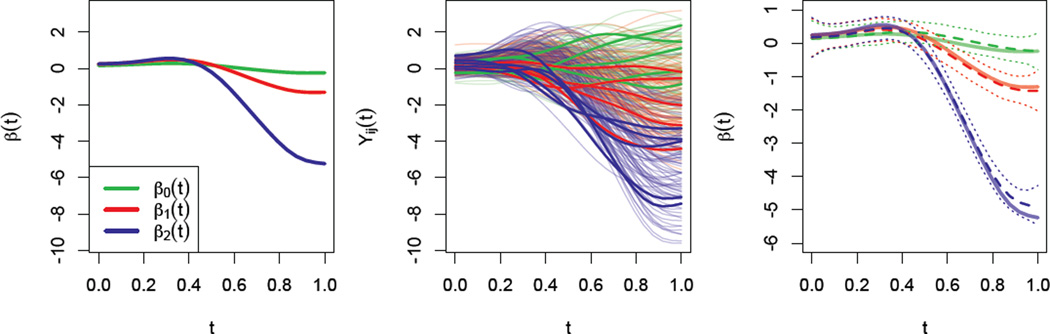
The quantities β, Σ^b and Σ^ε are chosen to resemble our motivating data. First, we focus on a subset of the full dataset that consists of the observed y-position curves from reaches to the target at 180°. In this subset, we find group-level average curves for each of the groups of interest; these become the coefficient functions in the rows of β. For each subject in our subset, we find the subject-level average curve and subtract the corresponding group-level mean, then calculate the covariance Σ^b of these curves. Finally, for each curve in our subset we subtract the subject-level mean, then calculate the covariance Σ^ε of these curves. The number of subjects I is set to (a) 60, (b) 120, or (c) 180. In all cases, we fix the number of observations per subject to be J_i = 5. To illustrate the simulation design, Figure 2 shows the coefficient functions in the left panel. The middle panel of Figure 2 shows a complete simulated dataset with I = 60, and highlights data for three subjects.

Figure 2.

The left panel shows the three coefficient functions used to simulate data. The middle panel shows a complete simulated data set, with three subjects (one from each group) highlighted. The right panel shows the true coefficient functions, as well as their estimates and credible intervals derived from the dataset shown in the middle panel.

For each sample size we generate 100 datasets. Parameters are estimated using the Gibbs sampler and variational Bayes algorithm described in Sections 2.1 and 2.2, respectively, with hyperparameters and initial values chosen as in Section 2.3. For the Gibbs sampler, we used chains of length 5000 and discarded the first 1000 as burn-in. To provide a frame of reference for our methods, we compare to the pffrGLS() function in the refund R package. This extends the the penalized function-on-function regression model assuming independent errors implemented in pffr() (Scheipl et al., 2013); generalized least squares is used to account for residual correlation in pffrGLS(), and a mixed model framework is used for parameter estimation. In a process similar to the GLS method described by Reiss et al. (2010) for cross-sectional function-on-scalar regression, we first fit the model assuming independence and use the residual curves to estimate the covariance matrix for use in pffrGLS(). Although it is not described in a manuscript or preprint at the time of writing, to the best of our knowledge pffrGLS() represents the current state-of-the-art in function-on-scalar regression with subject-level random effects.

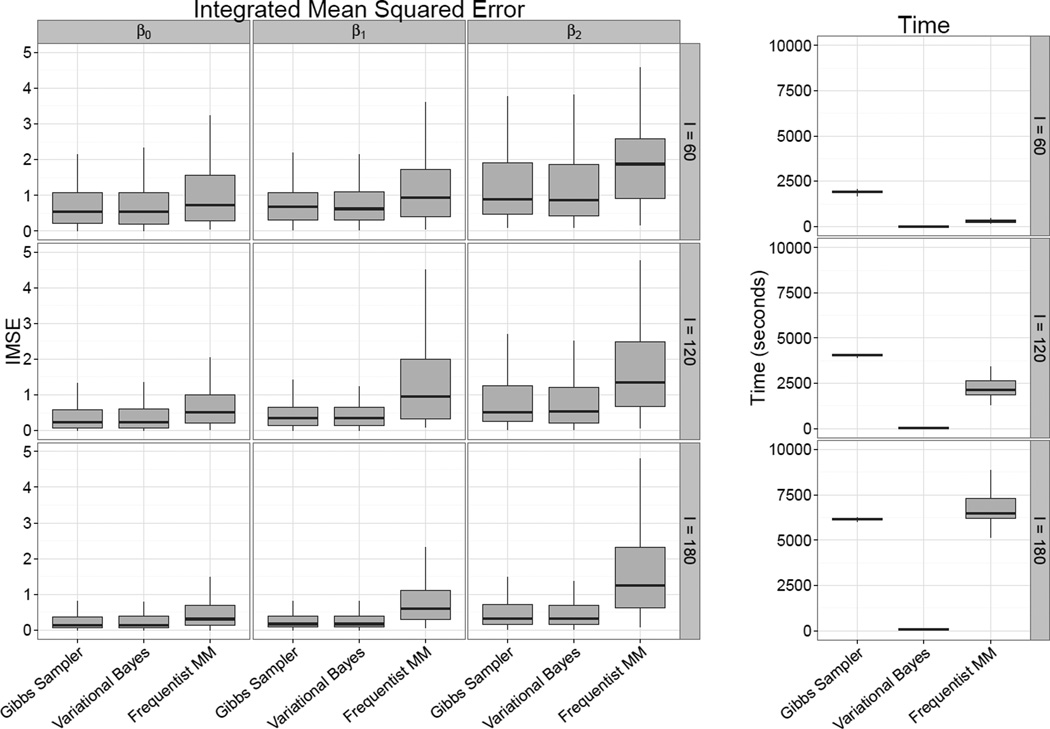
The left panels of Figure 3 show the integrated mean squared error IMSE = ∫ (β̂(t) − β(t))² dt for each coefficient function, estimation method, and sample size. IMSEs are indistinguishable for the Gibbs sampler and variational Bayes approaches, indicating that for posterior means the variational Bayes approximation is reasonable. As expected, IMSEs decrease as sample size increases. Both approaches are comparable to or outperform the mixed model approach, sometime substantially. The right panel of Figure 3 shows the computation time for each sample size and approach (simulations were executed in parallel on a compute cluster with Intel Xeon CPUs running at 2.30GHz; memory usage was 2, 4, and 6 GB for I = 60, 120 and 180, respectively). Not surprisingly, the variational Bayes algorithm is substantially faster than the complete Gibbs sampler. However, there are also meaningful improvements in computation time comparing the variational Bayes algorithm to the mixed model: for i = 180, the median computation time for the variational Bayes approach was roughly 15 seconds, while the median computation time for the mixed model was nearly two hours. This discrepancy in computation time is in part due to the need to fit both two models (one using pffr() and one using pffrGLS()) for the mixed model; also, the code for the variational Bayes algorithm is tailored to the model at hand while pffrGLS() uses the more general mgcv package for estimating parameters. However, we also note that our implementation of pffrGLS() used 5 (rather than 10) basis functions. For I = 180, using 10 basis functions in pffrGLS() required 20,000 seconds – roughly 3.5 times longer than the Gibbs sampler.

Figure 3.

Simualtion results. The left panels show IMSE, defined as IMSE = ∫ (β̂(t) − β(t))dt, for each coefficient function, sample size, and estimation technique. The right panel show computation time for each sample size and estimation method.

Table 1 presents the average coverage probability of 95% pointwise confidence intervals constructed using the Gibbs sampler, the variational Bayes algorithm, and the frequentist mixed moedl for each coefficient function and sample size. For both of the proposed Bayesian approaches, coverage slightly exceeds the nominal level and is often between .96 and .98. As expected, coverage improves as sample size increases. For the mixed model coverage is well below nominal levels for all coefficients and sample sizes; it is possible that the code is still under development and that future iterations may provide better inference. Although coverage for the variational Bayes approximation is reasonable in our simulations, we do not necessarily recommend basing inference in practice on this approach due to the difficulty in verifying the assumptions regarding the factorization of the posterior distribution. Rather, we favor the variational algorithm as a fast method for model building and base inference on a full Gibbs sampler.

Table 1.

Average coverage of 95% credible intervals constructed using the Gibbs sampler, variational Bayes algorithm, and pffr(). Coverages are expressed as percents.

	Gibbs Sampler			Variational Bayes			Frequentist MM
	β0(t)	β1(t)	β2(t)	β0(t)	β1(t)	β2(t)	β0(t)	β1(t)	β2(t)
I = 60	0.98	0.98	0.98	0.97	0.97	0.96	0.43	0.47	0.43
I = 120	0.98	0.99	0.98	0.97	0.99	0.96	0.37	0.34	0.34
I = 180	0.97	0.99	0.97	0.96	0.98	0.96	0.40	0.32	0.27

4 Application

We now apply the developed methods to the motivating data described in Section 1.1. In our dataset affected patients exhibit arm paresis, a weakness or motor control deficit affecting either the dominant or non-dominant arm, due to a unilateral stroke. Patients experienced stroke more than 6 months prior to data collection, meaning that observed motor control deficits are not due to short-term effects but rather are chronic in nature. To quantify the severity of arm impairment we use the Upper Extremity portion of the Fugl-Meyer motor assessment, a well known and widely used clinical assessment of motor impairmen. Fugl-Meyer scores were assessed for the affected arm only, and for upper extremity testing scores range from a 0 to 66 with 66 indicating healthy function. Controls were not scored and were assigned a Fugl-Meyer score of 66. Kinematic data collected for the left hand were reflected through the Y axis, and thus are in the same intrinsic joint space as data for the right hand (i.e., motions to the target at 180° reach across the body and involve both the shoulder and elbow).

Our focus is the effect of the severity of arm impairment on control of visually-guided reaching, where impairment is quantified using the Fugl-Meyer score. In addition to impairment severity, we control for important covariates in our regression modeling. We adjust for target direction (with 8 possible targets, treated as a categorical predictor); hand used (dominant and non-dominant); whether the arm is affected by stroke (affected and unaffected); and, potentially, interactions between these variables. Interactions of impairment severity and other covariates are possible, and are likely for target direction: the effect of stroke may be greatest to the more biomechanically difficult targets that involve coordination of multiple joints.

Our data analysis proceeds in two parts and focuses on estimation of the bivariate model (5). First, we use the variational Bayes algorithm developed in Section 2.2 to explore several possible models that include different combinations of target, hand used, affectedness, and impairment severity as well as potential interactions. In all models, subject-level random effects are estimated for each target and hand; these effects are a priori assumed to be independent. The computational efficiency of the variational Bayes algorithm is crucial at this stage, allowing the fast evaluation and comparison of models. The assumptions that underly the variational algorithm make in unsuitable for inference in our real-data application, and comparisons are made on the basis of percent variance explained. Therefore, after identifying a plausible final model, we estimate all model parameters using the complete Gibbs sampler described in Section 2.1 and base inference for the effect of stroke on this analysis.

4.1 Exploratory analyses using variational Bayes

In the following, we are interested in estimated fixed effects using a variety of structures for the population mean. We select hyperparameters as described in Section 2.3 and estimate models using the variational approximation described in Section 2.2. Computation time was under 20 minutes for each model we consider; the importance of fast computation in the model building stage cannot be understated, since it allows the consideration and refinement of many candidate models.

As a reference for the more complex structures that follow, we began with a model that uses only target direction as a predictor. This model addresses directional variation only, but the eight fixed effects account for roughly 90% of observed variance in the outcome. Following this, several models that included the Fugl-Meyer score, hand used, and affectedness as predictors were considered. Table 2 provides the fixed effects used in each of the models we consider, the number of fixed effects for each model, and the percent of outcome variance explained by fixed effects. Percent variance explained is given relative to the target-only model using

$$\text{Relative }\mathrm{P}\mathrm{V}\mathrm{E}=100\times [1-\frac{\text{Var }[\text{vec }(Y-{Ŷ}_m)]}{\text{Var }[\text{vec }(Y-{Ŷ}_0)]}]$$ (6)

for models m ∈ 1, …, 7, where Y is the matrix of observed trajectories and Ŷ_m is the matrix of estimated trajectories based on fixed effects in Model m.

Table 2.

Description and comparison of models considered.

Model	Fixed Effects	Number of fixed effects	Relative PVE for fixed effects
0	Tar	8	Reference
1	FM + Tar	9	0.1
2	FM × Tar	16	4.6
3	FM2 × Tar	32	5.2
4	FM × Tar × Hand	32	8.4
5	FM × Tar × Aff	32	8.8
6	FM2 × Tar × Aff	64	10.1
7	FM × Tar × Hand × Aff	64	11.9

Fixed effects structure is described in the second column, where “Tar” represents the target direction (as a categorical variable); “Hand” represents hand used (dominant, non-dominant); “Aff” indicates an affected hand; “FM” is the continuous Fugl-Meyer score; “+” indicates additive effects and “×” indicates interactions. The number of fixed effects induced by the model structure is given in the third column. The fourth column provides the percent of outcome variance explained by the model relative to a model with only target as a covariate (defined in equation (6)).

The poor performance of Model 1 compared to Model 2 indicates the importance of interaction between target and impairment severity, due to the target-specific direction of the effect of stroke and to differing levels of biomechanical difficulty. Models 3, 4 and 5 build on Model 2 by adding a quadratic effect of the Fugl-Meyer score and interactions with hand used and affectedness, respectively. The relatively small improvement of the quadratic model may support an assumption of linearity, and the comparability of Models 4 and 5 may be due to the fact that, in our dataset, the affected hand was more likely to be the dominant hand. Models 6 and 7 build on Model 5 by allowing a quadratic effect of the Fugl-Meyer score and an interaction with the hand used. Again, the improvement from using a quadratic term is models compared the effect of the added interaction. For all models, the fixed and random effects together explain roughly 50% of outcome variance; the remaining 50% is residual variance around subject-level means. This partitioning of variance usefully quantifies the extent to which motor control is explainable by covariates, subject-specific deviations, and trajectory-level variation. In Section 4.2 we discuss inference for Model 7.

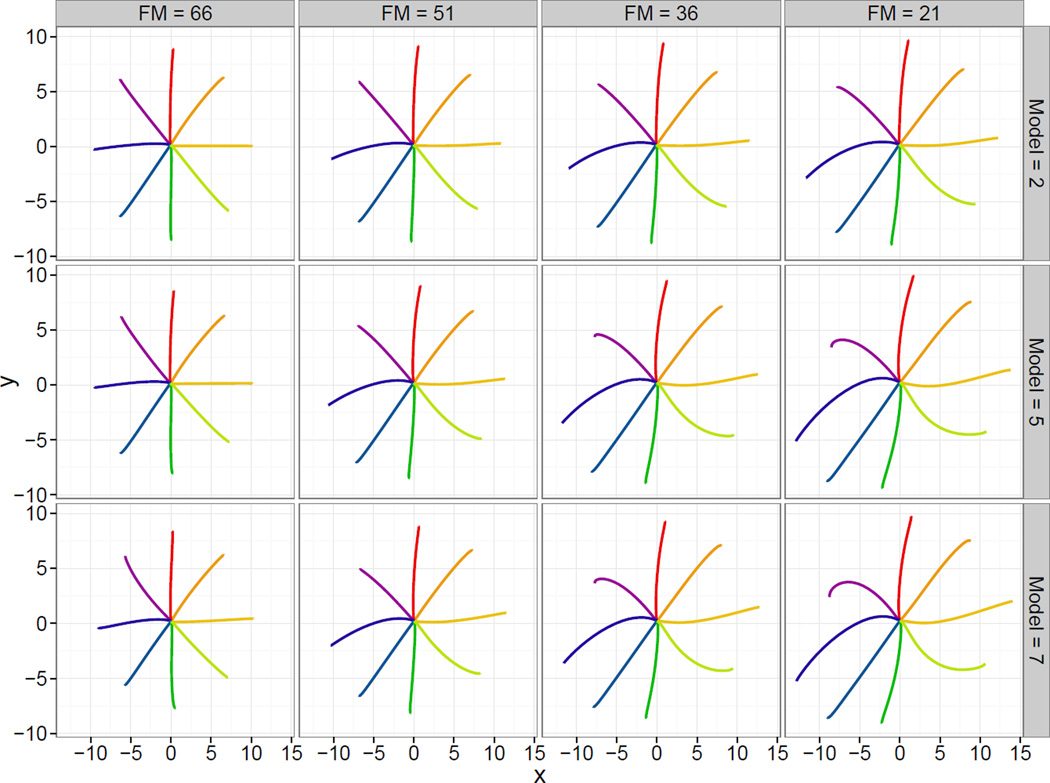
Figure 4 compares the estimated fixed effects from Models 2, 5, and 7. For each model (in rows), we show the estimated mean trajectories in an affected dominant hand for Fugl-Meyer scores 66, 51, 36, and 21 (in columns). In Model 2, the effect of increasing stroke severity is assumed to be the same in both the affected and unaffected hand. This is unlikely given that our data set consists of patients with unilateral stroke. Model 5 estimates separate effects of stroke severity for the affected and unaffected arm. Comparing Models 2 and 5 for an affected arm in Figure 4, Model 5 indicates large effects of increasing stroke severity; for an unaffected arm (not shown) Model 5 indicates small or no effect. Model 7 additionally separates the affected dominant from affected non-dominant hands, with the scientific interpretation that a stroke of the same severity could affect these limbs differently. The differences between Models 5 and 7 are subtle for affected dominant arms, but more noticeable for unaffected and non-dominant arms. An interactive version of Figure 4 is available on the first author’s website.

Figure 4.

Estimated motions for an affected dominant arm with Fugl-Meyer scores 66, 51, 36, and 21 (in columns) under Models 2, 5, and 7 (in rows). An interactive version of this Figure is available on the first author’s website.

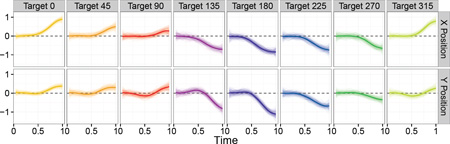
Estimates of subject-level effects are shown in Figure 5 for two subjects (separately by row) overlayed on the observed trajectories. Fixed effects estimates based on Model 7 are shown in bold solid lines and subject-level estimates including random effects are shown in bold dashed lines. In the top row is a control subject’s dominant hand; fixed effects and random effects estimates differ only slightly, indicating relatively little subject deviation from the population mean. In the bottom row is a severely affected (Fugl-Meyer 28) subject’s affected dominant hand. Here, fixed effects are noticeably curved for several targets indicating a systematic effect of stroke. Subject-level estimates differ from the fixed effects in some cases (particularly for targets at 0° and 180°), illustrating the idiosyncratic effects of stroke in this patient. Note that data for these patients is shown in Figure 1.

Figure 5.

Observed data (faint solid lines) overlayed with estimated fixed (bold solid lines) and random (bold dashed lines) effects. Data for two subjects are shown: in the top row, the dominant hand of a control subject, and in the bottom row the affected dominant hand of a severe stroke patient. Data for these subjects appear in Figure 1.

4.2 Full Bayesian analysis

After exploring several candidate fixed effects structures, we fit Model 7 using a fully Bayesian analysis to explore inferential properties of estimated coefficients. In particular, we are interested in the target-and hand-specific systematic effects of the Fugl-Meyer score as a continuous covariate. For our final model, we used five chains with random starting values, setting chain length to 2,000 iterations and discarding the first 500 as burn-in. Hyperparameters and initial values were chosen as described in Section 2.3. Analyses assessing the sensitivity to hyperparameter values appear in the web-based supplementary materials. Computations took 2.5 days per chain on a Intel Xeon CPUs running at 2.30GHz with 8 Gb memory, which emphasizes the importance of a fast approximation for data exploration and model building.

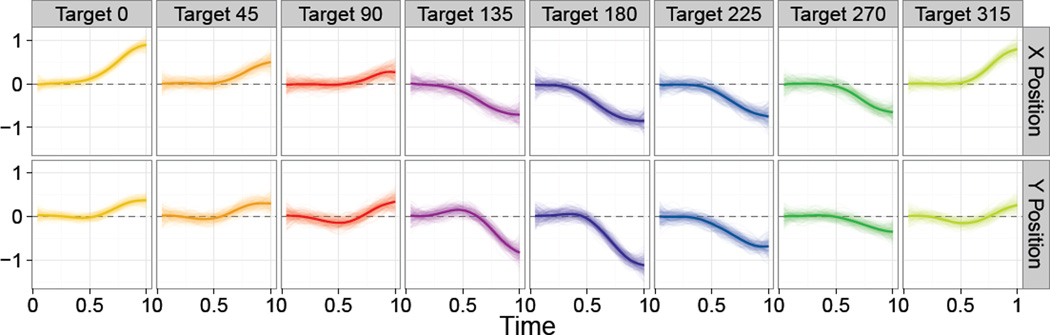
Figure 6 shows the estimated effect of a ten unit decrease in Fugl-Meyer score in a dominant hand affected by stroke for all target directions. The top and bottom rows show the marginal effect on the X and Y position curves, respectively. Panels show the posterior mean as a bold curve, and a sample from the posterior as translucent curves. These results show clear, significant effects to all targets, verifying that increasing stroke severity has a systematic effect on motor control. For motions to the target at 0°, increasing stroke severity leads to over-reach (increases in the X direction) as well as a vertical shift (increase in the Y position). Other targets can be interpreted similarly. The largest effects are generally in directions that require multi-joint coordination, and are thus more biomechanically difficult.

Figure 6.

Estimated effect of a 10-unit decrease in Fugl-Meyer score in an affected dominant hand. Effects to eight targets appear in columns; the effect in the X and Y positions appear in rows. Posterior means are shown as bold curves; a posterior sample is shown as translucent curves.

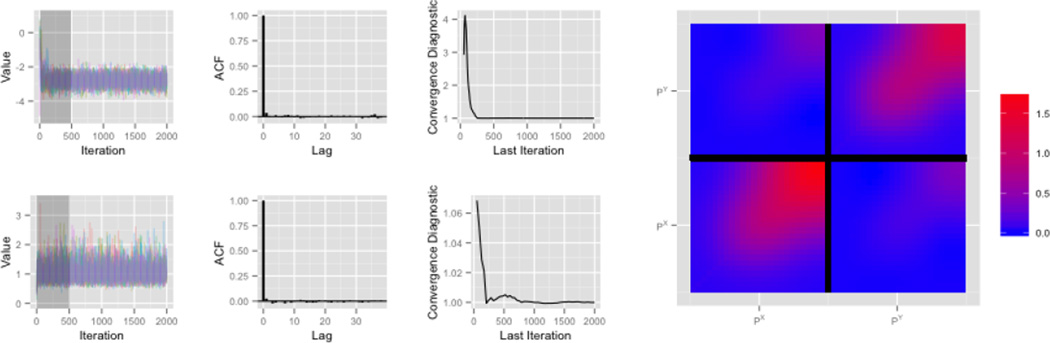
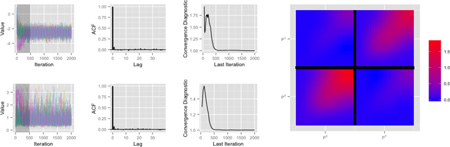
Figure 7 illustrates the quality and convergence of our Markov chains. The top row shows plots for a representative spline coefficient in a fixed effect function β_k(t); the bottom row shows the variance component σ_W,k that controls the degree of penalization in this function. In each row, the left panel shows the five posterior chains for the parameter of interest, started from randomly chosen values with the burn-in period shaded; this shows that chains converge quickly and there is little sensitivity to the choice of starting value. An autocorrelation function is shown in the second panel and indicates low autocorrelation. The third panel of each row shows the convergence criterion of Gelman and Rubin (1992) as a function of iteration number. Values near 1 indicate convergence, which is typically attained after only a few hundred iterations. Finally, at right we show the posterior mean residual covariance surface to illustrate the correlation within X and Y position residuals and the correlation between them.

Figure 7.

Diagnostic and convergence criteria for representative parameters are show in the grid on the left. The top row shows a spline coefficient in a fixed effect function and the bottom row shows the variance component associated with that coefficient function. The columns in this grid show, from left to right, the five chains with random start values, the autocorrelation function, and Gelman and Rubin’s diagnostic criterion. The plot at right show the residual covariance surface.

5 Concluding remarks

This manuscript has focused on the development of a regression framework for the analysis of kinematic data used to assess motor control in stroke patients. Our model allows flexible mean structures, subject-level random effects, bivariate outcomes and correlated errors. We develop a hierarchical Bayesian estimation framework; crucially, a fast and accurate variational Bayes approximation to the full Gibbs sampler allows extensive data exploration and model building before estimation with the full Bayesian approach. Implementations of both approaches and complete simulation code is publicly available.

Variational approximations are often quite inaccurate for the construction of credible intervals due to the factorization assumptions and use of parametric densities to approximate the posterior distribution. In that sense, the good inferential performance found in simulations is perhaps surprising. In part this performance is due to the hierarchical recentering in model (4), in which observed curves are centered around subject effects, subject effects are centered around fixed effects, and fixed effects are centered around zero. This formulation helps to decrease the posterior correlation between fixed and random effects and improves the quality of the approximation (and, importantly, the mixing for the Gibbs sampler). A direct implementation of model (3), which centers observed curves around the combination of fixed and random effects and centers both fixed and random effects around zero, had similar estimation accuracy but much poorer inference. Despite these results, we recommend caution when using the variational approximation for inference, and prefer this method for model building, cross-validation of results, bootstrapping, or other computationally intensive procedures. Finally, we note that the good performance of the variational approximation suggests that other approximate methods might be suitable for this model and should be explored carefully.

The application of our developed methodology to the motivating data yields novel insights into the effect of arm impairment on control of visually-guided reaching. We demonstrate consistent, systematic effects of stroke on reaching trajectories using the Fugl-Meyer score as a continuous covariate that are direction-dependent. Our final model indicates that roughly 10% of variability in observed trajectories is due to systematic effects of impairment severity; subject-specific idiosyncrasies account for an additional 40%. Although not of primary concern here, our application also allows comparisons of dominant and non-dominant hand among controls, as well as consideration of systematic effects in the unaffected hand following stroke. Additional work will examine the replicability of these findings in larger studies and quantify possible overfitting.

Future work may take several directions. In statistical methodology, additional exibility in the mean structure, for instance by allowing non-linear effects of covariates, could broaden the applicability of the model. Parameterizing the residual correlation structure as a function of impairment severity would more accurately reflect the disease process. Implementing and testing our methods for the case that curves are observed on a sparse grid would broaden the class of problems to which these methods can be applied. New general-purpose programming languages for Bayesian analysis (including sampling and optimization) will facilitate the implementation of more classes of prior distributions, potentially leading to better models and reducing the reliance on convenient priors (Stan Development Team, 2013). In the applied setting, extension to three-dimensional kinematics will be necessary as experiments allow more complex reaching motions. Longitudinal experiments to explore treatment effects and describe the natural history of recovery are underway; accompanying methods will be needed to account for within-subject correlations over time.

Appendices

This supplementary material consists of the following appendices: A, containing a graphical representation of our model and a brief discussion of induced factorings; B, containing sensitivity analyses for the choice of hyperparameters in our full Bayesian analysis; C, containing derivations of full conditional distributions for the Gibbs sampler; and D, containing derivations optimal densities for the variational Bayes algorithm. Throughout we consider the univariate model; for the bivariate outcome model presented in Section 2.4 slight augmentations are necessary but straightforward. For completeness, we briey describe the data and model of interest. The data are [Y_ij(t),w_i] for subjects i = 1, …, I and visits j = 1, … J_i, giving a total of n = ∑_i J_i observations. Univariate functional outcomes Y_ij(t) are observed on a regular grid of length D for all subjects and visits. We are interested in estimating the parameters in

$$Y=Z{B}_Z^T{\mathrm{\Theta }}^T+\epsilon$$

$$\epsilon ~\mathrm{N}[0,\mathrm{\Sigma }\otimes I_n];\mathrm{\Sigma }~\mathrm{I}\mathrm{W}[\nu ,\mathrm{\Psi }]$$

$$B_{Z,i}~\mathrm{N}[B_W{\mathit{w}}_i^T,{\sigma }_Z^2{P}^{-1}]\text{ for }i=1\dots I;{\sigma }_Z^2~\mathrm{I}\mathrm{G}[a_Z,b_Z]$$

$$B_{W,k}~\mathrm{N}[0,{\sigma }_{W,k}^2{P}^{-1}],{\sigma }_{W,k}^2~\mathrm{I}\mathrm{G}[a_{W,k},b_{W,k}]\text{ for }k=1\dots p.$$ (A.1)

In this model, B_W is the matrix of coefficients for fixed effects and B_Z is the matrix of coefficients for random subject effects; Σ is the residual covariance matrix, and the variance components n $\left\{{\sigma }_{W,k}^2\right\},{\sigma }_Z^2$ control the amount of smoothness in the fixed and random effects. Additionally, Y, W, Z, Θ, and P are the observed outcomes, the fixed and random effect design matrices, the b-spline basis matrix, and the known penalty matrix, respectively.

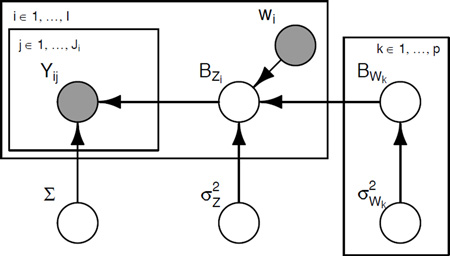
A Graphical model

The joint distribution corresponding to (A.1) is

$$\left[\prod _{i=1}^I\right[\prod _{j=1}^{J_i}p(Y_{ij}|B_{Z,i},\mathrm{\Sigma })]p(B_{Z,i}|B_W,{\sigma }_Z^2)]·[\prod _{k=0}^{p}p(B_{W,k}|{\sigma }_{W,k}^2)p({\sigma }_{W,k}^2)]·p(\mathrm{\Sigma })·p({\sigma }_Z^2).$$

Here we omit hyperparameters for the densities for the covariance matrix Σ and variances $\left\{{\sigma }_{W,k}^2\right\},{\sigma }_Z^2$. Also note that the “zeroth” column of B_W and the variance ${\sigma }_{W,0}^2$ correspond to the intercept β₀(t). A graphical representation of this model is shown in Figure A.1.

Figure A.1: Graphical illustration of model (A.1). Shaded nodes represent observed data; blank nodes denote inferred parameters; rectangles or plates denote indexing over a set of variables. For example, the plate surrounding only Y_ij indicates that for subject i, observations are indexed by j and are independent given parameters outside this plate.

Our variational approach assumes that the posterior distribution $p(B_Z,B_W,{\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma }|Y)$ can be approximated using

$$q(B_Z,B_W,{\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })=q(B_Z)q(B_W)q({\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })$$

where the functions q are distinguished by their argument rather than by subscript l. The additional factorizations $q(B_Z)={\prod }_{i=1}^{I}q(B_{Z,i})$ and $q({\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })=({\prod }_{k=0}^{p}q({\sigma }_{W,k}^2))q({\sigma }_Z^2)q(\mathrm{\Sigma })$ follow from the result

$$q_l^{*}({\varphi }_l)\propto \text{ exp }[E_{{\varphi }_{-l}}\text{ log }p(\mathit{y},\varphi )]\propto \text{exp }[E_{{\varphi }_{-l}}\text{ log }p({\varphi }_l|\text{rest})]K_{\theta }$$

and Figure A.1. In particular, the columns of B_Z are conditionally independent given B_W and the variance components are all conditionally independent given the remaining model parameters. These observations lead to our final factorization:

$$q(B_Z,B_W,{\sigma }_{W,0}^2,\dots ,{\sigma }_{W,p}^2,{\sigma }_Z^2,\mathrm{\Sigma })=(\prod _{i=1}^{I}q(B_{Z,i}))q(B_W)(\prod _{k=0}^{p}q({\sigma }_{W,k}^2))q({\sigma }_Z^2)q(\mathrm{\Sigma }).$$

B Sensitivity Analyses

In Section 2.3 of the manuscript, we describe a procedure for choosing hyperparameters. This procedure is based on an analysis of the data, and is developed to avoid default “uninformative” choices like a_z = b_z = a_W,k = b_W,k = .001, which places a large prior mass near zero for all variance components and can lead to overshrinkage of fixed and random effects toward zero. However there is the potential for sensitivity to these choices, and in this section we repeat our full data analysis using other choices for hyperparameters.

In this analysis, we set a_z = 10, b_z = 2.5, and a_W,k = b_W,k = 1 for all k as the hyperparameters for inverse-gamma densities. We set ν = 10 and Ψ = 10I, where I is an identity matrix. For reference, in the analysis presented in the manuscript, we set a_z = 4250 and b_z = 2600, a_W,k was set to 5 and b_W,k ranged between .001 and 100, with typical values near .05; we set ν = 19053 and Ψ was constructed using an FPCA decomposition. The choices of hyperparameters in this appendix result in more diffuse priors and encode relatively little information. Using these hyperparameters, we repeated our analysis by using five chains with random starting values, with each chain consisting of 2,000 iterations and discarding the first 500 as burn-in.

Figure A.2 shows the estimated effect of a 10-unit change in Fugl-Meyer score in a dominant hand affected by stroke for all target directions; this recreates Figure 6 from the main manuscript. Estimates of effects are very similar in both analysis, indicated that choices of hyperparameters can relax the degree of prior information with relatively little effect on estimation. The posterior sample in all panels of Figure A.2 tends to be more variable than the corresponding panel of Figure 6 in the manuscript, but not dramatically so.

Figure A.2: Estimated effect of a 10-unit decrease in Fugl-Meyer score in an affected dominant hand. Effects to eight targets appear in columns; the effect in the X and Y positions appear in rows. Posterior means are shown as bold curves; a posterior sample is shown as translucent curves. Figure is based on hyperparameters chosen for a sensitivity analysis.

Figure A.3 recreates Figure 7 in the main manuscript using the hyperparameter choices given above. The top row shows plots for the same representative spline coefficient in a fixed effect function β_k(t) as in Figure 7; the bottom row shows the variance component σ_W,k that controls the degree of penalization in this function. In each row, the left panel shows the five posterior chains; the second panel shows an autocorrelation function; and the third panel of each row shows the convergence criterion of Gelman and Rubin (1992) as a function of iteration number. Convergence is somewhat slower using the current hyperparameters, but is still reasonable. As seen in Figure A.2, distributions are a bit more variable, likely due to the spreading of prior mass for variance components.

Figure A.3: Diagnostic and convergence criteria for representative parameters are show in the grid on the left. The top row shows a spline coefficient in a fixed effect function and the bottom row shows the variance component associated with that coefficient function. The columns in this grid show, from left to right, the five chains with random start values, the autocorrelation function, and Gelman and Rubin’s diagnostic criterion. The plot at right show the residual covariance surface. Figure is based on hyperparameters chosen for a sensitivity analysis.

C Gibbs Sampler

In this section we provide derive full conditional distributions for the parameters in model (A.1). Let 1_m be a length m vector of 1’s and Y_i denote the rows of Y for subject i. Also recall that $n={\sum }_{i=1}^I{J}_i$ is the total number of observations.

• The full conditional distribution p(B_Z,i|rest) is

  $$p(B_{Z,i}|\text{ rest})\propto p(Y_i|B_{Z,i},\mathrm{\Sigma })p(B_{Z,i}|{\sigma }_Z^2,B_W)\propto \text{exp }[-\frac{1}{2}\{{(\text{vec }(Y_i^T)-({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })B_{Z,i})}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})(\text{vec }(Y_i^T)-({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })B_{Z,i})+{(B_{Z_i}-B_W{\mathit{w}}_i^T)}^T(\frac{1}{{\sigma }_Z^2}P)(B_{Z_i}-B_W{\mathit{w}}_i^T)\}]\propto \text{exp }[-\frac{1}{2}\{B_{Z,i}^T{(({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })+(\frac{1}{{\sigma }_Z^2}P))B_{Z,i}-2(\text{vec }{(Y_i^T)}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })+{(B_W{\mathit{w}}_i^T)}^T(\frac{1}{{\sigma }_Z^2}P))B_{Z,i}\left\}\right]\propto \text{exp }\{-\frac{1}{2}{(B_{Z,i}-{\mu }_{B_{Z,i}})}^T{\mathrm{\Sigma }}_{B_{Z,i}}^{-1}(B_{Z,i}-{\mu }_{B_{Z,i}})\}$$

  where

  $${\mathrm{\Sigma }}_{B_{Z,i}}={({({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })+\frac{1}{{\sigma }_Z^2}P)}^{-1}$$

  and

  $${\mu }_{B_{Z,i}}={\mathrm{\Sigma }}_{B_{Z,i}}({({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})\text{vec }(Y_i^T)+\frac{1}{{\sigma }_Z^2}P(B_W{\mathit{w}}_i^T)).$$

  Thus [B_Z,i | rest] follows a multivariate normal distribution with mean and variance as described above.

• Derivation of the full conditional distribution p(vec (B_W) |rest) follows very similarly to the above.

  In particular,

  $$p(\text{vec }(B_W)|\text{ rest})\propto p(B_Z|B_W,{\sigma }_Z^2)p(\text{vec }(B_W)|\{{\sigma }_{W,k}^2\})\propto \text{exp }[-\frac{1}{2}\{{(\text{vec }(B_Z)-(W\otimes I_{K_{\theta }})\text{vec }(B_W))}^T(\frac{1}{{\sigma }_Z^2}{I}_I\otimes P)(\text{vec }(B_Z)-(W\otimes I_{K_{\theta }})\text{vec }(B_W))+\text{vec }{(B_W)}^T(\text{diag }(1/{\sigma }_{W,k}^2)\otimes P)\text{vec }(B_W)\}]\propto \text{exp }\{-\frac{1}{2}{(\text{vec }(B_W)-{\mu }_{B_W})}^T{\mathrm{\Sigma }}_{B_W}^{-1}(\text{vec }(B_W)-{\mu }_{B_W})\}$$

  where

  $${\mathrm{\Sigma }}_{B_W}={(\frac{1}{{\sigma }_Z^2}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)(W\otimes I_{K_{\theta }})+\text{diag }(\frac{1}{{\sigma }_{W,k}^2})\otimes P)}^{-1}$$

  and

  $${\mu }_{B_W}={\mathrm{\Sigma }}_{B_W}(\frac{1}{{\sigma }_Z^2}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)\text{vec }(B_Z)).$$

  Thus [vec (B_W) | rest] follows a multivariate normal distribution with mean and variance given above; the conditional distribution of B_W is given by inverting the vec (·) operation.
• The full conditional distribution $p({\sigma }_Z^2|\text{rest})$ is

  $$p({\sigma }_Z^2|\text{ rest})\propto p({\sigma }_Z^2)\prod _{i=1}^{I}p(B_{Z,i}|{\sigma }_Z^2)\propto {({\sigma }_Z^2)}^{-a_Z-1}\text{exp }\{-\frac{b_Z}{{\sigma }_Z^2}\}\prod _{i=1}^I{({\sigma }_Z^2)}^{-K_{\theta }/2}\text{exp }\{-\frac{1}{2}{(B_{Z,i}-B_W{\mathit{w}}_i^T)}^T(\frac{1}{{\sigma }_Z^2}P)(B_{Z,i}-B_W{\mathit{w}}_i^T)\}={({\sigma }_Z^2)}^{-a_Z-\frac{I*K_{\theta }}{2}-1}\text{exp }\{-\frac{1}{{\sigma }_Z^2}(b_z+\frac{1}{2}\sum _{i=1}^I{(B_{Z,i}-B_W{\mathit{w}}_i^T)}^T(\frac{1}{{\sigma }_Z^2}P)(B_{Z,i}-B_W{\mathit{w}}_i^T)\left)\right\}.$$

  Thus $[{\sigma }_Z^2|\text{rest}]$ is distributed $\mathrm{I}\mathrm{G}[a_z+\frac{I*K_{\theta }}{2},b_z+\frac{1}{2}{\sum }_{i=1}^I{(B_{Z,i}-B_W{\mathit{w}}_i^T)}^{T}P(B_{Z,i}-B_W{\mathit{w}}_i^T)]$.
• The derivation of the full conditional distribution for each of the ${\sigma }_{W,k}^2$ is the same, and is similar to that of ${\sigma }_Z^2$. For any k, the full conditional $p({\sigma }_{W,k}^2|\text{rest})$ is

  $$p({\sigma }_{W,k}^2|\text{ rest})\propto p({\sigma }_{W,k}^2)p(B_{W,k}|{\sigma }_{W,k}^2).$$

  Straightforward computation shows that $[{\sigma }_{W,k}^2|\text{rest}]$ is distributed $\mathrm{I}\mathrm{G}[a_{W,k}+\frac{K_{\theta }}{2},b_{W,k}+\frac{1}{2}{B}_{W,k}^{T}P{B}_{W,k}]$.
• For a given value of B_Z, let $R=Y-Z{B}_Z^T{\mathrm{\Theta }}^T$ be the matrix containing residual curves evaluated over the discrete grid of observation points such that R_ij contains the jth residual vector for subject i. The full conditional distribution p(Σ|rest) is

  $$p(\mathrm{\Sigma }|\text{ rest})\propto p(Y|B_Z,\mathrm{\Sigma })p(\mathrm{\Sigma })\propto {|\mathrm{\Sigma }|}^{-\frac{n}{2}}\text{ exp }\{-\frac{1}{2}\sum _{i=1}^I\sum _{j=1}^{J_i}{\mathit{R}}_{ij}{\mathrm{\Sigma }}^{-1}{\mathit{R}}_{ij}^T\}·{|\mathrm{\Sigma }|}^{\frac{\nu +D+1}{2}}\text{ exp }\{-\frac{1}{2}\text{tr }[\mathrm{\Psi }{\mathrm{\Sigma }}^{-1}]\}.$$

  Note that ${\sum }_{i=1}^I{\sum }_{j=1}^{J_i}{\mathit{R}}_{ij}{\mathrm{\Sigma }}^{-1}{\mathit{R}}_{ij}^T=\text{tr }[\mathit{R}{\mathrm{\Sigma }}^{-1}{\mathit{R}}^T]=\text{tr }[{\mathit{R}}^T\mathit{R}{\mathrm{\Sigma }}^{-1}]$. Combining terms, the full conditional is

  $$p(\mathrm{\Sigma }|\text{ rest})\propto p(Y|B_Z,\mathrm{\Sigma })p(\mathrm{\Sigma })\propto {|\mathrm{\Sigma }|}^{-\frac{\nu +n+D+1}{2}}\text{ exp }\{-\frac{1}{2}\text{tr }[(\mathrm{\Psi }+{\mathit{R}}^T\mathit{R}){\mathrm{\Sigma }}^{-1}]\}$$

  so that [Σ | rest] is distributed $\mathrm{I}\mathrm{W}[\nu +{\sum }_i{J}_i,\mathrm{\Psi }+{(Y-Z{B}_Z^T{\mathrm{\Theta }}^T)}^T(Y-Z{B}_Z^T{\mathrm{\Theta }}^T)]$.

D Variational Bayes Algorithm

In this section we derive the optimal densities and the iterative algorithm in the variational Bayes approximation to the full posterior of model (A.1). Additionally, we provide the q-specific lower bound L_q used to monitor convergence of the algorithm.

First, we recall that given a partition {ϕ₁, …, ϕ_L} of the parameter space ϕ, the explicit solution for q(ϕ_l), 1 ≤ l ≤ L has the form

$$q_l^{*}({\varphi }_l)\propto \text{exp }[E_{{\varphi }_{-l}}\text{ log }p({\varphi }_l|\text{rest})];1\le l\le L$$ (A.2)

where rest ≡ {Y, ϕ₁, …, ϕ_l−1,ϕ_l+1, …, ϕ_L}. Notationally, for a scalar random variable ϕ, let

$${\mu }_{q(\varphi )}\equiv {\mathrm{E}}_q[\varphi ]=\int {\varphi }_{0}q({\varphi }_0)d{\varphi }_0$$

$${\sigma }_{q(\varphi )}\equiv {\text{Var}}_q[\varphi ]=\int {({\varphi }_0-\mathrm{E}[\varphi ])}^{2}q({\varphi }_0)d{\varphi }_0$$

be the mean and variance with respect to the q distribution. For a vector parameter ϕ, we use the analogously defined μ_q(ϕ) and Σ_q(ϕ)

• For B_Z,i, we use the full conditional derivation in Section C to find that

  $$q^{*}(B_{Z,i})\propto \text{exp }[E_{-B_{Z,i}}\text{ log }p(B_{Z,i}|\text{rest})]\propto \text{exp }[E_{-B_{Z,i}}[-\frac{1}{2}\{\text{ vec }{(B_{Z,i})}^T({({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })+(\frac{1}{{\sigma }_Z^2}P))\text{ vec }(B_{Z,i})-2(\text{ vec }{(Y_i)}^T(I_{J_i}\otimes {\mathrm{\Sigma }}^{-1})({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })+{(B_W{\mathit{w}}_i^T)}^T(\frac{1}{{\sigma }_Z^2}P))B_{Z,i}\left\}\right]]\propto \text{exp }\{-\frac{1}{2}{(B_{Z,i}-{\mu }_{q(B_{Z,i})})}^T{\mathrm{\Sigma }}_{q(B_{Z,i})}^{-1}(B_{Z,i}-{\mu }_{q(B_{Z,i})})\}$$

  where

  $${\mathrm{\Sigma }}_{q(B_{Z,i})}={({({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mu }_{q({\mathrm{\Sigma }}^{-1})})({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })+{\mu }_{q(1/{\sigma }_Z^2)}P)}^{-1}$$

  and

  $${\mu }_{q(B_{Z,i})}={\mathrm{\Sigma }}_{q(B_{Z,i})}({({\mathbf{1}}_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mu }_{q({\mathrm{\Sigma }}^{-1})})\text{vec }(Y_i)+{\mu }_{q(1/{\sigma }_Z^2)}P({\mu }_{q(B_W)}{\mathit{w}}_i^T)).$$

  Thus the optimal density q*(B_Z,i) is multivariate normal with mean and variance as specified above.
• The derivation for B_W is similar to that for B_Z,i; specifically, we use the full conditional derivation in Section C to find that

  $$q^{*}(B_W)\propto \text{exp }[E_{-B_W}\text{ log }p(B_W|\text{rest})]\propto \text{exp }\{-\frac{1}{2}{(\text{vec }(B_W)-{\mu }_{q(B_W)})}^T{\mathrm{\Sigma }}_{q(B_W)}^{-1}(\text{vec }(q(B_W))-{\mu }_{B_W})\}$$

  where

  $${\mathrm{\Sigma }}_{q(B_W)}={({\mu }_{q(1/{\sigma }_Z^2)}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)(W\otimes I_{K_{\theta }})+\text{diag }({\mu }_{q(1/{\sigma }_{W,k}^2)})\otimes P)}^{-1}$$

  and

  $${\mu }_{q(B_W)}={\mathrm{\Sigma }}_{q(B_W)}({\mu }_{q(1/{\sigma }_Z^2)}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)\text{vec }({\mu }_{q(B_Z)})).$$

  Thus the optimal density q*(B_W) is multivariate normal with mean and variance as specified above.
  For ${\sigma }_Z^2$, we find that

  $$q^{*}({\sigma }_Z^2)\propto \text{exp }[E_{-{\sigma }_Z^2}\text{ log }p({\sigma }_Z^2|\text{rest})]\propto \text{exp }\{-(a_Z+\frac{I*K_{\theta }}{2}+1)\text{ log }({\sigma }_Z^2)-\frac{1}{{\sigma }_Z^2}{E}_{-{\sigma }_Z^2}((b_z+\frac{1}{2}\sum _{i=1}^I{(B_{Z,i}-B_W{\mathit{w}}_i^T)}^T(P)(B_{Z,i}-B_W{\mathit{w}}_i^T)\left)\right\}={({\sigma }_Z^2)}^{-a_Z-\frac{I*K_{\theta }}{2}-1}\text{ exp }\{-\frac{1}{{\sigma }_Z^2}{b}_{q({\sigma }_Z^2)}\}$$

  where

  $$b_{q({\sigma }_Z^2)}=b_Z+\frac{1}{2}\sum _i({\mu }_{q(B_{Z,i})}^{T}P{\mu }_{q(B_{Z,i})}+\text{tr }[P{\mathrm{\Sigma }}_{q(B_{Z,i})}]-2{\mathit{w}}_i{\mu }_{q(B_W)}^{T}P{\mu }_{q(B_{Z,i})}+{\mathit{w}}_i{\mu }_{q(B_W)}^{T}P{\mu }_{q(B_W)}{\mathit{w}}_i^T+{\mathit{w}}_i\text{diag }(\text{tr }\left[P{\mathrm{\Sigma }}_{q(B_W,k)}\right]\left){\mathit{w}}_i^T\right).$$

  Thus the optimal density $q^{*}({\sigma }_Z^2)$ is $\mathrm{I}\mathrm{G}[a_Z+\frac{I*K_{\theta }}{2},b_{q({\sigma }_Z^2)}]$. Note that the term ${\mu }_{q(1/{\sigma }_Z^2)}$ appearing in the optimal densities q*(B_Z,i) and q*(B_W) is equal to $\frac{a_Z+\frac{I*K_{\theta }}{2}}{b_{q({\sigma }_Z^2)}}$.
• The derivation for the ${\sigma }_{w,k}^2$ is similar to that of ${\sigma }_Z^2$. Specifically,

  $$q^{*}({\sigma }_{W,k}^2)\propto \text{exp }[E_{-{\sigma }_{W,k}^2}\text{ log }p({\sigma }_{W,k}^2|\text{rest})]\propto \text{exp }\{-(a_{W,k}+\frac{K_{\theta }}{2}+1)\text{ log }({\sigma }_{W,k}^2)-\frac{1}{{\sigma }_{W,k}^2}{\mathrm{E}}_{-{\sigma }_{W,k}^2}((b_{W,k}+\frac{1}{2}{B}_{W,k}^{T}P{B}_{W,k}\left)\right\}={({\sigma }_{W,k}^2)}^{-a_{W,k}-\frac{K_{\theta }}{2}-1}\text{exp}\{-\frac{1}{{\sigma }_{W,k}^2}{b}_{q({\sigma }_{W,k}^2)}\}$$

  where

  $$b_{q({\sigma }_{W,k}^2)}=b_W+\frac{1}{2}({\mu }_{q(B_{W,k})}^{T}P{\mu }_{q(B_{W,k})}+\text{tr }[P{\mathrm{\Sigma }}_{q(B_{W,k})}\left]\right).$$

  Thus the optimal density $q^{*}({\sigma }_{W,k}^2)$ is $\mathrm{I}\mathrm{G}[a_{W,k}+\frac{K_{\theta }}{2},b_{q({\sigma }_{W,k}^2)}]$. Note that the term ${\mu }_{q(1/{\sigma }_{W,k}^2)}$ appearing in the optimal density q*(B_W) is equal to $\frac{a_{W,k}+\frac{K_{\theta }}{2}}{b_{q({\sigma }_{W,k}^2)}}$.
• For Σ, we have

  $$q^{*}(\mathrm{\Sigma })\propto \text{exp }[E_{-\mathrm{\Sigma }}\text{ log }p(\mathrm{\Sigma }|\text{rest})]\propto {|\mathrm{\Sigma }|}^{\frac{\nu +n+D+1}{2}}\text{exp }\{-\frac{1}{2}(\text{tr }[\mathrm{\Psi }{\mathrm{\Sigma }}^{-1}]+\sum _{m=1}^n{E}_{-\mathrm{\Sigma }}[(Y_m-Z_m{B}_Z^T{\mathrm{\Theta }}^T){\mathrm{\Sigma }}^{-1}{(Y_m-Z_m{B}_Z^T{\mathrm{\Theta }}^T)}^T)]\}$$

  where m indexes rows of Y and Z and has values between 1 and n. For any m, the expectation above is

  $$Y_m{\mathrm{\Sigma }}^{-1}{Y}_m^T-Z_m{B}_Z^T{\mathrm{\Theta }}^T{\mathrm{\Sigma }}^{-1}{Y}_m^T-Y_m{\mathrm{\Sigma }}^{-1}\mathrm{\Theta }{B}_Z{Z}_m+Z_m{\mu }_{q(B_Z)}^T{\mathrm{\Theta }}^T{\mathrm{\Sigma }}^{-1}\mathrm{\Theta }{\mu }_{q(B_Z)}{Z}_m^T+\text{tr }\left[{\mathrm{\Theta }}^T{\mathrm{\Sigma }}^{-1}\mathrm{\Theta }{\mathrm{\Sigma }}_{q(B_{z,i^{*}})}\right]$$

  where Σ_q(BZ,i*) is the covariance matrix defined in the update for B_Z,i and subject i* is the subject to which row m corresponds. Taking the sum over m of this expectation we have that

  $$q^{*}(\mathrm{\Sigma })\propto {|\mathrm{\Sigma }|}^{\frac{\nu +n+D+1}{2}}\text{ exp }\{-\frac{1}{2}\text{tr }[{\mathrm{\Psi }}_{q(\mathrm{\Sigma })}{\mathrm{\Sigma }}^{-1}\left]\right\}$$

  with

  $${\mathrm{\Psi }}_{q(\mathrm{\Sigma })}=\mathrm{\Psi }+Y^{T}Y-Y^{T}Z{\mu }_{q(B_Z)}^T{\mathrm{\Theta }}^T+\mathrm{\Theta }{\mu }_{q(B_Z)}{Z}^{T}Y+\mathrm{\Theta }{\mu }_{q(B_Z)}{Z}^{T}Z{\mu }_{q(B_Z)}^T{\mathrm{\Theta }}^T+\sum _i{J}_i\mathrm{\Theta }{\mathrm{\Sigma }}_{q(B_{Z,i})}{\mathrm{\Theta }}^T.$$

  Thus the optimal density q*(Σ) is IW [ν + n, Ψ_q(Σ)]. Note that the term μ_q(Σ⁻¹) appearing in the optimal density q*(B_Z) is equal to ${\left(\frac{{\mathrm{\Psi }}_{q(\mathrm{\Sigma })}}{\nu +{\sum }_i{J}_i}\right)}^{-1}$.

From these individual updates, we arrive at the following iterative algorithm:

Algorithm 1.

Iterative scheme for obtaining the optimal density parameters in the function-on-scalar regression model (A.1).

Initialize: μq(BZ,i), Σq(BZ,i) for all i; μq(BW); Σq(BW); $b_{q({\sigma }_Z^2)},b_{q({\sigma }_{W,k}^2)}$ for all k; and Ψq(Σ). Initial values can be chosen at random, or based on the approach used to select hyperparameters described in Section 2.3 to speed convergence.

Cycle: For all i: ◦ ${\mathrm{\Sigma }}_{q(B_{Z,i})}\leftarrow {({(1_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mu }_{q({\mathrm{\Sigma }}^{-1})})(1_{J_i}\otimes \mathrm{\Theta })+{\mu }_{q(1/{\sigma }_Z^2)}P)}^{-1}$ ◦ ${\mu }_{q(B_{Z,i})}\leftarrow {\mathrm{\Sigma }}_{q(B_{Z,i})}({(1_{J_i}\otimes \mathrm{\Theta })}^T(I_{J_i}\otimes {\mu }_{q({\mathrm{\Sigma }}^{-1})})\text{vec }(Y_i)+{\mu }_{q(1/{\sigma }_Z^2)}P({\mu }_{q(B_W)}{\mathit{w}}_i^T))$ ${\mathrm{\Sigma }}_{q(B_W)}\leftarrow {({\mu }_{q(1/{\sigma }_Z^2)}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)(W\otimes I_{K_{\theta }})+\text{diag }({\mu }_{q(1/{\sigma }_{W,k}^2)})\otimes P)}^{-1}$ ${\mu }_{q(B_W)}\leftarrow {\mathrm{\Sigma }}_{q(B_W)}({\mu }_{q(1/{\sigma }_Z^2)}{(W\otimes I_{K_{\theta }})}^T(I_I\otimes P)\text{vec }({\mu }_{q(B_Z)}))$ $b_{q({\sigma }_Z^2)}\leftarrow b_Z+\frac{1}{2}{\sum }_i({\mu }_{q(B_{Z,i})}^{T}P{\mu }_{q(B_{Z,i})}+\text{tr }[P{\mathrm{\Sigma }}_{q(B_{Z,i})}]-2{\mathit{w}}_i{\mu }_{q(B_W)}^{T}P{\mu }_{q(B_{Z,i})}+{\mathit{w}}_i{\mu }_{q(B_W)}^{T}P{\mu }_{q(B_W)}{\mathit{w}}_i^T+{\mathit{w}}_i\text{diag }(\text{tr }\left[P{\mathrm{\Sigma }}_{q(B_{W,k})}\right]\left){\mathit{w}}_i^T\right)$ For all k: ◦ $b_{q({\sigma }_{W,k}^2)}\leftarrow b_W+\frac{1}{2}({\mu }_{q(B_{W,k})}^{T}P{\mu }_{q(B_{W,k})}+\text{tr }[P{\mathrm{\Sigma }}_{q(B_{W,k})}\left]\right)$ ${\mathrm{\Psi }}_{q(\mathrm{\Sigma })}\leftarrow \mathrm{\Psi }+Y^{T}Y-Y^{T}Z{\mu }_{q(B_Z)}^T{\mathrm{\Theta }}^T+\mathrm{\Theta }{\mu }_{q(B_Z)}{Z}^{T}Y+\mathrm{\Theta }{\mu }_{q(B_Z)}{Z}^{T}Z{\mu }_{q(B_Z)}^T{\mathrm{\Theta }}^T+{\sum }_i{J}_i\mathrm{\Theta }{\mathrm{\Sigma }}_{q(B_{Z,i})}{\mathrm{\Theta }}^T$ until the increase in Lq is negligible.

Finally, the expression for the q-specific lower bound of the marginal log-likelihood is

$$L_{q^{*}}=\int q(\varphi )\text{ log }\frac{p(\mathit{y},\varphi )}{q^{*}(\varphi )}d\varphi ==\frac{1}{2}\sum _i\text{ log }\left(\right|{\mathrm{\Sigma }}_{q(B_{Z,i})}\left|\right)+\frac{1}{2}\sum _k\text{ log }\left(\right|{\mathrm{\Sigma }}_{q(B_{W,k})}\left|\right)-(a_z+\frac{I*K_{\theta }}{2})\text{ log}(b_{q({\sigma }_Z^2)})-\sum _k(a_w+\frac{K_{\theta }}{2})\text{ log}(b_{q({\sigma }_{W,k}^2)})-\left(\frac{\nu +{\sum }_i{J}_i}{2}\right)\text{ log}(|{\mathrm{\Psi }}_{q(\mathrm{\Sigma })}|)+\text{const}.$$

where “const.” represents an additive constant not affected by updates to the q density parameters. It should be noted that this constant contains the term log(|P⁻¹|), thus necessitating a full rank penalty matrix if L_q is used to monitor convergence of the algorithm.