Approaching the ideal elastic strain limit in silicon nanowires

Single-crystalline silicon nanowires can be reversibly stretched above 10% elastic strain at room temperature.

Abstract

Achieving high elasticity for silicon (Si) nanowires, one of the most important and versatile building blocks in nanoelectronics, would enable their application in flexible electronics and bio-nano interfaces. We show that vapor-liquid-solid–grown single-crystalline Si nanowires with diameters of ~100 nm can be repeatedly stretched above 10% elastic strain at room temperature, approaching the theoretical elastic limit of silicon (17 to 20%). A few samples even reached ~16% tensile strain, with estimated fracture stress up to ~20 GPa. The deformations were fully reversible and hysteresis-free under loading-unloading tests with varied strain rates, and the failures still occurred in brittle fracture, with no visible sign of plasticity. The ability to achieve this “deep ultra-strength” for Si nanowires can be attributed mainly to their pristine, defect-scarce, nanosized single-crystalline structure and atomically smooth surfaces. This result indicates that semiconductor nanowires could have ultra-large elasticity with tunable band structures for promising “elastic strain engineering” applications.

INTRODUCTION

Because of their availability and attractive physical properties, Si nanowires are among the most important one-dimensional (1D) building blocks for nanoelectronics and nanoelectromechanical system devices, as well as many other functional applications (1). However, potential mechatronics applications that involve large deformation, such as flexible electronics, epidermal electronics, and recent bio-nano interfaces (2–5), place extreme demands on nanowire elasticity. In the past few decades, researchers have found that Si structures could become more deformable when their characteristic lengths are reduced to micro- and nanoscales, with much higher elasticity compared to their bulk counterparts (6–11). Recently, a new concept called “ultra-strength” has been proposed (12, 13) and experimentally demonstrated in many nanomaterials, in which the specimen-wide stress level in a component can reach a significant fraction (>¹/₁₀) of the theoretical strength without plastic relaxation or premature failure, over an extended time period at finite temperature. To experimentally achieve ultra-strength and ultrahigh elasticity in semiconductors, nanowires will be not only important to build up robust flexible/stretchable nanodevices, but also useful for the emerging “elastic strain engineering” applications (14), in which their functional properties (such as band gap, catalytic activity, and optoelectronic properties) can be significantly tuned by engineering the large elastic strain field (15–21). For example, strained silicon, whereby one achieves marked enhancement in electron mobility by applying less than 2% tensile strain, has already achieved great commercial success in the semiconductor industry (22–24).

In particular for Si nanowires, recent experiments showed that wires with diameters >20 nm could be stretched up to ~5 to 7% tensile strain, with maximum fracture strengths of ~12 GPa (25–27), reaching a considerable fraction of the ideal elastic limit of Si (predicted by theory to be 17% or more) (28). Although larger strains have been reported for ultrathin wires (diameter, <20 nm) (19), most of the existing works focused on measuring fracture strengths (11, 25–27). In some bending cases (27, 29, 30), the maximum stress at the edge of the samples has been inferred to reach up to ~18 GPa (maximum local strain, ~14%), on the basis of the measured radius of curvature, although the average stress and strain were much smaller. Although recent theoretical calculations suggest that it is possible in principle to achieve even >17% elastic/lattice strain (up to ~19 to 23%, depending on crystallographic directions) in a perfect Si crystal (21, 31), how closely one can really approach the theoretical elastic limit in Si nanowires is of great practical and fundamental interest. The theoretical limit is usually defined for a defect-free infinite Si lattice at 0 K, but thermally activated defect processes are possible at room temperature (32). In addition, the surface itself is a defect and could lower the elastic strain limit (21). Even more important are the practical limits due to crystal imperfections. However, if one can experimentally achieve >10% elastic strain in silicon components in a highly controllable, reversible, and reliable manner, the band structure and associated electronic and optical properties of the strained Si nanowires could undergo totally disruptive/revolutionary changes (20, 21). Here, using in situ tensile straining, we directly measure the elastic strains of single-crystalline Si nanowires, and try to probe their elastic strain limit and understand the origins of their significantly enhanced elasticity.

Here, vapor-liquid-solid (VLS)–grown single-crystal Si nanowires in <110> orientation were first chosen because of their pristine single crystallinity, uniform diameters, and atomically smooth surfaces (with a diameter of ~100 nm, as shown in Fig. 1, A and B). Uniaxial tensile strain was achieved by using “push-to-pull” micromechanical devices (MMDs) assisted by an in situ quantitative nanoindenter (33–35). The basic configuration of tensile testing is presented in Fig. 1 (D to H). Upon actuation by the nanoindenter, the indentation load applied from the indenter head (Fig. 1G) was converted to the uniaxial tensile load on the individual Si nanowire sample clamped at the MMD stages, as shown in Fig. 1 (E and F). The corresponding stress-versus-strain curves of the tested samples can be obtained from the force-versus-displacement data (such as that shown in Fig. 1H) read from the high-resolution nanoindenter, whereas the strains of the sample under deformation were further measured and corrected via in situ microscopy imaging (for more details, see Materials and Methods).

Fig. 1. Sample and experimental configuration.

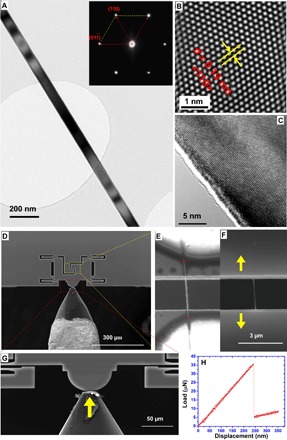
(A) VLS-grown Si nanowire sample with a uniform diameter of ~100 nm. Inset: Selected area electron diffraction (SAED) pattern indicates that Si nanowire is a single-crystal cubic diamond structure grown along the <110> orientation, which has been confirmed by the corresponding high-resolution transmission electron microscopy (HRTEM) image. (B) Lattice spacing of ~0.19 nm with respect to the <110> plane of Si. (C) HRTEM side view of a Si nanowire showing the atomically smooth surface. (D) In situ scanning electron microscopy (SEM) tensile testing of a single nanowire based on a push-to-pull MMD actuated by an external quantitative nanoindenter. (E to G) Zoom-in views (G) of the yellow frame in (D) are presented in (E) and (F), showing the detailed clamping configuration of a single nanowire sample at a lower voltage of 2 kV (E) and a regular working voltage of 20 kV (F). The tensile gauge length is indicated by the red bar in (E), whereas the yellow arrows in (F) indicate the uniaxial tensile loading direction. (H) Typical load-versus-displacement curve read from the nanoindenter for a monotonic tensile test under the displacement control mode. The abrupt force drop indicates the failure of the nanowire sample.

RESULTS

In situ tensile testing inside a scanning electron microscope

Figure 2 shows the results from quantitative in situ tensile tests of the VLS-grown single-crystal Si nanowires inside a scanning electron microscope. A representative example of our monotonic tensile tests is shown in Fig. 2 (A to G), in which the Si nanowire with a diameter of ~86 nm was stretched to ~13% tensile strain before fracture. This is much larger than the previously reported values for Si nanowires with similar diameters (8, 9, 25–27, 29, 30). The tensile straining process was under a constant strain rate of 0.003 s⁻¹, and the nanowire was elongated with a visible, uniform transverse thinning (Fig. 2, A to F). The measured transverse strain (ε_xx) was about −0.027 ± 0.011 (larger error was due to the limited image resolution in transversal direction), whereas the axial strain (ε_yy) was about 0.131, so the calculated Poisson’s ratio (ν) in this case is about 0.205 ± 0.085, consistent with the Poisson’s ratio of Si (11). (If the observed deformation were dominated by plasticity, one would observe an “apparent Poisson’s ratio” of ~0.5 due to the volume-conserving property of plasticity.) In addition, the corresponding stress-versus-strain curve (as shown in Fig. 2G) appears to be linear throughout the whole deformation, indicating a typical elastic deformation process without noticeable plastic yielding until the final fracture. The slope of the stress-strain curve gives a Young’s modulus of ~123 GPa, which is lower than the bulk Young’s modulus of Si along <110> (169 GPa) but in reasonable agreement with earlier reported values due to the decreased sample sizes (11, 25). It might also be noted that the fracture process of the nanowire presented an interesting “shattering” behavior, during which the broken nanowire pieces “flew away” instantly (see movie S1), with only the embedded sections remaining on the stages. These >10% large strains and shattering events of nanowires were consistently observed in our experiments, even in cyclic stretching experiments, with gradually increased strains until failure (see movie S2).

Fig. 2. In situ SEM tensile tests and postmortem TEM analysis.

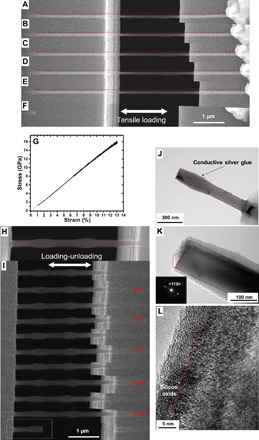
(A to F) Elongation of a single Si nanowire (diameter, ~86 nm). (A) Original status before test. (B to E) Extracted frames show gradual elongation of Si nanowire under tensile straining, with a maximum strain of 13% just before fracture (E). (F) Most of the nanowires flew away right after fracture, except the clamped portion. (G) The corresponding stress-versus-strain curve is nearly linear, with a fracture stress of ~16 GPa. (H and I) Loading-unloading test with increasing tensile strain amplitude and full unloading in each cycle. (H) Si nanowire before test (diameter, ~120 nm). (I) Loading–fully unloading process, in which the nanowire fully recovers its original length after strain values of ~5.8, ~8.1, ~9.7, and 13.2% are experienced. The nanowire finally broke at the fifth cycle with a strain value of ~13.5%, with one piece of broken nanowire remaining on the stage (as marked in the white frame); note that there is a thin, nonuniform layer of glue coating the nanowire [the red dashed lines in (H) indicate the true nanowire boundary]. (J and K) Bright-field TEM images showing a typical brittle fracture surface morphology, in which the nanowire remained in the single-crystalline structure [inset SAED pattern in (K)] with a uniform diameter [highlighted by red dashed lines in (J), with a small amount of conductive epoxy glue over the surface] and a flat fracture surface. All the images in (J) and (K) were taken in <1-11> zone axis. (L) The HRTEM image of the front end of the nanowire fracture surface [the red rectangular area in (K)] shows the single-crystalline structure with flat fracture surface (highlighted by red dashed lines); during the sample transfer and posttesting TEM analysis, a thin layer (~5 to 6 nm) of amorphous silicon oxide was formed at the fracture surface (L) with no visible sign of plastic deformation.

Loading-unloading tests with TEM analysis

To further confirm whether the deformation was fully elastic, we carried out repeated loading-unloading tests with increasing tensile strain amplitude (strain rate, ~0.005 s⁻¹) and full unloading in each cycle. After a strain value of up to ~13% was experienced (Fig. 2I), the Si nanowire could still recover its original length instantly upon unloading, with no evidence of plastic deformation and without any observable bending or buckling (see Fig. 2I and movie S3). Eventually, this particular Si nanowire with a diameter of ~120 nm failed at ~13.5% strain with a breaking stress of ~18 GPa (corresponding Young’s modulus of ~134 GPa). These ultra-large strains were visually striking (see movies S2 and S3), giving a rubber-like appearance with clearly visible transverse contraction. This contraction appears rather uniform, which allows us to measure a Poisson ratio of ~0.195 ± 0.045 (Fig. 2I), again indicating purely elastic deformation.

In the last frame of Fig. 2I, we see that half of the nanowire sample was fortunately left after fracture. That is, one-half did not “fly away” as in most other cases (which was the main reason we chose to present this case, despite a thin layer of conductive epoxy glue over the sample surface). On the other hand, the two glue “nodes” in Fig. 2I can also serve as “strain gauge” markers and show that the strain values are highly consistent with the measured data described previously. This allowed further TEM examination of the fracture surface and microstructure, as shown in Fig. 2 (J to L). Bright-field TEM images in Fig. 2 (J and K) show a flat fracture surface morphology, in which the broken nanowire remained in the original uniform diameter with no visible necking, suggesting that the nanowire fractured in a brittle manner. The SAED (Fig. 2K) of the sample also confirmed that the fractured nanowire remained in the same single-crystalline structure, whereas HRTEM imaging of a broken nanowire further showed a flat fracture surface with no visible indication of plastic deformation near the fracture area (Fig. 2L).

In situ tensile tests in ambient environment

Because there have been recent reports of large plastic strains in silicon nanowires due to electron beam effects (mainly performed in TEM) (36–38), we also performed additional tensile tests under optical microscope in an ambient laboratory environment to rule out electron beam effects in our findings, and confirmed that VLS-grown Si nanowires still showed ultralarge elastic behavior at room temperature, with the highest strain values ranging up to ~16% (corresponding fracture stress of ~20 GPa; see Supplementary Materials S1), just as inside the scanning electron microscope. Here, the nanowire deformation/strain in the transverse (thickness) direction could not be well characterized because of the diffraction limit of the optical microscope. However, the tensile strain (in the longitudinal direction) of the nanowire can still be precisely measured. We also performed loading-unloading experiments under the optical microscope (Fig. 3A), confirming that the Si nanowire strain could be fully recovered after very large strains (~10%) were experienced upon unloading. The nanowire was finally broken at a strain value of around 11.7% (stress, ~15 GPa; Young’s modulus, ~128 GPa) in the same brittle fashion as before, with the corresponding stress-versus-strain curves showing very linear and hysteresis-free shape during the full three cycles. Note that in this loading–fully unloading tensile experiment, the strain rate was relatively high at ~0.012 s⁻¹ (see movie S4).

Fig. 3. Tensile test in ambient environment under an optical microscope.

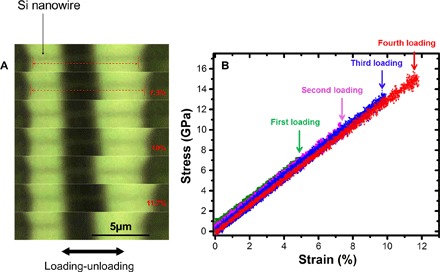
(A) Loading-unloading tensile test of a Si nanowire with increasing tensile strain amplitude and full unloading in each cycle. Again, the nanowire recovered its original length after strain values of ~5, ~7.3, and ~10% were experienced in each cycle and eventually fractured at the fourth cycle with strain value of ~11.7% (top to bottom: the last three cycles), where most of the broken nanowire flew away, as shown in the last frame. Note that the contrast in the optical images was slightly enhanced for clarity. (B) Corresponding stress-versus-strain curves of the multicycle loading–fully unloading test, using different colors to better illustrate the data from each cycle.

DISCUSSION

With the quantitative measurements and loading-unloading experiments, we can conclude that, despite extremely large fracture strains, Si nanowires essentially underwent pure elastic deformations up to the point of catastrophic brittle fracture. One interesting phenomenon is that the broken nanowires generally flew away after the fractures. This reflects the very large elastic potential energy (U_e) stored in the strained nanowires during the large deformation. For the sample shown in Fig. 2 (A to G), according to classical elasticity theory (39), the observed strain corresponds to an energy density of about 1.04 × 10⁹ J/m³ or about one-seventh of the volumetric energy density of TNT (2,4,6-trinitrotoluene). Upon fracture, stored energy was converted to kinetic energy as an elastic shock wave, causing secondary fractures near the nanowire clamping points. If this shock wave was efficiently converted to translational kinetic energy, the departing velocity of the broken nanowire fragments could reach up to 10³ m/s, which is so fast that it could not be visually captured. Therefore, unlike the “superplasticity” phenomena reported in Si nanowires under intense electron beam exposure, or the recently reported “anelasticity” case (40) in which p-doped Si nanowires took a long time for full recovery (41), our observations are essentially pure elasticity. In addition, because our elastic strains exceed one-half of the bulk theoretical limit of Si (~17 to 20% for <110> uniaxial tension) (28, 31), they go far beyond the definition (¹/₁₀) of ultra-strength (12, 13). We refer to this behavior as “deep ultra-strength,” defined as exceeding one-half of the bulk ideal strength (which itself was defined at 0 K for an infinite perfect crystal).

Mechanisms of the enhanced elasticity and deep ultra-strength

To understand the deep ultra-strength and ultrahigh elasticity observed here, we first note that theoretical studies and simulations (21, 28, 31) already showed that the ideal strength of bulk Si crystal can be extremely high (~21 to 23 GPa) (11), with the corresponding theoretical elastic strain limit of ~17 to 20% in <110> uniaxial tension. In addition, ab initio calculations suggested that the presence of an ideal flat surface in Si does not significantly decrease the ideal strength, except in extremely thin cases (on the order of 1 nm or less) (21). The question is then how nearly we can experimentally approach the ideal strength at 0 K in our ~100-nm-diameter Si nanowires at ~300 K.

Inhibiting both plasticity and brittle fracture, either of which typically occurs already at much smaller strains in bulk materials, is required to approach the theoretical strength limit. As in earlier works, the two key factors are the nanoscale sample size and pristine single-crystal structure, both of which greatly reduce the number of sources of failure. In our experiments, the high-quality VLS growth method provided pristine single-crystalline nanowires in a nearly defect-free state (Fig. 1, A to C). Regarding plasticity, because of the nanometer-sized volumes, the number of potential dislocation sources in the pristine single-crystalline Si nanowires is severely limited. Even with a few initial dislocations present, because of the small transverse dimensions, dislocations in nanowires can only travel very short distances before annihilating at a free surface, thereby further reducing the overall dislocation multiplication and dislocation density, effectively suppressing plasticity. The same mechanism allows increased elastic strains in submicrometer/nanometer-sized metal crystals, though to a lesser extent (42, 43). With increased stress during loading, these processes would lead to a dislocation-starved state that requires even higher stresses to nucleate new mobile dislocations, contributing to the ultrastrength (13, 44).

The second failure mechanism, brittle fracture, is more common for materials like silicon. In the simplest case, a crack forms at some local weak point or defect, without any contribution from dislocations. Then, an important factor for a thin wire might be statistical—that the probability of having a defect that could start a surface Griffith crack or nanocrack is proportional to the size. However, it is probably at least equally important that our VLS-grown <110>-oriented nanowires have almost atomically smooth surfaces (Fig. 1C). This nearly perfect surface structure could be another key factor to achieving such high strain in reality without early-stage local stress concentration and resultant crack initiation. To confirm this, we also tested top-down etched Si nanowires (Fig. 4, A to C) with a similar strain rate (~0.002 to 0.006 s⁻¹) and compared them with the abovementioned VLS-grown Si nanowires. Despite their uniform diameters (also around 100 nm) and same <110> single-crystalline orientation, the surfaces of those top-down etched nanowires were less smooth (Fig. 4A). One representative result is shown in Fig. 4B and movie S5. The maximum fracture strain was ~3.7% (Fig. 4C), which is still much greater than that of bulk Si but much smaller than our results for VLS-grown samples. By summarizing all successful tests on both VLS-grown Si nanowires and top-down etched Si nanowires in Fig. 4D for statistical analysis, we can see that the presence of surface roughness and possibly other etch-induced defects, such as porosity (45, 46), can significantly reduce the elastic limit of Si nanowires, which agrees with previous experiments (with fracture strengths of ~4 to 5 GPa) on metal-assisted, catalytically etched Si nanowires (47) as well as a recent molecular dynamics simulation result (48). It might also be noted that earlier studies on VLS growth of Si nanowires suggested that <110>-oriented nanowires could generally have smoother sidewalls compared to <111>-oriented wires (49), so again we believe that the smooth surfaces make a big difference.

Fig. 4. Comparison between VLS-grown Si nanowires and top-down etched Si nanowires.

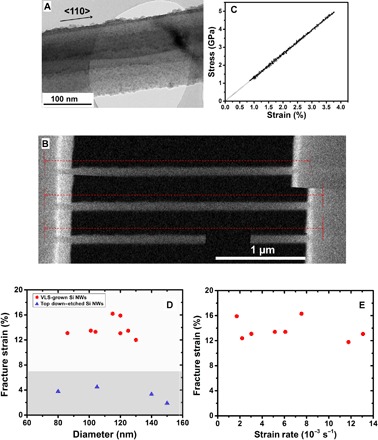
(A) Bright-field TEM showing a top-down etched single-crystal Si nanowire (also in <110> orientation) with a uniform diameter but a relatively rough surface. (B) Deformation process of a top-down etched Si nanowire upon tensile straining (diameter, ~140 nm) with the corresponding stress-versus-strain curve. (C) Si nanowire broken in an elastic manner with a fracture strain of ~3.7% (fracture stress, ~5 GPa; calculated Young’s modulus, ~135 GPa). (D) Summary of the comparison for the fracture strain versus nanowire (NW) diameter between the VLS-grown (red dots) and top-down etched (blue triangles) Si nanowires. The shaded bottom area indicates the range of previously reported tensile strain values for Si nanowires with diameters of >20 nm (25–27). (E) Summary of the fracture strains of VLS-grown Si nanowires versus their strain/loading rates, indicating that the elastic limit is insensitive to strain rate in this range.

Finally, the uniaxial tensile loading geometry could be another favorable factor, giving less local stress concentration and more uniform strain distribution throughout the whole specimens compared to earlier Si nanowire measurements (8, 9, 29, 30), mainly with the bending or deflection method. Compared to some recent results from atomic force microscopy cantilever–based tensile testing methods (25–27), our push-to-pull tensile mechanism could ensure more uniform and homogeneous loading through the whole deformation process, and introduce less bending/shearing misalignment when strains became large. In addition, we avoided the use of focused ion beam (FIB) or electron beam–induced deposition (EBID) (25, 27) in clamping the nanowire ends (see Materials and Methods), because they might introduce potential damage/change on the sample crystalline structure and surface morphology, as well as possibly introduce doping effects (50–52).

CONCLUSIONS

In conclusion, VLS-grown single-crystalline Si nanowires with diameters of around 100 nm were characterized by in situ tensile testing at room temperature and demonstrated ultrahigh elasticity, with maximum tensile strains and strengths approaching the theoretical elastic strain limit and ideal strength of silicon. Loading-unloading experiments further confirmed that the samples can consistently achieve above 10% elastic strain with full recovery during large cyclic straining. These deep ultra-strength behaviors observed in VLS-grown Si nanowires at room temperature, and presumably accessible in other defect-scarce semiconductor nanowires, could open up opportunities in flexible electronics and bio-nano integrated systems, as well as the promising elastic strain engineering that takes advantage of the drastically changed electronic and optical properties under ultra-large lattice strains (14, 18–21, 53).

MATERIALS AND METHODS

Sample fabrications

Here, the main experiments were performed on Si nanowires grown via a standard VLS growth method (54). In this fabrication process, a 304 stainless steel (0.5 mm thick) substrate was decorated with a 10-nm-thick Au catalyst film by using electron beam evaporation and then transferred into a chemical vapor deposition tube furnace. Under H₂ flow, the gold thin film was first annealed at ~600°C for 2 hours. Subsequently, Si nanowires were grown at ~540°C with SiH₄/H₂ mixed gas as the precursor (54), whereas for the top-down etched Si nanowires, they were prepared using a metal-assisted chemical etching method as previously reported by Peng et al. (55) and Jie et al. (56). Briefly, a clean wafer was electroplated with Ag nanoparticles by immersing in a solution containing 4.8 M HF and 0.005 M AgNO₃, followed by etching in 4.8 M HF and 0.1 M H₂O₂. The wafer was then immersed in dilute HNO₃ to remove the Ag catalyst and obtain a uniform array of Si nanowires. Finally, free-standing individual nanowires were obtained by scratching them off from the wafer (55).

In situ nanomechanical characterizations

The basic mechanism of the in situ tensile test for Si nanowires was based on the use of push-to-pull MMDs (33–35) assisted with a quantitative nanoindenter (Hysitron PI 85 PicoIndenter) (Fig. 1). To prevent possible damage on sample structure and morphology, we applied conductive silver epoxy glue (Chemtronics, CircuitWorks Conductive Epoxy) to clamp the individual nanowires onto the stages of the MMD, instead of the commonly used FIB or EBID clamping. To ensure firm bonding between the nanowire and MMD sample stages, a multilayer coating of the silver glue was applied (for more sample clamping details, see Supplementary Materials S2). The nanoindenter was used either inside a scanning electron microscope or under an optical microscope, and the corresponding deformation process of the tested samples was directly monitored and recorded by a field-emission scanning electron microscope (FEI Quanta 450 FE-SEM) or an optical microscope (A-Zoom μ microscope, equipped with a 100× objective lens). The tensile tests were performed under displacement control mode with constant strain rates (ranging from ~0.0017 to 0.013 s⁻¹). The force and displacement changes could be directly read out from the piezoelectric transducer of the nanoindenter at a high resolution of 3 nN for the load output and 0.02 nm for the displacement output. To ensure accurate measurements of the strain values of the samples, we used digital image correction to obtain an accurate sample elongation measurement, and the gauge sections were carefully imaged and marked at extra low electron beam voltage (2 kV; Fig. 1E) to better capture the glue boundaries of the clamping points (see more details in Supplementary Materials S2). After each test, both clamping points with the remaining bonded nanowires were carefully examined and compared with their original lengths before testing to ensure no interfacial sliding. TEM analysis (bright-field imaging and SAED) for the pristine and tested Si nanowires was conducted with a field-emission transmission electron microscope (JEOL, model JEM-2100F FE-TEM).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/8/e1501382/DC1

fig. S1. Monotonic tensile straining of a VLS-grown Si nanowire under an optical microscope.

fig. S2. Additional details about sample clamping and gauge length/strain measurement.

movie S1. Monotonic tensile test of a VLS-grown Si nanowire inside a scanning electron microscope (as shown in Fig. 2, A to G); video speed is played at ~3× speed.

movie S2. Loading–partially unloading tensile test of a VLS-grown Si nanowire with increased strain values until finally fractured at a stress of ~20 GPa; video speed is played at ~10× speed.

movie S3. Loading–fully unloading tensile test of a VLS-grown Si nanowire inside a scanning electron microscope (as shown in Fig. 2, H and I); video speed is played at ~9× speed.

movie S4. Loading–fully unloading tensile test of a VLS-grown Si nanowire in ambient environment under an optical microscope (as shown in Fig. 3); video speed is played at ~8× speed.

movie S5. Monotonic tensile test of a top-down etched Si nanowire (as shown in Fig. 4, B and C); video speed is played at ~2× speed.