Abstract
Efficiently avoiding inappropriate actions in a changing environment is central to cognitive control. One mechanism contributing to this ability is the deliberate slowing down of responses in contexts where full response cancellation might occasionally be required, referred to as proactive response inhibition. The present electroencephalographic (EEG) study investigated the role of attentional processes in proactive response inhibition in humans. To this end, we compared data from a standard stop-signal task, in which stop signals required response cancellation (“stop-relevant”), to data where possible stop signals were task-irrelevant (“stop-irrelevant”). Behavioral data clearly indicated the presence of proactive slowing in the standard stop-signal task. A novel single-trial analysis was used to directly model the relationship between response time and the EEG data of the go-trials in both contexts within a multilevel linear-models framework. We found a relationship between response time and amplitude of the attention-related N1 component in stop-relevant blocks, a characteristic that was fully absent in stop-irrelevant blocks. Specifically, N1 amplitudes were lower the slower the response time, suggesting that attentional resources were being strategically down-regulated to control response speed. Drift diffusion modeling of the behavioral data indicated that multiple parameters differed across the two contexts, likely suggesting the contribution from independent brain mechanisms to proactive slowing. Hence, the attentional mechanism of proactive response control we report here might coexist with known mechanisms that are more directly tied to motoric response inhibition. As such, our study opens up new research avenues also concerning clinical conditions that feature deficits in proactive response inhibition.
Keywords: response inhibition, attention, single-trial EEG, proactive control, drift diffusion models
INTRODUCTION
Adaptive motor behavior requires a complex coordination of motor activation and inhibition. Inhibitory mechanisms play a fundamental role in everyday behavior, in cognitive development, and in a range of neurological and psychiatric conditions, including attention-deficit hyperactivity disorder (ADHD), Parkinson's disease, and substance abuse (Chambers et al., 2009). In a laboratory setting the stop-signal paradigm has often been used to quantify the latency and efficiency of response inhibition (Logan and Cowan, 1984), and to investigate its underlying neural processes (Aron, 2011; Huster et al., 2013).
In the stop-signal task, a go-stimulus requiring a rapid choice-reaction is infrequently followed by a stop-stimulus, signaling the participant to halt the initiated response. Task behavior can be characterized as a race between a process that triggers (go-process) and cancels (stop-process) a motor action. The stop-process latency (“stop-signal response time”; SSRT) is covert, but can be recovered by assuming a stochastic model, such as the Independent Race Model (Verbruggen and Logan, 2009b).
Traditionally, the research focus was on processes related to this reactive form of inhibition (triggered by the stop-stimulus), which has been found to be related to a “response-inhibition network” involving the right inferior frontal gyrus, the pre-supplementary motor area, and the subthalamic nucleus (Aron et al., 2014; see also Cai et al., 2014). Recently, however, proactive response inhibition has received increasing attention. Proactive response inhibition is considered potentially more ecologically relevant, in that it describes the tendency of slowing down responses when outright stopping might be required, which likely relates to response caution in everyday situations (Aron, 2011). Mathematical modeling has mostly related this effect to an increased decision threshold of the go-process (e.g., Verbruggen and Logan, 2009a), and a range of experimental studies have implicated the (reactive) response-inhibition network in this process as implementing gradated instead of complete response inhibition (Aron et al., 2014).
Although the core neural processes of reactive and probably also proactive inhibition likely reside within the response-inhibition and extended motor network, recent behavioral research and theorizing has highlighted a possible role of earlier sensory/attentional processes in response inhibition (Bari and Robbins, 2013; Logan et al., 2014; Verbruggen et al., 2014b; Huster et al, 2014). Consistent with such notions, differences in the attentional processing of stop-stimuli have been found to contribute to the behavioral outcome in the stop-signal task, with increased attention to the stop-stimulus being associated with successful response inhibition (Bekker et al., 2005; Boehler et al., 2009; Kenemans, 2015).
Yet, some recent findings suggest that attentional processes may also play a role in proactive response inhibition; specifically, we have reported magnetoencephalograpic data showing that the attentional processing of the go-stimulus in a stop-trial is enhanced when response inhibition is ultimately unsuccessful (Boehler et al., 2009; see also Knyazev et al., 2008). While this implies that varying attentional processing of the go-stimulus is behaviorally relevant, this earlier work was limited in important ways with respect to the study of proactive response inhibition. Specifically, it involved only a small subset of trials (i.e., stop-trials), which furthermore could theoretically have been affected by the overlapping processing of Stop-stimuli in trials where those were presented particularly rapidly after the onset of the Go-stimulus. Additionally it was not clear whether participants actively engaged differential attentional processing as a means of strategic proactive inhibition. Rather, this earlier work might have identified the influence of randomly oscillating variations in attentional focus towards the go-stimuli, and not strategically deployed levels of attention driven by task-relevant stimuli. Here, we address these questions by (i) using EEG measures for which we adopt a single-trial framework to model electroencephalographic activity during go-trials as a function of response slowing (Pernet et al., 2011), and (ii) by including additional task blocks in which stop-stimuli were task-irrelevant to provide a baseline condition which should be devoid of proactive response inhibition.
METHODS
Participants
Sixteen healthy right-handed subjects (mean age 24.7 years, SD 5.0, 8 males) took part in the study. Subjects gave written informed consent before the experiment in accordance with the Duke Medical Center Institutional Review Board for Human Subjects. The experiments were performed at Duke University. All subjects were neurologically intact and had normal or corrected-to-normal visual acuity.
Stimuli
On each trial a traffic light symbol was presented above a central fixation dot on a gray background. The traffic symbols were green go-signs, directed to either the LEFT or the RIGHT, and red stop-signs. The LEFT-pointing go-sign required a button press with the right index finger, and the RIGHT-pointing one required a button press with the right middle finger. In contrast to our earlier related work (e.g., Boehler et al., 2009) the target stimuli were presented in isolation without additional distractor items. This choice-reaction stimulus either lasted for the full stimulus duration (go-trial) or was rapidly followed by a stop stimulus (stop-trial). Two block types were used: stop-relevant and stop-irrelevant (see Schmajuk et al., 2006 and Boehler et al., 2010, for similar task designs that used stop-irrelevant stop-trials as a sensory baseline condition to investigate reactive response inhibition). In stop-relevant blocks subjects were instructed to withhold their response when a stop-stimulus was encountered, whereas in stop-irrelevant blocks subjects were instructed to ignore the stop-stimulus completely and to always respond LEFT or RIGHT to the go-stimulus, see Figure 1. Participants were told not to slow down their response strategically. Still, proactive slowing is typically observed in such settings (Verbruggen et al., 2005).
Figure 1. Paradigm.
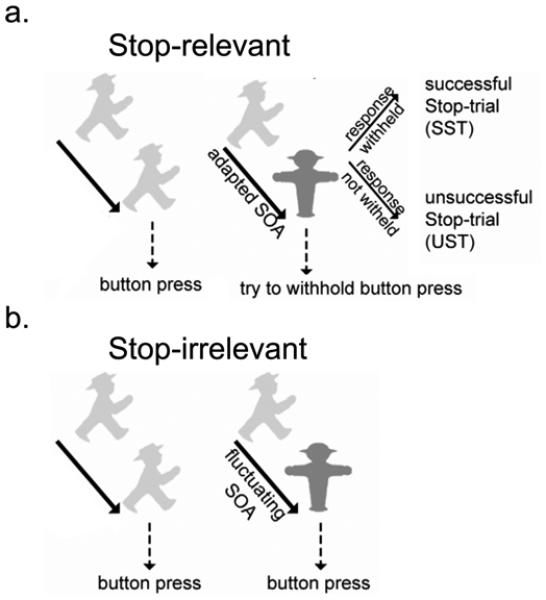
Participants performed a standard (stop-relevant) stop-signal task (a) and a stop-irrelevant version (b) in separate blocks. Response inhibition was required upon presentation of a stop-stimulus in the stop-relevant but not the stop-irrelevant blocks.
Procedure
Go-trials accounted for 75 percent of all trials, and stop-trials for the remaining 25 percent. There were twelve experimental blocks each consisting of approximately 90 trials. At the midpoint there was a small break and instructions were changed (e.g., stop-relevant to stop-irrelevant), with the next run having the opposite sequence. In total, there were 285 stop-trials and 846 go-trials, equally distributed across the stop-relevant and stop-irrelevant task blocks. Given the fast ABBA sequence of different block types, the actual block order was not further counterbalanced across participants. The overall duration of stimulus presentation was 700 ms for each trial, and trials were interleaved by intertrial intervals that varied randomly between 1000 and 1400 ms. For go-trials in both stop-relevant and stop-irrelevant blocks the visual display was constant for the 700 ms duration, whereas for stop-trials the go-stimulus was replaced by a stop-sign after a certain stop-signal delay (SSD), which would then stay on screen until the end of the 700 ms duration. For relevant stop trials an adaptive staircase procedure was used to control stopping performance by incrementing (after a successful stop trial) or decrementing (after an unsuccessful stop trial) the stop-signal delay by 17 ms. This procedure enabled the reliable calculation of the stop-signal response time (SSRT), which reflects the time required to inhibit a motor response. As a matched routine, we took the end value of the adapted stop-signal delay from stop-relevant blocks as the initial value in subsequent stop-irrelevant blocks and then randomly alternated it by 17 ms on each subsequent irrelevant trial.
Recording and Analysis
Basic Behavioral Analyses
All response time analyses were performed using repeated-measures analysis of variance (rANOVA). Differences in accuracy for go-trials were tested between blocks using a non-parametric Χ2 test of differences in proportions. To estimate the SSRT the integration approach was used. This approach defines the SSRT = (nth rank-ordered RT) − (mean stop-signal delay), with n equal to the number of RTs in the go-trial RT distribution multiplied by the overall probability of responding given a stop signal. Simulations showed that under most circumstances the integration approach yields consistent and unbiased estimates of the SSRT (Verbruggen et al., 2013). Note, however, that stop-trial data were only of peripheral interest here, as the main analyses focus on the go-trials from the two different task blocks1.
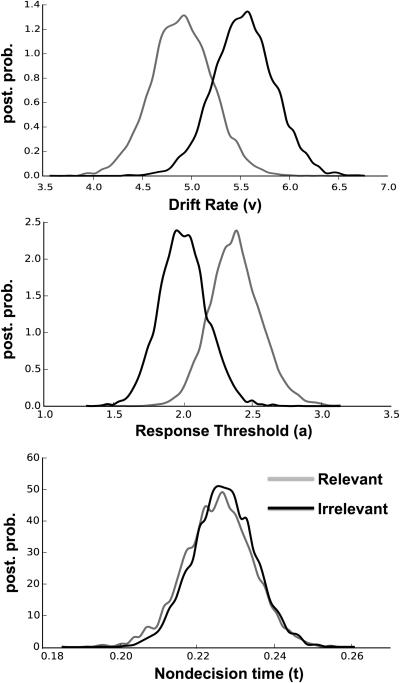
Drift Diffusion Models
Drift diffusion models are a description of a binary choice process defined by three main parameters (Ratcliff, 1978), and have been used frequently in the study of proactive inhibition (e.g., Verbruggen and Logan, 2009a). These parameters are the response threshold (a), the mean rate of approach to a threshold, known as drift rate (v), and processes that precede and succeed the actual decision process and give rise to a nondecision time (t0). Hierarchical Bayesian estimation was used to model the parameters using the Hierarchical Drift Diffusion Model (HDDM) software (Wiecki et al., 2013). Model fit was assessed using the deviance information criterion (Spiegelhalter et al., 2002; DIC, with smaller DIC indicating better fit). Five nested candidate models were fit to the data; a null model (model 0), a full model (model 1, including a, v, and t0), and 3 reduced models; a model without t0 (model 2), a model without v and t0 (model 3), and a model without a and t0 (model 4). These models were chosen to test for differences in the parameters in a principled sequential manner, and for alignment with previous modeling efforts (Verbruggen and Logan, 2009a). 20,000 posterior samples were drawn for each model using Markov-Chain Monte Carlo methods. We used a burn-in of 5,000 and a thinning factor of 3. Each model was checked for convergence using the Gelman-Rubin diagnostic (Gelman and Rubin, 1996). Furthermore, posterior-predictive checks were made as an added assurance of proper fit. After model selection, posterior distributions were probed to determine differences directly in the parameters between the stop-relevant and stop-irrelevant task contexts. This is accomplished by examining the proportion of posterior samples falling above or below the two estimated posterior distributions of any specific parameter, resulting in a probability that one posterior distribution is greater or less than the other (see Kruschke, 2010 for an overview of Bayesian methodology).
EEG Recording
EEG was recorded from 64 electrodes mounted in a custom-designed electrocap (Electro-Cap International, Eaton, Ohio), referenced to the right mastoid during recording (SynAmps amplifiers from Neuroscan; El Paso, TX). Additionally, horizontal and vertical EOG electrodes recorded blinks and eye movements, for which participants were additionally monitored online via a video camera in the EEG chamber. Electrode impedances were kept below 2Ω for the mastoids, below 10Ω for the electro-oculogram (EOG) electrodes, and below 5Ω for all the remaining electrodes. All EEG channels were continuously recorded with a band-pass filter of 0.01-100 Hz at a sampling rate of 500 Hz per channel.
EEG Preprocessing
EEG data were algebraically re-referenced to the average-mastoid offline. A coarse (visual) inspection was performed on the continuous data of each subject to exclude stretches of data with common EEG artifacts. This was followed by an Ocular-correction ICA analysis using the vertical EOG as the blink marker channel in Brain Vision Analyzer 2 (Brain Vision analyzer software, Brain Products GmbH, Munich, Germany). The correct responses of the go-trials from the two task blocks were then epoched from −200 to 1200 ms and corrected using the pre-stimulus baseline prior to further analysis. In the end, 97.8% of the data epochs were preserved.
Go-locked event-related potential (ERP) analyses
In order to focus on the inferoposterior visual N1 component, an averaged topography was plotted across both block types and used to define 10 posterior electrodes, 5 on the right and 5 on the left, as well as the time-range of interest, determined as 130 ms to 190 ms, to represent the visual N1 elicited by the Go-signal. This time-range and set of electrode averages was then also used for the statistical analysis (see e.g. Vogel and Luck, 2000, for similar a similar choice of channels and time-range). It is important to note, however, that the ERP analysis here is of peripheral interest, given that the between-block comparison is rather unspecific.
Single-trial ERP data
The main analysis of interest investigated the relationship between single-trial ERP data and response speed on go-trials in the two different task blocks. To this end, single-trial ERP analysis was carried out using the software package LIMO EEG (Pernet et al., 2011; also see Gaspar et al., 2011). Single-trial analysis fits a general linear model of the form [ye,s = XBe,s + noise] to trials of EEG data (y), for all analyzed electrodes (e) and sampling points (s) in the N1 time window. The five predictors in the design matrix X were the categorical stop-relevant and stop-irrelevant go-trial types, the single-trial normalized (per subject, per condition) response times, and a noise variable. Below, we describe some more details of the statistical analysis, as implemented in LIMO EEG (see Pernet et al., 2011 for more details).
A generalized Moore-Penrose pseudo-inverse algorithm was used to estimate the beta parameters for each subject. Model fit was assessed per individual by examining R2, the amount of variance explained in the EEG by the design matrix. These coefficients were tested using a restricted intercept-only model to develop an F-test that determines the amount of variance being explained over this restricted model with the full model. This results in F-values for each sampling point and electrode considered in the model, with degrees of freedom dependent on total number of predictors in the restricted model (i.e. number of predictors in the full model − 1) and trial number.
At the second level of the analysis each of the subjects' five estimated beta coefficients were “synthesized” to probe for statistical significance using nonparametric (bootstrapping) methods. The general linear model allows directly testing for the covariation of single-trial ERPs with response time using a bootstrap-t approach. This determines the significance and direction of beta parameters per sample point. We used a robust one sample t-test that tests if the average effect significantly differs from zero. The observed t-values were first computed. The data were then centered and five-thousand bootstraps were made. Subjects were drawn randomly with replacement. For every bootstrap, a one-sample t-test was performed on the bootstrap sample, subsequently storing the t-value. These bootstrapped t-values provide an approximation of the t-distribution under H0. The p-values are then computed by comparing the observed t-values to the bootstrapped t-distribution. Since tests are performed on multiple electrodes and sampling points, as is typical for this approach (e.g., Pernet et al., 2011; Gasper et al., 2011), testing will give rise to false positives. To account for multiple comparisons, we used temporal clustering by which only clusters with a mass (sum of t values) bigger than the 95% percentile of the null distribution are considered significant. In this case, the null distribution corresponds to the maximum cluster value across electrodes measured at each bootstrap computed on nullified data (Pernet et al. 2015).
In a similar vein, for a repeated-measures ANOVA, the observed F-values were first calculated. Following this, an F-table under H0 was made. First, the data was centered for each condition so that each cell of the ANOVA had a mean of zero. Second, the centered data was used to estimate F-distributions under H0. Subjects were sampled with replacement and the associations between observations were kept. Five-thousand bootstraps were made. P-values were obtained by comparing the observed and bootstrapped F-values, and multiple comparison corrections were handled in the same manner as the 1-sample t-tests.
Results
Behavioral Performance
The average response times to go-stimuli in the stop-relevant blocks were 466.7 ms (SD 116.6), which were slower than (F(1,15) = 50.37; p < .0001) those in the stop-irrelevant blocks 402.3 ms (SD 85.2). This result indicates that participants were employing proactive response slowing in the stop-relevant blocks, as expected. Overall, accuracy in go-trials was high: in the stop-relevant blocks it was 98.9 percent, but slightly lower (Χ2 = 8.12, p = 0.004) in the stop-irrelevant blocks at 98.3 percent. The SSRT was calculated using the integration method yielding an estimate of 242.8 ms (SD 37.5), a value in line with previous research.
The DIC-based model selection procedure evidenced that the full model (model 1, DIC = −25009.1) best accounted for the data. The next closest candidate model was the reduced model 2 (DIC = −24915.6), followed by model 3 (DIC = −24782.1), model 4 (DIC = −24658.7), and the model 0 (DIC = −22925.4). Based on this selection criteria and posterior predictive checks, model 1 was chosen for further analysis. Two of the three estimated main parameters showed significant differences between block types. In particular, robust effects were observed for a raised response threshold (a) and lower drift rates (v) in the stop-relevant blocks. Posterior distributions of the three main parameters are shown in Figure 2. With respect to the response threshold, the p(arelevant > airrelevant) = 0.94, showing that indeed the response threshold is raised in the relevant blocks. The drift rate is lower in the relevant blocks, p(Virrelevant > Vrelevant) = 0.92. As seen in Figure 2, non-decision time did not show evidence of being different between the blocks, p(t0irrelevant < t0relevant) = 0.46. Overall, the results evidence a more conservative response process in the stop-relevant blocks, and the fact that the effects were seen on two parameters suggests that this was brought about by multiple processes. Indeed, it is possible that model 2 (full model sans t0) is the better fitting model, given that DIC is known to be somewhat biased towards a model with greater complexity (Plummer, 2008). However, the parameter estimates of model 1 and model 2 are similar, so interpretation of the other two parameters remains exactly the same.
Figure 2. Hierarchical drift diffusion model results.
Drift rate (top), response threshold (middle), and non-decision time (bottom) posterior probability densities for both the irrelevant and relevant conditions of Model 1.
Go-locked N1 ERP Analysis
The average topography between 130 and 190 ms post Go-stimulus is shown in Figure 3a for correct Go-trials collapsed across the stop-relevant and stop-irrelevant blocks. Channel locations and time range for further analysis were selected based on this average across both block types. The N1 electrodes were separately averaged in the left and right hemisphere (see black dots in Fig. 3a) and a rANOVA was used to test for differences between block type (stop-relevant vs. stop-irrelevant) and laterality (left vs. right hemisphere) for the data averaged between 130 and 190 ms post go-stimulus. Both block type (F(1, 15) = 5.60, p = 0.032, η2 = 0.004) and laterality (F(1, 15) = 6.12, p = 0.026, η2 = 0.049) showed significant differences, but there was no significant interaction between the two (F(1, 15) = 1.19, p = 0.29, η2 = 0.0002). Note, that laterality was only of peripheral interest, that we had no clear expectations, and that the main effect only indicates that N1 amplitudes were generally larger over one hemisphere. The mean amplitudes of the stop-relevant N1 were slightly more negative than in the stop-irrelevant condition. Thus, a simplistic mapping between response speed and mean N1 amplitudes did not hold2. Yet, these effects are, as indicated by the effect size, quite small. Indeed, this between-block comparison is necessarily quite unspecific, and our a-priori analysis plan was to investigate the relationship between response time and N1 amplitudes within the two different block types, for which we applied the single-trial-based analysis presented below.
Figure 3. ERP results.
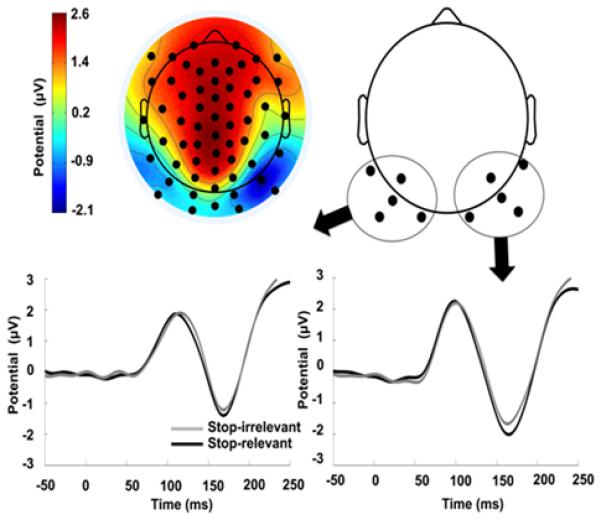
Topography for go-trials averaged between 130 and 190 ms collapsed across the two task blocks on the top left, and sensors chosen to represent visual N1 on the right. Sensor plots from the average of the five electrodes averaged on the left and the right are displayed at the bottom (plotted using a 30-Hz low-pass filter for displaying purposes).
Systematic Variation in Sensory Processing of Go-signals
Single Subject Analysis and Model Fit
For each participant, all ten inferoposterior N1 electrodes were individually taken into an analysis with the EEG signal modeled as a linear function of the response time to investigate relationships to go-stimulus processing across sampling points. Only correct go-trials were taken into consideration. For the first-level statistical analysis, single-trial ERPs were estimated for each individual at each of the 10 electrodes selected above between 130 and 190 ms. This resulted in beta coefficients for the categorical block parameters, response time parameters, and noise, for each of these 10 electrodes and for each sample point.
As expected, there was variation between individuals, electrodes, and sampling points modeled in terms of the estimated R2. The F-values were queried for a maximum value F-statistic across individuals and sampling points. The maximum F-values had a range from 4.14 to 16.18 over all individuals, with a mean of 8.35 (SD = 3.8). For each participant the max F-values were found to be significantly different from a restricted model, using number of linear predictors in the restricted model and participant trial numbers to calculate the appropriate degrees of freedom. Given that each individual’s model had sample points within the N1 range that were significantly explained by the design matrix, it was concluded that the model fit was adequate to continue testing at the second level.
Second Level Analyses
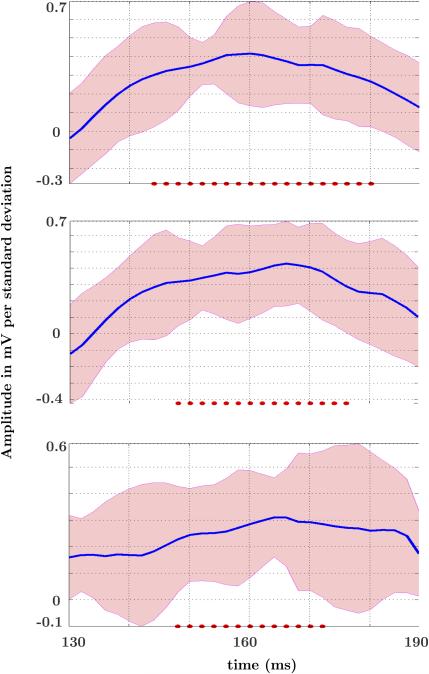
Group-level differences in the stop-relevant blocks of the RT beta parameters were tested using a bootstrapping 1-sample t-test procedure to synthesize individuals. Within the N1-related electrodes chosen for analysis, a generalized pattern of N1 attenuation emerged as RT increased. Estimated t-values peaked with significant effects that were centered roughly on 160 ms. Seven of the 10 electrodes showed significant effects using uncorrected t-tests and an α level of 0.05. Electrodes started to show RT effects in the relevant beta parameters capturing the relationship between RT and EEG amplitude starting at 138 ms and lasting until 190 ms. A 1-dimensional temporal cluster analysis was further run on the model to correct for multiple comparisons. This analysis evidenced 3 electrodes, 2 confined to the right posterior, and 1 to the left at a corrected p = 0.05 alpha level. The bootstrapped mean Betas and 95% confidence interval for each of the three electrodes that survived temporal cluster correction are plotted in Figure 4. This shows the mean change in mV per standard deviation unit of RT for the stop-relevant blocks to further illustrate this relationship.
Figure 4. Bootstrap mean Beta and 95% Confidence Intervals.
Evolution of mean Beta parameter for the three electrodes that survived multiple comparison correction in the 1-sample t-test of the stop-relevant block. Sampling points that survived correction are marked as red dots.
Differences in Slowing Between Blocks
A rANOVA was used to directly test the differences between the stop-relevant and stop-irrelevant trials and their relationship to response slowing. The purpose of testing the difference between the blocks was to ensure that the differences seen in the relevant blocks was not simply due to response time fluctuations that would be seen in an arbitrary forced choice task. Five thousand bootstrapped F-statistics were used in the analysis. Significant differences were found to begin at 155 ms, and continue until 175 ms post stimulus dependent on electrode, peaking at 164 ms, which is clearly within the time course seen for the 1-sample t-test. As in the 1-sample test, 7 of the 10 electrodes were found to be different between the two beta parameters in the uncorrected tests, and these differences overlapped between the tests. Three electrodes were found to be significant at α = 0.05 using the same clustering correction technique used in the 1-sample test. Two of these cluster-corrected electrodes overlapped with the previous 1-sample cluster-corrected analysis, both in the right hemisphere. Thus, to summarize, Go-trials in stop-relevant blocks displayed a systematic positive relationship between N1 amplitudes and RTs, and this relationship was significantly stronger than in the stop-irrelevant blocks, for which no clear relationship was found.
Discussion
The present EEG study investigated the neural processes underlying proactive response inhibition during the stop-signal task in human subjects, focusing on early attentional mechanisms. Based on a comparison of go-trials from different trial blocks in which stop-stimuli were either task-relevant or not, we found that participants indeed employed proactive response slowing in the relevant blocks, and a hierarchical drift diffusion model indicated that this mostly relied on a combination of differences in decision thresholds as well as in drift rates. This effect was accompanied by a significant relationship between the single-trial amplitudes in the visual N1 component in the stop-relevant but not the stop-irrelevant task blocks. Given that the N1 component is believed to index the level of attention paid to the go-stimulus, these results seem to reflect a down-regulating strategic process that proactively slows go-stimulus processing when the response to this stimulus might have to be canceled.
The role of visual attention in response inhibition
Go-stimuli elicited a classic inferoposterior N1 component. This component has been found to be larger the more attention that is paid to a stimulus, which is thought to index the selective attentional processing of the visual stimulus in mid- and high-level visual areas (Vogel and Luck, 2000), and which has been found to ramify into differences in response speed in attentional tasks (e.g., Talsma et al., 2007). The traditional ERP analysis did not find evidence for an inverse link between overall N1 amplitude and response speed, given that the condition with slower responses had slightly larger N1 amplitudes (and a very small effect size). Yet, given the difference in task requirements this between-block comparison is necessarily quite unspecific (see also below) and our main interest was to look at the relationship between fluctuations of response times and EEG activity within the respective blocks. In line with our expectation, a multilevel single-trial EEG framework indicated that such a link does exist when looking at fluctuations within the stop-relevant condition. Specifically, this analysis demonstrated that as response time increased, the N1 component attenuated, but only in the stop-relevant blocks.
In general, the role of attention and other perceptual mechanisms has mostly been neglected in the response inhibition literature (although see e.g. Sharp et al., 2010 for a discussion concerning whether response-inhibition-related fMRI activity might not in fact reflect activity in the ventral attentional system). Yet, in order to cancel a pre-potent response it is clear that first all relevant external stimuli need to be detected. The overarching view is to attribute differences in stopping latencies solely to differences seen in the efficacy of a single centralized response-related inhibitory control process (Verbruggen et al., 2014a). The current research suggests a clear role for early perceptual/attentional modulations in the stop-signal task. In this vein, the attenuation of N1 amplitudes as responses slow can be considered as an index of the discrimination dedicated to the go-stimulus. A down-modulated go-stimulus processing therefore appears to be advantageous for later inhibition via the positive relationship between successful inhibitory behavior and longer response times in the independent race model. While our inference is in principle a reverse one (inferring that attention was affected by looking at a neurophysiological marker without explicitly modulating it through our task design), we point to the tight and rather specific link between the N1 component and attention.
Crucially, the present data indicate that the relationship between response slowing and attentional processing of the go-stimulus is indeed under proactive control. An alternative notion would have been that attentional go-stimulus processing randomly fluctuates (e.g., as a function of general attentiveness). Yet, under a random-fluctuation account one would expect similar modulations also in a task context when Stop-stimuli are not task-relevant, which is counter to what we found here. Although this between-block comparison might by itself not rule out non-strategic contributions, our notion dovetails with recent work on Bayesian dynamic belief models, which have found a very strong relationship between Go-trial response time and the inferred subjective probability of a stop-stimulus, which was also interpreted as being strategic in nature (Ide et al., 2013).
Although perceptual mechanisms are usually neglected in response-inhibition studies, there is still some supporting evidence that attention to go-stimuli plays a role in adjusting response tendencies. Previous MEG work has shown that the go-stimulus N1 component was less pronounced in successful stop-trials as opposed to unsuccessful stop trials, suggesting that paying less attention to the Go-stimulus slows down responding, which in turn makes successful inhibition more likely (Boehler et al., 2009; see also Knyazev et al., 2008). Furthermore, when perceptual distractors in a stop-signal task were presented over whole trials, inhibitory behavior was impaired, and this impairment scaled with the degree of discrimination difficulty (Verbruggen et al., 2014b). To add to this, using pre-stimulus oscillatory EEG it was shown that a failure to lateralize occipital alpha activity in response to an attentional cue was predictive of false alarms (Bengson et al., 2011). Taken together, these studies suggest that the way in which sensory systems are adjusted to detect relevant stimuli is an important aspect of response inhibitory behavior.
Turning from go- to stop-stimulus processing, related studies have shown that the attentional processing of the stop-stimulus plays an important role in determining behavioral outcome, with enhanced attention for successful stop-trials (e.g. Dimoska and Johnstone, 2008; Bekker et al., 2005; see also Salinas and Stanford, 2013 for a related finding in a countermanding saccade task, and Kramer et al., 2013), or alternatively with the N1 as a marker of visual attention already reflecting an inhibitory mechanism (Kenemans, 2015). One interesting question here relates to the relationship between these modulations of the attentional processing of the go-stimulus vs. stop-stimulus in a given stop-trial, with one suggestion being that attentional resources need to be shared across these different components (Boehler et al., 2009; Pessoa, 2009). Given that at the moment of go-stimulus presentation participants cannot know yet that a given trial will be a stop-trial, this implies that such “anticipatory” resource sharing with a potentially upcoming stop-stimulus should also happen on regular go-trials. Yet, on the basis of the present data we cannot decide whether the observed effects relate to the anticipation of possible (relevant) Stop-stimuli or whether the attentional processing of go- and stop-stimuli proceed largely independently.
Although go-stimulus processing naturally precedes stop-stimulus processing, this does not necessarily imply that such effects are the earliest in time that possible mechanisms contributing to proactive slowing could be occurring. For example, a number of studies have related proactive response slowing to neural activity that precedes a given stop-trial altogether (Cai et al., 2011; Majid et al., 2013; Zandbelt et al., 2013). Similarly, it is likely that attentional control settings are implemented before the presentation of a given trial. Such preparatory effects may in fact be particularly likely in the present case in a blocked strategic way because of the non-selective nature of our manipulation. In contrast, other work investigating proactive inhibition has employed selective stopping paradigms in which, for example, one of two possible go-responses might have to be inhibited (Aron, 2011), which might require a more refined and selective mechanism than in our case where a global mechanism of slowing down all responses is likely applied.
Relationship to motor-level inhibition and drift diffusion models
Given the wealth of existing research linking proactive slowing to parts of the response-inhibition network (see, e.g., Zandbelt and Vink, 2010; Van Belle et al., 2014; Boehler et al., 2011; Jahfari et al., 2010; Chikazoe et al., 2009; Lavallee et al., 2014), we do not consider the present effect as the only mechanism underlying proactive response slowing. Rather, we assume that different mechanisms co-exist, and that neurophysiological measures might be more sensitive to the transient effect described here (but see an fMRI study by Li et al., 2009 for possible involvement of sensory areas in response slowing, as well as van Belle et al., 2014, for the involvement of dorsal attentional control areas in proactive response inhibition; and Jahfari et al., 2015, for the interplay between the prefrontal cortex and basal ganglia system with perceptual systems in response inhibition), but which may be less sensitive than fMRI to mechanisms that act more directly on the motoric level. Consistent with this notion of multiple mechanisms, our diffusion drift model of the behavioral data indicated that more than one parameter was affected. Specifically, we replicated an effect on decision thresholds that has been described previously (Verbruggen and Logan, 2009a), but we also found a pronounced effect on drift rates. The latter has also been reported before, but was found to be difficult to interpret (Logan et al., 2014; but see, White et al., 2014). One possible explanation is that decision-threshold adjustments are implemented within the stopping network, whereas drift rate reflects the attentional mechanism we describe here. The latter seems to intuitively fit well, given that the attentional processing of a task stimulus clearly relates to the speed with which it is being discriminated. It seems possible that the balance between these different mechanisms is adjusted based on strategy differences, as well as possibly being related to specific features of a given task. In the present study, we have focused a-priori on attentional processes. Additionally, possible subsequent mechanisms in frontal or even subcortical areas that might be more directly related to adjusted decision thresholds might be difficult to pick up with EEG due to anatomical reasons (but see, O’Connell et al., 2012; Twomey et al., 2015).
Another aspect in which the drift diffusion data seems relevant concerns the fact that the comparison between the stop-relevant and the stop-irrelevant blocks is necessarily somewhat unspecific. Specifically, it is likely that more than just proactive inhibition differed between the blocks. The fact that the stop-relevant blocks featured the possibility of having to cancel a response creates a dual-task situation (and as far as representing this task rule, this is also true for Go-trials), which has been suggested as an additional contributing factor to response time differences (Verbruggen and Logan, 2009a; see Zandbelt and Vink, 2010 for an attempt to circumvent this problem by parametrically varying the expectation of Stop-trials). Yet, the fact that non-decision time appears to not exert its effect between blocks in the response process indicates that a dual-task hypothesis is not very likely to account significantly for the observed data (see Verbruggen and Logan, 2009a for an extended discussion related specifically to the stop-signal task). Consistent with this, the faster response times in stop-irrelevant blocks were accompanied by lower accuracy, in line with a generally faster response mode that comes at some cost for response accuracy. Still, the comparison probably suffers from some global differences between the blocks, which in our opinion might in part have given rise to the N1 differences in the ERP between blocks, which featured larger N1s in the stop-relevant blocks and might reflect the generally increased task requirements of the stop-relevant blocks. In contrast to that, we consider it a major strength of the single-trial-based approach, which was the main analysis of interest here, that such global differences should play less of a role as far as differences in behavior and EEG activity across trials within the different blocks is concerned. Given that the task requirements remain stable across those trials, we believe that our main finding of a single-trial-based covariation between response time and the N1 component should be mostly unaffected by global block differences.
Conclusion
In the current report we present evidence that strategic modulations of the attentional processing of go-stimuli in a stop-signal task relate to the degree of proactive response slowing on a single-trial level. Specifically, an inverse relationship between single-trial amplitudes of the visual N1 component and response speed during go-trials was found in a context that might require response inhibition, while no such relationship existed when response inhibition was never required. This is in accordance with recent results suggesting a strong dependency between go-trial behaviors and stopping (White et al., 2014). The present attention-related effect likely coexists with additional proactive inhibition mechanisms. Our findings specifically emphasize the role of proactive attentional modulations in inhibitory control, thus contributing to a more multifaceted view of proactive control. Yet, integration of these disparate parts will be important to better understand inhibitory deficiencies in the future.
Acknowledgements
This research was supported by the Ghent University Multidisciplinary Research Platform “The integrative neuroscience of behavioral control”, and U.S. NIH grants R01-NS051048 and R01-MH060415 to M.G.W. The authors gratefully acknowledge Cyril R. Pernet and Guillaume A. Rousselet for statistical modeling support.
Footnotes
Note that the assumptions of the independent race model were nevertheless tested in order to evaluate whether the SSRT could reliably be estimated. Specifically, (1) the SSD was longer during unsuccessful than successful Stop-trials, t(15) = 7.65, p < 0.001; (2) that go-trial RT was slower than RTs on unsuccessful Stop-trials, t(15) = 8.94, p < .001; and (3) to show that RT on unsuccessful stop trials increase as a function of SSD we tested a correlations difference from zero (r = 0.34, t(779) < 0.001).).
In fact, in our further linear models N1 analyses there were no categorical differences between block type in a similar (the models also included RT, an error term, and were bootstrap tests) repeated measures ANOVA.
Bibliography
- Aron AR. From reactive to proactive and selective control: developing a richer model for stopping inappropriate responses. Biological psychiatry. 2011;69:e55–68. doi: 10.1016/j.biopsych.2010.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aron AR, Robbins TW, Poldrack RA. Inhibition and the right inferior frontal cortex: one decade on. Trends in cognitive sciences. 2014;18:177–185. doi: 10.1016/j.tics.2013.12.003. [DOI] [PubMed] [Google Scholar]
- Aron AR, Durston S, Eagle DM, Logan GD, Stinear CM, Stuphorn V. Converging evidence for a fronto-basal-ganglia network for inhibitory control of action and cognition. The Journal of neuroscience. 2007;27:11860–11864. doi: 10.1523/JNEUROSCI.3644-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bari A, Robbins TW. Inhibition and impulsivity: behavioral and neural basis of response control. Progress in neurobiology. 2013;108:44–79. doi: 10.1016/j.pneurobio.2013.06.005. [DOI] [PubMed] [Google Scholar]
- Bekker EM, Kenemans JL, Hoeksma MR, Talsma D, Verbaten MN. The pure electrophysiology of stopping. International journal of psychophysiology. 2005;55:191–198. doi: 10.1016/j.ijpsycho.2004.07.005. [DOI] [PubMed] [Google Scholar]
- Bengson JJ, Mangun GR, Mazaheri A. The neural markers of an imminent failure of response inhibition. Neuroimage. 2011;59:1534–1539. doi: 10.1016/j.neuroimage.2011.08.034. [DOI] [PubMed] [Google Scholar]
- Boehler CN, Appelbaum LG, Krebs RM, Hopf JM, Woldorff MG. Pinning down response inhibition in the brain--conjunction analyses of the Stop-signal task. NeuroImage. 2010;52:1621–1632. doi: 10.1016/j.neuroimage.2010.04.276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boehler CN, Munte TF, Krebs RM, Heinze HJ, Schoenfeld MA, Hopf JM. Sensory MEG responses predict successful and failed inhibition in a stop-signal task. Cerebral cortex. 2009;19:134–145. doi: 10.1093/cercor/bhn063. [DOI] [PubMed] [Google Scholar]
- Boehler CN, Bunzeck N, Krebs RM, Noesselt T, Schoenfeld M, Heinze HJ, Munte TF, Woldorff MG, Hopf JM. Substantia Nigra Activity Level Predicts Trial-to-Trial Adjustments in Cognitive Control. Journal of cognitive neuroscience. 2011;23:362–373. doi: 10.1162/jocn.2010.21473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai W, Oldenkamp CL, Aron AR. A proactive mechanism for selective suppression of response tendencies. The Journal of neuroscience. 2011;31:5965–5969. doi: 10.1523/JNEUROSCI.6292-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai W, Ryali S, Chen T, Li CS, Menon V. Dissociable roles of right inferior frontal cortex and anterior insula in inhibitory control: evidence from intrinsic and task-related functional parcellation, connectivity, and response profile analyses across multiple datasets. The Journal of neuroscience. 2014;34:14652–14667. doi: 10.1523/JNEUROSCI.3048-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers CD, Garavan H, Bellgrove MA. Insights into the neural basis of response inhibition from cognitive and clinical neuroscience. Neuroscience and biobehavioral reviews. 2009;33:631–646. doi: 10.1016/j.neubiorev.2008.08.016. [DOI] [PubMed] [Google Scholar]
- Chikazoe J, Jimura K, Hirose S, Yamashita K, Miyashita Y, Konishi S. Preparation to inhibit a response complements response inhibition during performance of a stop-signal task. The Journal of neuroscience. 2009;29:15870–15877. doi: 10.1523/JNEUROSCI.3645-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimoska A, Johnstone SJ. Effects of varying stop-signal probability on ERPs in the stop-signal task: do they reflect variations in inhibitory processing or simply novelty effects? Biological psychology. 2008;77:324–336. doi: 10.1016/j.biopsycho.2007.11.005. [DOI] [PubMed] [Google Scholar]
- Gaspar CM, Rousselet GA, Pernet CR. Reliability of ERP and single-trial analyses. NeuroImage. 2011;58:620–629. doi: 10.1016/j.neuroimage.2011.06.052. [DOI] [PubMed] [Google Scholar]
- Gelman A, Rubin DB. Markov chain Monte Carlo methods in biostatistics. Statistical methods in medical research. 1996;5:339–355. doi: 10.1177/096228029600500402. [DOI] [PubMed] [Google Scholar]
- Huster RJ, Enriquez-Geppert S, Lavallee CF, Falkenstein M, Herrmann CS. Electroencephalography of response inhibition tasks: functional networks and cognitive contributions. International journal of psychophysiology. 2013;87:217–233. doi: 10.1016/j.ijpsycho.2012.08.001. [DOI] [PubMed] [Google Scholar]
- Huster RJ, Plis SM, Lavallee CF, Calhoun VD, Herrmann CS. Functional and effective connectivity of stopping. Neuroimage. 2014;94:120–128. doi: 10.1016/j.neuroimage.2014.02.034. [DOI] [PubMed] [Google Scholar]
- Ide JS, Shenoy P, Yu AJ, Li CR. Bayesian prediction and evaluation in the anterior cingulate cortex. Journal of Neuroscience. 2013;33:2039–2047. doi: 10.1523/JNEUROSCI.2201-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahfari S, Stinear CM, Claffey M, Verbruggen F, Aron AR. Responding with restraint: what are the neurocognitive mechanisms? Journal of cognitive neuroscience. 2010;22:1479–1492. doi: 10.1162/jocn.2009.21307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahfari S, Waldorp LJ, Ridderinkhof KR, Scholte HS. Visual information shapes the dynamics of cortico-basal ganglia pathways during response selection and inhibition. Journal of Cognitive Neuroscience. 2015;27:1344–1359. doi: 10.1162/jocn_a_00792. [DOI] [PubMed] [Google Scholar]
- Kenemans JL. Specific proactive and generic reactive inhibition. Neuroscience & Biobehavioral Reviews. 2015;56:115–126. doi: 10.1016/j.neubiorev.2015.06.011. [DOI] [PubMed] [Google Scholar]
- Knyazev GG, Levin EA, Savostyanov AN. A failure to stop and attention fluctuations: an evoked oscillations study of the stop-signal paradigm. Clinical neurophysiology. 2008;119:556–567. doi: 10.1016/j.clinph.2007.11.041. [DOI] [PubMed] [Google Scholar]
- Kramer UM, Solbakk AK, Funderud I, Lovstad M, Endestad T, Knight RT. The role of the lateral prefrontal cortex in inhibitory motor control. Cortex. 2013;49:837–849. doi: 10.1016/j.cortex.2012.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruschke JK. Bayesian data analysis. Wires Cogn Sci. 2010;1:658–676. doi: 10.1002/wcs.72. [DOI] [PubMed] [Google Scholar]
- Lavallee CF, Meemken MT, Herrmann CS, Huster RJ. When holding your horses meets the deer in the headlights: time-frequency characteristics of global and selective stopping under conditions of proactive and reactive control. Front Hum Neurosci. 2014;8:994. doi: 10.3389/fnhum.2014.00994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CSR, Chao HHA, Lee TW. Neural Correlates of Speeded as Compared with Delayed Responses in a Stop Signal Task: An Indirect Analog of Risk Taking and Association with an Anxiety Trait. Cerebral cortex. 2009;19:839–848. doi: 10.1093/cercor/bhn132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logan, Cowan On the ability to inhibit thought and action: A theory of an act of control. Psychological Review. 1984;91 doi: 10.1037/a0035230. [DOI] [PubMed] [Google Scholar]
- Logan, Van Zandt T, Verbruggen F, Wagenmakers E-J. On the ability to inhibit thought and action: General and special theories of an act of control. Psychological Review. 2014;121:66–95. doi: 10.1037/a0035230. [DOI] [PubMed] [Google Scholar]
- Majid DS, Cai W, Corey-Bloom J, Aron AR. Proactive selective response suppression is implemented via the basal ganglia. The Journal of neuroscience. 2013;33:13259–13269. doi: 10.1523/JNEUROSCI.5651-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Connell RG, Dockree PM, Kelly SP. A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nature Neuroscience. 2012;15:1729–1735. doi: 10.1038/nn.3248. [DOI] [PubMed] [Google Scholar]
- Pernet CR, Chauveau N, Gaspar C, Rousselet GA. LIMO EEG: a toolbox for hierarchical LInear MOdeling of ElectroEncephaloGraphic data. Computational intelligence and neuroscience. 2011;2011:831409. doi: 10.1155/2011/831409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pernet CR, Latinus M, Nichols TE, Rousselet GA. Cluster-based computational methods for mass univariate analyses of event-related brain potentials/fields: A simulation study. J Neurosc Methods. 2015;250:85–93. doi: 10.1016/j.jneumeth.2014.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pessoa L. How do emotion and motivation direct executive control? Trends in cognitive sciences. 2009;13:160–166. doi: 10.1016/j.tics.2009.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plummer M. Penalized loss functions for Bayesian model comparison. Biostatistics. 2008;9:523–539. doi: 10.1093/biostatistics/kxm049. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A Theory of Memory Retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Salinas E, Stanford TR. The countermanding task revisited: fast stimulus detection is a key determinant of psychophysical performance. The Journal of neuroscience. 2013;33:5668–5685. doi: 10.1523/JNEUROSCI.3977-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmajuk M, Liotti M, Busse L, Woldorff MG. Electrophysiological activity underlying inhibitory control processes in normal adults. Neuropsychologia. 2006;44:384–395. doi: 10.1016/j.neuropsychologia.2005.06.005. [DOI] [PubMed] [Google Scholar]
- Sharp DJ, Bonnelle V, De Boissezon X, Beckmann CF, James SG, Patel MC, Mehta MA. Distinct frontal systems for response inhibition, attentional capture, and error processing. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:6106–6111. doi: 10.1073/pnas.1000175107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BR, van der Linde A. Bayesian measures of model complexity and fit. J Roy Stat Soc B. 2002;64:583–616. [Google Scholar]
- Talsma D, Mulckhuyse M, Slagter HA, Theeuwes J. Faster, more intense! The relation between electrophysiological reflections of attentional orienting, sensory gain control, and speed of responding. Brain Res. 2007;1178:92–105. doi: 10.1016/j.brainres.2007.07.099. [DOI] [PubMed] [Google Scholar]
- Twomey DM, Murphy PR, Kelly SP, O’Connell RG. The classic P300 encodes a build-to-threshold decision variable. European Journal of Neuroscience. 2015;42:1636–1643. doi: 10.1111/ejn.12936. [DOI] [PubMed] [Google Scholar]
- Van Belle J, Vink M, Durston S, Zandbelt BB. Common and unique neural networks for proactive and reactive response inhibition revealed by independent component analysis of functional MRI data. NeuroImage. 2014;103:65–74. doi: 10.1016/j.neuroimage.2014.09.014. [DOI] [PubMed] [Google Scholar]
- Verbruggen F, Logan GD. Proactive adjustments of response strategies in the stop-signal paradigm. Journal of experimental psychology Human perception and performance. 2009a;35:835–854. doi: 10.1037/a0012726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verbruggen F, Logan GD. Models of response inhibition in the stop-signal and stop-change paradigms. Neuroscience and biobehavioral reviews. 2009b;33:647–661. doi: 10.1016/j.neubiorev.2008.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verbruggen F, Chambers CD, Logan GD. Fictitious inhibitory differences: how skewness and slowing distort the estimation of stopping latencies. Psychological science. 2013;24:352–362. doi: 10.1177/0956797612457390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verbruggen F, McLaren IP, Chambers CD. Banishing the Control Homunculi in Studies of Action Control and Behavior Change. Perspectives on psychological science. 2014a;9:497–524. doi: 10.1177/1745691614526414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verbruggen F, Stevens T, Chambers CD. Proactive and reactive stopping when distracted: an attentional account. Journal of experimental psychology Human perception and performance. 2014b;40:1295–1300. doi: 10.1037/a0036542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verbruggen F, Liefooghe B, Notebaert W, Vandierendonck A. Effects of stimulus-stimulus compatibility and stimulus-response compatibility on response inhibition. Acta psychologica. 2005;120:307–326. doi: 10.1016/j.actpsy.2005.05.003. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Luck SJ. The visual N1 component as an index of a discrimination process. Psychophysiology. 2000;37:190–203. [PubMed] [Google Scholar]
- White CN, Congdon E, Mumford JA, Karlsgodt KH, Sabb FW, Freimer NB, London ED, Cannon TD, Bilder RM, Poldrack RA. Decomposing Decision Components in the Stop-signal Task: A Model-based Approach to Individual Differences in Inhibitory Control. Journal of cognitive neuroscience. 2014;26:1601–1614. doi: 10.1162/jocn_a_00567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiecki TV, Sofer I, Frank MJ. HDDM: Hierarchical Bayesian estimation of the Drift-Diffusion Model in Python. Front Neuroinform. 2013;7 doi: 10.3389/fninf.2013.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandbelt BB, Vink M. On the Role of the Striatum in Response Inhibition. PloS one. 2010;5 doi: 10.1371/journal.pone.0013848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandbelt BB, Bloemendaal M, Neggers SFW, Kahn RS, Vink M. Expectations and violations: Delineating the neural network of proactive inhibitory control. Human brain mapping. 2013;34:2015–2024. doi: 10.1002/hbm.22047. [DOI] [PMC free article] [PubMed] [Google Scholar]