Abstract
Simultaneous Multi-Slice (SMS) magnetic resonance imaging (MRI) is a rapidly evolving technique for increasing imaging speed. Controlled aliasing techniques utilize periodic undersampling patterns to help mitigate the loss in signal-to-noise ratio (SNR) in SMS MRI. To evaluate the performance of different undersampling patterns, a quantitative description of the image SNR loss is needed. Additionally, eddy current effects in echo planar imaging (EPI) lead to slice-specific Nyquist ghosting artifacts. These artifacts cannot be accurately corrected for each individual slice before or after slice-unaliasing. In this work, we propose a hybrid-space sensitivity encoding (SENSE) reconstruction framework for SMS MRI by adopting a three-dimensional representation of the SMS acquisition. Analytical SNR loss maps are derived for SMS acquisitions with arbitrary phase encoding undersampling patterns. Moreover, we propose a matrix-decoding correction method that corrects the slice-specific Nyquist ghosting artifacts in SMS EPI acquisitions. Brain images demonstrate that the proposed hybrid-space SENSE reconstruction generates images with comparable quality to commonly used split-slice-generalized autocalibrating partially parallel acquisition reconstruction. The analytical SNR loss maps agree with those calculated by a Monte Carlo based method, but require less computation time for high quality maps. The analytical maps enable a fair comparison between the performances of coherent and incoherent SMS undersampling patterns. Phantom and brain SMS EPI images show that the matrix-decoding method performs better than the single-slice and slice-averaged Nyquist ghosting correction methods under the hybrid-space SENSE reconstruction framework.
Index Terms: Controlled aliasing in parallel imaging (CAIPI), echo planar imaging (EPI), geometry-factor (g-factor), Nyquist ghosting artifacts, sensitivity encoding (SENSE), simultaneous multi-slice (SMS)
I. Introduction
Simultaneous multi-slice (SMS) imaging is becoming increasingly popular because it enables acceleration along the slice dimension in addition to the in-plane dimension [1]-[5]. SMS accelerated echo planar imaging (EPI) has been widely applied to functional and diffusion-weighted brain imaging to achieve shorter scan time, larger brain coverage, higher spatial resolution, faster temporal sampling rate, or a combination of the above [6]-[8].
The most widely used algorithm to reconstruct the SMS images is the slice-generalized autocalibrating partially parallel acquisition (slice-GRAPPA) algorithm [5], [9], or its more recent version with improved interslice leakage artifact reduction, the split-slice-GRAPPA algorithm [10]. Another reconstruction algorithm is adapted from the SENSE/GRAPPA combination for three-dimensional (3D) imaging [4], [11]-[14], By adopting a 3D representation of the SMS acquisition [15], [16], two-dimensional GRAPPA (2D-GRAPPA) [15], [17] and two-dimensional sensitivity encoding (2D-SENSE) [18], [19] can also be used to reconstruct SMS images.
A commonly used metric to evaluate the signal-to-noise ratio (SNR) loss in SMS acquisitions is the geometry-factor (g-factor) [20], or its reciprocal, the retained SNR [5]. The g-factor maps are usually calculated by the pseudo multiple replica method [5], [21], [22], which reconstructs synthesized repeated acquisitions. Analytical g-factor maps can also be calculated under the GRAPPA [23] or the 2D-SENSE [19] reconstruction frameworks, but such reconstructions are only applicable to acquisitions with periodic undersampling patterns such as controlled aliasing in parallel imaging (CAIPI) [5], [24], [25].
Alternative SMS undersampling patterns, such as the multi-slice acquisition with incoherent aliasing (MICA) [26] and the zigzag [16] patterns, have also been introduced. A generic reconstruction and g-factor calculation method is needed to reconstruct and compare arbitrary SMS undersampling patterns. A generalized SENSE reconstruction is a good candidate for such purpose because it can handle arbitrary k-space trajectories [27]. Its high computational cost can be reduced by first transforming the data into the spatial domain along the fully sampled k-space dimension then performing the reconstruction in the hybrid-space. This idea is explored for conventional single-slice image reconstruction in an approach called sensitivity profiles from an array of coils for encoding and reconstruction in parallel (SPACE RIP) [28]. Generalized SENSE and SPACE RIP provide a foundation for the proposed work.
Additionally, the eddy current effects in EPI lead to slice-specific Nyquist ghosting artifacts, which can be accurately corrected only during the slice unaliasing process [29]. Applying an odd/even residual ghosting correction after slice unaliasing [4] introduces minor improvements [30]. For further improvements, one can apply two sets of interpolation kernels for the odd and even phase encoding (ky) lines in the splitslice-GRAPPA [30] or adapted SENSE/GRAPPA combination [31] reconstruction. We will refer to split-slice-GRAPPA with such kernel fittings as the odd/even split-slice-GRAPPA.
In this work, we propose a generic hybrid-space sensitivity encoding (hybrid-space SENSE) reconstruction framework for SMS acquisition with arbitrary phase encoding undersampling pattern. Based on our reconstruction framework, analytical g-factor maps can be derived to evaluate the SNR performances of both periodic and incoherent undersampling patterns. Extending the proposed reconstruction model, we further propose a “matrix-decoding” correction method for SMS EPI to accurately correct the slice-specific Nyquist ghosting artifacts. Brain and phantom images are shown to validate the proposed methods.
II. Hybrid-space SENSE
The 3D representation of SMS acquisitions [15], [16] is adopted to illustrate the hybrid-space SENSE [27] reconstruction. x, y and z denote the frequency encoding, the phase encoding and the slice directions, respectively. kx, ky and kz are the corresponding spatial frequencies. In the 3D view, an SMS acquisition fully samples the kx dimension and undersamples the ky-kz plane.
The hybrid-space SENSE reconstruction can be thought of as an extension to SPACE RIP [28] by including an additional slice dimension. First, a 1D inverse Fast Fourier Transform (iFFT) is conducted along kx to transform the 3D data into x-ky-kz space, as depicted in Fig. 1(a) and (b). There is an undersampled ky-kz plane for each fixed x = x0. Assuming there are receiving coils, the signal acquired by the c-th coil is as follows:
| (1) |
where n and Np denote the echo index and the total number of echoes on the ky-kz plane, Ny is the number of pixels in y, Ns is the number of simultaneous slices, m(x, y, z) is the unknown magnetization and S(c, x, y, z) represents the receiving sensitivity of the c-th coil.
Fig. 1.

Hybrid-space SENSE reconstruction for SMS acquisitions.
The undersampling pattern on the ky-kz plane is determined by ky(n) and kz(n). For a CAIPI [5], [24] acquisition with FOVy/Nshift shift between adjacent slices and no in-plane acceleration, ky(n) = −π + 2π(n−1)/Ny, and kz(n) = 2π × mod(n − 1, Nshift)/Nshift where mod is the modulus operation and FOVy is the field of view in y. With inplane acceleration or partial Fourier acquisition, Np < Ny, otherwise, Np = Ny. Here, in-plane acceleration means that the ky lines are skipped at regular intervals such that at a skipped ky position there are no samples at any kz position.
To solve the unknown magnetization, (1) is written into matrix form,
| (2) |
where contains the measured data and is the encoding matrix formed by coil sensitivities and ky-kz phase encodings. The unknown magnetization for x = x0, , can be solved as a Tikhonov regularized least-squares problem,
| (3) |
| (4) |
where H indicates the transposed complex conjugate, λ is a Tikhonov regularization factor and INyNs is an NyNs × NyNs identity matrix.
Finally, the 3D magnetization m(x, y, z) is reconstructed by performing (3) for every value of x.
III. Analytical G-factor
G-factor is a widely used metric to quantify the noise amplification in parallel imaging techniques [5], [20], [23], [27], [32]-[35]. It is useful for comparing between data sampling schemes [23], [34], reconstruction methods [23], [33], [34] and clinical imaging protocols [35]. In this section, analytical g-factor [20] is derived for an SMS acquisition with an arbitrary phase encoding undersampling pattern [36].
The g-factor for the ρ-th pixel in the reconstructed SMS images is
| (5) |
where X(ρ,ρ) represents the ρ-th diagonal element in the image noise covariance matrix X and R is the data reduction factor.
The image noise covariance matrix in (5) is derived by propagating noise through the reconstruction process. Generally, after a linear reconstruction step y = Ax, the noise covariance matrix of the reconstructed vector y is
| (6) |
The following subsections will track the noise propagation in each step of the hybrid-space SENSE reconstruction pipeline. A final image noise covariance matrix will be derived to be used in (5). A schematic plot for the calculation process is displayed in Fig. 2.
Fig. 2.
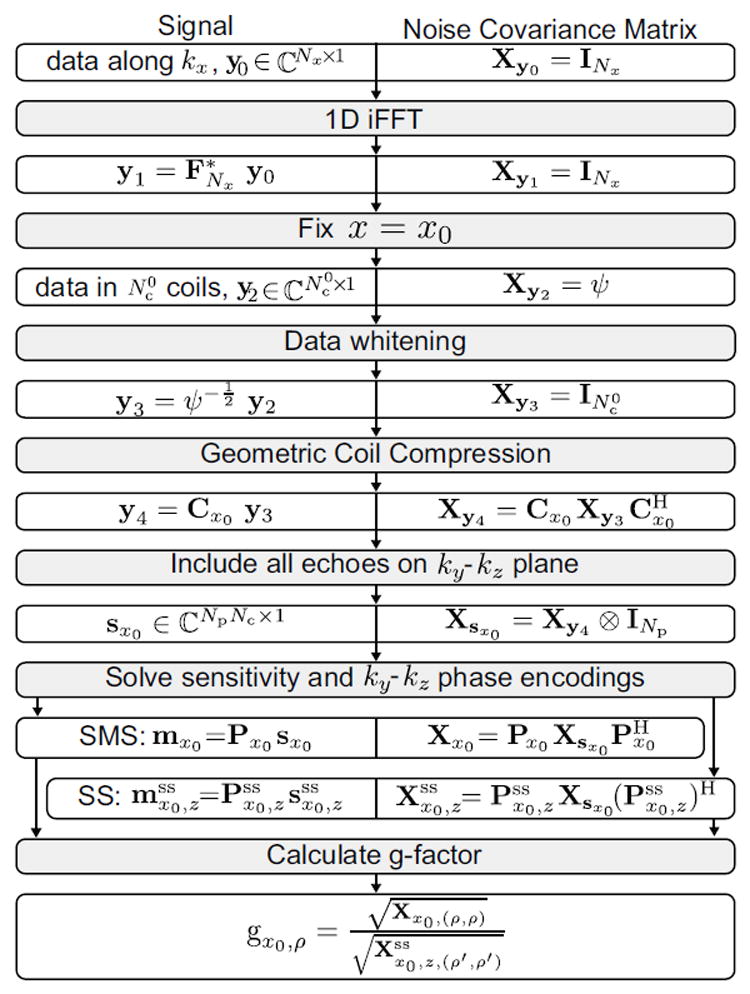
Schematic plot for the noise propagation through each step of the hybrid-space SENSE reconstruction pipeline. A final image noise covariance matrix is derived for a simultaneous multi-slice (SMS) acquisition (Xx0) and a single-slice (SS) acquisition to calculate the analytical g-factor. Please refer to the manuscript text for specific definitions of the matrices shown.
A. 1D Inverse FFT
The first step in the hybrid-space SENSE reconstruction is a 1D inverse FFT along kx. We write the Nx acquired kx points into a vector . The noise at different kx positions are independently identically distributed (IID). The data whitening operation, which will be described in detail later in Section III-B, scales the variance of the noise to one. The noise covariance matrix of y0 is therefore an Nx × Nx identity matrix,
| (7) |
The 1D inverse FFT operation is
| (8) |
where is a forward FFT matrix, * denotes the complex conjugate and contains the Nx points along x. The noise covariance matrix becomes
| (9) |
Equation (9) indicates that the noise at different x positions is IID.
B. Geometric-decomposition Coil Compression
Geometric-decomposition coil compression (GCC) [37] compresses multi-coil data in coils into a small number of Nc virtual coils and speeds up the reconstruction.
Data whitening can be conducted before GCC to transform the data into a set of coils in which the noise is IID [37]. Assume the zero mean Gaussian random noise in the receiving coils has a covariance matrix . Due to the fact that GCC is conducted in a sequence of different x positions and the noise at different x positions is IID, the noise propagation at different x positions can be tracked independently. For a fixed x = x0 (x0 = 0, 1, …Nx− 1), assume contains the raw k-space data in the coils, then the data whitening operation is y2, where contains data after the operation. The covariance matrix of the noise in the coils becomes an identity matrix,
| (10) |
The GCC operation is
| (11) |
where is the coil compression matrix for x = x0 and contains data in the compressed coils. The noise covariance matrix of y4 is
| (12) |
C. Solving Sensitivity and ky-kz Phase Encodings
The last step in the hybrid-space SENSE reconstruction is to solve the sensitivity and ky-kz phase encodings. Because this step is conducted in a sequence of different x positions and the noise at different x positions are independent, the noise propagation at different x positions can be tracked independently. For a fixed x = x0 (x0 = 0, 1, …Nx − 1), write data from all echoes and all coils into a vector . Since the noise in the Np echoes is IID, the noise covariance matrix of sx0 is
| (13) |
where ⊗ denotes the Kronecker product.
The reconstruction step, as illustrated in (3), is mx0 = Px0 sx0, where contains the final reconstructed single-slice images and is the reconstruction matrix for x = x0. The final NyNs × NyNs image noise covariance matrix for x = x0 is
| (14) |
The square root of the diagonal elements of Xx0 represent the noise levels in the NyNs reconstructed image pixels. They are used to calculate the g-factor values for x = x0.
D. Calculation of Analytical g-Factor
A conventional single-slice acquisition that applies the same in-plane acceleration as the SMS acquisition can be used as the reference full acquisition for calculating the analytical g-factor. The corresponding data reduction factor is R = 1.
At a specific slice location z (z = 0, 1, …Ns − 1) and for a fixed x = x0, the image noise covariance matrix for a conventional single-slice acquisition can be derived similarly to the above SMS case. Here, the number of simultaneous slices is one and all k-space echoes are acquired at kz = 0. The final reconstruction step is , where contains the final reconstructed single-slice images and is the reconstruction matrix. Because the noise propagation in a single-slice acquisition is identical to that in an SMS acquisition before the final reconstruction step, we have . The final Ny × Ny image noise covariance matrix for x = x0 is
| (15) |
The square root of the diagonal elements of represent the noise levels in the Ny reconstructed image pixels.
The analytical g-factor values for x = x0 are
| (16) |
where [ρ/Ny] is the largest integer not greater than ρ/Ny and mod is the modulus operation. By repeating this process for each value of x, a g-factor map for the reconstructed simultaneous slices is obtained.
For the above case where the reference full acquisition is a single-slice acquisition with the same in-plane acceleration as the SMS acquisition, the calculated g-factor map reflects the SNR loss only from the slice acceleration. A g-factor map that reflects the overall SNR loss can be calculated similarly by using a fully-sampled single-slice acquisition as the reference full acquisition and by setting the data reduction factor R to equal the in-plane acceleration factor.
E. Consideration of Correlated Noise at Different x Positions
The noise at different x positions may be correlated in some cases, for example, when ramp sampling is used with the readout gradient. Appendix A in the supplementary materials1 shows that in such cases the noise propagation at different x positions can still be calculated independently and the proposed g-factor calculation method is still valid.
IV. Matrix-decoding Nyquist Ghosting Correction
In this section, we introduce a “matrix-decoding” Nyquist ghosting correction algorithm that corrects the slice-specific Nyquist ghosting artifacts in SMS EPI [38].
In EPI acquisitions, field inhomogeneities and the eddy current effects associated with the bipolar readout gradients cause echo shift and phase mismatch between the odd and even echoes. These effects in k-space cause Nyquist ghosting artifacts in image space. An example of such echo shift is shown in Fig. 3(a) with a CAIPI ky-kz undersampling pattern. In Fig. 3(a), all k-space data are acquired with one echo train and the echo indices are denoted on the acquired k-space lines. The odd and even echoes are acquired with positive and negative readout gradient lobes respectively and are shifted towards +kx and −kx respectively. Properties of the Fourier transform indicate that an echo shift and a constant phase term along kx correspond to a linear phase ramp along x. In the hybrid x-ky-kz space, therefore, the odd and even echoes exhibit linear phase ramps along x with positive and negative slopes respectively. This is depicted in Fig. 3(b). By transforming the k-space data into the x-ky-kz space and correcting these linear phase ramps along x, the corresponding Nyquist ghosting artifacts in the image space can be corrected. An estimation of the linear phase ramps is obtained from a reference scan with all phase encoding gradients turned off [39]. The linear phase ramp θ(x, n, z) = a(n, z)x + b(n, z) is both echo (n) and slice (z) specific [29], [40].
Fig. 3.
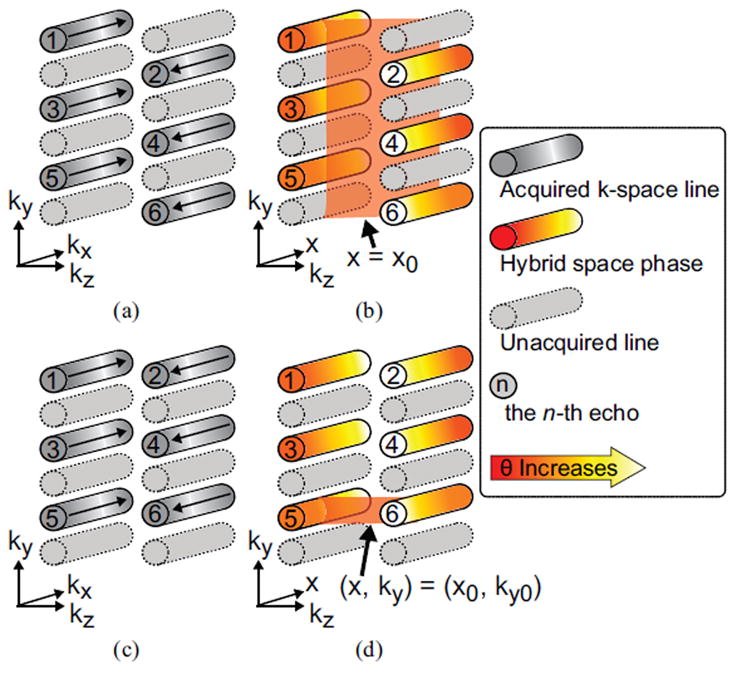
Matrix-decoding Nyquist ghosting correction for SMS EPI. (a), (c) Eddy current effects and field inhomogeneities cause echo shift and phase mismatch between odd and even echoes; (b), (d) These effects correspond to linear phase ramps along x. (a), (b) Matrix-decoding correction with arbitrary ky-kz undersampling patterns; (c), (d) with special undersampling patterns where kz is fully sampled.
A conventional Nyquist ghosting correction method for SMS EPI assumes that the individual slices exhibit the same Nyquist ghosting artifacts and the linear phase ramp θ(x, n) is slice independent. The multiband data are corrected with θ(x, n) before slice-unaliasing. Either a single-band or a multiband radiofrequency (RF) pulse can be used in the reference scan to get an estimation of θ(x, n). When a single-band RF pulse is applied, the estimated θ(x, n) corresponds to the ghosting artifacts in one of the simultaneous slices and we refer to such conventional Nyquist ghosting correction as the “single-slice” correction; When a multiband RF pulse is used, θ(x, n) corresponds to an averaged effect across the simultaneous slices and we call the corresponding correction “slice-averaged” correction.
To correct the slice-specific Nyquist ghosting artifacts, the “matrix-decoding” algorithm incorporates the echo and slice specific linear phase ramp θ(x, n, z) into the signal equation. This algorithm requires an estimation of the slice-dependent θ(x, n, z), which can be obtained from a single-slice reference scan covering each one of the simultaneous slices. The signal equation for a fixed x = x0 after a 1D inverse FFT becomes (Fig. 3(b))
| (17) |
Equation (17) is identical to (1) except for the phase term that causes the Nyquist ghosting artifacts in the individual slices. Equation (2), with the additional phase term added to the encoding matrix Ex0, can be used as a matrix form for (17). The 3D magnetization is reconstructed by performing (3) for each point along x. In this process, parallel imaging reconstruction and slice-specific Nyquist ghosting correction are conducted together in one single step.
The above generic matrix-decoding algorithm is applicable to SMS EPI acquisitions with arbitrary ky-kz undersampling patterns. For special undersampling patterns where the kz dimension is fully sampled, the matrix-decoding operations may become faster if being conducted independently before the parallel imaging reconstruction. Fig. 3(c) and (d) depicts one example for this case with fully sampled kz and 2× undersampled ky. The figure setups are analogous to those of Fig. 3(a) and (b). After transforming the k-space data into x-ky-kz space, as shown in Fig. 3(d), there are Nkz acquired points along the kz dimension for each pair of (x,ky) = (x0,ky0). The measured signal in the hybrid x-ky-kz space is
| (18) |
As long as Nkz ≥ Ns, the unknown magnetization in the hybrid x-ky-z space, m(x, ky, z), can be solved by inverting the Nkz × Ns encoding matrix. For data in each coil, the Nyquist ghosting artifacts in the individual slices are corrected and the kz encoding is solved by such matrix-decoding operations. If ky is undersampled, parallel imaging reconstruction is conducted as an additional step after all matrix-decoding operations to recover the missing ky lines.
V. Methods
A single-shot SMS EPI sequence is implemented on a GE 3T MR750 scanner (GE Healthcare, Waukesha, WI). For slice encoding, gradient blips along z are played out concurrently with those along y. At the beginning of the sequence, a set of fully sampled 3D SMS EPI data is acquired as the calibration data. For acquisitions with in-plane acceleration, the calibration data are acquired using a multishot scheme so that the echo train length matches between the calibration and accelerated data. A Hanning windowed sinc is modulated into a multiband RF pulse for signal excitation. A 32-channel head coil (Nova Medical, Wilmington, MA) is used for signal reception. The coil noise covariance matrix is estimated from 4096 noise data points saved during the prescan procedure. Ramp sampling is used for the EPI readouts. Reference scan data for Nyquist ghosting correction are acquired with all phase encoding blips turned off. In vivo experiments on healthy volunteers are approved by our university’s institutional review board.
Image reconstruction is performed offline in Matlab (the MathWorks, Natick, MA) on a 64-bit Linux workstation equipped with four Intel Xeon E5-4650 2.7GHz central processing units and 768 GB random access memory. Before reconstruction, GCC [37] is applied to compress the 32 coils into 10 coils. Non-cropped receiving coil sensitivity maps are estimated slice by slice from the coil-compressed calibration data using an eigenvalue approach [32] with a 6×6 kernel and a 64×64 calibration area. Because the calculated coil sensitivities are intrinsically normalized by the square root of sum of squares (SOS) combination of the true sensitivities, the intensity of the reconstructed image is weighted by this SOS coil combination. Although intensity correction can be conducted after the reconstruction as a post-processing step [41], [42], it is not carried out because it is independent of the proposed methods. The Tikhonov regularization factor λ for hybrid-space SENSE is empirically set to λ = (0.02/Nu) × ∥EHE∥F, where ∥ • ∥F denotes the Frobenius norm, E is the encoding matrix and Nu is the number of unknowns in the linear equations, i.e. the size of the second dimension of matrix E. When calculating the analytical g-factor maps, ramp sampling correction is also included in the noise propagation in addition to the steps discussed in section III. As a reference reconstruction method, split-slice-GRAPPA is conducted with a 7×7 kernel and the full matrix as the calibration area. The split-slice-GRAPPA kernels are regularized by Tikhonov regularization with an empirical regularization factor of (0.02/Nu) × ∥BHB∥F, where B is the source calibration data matrix and Nu is the number of unknown kernel coefficients, i.e. the size of the second dimension of matrix B. Coil images reconstructed by split-slice-GRAPPA are combined by an SOS operation. As a reference g-factor quantification method, the pseudo multiple replica simulation is conducted.
The linear phase ramps needed for correcting the Nyquist ghosting artifacts are estimated from the reference scan data using weighted least-squares fitting [43]. The single-slice or slice-averaged Nyquist ghosting correction is performed before the ramp sampling correction. Appendix B in the supplementary materials shows that a single-slice or slice-averaged Nyquist ghosting correction imposes no effects on the sample noise covariance matrix, assuming data whitening has been performed. Because of this, such operations are omitted when calculating the analytical g-factor maps. For the matrix-decoding Nyquist ghosting correction, a single-slice ghosting correction is first performed before the ramp sampling correction, then the residual eddy current effects are corrected by the matrix decoding approach after the ramp sampling correction. When applying the matrix-decoding approach to fully sampled SMS calibration data, (18) is used to set up the encoding matrix because the computation is faster than using (17). As a reference Nyquist ghosting correction method for CAIPI acquisitions, odd/even split-slice-GRAPPA is conducted.
Detailed acquisition parameters for all data sets are summarized in Table I.
Table I. Data Acquisition Parameters.
| Data Set | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Orientation* | Ax | Ax | Ax | Ax | Ax | Sag | Ax |
| Slice acceleration | 1 | 6 | 3 | 1 | 2 | 5 | 2 |
| In-plane acceleration | 1 | 1 | 2 | 1 | 1 | 1 | 1 |
| Partial Fourier | no | yes | no | no | no | no | no |
| FOV (cm) | 19.2 | 20.0 | 20.0 | 20.0 | 36.0 | 36.0 | 36.0 |
| In-plane resolution (mm) | 2.0 | 2.0 | 2.0 | 2.0 | 3.6 | 3.6 | 3.67 |
| Slice thickness (mm) | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Echo time (ms) | 2.48 | 13.9 | 17.6 | 32.3 | 21.7 | 21.7 | 30.0 |
| Repetition time (s) | 0.6 | 1.0 | 1.3 | 6.6 | 3.3 | 1.2 | 1.9 |
| Flip angle (degrees) | 90 | 62 | 68 | 90 | 85 | 54 | 77 |
| Number of reconstructed slices | 75 | 66 | 69 | 72 | 72 | 85 | 77 |
| Simultaneous slice gap (mm) | - | 22 | 46 | - | 72 | 34 | 54 |
| CAIPI shift (FOVy) | - | 1/3 | 1/4 | - | - | 1/3 | 1/2 |
| Readout direction* | L/R | L/R | L/R | L/R | L/R | S/I | L/R |
Ax: Axial; Sag: Sagittal; L/R: left-right; S/I: superior-inferior.
Data set 1
To compare hybrid-space SENSE reconstruction with split-slice-GRAPPA, single-slice brain data are acquired with a standard fast spoiled gradient echo sequence to provide ground truth for simulation. The single-slice data are used to simulate 2× slice and no in-plane accelerated CAIPI data with FOVy/2 shift between the simultaneous slices. Distance between simulated simultaneous slices is 72 mm.
Data set 2
To demonstrate the ability of hybrid-space SENSE to reconstruct SMS EPI data with partial Fourier acquisition, brain images are acquired by the SMS EPI sequence with a 6× slice accelerated CAIPI undersampling pattern. Matrix size is 100 × 100. Partial Fourier is used to acquire 70 ky lines. An iterative projection onto convex set [44] algorithm is conducted after the parallel imaging reconstruction to recover the ky lines missing from the partial Fourier acquisition.
Data set 3
To demonstrate that hybrid-space SENSE can reconstruct SMS data with in-plane acceleration and to compare the analytical maps with the pseudo multiple replica g-factor maps, brain images are acquired by the SMS EPI sequence with a 3× slice and 2× in-plane accelerated CAIPI undersampling pattern. The calibration data are used to compute g-factor maps.
Data set 4
To demonstrate that the analytical g-factor calculation is applicable to arbitrary SMS ky-kz undersampling pattern, a single-slice data set is acquired by the EPI sequence. Sensitivity maps derived from this data set are used to compute analytical g-factor maps for both periodic CAIPI patterns and randomized MICA patterns. The MICA kz traversal trajectory samples Np uniformly distributed points on the [−π, π] interval, and the order to take the Np samples is a bit-reversal permutation of the echo indices 1, 2, …Np. The ky traversal of MICA is the same as that of a conventional EPI acquisition.
Data set 5
To validate the matrix-decoding Nyquist ghosting correction method, axial phantom images are acquired by the SMS EPI sequence with a 2× slice accelerated MICA undersampling pattern. A large FOV of 36 cm is used so that some ghosting artifacts fall outside of the phantom. Phantom instead of in vivo data are acquired so that no physiological noise will confound the appearance of the residual ghosting.
Data set 6
To show the performance of the matrix-decoding method at a higher slice acceleration factor and with a different slice orientation, sagittal phantom images are acquired by the SMS EPI sequence with a 5× slice accelerated CAIPI undersampling pattern. Phantom instead of in vivo data are acquired in this case because elevated background noise at such acceleration factor would make the residual Nyquist ghosting artifacts hard to observe on in vivo images.
Data set 7
To demonstrate the in vivo performance of the matrix-decoding method, brain images are acquired by the SMS EPI sequence with a 2× slice accelerated CAIPI undersampling pattern. In the data whitening operation, only the diagonal elements of the coil noise covariance matrix are used because the full matrix is not available for this data set.
VI. Results
Fig. 4 shows the reconstructed and difference images from the 2× slice accelerated CAIPI data simulated using data set 1. The relative root mean squared (RRMS) error [45] for the head region is displayed under each image. Neither the split-slice-GRAPPA nor the hybrid-space SENSE images exhibit obvious visual artifacts. The difference images for both methods are mostly noise-like inside the head region. The hybrid-space SENSE images exhibit RRMS errors less than 0.0150, which is comparable to the reconstruction errors using split-slice-GRAPPA.
Fig. 4.
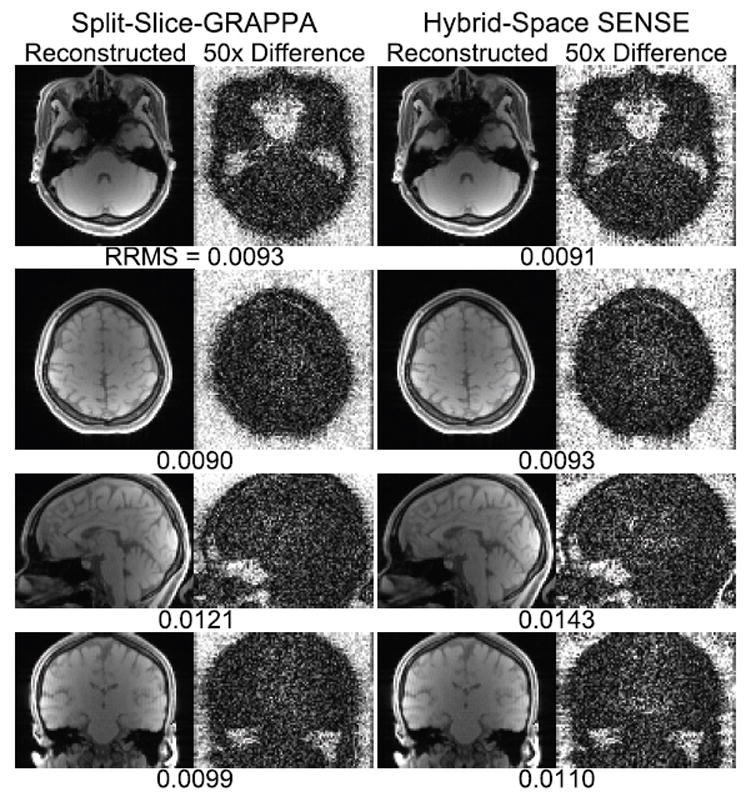
Reconstructed and difference images from simulated CAIPI acquisition with 2× slice and no in-plane acceleration. Relative root mean squared (RRMS) error inside the head is displayed under each image.
Fig. 5 displays the reconstructed images from data set 2, the CAIPI EPI acquisition with 6× slice, no in-plane acceleration and a partial Fourier acquisition. The split-slice-GRAPPA and hybrid-space SENSE reconstructions exhibit minor differences. The reconstruction time per group of simultaneous slices is approximately 18 s for split-slice-GRAPPA and 24 s for hybrid-space SENSE. The times spent on the individual steps of the two reconstruction methods are summarized in Table S1 in the supplementary materials.
Fig. 5.
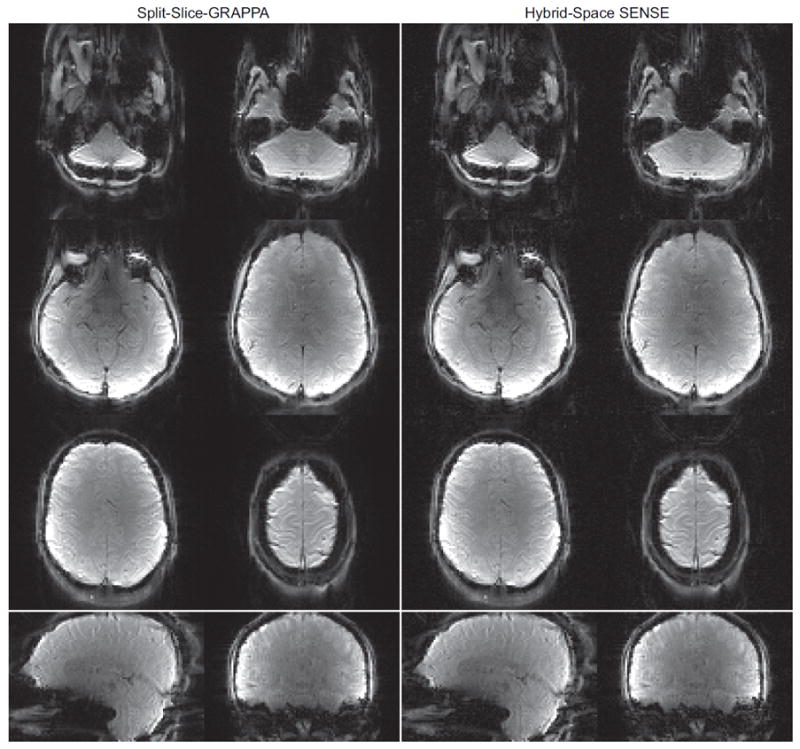
Images reconstructed from a CAIPI acquisition with 6× slice and no in-plane acceleration, FOVy/3 shift between adjacent slices and a partial Fourier acquisition.
Fig. 6 shows the reconstructed images and the corresponding retained SNR (i.e. one over g-factor) maps for data set 3, the CAIPI EPI acquisition with 3× slice and 2× inplane acceleration. The hybrid-space SENSE reconstruction exhibits no obvious visual artifacts, except signal dropout and image distortion intrinsic to EPI acquisitions. The analytical retained SNR maps that reflect the SNR loss from only slice acceleration agree with those from the pseudo multiple replica simulations. In contrast to the pseudo multiple replica maps, which become more accurate and less noisy with increased number of replicas [21], the analytical maps are noiseless. The retained SNR value is therefore always below 100% in the analytical maps but may exceed 100% in the pseudo multiple replica maps. The retained SNR calculation for one group of simultaneous slices needs approximately 40 s for pseudo multiple replica with 50 replicas, 327 s for pseudo multiple replica with 500 replicas and 22 s for the analytical maps. Fig. 6 also displays analytical retained SNR maps reflecting the overall SNR loss. The overall SNR loss closely resembles the SNR loss from slice acceleration only, indicating that the 2× in-plane acceleration introduces small SNR loss except the loss from data reduction for this experimental setup. Additionally, Fig. S1 in the supplementary materials displays retained SNR maps for a MICA acquisition, demonstrating that the analytical maps agree with the maps calculated by the pseudo multiple replica simulation for MICA data.
Fig. 6.
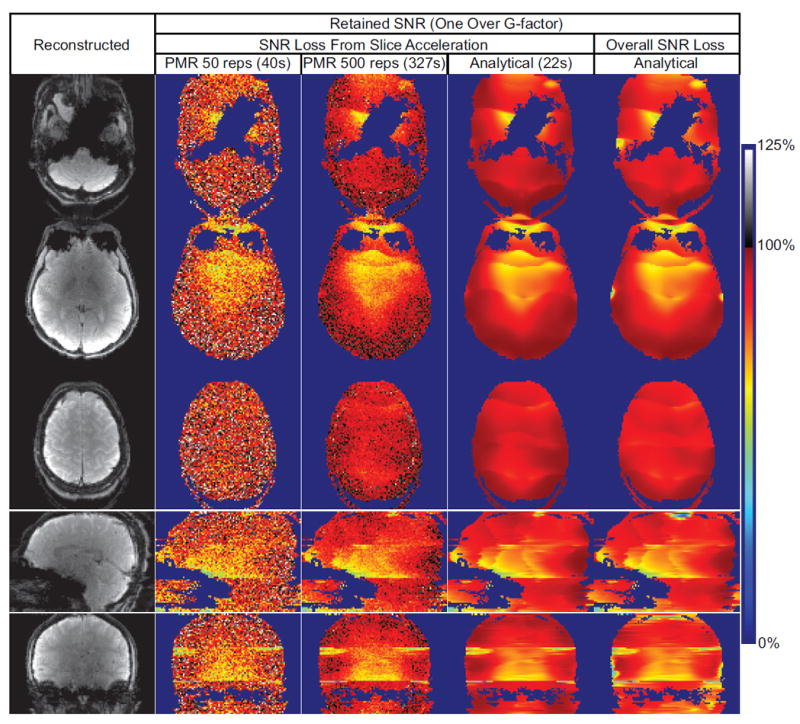
Hybrid-space SENSE reconstructed images and retained SNR maps of a CAIPI acquisition with 3× slice and 2× in-plane acceleration. The analytical maps that reflect SNR loss from slice acceleration only are compared with maps calculated using pseudo multiple replica (PMR) simulation with either 50 or 500 replicas. In addition, analytical maps that reflect the overall SNR loss are also displayed.
Fig. 7 displays the analytical retained SNR maps for three undersampling patterns: CAIPI with FOVy/2 shift, CAIPI with FOVy/3 shift and MICA with bit-reversal kz sampling. Retained SNR maps are computed using data set 4 for slice acceleration of 3 and 4 with no in-plane acceleration. Note that the ky-kz undersampling patterns are unrelated to the number of excited slices and are therefore identical for slice acceleration of 3 and 4. The displayed maps reflect the overall SNR loss, which comes solely from slice acceleration in this case. Fig. 7 demonstrates that the proposed analytical g-factor calculation is compatible with arbitrary SMS ky-kz undersampling pattern. Because the same sensitivity maps are shared, the differences in the resulting retained SNR maps are attributed solely to the differences in the undersampling patterns.
Fig. 7.
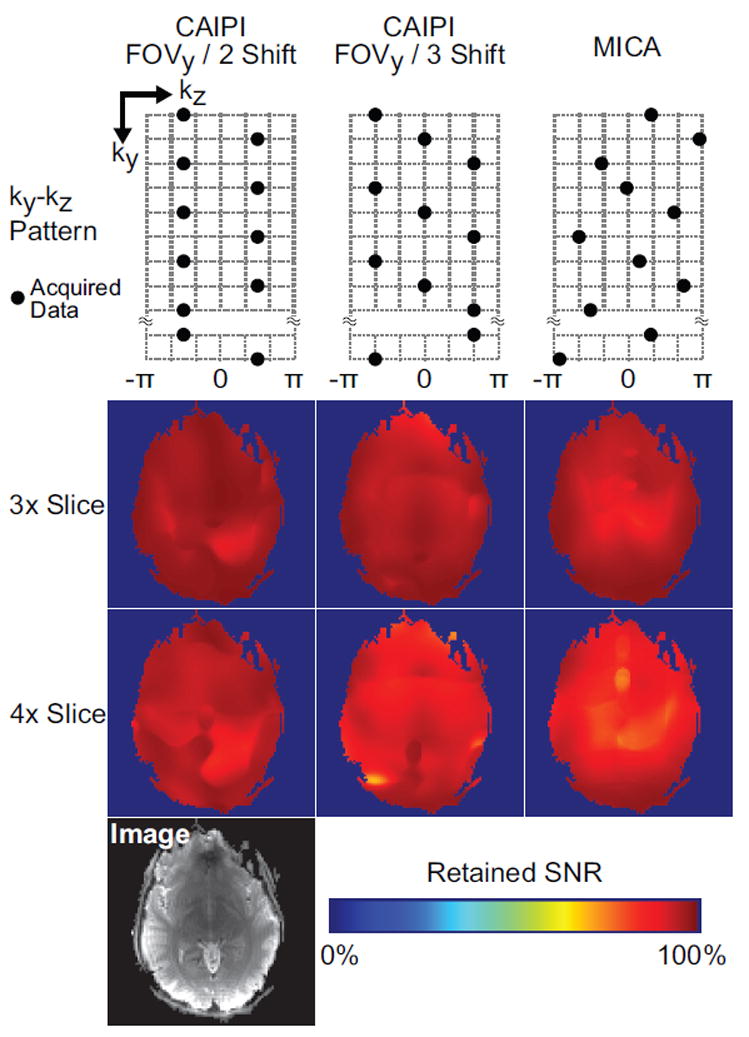
Analytical retained SNR maps of SMS acquisitions with different slice acceleration factors and ky-kz undersampling patterns. No in-plane acceleration or partial Fourier is applied. The CAIPI pattern with FOVy /2 (FOVy/3) shift periodically takes samples along 2 (3) kz lines. The MICA pattern takes samples along Np kz lines with a bit-reversal ordering. Np is the number of echoes on the ky-kz plane, which is 100 in this case. The corresponding single-slice image is displayed in the lower left corner for reference.
Fig. 8 shows the reconstructed axial phantom images from data set 5, the 2× slice accelerated MICA EPI data. The display window is adjusted so that the residual Nyquist ghosting artifacts are better visualized in the background. The same data set is reconstructed three times using hybrid-space SENSE with single-slice, slice-averaged and matrix-decoding Nyquist ghosting corrections, respectively. Split-slice-GRAPPA is not applicable to this data set. A residual Nyquist ghosting region of interest (ROI) is defined in each image and is denoted by a rectangle outside the phantom. The average signal level in the ghosting ROI is displayed next to the corresponding rectangle. The average ghosting level is calculated as a percentage of the average signal level in an ROI inside the phantom. The matrix-decoding method achieves the lowest residual ghosting level among the three correction methods for hybrid-space SENSE. The reconstructed images in Fig. 8 also demonstrate that the hybrid-space SENSE reconstruction and the matrix-decoding ghosting correction are both applicable to MICA acquisition with randomized ky-kz undersampling pattern. The additional phase term included in the signal model (17) for the matrix-decoding method is small and imposes little impact on the g-factor performance, as demonstrated by Fig. S2 in the supplementary materials.
Fig. 8.
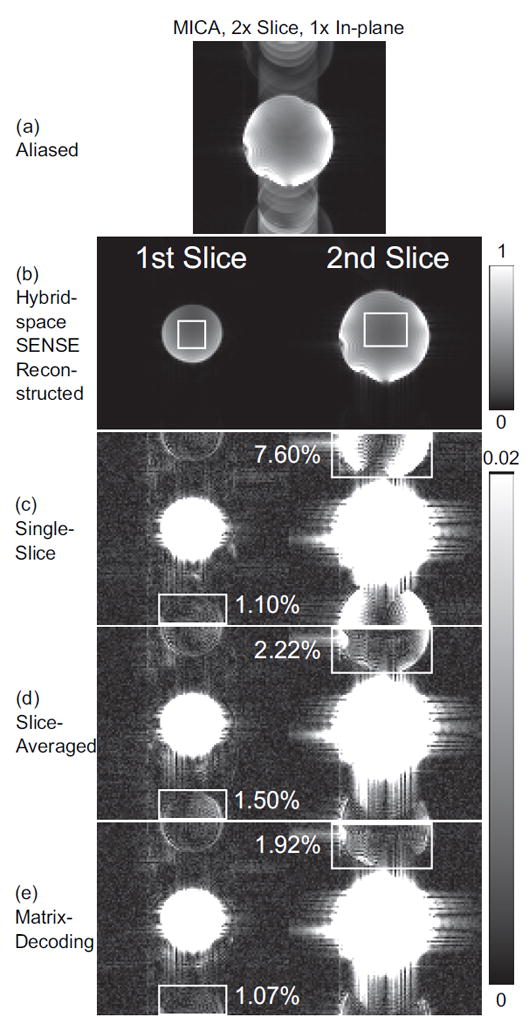
Nyquist ghosting correction for MICA EPI phantom images. Two axial simultaneous slices are displayed. (a): Slice aliased MICA image. (b): Images reconstructed by hybrid-space SENSE with the matrix-decoding Nyquist ghosting correction. A rectangle inside the phantom indicates a signal ROI. (c)-(e): Hybrid-space SENSE reconstruction with different Nyquist ghosting correction methods as labeled. Images are displayed under restricted window. A rectangle outside the phantom indicates an ROI for the residual Nyquist ghosting. A percentage indicates the average ghosting level in the ghosting ROI with respect to the average signal level in the corresponding signal ROI.
Fig. 9 shows the reconstructed sagittal phantom images from data set 6, the 5× slice accelerated CAIPI EPI data. Three out of five simultaneous slices are displayed. The figure setup is similar to that of Fig. 8. In addition to the three hybrid-space SENSE reconstructions, the same data set is also reconstructed by odd/even split-slice-GRAPPA. The average residual ghosting levels in the ghosting ROIs are displayed next to their corresponding ROI indicators. The matrix-decoding method achieves improved overall ghosting suppression than the single-slice and slice-averaged methods, although the performance of the slice-averaged method is close to the matrix-decoding method. The most improvement using the matrix-decoding method is seen in the 5th slice, which is the furthest away from and whose Nyquist ghosting is the most different from the middle slice. The odd/even split-slice-GRAPPA achieves the lowest residual ghosting level among all four methods.
Fig. 9.

Nyquist ghosting correction for CAIPI EPI phantom images. Three out of five sagittal simultaneous slices are displayed under restricted window. A percentage indicates the average ghosting level in the ghosting ROI with respect to the average signal level in the corresponding signal ROI.
Fig. 10 shows the reconstructed axial brain images from data set 7, the 2× slice accelerated CAIPI EPI data. The figure setup is similar to that of Fig. 9. The matrix-decoding method exhibits the lowest residual ghosting level among the three methods for hybrid-space SENSE reconstruction. The odd/even split-slice-GRAPPA reconstruction shows the lowest residual ghosting level among all four methods.
Fig. 10.
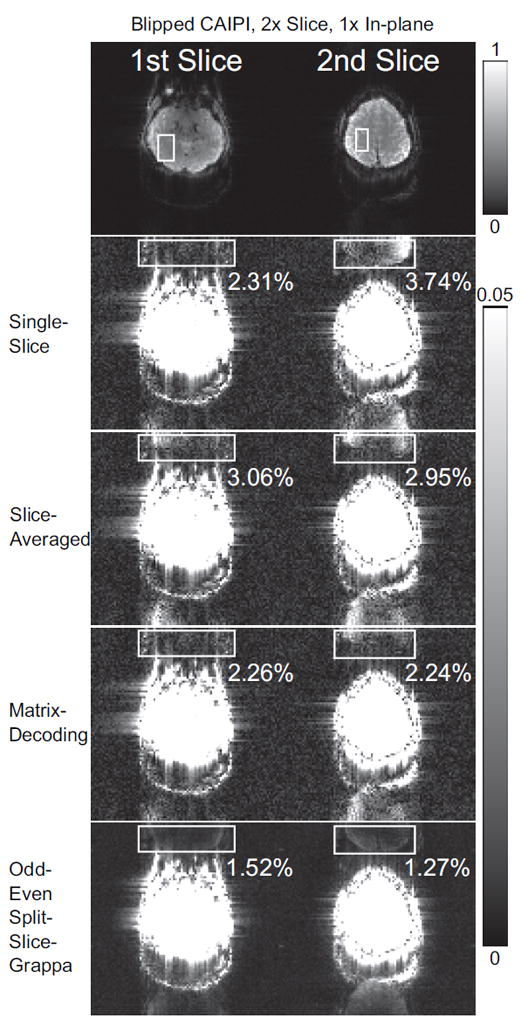
Nyquist ghosting correction for CAIPI EPI brain images. Two axial simultaneous slices are displayed. The figure setup is similar to that of Fig. 9.
VII. Discussion
The present work demonstrates that a hybrid-space SENSE reconstruction can be used for SMS MRI. For CAIPI-type acquisition, the hybrid-space SENSE images exhibit comparable quality to the split-slice-GRAPPA images. In addition, hybrid-space SENSE is a generic reconstruction that can handle arbitrary SMS ky-kz undersampling patterns, as long as the kx dimension is fully sampled. In principle, iterative reconstruction methods [27], [33], [46], [47] can also be used for such reconstruction. However, based on conventional 2D reconstructions [27], [33], [46], [47], these iterative methods can be computationally expensive.
It is of wide interest to optimize the SMS undersampling pattern and further improve the reconstruction. Along this direction, we derived the analytical g-factor, which is an essential tool for fair comparison of different SMS undersampling patterns. This method is compatible with arbitrary SMS ky-kz undersampling patterns, thus preventing bias to be introduced by different reconstruction methods in such comparisons. In addition, the analytical method is noise-free and faster than the pseudo multiple replica method to compute high quality g-factor maps for the hybrid-space SENSE reconstruction. It can be envisioned that the analytical g-factor maps may facilitate the design of dedicated receiving coils for SMS imaging, similar to what has been done in the conventional 2D imaging case [48]. Moreover, the hybrid-space SENSE reconstruction and the associated analytical g-factor calculations are applicable to both EPI and non-EPI acquisitions, although the SMS sequence used in this paper is an EPI sequence.
Furthermore, the matrix-decoding method allows us to improve the Nyquist ghosting correction. This method is integrated into the hybrid-space SENSE reconstruction and provides a one step solution for image reconstruction and slice-specific ghosting correction. This method is also compatible with arbitrary SMS ky-kz undersampling patterns. In this paper, the method is demonstrated using non-periodic MICA and periodic CAIPI undersampling patterns. For the MICA pattern, the matrix-decoding method achieves the lowest residual ghosting within the hybrid-space SENSE framework and the odd/even split-slice-GRAPPA method cannot be applied due to incompatibility. For the CAIPI patterns, both the matrix-decoding method and odd/even split-slice-GRAPPA suppress the ghosting level to a few percent of the signal level in the image. Although odd/even split-slice-GRAPPA achieves the lowest residual artifacts, the matrix-decoding method still improves the ghosting correction compared to conventional methods for hybrid-space SENSE.
The residual Nyquist ghosting artifacts are easier to observe when the background noise is smaller. When the background noise level increases with the increase of acceleration factor or with the inclusion of in vivo physiological noise, the residual Nyquist ghosting may become hard to notice. Even though the residual Nyquist ghosting seems too small to cause any problems in some cases, it still contaminates the signal when the ghosting overlaps with the object. Therefore a more accurate ghosting correction algorithm is always preferred whenever possible. Interestingly, the performance of the slice-averaged correction appears better than that of the single-slice correction and is even close to that of the matrix-decoding correction at the 5× slice acceleration factor. It is worth noting that the slice-averaged correction utilizes a multiband RF pulse to collect the reference scan data for estimating the ghosting correction coefficients and its reference scan data would have higher SNR than the other two methods for a fixed set of scan parameters. Mathematically, the matrix-decoding method is always more accurate than the slice-averaged correction. Practically, the advantage of the matrix-decoding method is better appreciated at a lower slice acceleration factor when the multiband pulse gains less SNR for the slice-averaged reference scan data and the Nyquist ghosting artifacts are more different in the further apart simultaneous slices.
The matrix-decoding Nyquist ghosting correction needs a reference scan for each individual slice, making the reference scan acquisition time Ns times that of a single-slice or slice-averaged correction, where Ns is the number of simultaneous slices. Nevertheless the increase in the total scan time of a time series is negligible because the reference scan is conducted only once.
The matrix-decoding Nyquist ghosting correction method we proposed [38] has been adapted into an image space approach called ghost-correcting SENSE (GhC-SENSE), in which the slice-specific ghosting phase terms are included when solving the signal equations for two sets of coil images reconstructed separately from the odd and even echoes [34]. GhC-SENSE is only applicable to periodic CAIPI patterns. GhC-SENSE is also built on an additional assumption that the phase error that causes Nyquist ghosting artifacts oscillates between two exactly opposite values for odd and even echoes. This assumption may break down sometimes when not all odd (or even) echoes are well aligned [40]. When the additional assumption holds and when the SMS acquisition uses a periodic undersampling pattern, GhC-SENSE generates identical images as the matrix-decoding method, but with reduced computation complexity and time [34]. The computation time reduction in GhC-SENSE, however, is not as significant as predicted from the problem complexity reduction alone due to associated overhead operations [34].
Both hybrid-space SENSE and split-slice-GRAPPA are applicable to CAIPI acquisitions. The performance of hybrid-space SENSE depends on the quality of the sensitivity maps, as in any SENSE-type reconstruction [20]. SNR loss and artifacts may arise at areas with poor or no sensitivity estimation. GRAPPA-type reconstruction may be more robust to imperfections in calibration data. With SENSE, Tikhonov regularization can be applied when solving the unknown magnetization in the spatial domain. With GRAPPA, similar regularization can be applied when solving the k-space interpolation kernels. The different ways of applying the regularization may lead to non-identical effects. These differences between hybrid-space SENSE and split-slice-GRAPPA may lead to differences in their reconstruction as well as Nyquist ghosting correction performances. Split-slice-GRAPPA may also cost less computation time, yet a more thorough comparison of the reconstruction properties of hybrid-space SENSE and split-slice-GRAPPA for CAIPI undersampling patterns awaits future investigations.
Besides the periodic CAIPI undersampling patterns, hybrid-space SENSE is also applicable to the randomly undersampled MICA pattern. Although MICA exhibits slightly lower overall retained SNR than CAIPI in Fig.7, it does have slightly higher retained SNR in some local regions. It is conceivable that for applications that have specific local ROIs, MICA might yield higher SNR for the targeted areas. The relative performance of different undersampling patterns also depends on the specific coil configuration and acquisition parameters. A thorough evaluation of the MICA SNR performance for different experimental setups would be a topic for future work.
It is worth noting that both the analytical and pseudo multiple replica g-factor maps reflect only the thermal noise properties of the images. Although these maps can reflect actual noise properties of phantom images, they do not reflect actual noise properties of in vivo data, which are contaminated by physiological noise in addition to thermal noise.
VIII. Conclusion
In this paper, hybrid-space SENSE reconstruction is proposed basing on the three-dimensional representation of SMS acquisitions. When periodic SMS undersampling patterns are applied, images reconstructed by hybrid-space SENSE exhibit comparable quality to those reconstructed by split-slice-GRAPPA. Furthermore, the hybrid-space SENSE reconstruction is compatible with arbitrary SMS phase encoding undersampling patterns, enabling an efficient reconstruction of randomly undersampled SMS data. Analytical g-factor quantifies the SNR performance and facilitates a fair comparison between different SMS undersampling patterns. In addition, the matrix-decoding method improves the Nyquist ghosting correction for hybrid-space SENSE reconstruction by incorporating the slice-specific EPI effects into the encoding model. The matrix-decoding method is compatible with arbitrary SMS phase encoding undersampling patterns, including CAIPI and MICA.
Acknowledgments
The authors thank Suchandrima Banerjee and Ajit Shankaranarayanan from GE Healthcare for their help with processing the EPI reference scan data. The authors thank Michael Lustig from University of California, Berkeley, for his help with computing sensitivity maps.
This work was supported in part by the National Institutes of Health under Grant P41 EB015891, Grant P01 CA159992 and Grant R01 EB008108. This work was also supported by GE Healthcare and the Center for Cognitive and Neurobiological Imaging at Stanford University. The work of Kangrong Zhu was supported in part by a Rambus Corporation Stanford Graduate Fellowship.
Footnotes
Supplementary materials are available online under the multimedia tab in IEEE Xplore.
Contributor Information
Kangrong Zhu, Email: kangrong@stanford.edu, Electrical Engineering Department, Stanford University, Stanford, CA 94305 USA.
Robert F. Dougherty, Center for Cognitive and Neurobiological Imaging, Stanford University, Stanford, CA 94305 USA
Hua Wu, Center for Cognitive and Neurobiological Imaging, Stanford University, Stanford, CA 94305 USA.
Matthew J. Middione, Applied Sciences Laboratory West, GE Healthcare, Menlo Park, CA 94025 USA
Atsushi M. Takahashi, Athinoula A. Martinos Imaging Center at MIT, McGovern Institute for Brain Research, Massachusetts Institute of Technology, Cambridge, MA 02139 USA
Tao Zhang, Email: tzhang08@stanford.edu, Electrical Engineering Department, Stanford University, Stanford, CA 94305 USA.
John M. Pauly, Email: pauly@stanford.edu, Electrical Engineering Department, Stanford University, Stanford, CA 94305 USA.
Adam B. Kerr, Email: akerr@stanford.edu, Electrical Engineering Department, Stanford University, Stanford, CA 94305 USA.
References
- 1.Glover GH. Phase-offset multiplanar (POMP) volume imaging: A new technique. J Magn Reson Imaging. 1991;1:457–461. doi: 10.1002/jmri.1880010410. [DOI] [PubMed] [Google Scholar]
- 2.Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging. 2001;13:313–317. doi: 10.1002/1522-2586(200102)13:2<313::aid-jmri1045>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- 3.Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain fMRI and fast diffusion imaging. PLoS One. 2010;5:e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010;63:1144–1153. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med. 2012;67:1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ugurbil K, Xu J, Auerbach EJ, et al. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. Neuroimage. 2013;80:80–104. doi: 10.1016/j.neuroimage.2013.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Feinberg DA, Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson. 2013;229:90–100. doi: 10.1016/j.jmr.2013.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Setsompop K, Kimmlingen R, Eberlein E, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage. 2013;80:220–233. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 10.Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn Reson Med. 2014;72:93–102. doi: 10.1002/mrm.24898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blaimer M, Breuer FA, Seiberlich N, Mueller MF, Heidemann RM, Jellus V, Wiggins G, Wald LL, Griswold MA, Jakob PM. Accelerated volumetric MRI with a SENSE/GRAPPA combination. J Magn Reson Imaging. 2006;24:444–450. doi: 10.1002/jmri.20632. [DOI] [PubMed] [Google Scholar]
- 12.Stäb D, Ritter CO, Breuer FA, Weng AM, Hahn D, Köstler H. CAIPIRINHA accelerated SSFP imaging. Magn Reson Med. 2011;65:157–164. doi: 10.1002/mrm.22600. [DOI] [PubMed] [Google Scholar]
- 13.Blaimer M, Choli M, Jakob PM, Griswold MA, Breuer FA. Multiband phase-constrained parallel MRI. Magn Reson Med. 2013;69:974–980. doi: 10.1002/mrm.24685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Moeller S, Vu AT, Auerbach E, Ugurbil K, Yacoub E. RO extended FOV SENSE/GRAPPA for multiband imaging with FOV shift. Proc 22nd Annu Meeting; Milan, Italy. ISMRM; 2014. p. 4396. [Google Scholar]
- 15.Zhu K, Kerr A, Pauly JM. Autocalibrating CAIPIRINHA: Reformulating CAIPIRINHA as a 3D problem. Proc 20th Annu. Meeting; Melbourne, Australia. ISMRM; 2012. p. 518. [Google Scholar]
- 16.Zahneisen B, Poser BA, Ernst T, Stenger VA. Three-dimensional fourier encoding of simultaneously excited slices: Generalized acquisition and reconstruction framework. Magn Reson Med. 2014;71:2071–2081. doi: 10.1002/mrm.24875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blaimer M, Breuer FA, Mueller M, Seiberlich N, Ebel D, Heidemann RM, Griswold MA, Jakob PM. 2D-GRAPPA-operator for faster 3D parallel MRI. Magn Reson Med. 2006;56:1359–1364. doi: 10.1002/mrm.21071. [DOI] [PubMed] [Google Scholar]
- 18.Weiger M, Pruessmann KP, Boesiger P. 2D SENSE for faster 3D MRI. MAGMA. 2002;14:10–19. doi: 10.1007/BF02668182. [DOI] [PubMed] [Google Scholar]
- 19.Zahneisen B, Ernst T, Poser BA. SENSE and simultaneous multislice imaging. Magn Reson Med. 2014 doi: 10.1002/mrm.25519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 21.Robson PM, Grant AK, Madhuranthakam AJ, Lattanzi R, Sodickson DK, McKenzie CA. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn Reson Med. 2008;60:895–907. doi: 10.1002/mrm.21728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xu J, Moeller S, Auerbach EJ, Strupp J, Smith SM, Feinberg DA, Yacoub E, Ugurbil K. Evaluation of slice accelerations using multiband echo planar imaging at 3T. Neuroimage. 2013;83:991–1001. doi: 10.1016/j.neuroimage.2013.07.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn Reson Med. 2009;62:739–746. doi: 10.1002/mrm.22066. [DOI] [PubMed] [Google Scholar]
- 24.Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med. 2005;53:684–691. doi: 10.1002/mrm.20401. [DOI] [PubMed] [Google Scholar]
- 25.Nunes RG, Hajnal JV, Golay X, Larkman DJ. Simultaneous slice excitation and reconstruction for single shot EPI. Proc 14th Annu. Meeting; Seattle, Washington, USA. ISMRM; 2006. p. 293. [Google Scholar]
- 26.Zhu K, Dougherty RF, Pauly JM, Kerr AB. Multislice acquisition with incoherent aliasing (MICA); Proc 22nd Annu. Meeting; Milan, Italy. ISMRM; 2014. p. 4403. [Google Scholar]
- 27.Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
- 28.Kyriakos WE, Panych LP, Kacher DF, Westin C-F, Bao SM, Mulkern RV, Jolesz FA. Sensitivity profiles from an array of coils for encoding and reconstruction in parallel (SPACE RIP) Magn Reson Med. 2000;44:301–308. doi: 10.1002/1522-2594(200008)44:2<301::aid-mrm18>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 29.Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA. Simultaneous multislice (SMS) imaging techniques. Magn Reson Med. 2015 doi: 10.1002/mrm.25897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Setsompop K, Cohen-Adad J, Gagoski BA, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage. 2012;63:569–580. doi: 10.1016/j.neuroimage.2012.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Koopmans PJ, Poser BA, Breuer FA. 2D-SENSE-GRAPPA for fast, ghosting-robust reconstruction of in-plane and slice accelerated blipped-CAIPI EPI. Proc 23rd Annu. Meeting; Toronto, Canada. ISMRM; 2015. p. 2410. [Google Scholar]
- 32.Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT - an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med. 2010;64:457–471. doi: 10.1002/mrm.22428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hennel F, Buehrer M, Deuster Cv, Seuven A, Pruessmann KP. SENSE reconstruction for multiband EPI including slice-dependent N/2 ghost correction. Magn Reson Med. 2015 doi: 10.1002/mrm.25915. [DOI] [PubMed] [Google Scholar]
- 35.Stemkens B, Tijssen RH, Andreychenko A, Crijns SPM, Sbrizzi A, Lagendijk JJW, van den Berg CAT. Optimizing CAIPIRINHA multi-band acquisition scheme for 2D multi-slice experiments in the abdomen. Proc 22nd Annu. Meeting; Milan, Italy. ISMRM; 2014. p. 645. [Google Scholar]
- 36.Zhu K, Dougherty RF, Wu H, Middione MJ, Pauly JM, Kerr AB. Theoretical g-factor for simultaneous multi-slice imaging. Proc ISMRM Workshop on Simultaneous Multi-Slice Imaging: Neuroscience and Clinical Applications; Pacific Grove, CA, USA. 2015. [Google Scholar]
- 37.Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn Reson Med. 2013;69:571–582. doi: 10.1002/mrm.24267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhu K, Dougherty RF, Takahashi AM, Pauly JM, Kerr AB. Nyquist ghosting correction for simultaneous multislice echo planar imaging. Proc 22nd Annu Meeting; Milan, Italy. ISMRM; 2014. p. 647. [Google Scholar]
- 39.Bruder H, Fischer H, Reinfelder H-E, Schmitt F. Image reconstruction for echo planar imaging with nonequidistant k-space sampling. Magn Reson Med. 1992;23:311–323. doi: 10.1002/mrm.1910230211. [DOI] [PubMed] [Google Scholar]
- 40.Buonocore MH, Gao L. Ghost artifact reduction for echo planar imaging using image phase correction. Magn Reson Med. 38:89–100. 1997. doi: 10.1002/mrm.1910380114. [DOI] [PubMed] [Google Scholar]
- 41.Wald LL, Carvajal L, Moyher SE, Nelson SJ, Grant PE, Barkovich AJ, Vigneron DB. Phased array detectors and an automated intensity-correction algorithm for high-resolution MR imaging of the human brain. Magn Reson Med. 1995;34:433–439. doi: 10.1002/mrm.1910340321. [DOI] [PubMed] [Google Scholar]
- 42.Murakami JW, Hayes CE, Weinberger E. Intensity correction of phased-array surface coil images. Magn Reson Med. 1996;35:585–590. doi: 10.1002/mrm.1910350419. [DOI] [PubMed] [Google Scholar]
- 43.Hinks RS, Mock BJ, Collick BD, Frigo FJ, Shubhachint T. Method and system for image artifact reduction using nearest-neighbor phase correction for echo planar imaging. 7,102,352. US Patent. 2006 Sep 5;
- 44.Haacke EM, Lindskogj ED, Lin W. A fast, iterative, partial-fourier technique capable of local phase recovery. J Magn Reson. 1991;92:126–145. [Google Scholar]
- 45.Brau AC, Beatty PJ, Skare S, Bammer R. Comparison of reconstruction accuracy and efficiency among autocalibrating data-driven parallel imaging methods. Magn Reson Med. 2008;59:382–395. doi: 10.1002/mrm.21481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Samsonov AA, Kholmovski EG, Parker DL, Johnson CR. POCSENSE: POCS-based reconstruction for sensitivity encoded magnetic resonance imaging. Magn Reson Med. 2004;52:1397–1406. doi: 10.1002/mrm.20285. [DOI] [PubMed] [Google Scholar]
- 47.Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE) Magn Reson Med. 2007;57:1196–1202. doi: 10.1002/mrm.21245. [DOI] [PubMed] [Google Scholar]
- 48.Weiger M, Pruessmann KP, Leussler C, Röschmann P, Boesiger P. Specific coil design for SENSE: A six-element cardiac array. Magn Reson Med. 2001;45:495–504. doi: 10.1002/1522-2594(200103)45:3<495::aid-mrm1065>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]


