Electronic Structure of a Cu^II-Alkoxide Complex Modeling Intermediates in Copper-Catalyzed Alcohol Oxidations

Abstract

In the copper-catalyzed oxidation of alcohols to aldehydes, a Cu^II-alkoxide (Cu^II-OR) intermediate is believed to modulate the αC-H bond strength of the deprotonated substrate to facilitate the oxidation. As a structural model for these intermediates, we characterized the electronic structure of the stable compound Tp^tBuCu^II(OCH₂CF₃) (Tp^tBu = (hydro-tris (3-tert-butyl-pyrazolyl) borate) and investigated the influence of the trifluoroethoxide ligand on the electronic structure of the complex. The compound exhibits an electron paramagnetic resonance (EPR) spectrum with an unusually large g_zz value of 2.44 and a small copper hyperfine coupling A_zz of 40·10⁻⁴ cm⁻¹ (120 MHz). Single-crystal electron nuclear double resonance (ENDOR) spectra show that the unpaired spin population is highly localized on the copper ion (≈ 68 %), with no more than 15 % on the ethoxide oxygen. Electronic absorption and magnetic circular dichroism (MCD) spectra show weak ligand-field transitions between 5000 and 12000 cm⁻¹ and an intense ethoxide-to-copper charge transfer (LMCT) transition at 24000 cm⁻¹, resulting in the red color of this complex. Resonance Raman (rR) spectroscopy reveals a Cu-O stretch mode at 592 cm⁻¹. Quantum chemical calculations support the interpretation and assignment of the experimental data. Compared to known Cu^II-thiolate and Cu^II-alkylperoxo complexes from the literature, we found an increased σ interaction in the Cu^II-OR bond that results in the spectroscopic features. These insights lay the basis for further elucidating the mechanism of copper-catalyzed alcohol oxidations.

Introduction

Copper(II)/radical systems are important catalysts for the oxidation of alcohols to aldehydes in both biology and synthesis. In nature, the fungal copper enzyme galactose oxidase (GAO) converts primary alcohols to aldehydes.^1,2 In organic synthesis, Cu/nitroxyl systems catalyze the same oxidation.^3–5 The currently accepted mechanisms of both biological and synthetic alcohol oxidation propose Cu^II-alkoxide complexes as relevant intermediates.^6,7 Deprotonation of the alcohol when it binds to copper is expected to significantly weaken the substrate αC-H bond strength in preparation for oxidation.⁸

During substrate oxidation in GAO, an alcohol binds to the Cu^II site and is deprotonated by an axially bound tyrosinate ligand, producing the proposed Cu^II-alkoxide intermediate. Ultimately H-atom transfer (HAT) to a coordinated 3′-(S-cysteinyl)tyrosinate radical^9,10 and electron transfer produce the aldehyde product and Cu^I, but the order and extent of kinetic coupling between the steps is still under investigation.^6,11 For the synthetic Cu/nitroxyl systems, several mechanisms of alcohol oxidation have been discussed in the literature. They all include a Cu^II-alkoxide as the first intermediate and differ in the binding mode of the exogenous nitroxyl moiety (which abstracts the αC-H hydrogen of the substrate producing the aldehyde product).^12–16

Understanding the geometric and electronic structure of these intermediates, including the extent to which the αC-H bond in the alcohol substrate is activated by copper, is of crucial importance to gain further insight into the mechanisms of both GAO and the synthetic Cu/nitroxyl systems. However, a detailed electronic structure characterization has not been performed on these intermediates and very few small molecule Cu^II-alkoxide complexes are known in the literature to serve as models.^17–20

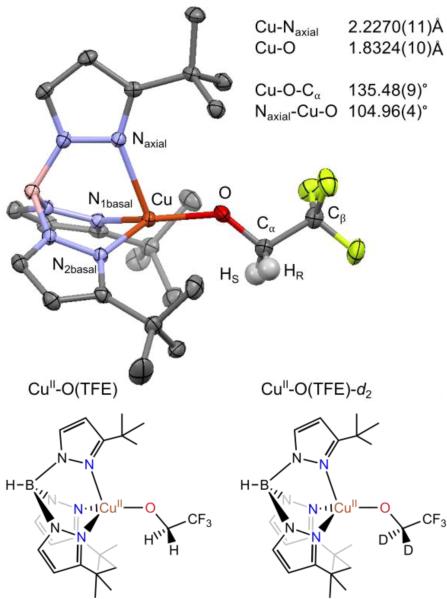
As a step toward understanding the structure of the intermediates in Cu-mediated alcohol oxidation, we examined a Cu^II-alkoxide complex, Tp^tBuCu^II(OCH₂CF₃)²¹ (abbreviated Cu^II-O(TFE) throughout). This complex does efficient H-atom abstraction when treated with H-atom donors such as TEMPO-H, yielding the corresponding radical, trifluoroethanol, and Cu^I. While this complex is not a direct functional model (i.e. alkoxide oxidation does not occur upon treatment with external oxyl radical H-atom acceptors),²¹ it serves as a general structural model for the proposed intermediates in Cu/radical alcohol oxidation systems. The complex, shown in Figure 1, features a tridentate Tp^tBu (Tp^tBu = (hydro-tris (3-tert-butyl-pyrazolyl) borate) ligand scaffold^22–24 and a 2,2,2-trifluoroethoxide ligand. Structurally, the bulky Tp^tBu ligand mimics the catalyst/enzyme supporting ligands, and the alkoxide functions as a substrate model. The complex has an approximately trigonal monopyramidal coordination geometry with a long Cu-N_axial bond²¹ (similar to type 1 copper sites).²⁵

Figure 1.

(Top) Crystal structure of Tp^tBuCu^II(OCH₂CF₃) with ellipsoids at the 50 % probability level and primary bond lengths and angles listed, from ref. 21. Hydrogen atoms are omitted for clarity, except on the trifluoroethoxide ligand. Additional relevant structural features include the bond lengths Cu-N_1basal (1.9717(11) Å) and Cu-N_2basal (1.9638(11) Å), and the dihedral angles Cu-O-C_α-H_S (37.43°) and Cu-O-C_α-H_R (−81.06°). (Bottom) Lewis structures of Cu^II-O(TFE) and Cu^II-O(TFE)-d₂ reproduced from ref. 21.

Here, we characterized the electronic structure of Cu^II-O(TFE). We used powder and single-crystal electron paramagnetic resonance (EPR) spectroscopy to probe the paramagnetic S = 1/2 ground state. This revealed the identity of the singly occupied molecular orbital (SOMO), the d_x²–y², and its orientation within Cu^II-O(TFE). It also revealed a large shift in g_zz (one of the largest recorded for copper in a biologically relevant ligand scaffold) and a small copper hyperfine ^CuA_zz, (similar in magnitude to type 1 blue copper sites²⁵). Using electron nuclear double resonance (ENDOR) spectroscopy, we measured the hyperfine couplings to determine the strength of the interaction between the unpaired electron and nearby magnetic nuclei (¹H, ¹⁹F, ¹⁴N). With these values, we mapped the extent of delocalization of the unpaired electron onto the Tp^tBu and trifluoroethoxide ligands and found much of the spin population localized on copper. Using UV-Vis/NIR, magnetic circular dichroism (MCD), and resonance Raman (rR) spectroscopies, we assigned the electronic transitions and characterized the nature of the Cu-O bond. We show Cu^II-O(TFE) has a near-UV ethoxide-to-copper charge transfer transition, giving it a red color, reminiscent of biological red copper sites (nitrosocyanin²⁶ and BSco^27,28). We compare Cu^II-O(TFE) to analogous thiolate (Cu^II-SR) and peroxo (Cu^II-OOR) ligated copper compounds to understand the influence of the ethoxide ligand on electronic structure. In addition, we summarize how the identifying spectroscopic features (large g_zz, small ^CuA_zz, near-UV transition) are related to biological copper sites.

Our data allow the following conclusions to be made. First, the spin population on the ethoxide ligand is small, leaving much of the spin localized on copper. The absence of substantial spin population on the ethoxide ligand suggests a relatively ionic Cu-O bond compared to related Cu^II complexes with similar distorted tetrahedral ligand environments. Despite the relatively ionic Cu-O bond, the αC-H bond of the trifluoroethoxide is not activated enough to promote ligand oxidation.²¹ Second, the Cu-O bond has contributions from both Cu d_xy/O(TFE) p_pseudo-σ and Cu d_x²–y²/O(TFE) p_π interactions. The σ bonding interaction between the O(TFE)-based p_pseudo-σ (abbreviated p_~σ) and the copper-based d_xy orbitals reduces the energy gap between the dominantly d_xy antibonding orbital and the singly occupied d_x²–y² orbital. This results in the small difference in energy, E_x²–y² – E_xy, observed by MCD spectroscopy, that drives the large shift in g_zz. Over all, these insights contribute to the understanding of the role of alkoxide intermediates in Cu^II-catalyzed alcohol oxidations.

Results

I. Field-swept EPR

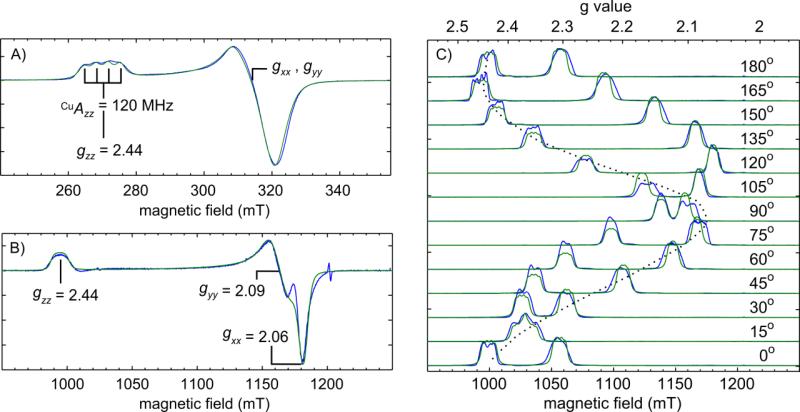
A combination of 9.2 GHz (X-band) and 34 GHz (Q-band) EPR spectroscopies reveal the magnetic parameters of the Cu^II-alkoxide. The continuous-wave (CW) 9.2 GHz EPR spectrum of Cu^II-O(TFE) in a frozen solution of toluene at 120 K is shown in Figure 2A. This spectrum resolved the unusually large g_zz = 2.44(1) and small Cu hyperfine coupling A_zz = 120(10) MHz (40(3)·10⁻⁴ cm⁻¹).²¹ 34 GHz EPR, shown in Figure 2B, of Cu^II-O(TFE) in DCM:toluene at 10 K further resolved the principal g values to g_xx = 2.060(6), g_yy = 2.093(6) and g_zz = 2.447(6) (simulation parameters in Table S1A). Based on the ligand field theory for a d⁹ system, the large g_zz shift away from the free electron g value (g_e = 2.0023) indicates that the molecule is in a d_x²–y² ground state.²⁹

Figure 2.

The copper hyperfine coupling, principal g values, and g tensor frame are resolved with multi-frequency and single-crystal EPR. A) Field-modulated 9.22 GHz CW EPR spectrum of a frozen solution of Cu^II-O(TFE) in a toluene glass acquired at 120 K with a microwave power of 2 mW (reported previously in ref. 21). B) First derivative of an echo-detected [π/2(30 ns) – τ(240 ns) – π(60 ns) – τ – echo] 34.061 GHz pulse field-swept spectrum of a frozen solution of Cu^II-O(TFE) in a DCM:toluene glass (10 K, 3 ms repetition time). C) FID-detected [π/2(1 μs) – FID] pulse field-swept spectra of 1% Cu^II-O(TFE) in a Zn^II-O(TFE) single-crystal (10 K, 2 ms repetition time, 0.1 mT steps). Spectra were acquired at 34.151 GHz (0°-75°) and 34.143 GHz (90°-180°). In all cases, experimental traces are shown in blue and simulations in green. Simulation parameters are summarized in Tables S1A, B.

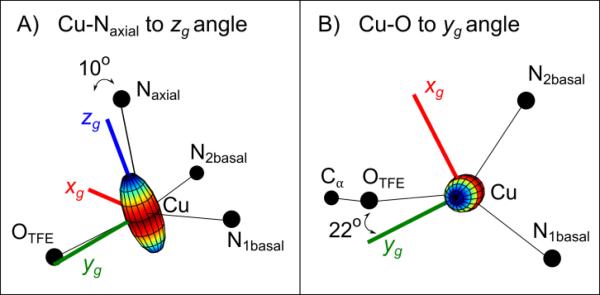
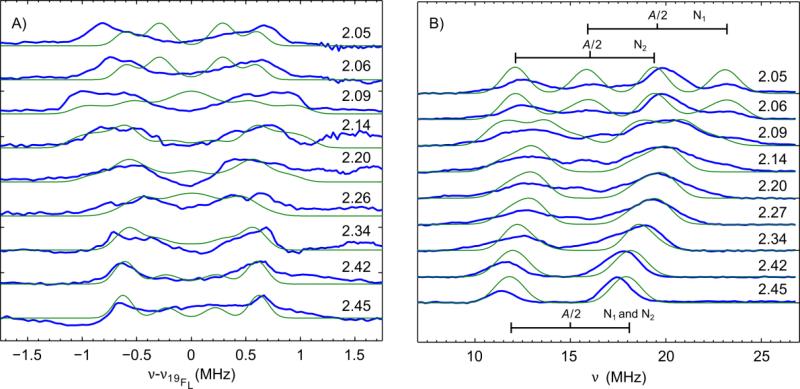
To determine the orientation of the g tensor principal axes and ultimately of the d_x²–y² orbital within the molecule, 34 GHz pulse field-swept EPR spectra of a doped single crystal sample were collected (1% Cu^II-O(TFE) in the zinc analog Zn^II-O(TFE)). In these experiments, a series of thirteen spectra were acquired by rotating a single crystal sample in the EPR spectrometer in 15° increments (Figure 2C). In each spectrum, two peaks from two sites in the unit cell are observed due to the P2₁/n space group of the crystal. Using the principal g values obtained from the powder 34 GHz spectrum, the orientation of the g tensor in the molecule was determined by a simultaneous least-squares fitting of the thirteen spectra with a model generated using the simulation parameters in Table S1B (fitting details in Experimental section). It was necessary to use g_zz = 2.453(4), slightly shifted compared to the frozen solution, to achieve adequate simulations of the data. This is likely due to slight structural differences between a frozen solution and a crystal. The data and simulations indicate the z axis of the g tensor (z_g) is tilted ≈ 10° away from the Cu-N_axial bond toward the ethoxide ligand and the y axis (y_g) is tilted ≈ 22° away from the Cu-O bond (shown in Figure 3). Least-squares fits of a data set from a second single crystal (Figure S2, Table S1B, using a g_zz value of 2.463(6)) produced a nearly identical g frame orientation. As a result, we determined the lobes of the singly occupied d_x²–y² orbital lie in a plane normal to the z_g axis and nearly normal to the long Cu-N_axial bond. Figure S6A shows the orientations of the static field in the molecule for this set of spectra.

Figure 3.

Orientation of the g tensor in Cu^II-O(TFE) determined from single-crystal EPR. An axial g tensor ellipsoid is centered on copper and the x_g, y_g, and z_g axes of the tensor are shown as thick red, green, and blue lines, respectively. A) The z_g axis lies 10° off the Cu-N_axial bond in crystal 1 (10° in crystal 2, see SI). B) The y_g axis lies 22° off the Cu-O bond in crystal 1 (37° in crystal 2, see SI).

II. ENDOR

II. A. ¹H ENDOR

To quantify the distribution of unpaired spin population in the molecule, we measured the hyperfine coupling interaction between the unpaired electron and surrounding magnetic nuclei using ENDOR spectroscopy. Frozen-solution ENDOR spectra of Cu^II-O(TFE) revealed broad ¹H peaks split by ≈ 25 MHz and centered around the ¹H Larmor frequency (peaks at ± 12 MHz in Figure S4). In ENDOR spectra of Cu^II-O(TFE)-d₂, these features shifted to lower frequency (centered at the ²H Larmor frequency). This indicates these features originate from the αC-H protons on the trifluoroethoxide ligand and these protons have isotropic hyperfine couplings of about 25 MHz.

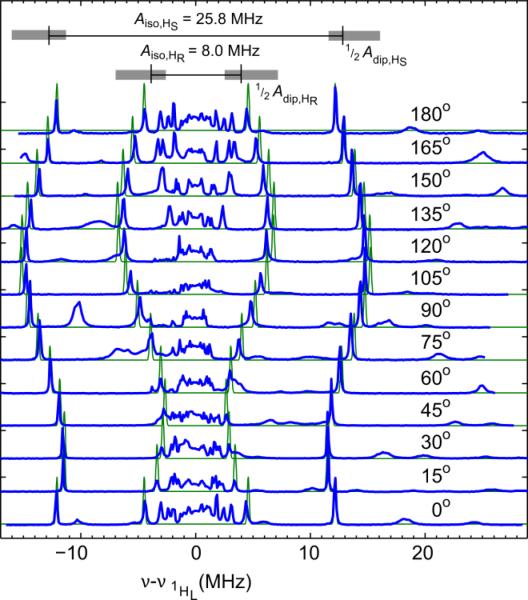
To determine the full hyperfine tensors of the two protons, including principal values and tensor orientations, we measured ¹H ENDOR on a doped single crystal (1% Cu^IIO(TFE), 99% Zn^II-O(TFE)). The corresponding spectra in Figure 4 show two pairs of orientation-dependent hyperfine lines due to the two ethoxide protons which we named H_R and H_S (referring to the prochirality of the hydrogens pictured in Figure 1). The total hyperfine coupling A_tot for each proton is modelled as the sum of an isotropic term and an anisotropic dipolar term, A_tot = A_iso + A_dip. The dipolar term of the hyperfine coupling produces the curved path of the peaks in the series of spectra collected as the orientation of the single crystal is rotated in the magnetic field.

Figure 4.

Single-crystal ¹H ENDOR resolves the hyperfine tensors of the trifluoroethoxide ligand protons H_R and H_S. (Top) The isotropic hyperfine couplings are marked by a black line and the spread of the dipolar hyperfine couplings (A_dip ≈ 9 MHz) is marked by a gray box. Shown in blue are echo-detected Davies ENDOR spectra [π(80 ns) – T – π/2(40 ns) – τ(230 ns) – π(80 ns) – τ – echo] of 1% Cu^II-O(TFE) in a Zn^II-O(TFE) single-crystal. Spectra were acquired at 34.151 GHz (0°-75°) and 34.143 GHz (90°-180°) (10 K, 3 ms repetition time). A 13 μs RF pulse was applied to excite nuclear transitions and was stepped in 0.1 MHz increments. Spectra were acquired at the g values corresponding to the transitions marked with a dotted line in Figure 2C. Simulations are shown in green (parameters in Table S1C).

Importantly, the dipolar term depends on the distance between the ¹H nucleus and the unpaired spin, which is delocalized in the molecule. We modelled the dipolar hyperfine coupling with a distributed point-dipole approximation assuming the spin population was distributed across the copper, the oxygen of the trifluoroethoxide ligand, and the two basal nitrogen atoms of the Tp^tBu ligand. For each proton, H_R and H_S, the total dipolar hyperfine tensor is the sum of four dipolar sub-tensors

$$A_{\mathrm{dip},\mathrm{H}}={\sigma }_{\mathrm{Cu}}{A}_{\mathrm{dip},\mathrm{CuH}}+{\sigma }_{\mathrm{O}}{A}_{\mathrm{dip},\mathrm{OH}}+{\sigma }_{\mathrm{N}1}{A}_{\mathrm{dip},\mathrm{N}1\mathrm{H}}+{\sigma }_{\mathrm{N}2}{A}_{\mathrm{dip},\mathrm{N}2\mathrm{H}},$$ (1)

where σ_i represents the spin population on atom i. Each subtensor was calculated using the point-dipole approximation

$$A_{\mathrm{dip},\mathrm{CuH}}=\frac{{\mu }_0}{4\pi }{\mu }_{\mathrm{B}}{\mu }_{\mathrm{N}}{g}_{\mathrm{N}}g\frac{1}{r_{\mathrm{CuH}}^3}\left[\left(\frac{3{\mathit{r}}_{\mathrm{CuH}}{\mathit{r}}_{\mathrm{CuH}}^{\mathrm{T}}}{r_{\mathrm{CuH}}^2}-\mathrm{I}\right)\right].$$ (2)

Here μ_B is the Bohr magneton, μ_N is the nuclear magneton, g_N is the nuclear g value, I is the 3×3 identity matrix, μ₀ is the vacuum permeability, and g is the full 3×3 g tensor obtained from fitting the single crystal pulse-field swept spectra. The distance vectors r_iH were taken directly from the coordinates of the X-ray crystal structure.²¹ In our simulations, the isotropic hyperfine coupling values (A_iso,HR, A_iso,HS) and the spin populations (σ_Cu, σ_O, σ_N1, and σ_N2) were adjustable parameters.

The proximity of the oxygen atom to the ¹H nuclei meant the dipolar contribution to the simulation was affected most significantly by the spin population on oxygen, σ_O. Even after significantly decreasing the spin density on copper (σ_Cu = 0.4), values for σ_O any larger than 0.15 produced simulations with too large a dipolar component. However, because the results of ¹⁴N ENDOR spectroscopy (in agreement with DFT calculations, see below) place upper bounds of 0.10 on both σ_N1 and σ_N2, it is reasonable to conclude σ_Cu is no less than 0.6. With σ_Cu = 0.6, values of σ_O any greater than 0.13 produced simulations with too large a dipolar coupling, allowing us to use this as an upper bound for spin population on oxygen in the single crystal.

Specifically, the values σ_N1 = 0.09 (or 9 %) and σ_N2 = 0.05 (or 5 %) were chosen based on ¹⁴N ENDOR data and are supported by DFT calculations as discussed below. Isotropic couplings, A_iso,HR = 25.8 MHz and A_iso,HS = 8 MHz, were used in the simulations and translate to spin populations on the protons of 0.018 (1.8 %) and 0.006 (0.6 %) respectively.³⁰ The remainder of the spin population (0.836, 83.6 %) was split between oxygen and copper. The simulations in Figure 4 used σ_O = 0.10(3) and σ_Cu = 0.73(3), or spin populations of 10±3 % and 73±3 %. Using these spin population values for σ_Cu, σ_O, σ_N1, and σ_N2, the principal values of the dipolar coupling were computed as (−3.3, −2.6, 6.3) MHz for H_S and (−2.5, −3.1, 5.5) MHz for H_R using Eq. (1) and (2) (tensor orientations shown in Figure S6B). The resulting principal values of the hyperfine coupling are (4.7, 5.4, 14) MHz for H_S and (23, 23, 31) MHz for H_R (summarized in Table S1C). These values for A_iso,HR, A_iso,HS, σ_Cu, σ_O, σ_N1, and σ_N2 also produced satisfactory simulations of ¹H ENDOR spectra for a second single crystal (Figure S3, Table S1C). These data suggest a relatively ionic Cu-O bond with little spin delocalization onto the trifluoroethoxide ligand.

The hyperfine couplings for H_R and H_S are dependent upon the site in the crystal unit cell used for the calculations. The two sites are related by a mirror plane which exchanges the dihedral angles (i.e. Cu-O-C-H_R = −81.06° and Cu-O-C-H_S = 37.43° become Cu-O-C-H_R = −37.43° and Cu-O-C-H_S = 81.06°). This exchanges the values of the hyperfine coupling and spin populations of the two protons.

II. B. ¹⁹F ENDOR

Higher resolution ENDOR spectra of a frozen solution of Cu^II-O(TFE) near the ¹H Larmor frequency show a peak pattern that is slightly asymmetric (Figure S5). This is due to fluorine peaks centered at the ¹⁹F Larmor frequency, which is 2.9 MHz lower than the ¹H Larmor frequency at 1160 mT. To separate the fluorine peaks from the proton peaks, the higher frequency half of the ¹H ENDOR spectrum, which contains purely proton features, was subtracted from the lower frequency half of the ENDOR spectrum. This yielded the difference spectrum in Figure 5A with ¹⁹F peaks only. Due to the three- to four-bond distance between the fluorine nuclei and the majority of the spin density, the isotropic hyperfine coupling was assumed to be negligible. Satisfactory simulations of these data were performed assuming a purely dipolar hyperfine coupling. The dipolar coupling principal values were computed using the distributed point-dipole approximation as described above using distance vectors obtained from crystal coordinates. To achieve the simulations shown in Figure 5A, the spin population of oxygen, σ_O, was increased to 0.15(3) and the spin population of copper, σ_Cu, decreased to 0.68(3) while the nitrogen spin populations were kept as 0.09 and 0.05. Principal ¹⁹F hyperfine values of (−1.1, −1.4, 2.4) MHz, (−0.65, −0.75, 1.4) MHz, and (−1.1, −1.3, 2.2) MHz were calculated (Table S1D). Hyperfine tensor frames were defined using the crystal structure coordinates assuming the unique axis A_zz points toward the copper nucleus (see Experimental section for details) and are visualized in Figure S6B. These simulations reproduce the orientation dependence and width of the spectra well, which supports the small σ_O and allows us to place an upper bound of 15±3 % spin population on oxygen when Cu^II-O(TFE) is in a frozen solution consistent with the small σ_O observed for the single crystal.

Figure 5.

¹⁹F and ¹⁴N ENDOR spectra of a frozen solution of Cu^II-O(TFE)-d₂ (A) and Cu^II-O(TFE) (B) in a DCM:toluene glass (10 K, 3 ms repetition time). A) Shown in blue are echo-detected Davies ENDOR spectra [π(100 ns) – T – π/2(50 ns) – τ(240 ns) – π(100 ns) – τ – echo] acquired at 34.068 GHz at the fields corresponding to g values listed in the figure. A 15 μs RF pulse was applied in 0.05 MHz steps. The ¹⁹F dipolar hyperfine coupling for simulations (green, parameters in Table S1D) were calculated with the distributed point dipole approximation assuming spin populations of σ_O = 0.15 and σ_Cu = 0.68. B) Shown in blue are echo-detected Davies ENDOR spectra [π(80 ns) – T – π/2(40 ns) – τ(240 ns) – π(80 ns) – τ – echo] acquired at 34.118 GHz at the fields corresponding to g values listed in the figure. A 14.5 μs RF pulse was applied. The ¹⁴N hyperfine couplings for simulations (green, parameters in Table S1D) are marked at the A/2 value (nitrogen in the strong coupling regime) for spectra acquired at g = 2.45 (bottom) and g = 2.05 (top). These coupling correspond to spin populations on the basal Tp^tBu nitrogen atoms of σ_N1 = 0.09 and σ_N2 = 0.05.

II. C. ¹⁴N ENDOR

Orientation-dependent 34 GHz ¹⁴N ENDOR supports the spin delocalization onto the Tp^tBu ligand (Figure 5B). At the low-field position (993 mT, g_zz = 2.45) where strong orientation selection is expected, the ENDOR spectrum shows only two features at 11.5 MHz and 17.5 MHz. These features are split by twice the Larmor frequency of ¹⁴N (3.05 MHz) and centered at ≈ 15 MHz, half the hyperfine coupling, A, for nitrogen in the strong coupling regime. At the highest field edge (g = 2.05), the ¹⁴N ENDOR spectrum splits into four lines indicating two nitrogen atoms are responsible for the coupling. Two less intense lines are centered at A/2 ≈ 20 MHz and two more intense lines are centered at A/2 ≈ 16 MHz (corresponding to axial hyperfine values for N_1basal of A_zz≈ 40 MHz, A_xx,yy≈ 30 MHz and for N_2basal of A_zz ≈ 32 MHz, A_xx,yy ≈ 30 MHz).

Observing only two peaks in the ENDOR spectrum collected at g_zz = 2.45 indicates that the two nitrogen nuclei contributing to the spectrum have identical hyperfine couplings in the direction of the z_g axis, known to be almost parallel to the long Cu-N_axial bond. For nitrogen atoms, we expect an approximately axial tensor, where the axis of the largest principal value (z_A) points toward copper and the majority of the spin density. In this case, only the two basal nitrogen atoms (N_1basal and N_2basal in Figure 1) will have equivalent hyperfine coupling in the z_g direction and are assigned as the source of these ¹⁴N features. Using this definition of the hyperfine tensor frames (details in Experimental section) and the values for A listed above in an initial simulation, the hyperfine couplings were adjusted to the final values (29, 29, 41) MHz and (30, 30, 35) MHz for N_1basal and N_2basal, respectively, to achieve the simulation in Figure 5B (parameters in Table S1D). From the DFT calculations, quadrupole couplings are expected to be small (see Table S1E) and were not included in the simulation.

The majority of the ¹⁴N hyperfine coupling comes from spin density in the 2s and 2p orbitals of the nitrogen atom of interest. Following Morton and Preston³⁰, one can calculate 2s orbital spin populations from the isotropic hyperfine couplings A_iso = 33 and 32 MHz for N_1basal and N_2basal, respectively. Similarly, one can use the dipolar values of the coupling (A_zz = 41 and 35 MHz and A_xx,yy = 29 and 30 MHz for N_1basal and N_2basal, respectively) to compute the 2p spin population (details in SI Section 1.f). The result yields a 2s orbital spin population of 0.02 for each nitrogen and 2p spin populations of 0.07 and 0.03 producing total spin populations of 0.09 (9 %) and 0.05 (5 %) on N_1basal and N_2basal, respectively. Contributions to the ¹⁴N hyperfine tensors due to dipolar coupling between nitrogen and spin population on other atoms (Cu, O, other N) were determined to be negligible (< 1 MHz) using the point-dipole approximation. In addition, we observed weak modulations in an ESEEM experiment (see SI section 1.g, Figure S7) that are likely due to the axial nitrogen. Since hyperfine coupling and spin population on the axial nitrogen are expected to be weak based on DFT calculations (A_iso < 1 MHz), this was not considered in the distributed point dipole approximation.

III. Electronic spectroscopy

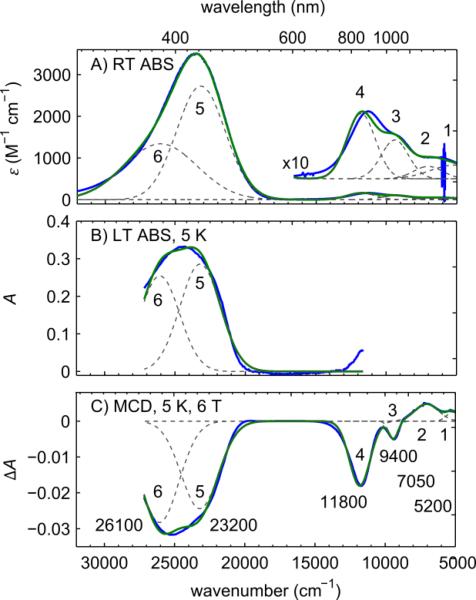
With a combination of room temperature electronic absorption (RT ABS),²¹ low temperature electronic absorption (LT ABS), and MCD spectroscopy, we resolved the near-UV and near-IR electronic transitions of Cu^II-O(TFE) (Figure 6). The RT ABS spectrum (Figure 6A) shows an intense near-UV transition at 24000 cm⁻¹ (ε > 3000 M⁻¹ cm⁻¹) which is not present in the precursor Tp^tBuCu^II(OTf).²¹ Additional weak near-IR features (ε < 300 M⁻¹ cm⁻¹) are seen below 13000 cm⁻¹. In the MCD spectrum (Figure 6C), two transitions underlying the near-UV transition become distinguishable. The near-IR features in the MCD spectrum are resolved into four distinct features which grow in intensity relative to the near-UV features.

Figure 6.

Optical spectra resolving six transitions in the near-IR and near-UV; bands 1-4 are copper based d → d_x²–y² transitions, bands 5-6 are O(TFE) → Cu d_x²–y² transitions. A) Room temperature UV-Vis and near-IR absorption spectrum of Cu^II-O(TFE) in DCM (from ref. 21). B) Electronic absorption of a thin film of Cu^II-O(TFE) collected simultaneously with MCD spectrum at 5 K and 0 T. C) MCD spectrum of a thin film of Cu^II-O(TFE) acquired at 5 K and 6 T. Individual fitted Gaussian resolved bands are shown as dashed gray lines, the total fit in green, and experimental data in blue. The λ_max of transitions 1-6 are labeled in the MCD spectrum.

Based on the resolution of the MCD spectrum we chose to model our electronic transitions as six Gaussian bands (see dashed lines in Figure 6) where each band consists of a peak center (transition energy), width, and integrated intensity. To constrain the simultaneous Gaussian fit of our model, we assumed the energy of the transitions did not change between the RT ABS, LT ABS, and MCD spectra, but allowed the width and integrated intensity of each band to vary freely. The near-IR bands 1-4 of the RT ABS and MCD spectra were simultaneously fit. In the LT ABS spectrum (Figure 6B), these features were detected with substantial noise and were not considered in the fit. Separately, the near-UV bands 5-6 of the RT ABS, LT ABS, and MCD spectra were simultaneously fit. Fitting parameters are summarized in Table S2. We found λ_max at 5200 cm⁻¹, 7050 cm⁻¹, 9400 cm⁻¹, 11800 cm⁻¹, 23200 cm⁻¹, and 26100 cm⁻¹ for bands 1-6, respectively. Significant figures in the near-IR region are based on a less than 100 cm⁻¹ measurement step size below 12500 cm⁻¹ and a less than 50 cm⁻¹ step size below 8000 cm⁻¹. Significant figures in the near-UV region are based on a less than 200 cm⁻¹ measurement step size.

Several factors allow assignment of bands 1-4 as d → d in character and bands 5-6 as trifluoroethoxide to copper charge transfer (CT) in character. First, bands 1-4 in the RT ABS are low intensity (ε < 300 M⁻¹ cm⁻¹) compared to bands 5-6. In transition metal complexes with incompletely filled d orbitals, low intensity features are usually the electric dipole forbidden d → d transitions. In contrast, the high intensity bands 5-6 are likely electric dipole allowed transitions such as from a ligand p orbital to a copper d orbital. Next, the relative intensities of the features in the RT ABS and MCD spectra suggest the near-IR transitions are predominantly d → d in character.^31,32 As shown in Figure S8, the intensity of all transitions in the MCD spectrum are temperature dependent indicating they are all C-term features. In low-symmetry sites, where all the electronic states are expected to be non-degenerate, C-term intensity is driven by spin-orbit coupling. The spin-orbit coupling is larger for copper than the ligand atoms (ξ_Cu = 830 cm₋₁, ξ_O,N ≈ 150, 76 cm⁻¹ for the free ions).²⁹ The magnitudes of intensities of copper-based d → d transitions are expected to increase relative to CT transitions when going from the RT ABS to the MCD spectrum. The ratio C₀/D₀ is commonly used to make this comparison between the C-term intensity (MCD), C₀, and the dipole transition strength (RT ABS), D₀, for each band.^33–35 Here, we use peak intensity maxima from the Gaussian fits to approximate C₀/D₀ ratios as MCD/ RT ABS ratios for bands 1-6. The MCD/ RT ABS ratios are larger in magnitude for bands 1-4 (MCD/ RT ABS = 0.076·10⁻³, 0.16·10⁻³, −0.053·10⁻³, and −0.12·10⁻³ respectively) compared to bands 5-6 (MCD/ RT ABS = −0.009·10⁻³ and −0.02·10⁻³ respectively) which supports the assignment of the low energy peaks as transitions within the d manifold.

Finally, the presence of the CT transition in Cu^IIO(TFE) but not in the precursor Tp^tBuCu^II(OTf) suggests the trifluoroethoxide ligand as the donor primarily responsible for bands 5-6 and the red color of Cu^II-O(TFE). Bands 5 and 6 are rationalized as transitions from two lone-pair orbitals O(TFE) p_π and O(TFE) p_~σ, named for their π and σ bonding orientation relative to the Cu-O bond, respectively. The σ bond to copper is expected to be stabilized in energy relative to the π bond to copper, making O(TFE) p_~σ → Cu d_x²–y² the higher energy transition, band 6. Additionally, we calculate the experimental oscillator strength f_exp = 4.61 × 10⁻⁹∈_maxν_1/2 from the RT ABS maximum ∈_max and the full width at half maximum ν_1/2 using the Gaussian fit parameters for bands 5-6 in Table S2. The oscillator strength of these transitions (f ∝ |〈ψ_i|μ|ψ_f〉|²) roughly correlates with the overlap of the donor orbitals (O(TFE) p_π and O(TFE) p_~σ) and acceptor orbital Cu d_x²–y²in the charge transfer transition and is used in the discussion section below.³⁶

Bands 1-4 are due to transitions from the four fully occupied copper-based d orbitals to the singly occupied copper based d_x²–y² orbital. We can assign the identity of each transition based on the literature assignments for Cu^II compounds in distorted tetrahedral environments. From lowest to highest energy (bands 1-4) the assignments are usually d_Z² → d_x²–y², d_xy → d_x²–y², d_yz+xz → d_x²–y², and d_yz–xz → d_x²–y².^33–35,37 The transitions have a +, +, −, − sign pattern in the MCD spectrum (Figure 6C). However, typically these transitions for Cu^II compounds in distorted tetrahedral ligand fields show a +, −, +, − sign pattern.

It is possible to fit the MCD spectrum with five Gaussian bands resulting in λ_max at 5100, 7100, 9500, 10500, and 11500 cm⁻¹ and the sign pattern +, +, −, +, − (Figure S10, Table S3). In this case the transitions are assigned as d_z² → d_x²–y², N(Pz) → d_x²–y², d_xy → d_x²–y², d_yz+xz → d_x²–y², and d_yz−xz → d_x²–y² with the sign pattern for the ligand field transitions consistent with the literature. The N(Pz) → d_x²–y² transition has been observed before in a similar Cu^II-thiolate complex.³³ However, we would expect a dipole allowed N(Pz) → d_x²–y² CT transition to have increased intensity in the RT ABS, which is not observed for Cu^II-O(TFE). The discrepancy in the signs of the MCD transitions compared to previous literature leaves the assignment of the ligand field transitions somewhat ambiguous. The implications of this for the electronic structure analysis are discussed below.

IV. Resonance Raman

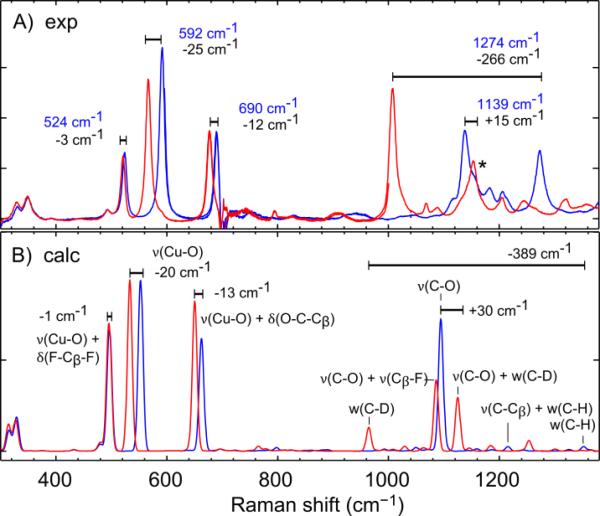
To further support the assignment of the LMCT transition, we performed resonance Raman (rR) spectroscopy on Cu^II-O(TFE) and the isotopically labeled Cu^IIO(TFE)-d₂ (deuteration only on the trifluoroethoxide ligand). Spectra were recorded with an incident wavelength of 426 nm (23474 cm⁻¹). In Cu^II-O(TFE), three low-energy peaks at 524, 592, and 690 cm⁻¹ and two high energy peaks at 1139 and 1274 cm⁻¹ were observed (Figure 7A, Table S4A). In Cu^IIO(TFE)-d₂, the three low energy peaks down-shifted to 521, 567, and 678 cm⁻¹, and two high energy peaks at 1008 and 1154 cm⁻¹ were observed. In both Cu^II-O(TFE) and Cu^IIO(TFE)-d₂ low intensity features are also observed at very low energies < 400 cm⁻¹ and are not affected by deuteration of O(TFE). The most intense features in the rR spectrum are all affected by deuteration of O(TFE), supporting assignment of the electronic transition at 23200 cm⁻¹ as an O(TFE) → Cu d_x²–y² CT. As such we expect the observed frequencies to correspond to normal modes involving displacement of copper and the trifluoroethoxide ligand.

Figure 7.

A) Room temperature resonance Raman spectra of Cu^IIO(TFE) (blue) and Cu^II-O(TFE)-d₂ (red) in DCM with an incident wavelength of 426 nm, exciting the O(TFE) → Cu d_x²−y² transition. Vibrational frequencies of Cu^II-O(TFE) are labeled in blue and the shifts upon isotopic labeling are listed in black. The peak in Cu^II-O(TFE)-d₂ that lies under a DCM solvent peak is labeled with a star. B) Calculated resonance Raman spectra of the optimized structure of Cu^II-O(TFE) (blue) and Cu^II-O(TFE)-d₂ (red). The dominant motions associated with each normal mode are labeled. Shifts upon isotopic labeling are listed for normal modes that closely correspond in Cu^II-O(TFE) and Cu^II-O(TFE)-d₂.

First, we will assign the three low-energy features from 500 to 700 cm⁻¹. These likely involve the heaviest atoms which indicates that these bands are ν(Cu-O) in character. The peak at 592 cm⁻¹ is the most intense indicating it has the most ν(Cu-O) stretch character of the three since these two atoms are involved in the CT. It is also substantially shifted by deuteration (−25 cm⁻¹) indicating movement of the oxygen atom may drag along the C_α-H₂ group. The lowest-frequency and least intense peak at 524 cm⁻¹ is also least effected by deuteration, shifting only −3 cm⁻¹. It likely has substantial movement of the heaviest fluorine atoms, furthest from the Cu-O bond, indicating distortions of C_β-F₃. The peak at 690 cm⁻¹ involves an intermediate amount of ν(Cu-O) character. However, it is also substantially shifted by deuteration (−12 cm⁻¹), indicating movement of the C_α-H₂ group. The peak at 592 cm⁻¹ with the most ν(Cu-O) stretch character constitutes one of the few known Cu^II-alkoxide stretch frequencies.

In support of our interpretation, we note Cu^II proteins and small molecule complexes in similar distorted tetrahedral environments exhibit similarly complicated Cu-ligand stretching patterns. Plastocyanin, a type 1 blue copper protein, has multiple Cu-S stretching frequencies between 350 and 500 cm⁻¹.^38–40 The five-coordinate thiolate-bound green and red copper sites in nitrite reductase, nitrosocyanin, and BSco exhibit multiple Cu-S frequencies between 340-450 cm⁻¹, 300-350 cm⁻¹, and 310-380 cm⁻¹ respectively.^26,28,41 Small molecules with similar pyrazolyl ligand scaffolds typically exhibit slightly simpler resonance Raman patterns. A type 1 blue copper mimetic molecule (HB(3,5-ipr₂pz)₃)Cu-SC(CH₃)₃ exhibits three frequencies at 348, 400, and 437 cm⁻¹ assigned as δ(C-C-S), δ(C-C-C), and ν(Cu-S), respectively.⁴² A Cu^II-alkylperoxo complex ((HB(3,5-ipr₂pz)₃)Cu-OOCMe₂Ph) exhibits a similar pattern with Raman shift frequencies at 536, 551, and 645 cm⁻¹ assigned as δ(C-C-O), δ(C-C-C), and ν(Cu-O), respectively.³⁴

Next, we will assign the features in the high-energy region above 1000 cm⁻¹, where we expect normal modes based on the O(TFE) ligand with little movement of the heavy copper atom. We suggest two interpretations of the data in this region. First, the peaks at 1139 cm⁻¹ and 1274 cm⁻¹ for Cu^II-O(TFE) can be assigned as dominantly ν(C-O) and w(C-H), respectively, based on the expected frequencies of these modes from IR and Raman spectroscopy (≈ 1090 cm⁻¹ for ν(C-O) and 1140-1400 cm⁻¹ for w(C-H)).⁴³ In Cu^II-O(TFE)-d₂, a w(C-D) is expected to appear at much lower frequency and is assigned as the peak at 1008 cm⁻¹. Deuteration of the αC-H is expected to slightly raise ν(C-O) (see calculations). We tentatively assign the low intensity peak at 1154 cm⁻¹ to ν(C-O); however, a DCM solvent peak appears at this frequency, which obscures the assignment.

In a second possible interpretation, the high-energy peaks in Cu^II-O(TFE) may be assigned as a Fermi resonance between a w(C-H) mode and the first overtone of the peak at 592 cm⁻¹ (expected to appear at 1184 cm⁻¹). The Fermi resonance red shifts the overtone peak by −45 cm⁻¹ so it appears at 1139 cm⁻¹. An equivalent blue shift of the w(C-H) up to 1274 cm⁻¹ means the true w(C-H) is expected to appear at ≈1229 cm⁻¹. In Cu^II-O(TFE)-d₂, a significant red shift of the w(C-D) would inactivate the Fermi resonance coupling and lead to one w(C-D) at 1008 cm⁻¹ with double the intensity of the peaks in Cu^II-O(TFE). DFT calculations (see below) support the first interpretation presented, but due to the solvent background, assignments remain uncertain.

Overall, our rR data confirm the assignment of the LMCT as predominantly O(TFE) p_π → Cu d_x²–y² in character. The main ν(Cu-O) stretch at 592 cm⁻¹ indicates that the Cu-O bond is softer than in a comparable Cu-peroxo compound with ν(Cu-O) of 645 cm⁻¹.

V. Quantum Chemistry

To support our analysis, we performed DFT and TDDFT calculations. An all-atom geometry optimization of Cu^II-O(TFE) was initiated from the geometry determined by X-ray crystallography.²¹ The atomic coordinates and most relevant structural features are compared in the supporting information (Section 5b, Figure S13). Between the crystal structure and the optimized geometry, the long Cu-N_axial bond (2.2270(11) vs. 2.26 (Å)), the Cu-O bond length (1.8324(10) vs. 1.87 (Å)), and the large Cu-O-C angle (135.48(9)° vs. 134°) were maintained, respectively. The optimized geometry was used in all further calculations.

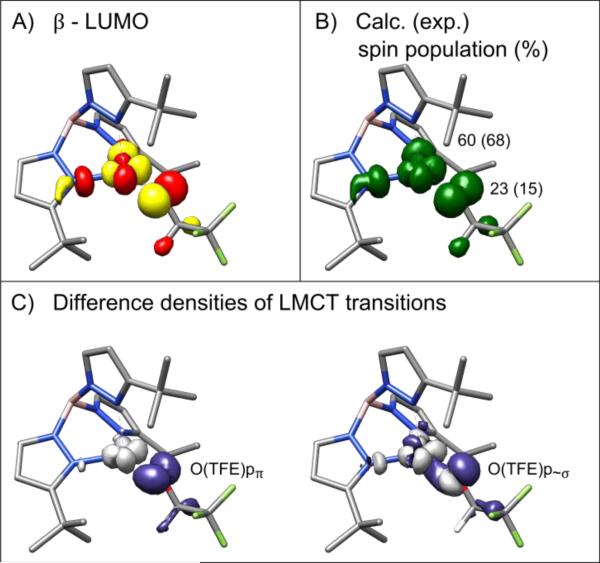
EPR property calculations support the interpretation of the experimental EPR data. Calculated Mulliken spin populations of ≈ 8 % on each of the two basal nitrogen atoms agree with the experimental spin populations derived from ¹⁴N ENDOR (σ_N1,N2 ≈ 9 %, 5 %). The hyperfine coupling values of the basal nitrogen atoms are in reasonable agreement with the values determined from simulation of the ¹⁴N ENDOR (compare Table S1D and S1E). However, the calculation predicts about 60 % spin population on copper and 23 % spin population on the trifluoroethoxide oxygen, which is larger than the experimental upper bound for σ_O of ≈ 10(3) % in a single crystal (≈ 15(3) % in solution). Also, DFT predicts hyperfine couplings for the trifluoroethoxide protons that are larger than observed. Overall, this suggests DFT over-delocalizes the spin density and overestimates the radical character on the trifluoroethoxide ligand. The DFT-predicted copper hyperfine coupling and g values are in poor agreement with experiment. Correct modeling of the electron correlation and the covalency of Cu^II-ligand bonds is essential for accurate g shift predictions. Multiple approaches have been used to improve EPR property calculations in related systems, although these were not pursued here.^44,45

DFT calculations support the assignment of the experimental rR shifts. Calculations were performed on Cu^IIO(TFE) and Cu^II-O(TFE)-d₂. Calculation of resonant enhancement of vibrational modes predicts three vibrations enhanced between 400 and 700 cm⁻¹ (Figure 7B, Table S4A). Dominantly, the modes are ν(Cu-O) + δ(F-C_β-F), ν(Cu-O), and ν(Cu-O) + δ(O-C-C_β) at 497, 553, and 663 cm⁻¹. In Cu^IIO(TFE)-d₂, three peaks with nearly identical normal modes are down shifted by −1, −20, and −13 cm⁻¹, respectively. This is in reasonable agreement with the experimental isotopic shifts of −3, −25, and −12 cm⁻¹ allowing more definitive assignment of the rough experimental mode assignments described above.

To higher energy, the rR calculation for Cu^II-O(TFE) predicts enhancement of a nearly pure ν(C-O) at 1094 cm⁻¹. The calculation for Cu^II-O(TFE)-d₂ predicts enhancement of two vibrational modes involving ν(C-O); ν(C-O) + ν(C_β-F) at 1086 cm⁻¹ and ν(C-O) + w(C-D) at 1125 cm⁻¹. The latter is isotopically shifted +30 cm⁻¹ from the calculated ν(C-O) for Cu^II-O(TFE). This is in reasonable agreement with the experimental isotopic shift of +15 cm⁻¹ for the features at 1139 cm⁻¹ and 1154 cm⁻¹ in Cu^II-O(TFE) and Cu^II-O(TFE)-d₂, respectively.

The experimental feature we assign as w(C-H) at 1274 cm⁻¹ in Cu^II-O(TFE) is not enhanced in the calculation. A numerical Raman calculation for Cu^II-O(TFE) (SI section 3.c) predicts that a ν(C-C_β) + w(C-H) mode at 1217 cm⁻¹ and a w(C-H) mode at 1359 cm⁻¹ will have Raman activity (appearing unenhanced at 1215 and 1353 cm⁻¹ in the analytical rR calculation). However, the calculation for Cu^II-O(TFE)-d₂ does predict enhancement of the w(C-D) mode at 964 cm⁻¹, isotopically shifted by −251 cm⁻¹ and −389 cm⁻¹ from the ν(CC _β) + w(C-H) and w(C-H) in Cu^II-O(TFE), respectively. The former is in closer agreement with the experimental isotopic shift of −266 cm⁻¹ from 1274 to 1008 cm⁻¹. Given this similar isotopic red shift between calculation and experiment, these experimental modes likely involve a w(C-H) and w(C-D), respectively.

Figure 8 shows a selection of DFT-calculated molecular orbitals, spin populations and transition difference densities. The β-LUMO (Figure 8A) and the spin density distribution (Figure 8B) support our selection of nuclei used in the distributed point-dipole approximation. As will be discussed below, the calculated β-LUMO also supports the orientation of the d_x²–y² orbital such that the lobes are nearly bisected by the Cu-O(TFE) bond. In Figure 8C, the TDDFT-predicted transition difference densities are shown for two O(TFE) p → Cu d_x²–y² transitions that make up the intense near-UV absorption band. The calculation incorrectly predicted the energy order of these two transitions so the images are used only to illustrate the orientation of the O(TFE) p orbitals as discussed below (TD-DFT discussion in SI section 5.a).

Figure 8.

DFT-predicted electronic structure. A) Ground state β-LUMO isosurface contoured at ±0.05 $a_0^{-3∕2}$. B) The spin population isosurface contoured at ±0.0025 $a_0^{-3}$. The calculation (UKS/B3LYP/EPR-II) predicts 60 % spin population on copper and 23 % spin population on oxygen in contrast to the experimentally determined spin populations of ≥ 68 % and ≤ 15 %, respectively. C) The isosurfaces of the difference density of the O(TFE) p_π → Cu d_x²−y² transition and the O(TFE) p_~σ → Cu d_x²−y² transition contoured at ±0.005 $a_0^{-3∕2}$. Purple represents the donor state and gray the acceptor state. The transitions demonstrate the π and σ interactions, respectively, in the Cu-O bond. Note that C) is for illustrative purposes only, as the TDDFT calculation incorrectly predicted the relative order in energy of the two transitions (details in SI).

Discussion

With our spectroscopic results, we characterized the electronic structure of this Cu^II-alkoxide complex. Below we examine the ligand field equations for a d⁹ transition metal in a d_x²–y² ground state to ascertain the physical origin of the unique EPR parameters. To understand the spectroscopic features engendered by the trifluoroethoxide ligand, we will compare the Cu^II-alkoxide to well-characterized small molecule Cu^II-thiolate (Cu^II-SR) and Cu^II-alkylperoxo (Cu^II-OOR) complexes in nearly identical geometries (see Table S5 for structural comparison).^46,47 These complexes exhibit similar EPR spectra, in particular the small ^CuA_zz hyperfine coupling. However, in contrast to the near-UV LMCT transition of Cu^II-O(TFE), the LMCT transitions (from thiolate and alkylperoxo ligand donors) in both of these complexes are in the near-IR region, which imparts a blue color to the compounds (see Tables 1 and S6 for spectroscopic comparison).^33,34,42 We will also compare the Cu^II-O(TFE) to the biological type 1 blue copper sites, type 2 red copper sites, and galactose oxidase (GAO). Finally, we will address the implications of the electronic structure of the Cu^II-alkoxide on alcohol oxidation.

Table 1.

Spectroscopic comparison of Cu^II-alkoxide, Cu^II-alkylperoxo,³⁴ and Cu^II-thiolate³³

	gzz (≈ g∥)	Ex2-y2 – Exy (cm−1)	% spin on Cua	|CuAzz| (×104 cm−1)	f~σ,exp/fπ,exp (CT donor → Cu dx2-y2)
Cu-O(TFE)	2.44	7050	68b (60)	40	0.735
Cu-OOR34	2.316	8050	62c (52)	55	0.161
Cu-SR33	2.23	9250	36d (34)	74	0.003

^aIn parentheses are results from a DFT/B3LYP calculations for Cu-OR, Cu-OOR, and Cu-SR using the Mulliken spin population, spin density and copper character in the ground state, respectively.

^bExperimental from distributed point dipole approximation using hyperfine coupling of remote nuclei.

^cExperimental from EPR g values and INDO/S-CI calculations.

^dExperimental from Cu-L edge XAS results.

I. Comparison of Cu^II-O(TFE), Cu^II-OOR, and Cu^II-SR

I. A. Large g_zz and NIR MCD transitions

The origins of the unusually large g_zz in Cu^II-O(TFE) can be rationalized via a ligand field theory argument for a d⁹ transition metal in the d_x²–y² ground state.²⁹ Assuming the simplified case of an axial g tensor, the g_zz = g_∥ value can be approximated as

$$\Delta g_{\parallel }=g_{\parallel }-g_{\mathrm{e}}=8{\zeta }_{\mathrm{Cu}}\frac{{\alpha }_{x^2-y^2}^2{\alpha }_{xy}^2}{E_{x^2-y^2}-E_{xy}}=\frac{C}{\Delta E_{\perp }}.$$ (3)

Here ζ_Cu is the one-electron spin-orbit coupling constant (830 cm⁻¹ for the free Cu^II ion). The coefficients α_x²–y² and α_xy quantify the d_x²–y² and d_xy character of the ground state and excited state, respectively. Larger α indicates increased d orbital character. ΔE_⊥ = E_x²–y² − E_xy is the transition energy for promoting one electron from the doubly occupied d_xy Cu-based molecular orbital (MO) to the d_x²–y² Cu-based singly occupied MO (SOMO).

ΔE_⊥ can be estimated from Eq. 3 by comparison to the alkylperoxo complex, Cu^II-OOR, using

$$\Delta E_{\perp ,\mathrm{CuOR}}=\Delta E_{\perp \mathrm{CuOOR}}\frac{C_{\mathrm{CuOR}}}{C_{\mathrm{CuOOR}}}\frac{\Delta g_{\parallel ,\mathrm{CuOOR}}}{\Delta g_{\parallel ,\mathrm{CuOR}}}$$ (4)

with Δg_∥,CuOOR = 0.316 and ΔE_⊥,CuOOR = 8050 cm⁻¹ (Table 1)³⁴ and Δg_∥,CuOR = 0.437. As ground-state DFT (B3LYP) predicts more spin population on copper in Cu^II-O(TFE) (60 %) versus Cu^II-OOR (52 %),³⁴ we expect increased copper character in the ground state and necessarily larger α_x²–y² in the Cu^II-alkoxide, and therefore C_CuOR/C_CuOOR > 1. With this, Eq. 4 yields ΔE_⊥,CuOR > 5821 cm⁻¹, and we can assign the peak at 7050 cm⁻¹ (band 2 in Figure 6C) to the d_xy → d_x²–y² transition. We assign the other three transitions in the near-IR region based on the expected energy order of the d orbitals in a distorted tetrahedral environment. Namely, we support the four-Gaussian model described in the Results section and assign band 1 (5200 cm⁻¹) to d_z² → d_x²–y², band 3 (9400 cm⁻¹) to d_yz/xz → d_x²–y², and band 4 (11800 cm⁻¹) to d_yz/xz → d_x²–y². As noted above, the signs of the MCD transitions differ from expectations based on the literature, but predicting signs can be challenging.^31,32 The small transition energy E_x²–y² − E_xy is the principal reason for the large g_zz.

I. B. Small ^CuA_zz

The hyperfine coupling can be derived from ligand field theory assuming a simplified axial hyperfine tensor with ^CuA_zz = A_∥ where

$$A_{\parallel }=P_{\mathrm{d}}\left[-\kappa {\alpha }_{x^2-y^2}^2-\frac{4}{7}{\alpha }_{x^2-y^2}^2+\frac{3}{7}(g_{\perp }-g_{\mathrm{e}})+(g_{\parallel }-g_{\mathrm{e}})\right].$$ (5)

P_d is a quasiatomic parameter that depends on the nucleus and is typically given the value ≈ 400·10⁻⁴ cm⁻¹ for copper. κ is a unitless parameter which represents the isotropic hyperfine coupling of the copper nucleus with a typical upper bound value of 0.43.²⁹

The difference in sign of terms one and two compared to terms three and four in Eq. 5 means a small A_∥ can be a result of cancellation of terms. Noting that g_⊥ ≈ 2.09 in both Cu^II-O(TFE) and Cu^II-OOR, one can simplify Eq. 5 to A_∥ = P_d(−C + Δg_∥) and estimate a parameter C_CuOOR for Cu^II-OOR from the literature Δg_∥ value (Table 1). Using C_CuOR ≈ C_CuOOR, this predicts copper hyperfine coupling for Cu^II-O(TFE) of A_∥,CuOR ≈ P_d(−C_CuOOR + Δg_∥,CuOR,) ≈ 80·10⁻ cm ¹, very close to the experimental value of 40·10⁻⁴ cm⁻¹. This again implies C_CuOR/C_CuOOR > 1, which indicates larger α_x²–y² and increased copper character in the ground state of the alkoxide complex. This analysis depends on the sign of the hyperfine coupling being the same in both cases (here assumed positive). The small ^CuA_zz is a result of the large g_zz value (term 4 in Eq. 5, driven by the small transition energy E_x²–y² − E_xy) and the large spin population on copper (terms 1 and 2 in Eq. 5, driven by σ_Cu ≥ 68 %) canceling terms in Eq. 5.

I. C. Nature of the Cu-O(TFE) bond

From single crystal EPR, we found the LMCT acceptor orbital (d_x²–y²) is oriented such that the lobes are in a plane approximately perpendicular to the Cu-N_axial bond. From resonance Raman and MCD spectroscopies, we know that the LMCT transition in the room temperature absorption spectrum has two components at 26100 and 23200 cm⁻¹ originating from the donor O(TFE) p_~σ and O(TFE) p_π orbitals, respectively. The orientations of the pseudo- σ and π p orbitals with the Cu-O bond are illustrated by the transition difference densities in Figure 8C.

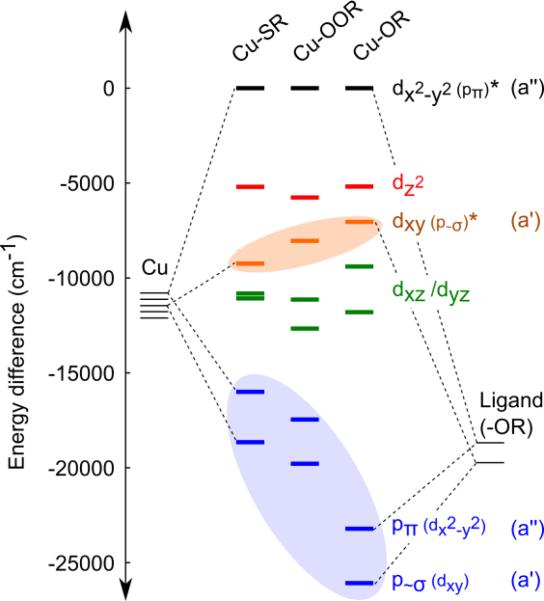
In the thiolate- and alkylperoxo-ligated Cu^II complexes, the LMCT transition is similarly comprised of two transitions from p orbitals. These are termed p_π and p_~σ in Cu^II-SR and π*_v and π*_σ in Cu^II-OOR due to their orientation with respect to the Cu-X(CT donor) bond.^33,34 The transition from the donor orbital with π orientation appears to lower energy and in both cases has a larger experimental oscillator strength than the transition from the donor orbital with σ orientation (see Table S6).^33,34 The larger intensity of the π transition relative to the pseudo-σ transition is rationalized as a rotation of the d_x²–y² acceptor orbital so that its lobes are bisected by the Cu-X bond. This allows for excellent overlap of the LMCT donor orbital with π orientation with the copper d_x²–y² acceptor orbital.

Similarly, in Cu^II-O(TFE), the oscillator strength of the lower-energy O(TFE) p_π → Cu d_x²–y² transition is larger (f_π,exp = 0.051) than for the O(TFE) p_~σ → Cu d_x²–y² transition (f_~σ,exp = 0.038, Table S2). This is evidence that the d_x²–y² orbital lies such that its lobes are bisected by the Cu-O bond (Figure 8A) and indicates a dominantly π bonding interaction. However, the ratios of the oscillator strengths f_~σ,exp/ f_π,exp for Cu^II-SR, Cu^II-OOR, and Cu^II-OR (0.003 < 0.161 < 0.735, respectively, Table 1) show an increase in the relative overlap of the p_~σ donor compared to the p_π donor with the Cu d_x²–y² acceptor. This ratio trend is due predominantly to a larger oscillator strength for the p_~σ → Cu d_x²–y² transition in Cu^II-O(TFE) (see Table S6).

The increase in relative intensity of the O(TFE) p_~σ → Cu d_x²–y² transition in Cu^II-O(TFE) may indicate increased σ bonding character compared to the Cu^II-alkylperoxo and Cu^II-thiolate. In a molecular orbital approach, we expect a bonding and antibonding combination of MOs to form between O(TFE) p_~σ and d_xy, where the bonding orbital is dominantly O(TFE) p_~σ and the antibonding is dominantly d_xy. The π bond results in an analogous set of bonding and anti-bonding MOs formed between O(TFE) p_π and d_x²–y² (see Figure 9). The bonding MO formed by the O(TFE) p_~σ /d_xy interaction will have increased metal character as the σ bonding interaction becomes stronger. An increase in metal character of the O(TFE) p_~σ donor orbital will increase overlap with the acceptor d_x²–y² orbital and result in the large integrated area of the O(TFE) p_~σ → Cu d_x²–y² transition that we observed in this work.

Figure 9.

An MO diagram based on experimentally determined transition energies for thiolate (Cu-SR), peroxo (Cu-OOR), and alkoxide (Cu-OR) ligated Cu^II complexes. Highlighted orbitals indicate major affectors of spectroscopic trends: 1) in orange, an increase in σ character of the Cu-OR bond drives the energy of the dominantly Cu d_xy orbital closer to the dominantly Cu d_x²–y² orbital; this small difference in energy results in a larger shift in g_zz, 2) in blue, p orbitals donors from the trifluoroethoxide ligand have a large ionization energy resulting in a near-UV LMCT that gives Cu^II-O(TFE) its red color; in Cu-SR and Cu-OOR, these donor orbitals are higher in energy (discussed in the text) resulting in the blue color. The singly occupied Cu d_x²–y² orbitals were set to zero and the vertical placement of each donor orbital reflects its experimental transition energy (data from ref. 33, 34 and this work). The ligand and copper orbital energies before bonding are illustrative only. Orbital symmetry is indicated for the C_s point group.

An increase in the σ bonding interaction would also raise the energy of the d_xy antibonding orbital closer to the d_x²–y² antibonding orbital, as illustrated in Figure 9. This is consistent with the small transition energy E_x²–y² − E_xy that drives the large shift in g_zz for Cu^II-O(TFE) (relative to g_zz = 2.21 and 2.316 for Cu^II-SR and Cu^II-OOR, respectively).

I. D. Origin of near-UV charge transfer

The red color (LMCT at 420 nm, 23800 cm⁻¹) of the Cu^II-alkoxide is notably different from the blue color of Cu^II-alkylperoxo and Cu^II-thiolate complexes (LMCT at 600 nm, 16600 cm⁻¹). This is a consequence of the nature of the trifluoroethoxide CT donor. The increased transition energy for an alkoxide donor is expected based on the increase in ionization energy for an alcohol compared to a alkylperoxide or thiol (10.48 > 9.36 > 9.31 eV for ethanol, n-butylperoxide, and ethanethiol, respectively).⁴⁸ The increased ionization energy for alcohols compared to peroxides comes in part from the nature of the molecular orbitals formed between the O-C_α bond in an alkoxide versus the O-O bond in a peroxide. The highest occupied MOs in an alkoxide are oxygen non-bonding orbitals, whereas in an alkylperoxo, they are destabilized π* antibonding orbitals.³⁴ In addition, the trifluoromethyl group is strongly electron withdrawing, further increasing the ionization energy of the trifluoroethoxide ligand (11.49 eV for trifluoroethanol) compared to a non-halogenated alcohol.⁴⁹

II. Comparison with copper sites in biology

Cu^II-O(TFE) shares a small hyperfine coupling ^CuA_zz with some members of the family of type 1 blue copper proteins. The type 1 blue copper site in plastocyanin (extensively reviewed by Solomon²⁵) is a distorted tetrahedral Cu^II site in a d_x²–y² ground state, which leads to an axial EPR spectrum. Plastocyanin is often described as possessing a uniquely small ^CuA_zz hyperfine coupling (g_zz = 2.23, ^CuA_zz = 63 · 10⁻⁴ cm⁻¹) compared to type 2 or “normal” copper sites such as D_4h [CuCl₄]²⁻ (g_zz = 2.22, ^CuA_zz = 164 · 10⁻⁴ cm⁻¹). A highly covalent Cu-S(Cys) bond decreases the spin density on the copper nucleus and leads to small ^CuA_zz hyperfine coupling (decrease of terms 1 and 2 in Eq. 5). In contrast, in Cu^II-O(TFE) we have found significant spin density on the copper nucleus of ≈ 68 %. The resulting increase in magnitude of the contact and spin-dipolar contributions (terms 1 and 2) to the hyperfine coupling is offset by the increased g_zz-dependent orbital contribution (term 4) of opposite sign, which is due to the small transition energy E_x²–y² – E_xy. Overall, this cancellation of terms in Eq. 5 drives the small ^CuA_zz.

Cu^II-O(TFE) shares the near-UV transitions of red copper sites such as those in the proteins nitrosocyanin and BSco (a cytochrome c oxidase assembly protein).^26,28 The copper sites in these proteins are five-coordinate and contain thiolate ligands which are the LMCT donors (S(Cys) p_σ and S(Cys) p_π). The increased copper coordination number (relative to type 1 blue copper) raises the energy of the d orbital manifold and shifts the LMCT transitions to the near-UV region, giving the proteins a distinct red color. In addition, the higher energy S(Cys) p_σ → Cu^II d_x²–y² transition is more intense, indicating that the lobes of the Cu^II d_x²–y² orbital lie along the Cu-S bond and that the bonding interaction is dominantly σ in character.^26,28 These five-coordinate red copper proteins generally have type 2 copper EPR spectra (large ^CuA_zz > 100 · 10⁻⁴ cm⁻¹ and g_zz ≈ 2.2 > g_yy ≈ g_xx) also indicative of a d_x²–y² ground state. Although Cu^II-O(TFE) shares the red color of nitrosocyanin and BSco, it is four-coordinate and the alkoxide ligand exhibits both π and σ bonding. The red color in Cu^II-O(TFE) is dominantly due to a less electron rich LMCT donor (oxygen compared to sulfur) containing a strongly electron withdrawing trifluoromethyl group.

Despite being a rough structural model for the Cu^II-alkoxide intermediate suggested in GAO, there are obvious differences in what is known of the electronic structures. The complete electronic structure of GAO when bound to the alkoxide substrate remains elusive due to the difficulty in trapping mechanistic intermediates.⁶ A catalytically inactive form of the enzyme (Cu^II bound to the reduced 3′-(S-cysteinyl)tyrosine residue) shows a type 2 copper EPR spectrum with g_zz value of ≈ 2.22 and large ^CuA_zz hyperfine coupling of ≈ 160 · 10⁻⁴ cm⁻¹ and near-UV charge transfer transition⁹ (indicative of Cu^II in a square planar environment, similar to red copper proteins described above). This indicates the open coordination site would support a dominantly sigma bonding interaction. We have shown that despite possessing a type 1 geometry (where covalent π bonding is expected), the alkoxide ligand imparts unique electronic structure with increased σ bonding to Cu^II-O(TFE). The nature of the suggested Cu^II-alkoxide bond in GAO still remains to be elucidated.

III. Implications for Alcohol Oxidation

We observe an increase in copper character in the ground state (≈ 68 % spin density on copper), indicating a more ionic Cu-O bond in Cu^IIO(TFE), relative to the comparable Cu^II-alkylperoxo (≈ 62 % spin density on copper)³⁴ and Cu^II-thiolate complexes (≈ 40 % spin density on copper).^33,50 The αC-H bond strength of an alcohol is known to depend on the hydroxyl group protonation state. It has been predicted that with ionic counter ions, such as Na⁺ and K⁺, the αC-H bonds in methanol are weakened from ≈ 91 kcal/mol to ≈ 81 kcal/mol and ≈ 79 kcal/mol, respectively.⁸ Similarly, the αC-D stretching frequency (which is roughly proportional to bond strength⁵¹) in trifluoroethanol-d₂ has been observed to decrease upon deprotonation with NaOH.⁵² We expect the ionic interaction between Cu^II and the trifluoroethoxide in Cu^II-O(TFE) to weaken the αC-H bond strength based on these findings from the literature. However, in a separate reactivity study, it was found that oxidation of the O(TFE) ligand with external oxyl radical hydrogen atom acceptors is not facile, indicating that the activation of the αC-H bond is not significant enough to promote bond cleavage in this system.²¹

Conclusion

In this study we have characterized in detail the electronic structure of a Cu^II-alkoxide complex as a model structural intermediate in copper catalyzed alcohol oxidation. EPR spectra reveal the orientation of the d_x²–y² SOMO with lobes bisected by the Cu-O bond. MCD and resonance Raman spectra show the donor in the LMCT transition is dominantly the O(TFE) ligand. The increased contribution from the O(TFE) p_~σ donor in the LMCT transition indicates both σ and π bonding interactions are present, relative to Cu^II-thiolate and Cu^II-alkylperoxo bonds. This increased ratio of σ/π bonding character reduces the energy of the d_xy → d_x²–y² transition. This small transition energy drives a large shift in g_zz and, together with small spin delocalization, contributes to the small hyperfine coupling ^CuA_zz. Single-crystal and solution ENDOR spectra, analyzed using a distributed point-dipole model, suggest the unpaired electron is highly localized on the copper atom with ≤ 15 % spin density on oxygen of the alkoxide ligand. A ligand field analysis using EPR and MCD data indicates substantial copper character in the ground state SOMO relative to related Cu^II-alkylperoxo and Cu^II-thiolate systems in nearly identical pyrazolyl ligand scaffolds. However, this relatively ionic bond does not sufficiently modulate the αC-H bond to promote ligand oxidation.²¹ This model complex serves as one of the only Cu^II-alkoxide complexes spectroscopically characterized to this extent. This insight lays the basis for further elucidating the mechanism of Cu-mediated alcohol oxidations.

Experimental Section

Synthesis and Characterization

Tp^tBuCu^II(OCH₂CF₃) and Tp^tBuCu^II(OCD₂CF₃) were synthesized as previously described and the structure of Tp^tBuCu^II(OCH₂CF₃) was determined previously.²¹ Tp^tBuCu^II(OCD₂CF₃) was used to assign hyperfine couplings of the αC-H protons of the trifluoroethoxide ligand and to assign vibrational modes in the resonance Raman spectra. Tp^tBuZn^II(OCH₂CF₃) was prepared through an analogous synthetic route. Tp^tBuCu^II(OCH₂CF₃ and Tp^tBu Zn^II(OCH₂CF₃) crystalize in the same space group (P2₁/n) with nearly identical unit cell dimensions (see SI section 6.a). All samples for spectroscopy were prepared in a nitrogen filled glovebox using deoxygenated and water-free solvents.⁵³

Single-Crystal 34 GHz EPR and ENDOR

Single crystals of Tp^tBuZn^II-OCH₂CF₃ doped with Tp^tBuCu^II-OCH₂CF₃ were grown from a concentrated pentane solution containing a ≈1:99 ratio of Cu/Zn complexes at −30 °C. The exact percent of Cu incorporation was not determined.

A single crystal was loaded into a 1 mm O.D. quartz capillary EPR sample tube and sealed in place with vacuum grease. A goniometer was mounted on to the sample rod and EPR sample tubes were placed into a Bruker EleXsys E580 X/Q spectrometer such that the long axis of the capillary was perpendicular to the direction of the magnetic field. The sample was rotated around the capillary axis (sample rod axis) in 15° increments from 0° to 180°. The orientation of the crystal relative to this rotation axis was determined by X-ray crystallography after recording EPR and ENDOR data.

At each rotation increment, a pulse field-swept EPR spectrum and a Davies ENDOR spectrum were recorded. All single-crystal measurements were carried out in a Bruker EN 5107D2 resonator at ≈ 34 GHz held at 10 K with an Oxford CF935O liquid helium cryostat and ITC503S temperature controller. Pulse field-swept EPR spectra were FID detected following a 1 μs pulse. The Davies ENDOR spectra were Hahn echo detected (π – T – π/2 – τ – π – τ – echo) with pulse lengths and timings given in specific figure captions. During time T, the RF pulse was applied. Microwave frequencies were measured with the built-in frequency counter, and accurate magnetic field values were obtained using a teslameter.

The above was repeated for a second single crystal. Data are shown in the electronic supporting information (section 1).

Frozen solution 9.2 and 34 GHz EPR and ENDOR

The continuous-wave (CW) EPR spectrum at 9.2 GHz, reported previously, was recorded on a Bruker EMX spectrometer in an SHQE resonator at 120 K in a frozen glass of ≈ 3 mM Tp^tBuCu^II(OCH₂CF₃) in toluene.²¹ The field axis was corrected for a 0.5 mT difference between nominal and teslameter-determined field values.

For pulse field-swept 34 GHz EPR spectroscopy, a 1.5 mM solution of Tp^tBuCu^II(OCH₂CF₃) in 1:1 DCM:toluene was flash frozen in a 1 mm O.D. quartz EPR sample tube. Pulse field-swept and Davies ENDOR spectra were recorded in the same spectrometer and resonator as described above at 10 K. The field swept spectrum was Hahn echo detected (π/2 – τ – π – τ – echo). Davies ENDOR was echo detected (π – T – π/2 – τ – π – τ – echo) with pulse lengths and timings given in the figure captions. Microwave frequencies were measured with the built-in frequency counter. Magnetic field values were corrected for a 1.5 mT shift between nominal and teslameter-determined field values.

Electronic Absorption and Magnetic Circular Dichroism

The UV-Vis spectrum was acquired previously and recorded with a 2 nm step size.²¹ The near-IR/IR spectrum was collected using an Agilent Cary 5000 spectrophotometer with a 1 cm path length.

MCD samples were prepared by saturating a pentane:toluene (9:1) solution with Tp^tBuCu^II(OCH₂CF₃). To this, a drop of paratone oil was added to increase the viscosity. The solution was pipetted dropwise onto a quartz disk and the solvent was allowed to evaporate, creating a thin film. Several layers of Tp^tBuCu^II(OCH₂CF₃) were deposited in this way and the film then sandwiched with a second quartz disk. The thin film sample was briefly exposed to atmosphere while mounting into the MCD sample rod which was then placed in a liquid helium cooled variable temperature, superconducting magneto-optical cryostat (Cryo-Industries SMC-1659 OVT) with the sample compartment oriented in Faraday configuration. Absorption and MCD spectra were collected simultaneously using an Aviv 40 DS spectropolarimeter equipped with an additional InGaAs (Teledyne Judson) detector for detection down to 5000 cm⁻¹ (2000 nm). Variable temperature, variable field measurements were carried out at 5, 10, 20, and 40 K with the magnetic field varied from 0 to 6 T in 1 T steps at each temperature. Data was collected with a 2 nm step size from 370 to 860 nm and a 5 nm step size from 800 to 2000 nm. At 5 K, the sample was screened for depolarization by matching the CD spectra of a chiral molecule placed before and after the sample. Depolarization was less than 10 %. The differential absorption of the MCD experiment is defined as ΔA = A_L-A_R, where A_L and A_R refer to the absorption of left and right circularly polarized photons in the sign convention of Piepho and Schatz.⁵⁴

Spectra were modeled using a sum of Gaussians defined in the Matlab program. The models were simultaneously fit to the data (using the assumptions presented in the Results section) using the least-squares fitting algorithms implemented in EasySpin.⁵⁵

Resonance Raman

Resonance Raman samples were prepared by dissolving Tp^tBuCu^II(OCH₂CF₃) to an optical density of 2 at 420 nm (1.38 mM) in DCM. The same was done for the deuterated Tp^tBuCu^II-OCD₂CF₃. These solutions were deposited in 5 mm OD NMR tubes and sealed with electrical tape before removing from the inert atmosphere glovebox.

The 426 nm Raman excitation beam was obtained from the frequency-doubled output of a titanium-sapphire laser (16 ns pulse, 5 μJ/pulse) pumped by a Q-switched (1 kHz), intracavity frequency-doubled Nd:YLF laser (Photonics Industries International). Excitation light was focused through a spherical lens onto the surface of the spinning sample tube, and backscattered (135°) light was collected and collimated with a camera lens and focused with an second lens onto the 0.200 mm entrance slit of a 0.8 m spectrometer (Spex 1401) equipped with a liquid N₂-cooled charge-coupled device detector (Roper Scientific). A 430 nm-cutoff notch filter (angle tuned) was placed at the slit to minimize the spectral contribution of Rayleigh scattering. The samples showed no signs of photodegradation after 15 minutes of continual laser irradiation. Samples showed decay of rR signal and color after more than 5 hours out of the glove box (data not shown). Experimental data shown here were collected in less than 3 hours.

EPR Simulations

All EPR and ENDOR simulations were performed using Easyspin 5.0.⁵⁵ For simulation of EPR spectra, the various frames were defined as follows. For P2₁/n symmetry (space group 14), the crystal frame C (principal axes x_C, y_C, z_C) was defined with y_C along the crystal b axis, z_C along the crystal c axis, and x_C along the a* axis normal to the bc plane of the crystal. The laboratory frame L (x_L, y_L, z_L) was defined with z_L along the static field and y_L along the axis of single crystal rotation (sample tube long axis).

To determine the orientation of the crystal in the EPR spectrometer, X-ray diffraction was recorded for the single crystal within the EPR tube (identical instrument described in SI section 6). Using the previously solved crystal structure, the rotation axis of crystal sample 1 (presented in article) was found to be along the (0, −3, 4) crystal direction in abc coordinates with 3° accuracy. The rotation axis of crystal sample 2 (presented in SI) was found to be along the (−7, −4, 5) direction in abc coordinates with 2° accuracy.

The molecular frame M (principal axes x_M, y_M and z_M) was defined with z_M along the Cu-N_axial bond and y_M perpendicular to z_M within the N_axial-Cu-O plane such that it points in the direction of the Cu-O bond. The initial g tensor frame before least-squares fitting was taken as collinear with the molecular frame. The copper hyperfine frame was assumed to be collinear with the g frame in all simulations.

With the above frame definitions, the starting orientation (azimuthal angle φ), of the crystal in the laboratory x_Lz_L plane and the three Euler angles relating the g tensor frame to the molecular frame remained unknown, for a total of four variables. These variables were determined by least-squares fitting. In increments of 3°, φ was varied, follow by a simultaneous least squares fit of the Euler angles of all 13 spectra in Figure 2C using a grid search algorithm implemented in EasySpin. This same procedure was carried out for crystal 2 and yielded a nearly identical set of Euler angles relating the g frame to the molecular frame.

The frequency change of spectra in Figure 2C is due to a small repositioning of the sample along the laboratory y_L axis (perpendicular to the field) to optimize sensitivity. This frequency change is negligibly small, but was nevertheless accounted for in the simulations.

Simulations of single-crystal ¹H ENDOR spectra used the full hyperfine tensors (calculated using the point dipole approximation) and the full g tensor. The hyperfine frames are visualized in Figure S6B.

Hyperfine frames (x_A, y_A, z_A) for simulation of the ¹⁴N and ¹⁹F frozen-solution ENDOR spectra were defined using the crystal structure coordinates. For each nucleus, its z_A axis was defined as the unit vector pointing from the nucleus to the copper atom. x_A and y_A were defined in the plane perpendicular to z_A, pointing in arbitrary but perpendicular directions. The frames are visualized in Figure S6B.

Density Functional Theory

Unrestricted Kohn-Sham (UKS) density functional theory (DFT) calculations were performed with Orca 3.0.2 or 3.0.3.⁵⁶ Geometry optimization was initiated from the crystal structure coordinates.²¹ All atom positions were optimized using the BP86^57,58 functional, the Ahlrichs tzvp⁵⁹ basis set, with grid size of 4 and SCF convergence criteria of 1·10⁻⁸ E_h. Convergence thresholds for the geometry optimization were as follows: energy change 5·10⁻⁶ E_h, maximum gradient 3·10⁻⁴ E_h/a₀, RMS gradient 1·10⁻⁴ E_h/a₀, maximum displacement 4·10⁻³ a₀, and RMS displacement 2·10⁻³ a₀.

EPR property calculations of the optimized geometry used the hybrid B3LYP^60–62 functional and Barone's EPR-II basis set.⁶³ The copper atom was modeled with a specialized CP(PPP) basis set to model core polarization.^64,65

In preparation for resonance Raman calculations, time-dependent DFT calculations were carried out with the B3LYP functional, the tzvp basis set and a grid size of 5.⁵⁹ The auxiliary basis set tzvp/j was used for the RI approximation for hybrid functionals.^66–68 The first 30 excited states were calculated. As solvent models are not available for the resonance Raman calculations in Orca, no solvent model was used. Separate TDDFT calculations using the COSMO⁶⁹ model for dichloromethane showed little difference in the predicted excited states (data not shown). States 10 and 12 showed O(TFE) p_σ → Cu d_x²–y² and O(TFE) p_π → Cu d_x²–y² character, respectively, and were used to predict resonance enhancement of Raman modes.

To obtain a Hessian file for resonance Raman calculations, an analytical frequency calculation was performed using an identical level of theory as for the geometry optimization. Additionally the tzvp/j auxiliary basis set was used for the RI approximation. The SCF was converged to an energy change tolerance of 1·10⁻⁸ E_h. Resonance enhancements were predicted using the Hessian file from the analytical frequency calculation for excited states 10 and 12 using the same level of theory as for TDDFT calculations. A sample input block is provided in the electronic supplemental information (section 3.b). Resonance Raman calculations for the isotopic molecule Cu^II-O(TFE)-d₂ were calculated by manually editing the masses of the appropriate hydrogen atoms in the Hessian input file. The new vibrational frequencies for the isotopically labeled molecule were calculated using the standalone orca_vib program. This adjusted Hessian was used in the input block for resonance Raman calculations of Cu^II-O(TFE)-d₂. In both cases, the resonance Raman calculation produced .asa input files which were fed into the orca_asa program to produce resonance Raman spectra.⁷⁰

Normal modes were visualized using Avogadro (version 1.0.3).⁷¹ Molecular orbitals, spin density, and transition difference densities were visualized using UCSF Chimera (version 1.8).⁷²