Accelerating Chemical Exchange Saturation Transfer (CEST) MRI by Combining Compressed Sensing and Sensitivity Encoding Techniques

Abstract

Purpose

To evaluate the feasibility of accelerated chemical-exchange-saturation-transfer (CEST) imaging using a combination of compressed sensing (CS) and sensitivity encoding (SENSE) at 3 Tesla.

Methods

Two healthy volunteers and six high-grade glioma patients were recruited. Raw CEST image k-space data were acquired (with varied radiofrequency saturation power levels for the healthy volunteer study), and a sequential CS and SENSE reconstruction (CS-SENSE) was assessed. The MTR_asym(3.5ppm) signals were compared with varied CS-SENSE acceleration factors.

Results

In the healthy volunteer study, a CS-SENSE acceleration factor of R = 2×2 (CS × SENSE) was achieved without compromising the reconstructed MTR_asym(3.5ppm) image quality. The MTR_asym(3.5ppm) signals obtained from the CS-SENSE reconstruction with R = 2×2 were well preserved compared to the reference image (R = 2 for only SENSE). In the glioma patient study, the MTR_asym(3.5ppm) signals were significantly higher in the tumor region (Gd-enhancing tumor core) than in the normal-appearing white matter (p < 0.001). There was no significant MTR_asym(3.5ppm) difference between the reference image and CS-SENSE-reconstructed image in the acceleration factor of R = 2×2.

Conclusion

Combining the SENSE technique with CS (R = 2×2) enables considerable acceleration of CEST image acquisition and potentially has a wide range of clinical applications.

INTRODUCTION

Chemical exchange saturation transfer (CEST) imaging is a unique detection enhancement technique that enables the measurement of endogenous low-concentration biomolecules with water-exchangeable protons (1–3). The distinct CEST contrast based on this proton exchange mechanism plays an important role in molecular MRI. Amide proton transfer (APT) imaging, a variant of the CEST-based molecular MRI technique, is based on the chemical exchange between free bulk water protons and the amide protons (-NH) of endogenous mobile proteins and peptides (4). APT MRI has the potential to detect cancers (5–8), as well as to differentiate high-grade from low-grade gliomas (9, 10) or radiation necrosis from tumor recurrence (11–13). In addition, it has been shown recently that the APT technique can detect an acute cerebral ischemia (14, 15) before a diffusion MRI abnormality is apparent (16, 17), and to differentiate hyperacute intracerebral hemorrhage from cerebral ischemia (18).

CEST effects are often assessed using a Z-spectrum generated by plotting the water signal intensity as a function of radiofrequency (RF) saturation frequency offsets. The measurement of a complete Z-spectrum based on the standard imaging scheme is time-consuming because a large number of RF saturation frequency offsets is inevitably acquired. Similarly, the clinical APT imaging acquisition is generally also slow because multiple RF saturation frequency offsets are needed for B₀ inhomogeneity corrections (19) or for the APT quantification (20–24), limiting its clinical translation despite the many benefits. Therefore, fast CEST imaging techniques remain an interesting research topic (25–30). In the recent years, many alternative strategies to accelerate MR image acquisition have been proposed: parallel MRI, such as SMASH (31), SENSE (32), and GRAPPA (33) using the spatial information from multiple receiver RF coils; k-t acceleration approaches, such as k-t BLAST/k-t SENSE (34, 35), k-t GRAPPA (36), k-t FOCUSS (37), and SPEAR (38) using the sparse property in the combined spatial and temporal Fourier domain; and compressed sensing (CS) using the inherent sparsity and compressibility of MR data (39). Notably, recent studies have demonstrated that a combination of CS and parallel MRI techniques can enable highly accelerated MRI by taking advantage of different redundancies in MRI data (40–42).

The purpose of this study was to demonstrate the feasibility of accelerated CEST imaging using a combined CS and SENSE technique (CS-SENSE) at 3 T. We evaluated the usability of the CS-SENSE reconstruction in the APT experiments on healthy volunteers and glioma patients, and the magnetization transfer ratio asymmetry at 3.5 ppm (namely, MTR_asym(3.5 ppm)) was calculated and compared with varied CS-SENSE acceleration factors.

THEORY

CS-SENSE Reconstruction

The CS-SENSE reconstruction for the high acceleration has two separate steps (40): (1) CS reconstruction for each coil channel using a set of aliased images in reduced FOV with randomly 2D-undersampled k-space data (39); and (2) SENSE reconstruction using coil sensitivity maps for a final unfolded image (32). The randomly undersampled k-space data with reduced FOV from each coil channel can be reconstructed by solving the linear combination of a data consistency term, total variation, and wavelet sparsity regularization:

$$\mathit{arg}\underset{x}{\mathit{min}}\left[\frac{1}{2}{\Vert Ax-b\Vert }_2^2+\alpha {\Vert x\Vert }_{TV}+\beta {\Vert \mathrm{\Psi }x\Vert }_1)\right],{\Vert x\Vert }_{TV}=\sum \sqrt{{\left|{\nabla }_1{x}_{ij}\right|}^2+{\left|{\nabla }_2{x}_{ij}\right|}^2}$$ [1]

where A is the undersampled Fourier encoding matrix, x is the image to be reconstructed, b is the undersampled k-space data, and α, β are two positive parameters. The total variation of x is defined by sum of the magnitudes of the discrete gradient at pixels. ∇₁ and ∇₂ in the total variation are the forward finite difference operators on the first and second coordinates. ψ is a sparsifying wavelet transform. To solve the differential equation with a non-smooth term, the L1-norm can be estimated by ${\Vert \mathrm{\Psi }x\Vert }_1\approx \sqrt{{(\mathrm{\Psi }x)}^{\ast }(\mathrm{\Psi }x)+\mu }$ where μ is positive and close to zero. Then, a nonlinear conjugate gradient solver can be applied to minimize the penalty (L1-norm) for each coil channel. When aliased reduced FOV images in each coil are reconstructed using CS, a SENSE algorithm is applied for the final unfolded image using the sensitivity maps from each coil channel. The final unfolded image can be reconstructed by using a pseudo-inverse formula of the sensitivity matrix C:

$$f={\left(C^{T}C\right)}^{-1}{C}^T{f}^A$$ [2]

where f ^A is a set of aliased images with reduced FOV, and f is the original full FOV image. The total acceleration factor R of CS-SENSE is equal to the product (R₁ × R₂) of the acceleration factor of CS (= R₁) and the acceleration factor of SENSE (= R₂).

METHODS

Subject Recruitment

The study was approved by the Johns Hopkins Institutional Review Board. Before involvement in this study, written, informed consent was obtained from each healthy volunteer and patient. Two healthy volunteers and six patients (five males, one female; median age, 47 years old) with pathology-confirmed high-grade gliomas were recruited for this study.

MRI Experiments

All healthy volunteers and patients were scanned on a Philips 3 T MRI scanner (Achieva 3.0 T; Philips Medical Systems, Best, The Netherlands) using a body coil for RF transmission and a 32-channel coil for reception (Invivo, Gainsville, FL). Several standard sequences were performed for each patient, including T₂-weighted (repetition time or TR = 2772 ms; echo time or TE = 80 ms; field of view or FOV = 212 × 190 mm²; slice thickness = 2.2 mm; matrix size = 512 × 512; 60 slices), fluid-attenuated inversion recovery (FLAIR; TR = 11 s; TE = 120 ms; inversion recovery time or TI = 2.8 s; FOV = 212 × 190 mm²; slice thickness = 2.2 mm; matrix size = 512 × 512; 60 slices), T₁-weighted, and gadolinium-enhanced T₁-weighted (three-dimensional, magnetization-prepared, rapid-gradient-echo sequence, MPRAGE; TR = 3 s; TE = 3.7 ms; TI = 843 ms; FA = 8°; 150 slices; isotropic voxel = 1.1 mm³). In the healthy volunteer study, only conventional T₂-weighted images were acquired to localize for the CEST experiment.

The CEST imaging sequence consisted of a pulse train of four block RF saturation pulses (200 ms duration each; 0.5, 1, 1.5, and 2 μT amplitude for healthy volunteers; each followed by a crusher gradient of 10 ms duration and 10 mT/m strength; 95.2 % duty cycle), followed by a fat-suppressed, spectral presaturation with inversion recovery (SPIR) and a fast spin-echo acquisition (TR = 3 s; TE = 6.4 ms; FOV = 212 × 190 mm²; matrix size = 256 × 256; slice thickness = 4.4 mm; turbo spin-echo factor = 45; single-slice acquisition). For patient studies, the RF saturation power of 2 μT was applied, because the negative MTR_asym(3.5ppm) background signal in the normal brain tissue at the relatively low RF saturation power (< 2 μT) may complicate the explanation of the MTR_asym(3.5ppm) image (43). The parallel imaging SENSE factor was set to 2 in the phase-encoding direction. In addition, the fully sampled k-space data was acquired to estimate the coil sensitivity profile. Following two dummy scans, the frequency sweep corresponded to a full Z-spectrum with 52 frequency offsets, 14 to −8 ppm at an interval of 0.5 ppm. Additional three acquisitions at ± 3.5 ppm were obtained for sufficient signal-to-noise ratios for APT images. An unsaturated image was acquired for signal normalization. The water saturation shift-referencing (WASSR) method (two block RF saturation pulses; 200 ms duration each and 0.5 μT amplitude) was used to determine B₀ maps (44). The WASSR had 26 frequency offsets from 1.5 to −1.5 ppm at an interval of 0.125 ppm.

Image Reconstruction and CEST Quantification

All image reconstruction and CEST processing were performed using MATLAB (The MathWorks, Inc., Natick, MA) and the toolbox SparseMRI (39). Figure 1 shows the flow chart of image reconstruction with CS-SENSE and APT processing procedures. Raw CEST image k-space data were retrospectively 2D-undersampled, using three different undersampling schemes: R₁ × R₂ of 1.3 × 2; 2 × 2; and 4 × 2. The variable density sampling is denser near the center of k-space because most of the energy of the MRI signal is concentrated near the central k-space. The aliased data with undersampled k-space for each coil channel was CS-reconstructed by the Daubechies-4 wavelet as a sparsifying transform ψ, together with a total variation penalty in Eq. [1]. The weights for TV minimization and L1 norm minimization were 0.001 and 0.035, respectively. For comparison, two linear reconstruction schemes were used, low-resolution sampling and zero-filling with density compensation (ZF-w/dc) based on complete Nyquist sampling (39). The additionally acquired fully sampled k-space data were apodized using a cosine taper window and normalized by the sum-of-square reconstruction to generate the coil sensitivity map. Finally, the full FOV images were reconstructed pixel-by-pixel using the image domain Cartesian SENSE reconstruction with the aliased CS-reconstructed image from all coil channels.

Figure 1.

Flow chart of APT-MRI processing with CS-SENSE. The proposed method reconstructs CEST images in three sequential steps: 1) CS reconstruction; 2) SENSE reconstruction; and 3) CEST quantification.

For CEST pre-processing, CEST data were registered to the saturated volume (3.5 ppm) (45) using the rigid body registration algorithm with a mutual information cost function and bicubic resampling using the analysis of functional neuroimages (AFNI) freeware (46). Next, the WASSR technique was used to correct for B₀ field inhomogeneity effects by resetting the water signal to 0 ppm for each voxel. CEST Z-spectra were interpolated and aligned correspondingly on a pixel-by-pixel basis along the direction of the saturation frequency offset. For APT imaging, the APT-weighted (APTw) signal is obtained by subtracting the MTR (= 1 – S_sat/S₀) at −3.5 ppm upfield, with respect to water, from that at +3.5 ppm downfield (4):

$${\mathit{MTR}}_{\mathit{asym}}(3.5\mathit{ppm})=\text{MTR}(+3.5\mathit{ppm})-\text{MTR}(-3.5\mathit{ppm})$$ [3]

In order to quantitatively estimate the fidelity of CS-SENSE accelerated acquisition, the correlation coefficients (CC) and normalized mean square error (NMSE) between the CS-SENSE-reconstructed and the reference (SENSE only) images were calculated within whole brain regions:

$$\mathit{NMSE}=\frac{\sum {\left|f_{\mathit{estimated}}(x,y)-f_{\mathit{reference}}(x,y)\right|}^2}{\sum f_{\mathit{reference}}^2(x,y)}$$ [4]

where f_reference is the reference image and f_estimated is the reconstructed image using the CS-SENSE. In addition, a region of interest (ROI) analysis was performed to compare the MTR_asym(3.5ppm) signals between the reference and the CS-SENSE accelerated acquisitions.

RESULTS

Figure 2 shows reconstructed brain images from a healthy volunteer derived from the undersampled k-space data using three CS-SENSE acceleration factors of 1.3 × 2, 2 × 2, and 4 × 2. In order to evaluate the performance of the CS-SENSE approach, CC and NMSE between the reference image and CS-SENSE-reconstructed images were calculated and compared with two linear reconstruction schemes: ZF-w/dc, and low-resolution sampling with the same number of data points of the undersampled datasets. The CC decreased while the NMSE increased as the CS acceleration factor increased due to elevated noise and aliasing-related artifacts resulting from sparse k-space sampling. The CC of CS-SENSE was higher than that of the ZF-w/dc and low-resolution sampling while the NMSE of CS-SENSE was lower than that of the ZF-w/dc and low-resolution sampling. Generally, the saturated images had relatively lower CC and higher NMSE values than the unsaturated (S₀) images probably because of low signal-to-noise ratio and the remaining B₀ inhomogeneity.

Figure 2.

CS-SENSE reconstruction of CEST images with various combinations of acceleration factors. The CS-SENSE reconstruction for unsaturated images (S₀) and saturated images at 3.5 ppm was compared to two linear reconstruction schemes, low-resolution sampling and ZF-w/dc.

Figure 3 shows MTR_asym images of a healthy volunteer brain with four RF saturation power levels (0.5, 1, 1.5, and 2 μT) under three different CS-SENSE accelerations. The CC and NMSE in the MTR_asym images followed the same trend as the unsaturated and saturated images shown in Fig 2. Note that the MTR_asym images had higher NMSE and lower CC values compared to the unsaturated images and saturated images at 3.5 ppm, as shown in Fig. 2, because the noise and artifacts related to the undersampling were added from saturated images at −3.5 ppm.

Figure 3.

CS-SENSE reconstructed MTR_asym(3.5 ppm) images with various combinations of acceleration factors under varied RF saturation power levels (0.5, 1, 1.5, and 2 μT). Aliasing-related artifacts from sparse sampling are seen at an acceleration factor of R=4 x 2.

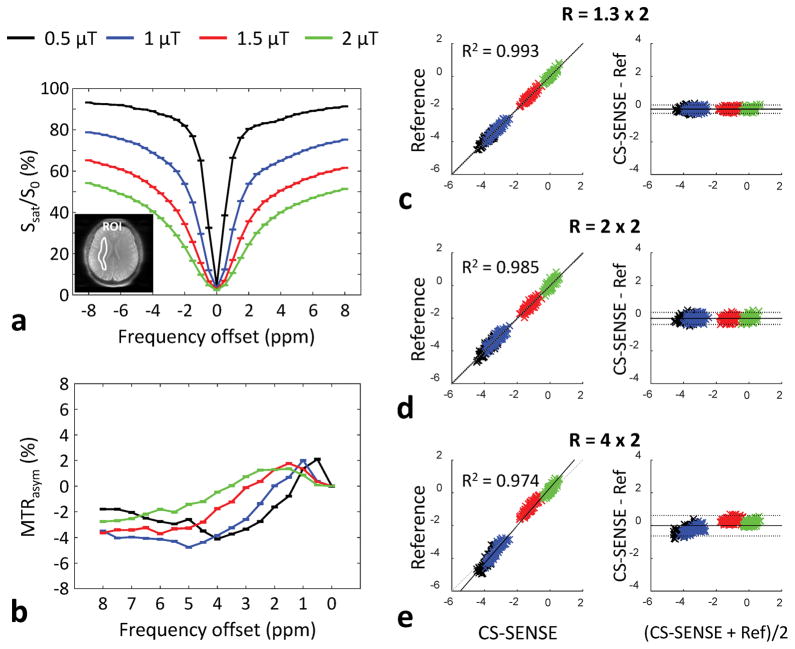
Figure 4a and b shows the average Z-spectrum and correspondent MTR asymmetry results from the normal-appearing white matter in the reference MTR_asym(3.5ppm) image, with four RF saturation power levels. The RF saturation power dependencies of the direct water saturation, semi-solid MT, and CEST effects can be seen clearly in the Z-spectrum. The MTR_asym(3.5ppm) was gradually increased with the RF saturation power level, as shown in Fig 4b. However, unlike at ultra-high B₀ fields (such as 7 T and 9.4 T), the APT peak at 3.5 ppm at 3 T was not observed in the MTR asymmetry, probably because of the small frequency width. In addition, many other water-exchangeable protons (for example, protein and peptide side-chain amide protons and various amine-related protons) may make some contributions to the CEST signals in a wide frequency range, including at 3.5 ppm. Figure 4c–e shows the correlation and Bland-Altman plots used to assess the bias and limits of agreement between the CS-SENSE-reconstructed and reference MTR_asym(3.5ppm) images. All CS-SENSE-reconstructed images showed high correlations with the reference, and the Bland-Altman analysis biases were significantly small, except for the acceleration factors of R = 4 × 2. The mean differences were 0.00055%, −0.004%, and −0.012% for R = 1.3 × 2, R = 2 × 2, and R = 4 × 2, respectively.

Figure 4.

(a) Average Z-spectrum, (b) MTR asymmetry from the normal-appearing white matter (ROI as shown in Fig. 4a) in the reference image with four RF saturation power levels, and (c)–(e) correlation plots and Bland-Altman plots of MTR_asym(3.5ppm) signals reconstructed by CS-SENSE and the reference standard (only SENSE) for two health volunteers. The small peak at 5 ppm at 0.5 μT may be an artifact due to the low signal-to-noise ratio and the small subject number, no CEST signal. In the Bland-Altman plot, the solid line is the mean of the difference and the dotted line brackets represent ± 1.96 times the standard deviations of the means.

Figure 5a shows an example of conventional MR images, MTR_asym(3.5ppm) images, and the corresponding error images for a representative patient with glioblastoma. The Gd-enhancing area (tumor core) on the post-Gd image was hyperintense on the MTR_asym(3.5 ppm) relative to the edema and normal tissue. There was no significant difference between reference and CS-SENSE-reconstructed MTR_asym(3.5ppm) images at acceleration factors of R = 1.3 × 2 and 2 × 2. The mean difference between reference and CS-SENSE (R = 2 × 2) was −0.0043% (95% confidence interval = +0.008 ~ −0.008) for MTR_asym(3.5 ppm) (n = 6). Figure 5b quantitatively compares the MTR_asym(3.5 ppm) in normal tissue and in glioma across three different acceleration factors. The MTR_asym(3.5 ppm) of the glioma was significantly higher than that of normal tissue (p < 0.001). The MTR_asym(3.5 ppm) signals measured by the different acceleration factors were quite similar for normal and for glioma tissue.

Figure 5.

(a) Conventional MR images and MTR_asym(3.5ppm) images with three acceleration factors (R = 1 × 2, 1.3 × 2, and 2 × 2) for a representative patient with a glioblastoma. MTR_asym(3.5 ppm) images show a hyperintense ring enhancement similar to that on the post-Gd image. (b) Average MTR_asym(3.5 ppm) signal intensities with three different acceleration factors from normal tissue and glioma tissue. Error bars depict standard deviations.

DISCUSSION

In this study, we introduce a robust approach for fast CEST imaging with highly accelerated acquisitions, which is applicable to many clinical applications. Combining a SENSE technique with CS enables us to further accelerate CEST image acquisition (or improve image quality) while maintaining the acceleration rate. To the best of our knowledge, this is the first study using a CS-SENSE approach for accelerated APT imaging in the human brain. Results in healthy volunteers and in tumor patients have shown that an acceleration factor for CS-SENSE of R = 4 (2 × 2) can be achieved without compromising CEST image quality.

The major limitation in the routine clinical use of CEST imaging is a relatively long acquisition time because of the use of a long RF saturation pulse (or multi-pulse train) and a series of multiple RF saturation frequencies. In addition, it is more likely vulnerable to motion during in vivo imaging. In a previous study, a keyhole imaging technique was applied to a CEST study for increased temporal resolution (25). The low frequency data collected in subsequent frames, along the saturation frequency dimension, were combined with the initial high spatial frequency data from the unsaturated image, thus reducing the scan time for each frame and increasing the temporal resolution of the technique. However, the keyhole approach might not be suitable in CEST MRI because there is a significant dynamic contrast change in the whole brain structure due to alternating RF saturation frequencies. In addition, the loss of a dynamic high frequency component (e.g., heterogeneous glioma feature) could also contribute to increased errors in the particular frequency offset (e.g., APT signal at 3.5 ppm). However, CS tolerates dynamic contrast changes quite well because it is dependent on an iterative approximation.

In the present study, the feasibility of the accelerated CEST imaging based on the CS-SENSE technique was demonstrated with a retrospective 2D variable-density random sampling. However, it is currently difficult to implement the 2D random sampling to any standard MRI scanners which requires a simultaneous switch of the phase- and frequency-encoding gradients randomly due to hardware constraints. A non-Cartesian sampling or a pseudo-random sampling by alternatively switching the two encoding directions during the image readout could be applied in practical MR imaging. Another study limitation includes the actual acquisition time reduction because most of the CEST imaging time is deployed in the RF saturation rather than data acquisition. However, RF irradiation is needed to be long enough for longitudinal magnetization of the free bulk water protons to reach a steady state. In this single slice imaging experiment, the CEST imaging acquisition is about 20% of the total imaging time (TR = 3000 ms, saturation time = 830 ms, image acquisition = 600 ms, recover time = 1570 ms). Therefore, CS-based CEST imaging must benefit from the multi-slice or 3D imaging requiring long image acquisition time and quantitative CEST imaging requiring many RF saturation frequency offsets. Lastly, the noise amplification in the parallel imaging is spatially variant and relies on the specific geometry of the multi-channel RF receiver coils, which may influence the performance of the CS reconstruction. However, no significant spatially-variant differences were observed in resulted CEST images probably due to a mild SENSE acceleration factor (=2) and higher receive coil elements (=32).

The accelerated CEST approach based on the CS-SENSE scheme can be extended in several directions. First, there are various ways to design incoherent sampling trajectories, such as radial and spiral samplings, although this work retrospectively explored a 2D random-sampled dataset to assess the performance of the acceleration scheme in CEST imaging (39). Three-dimensional whole-brain volume CEST imaging would be more favorable because the undersampling artifacts are more incoherent. Further, the golden-angle ordering scheme for radial sampling provides more temporal incoherence of the k-space acquisition (42). Second, joint sparsity in multi-coil images can be applied to improve reconstruction performance by exploiting the inter-correlation between the coils to reduce the overall number of measurements (35). Third, CS-SENSE can be combined with model-based compressed sensing using a dictionary learned from the data model as an adaptive sparsity transform (47–51). A partial k-space sampling scheme exploiting the conjugate symmetry of the Fourier transform of real images, as well as parallel imaging, can benefit from the CS-SENSE scheme because the CS, SENSE, and partial k-space sampling are applied separately (52). As a result, the combination could potentially allow much higher acceleration factors.

CONCLUSIONS

The application of the CS-SENSE technique to CEST acquisition offers a potentially significant scan time reduction and a robustness to motion artifacts. Accelerated CEST imaging based on CS-SENSE can be integrated easily into the clinical protocol and used for a wide range of clinical applications, particularly the rapid evaluation of acute stroke and pediatric patients.